1 Introduction

Linear convolution and morphological (nonlinear) operations are two types of operations that have wide applications in the field of surface metrology. While linear convolution is a good approximation to the blurring in optical systems, the morphological dilation operation resembles the tactile scanning process of some measurement instruments, such as the atomic force microscope (AFM) and the coordinate measurement machine (CMM). Another prime example is the Gaussian filter and morphological filters used for the evaluation of surface textures, e.g., the separation of surface roughness, waviness and form error. The Gaussian filtration is essentially a moving smoothing process created by convolving the measured surface data with the Gaussian weighting function specified by a given cutoff wavelength (ISO, 2011). Morphological filtration is usually obtained by rolling balls (disks) with a given radius upon a surface (profile) and taking the locus of the center of the balls (disks) (ISO, 2012).

Well-established computational and analytical methods are available for linear convolution, among which the Fourier transform is the most important one. It offers a dual description of the signal frequency by transferring the input signal from the physical-space (or time) into the frequency-space and converts the computationally expensive convolution in the spatial (or time) domain into the simple multiplication in the frequency domain (Bracewell, 1999). More importantly, the convolution operation can be explained as the frequency suppression in physics. It is of profound practical significance in many engineering disciplines, including surface metrology.

Morphological operations are an alternative method of combining two datasets. They aim to extract the geometrical structure of a surface data by matching it with small patterns (called structuring elements) at various locations of the data. By varying the shape and size of structuring elements, it can extract useful information of the shape of different parts of the surface data and their interrelation (Heijmans, 1995). Although morphological operations are straightforward in their spatial processing, more investigations are required to further find out how the structuring element is changing the original surface, just like the way that the weighting function is changing the frequency components of the surface data in a convolution operation. In this paper, we post our initial investigation on the slope transform, based on the work of Dorst and van den Boomgaard (1994) and Maragos (1995). It will be shown that the slope transform can provide an analytical ability for morphological operations, as is the Fourier transform to convolution operations in linear theory. This transform approach will offer a theoretical insight into morphological operations and initiate more potential uses in the field of surface measurement.

2 Linear convolution and morphological operations

2.1 Linear convolution

Linear convolution is a mathematical operation of combining two datasets to form a third one. The convolution of two continuous functions f(x) and g(x) is an integral that expresses the amount of overlap of g(x) as it is shifted over f(x):

$$f(x) \ast g(x) = \int_{ - \infty }^{ + \infty } {f(\tau)g(x - \tau){\rm{d}}\tau }.$$
(1)

Linear convolution is frequently observed in surface measurement as filtration techniques for surface roughness assessment. g(x) is usually called the weighting function. As g(x) is moving across the measured surface f(x), it tends to suppress high frequency/short wavelength components of f(x) and produce a smoothed reference surface f(x)*g(x) in which the original surface f(x) is compared to gain the roughness surface. Refer to Fig. 1 for an illustration. The weighting function works as a filter kernel and usually takes the form of symmetry with the biggest weight in the center and the smallest weight in the two ends. Thus, the convolution at a specific position is mainly determined by the central part of the surface portions and less effected by the far ends. This explains why the convolution is also called the moving weighted average.

Fig. 1
figure 1

Filtering by the linear convolution

Full size image

In the spatial domain, convolution, although only needing one basic step, requires a number of multiplications to obtain one convolved point. See Path A in Fig. 2. In practice, the convolution theorem is employed for computation, which states that the Fourier transform of a convolution is the product of Fourier transforms. The surface f(x) and the filter kernel g(x) are first transformed to the frequency domain by the Fourier transform to obtain their frequency spectrums F(ω) and G(ω). Their frequency spectrums are then multiplied, producing a combined result, F(ω)×G(ω). The transmission characteristic of the filter kernel determines which frequency bands can get through and which are suppressed. Finally, the multiplication F(ω)×G(ω) is transformed back by the inverse Fourier transform to achieve the convolved/filtered surface. This routine is of supreme efficiency and involves the following three steps, see Path B in Fig. 2. Denote the Fourier transform by and the inverse Fourier transform by F−1.

$${\cal F}\left[ {f(x)} \right] = F(\omega),\quad {\cal F}\left[ {g(x)} \right] = G(\omega);$$
(2)
$${\cal F}\left[ {(f \ast g)(x)} \right] = F(\omega) \times G(\omega);$$
(3)
$$(f \ast g)(x) = {{\cal F}^{ - 1}}[F(\omega) \times G(\omega)].$$
(4)
Fig. 2
figure 2

Convolution and the Fourier transform

Full size image

2.2 Morphological operations

Morphological operations are an alternative way of combining datasets. Dilation, erosion, opening, and closing are four basic morphological operations in mathematical morphology, which form the foundation of mathematical morphology (Serra, 1982).

The dilation of a function f(x) by the structuring function (element) g(x) is given by

$$(f \oplus g)(x) = \mathop {\rm{V}}\limits_u [f(u) + g(x - u)],$$
(5)

where V denotes the supremum (the least upper bound). It indicates that the dilated value at a given ordinate is the maximum value of f(x) in the window defined by g(x) when its origin is at (Soille, 1999).

Erosion is the morphological dual to dilation. The erosion of f(x) by g(x) is given by

$$\left({f \ominus g} \right)(x) = \mathop \Lambda \limits_u \left[ {f(u) - g(u - x)} \right],$$
(6)

where Λ means the infimum (the least lower bound). In other words, the eroded value at a given ordinate x is the minimum value of f(x) defined by g(x) when its origin is at x.

The combinations of dilation and erosion yield opening and closing. The opening of f(x) by g(x) is given by the erosion of f(x) by g(x) followed by the dilation:

$$(f \circ g)(x) = \left[ {(f \ominus g) \oplus g} \right](x).$$
(7)

The dual operation of opening is closing. The closing of f(x) by g(x) is given by applying the dilation of f(x) by g(x) followed by the erosion:

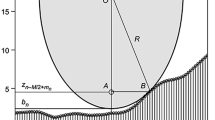
$$(f \bullet g)(x) = \left[ {(f \oplus g) \ominus g} \right](x).$$
(8)

In contrast to widely used linear convolution techniques, although may not universally recognized, morphological methods found many of their applications in the field of surface measurement (Lou et al., 2013b). To measure a surface by tactile instruments, traversing over workpiece surfaces by probe tips is the very initial application of morphological operations. See Fig. 3 as an illustration. This process can be explained in terms of morphological operations: the workpiece surface (as the input function) is dilated by the probe tip (as the structuring function). The traced surface is the dilation result. Obviously the traced surface is not identical to the real workpiece surface, but a dilated one. Thus, it always wants to correct the traced surface in order to recover the real workpiece surface. As Fig. 4 illustrates, the reconstruction is done by rolling an ideal tactile sphere (also with radius r) over the dilated surface from below. This process is exactly an erosion operation. The traced surface (the input function), is eroded by the probe tip (the structuring function) to generate the recovered workpiece surface. However, the reconstruction is not perfect. Although peaks are nicely reconstructed, parts of the valley features are not yet fully recovered.

Fig. 3
figure 3

Scanning of the workpiece surface by a tactile probe tip

Full size image
Fig. 4
figure 4

Reconstruction of the workpiece surface

Full size image

Morphological opening and closing have more uses in surface measurement. They appear as morphological filters which can suppress valleys and peaks on the surface respectively (ISO, 2006). Their combined effects, alternating symmetrical filters, remove both surface peaks and valleys. Thus the resulted reference surface travels through the inside of the original surface. In this aspect, it resembles the “mean” surface generated by convolution techniques. Morphological operations were successfully employed to extract topographical features from engineering surfaces (Lou et al., 2013c). They can also give an approximation to the form of conformable surfaces in a functional sense of sealing (Malburg, 2003). Moreover, morphological operations were used to simulate the interaction of two mating surfaces by rolling a ball upon the underlying surface. The ball is sized to simulate the largest reasonable radius at a contact, e.g., peak curvature (Lou et al., 2013a).

It can be shown that the structuring element is modifying the shape of the original surface during the traversing process. As is already stated, valleys in Fig. 4 are partially cut off on its dilation and closing profiles. However, how the shape (including slope and curvature) is modified is still unclear. Just as the Fourier transform nicely explains the linear convolution as frequency filtering, a counterpart transform, called the slope transform, may help with studying shape changes induced by morphological operations.

3 Tangential morphology

The tangential dilation is extended from the classical morphological dilation with less restriction. It was first introduced by Dorst and van den Boomgaard (1994) to construct the basis of the slope transform.

3.1 Tangential dilation

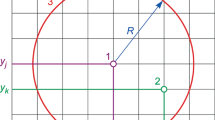
Eq. (5) presents the definition of the classical dilation of two functions, which is the supreme of the vector addition. Take Fig. 5 as an example, where the input function f(x) represents a profile and the structuring function g(x) is a disk. To compute the dilation at a given \(\overline{x}\), the center of the disk is placed at the abscissa \(\overline{x}\) and the disk g(x) is touching f(x) at the abscissa \(\overline{u}\). Thus, the height of the dilated curve at \(\overline{x}\) is: \((f\oplus g)(\overline{x})=f(\overline{u})+g(\overline{x}-\overline{u})\) At the touching point, f(x) and g(x) have a common tangent line. Therefore, the slope of f(x) and g(x) at the touching point is equal to: \(\nabla f(\overline{u})=\nabla g(\overline{x}-\overline{u})\).

Fig. 5
figure 5

Computation of the classical dilation and the tangential dilation

Full size image

The tangential dilation is a weak version of the classical dilation, which does not keep the supremum. To compute the tangential dilation of f(x) and g(x), first find the slope of f(x) at \(\overline{u}\), i.e., \(\nabla f(\overline{u})\) Then find an abscissa \(\overline{v}\) such that \(\nabla g(\overline{v})=\nabla f(\overline{u})\) Thus, the tangential dilation at the abscissa \(\overline{x}=\overline{u}+\overline{v}\) is: \((f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(\overline x) = f(\overline u) + g(\overline v)\).

The tangential dilation is formally defined as

$$(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = \mathop {{\rm{stat}}}\limits_u \left[ {f(u) + g(x - u)} \right],$$
(9)

where \(\mathop {{\rm{stat}}}\limits_u f(u)\) means the stationary values of f(u):

$$\mathop {{\rm{stat}}}\limits_u f(u) = \left\{ {f(\bar u)\vert\nabla f(\bar u) = 0} \right\}.$$
(10)

The relationship between the classical dilation and the tangential dilation is that the supremum of the tangential dilation is equal to the classical dilation, i.e.,

$$(f \oplus g)(x) = {\rm{V(}}f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g{\rm{)}}(x).$$
(11)

While Eq. (11) reveals the link of the classical dilation and the tangential dilation, it also evidently suggests the differences between two operations. The later operation will yield overlapping regions in its dilated result where the curvature of g(x) is larger than that of f(x). Nonetheless, the former one only retains the supremum of the result, as if the overlapping (crossed-over) regions are trimmed off. Fig. 6 presents such an example. The parabola function f(x)=0.5x2+1 is dilated by disks with radii 1 mm and 2 mm, respectively. The dilation with disk radius 2 mm causes crossing-over while the 1 mm disk does not.

Fig. 6
figure 6

Tangential dilation of a parabola with disk radii 1 mm and 2 mm

Full size image

The erosion operation is similar to the dilation, but takes the infimum (greatest lower bound). However, it can be easily converted into the dilation by first flipping the input function f(x) followed by flipping the result of the dilation \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over f} (x) \oplus g(x)\) where \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over f} (x)\) is the flip of f(x).

3.2 Slope and curvature changes of the tangential dilation

As shown in Fig. 5, let the abscissa of the center of the structuring function g(x) be at and the abscissa of the touching point of f(x) and g(x) be \(x_{f}=\overline{u}\) and \(x_{g}=x-\overline{u}\) respectively. It is obvious that the height of the tangential dilation function is the addition of the height of f(x) and g(x) at the touching point:

$$(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = f({x_f}) + g({x_g}).$$
(12)

At the touching point, the slopes of f(x), g(x), and \((f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x)\) coincide with each other:

$${(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)^{\prime} }(x) = f^{\prime}({x_f}) = g^{\prime}({x_g}).$$
(13)

This relationship clearly indicates that slopes are not modified by the tangential dilation. However, the point carrying that slope is transported by a distance. The curvature at the contact point is broadened, being the addition of those of f(x) and g(x) (Keller, 1991):

$${R_{f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g}}(x) = {R_f}({x_f}) + {R_g}({x_g}),$$
(14)

where R f (x) denotes the curvature of f(x), and so on.

4 Slope transform

4.1 Slope transform and inverse slope transform

Since the tangential dilation only parallelly offset the point carrying that slope, an input function with a constant slope will only be translated by a certain distance without changing its shape. These types of functions are planar functions e ω :<ω, x> with the constant slope ω, and it follows that:

$$({e_\omega }\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = {e_\omega } + s[g](\omega),$$
(15)

where s[g] is the translation shift, depending on g. Planar functions e ω are called morphological eigenfunctions (Maragos, 1995). If an arbitrary function can be decomposed into a series of planar eigenfunctions, then a tangential dilation can be constructed by the composition of these shifted eigenfunctions.

To be more precise, given a function f(x), find the tangent plane at the point \((\overline{x},f(\overline{x}))\). The slope of this tangent plane is \(\omega=\nabla f(\overline{x})\) the tangent plane intersects the height axis at \(f(\overline{x})-\langle\overline{\omega},\overline{x}\rangle\). Thus, the intercept can be expressed as a function of the slope. Formally the slope transform of f at ω is defined as

$${\cal S}[f](\omega) = \mathop {stat}\limits_x \left[ {f(x) - \left\langle {\omega, x} \right\rangle } \right].$$
(16)

It transfers the function f(x) in the spatial domain to the function S[f](ω) in the slope domain. Conversely, given a slope function S[f](ω), the original function f(x) can be reconstructed by the inverse slope transform:

$$f(x) = \mathop {stat}\limits_\omega \left[ {{\cal S}[f](\omega) + \left\langle {\omega, x} \right\rangle } \right].$$
(17)

4.2 Addition theorem

It has been proved that the slope transform occupies a critical property, which makes it resemble the Fourier transform of the linear theory (Dorst and van den Boomgaard, 1994). The slope transform of the tangential dilation is the addition of the slope transforms:

$${\cal S}[f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g](\omega) = {\cal S}[f](\omega) + {\cal S}[g](\omega).$$
(18)

This property enlightened an important perception into morphological operations. An arbitrary function can be invariably decomposed into a number of planar eigenfunctions, each of which corresponds to a point in the slope domain as the pair of the slope and the intercept of the eigenfunction. Thus, to compute the tangential dilation of f(x) by g(x), f(x) and g(x) are first transformed into the slope domain as and Then the addition of and are transformed back to the spatial domain by the inverse slope transform, giving the result of \((f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x)\). See Fig. 7 for an illustration. Similar to the Fourier transform of the convolution, the slope transform of the tangential dilation involves the following three basic steps. Denote the inverse slope transform by S−.

$${\cal S}\left[ {f(x)} \right] = F(\omega),\quad {\cal S}\left[ {g(x)} \right] = G(\omega);$$
(19)
$${\cal S}\left[ {(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x)} \right] = F(\omega) + G(\omega);$$
(20)
$$(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = {{\cal S}^{ - 1}}\left[ {F(\omega) + G(\omega)} \right].$$
(21)
Fig. 7
figure 7

Morphological tangential dilation and the slope transform

Full size image

Path A in Fig. 7 is a direct implementation of the tangential dilation in the spatial domain. Similar to the convolution operation, the computation of dilation of each point requires a number of additions and then takes the maximum. Following Path B, the dilation converts into the simple addition in the slope domain.

The slope transform indicates that the intercept is a function of the slope. Thus, the addition in the slope domain reveals that the tangential dilation does not modify the slope, but only changes the intercept at the point carrying that slope. Going back to the spatial domain by applying the inverse slope transform, it means that the point is offset and the tangent plane of the dilated function at this point has the same slope as before but with a different intercept. The change of intercept is determined by the structuring function and also the slope at that point.

5 Examples

In surface metrology, structuring functions are usually circular, e.g., disks for profile data and balls for areal data. In the following examples, the profile is taken as the input function and the disk as the desired structuring function.

5.1 Example 1: a sine wave dilated by a disk

Given a sine wave profile f(x)=sin(x) and a disk \(g(x) = \sqrt {{R^2} - {x^2}}\) with radius R, solve the dilated profile.

Apply the slope transform to the sine wave: \(F(\omega) = \mathop {{\rm{stat}}}\limits_x [\sin (x) - \omega \cdot x]\). Then it follows: \(\cos\overline{x}=\omega\Rightarrow\overline{x}=\arccos(\omega)\). Thus, \(F(\omega) = \sqrt {1 - {\omega ^2}} - \omega \arccos (\omega)\).

Apply the slope transform to the disk function: \(G(\omega) = \mathop {{\rm{stat}}}\limits_x [\sqrt {{R^2} - {x^2}} - \omega x]\). Then it has: \({{ - \bar x} \over {\sqrt {{R^2} - {{\bar x}^2}} }} = \omega \Rightarrow \quad \bar x = - {{\omega R} \over {\sqrt {1 + {\omega ^2}} }}\) Thus, it leads to: \(G(\omega) = R\sqrt {1 + {\omega ^2}}\).

In the slope domain, two transformed functions are added: \(F(\omega) + G(\omega) = \sqrt {1 - {\omega ^2}} - \omega \arccos (\omega) + R\sqrt {1 + {\omega ^2}}\). The inverse slope transform carries the addition back to the spatial domain:

$$\matrix{{(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = \mathop {{\rm{stat}}}\limits_\omega \left[ {\sqrt {1 - {\omega ^2}} - \omega \arccos (\omega)} \right.} \hfill \cr {\quad \quad \quad \quad \quad \left. { + R\sqrt {1 + {\omega ^2}} + \omega x} \right].} \hfill \cr}$$

However, it is difficult to find the stationary points by solving \(\overline{\omega}\) in the expression of x. Therefore, it is unable to obtain an analytic solution with the exact expression of the tangential dilation of the sine wave by a disk. Nevertheless, it will be illustrated in the following example that in certain cases such an analytic solution can be obtained.

5.2 Example 2: a disk dilated by a disk

Given a disk \(f(x) = \sqrt {R_1^2 - {x^2}}\) with radius R1 and another disk \(g(x) = \sqrt {R_2^2 - {x^2}}\) with radius R2, to solve the dilated profile, which is expected to be a disk with the combined radius (R1+R2), namely the disk is expanded by R2 in radius.

As aforementioned, it has \(F(\omega) = {R_1}\sqrt {1 + {\omega ^2}}\) and \(G(\omega) = {R_2}\sqrt {1 + {\omega ^2}}\).

Thus, in the slope domain, the tangential dilation becomes the addition of \(F(\omega) + G(\omega) = ({R_1} + {R_2})\sqrt {1 + {\omega ^2}}\). Applying the inverse slope transform: \((f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = \mathop {{\rm{stat}}}\limits_\omega [({R_1} + {R_2})\sqrt {1 + {\omega ^2}} + \omega \cdot x]\) then we can obtain:

$$({R_1} + {R_2}){{\bar \omega } \over {\sqrt {1 + {{\bar \omega }^2}} }} = - x \Rightarrow \bar \omega = - \sqrt {{{{x^2}} \over {{R^2} + {x^2}}}} \,{\rm{with}}\,R = {R_{\rm{1}}} + {R_2},$$

and thus,

$$(f\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \oplus } g)(x) = R \cdot \sqrt {1 + {{{x^2}} \over {{R^2} - {x^2}}}} + \sqrt {{1 \over {{R^2} - {x^2}}}} {x^2} = \sqrt {{R^2} - {x^2}}.$$

This result verifies the expectation that the dilated disk is an expanded disk having a radius equivalent to the sum of those of the input disk and the structuring disk.

6 Discretization

As indicated by Example 1 in Section 5, analytic solutions of the tangential dilation are not always possible. However, discretization solutions can be found. The discrete slope transform and inverse slope transform are given by the following formulas, respectively (Dorst and van den Boomgaard, 1994):

$$\left({\matrix{x \cr y \cr} } \right)\buildrel {\cal S} \over \longleftrightarrow \left({\matrix{{{{y^{\prime}} \over {x^{\prime}}}} \cr {{{x^{\prime}y - xy^{\prime}} \over {x^{\prime}}}} \cr } } \right) = \left({\matrix{X \cr Y \cr} } \right),$$
(22)

and

$$\left({\matrix{X \cr Y \cr } } \right)\buildrel {{{\cal S}^{ - 1}}} \over \longleftrightarrow \left({\matrix{{ - {{Y^{\prime}} \over {X^{\prime}}}} \cr {{{X^{\prime}Y - XY^{\prime}} \over {X^{\prime}}}} \cr } } \right) = \left({\matrix{x \cr y \cr} } \right).$$
(23)

Eqs. (22) and (23) require derivatives with respect to the variables. Thus, a derivative can be determined with a specific form. For instance, if it takes the forward difference:x′[i]=x[i]−x[i−1], then Eqs. (22) and (23) lead to:

$$\left({\matrix{{{x_i}} \cr {{y_i}} \cr} } \right)\buildrel {\cal S} \over \longleftrightarrow \left({\matrix{{{{{y_i} - {y_{i - 1}}} \over {{x_i} - {x_{i - 1}}}}} \cr {{{{x_i}{y_{i - 1}} - {x_{i - 1}}{y_i}} \over {{x_i} - {x_{i - 1}}}}} \cr} } \right) \equiv \left({\matrix{{{X_i}} \cr {{Y_i}} \cr} } \right),$$
(24)

and

$$\left({\matrix{{{X_i}} \cr {{Y_i}} \cr} } \right)\buildrel {{{\cal S}^{ - 1}}} \over \longleftrightarrow \left({\matrix{{ - {{{Y_{i + 1}} - {Y_i}} \over {{X_{i + 1}} - {X_i}}}} \cr {{{{X_{i + 1}}{Y_i} - {X_i}{Y_{i + 1}}} \over {{X_{i + 1}} - {X_i}}}} \cr} } \right) \equiv \left({\matrix{{{x_i}} \cr {{y_i}} \cr} } \right).$$
(25)

Fig. 8 presents an example where a sine wave f(x)=0.5sin(2x) is tangentially-dilated by a disk with radius 0.5 mm. The tangential dilation is implemented by the discrete slope transforms. The transformed sine wave and disk in the slope domain are depicted in Fig. 9. The disk is observed as a hyperbola in the slope domain. The bold dot lines are the result of the addition of two transformed curves. The added result is then converted back to the spatial domain, yielding the dilated profile. In this example, the tangential dilation is equal to the classical dilation due to the fact that there are no crossed-over regions of the tangential dilation profile. However, as the disk radius grows, this problem can arise. Fig. 10 illustrates the tangential dilation of the same sine wave but with disk radius 1 mm. It is evident that the region on the sine wave having a radius curvature smaller than the given disk radius will result in this problem occurring. This is definitely undesired because the dilation operation only keeps the supremum and the crossed regions should be trimmed off.

Fig. 8
figure 8

Tangential dilation of the sine wave by a 0.5 mm disk

Full size image
Fig. 9
figure 9

Addition of the slope transform of the sine wave and the disk

Full size image
Fig. 10
figure 10

Tangential dilation of the sine wave by a 1 mm disk

Full size image

7 Conclusions and future work

In contrast to linear convolution which is well studied and exploited, morphological operations are not fully understood and developed. By introducing the slope transform into the field of surface metrology, a deeper perception into morphological operations is gained. As the Fourier transform switches the convolution into the multiplication in the frequency domain, the slope transform converts the tangential dilation into the addition in the slope domain. As such, the slope and curvature changes caused by the structuring element are revealed. The derivation of the analytical solutions to the tangential dilation of a sine wave and a disk by a disk are illustrated respectively. It is found that the analytic solution is not always available. The discretized tangential dilations of a sine wave by the disks with two different radii are presented. The result clearly shows that the supremum of the tangential dilation is identical to the classical dilation. However the tangential dilation tends to produce the overlapping regions, which is undesireable in practice.

A key area of future research will be the investigation of the feasibility of the slope transform in real practice. If the crossing point can be located and the crossed regions trimmed off, the result of tangential dilation will be the same as that of the classical dilation. Then the boosts of the slope transform can be envisioned. Another research target will be the areal extension of the tangential dilation and the slope transform.