1 Introduction

One of the important issues during the construction of deep tunnels in saturated ground is the appropriate design of the tunnel liners. The convergence-confinement method (CCM) has become very popular for tunnel construction throughout the world due to its technical feasibility, safety, and economic competitiveness (Carranza-Torres and and Fairhurst, 2000; Oreste, 2003a; 2003b; González-Nicieza et al., 2008). According to the concept of the CCM, the tunnel liners should be designed to sustain the loads transmitted from the surrounding ground during excavation as well as the seepage forces due to the water flow towards the tunnel, if any (Lee and Nam, 2001; Bobet, 2003; Nam and Bobet, 2006). The effects of seepage force and in-situ stress on displacements and stress distributions for deep tunnels in saturated ground have been investigated by numerous researchers (Schweiger et al., 1991; Lee and Nam, 2001; Bobet, 2001; 2003; Arjnoi et al., 2009; Li, 2011).

Although there are a lot of numerical procedures capable of estimating the ground displacements and liner stresses, analytical solutions are still desirable in direct applications or in the validation and verification of numerical models for their advantages of conciseness and convenience (Huangfu et al., 2010).

Analytical solutions of the distribution of the pore pressure in the rock mass for steady seepage of deep tunnles are also obtained in previous studies. For instance, based on the theory of complex potentials, the theory of Cauchy integrals, and of singular integral equations, the steady-state fluid flow solution for fractured porous media was obtained by Liolios and Exadaktylos (2006). They also provided a numerical method for the accurate estimation of pore pressure and pore pressure gradient fields due to specified hydraulic pressure or pore pressure gradient acting on the lips of one or multiple non-intersecting curvilinear cracks in a homogeneous and isotropic porous medium, but there is a fly in the ointment for which they could not provide the complete analytical solutions of displacements and stresses for tunnels in saturated ground.

Complete analytical solutions of displacements and stresses for tunnels in saturated ground are obtained by Bobet (2001; 2003) and Nam (2006). These solutions cover different construction processes and ground conditions, including dry or saturated ground, shallow or deep, with or without air pressure, and with or without a gap between the ground and the liner. However, these solutions are restricted to cases where ground displacements are small, since the ground and the liner are assumed to behave elastically.

Based on the assumptions that circular tunnels are excavated in elasto-plastic homogeneous ground under hydrostatic stress conditions, a series of analytical or semi-analytical analyses have been performed (Fenner, 1938; Brown et al., 1983; Carranza-Torres and Fairhurst, 2000; Sharan, 2005; Lee et al., 2000; Fang et al., 2013; Han et al., 2013). All these studies have contributed to the understanding of the surrounding ground-liner interaction mechanism, but the results do not apply to the tunnels in saturated ground.

Considering the effect of seepage forces, ground stresses are obtained by Li et al. (2004) and Liu et al. (2009) for deep circular tunnels in elastic-perfectly plastic material with a Mohr-Coulomb type yield criterion while neglecting the existence of liners. Their studies were complemented by Lu and Xu (2009), who proposed an analytical model to solve the stresses for a subsea tunnel with liner. Note that all these studies are not capable of providing the solutions of ground displacements in the plastic zone.

In this study, elasto-plastic plane strain solutions of the stress and displacement distributions around deep circular lined tunnels in isotropic saturated ground due to uniform ground loads and seepage forces are presented. The derivation process for the expression of displacements in the plastic zone is a highlight in this paper. A gap between the ground and the liner, which represents a certain ground displacement along the tunnel circumference occurred before the installation of the liner is also considered. The proposed model is particularly suitable for the investigation of deep circular tunnels excavated in soft saturated ground.

2 Problem description

The fundamental objective of this paper is to study the stresses and displacements of tunnels with liners in saturated ground considering the effect of both the seepage force and in-situ stress. To derive the analytical solution for the proposed problem, the following assumptions are made: (1) The circular tunnel is located in a fully saturated, homogeneous and isotropic aquifer subjected to uniform in-situ stress. (2) Plane strain conditions are applicable at any tunnel cross-section. (3) The liner behaves in a linear elastic manner. (4) The ground behaves in an elastic-perfectly plastic manner, obeys the linear Mohr-Coulomb yield criterion, and is considered weightless. (5) The water is incompressible, and Darcy’s law is applicable. (6) Before the installation of the liner, certain ground displacements along the tunnel circumference have already occurred. Therefore, there is a constant gap between the ground and the liner along the perimeter of the tunnel (Bobet, 2001), which can represent the displacements due to any physical gap, the unsupported tunnel face, the liner construction lag, or the time effect of shotcrete hardening process. For example, the installation delay of the support will inevitably cause certain ground displacements. Moreover, even though the shotcrete lining is installed immediately after the excavation, certain ground displacements will gradually take place as the shotcrete hardens (Oreste, 2003b).

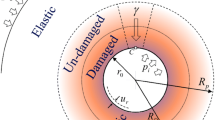
A schematic model of the proposed problem is shown in Fig. 1. In this model, r i is the inner radius of the liner, r l is the outer radius of the liner, and r 0 is the outer boundary of the problem. In this study, r 0=20r i. The outer boundary is far enough from the inner tunnel boundary, therefore the presence of the outer boundaries have limited impact on the solutions. This method has been adopted by numerous researchers (Bobet, 2003; Li et al., 2004; Nam and Bobet, 2006; Liu et al., 2009). There are no displacement constraints at the boundaries (Nam and Bobet, 2006). Ambient stresses σ i and σ 0 are the radial pressures (the tension is positive) at the inner boundary and the outer boundary, respectively. h i and h 0 are the water head on the inner boundary and the outer boundary, respectively. k l is the hydraulic conductivity of the liner. k p and k e are the hydraulic conductivities of the plastic zone and the elastic zone, respectively. E l and μ l are the elasticity modulus and the Poisson’s ratio of the liner, respectively. E p and μ p are the elasticity modulus and the Poisson’s ratio of the ground in the plastic zone, respectively. E e and μ e are the elasticity modulus and the Poisson’s ratio of the ground in the elastic zone, respectively. c p, φ p, and ψ p are the cohesion, the internal friction angle, and the dilation angle of the ground, respectively.

Fig. 1
figure 1

Schematic illustration of the analytical model

Full size image

The yield zone radius, r p, the water head on the outer of the liner, h l, the water head on the plastic zone, h p, the radial stress at the ground-liner interface, σ l, and the radial stress at the plastic-elastic interface, σ p can be derived by using the seepage and mechanical theory.

The radial stress, σ r, the tangential stress, σ θ , the water head, h, the displacement, u, are the functions of the radial distance from the tunnel center, r, and will be given analytically by a theoretical model in this study.

3 Proposed analytical model

3.1 Analytical solutions of the seepage field

It follows from the symmetry with respect to the axis of the tunnel that the flow is radial, and the discharge vectors at all points are directed toward the center of the tunnel. According to Bear (1972), following the continuity equation, there is

$${{\rm{d}} \over {{\rm{d}}r}}\left({r{{{\rm{d}}h} \over {{\rm{d}}r}}} \right) = 0,$$
(1)

then

$$h = {C_1}\ln r + {C_2},$$
(2)

where C 1 and C 2 are two integration constants.

The corresponding boundary conditions for the problem are

$$\eqalign{ & h\left| {_{r = {r_i}}} \right. = {h_i},\quad h\left| {_{r = {r_l}}} \right. = {h_l}, \cr & h\left| {_{r = {r_p}}} \right. = {h_p},\quad h\left| {_{r = {r_0}}} \right. = {h_0}. \cr}$$
(3)

Substituting Eq. (3) into Eq. (2), we can obtain:

$$h = \left\{ {\matrix{ {{{{h_i}\ln ({r_l}/r) + {h_l}\ln (r/{r_{\rm{i}}})} \over {\ln ({r_l}/{r_i})}},\quad {r_i} \le r \le {r_l},} \cr {{{{h_l}\ln ({r_p}/r) + {h_p}\ln (r/{r_l})} \over {\ln ({r_p}/{r_l})}},\quad {r_l} < r \le {r_p},} \cr {{{{h_p}\ln ({r_0}/r) + {h_0}\ln (r/{r_p})} \over {\ln ({r_0}/{r_l})}},\quad {r_p} < r \le {r_0}.} \cr}} \right.$$
(4)

Let Q l, Q p, and Q e be the water discharge through the ground in the elastic zone, in the plastic zone, and the liner, respectively. According to Wang et al. (2008), when r i≤r≤r l, there is

$${Q_l} = 2{\rm{\pi}}{k_l}({h_l} - {h_i})/\ln ({r_l}/{r_i}),$$
(5a)

analogously,

$${Q_p} = 2{\rm{\pi}}{k_p}({h_p} - {h_l})/\ln ({r_p}/{r_l}),\;\;{r_l} \le r \le {r_p},$$
(5b)
$${Q_e} = 2{\rm{\pi}}{k_e}({h_0} - {h_p})/\ln ({r_0}/{r_p}),\;\;{r_p} < r \le {r_0}.$$
(5c)

For Q l= Q e=Q, we can obtain:

$${h_l} = {{{h_0}\ln {{{r_l}} \over {{r_i}}} + {h_i}\left({{{{k_l}} \over {{k_p}}}\ln {{{r_p}} \over {{r_l}}} + {{{k_l}} \over {{k_e}}}\ln {{{r_0}} \over {{r_p}}}} \right)} \over {\ln {{{r_l}} \over {{r_i}}} + {{{k_l}} \over {{k_p}}}\ln {{{r_p}} \over {{r_l}}} + {{{k_l}} \over {{k_e}}}\ln {{{r_0}} \over {{r_p}}}}},$$
(6)
$${h_p} = {{{h_0}\left({{{{k_e}} \over {{k_p}}}\ln {{{r_p}} \over {{r_l}}} + {{{k_e}} \over {{k_l}}}\ln {{{r_l}} \over {{r_i}}}} \right) + {h_i}\ln {{{r_0}} \over {{r_p}}}} \over {\ln {{{r_0}} \over {{r_p}}} + {{{k_e}} \over {{k_p}}}\ln {{{r_p}} \over {{r_l}}} + {{{k_e}} \over {{k_l}}}\ln {{{r_l}} \over {{r_i}}}}},$$
(7)
$$Q = {{2{\rm{\pi}}{k_e}({h_0} - {h_i})} \over {\ln {{{r_0}} \over {{r_p}}} + {{{k_e}} \over {{k_p}}}\ln {{{r_p}} \over {{r_l}}} + {{{k_e}} \over {{k_l}}}\ln {{{r_l}} \over {{r_i}}}}}.$$
(8)

3.2 Analytical solutions of stresses and displacements

3.2.1 Basic equations and boundary conditions

The seepage force is a body force (Lambe and Whitman, 1969), of which the direction is radial due to the symmetry of the flow. The seepage force per unit volume is

$${f_r} = - {\gamma _w}{{{\rm{d}}(\xi h)} \over {{\rm{d}}r}},$$
(9)

where γ w is the specific weight of the water, ξ is the equivalent surface porosity of the fractured mass. Terzaghi (1936) and Leliavski (1947) determined from field and laboratory studies that ξ, the surface porosity, is generally close to unity and always greater than 0.85.

The solution of a deep tunnel in saturated ground must satisfy the equilibrium equation as follows:

$${{{\rm{d}}{\sigma _r}} \over {{\rm{d}}r}} + {{{\sigma _r} - {\sigma _\theta}} \over r} - {\gamma _w}{{{\rm{d}}(\xi h)} \over {{\rm{d}}r}} = 0,$$
(10)

where the subscripts r and θ denote the radial and tangential directions, respectively. Eq. (10) can be solved with the following boundary conditions:

$$\sigma _r^l\left| {_{r = {r_i}}} \right. = {\sigma _i},$$
(11a)
$$\sigma _r^e\left| {_{r = {r_0}}} \right. = {\sigma _0},$$
(11b)
$$\sigma _r^l\left| {_{r = {r_l}}} \right. = \sigma _r^p\left| {_{r = {r_l}}} \right. = {\sigma _l},\;$$
(11c)
$$\;\sigma _r^p\left| {_{r = {r_p}}} \right. = \sigma _r^e\left| {_{r = {r_p}} = {\sigma _p}} \right.,$$
(11d)
$${u^l}\left| {_{r = {r_l}}} \right. = u_{{r_l}}^l = {u^p}\left| {_{r = {r_l}} - w} \right. = u_{{r_l}}^p - w,$$
(11e)
$${u^p}\left| {_{r = {r_p}}} \right. = {u^e}\left| {_{r = {r_p}}} \right. = {u_{{r_p}}},$$
(11f)

where \(\sigma _r^l,\,\sigma _\theta ^l\) and u 1 are the radial stress, the tangential stress, and the radial displacement of the liner, respectively; \(\sigma _r^p,\,\,\sigma _\theta ^p\), and u p are the radial stress, the tangential stress, and the radial displacement of the ground in the plastic zone, respectively; \(\sigma _r^e,\,\,\sigma _\theta ^e\), and u e are the radial stress, the tangential stress, and the radial displacement of the ground in the elastic zone, respectively. w is the gap between the ground and the liner.

3.2.2 Stresses and displacements of liner

The analytical solutions of stresses and displacements acting on the liner due to the ground loads and seepage forces are obtained by a theoretical model based on the solutions of Li (2004):

$$\sigma _r^l = {K_1} + {K_2}{(1/r)^2} - {K_3}\ln r,$$
(12)
$$\sigma _\theta ^l = {K_4} - {K_2}{(1/r)^2} - {K_3}\ln r,$$
(13)
$$u_r^l = {K_5}r - {K_6}r_i^2/r - {K_7}r\ln r,$$
(14)
$${K_1} = {{{\sigma _l}r_l^2 - {\sigma _i}r_i^2} \over {r_i^2 - r_l^2}} + {{{\gamma _w}\xi ({h_l} - {h_i})(r_l^2\ln {r_l} - r_i^2\ln {r_i})} \over {2(1 - {\mu _l})(r_i^2 - r_l^2)(\ln {r_l} - \ln {r_i})}},$$
(15)
$${K_2} = {{r_i^2r_l^2({\sigma _l} - {\sigma _i})} \over {(r_l^2 - r_i^2)}} + {{r_i^2r_l^2{\gamma _w}\xi ({h_l} - {h_i})} \over {2(1 - {\mu _l})(r_l^2 - r_i^2)}},$$
(16)
$${K_3} = {{{\gamma _w}\xi ({h_i} - {h_l})} \over {2(1 - {\mu _l})(\ln {r_l} - \ln {r_i})}},$$
(17)
$$\eqalign{ & {K_4} = {{{\sigma _l}r_l^2 - {\sigma _i}r_i^2} \over {r_i^2 - r_l^2}} \cr & + {{{\gamma _w}\xi ({h_l} - {h_i})[(r_l^2\ln {r_l} - r_i^2\ln {r_i}) - (1 - 2{\mu _l})(r_i^2 - r_l^2)]} \over {2(1 - {\mu _l})(r_i^2 - r_l^2)(\ln {r_l} - \ln {r_i})}}, \cr}$$
(18)
$${K_5} = {{- {A_1}r_i^2 + {A_2}r_{\rm{l}}^2} \over {r_{\rm{l}}^2 - r_i^2}},$$
(19)
$${K_6} = {{({A_1} - {A_2})r_{\rm{l}}^2} \over {(1 - 2{\mu _l})(r_{\rm{l}}^2 - r_{\rm{i}}^2)}},$$
(20)
$${K_7} = {{(1 + {\mu _l})(1 - 2{\mu _l}){\gamma _w}\xi ({h_i} - {h_l})} \over {2{E_l}(1 - {\mu _l})(\ln {r_l} - \ln {r_i})}},$$
(21)
$${A_1} = {{(1 + {\mu _l})(1 - 2{\mu _l})} \over {{E_l}}}\left[ {{{{\gamma _w}\xi ({h_i} - {h_l})(\ln {r_i} + 1 - {\mu _l})} \over {2(\ln {r_l} - \ln {r_i})(1 - {\mu _l})}} - {\sigma _i}} \right],$$
(22)
$${A_2} = {{(1 + {\mu _l})(1 - 2{\mu _l})} \over {{E_l}}}\left[ {{{{\gamma _w}\xi ({h_i} - {h_l})(\ln {r_l} + 1 - {\mu _l})} \over {2(\ln {r_l} - \ln {r_i})(1 - {\mu _l})}} - {\sigma _l}} \right].$$
(23)

3.2.3 Stresses and displacements of the ground in the plastic zone

The excavation produces unloading in the radial direction and loading in the tangential direction according to the proposed problem. Therefore, the major principal stress is the tangential stress and the minor principal stress is the radial stress in the plastic zone. At failure, the 2D Mohr-Coulomb criterion can be expressed as f(σ r , σ θ )=0, i.e.,

$$f({\sigma _r},{\sigma _\theta}) = \sigma _\theta ^p - {{1 + \sin {\varphi _p}} \over {1 - \sin {\varphi _{\rm{p}}}}}\sigma _r^p + {{2{c_p}\cos {\varphi _p}} \over {1 - \sin {\varphi _{\rm{p}}}}} = 0.$$
(24)

According to the equilibrium equation (Eq. (10)), the boundary conditions (Eqs. (11c) and (11d)), and the failure criterion (Eq. (24)), the ground stresses in the plastic zone are:

$$\sigma _r^p = B - ({\sigma _{{r_l}}} + B){(r/{r_l})^{2\sin {\varphi _p}/(1 - \sin {\varphi _p})}},$$
(25)
$$\sigma _\theta ^p = {{1 + \sin {\varphi _p}} \over {1 - \sin {\varphi _p}}}\left[ {B - ({\sigma _{{r_l}}} + B){{\left({{r \over {{r_l}}}} \right)}^{{{2\sin {\varphi _p}} \over {1 - \sin {\varphi _p}}}}}} \right] - {{2{c_p}\cos {\varphi _p}} \over {1 - \sin {\varphi _p}}},$$
(26)

where B is a constant and can be expressed as follows:

$$B = {{1 - \sin {\varphi _{\rm{p}}}} \over {2\sin {\varphi _{\rm{p}}}}}{{{\gamma _w}\xi ({h_l} - {h_p})} \over {\ln {r_p} - \ln {r_l}}} + {c_p}\cot {\varphi _{\rm{p}}}.$$
(27)

Under the axisymmetric plain strain condition, the strains and the displacements are given by

$${\varepsilon _r} = {{d{u_r}} \over {dr}},\quad {\varepsilon _\theta} = {{{u_r}} \over r}.$$
(28)

The compatibility condition is expressed as

$${{{\rm{d}}{\varepsilon _\theta}} \over {{\rm{d}}r}} = {{{\varepsilon _r} - {\varepsilon _\theta}} \over r}.$$
(29)

Assuming a small strain deformation analysis, the total strains are decomposed into elastic and plastic components, as follows:

$${\varepsilon _r} = \varepsilon _r^e + \varepsilon _r^p,\quad {\varepsilon _\theta} = \varepsilon _\theta ^e + \varepsilon _\theta ^p,$$
(30)

where the superscripts e and p denote elastic and plastic strains, respectively.

Hooke’s law is applied to determine the radial and tangential strains in the elastic region under the plane strain condition:

$$\left\{ \matrix{ \varepsilon _r^e = [{\sigma _r} - {\sigma _\theta}{\mu _e}/(1 - {\mu _e})](1 - \mu _e^2)/{E_e}, \hfill \cr \varepsilon _\theta ^e = [({\sigma _\theta} - {\sigma _r}{\mu _e}/(1 - {\mu _e})](1 - \mu _e^2)/{E_e}, \hfill \cr} \right.$$
(31)

where E e and μ e denote the elastic modulus and Poisson’s ratio, respectively.

The elastic strains in the plastic zone can be readily obtained by substituting the stresses in the plastic zone into Hooke’s law (Eq. (31)). The plastic strains in the plastic zone are instead governed by an appropriate flow rule postulated for the yielding behavior. The flow rule of plasticity relating the plastic strain increment dε p to the plastic potential g is governed by

$${\rm{d}}{\varepsilon ^p} = {\rm{d}}\lambda {{\partial g} \over {\partial \sigma}},$$
(32)

where dλ is a non-negative scalar function present throughout the plastic loading process. With the Mohr-Coulomb model, it is often assumed that the plastic potential takes the same form as the yield function while the friction angle is replaced by the dilation angle (which is commonly a smaller angle). The plastic potential can therefore be written as

$$\eqalign{ & g(\sigma _r^p,\sigma _\theta ^p) = \sigma _r^p(1 + \sin {\psi _p}) - (1 - \sin {\psi _p})\sigma _\theta ^p \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 2{c_p}\cos {\psi _p}, \cr}$$
(33)

where ψ p is the dilation angle.

By substituting the plastic potential (Eq. (33)) into the flow rule (Eq. (32)), radial and tangential plastic strain increments can be obtained:

$${\rm{d}}\varepsilon _\theta ^p = {\rm{d}}\lambda,\;\;{\rm{d}}\varepsilon _r^p = - {N_\psi}{\rm{d}}\lambda,$$
(34)

where N ψ =(1+sinψ p)/(1−sinψ p). Integration for (Eq. (34)), there is

$$\varepsilon _\theta ^p = \lambda,\;\;\varepsilon _r^p = - {N_\psi}\lambda = - {N_\psi}\varepsilon _\theta ^p.$$
(35)

By substituting Eqs. (35) and (31) into Eq. (30), then into Eq. (29), a differential equation can be obtained:

$$\eqalign{ & {{{\rm{d}}\varepsilon _\theta ^p} \over {{\rm{d}}r}} + {{{N_\psi} + 1} \over r}\varepsilon _\theta ^p \cr & \;\;\;\;\;\; = {{4(1 - \mu _p^2)\sin {\varphi _p}({\sigma _l} + B){r_l}} \over {{E_p}{{(1 - \sin {\varphi _p})}^2}}}{\left({{r \over {{r_l}}}} \right)^{{{3\sin {\varphi _p} - 1} \over {1 - \sin {\varphi _p}}}}} \cr & \;\;\;\;\;\;\;\;\; + {{21 + {\mu _p})({c_p}\cos {\varphi _p} - B\sin {\varphi _p})} \over {{E_p}(1 - \sin {\varphi _p})}}{1 \over r}. \cr}$$
(36)

The solution is

$$\eqalign{ & \varepsilon _\theta ^p = {{4(1 - \mu _p^2)\sin {\varphi _p}({\sigma _l} + B)} \over {{E_p}{{(1 - \sin {\varphi _p})}^2}({N_\varphi} + {N_\psi})}}{\left({{r \over {{r_l}}}} \right)^{{N_\varphi} - 1}} \cr & \;\;\;\;\;\; + {{21 + {\mu _p})({c_p}\cos {\varphi _p} - B\sin {\varphi _p})} \over {{E_p}(1 - \sin {\varphi _p})(1 + {N_\psi})}} + {K_x}{r^{- (1 + {N_\psi})}}, \cr}$$
(37)

where K x is a coefficient which can be determined by the plastic strain at the plastic-elastic interface, \(\varepsilon _\theta ^p\left| {_{r = {r_p}}} \right. = 0\), as follows:

$$\eqalign{ & {K_x} = - {{r_p^{1 + {N_\psi}}} \over {{E_p}(1 - \sin {\varphi _p})}} \cr & \;\;\;\;\;\;\;\; \times \left[ {{{4(1 - \mu _p^2)\sin {\varphi _p}({\sigma _l} + B)} \over {(1 - \sin {\varphi _p})({N_\varphi} + {N_\psi})}}{{\left({{{{r_p}} \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}} \right. \cr & \;\;\;\;\;\;\;\;\left. { + {{2(1 + {\mu _p})({c_p}\cos {\varphi _p} - B\sin {\varphi _p})} \over {(1 + {N_\psi})}}} \right]. \cr}$$
(38)

By substituting Eq. (38) into Eq. (37), the plastic strain can be written as

$$\left\{ \matrix{ \varepsilon _r^p = - {N_\psi}\varepsilon _\theta ^p, \hfill \cr \varepsilon _\theta ^p = {{4(1 - \mu _p^2)\sin {\varphi _p}({\sigma _l} + B)} \over {{E_p}{{(1 - \sin {\varphi _p})}^2}({N_\varphi} + {N_\psi})}} \hfill \cr \;\;\;\;\;\;\; \times \left[ {{{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}} - {{\left({{{{r_p}} \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}{{\left({{{{r_p}} \over r}} \right)}^{1 + {N_\psi}}}} \right] \hfill \cr \quad \quad + {{2(1 + {\mu _p})({c_p}\cos {\varphi _p} - B\sin {\varphi _p})} \over {{E_p}(1 - \sin {\varphi _p})(1 + {N_\psi})}}\left[ {1 - {{\left({{{{r_p}} \over r}} \right)}^{1 + {N_\psi}}}} \right]. \hfill \cr} \right.$$
(39)

The tangential strain in the plastic zone can be derived as follows:

$$\eqalign{ & {\varepsilon _\theta} = {{1 - \mu _p^2} \over {{E_p}}}\left[ {\left[ {B - ({\sigma _l} + B){{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}} \right]\left({{N_\varphi} - {{{\mu _p}} \over {1 - {\mu _p}}}} \right)} \right. \cr & + {{4\sin {\varphi _p}({\sigma _l} + B)} \over {{{(1 - \sin {\varphi _p})}^2}({N_\varphi} + {N_\psi})}}\;\left[ {{{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}} - {{\left({{{{r_p}} \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}{{\left({{{{r_p}} \over r}} \right)}^{1 + {N_\psi}}}} \right] \cr & \left. { + {{2({c_p}\cos {\varphi _p} - B\sin {\varphi _p})} \over {(1 - {\mu _p})(1 - \sin {\varphi _p})(1 + {N_\psi})}}\left[ {1 - {{\left({{{{r_p}} \over r}} \right)}^{1 + {N_\psi}}}} \right]\;\;\; - {{2{c_p}\cos {\varphi _p}} \over {1 - \sin {\varphi _p}}}} \right]. \cr}$$
(40)

By substituting Eq. (40) into Eq. (28), the solution of displacements U p can be written as

$$\eqalign{ & {U^p} = {{r(1 - \mu _{^p}^2)} \over {{E_{\rm{p}}}}}\left[ {\left[ {B - ({\sigma _l} + B){{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}} \right]\left({{N_\varphi} - {{{\mu _{\rm{p}}}} \over {1 - {\mu _{\rm{p}}}}}} \right)} \right. \cr & + {{4\sin {\varphi _{\rm{p}}}({\sigma _l} + B)} \over {{{(1 - \sin {\varphi _{\rm{p}}})}^2}({N_\varphi} + {N_\psi})}}\left[ {{{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}} - {{\left({{{{r_{\rm{p}}}} \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}{{\left({{{{r_{\rm{p}}}} \over r}} \right)}^{1 + {N_\psi}}}} \right] \cr & \left. { + {{2({c_{\rm{p}}}\cos {\varphi _{\rm{p}}} - B\sin {\varphi _{\rm{p}}})} \over {(1 - {\mu _{\rm{p}}})(1 - \sin {\varphi _{\rm{p}}})(1 + {N_\psi})}}\left[ {1 - {{\left({{{{r_{\rm{p}}}} \over r}} \right)}^{1 + {N_\psi}}}} \right] - {{2{c_{\rm{p}}}\cos {\varphi _{\rm{p}}}} \over {1 - \sin {\varphi _{\rm{p}}}}}} \right]. \cr}$$
(41)

Note that for the proposed problem, the initial radial displacement of ground in the plastic zone u 0 p induced by the initial stress σ 0 should be subtracted from the total displacement in order to calculate the net displacements induced by tunnelling alone. The expression of u 0 p is given by

$$u_0^{\rm{p}} = {{(1 + {\mu _{\rm{p}}})(1 - 2{\mu _{\rm{p}}}){\sigma _0}r} \over {{E_{\rm{p}}}}}.$$
(42)

The expression for displacements due to tunnelling in the plastic zone can be derived as follows:

$$\eqalign{ & {u^{\rm{p}}} = {{(1 - \mu _{\rm{p}}^2)r} \over {{E_{\rm{p}}}}}\left[ {\left[ {B - ({\sigma _{{r_l}}} + B){{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}} \right]\left({{N_\varphi} - {{{\mu _{\rm{p}}}} \over {1 - {\mu _{\rm{p}}}}}} \right)} \right. \cr & + {{4\sin {\varphi _{\rm{p}}}({\sigma _{{r_l}}} + B)} \over {{{(1 - \sin {\varphi _{\rm{p}}})}^2}({N_\varphi} + {N_\psi})}}\left[ {{{\left({{r \over {{r_l}}}} \right)}^{{N_\varphi} - 1}} - {{\left({{{{r_p}} \over {{r_l}}}} \right)}^{{N_\varphi} - 1}}{{\left({{{{r_p}} \over r}} \right)}^{1 + {N_\psi}}}} \right] \cr & + {{2({c_{\rm{p}}}\cos {\varphi _{\rm{p}}} - B\sin {\varphi _{\rm{p}}})} \over {(1 - {\mu _{\rm{p}}})(1 - \sin {\varphi _{\rm{p}}})(1 + {N_\psi})}}\left[ {1 - {{\left({{{{r_{\rm{p}}}} \over r}} \right)}^{1 + {N_\psi}}}} \right] \cr & \left. {- {{(1 - 2{\mu _{\rm{p}}}){\sigma _0}} \over {1 - {\mu _{\rm{p}}}}} - {{2{c_{\rm{p}}}\cos {\varphi _{\rm{p}}}} \over {1 - \sin {\varphi _{\rm{p}}}}}} \right].\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cr}$$
(43)

3.2.4 Stresses and displacements of ground in the elastic zone

Note that the initial radial displacement of ground in the elastic zone \({u_0}^{\rm{e}}\) induced by the initial stress σ 0 should be subtracted from the total displacement to calculate the net displacements induced by tunnelling alone (Fang et al., 2013). The expression of u 0 e is given by

$$\eqalign{ & u_0^e = {{(1 + {\mu _{\rm{p}}})(1 - 2{\mu _{\rm{p}}}){\sigma _0}{r_{\rm{p}}}} \over {{E_p}}} \cr & \;\;\;\;\;\;\; + {{(1 + {\mu _e})(1 - 2{\mu _e}){\sigma _0}(r - {r_{\rm{p}}})} \over {{E_e}}}. \cr}$$
(44)

The ground stresses and displacements in the elastic zone can be derived by using the same methods as calculating the distributions of liner stresses and displacements. Therefore, the solutions can be written as

$$\sigma _r^e = {K'_1} + {K'_2}{(1/r)^2} - {K'_3}\ln r,$$
(45)
$$\sigma _\theta ^e = {K'_1} - {K'_2}{(1/r)^2} - {K'_3}\ln r,$$
(46)
$$\eqalign{ & {u^e} = {{K'}_5}r - {{K'}_6}{{r_p^2} \over r} - {{K'}_7}r\ln r + {{(1 + {\mu _p})(1 - 2{\mu _p}){\sigma _0}{r_p}} \over {{E_p}}} \cr & \;\;\;\; + {{(1 + {\mu _e})(1 - 2{\mu _e}){\sigma _0}(r - {r_p})} \over {{E_e}}}, \cr}$$
(47)

where K′ 1–K′ 7 have the same expressions as K 1–K 7 but replacing r i, r l, h i, h l, μ l, σ i, and σ l by r p, r 0, h p, h 0, μ e, σ p, and σ 0, respectively.

3.2.5 Expressions of \(\sigma _{r_i } \), \(\sigma _{r_p } \), and r p

The solutions in this study must satisfy the equilibrium equations, the strain compatibility equations, and the boundary conditions (Eqs. (11c) –(11f)).

According to Eqs. (11c), (11d), and (11f), we can obtain

$${\sigma _l} = \left[ {B - {{{{{u_{{r_p}}}{E_p}} \over {(1 - \mu _p^2){r_p}}} + {{2{c_p}\cos {\varphi _p}} \over {1 - \sin {\varphi _p}}}} \over {{N_\varphi} - {{{\mu _p}} \over {1 - {\mu _p}}}}}} \right]{\left({{{{r_l}} \over {{r_p}}}} \right)^{{N_\varphi} - 1}} - B,$$
(48)
$$\eqalign{& {\sigma _p} = \left[ {{{{E_p}\left[ {(1 - 2{\mu _e})r_p^2 - r_0^2} \right]{A_3} + 2{E_p}{\mu _e}r_0^2{A_2}^\prime} \over {(1 - \mu _p^2)(1 - 2{\mu _e})(r_0^2 - r_p^2)}}} \right. \cr & \;\;\;\;\;\;\;\left. { + {{{E_p}{K_7}^\prime \ln {r_p}} \over {1 - \mu _p^2}} - {{2{c_p}\cos {\varphi _p}} \over {1 - \sin {\varphi _p}}}} \right] \cr & \;\;\;\;\;\;\;\left. {{{} \mathord{\left/{\vphantom {{} {\left({{N_\varphi} - {{{\mu _p}} \over {1 - {\mu _p}}}} \right. + {{{E_p}(1 + {\mu _e})\left[ {(1 - 2{\mu _e})r_p^2 + r_0^2} \right]} \over {{E_e}(1 - \mu _p^2)(r_0^2 - r_p^2)}}}}} \right. \kern-\nulldelimiterspace} {\left({{N_\varphi} - {{{\mu _p}} \over {1 - {\mu _p}}}} \right. + {{{E_p}(1 + {\mu _e})\left[ {(1 - 2{\mu _e})r_p^2 + r_0^2} \right]} \over {{E_e}(1 - \mu _p^2)(r_0^2 - r_p^2)}}}}} \right), \cr}$$
(49)

where

$${A_3} = {{(1 + {\mu _e})(1 - 2{\mu _e}){\gamma _w}\xi ({h_p} - {h_0})(\ln {r_p} + 1 - {\mu _e})} \over {2{E_e}(\ln {r_0} - \ln {r_p})(1 - {\mu _e})}},$$
(50)
$$\eqalign{& {A_2}' = {{(1 + {\mu _e})(1 - 2{\mu _e})} \over {{E_e}}} \cr & \;\;\;\;\;\;\;\; \times \left[ {{{{\gamma _w}\xi ({h_p} - {h_0})(\ln {r_0} + 1 - {\mu _e})} \over {2(\ln {r_0} - \ln {r_p})(1 - {\mu _e})}} - {\sigma _0}} \right]. \cr}$$
(51)

By substituting Eqs. (48) and (49) into Eq. (11e), a transcendental equation can be obtained to find the value of r p. By substituting the value of r p into Eq. (6) and Eq. (7), the values of h l and h p can be obtained. Then, (\(\sigma_{r}^{l}\), \(\sigma_{\theta}^{l}\), u l), (\(\sigma_{r}^{p}\), \(\sigma_{\theta}^{p}\), u p), and (\(\sigma_{r}^{e}\), \(\sigma_{\theta}^{e}\), u e) can be obtained, and so forth.

4 Validation of the analytical solutions

4.1 Parameters used in validation

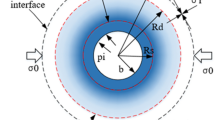
To validate the analytical model, the results of the analytical model are compared with those obtained from numerical computations. A MATLAB program is used to carry out the computations for the analytical model. The numerical computations are carried out by using a 3D finite difference code FLAC3D (Itasca Consulting Group, Inc., 1997; 2002) which can address 3D continuum problems with coupled groundwater flow. This comparison is intended to validate the solutions. A group of typical parameter values are employed, w=0, 7.5, 15, 23, 30.5, 38, 46, 53.5, 61, 68.5, and 76.5 (unit: mm), varied to simulate different stress releases before liner construction, and the others are shown in Table 1. Only a quarter of the geometry needs to be modeled due to symmetry. The geometry of the mesh and the boundary conditions are shown in Fig. 2. The normal velocities of the gridpoints along the bottom, vertical lateral, front and back boundary planes are fixed to be zero (Fang et al., 2013).

Fig. 2
figure 2

Calculation model (a) and boundary conditions (b)

Full size image
Table 1 Parameters used in the validation
Full size table

4.2 Relationship between r p-r l and w

The results of the calculations for the relationship between r p-r l and w are given in Fig. 3. It is clear from the plot that the solutions of the study and FLAC3D match well. All illustrative comparisons of the solution and the numerical results show little effect on the FLAC3D boundary constraints along the edges of the mesh. The yield zone radius increases significantly with the increase of w. This shows that the earlier the liner is carried out, the more significant the decreases in the plastic zone.

Fig. 3
figure 3

Relationship between r p -r l and w

Full size image

4.3 Results of the calculation

Results of the calculation for the stresses and displacements are given in Figs. 4 and 5. The solutions of the study and FLAC3D are matched well.

From the relationship between σ rl/σ 0 and w in Fig. 4, it is clear that contrary to r p, the effective radial stress at the ground-liner interface, σ rl decreases significantly with the increase of w, and σ rl≈0 when w=76.5 mm. This shows that the earlier the liner is carried out, the more significant will be the increase in the liner stress. Thus, appropriate time for the liner construction should be selected for a safe and economical design.

Fig. 4
figure 4

Relationship between σ r 1 /σ 0 and w

Full size image

Fig. 5 shows stresses distributions around the tunnel when w=15 mm. We can find that: (1) with the increase of distance from the tunnel centerline, the radial stress increases until it ceases to the in site stress, and yet the tangential stress in the ground increases to the maximum equaling two times that of the in site stress and then decreases until it ceases to the in site stress; (2) The tangential stress in the liner decreases with the increase of the distance from the tunnel centerline, and the discontinuity appears at the ground-liner interface because of different elastic moduli between the ground and liner.

Fig. 5
figure 5

Stress distributions around the tunnel when w =15 mm

Full size image

5 Conclusions

The analytical solutions presented in this paper expand and complete previous studies, in that we have now obtained complete analytical solutions for a deep tunnel in saturated ground. Although the analytical solutions are valid only for cases under the given assumptions, it appears to be useful for a preliminary design of deep tunnels under high water levels to predict the water pressure, stresses and displacement distributions around the tunnel. Stresses and displacement distributions using the proposed analytical solutions are compared to the numerical solution of FLAC3D, which appears to match well. For more complicated scenarios, a numerical model would be flexible. Nevertheless, the theoretical expressions derived in this study can be used in validating the numerical models.