1 Introduction

Flexible membranes have been increasingly used in a wide variety of engineering fields such as large-span structures on roofs, temporary exhibitions, storage facilities, and automobile air-bags (Jenkins and Korde, 2006). Due to their lightweight, flexibility and high susceptibility to external actions, they possess inherent advantages in covering large areas and constructing aesthetically pleasing architectures. However, membranes, owing to their negligibly small thickness, are usually assumed to have near-zero flexural stiffness and cannot sustain compressive stress beyond a certain minimal level. Thus, when membranes suffer stress based on a compressive direction, membranes tend to avoid it by out-of-plane deformation and then wrinkles are formed. As a result, the stiffness perpendicular to the direction of the wrinkles is reduced to zero, leading to a dramatic altering of the load transfer path and thereby affecting the static and dynamic performances (Du et al., 2006). Hence, the modeling of wrinkling behaviors is imperative in high precision design of membrane structures, and more attention has been given to develop computationally efficient and numerically accurate methods for a better understanding of the influence of wrinkles.

The wrinkling behavior of membrane structures has been studied previously by numerous researchers. Traditionally the wrinkling phenomena are analyzed with the tension field theory (TFT) which was firstly conceived by Wagner (1929). The fundamental assumption of this theory is that the compressive stress and the bending stress induced by the out-of-plane deformation are negligible in comparison with the tension stress (Jenkins et al., 2006). Based upon this theory, two major groups of techniques for wrinkling analysis, endowed with a modified constitutive law (Stein and Hedgepeth, 1961; Miller and Hedgepeth, 1985) or deformation gradient tensor (Roddeman et al., 1987a; 1987b; Kang and Im, 1997; Shaw and Roy, 2007), have been established to guarantee the absence of compressive stresses. Although these tension field theory approaches may provide efficient predictions for in-plane stress distribution and wrinkling regions, it is impossible for them to provide wrinkle details such as the amplitude, wavelength, and number of wrinkles.

Different from the classical TFT, the bifurcation buckling theory can be employed to obtain the precise shapes of wrinkles, which is also a topic of interest in this paper. Recent work in numerical studies based on buckling theory has advanced rapidly with the improvement of nonlinear computational methods and shell-based modeling technology that takes into account both the membrane and the bending stiffness. Lee and Lee (2002) developed an assumed strain formulation solid shell element with modified transverse shear modulus and Young’s modulus to compute a wrinkled deformation state for a square membrane. Wong and Pellegrino (2002; 2006a; 2006b; 2006c) studied the onset and development of wrinkles by using a thin-shell element in ABAQUS and obtained detailed information of wrinkles. They also performed some comparisons between the numerical results and experimental measurements, and showed that they were in a good agreement. Similar work based on an enhanced rotation-free shell triangular element was conducted by Flores and Onãte (2011), and accurate solutions for wrinkles with relatively coarse meshes were obtained.

Since wrinkling is a highly nonlinear behavior induced by the local rigid body motions, it is commonly recognized that the inclusion of this phenomenon in the computational simulation may lead to ill-conditioned or near-singular tangent stiffness matrices that would cause difficulties in the linearization of the nonlinear discrete equations. Therefore, instead of using an implicit solver, quasi-static modeling using an explicit integration of the damped motion equations can avoid the numerical difficulties such as inverting a singular matrix and may be a more appropriate method to deal with the instabilities associated with wrinkling. This strategy allows you to easily determine the final static equilibrium state as the limit of a number of pseudo-dynamic steps (Lee and Youn, 2006). However, the pseudo-dynamic method has the drawback that a very small time step is required to ensure numerical stability and accuracy, and thus generally a long computation time is required to obtain the converged solution. To overcome this drawback, several approaches (Rezaiee-pajand and Alamatian, 2010; Rodriguez et al., 2011) have been employed to rapidly obtain the equilibrated configuration.

According to the deformable body mechanics, a membrane is supposed to be a 2D solid in a state of plane stress, whereas it generally possesses 3D component motion. The numerical discrete models for solid structures may be classified into two groups, i.e., the intrinsic model and the analytical model (Ting et al., 2004). In view of natural physical properties, the intrinsic model for a true membrane is essentially a thin shell with near-zero flexural rigidity for its small thickness. However, the bending stiffness, albeit very small, is important in acquiring the detailed wrinkle shape. In fact, the out-of-plane deflections of the wrinkled membrane are actually induced by the membrane-to-bending coupling during the dynamic deformations. In this process, when compressive stresses breach the minimal critical level, they would be gradually reduced due to local instabilities (in the form of out-of-plane waves) with progressive oscillations and finally maintained constants at an extremely low level supported by the extremely small bending stiffness. Therefore, the variation of compressive stresses can be attributed to the actual interactions in membranes, and it is assumed to be reasonable to adopt an intrinsic membrane model when we attempt to simulate the wrinkling details in terms of the bifurcation theory.

In addition to the aforementioned models that have been extensively applied to the analysis of wrinkled membranes, the vector-form hybrid particle-element method (VHPEM) that is constructed by a theory based on vector mechanics (Ting et al., 2012), can be another viable choice for this problem. The concept of VHPEM resembles that of intrinsic approaches. It also can be considered as an extension of the finite element method (FEM) by involving some concepts of particle methods. The fundamental variables are discrete point values, rather than functions. That means in VHPEM, the analyzed domain is regarded as a body composed of a finite number of particles, instead of a continuous mathematical body adopted in the traditional methods based on analytical mechanics. The motion path of each particle can be modeled via a set of discrete path units. Within each path unit, Newton’s second law, rather than the weak equivalent variational formulations of the governing partial differential equations (PDEs), is adopted to directly form the motion equations of the particles. For conventional energy-based methods, the variational principle only imposes a global equilibrium on the entire analyzed domain without ensuring equilibrium within each element. These unbalanced residual forces will introduce some non-zero work under rigid body motion. Different from the global equilibrium condition employed in the standard FEM, VHPEM maintains the intrinsic nature of early finite elements which enforce a strong form of dynamic equilibrium on each particle. In addition, the formulation of each force term in the governing equation can be derived in a manner somewhat similar to that of FEM. For example, internal forces amid particles are determined by the deformation of a set of canonical elements connecting to them. However, the VHPEM does not directly employ the complicated strain/stress tensor formulations to evaluate the deformation as in a standard FEM. Instead, a set of physical modeling procedures, e.g., a special kinematics and a group of deformation coordinates, are proposed to separate rigid body motion and pure deformation. In the solution procedure, an incremental theory based on the concept of the convected material frame (Shih et al., 2004) and an explicit time integration scheme are also adopted. As a result, it may provide efficient solutions for the large-deflection study of structures. In recent years, Ting’s (2004) concept and theory has been accepted by many researchers and successfully applied to solving some practical engineering problems (Wang et al., 2005; Lien et al., 2010).

The prominent advantage of this method is that no nonlinear iterations are necessary and no global stiffness matrices should be formed, which allows it to avoid the numerical difficulties in solving matrix equations with ill-condition or singularity. Therefore, VHPEM is well-suited for treating with membrane wrinkling, a particular partly buckling phenomenon with typical characteristics of large deflections and rotations but moderate strains. By designing a generalized shell analysis framework of VHPEM in compliance with the buckling theory, this paper will expand the application of VHPEM to such an instability problem of thin membranes.

2 Vector-form hybrid particle-element formulation for shell-like membranes

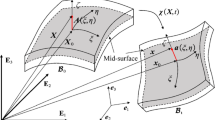
The VHPEM is a vector mechanics based numerical method. The primary objective of this method is to simulate the motions and geometrical changes of a system of multiple rigid and deformable bodies simultaneously. It contents four fundamental concepts: (a) point value description, (b) path unit description, (c) a kinematical description of particle motion and deformation by incorporating an adaptive convected material frame, and (d) strong formed equations of motion governed by Newton’s second law. For a further discussion about these subjects, one can consult references (Shih et al., 2004; Ting et al., 2004; Yu, 2010; Yang et al., 2014) where a complete and detailed vision can be found.

Considering a membrane as shown in Fig. 1, on the mid-surface some particles are properly allocated. The interaction forces evaluation of each particle between its neighbors is the most important work in VHPEM, which will be presented at length in the following paragraphs.

Fig. 1
figure 1

Motion of particle j in a membrane modeled by a group of particles

Full size image

As mentioned above, membranes are essentially ultra thin shell-like structures and we should not neglect their bending stiffness when attempting to acquire the deformed geometry of the wrinkled membranes in detail. Hence, a geometrically nonlinear shell model, accounting for both membrane and flexure deformations, is an obviously proper choice. In terms of the shell theory, the generalized internal forces of the shell-like membrane are also composed of two components with regard to the membrane and bending rigidity, respectively. In this work, these interaction forces are modeled by a set of triangular shell elements connected with particles, and thus the stress state of this kind of elements can be considered as a simple superposition of the membrane stress and the plate bending stress. Regarding the evaluation of the former effect caused by the in-plane deformation of the mid-surface, the detailed formulations can be found in our former work of shape analysis of membranes (Yang et al., 2014) and does not specify here in depth. This section is focused on the derivation for the formulations of particle interaction forces related to the non-zero bending rigidity of a membrane, i.e., the moments.

Fig. 2a shows an arbitrary 3D triangular thin shell element with thickness h. The geometry of the shell element is represented by the mid-plane defined by three particles with numbers (1, 2, 3). Each particle has three translational and three rotational degrees of freedom in the global coordinate. Because the element nodes are rigidly connected with particles, the position vectors and the rotation angles of the node i at times t a and t can be defined as (\({\bf{x}}_i^a,\,\,{\bf{\beta}}_i^a\)) and (x i , β i ) (i=1, 2, 3), respectively. Since the time interval between t a and t is very small, both the material property and the configuration are assumed to be unchanged within this time segment. If the configuration of the element at time t a is chosen as the material reference frame, the displacement increment and the rotation angle increment of node i between t a and t are \(\Delta {{\bf{u}}_i} = {{\bf{x}}_i} - {\bf{x}}_i^a\) and \(\Delta {{\bf{\beta}}_i} = {{\bf{\beta}}_i} - {\bf{\beta}}_i^a\) (i=1, 2, 3) (Fig. 2).

Fig. 2
figure 2

Motion of a 3D triangular shell element

(a) Position and rotation angles of particles at three corners of the mid-plane of an element; (b) Rigid body rotations and relative rotation angles

Full size image

Note that both the total nodal displacement increment Δu i and the rotation angle increment Δβ i include pure deformation, rigid body translation and rotation. However, the generalized internal forces in shells are contributed by the deformation displacements and rotations only, and thus the most important work here is to adopt a convected material reference frame and a procedure of fictitious reverse motion, as shown in Fig. 3a, for deducting the rigid body motions from the total displacement and rotation increments of particles. Yang et al. (2014) exhaustively discussed the fictitious reverse motion and provided the detailed derivations of the rotation angle θ and the corresponding direction vector of rotation axis e θ . Thus, the deformation displacement vector of node i from t a to t can be evaluated by

$${\bf{\eta}}_1^d = 0,$$
(1a)
$$\eqalign{& {\bf{\eta}}_i^d = {\bf{\eta}}_i + {\bf{\eta}}_i^r = (\Delta {{\bf{u}}_i} - \Delta {{\bf{u}}_1}) + {{\bf{R}}^*}(- \theta)({{\bf{x}}_i} - {{\bf{x}}_1}), \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 2,\;\;3, \cr}$$
(1b)

where η i and η r i are the total relative displacement increments of node i to node 1 and the rigid body displacement increment induced by the fictitious reverse rotation of node i, respectively, and R is a rotation matrix of rotation vector θ.

Fig. 3
figure 3

Particle internal force calculations

(a) Fictitious reverse translation (−Δu 1) and rotation (−θ); (b) Deformation displacements and rotation angles in the deformation coordinate system

Full size image

In addition, the effect of the rigid body rotation on the nodal rotations can be conveniently determined by

$${\bf{\omega}}_i^{\rm{d}} = \Delta {{\bf{\beta}}_i} + (- {\bf{\theta}}),\;\;\;i = 1,\;2,\;3.$$
(2)

To evaluate the work equivalent internal forces, a shape function with the same form as that developed in the FEM is introduced for describing the strain distribution within an element. Different from the total displacements in the traditional FEM, the nodal variables used in the VHPEM only account for the deformation. Therefore, a set of deformation coordinates (\(\hat x,\hat y,\hat z\)) are specifically introduced to remove the modes related to the rigid body motion as well as to reduce the total independent variables to the correct number. As shown in Fig. 3b, the basic vectors of \(\hat x,\hat y\) and \(\hat z\) axes are denoted by \({{\bf{\hat e}}_x},\,{{\bf{\hat e}}_y}\) and \({{\bf{\hat e}}_z}\), respectively, that is

$${{\bf{\hat e}}_x} = {1 \over {|{\bf{\eta}}_2^d|}}{\bf{\eta}}_2^{\rm{d}}, {{\bf{\hat e}}_z} = {{\bf{n}}_a}, {{\bf{\hat e}}_y} = {{{{{\bf{\hat e}}}_z} \times {{{\bf{\hat e}}}_x}} \over {|{{{\bf{\hat e}}}_z} \times {{{\bf{\hat e}}}_x}|}}.$$
(3)

Before the internal force evaluation can be implemented in the deformation coordinates, the deformation vector \({\bf{\eta}}_i^{\rm{d}}\) should be transformed to the new coordinate system by

$${{\bf{\hat u}}_i} = {\bf{\hat Q\eta}}_i^{\rm{d}} = {[{\hat u_i} {\hat v_i} {\hat w_i}]^{\rm{T}}}{\rm{,}}\;\;i = 1,\;2,\;3,$$
(4)

where \({\bf{\hat Q}} = {[{\bf{\hat e}}_x^{} {\bf{\hat e}}_y^{} {\bf{\hat e}}_z^{}]^{\rm{T}}}\) represents the coordinate transformation matrix from the global coordinates (x, y, z) to the local deformation coordinates (\(\hat x,\hat y,\hat z\)).

With regard to the other deformation component (i.e., the nodal rotation deformation \({\bf{\omega}}_i^{\rm{d}}\)), both the rotation angle increment Δβ ι and rigid body rotation θ corresponding to each axis should also be transformed to the local deformation coordinate. The former transformation can be straightforwardly presented as

$$\Delta {{\bf{\hat \beta}}_i} = {\bf{Q}}(\Delta {{\bf{\beta}}_i}),\;\;i = 1,\;2,\;3.$$
(5)

As for the rigid body rotation θ that consists of the out-of-plane rotation θ 1=θ 1 n 1 and the in-plane rotation θ 2=θ 2 n 2 as shown in Fig. 2b, in the deformation coordinate it can be obtained by a set of geometric operations,

$${\hat \theta _x} = {\bf{\theta}} \cdot {{\bf{\hat e}}_x} = {\theta _1}({{\bf{n}}_1} \cdot {{\bf{\hat e}}_x}),$$
(6a)
$${\hat \theta _y} = {\bf{\theta}} \cdot {{\bf{\hat e}}_y} = {\theta _1}({{\bf{n}}_1} \cdot {{\bf{\hat e}}_y}),$$
(6b)
$${\hat \theta _z} = {\bf{\theta}} \cdot {{\bf{\hat e}}_z} = {\theta _1}({{\bf{n}}_1} \cdot {{\bf{\hat e}}_z}) + {\theta _2}.$$
(6c)

Thus, the nodal deformation rotation of node i within time segment t a -t can be obtained when every term in Eq. (2) is written corresponding to each axis in the deformation coordinate as follows:

$$\begin{array}{*{20}c} {\Delta \hat \phi ^i = \left\{ {\begin{array}{*{20}c} {\Delta \hat \phi _x^i } \\ {\Delta \hat \phi _y^i } \\ {\Delta \hat \phi _z^i } \\ \end{array} } \right\} = \Delta \hat \beta _i + ( - \hat \theta ) = \left\{ {\begin{array}{*{20}c} {\Delta \hat \beta _x^i + ( - \hat \theta _x )} \\ {\Delta \hat \beta _y^i + ( - \hat \theta _y )} \\ {\Delta \hat \beta _z^i + ( - \hat \theta _z )} \\ \end{array} } \right\},} \\ {i = 1,2,3,} \\ \end{array}$$
(7)

where \(\Delta \hat \varphi _z^i\) represents the torsion angle around the mid-surface normal of a plane shell element, and it may be neglected in terms of the basic assumption in the classical shell theory.

Now in the new coordinate system six components, \({\hat u_1}, {\hat v_1}, {\hat w_1}, {\hat v_2}, {\hat w_2}, {\hat w_3}\) are zero, which implies that six DOFs are deleted. Thus, considering the remaining non-zero independent variables of deformations related to the bending stress, only rotating angles of each node corresponding to axes of \(\hat x\) and \(\hat y\) (i.e., \(\Delta \hat \varphi _x^i\) and \(\Delta \hat \varphi _y^i\)), totally six DOFs are left while the small transverse deformation displacements \({\hat w_i}\) may be neglected. For convenience, the deformation variables \(\Delta {{\bf{\hat \varphi}}^i}\) are expressed in a vector form, i.e.,

$$\eqalign{& \;{{{\bf{\hat \Omega}}}^{\rm{T}}} = \left[ {0\;\;\Delta \hat \varphi _x^1\;\;\Delta \hat \varphi _y^1\;\;0\;\;\Delta \hat \varphi _x^2\;\;\Delta \hat \varphi _y^2\;\;0\;\;\Delta \hat \varphi _x^3\;\;\Delta \hat \varphi _y^3} \right] \cr & \;\;\;\;\;\;\; = \left[ {{{{\bf{\hat \Omega}}}_1}\;\;{{{\bf{\hat \Omega}}}_2}\;\;{{{\bf{\hat \Omega}}}_3}} \right]. \cr}$$

To calculate the bending strain in a triangle shell element, consider \(\hat w(\hat x,\hat y)\) as the deformation deflection of an arbitrary point on the mid-surface of the element, which can be described by a set of cubic polynomial shape functions similar to those in the FEM. Then, according to the classical thin shell theory that conforms with the Kirchhoff-Love hypothesis, the deformation field can be written as

$$\left\{{\matrix{{\hat w} \cr {{{\hat \varphi}_x}} \cr {{{\hat \varphi}_y}} \cr}} \right\} = \left\{{\matrix{{\hat w} \cr {{{\partial \hat w} \over {\partial \hat y}}} \cr {- {{\partial \hat w} \over {\partial \hat x}}} \cr}} \right\} = \left[ {\matrix{{{\bf{\hat P}}} \cr {{{{\bf{\hat P}}}_{,\hat y}}} \cr {- {{{\bf{\hat P}}}_{,\hat x}}} \cr}} \right]{\bf{\alpha}},$$
(8)

where \(\hat P = [1 \hat x \hat y \hat x^2 \hat x\hat y \hat y^2 \hat x^3 \hat x^2 \hat y + \hat x\hat y^2 \hat y^3 ], \hat P_{,\hat x} \) and \(\hat P_{,\hat y} \) denote the first-order partial derivatives of \({\bf{\hat P}}\) with respect to \(\hat x\) and \(\hat y\) axes, respectively. α is a coefficient vector and it can be determined by the compatible conditions for deformation at the nodes, namely, at \({\bf{\hat x}} = {\left[ {{{\hat x}_i},{{\hat y}_i}} \right]^{\rm{T}}}\)

$$\left\{{\matrix{{\hat w} \cr {{{\hat \varphi}_x}} \cr {{{\hat \varphi}_y}} \cr }} \right\} = \left\{{\matrix{0 \cr {\Delta \hat \varphi _x^i} \cr {\Delta \hat \varphi _y^i} \cr }} \right\},\;\;\;\;i = 1,\;2,\;3.$$
(9)

The coefficients α i (i=1, 2, …, 9) in the vector α can be obtained by substituting the coordinate of each node \(({\hat x_i},{\hat y_i})\;(i = 1,\;2,\;3)\) and the compatibility conditions in Eq. (9) into Eq. (8). Then, the transverse deformation deflection \(\hat w(\hat x,\hat y)\) can be expressed in the form of interpolation functions, namely,

$$\hat w = {\bf{\hat P}}{{\bf{\hat A}}^{- 1}}{\bf{\hat \Omega}} = {\bf{\hat N\hat \Omega}} = {{\bf{\hat N}}^*}{{\bf{\hat \Omega}}^*} = \sum\limits_i^3 {{\bf{\hat N}}_i^*{\bf{\hat \Omega}}_i^*},$$
(10)

where \({\bf{\hat N}}\) and \({{\bf{\hat N}}^*}\) are the shape function matrices in the deformation coordinate, and the latter one is obtained by deleting the useless elements in \({\bf{\hat N}}\) which corresponds to the zero components in the nodal deformation vector \({\bf{\hat \Omega}};\,\,{{\bf{\hat \Omega}}^*} = {\left[ {\Delta \hat \varphi _x^1\;\Delta \hat \varphi _y^1\;\Delta \hat \varphi _x^2\;\Delta \hat \varphi _y^2\;\Delta \hat \varphi _x^3\;\Delta \hat \varphi _y^3} \right]^{\rm{T}}} = {\left[ {{\bf{\hat \Omega}}_1^*\;\;{\bf{\hat \Omega}}_2^*\;\;{\bf{\hat \Omega}}_3^*} \right]^{\rm{T}}}\) is a condensed nodal deformation vector, which is composed of independent variables only.

According to the basic concepts of “path unit description”, the deformation of an element within the time segment t a -t should be very small as compared with the reference configuration at time t a . Thus, with the deformation distribution functions, one can formulate the incremental strain and stress in terms of the elastic mechanics theory, i.e.,

$$\Delta \hat \varepsilon = \hat z\hat B^* \hat \Omega ^ * = \hat z[\hat B_1^* \hat B_2^* \hat B_3^* ]\hat \Omega ^ * = \hat z\left[ {\begin{array}{*{20}c} {\hat N_{1,\hat x\hat x}^* } & {\hat N_{2,\hat x\hat x}^* } & {\hat N_{3,\hat x\hat x}^* } \\ {\hat N_{1,\hat y\hat y}^* } & {\hat N_{2,\hat y\hat y}^* } & {\hat N_{3,\hat y\hat y}^* } \\ {\hat N_{1,\hat z\hat z}^* } & {\hat N_{2,\hat z\hat z}^* } & {\hat N_{3,\hat z\hat z}^* } \\ \end{array} } \right]\hat \Omega ^ * ,$$
(11)
$$\Delta {{\bf{\hat \sigma}}_r} = {{\bf{\hat D}}_a}\Delta {\bf{\hat \varepsilon}} = \hat z{{\bf{\hat D}}_a}{{\bf{\hat B}}^*}{{\bf{\hat \Omega}}^*},$$
(12)

where \({{\bf{\hat D}}_a}\) denotes the constitutive matrix of the material referring to the stress state, and \({{\bf{\hat \sigma}}_a}\) is the stress value at time t a .

For the calculation of internal forces, the principle of virtual work is adopted here. The internal virtual work induced by stresses and virtual strains can be written as

$$\eqalign{& \delta U = {(\delta {\bf{\Omega}}^*)^T} \cr & \;\; \times \left\{{\int_{{A_a}} {\int_{- {h_a}/2}^{{h_a}/2} {[\hat z{{({\bf{\hat B}}^*)}^T}{{{\bf{\hat \sigma}}}_a} + {{\hat z}^2}{{({\bf{\hat B}}^*)}^T}{{{\bf{\hat D}}}_a}{\bf{\hat B}}^*{\bf{\Omega}}^*{\rm{]d}}\hat z{\rm{d}}\hat A}}} \right\}, \cr}$$
(13)

where A a and h a respectively denote the area and the thickness of the element at time t a .

The external virtual work caused by the internal nodal moments is

$$\delta W = {(\delta {{\bf{\hat \Omega}}^*})^{\rm{T}}}{{\bf{\hat m}}^*} = {(\delta {{\bf{\hat \Omega}}^*})^{\rm{T}}}({\bf{\hat m}}_a^* + \Delta {{\bf{\hat m}}^*}),$$
(14)

where \({{\bf{\hat m}}^*}\) is the internal nodal moment at time t, \({\bf{\hat m}}_a^*\) is assumed as the internal nodal moment at time t a , and \(\Delta {{\bf{\hat m}}^*}\) is the incremental internal nodal moment.

Combining Eqs. (13) and (14) yields the equivalent internal moments

$${{\bf{\hat m}}^*} = \int_{{A_a}} {\int_{- {{{h_a}} \over 2}}^{{{{h_a}} \over 2}} {[\hat z{{({\bf{\hat B}}_{}^*)}^T}{{{\bf{\hat \sigma}}}_a} + {{\hat z}^2}{{({\bf{\hat B}}_{}^*)}^T}{{{\bf{\hat D}}}_a}{\bf{\hat B}}_{}^*{\bf{\Omega}}_{}^*]{\rm{d}}\hat z{\rm{d}}\hat A}}.$$
(15)

Eq. (15) only gives six components of the generalized internal nodal forces. Because the displacement components corresponding to the remaining three shearing forces \({{\bf{\hat f}}_{iz}}\;(i = 1,\;2,\;3)\) are relevant to the out-of-plane rigid body motions that have been eliminated in the deformation coordinates, these forces should be determined by the static equilibrium conditions of the element, namely

$$\sum {\hat F_z = 0, \hat f_{1z} + \hat f_{2z} + \hat f_{2z} = 0,}$$
(16a)
$$\sum {\hat M_x = 0, (\hat m_{1x} + \hat m_{2x} + \hat m_{3x} ) + \hat f_{2z} \hat y_2 + } \hat f_{3z} \hat y_3 = 0,$$
(16b)
$$\sum {\hat M_y = 0, (\hat m_{1y} + \hat m_{2y} + \hat m_{3y} ) - \hat f_{2z} \hat x_2 - } \hat f_{3z} \hat x_3 = 0.$$
(16c)

Next, to assemble the equivalent interaction forces acting on a conjunct particle, all the force and moment components caused by both membrane and bending deformations need to be transformed to the global coordinate. Besides, the element needs to undergo a forward motion, including a translation (+Δu 1) and a rotation (+θ), and move back to its original position at time t. Therefore, the actual internal forces and moments of node i at the current time can be determined by

$${\bf{f}}_i^{{\mathop{\rm int}}} = {\left[ {\matrix{{{f_{ix}}} & {{f_{iy}}} & {{f_{iz}}} \cr }} \right]^{\rm{T}}} = {\bf{R}}(+ \theta){{\bf{Q}}^{\rm{T}}}{\bf{\hat f}}_i^{}{\rm{,}}\;\;i = 1,\;2,\;3,$$
(17a)
$${\bf{m}}_i^{{\mathop{\rm int}}} = {\left[ {\matrix{{{m_{ix}}} & {{m_{iy}}} & {{m_{iz}}} \cr }} \right]^{\rm{T}}} = {\bf{R}}(+ \theta){{\bf{Q}}^{\rm{T}}}{\bf{\hat m}}_i^{}{\rm{,}}\;\;i = 1,\;2,\;3.$$
(17b)

3 Solution strategy: a pseudo-dynamic scheme

The ability of membranes to barely support compression may lead to near-singular system matrices and numerical difficulties. A straightforward application of the Newton-Raphson method may cause divergence. To solve the equations of motion of discrete particles (Eq. (1) in (Yang et al., 2014)) and achieve the solutions at equilibrium state, it is appropriate to employ a pseudo-dynamic scheme based on the explicit central difference time integration algorithm (de Borst et al., 2012). To maintain the efficiency and ensure that the mode associated with the applied loads is rapidly converged to the steady-state solution, as well as to be closer to the real dynamic course, the damping force \({\bf{F}}_\alpha ^{{\rm{dmp}}}\) adopted in this study for the pseudo-dynamic formulation is based on a viscous damping form (Rezaiee-pajand and Alamatian, 2010), i.e.,

$${\bf{F}}_\alpha ^{{\rm{dmp}}} = \mu {{\bf{M}}_\alpha}{{\bf{\dot d}}_\alpha},$$
(18)

where μ is the damping coefficients that determine the dissipation rate of the kinetic energy of the system, M α is the value of the particle mass and mass moment of inertia, and \({{\bf{\dot d}}_\alpha}\) is the acceleration vector.

For an arbitrary particle α, its motion within each path unit is governed by the equation that follows Newton’s second law, that is

$${{\bf{M}}_\alpha}{{\bf{\ddot d}}_n} = {\bf{F}}_n^{{\rm{ext}}} - {\bf{F}}_n^{{\rm{int}}} - {\bf{F}}_n^{{\rm{dmp}}},$$
(19)

where \({{\bf{\ddot d}}_n}\) is the acceleration vector, \({\bf{F}}_n^{{\rm{ext}}}\) is the summation of the prescribed external forces/moments and \({\bf{F}}_n^{{\rm{int}}}\) is the summation of the internal forces/moments exerted by the membrane elements connecting to particle α at time t n .

The approximations to the acceleration and velocity vectors of particle α at time t n can be obtained by linear interpolation, i.e.,

$${{\bf{\ddot d}}_n} = {1 \over {\Delta t}}({{\bf{\dot d}}_{n + 1/2}} - {{\bf{\dot d}}_{n - 1/2}}),$$
(20a)
$${{\bf{\dot d}}_n} = {1 \over 2}({{\bf{\dot d}}_{n + 1/2}} + {{\bf{\dot d}}_{n - 1/2}}),$$
(20b)

where the subscripts n and n−1/2, n+1/2 refer to the step number and mid-step numbers, \({{\bf{\dot d}}_{n - 1/2}}\) and \({{\bf{\dot d}}_{n + 1/2}}\) represent the velocities at times t+Δt/2 and t−Δt/2, respectively, and Δt is a constant time increment. Substituting Eqs. (18) and (20) into Eq. (19) and rearranging terms yields

$${{\bf{\dot d}}_{n + 1/2}} = \left({{{2 - \mu \Delta t} \over {2 + \mu \Delta t}}} \right){{\bf{\dot d}}_{n - 1/2}} + {{2\Delta t} \over {(2 + \mu \Delta t)}}{\bf{M}}_\alpha ^{- 1}({\bf{F}}_n^{{\rm{ext}}} - {\bf{F}}_n^{{\rm{int}}}).$$
(21)

Then the displacements vector at time t n +1=t n +Δt is calculated as

$${{\bf{d}}_{n + 1}} = {{\bf{d}}_n} + \Delta t{{\bf{\dot d}}_{n + 1/2}}.$$
(22)

It can be found that in the proposed time integration scheme, only simple algebraic manipulations for vectors are needed. In addition, the displacements of the particles are completely uncoupled. Consequently, global stiffness matrices are not required, and the computation cost and the memory storage requirement are very small.

Note that such the explicit operator is conditionally stable. So the time step has to be maintained at values below a critical time step value Δt crit according to the CFL stability condition (Cook et al., 1989), i.e., Δt crit=L min/c, where L min is the smallest characteristic element dimension, and c is the current effective dilatational wave speed of material, which is a function of material properties. The physical meaning is that stability is only ensured when the time increment is shorter than the time for the acoustic sound wave to travel the smallest distance between two adjacent nodes in a discrete modal.

Given that the choice of some parameters such as mass, the positive damping coefficient, and the time step has few influences on the desired quasi-static solution for path- and rate-independent materials, the fictitious values for these quantities that do not represent the real physical system may be artificially chosen to produce a faster convergence to the steady static solution while satisfying the stability conditions (Underwood, 1983). To get a larger stable time step in the time integration, the mass scaling approach (Hallquist, 2006) is used in this study, namely the mass density of each element in the model is adjusted to an artificially specified larger time step size Δt s, i.e.,

$${\rho _i} = {{\Delta t_s^2E} \over {L_i^2(1 - {\nu ^2})}},$$
(23)

where ρ i is the adjusted material density, E is the Young’s modulus, L i is the characteristic dimension of element i, and ν is the Poisson’s ratio. To provide a wide safety margin for stability, in the program the iterations are performed with an initial time step reduced by multiplying a scale factor, i.e., Δt 0=0.9Δt s.

Besides, a critical damping coefficient that is used to attenuate the transient may be estimated to be proportional to the lowest frequency (Underwood, 1983), namely

$$\mu = \sqrt {\omega _{\min}^2(4 - \Delta {t^2}\omega _{\min}^2)},$$
(24)

where ω min is the fundamental angular frequency of a structure in free vibration and its estimate may be obtained from the Rayleigh principle.

4 Modeling strategy for wrinkling initiation

Due to the fact that no mechanism exists to automatically initiate the out-of-plane wrinkling deformation, even in the presence of compressive stresses, when perfect flat membranes are only subjected to in-plane loading, a probable way for an efficient numerical modeling of the wrinkled shape is to perform a pseudo bifurcation analysis by perturbing the membrane slightly out of plane to trigger the membrane-to-bending coupling. From the point of buckling theory, the access to a solution on the post-buckling path can be conveniently obtained in this manner without implementing the bifurcation buckling analysis. Several approaches are possible for the introduction of such disturbs, where amplitude and distribution are particularly crucial. A possibility for providing useful information on the choice of initial imperfections is the first-order characteristic vector corresponding to the first wrinkling value at the bifurcation point (Su et al., 2003), or the linear combination of several modes that are scaled depending on the thickness of the membrane (Wong and Pellegrino, 2006b). In this simulation technique, the choice of the imperfection modes seeded in the membrane is based on the expected final wrinkling patterns. However, in general, in a pure membrane analysis, the wrinkling pattern is not known as a priori, so the requirement becomes that of the introduction of an arbitrary distribution of imperfection for inducing the out-of-plane deformation. Thus, another possibility is to impose an unbiased geometric imperfections pattern (Iwasa et al., 2004) on the initial flat membrane patch in the pseudo-random form, z i =αr i h, where α is a dimensionless amplitude parameter, r i is a pseudo-random number, and h is the membrane thickness.

It deserves to be noted that the imperfections generated by the aforementioned two schemes cannot be removed from the numerical model and may exert influence on the post-wrinkling behaviors. Particularly, for the ideal planar membrane model, the numerical errors caused by these schemes will be quite large. To accurately carry out the wrinkling analysis, an alternative way is to adopt a direct perturbed force approach (Leifer and Belvin, 2003) to introduce the imperfection and further the occurrence of the wrinkles. The basis of this approach is to apply a set of equal and opposite small forces perpendicular to the membrane surface on some selected points with a net resultant of zero to meet the self-equilibrium condition. The location of these disturbing forces may be in accordance with the first wrinkle mode characteristics or be arbitrarily specified across the membrane surface. A major advantage associated with the use of forces for wrinkling initiation is that the initial imperfection can be added to and removed from the model with ease. Moreover, to avoid the additional burden of the eigenvalue buckling analysis, the distribution of the disturbing forces adopted in the present study is in an arbitrary form.

Some guidelines for determining the amplitude of imperfection can be obtained from the investigation into the effects of the initial imperfections on wrinkling behavior conducted by Iwasa et al. (2004). It is confirmed that the magnitudes ranging from 0.01 to 1.0 of the membrane thickness are large enough to start the formation of wrinkles as well as to achieve the same final wrinkling distribution. This also implies that the effect of the initial imperfection on wrinkling behavior may be negligible when the given amplitude is within the recommended range. As a default rule in this study, the disturbing forces are determined according to the requirement that the amplitude of the out-of-plane perturbed deformation obtained is smaller than the membrane thickness at least by one order of magnitude.

5 Numerical examples and analysis

The present section is concerned with the numerical explorations of the proposed method for two typical membrane problems involving wrinkling. The numerical tests are implemented using a code designed following the above-mentioned formulations and modeling techniques. The performance of the new method will be displayed by comparisons with other numerical and analytical solutions, as well as experimental measurements reported in various literatures. The detailed characteristics of wrinkles can be used to validate the capability and accuracy of this method in geometrically nonlinear analysis of wrinkled membranes.

5.1 Rectangular thin-film membrane subject to in-plane shear loading

To investigate the functionality of the implemented code for a membrane wrinkling simulation, a benchmark example as in (Leifer and Belvin, 2003; Raible et al., 2005; Wong and Pellegrino, 2006b) is reproduced here first. This example presents a study of the formation and growth of wrinkles in an initially flat rectangular membrane, which was clamped along the lower edge while the upper one was allowed to move only in the horizontal direction under in-plane shear loadings. Both the left and right edges of the membrane were left completely unrestrained. This sheared membrane simulation is known as one of the most difficult tests. The thin film in this test was a kind of isotropic Kapton® membrane with thickness t 0=25 μm and density ρ=1.5×10−6 kg/mm3. The membrane mechanical properties were E=3500 N/mm2 and ν=0.31. The illustrations for the geometry, loading, and boundary conditions for this investigation are given in Fig. 4.

Fig. 4
figure 4

Geometry, boundary, and loading conditions of the flat membrane for the shear test calculation

(a) Problem setting of a rectangular thin membrane under in-plane shear loading; (b) Displacement control scheme

Full size image

The shear test calculation was conducted as follows. Firstly, the upper edge was slightly stretched by an upward displacement of δ y =0.025 mm, resulting in a certain prestress ranging from 0.82 N/mm2 to 0.95 N/mm2, to reproduce the true constraints and stress state existing in the experiment as well as to offer rigidity conditions for supporting the following load. For the second step, the influence of the imperfections as proposed in Section 4 was taken into account by specifying distributed disturbing forces perpendicular to the membrane surface. Each individual one was assigned 5×10−4 N. Then the prestress was kept constant while a small uniform shear load with displacement \({\delta _x}_{_{\rm{1}}} = \beta {\delta _y}\) along x direction was applied to the upper edge. As reported by Leifer and Belvin (2003), an empirical value of β=1.5 is a fair rationalization. In the last step, the initial disturbing forces were removed timely to eliminate the effect of the initial imperfections on the wrinkling behaviors. Meanwhile, small increments of shear load were gradually applied at the upper edge until the final horizontal displacement δ x reached 3 mm. In this way, the membrane wrinkling pattern without initial imperfections could be obtained. Throughout the entire period of analysis all calculations were only done with monotonic displacement control except for disturbing forces. The steady-state wrinkling solution was expected to be achieved using the pseudo-dynamic scheme with a larger artificially specified time step Δt s=1.0×10−5 s and a critical damping for shortening the computation time.

From the theoretical point of view, the pattern and number of wrinkles would be sensitive to the discretization of the membrane structure. To allow the model to reveal the fine wrinkle details, the maximum distance between the adjacent particles should be less than one half of the wrinkle wavelength λ (i.e., half the horizontal distance between two consecutive crests or troughs), which can be estimated from the formula derived by Epstein (2003). After considering the parameters of the membrane structure involved in this test, half of the theoretical wrinkle wavelength is obtained as λ=6.3 mm. In other words, a suitable distribution of particles deserves serious consideration based on this characteristic value to meet the requirements for describing complete wrinkle waves. Six uniformly discrete numerical models were considered with 21×61, 31×91, 46×136, 56×161, 61×176, 66×191 particles, respectively. In Figs. 5a and 5b, the dependency of the convergence behaviors for the number of wrinkles and the reaction shear force R x in x-direction on discretization is shown (δ x =3 mm, δ y = 0.025 mm). A clear convergence to an asymptotic value with an increasing number of particles is observed. Here, the total number of wrinkles is taken as the most important parameter for evaluating the effect of numerical prediction on the final wrinkle patterns, since it can be readily compared to the experimental observations. For the smallest discretization of 21×61 particles, 15 wrinkles were observed. Refining the discretization increased the number of wrinkles. When the distributions of particles changed from 56×161 to 66×191 (element sizes from 3.4 mm to 2.8 mm), the number of wrinkles was kept constant and matched with the results of the experiment in (Wong and Pellegrino, 2006a). It suggests that in the VHPEM analysis the number of wrinkles also depends on the fineness of particle distribution and element subdivision and the solution become discretization-independent after a particular level of refinement. Thus, considering the computation effort, the numerical model with 56×161 particles is suitable for the following wrinkling analysis. The results and discussion presented from now on are all based on this model.

Fig. 5
figure 5

Convergence behavior for the reaction shear force Rx (a) and the number of wrinkles (b)

Full size image

The wrinkles can be clearly observed from a contour map of the out-of-plane deformation in which each wrinkle is considered to extend from one peak to another peak. In Fig. 6 the formation and evolution of wrinkles under incremental shear displacements can be observed from a series of contour maps. The membrane exhibits antisymmetric deformation about the longitudinal central axis after shear load is applied. The first map (Fig. 6a) shows the situation of the perturbed state before the occurrence of wrinkles, where a slight pattern of out-of-plane deformation predicting the beginning of wrinkling can be observed, but the absolute value still remains in the same order of magnitude as that of the membrane thickness. In this study, the wrinkles are not believed to have formed until the magnitude of the out-of-plane deformation reaches the order of one tenth of a millimeter, which should be large enough as compared with the initial imperfection and the membrane thickness. Before this condition, we only consider the small and instable out-of-plane deformation as the original perturbed deflection added to the structure at the beginning of the analysis. This situation held up to a shear displacement of δ x =0.115 mm, when the wrinkling zone appearing from the edges around the corners became clearly visible first and then the maximum amplitude of wrinkles reached one order larger than that of the membrane thickness. Although at this time there also has been some out-of-plane deformation in the central region of the membrane, they were so small that they should not be considered as real wrinkles. Then, the number and distribution of wrinkles would change significantly until the shear displacement of δ x =0.17 mm when the membrane was full of wrinkles and the comparatively stable configuration has formed. Then the number and distribution of the wrinkles as well as the size of the central wrinkled region was stable while the amplitude expanded with the increasing shear displacement. The final completely developed wrinkles are shown in the last contour map when δ x =3 mm. It is shown that the wrinkles in the center region of the membrane are parallel to each other and are approximately inclined at a same angle to the horizontal edges while two fan regions form around the pair of corners. Note that all these wrinkling results were obtained after the elimination of the initial perturbations. It is obvious that the out-of-plane deformation still can be retained even though the initial disturbing forces have been removed at the point when δ x =0.0375 mm. Fig. 7 shows different profiles along the longitudinal mid-section of the membrane (at y=64 mm) under the corresponding increasing displacements δ x in Fig. 6. The wave crests and troughs can be explicitly observed from the plots of the wrinkle profiles. It is also noteworthy that as the number of wrinkles increases, the largest wrinkles near both edges remain fixed while a set of wrinkles of uniform amplitude exist between them. These deformed configurations are similar to the experimental evidence as well as the numerical results reported by Wong and Pellegrino (2006b).

Fig. 6
figure 6

Contour maps of out-of-plane deformation w (mm) for the development of wrinkles under the desired shear displacements δ x (mm)

(a) δ x =0.085 and δ y =0.025, w (max./min.)=0.063/–0.085; (b) δ x =0.095 and δ y =0.025, w (max./min.)=0.078/–0.098; (c) δ x =0.115 and δ y =0.025, w (max./min.)=0.102/–0.113; (d) δ x =0.15 and δ y =0.025, w (max./min.)=0.374/−0.368; (e) δ x =0.17 and δ y =0.025, w (max./min.)=0.441/−0.436; (f) δ x =3.0 and δ y =0.025, w (max./min.)=1.190/−1.139

Full size image
Fig. 7
figure 7

Profiles along the longitudinal mid-section of the membrane (at y=64 mm) under the desired shear displacements δ x (mm)

(a) δ x =0.085; (b) δ x =0.095; (c) δ x =0.115; (d) δ x =0.15; (e) δ x =0.17; (f) δ x =3.0

Full size image

Fig. 8 shows the overall final wrinkle pattern of the membrane obtained from both the reported experiment photograph and theoretical solutions, and it is encouraging to compare the locations of crests and troughs predicted by this method with them. Note that the last out-of-plane deformation contour map depicted in Fig. 6 shows a close agreement between the experimental and the numerical results in terms of the number of wrinkles and their orientations. Additionally, the general wrinkle shapes and distributions predicted by VHPEM are essentially consistent with those observed in the photograph. It can also be seen that the orientations of the wrinkles (1)–(4), inclined at 62°, 55°, 51°, and 46°, respectively, are close to those of the corresponding tension ray lines (Mansfield, 1969) that are at 5° intervals. A little difference between the results from this contribution and the tension field theory is the wrinkle orientation in the center region of the membrane. According to the analytical solutions, these wrinkles should be inclined at 45° to the upper/lower edges, but in the present study the angle is 46°. The major reason for this difference is that the length of the membrane is not infinite as that in the analytical model.

Fig. 8
figure 8

Comparison of wrinkle patterns

(a) Experimental photograph from Wong and Pellegrino (2006); (b) VHPEM solutions

Full size image

To test the accuracy of the VHPEM simulation, the detailed wrinkling information obtained by this method for any given shear, will be compared with the reference results. Fig. 9 compares the variation of the wrinkle half-wavelength and wrinkle amplitude with the shear angle applied in a rectangular membrane. Each figure shows both an analytical prediction curve according to (Wong and Pellegrino, 2002) and a set of experimental results obtained from a Kapton membrane mounted in a steel shear frame in (Jenkins et al., 1998), plotted together with a set of VHPEM simulation results. According to the out-of-plane deformation along the longitudinal mid-section of the membrane in Fig. 7, the wrinkle wavelength and amplitude can be directly determined as follows after disregarding the wrinkles near the edge. The amplitude of the wrinkle is the distance from the crest or trough to the undeformed membrane plane. The wrinkle wavelength is obtained from the ratio of the horizontal distance between the first and last wrinkle to the number of wrinkles. It can be observed from Fig. 9a that the half-wavelength λ obtained from the present simulation agrees well with the analytical and experimental results with the relative errors in the range of 5% throughout the analysis process. Increasing the shear displacement can visibly reduce the wavelength, and the same results can also be found in Figs. 6 and 7. Obtaining the results in Fig. 9b requires calculating the average value of each plot in Fig. 7. The wrinkle amplitude increases with the increased shear displacement. In Fig. 9b the amplitudes predicted in this simulation follow both the analytical and experimental results pretty closely for relatively small shear angles (γ≤0.015), probably due to the fact that the Kapton membrane remains linear elastic within this range. When the value of γ continues to increase, plastic deformation may occur with the maximum difference in predictions being up to about 0.025 mm, but they still follow similar trends.

Fig. 9
figure 9

Comparisons of wrinkle half-wavelength (a) and wrinkle amplitude (b)

Full size image

Note that in the experiment, the precision of measurement may be significantly influenced by the surrounding environment, including damping and gravity. Besides, there was some clearance between different equipment parts, and thus it was not easy to precisely control the prestress in the membrane. The actual initial imperfections induced by the local slightly curved configurations and a stochastic variation of material property before the application of the shear loadings were replaced by the arbitrary perturbations in the present numerical model, since they could not be adequately measured in the reported experiment. Moreover, in our wrinkling simulation, the membrane material was assumed as isotropic and elastic continuum. In fact, the membrane deformation was not totally linear elastic in the experiment, especially in the high tension regions. As a result of these factors, a certain discrepancy between the results of the present simulation and the experiment is reasonable and acceptable.

For a deeper investigation of the wrinkled membrane, Fig. 10 shows the distribution of stresses when the shear displacement δ x finally reaches 3 mm. One can observe that the stresses of two triangular regions near the vertical boundaries are very small, whereas the top right and bottom left corners play the role of the stress source where the stress concentrates with a upper limit of two times larger than the average value, which should be attributed to the specific mechanical behavior of the thin membrane under shear (Mansfield, 1969). Besides, it also shows that the major principal stress in the central region of the membrane is uniform and relatively small where the wrinkle deformation remains in the elastic stage, but in the stress concentration regions the unaccounted plastic deformation may appear and in turn affect the wrinkle deformation.

Fig. 10
figure 10

Distribution of major principal stress S 1 (a) and minor principal stress S 2 (b) (N/mm 2) (δ x =3 mm)

Full size image

Fig. 11 shows plots of the distribution of the major and minor principal stresses along the longitudinal mid-section of the membrane (at y=64 mm), corresponding to δ x =1.0 mm, 2.0 mm and 3.0 mm, respectively. It can be observed that the variation trend for every major principal stress curve is similar, namely keeping an approximately uniform value in most parts of the membrane and declining rapidly to a very small amount near the free edges due to the boundary conditions. On the other side, the minor principal stress remains small and varies slightly across the section. As mentioned above, if the particle distribution and the element subdivision are fine enough to represent the finest wrinkle pattern, the number of wrinkles should finally achieve a stable value. Thereafter, the compressive stresses should also converge to a small amount below but near zero when the particle distribution is sufficiently refined.

Fig. 11
figure 11

Principal stresses variation along the longitudinal mid-section of the membrane (at y =64 mm)

Full size image

5.2 Rectangular thin-film membrane loaded in uniaxial tension

Different from most of the previous studies where wrinkles were generally induced by direct actions, such as edge shearing, in-plane torsion, bending and so forth, in this example we use a non-uniform tension case to demonstrate the capability of the proposed method. As depicted in Fig. 12, after Cerda et al. (2002), the problem consisted of a rectangular membrane loaded in a longitudinal uniaxial tension that was laterally clamped at two opposite ends. The left edge of the membrane was fully constrained in all DOFs while at the right edge only the translation in the x-direction is allowed. The top and bottom edges were both free edges. This set of boundary conditions remained enforced in all analysis steps. To enable a valid comparison of results, all geometrical, material, and loading parameters comply with those specified by Zheng (2009). Before stretching, the original dimensions of the membrane were described as follows: length L 0=254 mm, width W 0=101.6 mm and thickness t 0=0.1 mm. A silicon rubber membrane was selected for the present example which was approximately assumed to be a linear elastic material with Young’s modulus E=1 N/mm2, Poisson’s ratio ν=0.495, and mass density ρ=1.14×103 kg/m3. A refined discrete model with 43×106 particles was used to simulate the behavior of the whole membrane structure, in order to capture the fine wrinkle details in the membrane. We should indicate that after a series of trial calculations similar to those presented in the first example this level of discretization has been proved to be dense enough for the following wrinkling analysis.

Fig. 12
figure 12

Problem setting of an end-clamped rectangular thin membrane loaded in uniaxial tension

Full size image

To perform the wrinkling analysis for this end-clamped rectangular membrane, the same strategies as described in the first example were also adopted, i.e., disturbing forces, displacement control, and a pseudo-dynamic scheme with an artificially specified larger time step (Δt s=1.0×10−4 s for this case) and critical damping. Indeed, the analysis procedure is essentially identical for a class of wrinkling simulations like these cases. Thus, the implementation of the stretch-induced wrinkling analysis was also subdivided into three stages. In the first stage, the right edge had imposed on a rightward displacement of 1 mm (i.e., ε≈0.4%) as specified in Fig. 12. Then, a set of disturbing forces were applied along the tension direction and distributed symmetrically about the center. The magnitude of each disturbing force was set at 1×10−6 N, and the resulting imperfection would be smaller than the membrane thickness by two orders of magnitude. In the third stage, the right edge was increasingly stretched in the x-direction to produce an expected tension strain, (e.g., 25.4 mm for 10% strain), whereas all the other DOFs were constrained. During this tension process, the initial disturbing forces were completely removed when the tension displacement reached 2.5 mm (i.e., ε≈1%).

We now briefly discuss the overall wrinkling behavior, primarily including the formation of the wrinkle pattern and its growth under increasing tension strain. By plotting a series of contour maps of out-of-plane deformation at the desired strain levels, Fig. 13 demonstrates the evolution of stretch-induced wrinkles for this rectangular membrane as the tension strain increases. It can be seen that the wrinkles formed parallel to the loading direction in a symmetric manner with the largest one at the center (Fig. 13b –13d), and this pattern and the number of wrinkles remained stable immediately after the wrinkles were formed (Fig. 13b) although the amplitude changes with the increasing tension strain. In this case, since the wrinkle amplitude is found to be fairly small, the formation of wrinkles is defined to be the moment at which the maximum out-of-plane deformation reaches the magnitude just one order smaller than the membrane thickness or the maximum wrinkle amplitude during the entire loading process. Before this moment, the amplitude of the out-of-plane deformation was negligibly small, and no significant instability could be observed (Fig. 13a). However, we should indicate these out-of-plane perturbed deformation generated by the removed disturbing forces are crucial for the occurrence of wrinkles when the increasing tension load arrives at a certain level. For displaying the development of the wrinkles further, the profiles along the transverse mid-section of the membrane (at x=127 mm) are plotted in Fig. 14. It can be observed that the membrane remained flat near the top and bottom edges while the wrinkle profiles were regulated by a wavelike mode, similar to the prediction in (Kim et al., 2012). Fig. 15 shows a perspective view of the final wrinkle profile for the stretched membrane. The out-of-plane deformation has been amplified ten times for visualization purpose. The deformed shape is essentially identical to the experimental and numerical results presented by Zheng (2009). Similar symmetric wrinkle patterns and distributions were also observed in an experiment with the polyethylene sheet (Huang et al., 2012).

Fig. 13
figure 13

Contour maps of out-of-plane deformation for the evolution of wrinkles at desired strain levels

(a) ε=1.5%, w (max./min.)=0.00725/−0.0044; (b) ε=3.9%, w (max./min.)=0.0155/−0.0143; (c) ε=11.0%, w (max./min.) =0.3128/−0.2484; (d) ε=30.0%, w (max./min.)=0.0105/−0.0.0102

Full size image
Fig. 14
figure 14

Profiles along the transverse mid-section of the membrane (at x=127 mm) at desired strain levels

Full size image
Fig. 15
figure 15

Overall perspective view of the final wrinkle profile for the stretched membrane

Full size image

Next, some comparisons, concerning the detailed characteristics of the wrinkles, with other experimental and numerical results available in the literature are provided to verify the accuracy of the present simulation. Fig. 16 shows the variation of wrinkle amplitudes at the center of the membrane with the applied tension strain, where the amplitude is taken as the value of the central peak. At the beginning, as the tension strain increases from zero to 3.9%, the amplitude grows quite slowly. This may be attributed to the magnitude of the compressive stress that is not sufficiently high or its area distribution that is sufficiently large at these strain levels. At the end of this stage, the wrinkles are considered to have been generated in the central region of the membrane in terms of the criterion on wrinkle formation stated above. Then the wrinkle amplitude increases rapidly until the tension strain reaches approximately 11%. Beyond this point, as the tension strain increases further, the wrinkle amplitude decreases at a slightly slower rate and eventually at ε=31% where the wrinkles almost disappear again. In other words, the wrinkle amplitude does not always monotonically increase with increasing strain but reaches the maximum value at an intermediate strain level. The dependence of the wrinkle amplitude on the tension strain has a similar trend to that of the maximum compressive stress in the unwrinkled membrane as shown in (Nayyar, 2010). It suggests that there may be some inherent correlations between them. In fact, in terms of the bifurcation bulking theory, the wrinkles are related with a certain stress level (Wong and Pellegrino, 2006c), and thus they should form only over a range of strain in which the compressive stress has the potential to cause wrinkles. When the strain is lower or higher than the critical values, the wrinkles diminish in amplitude and the membrane gets flattened again, as shown in Fig. 16. Then, the experimental measurements reported by Zheng (2009) for the changes of the wrinkle amplitude with the tension strain are also plotted in the same figure. It can be found that the amplitude predicted in the present simulation follows the same trend for the experimental results when the tension strain is between 11% and 18%, but the numerical one is smaller than the experimental one by about 10%. As for smaller tension strain the relatively large wrinkle amplitude obtained from the experiment may be caused by the initial undulant configuration in sample preparation and mounting stage that forced it to wrinkle immediately after the tension load was applied. Therefore, these experimental values should not be considered as real magnitudes of wrinkle amplitudes. Besides, the experimental specimen requires a much larger tension load to remove the wrinkles, probably due to the inelastic material behavior and inherent uneven thickness of the membrane. Generally, the trend for the variation of the wrinkle amplitude is still similar for the numerical and experimental results as the membrane is gradually stretched. Similar evolution of the wrinkle amplitude and possible reasons for the above discrepancy are also discussed by Huang (2012). Note that the aforementioned analysis is just for a particular geometrical and material property, and if any of these conditions get changed the range of strain in which the wrinkles can form would be different. However, given that the main focus of this study is to verify the efficacy of the proposed approach for wrinkling simulation, the results obtained based on the model in this example would be adequate.

Fig. 16
figure 16

Variation of wrinkle amplitudes at the center of the membrane with the applied tension strain

Full size image

As far as the wavelength is concerned, Fig. 17 shows a plot of the dimensionless wrinkle wavelength λ/(Lt)1/2 versus ε 1/4 obtained from this simulation, together with the prediction by a scaling analysis (Kim et al., 2012) for comparison, where the wavelength 2λ is a average value of the horizontal distance between two adjacent crests or troughs. Obviously, the results of the present simulation follow the analytical predictions based on scaling analysis, and both of them show the same linear trend with a slope of 2.05. This trend is also fairly well consistent with Cerda’s experimental measurements (Cerda et al., 2002).

Fig. 17
figure 17

Plot of dimensionless wrinkle wavelength λ /( Lt ) 1/2 versus ε 1/4

Full size image

In the following section, the changed stress field due to wrinkling will be illustrated. Fig. 18 shows the distribution of the major and minor principal stresses, S 1 and S 2, in the wrinkled membrane at 11% tension strain when the wrinkle amplitude is maximal. The variations of S 1 and S 2 along the mid-sections of the membrane (at x=127 mm or y=50.8 mm) at different strain levels are also obtained as shown in Fig. 19. It can be seen that the distribution patterns of the principal stresses are similar at different strains, with the only difference being in the magnitude. The variation range of the major principal stress is relatively small and remains positive across the sections at all strain levels. On the other hand, the minor principal stress increases rapidly from a near-zero value to a positive amount on the two clamped edges. The growth rate is dependent on the strain level. Moreover, in the wrinkled membrane, the distribution of the minor principal stress along the longitudinal mid-section is approximately uniform in the central region of the membrane and there are no obvious peaks. In addition, along the transverse mid-section, the minor principal stress remains a very small amount, but slight fluctuations in the central region can be observed through a closer look. On the basis of the aforementioned observations, one can conclude that in the wrinkled membrane, the transverse compressive stress is very close to zero, and thus its actual in-plane stress state is more analogous to a uniaxial stress state than it does in the completely flat membrane, as is described in the tension field theory.

Fig. 18
figure 18

Distribution of major principal stress S 1 (a) and minor principal stress S 2 (b) in the wrinkled membrane at 11% tension strain

Full size image
Fig. 19
figure 19

Distribution of principal stresses along the longitudinal mid-section (a) and the transverse mid-section (b)

Full size image

6 Conclusions

This study presents a general VHPEM framework for investigating the wrinkling phenomena of thin membranes. The basic ideas and formulations of VHPEM for modeling the configuration and motion of a membrane are first presented briefly. The internal forces of the shell-like membranes are derived in detail, especially those relating to bending stiffness, which are essential to ensure the completeness and continuity of the wrinkle waves and to obtain a further detailed knowledge of the wrinkled shape. Numerical examples of two benchmark wrinkling problems are solved using a pseudo-dynamic scheme to obtain the steady-state solutions, wherein the wrinkling behavior is initiated by applying a direct perturbed force approach.

Although the VHPEM contains some finite element basis, there are still some differences between the “element” proposed by this paper and the standard finite “element”. The major one is that VHPEM does not employ time-consuming matrix operations for extracting the exact deformation, or assume any superposition on convected coordinates to account for finite rotation. The internal forces are computed purely with physical modeling and implemented by a vector operation. Thus, the computational effort can be efficiently reduced.

In addition, the pseudo-dynamic scheme adopted in the present method allows it to avoid assembling a stiffness matrix or solving the motion equations iteratively even when dealing with nonlinear motion. In comparison with the nonlinear static scheme for wrinkling analysis employed in traditional methods, VHPEM no longer needs to address the numerical instability problems due to the low bending stiffness of the membrane. Numerical modeling of the intrinsic membrane based on classical shell theory (i.e., adopting Kirchhoff-Love hypothesis) provides freedom from shear locking and hour-glassing appearing in thin shells. Except for the modeling strategy for wrinkling initiation, no complicated treatments or modifications are necessary to be introduced into the present study during the entire analysis process. According to the comparisons with other approaches and experimental observations reported in literatures, the numerical results have demonstrated the ability of the proposed method to accurately predict the overall wrinkle patterns as well as quantitative solutions, such as amplitude, wavelength and so forth. Allowing for its generality and flexibility, it is believed that this method can be readily expanded to complex membrane problems with a nonlinear orthotropic material, which will be performed in the future work.