1 Introduction

External excitations, such as the oil-film force of journal bearings or the fluid exciting force inside the seal structure between a stator and rotor, are important factors that may induce instability in modern rotating machinery. The effect of the fluid exciting force in a multi-stage centrifugal pump, shrouded turbine, steam turbine, and other rotating machinery that includes a multi-level sealing structure can be very significant (Yuan et al., 2007; Megerle et al., 2013). Research on the mechanisms of fluid-solid interaction and the influence of nonlinear seal force on rotor-seal systems has become a priority for the safe operation of rotating machinery.

Many experimental studies have been carried out on the dynamic characteristics of various seals (Kaneko et al., 2003; Smalley et al., 2006; Childs et al., 2007). Muszynska (1988) and Muszynska and Bently (1990) proposed a nonlinear seal fluid dynamic force model that considered the circulating velocity as the key factor affecting the stability of the rotor system. Fei et al. (2013) developed a procedure, based on the finite element method (FEM), which can calculate the dynamics of dual rotor systems and obtain the coupling motion equations of the subsystems. Li et al. (2011) applied the Hamilton principle and the FEM to establish a new dynamic model of a rotor system. The model was used to analyze the dynamic behavior of a rotor system based on the Timoshenko model, with the coupled effects of the nonlinear oil film force, the nonlinear seal force, and the mass eccentricity of the disc. Ding et al. (2002) investigated the Hopf bifurcation behavior of a symmetric rotor-seal system using Muszynska’s nonlinear seal fluid dynamic force model. They discovered that for a perfectly balanced system, the instability from certain critical equilibrium positions proved to be the result of Hopf bifurcation and only the supercritical type was found for a specific rotor system using Poore’s algebraic criteria. Li et al. (2007) analyzed the influence of a labyrinth seal on the nonlinear characteristics of a rotor-labyrinth seal system with a sliding bearing, and judged the system’s stability using the Floquet theory and the bifurcation theorem. Wang and Wang (2010) researched the nonlinear coupling vibration and bifurcation of a high-speed centrifugal compressor with a labyrinth seal and two air-film journal bearings under different conditions of pressure drop and seal length. The Muszynska nonlinear seal model was also used successfully by Hua et al. (2005) to investigate the Hopf bifurcation and stability of a rotor-seal system using a high-precision direct integration method. Wang et al. (2009a; 2009b) established a nonlinear mathematical model for orbital motion of a rotor under the influence of leakage flow through a labyrinth seal. They found that the destabilization speed of the rotor was reduced due to the aerodynamic force induced by the leakage flow through the interlocking seal.

Although previous studies paid much attention to the dynamic behavior of rotor-seal or rotor-bearing-seal systems, only the Jeffcott rotor system was considered. No model was developed for a nonlinear double disc rotor-seal system with a coupled effect between the two discs based on the Lagrange equation and FEM. There is an urgent need to research the mechanisms of interaction of different levels of the impeller seal force in multi-stage sealing systems. In this paper, a nonlinear double disc rotor-seal system model is established, based on the Lagrange equation and FEM. Equations of motion, considering the Muszynska nonlinear seal force, are solved by the fourth-order Runge-Kutta method. The nonlinear characteristics of the double disc rotor-seal system are presented in the form of bifurcation diagrams, time-history diagrams, axis orbit diagrams, Poincaré maps, and amplitude spectrums. The effects of the distance between the two discs, the mass of the discs, seal clearance, seal length and seal drop pressure on the dynamic behavior of the system are also studied, and linear and nonlinear seal models are compared.

2 Model of a double disc rotor-seal system

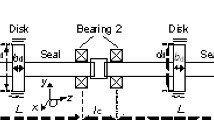
A typical double disc rotor-seal system, consisting of a rotating shaft, wheel, nonlinear seal force and clamped support at each end of the shaft, was modeled (Fig. 1), where L 1 is the length between the left edge of the shaft and the left disc, L 2 is the length between the left and right discs, L 3 is the length between the right disc and the right edge of the shaft, d d is the diameter of the disc, m d1 is the mass of the left disc, and m d2 the mass of the right disc.

Fig. 1
figure 1

Double disc rotor-seal system

Full size image

A finite element model of the system was established (Fig. 2). The system is divided into a total of four nodes and three shaft elements. Each node has four degrees of freedom, including two translational and two rotational motions. Nodes 1 and 4 are the supporting points, which are allowed only rotational motions, and nodes 2 and 3 bear both the gravity force of the disc and the nonlinear seal force, where F sx is the seal force in the x-direction, and F sy the seal force in the y-direction. The subscripts 1 and 2 denote the left and right discs, respectively, where the subscript ‘s’ denotes the seal.

Fig. 2
figure 2

Finite element model of a double disc rotor-seal system

Full size image

3 Component equations and system motion equations

Considering the double disc rotor-seal system is a multi-degree of freedom and non-conservative system, the Lagrange equation was applied to establish the motion equation of the double disc rotor-seal system. The non-conservative system Lagrange equation usually can be described in the following form:

$${{\rm{d}} \over {{\rm{d}}t}}\left({{{\partial T} \over {\partial {{\dot u}_j}}}} \right) - {{\partial (T - V)} \over {\partial {u_j}}} = {Q_j},$$
(1)

where T is the kinetic, V is the strain energy, u j are independent generalized coordinates, and Q j are generalized forces.

3.1 Rotating coordinate

The kinetic energy and strain energy of the components, shaft units and disc, can be derived using the projected angle method (Li et al., 2011). Fig. 3 shows a schematic map of a rotating coordinate and A-xyz is the fixed coordinate. Because of the unbalanced force of the disc, at a certain rotation speed Ω, deformation of the shaft would occur, causing the center line of the disc to be no longer collinear with the undeformed rotor center line. A rotating coordinate system o′-ξηζ, is attached to the disc and rotates synchronously with the rotor. θ is the angle between the ζ and z axes, and θ x , θ y are the angular displacements, defined as the angles between the z axis and the projection of the ζ axis onto the x-z and y-z planes, respectively. L is the length of the shaft, L d is the place of disc center in the z direction, and r is the distance of disc center in x-y plane.

Fig. 3
figure 3

Schematic map of rotating coordinates

Full size image

The absolute angular speed ω in the o′-ξηζ coordinate can be transformed to be rotation speed, expressed by the A-xyz coordinate (Zhong, 1987). The relationship between the fixed A-xyz coordinate and the o′-ξηζ coordinate attached to the disc can be described as follows:

$$\left\{\matrix{{\omega_\xi} \hfill \cr {\omega_\eta} \hfill \cr {\omega_\zeta} \hfill \cr} \right\} = \left\{\matrix{{{\dot \theta}_\xi}\cos \phi + {{\dot \theta}_y}\cos {\theta_\xi}\sin \phi \hfill \cr - {{\dot \theta}_\xi}\sin \phi + {{\dot \theta}_y}\cos {\theta_\xi}\cos \phi \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot \phi - {{\dot \theta}_y}\sin {\theta_\xi} \hfill \cr} \right\},$$
(2)

where θ ξ , φ are relative rotation angles between the o′-ξηζ coordinate and the A-xyz coordinate when the ξ-axis and ζ-axis are respectively, fixed in turn. ω ξ , ω η , and ω ζ are the components of ω in o′-ξηζ coordinate.

Considering θ ξ ≈θ x and Eq. (2) can be written as

$$\left\{\matrix{{\omega_\xi} \hfill \cr {\omega_\eta} \hfill \cr {\omega_\zeta} \hfill \cr} \right\} = \left\{\matrix{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \phi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos {\theta_x}\sin \phi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \cr - \sin \phi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos {\theta_x}\cos \phi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin {\theta_x}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;{\kern 1pt} {\kern 1pt} 1 \hfill \cr} \right\}\left\{\matrix{{{\dot \theta}_x} \hfill \cr {{\dot \theta}_y} \hfill \cr \Omega \hfill \cr} \right\}.$$
(3)

3.2 Rigid disc

For a rigid disc, the strain energy would be ignored and its degrees of freedom can be expressed by two translational displacements x, y and two rotational displacements θ x , θ y . Let

$${u_{dx}} = {[x,{\theta_y}]^{\rm{T}}},\;\;{u_{dy}} = {[y, - {\theta_x}]^{\rm{T}}},$$

then the kinetic energy of the disc for lateral motion is given by (Zhong, 1987)

$$T_d = \frac{1} {2}\dot u_{dx}^T M_d \dot u_{dx} + \frac{1} {2}\dot u_{dy}^T M_d \dot u_{dy} + \Omega \dot u_{dx}^T J\dot u_{dy} + \frac{1} {2}J_p \Omega ^2 ,$$
(4)

where

$$M_d = \left[ {\begin{array}{*{20}c} {m_d } & 0 \\ 0 & {J_d } \\ \end{array} } \right],J = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & {J_p } \\ \end{array} } \right],$$

where J d is the diametric moment, and J p is the polar moment of inertia of the disc.

Substituting Eq. (4) into Eq. (1), the motion equations of a rigid disc can be obtained as

$$\left\{\matrix{{M_{\rm{d}}}{{\dot u}_{{\rm{d}}x}} + \Omega J{{\dot u}_{{\rm{d}}y}} = {q_{{\rm{d}}x}}, \hfill \cr {M_{\rm{d}}}{{\dot u}_{{\rm{d}}y}} - \Omega J{{\dot u}_{{\rm{d}}x}} = {q_{{\rm{d}}y}}, \hfill \cr} \right.$$
(5)

where the subscript ‘d’ denotes the disc and q dx , q dy are generalized forces corresponding with u dx , u dy , respectively.

3.3 Elastic shaft element

Fig. 4 shows an elastic shaft element, including two nodes A and B, i.e., with eight degrees of freedom. Define the generalized coordinates

$${u_{{\rm{e}}x}} = {[{x_A},{\theta_{yA}},{x_B},{\theta_{yB}}]^{\rm{T}}},$$

and

$${u_{{\rm{e}}y}} = {[{y_A}, - {\theta_{xA}},{y_B}, - {\theta_{xB}}]^{\rm{T}}}$$
Fig. 4
figure 4

Elastic shaft element

Full size image

The generalized coordinates of a typical point internal to the element can be described by the endpoint of the shaft (Nelson and McVaugh, 1976; Zhang, 1990):

$$x = N{u_{{\rm{e}}x}},\;\;y = N{u_{{\rm{e}}y}},$$
(6)
$${\theta_y} = N'{u_{{\rm{e}}x}},\;\; - {\theta_x} = N'{u_{{\rm{e}}y}},$$
(7)

where

$$\begin{array}{*{20}c} {N = [N_1 N_2 N_3 N_4 ], N' = [N'_1 N'_2 N'_3 N'_4 ],} \\ {N_1 = 1 - 3(s/l)^2 + 2(s/l)^3 , N_2 = 1[(s/l) - 2(s/l)^2 + (s/l)^3 ],} \\ {N_3 = 3(s/l)^2 - 2(s/l)^3 ], and N_4 = l[ - (s/l)^2 + (s/l)^3 ].} \\ \end{array}$$

Similarly, the kinetic energy and strain energy also can be described as a function of the displacements and velocity of the elastic shaft element nodes and obtained by computing an integral over the length of the element (Zhong, 1987). The kinetic energy and strain energy can be calculated as follows:

$$\eqalign{ {T_{\rm{e}}} = {1 \over 2}\dot u_{{\rm{e}}x}^{\rm{T}}({M_{{\rm{eT}}}} + {M_{{\rm{eR}}}}){{\dot u}_{{\rm{e}}x}} + {1 \over 2}\dot u_{{\rm{e}}y}^{\rm{T}}({M_{{\rm{eT}}}} + {M_{{\rm{eR}}}}){{\dot u}_{{\rm{e}}y}} \cr {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \Omega \dot u_{{\rm{e}}x}^{\rm{T}}{J_{\rm{e}}}{{\dot u}_{{\rm{e}}y}} + {1 \over 2}{j_{{\rm{pe}}}} \cdot l \cdot \Omega {\rm{,}} \cr}$$
(8)
$${V_{\rm{e}}} = {1 \over 2}u_{{\rm{e}}x}^{\rm{T}}{K_{\rm{e}}}{u_{{\rm{e}}x}} + {1 \over 2}u_{{\rm{e}}y}^{\rm{T}}{K_{\rm{e}}}{u_{{\rm{e}}y}},$$
(9)

where

$${M_{{\rm{eT}}}} = \int_0^l {\mu {N^{\rm{T}}}N} {\rm{d}}z,\;\;\;{J_{\rm{e}}} = \int_0^l {{j_{\rm{p}}}{{N'}^{\rm{T}}}N'} {\rm{d}}z,$$
$$_{{\rm{eR}}} = \int_0^l {{j_{\rm{d}}}{{N'}^{\rm{T}}}N'} {\rm{d}}z,\;\;\;{K_{\bf{e}}} = \int_0^l {EI{{N''}^{\rm{T}}}N''} {\rm{d}}z,$$

where μ is the mass of shaft element unit length.

Substituting Eqs. (8) and (9) into Eq. (1), the motion equations of the elastic shaft element can be obtained as

$$\left\{\matrix{{M_{\rm{e}}}{{\ddot u}_{{\rm{e}}x}} + \Omega {J_{\rm{e}}}{{\dot u}_{{\rm{e}}y}} + {K_{\rm{e}}}{u_{{\rm{e}}x}} = {q_{{\rm{e}}x}}, \hfill \cr {M_{\rm{e}}}{{\ddot u}_{{\rm{e}}y}} - \Omega {J_{\rm{e}}}{{\dot u}_{{\rm{e}}x}} + {K_{\rm{e}}}{u_{{\rm{e}}y}} = {q_{{\rm{e}}y}}, \hfill \cr} \right.$$
(10)

where subscript ‘e’ denotes the elastic shaft element and q ex , q ey are generalized forces corresponding with u ex , u ey , respectively, which are always ignored.

3.4 Nonlinear seal force model

Muszynska’s nonlinear seal fluid dynamic force model was adopted to describe the nonlinear seal force acting on the discs. Muszynska’s model has been widely used to describe the nonlinear characteristic of seal force and can be expressed as follows (Muszynska, 1988; Hua et al., 2005):

$$\left\{ {\begin{array}{*{20}c} {F_{sx} } \\ {F_{sy} } \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}c} {K_s - m_s \gamma ^2 \Omega ^2 } & {\gamma \Omega C_s } \\ { - \gamma \Omega C_s } & {K_s - m_s \gamma ^2 \Omega ^2 } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {C_s } & {2m_s \gamma \Omega } \\ { - 2m_s \gamma \Omega } & {C_s } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot x} \\ {\dot y} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {m_s } & 0 \\ 0 & {m_s } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot x} \\ {\ddot y} \\ \end{array} } \right\},$$
(11)

where \({K_{\rm{s}}} = {K_0}{(1 - {\varepsilon^2})^{- {n_1}}}\), \({C_{\rm{s}}} = {C_0}{(1 - {\varepsilon^2})^{- {n_1}}}\), \(\gamma = {\gamma_0}{(1 - \varepsilon)^{{n_2}}}\) n 1=0.5–3, n 2=0–1, γ 0<0.5, ε=(x 2+y 2)1/2/c, c is the radial clearance of the seal, and K 0, C 0, and m s are expressed through the short bearing model of Childs (1983).

3.5 System motion equations

For a double disc rotor-seal system, the motion equations of the system can be derived by assembling the motion equations of all elastic shaft elements and discs as follows:

$$\left\{\matrix{{M_{{\rm{de}}}}{{\ddot u}_x} + \Omega {J_{{\rm{de}}}}{{\dot u}_y} + {K_{{\rm{de}}}}{u_x} = {Q_{{\rm{d}}x}}, \hfill \cr {M_{{\rm{de}}}}{{\ddot u}_y} - \Omega {J_{{\rm{de}}}}{{\dot u}_x} + {K_{{\rm{de}}}}{u_y} = {Q_{{\rm{d}}y}}, \hfill \cr} \right.$$
(12)

where u x =[x 1, θ y1, x 2, θ y2, x 3, θ y3, x 4, θ y4]T, u y =[y 1, −θ x1, y 2, −θ x2, y 3, −θ x3, y 4, −θ x4]T, M de, J de, and K de are the mass matrix, gyroscopic matrix, and stiff matrix, respectively, including all elastic shaft elements and discs. Q dx and Q dy are generalized force vectors of discs.

Considering the constrained translational displacements in the x-axis and y-axis of nodes 1 and 4 respectively, the effect of gravity force and seal exciting force, but ignoring tiny rotational displacements, the motion equations of a double disc rotor-seal system can be expressed as follows:

$$M\ddot u + C\dot u + Ku = Q + G,$$
(13)

where

$$\matrix{{Q = {{[{Q_{d1x}} + {F_{sx}},{Q_{d2x}} + {F_{sx}},{Q_{d1y}} + {F_{sy}},{Q_{d2y}} + {F_{sy}}]}^T},} \cr {{Q_{d1x}} = {m_{d1}}{e_{d1}}{\Omega^2}\cos (\Omega t),{Q_{d1y}} = {m_{d1}}{e_{d1}}{\Omega^2}\sin (\Omega t),} \cr {{Q_{d2x}} = {m_{d2}}{e_{d2}}{\Omega^2}\cos (\Omega t),{Q_{d2y}} = {m_{d2}}{e_{d2}}{\Omega^2}\sin (\Omega t),} \cr {u = {{[{x_2},{x_3},{y_2},{y_3}]}^T},G = {{[0,0, - {m_d}_1g, - {m_{d2}}g]}^T}.} \cr}$$

Introducing the following non-dimensional transform:

$$\matrix{{X = x/{c_s},Y = y/{c_s},t' = \Omega t,} \cr {\dot x = \Omega {c_{\rm{s}}}\dot X,\dot y = \Omega {c_{\rm{s}}}\dot Y,} \cr {\ddot x = {\Omega^2}{c_{\rm{s}}}\ddot X,\ddot y = {\Omega^2}{c_{\rm{s}}}\ddot Y,} \cr}$$

where c s is the radial clearance of the seal.

Substituting the expressions into Eqs. (11) and (13), the dimensionless system motion equation can be obtained as

$$\ddot U + {C \over {\Omega M}}\dot U + {K \over {{\Omega^2}M}}U = {{Q + G} \over {{c_{\rm{s}}}{\Omega^2}M}},$$
(14)

where

$$Q = \left[ {m_{d1} e_{d1} \Omega ^2 \cos t' + F'_{sx} ,m_{d2} e_{d2} \Omega ^2 \cos t' + F'_{sx} ,m_{d1} e_{d1} \Omega ^2 \times \sin t'_{sy} ,m_{d2} e_{d2} \Omega ^2 \sin t' + F'_{sy} } \right]^T ,$$
$$\left\{ {\begin{array}{*{20}c} {F'_{sx} } \\ {F'_{sy} } \\ \end{array} } \right\} = - c_s \left[ {\begin{array}{*{20}c} {K_s - m_s \gamma ^2 \Omega ^2 } & {\gamma \Omega C_s } \\ { - \gamma \Omega C_s } & {K_s - m_s \gamma ^2 \Omega ^2 } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} X \\ Y \\ \end{array} } \right\} - c_s \Omega \left[ {\begin{array}{*{20}c} {C_s } & {2m_s \gamma \Omega } \\ { - 2m_s \gamma \Omega } & {C_s } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot X} \\ {\dot Y} \\ \end{array} } \right\} - c_s \Omega ^2 \left[ {\begin{array}{*{20}c} {m_s } & 0 \\ 0 & {m_s } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot X} \\ {\ddot Y} \\ \end{array} } \right\},$$
$$U = \left[ {X_2 ,X_3 ,Y_2 ,Y_3 } \right]^T .$$

Eq. (14) is a second-order differential equation including coefficient matrices, which describes the nonlinear motion of the double disc rotor-seal system. The dimensionless equation of motion is difficult to solve by conventional perturbation methods (Li, 2011). Therefore, the fourth-order Runge-Kutta method was applied to obtain the numerical response solutions of the system.

4 Numerical results and discussion

Considering the seal parameters K s, C s, and γ are nonlinear functions of displacements of the two discs, the motion equation, Eq. (14), shows strongly nonlinear characteristics. The bifurcation diagrams show the variation course of the motion of the system. Time-history diagrams, axis orbit diagrams, Poincaré maps and amplitude spectrums are also presented to analyze the nonlinear vibration of the double disc rotor-seal system. The main parameters and values of the seals, and of the discs and shaft used in the numerical calculation, are shown in Tables 1, 2, and 3, respectively. The experimental coefficients of the seal are listed in Table 4.

Table 1 Main parameters and values of seals
Full size table
Table 2 Main parameters and values of the discs
Full size table
Table 3 Main parameters and values of the shaft
Full size table
Table 4 Experimental coefficients of seal
Full size table

4.1 Influence of the rotor speed Ω

Rotor speed is an important parameter of rotating machinery which significantly influences the vibration characteristics and dynamic response of rotor-seal systems. To investigate bifurcation, we chose the rotor speed (changing from 500 r/min to 9200 r/min) as abscissa and the dimensionless displacements X 2 and X 3 as ordinates. The dimensionless time ranged from 0 to 600π and every period was divided into an average of 256 parts considering the fast Fourier transform (FFT). To ensure accuracy of the results, the preceding half iterative results were discarded. The results showed that the double disc rotor-seal system would exhibit periodic, double-periodic, multi-periodic, and quasi-periodic motion as the rotor speed increases (Fig. 5).

Fig. 5
figure 5

Bifurcation diagrams of left (a) and right (b) discs

Full size image

The bifurcation diagrams show that the vibration amplitude at a rotor speed of about 1050 r/min is higher because of the occurrence of primary resonance. When the rotor speed is less than 2180 r/min, there is just one solution, which indicates that the system is in period-one motion, that is, the motion of the two discs occurs with the same frequency as the rotor speed. However, once the rotor speed runs over 2180 r/min, the system loses stability and turns into period-two motion. In the range [2320, 2610] r/min, quasi-periodic, period-four, and period-eight motion appear. With increasing rotor speed, the period-two motion appears again until the rotor speed reaches 3120 r/min. Quasi-periodic, multi-periodic (including period-six and period-three motion), and chaotic motion are found in the range [3120, 5290] r/min. Then, the motion of the two discs returns to period-one bifurcation and subsequently changes from period-one motion to quasi-periodic and chaotic motion as the rotor speed increases. Finally, chaotic motion is encountered when the rotor speed is greater than 8310 r/min. The motion status of the two discs is also represented by the time-history diagrams, the axis orbit diagrams, the Poincaré maps and amplitude spectrums (Figs. 6–9, p.45–46).

Fig. 6
figure 6

Numerical analysis of left (a) and right (b) discs at Ω =1200 r/min

Full size image
Fig. 7
figure 7

Numerical analysis of left (a) and right (b) discs at Ω =4420 r/min

Full size image
Fig. 8
figure 8

Numerical analysis of left (a) and right (b) discs at Ω =6150 r/min

Full size image
Fig. 9
figure 9

Numerical analysis of left (a) and right (b) discs at Ω =8650 r/min

Full size image

Fig. 6 illustrates the dynamic response of the double disc rotor-seal system at Ω=1200 r/min. The system has the same whirl frequency as the frequency of excitation force and has an isolated point in the Poincaré map corresponding to one part of the frequency of the amplitude spectrum, collectively demonstrating that the system exhibits stable synchronous vibration. The axis orbits of the two discs are clearly elliptical, whirling around the points (0.42, −0.77) and (0.19, −0.46), respectively. When the rotor speed increases to Ω=4420 r/min (Fig. 7), the time-history shows the system no longer has stable synchronous vibration. The vibration period becomes three times greater than the period of the excitation force at this rotor speed and the axis orbits begin to diverge. Three isolated points in the Poincaré maps and three isolated frequency parts indicate period-three motion. Fig. 8 shows the numerical analysis results at Ω=6150 r/min, representing the quasi-periodic motion. The axis orbits of the two discs show irregular motion and no obvious period can be found in the time-history diagrams. There is a closed curve in the Poincaré maps and some frequency parts have no common divisor in the amplitude spectrum, clearly indicating that the motion of the system is quasi-periodic. At Ω=8650 r/min, the vibration amplitudes of the two discs are much higher than previously. The axis orbits are becoming completely disorganized. The Poincaré point no longer has finite isolated points or a closed curve, and in the amplitude spectrum diagram, continuous spectrum occurs, collectively demonstrating that the system exhibits chaotic motion.

To study the specific effects of other key parameters on the double disc rotor-seal system, we obtained the bifurcations of both discs, in which the distance of the right disc L 3, the mass of disc m d2, the seal clearance c s2, and the seal clearance L s2 are labeled as the abscissa, i.e., as variable parameters.

4.2 Influence of the distance of the right disc L 3

The bifurcation behavior diagrams are presented in Fig. 10 for when the distance of the right disc L 3 is employed as the variable parameter, ranging from 0.2 m to 1 m. The distance between the left and right discs also varies with L 3 because the distance of the right disc L 1 is fixed. The other main parameters are L 1=0.6 m, m d2=180 kg, c s2=0.8 mm, L s2=0.06 m, and Ω=4000 r/min. Other parameters remain unchanged. The main motion characteristics can be summarized from Fig. 10. As L 3 increases: multi-periodic motion→quasi-periodic motion→multi-periodic motion→quasi-periodic motion→periodic motion→multi-periodic motion→periodic motion. Note that the system shows stable synchronous vibration when L 3 ranges from 0.52 m to 0.66 m, which reveals that the stability of a symmetrical double disc rotor-seal system is better than that of an asymmetrical system. When L 3 is higher than 0.76 m, stable synchronous vibration becomes the main motion, though period-two motion occurs within a narrow range.

Fig. 10
figure 10

Bifurcation diagrams of left (a) and right (b) discs with increasing L 3

Full size image

4.3 Influence of the mass of disc m d2

The bifurcation behavior diagrams are presented in Fig. 11 for when the mass of disc m d2 is employed as the variable parameter, ranging from 20 kg to 150 kg. The other main parameters are L 1=0.7 m, L 3=1 m, c s2=0.8 mm, L s2=0.06 m, and Ω=3000 r/min. The main motion characteristics can be summarized as follows. As m d2 increases: periodic motion→multi-periodic motion alternating with quasi-periodic motion. Clearly when the mass of disc m d2 is less than 34 kg, the system shows stable synchronous vibration. But as m d2 increases, the system not only loses its stability, but the vibration amplitude also becomes larger and the motion state changes frequently in certain zones, ranging from [54.5, 63] to [72.5, 85] kg. The results indicate that a small mass is good for the stability of a double disc rotor-seal system.

Fig. 11
figure 11

Bifurcation diagrams of left (a) and right (b) discs with increasing m d2

Full size image

4.4 Influence of the seal clearance c s2

Fig. 12 shows the bifurcation behavior diagrams for when the seal clearance c s2 is adopted as the variable parameter, ranging from 0.3 mm to 0.9 mm. The other main parameters are L 1=0.7 m, L 3=1 m, m d2=180 kg, L s2=0.06 m, and Ω=3000 r/min. The main motion characteristics can be summarized as follows. As c s2 increases: multi-periodic motion→quasi-periodic motion→multi-periodic motion→periodic motion→multi-periodic motion→quasi-periodic motion→multi-periodic motion. The diagrams indicate that a proper seal clearance c s2, ranging from 0.376 mm to 0.54 mm, can make the double disc rotor-seal system stable. Quasi-periodic motion also occurs in narrow zones and as c 2 increases, period-four motion emerges and changes to period-two motion when c s2=0.617 mm and 0.662 mm, respectively.

Fig. 12
figure 12

Bifurcation diagrams of left (a) and right (b) discs with increasing c s2

Full size image

4.5 Influence of the seal length L s2

Fig. 13 shows the bifurcation behavior diagrams for when the seal length L s2 is adopted as the variable parameter, ranging from 0.06 m to 0.15 m. The other main parameters are L 1=0.7 m, L 3=1 m, m d2=180 kg, c s2=0.8 mm, and Ω=3000 r/min. With increasing L s2, the main motion characteristics can be summarized as follows: period-two motion→quasi-periodic motion→periodic motion. Fig. 13 shows that compared with the previous bifurcation diagrams, the vibration form is single and the system shows period-two motion over a large range as the seal length L s2 increases, turning to quasi-periodic motion when L s2 reaches 0.121 m. The oscillating region of the system then starts to decrease and becomes periodic motion when L s2 is larger than 0.13 m. The results indicate that a larger seal length is beneficial for improvement of the system.

Fig. 13
figure 13

Bifurcation diagrams of left (a) and right (b) discs with increasing L s2

Full size image

4.6 Influence of the seal drop pressure ΔP 2

The bifurcation behavior diagrams are presented in Fig. 14 for when the seal drop pressure ΔP 2 is employed as the variable parameter, ranging from 0.05 MPa to 0.4 MPa. The other main parameters are L 1=0.7 m, L 3=1 m, m d2=180 kg, L s2=0.06 m, Ω=3000 r/min, and c s2=0.8 mm. The main motion characteristics can be summarized as follows. As ΔP 2 increases: quasi-periodic motion→multi-periodic motion→periodic motion. The diagrams clearly indicate that within the range [0.05, 0.4] MPa, the rotor-seal system becomes more stable with a higher seal drop pressure than with a lower one. Unstable quasi-periodic and multi-periodic motion occurs within the range [0.05, 0.104] MPa and the system becomes stable with increasing ΔP 2.

Fig. 14
figure 14

Bifurcation diagrams of left (a) and right (b) discs with increasing Δ P 2

Full size image

4.7 Comparing linear and nonlinear models

Noah and Sundararajan (1995) discussed the limitations of linearized analysis and the significance of considering nonlinear effects in predicting the dynamic characteristics of rotating systems. They pointed out that nonlinear analysis presents a more realistic representation of a rotating system than linear analysis. Fluid-film forces, including journal bearings, squeeze-film dampers, and annular liquid/gas seals, are highly nonlinear functions of journal displacement and velocity. The linear seal fluid dynamic force model proposed by Childs (1983) was adopted to describe the linear seal force. The linear model can be expressed as follows:

$$\left\{ {F_{sx} } \right\} = - \left[ {\begin{array}{*{20}c} {K_1 } & {K_2 } \\ \end{array} } \right]\left\{ x \right\} - \left[ {\begin{array}{*{20}c} {C_1 } & {C_2 } \\ \end{array} } \right]\left\{ {\dot x} \right\}$$
(15)

where K 1=μ 3(μ 0−μ 2 Ω 2 T 2/4), K 2=μ 1 μ 3 ΩT/2, C 1=μ 1 μ 3 T, C 2=μ 2 μ 3 ΩT 2, m s=μ 1 μ 3 T 2, μ 0, μ 1, μ 2, μ 3, and T are expressed through the short bearing model (Childs, 1983).

The bifurcation diagrams of the system using a linear seal force model are shown in Fig. 15. The parameters used in the system are in accord with those of the nonlinear model. The bifurcation diagrams demonstrate that when the rotor speed is less than about 1000 r/min, the vibration amplitudes of the two discs are similar to those of the nonlinear model and the system exhibits stable motion. However, as the rotor speed continues to rise, the vibration amplitudes increase first, and then decrease until the rotor speed reaches 2400 r/min. When the rotor speed runs over 2400 r/min, the system changes from stable period-one motion to unstable motion. The system loses some vibration characteristics compared with the bifurcation diagrams in Fig. 5, which is consistent with the results of Noah and Sundararajan (1995). Not only are vibration characteristics lost, but also the rub phenomenon emerges. In fact, Child (1983)’s linear seal model strictly applies only for small motion about the centered position and the nonlinear seal force model can be transformed into a linear seal force model under specific conditions. Thus, Child (1983)’s linear seal model is an instantiation of the nonlinear seal model of Muszynska (1988). Although the dynamic coefficients of the linear seal model consider the effects of seal clearance and fluid inertia, they are still far from the actual seal force compared with Muszynska (1988;s nonlinear seal model, especially when solving nonlinear problems.

Fig. 15
figure 15

Bifurcation diagrams of left (a) and right (b) discs with a linear model

Full size image

5 Conclusions

This paper deals with nonlinear vibration characteristics of a double disc rotor-seal system with coupled nonlinear seal forces. The model and the motion equations of the double disc rotor-seal system are established by FEM and the Lagrange equation. Compared with traditional modeling methods, this method is more convenient for studying complex multi-stage rotor-seal systems. The fourth-order Runge-Kutta method is used to solve the motion equations of the system and numerically determine the vibration response of the two discs. The nonlinear dynamic characteristics of the double disc rotor-seal system are represented by bifurcation diagrams, time-history diagrams, axis orbit diagrams, Poincaré maps, and amplitude spectrums, with the rotor speed increasing. The results show that the coupled seal force has great influence on the dynamic stability of the rotor-seal system. The effects of the key parameters, including distance between the two discs, mass of the disc, seal clearance, seal length, and seal drop pressure, are also analyzed. The numerical results show that the system exhibits rich forms of periodic, multi-periodic, quasi-periodic, and chaotic motion, and that a symmetrical disc structure, small disc mass, proper seal clearance, long seal length, and high seal drop pressure are propitious for improving the stability of the system and avoiding severe vibration. Compared with a linear seal model, the nonlinear seal model is more suitable for solving nonlinear vibration problems and analyzing actual situations. These results provide a theoretical foundation for further research on multi-stage rotor-seal systems.

In actual structures of rotating machinery with multi-stage sealing, in addition to the sealing of the impellers, bearings are applied at both ends to support the rotor system. These have a significant impact on the vibration performance of the rotor system. For future research to improve multi-stage rotor-seal systems, further work is needed on the effect of such bearings.