1 Introduction

The structural assessment of historical masonry buildings is a complex task because of several motivations, such as a significant variability in geometric and mechanical properties of masonry that are rather difficult to be characterised, epistemic uncertainties related to construction detailing, and nonlinear behaviour of structural systems under different loading conditions. In many cases, existing unreinforced masonry (URM) structures were built according to past rules of thumb and historical treatises, which do not comply with current design criteria. Furthermore, historical URM constructions have usually undergone changes over time compared to their original configuration, accelerating deterioration due to environmental actions, material aging, and/or damage caused by other loads such as soil settlements, earthquake ground motion, or impact. It is also emphasised that mechanical properties of masonry constituents (i.e., stones/bricks and, if any, mortar) and assemblages are highly variable due to variations in the quality of workmanship, environmental conditions during construction, and material characteristics, both between different URM structures (inter-structure variability) and within the same structure (intra-structure variability). Therefore, the huge variability in material properties and masonry assemblage, together with the highly nonlinear response to loads, should be considered [1,2,3]. In addition to the mechanical variability within masonry, especially in historical buildings, there are many difficulties in mechanical and geometric modelling when the concern is quantifying the effects of alterations in physical–mechanical properties of the materials due to, for example, water infiltration in the foundation, capillary rise of water, or corrosion of metallic ties. To make the modelling and capacity assessment of masonry structures even more challenging is the different role played by nonlinear mechanical properties such as strength [4] and fracture energy, as observed in [5,6,7]. Fracture energy plays a crucial role in the post-peak behaviour and displacement capacity of individual URM walls, while its impact is less crucial at larger scales of masonry walls with openings and at building scale [8].

After recent major seismic events such as the L’Aquila earthquake in 2009 and the Amatrice earthquake in 2016, the awareness of the importance of preserving historic buildings and the implementation of structural health monitoring (SHM) techniques has grown [9]. Structural monitoring is also one of the main tools supporting engineers to ensure an acceptable level of safety during different phases of facility lifetime, from construction to demolition. SHM can be based on wide variety of parameters, namely, displacements, rotations, accelerations, stresses, and strains. In this context, the challenge is to correctly identify when damage detected through SHM measurements is caused by, for example, structural deterioration or earthquakes, such as in [10, 11] where a theoretical investigation on the application of smart bricks to full-scale masonry structures for seismic assessment is presented. In the SHM framework, the damage modelling strategy within the finite element method (FEM) plays an important role in the implementation of automatic damage detection algorithms, allowing the development of simplified macro-element models from FEM. Indeed, although the macro-element modelling approach allows accurate nonlinear seismic analyses of masonry buildings [12,13,14], it requires calibration and validation studies on masonry buildings subjected to other loads and, more specifically, under operating conditions and in the presence of material aging and degradation. The aforementioned issues motivated this study, which is part of the DETECT-AGING research project that aims at developing a multi-scale numerical approach for the identification and quantification of the effects of material aging and degradation on the structural safety of cultural heritage, with a focus on URM constructions. More specifically, this study is focused on prediction of the in-plane capacity and stiffness of URM single walls made of tuff stone masonry (TSM), the behaviour of which [15,16,17,18] is different from other masonry types such as clay brick masonry [19, 20] (where mortar is usually weaker than clay brick units) and adobe masonry [21, 22] (where mud mortar and adobe bricks may have very similar properties). FEM was used to simulate the global behaviour of TSM walls, allowing force–displacement curves and cracking patterns to be investigated. FEM micro-models were developed using constitutive models calibrated against experimental data from previous full-scale tests [15, 23, 24]. So, based on a calibrated model, new numerical simulations of walls subjected to in-plane lateral loading were carried out under varying mechanical properties of tuff stones and mortar. To that aim, the variability in material properties was simulated through different combinations of their statistics because of lacking data on tuff stone masonry to characterise stochastic processes over time and, if any, in space. Indeed, previous studies focusing on other masonry types investigated the response of URM walls, making use of stochastic models (e.g., see [25, 26]). This work employs the materials values used to construct several masonry walls and a full-scale masonry building [16, 23] where experimental results on tuff stone masonry showed a well defined rising branch of the stress–strain curve, a peak strength associated with the typical value of 0.20% assumed as yielding strain by masonry standards, but the post-peak behaviour depends not only on imperfections but also on the randomness in the fracture process, so values of residual strength, fracture energy are complex to be defined. Tested tuff stone masonry had similar elastic modulus, 1540 MPa and 1520 MPa respectively for tuff and mortar with a compressive strength of 4.13 MPa and 2.5 MPa. The main goal of the overall study is to define a simple tool to support the prediction of the effects of material aging on structural capacity features such as stiffness, that can be inferred from continuous monitoring over time, and strength, that affect the peak load-bearing capacity.

2 Methodology of the study

Nonlinear FEM analyses were carried out on TSM single walls, which were subjected to a uniformly distributed vertical load to simulate gravity loads and horizontal loading in the form of a monotonically increasing displacement assigned on top of the wall. Therefore, in-plane shear-compression tests on case-study walls were simulated in DIANA FEA ver. 10.3 [27] through displacement-controlled static pushover analysis based on Newton–Raphson incremental iterative procedure and a mixed force–displacement convergence criterion. Numerical analyses were performed in the same way of previous studies where the FEM modelling approach was validated against experimental data [15, 23, 24]. Thus, this study builds upon those previous numerical investigations, assuming the same computational strategy without need for further calibration or validation. The methodology has a general nature, but FEM analysis and related models do not refer to a specific tested tuff masonry since a large variability was to be assessed, so scaling criteria between properties have been implemented using design code formula to deal with a generic tuff masonry, with results closely linked to the type of masonry investigated in this study. The methodology could be applied to analyse any type of masonry. The main aim is to investigate how the aging of mechanical properties of masonry constituents influences the overall in-plane lateral capacity and stiffness of single TSM walls, using parametric analysis based on design of experiments according to statistics under increasing aging level. The latter is assumed to be a time proxy in the long-term behaviour of masonry, because the temporal evolution and spatial variability of material properties in the case of tuff stone masonry has not been yet investigated and hence, cannot be stochastically modelled with proper support by data. The degradation modelling is explained in detail in Sect. 3.3. The starting point of this numerical investigation was the experimental compressive strength \({f}_{c}\) of tuff masonry described in [23, 24]. The following material properties have been considered to gradually change over time due to environmental degradation: uniaxial compressive strength \({f}_{c}\); was the driving parameter to associate tensile strength \({f}_{t}\); Young’s modulus \(E\); shear modulus \(G\); tensile fracture energy \({G}_{f}^{I}\); and compressive fracture energy \({G}_{c}\). The numerical investigation makes use of a multi-scale approach, moving from the above-mentioned mechanical properties of the masonry constituents (which are supposed to be modified by aging deterioration) to the following global in-plane capacity properties of single TSM walls: initial stiffness \({K}_{0}\); cracked stiffness \({K}_{F}\); elastic limit shear force \({V}_{Y}\) and peak shear force \({V}_{P}\).

Starting from modelling the environmental degradation of material properties, where degradation is not due to previous horizontal forces and masonry is not already cracked, numerical analysis becomes a fundamental part of the proposed integrated approach (Fig. 1). The numerical model was defined in terms of geometry, material behaviour, boundary conditions and loads, after that the variability in mechanical properties related to their inherent randomness and degradation phenomena was modelled. Based on nonlinear static FEM analysis, the influence of material variability on nonlinear behaviour of case-study walls was investigated not only in terms of force–displacement curves and corresponding capacity features, but also in terms of failure modes. Numerical results were processed to develop regression models that allow the estimation of conditional mean values of the above-mentioned capacity features (i.e., initial stiffness, cracked stiffness and load-bearing capacity) given the degradation level of masonry constituents strength, which can be either assumed or measured. As material properties reduce due to progressive degradation, regression models allow to quickly predict the progressive reduction in stiffness and load-bearing capacity. Effects of material aging on TMS wall capacity, in term of stiffness and peak load-bearing could be used as a starting point to examine how the global capacity and failure mode of more complex structures change. Effects of environmental ageing or capillary rise of water may affect a limited number of walls in the building and therefore may result in different effects depending on the wall's contribution to the overall response. Reduction in stiffness and load-bearing capacity due to material aging can be confirmed or anyway reported if structural monitoring is provided. Indeed, when a frequency decay of a monitored structure is recorded, some damage is expected to occur in the absence of inertia mass variations. It can be argued that aging does not lead to mass changes, but it does affect stiffness which impacts on dynamic monitoring. Hence, a change in stiffness can be directly used either forward to predict potential drops in peak load-bearing capacity because of material properties degradation, or backward to estimate the reduction in material properties that could have caused the recorded stiffness drop.

Fig. 1
figure 1

Flow-chart of methodology and potential implementation in structural safety assessment

Full size image

3 Numerical modelling accounting for degradation

Probabilistic seismic assessment of masonry structures, considering uncertainty in the material properties has recently been explored by researchers [28,29,30]. In the approach used in this study, the following assumptions played an important role in model development:

  1. (1)

    Probability distributions for mechanical properties;

  2. (2)

    The correlation between mechanical properties which influence the behaviour of masonry structures.

Due to the lack of data regarding tuff stone masonry, the same mechanical properties were assigned to the entire numerical model, hence neglecting the possible spatial variability associated with, e.g., construction process. A non-spatial analysis will over-estimate the probability of wall failure compared to a spatial analysis. For walls with unit-to-unit spatial variability, both the shear strength and the random presence of lower-than-average unit tensile strengths will determine the locations that the cracking first occurs. Moreover, as illustrated in [30] non-spatial analysis is a part of spatial analysis, representing the cases where the parameters are distributed with much less variance. Aging as a natural phenomenon may concern a specific area of the wall, or rather it could not affect a widespread area. In this sense, spatial variability could be expected and a diffuse degradation at the base of masonry piers could occur, e.g. with alterations in physical–mechanical properties of the materials due to water infiltration in the foundation or capillary rise of water. A set of two-dimensional (2D) nonlinear finite element models were generated, adopting different combinations of statistics for uniaxial compressive strengths of mortar and tuff stones. The following sub-sections describe the FEM micro-modelling approach, material properties, modelling criteria for material degradation, as well as the geometry and mesh of case-study TSM walls.

3.1 Finite element micro-modelling

Numerical analysis was carried out using DIANA FEA software [27], defining the mortar and tuff elements separately as continuous isotropic elements without friction interfaces between them, assuming a smeared-crack approach. The choice of simple micro-modelling is motivated to examine the uncertainty in the properties of each constituent material. Furthermore, such models are adequate for non-linear analysis with a minimum set of data, as validated against experimental data in [23, 24] confirming that simple micro-modelling without interface allows not only a good simulation of tuff masonry behavior but also a trade-off between accuracy and computational cost. The use of interfaces and refined modelling requires a larger number of parameters and a considerable amount of experimental data, supporting degradation effects, while the proposed simple micro-modelling allows for separate evaluation of mortar and tuff degradation. For these analyses, the wall thickness is set to 0.25 m. The mesh of the FEM model was generated using squared, plane-stress CQ16M elements with 8 nodes and isoparametric formulation. The displacements ux and uy in the directions of global axes x and y were defined through the following polynomial equation:

$${u}_{i}\left(\xi ,\eta \right)={\alpha }_{0}+{\alpha }_{1}\xi +{\alpha }_{2}\eta +{\alpha }_{3}\xi \eta +{\alpha }_{4}{\xi }^{2}+{\alpha }_{5}{\eta }^{2}+{\alpha }_{6}{\xi }^{2}\eta +{\alpha }_{7}{\xi \eta }^{2}$$
(1)

In the case of undistorted elements, this polynomial produces a strain εxx that varies linearly in the x direction and quadratically in the y direction. Similarly, Eq. (1) produces a strain εyy that varies linearly in the y direction and quadratically in the x direction. Besides, the shear strain γxy varies quadratically in both directions. By default, the DIANA FEA software applies 4 integration points [nξ = 2; nη = 2], the formulation of which is based on the concepts of quadratic interpolation and Gauss integration (i.e., the calculation of the stiffness matrix is not carried out analytically, but numerically using Gauss points).

3.2 Material properties

A nonlinear, isotropic, constitutive relationship was attributed to each finite element, accounting for strain softening both in tension and compression through fracture energies. As shown in Fig. 2, the same stress–strain functional forms were assigned to mortar and tuff stones, while considering different values of mechanical properties. More specifically, a nonlinear behaviour was considered in compression, whereas the tensile behaviour was assumed to be linear elastic up to peak strength with post-peak nonlinear softening up to complete failure.

Fig. 2
figure 2

Stress–strain diagrams used in FEM analysis for tuff stones and mortar

Full size image

Tensile strength (ft), Young’s modulus (E), tensile fracture energy (\({G}_{f}^{I}\)) and compressive fracture energy (Gc) were defined as functions of compressive strength (fc). Based on experimental data [31,32,33] available in the literature, tensile strength was set to ft = 0.1fc. The Young’s modulus was defined so that the axial strain corresponding to peak strength was εc = 0.2%. The following relationship was derived by referring to the expression used by DIANA (i.e., \({\varepsilon }_{c}=\frac{5}{3}\frac{{f}_{c}}{E}\)):

$$E=833 {f}_{c}$$
(2)

Tensile fracture energy for mortar was evaluated using the following equation proposed in [28]

$${G}_{f}^{I}=0.01571 {f}_{t}+0.0004882$$
(3)

where \({f}_{t}\) is measured in MPa and \({G}_{f}^{I}\) in Nmm/mm2. This relationship is reliable for general purpose mortar (1:1:6 + air-entrainer) and calibrated for the range [0.13–3.51] MPa. Tensile fracture energy for tuff stones was instead evaluated through the following equation [34] calibrated for the range [0.53–1.42] MPa:

$${G}_{f}^{I}={\left(\frac{{f}_{t}}{0.68}\right)}^{2}{18.10\bullet 10}^{-3}$$
(4)

An exponential relationship was considered for the behaviour of the material in the post-elastic phase taking into account the following parameters:

$$\frac{{\sigma }_{nn}^{cr}({\varepsilon }_{nn}^{cr})}{{f}_{t}}=\mathrm{exp}\left(\frac{{\varepsilon }_{nn}^{cr}}{{\varepsilon }_{nn,ult}^{cr}}\right)$$
(5)
$${\varepsilon }_{nn,ult}^{cr}=\frac{{G}_{f}^{I}}{{{h}_{cr}f}_{t}}$$
(6)

where: \({\sigma }_{nn}^{cr}\) is the crack stress, \({\varepsilon }_{nn}^{cr}\) is the crack strain, \({\varepsilon }_{nn,ult}^{cr}\) is the ultimate crack strain and \({h}_{cr}\) is the crack bandwidth.

To define the values of compressive fracture energy, a parabolic softening law [35] related to the equation used by DIANA was adopted as follows:

$${\varepsilon }_{c/3}=-\frac{1}{3}\frac{{f}_{c}}{E}$$
(7)
$${\varepsilon }_{c}=-\frac{5}{3}\frac{{f}_{c}}{E}=5{\varepsilon }_{c/3}$$
(8)
$${{\varepsilon }_{u}=\varepsilon }_{c}-\frac{3}{2}\frac{{G}_{c}}{{{h}_{cr} f}_{c}}$$
(9)
$$f = \left\{ {\begin{array}{*{20}l} { - f_{c} \cdot \frac{1}{3}\frac{{\varepsilon_{j} }}{{\varepsilon_{\frac{c}{3}} }} } \hfill & {{\text{if}}\;\varepsilon_{c/3} < \varepsilon_{j} \le 0 } \hfill \\ { - f_{c} \cdot \frac{1}{3}\left( {1 + 4\left( {\frac{{\varepsilon_{j} - \varepsilon_{\frac{c}{3}} }}{{\varepsilon_{c} - \varepsilon_{\frac{c}{3}} }}} \right) - 2 \left( {\frac{{\varepsilon_{j} - \varepsilon_{\frac{c}{3}} }}{{\varepsilon_{c} - \varepsilon_{\frac{c}{3}} }}} \right)^{2} } \right)} \hfill & {{\text{if}}\;\varepsilon_{c} < \varepsilon_{j} \le \varepsilon_{c/3} } \hfill \\ { - f_{c} \left( {1 - \left( {\frac{{\varepsilon_{j} - \varepsilon_{\frac{c}{3}} }}{{\varepsilon_{c} - \varepsilon_{\frac{c}{3}} }}} \right)^{2} } \right)} \hfill & {{\text{if}}\;\varepsilon_{u} < \varepsilon_{j} \le \varepsilon_{c} } \hfill \\ 0 \hfill & {{\text{if}}\;\varepsilon_{j} \le \varepsilon_{u} } \hfill \\ \end{array} } \right.$$
(10)

where: \({\varepsilon }_{c/3}\) is the elastic strain corresponding to a stress equal to one-third of the maximum compressive strength, \({\varepsilon }_{c}\) is the strain at the maximum compressive strength, and \({\varepsilon }_{u}\) is the ultimate strain at which the material is completely softened in compression.

Compressive fracture energy was calibrated so that a 20% strength degradation is associated with conventional ultimate axial strain of 0.35%, in addition to the above-mentioned assumption of axial strain εc = 0.2% [16]. Hence it is \({\varepsilon }_{u}=0.535\%\) (see Fig. 2), and the following equation was obtained:

$$\frac{{G}_{c}}{h}=\left({\varepsilon }_{u}-{\varepsilon }_{c}\right)\frac{2}{3}{f}_{c}$$
(11)

3.3 Degradation modelling

Typical analyses of masonry structures assume spatially-invariant mechanical properties throughout structural elements [26, 28,29,30, 36], with compressive strength obtained in accordance with the literature (e.g., [37, 38]). This type of analysis considers mechanical parameters as deterministic values to assess load-bearing capacity of the structure, even if some of those parameters are probabilistic in nature and their assessment through in-situ testing is rather complex. The choice of the suitable parameter to be correlated to other mechanical properties fell on compressive strength \({f}_{c}\), as it is considered to be representative of any masonry type. Compressive strength could be assumed random variable from a truncated distribution chosen to prevent unrealistic values in the subsequent degradation phase, obtained from hardened mortar cubes which usually occurs when mortar includes pozzolana-like or even cement as single or primary binder, but in this paper hardened mortar at early ages has been neglected. Therefore, sensitivity analysis was run under varying the compressive strength that was defined separately for mortar and tuff stones through a normal probability distribution truncated between mean (μ) minus standard deviation (σ) and mean plus standard deviation (Fig. 3), because this type of distribution agrees with lower and upper bounds to experimental data. After that the compressive strength value was assigned, other mechanical parameters were defined according to their correlation with \({f}_{c}\).

Fig. 3
figure 3

Truncated normal probability distribution for mortar compressive strength

Full size image

Due to lack of experimental data supporting the assumption of realistic correlation coefficients for tuff stone masonry (see, e.g., [28, 39]), spatial analysis was not carried out. A statistics-based sensitivity analysis was used to overcome the definition of a priori correlation coefficients between flexural tensile strength and shear strength or other material properties, linked to the lack of data on tuff stones. As technicians need to characterise the properties of mortar and tuff on structures affected by degradation, the ambition is to evaluate the effects of degradation on the response of single masonry walls in terms of both stiffness and load-bearing capacity. Mechanical properties were assumed as a proxy of material degradation over time, defining discrete changes in their probability distributions regardless of when they actually occur. Aging is here assumed as not linked to a specific physical process of material, but is defined by a condition that can be obtained after a certain time, i.e. a reference is made with the state in which the masonry may be. This also allows more generalised analysis results and their wider implementation, irrespective of the actual temporal variability of mechanical properties that depend on several case-specific factors, most of which associated with environmental conditions, use and maintenance of constructions. Hence, material degradation was not treated as temporal variability of mechanical properties of masonry constituent elements, but by defining specific levels of degradation. Each level of degradation was assigned to probability distributions obtained by progressively reducing the initial value taken as the mean of the distribution and increasing the coefficient of variation (CoV). In detail, five different combinations were defined by varying compressive strength, not among randomly generated values within the probability distribution, but between maximum and minimum values, and also considering a combination where both mortar and tuff were taken as average values. The compressive strength value, which was chosen as initial value of parametric analysis, was taken from experimental data [23, 24]. So, the mean value for tuff and mortar was set respectively to 4.13 MPa and 2.5 MPa, while the COV, experimentally characterised by the authors, was set for both tuff and mortar to 0.20 as it was the most recurrent COV value for all properties. It is noted that this study accounts for the variability in mechanical properties of masonry, neglecting degradation phenomena that produce geometric alterations (e.g., loss of mortar in joints close to masonry faces, erosion or void formation of tuff stones). However, this aspect could be the basis for future studies as it is not difficult to assume a close correlation between the physical mechanical and geometric alterations. Five levels of degradation were identified and for each level a higher reduction rate of the mean value and a lower increase rate of CoV was assumed (Fig. 4).

Fig. 4
figure 4

Truncated normal probability distribution of compressive strength under increasing degradation: a mortar; b tuff stones

Full size image

Due to the lack of data regarding environmental aging on tuff masonry walls, reference was made to similar studies on brick masonry. For the rate variation of CoV, the value was set from [40, 41]. The authors estimated that the change in the compressive strength of bricks is negligible in all hygrothermal exposure conditions with a low COV, maximum 10%. The reduction rate of the mean value was set to 15%, which on average resumes the degradation effects proposed by degradation models obtained from a regression analysis on the experimental data in [40, 41].

Table 1 outlines the assumptions regarding the degradation levels, moving from the initial condition without degradation (DL0) to the final, severe, degradation level (DL4). Variations from initial values of mean and CoV were gradually increased from 15 and 10% (DL1) to 48% and 46% (DL4).

Table 1 Mean value and CoV of truncated distribution of compressive strength: mortar and tuff at different degradation levels
Full size table

In the numerical analyses, each combination of degradation level and property statistics was denoted as DLn (fb, fm), where n = {0,…,4} refers to the degradation level considered and bracketed values include different permutations of the statistics assigned to compressive strength of tuff stone, i.e., fb = {μ − σ, μ, μ + σ}, and mortar, i.e., fm = {μ − σ, μ, μ + σ}. For each degradation level, the combinations were defined as follows:

  • Combination 1, where compressive strength was set to the maximum value of its probability distribution for both mortar and tuff stones, so it was denoted as DLn(μ + σ, μ + σ);

  • Combination 2, where compressive strength of tuff stones was set to the maximum value of the considered probability distribution and compressive strength of mortar was set to the minimum value of the considered probability distribution, so it was denoted as DLn (μ + σ, μ − σ);

  • Combination 3, where, for tuff, the compressive strength value is given by the minimum value of the considered probability distribution and for mortar the compressive strength value is given by the maximum value of the considered probability distribution DLn (μ − σ, μ + σ);

  • Combination 4, where for both mortar and tuff the compressive strength of tuff stones was set to the minimum value of the considered probability distribution DLn (μ − σ, μ − σ);

  • Combination M, where the mean values of compressive strengths of both mortar and tuff stone were assumed, so it was denoted as DLn (μ, μ).

Table 2 summarises the other parameters for combination M, corresponding to mean values as explained, assumed in the analyses.

Table 2 Comparison between numerical and theorical results for combination M at different degradation levels with their assumed mechanical properties
Full size table

3.4 Geometry and boundary conditions

This study focused on a simple masonry wall both to prevent further variability in the geometric modelling, but also it is noted that starting from local wall response variations, due to the effect of aging, more complex masonry buildings can be analyzed in terms of global response, starting from single wall data.

Case-study TSM walls were 1230 × 1200 × 250 mm3 in size (Fig. 5), with masonry consisting of a running bond assemblage of tuff stones and pozzolana-like mortar joints. Tuff stones have nominal dimension of 300 × 100 × 120 mm3 while masonry joints were nominally 10 mm. According to a shear-compression loading condition simulating the in-plane lateral loading induced by, e.g., seismic actions, a vertical compressive load per unit length of 37.5 kN/m was uniformly distributed on top of each wall to simulate the effects of gravity loads corresponding to an axial stress of 0.15 MPa, whereas in-plane horizontal loading was modelled as a monotonically increasing displacement on top of the wall since monotonic response provides a good fit of the load–displacement envelope of cyclic loading [26].

Fig. 5
figure 5

Geometry of case-study TSM walls

Full size image

Regarding boundary conditions, constraints were assigned to the base to prevent horizontal and vertical translations. A further constraint was applied on top of each wall to prevent rotations (Fig. 6), assigning to all points a kinematic link (tying type) for horizontal and vertical translations. The choice of studying squat masonry walls was based on greater influence of compressive load on the failure mode compared to the case of slender walls, as shown by several studies [42].

Fig. 6
figure 6

FEM model

Full size image

4 Impact of degradation on nonlinear behaviour and ultimate failure mode

4.1 Evaluation of compressive strength

Variations in mechanical properties for the simulation of degradation effects induces different values of compressive strength for the whole masonry. Hence, a numerical characterisation of tuff stone masonry under uniaxial compression was carried out on 760 × 300 × 150 mm3 single-leaf running bond specimens according to EN 1052–1 shown in Fig. 7, under varying mechanical behaviour of the mortar and tuff stones, separately. Constraints were assigned to the base to prevent both horizontal and vertical translations. Uniaxial load test for each degradation level and for all assumed combinations was simulated to assess the masonry compressive strength and thus define the load ratio for the walls subjected to lateral loading, whose configuration is illustrated in Fig. 5.

Fig. 7
figure 7

FE model for mechanical characterisation of the material

Full size image

Fig. 8a shows that numerical analysis produced significantly higher compressive strength values than those obtained through the following equation provided by Eurocode 6 (EC6) [43]:

$${f}_{k}=K{{f}_{b}}^{0.7}{{f}_{m}}^{0.3}$$
(12)

where \({f}_{k}\) is the characteristic compressive strength of the masonry, \(K\) is a factor that is set to 0.45 in case of natural stones and general purpose mortar, \({f}_{b}\) is the compressive strength of masonry units and \({f}_{m}\) is the mortar compressive strength. Comparison of \({f}_{k}\) values show significative differences for some combinations, but Eq. (12) is not questioned because in fact it has a statistical meaning and allows the assessment of characteristic value of compressive strength for design purposes, rather than a deterministic value related to deterministic strengths of mortar and tuff element, as discussed in this paper, for assessment purposes of average behaviour. A comparison in terms of vertical load ratio \(\overline{N }\) (i.e., the ratio between compressive load of the wall subjected to lateral loading (0.15 MPa) and compressive strength values of the wall cross section) associated with compressive strength values obtained from EC6 [43] and FEM is shown in Fig. 8b. The vertical load ratio corresponding to the compressive strength evaluated in accordance with EC6 varies from 8 to 25%, due to inherent variability and degradation levels. Lower variations were found by assuming the compressive strength evaluated through FEM analysis, which ranged from 4 to 13%; such values, instead of design EC6 values, were used in the following for consistent evaluations of FEM simulations. In any case, the analysed masonry was subjected to a low-medium level of vertical load ratio.

Fig. 8
figure 8

Numerical-analytical comparison obtained from EC6 [43] and FEM analysis for: a compressive strength values; b vertical load ratios

Full size image

4.2 Force–displacement curves

FEM results were processed to assess the load–displacement behaviour varying material properties and degradation level, which can be combined with the crack pattern observed in near-collapse conditions and corresponding failure mode (see Sect. 4.3). For each wall model, force–displacement curves were also used to record the initial stiffness, cracked stiffness and peak shear capacity, for development of regression models that are presented in Sect. 5.

Main focus of this study is the numerical analysis of peak lateral force capacity and monitorability, in terms of stiffness changes of tuff masonry walls. It is noted that in all the analyses, peak load was achieved with a limited post peak plateau mainly related to ultimate strain and energy (in numerical simulations) and rocking in experimental tests [8], not covered in this study. Some analyses do not show a marked post peak, but this is due to numerical convergence issues related to the assumed fracture energy value. Post peak is more evident for walls exhibiting flexural failure and less so for those exhibiting a shear failure. Peak loads are in agreement with theoretical formulations provided by the current Italian building code [37, 38], adopting mean values without safety factors (for mean behaviour assessment) as expected in the code, as can be seen in Table 2 for combination M with formulations briefly reported. In Table 2 for the theoretical formulations, the value of the minimum resistance is given with the relative equation reported in round parentheses. The flexural strength is provided by the equation:

$${V}_{f}={B}^{2}s\frac{{\sigma }_{0}}{{2H}_{eff}}(1-\frac{{\sigma }_{0}}{{0.85f}_{c}})$$
(13)

For regular masonry walls made of regular arrangements of units bonded with horizontal and vertical mortar joints the following equations for shear strength, both based on the well-known Mohr–Coulomb criterion, are provided:

$${V}_{s1}={B}^{^{\prime}}s\frac{{f}_{v0}+\mu {\sigma }_{0}}{{\gamma }_{m}}$$
(14)
$${V}_{s2}=\frac{Bs}{b}{(f}_{v0}^{^{\prime}}+{\mu }^{^{\prime}}{\sigma }_{0}) {f}_{v0}^{^{\prime}}=\frac{{f}_{v0}}{1+\mu \varphi }; {\mu }^{^{\prime}}=\frac{\mu }{1+\mu \varphi }; \varphi =\frac{2{h}_{b}}{{b}_{b}};$$
(15)

Both formulations depend on the geometry of the walls, (the base B and the height H, the thickness s) and on the vertical compressive stress σ0. Equation (14) is provided for predicting the shear strength in the case of sliding along horizontal joints while Eq. (15), formulated by [44], is provided in the case of sliding along diagonal stepped cracks in the mortar. In the Eq. (14) the partial safety coefficient \({\gamma }_{m}\) appears. In the formulation (14) μ is the friction coefficient and fv0 is the cohesion, defined as ‘local’ parameters; in Eq. (15) the ‘global’ parameters f′v0 and μ′ are used to account for the interlocking between the units expressed by parameter \(\varphi\), which depends on the units height hb and length bb. In addition to Eq. (15), the Commentary to the Italian code [38] specifies that the achievement of the tensile strength of the block is set as upper bound for the shear capacity. Equation (13) also depends on the shape factor b that according to the Commentary to the Italian code [38], is herein assumed equal to the in-plane slenderness of the wall b = λ = H/B but limited to the range 1.0–1.5. Equation (13) also depends on the compressive strength of masonry fc, and on the effective height Heff, assumed as the shear length and, thus, equal to 0.5 H in the case of double-fixed constraint, while B′ is the uncracked length of the end sections of the walls. The values of \({f}_{v0}\) and \(\mu\) used for the analytical predictions have been obtained from [4].

Figures 9a–e show the shear–displacement diagrams under varying degradation level, given the same combination of compressive strengths of tuff stones and mortar. As the degradation level increases, almost all curves gradually change indicating a progressive reduction in stiffness and peak load-bearing capacity. From combination 3 to M an increased bandwidth stiffness as a result of their variations due to degradation (i.e. from DL0 to DL4) is point out.

Fig. 9
figure 9

Effects of degradation on force–displacement behaviour given the combination of stone and mortar compressive strengths: a combination 1, b combination 2, c combination 3, d combination 4, e combination M

Full size image

In some analyses, particularly for combination 1, combination 2, and for the first two levels of degradation for the other combinations, an initial peak load related to the attainment of cracking is noted, followed by a stress distribution that leads to an initial unloading and a subsequent phase in which TSM wall resumes load bearing capacity (keeping in mind that constitutive relationship has a softening both in tension and compression through fracture energies).

Figure 10a–e outline the effect of uncertainty in the compressive strengths of masonry constituents and hence their different combinations of statistics, given the level of degradation. As the degradation level increases, Figs. 10a–e, the cracking force significantly reduces with negligible change in the corresponding displacement for all combinations, with a less marked reduction in stiffness for the first two degradation levels, while for the others, the stiffness reduction is more evident. It is also interesting to note that as the degradation level increases, combinations 1 and M show parallel trend to each other after crack peak, while combinations 3 and 4 show similar trends overall. Besides, the load-bearing capacity of the walls reduces as well, highlighting a potential correlation between those capacity features, that is discussed in detail in Sect. 5.

Fig. 10
figure 10

Effect of mechanical variability on force–displacement behaviour given the degradation level: a DL0, b DL1, c DL2, d DL3, e DL4

Full size image

As expected, lower and upper bounds to material strengths result in extreme values of peak resisting force, regardless of the degradation level under consideration. Furthermore, it is observed that, in the early phases of degradation (i.e., from DL0 to DL2) and when mortar and tuff stones are not simultaneously set to the same statistics (combinations 2 and 3) or when are set to their lower bound (combinations 4), the peak resistance does not show marked variations. In all material degradation levels (i.e., from DL0 to DL4), the variability in the mortar strength does not affect the peak resisting force when minimum values of stone strength are assumed (combinations 3 and 4). Also, for final stages of material degradation (i.e., DL3 and DL4), the variability in the mortar strength from μ to μ – σ and in stone strength from μ to μ + σ (combinations 2 and M) does not affect the wall response.

Force–displacement envelopes associated with increasing degradation level (Fig. 11) allow joint considerations on the influence of both the variability in mechanical properties and the degradation level on the in-plane capacity of the single TSM walls. As the environmental degradation level increases, the walls develop a bilinear elasto-plastic behaviour with decreasing variability, graphically represented by a reducing bandwidth of the force–displacement envelopes. Although the stiffness and load-bearing capacity gradually reduces under increasing degradation, the displacement corresponding to the peak resisting forces does not significantly change.

Fig. 11
figure 11

Force–displacement envelopes associated with different degradation levels

Full size image

For the load-bearing capacity, if TMS walls are no longer able to withstand the loads for which they were designed, in the case of assessing the vulnerability of buildings may be necessary to change the final destination. Stiffness reduction has a dual effect. TMS wall stiffness decrease entails a greater instability at increased axial loads due to seismic action, limiting the load-bearing capacity under seismic conditions, but wall stiffness reduction compromises also the estimation of the building fundamental vibration period and the calculation of vibrational modes resulting in incorrect design stress evaluations.

Modal frequencies analysis reveals a variation in the frequency of the first in-plane mode of vibration considering variations due to degradation (i.e. DL0 to DL4), from 25% for combination 1 to 32% for combination 4 slightly less than reduction in initial elastic stiffness as illustrated in Sect. 5.1.

Analyses focused on the individual TMS walls and the variations in strength and stiffness (with same boundary conditions and axial load but varying vertical load ratio due to variations in mechanical properties), the effects of which on a structure are to be assessed on a case-by-case basis, by modelling the entire structure using as input parameters the properties of single TMS walls with degradation (macro-elements).

4.3 Failure modes

Based on the interaction domain defined by equations available in the literature (see, e.g., [42, 45, 46]) with the mean values of masonry compressive strength and the corresponding dimensionless axial force acting on the wall (i.e. load ratio), flexural failure was found to be the most probable failure mode.

The failure patterns are not very obvious, as analysed in [47, 48] where the shear walls response is highly influenced by axial load ratio and material properties. In the numerical analyses different combinations of constituent strengths and their variations due to degradation can produce different failure modes, even if compressive load of the wall is constantly equal to 0.15 MPa but vertical load ratio \(\overline{N }\) changes. As discussed in [47] lower axial pre-compression load caused flexural or rocking failures and higher pre-compression load caused toe crushing and diagonal shear failures along the diagonal direction. Shear failures in FEM analyses occur for highest vertical load ratio \(\overline{N }\) which ranged from 10 to 13% with tensile mortar strength similar or lower than that of tuff.

In Figs. 12, 13 and 14, three different failure modes are defined through their respective cracking patterns, with a full panel view and one only with tuff elements where the vectors represent the normal crack strain in the integration points, as derived from parametric FEM analysis, as follows:

  • Flexural failure (abbreviated as ‘F’ below), which affects the first layers of tuff stone masonry at the base and on top of the wall without damage at the mortar joints.

  • Mixed failure (abbreviated as ‘M’), which consists of (i) bending-related cracks affecting penultimate mortar layers above the first masonry layer at the base and below the first layer on top, and (ii) diagonal shear-related cracks, which involve both head and bed joints along the compressed diagonal of the wall according to a stair-stepped path. In those conditions, the portion of masonry affected by rocking is almost the entire wall, with the exception of the first and last masonry layers, which keep a horizontal configuration.

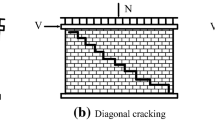
  • Shear failure (abbreviated as ‘S’), which consists of a diagonal cracking failure in the mortar joints at the centre of the wall, with flexural cracks lumped in the end mortar bed joints.

Fig. 12
figure 12

Cracking pattern corresponding to flexural failure (F): a complete model; b partial model without mortar

Full size image
Fig. 13
figure 13

Cracking pattern corresponding to mixed failure (M): a complete model; b partial model without mortar

Full size image
Fig. 14
figure 14

Cracking pattern corresponding to shear failure (S): a complete model; b partial model without mortar

Full size image

Table 3 outlines the occurrence of the above-mentioned failure modes under varying degradation level and combination of constituent strengths.

Table 3 Type of failure under varying degradation level and combinations of strength statistics
Full size table

Analysis results show that combinations of constituent strength statistics denoted as 1, 2 and 3 always resulted in the same failure modes (i.e., flexural, mixed and flexural, respectively) under any level of degradation, highlighting a major influence of the variability in material properties. Conversely, TSM walls with property combinations 4 and M, which were respectively characterised by stone and mortar strengths set to (μ–σ, μ–σ) and (μ, μ), were more sensitive to degradation. Indeed, walls with those property combinations experienced an F-to-S failure mode transition as the degradation level increased from 2 to 3 and 3 to 4, respectively. This is an important outcome that is related to possibly different cracking patterns and capacity features of TSM walls under increasing degradation.

Considering different combinations of constituent strengths and their variations due to degradation, it is noted that if mortar has values of mechanical properties set to the maximum values, flexural failure is expected regardless of tuff stone properties and property variations due to degradation. If mortar value is equal to the minimum value of the probability distribution, as mechanical degradation progresses, the central part of the wall will mostly experience cracks in mortar joints and a mixed failure will be observed in case of maximum value assigned to tuff stone. On the other hand, if the tuff stone strength is set to its minimum value, cracks in mortar joints are caused by shear failure with mortar compressive strength equal to approximately 1 MPa. In such conditions, if mortar compressive strength is greater than 1 MPa, flexural failure is expected. If tuff and mortar are set to their mean values, a flexural failure will be observed, with possible shear failure occurring only when Young’s modulus of mortar is approximately equal to 1 GPa.

5 Regression models

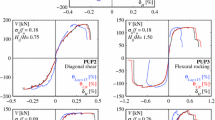
Based on the parametric analysis presented in previous sections, capacity features that summarise the global behaviour of single TSM walls under in-plane loading were recorded at each level of degradation. According to the methodology and objectives presented in Sect. 2, compressive strength was used as main local property of masonry that is related to other mechanical properties, whereas the following global capacity features of walls were recorded: initial stiffness \({K}_{0}\); cracked stiffness \({K}_{F}\); elastic limit shear force \({V}_{Y}\) and peak shear force \({V}_{P}\), indicated with a generic shear-displacement capacity curve in Fig. 15a. Local–global data sets were then used to develop regression models for their use in structural safety assessment of masonry structures. Indeed, starting from the aging effects of the constituents on the elastic stiffness of TSM wall, other correlations have been defined between elastic stiffness and other properties such as the cracked stiffness, the elastic shear and the peak shear capacity, so that it is possible to define step by step the entire response of the wall for different conditions when the mechanical properties of the constituents have changed. Let denote by \({K}_{00}\) and \({V}_{P0}\) the values of initial stiffness and peak shear force corresponding to intact TSM walls, i.e., walls with zero degradation defined as DL0. Similarly, \({f}_{b0}\) and \({f}_{m0}\) indicate the initial values of stone and mortar compressive strengths, respectively.

Fig. 15
figure 15

a Generic Shear-Displacement capacity curve with linear regression models for prediction of: b mean initial stiffness loss given compressive strength of tuff stone; c mean initial stiffness loss given compressive strength of mortar; d mean cracked stiffness given initial elastic stiffness; e mean elastic capacity loss given the initial stiffness loss; f mean load-bearing capacity loss given the initial stiffness loss

Full size image

5.1 Models for initial stiffness

The first regression analysis was performed to derive simple models for prediction of the conditional mean value of \({K}_{0}/{K}_{00}\) given \({f}_{b}/{f}_{b0}\) or \({f}_{m}/{f}_{m0}\). Hence, one can use either the regression model related to tuff stones or that related to mortar, depending on whether TSM degradation is measured as reduction of \({f}_{b}\) or \({f}_{m}\). In this respect, it should be noted that tuff stone masonry often suffers degradation of stones rather than mortar, if the latter material includes pozzolana-like or even cement as single or primary binder. In that case, it is suggested to measure TSM degradation as \({f}_{b}/{f}_{b0}\), namely, as progressive reduction of stone strength. To get more general findings, regression analysis was thus carried out on normalised values of both initial stiffness and compressive strengths, as shown in Figs. 15b, c. Linear regression models for tuff stones and mortar are respectively provided by Eqs. (16) and (17):

$$\frac{{K}_{0}}{{K}_{00}}=1.0033\frac{{f}_{b}}{{f}_{b0}}-0.0040$$
(16)
$$\frac{{K}_{0}}{{K}_{00}}=0.9943\frac{{f}_{m}}{{f}_{m0}}+0.0022$$
(17)

which are characterized by a coefficient of determination R2 equal to 0.998 and 0.9579, indicating a satisfactory goodness of fitting to numerical data.

Figure 15b shows that tuff stone strength has a greater effect on the behaviour of the TMS wall with a direct proportionality between the tuff strength loss and the initial stiffness reduction of TSM. Proportionality between mortar strength loss and stiffness reduction is less linear as shown in Fig. 15c with values that deviate from the regression line related to combinations when mortar and tuff stones are not simultaneously set to the same statistics (combinations 2 and 3).

It is worth noting that the maximum loss of compressive strength considered in regression analysis was approximately equal to 55%. That level of material degradation caused an initial stiffness loss of approximately 50%.

The proposed regression models could be integrated with SHM algorithms to understand possible frequency decays, which might be caused by material environmental degradation over time. Indeed, a frequency decay denotes a stiffness loss, which is here measured through the ratio \({f}_{b}/{f}_{b0}\) or \({f}_{m}/{f}_{m0}\). In such a case, time becomes only an implicit variable that does not influence damage detection.

The goal of relating correlation models to results from long-term monitoring is a motivation that, due to the lack of data from SHM, has not been used, but this link is presented as a potential future implementation in SHM damage detection methodology.

5.2 Models for cracked stiffness

As a result of the degradation of the mechanical properties, the question arises also on its influence on the cracked stiffness \({K}_{F}\) trend (Fig. 15d). The cracked stiffness \({K}_{F}\) is defined as the slope of the branch connecting the elastic shear force limit (i.e. at the end of the elastic phase) with the point where the peak shear force is reached. A third regression analysis then allowed the derivation of the following linear model:

$${K}_{F}=0.1228{K}_{0}+19.146$$
(18)

with R2 = 0.546 indicating a good correlation between \({K}_{F}\) and \({K}_{0}\). According to the force–displacement curves (see Sect. 4.2), material degradation produced a progressive decrease in initial stiffness \({K}_{0}\) while inducing a gradual increase in cracked stiffness \({K}_{F}\). This finding agrees with the fact that the regression models presented in Sects. 5.1 and 5.3 highlight approximately 50% loss of initial stiffness compared to a 13% drop in peak shear capacity at the maximum level of compressive strength degradation (i.e., around 55%). Thus, initial stiffness reduced more significantly than peak shear capacity under increasing degradation. In the proposed integrated approach, the derivation of another regression model for cracked stiffness allows a quick characterization of the in-plane behaviour of the case-study walls, assuming a bilinear load–displacement curve to represent the response until peak.

5.3 Models for shear capacity

A fourth regression analysis was performed on \(\left({V}_{Y},{K}_{0}\right)\) data sets, allowing the derivation of the following linear model (Fig. 15e):

$$\frac{{V}_{Y}}{{V}_{Y0}}=0.4574\frac{{K}_{0}}{{K}_{00}}+0.5517$$
(19)

with R2 = 0.898, highlighting a very good correlation between elastic limit capacity loss \({V}_{Y}/{V}_{Y0}\) and initial stiffness loss \({K}_{0}/{K}_{00}.\) Elastic limit shear was defined by an elastic-perfectly plastic bilinear law equivalent to the force–displacement curve in terms of energy dissipated up to the peak shear. Figure 15e shows values that deviate from the regression line related to combinations 2,3 and M. Regarding the DL1(μ, μ) combination the stiffness loss was not accompanied by a reduction in elastic peak resistance, which was found to be equal to that of DL0(μ, μ) combination. Same repeats for DL2(μ + σ, μ – σ) and DL1(μ + σ, μ – σ). and for the pair DL2(μ—σ, μ + σ) and DL1(μ—σ, μ + σ).

A fifth regression analysis was performed on \(\left({V}_{P},{K}_{0}\right)\) data sets, allowing the derivation of the following linear model (Fig. 15f):

$$\frac{{V}_{P}}{{V}_{P0}}=0.2481\frac{{K}_{0}}{{K}_{00}}+0.7519$$
(20)

with R2 = 0.917, highlighting a very good correlation between load-bearing capacity loss \({V}_{P}/{V}_{P0}\) and initial stiffness loss \({K}_{0}/{K}_{00}\). More specifically, this regression model allows the estimation of the conditional mean value of \({V}_{P}/{V}_{P0}\) given the loss of initial stiffness related to material degradation, and hence after that the loss of compressive strength of masonry constituents is known. This also provides evidence that initial stiffness \({K}_{0}\) is more informative than material strengths when the degree of detail moves from the material to the wall scale. Figure 15f shows values that deviate more than others from the regression line, generating the maximum residuals of the regression model. With regard to the combination DL3(μ + σ, μ – σ) the stiffness loss was not accompanied by a reduction in load-bearing capacity, which was found to be equal to that of DL2(μ, μ) combination. Same repeats for DL4(μ + σ, μ – σ) and DL3(μ + σ, μ + σ). For DL4(μ − σ, μ + σ), the same values of initial elastic stiffness and peak resistance of DL4(μ − σ, μ − σ), were obtained.

A limitation of the applicability of all these regressions is that they can be used for interpolation only, never for data extrapolation.

Even if these analyses are limited to this typology of tuff masonry, to the geometrical parameters of the walls (the width, the height and the thickness), to boundary conditions and to axial stress level also, this approach shows a methodology that takes into account material and stiffness degradation leading from a local to global degradation, which can be used as a starting point to assess the global capacity and failure mode of more complex structures, a scaling up that can also be extended to other materials and geometries.

6 Conclusions

Nonlinear analysis results on unreinforced TSM walls subjected to compression and in-plane shear loading have been presented and discussed. Numerical analyses were performed to evaluate the influence of the variability in mechanical properties of tuff stone masonry and to quantify the effect of degradation at the wall scale through a statistics-based sensitivity analysis and subsequent regression analysis. This study is part of an integrated approach where numerical analyses not only provide a prediction of performance decay, but they can also become useful in structural health monitoring of historical masonry buildings.

Numerical analysis results indicate how the degradation is not only the reason of a capacity loss in terms of stiffness and resistance, but it also affects the expected failure mode, changing from flexural failure (with cracks mostly lumped at wall ends) to either a mixed or shear failure (with crack patterns involving the mortar joints in the middle of the wall).

A flexural failure was observed when mortar strength was set to its maximum value, irrespective of the degradation level. Conversely, when mortar strength was set to its minimum value, TSM walls experienced either mixed or flexural failure at zero-to-slight degradation levels, showing a transition from flexural to shear failure at moderate-to-high degradation levels in case of minimum stone strength. Mean values of both tuff stones and mortar resulted into a flexural failure, exception made for the maximum degradation level that induced a transition to shear failure.

The influence of the variability in material properties becomes evident when compressive strength of tuff stones is set to minimum values. In those cases, variability produces either a sudden increase in cracked stiffness or a sudden decrease in the initial stiffness of the wall, and did not affect the overall response, regardless of the mortar compressive strength and degradation level. When mortar and tuff stones were not assigned the same statistics equal to the lower- or upper-bound values and the early degradation levels were assumed, the peak shear force did not significantly change. The same when the two maximum degradation levels were assumed, with the transition of mortar strength from the mean to the minimum value and that of the stone strength from the mean to the maximum value.

When masonry compressive strength values are lower than those initially known due to the decay of the mechanical properties, one can quickly estimate the expected reduction in elastic stiffness and also assess the global performance to understand how urgent it is to intervene.

Based on regression analysis, five simple models were obtained for quick prediction of conditional mean value of initial stiffness loss, cracked stiffness, elastic and load-bearing capacity loss, showing a satisfactory correlation between such capacity features of TSM walls and material strength used as degradation measure.

On the other hand, if monitoring tools are available, when a reduction in stiffness is observed, the proposed tools can be used to investigate whether a degradation phenomenon is taking place, allowing its identification, location, and quantification of the extent of the degradation. This can set alarm thresholds because a reduction in stiffness can be traced back to a reduction in load-bearing capacity with a consequent increase in the collapse potential, but this requires further analyses on the global behaviour of structures.

Those regression models give room to structural health monitoring and damage detection of historical TSM buildings, allowing the estimation of degradation effects based on the loss of frequency, and hence stiffness in some load-bearing walls. Future developments of this study might include (i) a correlation between capacity features of TSM walls and geometrical alterations (e.g., loss of mortar from the exterior part of joints), (ii) the use of stochastic FEM models based on future data regarding TSM degradation and spatial variability of TSM properties whose distribution can be obtained from future accelerated degradation test and evaluate also hardened mortar at early ages effect with mortar including pozzolana-like or event cement as single or primary binder, and (iii) the implementation of stiffness and strength degrading properties to evaluate response variation to horizontal actions and the consequent monitoring of complex masonry buildings both with FEM modelling and equivalent frame models, using the regression models for quick estimation of macro-element properties. Similar studies might also be carried out on other types of masonry walls, which can develop different behavioural and failure modes depending on their different material properties and degradation processes.