1 Introduction

Nowadays, there is growing environmental awareness and increasing demands for sustainability, in response to which wood is established as one of the most suitable materials for building as a natural and renewable resource.

Although the vast majority of products used in timber engineering are made of softwoods, hardwood species are gaining increasing attention for structural applications in the European market. This is mainly due to the large stocks of structurally unused hardwood resources in Central and Southern Europe, to the shortage of softwoods and consequent higher costs, and to continuous changes in reforestation policies toward hardwoods due to the greater suitability of several broadleaf species for soil and climate conditions [1]. This interest is demonstrated by emerging hardwood products, mainly glued laminated products [e.g., 2–4].

In this regard, Eucalyptus globulus Labill (also known as southern blue gum) stands out as a high-performance hardwood of significant interest, due to its fast growth, high mechanical properties, and good natural durability. Recently, there has been increasing industrial and institutional interest driving scientific research on E. globulus in different fields, such as silviculture [5,6,7,8], mechanical characterisation of the material with small clear specimens [9, 10] and structural size [11, 12], performance of bonded joints for laminated products [13, 14], as well as research related to the development of higher added value building and engineering wood products using this species, such as finger-jointed solid timber [11], glued laminated timber [15], cross-laminated timber (CLT) [16, 17], laminated veneer lumber (LVL) and plywood [18,19,20] or nail-laminated timber (NLT) and NLT-concrete composite floor panels [21].

In the last century, eucalyptus has become one of the most widely cultivated fast-growing species worldwide in forestry exploitations for production purposes, mainly focused on pulp and paper industries. The Eucalyptus globulus species is the most dominant hardwood plantation in Australia together with Eucalyptus nitens [22]. It is also one of the main hardwood species in South America. The Iberian Peninsula (Europe) hosts the most extensive E. globulus plantations, distributed primarily along the western and northern coasts, comprising Portugal and northern Spain [23].

In Europe, Eucalyptus globulus is assigned to the D40 strength class for structural use according to the European standard EN 1912:2012 [24]. The Spanish visual grading standard UNE 56546:2013 [25] only applies to E. globulus solid wood with maximum cross-sections of 60 × 200 mm2 because, in practice, larger cross-sections are difficult to obtain due to drying problems. For such larger cross-sections, glued laminated products would be a choice.

Thanks to the high performance of this species, eucalyptus solid timber or finger jointed solid timber with small cross-sections could be used in efficient structures, such as trusses, lattice structures, or gridshells [11, 26]. The timber elements that form these structures are often joined by dowel-type connections, which, if loaded perpendicular to the grain, may lead to brittle splitting failure of the timber member at load levels below the bearing capacity required for desirable ductile behaviour [27] (as is well known, the strength and stiffness perpendicular to the grain are particularly low in wood). Therefore, this brittle failure is one of the most critical in timber structures and deserves special attention in design to achieve adequate reliability.

Most design codes for timber structures currently include explicit expressions to quantify the splitting capacity of connections. These approaches are mainly based on a strength criterion (the former German DIN 1052:2008 [28] based on Ehlbeck et al. [29]) or on an energetic approach within the framework of fracture mechanics (Eurocode 5 [30], Canadian OS86:19 [31]).

In particular, the expression adopted in Eurocode 5 describing the splitting capacity of a connection loaded perpendicular to grain by means of fasteners other than punched metal plates is a quite simple formula applicable only to softwoods, which considers only geometrical parameters (the dimension of the beam cross-section and the distance from the fastener to the loaded edge of the beam). The expression is based on the analytical model originally formulated by Van der Put [32] in the framework of linear elastic fracture mechanics (with a further publication by Van der Put and Leijten [33] in an effort to make the theory more transparent).

As a drawback to its simplicity, the Eurocode 5 splitting capacity expression does not consider the influence of important parameters such as connection layout, type and number of fasteners, different loading cases, etc. Ongoing research has been addressed to propose alternative analytical expressions in order to extend or adapt the original expression, considering to a greater or lesser extent the effect of different geometrical and material parameters based on experimental tests or numerical analysis [34,35,36,37,38,39,40]. However, there is no general agreement between the results and the expression derived by Van der Put and Leijten still remains in the code. A comprehensive review of existing approaches can be found in Schoenmakers [41] and Jockwer and Dietsch [42].

Both the original van der Put and Leijten equation and the analytical variants based on fracture mechanics proposed in the literature consider the material fracture energy in their formulations, whereas the strength approaches are based on tensile strength perpendicular to the grain as a material property. There is no compilation of fracture energies for the different species in the standards, but this property must be obtained experimentally. The fracture energies in Modes I and II loading of E. globulus have been achieved in previous work by the authors [43,44,45]. However, there are no studies on the splitting capacity in eucalyptus.

Furthermore, as mentioned above, the Eurocode 5 expression is only applicable to softwoods. Most subsequent research has also focused mainly on solid wood or timber products with softwoods. Therefore, the suitability to hardwood species of this or other analytical proposals in the literature requires particular research, considering that hardwoods show greater mechanical properties than softwoods, including higher fracture energy and higher tensile strength perpendicular to the grain. Therefore, the use of expressions calibrated for softwoods might be too conservative for hardwoods.

The aim of the present work was to study, for the first time to the best of the authors’ knowledge, the splitting capacity of Eucalyptus globulus L. solid wood loaded perpendicular to the grain by steel dowel-type connections. Experimental tests were carried out on beams with single and double dowel connections placed at different loaded edge distances to derive the splitting capacity of this species. The adequacy to eucalyptus hardwood of the expression included in Eurocode 5 for softwoods was discussed. The correlation between experimental splitting failure loads and those predicted theoretically by different analytical models from the literature based on the experimentally determined fracture energy of the material was also addressed.

2 Materials and methods

2.1 Material properties

7 boards of Eucalyptus globulus Labill. from the Galicia region of northern Spain were used to prepare the 32 specimens used in the splitting tests (Sect. 2.2). All boards met the visual classification criteria of the Spanish standard UNE 56546:2013 [25]. It should be noted that the boards were approximately free of knots. This is usually the case in E. globulus because it develops a natural pruning, so from the starting point the knots are few and very small. The boards were conditioned at 20 °C and 65% relative humidity prior to specimen preparation, reaching an equilibrium moisture content of 12.8%.

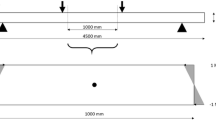
The 7 boards were subjected to edgewise bending tests under four-point loading according to EN 408:2011 [46] to obtain their static longitudinal modulus of elasticity (EL). The boards were planed before testing to a final dimension of 29 × 116 × 3042 mm3. The test span was set at 18 times the depth (width of cross-section). Table 1 shows the result obtained for each board (identified with a reference number that will also identify the splitting specimens to be extracted from each of them). Table 1 also includes the densities (ρ) determined from its dimensions and total weight for a reference moisture content of 12%.

Table 1 Density and longitudinal modulus of elasticity of E. globulus boards
Full size table

The mechanical properties of the material required in the different analytical models for the splitting analysis carried out in the present work (see Sect. 3) are the longitudinal modulus of elasticity (EL), the shear modulus of elasticity in the LR plane (GLR), the tensile strength perpendicular to the grain (ft,90), and the fracture energy in Mode I loading in most of the models (GIc) and in Mode II (GIIc).

The EL value of each splitting specimen was taken from the board from which it was extracted. The rest of the material properties (GLR, ft,90, GIc and GIIc) were taken from previous experimental work by the authors.

Specifically, for the determination of GLR and ft,90, eucalyptus boards with similar EL and ρ to those referred to above were used. A mean value of GLR = 1926 MPa was obtained from compression tests on ten small clear specimens [9] and a mean value of ft,90 = 7.5 MPa from perpendicular-to-grain tensile tests on thirty-six specimens [10].

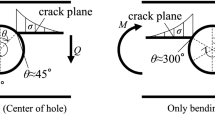
Regarding the fracture properties of E. globulus, the evaluation of Mode I fracture energy is detailed in [43] and [44] using Double Cantilever Beam (DCB) specimens (Fig. 1a). A mean value of the critical strain energy release rate GIc = 0.77 N/mm was derived from the resistance curves (R-curves) following the compliance-based beam method (CBBM) as a data reduction scheme. This method was also applied to determine the critical strain energy release rate in Mode II loading from end-notched flexure (ENF) tests (Fig. 1b), resulting in a mean value of GIIc = 1.54 N/mm [45].

Fig. 1
figure 1

a Double cantilever beam test; b end-notched flexure test

Full size image

Table 2 summarises the mean values of these properties that will be considered in the different analytical models to study the splitting behaviour of E. globulus.

Table 2 Number of specimens (n), mean value, and coefficient of variation (CoV) of the different properties of E. globulus
Full size table

2.2 Splitting tests

32 splitting tests were conducted on planed E. globulus specimens of 29 × 116 mm2 cross-section, 580 mm length and 500 mm span. This and similar cross-sections are readily available in this species.

Two series of three-point bending tests were carried out on single and double dowel connections with different arrangements of loaded edged distances (he):

  1. (a)

    A single steel dowel of d = 16 mm diameter and of S355 quality placed in the middle of the beam. Three he were evaluated: 2d , 3d and 4d (32 mm, 48 mm, and 64 mm) (Fig. 2a). The relative height of the connection is sometimes simplified by the parameter α (= he/h). The configurations mentioned correspond to α values of 0.27, 0.41 and 0.55, respectively (test data reported in the literature have shown that α values up to 0.7 may fail by splitting [37], with the splitting check restricted to α ≤ 0.7 in the former German standard [28]). It should be noted that he = 4d corresponds to the minimum loaded edge distance set out in Eurocode 5 [30], but there is always the possibility of execution errors when drilling holes on site, which are particularly relevant in structures with small depth elements, such as the ones studied here. Between seven and nine beams were tested for each configuration.

  2. (b)

    Two steel dowels in a row of d = 16 mm in diameter and quality S355, spaced 3d (48 mm) apart between their centres and placed at he = 4d (64 mm) as shown schematically in Fig. 2b. Eight beams were tested with this layout.

Fig. 2
figure 2

Connection geometries: a Single-dowel; b double-dowel

Full size image

The diameter of the steel dowels was chosen to be sufficiently thick to prevent yielding. These were loaded by two outer plates made of Eucalyptus globulus with characteristics similar to those of the beams (note that no embedment damage occurred in the plates). A load cell of 50 kN maximum capacity was used. The tests were carried out at a constant cross-head displacement rate of the test device, adjusted to reach failure in approximately 5 min (2 mm/min, 1 mm/min and 0.5 mm/min for he = 4d, he = 3d and he = 2d layouts, respectively, in the single-dowel tests; 0.7 mm/min velocity in the double-dowel tests). During the loading process, the applied load (P) and the displacement (δ) were recorded. For the latter, two Linear Variable Differential Transformer (LVDT) displacement sensors, Solartron AX/10/S, with ± 10 mm measurement range and 20 mV/V/mm sensitivity, were used: one was located on the middle bottom side of the specimen and the other at the top of the steel dowel.

3 Analytical models studied

The considered analytical fracture mechanics models for the analysis of the splitting capacity of beams loaded perpendicular to grain by connections are shown in Table 3. A comprehensive review of most of these approaches can be found in [35, 41]. Therefore, in this work, only a summary of these models will be presented. Most of the models are related and appear as special cases of a general one, where the failure load is determined for a linear elastic body loaded with a single force, based on the energy balance approach [47] and the fracture mechanics compliance method according to Eq. (1):

$$P_{u} = \sqrt {\frac{{2G_{f} }}{{\frac{dC(A)}{{dA}}}}}$$
(1)
Table 3 Analytical models for the analysis of the splitting capacity of beams loaded perpendicular to grain by connections
Full size table

being A and C the crack area and the model compliance, respectively.

The different analytical models in Table 3 are derived using Eq. (1) making certain assumptions on how to calculate the compliance C(A), which leads to a good agreement with the experimental data. The external load is assumed to act at a single point in the middle of the beam. The parameters considered by the models are both material and geometrical. The material properties are the fracture energy, Gf (GIc of the Mode I loading in most models); the shear modulus of elasticity, G; the longitudinal modulus of elasticity, E; and the tensile strength perpendicular to the grain, ft. The main geometric parameters are the width of the beam, b; the height of the beam, h; the distance from the connector to the loaded edge of the beam, he; the relative height of the connection, α (= he/h); the shear correction factor, βs, which takes the value of 6/5 for a rectangular cross-section according to ordinary beam theory; the number of rows of dowels parallel to grain, n; and the connection width, ar.

Jensen [34] formulated one of the most general models as an extended version of the original Van der Put and Leijten model [33], which will be discussed below, but without any simplifying assumptions, such as neglecting the normal forces in the cracked parts of the beam. The model was derived considering a cracked beam structure modelled by beam elements, all rigidly connected. The failure load is given by Eq. (2).

Another model which appears as a special case of the model expressed by Eq. (2) was later proposed by Jensen et al. [35], derived this time from considering that the part of the beam below the crack behaves like a beam with fixed ends, of length the crack and depth he. The expression is shown in Eq. (3), which would also be arrived at by assuming h → ∞ for a finite value of he (i.e. α → 0) in Eq. (2), that is, all beams except the beam with depth he are assumed to be infinitely stiff.

When only shear deformations are considered and thus bending deformations are neglected (i.e., finite G, E → ∞), the ratio G/E → 0 and Eq. (3) is reduced to the form expressed in Eq. (4). This expression is similar to the solution proposed by Larsen and Gustafsson [36] when βs = 1 is assumed.

A renowned simple analytical model that forms the basis for the design in Eurocode 5 [30] is the one proposed by Van der Put and Leijten [33] expressed in Eq. (5). Due to the similarity in behaviour, the same principle was followed as in the mechanical fracture model for the splitting of beams with notches previously derived by Van der Put [32]. The expression is obtained by analysing the cracked state of a beam under an energy balance approach when the joint load is perpendicular to the grain near the loaded edge, using experimental results from the literature as calibration. Although today it is still the model basis of the normative expression, it has been subject to subsequent alterations and adjustments by different researchers. In this sense, the resulting expression could again be seen as a special case of the general model presented in Eq. (2) neglecting bending deformations and taking into account only shear deformations (that is, G/E → 0) and βs = 6/5 for rectangular cross-section. In the cases where he/h → 0, the van der Put model would lead back to the solution presented in Eq. (4).

Ballerini [37] proposed a semiempirical model given by Eq. (6), in an effort to better fit the experimental data than using the van der Put and Leijten formula for single-dowel connections. The work also provides an approach for multiple-dowel connections and is further elaborated with parametric numerical analysis by Ballerini and Rizzi [48]. It considers the influence of the connection width and depth using correction functions applied to the single-dowel formula. In particular, the correction factor to account for the influence of the width of the connection is fw = 1 + 0.75(lr + l1/h) ≤ 2.2, where lr is the spacing between the dowels and l1 is the distance between the dowel clusters (this correction function will be applied in the case of double dowel connections studied in the present work).

Jensen postulated other analytical models based on the beam-on-elastic foundation (BEF) [38]. In this case, the crack plane is modelled by springs to which the fracture properties are assigned. After cracking, the beam below the fictitious fracture layer is considered as a beam resting on elastic Wrinkler springs connected to the upper part, which is assumed to be infinitely rigid (foundation). For a single load acting far from the end of the beam and small crack lengths, the failure load is given by Eq. (7), where γ is the effectiveness factor. Unlike the models mentioned above, this expression includes the tensile strength ft in the parameter ζ, and the splitting failure load is not proportional to the square root of the fracture energy. Therefore, solutions cannot be encompassed within either linear elastic fracture mechanics (LEFM) or nonlinear fracture mechanics (NLEFM). They belong to quasi-nonlinear fracture mechanics, and LEFM solutions are considered special cases.

Assuming E → ∞ or ft → ∞ in the analytical approach of Eq. (7), the solution Pu = Pu,LEFM would be obtained. The same solution could also be derived from Eq. (4) for βs = 6/5, and from Eq. (5) when he/h → 0. Therefore, it seems feasible to use, as Pu,LEFM in Eq. (7) the linear elastic fracture mechanics solution given by Eq. (5). In this way, the analytical model expressed by Eq. (8) is obtained. When he/h → 0, Eq. (8) leads to Eq. (7), and when E → ∞ or ft → ∞ it becomes Eq. (5). Equation (8) is therefore a semi-empirical generalization of Eq. (7) that considers the effect of the total beam height.

Franke and Quenneville [39] presented a complete approach based on a quadratic failure criterion in which fracture modes I and II for tension and shear are considered using the corresponding fracture energies GI and GII. It should be noted that virtually all fractures are, in fact, mixed-mode fractures, but the mixed-mode ratio is not considered by the aforementioned compliance method. As the GI of wood is usually much lower than the GII, the GI is usually considered in most splitting models as a conservative assumption and reasonably accurate approximation, but the mixed-mode fracture energy would represent the most realistic situation. The Franke and Quenneville formula also takes into account the width of the connection and the number of rows of dowels, and they found that the geometry of the connection influenced the ratio between fracture modes I and II. The design proposal is given by Eq. (9) as a result of an experimental and numerical investigation by finite element analysis of more than 100 different connection arrangements.

All of the above models are similarly acceptable from a modelling perspective. From a practical design point of view, simple and robust models seem to be more attractive.

4 Results and discussion

4.1 Experimental failure loads

The failure behaviour of the series of specimens with one and two dowels in a row and different distances from the loaded edges subjected to splitting tests is herein presented.

In the single-connection tests, a main crack could always be observed growing from both sides of the dowel (Fig. 3a). This crack developed at slightly different positions, starting at the mid-down part of the dowel contact. The smaller the loaded edge distance, the faster the crack developed with respect to the maximum load capacity. In these test groups, the crack never reached the ends of the beam.

Fig. 3
figure 3

a Representative failure behaviour of single-dowel test series; b detail of the local failure around the dowel for the three loaded edge distances

Full size image

Some of the specimens with the largest loaded edge distance (4d) showed embedding deformations under the dowels, but no bending of the dowels, as well as some cracks with small lengths beside the dowel (Fig. 3b). The beams with 2d and 3d loaded edge distances did not exhibit any significant embedment under the dowels. In any case, the brittle failure was always characterised by one main crack.

Regarding the double-dowel tests, a similar crack growth process was observed as for the single-dowel batches in the sense that just one main crack developed on both sides of the beams. However, in all tests, the crack reached the beam ends, producing a complete separation of the specimen into two parts with a very brittle and sudden failure (Fig. 4a).

Fig. 4
figure 4

a Representative failure behaviour of the double-dowel test series; b detail of local failure around the dowels

Full size image

No embedment deformations were observed under the two dowels (Fig. 4b, unlike in the case of a single dowel for the same loaded edge distance (4d), as the bearing area increases with the two closely spaced dowels.

These failure modes are well represented by the corresponding load versus displacement curves measured at the top of the dowels. The results of the single-dowel splitting tests are shown in Fig. 5a, which reveal the different failure behaviour of the investigated connection arrangements.

Fig. 5
figure 5

Load–displacement curves. a Single-dowel splitting tests with 2d, 3d and 4d loaded edge distances; b double-dowel splitting tests with 4d loaded edge distance

Full size image

As can be seen, the load–displacement curves obtained from the beams with the greatest edge distance (4d) show a ductile behaviour characterised by embedment stresses and yielding followed by hardening. The connection is still able to force a splitting failure after considerable slip, although splitting is not the primary failure mode. On the contrary, a brittle failure response is displayed for lower edge distances (3d and 2d).

The load–displacement curves of the double-dowel splitting tests with a 4d loaded edge distance are shown in Fig. 5b. In this case, a clear brittle behaviour is observed in all specimens for the α-value studied.

Failure loads (Pu) achieved in all splitting tests for the beams with single- and double-dowel arrangements as well as the mean value, the standard deviation (SD) and the coefficient of variation (CoV) are compiled in Table 4.

Table 4 Failure loads from the single- and double-dowel splitting tests
Full size table

As can be seen from the results of the single-dowel beams, the load-carrying capacity increases with increasing loaded edge distance.

The failure loads reached by the beams with two dowels are not necessarily twice as high as those achieved by the beams with a single dowel arrangement at the same loaded edge distance 4d (α = 0.55), but the mean value is only slightly higher (21% higher). These results are in agreement with those obtained by Quenneville and Mohammad [49], who tested different connection arrangements on spruce-pine glulam beams, including series of one and two fasteners spaced horizontally 5d apart, with α = 0.6. The mean maximum loads in the case of double fasteners were found to be 23% higher compared to the single connection. Previous experimental investigations by Reshke [50] for the same material and joint geometry as specified for [49], also resulted in a small difference of approximately 14% higher failure load for specimens with two dowels compared to those with one dowel.

The fact that two closely spaced dowels give basically the same splitting failure load as a single dowel was also stated by Kasim and Quenneville [51] using the concept of cluster (group) of fasteners. In their research, the capacity of two rows of bolts separated 4d in the direction parallel to the grain turned out to be lower or statistically not different from that of one row of bolts on spruce glulam beams with α = 0.44 and α = 0.70. As the spacing of the rows increased, so did the splitting capacity of the connection. The two-row joint behaved almost as two separate single rows if the spacing between the rows was ≥ 2he (75% of twice the capacity of the one-row connection was obtained). The angle of load distribution from a bolt towards the loaded edge was estimated to be 45°. In this regard, the former German code [28] limited to less than 0.5h the distance between groups of fasteners in the direction parallel to the grain to be considered as one group. For distances ≥ 2 h between them, they are treated as separate groups. For distances between 0.5h and 2h, the groups are considered as one group, but a reduction factor is applied. Quenneville and Mohammad [49] stated that a connection can be assumed to be one cluster if the distance parallel to the grain between the rows of bolts does not exceed he. The assumed angle of load distribution was 63º in this case.

4.2 Comparison of theoretical and experimental failure loads

The adequacy of the different analytical models compiled in Sect. 3 based on fracture mechanics for the prediction of the splitting capacity in timber connections loaded perpendicular to the grain in relation to the experimental data obtained for eucalyptus is discussed here. The material properties EL, GLR, GIc, GIIc and ft,90 experimentally determined for this species (Sect. 2.1) were used as input parameters in the corresponding models.

The ratios of the theoretically predicted failure loads to the experimental values for the single connection arrangement are presented in Table 5. These ratios normalise the strength estimates, allowing for easier comparison. Ratio < 1 represents a conservatively predicted connection strength; ratio ≈1 means an accurately predicted connection strength; and ratio > 1 depicts an overpredicted connection strength.

Table 5 Theoretical vs. experimental failure load ratios of single-dowel connection tests
Full size table

Figure 6 shows graphically these failure load ratios for the single-dowel connection. The results of the he = 2d specimens are represented in red, he = 3d in blue, and he = 4d in green. The results of each analytical model compiled in Table 3 are represented by a different symbol.

Fig. 6
figure 6

Experimental versus theoretical failure loads predicted by the analytical models for single dowel connections

Full size image

As can be observed from Table 5 and Fig. 6, most analytical models overpredict the splitting capacity for single-dowel beams of eucalyptus, which could lead to a dangerous design situation.

The models given by Eqs. (2) and (5) produce the worst predictions in single-dowel specimens (it should be noted that Eq. (5) is the basis for the Eurocode 5 splitting capacity formula). This performance is in line with that obtained by Jensen et al. [35] in research using Radiata pine LVL beams. In such research, Eqs. (2) and (5) did not lead to good agreement with the experimental data if the fracture energy obtained by the single edge notched beam (SENB) fracture tests was used directly. However, the agreement was fair if the fracture energy estimated from plate specimen tests was used instead, as its formulation is closely related to the models given by these two equations. This fact seems to suggest that the linear fracture mechanics model, on which Eqs. (2) and (5) are based on, may have some shortcomings.

The models given by Eqs. (3) and (4) provide better predictions than Eqs. (2) and (5) but still overestimated. It is worth noting that the former are just special cases of the latter. A similar overestimation is also found by the semiempirical Ballerini model expressed by Eq. (6).

Equation (7) stands out with the best predictions of experimental results in eucalyptus from all models related to the original Van der Put and Leijten equation, where only Mode I is taken into account in terms of fracture energy (Eqs. (2)–(8)). These findings are in line with those of Hindman et al. [52] and Patel and Hindman [53], who concluded that Eq. (7) performed better than Eq. (5) for Southern pine machined stress rated (MSR) lumber, laminated veneer lumber (LVL) composed mostly of southern pine with some eucalyptus, and also for yellow poplar parallel strand lumber (PSL). This can be justified by the fact that in Eq. (7), the tensile strength perpendicular to the grain of the member is added besides the fracture energy. It is worth remembering that Eq. (7) is enclosed within quasi-nonlinear fracture mechanics and the LEFM model described by Eq. (5) could be considered a special case of it.

Equation (8) also includes the tensile strength perpendicular to the grain, and it should be recalled that it was postulated as a semi-empirical modification of Eq. (7) to take into account the total height of the beam. Thus, in the work of the authors who formulated this model [35], Eqs. (7) and (8) gave similar predictions on Radiata pine LVL beams with two dowels aligned along the grain, when the distance to the loaded edge was 4d (α = 0.21). However, for larger loaded edge distances of 8d (α = 0.43), predictions from Eq. (8) were clearly better. However, this improvement in results using Eq. (8) instead of (7) is not satisfied in the eucalyptus beams of the present study for any configuration of loaded edge distances in single-dowel joints (nor in beams with two dowels, as will be seen below).

The only model that provides a conservative prediction of splitting failure for most of the eucalyptus specimens tested with a single dowel connection is the one presented by Franke and Quenneville (Eq. (9)) [39], which, unlike the previous ones, also considers the fracture energy in Mode II as a material parameter. In this respect, the authors stated that the fracture values achieved showed that the geometry of the connection, the distance from the loaded edge, and the depth of the beam influence the relationship between fracture Mode I and Mode II.

Regarding the influence of loaded edge distance on the theoretical/experimental ratios, there seems to be a tendency for the mean ratio to increase as the distance increases from 2 to 3d for all models. However, in the case of the 4d distance, the ratio decreases to a greater or lesser extent for most models. Even so, the magnitudes of the differences are not uniform. Uniformity of the trends of the theoretical/experimental ratio in relation to the loaded edge distance was also not found by Hindman et al. [52] using the models described in Eqs. (5) and (7) for beams with the same span/depth ratio as those studied in the present work.

Similarly, the ratios of the theoretically predicted failure loads to the experimental values of the specimens with double-dowel connections are presented in Table 6, together with the main values of each set of results.

Table 6 Theoretical vs. experimental failure load ratios of double-dowel connection tests
Full size table

A visual comparison of these failure loading ratios for the double-dowel connections is shown in Fig. 7, where each symbol represents the ratio obtained using a different analytical model.

Fig. 7
figure 7

Experimental versus theoretical failure loads predicted by the analytical models for double dowel connections

Full size image

For this arrangement, the Eq. (7) based on quasi-nonlinear fracture mechanics and including tensile strength perpendicular to the grain, again stands out, being in this case the one that provides the most conservative predictions. In any case, it is worth noting that for the two-dowel configuration, there is a higher number of specimens giving ratios below 1 compared to the single dowel arrangements, although most analytical formulations were developed considering a single connector (and mostly softwoods).

Although all the models studied give load capacity predictions closer to the experimental values for beams with two dowels than for single dowels, Eqs. (2) and (5), the latter basis of the Eurocode 5 formula, are again the least appropriate for eucalyptus.

The models described by Eqs. (6) and (9) are the only ones in the studied that include some parameter related to the multiple dowel connection. In particular, Eq. (6) includes a correction factor for the splitting capacity to account for the influence of the connection width (fw = 1.31 for the double connection studied), but also gives a poor prediction of the experimental values (ratio = 1.34, see Table 6). However, if this correction factor had not been considered, the average value of the experimental versus theoretical failure load ratio would result in 1.02, similar to the ratios obtained using Eq. (4), and therefore significantly better predictions than considering the correction factor.

In turn, Eq. (9) formulated by Franke and Quenneville, considering the mixed mode of fracture, again gives good estimates of the experimental values, as in the case of single bolt connections, although this formula was calibrated using spruce laminated beams [39] and extended to Radiata pine LVL [54].

The results suggest that more comprehensive analytical models, where more material parameters are considered, such as Mode I and II fracture energies and tensile strength perpendicular to the grain, lead to more reliable predictions. In any case, further studies with different connection geometries and species and products should be performed to come up with an expression that can be optimally applicable to hardwoods.

4.3 Applicability of the Eurocode 5 expression

As mentioned above, a manifestation of Eq. (5) proposed by van der Put and Leijten [33] appears in Eurocode 5 [30] as a specific splitting capacity check for connections in softwoods loaded perpendicular to the grain (however, application to hardwoods and other wood-based products is not specified). It considers the verification of the shear force acting on the beam by the following expression,

$$F_{v,Ed} \le F_{90,Rd}$$
(10)

being \(F_{v,Ed} = \max \left( {F_{v,Ed,1} ,F_{v,Ed,2} } \right)\), where Fv,Ed,1 and Fv,Ed,2 are the design shear forces acting on both sides of the joint.

For softwoods connected by fasteners other than punched metal plates type, the characteristic value of the splitting load is described in the code as,

$$F_{90,Rk} = bC_{1} \sqrt {\frac{{h_{e} }}{{1 - \frac{{h_{e} }}{h}}}}$$
(11)

where b and h are the width and depth of the beam, respectively, he is the distance from the loaded edge to the dowel location, and C1 = 14 N/mm1.5. From its origins, this 14 value derives from what is known as the apparent fracture parameter, (GGc)0.5, which represents the square root of the shear modulus, G, times the critical energy release rate, Gc, in the form C1 = (GGc/0.6)0.5.

The apparent fracture parameter was used by Van der Put and Leijten as a fitting parameter by taking test data from a limited number of sources with different connection types. The mean lower bound of the apparent fracture parameter of 12 N/mm1.5 was selected, leading to a factor C1 = 15.5 N/mm1.5. To obtain a characteristic value, the factor C1 was further reduced to 15.5⋅2/3≈10 N/mm1.5, and this was the value suggested for use in the code design criterion. Even so, the value finally adopted by Eurocode 5 was C1 = 14 N/mm1.5, which corresponds to an apparent fracture parameter of (GGc)0.5 = 10.84 N/mm1.5 (= 14·0.60.5).

This apparent fracture energy parameter assumed in the expression of the European code has been discussed since its origins. Some studies suggest obtaining individual C1 factors for each species [54] as GI fracture energy values are not specified in Eurocode 5 or related product standards. Therefore, a comprehensive experimental determination of this parameter would be desirable for each species or wood product.

Proceeding in a similar way to that mentioned above, the values of factor C1 of the Eurocode 5 formula that would correctly predict the experimental failure loads obtained for eucalyptus are shown in Table 7. As can be seen, the lowest characteristic value of factor C1 (calculated as 2/3C1) results in 19.45 N/mm1.5, which is 1.39 times the value established by Eurocode 5 for softwoods (C1 = 14 N/mm1.5).

Table 7 Factor C1 of Eq. (11) that would predict the experimental failure loads of eucalyptus
Full size table

However, when considering the mean values of G and Gc obtained from the experimental tests on Eucalyptus globulus (GLR = 1926 MPa and GIc = 0.77 N/mm, respectively), the apparent fracture parameter (GGc)0.5 results in 38.51 N/mm1.5. It leads to a C1 = 49.71 N/mm1.5, which can be reduced by 2/3 and gives the characteristic value of 33.14 N/mm1.5, 2.37 times the value stablished by Eurocode 5 and higher than the value obtained from the process shown in Table 7. This high C1 value of eucalyptus respond to the high performance of hardwoods compared to softwoods due to their anatomical differences.

The splitting capacity of the eucalyptus specimens was also predicted by directly applying the Eurocode 5 formula developed for softwoods (Eq. (11)), where C1 = 14 N/mm1.5. The results are presented in Table 8. In this case, the design capacity does not explicitly depend on any material parameter. The only input parameters are the beam depth and width and the loaded edge distance from the dowel. The results were adjusted to the design values to account for the type of material, the duration of loading, and the effects of the moisture content (kmod = 0.9 and γM = 1.3). Table 8 also includes the averages and CoV values of the design factor of safety (DFS) for each configuration, defined as the ratio of the test capacity strength to the Eurocode 5 design splitting capacity.

Table 8 Characteristic and design values of the eucalyptus splitting capacity applying the Eurocode 5 expression and design factors of safety (DFS)
Full size table

The DFS values generally ranged between 2.5 and 4.6, with no clear trend with respect to the loaded edge distance. Therefore, the prediction formula included in Eurocode 5 for softwoods is prone to underestimate the splitting capacity of the eucalyptus specimens, leading to very conservative predictions.

5 Conclusions

The results of the splitting capacity of Eucalyptus globulus L. beams loaded perpendicular to the grain by single and double steel dowel connections with different loaded edge distances are provided. These are essential preliminary data to gain knowledge on the splitting behaviour in hardwoods as there is no specific equation for its prediction included in Eurocode 5, only for softwoods.

From the experimental study for the geometry of the tested beam, the load carrying capacity considering a single dowel increases with increasing distance to the loaded edge. Distances of 4d result in ductile failures and smaller distances in brittle failures. However, in the case of two dowels at 4d, the load carrying capacity is similar to that of one dowel and the failure is clearly brittle. This is of particular relevance, as the Eurocode 5 formula does not take into account the number of dowels.

Of the eight analytical models based on fracture mechanics studied (including the model basis of the Eurocode 5 formula) and considering the actual eucalyptus properties required as input of these models, in general, all of them overestimate the splitting failure load of single-dowel eucalyptus beams, except the only model that considers Mode II fracture energy in addition to Mode I fracture energy in its expression. For the double dowel layout, an analytical model based on quasi-nonlinear fracture mechanics, which also includes the tension perpendicular to grain of the member, provides the most conservative predictions and also good agreement for the single dowel beams. In all arrangements, the analytical model basis of the Eurocode 5 expression gives the worst agreement with the experimental eucalyptus results.

The splitting capacity formula adopted by Eurocode 5 for softwoods, which does not take into account any material parameter, only the depth and width of the beam and the distance from the dowel to the loaded edge, proves to be very conservative in predicting the ultimate failure load of Eucalyptus globulus with the connection geometries analysed in this study.

Further experimental research on the splitting behaviour of this and other hardwood species would be desirable in order to derive an optimal general formula valid for all of them, taking into account the different material properties, as well as the geometry and type of connection.