Century-long expansion of hydrating cement counteracting concrete shrinkage due to humidity drop from selfdesiccation or external drying

Abstract

A physically based model for auotgenous shrinkage and swelling of portland cement paste is necessary for computation of long-time hydgrothermal effects in concrete structures. The goal is to propose such a model. As known since 1887, the volume of cement hydration products is slightly smaller than the original volume of cement and water (chemical shrinkage). Nevertheless, this does not imply that the hydration reaction results in contraction of the concrete and cement paste. According to the authors’ recently proposed paradigm, the opposite is true for the entire lifetime of porous cement paste as a whole. The hydration process causes permanent volume expansion of the porous cement paste as a whole, due to the growth of C–S–H shells around anhydrous cement grains which pushes the neighbors apart, while the volume reduction of hydration products contributes to porosity. Additional expansion can happen due to the growth of ettringite and portlandite crystals. On the material scale, the expansion always dominates over the contraction, i.e., the hydration per se is, in the bulk, always and permanently expansive, while the source of all of the observed shrinkage, both autogenous and drying, is the compressive elastic or viscoelastic strain in the solid skeleton caused by a decrease of chemical potential of pore water, along with the associated decrease in pore relative humidity. As a result, the selfdesiccation, shrinkage and swelling can all be predicted from one and the same unified model, in which, furthermore, the low-density and high-density C–S–H are distinguished. A new thermodynamic formulation of unsaturated poromechanics with capillarity and adsorption is presented. The recently formulated local continuum model for calculating the evolution of hydration degree and a new formulation of nonlinear desorption isotherm are important for realistic and efficient finite element analysis of shrinkage and swelling. Comparisons with the existing relevant experimental evidence validate the proposed model.

1 Introduction and objective

It is usually required that concrete structures such as bridges be designed for a lifespan of at least hundred years. But durability problems often shorten the lifespan drastically [1,2,3]. Although studied for more than a century, they are not yet understood satisfactorily. The long time volume changes of concrete are a parituclar problem.

The difficulty is to find a model that agrees with all the basic experimentally observed phenomena and, in particular, captures the interaction of creep, shrinkage, pore humidity changes, water transport, and cement hydration. The general form of such a model was proposed in Bažant et al. [4] and was developed in more detail in Bažant et al. [5]. In this study, this previous model is refined, put on a solid thermodynamic basis, and made comprehensive so that it would agree with all the basic types of experiments reported in the literature. They include:

• 1. Autogenous shrinkage tests of long duration.

• 2. Long-time drying shrinkage tests for specimens of various sizes, in which the autogenous shrinkage is under way in the core until the drying front arrives.

• 3. Long-time tests of swelling under water and in fog room, for specimens of various sizes.

• 4. Measurements of the evolution of pore humidity in selfdesiccating sealed specimens.

• 5. Tests of sorption isotherms.

• 6. Abuhaikal et al.’s [6] test of a specimen under constant saturation and constant pore pressure.

A selection of some of these tests, e.g., drying and autogenous shrinkage, can be described by diverse models. But a model that fits them all ought to be virtually unique. Its formulation is our objective.

The analysis that follows recognizes that data fitting must employ realistic models for: (1) creep [7], (2) hydration [8], (3) moisture diffusion [9], and (4) cracking damage due to tensile stresses caused, e.g., by drying shrinkage (for 2 and 3, see “Appendices 1 and 2”).

2 Some basic phenomena

A serious problem with most models has been that they assume the autogenous shrinkage, drying shrinkage and swelling to terminate with a horizontal asymptote. This erroneous assumption has been caused by scarcity of long-time tests and by the widespread deplorable habit to plot the observed data in a linear time scale, which cannot reveal the long term trend. There exist, nevertheless, a few test data [10, 11] whose logarithmic scale plots document that no asymptotic bound is approached even after 30 years (Fig. 1a, b). The present analysis shows that the autogenous shrinkage and swelling evolve logarithmically for decades, and probably even for centuries. What is the physical source of such behavior?

Fig. 1

Long-term measurements of volume changes: a autogenous shrinkage, b swelling

To answer this vital question, consider first the autogenous shrinkage, which is, in modern concretes with low water-cement ratios and certain admixtures, much more intense than it used to be decades earlier. Following Bažant et al. [5, 12], its primary cause must be the decrease of pore relative humidity h during selfdesiccation, which is physically no different from a decrease of h due to external drying. It is inconceivable that shrinkage would be caused by pore humidity drop due to external drying and not due to selfdesiccation.

According to RILEM TC 196-ICC [13], the selfdesiccation is defined as the “reduction of the relative humidity, h, in a sealed system when empty pores are generated”. However, the wording of this definition is unrealistic and misleading. Empty pores are unlikely to be ‘generated’.

Fig. 2

a Subsequent menisci of increasing curvature receding into a narrowing pore as a vapor bubble expands into the pore during selfdesiccation or external drying, and b evolution of pore relative humidity in pores with different sizes

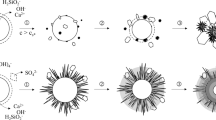
Vapor bubbles must form in liquid water at the time of set, produced by precipitation of dissolved gases or triggered by various dissolved ions. But they must immediately coalesce into large sparse bubbles of smallest possible surface curvature in the biggest pores [14]. Later on, generation of new vapor bubbles is not necessary, and is even very unlikely, due to the high resistance of liquid water to cavitation. What is doubtless happening is that the existing pore vapor space expands at decreasing h as the existing capillary menisci increase their curvature and gradually recede into narrower and narrower pores; see Fig. 2. This is how selfdesiccation mechanism should be explained.

Consequently, the main source of the long-term autogenous shrinkage is the long-lived hydration reaction (for its prediction, see “Appendix 1”). It was a widely held belief that the hydration stops after about 1 year. However, that can be correct only for specimens thin enough to dry up uniformly within a year. In the cores of a massive wall exposed to drying, high enough h may persist for decades, even for centuries.

What causes the hydration process to be long-lived and progressively slower is that, after the first day, the anhydrous cement grains become enveloped in contiguous shells of cement hydrate. These shells have very low permeability, and the transport of water toward the anhydrous grain interface is very slow. In addition, as these shells gradually thicken, the pore relative humidity, h, as well as the chemical potential of water, $\mu$, decreases, causing the hydration to slow down further (which experimentally illustrated by [15,16,17,18] and mathematically described by Rahimi-Aghdam et al. [8]). If h in the pores is not below about 0.8, the hydration reaction proceeds logarithmically for many decades, probably even for centuries. This causes similar long-time evolution of autogenous shrinkage.

Locally, at a point of macroscale homogenizing continuum, all the phases of water must be in thermodynamic equilibrium. This means that the chemical potential $\mu$ in all the phases must be the same. Therefore, a decrease of pore humidity h must produce tensile stress changes in all the phases of water (i.e., the vapor, liquid, and free and hindered adsorbed water). These stress changes must be balanced by compressive stress changes in the solid skeleton, which in turn must cause some compressive elastic deformation and creep in the solid skeleton of cement paste.

When immersed in water, most concretes swell. There exist data showing that the swelling is also a long-lived, multi-decade, phenomenon. Specimens immersed for a decade continue to expand logarithmically, with no bound in sight [10]. In these specimens, the pores near the surface must be saturated, $h=1$, and those in the core must undergo selfdesiccation until the water saturation front arrives. Since these specimens were not thick, the relative humidity was near saturation in all pores. Therefore, expansion cannot be driven by a change of pore humidity, which was almost constant throughout the experiment. The remaining reasonable candidate to drive the swelling is the expansiveness of hydration. Because it is inconceivable for the hydration to be both expansive in water immersion and contractive without immersion, the swelling must be driven by chemical expansion during hydration.

Indeed, if the hydration were contractive, the swelling in water immersion would not be physically explicable. But if it is expansive, both the swelling and the (autogenous and drying shrinkage) become explicable. Thus, in contrast to traditional thinking, we have a new paradigm (proposed in 2015 [4, 5]): The cement hydration is permanently expansive in terms of apparent volume (solid with pores) although the absolute volume of hydration products is smaller than initial reactants (chemical shrinkage).

There is another phenomenon that probably also prolongs shrinkage, whether autogenous or drying—nanoscale viscoelasticity (Bažant et al. [12]) of the solid skeleton of the hardened cement paste. The increase of capillary tension, the increase of solid surface tension on nanoscale globules of hydrated cement, and the decrease of disjoining pressure of hindered adsorbed water in nanopores (< 3 mm thick), as produced by pore humidity decrease, must be balanced by compressive stress changes in the solid skeleton; see Fig. 3 (all of these stress changes are proportional to $\rho _{l} (RT/M) \ln \, h$, as defined later; cf. [4, 19]).

Fortunately, all the three sources of pressure depend on the relative humidity, h, in a similar way, as follows:

$$p_{i}=C\ln h$$

(1)

where $p_i=$ capillary tension, solid surface tension or disjoining pressure. Therefore, it is logical to consider the average fluid pressure $p_{l}$ to depend on the relative humidity similarly:

$$p_{l}=C_{w}\ln h$$

(2)

where $C_w$ is a coefficient, here considered as empirical. Therefore, h may be used as a parameter controlling all these internal forces.

Fig. 3

Schematic diagram of equilibrium of various internal forces within hardened cement paste

Note in the writers’ opinion, which is not shared by some experts and has not yet been quantitively verified by anyone, the tensile stress changes in the nanopores caused by a drop of disjoining pressure are probably most important. The reason is that the nanopore water is a major part of water content and fills the nanopores completely, whereas the larger capillary pores are unsaturated. The disjoining stress drop must be expected to produce viscoelastic compressive strain in the skeleton, extending shrinkage in the long term, much beyond the drying process termination. But these stress drops (tensile) may be expected to produce smaller compressive volumetric strain than an externally applied pressure since they act, within the nanostructure, only on reduced cross section areas, which alternate with areas under balancing stress change of opposite sign [4].

3 Expansiveness of the hydration reaction in hardened cement paste

Already in 1887, Le Chatelier showed that the cement hydration reaction is always contractive, i.e., the volume of the cement gel produced by hydration is always smaller than the sum of the original volumes of anhydrous cement and water. Later this conclusion was supported by Powers and others. However, this conclusion is valid only in terms of absolute volume, not bulk volume (apparent volume). In the bulk, with a sufficient pore volume growth and constant relative humidity in the pores, the porous hydrated cement must always expand, even if the volume of the solid phase in the material decreases (for analogy, imagine a truss in which the bars are growing longer while the cross sections are shrinking even more to reduce the bar weight).

In hardened portland cement paste, the growth of two mutually contacting C–S–H shells around neighboring anhydrous cement grains must push the neighbors apart; Fig. 4. This must cause volume expansion of the porous skeleton of cement paste during hydration [4]. The compression force within each pair of contacting neighbors, akin to the crystal growth pressure, must be balanced by overall tension in the solid skeleton of cement paste. Like hydration, the overall tension evolves for decades, and so does the swelling. Thus the long-term hydration causes not only autogenous shrinkage, via selfdesiccation, but also swelling. Furthermore, the long-time loading of the solid skeleton by pore pressure must, of course, produce not only elastic deformation but also creep.

Several studies suggested a different source of swelling—the growth of ettringite crystals [20, 21]. There are two reasons why this could be only one minor contribution and not the basic source of the long-term expansion: (1) Ettringite crystals do not form with a delay of many years. Rather, they dissolve at an early age and thus cannot affect the long-term swelling. (2) The long-term swelling can be seen in any type of cement regardless of the amount of C$_{3}$A phase. Therefore, even if we would admit the ettringite crystal growth to be the cause of swelling in the initial days, it could not explain the swelling in the long term.

The final conceivable source of long-term swelling of concrete is the alkali-silica reaction (ASR). With a typical delay of 20–50 years, it can, of course, engender considerable swelling, but only if the alkali-content of the cement paste is high enough, if the aggregates are reactive, and if the pore humidity remains sufficiently high [22, 23]. This is not the case in normal laboratory experiments.

4 Thermodynamics of unsaturated poromechanics and Biot coefficient

For normal saturated elastic porous materials, the volumetric part of the constitutive equations is written as [24]:

$$\epsilon = \frac{\sigma + b p}{K} = \frac{\sigma _{\mathrm{ef}}}{K}$$

(3)

$$-\,\zeta = \frac{c \sigma + p}{R}$$

(4)

$$\hbox {with}\quad \frac{b}{K} = \frac{c}{R}$$

(5)

where $\epsilon$ = volumetric strain, $\sigma _{\mathrm{ef}}$ = effective stress, $\zeta$ = relative expansion of fluid phase (measured in terms of liquid water); $\sigma$ = volumetric Stress (positive for tension), p = pore pressure (positive for compression), K = bulk elastic modulus of the dry solid skeleton, R = elastic modulus of fluid phase characterizing its compressibility, b = Biot coefficient, c = Skempton coefficient. Equation (5) is a symmetry relation required by the existence of thermodynamic potential, $\varPsi$.

For porous materials fully saturated by liquid water, Biot and Willis [25] proposed the estimate $b = 1 - K /K_{\mathrm{S}}$ where $K_{\mathrm{s}}$ = bulk modulus of the material forming the solid skeleton; for cement paste, $K_{\mathrm{s}}$ = bulk modulus of the C–S–H gel, and $K_{\mathrm{s}}\approx$ = 45 GPa [26]. It must be stressed, however, that this estimate of b cannot be applied to the cement paste and other partly saturated media. The reason is that, due to selfdesiccation beginning right after the set, the hardened cement paste is always unsaturated, containing water vapor, liquid water, adsorbed water and air (usually, the water vapor and air may be combined as a single gas phase).

To deal with the unsaturated case, Coussy et al. [27] ignored the adsorbed water and considered the Helmholtz free energy. Here we take the adsorbed water into account and find it clearer to use the Gibbs free energy, $\varPsi$ (per unit volume of the porous material):

$$\begin{aligned} \varPsi = \frac{\sigma ^2}{2 K} +\varphi (1+\chi \epsilon )[S_{l} \rho _{l} + \varGamma _a(h) + (1-S_{l}) \rho _{\mathrm{v}}] \mu (h) \end{aligned}$$

(6)

$$\begin{aligned} \hbox {where}\quad p_{l}&=\rho _{l} \mu ,\quad \rho _{\mathrm{v}} = \frac{p_{\mathrm{v}}}{RT},\quad \mu = \frac{RT}{M}\,\ln \,h\end{aligned}$$

(7)

$$\varGamma _a(h)=\theta (h) \varGamma _1,\quad \theta (h) = \frac{1}{1-h} - \frac{1}{1 - h + c_T h}$$

(8)

Here $\theta (h)$ is the well-known BET isotherm of gas adsorption in multimolecular layers [19, 28,29,30] (derived mathematically by Edward Teller); $c_T = c_0 e^{\Delta Q_0 /RT}$, $c_0$ = constant, $\Delta Q_0$ = latent heat of adsorption minus latent heat of liquefaction; $\varGamma _a(h)$ = mass of free adsorbed water at pore humidity h per unit pore surface area ($\approx \rho _{l} \times$ effective thickness of adsorption layer); $\varGamma _1$ = constant = value of $\varGamma _a$ for a full monomolecular layer; R = universal gas constant, $\varphi$ = porosity, T = absolute temperature, M = molecular weight of water; $p_{l}$ = pressure in liquid (capillary) water; $S_{l}$ = liquid water saturation degree $\approx$ volume fraction of liquid water per unit volume of porous material; $h = p_{\mathrm{v}} /p_{\mathrm{sat}}(T)$ = relative vapor pressure, or humidity, in the pores; $\rho _{l}, \rho _{\mathrm{v}}$ = mass densities of liquid water and water vapor ($\rho _{l} \approx$ constant, even in the case of unsaturated material); $\chi$ = parameter introduced as an empirical coefficient (close to 1) such that $\chi \epsilon$ represent the relative change of pore volume. Equations (7) are based on the ideal gas equation for water vapor and on the Laplace and Kelvin equations of capillarity [19, e.g.].

Equation (8) is contingent upon the assumption that the surface area of the adsorbed water layers exposed to water vapor is constant. This is not really true, even if there is no change in pore volume due to hydration. The reason is that much of the pore volume in hydrated cement has a width less than 10 molecular layers of water (2.67 nm), and the width of many pores is $<\,$0.5 nm. The adsorbed water layer in such pores completely fills the pore and is not exposed to vapor (while developing disjoining pressure [19]). As the drying penetrates into narrower and narrower pores, more of the surface area gets in contact with vapor and becomes available for free (unhindered) adsorption; see the schematic of a wedge pore in Fig. 2. This phenomenon is neglected in the BET isotherm, Eq. (8). Important though it might be, it is beyond the scope of this study and is solved separately [31] .

The advantage of using the Gibbs, rather than Helmholtz, potential is that the Gibbs free energy per unit mass of the pore water, called the chemical potential, $\mu$, must be the same in all the phases of water (at the same point of homogenizing macro-continuum) [19, e.g.]. For our purposes, we can neglect $\chi \epsilon$ compared to 1 and $\rho _{\mathrm{v}}$ compared to $\rho _{l}$ (for high temperatures, though, it could not be neglected). Then we have

$$\varPsi = \varPsi (\sigma , p_{l}) = \frac{\sigma ^2}{2 K} + \varphi S(h) p_{l}(h)$$

(9)

(10)

Here S(h) = effective volume expansion of the combined liquid and adsorbed phases measured in terms of the liquid phase, such that $S(h) p_{l}(h)$ give the work of the combined liquid and adsorbed water phases per unit pore volume within the material, while stress $\sigma$ works on volumetric strain $\epsilon$; $\varGamma _1/\varphi$ is the mass of monomolecular adsorption layer per unit volume of the pores. Equation (7) shows that capillary pressure $p_{l}$ is controllable as a function of h. Since the independent thermodynamic variables in Gibbs free energy $\varPsi$ are $\sigma$ and $p_{l}$, the first variation of $\varPsi (\sigma , p_{l})$ is

$$\delta \varPsi =\frac{\partial \varPsi }{\partial \sigma }\, \delta \sigma + \frac{\partial \varPsi }{\partial p_{l}}\, \delta p_{l}$$

(11)

$$= \epsilon \, \delta \sigma \, -\, \zeta \, \delta p_{l}$$

(12)

$$\hbox {or}\quad \delta \varPsi=\frac{\sigma }{K}\, \delta \sigma + \varphi \, S(h)\, \delta p_{l}$$

(13)

(if $\delta$ is replaced by d, these equations represent the total, or exact, differential of $\varPsi$). Note that the last term in the last equation can be neither $\varphi \delta (S p_{l})$ nor $\delta (v_f S p_{l})$, since neither S nor $\varphi$ do any work, although they are variable (due to drying or hydration).

According to the Taylor series expansion, the second variation of $\varPsi$ may be written as

$$\delta ^2 \varPsi = \frac{\delta ^2 \sigma }{K} + 2\, \frac{\delta \sigma \, \delta p_{l}}{H} + \frac{\delta ^2 p_{l}}{R}$$

(14)

$$\hbox {where}\quad \frac{1}{K} = \frac{\partial ^2 \varPsi }{\partial \sigma ^2},\quad \frac{1}{H} = \frac{\partial ^2 \varPsi }{\partial \sigma \, \partial p_{l}},\quad \frac{1}{R} = \frac{\partial ^2 \varPsi }{\partial p_{l}^2}$$

(15)

where K, H, R are the poromechanical stiffness moduli of the material, and the symmetry, manifested in the equality of the cross-diagonal coefficient H, is required by the existance of Gibbs potential. It follows that the elastic volumetric constitutive equation of the unsaturated elastic porous material may be written as

$$\epsilon =\frac{\sigma }{K} + \frac{p_{l}}{H} = \frac{\sigma + b\, p_{l}}{K}$$

(16)

$$-\, \zeta =\frac{\sigma }{H} + \frac{p_{l}}{R} = \frac{c\, \sigma + p_{l}}{R}$$

(17)

Here b = Biot coefficient and c = Skempton coefficient,

$$b = \frac{K}{H},\quad c = \frac{R}{H}$$

(18)

According Eqs. (16), (17),

$$\begin{aligned} \frac{1}{K} = \left[ \frac{\partial \epsilon }{\partial \sigma } \right] _{p_{l}},\quad \frac{1}{H} = \left[ \frac{\partial \epsilon }{\partial p_{l}} \right] _{\sigma } = -\, \left[ \frac{\partial \zeta }{\partial \sigma } \right] _{p_{l}},\quad \frac{1}{R} = -\, \left[ \frac{\partial \zeta }{\partial p_{l}} \right] _{\sigma } \end{aligned}$$

(19)

Therefore, the definitions of the Biot and Skempton coefficients are

$$\begin{aligned} b = \left[ \frac{\partial \sigma }{\partial p_{l}} \right] _\epsilon , \quad c = \left[ \frac{\partial p_{l}}{\partial \sigma } \right] _\zeta \end{aligned}$$

(20)

If the porous material undergoes inelastic deformations or change of pore volume due to hydration or microcracking, $\varPsi$ must be considered as a small increment of Gibbs free energy per unit volume, and a similar derivation can then show that Eqs. (16), (17) must be replaced by the incremental volumetric constitutive relation

$$\begin{aligned} \delta \epsilon =\frac{\delta \sigma }{K} + \frac{\delta p_{l}}{H} = \frac{\delta \sigma + b\, \delta p_{l}}{K} \end{aligned}$$

(21)

$$\begin{aligned} - \delta \zeta=\frac{\delta \sigma }{H} + \frac{\delta p_{l}}{R} = \frac{c\, \delta \sigma + \delta p_{l}}{R} \end{aligned}$$

(22)

The equivalent pore pressure, $\pi$, in unsaturated material must be defined as a stress variable that works on the pore volume $\varphi$ when it is imagined to expand by $\text{d}\varphi$. This work is $\pi \, \text{d}\phi$ and the complementary work is $\varphi \, \text{d}\pi$. So, the expression of Gibbs free energy increment may be written as

$$\text{d}\varPsi \, =\, \frac{\sigma }{K}\, \text{d}\sigma + \varphi \ \text{d}\pi$$

(23)

Comparing this to Eq. (13), we conclude that

(24)

$$\hbox {and}\quad \text{d}\sigma _{\mathrm{ef}}\, =\, \text{d}\sigma \, +\, b\, \text{d}\pi$$

(25)

which is the increment of the total stress acting on the solid skeleton.

To allow using thermodynamics, the foregoing derivation had to treat K and H as material constants, which also implied b to be a constant.. Thus the potential, $\varPsi$, applies only to a short time interval in which the progress of hydration is negligible, and is different in subsequent intervals. For an interval with negligible advance of hydration, integration of the last equation gives,

$$\sigma _{\mathrm{ef}} = \sigma + b \pi$$

(26)

The Biot coefficient (as well as K and H) must obviously change if the pore volume $\varphi$ decreases due to hydration or increases due to microcracking. Since Eq. (26) must hold true for any porosity $\varphi$ and any b, differentiation of the last equation furnishes the final general expression for the effective stress increments:

(27)

Fig. 4

Contacting C–S–H shells, surrounding diminishing C$_3$S grains, push each other apart as they grow during hydration

This means that the volume change of an elastic porous solid is $\text{d}(\sigma _{\mathrm{ef}} /K)$. The added term $\pi \,\text{d}b$ is physically supported by the fact that, if the pore volume increases due to, e.g., microcracking, the pore fluid must penetrate the additional pore space $\varphi \Delta b$ and exert on the pore boundary additional pressure $\pi \Delta b$, which is proportional to the added pore volume (because pressure $\times$ volume change = work). This fact is graphically illustrated in Fig. 5.

Fig. 5

The increase of Biot coefficient due to damage adapted from [32]

Note that, for a big change of the Biot coefficient, the term $\pi \text{d}b$ is quite significant. This is the case at the early age of concrete after casting. Unfortunately, the term $\pi \text{d}b$ seems to have been neglected in all the literature. Neglecting this term for a saturated soil with an almost constant Biot coefficient is acceptable, but causes a large error in predicting the deformation of young concrete. This error is discussed in more detail later, at Eq. (54). Note that there is similarity with the variation of Biot coefficient on hydraulic cracks in shale, which was intuitively explained and modeled in Chau et al. [32].

The adsorption part, Eq. (8), has no effect on the present data fitting, because the humidities in the selfdesiccation and swelling experiments are not low enough. But it would matter for various applications.

Note also that the Gibbs free energy, $\varPsi$, cannot be used when the solid skeleton of the material undergoes strain softening, because the response becomes non-unique. In that case, it may be preferable to use the Helmholtz free energy $\varPhi$, which is related to $\varPsi$ by the Legendre transformation:

$$\varPhi (\epsilon , \zeta ) = \sigma \epsilon - p_{l} \zeta - \varPsi (\sigma , p_{l})$$

(28)

In practice, though, this is unimportant. One can simply deal with the solid part as if loaded by $\sigma _{\mathrm{ef}}$.

Since concrete is not elastic but viscoelastic, the expression for the volumetric viscoelastic strain of the porous solid must be generalized as:

$$\epsilon (t) = \int _{0}^{t} J(t, t',h,T) \text{d}\sigma _{\mathrm{ef}}(t')$$

(29)

where $t'$ is the time at which stress increments $\text{d}\sigma _{\mathrm{ef}}(t')$ are applied, and J is the compliance function for creep plus elastic deformation. It should be noted that creep compliance has been considered to be a function of relative humidity, h, and temperature, T, since several studies showed viscosity of concrete depends significantly on relative humidity and temperature.

5 Equations governing both shrinkage and swelling

As established at the dawn of cement research by Le Chatelier and confirmed by Powers and others, the cement hydration reaction is always contractive, i.e., the volume of the cement gel produced by hydration is always smaller than the sum of the original volumes of anhydrous cement and water. So how can the hardened cement paste swell? The reason is porosity. The growth of adjacent C–S–H shells around the cement grains pushes the adjacent shells apart, producing crystallization pressure [4]. This is what causes the porous solid to expand (Fig. 4).

Until now we have disregarded the effect of swelling due to the hydration process. To this end, we can consider an additional pressure (akin to crystal growth pressure) that is induced by the macro-expansive hydration process, $\sigma _{\mathrm{hyd}}$. For simplicity, we can assume it to depend linearly on the hydration degree (for its calculation, see “Appendix 1”). Adding this pressure, we can rewrite Eq. (27) as:

$$\text {d}\sigma _{\mathrm{ef}}=\text {d}\sigma + \pi \,\text {d}b + b\,\text {d}\pi$$

(30)

$$=\text {d}\sigma +\pi \text {d}b + b\left( C_{w}S_{w}\frac{\text {d}h}{h} + C_{\mathrm{hyd}}\text {d}\alpha \right)$$

(31)

where $C_{\mathrm{hyd}}$ is a calibration parameter.

So far we have shown how the pressure should be modified for unsaturated media. However, pressure is not the only parameter that needs modification. Recently, Bažant et al. [5] showed, for unsaturated medium, that the Biot coefficient depends not only on the relative stiffness of matrix to solid constituents, but also on the relative humidity of pores. Fortunately, at high relative humidity values ($h>0.8$) the dependence of Biot coefficient on relative humidity is negligible. Therefore, the traditional definition of Biot coefficient for simulating autogenous shrinkage and swelling when the pore humidity stays high leads to no significant error and is used here. To calculate the Biot coefficient, the effect of aging on the bulk modulus of concrete needs to be determined first. For simplicity, we consider the stiffness of cement paste to be related to the hydration degree linearly:

$$K(\alpha )=K_{u}\left( \frac{\alpha -\alpha _{\mathrm{set}}}{\alpha _{u}-\alpha _{\mathrm{set}}}\right)$$

(32)

The Biot coefficient depends on the bulk modulus K and can be calculated as

$$b(\alpha )=1-\frac{K(\alpha )}{K_{\mathrm{S}}}$$

(33)

Finally, we must introduce a realistic equation for the creep compliance, J, of solid skeleton (dry material) loaded by pore water pressure.

This compliance should be different from the creep compliance of the cement paste as a whole (which includes water in capillary pores and the load-bearing adsorbed water in nanopores). For lack of deeper information, we assume a simple power function:

$$J(t,t',h,T) = \, \alpha _u/\alpha \,\left[ c_{0} +\beta _{\eta }(T,h) c_{1}(t-t')^{n}\right]$$

(34)

where $c_{0}$ corresponds to the instantaneous response; constant $c_{1}$ and exponent n are two calibration parameters; $\alpha$ = hydration degree and $\alpha _u$ = ultimate hydration degree which is function of w/c. The purpose of factor $\alpha _u/\alpha$ is to consider the effect of aging. The effect of this factor is significant at early ages; finally, $\beta _{\eta }(T,h)$ is a function to consider the change of viscosity due to the change of relative humidity or temperature. In this study, the same relation as the one in the XMPS model [7] is used to calculate the $\beta_\eta$.

$$\beta _{\eta }(T,h) = \exp \left[ \frac{Q_{\eta }}{R}\left( \frac{1}{T_{0}} - \frac{1}{T(t)}\right) \right] \left( p_{0} + \frac{1 - p_0}{ 1 + \left( \frac{1-h}{1-h^{*}}\right) ^{n_{h}} } \right)$$

(35)

Now we try to predict the autogenous shrinkage for cement pastes with different water–cement ratios, w/c. A change in w/c changes not only the amount of selfdesiccation but also the strength, as well as stiffness, i.e, Young’s modulus E. Therefore, to predict the autogenous shrinkage correctly, we need a model that can predict the stiffness, E, for different cement pastes correctly. In the literature, there are several empirical models for predicting the stiffness of concrete from its strength $f'_{c}$, but they are not suitable for the hardened cement paste. Therefore, we propose the following simple, empirically calibrated, equation that can predict the stiffness of cement paste for different w/c (Fig. 6a):

$$E = A - B\, {w/c}\quad (A = 52\,\hbox {GPa}, \quad B = 62\,\hbox {GPa})$$

(36)

The Poisson ratio for cement pastes with different w/c is considered the same, $\nu =0.2$.

6 Desorption and resorption isotherms

The dependence of the evaporable water mass, $w_{\mathrm{e}}$, per unit volume of material, on the relative humidity, h, in the pores, at a constant temperature, is called the sorption isotherm. Because of hysteresis, one must distinguish between the desorption isotherm, at drying, and the absorption isotherms, at wetting (the latter is also called the sorption or resorption isotherm). In what follows, we deal only with the desorption isotherm.

Fig. 6

Stiffness of hardened cement paste and desorption: a Decrease of stiffness, or E-modulus, at increasing water-cement ratio, w/c; b nonlinear desorption isotherm anchored by bilinear tangents; c experimental versus simulated desorption isotherms for two different water-cement ratios

To be able to compare the isotherms for different concretes, the sorption isotherm is preferably formulated in a dimensionless form, as a relation between the relative humidity, h, in the pores and the saturation degree, S, which may be defined as

$$S = \frac{w_e}{w_1}$$

(37)

where $w_e$ is the current mass of evaporable water (all per unit volume of concrete) and $w_1$ is the mass of evaporable water at the beginning of desorption, i.e., at $h = 1$. It is important to note that $w_1$ need not, and typically does not, represent the maximum possible mass, $w_{\max }$, of the evaporable water that could be accommodated in the pores. Even at, or above, the saturation vapor pressure (i.e., at $h \ge 1$), the pores need not be, and in reality are not, filled completely (i.e., $w_e < w_{\max }$) because the vapor still exists in numerous bubbles whose menisci are saddle (anticlastic) surfaces with zero or negative total curvature, and because of reverse ink-bottle effects [19, p.825]. Even though no tests of sorption isotherm for $p > p_{\mathrm{sat}}$ exist, the mass, $w_{\max }$, for complete saturation is reachable, because of selfdesiccation, only at $h \gg 1$, i.e., at pore vapor pressures $p \gg p_{\mathrm{sat}}(T)$ where $p_{\mathrm{sat}}(T)$ = thermodynamic saturation vapor pressure at temperature T. The equality $w_e = w_{\max }$ applies only immediately after the set, before selfdesiccation begins. Unfortunately, ignoring these facts has caused much confusion in the literature and in interpretation of experiments. Since $w_{\max }$ is variable and hard to measure, it is not suitable to define S as the ratio $w_e{/}w_{\max }$.

Several studies [26, 30] showed that the desorption isotherm is nonlinear and its shape depends on the properties of concrete. The most important parameters are the water-cement ratio and age. In addition, certain admixtures have a significant effect. Especially, adding silica fume fills the smallest pores and makes the isotherm at low humidities steeper [33, 34]. Various equations for the desorption isotherm have been proposed, but they are either too complicated to use or necessitate several calibration parameters hard to determine. Here we aim at realistic but simple formulation.

Based on experimental evidence, the desorption isotherm for $h >50\%$ can be roughly approximated by two straight line segments. But a smooth curve is preferable and can be formulated so as to have the two straight lines as a tangent and an asymptote (see Fig. 6b), as follows:

$$\text {d}h=k(h,\alpha )\text {d}S$$

(38)

$$\frac{1}{k(h,\alpha )}=m_{2} + \frac{m_1 - m_2}{1+\left( \frac{1-h}{1-h^{*}}\right) ^{2}}$$

(39)

where $k(h,\alpha )$ is the inverse slope of the desorption isotherm; $m_{1}$ and $m_{2}$ are the slopes of the two straight lines (which can be more simply used to approximate desorption isotherm), and $h^{*}$ is the intersection point of the two straight lines. These parameters can be empirically estimated as follows:

$$m_{1}=\frac{f_{\alpha }}{c_{SF}}\left[ 2.4 + \left( \frac{{w/c}-0.13}{0.19} \right) ^{1.5}\right]$$

(40)

$$m_{2}=c_{SF}^{0.5}\ 1.18\, {w/c}^{0.4}$$

(41)

$$h_{\mathrm{s}}=1-fc_{SF}\frac{0.03}{{w/c}^{2}}$$

(42)

$$f_{\alpha }=(\alpha _{u}-\alpha _{0})/(\alpha -\alpha _{0})$$

(43)

The factor $c_{\mathrm{SF}}$ is included to account for possible addition of silica fume. In its absence $c_{\mathrm{SF}} = 1$ and, generally, for a finite specific content $\xi _{\mathrm{SF}}$ of silica fume (mass of silica fume/mass of cement):

$$c_{\mathrm{SF}} = 1 + 2\xi _{\mathrm{SF}}$$

(44)

Figure 6c compares the calculation results (solid curves) with measurements. Evidently, the simulated desorption isotherms are in a good agreement with the experimental results. It should be mentioned that some studies showed some minor effect of temperature on the isotherm, but for simplicity this effect has been neglected.

7 Selfdesiccation

As already mentioned, contrary to the definition in RILEM TC 196-ICC, the selfdesiccation does not occur “when empty pores are generated”. Rather, the existing vapor bubbles in large pores grow and their menisci recede into narrower pores (Fig. 2). The decrease of h is controlled by the size of these bubbles, which depends mainly on the water-to-cement ratio (w/c), the degree of hydration, the particle size distribution of cement, and the type of admixtures. The pore sizes are smaller for lower w/c and for finer cements. Smaller pore sizes intensify selfdesiccation. Some fine admixtures such as the silica fume decreases the pore sizes.

To calculate the selfdesiccation, one must begin with the hydration reaction and the amount of water consumed in this reaction. The ordinary Portland cement (OPC) consists of various phases such as alite ($\hbox {C}_{3}\hbox {S}$), belite ($\hbox {C}_{2}\hbox {S}$), calcium aluminate ($\hbox {C}_{3}\hbox {A}$), tetracalcium aluminoferrite ($\hbox {C}_{4}\hbox {AF}$) and gypsum, as well as minor other phases (we use cement chemistry notation in which C, S, A and F stand, respectively, for CaO, $\hbox {SiO}_{2}$, $\hbox {Al}_{2}\hbox {O}_{3}$ and $\hbox {Fe}_{2}\hbox {O}_{3}$; Taylor [21]). $\hbox {C}_{3}\hbox {S}$ and $\hbox {C}_{2}\hbox {S}$ are two major components of ordinary Portland cement (OPC) and their ratio depends on the cement type. To measure the amount of water consumed in the hydration reaction, we consider, for simplicity, only $\hbox {C}_{3}\hbox {S}$ and $\hbox {C}_{2}\hbox {S}$ and we assume the cement to be composed of 80% $\hbox {C}_{3}\hbox {S}$ and 20% $\hbox {C}_{2}\hbox {S}$, whose nano-scale reaction can be summarized as [35],

$$\begin{aligned} \begin{array}{cc} \text {C}_{2}\text {S}+2.1\text {H}\rightarrow \text {C}_{1.7}\text {SH}_{1.8}+0.3\text {CH}\\ \text {C}_{3}\text {S}+3.1\text {H}\rightarrow \text {C}_{1.7}\text {SH}_{1.8}+1.3\text {CH} \end{array} \end{aligned}$$

(45)

Here $\text {C}_{1.7}\text {SH}_{1.8}$ and H are the typical C–S–H types in OPC pastes. Table 1 summarizes the molar volume and density of different components in hydration reactions. Note that water is not included in Eq. (45), as if the C–S–H pores were empty, and so one must include additional water trapped in the C–S–H pores.

Nowadays it is well established that calcium–silicate–hydrates (C–S–H) in cement-based materials exist in, at least, two different forms. This phenomenon was observed in Taplin [36], who attributed the two forms to the inner and outer hydration products. Recently Constantinides and Ulm [37] (see also [38, 39]) studied it far more detail and demonstrated by ingenious statistical sampling that two types of C–S–H are produced during hydration reaction: low-density C–S–H (LD), with porosity 36%, and high-density C–S–H (HD) with porosity 26%. Jennings and Thomas [38] showed that, for different w/c, the ratio between these two C–S–H types varies. For instance, their model (JT model) predicted that for ${w/c}=0.45$, there is 50% HD and 50 %LD, while for ${w/c}=0.25$ there is 80% HD and 20% LD. Therefore, the average porosity of C–S–H, $\varphi _{gp}$, depends mainly on w/c. Here, for simplicity, we assume a linear relation subjected to lower and upper bounds:

$$0.27<\varphi _{gp} = 0.28 + 0.2({w/c}-0.3) < 0.35$$

(46)

The lower and upper bounds on $\varphi _{gp}$ are necessary because it does not suffice to consider only the LD or HD phases.

Table 1 Molar volume and density of calcium-silicate phases in hardened cement paste

Fig. 7

Comparisons of predicted and experimental results: a Relative humidity decrease in selfdesiccating sealed specimens for tests by Jiang et al. [34], for different w/c; b Ditto, for tests by Kim and Lee [40]; c Measurements of autogenous shrinkage predicted from either average porosity or variable porosity

After quantifying the hydration relation and calculating the porosity of C–S–H, we can calculate the total volume of water, $\xi _{gc}$, per unit volume of cement, that is used in hydration to produce a C–S–H gel, the volume of empty pores, $\xi _{bw}$, and the volume of water that fills gel pores, $\xi _{fp}$:

$$\xi _{wc}=\xi _{bw}+\xi _{fp}$$

(47)

$$\begin{aligned}&\xi _{bw}=w_{\text {C}_{2}\text {S}}\xi _{bw}^{\text {C}_{2}\text {S}} + w_{\text {C}_{3}\text {S}}\xi _{bw}^{\text {C}_{3}\text {S}} \end{aligned}$$

(48)

$$\xi _{fp}=\varphi _{gp}\xi _{gc}S_{gp}$$

(49)

where $S_{gp}$= saturation degree of gel pores; $w_{\text {C}_{2}\text {S}}$ and $w_{\text {C}_{3}\text {S}}$ = volume ratio of C$_{2}$S and C$_{3}$S respectively; $\xi _{bw}^{\text {C}_{2}\text {S}}$ and $\xi _{bw}^{\text {C}_{3}\text {S}}$ = volumes of water that are consumed to hydrate one unit volume of C$_{2}$S and C$_{3}$S, respectively, and produce C–S–H gel with empty pores. If 80% of cement is assumed to consist of the C$_{3}$S and 20% C$_{2}$S, we have

$$\xi _{bw} = 0.2 (37.8/52.7) + 0.8 (55.8/72.9) = 0.755 \xi _{gc} = 0.2 (110 /52.7) + 0.8 (110 /72.9) = 0.487$$

Since the gel pores are smaller than the capillary pores, the gel pores, in the simulation of hydration process, have usually been considered to be saturated. However, several experiments illustrate the gradual desorption of gel pores [41,42,43]. In addition, Rahimi-Aghdam et al. [8] show computationally that this cannot be correct and that some of the gel pores must be treated as unsaturated capillary pores. Otherwise, the gel pore water would always have a uniform chemical potential and one could not explain the termination of hydration below a certain low relative humidity. Here, 33% of gel pores are assumed to have the same saturation degree as the capillary pores, and 67% the same as nanopores (which, at high relative humidities, are always saturated). Therefore, for a high relative humidity, the saturation degree of capillary pores is:

$$S_{gp} = 0.67 + 0.33 S_{cp}$$

(50)

Figure 7a, b shows the resulting prediction of selfdesiccation. As seen, the predictions agree with the experiments well, although the predicted autogenous shrinkage curves show some delay (see Fig. 7c). The probable cause is that, initially, most of the C–S–H gel produced is LD and, as the hydration reaction proceeds, the HD ratio increases and generally the density of C–S–H increases [44]. This may be formulated as,

$$\begin{aligned}&\begin{aligned} \varphi _{gp}=r_{LD}\varphi _{LD}+r_{HD}\varphi _{HD} =\\ 0.36r_{LD}+0.26(1-r_{LD}) \end{aligned} \end{aligned}$$

(51)

$$r_{LD}=\exp \left( -c_{{w/c}}\ \frac{\alpha }{\alpha _{u}}\right)$$

(52)

$$c_{{w/c}}=\frac{0.17}{\left({w/c} - 0.05\right) ^{4}}$$

(53)

where $r_{LD}$ and $r_{HD}$ are the volume fractions of the C–S–H gel produced. Using either the average porosity or a variable porosity C–S–H, one finds the predicted selfdesiccation curves to be almost the same but, as seen in Fig. 7c, the use of average porosity causes a delay in the predicted autogenous shrinkage. Therefore, only the variable density method is employed here. It should be mentioned that Masoero et al. [45] showed the effect of C–S–H densification on predicting selfdesiccation as well.

To analyze more deeply the ability of the model in predicting self-desiccation, several experiments were simulated. Figure 8 [46, 47] illustrates the comparison between the predicted vs. experimental results. As it can be seen, the results are in very good agreement. It should be mentioned that, using other hydration models, selfdesiccation can be simulated with almost the same accuracy [48], but the computation time is drastically longer. Also, note that several studies showed the effect of humidity decrease due to dissolved ions and they found that the effect can vary significantly for different concrete types [49]. But for simplicity, for all simulations, 1% decrease in saturation degree was assumed in this study. Note that no calibration parameters were used and the computation time for each simulation was less than 5 seconds. This computation time is negligible compared to other models currently available.

Fig. 8

Comparisons of predicted and experimental results for pore humidity evolution during selfdesiccation of sealed specimens

8 Prediction of autogenous shrinkage

To check how good the predictions of the present model are, we begin with the experiments of Baroghel-Bouny et al. [33], in which the autogenous shrinkage of cement pastes was measured for different water-cement ratios. Figure 9a compares the calculated curves with the measured points. As seen, the agreement is good. Note that the model was calibrated only by matching of the measured bulk modulus of the cement paste, and only for ${w/c}=0.4$. The rest is the prediction. Also, it should be mentioned that, due to considering hydration to be expansive, the model was able to predict the initial swelling in cement pastes with high w/c correctly.

Fig. 9

Comparison of calculated curves with measured evolution of autogenous shrinkage, for cement pastes with different water-cement ratios

Next, consider the experiments of Jiang et al. [34]. This experiment is almost similar to experiment by Baroghel-Bouny et al. [33]. The only main differences are having cement with a higher percentage of $\hbox {C}_3\hbox {A}$ and the use of high range water reducer for cement pastes with low water cement ratio. However, as the autogenous values show, the autogenous shrinkage values of this experiment are higher than the ones for Baroghel-Bouny et al. [33]. Especially, for the cases in which water reducer is used (${w/c}= 0.2$ and 0.3), the autogenous shrinkage is significantly larger. This is due to the fact that water reducing admixtures lower the viscosity and thus increase the creep compliance [12]. In addition, the bigger autogenous shrinkage value for the cases in which water reducer hasn’t been used is due to a greater amount of $\hbox {C}_3\hbox {A}$. $\hbox {C}_3\hbox {A}$ hydration process consumes significantly larger amount of water thus increases the selfdesiccation. To consider the effect of greater amount of $\hbox {C}_3\hbox {A}$, the value of $\xi _{bw}$ was modified from 0.755 to 0.76. All the other calibration parameters are the same. As shown in Fig. 9b, the predicted results are in good agreement with the experimental ones.

9 Combined autogenous shrinkage and swelling

Let us now analyze the ability of the model to predict deformations when both swelling and autogenous shrinkage happen simultaneously. This is the case for all swelling experiments. The core undergoes autogenous shrinkage until the front of wetting arrives from the exposed surface (if the environmental humidity is not too high). Only the region between the surface and the wetting front experiences swelling. Therefore, and because the diffusion times depend on specimen size, the evolution of deformation and its final value are size dependent. As the volume-surface ratio increases, the parts that undergo swelling play a smaller role and the autogenous shrinkage begins to dominate. The opposite happens for thin specimens, with low volume-surface ratios, in which the swelling dominates.

Miyazawa and Monteiro [50] illustrate this phenomenon by experiment. They tested mortar prisms with ${w/c}=0.30$ and different sizes. On the first day, the samples were sealed and then placed in fog room. The bottom and top of the test specimens were sealed to ensure two-dimensional (rather than three-dimensional) diffusion. In the literature, there seems to be no model that could predict these experiments well.

Figure 10a compares the predicted versus experimental results for three different specimen sizes. As it can be seen, the predicted results are in good agreement with the experimental ones. In addition, the present model is able to predict the size effect in swelling. It should also be noted that these authors started measuring deformation at 1 day. This way, they ignored a significant part of autogenous shrinkage. Figure 10b shows the predicted results starting from the time of set. As seen, the difference is very significant.

Considering all these complexities, it appears that the finite element simulation is the only reliable method for predicting swelling. All the prediction formulae have significant errors.

Fig. 10

Predictions of swelling of specimens of different sizes (given in mm) sealed up to 1 day and then exposed to fog, measured from the moment of exposure; b Ditto, for 25$\times$ 25 mm, when the autogenous shrinkage during the first day is included (lower curve) and when it is not

10 Importance of considering the variation of Biot coefficient

To illustrate the significant effect of variation of the Biot coefficient, a recent highly interesting and original experiment of Abuhaikal and Ulm [6] must be considered. In their experiment, the specimen was kept constantly saturated while both the external load (compressive) and the pore pressure were kept nearly the same, at $p \approx$ − 1 MPa; Fig. 11a. Their experiment ran from the time of set and the concrete was hydrating during the experiment. Therefore, the Biot coefficient must have been decreasing as the matrix was gaining strength; Fig. 11b. Whereas the material is hydrating and the masses of constituents are changing, the Biot relation can be used only at constant hydration degree $\alpha$, i.e.,

$$\sigma =\sigma _{\mathrm{solid}}(\alpha )-b(\alpha )\pi$$

(54)

where π initially starts from its value in a sealed specimen but, as water diffuses and material becomes fully saturated, its value becomes equal to p. Since $p = -\, \sigma = 1$ MPa is maintained, the stress (in MPa) in the solid part, after full saturation, should be calculated as,

$$\sigma _{\mathrm{solid}}(\alpha ) = -\, 1 + b(\alpha )$$

(55)

The stress evolution in the solid part, $\sigma _{\mathrm{solid}}$, after full saturation is portrayed schematically in Fig. 11c. Note that prior to full saturation, the stress value is not uniform throughout the specimen and its value depends on the distance from wetting front. As the figure shows, the stress in the solid part, $\sigma _{\mathrm{solid}}$, after saturation is always compressive and increases in magnitude. This stress can cause significant deformation, especially when the creep due to this stress is taken into account.

The total strain, $\epsilon _{tot}$, in Abuhaikal et al.’s experiment should be divided into two parts Fig. 12: (1) the normal shrinkage and swelling of young concrete neglecting the effect of externally applied load and fluid pressure, $\epsilon _{\mathrm{swell}}$, and (2) the strain due to compressive load on the solid constituent, $\epsilon _{\mathrm{load}}$. To calculate the strain increment due to the stress in solid, $\text {d}\epsilon _{\mathrm{load}}$, the strain due to $\sigma _{\mathrm{solid}}$ needs to be divided into two parts.

The first part is the strain at constant hydration degree due to the increments in loads, and the second part is the strain at constant loads due to the change of the properties of hydrating concrete, i.e.,

$$\text {d}\epsilon _{\mathrm{load}} = \text {d} \epsilon _{{1,{\alpha }}} + \text {d} \epsilon _{{2,{\text{load} }}}$$

(56)

As mentioned, at constant hydration degree, both the external load and the pressure are kept constant, and so after full saturation $\text {d} \epsilon _{{1,{\alpha }}} = 0.$ However, the second part, $\text {d} \epsilon _{{2,{\text{load} }}}$, is not zero even after full saturation  and can be calculated as,

$$\text {d} \epsilon _{{2,{\text{load} }}}\,= J\, \text {d} \sigma _{\text {solid, load}} = J\, \text{d}b$$

(57)

where J is the creep compliance value for the given time (including the elastic strain). Finally, $\epsilon _{\mathrm{load}}$ can be obtained as,

$${{\epsilon _{\mathrm{load}}}}(t)={{\epsilon _{\mathrm{load}}}}(t_{sat})+\int _{t_{sat}}^{t}J(\alpha ,t') \, \mathrm{d}b(t')$$

(58)

where the first term in right hand side is added to include the initial unsaturated condition. The effect of $\epsilon _{\mathrm{load}}$(t) is not negligible. But it has, unfortunately, been neglected by Abuheikal et al. [6], which led them to attribute the shrinkage solely to eigenstresses in concrete.

Fig. 11

Schematic predicted responses in Abuheikal et al. [6] test. a Applied forces; b evolution of Biot coefficient; c schematic evolution of stress in solid skeleton; d strain due to swelling, summed with e strain due to stress in solid skeleton, to obtain f total strain

Fig. 12

Measured versus predicted strains for Abuheikal et al. [6] experiment

11 Conclusions

• 1. The present analysis and comparisons with tests confirm a new paradigm [4]: On the porous material scale, the hydration reaction is always and permanently expansive (Bažant et al. [5, 12]), even though it is contractive on the nanoscale. All shrinkage is caused by a decrease of pore humidity. Limited periods of early expansiveness of hydration might have been suspected by earlier researchers.

• 2. Recognizing the expansiveness property leads to a grand unification of models for drying shrinkage, autogenous shrinkage and swelling at water immersion, and especially their long-time, multi-decade and century-long, evolution.

• 3. Consequently, these seemingly diverse phenomena can all be predicted from one and the same material model, even for decades-long (and probably century-long) duration.

• 4. When used in computer-aided design, this grand unification should help to design for century-long durability, a goal that has rarely been achieved for large concrete bridges and other structures [2].

• 5. Selfedsiccation is explicable without assuming any cavitation in liquid water. It is explained by gradual recession of existing capillary menisci into narrower and narrower pores.

• 6. Without a realistic model for long-term selfdesiccation, autogenous shrinkage, swelling and moisture diffusion, the present test data could not be fitted, in their entirety, by one-and-the same model.

• 7. The importance of considering the Biot coefficient to decrease with increasing degree of hydration and to increase with increasing cracking damage is demonstrated.

• 8. The present new thermodynamic formulations of poromechanics with capillarity and adsorption, based on the Gibbs energy potential, lends the present model general applicability, although the present data except those for very low humidities can be fitted without the adsoprtion part.

• 9. The recently developed computationally efficient hydration model [8] using local continuum variables to bypass Bentz’s simulation of a three-dimensional system of hydrating particles makes feasible finite element analysis of shrinkage, swelling and hydration degree evolving differently at each integration point.

• 10. The present introduction of a nonlinear desorption isotherm improves shrinkage and swelling predictions.

Appendices

Appendix 1: Algorithm to calculate the degree of hydration

A realistic model for calculating the degree of hydration is essential for predicting selfdesiccation, shrinkage, swelling and creep. Therefore, the algorithm of such a model, developed recently [8], is now presented. It is simpler and computationally faster than the widely accepted classical model of Bentz [51], which uses random particle simulations of hydrating cement grains and would be too time consuming for use at integration points in finite elements computations.

• 1. For the cement paste or concrete with a known water-cement ratio, w/c, and aggregate-cement ratio, a/c, ratios, calculate the initial volume fraction of cement $V_{0}^{c}$and water $V_{0}^{w}$:

  $$V_{0}^{c}=\frac{\rho _{a}\rho _{w}}{\rho _{a}\rho _{w} +\rho _{c}\rho _{w}a/c+\rho _{c}\rho _{a}w/c}$$

  (59)
  $$V_{0}^{w}=\frac{\rho _{a}\rho _{c}w/c}{\rho _{a}\rho _{w} +\rho _{c}\rho _{w}a/c+\rho _{c}\rho _{a}w/c}$$

  (60)

  where $\rho _{\mathrm{l}}$, $\rho _c$ and $\rho _a$ are, respectively, the specific mass of water (in 1000 kg/m$^3$), of cement (here considered as 3150 kg/m$^3$), and of aggregates (here 1600 kg/m$^3$) (for gravel and sand combined).

• 2. Calculate the average cement particle size (i.e., particle radius) $a_{0}$, based on the cement type. Here the Blaine fineness of cement, $f_{bl}$, equal to 350m$^{2}$/kg, is considered to correspond to particle radius 6.5$\upmu$m. Further calculate the number of cement particles, $n_{g}$, per unit volume of cement:

  $$a_{0}=6.5(\mu \hbox {m})\ \frac{350}{f_{bl}}$$

  (61)
  $$n=\frac{V_{0}^{c}}{\frac{4}{3}\pi a_{0}^{3}}$$

  (62)

• 3. Choose a reasonable hydration degree for setting the time at set, $\alpha _{\mathrm{set}}$, and time $\alpha _{c}$ at which a continuous C–S–H barrier shells gets completed, i.e., the critical hydration degree at which a complete C–S–H barrier will form around the anhydrous cement grains (about 1 day). For a normal cement with $a_{0}^{n}=6.5\upmu$m, $w/c=0.3$ at $T=20C$ $^{\circ }$C, the values $\alpha _{\mathrm{set}}^{0}=0.05$ and $\alpha _{c}=0.36$ are good approximations. For the given cement type and the given values of T and w/c, realistic estimates may be calculated as follows:

  $$\alpha _{c}=\alpha _{c}^{0}f_{1}(a)f_{2}(w/c)f_{3}(T)<0.65$$

  (63)
  $$f_{1}(a)=\dfrac{a_{0}^{n}}{a}$$

  (64)
  $$f_{2}(w/c)=1+2.5(w/c-0.3)$$

  (65)
  $$\begin{aligned}&f_{3}(T)=\hbox {exp}\left[ \frac{E_{\alpha }}{R}\left( \frac{1}{273+T_{0}}-\frac{1}{273+T}\right) \right] \end{aligned}$$

  (66)
  $$\frac{\alpha _{\mathrm{set}}}{\alpha _{\mathrm{set}}^{0}} =\frac{\alpha _{c}}{\alpha _{c}^{0}}$$

  (67)

• 4. Then calculate the volume fraction of cement, $V_{\mathrm{set}}^c$, portlandite, $V_{\mathrm{set}}^{CH}$, gel (C–S–H plus ettringite) and $V_{\mathrm{set}}^g$. Using these fractions, calculate the radius of the anhydrous cement remnants, $a_{\mathrm{set}}$, and the outer radius of C–S–H barrier, $z_{\mathrm{set}}$. To describe the chemical reaction of hydration, use the volume ratios $\zeta _{gc} = 1.52$ and $\zeta _{CHc} = 0.59$ in the following equations:

  $$\begin{aligned}&\begin{aligned} V_{\mathrm{set}}^{c}=(1-\alpha _{\mathrm{set}})V_{0}^{c}\,\,\,\,\,\,\,\,V_{\mathrm{set}}^{CH} =\zeta _{CHc}\alpha _{\mathrm{set}}V_{0}^{c}\,\,\,\, V_{\mathrm{set}}^{g}=\zeta _{gc}\alpha _{\mathrm{set}}V_{0}^{c} \end{aligned} \end{aligned}$$

  (68)
  $$\begin{aligned}&a_{\mathrm{set}}=\left( \frac{V_{{{\mathrm{set}}}}^{c}}{\frac{4}{3}\pi n_{g}}\right) ^{\frac{1}{3}},\quad z_{\mathrm{set}}=\left( \frac{V_{\mathrm{set}}^{c} +V_{\mathrm{set}}^{g}}{\frac{4}{3}\pi n_{\mathrm{g}}}\right) ^{\frac{1}{3}} \end{aligned}$$

  (69)

• 5. In each time step, use the hydration degree $\alpha$ and humidity h from previous step to calculate the water diffusivity $B_{\mathrm{ef}}$:

  $$\begin{aligned} B_{\mathrm{ef}}=B_{0}f_{0}(h_{\mathrm{p}})f_{4}(\alpha ) \end{aligned}$$

  (70)
  $$\begin{aligned} f_{0}=c_{\mathrm{f}}+\frac{1-c_{\mathrm{f}}}{1+\left( \frac{1-h_{\mathrm{t}}^{p}}{1-h^{*}} \right) ^{n_{\mathrm{h}}}} \end{aligned}$$

  (71)
  $$f_4(\alpha )\ =\ \gamma \, e^{-\gamma }\quad \hbox {for}\quad \alpha \le \alpha ^{*}$$

  (72a)
  $$\begin{aligned}&f_4(\alpha )\ =\ (\beta /\alpha _{\mathrm{s}})^m e^{(\beta /\alpha _{\mathrm{s}})^m} \quad \hbox {for}\quad \alpha > \alpha ^{*} \end{aligned}$$

  (72b)

  where

  $$\begin{aligned} \gamma = \left( \frac{\alpha }{\alpha _{\max }} \right) ^m, \,\, \beta = \alpha -\alpha ^*+\alpha ^{*}\alpha _{s}/\alpha _{\max } \end{aligned}$$

  (73)

  Use $\alpha _{\mathrm{s}}=0.3$, $\alpha _{\max }=\alpha _c/2$, $\alpha ^{*}=0.75\alpha _c$ and $m=1.8$. Furthermore, the empirical parameters c, $h^{*}$, $n_h$, $c_f$ need to be set. In this study, we set $n_h = 8$, $h^{*} = 0.88$ and $c_f = 0$.

• 6. In each step, calculate the radius of the equivalent contact-free C–S–H shells, $\hat{z}$, that give the same free surface area as the actual shell radius z would if the shell surfaces were free, with no contacts;

  $$\hat{z}_{t}\ =\ \frac{z_{t}}{1+\left( \frac{z_{t}-a_{0}}{u}\right) ^{5}}$$

  (74)

  where $u = a_{0} / 6.4$. This relation has been modified compared to that in Rahimi-Aghdam et al. [8], so as to represent the multi-decade continuation of hydration better (this change has no effect on model performance up to 10 years).

• 7. In each time step, using pore humidity h, the size of the anhydrous cement remnant, a, and the outer radius z of C–S–H barrier from the previous time step, as well as the latest diffusivity value, calculate the water discharge $Q_t^1$:

  $$Q_{t}^{1} = 4\pi a_{t}z_{t}B_{ef}(\alpha ,h_{p})\frac{h_{p}-h_{c}}{z_{t}-a_{t}} \left( \frac{\hat{z}^{2}}{z_{t}^{2}}\right)$$

  (75)

  The last factor on the right-hand side, $\frac{\hat{z}^2}{ z_{t}^2 }$, serves to consider the reduction of C–S–H shell surfaces due to mutual contacts.

• 8. In each step, using the calculated water discharge $Q_t^1$, calculate the increment of cement volume, $\text{d}V_t^c$, of portlandite, $\text{d}V_t^{CH}$, and cement gel $\text{d}V_t^{g}$:

  $$V_{t+\text{d}t}^c=V_t^c+\hbox {d}V_t^c=V_t^c-n_gQ_t^1\zeta _{cw}\hbox {d}t$$

  (76a)
  $$V_{t+\text{d}t}^g=V_t^g+\hbox {d}V_t^g=V_t^g+n_gQ_t^1\zeta _{gw}\hbox {d}t$$

  (76b)
  $$V_{t+\text{d}t}^{CH} = V_t^{CH}+\hbox {d}V_t^{CH} = V_t^{CH}+n_gQ_t^1\zeta _{CHw}\hbox {d}t$$

  (76c)

  where $V_{t} = V(t)$, etc.; $\zeta _{cw}$, $\zeta _{gw}$ and $\zeta _{CHw}$ are, respectively, the volumes of the cement consumed, of the C–S–H gel produced, and of the portlandite produced per unit volume of discharged water. These volume fractions are calculated as: $\zeta _{cw}=\frac{1}{\zeta _{wc},}$, $\zeta _{gw}=\zeta _{gc}\zeta _{cw}$ and $\zeta _{CHw}=\zeta _{CHc}\zeta _{cw}$.

• 9. In each time step, use the calculated $\text{d}V_t^c$ to evaluate the increment of hydration degree $\text{d}\alpha _t$, and the cement particle radius $\text{d}a_t$:

  $$a_{t+\text{d}t} = a_t+\hbox {d}a_t = a_t +\dfrac{1}{4\pi a_0^2n_g}\hbox {d}V_t^c$$

  (77a)
  $$\alpha _{t+\text{d}t} = \alpha _t+\hbox {d}\alpha _t=\alpha _t-\dfrac{3}{4\pi a_0^3n_g}\hbox {d}V_t^c$$

  (77b)

• 10. At each time step calculate the increment of gel barrier $\text{d}z_t$

  $$\hbox {d}z_{t} = \frac{\hbox {d}V_{t}^{g} + \hbox {d}V_{t}^{c}}{4\pi \hat{z}^{2}}\quad \hbox {for}\quad \alpha _{t}>\alpha _{c}$$

  (78)

• 11. Finally, calculate the selfdesiccation increment of relative humidity, $\text{d}h_t^s$, of saturation degree, $\text{d}S_t^{cap}$, and of inter-particle porosity, $\text{d}\varphi _t^{cap}$;

  $$\text{d}h_{t}^{s} = K_{h}\left( \frac{\hbox {d}V_{t}^{c}(\zeta _{bw} + \varphi _{np}\zeta _{gc}) - \hbox {d}\varphi _{t}^{cap}S_{t}^{cap}}{\varphi _{t}^{cap}}\right)$$

  (79)

  where

  $$\begin{aligned} \begin{aligned} \hbox {d}\varphi _{t}^{cap} = -\, (\hbox {d}V_{t}^{g} + \hbox {d}V_{t}^{CH} + \hbox {d}V_{t}^{c}) + (\varphi _{gp}-\varphi _{np}) \zeta _{gc} \end{aligned} \end{aligned}$$

  (80)

  Here $\varphi _{np}$ is the nano-pore part of gel porosity in which the pores are assumed to be always saturated during hydration process. In this study, 2/3 of gel pores are assumed to be nano-pores.

Appendix 2: Algorithm to determine the permeability and diffusivity

Based on Bažant-Najjar [52] model, which has been embodied in the fib Model Code 2010 (Fédération internationale de béton 2013), the equation for moisture diffusion in concrete reads:

$$\frac{\partial h}{\partial t} = k(\alpha ,h)\nabla \cdot \left( c_{p} \nabla h\right) + \frac{\partial h_{s}}{\partial t}$$

(81)

where $k(\alpha ,h)$ (dimension m$^{3}$/kg) is the reciprocal moisture capacity (i.e, the inverse slope of the isotherm), and $\alpha$ is the hydration degree, $c_p$ is the permeability and the last term on the right-hand side is a distributed sink representing the selfdesiccation. Same as in Bažant-Najjar model, the dependence of moisture permeability $c_{p}$ on h may again be expressed as follows:

$$c_{p}(h,\alpha ) = c_{1} \left( \beta + \frac{1 - \beta }{1 + \left( \frac{1-h}{1-h_{c}} \right) ^{r}} \right)$$

(82)

where $c_{1}$, $\beta$, $h_{c}$ and r were four unknown parameters which should be determined based on experiments of relative humidity evolution. Usually, though, the creep and shrinkage testers do not report the relative humidity values, and so these values and the parameters needs to be guessed. This can cause significant error.

To address this issue, some methods have been suggested [9, 53, 54]. Among these methods, the new model by Rahimi-Aghdam et al. [9] proposed simple empirical relations to determine these parameters based on concrete admixtures. They set $r=2$ and proposed calculating the other three parameters as follows.

$$c_{1} = 60 [1+12(w/c-0.17)^2]\, \alpha /\alpha _{u}$$

(83)

$$\begin{aligned}&h_{c} = 0.77 + 0.22\left( w/c - 0.17\right) ^{1/2} + 0.15 \left( \frac{\alpha _{u}}{\alpha }-1 \right) \quad \hbox {but}\quad h_c < 0.99 \end{aligned}$$

(84)

$$\beta = c_{f} /c_{1}$$

(85)

$$c_{f}^{0} = 60[1 + 12(w/c-0.17)^2]\, \alpha /\alpha _{u}$$

(86)

$$\begin{aligned}c_{f}& = {\left\{ \begin{array}{ll} c_{f}^{0}\quad &{} (h>h_{s}) \\ 0.1c_{f}^{0} + 0.9 c_{f}^{0} (h / h_{\mathrm{s}})^4\quad &{} (h < h_{s}) \end{array}\right. } \end{aligned}$$

(87)

Here $\alpha _{u}$ is the ultimate hydration degree in sealed concrete, which is a function of w/c; it is estimated as

$$\alpha _{u} = 0.46 + .95(w/c-0.17)^{0.6} \quad \hbox {but}\quad \alpha _{u} < 1$$

(88)