1 Introduction and nature of problem

Because of the tremendous variety of concrete compositions, prior to designing or building a structure it is often necessary to perform short-time creep and shrinkage tests of the concrete to be used. Typically, the acceptable test duration, \({t_e}\), is 1–3 months. Extrapolation of the basic creep test (i.e., the test of a sealed specimen) is relatively easy [1–3] since the compliance curve of concrete is, in the logarithmic time scale, rising at nearly constant slope and no final asymptotic final value exists. However, extrapolation of the drying shrinkage test is far more difficult (so is the extrapolation of the additional creep due to simultaneous drying, called the drying creep).

The difficulty is made clear in Fig. 1 (adapted from Fig. 2c in [1] and Fig. 1.4 in [3]). It shows three curves plotted in the logarithmic time scale according to the drying shrinkage formula of models B3 [1, 3] and B4 [4] with different parameter values (see Eqs. 9–14 in [1]). Curve c is almost identical to curve a for the duration of the short-time test but leads to a much higher final shrinkage. Mathematically it means that the shrinkage extrapolation problem is ill-conditioned, leading to a nearly singular system of equations. In other words, a very small change in short-time data can cause a very large change in the optimum fit by the shrinkage formula (this is true not only for the B3 or B4 formula but also for the formulas of ACI-209, fib and other codes or recommendations). Furthermore, curve b, for modern concrete of very low diffusivity, gives a much lower short-time shrinkage than curve a for normal concrete, but may eventually lead to a much higher final shrinkage.

Fig. 1
figure 1

Three examples of possible very different shrinkage evolutions demonstrating the difficulty of extrapolating short-time data

Full size image

Why the basic creep extrapolation does not suffer from this problem?—The basic creep curve has no characteristic time, called the halftime, and no final asymptotic value (if one uses a realistic formula with a logarithmic terminal trend, such as that from B3 or B4 models). For shrinkage, these two characteristics are essential but can be determined only if the shrinkage test is long enough for the slope in the logarithmic time plot to approach closely the horizontal asymptote (Fig. 1).

In [1] it was proposed to aid shrinkage extrapolation by carrying out simultaneous measurements of weight loss, i.e., loss of water from the pores, which drives the drying shrinkage. The motivation was that, in contrast to shrinkage, the final water loss can be estimated in advance, either from the water-cement ratio of the concrete mix, or by drying the specimen in the oven and then interpolating the water loss from perfect dryness in the oven to the given environmental humidity. Initial studies [5, 6] indicated some good results but, unfortunately, some recent studies have shown poor extrapolations [7]. One problem has been that the estimate of the final water loss is often not good enough. Other problems may be that the aging due to hydration and the development of shrinkage cracks affect the shrinkage curve and the water loss curve somewhat differently. Therefore, a different method is suggested now for consideration.

2 Shrinkage formula and diffusion size effect

The formula for the drying shrinkage strain used in Model B3 [1, 3] as well as the improved model B4 [4] may be written in the form:

$$\begin{aligned}&\epsilon _{\text{sh}} = {\epsilon _s}_\infty r\, \tanh {\sqrt{\frac{\hat{t}}{\tau _{\text{sh}}}}}\end{aligned}$$
(1)
$$\begin{aligned} \text{ where }\quad &\tau _{\text{sh}}= {k_1} {k_s^2} {D^2}\end{aligned}$$
(2)
$$\begin{aligned}D = 2v/s,\quad \hat{t} = t - t_0\end{aligned}$$
(3)
$$\begin{aligned}&r = k_h \sqrt{ 0.99 + \frac{4.63}{t_0 + \tau _{\text{sh}}}}. \end{aligned}$$
(4)

  • \(t, {t_0} =\) current time and concrete age at exposure to drying (all times are in days);

  • \(\tau _{\text{sh}} =\) shrinkage halftime;

  • D = 2v/s = effective thickness of specimen, also called the size, where v/s = ratio of specimen’s volume v to its exposed surface area s (factor 2 is used to make D equal to the actual thickness when an infinite flat slab is considered);

  • \({\epsilon _s}_\infty =\) final shrinkage strain for reference conditions h = 0, \({t_0} =\) 7 days and \(\tau _{\text{sh}} =\) 600 days;

  • \({k_h} = 1 - {h^3} =\) empirical correction factor for environmental relative humidity h (if \(h < 0.98\));

  • \({k_1} =\) empirical factor depending on concrete strength;

  • \({k_s} =\) correction factor (theoretically derived from diffusion theory) for the cross section shape, equal to 1 for an infinite slab, 1.15 for an infinite cylinder, and 1.25 for an infinite square prism.

In contrast to other shrinkage functions used in design codes and recommendations, the form of Eq. (1) was theoretically derived by asymptotic matching, based on three physical requirements (of which the first two follow from the diffusion theory):

  1. (1)

    the shrinkage halftime must initially increase as \({D^2}\);

  2. (2)

    \(\epsilon _{\text{sh}}\) must initially evolve as \(\sqrt{\hat{t}}\); and

  3. (3)

    the approach to the final value must be asymptotically much closer to a decaying exponential than to a power law.

The first two requirements have also been well verified by shrinkage tests [10, 11].

Eq. (4) is derived by substituting the empirical formula for aging of elastic modulus, \(E(t) = [E_{28}t/(4 + 0.85 t)]^{1/2}\), into the equation \({\epsilon _{\text{sh}}}_\infty = {\epsilon _s}_\infty E(607) /E(t_0 +\tau _{\text{sh}})\), which introduces the hypothesis that shrinkage is caused by a compressive stress increment in the solid microstructure generated by an increase in solid surface tension and drop in disjoining pressure. It reflects the fact that an older and stiffer concrete shrinks less.

3 Extrapolation via least-square optimization

We want to extrapolate the short time data on \(\epsilon _{\text{sh}}\) for specimens of size \({D_1}\), typically cylinders of diameters d = 6 in. or 1 in. (for which \(D = 2v/s = 2(\pi d^2 /4) /(\pi d) = d/2\) = 3 in. or 0.5 in.), or for square prisms of side c = 1 in. or 3 in. (for which \(D = 2v/s = 2 c^2/(4c) = c/2\) = 0.5 in. or 1.5 in.). The data terminate at not too long test duration \({t_1}\) such as 3 months or 1 month, causing a tolerable delay.

Given that the short-time data for specimens of one size alone cannot be extrapolated (because of the afore-mentioned ill-conditioning), and that the use of water loss data might be questionable, it is proposed to exploit the diffusion size effect on shrinkage. This size effect has been derived theoretically and verified experimentally; see, e.g., [8, 9]. Its characteristic is a quadratic size dependence of shrinkage halftime, as in Eq. (2).

Thus it is proposed that, in addition to measuring the shrinkage strains, \(\epsilon _1(\hat{t})\), of standard specimens of size \({D_1}\), one should also measure the shrinkage strains, \(\epsilon (\hat{t})\), of companion specimens of a much smaller size \({D_2}\). According to the diffusion theory, the shrinkage curves of both should be mutually shifted by distance \(\Delta = 2 \log (D_1k_{s,1} /D_2k_{s,2})\) when plotted in the logarithmic time scale. The standard short-time shrinkage test of 1 or 3 months duration typically reaches up to only 20–40 % of the final shrinkage, \(\epsilon _1(\infty )\) of the standard specimen. But if the companion size \({D_2}\) is small enough, the measured companion data should reach up to about 95 % of the final shrinkage, \(\epsilon _2(\infty )\). Due to inevitable experimental scatter, a number of specimens should be tested. To deal with the scatter, statistical optimization of data fits must be used. How many parameters of Eq. (1) should be optimized? Only two, x and y, because for more the optimization problem would become ill-conditioned. And which parameters should be optimized? One must be a parameter controlling the final asymptotic value, and the other controlling the halftime. So we set

$$\begin{aligned} x = {\epsilon _s}_\infty ,\quad y = k_1 \end{aligned}$$
(5)

The objective function to be minimized by least-square optimization may now be formulated as follows:

$$\begin{aligned} \Phi (x,y) = {w_1} {w_0} \sum _{i=1}^N \left( {\epsilon _1}_i - x r \tanh \sqrt{ \frac{\hat{t}_i}{k_{s,1}^2 y D_1^2} }\ \right) ^2\,+\, w_2 \sum _{j=m+1}^n \left( {\epsilon _2}_j - x r \tanh \sqrt{ \frac{\hat{t}_j}{k_{s,2}^2 y D_2^2} }\ \right) ^2\end{aligned}$$
(6)
$$\begin{aligned} w_1 = \frac{1}{N}, \quad w_2= \frac{1}{n-m} \end{aligned}$$
(7)

  • \({\epsilon _1}_i\) for \(i = 1,2,\ldots N\) are the data measured at increasing discrete times \(\hat{t}_i\) on the standard-size specimens;

  • \({\epsilon _2}_j\) for \(j = 1,2,\ldots n\) are the data measured at increasing discrete times \(\hat{t}_j\) on the reduced-size companion specimens;

  • \({\epsilon _2}_j\) for \(j = 1,2,\ldots m\) are those data for which \({\epsilon _2}_j < {\epsilon _1}_N\). These data are excluded from the optimization to prevent them from modifying the fit of the data measured on the standard-size specimens, which are the shrinkage data to be extrapolated (however, should an overall optimum fit be desired, then these data may be included, in which case \(m=0\)).

  • \({w_1}, {w_2}\) are the chosen bias-countering weights for the standard and companion specimens, ensuring that both sums in \(\Phi\) have equal total weights. The weight values chosen in Eq. (7) prevent. e.g., the second sum from dominating when it contains many more data points than the first sum.

  • \({w_i}\) is a chosen importance weight. To ensure a very close fit of the data measured on the standard-size specimens that are to be extrapolated, a large value may have to be used; here \({w_i} =\) 5 or 1,000 has been used (however, if the sole objective were the best fit of all the data, then \({w_i}\) would have to be chosen as 1).

  • \(k_{s,1}, k_{s,2}\) are the values of shape parameter \({k_s}\) for specimens of sizes \({D_1}\) and \({D_2}\).

Upon identifying parameters x and y by optimization, there is enough information for extrapolation. The objective function is not a quadratic form in terms of the unknown parameters x and y. So the optimization problem is nonlinear; it cannot be reduced to linear equations for x and y. Nevertheless, easy and fast solution is obtained by means of the Levenberg–Marquardt algorithm, which also gives the coefficients of variation of x and y. Once x and y are known, Eqs. (1) and (2) deliver the extrapolation. Furthermore, the coefficient of variation (CoV) of the extrapolations can be calculated from those of x and y.

4 Test data used for evaluation

Although thousands of measured shrinkage curves are available in the new NU database of creep and shrinkage [10], only the shrinkage data sets of Burg and Ost [11] and of Wittmann and Bažant [8, 9] feature the minimal range of different specimen sizes, necessary to appraise the proposed method.

The tests of Wittmann and Bažant were intended to study the random scatter of shrinkage among identical specimens. They included one group of 36 identical cylinders of diameters 83 mm, one group of 35 identical cylinders of diameters 160 mm, and one group of 3 identical cylinders of diameters 300 mm. The length of each cylinder was double the diameter. The ends always remained protected against drying. The mean standard 28-day cylindrical strength was \(\bar{f}_c\) = 33.2 MPa (4815 psi) and the 28-day E-modulus was 36.3 GPa (5,265,000 psi).

The water-cement ratio was 0.48, which was probably high enough to ensure that the autogenous shrinkage in the wet portion of the cross section was not too large. No admixtures, plasticizers or air-entraining agents were used. All the specimens were cast from one batch of concrete, and the coefficient of variation of measured shrinkage values was mostly between 6 and 9 % with outliers up to 47 %. The specimens were cured in molds for 7 days, until the instant of exposure to controlled environment of relative humidity 65 ± 5 % and temperature was 18 ± 1 °C. The shrinkage was measured as the change of distance between the ends of specimens along the axis, and the readings began within one minute after the stripping of the mold.

The shrinkage tests of Burg and Ost used high-strength concretes with water-cement ratios ranging from 0.26 to 0.43; and water-to-cementitious material ratios ranging from 0.22 to 0.32. The concretes used contained either no mineral admixtures except silica fume, or both fly ash and silica fume, and were delivered to the laboratory by a ready-mix supplier. The compressive strength values ranged from 69 to 138 MPa (10,000–20,000 psi). The environmental relative humidity was 50 ± 4 % and the temperature 23 ± 1.7 °C. The ASTM C157 and C512 procedures were followed, i.e., the environmental conditions were the same for all the drying shrinkage specimens. The curing period was 28 days. Creep and many other properties were also tested. The autogenous shrinkage was not measured.

5 Optimal fitting, extrapolation and evaluation of actual data

The data points in Figs. 2, 3 and 4 represent the averages of the measured data for each time and each specimen size D, plotted in the logarithmic scale of the time \(t-t_0\) elapsed from the moment \(t_0\) of exposure to drying (all the times are in days). There are two kinds of data points: (1) The circle points are those that have been used in the optimization of the shrinkage formula; and (2) the cross points are those that have not been used and are intended for comparison with the optimum fit of the circle points.

Fig. 2
figure 2

a–d Various shrinkage data of Burg and Ost [12] for water-cement ratio 0.28 and their extrapolations; C.o.V = coefficient of variation of the errors (root mean square of the errors divided by the average of data used); \({w_x}\), \({w_y} =\) coefficient of variations of parameters x and y, obtained by optimization

Full size image
Fig. 3
figure 3

a–d Further shrinkage data of Burg and Ost [12] for water-cement ratio 0.34 and their extrapolations

Full size image
Fig. 4
figure 4

a–d Shrinkage data of Bažant and Wittmann [10, 11] and their extrapolations

Full size image

In Figs. 2a, 3a and 4a all the data points are used in calculations. These figures document that Eq. (1) can fit the test data as well as can be expected in view of the inevitable experimental scatter (6–9 %).

The durations \({t_e}\) of the short-time shrinkage tests to be extrapolated are here considered to be either 90 days or 30 days. These times are marked in all the figures by vertical lines. All the data points beyond the duration \({t_e}\) are crosses, which means they are not used for fitting and serve only for evaluating the extrapolations. The shrinkage strain reached in these large specimens at time \({t_e}\) is denoted as \(\epsilon _e\) and is marked in the figures by a horizontal line.

The smaller-size companion specimens to aid the extrapolation reach much higher shrinkage strains before time \({t_e}\) and their sizes should obviously be so small to their strain attained at time \({t_e}\) would be at the beginning of the terminal concave portion of the shrinkage curve revealing approach to the final shrinkage value. The strains of the companion specimens that are smaller then \(\epsilon _e\) (and are shown by crosses below the horizontal line) are not considered for data fitting by shrinkage formula (1) because the aim is to extrapolate only the shrinkage test of the larger, standard size, specimen. Nevertheless, the early companion specimen strains, which are smaller than \(\epsilon _e\), can be used to judge the quality of fit. Also, it has been checked that if these early strains were included in the data fitting, the resulting fits would be almost the same.

For Wittmann–Bažant data, the main tests to be extrapolated are considered to be the tests of cylinders of diameter either 160 mm (6.30 in.) (for which D = 3.15 in.) or 83 mm (or 3.27 in.) (for which D = 1.63 in.). For Burg–Ost data, the main tests are assumed to be the tests of cylinders of diameter 152 mm. (6 in.) (for which D = 3 in.) or prisms of side 76 mm (or 3 in.) (for which D = 1.5 in.).

Figs. 2a–d, 3a–d and 4a–d show a number of different combinations of test sizes and durations of exposure. First we consider the test pairs for actually measured shrinkage curves in Figs. 2a, b, 3a, b, and 4a, c, d. As seen in the figures, in some cases the extrapolations of the measured data aided by the small-size specimens agree well with the subsequently measured data marked by the crosses; see Figs. 2b and 3b.

In other cases, however, the agreement is not too good and, more seriously, the extrapolation seems not to give the correct final shrinkage value, which is of main interest. The cause of these poor results is thought to be that the smaller specimen sizes considered were not small enough, and particularly that their shrinkage curves did not extend within time \({t_e}\) into the concave approach to the final shrinkage value.

6 Optimal fitting, extrapolation and evaluation of artificially shifted data

Unfortunately, no data pairs for companion specimens of sufficiently small sizes are available in the literature. Therefore, strictly for the purpose of evaluating the method, it was decided to create artificial data for smaller-size specimens according to the assumption that Eq. (1) based on the diffusion theory of shrinkage is sufficiently realistic [1, 2, 4, 5]. According to the diffusion theory, a decrease of specimen size from \({D_1}\) to \({D'_1}\) corresponds to a leftward shift of the shrinkage curve in the logarithmic time scale. The shift distance is \(\Delta = 2 \log (D'_1k'_{s,1}/D_1k_{s,1})\). However, after the shift, the artificial data must also be slightly scaled up vertically in the same ratio as the final value \({\epsilon _{\text{sh}}}_\infty\), which is changing due to cement hydration (aging). The vertical scaling ratio is obtained from Eq. (4) as the ratio of the \({\epsilon _{\text{sh}}}_\infty\) values corresponding to the \(\tau _{\text{sh}}\)-values for the reduced size \({D'_1}\) and the original size \({D_1}\).

While the standard size shrinkage specimens are usually cylinders, for making specimens of greatly reduced size it would be preferable to use square prisms. Such specimens could be cast horizontally, with one size open, and if the specimens are not wide enough compared to the aggregate size, they could be cut from a wider specimen by a saw (in that case, an additional correction would be required for the wall effect, which differs between cast and sawed surfaces and can be determined by diffusion and shrinkage simulations with a lattice-particle model).

The shrinkage plots with the shifted data are shown in Figs. 2c, d, 3c, d and 4b. They are again optimally fitted in the same way as before. Comparing the fits to those of the unshifted data confirms that if the smaller companion specimen is small enough, the extrapolation is improved.

However, the extrapolation is found not to improve as much as might be desired. There are still cases in which the final shrinkage value is not predicted correctly; see Fig. 4c, d. Obviously, to get perfect extrapolations, the B3 (or B4) Eq. (1) would need to be improved, or the extrapolation would need to be made by inverse analysis with a sophisticated three-dimensional finite element code that simulates the diffusion of moisture, distributed cracking and its localization, the aging due to hydration and the creep due to shrinkage stresses. The autogenous shrinkage in the parts of the cross section not yet reached by the drying front would have to be considered, too. To this end, tests of combined drying and autogenous shrinkage, necessitating a sophisticated evaluation, would have to be devised and carried out. This would be a major task beyond the scope of this paper and would require an extensive project.

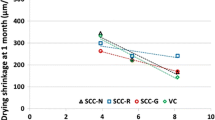
The fact that neither the present method nor the water loss method are completely satisfactory must be viewed in the context of the present practice, whose errors are even bigger. The short-time data are plotted graphically, often in the linear scale (Fig. 5), and then an asymptote is intuitively sketched by eye or obtained by fitting an obsolete formula with poor asymptotics, such as that of ACI-Committee 209. In the linear scale plots, it often looks as if the final shrinkage value (such as that shown by the dashed horizontal line in Fig. 5a) were close, even though much more shrinkage is still to take place.

Fig. 5
figure 5

a, b Comparison of extrapolations in the linear and logarithmic time scales (the data points in both diagrams are exactly the same)

Full size image

In view of the uncertainties about both methods, it would make sense to use them both. If they happen to agree, the extrapolation is more likely to be realistic. If not, a conservative approach is to take the larger value, which is still better than an intuitive extension of the curve.

7 Conclusions

  1. 1.

    Since the extrapolation of shrinkage aided by weight loss measurement has recently been shown to be insufficiently reliable, an alternative extrapolation may be based on testing the shrinkage of small-enough companion specimens.

  2. 2.

    An alternative concept is to improve the long-time extrapolation of shrinkage by adding a test of companion specimen of sufficiently small size. But again this concept is not sufficiently reliable. The reality is that, in some cases, it can significantly underestimate the long-time value. Further research, which will require a properly designed testing program and analysis, is needed.

  3. 3.

    Both the present method and the weight-loss method are nevertheless better than the estimates made by intuitive extrapolation by eye or by fitting a formula to one-size data (especially if one uses an outdated formula, such as the ACI-209 formula which has incorrect short- and long-time asymptotics).