Advertisement

Materials and Structures

, Volume 48, Issue 12, pp 3863–3874 | Cite as

Steel fibre spacing in self-compacting concrete precast walls by X-ray computed tomography

  • Tomasz Ponikiewski
  • Jacek Katzer
  • Monika Bugdol
  • Marcin Rudzki
Open Access
Original Article
First Online:

Abstract

In the paper, a research programme focused on determination of steel fibre dispersion in self-compacting concrete using the X-ray computed tomography method is presented. Large scale specimens were cast (in the form of walls 1.2 m × 1.2 m × 0.15 m), containing different types of steel fibre. The tests were conducted on beam specimens cut from each wall. Both traditional destructive tests (compressive strength, three point bending) and non-destructive tests (X-ray computed tomography imaging followed by image analysis) were performed. The X-ray computed tomography method allowed to precisely determine fibre dispersion in the whole volume of the walls. These results were compared with mechanical properties of cut beams and their original location in the walls. Differences in fibre volume and dispersion between top and bottom parts of the walls were observed. The influence of the fibre type and the casting point location was also significant. Longer fibres became more effectively orientated in parallel to the bending loading direction, resulting in enhancement of the mechanical properties of the concrete. Tests on 16 beams (cut from each wall), through load–deflection relations, provided a thorough picture of mechanical uniformity of the material properties inside the walls. The X-ray computed tomography imaging proved to be intuitive and accurate in the assessment of steel fibre dispersion.

Keywords

Concrete SFRC Steel fibres Self-compacting concrete X-ray computed tomography Image processing 

1 Introduction

Steel fibre reinforced concrete (SFRC) has been known since 1874 when the patent describing the idea of strengthening ordinary concrete through addition of irregular steel scrap was filed by A. Berard. Modern SFRC, based on engineered steel fibre, entered civil engineering in early 1960s. The addition of fibre mainly influences tensile and flexural toughness and all dynamic properties of concrete including blast load and projectile load resistance [25, 27, 29]. The benefit of adding fibre to concrete, is determined by the type, content and dispersion of the fibres [45]. Fibre dispersion is an important aspect to be considered when designing and analysing the structural response of SFRC elements [36, 43]. Current worldwide yearly consumption of engineered fibres for concrete reinforcement is equal to 300,000 tons [24] and is growing every year by 20 % [27]. For the last 50 years a broad range of applications has been developed for this kind of cement composite. However, current use of SFRC is often limited to pavements and tunnel linings [7, 32]. The limited applications are caused by lack of reliable and easy to use designing methods of SFRC and by unpredictable fibre dispersion in cast element influencing both its mechanical properties and homogeneity [1, 20]. To overcome these limitations a new approach to SFRC is needed. Firstly, the correlation between fibre dispersion and properties of SFRC (in both fresh and hardened state) deserves much deeper investigation. The knowledge about fibre dispersion would enable efficient and precise designing of enhanced cement composites “tailored” for specific structural applications [2, 7, 18]. Secondly, combining SFRC and self-compacting concrete (SCC) into a new type of cement composite would create a material opening wide possibilities in civil engineering mainly associated with its previously unknown flexibility in creating a concrete structure. The future successful use of steel fibre reinforced self-compacting concrete (SFR-SCC) implies the thorough analysis of fibre dispersion, especially when considering thin elements [4, 21]. The results of previous research programmes [8, 9, 32, 35, 45] show that fibre dispersion in SFR-SCC structural elements varies due to: the type of casting process, the flow rate, the wall effect, the thickness of elements and the proximity to the bottom of moulds. Since the best fibre reinforced concrete performance is expected when fibres are parallel to the direction of the applied tensile stress, it is essential to determine the actual angle between any given fibre and this axis [16, 17]. It is impossible to predict the fibre dispersion without undertaking sophisticated destructive and/or non-destructive testing [11, 12, 42, 45]. The main idea of the planned research programme was to cast large SFR-SCC “wall specimens” (scale 1:2 comparing to ordinary pre-cast wall elements) and harness X-ray computed tomography (XCT) imaging for non-destructive testing (NDT). XCT imaging is a NDT method for obtaining a large number of consecutive sectional images of the internal structure of the specimens. It has been successfully used in several previous studies to characterize the mechanical properties of cement-based materials [22, 26, 41, 44] while taking into consideration air-voids volume, spatial distribution of air and clogging.

2 Used materials and experimental programme

The matrix composition was constant for all tested SFR-SCC. Portland cement CEM I 42.5R, was applied as a binder. The water/cement ratio was equal to 0.41. The cement content was high (490 kg/m3), but successfully harnessed by other researchers in previous research programmes [10, 33, 40]. The aggregate was in a form of natural sand (804.1 kg/m3) and fine aggregate (804.1 kg/m3) characterized by maximum diameters of 2 and 8 mm respectively. Two admixtures: a superplasticizer and a stabilizer, were used. The superplasticizer was based on polycarboxylate ether (solid concentration 20 %) and the base constituent of the stabilizer was a synthetic co-polymer. The superplasticizer and the stabilizer were characterized by the density of 1.07 and 1.01 g/cm3 respectively. Both admixtures were chosen according to the suggestions described by Kim et al. [22]. The superplasticizer was dosed at the rate of 3.5% by weight of cement in order to maintain a slump-flow range of 720–800 mm. Mixes were modified by two types of steel fibre (code names F35 and F50). Both fibre types were crimped and produced out of low carbon steel wire characterized by tensile strength of 800 MPa.

The choice of fibres was based on previous experience with SFR-SCC. The commercial availability and commonness of civil engineering applications of specific fibre types were also studied and taken into consideration [18]. The volume of added fibre was equal to 1.00 %. The fibres geometry, which is presented in detail in Table 1, was the only variable factor.
Table 1

Geometrical properties of steel fibres

Code name

Length (mm)

Width (mm)

Cross section

Shape

Number of fibres per kg

F 35

35

2.60

Segment of a circle

Open image in new window

2,884

F 50

50

2.60

Segment of a circle

Open image in new window

1,128

The mix proportioning system proposed by Okamura and Ozawa [31], which assumes a supply of concrete fresh mix as a ready-mix provided by a concrete plant was implemented. Due to the fixed amounts of sand and fine aggregate the self-compatibility is achieved by adjusting only the water–binder ratio and associated with it superplasticizer dosage [23, 30]. During both castings, it was observed that the fibres disperse homogeneously without any clumping. The detailed mixing procedure is presented in Fig. 1.
Fig. 1

Mixing procedure of SFR-SCC (S sand, FA fine aggregate, C cement, W water, F fibre, SP superplasticizer, ST stabilizer)

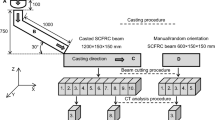
In order to characterize the flow and workability properties of SFR-SCC, the traditional slump-flow test was performed according to RILEM TC 145-WSM [37]. Scaled (1:2) concrete walls with dimensions of 150 × 1,210 × 1,240 mm were chosen as specimens for the tests. The specimens are thinner than actual wall structures of this type. This dimension was limited by the testing standard for compressive strength (dimensions of ordinary cube specimen) [32]. The concrete was pumped from the upper middle point and therefore it flowed along the formwork to fill the structure. The SFR-SCC mixes were cast to the formwork from the top. After hardening, the walls were cut into 16 beams with dimensions of 150 × 150 × 600 mm each. The code names of these beams were T1.1–T1.16 and T2.1–T2.16 (totalling 32 beams). The formwork used, the location of the casting point, the wall cut scheme and the global system of coordinates are presented in the Fig. 2.
Fig. 2

Used formwork, location of casting point, wall cut scheme (x = 1 for first wall and x = 2 for second wall) and global system of coordinates

The research programme was divided into two main stages. The first stage covered acquisition of XCT images of SFR-SCC specimens and processing of these images. XCT medical scanner equipped with 64 rows of detectors, and the thickness of a series of reconstructed native Computed Tomography scans of 0.625 mm (the width of a single detector) was used during this part of the research programme. The examined surface of each layer of concrete was 150 × 150 mm. For each X-ray beam the results consisted of a native series written in DICOM format with at least 950 images, and a reconstructed series with at least 1,500 images (taking into account the interval in the range 50–80 % of the thickness of the native layer). The acquisition parameters were not less than 140 kV for lamp voltage and 400 mAs for current strength. The acquired CT volumetric images were processed by in-house-built software using C++ libraries for medical image processing, the “Insight Toolkit” (ITK) [14]. After tomography reconstruction, the image data to be analysed for each specimen was characterized by (0.47 × 0.47 × 0.4) [mm] voxel size, total image size (512 × 512 × 1,600) voxels with intensity expressed in hounsfield units (HU) that define the extent of X-ray radiation absorption. The image processing consisted of two stages: automatic selection of volume of interest (VOI) and analysis of VOI. The automatic selection of the region of interest consists of: binarization (thresholding) above 500 HU, selection of the largest 3D object (small objects due to cracking were disregarded) and calculation of cuboid vertices that contain the object. The analysis of VOI consisted of: image framing (cropping) to specimen volume, binarization above 3,000 HU, binary smoothing in order to remove spurious voxels assigned value, binary median filtering (voxel radius 1), separation of objects, binary object labelling, calculating geometrical properties of objects (centre and orientation). Each specimen underwent XCT imaging with the custom acquisition protocol (the spatial resolution was 0.47, 0.47, 0.4 mm). Three cross-sections of an exemplary beam after VOI selection and after steel fibre segmentation are presented in Fig. 3.
Fig. 3

Cross sections of the beam T1.1 after VOI selection (upper left X–Y plane; upper right 3D visualization; lower left Y–Z plane; lower right X–Z plane)

The second stage covered tests of mechanical properties of SFR-SCC. Initially, three-point bending tests according to RILEM TC 162-TDF (2002) were performed. After the three-point bending test, the beams were cut into 150 × 150 × 150 mm cubes and the compressive strength was tested.

3 Test results

The slump-flow test results in the form of the diameter (SFD) and the time when fresh mix reaches the 500 mm diameter (T500) are presented in Tables 1, 2 and 3. Both achieved values of SFD and both values of T500 were within the accepted ranges given in the EFNARC Specification and Guidelines for SCC [6].
Table 2

Properties of fresh and hardened SFR-SCC

Wall

Fibre code name

Slump-flow test

Fresh mix density (kg/m3)

Compressive strength after 28 days

T 50 (s)

SFD (mm)

f c, cube (MPa)

SD

T1

F 35

2.5

760

2,383

74.98

5.76

T2

F 50

2.6

765

2,389

81.25

5.28

Table 3

SFR-SCC classification in compliance to “fib Model Code 2010”

Specimen

f R1 (MPa)

f R3/f R1

Class

f R1/f LOP

Reinforcement substitution

T1.1

2.04

0.509

2a

0.555

Enabled

T1.2

2.11

0.469

–

0.590

–

T1.3

1.98

0.241

–

0.550

–

T1.4

2.65

0.031

–

0.829

–

T1.5

1.04

0.505

1.0a

0.303

–

T1.6

1.07

0.405

–

0.379

–

T1.7

1.71

0.547

1.5a

0.424

Enabled

T1.8

1.54

0.350

–

0.445

–

T1.9

3.06

0.290

–

0.718

–

T1.10

1.50

0.474

–

0.408

–

T1.11

2.52

0.761

2.5a

0.600

Enabled

T1.12

2.69

0.141

–

0.785

–

T1.13

2.28

0.805

2.0b

0.614

Enabled

T1.14

1.45

0.803

1.0b

0.465

Enabled

T1.15

4.48

0.467

–

0.891

–

T1.16

1.33

0.453

–

0.372

–

Wall 1 average

2.09

0.453

–

0.558

–

T2.1

2.98

0.724

2.5a

0.718

Enabled

T2.2

4.52

0.937

4.0b

0.980

Enabled

T2.3

5.52

0.615

5.0a

0.989

Enabled

T2.4

1.38

0.806

1.0b

0.403

Enabled

T2.5

4.42

0.733

4.0a

0.991

Enabled

T2.6

1.01

0.597

1.0a

0.315

–

T2.7

4.59

0.776

4.0a

0.916

Enabled

T2.8

2.60

0.274

–

0.780

–

T2.9

4.60

0.846

4.0b

0.983

Enabled

T2.10

3.26

0.067

–

1.000

–

T2.11

3.66

0.780

3.0a

0.876

Enabled

T2.12

3.05

0.201

–

0.926

–

T2.13

6.70

0.710

6.0a

0.970

Enabled

T2.14

1.50

0.788

1.5a

0.492

Enabled

T2.15

8.05

0.745

8.0a

0.996

Enabled

T2.16

2.15

0.850

2.0b

0.572

Enabled

Wall 2 average

3.75

0.653

3.0a

0.807

Enabled

Both SFR-SCC walls, after being cut into 16 beam specimens, were subjected to XCT imaging. For each specimen there were calculated: the number of the steel fibres, the coordinates of the fibre centre in 3D, the orientation and the distance to the casting point of each fibre (eigenvector of the fibre’s rotation matrix corresponding to the smallest eigenvalue). The volume of each fibre was also assessed. In this way the computed numbers of fibre in the first wall and in the second wall were equal to 54,008 and 46,693 respectively. Having all the above-described data, spherical histograms were generated, following the steps thoroughly described in a previous publication [39]. For each fibre, the vector U k assigned to the fibre is provided using spherical coordinates (see Fig. 4).
Fig. 4

Transformation of orientation vector to spherical coordinates with the z-axis aligned with the long axis of the beam

For each vector parallel to a fibre υ k a new vector \(\omega_{k}\) is assigned, whose first two coordinates are angles \(\phi_{k} ,\theta_{k}\) and its third coordinate equals 1. The achieved spherical histogram consists of a sphere, serving as a reference object, and up to c 2 (where c is a divisor of 180) cylinders, whose main axes of symmetry are parallel to the vectors that are representative of each class and whose heights equal appropriate n i,j values. First two spherical coordinates of the class representatives should be calculated using the following formula (1).
$$\phi = \frac{180}{c} \cdot \left( {i - \frac{1}{2}} \right),\quad \theta = \frac{180}{c} \cdot \left( {j - \frac{1}{2}} \right)$$
(1)
The fibre distribution along the X-axis, which is parallel to the shorter side of the wall, is presented in Fig. 5. It can be seen that, in the case of Wall 2 the number of fibres depends very little on the coordinate X, whereas in the case of Wall 1 clearly more fibres can be found closer to the wall edges. The fibre distribution along the Y-axis, defined by the vertical wall axis, is presented in Fig. 6. Wall 2 is characterized by almost homogeneous fibre dispersion along its height. In the case of Wall 1 fibre dispersion is divided into three areas: fibre congestion at 180 mm from the top of the wall, sparse fibre in the middle part of the height of the wall and second fibre congestion at the bottom of the wall.
Fig. 5

Fibre distribution along the X-axis in Wall 1 (a) and Wall 2 (b)

Fig. 6

Fibre distribution along the Y-axis in Wall 1 (a) and Wall 2 (b)

The Z-axis is parallel to the wider wall side (see Fig. 2). The distribution of the fibres along that axis is illustrated in Fig. 7. In the upper part of Wall 1, there is a fibre congestion area near the casting point followed by sparse fibre. The second fibre congestion area is located at both edges of the wall. There is also a local minimum of fibre number under the casting point. The fibre dispersion in the lower part of Wall 1 is more homogeneous comparing to the upper part.
Fig. 7

Fibre distribution along the Z-axis in Wall 1 (a) and Wall 2 (b)

In the Fig. 8 the distribution of the angle Θ (theta), which describes the fibre orientation with respect to the horizontal plane, is presented. It is clear that the fibres in the walls are arranged more vertically than horizontally.
Fig. 8

Distribution of the angle Θ (which describes the fibre orientation with respect to the horizontal plane) in Wall 1 (a) and Wall 2 (b)

In Fig. 9 the distribution of the angle Φ (phi) between the fibres and the Z-axis is presented. The analysis of this chart allows to assess whether the fibres are arranged along the shorter or the longer side of the wall. It should be noted that, in the lower part of the wall, the fibres are orientated more evenly in comparison to the upper part of the wall where 50 % less of the fibres are aligned parallel to the longer side. These results show a clear effect of fibre orientation along the Y-axis in both walls.
Fig. 9

Distribution of the angle Φ (which describes the fibre orientation with respect to the Z-axis) in Wall 1 (a) and Wall 2 (b)

The load–deflection curves (according to RILEM TC 162-TDF) of the specimens cut from the Wall 1 and Wall 2 are shown in Figs. 10 and 11 respectively.
Fig. 10

Load–deflection curves of specimens cut from Wall 1 (T1.1–T1.16)

Fig. 11

Load–deflection curves of specimens cut from Wall 2 (T2.1–T2.16)

4 Discussion

On the basis of the obtained Load–CMOD diagram (according to RILEM TC 162-TDF [38]), four different values of the residual strengths (f R1, f R2, f R3, f R4) were calculated for all tested SFR-SCC beam specimens. These strengths correspond to different values of the CMOD and are contested by some researchers as difficult to be directly used in SFR-SCC design procedures [5, 19]. Nevertheless, some of the residual strengths are commonly assumed as representative of serviceability limit states (SLS) and ultimate limit states (USL). The residual strengths f R1 and f R3 which are significant for service and ultimate conditions are most often pointed as those which characterize the global residual strength. These strengths can be harnessed for SLS analysis and USL analysis. In “fib Bulletin 55, Model Code 2010” it was proposed that material behaviour at ULS will be related to the behaviour at SLS employing the f R3/f R1 ratio. Basically, in order to classify the post-cracking strength of SFR-SCC linear elastic behaviour can be assumed by considering the characteristic residual strength significant for service (f R1) and ultimate (f R3) conditions. According to this procedure SFR-SCC post-cracking residual strength is described by two parameters: namely f R1 (representing the strength interval) and a letter a, b, c or d (representing the ratio f R3/f R1). This classification properly represents the most common cases of softening and hardening of fibre reinforced concrete. Traditional reinforcement substitution is enabled if relationships 2 and 3 are fulfilled. Full classification of all tested specimens according to “fib Bulletin 55, Model Code 2010” is summarized in Table 3.
$$f_{{{\text{R}}1}} /f_{\text{LOP}} > \, 0.4$$
(2)
$$f_{{{\text{R}}3}} /f_{{{\text{R}}1}} > \, 0.5$$
(3)

Only 6 out of 16 specimens cut from Wall 1 fulfil the requirements to have the strength class assigned (according to “fib Bulletin 55, Model Code 2010”). In contrast, 13 out of 16 specimens cut from Wall 2 fulfil the same requirements. On average the specimens cut from Wall 1 are characterized by f R1 = 2.09 MPa, with no strength class assigned and no option for traditional reinforcement substitution. Specimens originating from Wall 2 are on average characterized by f R1 = 3.75 MPa, with 3.0 a strength class assigned and enabled reinforcement substitution. Both analysed walls are characterized by heterogeneous mechanical properties (e.g. specimens cut from the bottom-left corner of the walls are characterized by much higher f LOP, than specimens cut from the bottom-right corner). On average, all residual strengths of specimens cut from Wall 2 are significantly larger than those of Wall 1. Nevertheless, both walls suffer from lack of mechanical properties uniformity, putting in question their engineering use.

Comparing curves presented in Figs. 10 and 11 it can be observed that there are significant differences between the specimens cut from Wall 1 and Wall 2. In general, lower values of applied loads were observed for the specimens cut from Wall 1 containing shorter (35 mm long) fibres. It should be noted that specimens T1.1, T1.2, T1.3 and T1.4 showed a clear softening-type post-cracking behaviour. These specimens were located close to the top of the wall and the velocity of fresh mix flow was probably insufficient to orient the fibres. By increasing the length of the fibres (Wall 2), they tend to be more vertically orientated to the loading direction (in bending). The best mechanical behaviour of an SFR-SCC is expected when the fibres are completely perpendicular to the crack so that they can fully arrest it [28]. This results in the enhancement of the mechanical properties of the SFR-SCC. The specimens from the bottom part (T2.15, T2.13) and the top part (T2.2, T2.3) of Wall 2 are characterized by the best post-cracking behaviour. This phenomenon was also observed during another research programme conducted by Zhu et al. [45]. In the case of both walls, specimens characterized by best mechanical performance were number 15 (bottom-left part of a wall). Specimen T1.15 failed when the applied load reached 15.30 kN (the maximum value for a specimen cut from Wall 1) while specimen T2.15 failed when the applied load reached 24.92 kN (the maximum value for a specimen cut from Wall 2).

The XCT determination of the fibre dispersion is in good agreement with the outcome of the load–deflection curves. Significant differences in mechanical properties of both walls are mirrored in the results of XTC imaging. Dissimilarities of the mechanical properties of specimens cut from lower and upper part of walls are also clearly visible.

Probably the most interesting phenomenon observed during the research programme is the lack of symmetry around the vertical axis in mechanical properties of specimens located at the bottom of both walls. The bottom specimens cut from both walls (T1.15, T1.16, T1.13, T1.14 and T2.15, T2.16, T2.13, T2.14) are characterized by significantly different mechanical properties. In the case of Wall 1 the symmetry is mostly recovered the farther a specimen was located from the bottom inlet point. Wall 2 is characterized by this “lack of symmetry” throughout its height. The Authors believe that this lack of symmetry was created during the casting procedure. Both SFR-SCC mixes were cast (free-fall) through a steel funnel with a rubber tube. Due to the shape of the formwork it was very difficult to control the position of the bottom part of a rubber tube feeding the mix into the formwork. Lower parts of the walls were subjected to the largest differences in position of the tube ending over the current mix level and “left-right” alignment to keep the casting in vertical axis of the formwork. The higher the formwork was filled the easier it was to keep the position of the tube ending steady. One must also keep in mind ordinary turbulences of a fresh mix being fed through a funnel and rubber tube from a height of 2.0 m. It would be also interesting to observe (if a formwork was made out of see-through material) whirls and all other turmoil of a mix being cast especially in a bottom part of a formwork. The mechanical properties of the specimens cut from the walls prove that type of fibre significantly influences the quality of casting procedure.

The future of fibre reinforced concretes seems to be associated with orienting the fibres along a certain direction [28]. Taking into account effectiveness of XTC imaging orienting of the fibres can be now improved and controlled allowing very precise designing of elements and structures, especially these subjected to dynamic loads [3]. Other promising, but still uncharted research territory for XTC imaging are concretes reinforced by waste fibre [13]. The growing importance of environment protection would force research effort to be more and more focused on non-conventional cement composites [34] such as SFR-SCC.

5 Conclusions

Conducted research programme allows to state that:

  • harnessing medical XCT imaging to fibre distribution characterization is feasible,

  • 3D image reconstruction and coordinate extraction of fibre position is possible and the complete distribution curves of fibre orientation and dispersion can be extracted,

  • there are significant distortions in fibre dispersion randomness caused by multiple technological factors,

  • in general, the fibres are aligned along the fresh mix’s flow (Y) vertical direction,

  • the medical XCT methodology used for assessment of SFR-SCC has its limitation and improved (concrete dedicated) processes should be developed,

  • the reconstruction of fibre dispersion in 3D, can be used for the subsequent finite element analysis of SFR-SCC,

  • the prediction of the mechanical characteristics, based on the actual fibre dispersion in SFR-SCC precast walls is fairly reliable. Yet constitutive models of SFR-SCC given by Jiaping et al. [15] need to be established and validated.

  • SFR-SCC modified by longer fibres (Wall 2) is characterized by better mechanical performance than the one modified by shorter fibres (Wall 1),

  • Wall 2 is characterized by better uniformity of mechanical properties than Wall 1,

  • longer fibres used as reinforcement for SFR-SCC allow to achieve better static mechanical properties of cast wall elements,

  • dynamic properties and walls of different shapes and sizes should be tested.

References

  1. 1.
    Barnett SJ, Lataste JF, Parry T, Millard SG, Soutsos MN (2010) Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength. Mater Struct 43(7):1009–1023CrossRefGoogle Scholar
  2. 2.
    Bui VK, Geiker MR, Shah SP (2003) Rheology of fiber reinforced cementitious materials. In: Naaman AE, Reinhardt HW (eds) Proceedings of the HPFRCC4 Workshop, Ann Arbor. RILEM Publications, Cachan, pp 221–231Google Scholar
  3. 3.
    Cichocki K, Ruchwa M (2011) Propagation of damage in structures under blast load. In: Proceedings of 57th annual conference on scientific problems of civil engineering, Krynica-Rzeszow, 18–22 September 2011, pp 98–99Google Scholar
  4. 4.
    Corinaldesi V, Moriconi G (2011) Characterization of self-compacting concretes prepared with different fibers and mineral additions. Cem Concr Compos 33(5):596–601CrossRefGoogle Scholar
  5. 5.
    di Prisco M, Plizzari G, Vandewalle L (2009) Fibre reinforced concrete: new design perspectives. Mater Struct 42:1261–1281. doi: 10.1617/s11527-009-9529-4 CrossRefGoogle Scholar
  6. 6.
    EFNARC (2002) Specification and guidelines for self-compacting concrete. English ed. European federation for specialist construction chemicals and concrete systems. Norfolk, UK; February 2002Google Scholar
  7. 7.
    Ferrara L, Meda A (2006) Relationships between fibre distribution, workability and the mechanical properties of SFRC applied to precast roof elements. Mater Struct 39:411–420CrossRefGoogle Scholar
  8. 8.
    Ferrara L, Park YD, Shah SP (2008) Correlation among fresh state behaviour, fiber dispersion and toughness properties of SFRCs. ASCE J Mater Civ Eng 20(7):493–501CrossRefGoogle Scholar
  9. 9.
    Ferrara L, Ozyurt N, di Prisco M (2011) High mechanical performance of fiber reinforced cementitious composites: the role of ‘‘casting-flow’’ induced fiber orientation. Mater Struct 44(1):149–168CrossRefGoogle Scholar
  10. 10.
    Ferrara L, Bamonte P, Caverzan A, Musa A, Sanal I (2012) A comprehensive methodology to test the performance of steel fibre reinforced self-compacting concrete (SFR-SCC). Constr Build Mater 37:406–424CrossRefGoogle Scholar
  11. 11.
    Ferrara L, Faifer M, Toscani S (2012) A magnetic method for non destructive monitoring of fiber dispersion and orientation in steel fiber reinforced cementitious composites—part 1: method calibration. Mater Struct 45:575–589CrossRefGoogle Scholar
  12. 12.
    Ferrara L, Faifer M, Muhaxheri M, Toscani S (2012) A magnetic method for non destructive monitoring of fiber dispersion and orientation in steel fiber reinforced cementitious composites. Part 2: correlation to tensile fracture toughness. Mater Struct 45:591–598CrossRefGoogle Scholar
  13. 13.
    Graeff AG, Pilakoutas K, Neocleous K, Peres MVN (2012) Fatigue resistance and cracking mechanism of concrete pavements reinforced with recycled steel fibres recovered from post-consumer tyres. Eng Struct 45:385–395CrossRefGoogle Scholar
  14. 14.
    Ibáñez L, Schroeder W, Ng L, Cates J. (2005) The ITK Software Guide. KitwareGoogle Scholar
  15. 15.
    Jiaping L, Changfeng L, Jianzhong L, Gong C, Zhiqian Y (2013) Study on 3D spatial distribution of steel fibers in fiber reinforced cementitious composites through micro-CT technique. Constr Build Mater 48:656–661CrossRefGoogle Scholar
  16. 16.
    Kang ST, Kim JK (2011) The relation between fiber orientation and tensile behavior in an ultra high performance fiber reinforced cementitious composites(UHPFRCC. Cem Concr Res 41:1001–1014CrossRefGoogle Scholar
  17. 17.
    Kang ST, Lee BY, Kim JK, Kim YY (2011) The effect of fibre distribution characteristics on the flexural strength of steel fibre-reinforced ultrahigh strength concrete. Constr Build Mater 25:2450–2457CrossRefGoogle Scholar
  18. 18.
    Katzer J, Domski J (2012) Quality and mechanical properties of engineered steel fibres used as reinforcement for concrete. Constr Build Mater 34:243–248CrossRefGoogle Scholar
  19. 19.
    Katzer J, Domski J (2013) Load–deflection characteristic of fibre concrete based on waste ceramic aggregate. Rocznik Ochrona Środowiska (Annu Set Environ Protect) 15:213–230Google Scholar
  20. 20.
    Kaufmann J, Frech K, Schuetz P, Münch B (2013) Rebound and orientation of fibers in wet sprayed concrete applications. Constr Build Mater 49(2013):15–22CrossRefGoogle Scholar
  21. 21.
    Khayat KH, Manai K, Trudel A (1997) In suit mechanical properties of wall elements cast using self-consolidating concrete. ACI Mater J 94(6):491–500Google Scholar
  22. 22.
    Kim KY, Yun TS, Choo J, Kang DH, Shin HS (2012) Determination of air-void parameters of hardened cement-based materials using X-ray computed tomography. Constr Build Mater 37:93–101CrossRefGoogle Scholar
  23. 23.
    Łaźniewska-Piekarczyk B (2013) The influence of admixtures type on the air-voids parameters of non-air-entrained and air-entrained high performance SCC. Constr Build Mater 41:109–124CrossRefGoogle Scholar
  24. 24.
    Li VC (2002) Large volume, high-performance applications of fibers in civil engineering. J Appl Polym Sci 83:660–686CrossRefGoogle Scholar
  25. 25.
    Maidl BR (1995) Steel fibre reinforced concrete. Ernst & Sohn, BerlinGoogle Scholar
  26. 26.
    Manahiloh KN, Muhunthan B, Kayhanian M, Gebremariam SY (2012) X-ray computed tomography and nondestructive evaluation of clogging in porous concrete field samples. J Mater Civ Eng 24(8):1103–1109CrossRefGoogle Scholar
  27. 27.
    Mehta PK, Monteiro PJM (2006) Concrete—microstructure properties and materials, 3rd edn. McGraw-Hill, New YorkGoogle Scholar
  28. 28.
    Montero F, Schlangen E (2012) Modelling of fracture in fibre-cement based materials. In: Brandt AM, Olek J, Glinicki MA, Leung CKY (eds) Proceedings of the international symposium on brittle matrix composites, vol 10. IFTR and Woodhead Publications, Warsaw, pp 51–60Google Scholar
  29. 29.
    Nawy EG (1996) Fundamentals of high strength high performance concrete. Longman, EnglandGoogle Scholar
  30. 30.
    Okamura H, Ouchi M (2003) Self-compacting concrete. J Adv Concr Technol 1(1):5–15CrossRefGoogle Scholar
  31. 31.
    Okamura H, Ozawa K (1995) Mix design for self-compacting concrete. Concr Lib JSCE 1995Google Scholar
  32. 32.
    Orbe A, Cuadrado J, Losada R, Rojí E (2012) Framework for the design and analysis of steel fiber reinforced self-compacting concrete structures. Constr Build Mater 35:676–686CrossRefGoogle Scholar
  33. 33.
    Pająk M, Ponikiewski T (2013) Flexural behavior of self-compacting concrete reinforced with different types of steel fibers. Constr Build Mater 47:397–408CrossRefGoogle Scholar
  34. 34.
    Piecuch I, Piecuch T (2013) Environmental education and its social effects. Annu Set EnvironProtect 46(9):1561–1568Google Scholar
  35. 35.
    Ponikiewski T, Cygan G (2011) Some properties of self compacting concretes reinforced with steel fibres. Cem Wapno Beton 16(4):203Google Scholar
  36. 36.
    Ponikiewski T, Golaszewski J (2012) The new approach to the study of random distribution of fibres in high performance self-compacting concrete. Cem Wapno Beton 17(3):165Google Scholar
  37. 37.
    RILEM TC 145-WSM (2002) Workability and rheology of fresh concrete: compendium of tests In: Bartos PJM, Sonebi M, Tamimi AK (eds) Report of RILEM technical committee TC 145-WSM workability of special concretes. RILEM Publications, CachanGoogle Scholar
  38. 38.
    RILEM TC 162-TDF (2002) Test and design methods for steel fiber reinforced concrete bending test, final recommendation. Mater Struct 35:579–582CrossRefGoogle Scholar
  39. 39.
    Rudzki M, Bugdol M, Ponikiewski T (2013) Determination of steel fibers orientation in SCC using computed tomography and digital image analysis methods. Cem Wapno Beton 80:257–263Google Scholar
  40. 40.
    Şanal İ, Ozyurt N (2013) To what extent does the fiber orientation affect mechanical performance? Constr Build Mater 44:671–681CrossRefGoogle Scholar
  41. 41.
    Suuronen JP, Kallonen A, Eik M, Puttonen J, Serimaa R, Herrmann H (2013) Analysis of short fibres orientation in steel fibre-reinforced concrete (SFRC) by X-ray tomography. J Mater Sci 48(3):1358–1367CrossRefGoogle Scholar
  42. 42.
    Torrents JM, Blanco A, Pujadas P, Aguado A, Juan-García P, Sánchez-Moragues MÁ (2012) Inductive method for assessing the amount and orientation of steel fibers in concrete. Mater Struct 45:1577–1592CrossRefGoogle Scholar
  43. 43.
    Wong RCK, Chau KT (2005) Estimation of air void and aggregate spatial distributions in concrete under uniaxial compression using computer tomography scanning. Cem Concr Res 35(8):1566–1576CrossRefGoogle Scholar
  44. 44.
    Zerbino R, Tobes JM, Bossio ME, Giaccio G (2012) On the orientation of fibres in structural members fabricated with self compacting fibre reinforced concrete. Cem Concr Compos 34:191–200CrossRefGoogle Scholar
  45. 45.
    Zhu YT, Blumenthal WR, Lowe TC (1997) Determination of non-symmetric 3-D fiber orientation distribution and average fiber length in short-fiber composites. J Compos Mater 31(13):1287–1301CrossRefGoogle Scholar

Copyright information

© The Author(s) 2014

Open AccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Authors and Affiliations

  • Tomasz Ponikiewski
    • 1
  • Jacek Katzer
    • 2
  • Monika Bugdol
    • 3
  • Marcin Rudzki
    • 3
  1. 1.Faculty of Civil EngineeringSilesian University of TechnologyGliwicePoland
  2. 2.Faculty of Civil Engineering, Environmental and Geodetic SciencesKoszalin University of TechnologyKoszalinPoland
  3. 3.Faculty of Biomedical EngineeringSilesian University of TechnologyGliwicePoland

Personalised recommendations