1 Introduction

The resistance of concrete to frost damage is largely controlled by its air void system. This air void system is created by deliberately incorporating air into the fresh mix using an air-entraining agent. The resulting air bubbles are characterized by their volume, size, shape, specific surface, frequency, and spacing. These quantities can be estimated by applying the principles of stereology on a statistically representative two-dimensional plane through a sample. Traditionally, the air bubble system is quantified by using either the linear traverse method or point counting method described in ASTM C457 [1]. These methods require manually counting bubbles and measuring chord lengths on a sample surface with a stereoscopic microscope. However, the ASTM C457 method is time consuming, requiring several hours of measurement to gain a statistically representative amount of information.

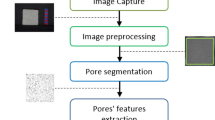
As an alternative, we developed a procedure to rapidly quantify the air void system of a mortar or concrete sample using automatic image analysis. This manuscript recommends an improved sample preparation method and then implements an image analysis procedure using a customizable Matlab script. This script obtains more complex information from a sample surface than what is described in ASTM C457. As a result, the accuracy of the computed air void properties ought to improve. Further, new information is computed, such as the shape and size distribution of the bubbles.

The method of using automatic image analysis to determine the air void system of concrete was first reported in 1977 by Chatterji and Gudmundsson [3], who proposed a sample preparation technique that would provide contrast to illuminate the air voids. This technique involved darkening the sample background with black ink and pressing white powder into the voids prior to scanning the surface with a microscope. This method of providing contrast is still used today, however, the most commonly used materials to prepare the sample surface are not always effective. We compare the effectiveness of various darkening agents and white powders and recommend a sample preparation procedure for more accurate results.

Advancements have been made toward developing commercial software to analyze the air void system of hardened concrete [13, 30], [16], including the introduction of a flatbed scanner for capturing digital images [14]. Because commercial software packages are based on automation, its use can minimize user error. We build upon this work, including the use of a high-resolution, flatbed scanner. However, unlike current available commercial code, our image analysis method is delivered as a platform-independent, Matlab script that can be downloaded and modified by the operator. Our script implements image processing methods and computes properties of the air void system using stereological analysis described in this manuscript. As a result, the user is able to quantify the air void system by computing the total air content, specific surface, spacing, and size distribution of the bubbles.

2 Sample preparation

Mortar specimens were cast and wet-cured into 6-in. × 3-in. (15-cm × 7.6-cm) cylinders with both air-entrained and non-air-entrained Portland cement mix proportions. The air entraining agent used in these tests was manufactured by Sika Air. Curing times varied from 3 days to 6 months. Ottawa sand, conforming to ASTM C778, was chosen as the only aggregate because it is particularly useful when studying small samples. Approximately 4-cm × 4-cm × 1-cm samples were cut from the cylinders with a diamond saw. To compare the entrained air content with that determined by image analysis, the bulk density was computed for both air-entrained and control samples in the saturated surface dry (SSD) condition by weighing and measuring the sample dimensions. The computed percent difference in density indicated the percent of entrained air. This estimation is based on the assumption that the entrapped air content for both air-entrained and control samples was the same.

To achieve a flat surface, each sample was carefully lapped on an Allied Multi Prep Polisher using successively finer silicon carbide grinding paper [320 grit (40.5 μm), then 400 grit (25.8 μm), 600 grit (15.3 μm), and finally 2400 grit (2.5 μm)]. The polisher was set to hold the samples automatically, maintaining the abrasive plane during polishing. Compressed air was used to remove dust from the specimen between each lapping stage. One of the challenges with grinding/polishing is to prevent defects on the surface because these defects could be mistaken for air voids. Another issue is that the perimeter of the air voids can easily erode, causing an overestimation of air void sizes and total air content. Both problems were mitigated by applying a 3:1 mixture of acetone and red nail polish (for visibility) to the surface as reinforcement prior to grinding. Polishing was considered complete when the red nail polish was removed entirely from the flat surface (but remained in the voids). Acetone was used to remove the remaining nail polish. The quality of polish was considered acceptable if the reflectivity of the surface was uniform and there was an absence of striations from the grinding paper.

The polished surfaces were then blackened using a water-soluble acrylic ink applied with a rubber brayer (Speedball Deluxe 3-inch Soft Rubber Brayer), a tool conventionally used for inking blocks for print making. Various brands of permanent marker (Sharpie, Bic, and Sanford) were also tested as a surface blackening agent, but it was found that while permanent markers could effectively blacken the surface of the paste and some types of large aggregate, it was ineffective in masking the reflectivity of the Ottawa sand used in our samples. The light source from the scanner picked up on this reflectivity, causing the corresponding pixels to look bright enough to be mistaken for air voids. Furthermore, because permanent markers typically contain resin, its ink was somewhat sticky. This sticky surface prevented the powder from being fully removed from the paste surface, causing an overestimation of the air content. On the other hand, the acrylic ink provided a very thin, dark matte black ink to the entire surface free of resin. This ink was effective at masking the reflectivity of the sand particles.

After the blackened mortar surfaces fully dried, a barium sulfate powder with an average particle size of 3-μm was pressed into the air voids. The powder was then wiped off with the edge of a a silicone spatula, resulting in a black background with white air void profiles. Other white powders were tested, including 0.5-μm titanium dioxide, 2-μm silicon oxide, and 9-μm corn starch (mean particle sizes). As with any cementitious material, grinding and polishing a “flat” plane is an imperfect process since it is impossible to remove all surface defects. As a result, the 0.5-μm titanium dioxide particles were too small because the tiny particles filled many of these imperfections. This effect was apparent because the particles would not wipe away from the cement surface. In contrast, the corn starch proved to be too coarse. These 9-μm particles created a “wall effect” around the perimeter of the bubbles, especially bubbles that were 50 μm in diameter or smaller. The empty space between the starch and the bubble perimeters resulted in an underestimation of the air void content. The silicon oxide powder was an acceptable powder choice, but the barium sulfate was whiter and provided better contrast more suitable for image processing. Figure 1 compares SEM images of polished mortar samples containing barium sulfate, silicon oxide, and corn starch showing the suitability of each powder in terms of particle size.

Fig. 1
figure 1

Backscattered SEM images of air voids filled with white powder from a 2-μm silica b 3-μm barium sulfate c 9-μm corn starch. Silica and barium effectively filled the air voids, making each of these powders suitable for image analysis. Because of its relatively large particle size, the corn starch created a wall effect, rendering it less effective at capturing the full profile area of the air voids. Using a powder of this size tends to cause an underestimation of the air content and overestimation of the spacing factor. On the other hand, smaller powders tended to scatter on the surface, so it was necessary to carefully wipe the surface after application to ensure that the air content was not overestimated

Full size image

3 Image capture

The inked and powdered samples were placed face down on a Canon CanoScan 8400F flatbed scanner. To prevent scratching of the platen (the glass flatbed), a border made from electrical tape was placed along the four edges of the sample surface, raising the sample slightly from the glass. The scanner was set to capture images at 3200 dpi resolution, corresponding to a 7.94-μm pixel size. This resolution was the highest optical scanning capability of the scanner. Each sample was scanned using 8-bit grayscale digital imaging so that each image was represented by a matrix of integers corresponding to 256 different intensities ranging from 0 (pure black) to 255 (pure white).

The first step in image processing was converting the grayscale image to binary format so that each pixel was assigned either a value of 0 (black) representing a background pixel, or a value of 1 (white), representing an object pixel. Background pixels corresponded to the paste/aggregate and object pixels corresponded to air void. The threshold is the grayvalue between 0 and 255 that separates these two sets, or classes. It is possible to select a thresholding algorithm that does not rely on user input [13] [14]. Typically such an algorithm involves a statistical analysis of the graylevel data. Such algorithms are typically based on the shape of the histogram, where graylevel data is analyzed in clusters and the results depend on statistical interpretation. These types of algorithms can give satisfactory results, but depending on the range of the graylevel pixels values for each set, the results may not always be satisfactory.

Consider Otsu’s method, a commonly used thresholding algorithm. Otsu’s method minimizes the intra-class variance of gray values [11]. The result is a maximization of the separability of the two resultant classes: the class of background pixels and the class of object pixels. In the case of the air-entrained concrete images, the problem with relying solely on this algorithm or any statistical method is that the threshold can depend on the quantity and spread of each class of pixels. For example, a sample with 3 % air content would likely have a different computed threshold compared to a sample with a 20 % air content, even if the samples were prepared using the same blackening agent and same powder. Even a cropped portion of the same image could end up with a different threshold compared to the sample as a whole or compared to a different cropped section. For this reason, it is advised that the user check and possibly re-evaluate the computed threshold.

A proper threshold should provide a binary matrix that is representative of the grayscale image. In the case of air-entrained concrete images, the most obvious indicator of a satisfactory threshold is one that results in accurate air void profile diameters. To this end, the threshold was chosen using the following steps: (1) We computed the threshold using Otsu’s statistical algorithm. (2) We create a binary image of black background pixels and white object pixels using this threshold. (3) We zoomed in on a random selection of air voids and compared the diameters between the grayscale image and the binary image. (4) If the diameters did not match, we slightly adjusted the threshold. A lower threshold generally increased the diameters of the air voids in the binary image and conversely, a higher threshold generally decreased the diameters in the binary image. If necessary, we repeated steps 2 through 4, particularly when testing a new material. The result was a binary image that was segmented from the original grayscale image. An example of the original grayscale image and corresponding binary image obtained using this procedure is shown in Fig. 2.

Fig. 2
figure 2

a Grayscale image of powder-filled air voids on a polished and inked mortar sample. b Corresponding binary image segmented using Otsu’s thresholding algorithm

Full size image
Fig. 3
figure 3

Grayscale (a) and corresponding binary (b) image of one bubble with approximately a 22-pixel (175 μm) diameter. c The gray value of each pixel versus the distance along the blue line shown in a. Here, the computed threshold was 85. (Color figure online)

Full size image

Threshold adjustments are sometimes necessary because there is typically a reduction of contrast at the perimeters of the air void boundaries. At the region just inside the bubble perimeters, the depth of the bubble profile is shallow compared to the center, therefore increasing the likelihood that black ink will show through the white powder. As a result, the whiteness of the object pixels at those locations decrease. Figure 3a, b compares grayscale and binary images of just one bubble from Fig. 2. Visually, it appears that the bubble boundary in the binary image matches that of the grayscale image. This feature is important when computing air content, specific surface, bubble spacing, distribution, etc. Fig. 3c is a plot of the gray values of one line through the center of the bubble, confirming that the brightness of the pixels decrease as the location becomes closer to the bubble boundary. If sample preparation is performed carefully, the diameter of the binary bubble should not be sensitive to the threshold. In this example, the threshold was 85, computed using Otsu’s method. At the horizontal centerline, 22 pixels had graylevels above 85. Yet if the threshold were reduced to 81 or increased to 94, the quantity of white object pixels on this line is the same.

Generally, the more careful the sample preparation technique, the less likely any threshold adjustments are needed. The reason is because noisy images tend to have more uniform graylevels, reducing the effectiveness of an algorithm that is based on class separability. Indeed, the more careful the sample preparation technique, the more effective Otsu’s method is in determining a proper threshold and the less likely any adjustments are needed. For example, if the white powder is not cleanly wiped, excess powder particles could spill over the edge of a bubble profile onto the black surface. A scattering of white particles on a black surface will result in the averaging of gray values at those pixel locations, therefore reducing class separability and raising the sensitivity of the threshold. In general, the user should strive to reduce threshold sensitivity through careful application and removal of the white powder.

The sample preparation technique is rarely perfect. Because of this imperfection, some scattering of white powder may occur. This scatter can manifest itself as single disconnected object pixels. As an option, single disconnected object pixels can be removed from the binary image by scanning every white pixel and checking if the value of all adjacent pixels are black. We chose to perform this step because it slightly reduced the noise and negligibly changed the fraction of white pixels (typically less than 0.01 %).

At this point, it is possible to compute the air void content by simply computing the ratio of the white pixels to the total number of pixels from the image. However, in order to compute more advanced properties, such as specific surface, spacing factor, and air void distribution, the connectivity of each object must be defined. In image processing, connectivity refers to the way pixels relate to their immediate neighbors. In 2-dimensions, there are two common neighborhood types: the 4-connected neighborhood and the 8-connected neighborhood. The 4-connected neighborhood specifies that connected pixels are neighbors to every pixel that touch edge to edge. Therefore, since pixels lie on a square grid, there is a maximum of 4 possible neighbors for any pixel. The 8-connected neighborhood specifies that connected pixels are neighbors to every pixel that touches edge to edge or corner to corner, resulting in a maximum of 8 possible neighbors for any pixel. Although the results were not too sensitive to connectivity, the 8-connected neighborhood tended to erroneously promote connectivity between air voids that were in very close proximity to each other. Therefore, the 4-connected neighborhood was chosen to most closely resemble the structure of the convex air voids. By systematically scanning the grid, each connected pixel was identified and grouped into objects that represented a 2D slice through each air void.

4 Image analysis

Once the image of the sample has been scanned, converted into a binary matrix, and processed using pixel connectivity, our script can determine a number of properties. These properties are based on the assumption that all connected components (connected white pixels) are “objects” representing the 2-D image generated by a random plane through a 3-D sample of mortar. Using information from the 2-D image, real 3-D properties can be estimated based on principles of stereology.

4.1 Air content

The simplest property of air-entrained mortar computed from a plane section is the volumetric air content. Air content is computed using the Principle of Delesse [5], a fundamental principle of stereology that states the following: if a structure containing objects is randomly sectioned, then the areal density A A of the profiles of those objects is equal to the volumetric density V V of the objects in the structure:

$$\begin{aligned} V_V = A_A \end{aligned}$$
(1)

The script computes the areal density of the air voids by counting the number of white pixels in the image and dividing by the total number of pixels. This value is equivalent to the air content in the sample.

4.2 Powers spacing factor and specific surface

In Powers’s 1949 paper [15] on the role of air in frost resistant concrete, Powers defined an air void spacing factor \(\bar{L}\) as the distance between the surface of a bubble and its sphere of influence, such that

$$\begin{aligned} \bar{L} = \left\{ \begin{array}{ll} \displaystyle \frac{3}{\alpha } \left[1.4 (\frac{p}{A} + 1)^{1/3} - 1\right] &{} \displaystyle \frac{p}{A} \ge 4.33\\ \\ \displaystyle \frac{p}{\alpha A} &{} \displaystyle \frac{p}{A} < 4.33 \end{array} \right. \end{aligned}$$
(2)

where α is the specific surface, defined as the ratio of the average void surface area to the average void volume, and p/A is the volumetric paste to air ratio, where p is the volume fraction of cement, water, and supplementary cementitious materials (if any). In this study, p is computed from the mix proportions.

Equation 2 shows that it is necessary to determine the specific surface of the air voids to compute the Powers spacing factor. In a discussion appended to [15], T.F. Willis showed that

$$\begin{aligned} \alpha = \frac{4}{l} = \frac{4n}{A} \end{aligned}$$
(3)

where l is the average chord length through the air voids along a line of traverse, n is the number of air voids intersected per unit length of traverse, and A is the air content.

The conventional technique for determining α is to use a stereoscopic microscope and employ either the linear traverse method or the point-count method described in ASTM C457. It is also possible to replicate the same action using automatic image analysis. For example, one could take lines of traverse on a matrix and determine the number of times an air void was encountered by counting the number of times the pixel value changes from 1 to 0 or from 0 to 1. This change in pixel value represents the movement between the paste/aggregate matrix and the air void.

However, a limitation to this method is that Eq. 3 assumes that all the air voids in the sample are convex in shape. Although this assumption should be valid for entrained air voids, which should be spherical, the assumption of convexity is not always true for entrapped air voids, which can be irregularly shaped. Here, we develop a more general equation of the specific surface of objects in a matrix. Beginning with two independent derivations by Saltykov [19] and Tomkeieff [25],

$$\begin{aligned} S_V = 2 I_L \end{aligned}$$
(4)

where S V is the surface density of objects within another object and I L is the number of intersects per length of random line of traverse.Footnote 1

The surface density is defined as the set of points at the interface between the objects and the matrix divided by the volumetric sum of the objects and the matrix. S V therefore is in units of [length]−1. In the case of air voids within a paste matrix,

$$\begin{aligned} S_V = \frac{S_{ap}}{V_p+V_a} \end{aligned}$$
(5)

where S ap is the surface of the air-paste interface, V p is the volume of the paste/aggregate matrix, and V a is the volume of the air voids. Note that S V is not the same definition as the specific surface α. Knowing that \(V_V = A_A\), we rewrite S V as follows:

$$\begin{aligned} \alpha = \frac{S_{ap}}{V_a} = S_V (\frac{V_p + V_a}{V_a}) = \frac{S_V}{V_V} = \frac{S_V}{A_A} \end{aligned}$$
(6)

Substituting Eq. 4 into Eq. 6,

$$\begin{aligned} \alpha = \frac{2 I_L}{A_A} \end{aligned}$$
(7)

If all the objects are convex, then \(I_L = 2 n\) and \(\alpha = 2n/A_A = 2n/V_V\), where n is the number of intercepted objects per unit length of traverse, since every object crossed by a line of traverse would intersect at the boundary of any convex object exactly twice. Therefore, for convex objects within a matrix, such as entrained air voids dispersed with a cement or concrete sample, the specific surface of the air voids presented in Powers’ 1949 paper (Eq. 3) is equivalent to Saltykov’s 1945 equation (Eq. 4) of surface density.Footnote 2

Many methods of stereology, such as Eqs. 3 and 4, were developed for the computing capabilities of the middle 20th century. Using image processing, it is possible to use stereological principles that were once considered to be impractical or useful for academic exercise only. For example, the specific surface of objects can be determined by directly computing the perimeter of those objects on a representative 2D plane. Measuring a perimeter is never straightforward, but if an image finely discretizes the object boundaries, the perimeter can be computed by counting pixels. It can be shown from Buffon’s 1777 needle problem that

$$\begin{aligned} B_A = \frac{\pi }{2} I_L \end{aligned}$$
(8)

where B A is the boundary length density of objects in a representative 2D plane, where “boundary length density” is defined as the perimeter of the objects divided by the area of the plane. Equating Eq. 7 and Eq. 4, we find that

$$\begin{aligned} \alpha = \frac{4}{\pi } \frac{B_A}{A_A} \end{aligned}$$
(9)

Eq. 9 shows that given the perimeter and area of objects on a representative 2D plane through a 3D sample, it is possible to determine the specific surface of those objects. Note that this formulation is more general than Eq. 3 which is used in ASTM C457, since Eq. 9 does not require the objects to be convex. However, because the objects in question area primarily spherical air voids, in our samples, Eq. 3 and Eq. 9 agree well with each other.

4.3 Air void perimeters

To use Eq. 9, it is necessary to compute the boundary length, or perimeter, of those air voids on a representative 2D plane.

An estimation of the perimeter of the air voids can be obtained by taking each connected component from the image and determining the equivalent circumference, assuming that each connected component is a circular intersection of the spherical air voids with the plane. However, this method is problematic because of the imperfections related to sample preparation. For example, there are cases where two air voids are in very close proximity to each other. Either sample grinding/polishing and/or imperfect placement of white powder on these air voids causes the voids to appear connected together on the surface. When two or more air voids appear to come in contact, it becomes difficult to separate these air voids as distinct objects through automatic image processing, especially if the objects are not always regular in shape. Therefore, assuming each connected component is a discrete, circular intersection would lead to an underestimation of the true perimeter of the air voids.

We developed a more accurate method of computing air void perimeters by identifying the boundary pixels and computing the distance between each neighboring boundary pixel. These boundary pixels were determined by identifying white pixels that neighbored black pixels. The length of the boundary was determined by identifying the manner in which successive white boundary pixels connect to each other. We designated a 4-connected neighborhood as described in Sect. 3 to define boundary pixel connectivity. Once the boundary pixels were identified, the straight-line Pythagorean distances between the centers of successive boundary pixels were computed to estimate the perimeter of each object.Footnote 3 This perimeter value was used to compute the specific surface in Eq.9.

4.4 Reconstruction of the air void size distribution

To study the effect of air-entraining agents on the air void distribution, it is desirable to estimate the size distribution of the air-entrained bubbles. In general, the process of estimating the 3D size distribution of objects using the apparent sizes, or profiles on a 2D plane is called “unfolding” or “reconstruction.” Sphere reconstruction can be accomplished by taking either a parametric or non-parametric approach. In a parametric approach, a distribution function representing the apparent circle sizes is first assumed and then transformed into a sphere distribution function. An analytical solution to this transformation was first published in 1925 by S. D. Wicksell [29]. Another noteworthy solution was published in 1955 by Reid [17], who included a transformation between spheres and chord lengths as well.

For an excellent review of stereological properties of air voids, including parametric methods, we refer the reader to Snyder et al. [24].

A non-parametric approach to sphere reconstruction does not assume an analytical form of the circle size distribution. Rather, the method operates on the collected data directly. The first mention of a non-parametric reconstruction method was included in the 1925 Wicksell paper, but the solution was greatly modified and expanded by Scheil [21] in 1931. In 1934, Schwartz [22] modified Scheil’s method, which was later improved on by Saltykov in 1958 [20]. Saltykov’s method, which is fully described by Underwood [26, 27], was chosen for this analysis and is briefly described here.

Consider a sphere of radius R. A rule of geometric probability states that if a large number of planes intersect the sphere, the profile circles will have a probability distribution ϕ(r) such that

$$\begin{aligned} \phi (r) = \frac{r}{R \sqrt{R^2 - r^2}} \end{aligned}$$
(10)

where r is the radius of each profile circle. Equivalently, ϕ(r) is the probability that a large quantity of identically sized spheres in a sample is randomly sectioned once. Note that the form of the curve of Eq. 10 increases asymptotically to \(r = R\). However, as expected, the area under the curve is equal to unity since ϕ(r) is a probability density function. An alternative representation of the curve is a histogram, where each bin corresponds to a class of profile radii. Figure 4a, b compare the smooth and discrete versions of Eq. 10.

Fig. 4
figure 4

Probability distribution function a and corresponding discrete histogram b of the profile radius r if a sphere of radius R is randomly sectioned by a plane

Full size image

Consider now a more realistic situation in which a sample is composed of a polydispersed system of spheres. For each discrete group, or class of spheres, the corresponding profile sizes will vary according to Eq. 10. Because there are multiple sphere sizes, the total distribution of profile sizes is a summation of the histograms corresponding to each sphere class. In order to compute the sphere sizes from an image of circular profiles, the histogram of profiles corresponding to the largest sphere class is subtracted from the total histogram, revealing the profiles of all spheres smaller than the largest sphere class. This “histogram stripping” method is repeated for the next-largest sphere class until only the smallest class remains.

If the diameter of the largest spheres is D m , then the class width \(\Delta\) is defined as \(\Delta = D_m/k\), where k is the number of classes. If i is the profile class number and j is the sphere class number, Saltykov’s expression relating the number density of profiles to the number density of spheres is

$$\begin{aligned} N_A(i,j) = N_V(j) \Delta [\sqrt{j^2 - (i-1)^2} - \sqrt{j^2 - i^2}] \end{aligned}$$
(11)

where N A is the number of profiles per unit area and N V is the number of spheres per unit volume. For a discrete sphere distribution, Eq. 11 is applied separately for each class. The result is a reconstruction of the 3D sphere distribution. Saltykov originally solved for N V in terms of N A and \(\Delta\) in the form of a table of coefficients using a maximum of 15 classes. However, it is no longer necessary to use this table because the computation can be performed rapidly on a computer using any desired number of classes.

One known problem that can arise with this classical reconstruction method involves negative binning. Because of sampling statistics and other practical measurement problems, a negative number of spheres from a smaller class may be computed. This phenomenon occurs when the measured number of profiles in a class is lower than its expected value and occurs most frequently with the smallest spheres in a sample [26]. In general, the problem can be solved by using an expectation-maximization algorithm [6][10], error bars [12], and/or histogram smoothing. In our image analysis, we avoided negative binning by choosing a large enough bin width that avoided gaps in the histogram. For our images, using a bin width = 4 μm was large enough to avoid negative binning during reconstruction.

5 Example of results

Using the image processing techniques discussed in Sects. 2, 3, 4, the air void structure of a number samples were analyzed. This image analysis procedure was verified by comparing the bulk densities with computed air contents. First, the bulk densities were measured by weighing and measuring the volumes of both air-entrained and control samples. Because an air-entrained specimen contains both entrapped and entrained air, and a control specimen contains only entrapped air, the percent difference in bulk density was therefore equivalent to the amount of entrained air only. An example of these values are shown in Table 1, which shows that the entrained air content for this sample was 5.29 %. This value assumes that amount of entrapped air in an air-entrained and control sample is nearly the same.

The air content obtained by image analysis computes the total volume of air in a sample. Therefore, the entrained air content can also be estimated by computing the air content for both air-entrained and control samples and taking the difference. These values were computed using the image of a plane through the sample volume. The results are shown in Table 2 . Here, the difference in air content was 5.15 %. Because this value agrees well with the percent difference in bulk density, we can have confidence that the quantities computed by image analysis are accurate.

Table 2 also reports the specific surface α and Powers spacing factor \(\bar{L}\) for the same example specimens. Note that while α was similar for both the air-entrained and control sample, \(\bar{L}\) was much greater in the control sample. This result was expected since the air content was much lower in the control. Typically, \(\bar{L}\) is computed as an average value for the entire scanned image. However, it is possible to segment the image into a grid of sub-images. By computing \(\bar{L}\) for each sub-image, it would be possible to determine if local variations exist throughout the sample.

Table 1 Example saturated surface dry (SSD) bulk density measurements for air-entrained and non-air-entrained mortar
Full size table
Table 2 The first column is an example of the computed air content for both air-entrained and non-air-entrained mortar using image analysis
Full size table

The mean profile diameter, which was computed by associating the area of each observed air void as a circular section, was 66 μm. Using Saltykov’s method described in §4.4, the size distribution of the air voids was reconstructed from the profile distribution. Histograms of the profile and sphere distributions are compared in Fig. 5. Note that the mean sphere diameter, which was 40 μm, is smaller than the mean profile diameter. This trend follows from the tendency to capture the larger profile diameters when taking a random plane through a random assembly of spheres, but never larger than the actual size of the spheres (see Fig. 4).

Fig. 5
figure 5

a Distribution of the observed bubble profiles from images of typical air-entrained mortar. These distributions are normalized per mm2. b The computed sphere distribution per mm3 is shown using Saltykov’s classical sphere reconstruction method described in Sect.4.4. A best fit lognormal distribution is plotted in red. The observed mean profile radius was 33 μm and the computed mean sphere radius was 20 μm. The absence of reconstructed bubbles in the lowest size range (less than 8 μm) is a result of the limitation in scanning resolution. (Color figure online)

Full size image

A Matlab script was written to perform the image analysis and is available as supplementary material with this manuscript. The code takes in as arguments the scanned image file and the volumetric ratio of cement paste to total solids, where the total solid content is the sum of the paste and aggregate. In the example shown here, paste to solids ratio was 0.8 as determined by the mix proportions.

6 Conclusion

This manuscript presents a technique for analyzing the air void system of mortar or concrete using automatic image analysis. First, the bulk densities of air-entrained and non-air-entrained companion samples were compared to approximate the entrained air content. The same samples were also ground and polished prior to applying a thin coat of black acrylic ink and filling the exposed voids with a fine white barium sulfate powder. These samples were scanned at 3,200 dpi using a flatbed scanner and processed into binary images using Otsu’s method of thresholding. The resulting image contained black pixels that represented cement paste or aggregate and white pixels that represented air voids. Using stereological methods, 3D quantities of interest were approximated. The determined quantities were the total volumetric air content, Powers spacing factor, specific surface, and the approximate size distribution of the air voids. The analysis was performed by writing a Matlab script which is available as supplementary material to download and modify.

Using this method of air void analysis, the air void structure of various mortar or concrete samples can be rapidly compared. For example, the effectiveness of air-entraining agents or the interactions between the air-entraining agents and various admixtures can be quantified. By determining the total volume, spacing, fineness, and distribution of air bubbles, these parameters can be directly linked to strength and workability, as well as resistance to frost damage.