Gradient and lamellar heterostructures for superior mechanical properties

Abstract

Heterostructured (HS) materials are a novel class of materials with mechanical properties that are superior over their conventional homogeneous counterparts. They are composed of HS zones with a dramatic difference in mechanical behaviors, which produces a synergistic effect on mechanical properties that are above the prediction by the rule-of-mixtures. Among all heterostructures, the two most studied are grain-size gradient structure and heterolamellar structure. These two heterostructures produce typical heterogeneous deformation during tensile deformation, producing long-range back stress in the soft zones and forward stress in the hard zones, which collectively produces hetero deformation-induced (HDI) stress to enhance the yield strength before yielding, and HDI hardening after yielding to retain ductility. In this article, we will focus on these two types of heterostructures. The issues, concerns, and progress are reviewed with the emphasis on the synergistic effect of mechanical properties, the fundamentals of several special plastic behaviors (e.g., strain gradient, HDI hardening and strain hardening), the plastic deformation mechanism, and the relationship between the microstructure and properties.

Introduction

Heterostructured (HS) materials are attracting extensive interest due to their superior mechanical properties, which are not attainable by their conventional homogeneous counterparts.^{1,2,3,4,5,6,7,8,9,10} HS materials are defined as materials that have HS zones with dramatically different (> 100%) mechanical properties, and the interzone interactions are able to produce significant synergistic effect on mechanical properties.¹ A typical class of heterostructures involves a multilevel architecture of trans-scale grains,⁶ among which the most studied are gradient structure (GS)^{2,6,10,11,12,13,14,15,16,17} and heterogeneous lamellar structure (HLS).^18,19 This article focuses on these two types of heterostructures. Other HS materials include the precipitates, second phase, and multilevel grain and multiphase microstructures.^{20,21,22,23,24,25,26,27}

Tailoring microstructural heterogeneity is needed to enhance the synergistic effect in HS materials.^{1,2,3,4,5,6,7,8,9,10} Nanoscale grains produce high strength but low ductility, while coarse grains do the opposite. However, the combination of soft coarse grains with strong nanoscale grains can produce a synergistic effect, especially for the ductility.^1,5 Both GS and HLS are trans-scale from the coarse grains to nanoscale grains and/or nanostructures,^11,12 with polarizing mechanical responses. More importantly, the heterozone boundaries play a critical role in producing the synergistic effect as compared to normal grain boundaries.^1,5 A heterozone boundary affected region (HBAR) appears at and near the heterozone boundaries with strain gradient during plastic deformation.^1,18,19 Note that the HBAR was previously defined as interface-affected zone (IAZ).¹⁹ The interaction and coupling between the HS zones occur in the HBARs, leading to a synergistic effect.^1,19

The synergistic effect is a hallmark of HS materials.^12,13,15 Specifically, extra strengthening,^12,13 extra strain hardening,¹² and high ductility^11,12,13,18 are produced by the synergistic effect in GS and HLS materials.^{11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47} This makes the yield strength exceed what is predicted by the rule-of-mixtures.^13,15 Furthermore, ductility in HS materials is much higher than that measured in standalone nanostructured materials.^11,12,13 This is associated with the strain gradient and stress state change.¹² In other words, strain gradient in the HBAR is accommodated by geometrically necessary dislocations (GNDs),^{1,4,5,6,12,18,19} which leads to the hetero deformation-induced (HDI) strengthening and HDI strain hardening.^1,5,6,40,43 This produces the synergistic effect in HS materials. As a result, the tradeoff in strength and ductility can be largely alleviated.^{11,12,13,14,18,19,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45}

In this article, we focus on the trans-scale GS and HLS, containing the nanograins (NG)/nanostructures (NS) and coarse grains (CG). Both the GS and HLS induce hetero deformation, which produces extraordinary strain hardening. This review concerns the synergy in mechanical properties, strain gradient-based design of HS materials, and HDI strengthening and strain hardening.

Producing synergy by heterostructuring

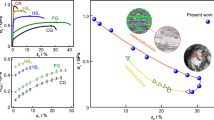
The synergistic effect is a characteristic feature of HS materials^{1,2,3,4,5,6,7,8,9,10} (Figure 1a). The goal is to raise yield strength ${\upsigma }_{y}$ while retaining ductility (uniform elongation ${\upvarepsilon }_{u}$). This is challenging because ${\upsigma }_{y}$ and ${\upvarepsilon }_{u}$ usually show a tradeoff with each other. This tradeoff in (${\upsigma }_{y},{\upvarepsilon }_{u}$) is, however, dramatically alleviated or even avoided in HS materials, by introducing the heterogeneities into the microstructure such as the grain/twin gradient, lamellar, and hierarchical structure. Interestingly, the conventional banana-like (${\upsigma }_{y},{\upvarepsilon }_{u}$) relationship can be reversed. The heterogeneities cause strain hardening and promote heterogeneous plastic deformation, both acting as the dominant mechanisms for toughening.^16,46,47 This is the reason for superior combination of the strength and fracture toughness (K_1C) (Figure 1b) and v-notch impact fracture toughness (A_K) (Figure 1c) in HS materials.

Figure 1

Superior mechanical properties of heterostructured (HS) materials. (a) Schematic (${\upsigma }_{y}, {\upvarepsilon }_{u}$) plot. The sequence of various HS materials is arbitrary. (b) (K_1C$,{\upsigma }_{y}$) plot. (c) (A_K$,{\upsigma }_{y}$) plot.${\upsigma }_{y}$: yield strength. ${\upvarepsilon }_{u}$: ductility (uniform elongation). K_1C: fracture toughness. A_K: v-notch impact fracture toughness.

Fundamentals: Hetero deformation-induced stress and hetero deformation-induced strain hardening

Hetero deformation reigns in both GS and HLS materials during tensile deformation.^{1,4,5,6,12,18,26} Hetero deformation-induced (HDI) stress is generated in the HBARs as a result of mechanical incompatibility.^1,5 The HDI stress is collectively produced by the back stress in the CG zones and forward stress in the NG/NS zones.⁵ It has been proposed that the back stress is produced by GNDs,^{48,49,50,51,52} typically in the form of GND pileups.^1,5,18,49 The back stress acts to offset applied stress to impede the emission and slip of dislocations from dislocation sources in the CG zones.^1,5

The GND pileup exerts a stress concentration at the heterozone boundary, which needs to be balanced by a forward stress in the hard zone. The forward stress is in the same direction as the applied stress, and therefore promotes plastic deformation in the hard zone. In other words, it acts to soften the hard zone. At the heterozone boundary, the forward stress and the back stress are the same in magnitude, but in opposite directions. However, they decay in different manner away from the heterozone boundary, which collectively produces HDI stress.

Before the hard zone starts to yield, the HDI stress primarily comes from the back stress since the forward stress cannot make the hard zone to deform yet. In other words, the back stress acted to increase the yield strength of HS materials. After the yield point, the balance between the back stress and forward stress produces HDI strain hardening with applied strain to retain ductility.^1,5,40,43

The mechanism of HDI strain hardening has been reported in various HS materials. The presence of a wide hysteresis loop and residual plastic strain as large as 0.2% during unload-reload tensile testing indicate the presence of HDI stress and HDI hardening in the GS, LS, and HGS materials^17,18,34 (Figure 2). GND density gradient was detected in the HBARs, which increases with increasing applied tensile strain in HS copper-brass laminates.¹⁹ This is consistent with the GND pileup model,^5,9,18 in which GNDs are emitted from a Frank–Read source in the grain interior, and piled up in front of the hetero-zone boundary with a GND density gradient.

Figure 2

Experimental evidence for hetero deformation-induced (HDI) strain hardening. (a) Hysteresis loop at uniform tensile strain (ε_u) of 18.2% in the gradient-structured (GS) IF steel during unload-reload tensile testing. ${\upsigma }_{u}$ and ${\upsigma }_{L}$ are yield stress under unload and reload, respectively. (b) Hysteresis loop during unload-reload tension at 77 K in CoCrNi medium-entropy alloy.²⁶ Note residual plastic strain (${\upvarepsilon }_{rp}$) larger than 0.2 percent. (c) HDI stress (σ_b) at various offset strain (0.05, 0.10, 0.15) during tensile deformation in IF steel. (d–f) Hysteresis loops in hetero-lamellar structured Ti,¹⁸ a high-entropy alloy (HEA), and a gradient-structured Ni-based alloy.³⁴

Strain gradient and geometrically necessary dislocations

The strain gradient is the inevitable result of hetero-deformation in HS materials.^{1,4,5,6,9,10,12,18} In the trans-scale GS and LS materials, hard NG zones exert a strong constraint on adjacent soft CG zones, which are subjected to larger plastic strain. The strain gradient thus forms to maintain the strain continuity across the hetero-zone boundaries.^50,51,52 To accommodate the strain gradient, GNDs are generated to provide compatible deformation in the HBARs.^50,51,52

The larger the grain-size difference, the larger the strain gradient in the HBARs, and the higher the GND density, which leads to higher HDI strain hardening. Both the GS and HLS are the strain gradient-based designs to produce high density GNDs for higher HDI stress. As shown in Figure 3a, the strain gradient distribution is macroscopic and inter-layered, which enables the strain delocalization in the nanostructured layer.^53,54,55 In the HLS material (Figure 3b),¹⁸ the coarse-grained lamellae are distributed discontinuously in the nanostructured matrix. The heterogeneous grain structure (HGS) is the third version of trans-scale HS materials.²⁶ The three-level of grains are formed as shown in Figure 3c. Nanograins (grain size $<$ 0.2 μm) were formed at the boundaries of ultrafine-grains (0.2–1 μm), which are formed at the boundaries of coarse grains (average 5 μm).

Figure 3

Strain gradient distribution in heterogeneous grain structures. (a) Gradient structure. (b) Heterogeneous lamellar structure. (c) Heterogeneous grain structure. (d) Gradient nano-twinned structure. Color scale bar: qualitative comparison of strain gradient.

Recently, dual-gradient structure (i.e., the grain-size gradient and intragranular twin-spacing gradient) was reported in copper¹³ (Figure 2d). Long-range and short-range strain gradients were found at the hetero-zone boundaries and twin boundaries, respectively. This dual-gradient structure induced an extraordinary extra strengthening and strain hardening for a superior combination of strength and ductility.¹³ This is because they can produce abundant hetero-zone boundaries and twin boundaries for strain gradient where high density of GNDs are formed, which produces additional HDI strain hardening.

Strain gradient and GND density gradient have been observed in the HBARs of GS and HLS materials.^{12,19,30,53,54,55} Note that the HBAR was earlier named the interface affected zone (IAZ).¹⁹ The HBAR width was found to remain constant with increasing applied strain, but the strain gradient increased linearly. The HBAR width is considered to be a critical parameter for the design of HS materials. Moreover, in situ TEM observations revealed that a GND gradient was formed by the dynamic generation and deactivation of Frank–Read sources in the HBAR.⁵⁶

Strain gradient and HDI stress always occur during the plastic deformation of HS materials. Computational modeling and simulations at continuum and atomic scales revealed the key role of GNDs in plastic deformation of GS, resulting in extra strengthening or strain hardening.^{9,10,13,14,27,30,39} Crystal plasticity finite element modeling of two-dimensional and three-dimensional gradient samples demonstrated the presence of plastic strain and tensile stress gradients during plastic deformation.^30,39 The plastic strain is larger in the soft center and smaller in the hard surface layer, while the tensile stress gradient has an opposite distribution. Finite element modeling and simulations based on the strain-gradient plasticity theory showed both the GNDs and HDI stress induced by GND pileup during uniaxial tension of gradient nanograined metals. The predictions on the uniform elongation and extra-strain hardening from the modeling agree well with the experimental results.^9,10

Deformation mechanism in gradient structure

The heterostructures cause unique deformation mechanisms in HS materials, which in turn produce the observed superior mechanical properties. There are still many issues and details in the deformation mechanisms that are not well understood.^1,2,6,9,10 The difficulty lies mainly in the hetero deformation and correlation with the polarizing plastic responses,^6,53 such as the rapid strain localization in NG/NS zones and stabilization in the CG zones. So far, several key issues have been investigated, including the strain gradient near hetero-zone boundaries and concurrent GNDs, HDI stress, and HDI strengthening and HDI strain hardening. However, the picture is not yet complete. For example, it is not clear that during a tensile deformation whether the NS layer uniformly deforms together with the CG layer.⁵³ It has been believed that tensile strain is uniform and equal for all layers in the GS materials. This assumption is derived from the engineering stress–strain curves showing a long stage of strain hardening prior to necking. This strain hardening is a macroscopic response of the global GS sample.

In situ layer-by-layer testing can be used to evaluate plastic deformation in each layer of the GS sample.^{19,34,53,54,55,56} For example, the NS layer has high strength, a two-stage work hardening with a large work hardening exponent, and back stresses by GNDs.³⁴ The intergranular back stress contributed to high strain hardening. More recently, the in situ digital-imaging-correlation full-field strain measurements revealed that the NS layer deforms heterogeneously by nucleation and propagation of a single strain-band (SB).⁵³ Specifically, strain localization occurs in NS surface layer, in contrast to uniform deformation in the CG core, even though both were subjected to the same applied strain. Strain gradient appears in the cross section between NS and CG layer and in axial and in-plane ahead of propagating SB. HDI hardening is thus induced not only to prevent SB from propagating into the depth, but also to slow down and stabilize the propagating SB. Both renders strain delocalization in the SB. Further, the microhardness shows a drop at first and rise later in SB, indicating strain softening and recovery strain hardening capability in the SB. In addition, the degree of microstructural heterogeneities probably plays a role in strain localization of the NS layer.

On the other hand, highly dispersed strain bands were observed in GS Ni.⁵⁴ This is another way to delocalize the strain in the NS layer. Strain banding seems to be a unique deformation mechanism in HS materials. Strain bands are usually found to be highly dispersed to delocalize the global strain.⁵⁴ This is in sharp contrast to homogeneous nanostructures, where a single intense strain localization leads to the failure of the whole sample.

Relationship between microstructure and tensile property

The relationship between mechanical properties and heterostructures shed light on what the synergistic effect is and how to correlate them. Lu² first predicted a moderate (${\upsigma }_{y},{\upvarepsilon }_{u}$) relationship in GS (see Figure 4a), which shows an inverse banana relationship, as evidenced in the GS IF steel (Figure 4b), gradient nano-twinned Cu¹³ (Figure 4c), laminate copper/brass¹⁹ (Figure 4d), heterogeneous HLS Ti (Figure 4e),¹⁸ and dual-phase high strength steel²⁰ (Figure 4f). The prominent feature is the retaining and even increasing ductility even at high yield strength. This is caused by the HDI strain hardening.

Figure 4

Relationship of heterostructure and tensile properties. (a) Predicted (${\upsigma }_{y},{\upvarepsilon }_{u}$) in GNG.² (b–f) (${\upsigma }_{y},{\upvarepsilon }_{u}$) in the gradient structured interstitial-free steel (b), gradient nano-twinned (GNT) Cu¹³ (c), laminate copper/brass¹⁹ (d), heterogenous lamellar structured Ti¹⁸ (e), and dual-phase steel (blue spheres)²⁰ (f).

Summary and outlook

Gradient structured and heterogeneous lamella structured materials are two typical HS materials. Their superior mechanical properties have attracted great attention in the materials community because of their easy fabrication and promising practical applications as well as the new materials science in HS materials. Since HS materials are an emerging materials field, there are still many fundamental issues for further study.¹ It will take multidisciplinary approaches by researchers from materials and mechanics communities to solve these issues. A key advantage of HS materials is their easy production using current industrial facilities at low cost. It is the combination of new materials science and great commercialization potential that are driving the fast development of this field, which is on track to become a hot research topic post nano-materials era.

Issues for future studies include, but are not limited to, the interactions of geometrically necessary dislocations with the heterozone boundaries, the nucleation and growth of dispersive local strain bands and their relations to the GND piles and transmissions across the heterozone boundaries. There is also a need to develop analytical modeling and equations for predicting the optimal heterostructural parameters such as the shape and size of the soft zones. In addition, more processing and production technologies need to be developed for the commercialization of the HS materials.