1 Introduction

Starting from the Bronze Age,[1] metallic materials have been used by mankind for over five thousand years. After extensive research for more than a century, metallurgy is generally regarded as a mature discipline in which major materials sciences have been studied and understood. Nevertheless, during the past few decades, nanostructured metals and alloys, which was initiated by Prof. Gleiter,[2,3,4,5] have attracted worldwide attention and extensive research. Nanostructured metallic materials explore the well-known materials principle of Hall–Petch effect[6] to increase the strength, as predicted by the Hall–Petch equation, \(\sigma = \kappa d^{ - 1/2}\), where σ is yield strength, κ is constant, and d is the average grain size. It predicts very high strengths for nanocrystalline metals (grain sizes below 100 nm), which was confirmed experimentally.[7,8,9,10] However, when the grain size is smaller than a critical value for a particular nanocrystalline metal, an inverse Hall–Petch relationship was observed, which has been rationalized by a number of models.[9,11,12,13,14,15,16,17,18,19,20,21,22] In addition, it has been found that the deformation mechanisms in the nanocrystalline metals[23,24] are different from those in their coarse-grained counterparts because nanograins can activate different deformation mechanisms, including partial dislocation emissions from grain boundaries,[25,26,27,28] deformation twinning,[23,29,30,31] as well as grain boundary sliding[19,32,33,34,35,36,37] and grain rotation.[34,38,39,40,41,42] The change in deformation mechanisms is responsible for the deviation from the Hall–Petch relationship.

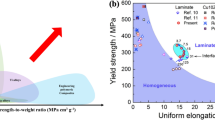
The advantage of nanostructured metallic materials is their high strength, which can be several times higher than those of their coarse-grained counterparts.[43,44,45,46] Nanostructured materials are defined as materials with grain or subgrain structures such as dislocation cells and/or subgrains smaller than 100 nm.[47] High strength is highly desired for structural applications, especially for aerospace applications and energy efficient vehicles such as electric cars. High strength helps reduce the weight of structural components, making transportation vehicles more energy efficient. However, high strength alone is often not sufficient for structural applications. Good ductility is also needed to maintain good safety, which is required for structural components. Unfortunately, there is often a trade-off between the strength and ductility. Metallic materials are usually strong or ductile, but rarely both at the same time.[24,43,48,49] This strength-ductility trade-off leads to the well-known “banana curve”, as shown in Figure 1, which also exists in physical properties of some functional materials.[50] Unfortunately, this banana curve also rules over nanostructured metallic materials.[24,43,44,48,50]

Fig. 1
figure 1

The trade-off between strength and ductility of metallic materials produces a typical “banana curve”

Full size image

There are several other well-known mechanisms for strengthening metallic materials, in addition to refining grains,[6,51] which include solution hardening, dislocation (cold work) hardening, and precipitation (second-phase particle) hardening. However, these strengthening mechanisms are also often accompanied with reduction in ductility, i.e., the banana curve. There has been no effective way to overcome the banana curve to improve the strength while improving or retaining good ductility. For nanostructured structured metals, a few mechanisms have been reported to be able to improve ductility while maintaining or even improve their high strengths to some extent,[24] including deformation twinning,[52,53,54,55] introducing pre-existing twins,[56,57,58] second-phase precipitations,[59,60] etc. However, their ductility is still much lower than their coarse-grained counterparts, i.e., there is still an overall trade-off between strength and ductility.

2 Issues Concerning Ductility

As discussed above, there are many effective ways to increase the yield strength of metallic materials. However, it is much more challenging to improve the ductility, especially for materials with high strength.[24] To further complicate the issue, there has been a confusion in the community on the difference between ductility and plasticity.[49] For conventional coarse-grained materials, high plasticity often comes with high ductility, in which the misuse/interchange of these two terms may not pose a serious problem in practice. However, for some high-strength advanced materials such as nanostructured materials, the misuse often leads to serious problems.[49]

Clarification of ductility and plasticity will help us to understand the mechanisms of heterostructured materials. Here we first delineate the difference and definitions of these two terms.[49] Plasticity is the capability of a material to be deformed plastically, and it is affected by the deformation mode for a given ambient condition such as room temperature. Plasticity is an important property for material processing, shaping, and forming, which often involves plastic deformation. Materials with no apparent plastic deformation before fracture under any of the common plastic deformation modes such as compression, tension, and shear are deemed to be brittle. Very little dislocation slip is activated during the deformation and fracture process of brittle materials. Tensile fracture surface of brittle materials is typically cleavage type with crack propagation across samples along crystalline planes in grains or along grain boundaries,[6] which can be clearly revealed using scanning electron microscopy (SEM). Common examples of brittle materials include ceramics and glasses.

Most metallic materials have plasticity to some extent, and their fracture typically involves dislocation activities, which produces dimples on the fracture surface observed under SEM. Such a fracture is called ductile fracture.[6]

Ductility is measured as elongation to failure or uniform elongation during tensile testing. In other words, ductility can be regarded as tensile plasticity,[49] i.e., plasticity under tensile deformation.

Plasticity is largely controlled by the intrinsic crystal structure of the metal. For example, face-centered cubic (fcc) and body-centered cubic (bcc) metals generally have much higher plasticity than hexagonal close packed (hcp) metals because fcc and bcc metals possess more slip systems than hcp metals. High plasticity is a necessary requirement for high ductility, but not a sufficient one. In other words, high plasticity does not guarantee high ductility, as clearly demonstrated in nanostructured metals. Nanostructured metals typically have high plasticity under compression, or cold rolling, but poor plasticity under tensile loading, i.e., poor ductility.[24,49,61,62] Furthermore, nanostructured metals typically exhibit ductile fracture behaviors, with significant necking before fracture, and dislocation dimples on the fractured surface,[61] despite of its low ductility. For conventional coarse-grained materials, the percent reduction in area at the fractured section after tensile testing is sometimes used as an indicator of ductility, which is reasonable because it usually co-relates well with the elongation to failure. However, for nanostructured metals, these two are disconnected, and the percent reduction in area can no longer be used as an indicator of ductility.

Improving ductility of high-strength materials has been a challenge for over a century due to the strength-ductility trade-off. To solve this problem, we need to first understand the two failure modes of metallic materials during a tensile test.[24] The first type is dominated by the crack/void formation and propagation, which leads to abrupt fracture without much necking. Such materials typically have low plasticity, and consequently low ductility. Their engineering tensile stress-grain curves often exhibit a sudden stress drop, from a point when the sample still exhibits strong strain hardening. Such a failure mode can be considered as a premature failure caused by crack nucleation and quick propagation. The second type exhibits significant necking before final failure and the stress often drops gradually during the necking process. On a typical tensile engineering stress-strain curve, the necking occuring at the highest engineering flow stress, before which the deformation is uniform. Therefore, the engineering strain at the highest stress is also called the uniform elongation than elongation to failure, which is a more appropriate measurement of ductility, especially when non-standard small tensile samples are used.[49,63,64]

In this paper, we focus on the second type of failure mode, in which the failure starts with necking. Logically, to improve ductility, we need to delay the onset of the failure, i.e., the necking process. According to Hart’s criterion, to prevent necking, the strain hardening and strain rate sensitivity during a tensile test need to be high enough to satisfy the following equation[49,65]:

$$ \left( {\frac{{d\sigma_{t} }}{{d\varepsilon_{t} }}} \right)\frac{1}{{\sigma_{t} }} + m \ge 1 $$
(1)

where σt is true stress, εt is true strain, and m is the strain rate sensitivity.

At room temperature, for most metallic materials including nanostructured materials, the strain rate sensitivity m is very small, and its contribution to the ductility is often negligible, in which case the above equation can be simplified as

$$ \frac{{d\sigma_{t} }}{{d\varepsilon_{t} }} \ge \sigma_{t} $$
(2)

Equation 2 is the well-known Considère criterion for preventing necking.[24,49] It indicates that high-strength materials require high strain hardening rate, i.e., high slope of the tensile true stress-strain curves, to maintain the same ductility. Unfortunately, most strengthening mechanisms that are commonly used to improve the strength of metallic materials often decrease dislocation accumulation capability, which decreases the strain hardening rate, leading to low ductility. This is why the banana curve generally represents the strength-ductility relationship of metallic materials.

The strength-ductility trade-off is well demonstrated in nanostructured materials, which have high strength due to the Hall–Petch effort, i.e., strengthening by grain refinement.[24] As shown in Figure 2(a), nanostructured Ti is several times stronger than coarse-grained Ti under compression. However, its strain hardening rate (the slope of the true stress-strain curve) quickly falls to zero after yielding. Consequently, during the tensile test (Figure 2(b)), necking quickly sets in, which leads to low ductility. It is clear from Figure 2 that the nano-Ti has very high plasticity under compression, but very low tensile plasticity (ductility).[61]

Fig. 2
figure 2

Adapted from Ref. [61]

Mechanical behavior of nanostructured Ti as compared with coarse-grained Ti. (a) Compressive testing and (b) Tensile testing.

Full size image

3 Heterostructured Materials: definition and superior properties

As discussed above, there has been a strength-ductility trade-off that cannot be solved using our textbook knowledge on metallurgy. A question arises on if there are still any unknown mechanisms that can solve this problem. The answer is yes. A new type of microstructure, heterostructure, can activate a new mechanism, hetero-deformation induced (HDI) strengthening and HDI strain hardening, to alleviate or even totally avoid the strength-ductility trade-off.[66,67,68,69] HDI strengthening is caused by the HDI stress before yielding, which acts to increase the yield strength, while HDI strain hardening is the increase rate of HDI stress with applied strain, which acts to improve ductility. Heterostructure is defined as a non-uniform structure consisting of heterogeneous zones whose strength are more than 100 pct different, and the inter-zone interaction produces a significant synergy, making the heterostructured (HS) materials much stronger than what is predicted by the rule of mixtures.[50]

It should be noted that there are differences between the heterostructured materials defined here and the conventional composite materials in the literature. The latter typically has a strong and brittle component to reinforce a softer matrix. If the matrix is metallic, HDI strengthening will be produced to enhance its strength, but ductility enhancement is limited because such composite typically fails by the fracture of reinforcement or failure in the reinforcement matrix interface, which limits their plasticity. In contrast, in a typical heterostructured material both the hard and soft zones are plastically deformable to allow effective HDI strain hardening for higher ductility.

According to the definition, heterostructured materials can be classified as materials with structures including, but not limited to, heterostructured lamella structure,[66,70,71,72,73,74,75] gradient structure,[76,77,78,79,80,81,82] laminate structure,[83,84,85,86,87,88,89,90,91,92,93,94,95,96,97] dual/multi-phase structures,[98,99,100] harmonic (core-shell) structure,[101,102,103] multi-modal structure,[104,105,106,107] and heterostructured composite.[108] These microstructures are very diverse, but their superior mechanical properties are all rendered by the HDI strengthening and HDI strain hardening.

The superiority of heterostructured (HS) materials is best demonstrated in HS lamellar Ti (commercially pure, hcp structure), which has been found to possess the high strength of ultrafine-grained Ti and the ductility of coarse-grained Ti, which is believed almost impossible according to our textbook knowledge of materials science (see Figure 3).[66] As shown in Figure 4, the heterostructure of the HS lamellar Ti consists of 25 pct of recrystallized grains with an average grain size of 4 μm, which are embedded in the ultrafine-grained (UFG) matrix. According to the Hall–Petch equation[6]

$$ \sigma = \sigma_{0} + \kappa d^{ - 1/2} $$
(3)
Fig. 3
figure 3

Reprinted from Ref. [66]

The superior properties and strain hardening of heterostructured lamella Ti. (a) Heterostructured (HS) Ti samples (HL60 and HL80) have the strength of ultrafine-grained Ti, and its ductility (uniform elongation) is slightly better than that of coarse-grained (CG)Ti. (b) HS Ti samples have higher strain hardening rate than CG Ti.

Full size image
Fig. 4
figure 4

Reprinted from Ref. [66]

Microstructure of the coarse-grained and heterostructured Ti. (a) Electron back-scattered diffraction (EBSD) image shows initial coarse-grained Ti with an average grain size of 43 μm. (b) EBSD image of the HS lamellar Ti. (c) Recrystallized polycrystalline lamellae embedded in the UFG matrix (black color). (d) TEM micrograph shows a clean recrystallized polycrystalline lamellar and its surrounding UFG matrix

Full size image

where σ is the strength, σ0 and κ are constants, and d is the average grain size, the strength of the HS lamellar Ti should be lower than that of the UFG Ti because the grain size d increased after partial recrystallization. In other words, the high strength of HS lamellar Ti violated the well-known Hall–Petch relationship.

As shown in Figure 4(d), the recrystallized grains are very clean with almost no dislocations in the grain interior. In addition, the un-recrystallized UFG matrix should have gone through a recovery process, leading to lower dislocation density. The effect of dislocation density on flow stress of a metal can be described by the dislocation hardening,[109,110] which is also called Taylor hardening[111]:

$$ \tau = \alpha Gb\sqrt {\rho_{t} } $$
(4)

where τ is the shear strength, α is a constant, G is the shear modulus, b is the magnitude of the Burgers vector, and ρt is the total dislocation density, which is the sum of densities of the statistically stored dislocations (SSDs) and geometrically necessary dislocations (GNDs). According to Eq. [4], the lower dislocation density of the HS lamellar Ti should make its strength lower than that of the UFG Ti. In other words, the high strength of the HS lamellar Ti shown in Figure 3(a) violated the well-known dislocation hardening.

Another extraordinary observation is that the strain hardening rate of the HS lamellar Ti is higher than that of CG Ti (Figure 3(b)), which is totally unexpected from our conventional textbook knowledge. It is experimentally observed that UFG Ti has approximately zero strain hardening rate during plastic deformation.[61] One would expect the HS lamellar Ti to have a very low strain hardening rate that is closer to that of the UFG Ti than that of the CG Ti, since it contains 75 pct of UFG Ti. The high strain hardening rate of the HS lamellar Ti is totally unexpected. This extraordinarily high strain hardening rate of the HS lamellar Ti rendered it high ductility (Figure 3(a)).

As discussed above, the HS lamellar Ti is expected to have lower strength than the UFG Ti according to both the Hall–Petch equation and dislocation hardening. It is also expected to have much lower strain hardening rate than the CG Ti. All of these expectations are surpassed by the HS Ti. The superior mechanical behavior and properties of the HS lamellar Ti cannot be explained by our conventional textbook knowledge of materials science. A new scientific principle must have played a critical role in the observed superior mechanical properties of HS lamellar materials. It should be noted that similar effect of superior combination of strength and ductility has also been observed in other heteorostructured lamellar materials systems, including stainless steel,[70] brass,[73] Cu-Fe dual-phase material,[71] and Ni.[75]

4 New Science of Heterostructured Materials

As discussed above, a new scientific principle, hetero-deformation induced (HDI) strengthening and HDI strain hardening, is responsible for the extraordinary mechanical properties of heterostructured (HS) materials. HDI stress can be effectively produced by the piling up of geometrically necessary dislocations (GNDs), as illustrated in Figure 5.[50] As shown, with increasing applied shear stress τa, a Frank-Read dislocation source (the red dot) in the soft zone is first activated to emit dislocations with the same Burgers vector. These dislocations glide on a slip plane toward the zone boundary, and stopped and piled up against the boundary. Since these dislocations have the same Burgers vector, they will distort, i.e., change the orientation of the slip plane, which is why they are called GNDs. The elastic fields of these GNDs superimpose on each other to produce a long-range stress in the soft zone, which is called back stress because it is opposite to the applied stress. The back stress offsets the applied stress in such a way that following GNDs do not have enough driving force to slip forward or to be emitted from the Frank–Read source. In other words, the back stress makes the soft zones apparently stronger.

Fig. 5
figure 5

Reprinted from Ref. [50]

(a) A schematic of piling up of geometrically necessary dislocations (GNDs) against a zone boundary. The GND piling up generates back stress in the soft zone and forward stress in the hard zone. The curve on the left of the boundary is the distribution of the forward stress in the hard zone. (b) The plastic strain gradient in the soft zone due to the GND piling up, assuming these GNDs are from a Frank-Read dislocations source marked as the red dot in (a). (c) The schematic of back stress profile in the soft zone (Color figure online).

Full size image

Since plastic strain is produced by the slip of dislocations, no plastic strain is produced by the GND pile-up at the zone boundary because no dislocation has reached it, while the location at the dislocation source should have the highest plastic strain. Also considering the non-uniform dislocation distribution in a GND pile-up, a smoothed strain profile as a function of distance from the boundary is schematically shown in Figure 5(b). The slope of this strain profile is the strain gradient near the boundary. In other words, the GND pile-up produces a strain gradient. In addition, a stress distribution profile should also exist near the boundary (Figure 5(c)) due to the non-uniform distribution of GNDs in a pile-up.

It is known that at the head of a GND pile-up, there is a stress concentration of nτa, where n is the total number of GNDs in the pile-up. This stress concentration is applied onto the hard zone at the zone boundary to produce a forward stress. At the zone boundary, the forward stress and back stress are a pair of stresses with the same magnitude but opposite direction. In other words, they cancel each other at the zone boundary. However, their distributions away from the boundary are different, which collectively produce the hetero-deformation induced (HDI) stress. It is hypothesized that the HDI stress monotonically increases with the back stress. More detailed analysis is presented in Reference [50].

The GND pile-up in Figure 5 presents an idealized scenario that is most effective in producing the HDI stress. The situation in real heterostructured materials could be much more complex. For example, some GNDs may not exist in a pile-up formation, but still produce HDI stress, albeit in a less effective manner. Some GNDs may also form an array to produce a low-angle grain boundary, which do not produce long-range back stress or HDI stress.

Experimentally, extensive GND pile-ups were found in the soft, recrystallized large grains in the heterostructured lamellar Ti, which is deemed responsible for its high yield strength.[66] The schematic in Figure 5 also presents a gradient of GND density near the zone boundary, which was indeed observed in a Cu-bronze laminate structured sample after various tensile straining.[83] The GND gradient was found to increase with increasing tensile strain, which indicates an HDI strain hardening. Furthermore, Figure 5 predicted a positive strain gradient near the zone boundary, i.e., plastic strain increases with distance from the boundary. However, digital image correlation (DIC) measurement revealed a negative strain gradient in the same Cu-bronze laminate structure,[112] which seems to suggest the zone boundary as the dislocation source. This puzzle was solved by in situ TEM observations.[38] It turned out that the Frank-Read dislocation sources are indeed dominant in the deformation of the soft large Cu grains, but they are dynamically generated and deactivated after emitting some GNDs. There exists a density gradient of Frank-Read sources with more Frank-Read sources activated nearer the boundary. In addition, most GNDs emitted from the Frank-Read sources are pushed into the zone boundary, which together with the density gradient of Frank-Read sources produced a negative strain gradient. More experimental studies are needed to probe the GND pile-up behavior in other material systems.

The HDI stress at varying tensile strain during a tensile testing can be measured using an unloading-reloading procedure.[113] As shown in Figure 6, the HDI stress at point A of the tensile stress-strain curve can be calculated as

$$ \sigma_{{{\text{HDI}}}} \; = \; \frac{{\sigma_{u} + \sigma_{r} }}{2} $$
(5)

where σu is the unloading yield stress, which is decided as the point at which the unloading curve deviates from the linear slope by x pct (x can be chosen as 5, 10 or other values), and σr is the reloading yield stress, which is decided as the point at which the reloading curve deviates from the linear slope by the same x pct. The HDI stress σHDI is not affected much by the x pct value because σu and σr changes to the opposite direction with x pct. This is a big advantage of Eq. [5]. The HDI stress at different points on the tensile stress-strain curve can be measured by repeating this unloading–reloading experiments. More details on this procedure and discussions of its issues can be found in References [50] and [113]

For the heterostructured lamella Ti,[66] it is found that the HDI hardening is much higher than dislocation hardening. As shown in Figure 7, σHDI is several times higher than the hardening by dislocation accumulation σdis. Note that the σHDI at yielding (first data point) is about 400 MPa, which means that the HDI stress contributed about 400 MPa to the enhancement of yield strength. In addition, the HDI stress also increased with increasing tensile strain, which means it contributed to strain hardening to enhance the ductility. The strain hardening is very high at low plastic strains (< 2 pct), which explains the quick uptick of strain hardening for some samples shown in Figure 3b. These observations demonstrate that the superior combination of strength and ductility of heterostructured lamella Ti is indeed due to the HDI strengthening and HDI strain hardening.

Fig. 6
figure 6

Reprinted from Ref. [50]

Schematics of an unloading-reloading experiment to measure the HDI stress σHDI at point A of a tensile testing curve.

Full size image
Fig. 7
figure 7

HDI hardening is much higher than the conventional dislocation hardening during the tensile deformation of a heterostructured lamella Ti

Full size image

HDI stress is a new terminology,[68] which is more accurate than back stress in describing the effect of GNDs on the mechanical behaviors of heterostructured materials. The direct consequence of GNDs is the generation of long-range back stress in the soft zone to make the soft zone stronger, i.e., back stress strengthening. This is why back stress was used inadvertently in early literature[113,114,115] to explain the superior mechanical behaviors of composites and other materials with heterogeneous microstructures. As discussed in the last section, the experimentally measured extra strengthening and strain hardening in heterostrctured materials is actually the HDI stress, not the back stress.

HDI stress can be produced at three structural levels[50]: (i) near the heterostructured zone boundaries, (ii) near the grain boundaries, and (iii) in subgrains or dislocation cells. The HDI stress at levels (ii) and (iii) also exists in conventional coarse-grained metals, and is relatively small, which is why it is often not considered when explaining mechanical behavior of conventional coarse-grained metals. In other words, in conventional coarse-grained metals, the HDI contribution to the mechanical behavior is usually so small that only dislocation hardening as described by the Taylor equation (Eq. [4]) is usually used.[109,110] In contrast, in heterostructured materials the HDI stress at level (i) is so high that it can no longer be ignored.[66] This is because of the huge strength difference across the zone boundaries, where GNDs in the soft zones can be effectively blocked and piled up.

There are distinct differences between the HDI hardening and the conventional dislocation hardening. The HDI hardening is kinematic in nature, caused by long-range internal stresses (back stress and forward stress), and is directional. The HDI stress is produced by GNDs. It is also related to the Bauschinger effect because they have the same physical origin. Generally, higher HDI stress also means higher Bauschinger effect.[116] In comparison, the dislocation hardening is caused by short-range dislocation interactions, and isotropic. It is only related to the total dislocation density. It should be noted that the mechanics community has used terminology of kinematic hardening to describe HDI hardening phenomenon. However, this does not convey its physical origin, or its potential application to enhance mechanical properties.

Lastly, there is a question on why HDI strengthening and HDI work hardening have not been explored/considered before. In fact, the strengthening by GND pile-ups was first proposed by Petch,[117,118,119] which is one of the theories to explain the well-known Hall–Petch relationship. This is essentially the HDI strengthening that enhances the yield strength of metals by grain boundaries. In other words, the HDI strengthening in homogeneous materials has been regarded as the so-called Hall–Petch effect. It should be noted that the grain boundary is less effective than the zone boundary in blocking GNDs because there is a huge strength difference across the zone boundaries, which makes it much harder to activate the dislocation slip across zone boundaries than across grain boundaries. In other words, zone boundaries in heterostructured materials are much more effective than grain boundaries in producing HDI strengthening. Consequently, the HDI strain hardening in conventional homogeneous materials is much lower than hardening caused by dislocation hardening,[66] as described by the Eq. [4].[109,110] Specifically, the dislocation hardening alone can often explain the mechanical behavior of homogeneous materials very well without invoking HDI hardening. One exception is the high strain hardening and ductility of dual-phase steels,[98,99,100] which was attributed to the strain partitioning, without further linking the dots to HDI hardening caused by the strain partitioning. These facts attest to the difficulty in the conception and acceptance of new physics in the well-developed field of metallurgy. The HDI stress concept has been invoked recently only because our textbook knowledge can no longer explain the experimentally observed superior properties in the heterogeneous lamellar Ti.[66]

5 Design of Heterostructures

There are several basic principles that govern the performance of heterostructured materials. From the above discussions, the superior mechanical properties of heterostructured materials comes from high HDI stress, which can be most effectively produced by piling up of GNDs. Therefore, an effective heterostructure must facilitate GND piling up. Since the GNDs are piled up against zone boundaries, an effective heterostructure should have high densities of zone boundaries per unit volume. In other words, the zone boundary spacing should be small. This is why the lamellar geometry[66] is an effective geometry for soft zones. It is known that a spherical geometry has the lowest boundary area/volume ratio, while a lamellar geometry has much larger boundary area/volume ratio. Another potential effective geometry for soft zones is a needle geometry, which has even higher boundary area/volume ratio than the lamella geometry. Note that when lamella soft zones become continuous across a whole sample, it will form a laminate structure with alternative soft and hard layers. However, such a laminate structure is not very effective in producing HDI stress because no strain gradient can be established in the tensile direction since all layers are subjected to the same strain.

After optimizing the geometry of the soft zones, the size of the soft zones also needs to be optimized. GNDs need a certain spatial room to pile up in the soft zones. Therefore, the boundary spacing cannot be too small. The optimal spacing for Cu-bronze laminated heterostructure is found to be about 15 μm,[112] above which both strength and ductility increases with decreasing spacing. Below this critical spacing, further decreasing the spacing will enhance the strength but decreases the ductility. The optimal boundary spacing should be related to the length of GND pile-up, which is an issue that needs to be studied.

In the heterostructured lamellar Ti,[66] the soft coarse-grained zones are embedded in hard ultrafine-grained (UFG) matrix. It turns out that this is the best structure for enhancing the HDI stress. When a soft zone is surrounded by hard matrix, it is fully constrained by the hard matrix and therefore cannot deform plastically until its hard matrix allows it to. This allows GNDs to build up in the soft zone to increase its back stress to effectively improve the yield strength, as shown in Figure 8(a). In addition, after yielding, the soft zones sustain more plastic strain than the hard matrix. As shown in Figure 8(b), the initial equiaxed grains in the soft zones (colored) sustained 45 pct plastic strain, although the sample was subjected to only a global strain of 9.4 pct. This indicates that the hard UFG matrix sustained much less plastic strain. Since the zone boundary should have the same strain for both zones, there has to be a strain gradient near the boundary to accommodate the strain difference. This strain gradient is related to gradual GND buildup and HDI strain hardening for higher ductility. Therefore, embedding the soft zones in hard matrix is a good strategy to improve both yield strength and strain hardening. On the contrary, if the hard zones are embedded in a continuous soft matrix, the soft matrix would be able to flow freely around the hard zones, which is not effective in improving yield strength.

Fig. 8
figure 8

Reprinted from Ref. [66]

Microstructure and defect structure in the heterostructured lamella Ti. (a) Large number of GND pile-ups (marked by green lines). (b) Elongation of grains in soft zones after tensile testing to 9.4 pct global strain (Color figure online).

Full size image

Another parameter for designing the heterostructured materials is the volume fraction of the soft zones, Vf. Since the soft zone is embedded in the hard matrix, the Vf apparently should be less than 50 pct. Our current data from several studies indicate that 20 to 30 pct is the optimal Vf range for producing the best mechanical properties. The optimum volume fraction may vary with the strength difference between the zones. The hard zone matrix should be thick enough to fully constrain the soft zones as well as to resist the forward stresses produced by the GND pile-ups. It follows that the higher the strength difference, the less fraction of hard zones is needed to constrain the soft zones, which leads to higher optimum fraction of soft zones. Since soft zones are where the GND pile-up occur to produce back stress, higher volume fraction of soft zones will produce higher HDI stress to improve the mechanical properties.

It is also important for the hard zone to be able to deform plastically. Otherwise, the zone boundaries may fail prematurely during tensile testing. Such a failure mode is common in ceramic particle reinforced metal matric composites. In addition, the hard matrix may develop cracks, leading to premature failure.

Lastly, intrinsic material properties such as stacking fault energy (SFE) may affect the HDI hardening. Logically, lower SFE makes it easier for GNDs to pile up without cross-slip, which should enhance the HDI hardening. This is certainly true for fcc metals and alloys. However, very low SFE may activate twinning, which complicates the situation. More study is needed to understand this.

6 Processing of Heterostructured Materials

Several types of heterostructures have been reported, each can be produced by one or more unique processing techniques. Here I will give a brief description of a few major processing techniques that are suitable for industrial scaling-up. More details can be found in the original publications.[66,77,79,80,81,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,100,101,102,103,104,105,106,107,108]

6.1 Cold Deformation + Partial Recrystallization

This technique has been used to process heterostructured lamella structures.[66,70] The process starts with coarse-grained sample. During the plastic deformation, individual coarse grains with different orientations will accumulate dislocations and other crystalline defects at different rates to form zones with different defect densities and different energies. During the recrystallization annealing, zones with higher defect density will recrystallize first to form soft recrystallized zones, where the un-recrystallized initial coarse grains will form hard zones. The volume fraction of the soft zones and size of recrystallized grains can be controlled by tuning the recrystallization temperature and time. In the case of heterostructured lamella structures,[66] the cold deformation was performed via cold rolling, and the initial coarse grains were all deformed into a lamellar geometry, which is why the soft zones are lamellar shaped. Other cold deformation techniques may produce different soft zone geometries. For example, cold extrusion will deform the initial coarse grains into a needle geometry, and consequently produce soft zones with a needle geometry.

The cold deformation strain needs to be controlled to produce the desired geometry and interfacial spacing of the soft zones. The deformation strain can be calculated based on the desired thickness/length ratio of the soft zone, assuming the initial coarse grains are equiaxed.

It should be noted that if a coarse-grained metal is severely deformed as in the severe plastic deformation,[120] the initial coarse grains will be refined to equiaxed ultrafine grains and the initial coarse grains may lose their identity. In such cases, polycrystalline soft zones in the lamella or needle geometry may not form. Instead, a bi-modal microstructure may form with individual large grains embedded in ultrafine-grained matrix.[104]

6.2 Surface Mechanical Attrition Treatment (SMAT)[121]

This technique uses high-speed, high-energy balls to pound the surface of a metal sample to produce a nanocrystalline surface layer and a gradual grain size increase toward the coarse-grained center, which together forms a gradient surface layer. It is similar to the conventional shot peening but larger balls at higher energy are used to deform the metal to a larger depth. In addition to producing nanocrystalline surface, it also produces compressive stress in the surface layer,[77] which can not only improve the fatigue property of mechanical parts, but also ductility of sheet samples. Due to the limited depth of the gradient layer, this technique can only produce gradient material sheets with a thickness of a few millimeters or wires with a diameter of a few millimeters. There are a few variants of the SMAT technique, including ultrasonic peening[122,123] and rotationally accelerated shot peening (RASP),[124,125] etc.

6.3 Powder Metallurgy Plus Deformation

Powder metallurgy is a mature industrial technology and has some unique advantages for producing heterostructured materials and components. The volume fraction and geometry of the soft zones can be easily controlled using this technology. First, a mixture of powers with precise ratio of soft to hard constituents is first consolidated using conventional powder metallurgy, producing a heterostructure with equiaxed soft zones embedded in hard matrix. The soft and hard components may have difference in crystal structure, composition, grain size, etc. If a nanostructured and coarse-grained powder mixture is used, it is important that the nanostructured powder has high enough thermal stability to survive the sintering. Nanostructured powders processed by some ball-milling technique such as liquid nitrogen milling have been reported to have very high thermal stability[126,127] and are ideal for this purpose. Subsequent cold rolling deforms the equiaxed zones into the lamellar geometry. This approach has been successfully used to make Fe-Cu heterostructured lamella structure.[71] In addition, Lavernia et al has used powder consolidation plus hot extrusion to produce a heterostructure with soft large needle-shaped grains embedded in nanostructured matrix, which exhibit excellent mechanical properties.[105,106,128]

6.4 Accumulative Roll Bonding (ARB)[129]

ARB is one of the severe plastic deformation (SPD) techniques.[47] It has been extensively used to process ultrafine-grained (UFG) metals and alloys because it can process materials to very high strains.[130,131] ARB involves rolling of stacked metal sheets into the thickness of one original sheet so that the sheet can be repetitively stacked and rolled for multiple passes, and the sheets are cold-welded together by the rolling strain. If the starting sheets have different composition or crystal structure, a type of heterostructure, laminate structure, can be formed.[83,129,132]

7 Summary

Heterostructured materials are quickly emerging as a major materials field because of their new materials science and the great potential for real industrial applications. A new scientific principle, hetero-deformation-induced (HDI) strengthening and HDI hardening, is responsible for their superior mechanical properties. It becomes a major factor in determining the mechanical behavior of heterostructured materials, which is superimposed on the conventional dislocation-based strengthening and hardening. The major advantage of heterostructured materials is their easy production using current industrial facilities, which makes their commercial applications readily feasible.

Our understanding of this new field is still limited and there are many known and unknown fundamental issues that need to be studied by researchers in the communities of materials, mechanics, and computer modeling. Here I would deliberate further on the most fundamental issue that needs to be solved: GND interaction with the zone boundaries during GND piling up. Theoretically, when GNDs pile up against a zone boundary, the GNDs may be stopped at the boundary, pushed into the boundary, transmitted across the boundary, reflected from the boundary, or cross-slip to escape the pile-up. These scenarios will affect the effectiveness in producing the back stress and HDI stress. The occurrence of these scenario will be affected by the intrinsic properties of materials such as the stacking fault energy and crystal structure, as well as the microstructural characteristics such as zone boundary structure and misorientation, strength difference across the boundary, crystal structure difference across the boundary, etc.

Lastly, the heterostructure concept has also been successfully applied to functional materials, although the mechanism is different from that of structural materials.[133] However, it can be stated that the superior properties of heterostructured materials are derived from the coupling/interaction of heterostructured zones. The mechanical coupling produces superior mechanical properties, while the physical coupling produces superior physical properties.