Fracture ab initio: A force-based scaling law for atomistically informed continuum models

Abstract

In fracture mechanics, established methods exist to model the stability of a crack tip or the kinetics of crack growth on both the atomic and the macroscopic scale. However, approaches to bridge the two scales still face the challenge in terms of directly converting the atomic forces at which bonds break into meaningful continuum mechanical failure stresses. Here we use two atomistic methods to investigate cleavage fracture of brittle materials: (i) we analyze the forces in front of a sharp crack and (ii) we study the bond breaking process during rigid body separation of half crystals without elastic relaxation. The comparison demonstrates the ability of the latter scheme, which is often used in ab initio density functional theory calculations, to model the bonding situation at a crack tip. Furthermore, we confirm the applicability of linear elastic fracture mechanics in the nanometer range close to crack tips in brittle materials. Based on these observations, a fracture mechanics model is developed to scale the critical atomic forces for bond breaking into relevant continuum mechanical quantities in the form of an atomistically informed scale-sensitive traction separation law. Such failure criteria can then be applied to describe fracture processes on larger length scales, e.g., in cohesive zone models or extended finite element models.

I. INTRODUCTION

Resistance to crack propagation is undoubtedly one of the most important properties of structural materials. However, our current mechanistic understanding of the energy-dissipation processes involved on the various scales and of their interplay is not sufficiently advanced to predict the fracture behavior of materials ab initio.1,2 As fracture is ultimately caused by the breaking of atomic bonds,3 there is a high demand for atomistically informed fracture criteria. An overview of ongoing attempts to realize them in hierarchical and concurrent schemes can be found, e.g., in Refs. 4 and 5. Here we propose a hierarchical scheme that meets two common challenges: to extract information on the atomic scale in an efficient manner and to coarse-grain this information to obtain practical and meaningful failure criteria for a finite element (FE) implementation on the mesoscale. Our approach is demonstrated by making use of cohesive zones (CZs), but is not limited to this model.

A so-called cohesive zone model is a seemingly natural way to incorporate atomistic information in a continuum model of fracture. In a traditional CZ model, the fracture process zone (i.e., the region in which nonlinear processes occur) ahead of the crack tip is represented by cohesive surfaces (respectively a narrow band of vanishing thickness) which experience cohesive tractions described by a constitutive law, the so-called traction-separation (TS) law. Crack growth occurs when the separation at the tail of the CZ, i.e., at the physical crack tip, reaches a critical value at which the cohesive traction vanishes. The strip yield model of Dugdale,6 which was originally proposed for estimating the size of the plastic zone around a crack tip, is regarded as one of the first CZ-type models. Barenblatt7 also proposed a cohesive fracture concept with the aim to eliminate the crack tip stress singularity in classical linear elastic fracture mechanics (LEFM). For fracture of perfectly brittle materials, the descriptions by LEFM and the CZ model approach are equivalent if the material behavior in the zone around the crack tip is determined by the stress-intensity (K) field and if the cohesive energy density is identical to the critical energy release rate.8 The first condition is met when the fracture process zone is smaller than the K-dominated zone (the region with a significant gradient in the stress), which is the case in brittle materials.9,10

A crucial point to consider in practical applications within a finite element method (FEM) implementation is that CZ-based numerical techniques require cracks to propagate along the element boundaries. Therefore, an inherent nonvanishing amount of mesh dependency arises, which can become dominant for three-dimensional simulations in a homogeneous material.11 For instance, no converged solutions from the simulation of progressive delamination were obtained above a critical mesh size.12 As a general rule, Hillerborg et al.13 suggested a maximum characteristic length ${l_{{\rm{coh}}}} \approx {G_{\rm{c}}}/{\rm{\sigma}}_{\rm{c}}^2$ for the CZ under mode I loading, based on the cohesive energy G_c and the critical stress to initiate crack advance σ_c. This characteristic length is always smaller than the radius of the K-dominated zone at critical loading, but also larger than the fracture process zone. In our approach, we couple the mesh size to the critical stress, which is the object of a scaling procedure explained in Sec. III. Furthermore, we do not only treat the fracture process zone as a CZ, but sample the complete K-dominated region on the cleavage plane with cohesive elements. This way, we obtain mesh-independent results for the fracture toughness under mode I loading.

In principle, the TS law can capture the physics of deformation and failure on the microscale, provided its shape is chosen carefully and that it includes important parameters such as maximum strength, work of separation, and critical displacement.14 Within the hierarchical modeling approaches, there are basically two philosophies about how to incorporate this information in TS laws, which differ in the way in which dissipative processes enter the modeling framework.

TS laws derived from atomistic simulations of homogeneous deformation of a single crystal, a bicrystal, or even model sections of polycrystalline microstructures can produce a stress–strain curve which reflects both elastic and dissipative processes during fracture.15–21 However, dissipating the energy which is released during crack initiation and growth can be severely constrained in microstructures22 so that the fracture toughness becomes dependent on length scale and geometry. This means that the TS law would have to be adapted for each specific microstructure. Instead, we want to promote an approach in which the process of material separation by breaking of atomic bonds is separated from energy dissipative processes, such as plastic deformation accommodated by generation and motion of dislocations. The description of bond breaking within the CZ can be combined with different levels of description of the plastic deformation in the material adjacent to the CZ. On the smallest scale, plasticity is described based on discrete dislocation dynamics models in two23–25 or three dimensions.26 Further developments include the formulation of the virtual internal bond model of cohesive fracture and its application to nanomaterials.27,28

Following the failure criterion by Griffith, the TS law for the bond-breaking process will have to capture the work of separation of the material, but to predict reliably the trends in cohesive behavior, the strength of the bonds is required as well.29 The strength of interatomic bonds is reflected in the theoretical strength of a material, which can be determined via ab initio density functional theory (DFT) calculations for single crystals30,31 as well as interfaces with and without impurities.32–34 However, this procedure assumes homogeneous expansion perpendicular to, or cleavage along, an infinite crystallographic plane. During such a process, all bonds across the anticipated cleavage plane are elongated by the same amount and rupture at the same time. By contrast, individual pairs of atoms across the cleavage plane in the vicinity of the crack tip experience different environments, due to the gradient of the elastic displacement ahead of a crack tip, as shown in Fig. 1. Thus, the equivalence of the stresses obtained from such a rigid body separation (RBS)-type calculation with the critical stress needed to advance a crack tip still has to be demonstrated. This is one of the aims of the present paper (see Sec. II).

FIG. 1

Simulation setups for rigid-body separations (a) and crack-tip configurations (b). Note that not all interacting nearest-neighbor (NN) pairs (green; color online) are shown here due to the two-dimensional visualization. In fact the number of interacting NN pairs is twice the number of interacting 2nd NN pairs.

Embedding an atomistics-based TS law into a fracture model via CZs in a FE scheme has also practical issues because the theoretical strength is of the order of GPa and the critical separation is of the order of Å.35 The stresses on the order of the theoretical strength occur very locally in the extreme stress gradient in front of the crack tip, i.e., usually within the first few layers of atoms. In contrast to this, any continuum modeling is based on describing average stresses in some finite volume such that typical stresses occurring in FE models are much smaller. Therefore, Serebrinsky et al. first used a scaling relation for TS laws36 derived from the results of ab initio calculations based on the concepts introduced in Refs. 37 and 38. It assumes that the critical stress needed to separate two half crystals depends on the amount of elastic energy that is stored and released from the material next to the cleavage plane, which in turn scales with the system size. This can easily be observed in atomistic supercell calculations in which two half crystals are shifted and the atomic positions are relaxed afterwards. If the theoretical strength is simply identified with the maximum of the derivative of the energy–displacement curve, it decreases with an increasing number of planes parallel to the cleavage plane.37 However, the amount of energy that localizes and is subsequently released during the fracture process is in fact finite,39 and the seemingly size-dependent fracture stress can be normalized to obtain the unique strength of the material.40 Thus, a scaling approach via the elastic energy is practical, but not well justified, and a physically meaningful coarse-graining scheme providing an unambiguous connection between the macroscopic and microscopic stresses is still needed.

With the work at hand, we want to promote tensile tests carried out by RBSs and translations in combination with a scaling approach based on pairwise forces. RBS schemes can be used to characterize single crystals and grain boundaries on the same footing,41 provide a three-dimensional description of single crystal42 and grain boundary separation,43 and can be extended to include impurity effects.35 Most importantly, the derived critical stresses are size independent without any normalization. Our scaling approach based on interatomic forces will allow us to relate this fundamental atomistic quantity to the required mesh-sensitive model parameters in a rigorous way.

In the following, the results of atomistic simulations of RBS are compared with those of simulations of K-dominated cracks to demonstrate the equivalence of the interatomic forces in both situations; see Sec. II. This is the starting point for our novel approach to scale the atomic-level properties into parameters for continuum models in a physically motivated way, which is presented in Sec. III. This novel approach is tested in the framework of CZ modeling of cleavage fracture in an FE model, which demonstrates its advantages and shortcomings. Our findings are summarized in Sec. IV.

II. COMPARISON OF INTERATOMIC FORCES AT CRACK TIPS AND DURING RIGID-BODY SEPARATION

A. Interatomic potentials and simulation setups

We chose tungsten as a brittle, elastically isotropic model material to study cleavage fracture under static loading conditions. The atomic interactions were described either in the framework of ab initio DFT calculations using the local density approximation (LDA) or by using different potentials of the embedded atom method (EAM) type. DFT calculations were carried out using the ABINIT electronic structure code,44–46 employing the ultra-soft pseudopotential of Hartwigsen, Goedecker and Hutter.47 For the RBSs described below, a k-point mesh of 8 × 8 × 2 k-points was used, which, after Fourier transformation, corresponds to a maximum k-point spacing of 47.45 a.u. (25 Å). The energy cut-off for the plane-wave basis set was 16 Ha (435 eV).

The EAM potentials used are the classical Ackland–Thetford–Finnis–Sinclair (ATFS) potential from the 1980s48,49 and the more recent potential by Wang.50 Their fracture-relevant properties and cutoff radii r_cut are presented in Table I. All atomistic simulations were performed with the molecular dynamics software package IMD51,52 using the MIK53 and FIRE54 relaxators.

TABLE I Summary of fracture-relevant potential properties of the EAM potentials used for tungsten (ATFS48,49 and Wang50): the lattice parameter a₀ at 0 K, the bulk equilibrium energy E₀, and the elastic constants C_ij, the (100) surface energy, and the cut-off radius.

The simulation setups for the corresponding atomistic simulations are shown in Fig. 1. Figure 1(a) shows the case of rigid-body separations, which is often used to determine the theoretical strength via ab initio tensile tests. In this setup, two crystal halves are iteratively separated without allowing the atoms to relax their positions. As mentioned in the introduction, this strategy prevents size effects, which would occur if the crystallographic layers were allowed to relax, and furthermore enables a unified description of single crystals and grain boundaries.41 Note, however, that the strength values determined from methods that include atomic relaxations and lateral contraction of the sample can differ significantly, particularly in the presence of defects, such as grain boundaries.55 The implications will be discussed below. Periodic boundary conditions (PBC) are used in all directions. In the case of a grain boundary calculation, this actually requires the inclusion of two cleavage planes as there would be two grain boundaries in the simulation cell. This is not necessary in the single crystal, but to be able to use the same setup, we did so for consistency.

The size of the simulation box in the present study was L_x × L_y × L_z ≈ 10 × 60 × 10 ų. The separation distance Δ_y was varied from −0.5 Å to 2.5 Å in incremental steps of dΔ_y = 0.025 Å. The normal stress σ_at acting between the atoms of the two crystal halves at a certain separation distance Δ_y was then calculated from the average potential energy per atom, E_pot, as

$${{\rm{\sigma}}_{{\rm{at}}}} = {{{N_{{\rm{atoms}}}}} \over {2{A_{xz}}}}{{{\rm{d}}{E_{{\rm{pot}}}}} \over {{\rm{d}}{{\rm{\Delta}}_y}}}\quad ,$$

(1)

where N_atoms is the number of atoms in the configuration and A_xz is the cross-sectional area of the created surface. The factor of 2 results from the PBC.

Figure 1(b) shows the setup used to determine the fracture toughness and structure of an atomistically sharp crack. Although this setup can also be used to study cracks with DFT,56 it is usually used in classical atomistic simulations with interatomic potentials. In this setup, the linear-elastic solution of the crack-tip displacement field under plane-strain conditions, u_x,y(r, θ) is directly applied to a cylindrical atomistic configuration with PBC.57,58 The displacements are determined for a given stress intensity factor K_I and depend on the distance from the central crack tip, r, and the inclination angle θ of the direction of r and the crack plane. The critical stress intensity factor for the onset of crack propagation, K_Ic, was determined by iteratively increasing K_I, the corresponding Δu_x,y, and the subsequent relaxation of the atoms in the interior of the configuration (with a minimum distance of 2r_cut from the outer surface). The value of K_I at which the crack propagates by brittle bond breaking was then defined as K_Ic (we will denote this quantity as $K_{{\rm{Ic}}}^{{\rm{at}}}$ hereafter to emphasize that it was obtained by atomistic simulations). For more details on the setup and simulation methodology, see Refs. 59 and 60. In the present study, a cylinder of radius 150 Å and length L_z ≈ 10 Å was used to study a crack on the (100) crack plane along the crack-front direction [011], which is the natural crack system in tungsten.61

B. Results

1. Simulations of rigid-body separation

The dependence of the binding energy per unit area, i.e., the energy difference of a configuration with respect to the fully separated crystal halves, on the separation distance is shown in Fig. 2 for the two interatomic potentials in comparison to DFT results. From this, the cleavage energy G_c is obtained as the difference between the energy at infinite and that at zero separation. The values are summarized in Table II. By comparing with Table I, it can be seen that the cleavage energy approximately equals 2γ_s(100), which would be the (relaxed) work of separation. The work of separation (WoS) obtained from the DFT calculations (not shown in Table I) equals 8.58 J/m², which is in good agreement with other DFT values.62,63 The values for the cleavage energies obtained with the EAM potentials are significantly different from the DFT data. Such deviations are not uncommon: see, e.g., Ref. 64 for a review of the applicability of various classes of potentials for bcc transition metals to fracture-like situations. However, for the aim of the present study, it is sufficient to show that the atomistically determined fracture toughness can be reproduced independently of the mesh size of our CZ model. In addition, we will show how the DFT results from the simpler RBS calculations can be used in the same approach, opening up the possibility of a more accurate determination of K_Ic without performing the actual DFT crack-tip simulations.

FIG. 2

(a) Binding energy versus separation of crystal halves for two different tungsten potentials and as obtained by DFT. (b) Derivatives of the binding curves, i.e., traction versus separation of crystal halves.

TABLE II Summary of the characteristic values for rigid-body separations (cleavage energy G_c, threshold stress σ_th, critical separation δ_crit, final separation δ_f) and crack-tip configurations ($K_{{\rm{Ic}}}^{{\rm{at}}}$) obtained with the ATFS48,49 and Wang50 potentials as well as by DFT calculations.

The TS relationships for the different potentials were readily obtained by applying Eq. (1), i.e., by derivation of the binding-energy versus separation-distance data. The corresponding TS plots are shown in Fig. 2(b). Three characteristic values can be obtained from these plots: the threshold stress, σ_th, the critical separation distance δ_crit (where σ_th is reached), and the ‘final’ distance δ_f (where the traction across the surface is zero). All characteristic values are summarized in Table II and compared to values obtained by DFT calculations.

Based on the experience with previous studies on RBS,35,41 the shape of the TS relationships of the Wang potentials appears to be somewhat unexpected as it shows two local maxima and a local minimum at around Δ_y ≈ 0.65 Å. The origin lies in the not-completely-smooth energy–displacement curves [see Fig. 2(a)]. Both potentials were optimized to reproduce several material properties, but an interplanar separation along the [001] axis was not included. However, as we will see in Sec. III, it is sufficient if the TS law includes the peak stress, and this is reasonably well reproduced by both potentials.

2. Crack-tip simulations

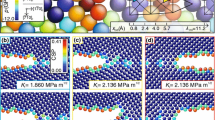
The fracture toughness $\left({K_{{\rm{Ic}}}^{{\rm{at}}}} \right)$ values determined by atomistic simulations are summarized in Table II. According to the Griffith criterion65 ${K_{\rm{G}}} = \sqrt {2{{\rm{\gamma}}_{\rm{s}}}\left({100} \right)\cdot{E}}$ (with E being the appropriate orientation-dependent elastic constant), critical values in the range of 1.61–1.64 MPa m^1/2 are expected for both potentials. These theoretically expected values using the potential parameters are markedly smaller than the atomistically determined ones; see Sec. II. This well-known behavior66 is generally attributed to the lattice-trapping effect.67 The atomistic crack-tip configurations showing crack propagation by cleavage on the original (100) plane are provided in Fig. 3.

FIG. 3

Atomistic crack-tip configurations in the (100)[011] crack system for the ATFS (a) and Wang (b) potentials at the critical stress intensity factors $K_{{\rm{Ic}}}^{{\rm{at}}}$; see Table II. The original crack-tip atoms are colored black.

3. Comparison of interatomic forces

There are different ways to calculate the force acting across the cleavage plane from the present simulation results: $F_{{\rm{ct}}}^{{\rm{at}}}$ is the y-component of the individual atomic (superscript ‘at’) force vectors calculated during the simulation of crack-containing configurations (subscript ‘ct’). To compare the evolution of the crack-tip forces with the forces during rigid-body separations, the crack-tip distance r_ij has to be related to the corresponding separation in the [100] direction, Δ_y, as follows:

$${{\rm{\Delta}}_y} = - {a_0}/2 + \sqrt {r_{ij}^2 - a_0^2/2} \quad ,$$

(2)

where a₀ denotes the bulk lattice parameter. Strictly, this correction is only valid under the assumption that the distance between next-nearest (NN) neighbors (and for cracks on the (100) plane NN neighbor bonds are the critical bonds) changes with Δ_y, as follows:

$${r_{ij}} = \sqrt {2{{\left({{a_0}/2} \right)}^2} + {{\left({{{\left({{a_0}/2} \right)}^2} + {{\rm{\Delta}}_y}} \right)}^2}} \quad ,$$

(3)

i.e., when applying a homogeneous uniaxial strain without allowing Poisson contraction, as is the case in the present study.

$F_{{\rm{rb}}}^{{\rm{at}}}$ is the y-component of the individual atomic force vectors calculated during the simulation of rigid-body separations (subscript ‘rb’). Since there are N_surface interacting NN pairs and ${{{N_{{\rm{surface}}}}} \over 2}$ 2nd NN pairs for each (100) surface [Fig. 1(a)], the total force $F_{{\rm{rb}}}^{{\rm{at}}}$ per surface atom is obtained from the individual forces between NN and 2nd NN neighbors, $F_{{\rm{NN}}}^{{\rm{at}}}$ and $F_{2{\rm{NN}}}^{{\rm{at}}}$, by

$$F_{{\rm{rb}}}^{{\rm{at}}} = F_{{\rm{rb}},{\rm{NN}}}^{{\rm{at}}} + 1/2F_{{\rm{rb}},{\rm{2NN}}}^{{\rm{at}}}\quad ,$$

(4)

$F_{{\rm{rb}}}^{{\rm{avg}}}$ is calculated from the change of the average potential energy per atom in rigid-body separations:

$$F_{{\rm{rb}}}^{{\rm{avg}}} = {{{N_{{\rm{atoms}}}}} \over {2{N_{{\rm{surface}}}}}}{{{\rm{d}}{E_{{\rm{pot}}}}} \over {{\rm{d\Delta}}}}\quad ,$$

(5)

which corresponds to the calculation of the tractions in Eq. (1) but normalized to the number of surface atoms rather than the surface area.

F^eff is the derivative of the effective pair potential.68 In this case, the same correction regarding r_ij and Δ_y has to be made as for the crack-tip forces; see Eq. (2).

The evolution of these forces as a function of lateral separation Δ_y is shown in Figs. 4(a) and 4(b) for the two potentials. The truly remarkable result of this comparison is how well the force laws from the by-far-simpler model systems (rigid-body separations and effective pair potential) agree with the actual forces at the crack tips, considering that the environments in which the forces have been determined (or calculated as in the case of F^eff) are completely different.

FIG. 4

Comparison of the relationship between per-atom forces on crack-tip atoms $\left({F_{{\rm{ct}}}^{{\rm{at}}}} \right)$, the NN and 2NN contributions to the forces on atoms across the cleavage plane during rigid-body separations $\left({F_{{\rm{rb}}}^{{\rm{at}}}} \right)$, the derivative of the average potential energy during rigid-body separations $\left({F_{{\rm{rb}}}^{{\rm{avg}}}} \right)$, and the derivative of the effective pair potential (F^eff) on the separation distance Δ_y (a) for the ATFS potential and (b) for the Wang potential.

Second, it should be noted that the unexpected camel-hump shape of the T(Δ_y) curve for the Wang potential shown in Fig. 2(b), which is essentially the per-area instead of per-atom versions of $F_{{\rm{rb}}}^{{\rm{avg}}}\left({{{\rm{\Delta}}_y}} \right)$ and thereby $F_{{\rm{rb}}}^{{\rm{at}}}\left({{{\rm{\Delta}}_y}} \right)$, can now be understood by the separation of the total acting force into contributions from NN and 2nd NN neighbors.

Third, the individual force–separation relationships ($F_{{\rm{rb}},{\rm{NN}}}^{{\rm{at}}}$ and $F_{{\rm{rb}},2{\rm{NN}}}^{{\rm{at}}}$) are very similar to each other, and their shape can be qualitatively understood by comparing it to the shape of the derivative of the effective pair potential, F^eff. This implicitly shows that the correction made in Eq. (2) is applicable even if it does not account for changes in the electron density due to uniaxial straining, which might, however, be the reason for the minor differences in the magnitudes of $F_{{\rm{rb}},{\rm{NN}}}^{{\rm{at}}}$ and F^eff.

An important conclusion which can be drawn from these results is that the forces necessary to break the bond between the crack-tip atoms show only a small—if any at all — dependence on the local atomic surrounding at the crack tip. Even if our observations cannot prove that all EAM potentials will show the same behavior or that crack-tip bonds in metals in general do not show a strong dependence on their local bonding environment, this is to our knowledge the first time that it has been shown that the forces to separate crack-tip atoms can indeed be estimated from simulations of rigid-body displacements. In particular, the comparison between $F_{{\rm{ct}}}^{{\rm{at}}}$ and $F_{{\rm{rb}}}^{{\rm{avg}}}$ in Fig. 4 shows that the characteristics of TS laws derived from simple rigid-body separations, i.e., the maximum force and the critical separation distance δ_crit, are in very good agreement with the actual crack-tip forces. This has important consequences for multiscale modeling, as it validates the long-standing use of DFT calculations to determine traction separation laws. Whether the correspondence of forces from rigid-body separation and fracture simulations still holds for systems with complex chemical compositions or grain- and interphase boundaries would still need to be shown. However, an averaging of forces over one structural or chemical unit would be a possible way to extend our approach.

III. ATOMISTICALLY INFORMED TRACTION SEPARATION (TS) LAW

A. Derivation of a scalable TS law

In this section, a method is derived to convert the atomic forces at the crack tip into meaningful continuum quantities, i.e., TS laws describing the cohesive behavior of the material in front of the crack tip. To accomplish this, we consider a chain of N pairs of atoms in front of the crack tip on the crack plane (see Fig. 5). The atom pairs under consideration are those that are affected by the stress concentration of the crack tip and that lie in the crack plane.

FIG. 5

Schematic drawing of the strained atom pairs in the CZ in front of the crack tip.

Formally, the atomic forces F⁽ⁱ⁾, defined in Sec. II.B.2, can be converted into atomic stresses by normalization with the atomic area A_at as

$${{\rm{\sigma}}_{{\rm{at}}}}\left({{x^{\left(i \right)}}} \right) = {{{F^{\left(i \right)}}} \over {{A_{{\rm{at}}}}}}\quad ,$$

(6)

where x⁽ⁱ⁾ = ia_cd is the distance of the atom pair i = 1, 2, …, N to the crack tip and A_at = a_cfa_cd is the projected atomic area on the crack plane, given by the interplanar distance a_cf along the crack front and the interplanar distance a_cd in crack direction, respectively. The crack itself is defined by the pairs of atoms that are separated by a distance of more than the critical displacement δ_f, such that the position of the crack tip is located at the last pair of atoms with a larger separation than δ_f. It is noted here that the elastic distortion of the atomic distances along the crack front and in the crack direction is neglected to obtain a closed-form solution for the scaling relation.

From LEFM, it is known that the stress field in front of a crack tip decays as $1/\sqrt {{x^{\left(i \right)}}}$. Figure 6(a) shows that this linear-elastic theory holds excellently at the atomic scale, even very close to the crack tip, in agreement with the findings of Ref. 9. The deviation for the crack-tip atom is partly due to the 20% increased Voronoi volume compared to the atoms in front of the crack tip. In contrast to the atomic stresses, the atomic forces are largest for the crack-tip atom pair. The atomic stresses along the cleavage plane in front of the crack tip can be reasonably expected to follow

$${{\rm{\sigma}}_{{\rm{at}}}}\left({{x^{\left(i \right)}}} \right) = {{\rm{\sigma}}_{{\rm{at}}}}\left({{x^{\left(1 \right)}}} \right)\sqrt {{{{x^{\left(1 \right)}}} \over {{x^{\left(i \right)}}}}} = {{{F^{\left(1 \right)}}} \over {{A_{{\rm{at}}}}}}\sqrt {{{{x^{\left(1 \right)}}} \over {{x^{\left(i \right)}}}}} = {{{K_{\rm{I}}}} \over {\sqrt {2{\rm{\pi}}{x^{\left(i \right)}}}}}\quad ,$$

(7)

with the stress intensity factor

$${K_{\rm{I}}} = {{{F^{\left(1 \right)}}\sqrt {2{\rm{\pi}}{a_{{\rm{cd}}}}}} \over {{A_{{\rm{at}}}}}}\quad ,$$

(8)

fully defined by atomistic quantities.

FIG. 6

(a) Atomic stresses (black diamonds) in front of the crack tip in the atomistic simulation using the Wang potential at a load of K_I = 1.67 MPa m^1/2 together with the corresponding analytic LEFM solution, which results in a finite stress at the boundary of our model. The blue points (color online) show the corresponding atom positions (right ordinate axis). (b) Schematic drawing of the stress, with step-wise functions, which indicate the average stress per element in FEM simulations with two different mesh sizes, FE1 and FE2. The region with a significant gradient in the average stress is called the K-dominated region. At the end of the K-dominated zone, the stress gradient decays into a constant far-field stress σ₀, which needs to be considered for finite crack sizes; see Eq. (15).

The fundamental relation between the atomistic and the continuum description is demonstrated by calculating the fracture toughness K_Ic from Eq. (8), as

$${K_{{\rm{Ic}}}} = {F_{\rm{c}}}\sqrt {2{\rm{\pi}}{a_{{\rm{cd}}}}} /{A_{{\rm{at}}}} = {\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}\sqrt {2{\rm{\pi}}{a_{{\rm{cd}}}}} \quad ,$$

(9)

with the critical force F_c at which the bond between the first pair of atoms breaks; i.e., this pair of atoms is separated beyond the critical distance δ_f, and consequently the crack tip advanced by one atomic distance. This force corresponds to the theoretical strength defined in Sec. II.B.1 and can thus be conveniently calculated with atomistic methods. With the values obtained from atomistic calculations with the Wang potential (see Table II), a fracture toughness of K_Ic = 1.70 MPa m^1/2 is calculated from the critical force, $F_{{\rm{rb}},{\rm{max}}}^{{\rm{avg}}}$, and K_Ic = 1.84 MPa m^1/2 from the theoretical strength σ_th with ${a_{{\rm{cd}}}} = {a_0}/\sqrt 2$. The force-based value corresponds very well to the K_Ic values obtained from direct atomistic simulation ($K_{{\rm{Ic}}}^{{\rm{at}}} = 1.68$ MPa m^1/2) and from the Griffith criterion ($K_{{\rm{Ic}}}^{\rm{G}} = 1.64$ MPa m^1/2). The value from the critical strength is roughly 8% higher as can be expected from the difference in $F_{{\rm{eff}}}^{{\rm{max}}}$ and $F_{{\rm{rb}},{\rm{max}}}^{{\rm{avg}}}$ (see Fig. 4).

However, for most continuum fracture models, a fracture energy or WoS is required in addition to the fracture strength ${{\rm{\tilde \sigma}}_{\rm{c}}}$ and a critical separation ${{\rm{\tilde \delta}}_{\rm{c}}}$. These parameters represent the main quantities defining the TS law describing the cohesive behavior of a material in front of a crack tip [see Fig. 6(b)]. While the WoS is scale independent, the fracture strength and the critical separation both depend on the spatial resolution of the applied method. The fundamental material constants are obtained from atomistic methods, but a proper scaling must be developed for the scale-dependent model parameters that takes an appropriate length scale or mesh size into account, as outlined in the introduction.

Since all values used in continuum methods represent average values over a finite volume or a FE, we start by defining the critical fracture strength as average stress over the K_I-dominated region

$${{\rm{\tilde \sigma}}_{\rm{c}}} = {{\sum\limits_{i = 1}^N {{F^{\left(i \right)}}}} \over A}\quad ,$$

(10)

as the sum over all atomic forces in this region normalized by the corresponding area. From relation Eq. (7), we also conclude that the atomic forces decay as

$${F^{\left(i \right)}} = {F^{\left(1 \right)}}\sqrt {{{{x^{\left(1 \right)}}} \over {{x^{\left(i \right)}}}}} = {{{F^{\left(1 \right)}}} \over {\sqrt i}}\quad .$$

(11)

With Eq. (11), the relation A = NA_at and the condition that F⁽¹⁾ = F_c, because the onset of crack advance is considered, we obtain

$${{\rm{\tilde \sigma}}_{\rm{c}}} = {{{F_{\rm{c}}}\sum\limits_{i = 1}^N {{1 \over {\sqrt i}}}} \over {N{A_{{\rm{at}}}}}} = {\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}{1 \over N}\sum\limits_{i = 1}^N {{1 \over {\sqrt i}}} \quad .$$

(12)

The sum on the right hand side of this equation can be approximated by

$$\tilde S\left(N \right) = {1 \over N}\sum\limits_{i = 1}^N {{1 \over {\sqrt i}}} \approx {2 \over {\sqrt N}} - {{1.4} \over N}\quad .$$

(13)

Numerical evaluation of the approximation shows that the relative error is less than 10⁻⁴ for values of N between 10⁵ and 10⁶; for the latter value, the sum amounts to $\tilde S\left(N \right) = 0.002$. The precision of the approximation gets better for larger values of N, which is the usual case for applications. Since the sum is finite, a precise numerical evaluation is always possible, although the simple approximation function is still easier to handle.

To calculate a properly scaled final separation of atoms ${{\rm{\tilde \delta}}_{\rm{f}}}$, we consider a simple bilinear TS law [see Fig. 7(b)] such that ${\rm{\Gamma}} = 1/2{\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}{\rm{\delta}}_{\rm{f}}^{{\rm{at}}} = 1/2{{\rm{\tilde \sigma}}_{\rm{c}}}{{\rm{\tilde \delta}}_{\rm{f}}}$. It follows

$${{\rm{\tilde \delta}}_{\rm{f}}} = {{2{\rm{\Gamma}}} \over {{{{\rm{\tilde \sigma}}}_{\rm{c}}}}} = {{{\rm{\delta}}_{\rm{f}}^{{\rm{at}}}} \over {\tilde S\left(N \right)}}\quad .$$

(14)

FIG. 7

(a) Schematic drawing of the region around a crack-opening sampled by elements of different sizes r_FE. At each node, the crack opening is characterized by a δ. (b) Bilinear TS law in which critical stress and final displacement depend on the mesh size.

In the final step, a reasonable estimate for the length of the K-dominated region and thus the number N of atom pairs to consider is developed. The criterion for the length of this region is the decay of the stress to a value of σ₀, which can be either the yield strength of a plastic material or the far-field stress ${{\rm{\sigma}}_0} = {K_{\rm{I}}}/\sqrt {{\rm{\pi}}{a_{{\rm{crack}}}}}$ considered in linear-elastic fracture mechanics, where a_crack is the crack length. Hence, N is defined by the requirement that

$${{{F^{\left(N \right)}}} \over {{A_{{\rm{at}}}}}} = {{{F^{\left(1 \right)}}} \over {{A_{{\rm{at}}}}\sqrt N}} = {{\rm{\sigma}}_0}\quad .$$

(15)

For the critical condition, when the crack starts to propagate (F⁽¹⁾ = F_c), we obtain

$${N_{\rm{c}}} = {\left({{{{F_{\rm{c}}}} \over {{{\rm{\sigma}}_0}{A_{{\rm{at}}}}}}} \right)^2} = {\left({{{{\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}} \over {{{\rm{\sigma}}_0}}}} \right)^2}\quad .$$

(16)

Noting that the critical atomic stresses are typically a 1000 times larger than the yield strength or far-field stress, a reasonable estimate for the number of atom pairs in the K-dominated region is N_c ≈ 10⁶. This yields a size of K-dominated zone r_coh = N_ca_cd ≈ 200 μm.

In summary, a scaling relation for the atomistic strengths and separations has been derived, in the form

$${{\rm{\tilde \sigma}}_{\rm{c}}} = {\rm{\kappa \sigma}}_{\rm{c}}^{{\rm{at}}}\quad ,$$

(17)

$${{\rm{\tilde \delta}}_{\rm{f}}} = {{{\rm{\delta}}_{\rm{f}}^{{\rm{at}}}} \over {\rm{\kappa}}}\quad ,$$

(18)

with the scaling factor

$${\rm{\kappa}} = \tilde S\left(N \right) = {2 \over {\sqrt N}} - {{1.4} \over N} = 2{{{{\rm{\sigma}}_0}} \over {{\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}}} - 1.4{\left({{{{{\rm{\sigma}}_0}} \over {{\rm{\sigma}}_{\rm{c}}^{{\rm{at}}}}}} \right)^2}\quad .$$

(19)

For practical applications, N is replaced by the ratio of the size of each element to the lattice parameter in crack propagation direction, and Eq. (19) becomes

$${{\rm{\kappa}}_{{\rm{FE}}}} = 2\sqrt {{{{a_{{\rm{cd}}}}} \over {{r_{{\rm{FE}}}}}}} - 1.4{{{a_{{\rm{cd}}}}} \over {{r_{{\rm{FE}}}}}}\quad .$$

(20)

This results in a critical stress and a final displacement, which are both adjusted to the element size, as shown in Fig. 7(b).

It is noted that the directional dependence of the model parameters in Eq. (20) is artificially introduced by the scaling of the FE size with the atomic interplanar distance in the crack propagation direction. A proper directional dependence could be introduced by using a direction-sensitive energy release rate as WoS.

B. Application and validation

As an application of the novel scaling relation, we conducted FE fracture simulations for a linear elastic material representing tungsten to calculate the fracture toughness K_Ic. The numerical simulations have been performed using the commercial FE software ABAQUS. All simulations have been performed using an implicit time integration scheme. The surface-based CZ method is used to simulate fracture. The geometry of the model is the same as in the atomistic simulation [see Fig. 1(b)], whereas the ratio between the radius of the sample and the mesh at the crack tip is kept constant at 10,000. This is done to avoid the variation of results due to mesh-size variation in comparison to the sample size. This mesh size is applied to the area around crack tip up to 1% of the total size of the model and then increased gradually toward the outer boundary of the specimen to avoid too much computational cost. The geometry has been meshed with fully integrated 4-node quadratic elements with linear shape functions (CPE4) for the plane strain case. The mechanical boundary conditions have been applied as K_I-displacement field in a similar way as in the atomistic simulations. This is achieved by selecting the outermost nodes of the FE model and applying the boundary conditions to those nodes. Isotropic elastic constants, Young’s modulus E and Poisson ratio ν, were determined according to the elastic constants for the Wang potential in Table I, which yields E = 410 GPa and ν = 0.281.

A series of FE simulations has been performed for K_I loading using scaled parameters for the TS law according to different mesh sizes, i.e., the scaled critical stress ${{\rm{\tilde \sigma}}_{\rm{c}}}$, and the displacement at failure ${{\rm{\tilde \delta}}_{\rm{f}}}$ according to Eq. (20). The value for the initial slope of the TS law has been kept constant at 1.634 × 10⁵ GPa for all cases. The fracture toughness K_Ic is defined as the loading at which the first cohesive surface element breaks (δ ≥ δ_f).

In Fig. 8(a), it can be seen that the values of scaled critical stresses decrease over several orders of magnitude with the increasing mesh size. The values of final displacements (not shown) increases correspondingly to keep the cleavage energy (WoS) constant.

FIG. 8

(a) Scaling of the model parameter of the TS law with the mesh size. (b) Fracture toughness resulting from a FE simulation for a linear elastic material law with the properly scaled TS law (left ordinate axis) and with constant TS law (right ordinate axis) for the cohesive behavior.

Figure 8(b) shows the obtained values of K_Ic for different mesh sizes. The value K_Ic varies between 1.35 and 1.49 MPa m^1/2 over variation of mesh size by 5 orders of magnitude. The average of the K_Ic values over the range of mesh sizes is 1.45 MPa m^1/2, which is close to the atomistic value $K_{{\rm{Ic}}}^{{\rm{at}}} = 1.68$ MPa m^1/2. This is remarkable because there is no fitting of parameters, but rather a consistent scaling of the atomistic quantities according to the mesh size over a range of five orders of magnitude. It can be seen that there is no pronounced scatter around the average value in the sense of a pronounced mesh-size dependence. To emphasize the importance of our scaling procedure, the calculation of K_Ic with a constant TS law was also performed. In this case, the scaling is done only for the 10⁻⁷ m mesh and the same parameters for the TS law are used for the calculation of K_Ic with the 10⁻⁶ m mesh (4.59 MPa m^1/2) and the 10⁻⁴ m mesh (45.82 MPa m^1/2). It can be seen in Fig. 8(b) that in this case the critical stress intensity factor scales with the square root of the mesh size (or in other words, the size of the sample), in agreement with the observation of Bazant69 of K_Ic variation for self-similar geometries but different sizes.

IV. CONCLUSIONS

In the strong stress gradient ahead of the crack tip, the definition of mechanical stress is necessarily scale-dependent. Thus, only fundamental atomistic methods provide a rigorous way to define stress-related material properties, e.g., the fracture strength.

In this work, it is shown that the widely used approach to derive the critical bond separation stress from ab initio calculations of RBSs is well justified. To accomplish this, we have compared forces occurring in atomistic simulations of RBS with those at crack tips under K_I loading. The results demonstrate that they are indeed equivalent, which means that they are less environment-dependent than commonly expected. As a consequence, we can derive meaningful TS laws from much simpler model systems than from actual fracture simulations. This enables the use of computationally expensive, but quantitatively reliable methods such as ab initio DFT calculations.

Since the mesh sizes commonly used in continuum methods do not resolve the high atomistic stresses and the strong stress gradient at crack tips, we have introduced a physically meaningful approach to scale atomistic TS laws with the mesh size. It is based on the insight that the atomistically determined stresses ahead of the crack tip agree well with the prediction of LEFM. The approach defined in this work is based on properly averaging atomic forces over cohesive surface elements to convert them in mechanical stresses. This enables the use of fundamental atomistic material constants, such as theoretical strength, theoretical final separation, and work of separation as parameters in continuum fracture models.

It has also been demonstrated that the fracture toughness resulting from the thus-parameterized continuum model is independent of the mesh size, although numerical fluctuations occur. In this way, the atomistic data can be used directly to calculate TS parameters for continuum fracture models, such as CZ models or XFEM.

In our approach, the fracture model describes only the bond-breaking processes during cleavage; any additional (plastic) energy dissipation needs to be taken into account in the constitutive model of the material surrounding the crack. Therefore, the scaling method is ideally used in conjunction with micromechanical plasticity models or discrete dislocation dynamics simulations.

As ab initio tensile tests can be carried out using complex chemical compositions and including grain or interphase boundaries, the scheme enables the material-specific atomistically informed continuum modeling of fracture of engineering materials.