Modeling of phase transitions in three-phase polymorphic systems: Part I. Basic equations and example simulation

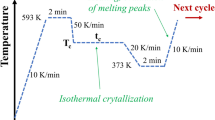
Abstract

Development of phase composition in one-component, three-phase systems containing a liquid phase (melt) and two polymorphic solids has been discussed. Two types of polymorphic systems have been analyzed: enantiotropic systems composed of three thermodynamically stable phases and monotropic systems with two stable and one metastable phase. Detailed relations between transition rates, molecular characteristics, and external conditions have been derived. Simulation of isothermal crystallization of a model system has been performed and discussed.

Appendix: Nucleation And Growth Of Cubic Clusters

Nucleation and crystal growth characteristics are based on the classical theory of Turnbull and Fisher,7 Lauritzen and Hoffman,8 Frank and Tosi,9 Frenkel,17 and Zeldovich.18 For the sake of simplicity, the aggregating kinetic units (atoms, molecules, chain segments) are assumed as cubes of volume ${v_0} = a_0^3$.

A1. Primary nucleation

Consider a cubic primary cluster of the target phase characterized by volume v = a3. Free enthalpy of cluster formation per unit volume of the target phase is

$$\Delta g = \left( {\Delta h - T\Delta s} \right) \cdot \gamma = {{\Delta h\gamma \left( {{T_{\rm{m}}} - T} \right)} \over {{T_{\rm{m}}}}}.$$

((A1))

The enthalpy density, ∆h, and entropy density, As, related to unit mass are assumed constants. γ denotes the density of the target phase. Following Refs. 17–19, nucleation is described as a motion of clusters in the continualized space of their volumes, v.

Free enthalpy of formation a cubic cluster with volume, v, from single kinetic elements includes a negative bulk term proportional to ∆g and a positive surface term proportional to interface tension σ

$$\Delta G\left( v \right) = \Delta g \cdot v + 6\sigma \cdot {v^{2/3}}.$$

((A2))

Differentiation of ∆G with respect to v yields characteristics of the thermodynamic barrier

$${{{{\partial \Delta G} \over {\partial v}} = 0\quad \Rightarrow \quad \left\{ {{{{v^*} = {{64{\sigma ^3}} \over {{{\left| {\Delta g} \right|}^3}}}} \;\;\;\; {\Delta {G^*} = {{32{\sigma ^3}} \over {\Delta {g^2}}}} \;\;\;\; } } \right.,} \;\;\;\; {{{{\partial ^2}\Delta G} \over {\partial {v^2}}} = {{ - 4\,\sigma {v^{ - 4/3}}} \over 3},} \;\;\;\; {{{\left. {{{{\partial ^2}\Delta G} \over {\partial {v^2}}}} \right|}_{{v^*}}} = {{ - \Delta {g^4}} \over {192\,{\sigma ^3}}},} \;\;\;\; {Z = \sqrt {{{ - 1} \over {2kT}}{{\left. {{{{\partial ^2}\Delta G} \over {\partial {v^2}}}} \right|}_{{v^*}}}} = {{\Delta {g^2}} \over {8\sqrt {6kT} {\sigma ^{3/2}}}}.} \;\;\;\; } $$

((A3))

Z, often called “Zeldovich factor,” results from expansion of the free enthalpy ∆G with respect to cluster volume v (cf. Eqs. A7 and A8 below).

Nucleation frequency is controlled by cluster-size distribution ρ(v) in the vicinity of v*. The function ρ(v) can be obtained from the continuity (diffusion) equation

(A4)

where j(v,t) denotes flux in the space of cluster volumes and D(v) denotes diffusion coefficient in this space. The boundary conditions include constant concentration of single kinetic units (v = v₀) and zero concentration of clusters larger than some maximum value v_max (assumed as 2v*).

The diffusion coefficient D related to absolute reaction rate theory20 is proportional to the frequency of thermal motions and to the number of sites on the surface of the growing cluster, P, available for aggregation-dissociation reactions. For a cube with edge a composed of small cubes each of edge a₀

$${{P\left( v \right)} \;\;\;\; = \;\;\;\; {{{6{a^2}} \over {a_0^2}} = 6{{\left( {{v \over {{v_0}}}} \right)}^{2/3}},} \;\;\;\; {D\left( v \right)} \;\;\;\; = \;\;\;\; {v_0^2P\left( v \right){{kT} \over h}{e^{{{ - {E_D}} \over {kT}}}} = 6{{\left( {{v \over {{v_0}}}} \right)}^{2/3}}v_0^2{{kT} \over h}{e^{{{^{ - {E_D}}} \over {kT}}}}.} \;\;\;\; } $$

((A5))

where E_D is activation energy of molecular motions. At the point of the maximum,

$$D\left( {{v^*}} \right) = {{96\,{\sigma ^2}v_0^{4/3}} \over {\Delta {g^2}}}{{kT} \over h}{e^{{{ - {E_D}} \over {kT}}}}.$$

((A6))

Expansion of the free enthalpy around v = v* yields

$${{{{\Delta G\left( v \right)} \over {kT}}} \;\;\;\; = \;\;\;\; {{{\Delta G\left( {{v^*}} \right)} \over {kT}} + {1 \over {kT}}{{\left. {\left( {{{\partial \Delta G} \over {\partial v}}} \right)} \right|}_{{v^*}}}\left( {v - {v^*}} \right)} \;\;\;\; {} \;\;\;\; {} \;\;\;\; { - {1 \over {2kT}}{{\left. {\left( {{{{\partial ^2}\Delta G} \over {\partial {v^2}}}} \right)} \right|}_{{v^*}}}{{\left( {v - {v^*}} \right)}^2} + \cdots \,.} \;\;\;\; } $$

((A7))

Considering disappearance of the linear term at v = v* and neglecting terms higher than quadratic

$${{\Delta G\left( v \right)} \over {kT}} \cong {{\Delta G\left( {{v^*}} \right)} \over {kT}} + {Z^2}{\left( {v - {v^*}} \right)^2}.$$

((A8))

Frenkel17 and Zeldovich18 arrived at the simple steadystate cluster distribution

(A9)

where erf(x) is error function. Frequency of primary nucleation, i.e., steady-state flux of clusters reaching critical size is obtained in the form

(A10)

and nucleation rate, i.e., the number of nuclei produced in unit time and unit volume

(A11)

A2. Growth of crystals. Secondary nucleation on crystal surface

In the classical theory of crystallization, crystal growth is implied as formation of secondary, 2D nuclei on crystal surface, followed by instantaneous spreading of the 2D nucleus to cover crystal face with a monomolecular layer. Secondary clusters with dimensions (a₀ × a × a) grow in the two lateral dimensions (a) parallel to crystal face. Formation of a secondary cluster with volume v_gr = a₀a2 is accompanied by the change of free enthalpy

$${{\Delta {G_{gr}}\left( {{v_{gr}}} \right)} \;\;\;\; = \;\;\;\; {\Delta g\,{a_0}{a^2} + 4\,\sigma \,{a_0}a} \;\;\;\; {} \;\;\;\; = \;\;\;\; {\Delta g\,{v_{gr}} + 4\,\sigma \,v_{gr}^{1/2}v_0^{1/6}.} \;\;\;\; } $$

((A12))

Differentiation with respect to cluster size, v_gr, yields

$${{{{\partial \Delta {G_{gr}}} \over {\partial {v_{gr}}}} = 0\quad \Rightarrow \,\left\{ {{{v_{gr}^* = {{4\,{\sigma ^2}v_0^{1/3}} \over {\Delta {g^2}}}} \;\;\;\; {\Delta G_{gr}^* = {{4\,{\sigma ^2}v_0^{1/3}} \over {\left| {\Delta g} \right|}}} \;\;\;\; },} \right.} \;\;\;\; {{{{\partial ^2}\Delta {G_{gr}}} \over {\partial v_{gr}^2}} = - \sigma \,v_0^{1/6}v_{gr}^{ - 3/2},} \;\;\;\; {{{\left. {{{{\partial ^2}\Delta {G_{gr}}} \over {\partial v_{gr}^2}}} \right|}_{v_{gr}^*}} = - {{{{\left| {\Delta g} \right|}^3}} \over {8\,{\sigma ^2}v_0^{1/3}}}} \;\;\;\; {{Z_{gr}} = \sqrt {{{ - 1} \over {2kT}}{{\left. {{{\partial {G_{gr}}} \over {\partial v_{gr}^2}}} \right|}_{v_{gr}^*}}} = {{{{\left| {\Delta g} \right|}^{3/2}}} \over {4\sqrt {kT} \sigma v_0^{1/6}}}.} \;\;\;\; } $$

((A13))

In an analogy to primary nucleation, steady-state flux of secondary clusters results in the form

(A14)

In isothermal, steady-state conditions, the distribution of secondary clusters reduces to

(A15)

The total number of sites available for additiondissociation reactions on the four growing faces (a × a₀) of the secondary cluster reads

$${P_{gr}}\left( {{v_{gr}}} \right) = {{4\,a} \over {{a_0}}} = 4{\left( {{{{v_{gr}}} \over {{v_0}}}} \right)^{1/3}}.$$

((A16))

and the diffusion coefficient, ${D_{gr}}\left( {v_{gr}^*} \right)$

$${D_{gr}}\left( {v_{gr}^*} \right) = v_0^2P\left( {v_{gr}^*} \right){{kT} \over h}{e^{{{ - {E_D}} \over {kT}}}} = {{8\,\sigma \,v_0^{5/3}} \over {\left| {\Delta g} \right|}}{{kT} \over h}{e^{{{ - {E_D}} \over {kT}}}}.$$

((A17))

Steady-state flux of secondary nuclei, ${j_{gr,st}}\left( {v_{gr}^*} \right)$ (nucleation frequency) results in the form

(A18)

Steady-state rate of secondary nucleation, Ṅ_gr,st, results in the form

(A19)

Each act of secondary nucleation leads to the creation of a monomolecular layer of thickness a₀ on crystal face. To obtain linear growth rate normal to crystal face, $\dot R$, frequency of secondary nucleation, ${j_{gr,st}}\left( {v_{gr}^*} \right)$, is multiplied by the increment of growth, i.e., thickness of the growth layer, ${a_0} = v_0^{1/3}$

(A20)

A3. Global transition rate characteristics

Combination of sporadic nucleation rate Ṅ_st from Eq. (A10) with 3D growth rate $\dot R$ from Eq. (A20) yields isothermal transition characteristic E^spc in the form

(A21)

The characteristic frequency based on sporadic nucleation is

(A22)

Similarly, the transition progress characteristic controlled by predetermined nucleation

(A23)

yields

(A24)

$v_{ij}^{{\rm<Prefix>e</Prefix>}}$ and $v_{ij}^{{\rm{spc}}}$ provide measures of isothermal transition rates “i” → “j.” After time t = 1/v_ij, (1/e) part of the source phase “i” is converted into the target phase “j.”