Abstract
The structure and dynamics of the solar corona is dominated by the magnetic field. In most areas in the corona magnetic forces are so dominant that all non-magnetic forces like plasma pressure gradient and gravity can be neglected in the lowest order. This model assumption is called the force-free field assumption, as the Lorentz force vanishes. This can be obtained by either vanishing electric currents (leading to potential fields) or the currents are co-aligned with the magnetic field lines. First we discuss a mathematically simpler approach that the magnetic field and currents are proportional with one global constant, the so-called linear force-free field approximation. In the generic case, however, the relation between magnetic fields and electric currents is nonlinear and analytic solutions have been only found for special cases, like 1D or 2D configurations. For constructing realistic nonlinear force-free coronal magnetic field models in 3D, sophisticated numerical computations are required and boundary conditions must be obtained from measurements of the magnetic field vector in the solar photosphere. This approach is currently of large interests, as accurate measurements of the photospheric field become available from ground-based (for example SOLIS) and space-born (for example Hinode and SDO) instruments. If we can obtain accurate force-free coronal magnetic field models we can calculate the free magnetic energy in the corona, a quantity which is important for the prediction of flares and coronal mass ejections. Knowledge of the 3D structure of magnetic field lines also help us to interpret other coronal observations, e.g., EUV images of the radiating coronal plasma.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The magnetic activity of the Sun has a high impact on Earth. As illustrated in Figure 1, large coronal eruptions like flares and coronal mass ejections can influence the Earth’s magnetosphere where they trigger magnetic storms and cause aurorae. These coronal eruptions have also harmful effects like disturbances in communication systems, damages on satellites, power cutoffs, and unshielded astronauts are in danger of life-threatening radiation.Footnote 1 The origin of these eruptive phenomena in the solar corona is related to the coronal magnetic field as magnetic forces dominate over other forces (like pressure gradient and gravity) in the corona. The magnetic field, created by the solar dynamo, couples the solar interior with the Sun’s surface and atmosphere. Reliable high accuracy magnetic field measurements are only available in the photosphere. These measurements, called vector magnetograms, provide the magnetic field vector in the photosphere.
To get insights regarding the structure of the coronal magnetic field we have to compute 3D magnetic field models, which use the measured photospheric magnetic field as the boundary condition. This procedure is often called “extrapolation of the coronal magnetic field from the photosphere”. In the solar corona the thermal conductivity is much higher parallel than perpendicular to the field so that field lines may become visible by the emission at appropriate temperatures. This makes in some sense magnetic field lines visible and allows us to test coronal magnetic field models. In such tests 2D projection of the computed 3D magnetic field lines are compared with plasma loops seen in coronal images. This mainly qualitative comparison cannot guarantee that the computed coronal magnetic field model and derived quantities, like the magnetic energy, are accurate. Coronal magnetic field lines which are in reasonable agreement with coronal images are, however, more likely to reproduce the true nature of the coronal magnetic field.
To model the coronal magnetic field B we have to introduce some assumptions. It is therefore necessary to get some a priori insights regarding the physics of the solar corona. An important quantity is the plasma β value, a dimensionless number which is defined as the ratio between the plasma pressure p and the magnetic pressure,
. Figure 2 from Gary (2001) shows how the plasma β value changes with height in the solar atmosphere. As one can see a region with β ≪ 1 is sandwiched between the photosphere and the upper corona, where β is about unity or larger. In regions with β ≪ 1 the magnetic pressure dominates over the plasma pressure (and as well over other non-magnetic forces like gravity and the kinematic plasma flow pressure). Here we can neglect in the lowest order all non-magnetic forces and assume that the Lorentz force vanishes. This approach is called the force-free field approximation and for static configurations it is defined as:
,
,
, or by inserting Equation (3) into (2):
,
. Equation (5) can be fulfilled either by:
or by
.
Plasma β model over active regions. The shaded area corresponds to magnetic fields originating from a sunspot region with 2500 G and a plage region with 150 G. The left and right boundaries of the shaded area are related to umbra and plage magnetic field models, respectively. Atmospheric regions magnetically connected to high magnetic field strength areas in the photosphere naturally have a lower plasma β. Image reproduced by permission from Figure 3 of Gary (2001), copyright by Springer.
Current free (potential) fields are the simplest assumption for the coronal magnetic field. The line-of-sight (LOS) photospheric magnetic field which is routinely measured with magnetographs are used as boundary conditions to solve the Laplace equation for the scalar potential φ,
, where the Laplacian operator Δ is the divergence of the gradient of the scalar field and
. When one deals with magnetic fields of a global scale, one usually assumes the so-called “source surface” (at about 2.5 solar radii where all field lines become radial): see, e.g., Schatten et al. (1969) for details on the potential-field source-surface (PFSS) model. Figure 3 shows such a potential-field source-surface model for May 2001 from Wiegelmann and Solanki (2004).
Global potential field reconstruction. Image reproduced by permission from Wiegelmann and Solanki (2004), copyright by ESA.
Potential fields are popular due to their mathematical simplicity and provide a first coarse view of the magnetic structure in the solar corona. They cannot, however, be used to model the magnetic field in active regions precisely, because they do not contain free magnetic energy to drive eruptions. Further, the transverse photospheric magnetic field computed from the potentialfield assumption usually does not agree with measurements and the resulting potential field lines do deviate from coronal loop observations. For example, a comparison of global potential fields with TRACE images by Schrijver et al. (2005) and with stereoscopically-reconstructed loops by Sandman et al. (2009) showed large deviations between potential magnetic field lines and coronal loops.
The B ‖ ∇ × B condition can be rewritten as
,
, where α is called the force-free parameter or force-free function. From the horizontal photospheric magnetic field components (Bx0, By0) we can compute the vertical electric current density
and the corresponding distribution of the force-free function α(x, y) in the photosphere
. Condition (12) has been derived by taking the divergence of Equation (11) and using the solenoidal condition (4). Mathematically, Equations (11) and (12) are equivalent to Equations (2) – (4). Parameter α can be a function of position, but Equation (12) requires that α be constant along a field line. If α is constant everywhere in the volume under consideration, the field is called linear force-free field (LFFF), otherwise it is nonlinear force-free field (NLFFF). Equations (11) and (12) constitute partial differential equations of mixed elliptic and hyperbolic type. They can be solved as a well-posed boundary value problem by prescribing the vertical magnetic field and for one polarity the distribution of α at the boundaries. As shown by Bineau (1972) these boundary conditions ensure the existence and unique NLFFF solutions at least for small values of α and weak nonlinearities. Boulmezaoud and Amari (2000) proved the existence of solutions for a simply and multiply connected domain. As pointed out by Aly and Amari (2007) these boundary conditions disregard part of the observed photospheric vector field: In one polarity only the curl of the horizontal field (Equation (13)) is used as the boundary condition, and the horizontal field of the other polarity is not used at all. For a general introduction to complex boundary value problems with elliptic and hyperbolic equations we refer to Kaiser (2000).
Please note that high plasma β configurations are not necessarily a contradiction to the forcefree condition (see Neukirch, 2005, for details). If the plasma pressure is constant or the pressure gradient is compensated by the gravity force (∇p = ρ∇Ψ, where ρ is the mass density and Ψ the gravity potential of the Sun) a high-β configuration can still be consistent with a vanishing Lorentz force of the magnetic field. In this sense a low plasma β value is a sufficient, but not a necessary criterion for the force-free assumption. In the generic case, however, high plasma β configurations will not be force-free and the approach of the force-free field is limited to the upper chromosphere and the corona (up to about 2.5R⊙).
2 Linear Force-Free Fields
Linear force-free fields are characterized by
,
, where the force-free parameter α is constant. Taking the curl of Equation (15) and using the solenoidal condition (16) we derive a vector Helmholtz equation:
which can be solved by a separation ansatz, a Green's function method (Chiu and Hilton, 1977) or a Fourier method (Alissandrakis, 1981). These methods can also be used to compute a potential field by choosing α = 0.
For computing the solar magnetic field in the corona with the linear force-free model one needs only measurements of the LOS photospheric magnetic field. The force-free parameter α is a priori unknown and we will discuss later how α can be approximated from observations. Seehafer (1978) derived solutions of the linear force-free equations (local Cartesian geometry with (x, y) in the photosphere and z is the height from the Sun's surface) in the form:
,
,
, with \(\lambda _{mn} = \pi ^2 \left( {m^2 /L_x^2 + n^2 /L_y^2 } \right)\) and \(r_{mn} = \sqrt {\lambda _{mn} - \alpha ^2 } \).
As the boundary condition, the method uses the distribution of Bz(x, y) on the photosphere z = 0. The coefficients Cmn can be obtained by comparing Equation (20) for z = 0 with the magnetogram data. In practice, Seehafer's (1978) method is used for calculating the linear force-free field (or potential field for α = 0) for a given magnetogram (e.g., MDI on SOHO) and a given value of α as follows. The observed magnetogram which covers a rectangular region extending from 0 to Lx in x and 0 to Ly in y is artificially extended onto a rectangular region covering -Lx to Lx and -Ly to Ly by taking an antisymmetric mirror image of the original magnetogram in the extended region, i.e.,
. This makes the total magnetic flux in the whole extended region to be zero. (Alternatively one may pad the extended region with zeros, although in this case the total magnetic flux may be non-zero.) The coefficients Cmn are derived from this enlarged magnetogram with the help of a Fast Fourier Transform. In order for rmn to be real and positive so that solutions (18) – (20) do not diverge at infinity, α2 should not exceed the maximum value for given Lx and Ly,
Usually, α is normalized by the harmonic mean L of Lx and Ly defined by
. For Lx = Ly we have L = Lx = Ly. With this normalization the values of α fall into the range \( - \sqrt 2 \pi < \alpha < \sqrt 2 \pi \).
2.1 How to obtain the force-free parameter α
Linear force-free fields require the LOS magnetic field in the photosphere as input and contain a free parameter α. One possibility to approximate α is to compute an averaged value of α from the measured horizontal photospheric magnetic fields as done, e.g., in Pevtsov et al. (1994), Wheatland (1999), Leka and Skumanich (1999), and Hagino and Sakurai (2004), where Hagino and Sakurai (2004) calculated an averaged value \(\alpha = \Sigma \mu _0 J_z sign(B_z )/\Sigma \left| {B_z } \right|\). The vertical electric current in the photosphere is computed from the horizontal photospheric field as \(J_z = \frac{1} {{\mu _0 }}\left( {\frac{{\partial B_y }} {{\partial x}} - \frac{{\partial B_x }} {{\partial y}}} \right)\). Such approaches derive best fits of a linear force-free parameter .. with the measured horizontal photospheric magnetic field.
Alternative methods use coronal observations to find the optimal value of α. This approach usually means that one computes several magnetic field configurations with varying values of α in the allowed range and to compute the corresponding magnetic field lines. The field lines are then projected onto coronal plasma images. A method developed by Carcedo et al. (2003) is shown in Figure 4. In this approach the shape of a number of field lines with different values of α, which connect the foot point areas (marked as start and target in Figure 4(e)) are compared with a coronal image. For a convenient quantitative comparison the original image shown in Figure 4(a) is converted to a coordinate system using the distances along and perpendicular to the field line, as shown in Figure 4(b). For a certain number of N points along this uncurled loop the perpendicular intensity profile of the emitting plasma is fitted by a Gaussian profile in Figure 4(c) and the deviation between field line and loops are measured in Figure 4(d). Finally, the optimal linear force-free value of α is obtained by minimizing this deviation with respect to α, as seen in Figure 4(f). The method of Carcedo et al. (2003) has been developed mainly with the aim of computing the optimal α for an individual coronal loop and involves several human steps, e.g., identifying an individual loop and its footpoint areas and it is required that the full loop, including both footpoints, is visible. This makes it somewhat difficult to apply the method to images with a large number of loops and when only parts of the loops are visible. For EUV loops it is also often not possible to identify both footpoints. These shortcomings can be overcome by using feature recognition techniques, e.g., as developed in Aschwanden et al. (2008a) and Inhester et al. (2008) to extract one-dimensional curve-like structures (loops) automatically out of coronal plasma images. These identified loops can then be directly compared with the projections of the magnetic field lines, e.g., by computing the area spanned between the loop and the field line as defined in Wiegelmann et al. (2006b). This method has become popular in particular after the launch of the two STEREO spacecraft in October 2006 (Kaiser et al., 2008). The projections of the 3D linear force-free magnetic field lines can be compared with images from two vantage viewpoints as done for example in Feng et al. (2007b,a). This automatic method applied to a number of loops in one active region revealed, however, a severe shortcoming of linear force-free field models. The optimal linear force-free parameter α varied for different field lines, which is a contradiction to the assumption of a linear model. A similar result was obtained by Wiegelmann and Neukirch (2002) who tried to fit the loops stereoscopically reconstructed by Aschwanden et al. (1999). On the other hand, Marsch et al. (2004) found in their example that one value of α was sufficient to fit several coronal loops. Therefore, the fitting procedure tells us also whether an active region can be described consistently by a linear force-free field model: Only if the scatter in the optimal α values among field lines is small, one has a consistent linear force-free field model which fits coronal structures. In the generic case that α changes significantly between field lines, one cannot obtain a self-consistent force-free field by a superposition of linear force-free fields, because the resulting configurations are not force-free. As pointed out by Malanushenko et al. (2009) it is possible, however, to estimate quantities like twist and loop heights with an error about of 15% and 5%, respectively. The price one has to pay is using a model that is not self-consistent.
Low and Lou's (1990) analytic nonlinear force-free equilibrium. The original 2D equilibrium is invariant in ϕ, as shown in panel a. Rotating the 2D-equilibrium and a transformation to Cartesian coordinates make this symmetry less obvious (panels b.d), where the equilibrium has been rotated by an angle of \(\phi = \frac{\pi } {8},\frac{\pi } {4}, and \frac{\pi } {2}\), respectively. The colour-coding corresponds to the vertical magnetic field strength in G (gauss) in the photosphere (z = 0 in the model) and a number of arbitrary selected magnetic field lines are shown in yellow.
3 Analytic or Semi-Analytic Approaches to Nonlinear Force-Free Fields
Solving the nonlinear force-free equations in full 3-D is extremely difficult. Configurations with one or two invariant coordinate(s) are more suitable for an analytic or semi-analytic treatment. Solutions in the form of an infinitely long cylinder with axial symmetry are the simplest cases, and two best known examples are Lundquist's (1950) solution in terms of Bessel functions (α = constant), and a solution used by Gold and Hoyle (1960) in their flare model (α ≠ constant, all field lines have the same pitch in the direction of the axis). Low (1973) considered a 1D Cartesian (slab) geometry and analyzed slow time evolution of the force-free field with resistive diffusion.
In Cartesian 2D geometry with one ignorable coordinate in the horizontal (depth) direction, one ends up with a second-order partial differential equation, called the Grad-Shafranov equation in plasma physics. The force-free Grad-Shafranov equation is a special case of the Grad-Shafranov equation for magneto-static equilibria (see Grad and Rubin, 1958), which allow to compute plasma equilibria with one ignorable coordinate, e.g., a translational, rotational or helical symmetry. For an overview on how the Grad-Shafranov equation can be derived for arbitrary curvilinear coordinates with axisymmetry we refer to (Marsh, 1996, Section 3.2.). In the Cartesian case one finds (see, e.g., Sturrock, 1994, Section 13.4)
, where the magnetic flux function A depends only on two spatial coordinates and any choice of f(A) generates a solution of a magneto-static equilibrium with symmetry. For static equilibria with a vanishing plasma pressure gradient the method naturally provides us force-free configurations. A popular choice for the generating function is an exponential ansatz, see, e.g., Low (1977), Birn et al. (1978), and Priest and Milne (1980). The existence of solutions (sometimes multiple, sometimes none) and bifurcation of a solution sequence have been extensively investigated (e.g., Birn and Schindler, 1981). We will consider the Grad-Shafranov equation in spherical polar coordinates in the following.
3.1 Low and Lou’s (1990) equilibrium
As an example we refer to Low and Lou (1990), who solved the Grad-Shafranov equation in spherical coordinates (r, θ, ϕ) for axisymmetric (invariant in ϕ) nonlinear force-free fields. In this case the magnetic field is assumed to be written in the form
, where A is the flux function, and Q represents the ϕ-component of the magnetic field B, which depends only on A. This ansatz automatically satisfies the solenoidal condition (6), and the force-free equation (5) reduces to a Grad-Shafranov equation for the flux function A
, where μ = cos θ. Low and Lou (1990) looked for solutions in the form
with a separation ansatz
. Here n and λ are constants and n is not necessarily an integer; n = 1 and λ = 0 corresponds to a dipole field. Then Equation (23) reduces to an ordinary differential equation for P(μ), which can be solved numerically. Either by specifying n or λ, the other is determined as an eigenvalue problem (Wolfson, 1995).The solution in 3D space is axisymmetric and has a point source at the origin. This symmetry is also visible after a transformation to Cartesian geometry as shown in Figure 5(a). The symmetry becomes less obvious, however, when the symmetry axis is rotated with respect to the Cartesian coordinate axis; see Figures 5(b)–(d). The resulting configurations are very popular for testing numerical algorithms for a 3D NLFFF modeling. For such tests the magnetic field vector on the bottom boundary of a computational box is extracted from the semi-analytic Low-Lou solution and used as the boundary condition for numerical force-free extrapolations. The quality of the reconstructed field is evaluated by quantitative comparison with the exact solution; see, e.g., Schrijver et al. (2006). Similarly one can shift the origin of the point source with respect to the Sun center and the solution is not symmetric to the Sun's surface and can be used to test spherical codes.
3.2 Titov-Démoulin equilibrium
Another approach for computing axisymmetric NLFFF solutions has been developed in Titov and Démoulin (1999). This model active region contains a current-carrying flux-tube, which is imbedded into a potential field. A motivation for such an approach is that solar active regions may be thought of as composed of such flux tubes. The method allows to study a sequence of force-free configurations through which the flux tube emerges. Figure 6 shows how the equilibrium is built up. The model contains a symmetry axis, which is located at a distance d below the photosphere. A line current I0 runs along this symmetry axis and creates a circular potential magnetic field. This potential field becomes disturbed by a toroidal ring current I with the minor radius a and the major radius R, where a ≪ R is assumed. Two opposite magnetic monopoles of strength q are placed on the axis separated by distance L. These monopoles are responsible for the poloidal potential field. This field has its field lines overlying the force-free current and stabilizes the otherwise unstable configuration. Depending on the choice of parameters one can contain stable or unstable nonlinear force-free configurations. The unstable branch of this equilibrium has been used to study the onset of coronal mass ejections; see Section 5.5. Stable branches of the Titov-Démoulin equilibrium are used as a challenging test for numerical NLFFF extrapolation codes (see, e.g., Wiegelmann et al., 2006a; Valori et al., 2010).
4 Azimuth Ambiguity Removal and Consistency of Field Measurements
4.1 How to derive vector magnetograms?
NLFFF extrapolations require the photospheric magnetic field vector as input. Before discussing how this vector can be extrapolated into the solar atmosphere, we will address known problems regarding the photospheric field measurements. Vector magnetographs are being operated daily at NAOJ/Mitaka (Sakurai et al., 1995), NAOC/Huairou (Ai and Hu, 1986), NASA/MSFC (Hagyard et al., 1982), NSO/Kitt Peak (Henney et al., 2006), and U. Hawaii/Mees Observatory (Mickey et al., 1996), among others. The Solar Optical Telescope (SOT; Tsuneta et al., 2008) on the Hinode mission has been taking vector magnetograms since 2006. Full-disk vector magnetograms are observed routinely since 2010 by the Helioseismic and Magnetic Imager (HMI; Scherrer et al. (2012)) onboard the Solar Dynamics Observatory (SDO). Measurements with these vector magnetographs provide us eventually with the magnetic field vector on the photosphere, say Bz0 for the vertical and Bx0 and By0 for the horizontal fields. Deriving these quantities from measurements is an involved physical process based on the Zeeman and Hanle effects and the related inversion of Stokes profiles (e.g., LaBonte et al., 1999). Within this work we only outline the main steps and refer to del Toro Iniesta and Ruiz Cobo (1996), del Toro Iniesta (2003), and Landi Degl'Innocenti and Landolfi (2004) for details. Actually measured are polarization degrees across magnetically sensitive spectral lines, e.g., the line pair Fe i 6302.5 and 6301.5 .A as used on Hinode/SOT (see Lites et al., 2007) or Fe i 6173.3 Å as used on SDO/HMI (see Schou et al., 2012). The accuracy of these measurements depends on the spectral resolution, for example the HMI instruments measures at six points in the Fe i 6173.3 Å absorption line. In a subsequent step the Stokes profiles are inverted to derive the magnetic field strength, its inclination and azimuth. One possibility to carry out the inversion (see Lagg et al., 2004) is to fit the measured Stokes profiles with synthetic ones derived from the Unno.Rachkovsky solutions (Unno, 1956; Rachkovsky, 1967). Usually one assumes a simple radiative transfer model like the Milne-Eddington atmosphere (see, e.g., Landi Degl'Innocenti, 1992) in order to derive the analytic Unno-Rachkovsky solutions. The line-of-sight component of the field is approximately derived by Bl ∝ V/I, where V is the circular polarization and I the intensity (the so-called weak-field approximation). The error from photon noise is approximately \(\delta B\ell \propto \frac{{\delta V}} {I}\), where δ corresponds to noise in the measured and derived quantities. As a rule of thumb, δV/I ∼ 10-3 and δ Be ∼ a few gauss (G) in currently operating magnetographs. The horizontal field components can be approximately derived from the linear polarization Q and U as \(B_t^2 \propto \sqrt {Q^2 + U^2 } /I\). The error in δ Bt is estimated as \(B_t \delta B_t \propto \frac{{Q\delta Q + U\delta U}} {{\sqrt {Q^2 + U^2 } I}}\) from which the minimum detectable Bt(δ Bt ∼ is proportional to the square root of the photon noise \(\approx \sqrt {\delta Q^2 + \delta U^2 } /I \approx \sqrt {\delta V/I}\) namely around a few tens of G, one order of magnitude higher than δ Bl (Although δBt scales as 1/Bt and gives much smaller δBt for stronger Bt, one usually assumes a conservative error estimate that δ Bt ∼ a few tens of G regardless of the magnitude of Bt)
Additional complications occur when the observed region is far away from the disk center and consequently the line-of-sight and vertical magnetic field components are far apart (see Gary and Hagyard, 1990, for details). The inverted horizontal magnetic field components Bx0 and By0 cannot be uniquely derived, but contain a 180° ambiguity in azimuth, which has to be removed before the fields can be extrapolated into the corona. In the following, we will discuss this problem briefly. For a more detailed review and a comparison and performance check of currently available ambiguity-removal routines with synthetic data, see Metcalf et al. (2006).
To remove the ambiguity from this kind of data, some a priori assumptions regarding the structure of the magnetic field vector are necessary, e.g., regarding smoothness. Some methods require also an approximation regarding the 3D magnetic field structure (usually from a potential field extrapolation); for example to minimize the divergence of magnetic field vector or the angle with respect to the potential field. We are mainly interested here in automatic methods, although manual methods are also popular, e.g., the AZAM code. If we have in mind, however, the huge data stream from SDO/HMI, fully automatic methods are desirable. In the following, we will give a brief overview on the ambiguity removal techniques and tests with synthetic data.
4.2 Quantitative comparison of ambiguity removal algorithms
Metcalf et al. (2006) compared several algorithms and implementations quantitatively with the help of two synthetic data sets, a flux-rope simulation by Fan and Gibson (2004) and a multipolar constant-α structure computed with the Chiu and Hilton (1977) linear force-free code. The results of the different ambiguity removal techniques have been compared with a number of metrics (see Table II in Metcalf et al., 2006). For the discussion here we concentrate only on the first test case (flux rope) and the area metrics, which simply tells for what fraction of pixels the ambiguity has been removed correctly. A value of 1 corresponds to a perfect result and 0.5 to random. The result is visualized in Figure 7, where the ambiguity has been removed correctly in black areas. Wrong pixels are white. In the following, we briefly describe the basic features of these methods and provide the performance (fraction of pixels with correctly removed ambiguity).
4.3 Ambiguity removal algorithm
4.3.1 Acute angle methods
The magnetic field in the photosphere is usually not force-free and even not current-free, but an often made assumption is that from two possible directions (180° apart) of the observed field Bobs, the solution with the smaller angle to the potential field (or another suitable reference field) B0 is the more likely candidate for the true field. Consequently, we get for the horizontal/transverseFootnote 2 field components Bt the condition
. This condition is easy to implement and fast in application. In Metcalf et al. (2006) several different implementations of the acute angle method are described, which mainly differ by the algorithms used to compute the reference field. The different implementations of the acute angle methods got a fraction of 0.64 – 0.75 pixels correct (see Figure 7, panels marked with NJP, YLP, KLP, BBP, JLP, and LSPM).
Overview of the performance of different algorithms for removing the 180° azimuth ambiguity. The codes have been applied to synthetic data (a flux-rope simulation by Fan and Gibson, 2004). In black areas the codes found the correct azimuth and in white areas not. Image reproduced by permission from Figure 3 of Metcalf et al. (2006), copyright by Springer.
4.3.2 Improved acute angle methods
A sophistication of the acute angle method uses linear force-free fields (Wang, 1997; Wang et al., 2001), where the optimal force-free parameter α is chosen to maximize the integral
where Blff is the linear force-free reference field. A fraction of 0.87 pixels has been identified correctly (see Figure 7 second row, right panel marked with HSO).
Another approach, dubbed uniform shear method by Moon et al. (2003) uses the acute angle method (with a potential field as reference) only as a first approximation and subsequently uses this result to estimate a uniform shear angle between the observed field and the potential field. Then the acute angle method is applied again to resolve the ambiguity, taking into account the average shear angle between the observed field and the calculated potential field. A fraction of 0.83 pixels has been identified correctly. Consequently both methods significantly improve the potential-field acute angle method (see Figure 7 third row, center panel marked with USM).
4.3.3 Magnetic pressure gradient
The magnetic pressure gradient method (Cuperman et al., 1993) assumes a force-free field and that the magnetic pressure B2/2 decreases with height. Using the solenoidal and force-free conditions, we can compute the vertical magnetic pressure gradient as:
with any initial choice for the ambiguity of the horizontal magnetic field components (Bx,By). Different solutions of the ambiguity removal method give the same amplitude, but opposite sign for the vertical pressure gradient. If the vertical gradient becomes positive, then the transverse field vector is reversed. For the test this method got a fraction of 0.74 pixels correct, which is comparable with the potential-field acute angle method (see Figure 7 forth row, left panel marked with MS).
4.3.4 Structure minimization method
The structure minimization method (Georgoulis et al., 2004) is a semi-analytic method which aims at eliminating dependencies between pixels. We do not describe the method here, because in the test only for a fraction of 0.22 pixels the ambiguity has been removed correctly, which is worse than a random result (see Figure 7 third row, right panel marked with MPG).
4.3.5 Non-potential magnetic field calculation method
The non-potential magnetic field method developed by Georgoulis (2005) is identical with the acute angle method close to the disk center. Away from the disk center the method is more sophisticated and uses the fact that the magnetic field can be represented as a combination of a potential field and a non-potential part B = Bp + Bc, where the non-potential part Bc is horizontal on the boundary and only Bc contains electric currents. The method aims at computing a fair a priori approximation of the electric current density before the ambiguity removal. With the help of a Fourier method the component Bc and the corresponding approximate field B are computed. This field is then used as the reference field for an acute angle method. The quality of the reference field depends on the accuracy of the a priori assumed electric current density jz. In the original implementation by Georgoulis (2005) jz was chosen once a priori and not changed afterwards. In an improved implementation (published as part of the comparison paper by Metcalf et al. (2006) and implemented by Georgoulis) jz becomes updated in an iterative process. The original implementation got 0.70 pixels correct and the improved version 0.90 (see Figure 7 forth row, center and right panels marked with NPFC and NPFC2, respectively). So the original method is on the same level as the potential-field acute angle method, but the current iteration introduced in the updated method gives significantly better results. This method has been used for example to resolve the ambiguity of full-disk vector magnetograms from the SOLIS instrument (Henney et al., 2006) at NSO/Kitt Peak.
4.3.6 Pseudo-current method
The pseudo-current method developed by Gary and Démoulin (1995) uses as the initial step the potential-field acute angle method and subsequently applies this result to compute an approximation for the vertical electric current density. The current density is then approximated by a number of local maxima of jz. with an analytic expression containing free model parameters, which are computed by minimizing a functional of the square of the vertical current density. This optimized current density is then used to compute a correction to the potential field. This new reference field is then used in the acute angle method to resolve the ambiguity. In the test case this method got a fraction of 0.78 of pixels correct, which is only slightly better than the potential-field acute angle method (see Figure 7 fifth row, left panel marked with PCM).
4.3.7 U. Hawai’i iterative method
This method, originally developed in Canfield et al. (1993) and subsequently improved by a group of people at the Institute for Astronomy, U. Hawai'i. As the initial step the acute angle method is applied, which is then improved by a constant-.. force-free field, where .. has to be specified by the user (in principle it should also be possible to apply an automatic ..-fitting method as discussed in Section 4.3.2). Therefore, the result would be similar to the improved acute angle methods, but additional two more steps have been introduced for a further improvement. In a subsequent step the solution is smoothed (minimizing the angle between neighboring pixels) by starting at a location where the field is radial and the ambiguity is obvious, e.g., the umbra of a sunspot. Finally also the magnetic field divergence or vertical electric current density is minimized. This code includes several parameters, which have to be specified by the user. In the test case the code recognized a fraction of 0.97 pixels correctly. So the additional steps beyond the improved acute angle method provide another significant improvement and almost the entire region has been correctly identified (see Figure 7 fifth row, center panel marked with UHIM).
4.3.8 Minimum energy methods
The minimum energy method has been developed by Metcalf (1994). As other sophisticated methods it uses the potential-field acute angle method as the initial step. Subsequently a pseudo energy, which is defined as a combination of the magnetic field divergence and electric current density, is minimized. In the original formulation the energy was defined as \(E = \sum {(|\nabla \cdot B| + |j|)} \), which was slightly modified to
in an updated version. For computing jx, jy, and ∂Bz/∂z, a linear force-free model is computed, in the same way as described in Section 4.3.7. The method minimizes the functional (29) with the help of a simulated annealing method, which is a robust algorithm to find a global minimum. In a recent update (published in Metcalf et al., 2006) the (global) linear force-free assumption has been relaxed and replaced by local linear force-free assumptions in overlapping parts of the magnetogram. The method was dubbed nonlinear minimum energy method, although it does not use true NLFF fields (would be too slow) for computing the divergence and electric currents. The original linear method got a fraction of 0.98 of pixels correctly and the nonlinear minimum energy method even 1.00. Almost all pixels have been correct, except a few on the boundary (see Figure 7 fifth row, right panel and last row left panel, marked with ME1 and ME2, respectively.) Among the fully automatic methods this approach had the best performance on accuracy. A problem for practical use of the method was that it is very slow, in particular for the nonlinear version. Minimum energy methods are routinely used to resolve the ambiguity in active regions as measured, e.g., with SOT on Hinode or HMI on SDO.
4.4 Summary of automatic methods
The potential-field acute angle method is easy to implement and fast, but its performance of 0.64 – 0.75 is relatively poor. The method is, however, very important as an initial step for more sophisticated methods. Using more sophisticated reference fields (linear force-free fields, constant shear, non-potential fields) in the acute angle method improves the performance to about 0.83 – 0.90. Linear force-free or similar fields are a better approximation to a suitable reference field, but the corresponding assumptions are not fulfilled in a strict sense, which prevents a higher performance. The magnetic pressure gradient and pseudo-current methods are more difficult to implement as simple acute angle methods, but do not perform significantly better. A higher performance is prevented, because the basic assumptions are usually not fulfilled in the entire region. For example, the assumption that the magnetic pressure always decreases with height is not fulfilled over bald patches (Titov et al., 1993). The multi-step U. Hawai’i iterative method and the minimum energy methods showed the highest performance of > 0.97. The pseudo-current method is in principle similar to the better performing minimum energy methods, but due to several local minima it is not guaranteed that the method will always find the global minimum. Let us remark that Metcalf et al. (2006) introduced more comparison metrics, which, however, do not influence the relative rating of the discussed ambiguity algorithms. They also carried out another test case using the Chiu and Hilton (1977) linear force-free model, for which most of the codes showed an absolutely better performance, but again this does hardly influence the relative performance of the different methods. One exception was the improved non-potential magnetic field algorithm, which performed with similar excellence as the minimum energy and U. Hawai’i iterative methods. Consequently these three methods are all suitable candidates for application to data. It is, however, not entirely clear to what extent these methods can be applied to full-disk vector magnetograms and what kind of computer resources are required.
4.4.1 Effects of noise and spatial resolution
The comparison of ambiguity removal methods started in Metcalf et al. (2006) has been continued in Leka et al. (2009). The authors investigated the effects of Poisson photon noise and a limited spatial resolution. It was found that most codes can deal well with random noise and the ambiguity resolution results are mainly affected locally, but bad solutions (which are locally wrong due to noise) do not propagate within the magnetogram. A limited spatial resolution leads to a loss of information about the fine structure of the magnetic field and erroneous ambiguity solutions. Both photon noise and binning to a lower spatial resolution can lead to artificial vertical currents. The combined effect of noise and binning affect the computation of a reference magnetic field used in acute angle methods as well as quantities in minimization approaches like the electric current density and ∇ · B. Sophisticated methods based on minimization schemes performed again best in the comparison of methods and are more suitable to deal with the additional challenges of noise and limited resolution. As a consequence of these results Leka et al. (2009) suggested that one should use the highest possible resolution for the ambiguity resolution task and if binning of the data is necessary, this should be done only after removing the ambiguity. Recently Georgoulis (2012) challenged their conclusion that the limited spatial resolution was the cause of the failure of ambiguity removal techniques using potential or non-potential reference fields. Georgoulis (2012) pointed out that the failure was caused by a non-realistic test-data set and not by the limited spatial resolution. This debate has been continued in a reply by Leka et al. (2012). We aim to follow the ongoing debate and provide an update on this issue in due time.
4.4.2 HAO AZAM method
This is an interactive tool, which needs human intervention for the ambiguity removal. In the test case, which has been implemented and applied by Bruce Lites, all pixels have been identified correctly. It is of course difficult to tell about the performance of the method, but only about a human and software combination. For some individual or a few active regions the method might be appropriate, but not for a large amount of data.
4.4.3 Ambiguity removal methods using additional observations
The methods described so far use as input the photospheric magnetic field vector measured at a single height in the photosphere. If additional observations/measurements are available they can be used for the ambiguity removal. Measurements at different heights in order to solve the ambiguity problem have been proposed by Li et al. (1993) and revisited by Li et al. (2007). Knowledge of the magnetic field vector at two heights allows us to compute the divergence of the magnetic field and the method was dubbed divergence-free method. The method is non-iterative and thus fast. Li et al. (2007) applied the method to the same flux-rope simulation by Fan and Gibson (2004) as discussed in the examples above, and the method recovered about a fraction of 0.98 pixels correctly. The main shortcoming of this method is certainly that it can be applied only if vector magnetic field measurements at two heights are available, which is unfortunately not the case for most current data sets.
Martin et al. (2008) developed the so-called chirality method for the ambiguity removal, which takes additional observations into account, e.g., H.., EUV, or X-ray images. Such images are used to identify the chirality in solar features like filaments, fibrils, filament channels, or coronal loops. Martin et al. (2008) applied the method to different solar features, but to our knowledge the method has not been tested with synthetic data, where the true solution of the ambiguity is known. Therefore, unfortunately one cannot compare the performance of this method with the algorithms described above. It is also now obvious that fully automatic feature recognition techniques to identify the chirality from observed images need to be developed.
After the launch of Solar Orbiter additional vector magnetograms will become available from above the ecliptic. Taking these observations from two vantage positions combined is expected to be helpful for the ambiguity resolution. If separated by a certain angle, the definition of line-of-sight field and transverse field will be very different from both viewpoints. Removing the ambiguity should be a straightforward process by applying the transformation to vertical and horizontal fields on the photosphere from both viewpoints separately. If the wrong azimuth is chosen, then both solutions will be very different and the ambiguity can be removed by simply checking the consistency between vertical and horizontal fields from both observations.
4.5 Derived quantities, electric currents, and α
The well-known large uncertainties in the horizontal magnetic field component, in particular in weak field regions (see Section 4.1), cause large errors when computing the electric current density with finite differences via Equation (13). Even more critical is the computation of α with Equation (14) in weak field regions and in particular along polarity inversion lines (see, e.g., Cuperman et al., 1991). The nonlinear force-free coronal magnetic field extrapolation is a boundary value problem. As we will see later, some of the NLFFF codes make use of Equation (14) to specify the boundary conditions while other methods use the photospheric magnetic field vector more directly to extrapolate the field into the corona.
4.6 Consistency criteria for force-free boundary conditions
After Stokes inversion (see Section 4.1) and azimuth ambiguity removal, we derive the photospheric magnetic field vector. Unfortunately there might be a problem, when we want to use these data as the boundary condition for NLFFF extrapolations. Due to Metcalf et al. (1995), the solar magnetic field is not force-free in the photosphere (finite β plasma), but becomes force-free only at about 400 km above the photosphere. This is also visible in Figure 2 from Gary (2001), which shows the distribution of the plasma β value with height. Consequently, the assumption of a force-free magnetic field is not necessarily justified in the photosphere. Unless we have information on the magnetic flux through the lateral and top boundaries, we have to assume that the photospheric magnetic flux is balanced
, which is usually the case when taking an entire active region as the field-of-view.
In the following, we review some necessary conditions the magnetic field vector has to fulfill in order to be suitable as boundary conditions for NLFFF extrapolations. Molodenskii (1969); Molodensky (1974) and Aly (1989) defined several integral relations, which are related to two moments of the magnetic stress tensor.
-
1.
The first moment corresponds to the net magnetic force, which has to vanish on the boundary:
$$\int_S {B_x B_z dx dy} = \int_S {B_y B_z dx dy = 0}$$((31)),
$$\int_S {\left( {B_x^2 + B_y^2 } \right)dx dy} = \int_S {B_z^2 dx dy}$$((32)).
-
2.
The second moment corresponds to a vanishing torque on the boundary:
$$\int_S {x\left( {B_x^2 + B_y^2 } \right)dx dy} = \int_S {xB_z^2 dx dy}$$((33)),
$$\int_S {y\left( {B_x^2 + B_y^2 } \right)dx dy} = \int_S {yB_z^2 dx dy}$$((34)),
$$\int_S {yB_x B_z dx dy} = \int_S {xB_y B_z dx dy}$$((35)).
The total energy of a force-free configuration can be estimated directly from boundary conditions with the help of the virial theorem (see, e.g., Aly, 1989, for a derivation of this formula)
. For Equation (36) to be applicable, the boundary conditions must be compatible with the force-free assumption. If the integral relations (31) – (35) are not fulfilled then the data are not consistent with the assumption of a force-free field. A principal way to avoid this problem would be to measure the magnetic field vector in the low-gb chromosphere, but unfortunately such measurements are not routinely available. We have therefore to rely on photospheric measurements and apply some procedure, dubbed ‘preprocessing’, in order to derive suitable boundary conditions for NLFFF extrapolations. As pointed out by Aly (1989) the condition that α is constant on magnetic field lines (12) leads to the integral relation
, where S+ and S- correspond to areas with positive and negative Bz in the photosphere, respectively, and f is an arbitrary function. Condition (37) is referred to as differential flux-balance condition as it generalizes the usual flux-balance condition (30). As the connectivity of magnetic field lines (magnetic positive and negative regions on the boundary connected by field lines) is a priori unknown, relation (37) is usually only evaluated after a 3D force-free model has been computed.
4.7 Preprocessing
Wiegelmann et al. (2006b) developed a numerical algorithm in order to use the integral relations (31) – (35) to derive suitable NLFFF boundary conditions from photospheric measurements. To do so, we define the functional:
,
,
. The first and second terms (L1,L2) are quadratic forms of the force and torque balance conditions, respectively. The L3 term measures the difference between the measured and preprocessed data. L4 controls the smoothing, which is useful for the application of the data to finite-difference numerical code and also because the chromospheric low-β field is smoother than in the photosphere. The aim is to minimize Lprep so that all terms Ln are made small simultaneously. The optimal parameter sets μn have to be specified for each instrument separately. The resulting magnetic field vector is then used to prescribe the boundary conditions for NLFFF extrapolations. In an alternative approach Fuhrmann et al. (2007) applied a simulated annealing method to minimize the functional. Furthermore they removed the L3 term in favor of a different smoothing term L4, which uses the median value in a small window around each pixel for smoothing. The preprocessing routine has been extended in Wiegelmann et al. (2008) by including chromospheric measurements, e.g., by minimizing additionally the angle between the horizontal magnetic field and chromospheric Hα fibrils. In principle, one could add additional terms to include more direct chromospheric observations, e.g., line-of-sight measurements of the magnetic field in higher regions as provided by SOLIS. In principle, it should be possible to combine methods for ambiguity removal and preprocessing in one code, in particular for ambiguity codes which also minimize a functional like the Metcalf (1994) minimum energy method. A mathematical difficulty for such a combination is, however, that the preprocessing routines use continuous values, but the ambiguity algorithms use only two discrete states at each pixel. Preprocessing minimizes the integral relations (31 – 35) and the value of these integrals reduces usually by orders of magnitudes during the preprocessing procedure. These integral relation are, however, only necessary and not sufficient conditions for force-free consistent boundary conditions, and preprocessing does not make use of condition (37). Including this condition is not straight forward as one needs to know the magnetic field line connectivity, which is only available after the force-free configuration has been computed in 3D. An alternative approach for deriving force-free consistent boundary conditions is to allow changes of the boundary values (in particular the horizontal field) during the force-free reconstruction itself, e.g., as recently employed by Wheatland and Régnier (2009), Amari and Aly (2010), and Wiegelmann and Inhester (2010). The numerical implementation of these approaches does necessarily depend on the corresponding force-free extrapolation codes and we refer to Sections 6.2 and 6.4 for details.
5 Nonlinear Force-free Fields in 3D
In the following section, we briefly discuss some general properties of force-free fields, which are relevant for solar physics, like the magnetic helicity, estimations of the minimum and maximum energy a force-free field can have for certain boundary conditions and investigations of the stability. Such properties are assumed to play an important role for solar eruptions. The Sun and the solar corona are of course three-dimensional and for any application to observed data, configurations based on symmetry assumptions (as used in Section 3) are usually not applicable. The numerical treatment of nonlinear problems, in particular in 3D, is significantly more difficult than linear ones. Linearized equations are often an over-simplification which does not allow the appropriate treatment of physical phenomena. This is also true for force-free coronal magnetic fields and has been demonstrated by comparing linear force-free configurations (including potential fields, where the linear force-free parameter α is zero).
Computations of the photospheric .. distribution from measured vector magnetograms by Equation (14) show that α is a function of space (see, e.g., Pevtsov et al., 1994; Régnier et al., 2002; DeRosa et al., 2009). Complementary to this direct observational evidence that nonlinear effects are important, there are also theoretical arguments. Linear models are too simple to estimate the free magnetic energy. Potential fields correspond to the minimum energy configuration for a given magnetic flux distribution on the boundary. Linear force-free fields contain an unbounded magnetic energy in an open half-space above the photosphere (Seehafer, 1978), because the governing equation in this case is the Helmholtz (wave) equation (Equation (17)) whose solution decays slowly toward infinity. Consequently both approaches are not suitable for the estimation of the magnetic energy, in particular not an estimation of the free energy a configuration has in excess of a potential field.
5.1 Magnetic helicity
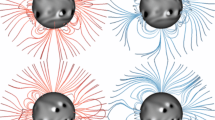
Magnetic helicity is a quantity closely related to a property of the force-free field (Woltjer, 1958), and is defined by
, where B = ∇ × A and A is the vector potential. When B is given, A is not unique and a gradient of any scalar function can be added without changing B. Such gauge freedom does not affect the value of Hm if the volume V is bounded by a magnetic surface (i.e., no field lines go through the surface). Figure 8 shows simple torus configurations and their magnetic helicities. As can be guessed from the figures, magnetic helicity is a topological quantity describing how the field lines are twisted or mutually linked, and is conserved when resistive diffusion of magnetic field is negligible. In the case of the solar corona, the bottom boundary (the photosphere) is not a magnetic surface, and field lines go through it. Even under such conditions, an alternative form for the magnetic helicity which does not depend on the gauge of A can be defined (Berger and Field, 1984; Finn and Antonsen Jr, 1985). On the Sun one finds the hemispheric helicity sign rule (see, e.g., Pevtsov et al., 1995; Wang and Zhang, 2010, and references therein). For various features like active regions, filaments, coronal loops, and interplanetary magnetic clouds the helicity is negative in the northern and positive in the southern hemisphere.
5.2 Energy principles
Energy principles leading to various magnetic fields (potential fields, linear force-free fields, and nonlinear force-free fields) were summarized in Sakurai (1989). For a given distribution of magnetic flux (Bz) on the boundary,
-
(a)
a potential field is the state of minimum energy.
-
(b)
If the magnetic energy is minimized with an additional condition of a fixed value of Hm, one obtains a linear force-free field. The value of constant α should be an implicit function of Hm. The obtained solution may or may not be a minimum of energy; in the latter case the solution is dynamically unstable.
-
(c)
If the magnetic energy is minimized by specifying the connectivity of all the field lines, one obtains a nonlinear force-free field. The solution may or may not be dynamically stable.
Item (c) is more explicitly shown by introducing the so-called Euler potentials (u, v) for the magnetic field (Stern, 1970),
. This representation satisfies ∇ · B = 0. Since B · ∇u = B · ∇v = 0, u and v are constant along the field line. The values of u and v on the boundary can be set so that Bz matches the given boundary condition. If the magnetic energy is minimized with the values of u and v specified on the boundary, one obtains Equation (5) for a general (nonlinear) force-free field.
By the construction of the energy principles, the energy of (b) or (c) is always larger than that of the potential field (a). If the values of u and v are so chosen (there is enough freedom) that the value of Hm is the same in cases (b) and (c), then the energy of nonlinear force-free fields (c) is larger than that of the linear force-free field (b). Therefore, we have seen that magnetic energy increases as one goes from a potential field to a linear force-free field, and further to a nonlinear force-free field. Suppose there are field lines with enhanced values of .. (carrying electric currents stronger than the surroundings). By some instability (or magnetic reconnection), the excess energy may be released and the twist in this part of the volume may diminish. However, in such rapid energy release processes, the magnetic helicity over the whole volume tends to be conserved (Berger, 1984). Namely local twists represented by spatially-varying .. only propagate out from the region and are homogenized, but do not disappear. Because of energy principle (b), the end state of such relaxation will be a linear force-free field. This theory (Taylor relaxation; Taylor, 1974, 1986) explains the commonly-observed behavior of laboratory plasmas to relax toward linear force-free fields. On the Sun this behaviour is not observed, however. A possible explanation could be that since we observe spatially-varying α on the Sun, relaxation to linear force-free fields only takes place at limited occasions (e.g., in a flare) and over a limited volume which magnetic reconnection (or other processes) can propagate and homogenize the twist.
5.3 Maximum energy
There is in particular a large interest on force-free configurations for a given vertical magnetic field Bn on the lower boundary and in which range the energy content of these configurations can be. For such theoretical investigations, one usually assumes a so-called star-shaped volume, like the exterior of a spherical shell and the coronal magnetic field is unbounded but has a finite magnetic energy. (Numerical computations, on the other hand, are mainly carried out in finite computational volumes, like a 3D-box in Cartesian geometry.) It is not the aim of this review to follow the involved mathematical derivation, which the interested reader finds in Aly (1984). As we saw above, the minimum energy state is reached for a potential field. On the other hand, one is also interested in the maximum energy a force-free configuration can obtain for the same boundary conditions Bn. This problem has been addressed in the so-called Aly-Sturrock conjecture (Aly, 1984, 1991; Sturrock, 1991). The conjecture says that the maximum magnetic energy is obtained if all magnetic field lines are open (have one footpoint in the lower boundary and reach to infinity). This result implies that any non-open force-free equilibrium (which contains electric currents parallel to closed magnetic field lines, e.g., created by stressing closed potential field lines) contains an energy which is higher than the potential field, but lower than the open field. As pointed out by Aly (1991) these results imply that the maximum energy which can be released from an active region, say in a flare or coronal mass ejection (CME), is the difference between the energy of an open field and a potential field. While a flare requires free magnetic energy, the Aly-Sturrock conjecture does also have the consequence that it would be impossible that all field lines become open directly after a flare, because opening the field lines costs energy. This is in some way a contradiction to observations of CMEs, where a closed magnetic structure opens during the eruption. Choe and Cheng (2002) constructed force-free equilibria containing tangential discontinuities in multiple flux systems, which can be generated by footpoint motions from an initial potential field. These configurations contain energy exceeding the open field, a violation of the Aly-Sturrock conjecture, and would release energy by opening all field lines. Due to the tangential discontinuities, these configurations contain thin current sheets, which can develop micro-instabilities to convert magnetic energy into other energy forms (kinetic and thermal energy) by resistive processes like magnetic reconnection. It is not clear (Aly and Amari, 2007), however, which conditions are exactly necessary to derive force-free fields with energies above the open field: Is it necessary that the multiple flux-tubes are separated by non-magnetic regions like in Choe and Cheng (2002)? Or would it be sufficient that the field in this region is much weaker than in the flux tubes but remains finite? (See Sakurai, 2007, for a related discussion.)
5.4 Stability of force-free fields
In principle, the MHD stability criteria can also be applied to force-free equilibria. Typical approaches (see the book by Priest, 1982) to investigate the stability of ideal MHD equilibria (which correspond to the assumption of infinite electrical conductivity) are normal mode analysis and an energy criterion. The basic question is how a small disturbance to the equilibrium evolves. Analytic methods typically linearize the problem around an equilibrium state, which leads to the so-called linear stability analysis. One has to keep in mind, however, that a linearly-stable configuration might well be nonlinearly unstable. The nonlinear stability of a system is usually investigated numerically with the help of time dependent simulations, e.g., with an MHD code (see also Section 5.5 for an application to NLFFF equilibria). In the following, we concentrate on linear stability investigations by using an energy criterion.
For a force-free configuration the energy is given by
where the subscript 0 corresponds to the equilibrium state. This equilibrium becomes disturbed by an displacement ξ(r0, t) in the form B = B0 + B1 with B1 = ∇0 × (ξ × B0). This form of the magnetic field displacement has its origin from the linearized induction equation \(\frac{{\partial B_1 }} {{\partial t}} = \nabla \times (v_1 \times B_0 )\), where the velocity field has been replaced by the displacement ξ. The MHD energy principle (Bernstein et al., 1958) reduces for force-free fields to (Molodensky, 1974):
A configuration is stable if W > 0, unstable for W < 0, and marginally stable for W = 0. For force-free fields and using the perturbed vector potential A1 = ξ × B, Equation (46) can be written as:
. From Equation (47) it is obvious that the potential field with α = 0 is stable. If we approximate |∇ × A1| ∼ |A1|/l with a typical length scale l of the system, the first term may remain larger than the second term (i.e., stability) in Equation (47) if
. This means that the scale of twist in the system, 1/α, should be larger than the system size l for it to be stable. This criterion is known as Shafranov’s limit in plasma physics. More precise criteria for stability can be obtained for specific geometries. For example the case of cylindrical linear force-free field (Lundquist’s field) was studied by Goedbloed and Hagebeuk (1972).
5.5 Numerical stability investigations
Török and Kliem (2005) investigated the stability of the nonlinear force-free Titov-Démoulin equilibrium numerically with the help of a time-dependent MHD code. Figure 9 shows snapshots from MHD simulation starting from in an unstable branch of the Titov-Démoulin equilibrium in comparison with a solar eruption observed with TRACE. The simulation shows a very good agreement with the observed eruptions and indicates that a helical kink instability can trigger coronal eruptions. Dependent on particular parameters of the original Titov-Démoulin equilibrium the eruption remains confined or leads to a coronal mass ejection (see Török and Kliem, 2005, for details).
6 Numerical Methods for Nonlinear Force-free Fields
In the following, we review five different approaches for the computation of nonlinear force-free coronal magnetic fields. The aim of all codes is to extrapolate photospheric vector field measurements into the corona, but the way how the measurements are used is different. MHD relaxation and optimization methods prescribe the three components of the magnetic field vector on the bottom boundary. Grad-Rubin methods use the vertical magnetic field and the vertical electric current density (or α-distribution) as boundary condition. The upward integration method and the boundary-element method require a combination of both boundary conditions. In the following, we will briefly discuss the main features of these five methods. Grad-Rubin, MHD relaxation, and optimization methods require first the computation of a potential field; then the appropriate boundary conditions are specified and eventually one iterates numerically for a solution of the NLFFF equations. Upward integration and boundary-element methods do not require first the computation of a potential field, but solve the NLFFF equations more directly. Both methods have, however, some shortcomings as explained later. Often one is interested anyway to get also the potential field, e.g., to derive the energy the NLFFF field has in excess of the potential field. A more detailed review on the mathematical and computational implementations and recent code updates can be found in Wiegelmann (2008).
6.1 Upward integration method
This straightforward method was proposed by Nakagawa (1974) and it has been first computationally implemented by Wu et al. (1985, 1990). The basic idea of this method is to reformulate Equations (2) – (4) and extrapolate the magnetic field vector into the solar corona. The method is not iterative and extrapolates the magnetic field directly upward, starting from the bottom layer, where the field is measured. From B0(x, y, 0) one computes the z-component of the electric current u0jz0 by Equation (13) and the corresponding α-distribution with Equation (14). Then the x- and y-components of the electric current are calculated by Equation (11):
,
. Finally, we get the z-derivatives of the magnetic field vector with Equations (3) and (4) as
,
,
. A numerical integration provides the magnetic field vector at the level z + dz. These steps are repeated in order to integrate the equations upwards in z. Naively one would assume to derive finally the 3D magnetic fields in the corona, which is indeed the idea of this method. The main problem is that this simple straightforward approach does not work because the method is mathematically ill-posed and the algorithm is unstable (see, e.g., Cuperman et al., 1990 and Amari et al., 1997 for details). As a result of this numerical instability one finds an exponential growth of the magnetic field with increasing height. The reason for this is that the method transports information only from the photosphere upwards. Other boundary conditions, e.g., at an upper boundary, either at a finite height or at infinity cannot be taken into account. Several attempts have been made to stabilize the algorithm, e.g., by smoothing and reformulating the problem with smooth analytic functions (e.g., Cuperman et al., 1991; Démoulin and Priest, 1992; Song et al., 2006). Smoothing does help somewhat to diminish the effect of growing modes, because the shortest spatial modes are the fastest growing ones. To our knowledge the upward integration method has not been compared in detail with other NLFFF codes and it is therefore hard to evaluate the performance of this method.
6.2 Grad-Rubin method
The Grad-Rubin method has been originally proposed (but not numerically implemented) by Grad and Rubin (1958) for the application to fusion plasma. The first numerical application to coronal magnetic fields was carried out by Sakurai (1981). The original Grad-Rubin approach uses the α-distribution on one polarity and the initial potential magnetic field to calculate the electric current density with Equation (12) and to update the new magnetic field B from the Biot-Savart equation (11). This scheme is repeated iteratively until a stationary state is reached, where the magnetic field does not change anymore. Amari et al. (1997, 1999) implemented the Grad-Rubin method on a finite difference grid and decomposes Equations (2) – (4) into a hyperbolic part for evolving α along the magnetic field lines and an elliptic one to update the magnetic field from Ampere’s law:
,
. This evolves α from one polarity on the boundary along the magnetic field lines into the volume above. The value of α0± is given either in the positive or negative polarity:
,
,
,
. An advantage from a mathematical point of view is that the Grad-Rubin approach solves the nonlinear force-free equations as a well-posed boundary value problem. As shown by Bineau (1972) the Grad-Rubin-type boundary conditions, the vertical magnetic field and for one polarity the distribution of α, ensure the existence and unique NLFFF solutions at least for small values of α and weak nonlinearities. See Amari et al. (1997, 2006) for more details on the mathematical aspect of this approach. The largest-allowed current and the corresponding maximum values of α for which one can expect convergence of the Grad-Rubin approach have been studied in Inhester and Wiegelmann (2006). Starting from an initial potential field the NLFFF equations are solved iteratively in the form of Equations (11) – (12). The horizontal component of the measured magnetic field is then used to compute the distribution of α on the boundary using Equation (14). While α is computed this way on the entire lower boundary, the Grad-Rubin method requires only the prescription of α for one polarity. For measured data which contain noise, measurement errors, finite forces, and other inconsistencies the two solutions can be different: However, see for example the extrapolations from Hinode data carried out in DeRosa et al. (2009). While both solutions are based on well-posed mathematical problems, they are not necessary consistent with the observations on the entire lower boundary. One can check the consistency of the α-distribution on both polarities with Equation (37).
As a further step to derive one unique solution the Grad-Rubin approach has been extended by Wheatland and Régnier (2009) and Amari and Aly (2010) by using these two different solutions (from different polarities) to correct the α-distribution on the boundaries and to find finally one consistent solution by an outer iterative loop, which changes the α-distribution on the boundary. An advantage in this approach is that one can specify where the α-distribution, as computed by Equation (14), is trustworthy (usually in strong field regions with a low measurement error in the transverse field) and where not (in weak field regions). This outer iterative loop, which aims at finding a consistent distribution of α on both polarities, allows also to specify where the initial distribution of α is trustworthy.
6.3 MHD relaxation method
MHD relaxation method means that a reduced set of time-dependent MHD equations is used to compute stationary equilibria:
,
,
,
. Here, v is a fictitious viscosity, v the fluid velocity, and e the electric field. For general MHD equilibria the approach was proposed by Chodura and Schlüter (1981). Applications to force-free coronal magnetic fields can be found in Mikić and McClymont (1994), Roumeliotis (1996), and McClymont et al. (1997). In principle, any time-dependent MHD code can be used for this aim. The first NLFFF implementation of this methods used the code developed by Mikić et al. (1988). MHD relaxation means that an initial non-equilibrium state is relaxed towards a stationary state, here NLFFF. The initial non-equilibrium state is often a potential field in the 3D-box, where the bottom boundary field has been replaced by the measurements. This leads to large deviations from the equilibrium close to this boundary. As a consequence one finds a finite plasma flow velocity v in Equation (60) because all non-magnetic forces accumulate in the velocity field. This velocity field is reduced during the relaxation process and the force-free field equations are obviously fulfilled when the left-hand side of Equation (60) vanishes. The viscosity v is usually chosen as
with μ = constant. By combining Equations (60), (61), (62), and (64) one gets a relaxation process for the magnetic Field
,
. For details regarding a currently-used implementation of this approach see Valori et al. (2005).
6.4 Optimization approach
The optimization approach as proposed in Wheatland et al. (2000) is closely related to the MHD relaxation approach. It shares with this method that a similar initial non-equilibrium state is iterated towards a NLFFF equilibrium. It solves a similar iterative equation as Equation (65)
, but F has additional terms, as explained below. The force-free and solenoidal conditions are solved by minimizing the functional
. If the minimum of this functional at L = 0 is attained then the NLFFF equations (2) – (4) are fulfilled. The functional is minimized by taking the functional derivative of Equation (68) with respect to an iteration parameter t:
. For vanishing surface terms the functional L decreases monotonically if the magnetic field is iterated by
. The first term in Equation (70) is identical with FMHS as defined in Equation (66).
A principal problem with the optimization and the MHD-relaxation approaches is that using the full magnetic field vector on the lower boundary does not guarantee the existence of a force-free configuration (see the consistency criteria in Section 4.6. Consequently, if fed with inconsistent boundary data, the codes cannot find a force-free configuration, but a finite residual Lorentz force and/or a finite divergence of the field remains in the 3D equilibrium. A way around this problem is to preprocess the measured photospheric data, as explained in Section 4.7. An alternative approach is that one allows deviations of the measured horizontal field vector and the corresponding field vector on the lower boundary of the computational box during the minimization of the functional (68). Wiegelmann and Inhester (2010) extended this functional by another term
, where v is a free parameter and the matrix W contains information how reliable the data (mainly measurements of the horizontal photospheric field) are. With this approach inconsistencies in the measurement lead to a solution compatible with physical requirements (vanishing Lorentz force and divergence), leaving differences between Bobs and the bottom boundary field B in regions where W is low (and the measurement error high). Consequently, this approach takes measurement errors, missing data, and data inconsistencies into account. Further tests are necessary to investigate whether this approach or preprocessing, or a combination of both, is the most effective way to deal with noisy and inconsistent photospheric field measurements. This approach, as well as a variant of the Grad-Rubin method, have been developed in response to a joint study by DeRosa et al. (2009), where one of the main findings w as that force-free extrapolation codes should be able to incorporate measurement inconsistencies (see also Section 6.6).
6.5 Boundary-element methods
The boundary-element method was developed by Yan and Sakurai (2000) and requires the magnetic field vector and the α-distribution on the boundary as input. The NLFFF equations relate the magnetic field values on the boundary with those in the volume:
with ci = 1 for points in the volume and ci = 1/2 for boundary points and B0 is the magnetic field vector on the boundary, where
and λi (i = x, y, z) are implicitly computed with integrals over the 3D volume,s
. The boundary-element method is slow for computing the NLFFF in a 3D domain. Rudenko and Myshyakov (2009) raised questions on this method.
6.6 Comparison of methods and the NLFFF consortium
Since 2004, a group of scientists chaired by Karel Schrijver compare, evaluate, and improve methods for the nonlinear force-free computation of coronal magnetic fields and related topics. The test cases are available at http://www.lmsal.com/~derosa/for_nlfff/. So far, six workshops have been organized and the consortium published four joint publications:
-
1.
Schrijver et al. (2006) performed blind tests on analytical force-free field models with various boundary conditions to show that in general the NLFFF algorithms perform best where the magnetic field and the electrical currents are strongest, but they are also very sensitive to the specified boundary conditions. Nevertheless, it was shown that the optimization method as proposed by Wheatland et al. (2000) and as implemented by Wiegelmann (2004) was the fastest-converging and best-performing one for this analytical test case.
-
2.
Metcalf et al. (2008) tested the performance of the NLFFF algorithms applied to a solar-like reference model including realistic photospheric Lorentz forces and a complex magnetic field structure. All the codes were able to recover the presence of a weakly twisted, helical flux rope. Due to the sensitivity to the numerical details, however, they were less accurate in reproducing the field connectivity and magnetic energy when applied to the preprocessed, more force-free, chromospheric-like boundary conditions. When applied to the forced, not preprocessed photospheric data the codes did not perform successfully, indicating that the consistency of the used boundary conditions is crucial for the success of the magnetic field extrapolations. It also showed that the magnetic field connection between the photosphere, chromosphere, and lower corona needs to be additionally precisely modeled.
-
3.
Schrijver et al. (2008) used four different codes and a variety of boundary conditions to compute 14 NLFFF models based on Hinode/SOT-SP3 data of an active region around the time of a powerful flare. When applied to this real solar data, the models produced a wide variety of magnetic field geometries, energy contents, and force-freeness. Force-free consistency criteria, like the alignment of electric currents with magnetic field lines, have been best fulfilled for computations with the Grad-Rubin approach. It was concluded that strong electrical currents in the form of an ensemble of thin strands emerge together with magnetic flux preceding the flare. The global patterns of magnetic fields are compatible with a large-scale twisted flux rope topology, and they carry energy which is large enough to power the flare and its associated CME.
-
4.
DeRosa et al. (2009) found that various NLFFF models differ remarkably in the field line configuration and produce different estimates of the free magnetic energy when applied to Hinode/SOT-SP data. This problem was recognized already in the first application to Hinode data in Schrijver et al. (2008) and it has been worked out that a small field-of-view vector magnetogram, which does not contain an entire active region and its surroundings, does not provide the necessary magnetic connectivity for successful NLFFF extrapolations. As visible in Figure 10 the stereoscopically-reconstructed loops by Aschwanden et al. (2008b) do not agree well with the NLFFF models. Unfortunately, the FOV of Hinode covered only a small fraction (about 10%) of area spanned by loops reconstructed from STEREO/SECCHI images. The quantitative comparison was unsatisfactory and NLFFF models have not been better as potential fields here. In other studies NLFFF methods have shown to be superior to potential and linear force-free extrapolations (Wiegelmann et al., 2005). NLFF field lines showed in particular excellent agreement with the observed loops, when both footpoints are within the FOV of the vector magnetogram and sufficiently far away from the boundaries.
A series of coaligned images of AR 10953. Blue lines are stereoscopically-reconstructed loops (Aschwanden et al., 2008b). Red lines are extrapolated nonlinear force-free field lines from Hinode/SOT with MDI data outside the Hinode FOV (the dotted line). Image reproduced by permission from Figure 1 of DeRosa et al. (2009), copyright by AAS.
When presented with complete and consistent boundary conditions, NLFFF algorithms generally succeed in reproducing the test fields. However, for a well-observed dataset (a Hinode/SOT-SP vector-magnetogram embedded in MDI data) the NLFFF algorithms did not yield consistent solutions. From this study we conclude that one should not rely on a model-field geometry or energy estimates unless they match coronal observations. It was concluded that successful application to real solar data likely requires at least:
-
1.
Large model volumes with high resolution that accommodate most of the field-line connectivity within a region and to its surroundings.
-
2.
Accommodation of measurement uncertainties (in particular in the transverse field component) in the lower boundary condition.
-
3.
‘Preprocessing’ of the lower-boundary vector field that approximates the physics of the photosphere-to-chromosphere interface as it transforms the observed, forced, photospheric field to a realistic approximation of the chromospheric, nearly-force-free, field.
-
4.
The extrapolated coronal magnetic field lines should be compared and verified by coronal observations.
In the meantime, some work has been done in reply to these conclusions. New implementations of the Grad-Rubin and optimization methods do accommodate the measurement errors; see Sections 6.2 and 6.4 for an overview and Wheatland and Régnier (2009), Wiegelmann and Inhester (2010), and Amari and Aly (2010) for the corresponding original publications. On the instrumentation side SDO/HMI provides us with full-disk measurements of the photospheric magnetic field vector, which should allow us to find suitable large model volumes. The first vector magnetograms from SDO/HMI have been released at the end of 2011 and currently research on using them for force-free extrapolations is ongoing.
6.7 Application of nonlinear force-free codes
Despite the difficulties outlined in Section 6.6 NLFFF-codes have been used to study active regions in various situations. Several studies deal with the energy content of the coronal magnetic field in active regions. Bleybel et al. (2002) studied the energy budget of AR 7912 before and after a flare on 1995 October 14 with a Grad-Rubin method and found that the magnetic energy decreased during the flare. The magnetic field lines computed from the nonlinear force-free model seem to be in reasonable agreement with a soft X-ray image from Yohkoh, as shown in the top panel in Figure 11. At least the nonlinear force-free model seems to agree better with the X-ray image than a linear force-free and a potential field model shown in the center and bottom panel, respectively. Régnier et al. (2002), also using the Grad-Rubin approach, studied the non-flaring active region AR 8151 in February 1998 and found that the available free magnetic energy was not high enough to power a flare. These results are consistent which the observation in the sense that nonlinear force-free field lines reasonably agree with coronal observations and a consistent flaring activity: The particular active regions flared (not flared) when the free magnetic energy computed with NLFFF-codes was high enough (too low). A decreasing free magnetic energy during flares has been confirmed in several studies. Thalmann and Wiegelmann (2008) and Thalmann et al. (2008), using the optimization approach, found that the force-free energy before a small C-class flare (observed in active region NOAA 10960 on 2007 June 7) was 5% higher than the potential field energy. Before a large M-class flare (observed in active region NOAA 10540 in January 2004) the force-free energy exceeded the potential field energy by 60%. In a statistic study, based on 75 samples extrapolate with the optimization approach, Jing et al. (2010) found a positive correlation between free magnetic energy and the X-ray flaring index. It seems that we can trust that there is a relation between computed free energy and flaring activity, whereas the results of Section 6.6 indicate that one might not fully trust in the exact numbers of magnetic energies computed with one NLFFF-code only. Recently, Gilchrist et al. (2012) pointed out that uncertainties in the vector magnetograms likely result in underestimating the computed magnetic energy. NLFFF-codes are, however, a strong tool to guide the investigation of coronal features. Régnier and Amari (2004), Valori et al. (2012), and Sun et al. (2012) applied the Grad-Rubin, MHD-relaxation and optimization approach, respectively and found at least qualitatively a good agreement of NLFFF-models with observed sigmoid or serpentine structures.
7 Summary and Discussion
In this review, we tried to give an overview of force-free magnetic fields, particularly model assumptions, which are important for understanding the physics of the solar corona. While the underlying mathematical equations describe stationary states and look relatively simple, solving them is by no means a trivial problem because of the nonlinear nature of the problem. Exact solutions are only available for further simplifications, like linearizing the equations or to restrict to 1D/2D for the nonlinear case. For force-free configurations in 3D, we know that (for given flux distributions in the photosphere) the magnetic field energy is bounded from below by a potential field. An upper-limit for the energy is more difficult to obtain. While the Aly-Sturrock conjecture (Section 5.3) claims that the upper limit is for the configurations with all magnetic field lines open, Choe and Cheng (2002) constructed solutions with energies above the Aly-Sturrock limit. These configurations contain discontinuities and the debate of the validity of the Aly-Sturrock limit is ongoing (Hu, 2004; Wolfson et al., 2012).
For practical computations of the 3D-field in the solar corona, one has to use numerical computations and several codes have been developed, compared, and applied. As input these codes require measurements of the magnetic field vector in the solar photosphere. However, the transverse field component contains an ambiguity in the azimuth, which has to be resolved before the data can be used for coronal magnetic field modeling. The accuracy of photospheric measurements is lower for the transverse field component compared with the line-of-sight field, and in weak field regions measurements and azimuth ambiguity removal are less trustworthy. Consequently the majority of coronal force-free field models are carried out in active regions, although methods for full-disk computations have been developed too. A further complication of using photospheric measurements as the boundary condition for force-free extrapolations is that the photospheric magnetic field is not necessarily consistent with the force-free assumption. Possible solutions are to use only the vertical magnetic field and the vertical electric current as boundary conditions, as done for the Grad-Rubin approach, to preprocess the photospheric measurements with the aim to make them compatible with force-free and other physical requirements, or to allow changes of the transverse magnetic field during the iteration of a force-free field. The latter approach has been implemented in the optimization approach and allows us to take measurement errors into account.
A major source for future research on force-free fields is SDO/HMI, which measures the photospheric magnetic field vector on the full disk, which in principle allows us to compute global coronal models as well as selecting appropriate isolated active regions with a sufficiently large field-of-view. Research on Stokes inversion, azimuth ambiguity removal, and force-free modeling for SDO/HMI data is ongoing. Another important aspect on coronal modeling is the comparison of force-free models as extrapolated from photospheric measurements with coronal images as observed, for example, with the Atmospheric Imaging Assembly (AIA; Lemen et al., 2012) on SDO. On the one hand, such a comparison is important to validate the models (see DeRosa et al., 2009, for details), and, on the other hand, the 3D models help to interpret the observations. With the 3D structure of magnetic loops from the models in hand, one has important tools for modeling of plasma loops, and may gain understanding of coronal heating and plasma flows along the loops. Further steps on the research of eruptive phenomena like flares and CMEs are planned with time-dependent MHD simulations. Force-free models are planned to be used as initial equilibria, which are disturbed by photospheric plasma flows (which can be deduced, e.g., from measurements with SDO/HMI). The temporal evolution and the potential occurrence of eruptions can be investigated with ideal or resistive MHD simulations in comparison with observations. Questions are if or to which extent the configurations remain approximately force-free during eruptions, the role of thin current sheets and discontinuities, and the energy and helicity content. We aim to report about the progress in these aspects in an update of this review in due time.
Notes
1 For an animation of a coronal mass ejection (CME) causing a substorm and aurora, see http://sohowww.nascom.nasa.gov/gallery/Movies/recon/reconsm.mpg
2 In the following, we assume observations close to the disk center for simplicity, when the vertical and LOScomponent are identical. For observations far away from the disk center one has to resolve first the ambiguity and apply coordinate transformations from LOS/transverse to vertical/horizontal fields afterwards.
References
Ai, G.-X. and Hu, Y.-F., 1986, “Principles of a solar magnetic field telescope”, Acta Astron. Sinica, 27, 173–180. [ADS] (Cited on page 16.)
Alissandrakis, C.E., 1981, “On the Computation of Constant α Force-free Magnetic Field”, Astron. Astrophys., 100, 197–200. [ADS] (Cited on page 10.)
Aly, J.J., 1984, “On some properties of force-free magnetic fields in infinite regions of space”, Astrophys. J., 283, 349–362. [DOI], [ADS] (Cited on page 27.)
Aly, J.J., 1989, “On the reconstruction of the nonlinear force-free coronal magnetic field from boundary data”, Solar Phys., 120, 19–48. [DOI], [ADS] (Cited on page 23.)
Aly, J.J., 1991, “How much energy can be stored in a three-dimensional force-free magnetic field?”, Astrophys. J. Lett., 375, L61–L64. [DOI], [ADS] (Cited on page 27.)
Aly, J.J. and Amari, T., 2007, “Structure and evolution of the solar coronal magnetic field”, Geophys. Astrophys. Fluid Dyn., 101, 249–287. [DOI], [ADS] (Cited on pages 8 and 27.)
Amari, T. and Aly, J.J., 2010, “Observational constraints on well-posed reconstruction methods and the optimization-Grad-Rubin method”, Astron. Astrophys., 522, A52. [DOI], [ADS] (Cited on pages 25, 31, and 35.)
Amari, T., Aly, J.J., Luciani, J.F., Boulmezaoud, T.Z. and Mikić, Z., 1997, “Reconstructing the solar coronal magnetic field as a force-free magnetic field”, Solar Phys., 174, 129–149. [DOI], [ADS] (Cited on pages 30 and 31.)
Amari, T., Boulmezaoud, T.Z. and Mikić, Z., 1999, “An iterative method for the reconstruction of the solar coronal magnetic field. I. Method for regular solutions”, Astron. Astrophys., 350, 1051–1059. [ADS] (Cited on page 31.)
Amari, T., Boulmezaoud, T.Z. and Aly, J.J., 2006, “Well posed reconstruction of the solar coronal magnetic field”, Astron. Astrophys., 446, 691–705. [DOI], [ADS] (Cited on page 31.)
Aschwanden, M.J., Newmark, J.S., Delaboudini`ere, J.-P., Neupert, W.M., Klimchuk, J.A., Gary, G.A., Portier-Fozzani, F. and Zucker, A., 1999, “Three-dimensional stereoscopic analysis of solar active region loops. I. SOHO/EIT observations at temperatures of (1.0.1.5)∼106 K”, Astrophys. J., 515, 842–867. [DOI], [ADS] (Cited on page 13.)
Aschwanden, M.J., Lee, J.K., Gary, G.A., Smith, M. and Inhester, B., 2008a, “Comparison of five numerical codes for automated tracing of coronal loops”, Solar Phys., 248, 359–377. [DOI], [ADS] (Cited on page 11.)
Aschwanden, M.J., Wülser, J.-P., Nitta, N.V. and Lemen, J.R., 2008b, “First three-dimensional reconstructions of coronal loops with the STEREO A and B spacecraft. I. Geometry”, Astrophys. J., 679, 827–842. [DOI], [ADS] (Cited on pages 35 and 36.)
Berger, M.A., 1984, “Rigorous new limits on magnetic helicity dissipation in the solar corona”, Geophys. Astrophys. Fluid Dyn., 30, 79–104. [DOI], [ADS] (Cited on page 26.)
Berger, M.A. and Field, G.B., 1984, “The topological properties of magnetic helicity”, J. Fluid Mech., 147, 133–148. [DOI], [ADS] (Cited on page 26.)
Bernstein, I.B., Frieman, E.A., Kruskal, M.D. and Kulsrud, R.M., 1958, “An energy principle for hydromagnetic stability problems”, Proc. R. Soc. London, Ser. A, 244, 17–40. [DOI], [ADS] (Cited on page 28.)
Bineau, M., 1972, “On the Existence of Force-Free Magnetic Fields”, Commun. Pure Appl. Math., 25, 77–84. [DOI] (Cited on pages 8 and 31.)
Birn, J. and Schindler, K., 1981, “Two-ribbon flares: Magnetostatic equilibria”, in Solar Flare Magnetohydrodynamics, (Ed.) Priest, E.R., pp. 337–378, Gordon and Breach Science Publishers, New York. [ADS] (Cited on page 14.)
Birn, J., Goldstein, H. and Schindler, K., 1978, “A theory of the onset of solar eruptive processes”, Solar Phys., 57, 81–101. [DOI], [ADS] (Cited on page 14.)
Bleybel, A., Amari, T., van Driel-Gesztelyi, L. and Leka, K.D., 2002, “Global budget for an eruptive active region. I. Equilibrium reconstruction approach”, Astron. Astrophys., 395, 685–695. [DOI], [ADS] (Cited on pages 36 and 37.)
Boulmezaoud, T.Z. and Amari, T., 2000, “On the existence of non-linear force-free fields in threedimensional domains”, Z. Angew. Math. Phys., 51, 942–967. [DOI], [ADS] (Cited on page 8.)
Canfield, R.C., de La Beaujardiere, J.-F., Fan, Y., Leka, K.D., McClymont, A.N., Metcalf, T.R., Mickey, D.L., Wülser, J.-P. and Lites, B.W., 1993, “The morphology of flare phenomena, magnetic fields, and electric currents in active regions. I. Introduction and methods”, Astrophys. J., 411, 362–369. [DOI], [ADS] (Cited on page 20.)
Carcedo, L., Brown, D.S., Hood, A.W., Neukirch, T. and Wiegelmann, T., 2003, “A quantitative method to optimise magnetic field line fitting of observed coronal loops”, Solar Phys., 218, 29–40. [DOI], [ADS] (Cited on pages 11 and 12.)
Chiu, Y.T. and Hilton, H.H., 1977, “Exact Green's function method of solar force-free magnetic-field computations with constant α. I. Theory and basic test cases”, Astrophys. J., 212, 873–885. [DOI], [ADS] (Cited on pages 10, 17, and 21.)
Chodura, R. and Schlüter, A., 1981, “A 3D code for MHD equilibrium and stability”, J. Comput. Phys., 41, 68–88. [DOI], [ADS] (Cited on page 32.)
Choe, G.S. and Cheng, C.Z., 2002, “Energy of force-free magnetic fields in relation to coronal mass ejections”, Astrophys. J. Lett., 574, L179–L182. [DOI], [ADS] (Cited on pages 27 and 38.)
Cuperman, S., Ofman, L. and Semel, M., 1990, “Extrapolation of photospheric potential magnetic fields using oblique boundary values: a simplified approach”, Astron. Astrophys., 227, 583–590. [ADS] (Cited on page 30.)
Cuperman, S., Démoulin, P. and Semel, M., 1991, “Removal of singularities in the Cauchy problem for the extrapolation of solar force-free magnetic fields”, Astron. Astrophys., 245, 285–288. [ADS] (Cited on pages 22 and 31.)
Cuperman, S., Li, J. and Semel, M., 1993, “Identification and elimination of the residual ambiguity in the sign of observed photospheric magnetic fields”, Astron. Astrophys., 278, 279–287. [ADS] (Cited on page 19.)
del Toro Iniesta, J.C., 2003, Introduction to Spectropolarimetry, Cambridge University Press, Cambridge; New York. [ADS], [Google Books] (Cited on page 16.)
del Toro Iniesta, J.C. and Ruiz Cobo, B., 1996, “Stokes Profiles Inversion Techniques”, Solar Phys., 164, 169–182. [DOI], [ADS] (Cited on page 16.)
Démoulin, P. and Priest, E.R., 1992, “The properties of sources and sinks of a linear force-free field”, Astron. Astrophys., 258, 535–541. [ADS] (Cited on page 31.)
DeRosa, M.L., Schrijver, C.J., Barnes, G., Leka, K.D., Lites, B.W., Aschwanden, M.J., Amari, T., Canou, A., McTiernan, J.M., Régnier, S., Thalmann, J.K., Valori, G., Wheatland, M.S., Wiegelmann, T., Cheung, M.C.M., Conlon, P.A., Fuhrmann, M., Inhester, B. and Tadesse, T., 2009, “A Critical Assessment of Nonlinear Force-Free Field Modeling of the Solar Corona for Active Region 10953”, Astrophys. J., 696, 1780–1791. [DOI], [ADS], [arXiv:0902.1007] (Cited on pages 25, 31, 33, 35, 36, and 38.)
Fan, Y. and Gibson, S.E., 2004, “Numerical simulations of three-dimensional coronal magnetic fields resulting from the emergence of twisted magnetic flux tubes”, Astrophys. J., 609, 1123–1133. [DOI], [ADS] (Cited on pages 17, 18, and 22.)
Feng, L., Inhester, B., Solanki, S.K., Wiegelmann, T., Podlipnik, B., Howard, R.A. and Wülser, J.-P., 2007a, “First stereoscopic coronal loop reconstructions from STEREO SECCHI images”, Astrophys. J. Lett., 671, L205–L208. [DOI], [ADS], [arXiv:0802.0773] (Cited on page 11.)
Feng, L., Wiegelmann, T., Inhester, B., Solanki, S.K., Gan, W.Q. and Ruan, P., 2007b, “Magnetic stereoscopy of coronal loops in NOAA 8891”, Solar Phys., 241, 235–249. [DOI], [ADS] (Cited on page 11.)
Finn, J.M. and Antonsen Jr, T.M., 1985, “Magnetic helicity: What is it, and what is it good for?”, Comments Plasma Phys. Contr. Fusion, 9, 111–126 (Cited on page 26.)
Fuhrmann, M., Seehafer, N. and Valori, G., 2007, “Preprocessing of solar vector magnetograms for forcefree magnetic field extrapolation”, Astron. Astrophys., 476, 349–357. [DOI], [ADS] (Cited on page 24.)
Gary, G.A., 2001, “Plasma beta above a solar active region: Rethinking the paradigm”, Solar Phys., 203, 71–86. [DOI], [ADS] (Cited on pages 6, 7, and 23.)
Gary, G.A. and Démoulin, P., 1995, “Reduction, analysis, and properties of electric current systems in solar active regions”, Astrophys. J., 445, 982–998. [DOI], [ADS] (Cited on page 20.)
Gary, G.A. and Hagyard, M.J., 1990, “Transformation of vector magnetograms and the problems associated with the effects of perspective and the azimuthal ambiguity”, Solar Phys., 126, 21–36. [ADS] (Cited on page 16.)
Georgoulis, M.K., 2005, “A new technique for a routine azimuth disambiguation of solar vector magnetograms”, Astrophys. J. Lett., 629, L69–L72. [DOI], [ADS] (Cited on page 19.)
Georgoulis, M.K., 2012, “Comment on ‘Resolving the 180° Ambiguity in Solar Vector Magnetic Field Data: Evaluating the Effects of Noise, Spatial Resolution, and Method Assumptions’“, Solar Phys., 276, 423–440. [DOI], [ADS], [arXiv:1106.4682 [astro-ph.SR]] (Cited on page 21.)
Georgoulis, M.K., LaBonte, B.J. and Metcalf, T.R., 2004, “On the resolution of the azimuthal ambiguity in vector magnetograms of solar active regions”, Astrophys. J., .602, 446–467. [DOI], [ADS] (Cited on page 19.)
Gilchrist, S.A., Wheatland, M.S. and Leka, K.D., 2012, “The Free Energy of NOAA Solar Active Region AR 11029”, Solar Phys., 276, 133–160. [DOI], [ADS], [arXiv:1110.4418 [astro-ph.SR]] (Cited on page 37.)
Goedbloed, J.P. and Hagebeuk, H.J.L., 1972, “Growth rates of instabilities of a diffuse linear pinch”, Phys. Fluids, 15, 1090–1101. [DOI], [ADS] (Cited on page 28.)
Gold, T. and Hoyle, F., 1960, “On the origin of solar flares”, Mon. Not. R. Astron. Soc., 120, 89. [ADS] (Cited on page 14.)
Grad, H. and Rubin, H., 1958, “Hydromagnetic Equilibria and Force-Free Fields”, in Peaceful Uses of Atomic Energy, Vol. 31: Theoretical and Experimental Aspects of Controlled Nuclear Fusion, Proceedings of the Second United Nations International Conference, Geneva, 1–13 September 1958, (Eds.) Martens, J.H., Ourom, L., Barss, W.M., Bassett, L.G., Smith, K.R.E., Gerrard, M., Hudswell, F., Guttman, B., Pomeroy, J.H., Woollen, W.B., Singwi, K.S., Carr, T.E.F., Kolb, A.C., Matterson, A.H.S., Welgos, S.P., Rojanski, I.D., Finkelstein, D., pp. 190–197, United Nations, Geneva. Online version (accessed 14 August 2012): http://www-naweb.iaea.org/napc/physics/2ndgenconf/sets/46.html (Cited on pages 14 and 31.)
Hagino, M. and Sakurai, T., 2004, “Latitude variation of helicity in solar active regions”, Publ. Astron. Soc. Japan, 56, 831–843. [ADS] (Cited on page 11.)
Hagyard, M.J., Cumings, N.P., West, E.A. and Smith, J.E., 1982, “The MSFC vector magnetograph”, Solar Phys., 80, 33–51. [DOI], [ADS] (Cited on page 16.)
Henney, C.J., Keller, C.U. and Harvey, J.W., 2006, “SOLIS-VSM Solar Vector Magnetograms”, in Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B.W., vol. 358 of ASP Conference Series, pp. 92–95, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:astro-ph/0612584] (Cited on pages 16 and 19.)
Hu, Y.Q., 2004, “Energy buildup of multipolar magnetic fields by photospheric shear motion”, Astrophys. J., 607, 1032–1038. [DOI], [ADS] (Cited on page 38.)
Inhester, B. and Wiegelmann, T., 2006, “Nonlinear force-free magnetic field extrapolations: Comparison of the Grad Rubin and Wheatland Sturrock Roumeliotis algorithm”, Solar Phys., 235, 201–221. [DOI], [ADS] (Cited on page 31.)
Inhester, B., Feng, L. and Wiegelmann, T., 2008, “Segmentation of loops from coronal EUV images”, Solar Phys., 248, 379–393. [DOI], [ADS], [arXiv:0801.3240] (Cited on page 11.)
Jing, J., Tan, C., Yuan, Y., Wang, B., Wiegelmann, T., Xu, Y. and Wang, H., 2010, “Free Magnetic Energy and Flare Productivity of Active Regions”, Astrophys. J., 713, 440–449. [DOI], [ADS] (Cited on page 37.)
Kaiser, G., 2000, “Complex-Distance Potential Theory and Hyperbolic Equations”, in Clifford Algebras and their Applications in Mathematical Physics, Vol. 2: Clifford Analysis, (Eds.)Ryan, J., Sprößig, W., vol. 19 of Progress in Mathematical Physics, p. 135, Birkhäuser, Boston. [ADS] (Cited on page 8.)
Kaiser, M.L., Kucera, T.A., Davila, J.M., St Cyr, O.C., Guhathakurta, M. and Christian, E., 2008, “The STEREO mission: An introduction”, Space Sci. Rev., 136, 5–16. [DOI], [ADS] (Cited on page 11.)
LaBonte, B.J., Mickey, D.L. and Leka, K.D., 1999, “The Imaging Vector Magnetograph at Haleakalä. II. Reconstruction of Stokes Spectra”, Solar Phys., 189, 1–24. [DOI], [ADS] (Cited on page 16.)
Lagg, A., Woch, J., Krupp, N. and Solanki, S.K., 2004, “Retrieval of the full magnetic vector with the He I multiplet at 1083 nm. Maps of an emerging flux region”, Astron. Astrophys., 414, 1109–1120. [DOI], [ADS] (Cited on page 16.)
Landi Degl'Innocenti, E., 1992, “Magnetic Field Measurements”, in Solar Observations: Techniques and interpretation, (Eds.) Sánchez, F., Collados, M., Vázquez, M., pp. 71–143, Cambridge University Press, Cambridge; New York}. [ADS], [Google Books] (Cited on page 1
Landi Degl'Innocenti, E. and Landolfi, M., 2004, Polarization in Spectral Lines, vol. 307 of Astrophysics and Space Science Library, Kluwer, Dordrecht; New York. [DOI], [ADS], [Google Books] (Cited on page 16.)
Leka, K.D. and Skumanich, A., 1999, “On the value of ‘αAR’ from vector magnetograph data. I. Methods and Caveats”, Solar Phys., 188, 3–19. [ADS] (Cited on page 11.)
Leka, K.D., Barnes, G., Crouch, A.D., Metcalf, T.R., Gary, G.A., Jing, J. and Liu, Y., 2009, “Resolving the 180. Ambiguity in Solar Vector Magnetic Field Data: Evaluating the Effects of Noise, Spatial Resolution, and Method Assumptions”, Solar Phys., 260, 83–108. [DOI], [ADS] (Cited on page 21.)
Leka, K.D., Barnes, G., Gary, G.A., Crouch, A.D. and Liu, Y., 2012, “rResponse to ‘Comment on Resolving the 180° Ambiguity in Solar Vector Magnetic Field Data: Evaluating the Effects of Noise, Spatial Resolution, and Method Assumptions’”, Solar Phys., 276, 441–450. [DOI], [ADS], [arXiv:1110.2697 [astro-ph.SR]] (Cited on page 21.)
Lemen, J.R., Title, A.M., Akin, D.J., Boerner, P.F., Chou, C., Drake, J.F., Duncan, D.W., Edwards, C.G., Friedlaender, F.M., Heyman, G.F., Hurlburt, N.E., Katz, N.L., Kushner, G.D., Levay, M., Lindgren, R.W., Mathur, D.P., McFeaters, E.L., Mitchell, S., Rehse, R.A., Schrijver, C.J., Springer, L.A., Stern, R.A., Tarbell, T.D., Wülser, J.-P., Wolfson, C.J., Yanari, C., Bookbinder, J.A., Cheimets, P.N., Caldwell, D., Deluca, E.E., Gates, R., Golub, L., Park, S., Podgorski, W.A., Bush, R.I., Scherrer, P.H., Gummin, M.A., Smith, P., Auker, G., Jerram, P., Pool, P., Soufli, R., Windt, D.L., Beardsley, S., Clapp, M., Lang, J. and Waltham, N., 2012, “The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO)”, Solar Phys., .275, 17–40. [DOI], [ADS] (Cited on page 38.)
Li, J., Cuperman, S. and Semel, M., 1993, “On the removal of the 180° sign ambiguity in vector magnetograph measurements: the divergence-free method (divergence of B identical to 0)”, Astron. Astrophys., 279, 214–224. [ADS] (Cited on page 22.)
Li, J., Amari, T. and Fan, Y., 2007, “Resolution of the 180° ambiguity for inverse horizontal magnetic field configurations”, Astrophys. J., 654, 675–686. [DOI], [ADS] (Cited on page 22.)
Lites, B.W., Elmore, D.F., Streander, K.V., Hoffmann, C.M., Tarbell, T.D., Title, A.M., Shine, R.A., Ichimoto, K., Tsuneta, S., Shimizu, T. and Suematsu, Y., 2007, “Performance Characteristics of the Solar-B Spectro-Polarimeter”, in New Solar Physics with Solar-B Mission, Proceedings of the Sixth Solar-B Science Meeting held at Kyoto, Japan, 8–11 November 2005, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, pp. 55–58, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 16.)
Low, B.C., 1973, “Resistive diffusion of force-free magnetic fields in a passive medium”, Astrophys. J., 181, 209–226. [DOI], [ADS] (Cited on page 14.)
Low, B.C., 1977, “Evolving force-free magnetic fields. I. The development of the preflare stage”, Astrophys. J., 212, 234–242. [DOI], [ADS] (Cited on page 14.)
Low, B.C. and Lou, Y.Q., 1990, “Modeling solar force-free magnetic fields”, Astrophys. J., 352, 343–352. [DOI], [ADS] (Cited on pages 13 and 14.)
Lundquist, S., 1950, “Magneto-hydrodynamic fields”, Ark. Fys., 2, 361–365} (Cited on page 14.)
Malanushenko, A., Longcope, D.W. and McKenzie, D.E., 2009, “Reconstructing the Local Twist of Coronal Magnetic Fields and the Three-Dimensional Shape of the Field Lines from Coronal Loops in Extreme-Ultraviolet and X-Ray Images”, Astrophys. J., 707, 1044–1063. [DOI], [ADS], [arXiv:0909.5141 [astroph. SR]] (Cited on page 13.)
Marsch, E., Wiegelmann, T. and Xia, L.D., 2004, “Coronal plasma flows and magnetic fields in solar active regions. Combined observations from SOHO and NSO/Kitt Peak”, Astron. Astrophys., 428, 629–645. [ADS] (Cited on page 13.)
Marsh, G.E., 1996, Force-Free Magnetic Fields: Solutions, Topology and Applications, World Scientific, Singapore; River Edge, NJ (Cited on page 14.)
Martin, S.F., Lin, Y. and Engvold, O., 2008, “A method of resolving the 180-degree ambiguity by employing the chirality of solar features”, Solar Phys., 250, 31–51. [DOI], [ADS] (Cited on page 22.)
McClymont, A.N., Jiao, L. and Mikić, Z., 1997, “Problems and progress in computing three-dimensional coronal active region magnetic fields from boundary data”, Solar Phys., 174, 191–218. [DOI], [ADS] (Cited on page 32.)
Metcalf, T.R., 1994, “Resolving the 180-degree ambiguity in vector magnetic field measurements: The ‘minimum’ energy solution”, Solar Phys., 155, 235–242. [DOI], [ADS] (Cited on pages 20 and 24.)
Metcalf, T.R., Jiao, L., McClymont, A.N., Canfield, R.C. and Uitenbroek, H., 1995, “Is the solar chromospheric magnetic field force-free?”, Astrophys. J., 439, 474–481. [DOI], [ADS] (Cited on page 23.)
Metcalf, T.R., Leka, K.D., Barnes, G., Lites, B.W., Georgoulis, M.K., Pevtsov, A.A., Balasubramaniam, K.S., Gary, G.A., Jing, J., Li, J., Liu, Y., Wang, H.N., Abramenko, V., Yurchyshyn, V. and Moon, Y.-J., 2006, “An overview of existing algorithms for resolving the 180° ambiguity in vector magnetic fields: Quantitative tests with synthetic data”, Solar Phys., 237, 267–296. [DOI], [ADS] (Cited on pages 16, 17, 18, 19, 20, and 21.)
Metcalf, T.R., DeRosa, M.L., Schrijver, C.J., Barnes, G., van Ballegooijen, A.A., Wiegelmann, T., Wheatland, M.S., Valori, G. and McTiernan, J.M., 2008, “Nonlinear force-free modeling of coronal magnetic fields. II. Modeling a filament arcade and simulated chromospheric and photospheric vector fields”, Solar Phys., 247, 269–299. [DOI], [ADS] (Cited on page 34.)
Mickey, D.L., Canfield, R.C., LaBonte, B.J., Leka, K.D., Waterson, M.F. and Weber, H.M., 1996, “The Imaging Vector Magnetograph at Haleakala”, Solar Phys., 168, 229–250. [DOI], [ADS] (Cited on page 16.)
Mikić, Z. and McClymont, A.N., 1994, “Deducing coronal magnetic fields from vector magnetograms”, in Solar Active Region Evolution: Comparing Models with Observations, Proceedings of the 14th International Summer Workshop, NSO / Sacramento Peak, Sunspot, New Mexico, USA, 30 August–3 September 1993, (Eds.) Balasubramaniam, K.S., Simon, G.W., vol. 68 of ASP Conference Series, pp. 225–232, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 32.)
Mikić, Z., Barnes, D.C. and Schnack, D.D., 1988, “Dynamical evolution of a solar coronal magnetic field arcade”, Astrophys. J., 328, 830–847. [DOI], [ADS] (Cited on page 32.)
Molodenskii, M.M., 1969, “Integral properties of force-free fields”, Sov. Astron., 12, 585–588. [ADS] (Cited on page 23.)
Molodensky, M.M., 1974, “Equilibrium and stability of force-free magnetic field”, Solar Phys., 39, 393–404. [DOI], [ADS] (Cited on pages 23 and 28.)
Moon, Y.-J., Wang, H., Spirock, T.J., Goode, P.R. and Park, Y.D., 2003, “A new method for resolving the 180° ambiguity in solar vector magnetograms”, Solar Phys., 217, 79–94. [DOI], [ADS] (Cited on page 17.)
Nakagawa, Y., 1974, “Dynamics of the solar magnetic field. I. Method of examination of force-free magnetic fields”, Astrophys. J., 190, 437–440. [DOI], [ADS] (Cited on page 30.)
Neukirch, T., 2005, “Magnetic Field Extrapolation”, in Chromospheric and Coronal Magnetic Fields, Proceedings of the International Scientific Conference, 30 August–2 September 2005, Katlenburg-Lindau, Germany, (Eds.) Innes, D.E., Lagg, A., Solanki, S.K., vol. SP-596 of ESA Conference Proceedings, ESA Publications Division, Noordwijk. [ADS] (Cited on page 8.)
Pevtsov, A.A., Canfield, R.C. and Metcalf, T.R., 1994, “Patterns of helicity in solar active regions”, Astrophys. J. Lett., 425, L117–L119. [DOI], [ADS] (Cited on pages 11 and 25.)
Pevtsov, A.A., Canfield, R.C. and Metcalf, T.R., 1995, “Latitudinal variation of helicity of photospheric magnetic fields”, Astrophys. J. Lett., 440, L109–L112. [DOI], [ADS] (Cited on page 26.)
Priest, E.R., 1982, Solar Magnetohydrodynamics, vol. 21 of Geophysics and Astrophysics Monographs, Reidel, Dordrecht; Boston. [ADS], [Google Books] (Cited on page 27.)
Priest, E.R. and Milne, A.M., 1980, “Force-free magnetic arcades relevant to two-ribbon solar flares”, Solar Phys., .65, 315–346. [DOI], [ADS] (Cited on page 14.)
Rachkovsky, D.N., 1967, “The reduction for anomalous dispersion in the theory of the absorption line formation in a magnetic field”, Izv. Krymsk. Astrof. Obs., 37, 56–61. In Russian (Cited on page 16.)
Régnier, S. and Amari, T., 2004, “3D magnetic configuration of the H.. filament and X-ray sigmoid in NOAA AR 8151”, Astron. Astrophys., 425, 345–352. [DOI], [ADS] (Cited on page 37.)
Régnier, S., Amari, T. and Kersalé, E., 2002, “3D coronal magnetic field from vector magnetograms: non-constant-.. force-free configuration of the active region NOAA 8151”, Astron. Astrophys., 392, 1119–1127. [DOI], [ADS] (Cited on pages 25 and 36.)
Roumeliotis, G., 1996, “The ‘stress-and-relax’ method for reconstructing the coronal magnetic field from vector magnetograph data”, Astrophys. J., 473, 1095. [DOI], [ADS] (Cited on page 32.)
Rudenko, G.V. and Myshyakov, I.I., 2009, “Analysis of reconstruction methods for nonlinear force-free fields”, Solar Phys., 257, 287–304. [DOI], [ADS] (Cited on page 34.)
Sakurai, T., 1981, “Calculation of force-free magnetic field with non-constant α”, Solar Phys., 69, 343. [DOI], [ADS] (Cited on page 31.)
Sakurai, T., 1989, “Computational modeling of magnetic fields in solar active regions”, Space Sci. Rev., 51, 11–48. [DOI], [ADS] (Cited on page 26.)
Sakurai, T., 2007, “Two fundamental MHD problems in solar physics”, in New Solar Physics with Solar-B Mission, Proceedings of the Sixth Solar-B Science Meeting held at Kyoto, Japan, 8–11 November 2005, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, pp. 587–592, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 27.)
Sakurai, T., Ichimoto, K., Nishino, Y., Shinoda, K., Noguchi, M., Hiei, E., Li, T., He, F., Mao, W., Lu, H., Ai, G., Zhao, Z., Kawakami, S. and Chae, J., 1995, “Solar flare telescope at Mitaka”, Publ. Astron. Soc. Japan, 47, 81–92. [ADS] (Cited on page 16.)
Sandman, A.W., Aschwanden, M.J., DeRosa, M.L., Wülser, J.P. and Alexander, D., 2009, “Comparison of STEREO/EUVI loops with potential magnetic field models”, Solar Phys., 259, 1–11. [DOI], [ADS] (Cited on page 7.)
Schatten, K.H., Wilcox, J.M. and Ness, N.F., 1969, “A model of interplanetary and coronal magnetic fields”, Solar Phys., 6, 442–455. [DOI], [ADS] (Cited on page 7.)
Scherrer, P.H., Schou, J., Bush, R.I., Kosovichev, A.G., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall Jr, T.L., Zhao, J., Title, A.M., Schrijver, C.J., Tarbell, T.D. and Tomczyk, S., 2012, “The Helioseismic and Magnetic Imager (HMI) investigation for the Solar Dynamics Observatory (SDO)”, Solar Phys., 275, 207–227. [DOI], [ADS] (Cited on page 16.)
Schou, J., Scherrer, P.H., Bush, R.I., Wachter, R., Couvidat, S., Rabello-Soares, M.C., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall Jr, T.L., Akin, D.J., Allard, B.A., Miles, J.W., Rairden, R., Shine, R.A., Tarbell, T.D., Title, A.M., Wolfson, C.J., Elmore, D.F., Norton, A.A. and Tomczyk, S., 2012, “Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO)”, Solar Phys., 275, 229–259. [DOI], [ADS] (Cited on page 16.)
Schrijver, C.J., DeRosa, M.L., Title, A.M. and Metcalf, T.R., 2005, “The nonpotentiality of active-region coronae and the dynamics of the photospheric magnetic field”, Astrophys. J., 628, 501–513. [DOI], [ADS] (Cited on page 7.)
Schrijver, C.J., DeRosa, M.L., Metcalf, T.R., Liu, Y., McTiernan, J., Régnier, S., Valori, G., Wheatland, M.S. and Wiegelmann, T., 2006, “Nonlinear force-free modeling of coronal magnetic fields part I: A quantitative comparison of methods”, Solar Phys., 235, 161–190. [DOI], [ADS] (Cited on pages 15 and 34.)
Schrijver, C.J., DeRosa, M.L., Metcalf, T., Barnes, G., Lites, B.W., Tarbell, T.D., McTiernan, J., Valori, G., Wiegelmann, T., Wheatland, M.S., Amari, T., Aulanier, G., Démoulin, P., Fuhrmann, M., Kusano, K., Régnier, S. and Thalmann, J.K., 2008, “Nonlinear force-free field modeling of a solar active region around the time of a major flare and coronal mass ejection”, Astrophys. J., 675, 1637–1644. [DOI], [ADS], [arXiv:0712.0023] (Cited on pages 34 and 35.)
Seehafer, N., 1978, “Determination of constant α force-free solar magnetic fields from magnetograph data”, Solar Phys., 58, 215–223. [DOI], [ADS] (Cited on pages 10 and 25.)
Song, M.T., Fang, C., Tang, Y.H., Wu, S.T. and Zhang, Y.A., 2006, “A new and fast way to reconstruct a nonlinear force-free field in the solar corona”, Astrophys. J., 649, 1084–1092. [DOI], [ADS] (Cited on page 31.)
Stern, D.P., 1970, “Euler potentials”, Am. J. Phys., 38, 494.501. [DOI], [ADS] (Cited on page 26.)
Sturrock, P.A., 1991, “Maximum energy of semi-infinite magnetic field configurations”, Astrophys. J., 380, 655–659. [DOI], [ADS] (Cited on page 27.)
Sturrock, P.A., 1994, Plasma Physics: An Introduction to the Theory of Astrophysical, Geophysical and Laboratory Plasmas, Cambridge University Press, Cambridge; New York. [ADS] (Cited on page 14.)
Sun, X., Hoeksema, J.T., Liu, Y., Wiegelmann, T., Hayashi, K., Chen, Q. and Thalmann, J., 2012, “Evolution of Magnetic Field and Energy in a Major Eruptive Active Region Based on SDO/HMI Observation”, Astrophys. J., .748, 77. [DOI], [ADS], [arXiv:1201.3404 [astro-ph.SR]] (Cited on page 37.)
Taylor, J.B., 1974, “Relaxation of toroidal plasma and generation of reverse magnetic fields”, Phys. Rev. Lett., 33, 1139.1141. [DOI], [ADS] (Cited on page 27.)
Taylor, J.B., 1986, “Relaxation and magnetic reconnection in plasmas”, Rev. Mod. Phys., 58, 741–763. [DOI], [ADS] (Cited on page 27.)
Thalmann, J.K. and Wiegelmann, T., 2008, “Evolution of the flaring active region NOAA 10540 as a sequence of nonlinear force-free field extrapolations”, Astron. Astrophys., 484, 495–502. [DOI], [ADS] (Cited on page 36.)
Thalmann, J.K., Wiegelmann, T. and Raouafi, N.-E., 2008, “First nonlinear force-free field extrapolations of SOLIS/VSM data”, Astron. Astrophys., 488, L71–L74. [DOI], [ADS], [arXiv:0809.1428] (Cited on page 36.)
Titov, V.S. and Démoulin, P., 1999, “Basic topology of twisted magnetic configurations in solar flares”, Astron. Astrophys., 351, 707–720. [ADS] (Cited on page 15.)
Titov, V.S., Priest, E.R. and Démoulin, P., 1993, “Conditions for the appearance of ‘bald patches’ at the solar surface”, Astron. Astrophys., 276, 564–570. [ADS] (Cited on page 21.)
Török, T. and Kliem, B., 2005, “Confined and ejective eruptions of kink-unstable flux ropes”, Astrophys. J. Lett., 630, L97–L100. [DOI], [ADS] (Cited on pages 28 and 29.)
Tsuneta, S., Ichimoto, K., Katsukawa, Y., Nagata, S., Otsubo, M., Shimizu, T., Suematsu, Y., Nakagiri, M., Noguchi, M., Tarbell, T.D., Title, A.M., Shine, R.A., Rosenberg, W., Hoffmann, C.M., Jurcevich, B.K., Kushner, G.D., Levay, M., Lites, B.W., Elmore, D.F., Matsushita, T., Kawaguchi, N., Saito, H., Mikami, I., Hill, L.D. and Owens, J.K., 2008, “The Solar Optical Telescope for the Hinode mission: An overview”, Solar Phys., 249, 167–196. [DOI], [ADS], [arXiv:0711.1715] (Cited on page 16.)
Unno, W., 1956, “Line Formation of a Normal Zeeman Triplet”, Publ. Astron. Soc. Japan, 8, 108–125. [ADS] (Cited on page 16.)
Valori, G., Kliem, B. and Keppens, R., 2005, “Extrapolation of a nonlinear force-free field containing a highly twisted magnetic loop”, Astron. Astrophys., 433, 335–347. [DOI], [ADS] (Cited on page 32.)
Valori, G., Kliem, B., Török, T. and Titov, V.S., 2010, “Testing magnetofrictional extrapolation with the Titov-Démoulin model of solar active regions”, Astron. Astrophys., 519, A44. [DOI], [ADS], [arXiv:1005.0254 [astro-ph.SR]] (Cited on page 15.)
Valori, G., Green, L.M., Démoulin, P., Vargas Domínguez, S., van Driel-Gesztelyi, L., Wallace, A., Baker, D. and Fuhrmann, M., 2012, “Nonlinear Force-Free Extrapolation of Emerging Flux with a Global Twist and Serpentine Fine Structures”, Solar Phys., 278, 73–97. [DOI], [ADS] (Cited on page 37.)
Wang, C. and Zhang, M., 2010, “A Hemispheric Helicity Sign Rule Indicated by Large-scale Photospheric Magnetic Fields at Three Phases of Solar Cycle 23”, Astrophys. J., 720, 632–638. [DOI], [ADS] (Cited on page 26.)
Wang, H., 1997, “Distribution of 2-D magnetic saddle points and morphology of flare kernels in solar active regions”, Solar Phys., 174, 265–279. [ADS] (Cited on page 17.)
Wang, H., Yan, Y. and Sakurai, T., 2001, “Topology of magnetic field and coronal heating in solar active regions”, Solar Phys., 201, 323–336. [DOI], [ADS] (Cited on page 17.)
Wheatland, M.S., 1999, “A better linear force-free field”, Astrophys. J., 518, 948–953. [DOI], [ADS] (Cited on page 11.)
Wheatland, M.S. and Régnier, S., 2009, “A self-consistent nonlinear force-free solution for a solar active region magnetic field”, Astrophys. J. Lett., 700, L88–L91. [DOI], [ADS], [arXiv:0906.4414] (Cited on pages 25, 31, and 35.)
Wheatland, M.S., Sturrock, P.A. and Roumeliotis, G., 2000, “An optimization approach to reconstructing force-free fields”, Astrophys. J., 540, 1150–1155. [DOI], [ADS] (Cited on pages 32 and 34.)
Wiegelmann, T., 2004, “Optimization code with weighting function for the reconstruction of coronal magnetic fields”, Solar Phys., 219, 87–108. [DOI], [ADS] (Cited on page 34.)
Wiegelmann, T., 2008, “Nonlinear force-free modeling of the solar coronal magnetic field”, J. Geophys. Res., 113(A12), 3. [DOI], [ADS], [arXiv:0801.2902] (Cited on page 30.)
Wiegelmann, T. and Inhester, B., 2010, “How to deal with measurement errors and lacking data in nonlinear force-free coronal magnetic field modelling?”, Astron. Astrophys., 516, A107. [DOI], [ADS] (Cited on pages 25, 33, and 35.)
Wiegelmann, T. and Neukirch, T., 2002, “Including stereoscopic information in the reconstruction of coronal magnetic fields”, Solar Phys., 208, 233–251. [DOI], [ADS], [arXiv:0801.3234] (Cited on page 13.)
Wiegelmann, T. and Solanki, S.K., 2004, “Why are Coronal Holes Indistinguishable from the Quiet Sun in Transition Region Radiation?”, in SOHO 15: Coronal Heating, Proceedings of the Workshop, 6 - 9 September 2004, St. Andrews, Scotland, UK, (Eds.) Walsh, R.W., Ireland, J., Danesy, D., Fleck, B., vol. SP-575 of ESA Conference Proceedings, pp. 35–40, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 7 and 8.)
Wiegelmann, T., Lagg, A., Solanki, S.K., Inhester, B. and Woch, J., 2005, “Comparing magnetic field extrapolations with measurements of magnetic loops”, Astron. Astrophys., 433, 701–705. [DOI], [ADS] (Cited on page 35.)
Wiegelmann, T., Inhester, B., Kliem, B., Valori, G. and Neukirch, T., 2006a, “Testing non-linear force-free coronal magnetic field extrapolations with the Titov-Démoulin equilibrium”, Astron. Astrophys., 453, 737–741. [DOI], [ADS] (Cited on page 15.)
Wiegelmann, T., Inhester, B. and Sakurai, T., 2006b, “Preprocessing of vector magnetograph data for a nonlinear force-free magnetic field reconstruction”, Solar Phys., 233, 215–232. [DOI] (Cited on pages 11 and 24.)
Wiegelmann, T., Thalmann, J.K., Schrijver, C.J., Derosa, M.L. and Metcalf, T.R., 2008, “Can we improve the preprocessing of photospheric vector magnetograms by the inclusion of chromospheric observations?”, Solar Phys., 247, 249–267. [DOI], [ADS], [arXiv:0801.2707] (Cited on page 24.)
Wolfson, R., 1995, “Shear-induced opening of the coronal magnetic field”, Astrophys. J., 443, 810–817. [DOI], [ADS] (Cited on page 15.)
Wolfson, R., Drake, C. and Kennedy, M., 2012, “Maximizing magnetic energy storage in the solar corona”, Astrophys. J., 750, 25. [DOI], [ADS] (Cited on page 38.)
Woltjer, L., 1958, “A theorem on force-free magnetic fields”, Proc. Natl. Acad. Sci. USA, 44, 489–491. [DOI], [ADS] (Cited on page 25.)
Wu, S.T., Chang, H.M. and Hagyard, M.J., 1985, “On the numerical computation of nonlinear force-free magnetic fields”, in Measurements of Solar Vector Magnetic Fields, (Ed.) Hagyard, M.J., vol. 2374 of NASA Conference Publication, pp. 17–40, NASA, Washington, DC (Cited on page 30.)
Wu, S.T., Sun, M.T., Chang, H.M., Hagyard, M.J. and Gary, G.A., 1990, “On the numerical computation of nonlinear force-free magnetic fields”, Astrophys. J., 362, 698–708. [DOI], [ADS] (Cited on page 30.)
Yan, Y. and Sakurai, T., 2000, “New boundary integral equation representation for finite energy forcefree magnetic fields in open space above the Sun”, Solar Phys., 195, 89–109. [DOI], [ADS] (Cited on page 34.)
Acknowledgements
TW was supported by DLR-grants 50 OC 0501 and 50 OC 0904.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wiegelmann, T., Sakurai, T. Solar Force-free Magnetic Fields. Living Rev. Sol. Phys. 9, 5 (2012). https://doi.org/10.12942/lrsp-2012-5
Published:
DOI: https://doi.org/10.12942/lrsp-2012-5
Keywords
- Magnetic Field Line
- Magnetic Field Vector
- Magnetic Helicity
- Coronal Magnetic Field
- Photospheric Magnetic Field
Article history
Latest
Solar force-free magnetic fields- Published:
- 11 January 2021
- Received:
- 10 July 2020
- Accepted:
- 05 November 2020
DOI: https://doi.org/10.1007/s41116-020-00027-4
Original
Solar Force-free Magnetic Fields- Published:
- 20 September 2012
DOI: https://doi.org/10.12942/lrsp-2012-5