Abstract
Solar eruptive phenomena embrace a variety of eruptions, including flares, solar energetic particles, and radio bursts. Since the vast majority of these are associated with the eruption, development, and evolution of coronal mass ejections (CMEs), we focus on CME observations in this review. CMEs are a key aspect of coronal and interplanetary dynamics. They inject large quantities of mass and magnetic flux into the heliosphere, causing major transient disturbances. CMEs can drive interplanetary shocks, a key source of solar energetic particles and are known to be the major contributor to severe space weather at the Earth. Studies over the past decade using the data sets from (among others) the SOHO, TRACE, Wind, ACE, STEREO, and SDO spacecraft, along with ground-based instruments, have improved our knowledge of the origins and development of CMEs at the Sun and how they contribute to space weather at Earth. SOHO, launched in 1995, has provided us with almost continuous coverage of the solar corona over more than a complete solar cycle, and the heliospheric imagers SMEI (2003–2011) and the HIs (operating since early 2007) have provided us with the capability to image and track CMEs continually across the inner heliosphere. We review some key coronal properties of CMEs, their source regions and their propagation through the solar wind. The LASCO coronagraphs routinely observe CMEs launched along the Sun-Earth line as halo-like brightenings. STEREO also permits observing Earth-directed CMEs from three different viewpoints of increasing azimuthal separation, thereby enabling the estimation of their three-dimensional properties. These are important not only for space weather prediction purposes, but also for understanding the development and internal structure of CMEs since we view their source regions on the solar disk and can measure their in-situ characteristics along their axes. Included in our discussion of the recent developments in CME-related phenomena are the latest developments from the STEREO and LASCO coronagraphs and the SMEI and HI heliospheric imagers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coronal mass ejections (CMEs) consist of large structures containing plasma and magnetic fields that are expelled from the Sun into the heliosphere. They are of interest for both scientific and technological reasons. Scientifically they are of interest because they remove built-up magnetic energy and plasma from the solar corona (Low, 1996), and technologically they are of interest because they are responsible for the most extreme space weather effects at Earth (Baker et al., 2008), as well as at other planets and spacecraft throughout the heliosphere. Most of the ejected material comes from the low corona, although cooler, denser material probably of chromospheric or photospheric origin is also sometimes involved. The CME plasma is entrained on an expanding magnetic field, which commonly has the form of helical field lines with changing pitch angles, i.e., a flux rope. This paper reviews the best-determined coronal properties of CMEs and what we know about their source regions, and some key signatures of CMEs in the solar wind. Observations of Earth-directed CMEs, often observed as halos surrounding the occulting disk of near-Earth coronagraphs, are important for space weather studies.
Until the early years of this century, images of CMEs had been made near the Sun primarily by coronagraphs on board spacecraft. Coronagraphs view the outward flow of density structures emanating from the Sun by observing Thomson-scattered sunlight from the free electrons in coronal and heliospheric plasma. This emission has an angular dependence which must be accounted for in the measured brightness (e.g., Billings, 1966; Vourlidas and Howard, 2006; Howard and Tappin, 2009). They are faint relative to the background corona, but much more transient, so some form of background subtraction is typically applied to identify them. CME-related phenomena such as flares and prominence eruptions have been known since the late 19th century, and energetic particles (Forbush, 1946), type II and IV radio bursts (Wild et al., 1954), and interplanetary shocks (Sonnett et al., 1964) have been observed since the 1940s, 50s and 60s. The first spacecraft coronagraph observations of CMEs were made by the OSO-7 coronagraph in the early 1970s (Tousey, 1973). These were followed by better quality and longer periods of CME observations using Skylab (1973 – 1974; MacQueen et al., 1980), P78-1 (Solwind) (1979 – 1985; Sheeley Jr et al., 1980), and SMM (1980; 1984 – 1989; Hundhausen, 1999). In late 1995, SOHO was launched and two of its three LASCO coronagraphs still operate today (Brueckner et al., 1995). Finally late in 2006, LASCO was joined by the STEREO CORs (Howard et al., 2008a). These early observations were complemented by white light data from the ground-based Mauna Loa Solar Observatory (MLSO) K-coronameter viewing from 1.2 – 2.9R⊙ (Fisher et al., 1981; Koomen et al., 1974) and green line observations from the coronagraphs at Sacramento Peak, New Mexico (Demastus et al., 1973) and Norikura, Japan (Hirayama and Nakagomi, 1974).
Throughout the early years also, at larger distances from the Sun, interplanetary transients were observed using interplanetary radio scintillation (1964 — present; Hewish et al., 1964; Houminer and Hewish, 1974; Vlasov, 1981) and from the zodiacal light photometers on the twin Helios spacecraft (1975 – 1983; Richter et al., 1982; Jackson, 1985). The Helios photometers observed regions in the inner heliosphere from 0.3 – 1.0 AU but with an extremely limited field of view. The new millennium witnessed the arrival of a new class of detector, the heliospheric imager, with the Solar Mass Ejection Imager (SMEI) launched on board the Coriolis spacecraft early in 2003 and the Heliospheric Imagers (HIs) launched on the twin STEREO spacecraft in late 2006. LASCO has detected well over 104 CMEs during its lifetime (Yashiro et al., 2004; Gopalswamy et al., 2009b; http://cdaw.gsfc.nasa.gov/CME_list/). SMEI observed nearly 400 transients during its 8.5 year lifetime (Webb, 2004; Webb et al., 2006; Howard and Simnett, 2008); it was switched off in September 2011. The number of “events” reported using the HIs is now over 1340 (http://www.stereo.rl.ac.uk/HIEventList.html), although less than 100 have been discussed so far in the scientific literature.
These mostly white light observations have been accompanied by those of the solar disk at coronal wavelengths including the SOHO Extreme Ultraviolet Imaging Telescope (EIT), SOHO Coronal Diagnostic Spectrometer (CDS) imagers, STEREO Extreme-UltraViolet Imager (EUVI), and instruments on board the Yohkoh, TRACE, RHESSI, and Hinode spacecraft (see Hudson and Cliver, 2001), as well as near and beyond 1 AU by in-situ experiments on spacecraft including the Voyagers, Ulysses, Helios, Wind, ACE, and STEREO. In February 2010 the Solar Dynamics Observatory (SDO) spacecraft joined the solar disk imaging ensemble, while EIT, Yohkoh, TRACE, SMEI and Ulysses no longer return scientific data. In addition, important new plasma diagnostics of CMEs have been obtained from ultraviolet spectroscopy from SOHO (CDS, SUMER, and UVCS, Hinode (EIS) and SDO (EVE). The UVCS instrument, in particular, which overlaps the same height range as LASCO C2, has provided a wealth of data on the evolution of hundreds of CMEs (see review by Kohl et al., 2006). Figure 1 shows a timeline of the launches of spacecraft relevant to CME study.
Timeline of the history of spacecraft relevant to CME study. Image adapted from Howard (2011b).
White light observations of CMEs reveal that, even near the sun, the CME can dwarf the solar disk (see Figure 2). Coronal images of CMEs have also been obtained at radio frequencies, beginning with the pioneering work at the Culgoora (Australia) Radioheliograph in the 1970s. Much of this involved the tracking of shocks (via type II bursts) through the corona and into the heliosphere, but both thermal (Gopalswamy and Kundu, 1992) and non-thermal CME radio emission (such as type IV bursts) have also been imaged. Figure 3 shows a rare image of a radio CME from the Nançay (France) Radioheliograph. The onset of CMEs has been associated with many solar disk phenomena such as flares (e.g., Feynman and Hundhausen, 1994), prominence eruptions (e.g., Hundhausen, 1999), coronal dimming (e.g., Sterling and Hudson, 1997; Thompson et al., 1999), arcade formation (e.g., Hanaoka et al., 1994; Hudson and Webb, 1997), and X-ray sigmoids (e.g., Canfield et al., 1999). However, the vast majority of the ejected energy assumes the form of mechanical energy carried by the CME and not the associated solar flare, even in the most energetic cases (Emslie et al., 2004). Many CMEs have also been observed to be unassociated with any obvious solar surface activity (Howard and Tappin, 2008; Robbrecht et al., 2009a). Most flares occur independently of CME eruptions and it now seems likely that any flare accompanying a CME is part of an underlying magnetic process rather than being a direct cause of the CME launch (Kahler, 1992; Gosling, 1993). Recent models describing the onset and early evolution of CMEs (e.g., Moore and Roumeliotis, 1992; Antiochos et al., 1999; Fan and Gibson, 2003; Lynch et al., 2005) provide a variety of mechanisms by which this may be accomplished.
Evolution of a “classic” CME observed by the LASCO C2 coronagraph on 2 June 1998. Note the circular structures just above the prominence, suggesting a flux rope. Image reproduced with permission from Plunkett et al. (2000), copyright by Springer.
a) Snapshot map of a radio CME at a frequency of 164 MHz at the time of maximum flux. The background emission from the Sun has been subtracted. Time variable radio emission from a noise storm is present to the northwest (upper right). The brightness of the CME is saturated in the corona because the map has been clipped at a level of 0.04 SFU beam-1, corresponding to a brightness temperature of 2.6 × 105 K. The radio CME is visible as a complex ensemble of loops extended out to the southwest (lower right). Also shown is the spectral index measured at four locations in the radio CME. b) Flux spectra measured at the four points shown in (a). All flux measurements have been normalized to SFU N -1beam , where Nbeam is the 164 MHz beam. Model spectra are also shown. Image reproduced with permission from Bastian et al. (2001).
We refer the reader to reviews of these models by, for example, Forbes et al. (2006), rather than discuss them at length here in this review of CME observations. We also draw the reader’s attention to other reviews of solar eruptive phenomena and CMEs, including Kahler (1992, 2006), Webb et al. (1996), Hundhausen (1997, 1999), Low (1997), St Cyr et al. (2000), Webb (2002, 2004), Gopalswamy (2004), Gopalswamy et al. (2006b), and Aschwanden (2006). Several recent journal special issue volumes are devoted to CMEs: LASCO-era CMEs (Kunow et al., 2006), CME and energetic particles (Gopalswamy et al., 2006a), STEREO results (Christian et al., 2009), and 3-D measurements (Mierla et al., 2011). In addition, see also the Living Reviews by Schwenn (2006) and Chen (2011), and other Living Reviews in Solar Physics articles on prominences, flares, space weather, and other related phenomena. One of us has also recently published an introductory text on CMEs (Howard, 2011b).
2 Properties of CMEs
The measured properties of CMEs include their occurrence rates, locations relative to the solar disk, angular widths, speeds and accelerations, masses, and energies (e.g., Hundhausen, 1972; Kahler, 1992; St Cyr et al., 2000; Webb, 2002; Yashiro et al., 2004; Gopalswamy et al., 2005, 2006b; Gopalswamy, 2010b; Kahler, 2006; Vourlidas et al., 2010). There is a large range in the basic properties of CMEs, although some of this scatter is likely due to imaging projection effects (e.g., Burkepile et al., 2004; Cremades and Bothmer, 2004). Their speeds, accelerations, masses, and energies extend over 2 – 3 orders of magnitude (e.g., Vourlidas et al., 2002a; Gopalswamy et al., 2006b), and their angular widths exceed by factors of 3 – 10 the sizes of flaring active regions (e.g., Yashiro et al., 2004). Note that the measured values in the above cited publications make the assumption that all the CME material is in the “plane of the sky”, i.e., in the plane orthogonal to the Sun-Earth line. Thus, for example, unless a CME is exactly at the solar limb, its derived properties will be an underestimate and the width an overestimate. Recent developments using auxiliary data (Howard et al., 2007, 2008b) and the multiple viewpoint capability of STEREO (e.g., Mierla et al., 2010, and references therein) have attempted to overcome this problem. These are discussed later. Table 1 summarizes the statistical properties from all of the near-Earth space borne coronagraph observations of CMEs (summaries of most CME parameters observed by the STEREO spacecraft are not yet available).
CMEs can exhibit a variety of forms, some having the classical “three-part” structure (Illing and Hundhausen, 1985), usually interpreted as compressed plasma ahead of a flux rope followed by a cavity surrounded by a bright filament/prominence (Figure 2). Other CMEs display a more complex geometry. Some CMEs appear as narrow jets, some arise from pre-existing coronal streamers (the so-called streamer blowouts), while others appear as wide almost global eruptions. CMEs spanning very large angular ranges are probably not really global, but rather have a large component along the Sun-observer line and so appear large by perspective. These include the so-called halo CMEs (Howard et al., 1982) — see Section 2.3. The CDAW CME catalog (Yashiro et al., 2004) defines a “partial halo” as a CME with an apparent position angle range > 120°. Hence, again, the definition of a CME is restricted by its viewing perspective. Figure 4 illustrates several examples of partial and full halo CMEs observed by LASCO.
Examples of a variety of halo CME observations, clockwise: a frontside full halo (arrow shows likely source near Sun center); a backside full halo; a partial halo; and an asymmetric full halo. Image reproduced with permission from Gopalswamy et al. (2003a).
Figure 5 shows images of the same event (the Earth-directed CME from early April 2010) observed from three different viewpoints. Figure 5b shows the perspective from LASCO, which is along the Sun-Earth line, where the CME appears as a halo. Figures 5a and c show the same CME as observed by each STEREO spacecraft, which were separated in longitude by around 70° from LASCO at the time. The event appears in each COR-2 image as a limb CME directed towards the left (right) relative to STEREO-A (-B). The dramatic change in the appearance of this CME, with the only physical change being the viewing location, demonstrates the importance of perspective with respect to measuring CME properties.
Images of the same Earth-directed CME obtained from three different viewing locations within an hour: a) from STEREO/COR2-B on 3 April 2010 at 11:39 UT, b) from LASCO/C2 at 10:55 UT, and c) from STEREO/COR2-A on the same day at 11:08 UT. At this time (April 2010) the STEREO spacecraft were approximately 70° in longitude from the Sun-Earth line and ∼ 140° from each other. The different appearances of this same CME observed at around the same time demonstrate the need to consider perspective in measuring CME properties.
2.1 CME identification and measurement
Traditionally CME observations were obtained by visual inspection of coronagraph images, and many of these “manual” catalogs of CMEs observed by the P78/Solwind (http://lasco-www.nrl.navy.mil/solwind_transient.list), SMM C/P (http://smm.hao.ucar.edu/smm/smmcp_catalog.html), and LASCO C2 and C3 coronagraphs (http://cdaw.gsfc.nasa.gov/CME_list/index.html) are now on-line (Boursier et al., 2009; Gopalswamy et al., 2009b). These catalogs have in recent times been augmented by additional on-line catalogs of CMEs detected by automatic methods. One is the CACTus CME catalog (Robbrecht et al., 2009a), which uses the Hough transform to detect motion of the brightest structures of CMEs. The SEEDS (Olmedo et al., 2008) and ARTEMIS (Boursier et al., 2009) catalogs are based on automated detection of CMEs in the LASCO C2 coronagraph observed at ∼ 2 – 6R⊙. ARTEMIS detects CMEs on synoptic Carrington maps. CACTus also catalogs CMEs detected by the STEREO COR2 coronagraphs, which are in near-1 AU solar orbits.
Comparisons among the LASCO catalogs have shown significant differences. For example, Robbrecht et al. (2009a) found that CACTus automatically identified many more events than in the CDAW (manual) catalog but half of them were narrow (< 20° of apparent angular width). In addition, as shown in Figure 6, the shapes of the CME rate curves were quite different with the CACTus and sunspot curves similar, but the CDAW curve flattened out during the cycle decline. This and other comparisons suggest that the CDAW catalog is affected by observer bias since it has been compiled by at least four different observers throughout the lifetime of the SOHO mission. One example of this bias appears in the occurrence rate in later years of the SOHO mission. Occurrence rate increased greatly after 2004, not because more CMEs were physically erupting, but rather because a decision was made to categorize very narrow LASCO features, which were previously disregarded, as CMEs. Another comparison of CME properties of the four LASCO catalogs shows best agreement between the ARTEMIS and SEEDS catalogs (Boursier et al., 2009), which better reflect the early stages of CMEs (i.e., within the LASCO C2 field of view). A recent analysis of LASCO CMEs based on a multiscale method convolving high and low-pass filters with CME images (Byrne et al., 2009) has shown that multiscale values agree much better with the generally smaller SEEDS CME widths than with the larger CACTus and CDAW values. A comparison of the LASCO fast (v > 1000 km s-1) CMEs between the CDAW and CACTus catalogs shows that the CDAW fast CME widths are considerably wider (Yashiro et al., 2008b). The CACTus CME width distribution is essentially scale invariant in angular span over a range of scales from 20 – 120° while previous catalogs present a broad maximum around 30°. Yashiro et al. (2008b) found that the CACTus catalog has a larger number of narrow CMEs than CDAW, and that the CDAW catalog missed many narrow CMEs during solar maximum. Another significant discrepancy was that the majority of the fast CDAW CMEs are wide and originate from low latitudes, while the fast CACTus CMEs are narrow and originate from all latitudes. In general, automatic catalogs do not always identify wide CMEs, including halos which are the most important ones for space weather applications when observing from near the Earth (e.g., see Figure 8 in Gopalswamy et al., 2010b).
Daily SOHO LASCO CME rates for Cycle 23 (thin curves: smoothed per month, thick curves: smoothed over 13 months) from 1997 — 2006. These have been extracted using CACTus (red) and the CDAW CME Catalog (blue). As reference, the daily and smoothed monthly sunspot number have been overplotted in gray (produced using the SIDC-Royal Observatory of Belgium). The CME rates have been adjusted to accommodate for duty cycle. Image reproduced with permission from Robbrecht et al. (2009a), copyright by IOP.
The above discussion demonstrates that CME identification and measurement remain somewhat subjective and no consensus has yet been achieved regarding the establishment of a standard definition of a CME or of the components within. The original definition of a CME as a new, discrete brightening in the field of view over a time-scale of tens of minutes which is always observed to move outward (e.g., Webb and Hundhausen, 1987) is still generally accepted. However, some workers tend to regard any eruption from the Sun observed in the corona, no matter how faint or narrow, as a CME while others regard an eruption as a CME only if it has a certain size or structure. Although a “typical” CME is now thought to involve the eruption of a magnetic flux rope, the structure and magnitude of any CME magnetic field near the Sun can only be inferred, since we cannot directly measure coronal magnetic fields. Efforts to make the connection between magnetic flux ropes measured in-situ with CME structure observed by coronagraphs have been made, most recently by Howard and DeForest (2012a).
2.2 Frequency of occurrence
The frequency of occurrence of CMEs observed in white light tends to follow the solar cycle in both phase and amplitude, which varies by an order of magnitude over the cycle (Webb and Howard, 1994). LASCO has now observed the entire Solar Cycle 23 (1996 – 2008) (Figure 7) and continues to observe through this current rising phase of Cycle 24. It has detected CMEs at a rate slightly higher than earlier observations, varying from around one per day around solar minimum to nearly five per day at solar maximum (St Cyr et al., 2000; Gopalswamy et al., 2005, 2006b). This has been attributed to the improved sensitivity of LASCO as opposed to any physical difference between CME activity in Cycle 23 and that in prior cycles. LASCO, for example, observes halo CMEs (Section 2.3) regularly whereas no prior coronagraph observed more than a few (Howard et al., 1985, for example, only identified 20 halos out of 998 CMEs observed with Solwind)]. This demonstrates that a fraction of CMEs were undetectable by coronagraphs prior to LASCO. A 13-month running average of the LASCO CME rate vs. sunspot number shows that both have double peaks, but that the CME peak lagged sunspots by many months (Figure 8). This lag has also been seen in previous cycles and is related to observations that high latitude CMEs arise from polar crown filaments which have a “rush to the poles” near maximum and disappear (erupt) with a frequency that slightly lags sunspot numbers at low latitudes (Cliver and Webb, 1998; Gopalswamy et al., 2003b).
LASCO CME occurrence rate (left) and mean speed (right) from 1996 to 2011 averaged over Carrington rotations. The large spike in CME speed is due to highly energetic CMEs that erupted in the late 2003 period. Image adapted from Gopalswamy (2010b), updated by S. Yashiro (2011).
The LASCO CME rate smoothed over 13 Carrington rotations and compared with the solar sunspot number. Arrows indicate the two maxima in CME rate and sunspot number. Large data gaps occurred during June 1998 to February 1999. Image reproduced with permission from Gopalswamy (2004), copyright by Springer.
As has been well documented, Solar Cycle 23 had an unusually long decline and flat minimum, extending the cycle to ∼ 13 years, with the “true” minimum in late 2008 or early 2009 (Hathaway, 2010). Referring back to the updated LASCO CDAW CME rate in Figure 6, Figure 9 tracks the CME rate from the CDAW, SEEDS and CACTus catalogs from 2007 into 2011 along with the current and predicted SWPC sunspot number. Despite differences in amplitude, it is clear that the CME rate continues to be correlated with the sunspot number through its minimum and initial rise of Cycle 24, with the CME rate minimum in late 2008 or early 2009. The linear relationship between CME rate and sunspot numbers was first shown by Webb and Howard (1994) and recently confirmed for Cycle 23 by Robbrecht et al. (2009a) (Figure 10), although some variation over a solar cycle has been found (Gopalswamy et al., 2010a). In Figure 9 we have added the counting rate from the STEREO COR1 coronagraphs, demonstrating that the CME rate is relatively constant despite the increasing longitudinal angle between the STEREO spacecraft and Earth from 0 – 90° during this period.
Daily CME rate for 2010 – 2011 in the context of the rate through recent solar minimum. CME data sources: LASCO = manual online CDAW catalog (black - NRL, CUA) and our counts since January 2010 (light blue); SEEDS = automatic catalog (dotted red) courtesy J. Zhang and J. Bannick (GMU); CACTus = automatic catalog courtesy E. Robbrecht & B. Bourgoignie (SIDC); STEREO COR1 = manual catalog (green) courtesy C. St. Cyr (NASA) and H. Xie (CUA); Sunspot number (SSN — dark blue is current, dotted blue is predicted) from NOAA SWPC. CDAW and SEEDS rates are for CME widths > 20. CDAW, SEEDS, and SSN plots are 13-month, COR1 6-month, and 2010 LASCO counts 6-week running averages. Image courtesy T. Kuchar.
Daily CME rate vs. SSN both averaged per year. The asterisks refer to rates for Cycle 23 derived from CACTUS (see Table 1). Its absolute scale is shown on the right y-axis. The daily CME rates derived by Webb and Howard (1994) are plotted with diamonds. Its absolute scale is shown on the left y-axis. A scaling factor of ∼ 4.7 applies between the CACTus and the Webb and Howard rates. Image reproduced with permission from Robbrecht et al. (2009a), copyright by IOP.
2.3 Halo CMEs
Because of their increased sensitivity, field of view and dynamic range, the SOHO/LASCO and STEREO/COR coronagraphs now frequently observe halo CMEs, which appear as expanding, circular brightenings that completely surround the coronagraphs’ occulting disks (Figure 4). Observations of associated activity on the solar disk are necessary to help distinguish whether a halo CME was launched from the front or backside of the Sun relative to the observer. This has had limited success, as frontsided CMEs that do not have a solar surface association can be mistaken for backsided events. Halo CMEs are important for three reasons:
-
1.
The source regions of frontside halo CMEs are likely to be located within a few tens of degrees of Sun center from the perspective of the observer (Cane et al., 2000; Webb, 2002; Gopalswamy, 2004; Gopalswamy et al., 2010b). Thus, these regions can be studied in greater detail than for most CMEs which are observed near the limb, but at the cost of reduced information about the CME itself because of projection. In recent years several CMEs have been observed by the “three eyes” of STEREO-B, LASCO and STEREO-A by a variety of viewing points, thus reducing this latter problem (e.g., Howard and Tappin, 2008; Wood and Howard, 2009; Robbrecht et al., 2009b; Möstl et al., 2009, 2010; Patsourakos and Vourlidas, 2009).
-
2.
Lacking significant deflections in the interplanetary medium, frontside halo CMEs should travel with part of their structure approximately along the Sun-observer line, so their internal material can be sampled in-situ by the observer.
-
3.
When they are Earth-directed (i.e., observed as halos by spacecraft on the Sun-Earth line like SOHO), they are the key link between solar eruptions and major space weather phenomena such as geomagnetic storms and solar energetic particle events. This “geoeffectiveness” of halo CMEs depends on the source location on the disk. CMEs that are aligned near the relative disk center tend to be more geoeffective while those nearer the relative solar limb are less so. This center-to-limb variation of the geoeffectiveness has been documented (e.g., Gopalswamy et al., 2007). The vast majority of the most intense geomagnetic storms of Cycle 23, for example, were caused by halo CMEs (Gopalswamy, 2010a). Three spacecraft, SOHO, Wind and ACE, provide solar wind measurements upstream of Earth, and the twin STEREO spacecraft provide similar measurements from their perspectives drifting away from the Sun-Earth line.
Partial and full halo CMEs occur at a rate of about 10% that of all CMEs, but 360° halo CMEs are only detected at a rate of ∼ 4% of all CMEs. It has been documented (e.g., Gopalswamy et al., 2010a) that halo CMEs appear to be faster and more energetic than non-halo CMEs. This, of course, does not imply that halo CMEs are somehow physically different, but rather it shows that even with LASCO some CMEs are not detected. LASCO does not observe faint (weak) CMEs near Sun center. Studies investigating this include those involving post-eruptive arcades (Tripathi et al., 2004), interplanetary transients and shocks (Cane and Richardson, 2003; Howard and Tappin, 2005), and heliospheric imagers (Howard and Simnett, 2008). All found that between 3–7% of the studied CME-associated events were not associated with LASCO CMEs. Howard and Simnett (2008) further deduced that around 15% of interplanetary transients observed far from the Sun by SMEI were associated with either very weak CMEs or with those that had measurement problems, e.g., related to the large height and time separations between the LASCO and SMEI fields of view. However, this study did not exclusively involve halo CMEs.
2.4 Locations, widths, geometry
The latitude distribution of the central position angles of CMEs tends to cluster about the equator around solar minimum but broadens over all latitudes near solar maximum. Hundhausen (1993) first noted that this CME latitude variation more closely parallels that of streamers and prominences than of active regions or sunspots. This pattern also is closely linked to the variation of the global solar magnetic field, as exemplified by the tilt angle of the heliospheric current sheet (HCS) when the Sun makes its transition from solar minimum to maximum. This pattern including the match between CMEs, prominence eruptions and the HCS has been confirmed with the LASCO data (Figure 11 — Gopalswamy, 2004; Gopalswamy et al., 2010a). On this figure also note the sharp decrease in the rate of CMEs and prominence eruptions in ∼ 2006 when the HCS became flatter below 30° solar latitude.
Latitudes of LASCO CMEs (filled circles) with known solar surface associations (identified from microwave prominence eruptions) plotted vs time, by Carrington Rotation number. The dotted and dashed curves represent the tilt angle of the heliospheric current sheet in the northern and southern hemispheres, respectively; the solid curve is the average of the two. The up and down arrows denote the times when the polarity in the north and south solar poles, resp., reversed. Note that the high latitude CMEs and PEs are confined to the solar maximum phase and their occurrence is asymmetric in the northern and southern hemispheres. PEs at latitudes below 40° may arise from active regions or quiescent filament regions, but those at higher latitudes are always from the latter. Image adapted from Gopalswamy (2004); Gopalswamy et al. (2010a), updated by S. Yashiro (2011).
In pre-SOHO coronagraph observations the angular size distribution of CMEs seemed to vary little over the cycle, maintaining an average width of about 45° (SMM — Hundhausen, 1993; Solwind — Howard et al., 1985). However, the CME size distribution observed by LASCO and the CORs is affected by their increased detection of very wide CMEs, especially halos. Including halo CMEs from January 1996 – June 1998, St Cyr et al. (2000) found the average (median) width of LASCO CMEs was 72° (50°). Including all measured LASCO CMEs of 20 – 120° in width through 2002, Yashiro et al. (2004) found the average widths to vary, from 47° at minimum to 61° at maximum (1999), then declining again. Figure 12 from Gopalswamy et al. (2010a) gives the updated distributions of LASCO CME speeds and widths. The average width of 41° corresponds to nonhalo (width ≤ 120°) CMEs, whereas inclusion of all CMEs yields an average width of 60°. On the bottom are the speed and width distributions of all LASCO CMEs with widths > 30°. That the CACTus automatic catalog contains many more narrow CMEs is illustrated in Figure 13 from Robbrecht et al. (2009b). Shown on a log-log scale are the CACTus and CDAW width distributions for each year from 1997 – 2006; CACTus does not measure structures with widths below 10°.
Speed and width distributions of all CMEs (top) and wider CMEs (W ≥ 30°; bottom). The average width of wider CMEs is calculated using only those CMEs with W ≥ 30°. Image reproduced with permission from Gopalswamy et al. (2010a), copyright by Springer.
Apparent CME width distributions, displayed per year in log-log scale. The CACTus distribution corresponds to the red curve; the CDAW distribution is represented by the light blue curve. The distributions are not corrected for observing time. Image reproduced with permission from Robbrecht et al. (2009a), copyright by IOP.
Along with their white light imaging capabilities, the benefits of polarized images have also been demonstrated with some instruments. A polarizing strip across a fixed radial was part of the C/P instrument on board SMM and polarizing capabilities were part of the Skylab and Solwind coronagraphs as well (Sheeley Jr et al., 1980; Crifo et al., 1983). Polaroid filters can help determine distances of CME material along the line of sight and, therefore, give an idea of its three-dimensional structure. This is because the Thomson scattered light that enables us to observe CMEs has a polarization degree that is dependent on the direction of observation (Billings, 1966; Howard and Tappin, 2009). In what has become two of only a few studies making use of the SOHO/LASCO polarizing capabilities, Moran and Davila (2004) and Dere et al. (2005) presented analyses of LASCO C2 polarized CME observations and showed loop arcades and filamentary structure in six CMEs. The STEREO coronagraphs provide a constant stream of polarized images enabling for the first time their regular utility for 3-D property extraction. Publications making use of this ability include Mierla et al. (2009), Moran et al. (2010), and de Koning and Pizzo (2011).
The STEREO instruments allow us to attempt to remove the projection effects using geometry, that is to use geometric triangulation on features commonly observed between observers. An early attempt to do this using LASCO and COR2 data was performed by Howard and Tappin (2008). They measured two events observed as southwest limb CMEs in LASCO observed in November 2007 when the STEREO spacecraft were each ∼ 20° from the Sun-Earth line (and ∼ 40° from each other). Figure 14 shows the results from a geometric localization technique, also using LASCO and COR2 data, devised by de Koning et al. (2009). Rather than attempt to perform 3-D triangulation on a series of points comprising the CME, they confine the CME to within a polygon bound by the limits of the CME’s extent. While this does not provide as much information as one may assume can be obtained with 3-D triangulation, it is actually a powerful technique, as the optical thinness of CMEs makes it nearly impossible to identify the same point in 3-D space when observing from different perspectives.
The 3-D spatial location of the CME on 17 October 2008 at 14:08 UT as calculated using geometric localization. The CME appeared as a west-limb event in STEREO-A, as an east-limb event in STEREO-B, and as a halo CME by LASCO. The absence of space weather disturbances at Earth associated with the CME suggests that it was a backside halo event. The green quadrilaterals indicate the bounding volume of the CME as a whole; the blue quadrilaterals indicate the bounding volume of the leading-edge shell. The hash marks on the plots indicate the scale used; the distance between each mark is 1R⊙. The viewing latitudes and longitudes on the plots refer to the observer’s position in HEEQ coordinates. The left plot is for an observer hovering over the west limb of the Sun; Earth is on the left-hand side of the plot. The center plot is for an observer at Earth. The right plot is for an observer looking down onto the north pole of the Sun; Earth is toward the bottom of the plot. Image reproduced with permission from de Koning et al. (2009), copyright by Springer.
Many workers have now devised geometrical techniques for determining 3-D information on CMEs, including forward modeling (e.g., Thernisien et al., 2006; Wood et al., 2009), tie-pointing (e.g., Mierla et al., 2009), and inverse reconstruction (Antunes et al., 2009). Other triangulation efforts have also been made by (for example) de Koning et al. (2009), Liewer et al. (2009), and Temmer et al. (2009). The review by Mierla et al. (2010) discusses many of these new and emerging techniques. Attempts to identify the 3-D structure using triangulation has proven to be difficult, and techniques that place the CME within a volume bound by a polygon (e.g., de Koning et al., 2009; Byrne et al., 2010; Feng et al., 2012) may have greater success.
2.5 Kinematics
Estimates of the apparent speeds of the leading edges of CMEs range from about 20 to > 2500 km s-1, or from well below the sound speed in the corona to well above the Alfvén speed (Figures 8 and 12). The annual average speeds of Solwind and SMM CMEs varied over the solar cycle from about 150 – 475 km s-1, but their relationship to sunspot number was unclear (Howard et al., 1986; Hundhausen et al., 1994). However, LASCO CME speeds did generally track sunspot number in Solar Cycle 23 (Yashiro et al., 2004; Gopalswamy, 2010b), from 280 to ∼ 550 km s-1 at the maximum and following it in 2003 (Figure 15). Above a height of about 2R⊙ the speeds of typical CMEs are relatively constant in the field of view of coronagraphs, although the slowest CMEs tend to show acceleration while the fastest tend to decelerate (St Cyr et al., 2000; Yashiro et al., 2004; Gopalswamy et al., 2006b). This may be expected, given that CMEs must push through the surrounding solar wind, believed to have a speed of around 400 km s-1 in the outer corona.
Annual mean and median speeds of LASCO CMEs from 1996 – 2010. There are two peaks, the first near solar activity maximum and the second in 2003. Thus, high speeds were still prevalent during the early declining phase. Image adapted from Gopalswamy (2004), updated by S. Yashiro (2011).
The early acceleration for most CMEs must occur low in the corona (< 2R⊙). Despite its increased field of view, only 17% of all LASCO CMEs exhibit acceleration out to 30R⊙ (St Cyr et al., 2000). St Cyr et al. (1999) compared ground-based Mauna Loa, HI MK3 and SMM observations of CMEs above 1.15R⊙. These had either constant speed or constant acceleration profiles. The average acceleration of the events was found to be +264 m s-2, clearly much faster than the near-zero values of acceleration for LASCO CMEs (Yashiro et al., 2004, and our Table 1). Those features associated with active regions were found to be more likely to have constant speeds and those associated with prominence eruptions to have constant accelerations. Using observations of flare-associated CMEs close to the limb in the LASCO C1 field of view (1.1 – 3.0R⊙), Zhang et al. (2001, 2004) found a three-phase kinematic profile: a slow rise (< 80 km s-1) over tens of minutes; a second phase with a rapid acceleration of 100 – 500 m s-2 in the height range 1.4 – 4.5R⊙ during the flare rise phase; and a final phase with propagation at a constant or declining speed. Gallagher et al. (2003) and others have narrowed the strong (> 200 km s-1) acceleration region of impulsive CMEs to ∼ 1.5 - 3.0R⊙. Using LASCO data, Sheeley Jr et al. (1999) and Srivastava et al. (1999) found that gradually accelerating CMEs were balloon-like in coronagraph images, whereas fast CMEs moved at constant speed even as far out as 30R⊙. However, when viewed well out of the sky plane, gradual CMEs looked like smooth halos which accelerated to a limiting value then faded, while fast CMEs had ragged structure and decelerate (Sheeley Jr et al., 1999). Yashiro et al. (2004) found that slow CMEs tend to accelerate and fast CMEs decelerated through the LASCO field of view, with those around the solar wind speed having constant speeds. Thus, CMEs attain fast acceleration low in the corona until gravity and other drag forces slow them further out. This process continues into the interplanetary medium. More recently, the high temporal and spatial resolution STEREO COR and EUVI and SDO AIA imagery has been used to investigate the initial formation and kinematics of CMEs erupting from active regions (see, e.g., papers by Zhang et al., 2012; Liu et al., 2011; Patsourakos et al., 2010a,b; Temmer et al., 2010).
Sheeley Jr et al. (1999) used LASCO data to suggest that there were two dynamical classes of CMEs: gradual CMEs, which are slower, accelerate in the coronagraph fields of view, and are preferentially associated with prominence eruptions; and impulsive CMEs, which are faster, decelerate in the coronagraph fields of view, and are preferentially associated with solar flares. This appeared to confirm the flare-prominence eruption distinction found by MacQueen and Fisher (1983) using Mauna Loa, Skylab and SMM data. The tendency for fast CMEs to be associated with solar flares has been known since the earliest observations of coronagraph CMEs (for example, Gosling et al. (1976), using Skylab observations of CMEs, found a tendency for faster CMEs to be associated with solar flares and slower ones to be associated with prominences). However, prominence eruptions are often associated with two-ribbon flares and flares can be also accompanied by prominence eruptions, especially in active regions. The basic question then is whether there are two physically different processes that launch CMEs or whether all CMEs belong to a dynamical continuum with a single physical initiation process. This issue was revisited at several SHINE workshops (e.g., Crooker, 2002), with no definitive answer. In addition, Low and Zhang (2002) proposed a model of two kinds of erupting prominence-CMEs depending on whether they had normal or inverse magnetic geometries. They found that CMEs arising in normal polarity eruptions have more energy and higher speeds. To the contrary, in a comparison of flare-associated and non-flare CMEs, Vršnak et al. (2005) found considerable overlap of accelerations and speeds between the two CME groups. While flare-associated CMEs are generally faster than those without flares, there is also a correlation between CME speeds and flare X-ray peak fluxes, in which CMEs associated with the smaller flares are similar to CMEs with filament eruptions. This argues for a CME continuum and against the two-class concept. Yurchyshyn et al. (2005) found that the speeds of both accelerating and decelerating LASCO CMEs are distributed lognormally, implying that the speeds of both groups result from many simultaneous processes or from a sequential series of processes. Recently, Howard and Harrison (2012), using historical observations, argue in favor of a single launch mechanism and a continuum of energies.
2.6 Masses and energies
CME mass calculations require a conversion from the coronagraph-observed intensity to electron (and therefore plasma) density using the physics of Thomson scattering. Most workers today follow the theory outlined in Billings (1966) (the necessary equations conveniently appear on a single page of this text) but more recent reviews of this theory, along with its adaption for heliospheric imaging appear in Howard and Tappin (2009), Howard (2011b) and Howard and DeForest (2012b). Masses and energy calculations of CMEs therefore require difficult instrument calibrations and have large uncertainties. The average mass of CMEs derived from the older coronagraph data (Skylab, SMM and Solwind) was a few times 1012 kg (see Table 1). LASCO calculations indicate a slightly lower average CME mass, 1.6 × 1012 kg (Figure 16), likely because LASCO can measure smaller masses down to the order of 1010 kg (Vourlidas et al., 2002a, 2010, 2011b; Kahler, 2006). Studies using Helios (Webb et al., 1996) and LASCO (Vourlidas et al., 2000, 2010, 2011b) data suggest that the older CME masses may have been underestimated because mass outflow may continue well after the CME’s leading edge leaves the instrument field of view. For example, Vourlidas et al. (2010) estimated that CME masses may be underestimated by a factor of two and CME kinetic energies by a factor of 8. LASCO results of the mass density of CMEs as a function of height suggest that this density rises until ∼ 7R⊙, then levels off — Figure 17). The implication is that CMEs with larger masses reach greater heights, and are more likely to escape the Sun. Indeed, there is a population with a mass peak < 7R⊙; these CMEs are less massive and slower and may not reach IP space. This begs the question whether the outward motion of coronal mass that is not clearly “ejected” should be called a “CME” or something else. Downward motions of prominence material during eruptions are common, but similar downward motions of mass in white light CMEs are rare, though it has been reported (e.g., Tripathi et al., 2007).
Histograms of LASCO CME mass distribution (upper left), kinetic energy (upper right), and total mechanical energy (bottom left) for 7668 events. Also shown are the histograms for events reaching maximum mass < 7R⊙ (dashed lines) and events reaching maximum mass 7R⊙ (dash-double dot). Not all detected CMEs have been included because mass measurements require: (i) a good background image, (ii) three consecutive frames with CMEs, and (iii) CMEs well separated from preceding CMEs. Image adapted from Vourlidas et al. (2010, 2011b), courtesy A. Vourlidas (2011).
Top: scatter plot of the logarithm of maximum CME mass vs. the height where it was measured. Two populations are present: CMEs reaching maximum mass < 7R⊙ and CME with maximum mass > 7R⊙. Bottom: scatter plot of the logarithm of CME surface density (e cm-2) vs. height. The CME density is constant above ∼ 10R⊙. A histogram with 1R⊙ bins is calculated and the average density (asterisks) and in each bin is overploted. Note the small spread of the CME density values above ∼ 10R⊙. Its average value is shown on the plot. The height spread is mostly due to the noise and flatness of the mass measurements at those heights which tend to shift around the height of the maximum mass. Image adapted from Vourlidas et al. (2010, 2011b), courtesy A. Vourlidas (2011).
Mass estimates of a few CMEs have also been made with radio (Gopalswamy and Kundu, 1993; Ramesh et al., 2003) and X-ray observations (e.g., Rust and Hildner, 1976; Hudson and Webb, 1997) and, more recently, in the EUV (e.g., Harrison et al., 2003; Aschwanden et al., 2009). Many X-ray and EUV measurements involve “coronal dimming” (Section 3.4) regions associated with a CME, and these estimates are usually lower than that of the equivalent white light masses. This is probably because the material leaving the coronal dimming region is only part of that comprised in the CME. The radio, X-ray, and EUV techniques provide an independent check on CME masses because their dependency is on the thermal properties of the plasma (density and temperature) vs only density in the white light observations. Likewise average CME kinetic energies measured by LASCO are less than previous measurements, 2.0 × 1030 erg (Vourlidas et al., 2010 — Figure 16). The CME kinetic energy distribution appears to have a power law index of -1 (Vourlidas et al., 2002a), different than that for flares (-2; Hudson, 1991; Yashiro et al., 2006).
Figure 18 shows plots of the solar-cycle dependence of the LASCO CME mass and kinetic energy (Vourlidas et al., 2010, 2011b). The bottom panel shows the total CME mass per Carrington rotation. The mass, mass density, and kinetic energy all have minima in 2007 that are 2 – 4 times below the 1996 minimum and reflect the unusual extended activity in Solar Cycle 23. The total mass reaches a minimum in 2009 and is roughly equivalent to the 1996 minimum. MacQueen et al. (2001) found that the mass density variation between Solar Cycle 22 minimum and maximum varied by a factor 4 even in the background corona.
Solar cycle dependence of the CME mass and kinetic energy. Top left: log CME mass. Top right: log CME mass density in g R-2. Middle left: log CME kinetic energy. Middle right: CME speed. All four plots show annual averages. Bottom panel: total CME mass per Carrington rotation. The data gaps in 1998 and the drop in 1999 are due to spacecraft emergencies. The plot is an update of Figures 14 and 1 in Vourlidas et al. (2010, 2011b) to include events to July 31, 2010, courtesy A. Vourlidas (2011).
Measuring CME masses and energies using white light images farther from the Sun has proven to be a difficult task (see Section 5.3), due to the lack of calibration information and the uncertainties imposed by the faintness of the CMEs compared to the background noise. Mass and energy estimates have also been made from 3-D density reconstructions of a few CMEs observed in the heliosphere by SMEI (Jackson et al., 2008a, 2010a). The mass estimates generally agree with the mass of the same CMEs as derived from LASCO data. Some attempts are currently being made using some highly developed processing techniques with the STEREO SECCHI images. DeForest et al. (2012) performed some mass measurements on a small disconnection event (i.e., not a CME) using photometric measurements and the theory of Thomson scattering. The technique is currently being applied to CME measurements.
The reader must note that as with the kinematical properties, mass calculations are based on coronagraph images and, therefore, subject to the same problems of projection and perspective. For example, the CME mass calculations in the CDAW catalog make the assumption that all of the CME mass is in the sky plane, as has always been the standard assumption. The Thomson scattering theory from which the density is derived includes a direction term χ, and so the direction of propagation is an integral component of the density calculations. Traditionally, auxiliary data such as solar flare or filament location have been used provide an estimate of CME direction but more recent work making use of the stereoscopic capabilities of STEREO have provided more accurate measurements (Colaninno and Vourlidas, 2009). Finally, the Thomson scattering theory provided by Billings differs somewhat from the initial treatment by Schuster (1879) and Minneart (1930). An alternative treatment of this theory and it applications to both coronagraphs and heliospheric imagers can be found in Howard and Tappin (2009), Howard (2011a) and Howard and DeForest (2012b). This latest theory implies that the sky plane assumption may be more appropriate than has been previously assumed (see also van Houten, 1950).
A poorly understood topic is that of the energy budget available to the eruption of CMEs and associated solar activity. The next section discusses many of the phenomena that are known to be associated with CMEs and all of them require substantial quantities of energy. If we assume that the total energy arises from magnetic energy stored in the pre-launch corona then we may allocate an energy budget for the CME and its associated phenomena. Few studies have been conducted to address this topic, largely because of the difficulty in acquiring accurate measurements of both the available budget and the energies available from each associated phenomenon. These publications have revealed that the mechanical energy consumed by the launch and evolution of a CME is much greater than that of all the associated eruptive phenomena combined. Canfield et al. (1980), Webb et al. (1980), and Emslie et al. (2004) found the CME mechanical energy to be an order of magnitude greater than that of the associated flare and to consume the majority of energy available from the magnetic field. Ravindra and Howard (2010) found the mechanical energy of the CME was over an order of magnitude greater than that of the associated flare, and that half-to-all of the energy removed from the magnetic field during the eruption was consumed by the flare-CME-associated eruption combination. The uncertainties associated with the calculations in all of these studies, unfortunately, are too large to draw any firm conclusions.
3 Signatures of CME Origins
As stated in the previous section, the early acceleration phase of typical CMEs has mostly ceased by the time it has reached around 2R⊙. This indicates that over this distance the CME, which has a mass of the order of 1013 kg must be accelerated to speeds of several hundred km s-1 (and sometimes exceeding 2000 km s-1). Hence, the erupting magnetic structure that becomes the CME must have access to a mechanism providing vast amounts of energy over a relatively short time scale. Some theoretical models suggest that this involves an interaction between the erupting and the surrounding field, perhaps via runaway magnetic reconnection. The CME onset itself must involve some instability disrupting the equilibrium between the closed magnetic field in the corona and the tendency of the corona towards its natural state of expansion. We have thus far been unable to directly observe this mechanism or the instability responsible for its onset, although we can find clues via near-solar-surface phenomena that are known to be associated with the initiation of CMEs. These are mostly observed with instruments other than coronagraphs, typically imagers observing various regions of the electromagnetic spectrum: this makes the direct association between a CME and the associated phenomena difficult. In this section we review these phenomena. We also draw the reader’s attention to other recent reviews, including Webb (2002), Cliver and Hudson (2002), Gopalswamy (2004, 2010b), Kahler (2006), and Howard (2011b).
The release of the stored free magnetic energy that probably drives a CME can take many forms including (predominantly) mechanical in the form of an expanding CME and erupting filament, electromagnetic emission in the form of a flare, and also in the acceleration of energetic particles, magnetic field reconfiguration and bulk plasma motion. We mentioned the energy budget of CMEs and associated phenomena earlier: the few reports that have discussed this are Canfield et al. (1980), Webb et al. (1980), Emslie et al. (2004, 2005), and most recently, Ravindra and Howard (2010).
As noted in the introduction (Section 1), the formation and early development of CMEs can now be observed and followed near the surface, especially in EUV images (see, e.g., Hudson and Cliver, 2001). The first well-defined observation of the initial development of a CME “bubble” was with SOHO EIT images by (Dere et al., 1997). More recently, the high temporal and spatial resolution STEREO COR and EUVI and SDO AIA imagery has been used to study the initial formation of CMEs (see, e.g., Patsourakos et al., 2010a,b; Vourlidas et al., 2012). These demonstrate the rapid expansion of CMEs and their associated cavities and flux ropes.
EUV spectral observations from the UVCS, CDS, and SUMER instruments on SOHO and the SOT and EIS instruments on Hinode have helped us to measure the densities, temperatures, ionization states, and Doppler velocities of CMEs (e.g., Raymond, 2002; Kohl et al., 2006; Landi et al., 2010). Table 2 is a summary of the spectral lines that have been observed in CMEs by the UVCS instrument (Kohl et al., 2006). The UVCS instrument is unique in that it can sample the CME material at relatively high heights, e.g., out to ∼ 10R⊙, in the corona compared to the other spectrometers. Most CME material observed in UVCS is cool (< 105 K) and concentrated in small regions (Akmal et al., 2001), although this is not the case for fast CMEs associated with X-class flares (Raymond et al., 2003). Heating rates inferred from models using UVCS observations show that heating of the material continues out to 3.5R⊙ and is comparable to the kinetic and gravitational potential energies gained by the CMEs (Akmal et al., 2001; Landi et al., 2009). The Doppler information from UVCS combined with the EIT and LASCO images has shown in one case the unwinding of a helical structure (Ciaravella et al., 2000). Doppler shifts are usually high, ∼ 1000 km-1, within halo CMEs, where compressed or deflected coronal material along the flanks of a CME is measured. H I Lyα emission also suggests that dense material is present (Kohl et al., 2006).
3.1 Coronal streamers and blowouts
CMEs in general are associated with previously closed magnetic field regions in the corona, the opening of which is a consequence of the eruption. Many CMEs viewed at the solar limb also appear to arise from large-scale, pre-existing coronal streamers which often overlie active regions (e.g., Hundhausen, 1993). Many energetic CMEs actually involve the disruption (“blowout”) of such a structure, which can increase in brightness and size for days before erupting as a CME (Howard et al., 1985; Illing and Hundhausen, 1986; Hundhausen, 1993). Possible causes of such disruptions include the emergence through the surface of new magnetic flux, the dynamical evolution of arcades, or the shearing of magnetic field lines. Other variants of streamer changes associated with different types of filament activity have been noted by Gopalswamy et al. (2004a).
A streamer is a bright (dense) structure containing closed and open fields, which help guide denser, outward-flowing solar wind material. They are observed by coronagraphs (and during solar eclipses) above the solar limb and are often found above active regions. Blowout CMEs viewed when the surface eruption is at the solar limb mostly display the classic three-part structure (Burkepile et al., 2004). In these cases prominence material can actually be followed from at or near the solar surface (as viewed in the Hα line) into the coronagraph field of view (Figures 2, 19, and 20), where it forms the bright core of the CME. CMEs exhibit radial velocity dispersion, with the leading edge being fastest, followed by the speed decreasing through the prominence material (Webb and Jackson, 1981; Simnett, 2000). The kinematic profiles of erupting prominences and their associated CMEs are usually similar in that both will exhibit acceleration, deceleration or constant speed with height. The SMM coronagraph had an Hα filter, which was used for studies of a few CMEs containing large prominences. Illing and Athay (1986) compared the Hα and white light images from eight prominence/CMEs finding that some CME prominence masses exceed 1012 kg: a large fraction of the total CME mass. They also concluded that the prominence material usually becomes nearly fully ionized as it moves outward through the low corona. UVCS results are limited in this regard, because its best diagnostics are for plasma typically in the 105 K range. The brightest UVCS emission seen during CMEs is likely in the core or prominence material. Proton temperatures and ionization states suggest plasma of 104.5 – 5.5 K, so the material has probably been heated from the original prominence temperatures and it must be heated continually as it moves out to counteract cooling and radiative losses (Kohl et al., 2006; J. Raymond, 2011, priv. comm.). In one event, Ciaravella et al. (2003b) noted that prominence material likely was heated to above 106 K. The cleanest evidence for heated prominence plasma is the EIS result for the 9 April 2008 event by Landi et al. (2010). Also, many EIT and TRACE observations of erupting prominences near the surface show them changing from absorption to emission, indicative of heating.
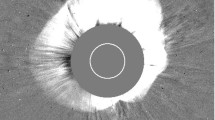
LASCO C2 image from 4 January 2002 image of a Coronal Mass Ejection (CME) showing detail in the ejected material. The solar limb Sun is represented by the white circle. Available from SOHO online image gallery: http://sohowww.nascom.nasa.gov/gallery/bestofsoho.html.
mpg-Movie (455.255859375 KB) Still from a movie showing LASCO C3 images of lightbulb shaped CME on 27 February 2000. Classic three-part structure with outer shell, void and inner bright structure, in this case an erupting prominence. From SOHO online movie gallery: http://sohowww.nascom.nasa.gov/gallery/Movies/flares.html. (For video see appendix)
3.2 Flares
Throughout most of the history of detailed solar observation (i.e., since ∼ 1850) it was generally accepted that the solar flare was the cause of interplanetary disturbances and major space weather effects on Earth. So when interplanetary shocks were discovered by Mariner 2 at the dawn of the space age (Sonnett et al., 1964), most believed them to be blast waves from solar flares. Likewise, when CMEs were discovered in 1973, many thought they were also flare-driven. Careful work through the 1970s and 1980s established that the CME is a separate and, in fact, the central phenomena responsible for both interplanetary shocks and geomagnetic storms. This was finally established in the controversial paper by Gosling (1993) which, however, was disputed in several other papers, best summarized in Hudson et al. (1995). Workers now typically regard CMEs and flares as sometimes related phenomena and not as one being the cause for the other.
There is no one-to-one relationship between CMEs and flares. Many CMEs are associated with solar flares but many are not, just as most flares are not associated with mass ejection. When CMEs and flares occur together, the CME onsets seem to precede the flares in many cases, and the CMEs contain far more total energy than that radiated by the flare itself (Section 2.6). It is now generally accepted that CMEs and flares are part of a single magnetically-driven “event” and, therefore, it is more appropriate to consider a unified model that accounts for both. A schematic of one such unified model is shown in Figure 21 (Lin, 2004). This “standard” flare model has been developed and refined over the last few decades and has become known as Flux Cancellation or the Catastrophe model (e.g., Švestka and Cliver, 1992; Shibata et al., 1995; Lin and Forbes, 2000; Lin, 2004). In this model a stressed magnetic arcade that may contain a magnetic flux rope at its core begins to rise. A current sheet develops beneath it as external pressure causes oppositely directed magnetic field lines to converge and reconnect. Some of the liberated energy heats the CME plasma and adds mass and magnetic flux to it. Other energy is directed downward in the form of shock waves, energetic particles, and/or rapidly moving plasma. This energy can heat the low-lying or reconnecting magnetic loops and travel down the loops to the chromosphere, producing the flare. In some cases, especially if a prominence lifts off slowly, there may be too little energy deposited in underlying structures to produce a detectable surface brightening, or flare. Typical flares are “confined” or “compact” and do not have sufficient energy or magnetic topology to open up the ambient field and produce an eruption or ejection. However, Shibata and colleagues have argued that impulsive, compact flares might also have narrow, plasma ejections yielding small CMEs.
Schematic diagram of a disrupted magnetic field that forms in an eruptive process (Lin, 2004). Catastrophic loss of equilibrium, occurring in a magnetic configuration including a flux rope, stretches the closed magnetic field and creates a Kopp-Pneuman-type structure. This diagram is created by incorporating the traditional two-ribbon flare model (bottom), from Forbes and Acton (1996) with the CME model (top) of Lin and Forbes (2000). Colors denote the different hierarchies of plasma in the configuration. Image reproduced with permission from Lin (2004), copyright by Springer.
Other models have been developed to describe the relationship between flares and CMEs. The so-called Breakout model of Antiochos et al. (1999), for example, involves the launch of the CME via magnetic reconnection between a core and the surrounding strapping magnetic field, which produces underlying magnetic reconnection (that may give rise to a flare) later in the process. It also allows for the passage of the core field past the strapping field, which is an essential process for ensuring that the net energy throughout the CME eruption is reduced.
Comparisons of low coronal soft X-ray, EUV and radio data with the white light observations provide many insights into the source regions of CMEs. Previous statistical association studies indicated that erupting prominences (EPs) and X-ray events, especially of long duration, were the most common near-surface activity associated with CMEs. Gopalswamy et al. (2003b) showed that 73% of microwave EPs, and nearly all those attaining high heights, were associated with CMEs, confirming results first found during Skylab (e.g., Munro et al., 1979). There is a strong correspondence between X-ray ejecta and CMEs. Nitta and Akiyama (1999) found that flares with X-ray ejecta were always associated with CMEs and the X-ray ejecta corresponded with CME cores, likely dense, heated prominence material (also see Rust and Webb, 1977).
Although most flares occur independently of CMEs, the fastest, most energetic CMEs do tend to be associated with bright flares, and reported flares are associated with most frontside, full halo CMEs (e.g., Webb, 2002; Gopalswamy et al., 2007). This rate may be high because the surface sources associated with halo CMEs can be clearly viewed near sun center and halo CMEs appear to be faster and more energetic than average CMEs. Thus, either or both mass motion or ejection speed seem to be critical for the association of a flare with a CME. This may be because there is a larger net energy reservoir available for both phenomena.
Sheeley Jr et al. (1983) first showed that the probability of associating a CME with a soft X-ray flare increased linearly with the flare duration, reaching 100% for flare events of duration > 6 hours. Confirming previous results with lower statistical validity, Yashiro et al. (2005) found that the LASCO CME association rate with X-ray flares also increased linearly with the peak X-ray intensity. Thus, the more energetic the flare, the more likely it was to be associated with mass ejection. When longitudinal visibility effects were accounted for, Yashiro et al. found that nearly all flares above the M5 level were associated with CMEs. The SMM CME observations indicated that the estimated departure time of flare-associated CMEs typically preceded the flare onsets. Harrison (1986) found that such CMEs were initiated along with weaker soft X-ray bursts that preceded any subsequent main flare by tens of minutes, and that the main flares were often spatially offset to one side of the CME. Also, the location of flares is more closely associated with the footpoint, rather than the center, of the CME (Simnett and Harrison, 1984, 1985). We note however, that more recent results using the LASCO data reported by Yashiro et al. (2008a) showed more variation between flare location and CME span, with X-flares usually centered under the CME. More details about solar flares appear in the Living Review by Benz (2008).
3.3 Erupting prominences
Prominences are observed in coronagraphs often as the bright, central core of the CME structure (the filament component of the classic three-part CME). They are also observed by instruments that observe the solar disk, so through erupting prominences a direct comparison between coronagraphs and solar data can be made. Prominences are believed to be caused by the formation of a flux rope low in the magnetic structure that eventually erupts to form the CME. Many CME onset models (e.g., flux cancellation, mass loading) require the presence or formation of a prominence in order for the CME to erupt.
The latitude distribution of LASCO CMEs peaks at the equator (Section 2.4), but the distribution of EIT EUV activity including prominence eruptions associated with these CMEs is bimodal with peaks 30° north and south of the equator (Plunkett et al., 2002). This offset is confirmed for the distribution of disk source regions associated with halo CMEs (Figure 22). This pattern indicates that many CMEs involve more complex, multiple-polarity systems (Webb et al., 1997) such as those modeled by Antiochos et al. (1999). Prominences themselves tend to be offset to one side of the CME axis and, occasionally, two prominences can erupt under the same CME canopy (Webb et al., 1997; Simnett, 2000). A particularly good example of the former is shown in Figures 7 – 11 of Hundhausen (1988) which combine Mauna Loa and SMM Hα and white light data of a CME (see also Webb, 1992).
Histograms of “source” longitudes of halo CMEs. Image reproduced with permission from Webb (2002).
Using SOHO LASCO, EIT, and MDI and ground-based Hα data, Cremades and Bothmer (2004) concluded that a simple scheme can be used to relate CME white light topology to the heliographic position and orientation of the underlying magnetic neutral line. When the neutral line is approximately parallel to the solar limb, the CME appears as a linear feature parallel to the limb having a broad, diffuse inner core. When the neutral line is approximately perpendicular to the solar limb, the CME is observed along its symmetry axis, and the core material lies along the line of sight. Joy’s law implies that the frontside neutral line will typically lie perpendicular to the east limb and parallel to the west limb. The neutral line and CME orientations are reversed for the solar backside, so backside CMEs are viewed predominately orthogonally to frontside CMEs at each limb. These CME orientations are generally valid only for CMEs with source regions in the active region belts, < 50° heliolatitude. The CME orientations will be different for polar crown filaments (McAllister et al., 2002; Gopalswamy et al., 2003a) or for CME source regions outside the active regions, where the neutral lines do not obey Joy’s law. However, in an older, related study using SMM data, Webb (1988) found no clear pattern between the orientation of filaments, i.e., neutral lines, and the morphology or widths of associated CMEs.
There have been several recent studies of the kinematics and rotations of prominences using STEREO EUVI data. Joshi and Srivastava (2011) used a stereoscopic reconstruction technique to study the motions of two polar crown prominences. They found evidence of two different motions, a helical twist in the prominence spine and overall non-radial equatorward motion of the entire prominence structure, and two phases of acceleration during the eruptions. Bemporad et al. (2011) used the tie-pointing technique with COR1 and EUVI data to reconstruct the 3-D shape and trajectory of an erupting prominence. They found evidence for a progressive clockwise rotation of the prominence by ∼ 90°, and helical motion providing evidence for the conversion of twist into writhe. Finally, (Vourlidas et al., 2011a) used SECCHI and LASCO data with a forward-fitting model to determine the 3-D orientation of a 3-part CME with embedded prominence. The found that the CME had a fast rotation rate, and suggested it was possibly due to disconnection of one of the CME footpoints.
The physical (as opposed to observational, defined earlier) definition of a CME involves material in a magnetic field that is expelled from the corona (Hundhausen, 1999), so we assume that all the material observed moving away from the Sun in coronagraphs escapes the corona. However, in a few CMEs with relatively slow speeds material in bright cores has been observed to collapse back to the Sun with speeds of ∼ 50 to 200 km s-1 (Wang and Sheeley Jr, 2002). These collapses have been interpreted in terms of gravitational and magnetic tension forces as well as the drag forces of the ambient solar wind. It is not clear whether these collapses are only a minor part of some CMEs or more generally important for the CME dynamics.
3.4 Coronal dimming to arcade formation
The most obvious coronal signatures of CMEs in the low corona are the arcades of bright loops that develop after the CME material has erupted (Kahler, 1977 – Skylab; McAllister et al., 1996; Hudson and Webb, 1997 — Yohkoh; Hanaoka et al., 1994 — radio; Tripathi et al., 2004 — EIT). Prior to the eruption, an S-shaped structure called a sigmoid can develop, typically observed in X-rays, sometimes in association with a filament activation. A sigmoid is indicative of a highly sheared, non-potential coronal magnetic field, and might be an important precursor to certain types of CMEs (e.g., Canfield et al., 1999). However, McKenzie and Canfield (2008) point out that X-ray sigmoids actually consist of separate J-shaped loops that support a bald-patch separatrix surface model for sigmoids. Eventually an eruptive flare can occur within or in the proximity of the sigmoid, resulting in the bright, long-duration arcade of loops. Sterling et al. (2000) call this process “sigmoid-to-arcade” evolution. These arcades suggest the eruption and subsequent reconnection of strong magnetic field lines associated with the CME system. Tripathi et al. (2004) found that nearly all (92%) EIT post-eruptive arcades (PEAs) from 1997 – 2002 were associated with LASCO CMEs (Figure 23). Recent analyses of Hinode XRT and SDO AIA data reveal new information of the space and temperature evolution of arcades (e.g., Reeves et al., 2010; Reeves and Moats, 2010; Reeves and Golub, 2011), which help to further constrain the “standard” eruptive flare model (e.g., Section 3.2 and Figure 20).
Erupting prominence, dimming regions and arcade associated with a fast CME on 12 September 2000. Top: SOHO EIT 195 Å running-difference images; bottom: CME leading edge and erupting prominence (EP) seen in SOHO LASCO C2 images. Image reproduced with permission from Tripathi et al. (2004), copyright by ESO.
Coronal dimming is the reduction in intensity on the solar disk across a large area, observed in X-ray, EUV and more recently in Hα, and coincident in timing with the launch of a CME above. Measurements imply that the reduction in intensity is due to the evacuation of mass from the low corona (Hudson and Webb, 1997) and not a temperature change (e.g., Harrison and Lyons, 2000; Harrison et al., 2003). The dimming regions can be much more extensive than any associated flaring activity and can map out the apparent base of the associated CME (Thompson et al., 2000; Harrison et al., 2003). They have also been shown to extend deep into the corona and possibly the chromosphere and photosphere (McIntosh et al., 2007), thereby indicating that the initial terminology of “transient coronal hole” is probably more physically appropriate. Coronal dimmings are good indicators of the area on the Sun corresponding to the CME and of the behavior of the local magnetic fields following the CME launch. It is likely that at least part of the mass observed leaving the low coronal dimming region becomes part of the CME (e.g., Webb et al., 2000a), but what part and how much are uncertain. In a recent survey of six STEREO events observed as dimmings by EUVI and as CMEs by COR2, Aschwanden et al. (2009) found a nearly 1:1 correspondence between the EUV and white light masses. The self-similar evolution of the mass from the low to outer corona was also successfully modeled. For their sample of EIT dimming events, Reinard and Biesecker (2008) found mean lifetimes of 8 hours, with most disappearing within a day. Other results suggest that there may be two types of dimming, “core” dimmings directly associated with the source active region and flare, and “secondary” dimmings farther away that may be associated with loop motions or evacuation (e.g., Attrill et al., 2010).
Surveys of solar activity associated with frontside halo CMEs have been made primarily with low coronal images from the SOHO EIT and Yohkoh Soft X-ray telescope (SXT) instruments, although surveys with STEREO and Hinode are emerging. The activity associated with halo CMEs includes the formation of dimming regions, long-lived loop arcades, flaring active regions, large-scale coronal waves and filament eruptions (Figure 24). Webb (2002) found that 2/3 of halo CMEs were associated with either or both filament eruptions and dimmings, and Reinard and Biesecker (2008) found that about half of all frontside halo CMEs have dimmings. Coronal dimming has not been observed as frequently as other associated eruptive phenomena but the most recent, very sensitive results (e.g., Schrijver and Title, 2011) from SDO imply that dimming is more common than measurements from previous instruments have implied.
A filament eruption and post-eruption arcade near Sun center on 17 February 2000 (top). It was associated with a symmetrical LASCO halo CME (bottom). Image reproduced with permission from Tripathi et al. (2004), copyright by ESO.
3.5 Coronal waves
The frequent detection of coronal waves observed in EUV was an exciting discovery from the SOHO EIT observations (e.g., Thompson et al., 1998). They were originally termed EIT waves, but are now often referred to as EUV waves or, more generally, as coronal waves. These waves were originally considered to be a candidate for a CME-associated Moreton wave. According to the theory by Uchida (1968), a flare may trigger an impulse that will propagate along the solar surface as a fast traveling front with an increase in emission. In the photosphere and chromosphere it can best observed in Hα as a Moreton wave. However, the EUV (EIT) waves propagate across the solar disk at typical speeds of 200 – 400 km s-1 (Thompson and Myers, 2009), slower than the 1000 km s-1 typical of Moreton waves. Observational evidence, such as the association of Type II radio bursts with coronal waves, suggests that at least some of them may be fast-mode MHD shocks. Although Biesecker et al. (2002) found a CME associated with nearly every EIT wave, it is accepted that not all CMEs are associated with waves. For example, Webb (2002) found that only about half of frontside halo CMEs have EIT waves, and Cliver et al. (2005) found that there are ∼ 5 times as many frontside CMEs as EIT waves. Thus, their nature is still under intense debate, Competing models include fast-mode MHD waves, slow-mode waves or solitons, and “pseudo waves” related to a current shell or successive restructuring of field lines at the CME front. Details of observations and models can be found in recent reviews (Warmuth, 2007; Vršnak and Cliver, 2008; Wills-Davey and Attrill, 2009; Gallagher and Long, 2011).
The relatively poor cadence (∼ 12 minutes) of the EIT observations of propagating EUV disturbances were partially alleviated by STEREO EUVI imagery. These have shown that the EUV wave kinematics are more consistent with coronal MHD waves (e.g., Long et al., 2008; Patsourakos and Vourlidas, 2009). Using the Atmospheric Imaging Assembly (AIA) on SDO, Liu et al. (2010) show that there can be multiple wave components with rippling effects. In one of the best observed wave events using the AIA EUV images, it was found that the shock and metric type II burst appeared simultaneously (Gopalswamy et al., 2012). Also the wave propagation can be inhibited and possibly reflected from coronal holes (e.g., Gopalswamy et al., 2009c). Veronig et al. (2010) presented evidence from STEREO/EUVI observations that the wave initially appears as a dome-shaped spherical structure surrounding the CME. Chen and Wu (2011) interpret an EUV event using SDO/AIA data as consisting of a fast mode wave followed by a slower disturbance.
3.6 Shock waves and SEPs
If the speed of a CME exceeds the local Alfvén speed in the corona and interplanetary medium it can drive a forward shock. Type II radio bursts, caused by Langmuir waves forming as a result of plasma motion ahead of a shock, are associated with CMEs. Type IV bursts, especially “moving” bursts associated with CMEs, imply magnetic plasma ejections, possibly associated with EPs, and nonthermal particles from field-line reconnection. Studies performed using SOHO data seem to confirm that metric type II bursts arise from shock waves driven by CMEs (Cliver et al., 1999) although the association between metric type II bursts and solar activity has been established since their discovery in the 1950s. Type II bursts in various wavelength domains appear to be organized by the kinetic energy of the CMEs: metric type II bursts (< 2R⊙) are associated with CMEs with above-average kinetic energy; those extending into decameter-hectometric (DH) wavelengths (> 2R⊙) have moderate CME kinetic energy; and type II bursts seen in both the metric and DH domains and extending to kilometric (km) wavelengths (covering the entire Sun-Earth distance) are associated with CMEs of the largest energy. This hierarchical relationship implies that all type II bursts are associated with CMEs, i.e., mass ejecta (e.g., Gopalswamy et al., 2005). More details about solar radio events will appear in an upcoming Living Review; also see Schwenn (2006).
Historically, identifying shocks in white light coronagraph images has been very difficult. Kinks in streamers deflected by CMEs and changes in type II dynamic spectra have been used to infer the existence of shocks on the flanks of CMEs. Sharp, bright rims ahead of fast CMEs occasionally observed by LASCO are now considered by some to be evidence of shocks (e.g., Vourlidas et al., 2003; Ontiveros and Vourlidas, 2009; Vourlidas and Ontiveros, 2009). The kinematics of a spherical shock ahead of a bubble CME has been determined in EUV data from SDO-AIA (Ma et al., 2011).
Ultraviolet spectroscopy provides an unambiguous means to observe coronal shocks and determine their properties (Kohl et al., 2006). Shock compression causes an immediate increase in the emissivity of dominant ions, and the bulk motion of the shocked plasma causes Doppler dimming of H I Lyα and O VI lines. Electron heating causes a more gradual change in the ionization state, and heating of the ions can be measured through line width increases. However, since the shocked gas passes quickly through the UVCS slit, the signatures of only a few shocks have been reported. In all these cases broad O VI profiles were detected and the O temperatures were > 108 K.
Using SOHO and radio observations of a fast CME, Bemporad and Mancuso (2010) were able to provide a complete characterization of pre- and post-shock plasma physical parameters in the corona. The UVCS slit was centered at 4.1R⊙ in the flank of the expanding CME, the highest UV detection of a shock obtained so far with UVCS. The white-light and EUV data were combined to estimate the shock compression ratio, plasma temperature, and the strength of the magnetic fields. For the compression ratio of 2.06, the coronal plasma was heated across the shock from an initial temperature of 2.3 × 105 K up to 1.9 × 106 K, while the magnetic field was compressed such that its strength increased from ∼ 0.02 G to ∼ 0.04 G. Magnetic and kinetic energy density increases at the shock were comparable and more than two times larger than the thermal energy density increase.
CME-driven shocks can accelerate electrons and ions producing solar energetic particle (SEP) events. The close association between SEP events and fast CMEs implies that SEPs are accelerated by CME-driven shocks (Reames, 1999). Early work with solar energetic particles in the 1960s suggested that a two-stage acceleration process must take place to achieve the energies observed in these particles (Wild et al., 1963), a process later confirmed using in-situ data in the 1980s and 1990s (e.g., Gloeckler et al., 1994). The first stage, up to around 100 keV for electrons, is provided by the flare, and the rest provided by a fast magnetohydrodynamic (MHD) shock, now believed to be produced by the CME. A few hundred large SEP events have been recorded during the SOHO period, most of them occurring around the solar maximum (e.g., Gopalswamy et al., 2008). The associated CMEs were fast (average speed ∼ 1500 km s-1), apparently wide (mostly full halos) and decelerating (possibly due to coronal drag). Large SEP events with the most energetic particles, ground level enhancements (GLEs — e.g., Forbush, 1946), are associated with the fastest CMEs (> 2000 km s-1; Gopalswamy et al., 2008). The fastest particles can arrive at Earth only minutes after the impulsive flare and associated shock. A comparison of the LASCO fast (v > 1000 km s-1) CMEs between the CDAW (manual) and CACTus (automatic) catalogs shows that the CDAW CME widths are considerably wider (Yashiro et al., 2008b), but nearly all of the CMEs associated with GLEs are halos (W > 180°) in both catalogs. The source regions of the SEP-associated CMEs are generally located in the Sun’s western hemisphere, because the particles travel along the Parker spiral interplanetary field lines. The SEP-CME distribution is different from that of the CMEs producing geomagnetic storms (Figure 25). Thus, all frontsided fast and wide CMEs are potentially important for Earth’s space weather. An important SOHO result is that the high-intensity SEPs are associated with active regions that are associated with repeated CMEs, suggesting that CME interactions may be important in accelerating the particles in large SEPs (e.g., Gopalswamy et al., 2004b).
Locations of associated solar surface activity related to CMEs that produce major (Dst ≤ -100 nT) geomagnetic storms (left) and large SEP events (right). The circle sizes represent the significance of the resultant event (Gopalswamy, 2010b).
Emslie et al. (2004) have shown that the CME kinetic energy is by far the largest component in the energy budget of an eruption. As much as 10% of the CME kinetic energy might go into SEPs, suggesting that CME-driven shocks are very efficient particle accelerators (Mewaldt, 2006). More details about Solar Energetic Particles will appear in an upcoming Living Review; also see Schwenn (2006).
3.7 Evidence of reconnection and current sheets
In Section 3.2, we discussed the Flux Cancellation flare-CME model involving field line reconnection. A consequence of this process is the formation of a current sheet that connects the outgoing CME/flux rope with the reforming coronal loop arcade near the surface (Figure 21). Evidence for this seems to have been observed by a number of instruments. Yohkoh/SXT and Hinode/XRT observations have provided substantial X-ray evidence of current sheet formation, such as cuspshaped loops (Shibata, 1999) and supra-arcade downflows (SADs — McKenzie and Hudson, 1999, 2001; Sheeley Jr et al., 2004; Savage et al., 2010), of post-CME reconnection occurring over long-duration flares. The supra-arcade downflows are downward motions that have been observed in Yohkoh, TRACE, Hinode, and SOHO SUMER above post-CME flare arcades. SADs have trajectories which slow as they reach the top of the arcade, consistent with post-reconnection magnetic flux tubes retracting from a reconnection site high in the corona until they reach a lower-energy magnetic configuration. Savage et al. (2010) showed for a single XRT event following a limb CME that SADs can also appear as shrinking loops rather than downflowing voids. In that event, for the first time both the current sheet and the outgoing CME were imaged in soft X-rays and followed into the LASCO C2 field of view.
Sui and Holman (2003) first discussed a hard X-ray event observed by RHESSI that showed a compact X-ray source above the top of a roughly vertical current sheet in which they claimed magnetic reconnection was occurring. Subsequently, Sui et al. (2005), Saint-Hilaire et al. (2009), and others have analyzed similar events in which the coronal sources appear to move both downwards and outwards with time. The hard X-ray emission indicates a very hot source, ∼ 107 – 8 K, with the outgoing packet associated with the magnetic X-point where oppositely-directed field lines reconnect. The downward source is likely hot plasma from the most-recently reconnected arcade loops that are shrinking, as well observed in the soft X-ray observations.
The current within the current sheet is confined to a surface. In MHD theory, an electric current passing through part of the volume of a fluid tends to be expelled by magnetic forces from the fluid, compressing the current into very thin layers within the volume. We now have growing evidence for the existence of such current sheets in the corona trailing CMEs when the observing conditions are appropriate. Following earlier studies of concave-outward structures and reforming helmet streamers after CMEs, Webb (1995; 2004) analyzed SMM CMEs with concave-outward bright regions, finding that about half were followed by coaxial, bright rays suggestive of newly formed current sheets lasting for several hours and extending more than five solar radii into the outer corona.
With the advent of LASCO data, cases of CMEs with rays and Y-shapes were reported by Simnett et al. (1997), and St Cyr et al. (2000) found such features in one third to one half of all LASCO CMEs. Bright narrow features with enhanced temperatures (3 – 6 × 106 K), densities (∼ 5 × 107 cm-3 at 1.5R⊙), and abundances of elements with low first ionization potentials (FIPs) were observed with the UVCS following slow (∼ 180 km s-1; Ciaravella et al., 2003b) and very fast (1800 km s-1; Ko et al., 2003; Lin et al., 2005) CMEs. Figure 26 shows enhanced images of the 18 November 2003 event; the CME had a concave-outward, flux-rope like appearance followed by a rapidly brightening ray (Lin et al., 2005). Blobs moved along the ray at ∼ 1000 km s-1 suggesting bursty reconnection in the current sheet, as MHD modeled for example by Riley et al. (2007). Figure 27 shows an example of SOHO observations of a classic three-part CME with narrow enhanced Fe XVIII emission centered under the CME where the current sheet should lie (as in the standard-flare-model cartoon sketched at the bottom of the figure). Yokoyama et al. (2001), Simnett (2004), Sheeley Jr and Wang (2007), Vršnak et al. (2009), and Savage et al. (2010) also identified bi-directional flows in SOHO and Hinode images moving away from a common point in the low to mid-corona that were interpreted in terms of reconnecting current sheets.
A very fast CME with flux-rope structure followed by a narrow ray on 18 – 20 November 2003. The ray also shows evidence of bursty reconnection in the current sheet (bottom panels). Image reproduced with permission from Lin et al. (2005).
A LASCO “Light-bulb CME” on 23 March 1998 (see Ciaravella et al., 2003a). The UVCS slit at 1.5R⊙ reveals hot Fe XVIII emission trailing the CME, an expected spectroscopic signature of a current sheet. Image courtesy A. Ciaravella.
Ciaravella and Raymond (2008) were the first to combine UVCS and white light data to derive both the density and thickness in a current sheet, rather than assuming one to estimate the other. Bemporad and Mancuso (2010) derived turbulent speeds and their evolution in time, which is the main constraint for turbulent current sheet models. In these and other results (e.g., Lin et al., 2009), the thickness of the current sheet was calculated to be much larger than classical or anomalous resistivity would predict, possibly indicating an effective resistivity much larger than anomalous resistivity, such as that due to hyperdiffusion. The Petschek reconnection mechanism (Petschek, 1964) and turbulent reconnection is consistent with these results.
3.8 “Problem” and “stealth” CMEs
So-called “problem” geomagnetic storms lack historically obvious signatures of related solar activity, such as flares and large disappearing filaments (e.g., Dodson and Hedeman, 1964; McAllister et al., 1996, and references therein). An event on 6 – 10 January 1997 was the first such problem storm for which the antecedent CME was actually observed (Webb et al., 2000b). The associated solar surface activity was so weak and unimpressive that, had the faint LASCO halo CME not been observed, the storm would not have been forecast. During the LASCO period, partial or full halo CMEs that had no obvious surface association were usually attributed to “backside” events directed away from the Sun-Earth line (e.g., Demastus et al., 1973; Munro et al., 1979; Webb and Hundhausen, 1987). Non-halo CMEs occurring near the limb were mostly attributed to unseen sources behind the limb.
The absence of solar surface activity with observed CME activity is not a new observation (Howard and Harrison, 2012). The launch of STEREO in 2006, however, afforded us the opportunity to study the origins of CMEs simultaneously from multiple lines of sight. Robbrecht et al. (2009a) presented a study of a streamer blowout CME without a clear source region. The STEREO spacecraft were sufficiently widely separated (53°) that the CME and its source region could be viewed edge-on in STEREO A and face-on in STEREO B. STEREO B saw the CME as a faint halo and it was detected in-situ as a magnetic cloud 5 days later. Robbrecht et al. suggested that the CME originated high enough up in the corona such that no surface signatures were evident. Subsequently, Ma et al. (2010) performed a statistical study of all CMEs observed during the first 8 months of 2009 when the STEREO lines of sight were nearly perpendicular to each other. They found that about a third of the CMEs were “stealth”, having no distinct surface association, and tending to be slow, i.e., < 300 km s-1. Faint coronal changes could be detected in about half of the stealth CMEs, again suggesting a higher launch site. It is noted that this period was during the recent unusual extended solar minimum, so the fraction of such CMEs may be different at other times. Howard and Harrison (2012) in a recent review paper discuss the use of the term “stealth CME”.
3.9 Precursors of CMEs
A currently popular paradigm is that the activation of coronal magnetic fields leading to a CME begins well before the appearance of any associated surface activity such as flares or erupting prominences. Some of the energy released during a CME could drive precursor activity, and there is some evidence of precursor activity tens of minutes to hours before the onset of surface activity and even before CME onset (see Webb, 1992 and Gopalswamy et al., 2006b for a recent review called “The Pre-CME Sun”).
Jackson and colleagues described evidence for two kinds of coronal precursors occurring before the onset of Skylab CMEs. The first were called “forerunners”, large, faint regions of enhanced brightness that were found to rim the CMEs themselves (Jackson and Hildner, 1978). The outer boundaries of the forerunners maintained a constant offset of 1 – 2R⊙ from the CME. The reality of such features would be significant for two reasons:
-
1.
The volume of the affected corona would be much larger than the subsequent CME;
-
2.
The onset of the material ejection would begin higher in the corona and earlier than previously thought.
Jackson (1981) noted that in some events forerunner material was actually in motion prior to the associated surface activity. However, using Solwind data, Karpen and Howard (1987) concluded that forerunners were either an artifact of the contouring process used or were structures not separate from the CME itself. Although this controversy was never fully resolved, with the larger dynamic range of LASCO rims of material detected ahead of fast LASCO CMEs are now considered evidence of shock waves, and emission can be detected ahead of slower speed CMEs as low-level brightness enhancements due to the expanding streamer (see Section 3.6).
A second type of CME precursor reported by Jackson et al. (1978) was the statistically significant temporal clustering of Culgoora type III radio bursts an average of 6 hours before Skylab CME onsets. Culgoora radioheliograph positional data revealed that these same type IIIs clustered spatially at the limb within 20° of the centroid of the CME. Recently, Jackson et al. (2010c) reported that imaging measurements from the French Nançay radio array showed similar activity before some solar disk events such as on 26 April 2008, but definitive studies are clearly necessary.
Data nearer the time of CME onset indicate the existence of precursor activity before some, but not all CMEs. During the SMM era it was found that the departure times of flare-associated CMEs often preceded flare onsets. Harrison (1991) concluded that CME onsets preceded any subsequent associated Hα or X-ray flares by an average of 17 minutes. CME onsets were associated with precursor X-ray arches having large scale sizes of ∼ 105 km and interconnecting two active regions. In addition, most X-ray flares observed by the SMM HXIS instrument were preceded by weak soft X-ray bursts, but more recent results using soft X-ray and EUV data do not show such a clear pattern (Harrison, 1991; Harrison et al., 1990; Yashiro et al., 2008a).
As discussed in Section 3.4, an S or reverse S-shaped structure called a sigmoid sometimes develops, and can be associated with a filament’s activation. Like the filaments themselves, sigmoids are indicative of sheared coronal magnetic fields. Since many CME onset models require a magnetic shear to be established for the field to erupt, these sigmoids may be a precursor of a CME. It is well known that various kinds of filament/prominence activity precede the eruption of the filament itself by tens of minutes. Since erupting prominences are the most common type of surface activity associated with CMEs and appear as bright cores within many CMEs (Webb and Hundhausen, 1987), pre-eruptive filament activity is a form of CME precursor. Tens of minutes before their eruption, some large filaments darken and get broader (e.g., Martin, 1980). The cancellation of magnetic flux near filament channels can also build energy prior to an eruption, a process already referred to as Flux Cancellation (Martin and Livi, 1992). Kahler et al. (1988) found that the eruption of Hα filaments began before the onset of associated flare impulsive phases, suggesting that these erupting filaments, and by analogy the CMEs associated with them, were driven before and independently of the flare and its impulsive phase.
Some of the most massive and energetic CMEs are the so-called streamer blowout events, which were first described in detail by Sheeley Jr et al. (1982) and Illing and Hundhausen (1986). The preliminary statistics of streamer-blowout CMEs observed by LASCO were presented by Vourlidas et al. (2002b). In such events, a pre-existing streamer typically increases in brightness for one to several days before erupting as a CME (Figure 2). Following the CME, the so-called helmet streamer disappears, and is often replaced by a thin ray and later a reforming helmet (Kahler and Hundhausen, 1992). These events appear on white light synoptic charts as “bugles”: portions of the streamer belt that brighten and widen with time until they disappear during a CME (Figure 28 — Hundhausen, 1993). Most streamer blowouts involve a pre-existing prominence sitting within a coronal void or cavity; this then erupts to form the classic “three-part” CME structure. Thus, the early filament/prominence activations discussed above are probably related to streamer swellings and blowouts.
Coronal synoptic maps from the SMM C/P coronagraph showing the white light emission at a height of 3.4R⊙ over the east (top) and west (bottom) limb. The coronal streamer belt is evident on these maps. Narrow vertical streaks on the maps indicate CMEs. These were first called “bugles” by Hundhausen (1993), since streamer-blowout CMEs appear on synoptic maps as vertical streaks usually preceded by brightening and widening streamers. Such bugle shapes are left-facing on synoptic maps because time runs from right to left. The locations and widths of all CMEs on this rotation are marked by dashed boxes. Image adapted from Hundhausen (1993), courtesy J. Burkepile, NCAR/HAO.
4 CME Models
As mentioned earlier, in the early years, most of the solar physics community believed that CMEs were shock waves caused by solar flares. Although this belief has since been disproven (refer to Kahler, 1992 and Gosling, 1993 for reviews debunking the “Solar Flare Myth”), some remnants still remain in some circles, particularly those outside the solar physics community. Early mathematical models (and some still in use today) regard solar mass ejections as eruptive solar flares in opposition to the majority of flares which are “confined”. Because the corona is a highly conducting medium, the plasma is essentially “frozen in” to the magnetic field such that for an eruption to occur, the field lines must open up to allow the plasma to escape. But flares and CMEs can have very different properties, not least their spatial scales, and CMEs can occur without flares, so most researchers now consider flares and CMEs to be different aspects of magnetic field reconfiguration on the Sun. For details of CME models in general, see the Living Review by Chen (2011). Here we describe only those models that pertain to material eruption (see, e.g., Aschwanden, 2006 and Forbes et al., 2006 for reviews).
Contemporary models describing the launch and early evolution of CMEs must overcome two major physical obstacles:
-
1.
How to provide vast quantities of energy over a short time period (mentioned previously);
-
2.
How to physically justify the CME as an opening of a magnetic field when the completely open field state is higher in energy than the pre-erupted closed state (the so-called Aly-Sturrock limit).
While the physical mechanism to launch the CME may vary between models, the overall picture is essentially the same: A magnetic field configuration held in equilibrium is disrupted somehow, causing the system to erupt. The initial configuration typically involves an underlying sheared field often called the core (e.g., Moore and Roumeliotis, 1992) held down by an overlying strapping field. The onset mechanism itself that causes the eruption is actually less important — eventually one will occur. It may take the form of magnetic reconnection or even a simple field reconfiguration could accomplish an equilibrium disruption. The core then erupts beyond the strapping field.
The most recent modeling work in this area (e.g., Rachmeler et al., 2009) has focused on the question of what happens to the strapping field when the CME erupts. Until recently it was accepted that the strapping field must be stretched by the erupting core, which must presumably stretch it out to infinity. This, however, violates the Aly-Sturrock limit meaning it has been difficult to explain physically why a CME would spontaneously move to a more energetic state. This problem has been overcome with the use of 3-D models. In three dimensions, the core can erupt without stretching the strapping field along with it — instead it can simply push the strapping field aside as it erupts. Hence, in 3-D the Aly-Sturrock limit does not pose a problem.
To overcome the first obstacle, that of energy provision, a number of models have emerged. Some, such as the breakout model (e.g., Antiochos et al., 1999; Lynch et al., 2008), involve runaway magnetic reconnection between the erupting core and the strapping field, while others, such as the kink instability (e.g., Török and Kleim, 2003; Török and Kliem, 2005; Fan and Gibson, 2004) involve the twisting of the core field. Figure 29 shows a 3-D diagram of the kink instability, also showing how the strapping field is pushed aside to make way for the erupting core.
Sequence showing the three-dimensional evolution of the coronal magnetic field via the kink instability model. The heavy blue/green lines represent the kinked flux rope, which erupts through the overlying strapping magnetic field (red). This field is pushed aside during this process. Image reproduced by permission from Fan (2005), copyright by AAS.
After the CME has erupted the magnetic field left behind eventually closes, probably via some form of large-scale magnetic reconnection. The recent models of this process describe the late phase of CMEs reasonably well (cf. Švestka and Cliver, 1992). Kahler and Hundhausen (1992) found that the bright structures following many SMM CMEs are streamers probably newly-formed by reconnection. Observations from Yohkoh and from MLSO of the reformation of a giant helmet streamer also provide strong evidence of reconnection following CMEs (Hiei et al., 1993). As discussed earlier, the white light and spectroscopic evidence for current sheets trailing CMEs also provide support for the reconnection of the surface fields. Reeves and Moats (2010) have examined the relationships among the CME kinematics, thermal energy release and soft X-ray emissions using the Lin and Forbes (2000) loss-of-equilibrium model, finding good correlations among the parameters.
An extensive survey of post-eruptive arcades in SOHO/EIT 195 Å images has shown that every arcade is associated with a LASCO CME (Tripathi et al., 2004). These observations have been interpreted in terms of a basic model of reconnecting magnetic fields behind a magnetic flux rope and over a magnetic arcade (e.g., Lin, 2004), which results in a disconnection of CME fields from the Sun, as shown in Figure 21. This model has been called the CSHKP model to reflect its provenance. The acronym stands for Carmichel, Sturrock, Hirayama, Kopp, and Pneuman, each of whom developed configurations which have now evolved into a “standard” model that continues to be supported by observations and simulations (see Švestka and Cliver, 1992, for the original CSHKP description). Correlations found between inferred magnetic reconnection rates in arcades and the speeds of associated CMEs provide further confirmation of the model (Jing et al., 2005). Radio imaging of the moving and quasi-stationary type IV bursts can provide upper limits to the current sheet length by bracketing the reconnection region (Pick et al., 2005).
Most of the models intended to describe the origin and propulsion of CMEs are not sufficiently developed to compare with observations. Many of them involve force free equilibria which cannot realistically describe the complex evolution of the pressure, magnetic and gravitational forces acting on a magnetically closed coronal structure (e.g., Hundhausen et al., 1994). The class of models which require a thermal or pressure pulse (i.e., flare) as driver no longer seem viable (cf. Dryer, 1994). For instance, such models are not consistent with CMEs that exhibit significant accelerations over large distances. Causes of the evolution of these coronal structures, especially streamer configurations, include the emergence of magnetic flux, the dynamical evolution of arcades (Mikić and Linker, 1994), and the shear of field lines across inversion lines (Wolfson and Low, 1992; Mikić and Linker, 1994). However, no strong consensus has yet emerged.
Models attempting to describe CME evolution at large distances from the Sun can be categorized in order of their increasing complexity. It is important to note that the most complex model does not necessarily indicate the more accurate; sometimes the simpler description can be the most appropriate. We divide models for CME evolution into three categories: 1) A disturbance in the ambient solar wind, 2) an embedded lump of plasma, and 3) an embedded magnetic flux rope. All of these essentially begin with the same foundation, that of a background solar wind into which some form of anomaly is introduced.
The first category, that of a disturbance in the solar wind, is really a derivative of the original idea that CMEs were blast waves from flares. This has since been proven to be a physically incorrect description of CMEs, but nonetheless some of these models have been able to sometimes reproduce well the appearance and propagation characteristics of CMEs. This is probably because at large distances from the Sun the most prominent observable feature is the built-up solar wind material in the sheath, which is governed by the theory of interplanetary shock propagation. The most popular of these models include the Shock Time Of Arrival (STOA) model (Dryer and Smart, 1984), its later version ISPM (Smith and Dryer, 1990), and HAFv2 (Hakamada and Akasofu, 1982; Fry et al., 2001).
The second category, which consists of a lump of material embedded into the solar wind, takes simple and more complex forms, but essentially is based on the assumption that the embedded material responds hydromagnetically to the surrounding solar wind. The simplest description is that of aerodynamic drag, where the CME speed is governed by momentum transfer between it and the solar wind until a kinematic equilibrium is reached. Examples of this include Cargill (2004) and Tappin (2006). A more complex version of this is the ENLIL model (Odstrčil, 2003) which takes into consideration plasma density, CME structure and extrinsic magnetic field as well as the kinematic properties of the CME and solar wind.
The third category treats the CME as a magnetic flux rope which is embedded into the solar wind. These models attempt to include the magnetic interaction between the CME and the interplanetary magnetic field (e.g., Chen, 1996; Manchester IV et al., 2005).
It is important to note that the models discussed above describe the evolution of the CME once it is some distance away from the Sun, i.e., they do not describe the physics of the onset and early evolution. The assumption is that the physics become simplified once the CME has escaped the gravitational and magnetic pressure forces at or near the Sun.
5 CMEs in the Heliosphere
CMEs carry into the heliosphere large amounts of coronal magnetic fields and plasma, which can be detected by remote sensing and in-situ spacecraft observations. Here they are known as interplanetary CMEs or ICMEs (Zhao and Webb, 2003; Dryer, 1994). The term ICME or “interplanetary CME” was originally devised as a means to separate the phenomena observed far from the Sun (e.g., by in-situ spacecraft) and those near the Sun (e.g., by coronagraphs). However, in the SMEI and STEREO era, where CMEs can now be tracked continuously from the Sun to 1 AU and beyond, the term has become largely redundant. Consequently, in a recent workshop on remote sensing of the heliosphere in Wales (June 2011) it was decided to no longer use the term ICME, and in this review we drop the term.
The passage of CME material past a single spacecraft is marked by distinctive signatures, but with a great degree of variation from event to event (e.g., Gosling, 1993). These signatures include transient interplanetary shocks, depressed proton temperatures, cosmic ray depressions, flows with enhanced helium abundances, unusual compositions of ions and elements, and magnetic field structures consistent with looplike topologies. Many of these signatures were first identified in the plasma which followed an IP shock by several hours and was considered to be the piston (CME) driving the shock. Some signatures can also be observed elsewhere in the solar wind where they may identify relatively slower CMEs not driving shocks.
Often observed in in-situ data are highly structured magnetic field configurations corresponding to the arrival of a CME. The field assumes the structure of a spiral (or helix), and is accompanied by other signatures including strong magnetic field with low field variance, low plasma beta, and low temperature. Such structures were called magnetic clouds by Burlaga et al. (1981) citing early theoretical work dating back to the 1950s (Morrison, 1954). Figure 30 shows a schematic of such a cloud impinging on the Earth in May 1997. Such a structure is often modeled as a flux rope, which is a series of helical field lines like the coils of a spring with pitch angles increasing toward the outer edge. Since, as we have seen, many if not all CMEs are now considered to contain flux ropes, it is logical to expect magnetic clouds to form the core of CMEs. In a recent report, one magnetic cloud observed in-situ was tracked continuously back to its coronagraph origins and it was found to be the cavity component of the three-part CME structure (Howard and DeForest, 2012a). This reinforced the largely-accepted view that the cavity component was the CME flux rope (e.g., Forsyth et al., 2006). Theoretical work involving the development of cavities includes Fuller et al. (2008).
Schematic drawing of modeled flux rope on 15 May 1997, including estimate of its dimensions and orientation with respect to the ecliptic plane; the axis of the cloud lay nearly in the ecliptic plane and pointed toward the east. Also drawn is the Sun-Earth line at time of cloud passage by Wind near the L1 point. Image reproduced with permission from Webb et al. (2000b), copyright by AGU.
Models have been developed for the force free (e.g., Lepping et al., 1990; Lynch et al., 2005) and non-force free (Hu and Sonnerup, 2001) states of magnetic clouds observed in-situ, the latter also known as the Grad-Shafranov technique. Around 30% (Gosling et al., 1991) to 50% (Cane et al., 1997) of CMEs observed in-situ show a clear signature of a magnetic cloud. It remains unknown whether the remainder does not show the signature because the imbedded flux rope is less structured, is absent, or whether the spacecraft did not pass through the flux rope component (i.e., skirted its flank).
Some magnetic clouds have been associated with solar filament disappearances. Since filament plasma is embedded in helical, horizontal magnetic fields, the close association of CMEs with filament eruptions and shearing fields near the surface also supports the view that flux ropes form the core of CMEs. One idea is that the interior fields of a rising, sheared CME reconnect, resulting in an ejected flux rope and new, closed coronal loops at the Sun. In several studies magnetic clouds have been found to have the same orientation and polarity as associated erupting filaments at the Sun. Furthermore, larger filaments always have twist in the same sense in a given hemisphere, even though the hemispherical polarity reverses every solar cycle. Filament eruptions and CMEs may be important ways that the Sun sheds magnetic helicity, as well as flux built up over the solar magnetic cycle.
Since the in-situ signatures of CMEs are well described in several recent reviews (Schwenn, 2006; Zurbuchen and Richardson, 2006; Richardson and Cane, 2010), we will not discuss them further here. We will, however, discuss the remote sensing of CMEs, especially as achieved recently by the new class of white light imagers: heliospheric imagers.
5.1 Remote sensing of CMEs at large distances from the Sun
Several techniques have been developed to remotely detect and track disturbances related to CMEs in the interplanetary medium (e.g. Jackson, 1992). These have utilized radio and white light wavelengths to detect and image these structures. The techniques are kilometric radio observations from space and metric radio interplanetary scintillation (IPS) observations from the ground. The kilometric observations can track the emission typically from strong shocks traveling ahead of fast CMEs. Such instruments have been flown on the ISEE-3 and Ulysses spacecraft and are currently on board Wind and STEREO.
5.2 Interplanetary scintillation (IPS) observations
The IPS technique relies on measurements of the fluctuating intensity level of a large number of point-like distant meter-wavelength radio sources. They are observed with one or more ground arrays operating in the MHz-GHz range. IPS arrays detect changes to density in the (local) interplanetary medium moving across the line of sight to the source. Disturbances are detected by either an enhancement of the scintillation level and/or an increase in velocity. When built up over a large number of radio sources a map of the density enhancement across the sky can be produced. The technique suffers from relatively poor temporal (24-hour) resolution and has a spatial resolution limited to the field of view of the radio telescope. For example, high-latitude arrays such as the long-deactivated 3.5 ha array near Cambridge in the UK could not observe sources in the mid-high latitude southern hemisphere. Scattering efficiency also poses a limitation on IPS measurements as increasing the frequency at which to measure the sources allows an observer to detect disturbances closer to the Sun. Higher frequencies means fewer sources, however, so the spatial resolution is effectively decreased. Finally, ionospheric noise limits viewing near the Sun and near the horizon, and a model-dependence for interpreting the signal as density or mass. Workers have, however, been working with these difficulties for 50 years and a number of techniques have evolved to extract reliable CME measurements using IPS. Recent papers involving such measurements include Jones et al. (2007), Bisi et al. (2008), Jackson et al. (2010b), Tappin and Howard (2010), and Manoharan (2010).
5.3 Heliospheric imagers
Today’s heliospheric imagers are the successors to the zodiacal-light photometers (Leinert et al., 1975) on the twin Helios spacecraft flown in solar orbits in the 1970s and early 1980s. SMEI, in particular, was designed to exploit the heliospheric remote sensing capability demonstrated by that instrument (Jackson, 1985; Webb and Jackson, 1990). Unlike Helios, which could only observe a few narrow strips across the sky, this new generation of imager could observe large areas simultaneously. SMEI was the first such imager, developed as a proof-of-concept U.S. Air Force experiment for operational forecasting. Launched in January 2003 on the Coriolis spacecraft, SMEI imaged nearly the entire sky in white light once per 102-minute spacecraft orbit, using three baffled camera systems. Individual frames are mapped into ecliptic coordinates to produce a nearly complete sky map (Figure 31). SMEI was deactivated in September 2011 and over its 8.5 year lifetime it observed nearly 400 CMEs (e.g., Webb et al., 2006; Howard and Simnett, 2008) many of which were Earth-directed (e.g., Tappin et al., 2004; Howard et al., 2006; Webb et al., 2009) allowing the comparison with in-situ spacecraft and prediction of arrival times and speeds. Unlike with in-situ spacecraft, however, SMEI enabled the comparison with coronagraph events in any direction, enabling large-scale tracking and 3-D reconstruction. Figure 32 is a movie of a halo-type CME that was tracked by SMEI until it produced a major geomagnetic storm at Earth.
A composite all-sky image from SMEI taken in February 2003. An equal-area Hammer-Aitoff projection centered on the Sun with North and South ecliptic poles at top and bottom. The dark circle is a zone of exclusion 20° in radius usually centered on the Sun. The inset box shows a large, loop CME in May 2003 superimposed on the all-sky image. CMEs can only be detected in the SMEI data by careful subtraction of backgrounds that include particle contamination because of its Earth orbit (for details see, e.g., Webb et al., 2006).
mpg-Movie (10681.5 KB) Still from a movie showing Orbit difference images of an Earthward halo from SMEI. Halo was visible as an arc over ≥ 150° of sky (arrows). Blacked-out areas are due to shuttering of bright sunlight and CCD noise from particles in Coriolis’ 840 km circular Earth orbit. (For video see appendix)
SMEI was used for CME tracking (Tappin et al., 2004; Webb et al., 2006; Howard et al., 2006, 2007), space weather forecasting (Howard et al., 2006; Webb et al., 2009; Howard and Tappin, 2010), and 3-D reconstruction (Tappin and Howard, 2009; Jackson et al., 2010b). SMEI observations have been compared with coronagraph and in-situ spacecraft measurements (Tappin et al., 2004; Tappin, 2006; Howard et al., 2006, 2007; Howard and Simnett, 2008; Webb et al., 2009) and compared with IPS observations (Jackson et al., 2008b; Bisi et al., 2008). While SMEI observed the entire sky beyond 20° elongation, its field of view was often obscured by energetic particle saturation during its passage through the magnetospheric polar caps and the South Atlantic Anomaly, and by hot pixel degradation.
In October 2006, the twin STEREO spacecraft were launched carrying the Heliospheric Imagers (HIs) (Howard et al., 2008a; Eyles et al., 2009). The HIs are part of the SECCHI suite of imaging telescopes on each spacecraft and view the inner heliosphere starting at an elongation of 4° from the Sun. HI-1 has a FoV of 20°, from 4 – 24° elongation (∼ 12 – 85R⊙), and HI-2 of 70°, from ∼ 19 – 89° elongation (∼ 68 – 216R⊙). There is a 5.3° overlap between the outer HI-1 and inner HI-2 FoVs. The HIs do not cover the entire position angle (PA) range around the Sun, but observe up to a 90° range in PA, usually centered on the ecliptic and viewing either east (HI-A) or west (HI-B) of the Sun. They do not suffer the same problems with particle saturation as SMEI did, but are constrained by their fields of view about the ecliptic plane. Combined with the coronagraphs, the HIs do provide for the first time a continuous view from the Sun to around 1 AU and the stereoscopic viewpoints enable the possibility for 3-D reconstruction using the coronagraphs and HI-1.
The STEREO spacecraft share similar ∼ 1 AU orbits about the Sun as the Earth but separate from the Sun-Earth line by 22.5° per year. STEREO-A (Ahead) leads the Earth in its orbit, while STEREO-B (Behind) lags. Figure 33 is a schematic showing the fields of view of the SECCHI telescopes. Figure 34 is a movie that illustrates these views from all the telescopes during a series of CMEs in early April 2010 that produced several geomagnetic storms at Earth (Davis et al., 2011). The bottom shows the B and A views of the EUVI disk, COR1 and COR2 coronagraph imagers out to 15R⊙, and the upper set shows the HI-1 and -2 fields viewing east (left, HI-A) and west (right, HI-B) of the Sun beyond the EUVI, COR1, COR2 set shown to scale. Most of the early work involving the STEREO-HIs and CMEs have focused on their detection and tracking, and comparison with in-situ spacecraft. Publications include Harrison et al. (2008); Davies et al. (2009); and DeForest et al. (2011).
The fields of view of the STEREO SECCHI HI telescopes flanking that of the SOHO/LASCO C3 instrument. The SECCHI EUVI, COR1, and COR2 telescopes are Sun-pointed like LASCO but the COR2 field extends to only half that of C3. Image adapted from Harrison et al. (2008).
mpg-Movie (28363.8935547 KB) Still from a movie showing Combined views from all of the STEREO SECCHI telescopes during a series of CMEs in early April 2010. The bottom panels show the ST-B and ST-A views of the EUVI disk, COR1 and COR2 imagers out to 15R⊙, and the upper set shows the HI-1 and -2 fields viewing east (left, HI-A) and west (right, HI-B) of the Sun beyond the EUVI, COR1, COR2 set shown to scale. From the online data at: http://secchi.nrl.navy.mil/index.php?p=movies. (For video see appendix)
As shown in Figures 33 and 34, the STEREO/SECCHI instrument suite provides an uninterrupted view from the Sun to around 90° elongation. While they do not have the full PA coverage of SMEI, their location outside the Earth’s magnetosphere removes noise sources that decreased the quality of SMEI images, such as energetic particle saturation from the cusp and South-Atlantic anomaly, glare from the moon, and the aurora. A number of large-scale solar wind transients have been tracked through the SECCHI field of view, including CMEs (e.g., Harrison et al., 2008; Davis et al., 2009; Möstl et al., 2010), corotating interaction regions (e.g., Sheeley Jr et al., 2008; Rouillard et al., 2008; Tappin and Howard, 2009), and solar wind “puffs” (e.g., Rouillard et al., 2010) and “blobs” (e.g., Sheeley Jr et al., 2009; Sheeley Jr and Rouillard, 2010).
The most recent scientific developments using SECCHI data involve a processing pipeline that reduces many sources of noise (starfield, F corona) from the dataset. This has permitted the tracking and measurement of features that were previously inaccessible. Analyses of these pipeline data are still in the preliminary stages, but early results include observations and measurements of CME flux ropes (Howard and DeForest, 2012a) and disconnection events (DeForest et al., 2012). Figure 35 shows an image from a HI-2 movie from DeForest et al. (2011), the movie is also included in this paper.
mpg-Movie (70268.6445312 KB)Still from a movie showing STEREO/HI2-A images following the latest data processing pipeline for SECCHI (DeForest et al., 2011). (For video see appendix)
The important difference between heliospheric imagers and coronagraphs is that 3-D information is available in heliospheric imagers that is not available in coronagraphs. This is because the assumptions imposed on coronagraphs (Thomson scattering assumptions, low angles) are not adequate at large elongations and across large distances. This increases the difficulty of the analysis, but makes available additional information on the structure and kinematics of the CME. This thereby removes the need for auxiliary data to provide this information. The theory describing this ability is developed by Howard and Tappin (2009). More recently, papers are beginning to emerge that consider the 3-D structure of the CME, including Wood and Howard (2009), Lugaz et al. (2009, 2010), and Howard and Tappin (2009, 2010). Techniques involving the extraction of 3-D properties from heliospheric image data are reviewed by Howard (2011a).
6 Conclusions
6.1 Summary
We have discussed the origins and characteristics of coronal mass ejections and their associated phenomena. These have been discussed as occurring near the Sun in terms of their basic coronal properties and what we know about their source regions, and their manifestation in the heliosphere and near Earth. Kinematically there appears to be a continuum of accelerations and speeds of CMEs ranging from gradually accelerating CMEs that have smooth and balloon-shaped profiles, to rapidly accelerating CMEs that are less homogeneous and move through the outer corona at relatively constant speed. The rate of occurrence of CMEs correlates with solar activity, but the size scales of CMEs are much larger and their latitude distributions different than those of nearsurface activity like flares or active regions. CMEs arise in large-scale closed coronal structures, the most evident being helmet streamers, which blow out and reform. Statistically, CMEs are most frequently associated with erupting filaments and X-ray long duration events, and not optical flares. However, new X-ray and EUV data are helping reshape our ideas on these associations. Large-scale coronal arcades are frequently observed, and may result from reconnection of closed field systems opened by CMEs , and indeed long current sheets are now observed connecting the arcade and the rising CME. The size scales and field strengths of these associated systems are a function of latitude. Thus, CMEs involve the destabilization of large-scale coronal structures which result in reconfiguration of the larger-scale, weaker fields at higher latitudes and of the smaller-scale, stronger fields at low latitudes. The magnetic structures involved with the source regions of CMEs can be complex and multipolar. The earliest X-ray signatures of the onset of a CME in the low corona appear to include outward-moving loops and the dimming or depletion of coronal material before and above the bright arcade. Against the disk the arcades are preceded by S-shaped structures associated with and aligned along the axis of filaments, which erupt forming cusp-shaped arcades. EUV waves are now frequently observed in association with CMEs.
CMEs carry into the heliosphere large quantities of coronal magnetic fields and plasma which are detected by remote sensing and in-situ spacecraft observations. Measured at a single spacecraft, this material has distinctive plasma and magnetic field signatures with a large amount of variation. One of the most important signature classes is of magnetic clouds which are thought to be the flux ropes embedded in CMEs and have been identified, for one case, as originating from the cavity component of the three-part coronagraph CME. These carry strong, directional fields that can be very geoeffective. As carriers of such magnetic structures, CMEs may provide an important way for the Sun to shed the magnetic flux and helicity that is built up over the solar magnetic cycle.
In terms of space weather, CMEs are now identified as a crucial link between activity at the Sun and its propagation through the heliosphere to the Earth and other locations. The interplanetary manifestations of CMEs can result in extensive transient disturbances that, when directed Earthward, can cause major geomagnetic storms at Earth. In addition, significant particle and radiation hazards at Earth can arise from CMEs launched from western solar longitudes and, thus, are not necessarily Earth-directed (see Figure 24). The association of erupting filaments and magnetic clouds with CMEs has led to the view that flux ropes form the cavity of a CME and help drive it outward. Halo CMEs are important in terms of forecasting space weather and enhancing our understanding of CMEs and flux ropes. It appears that shocks and magnetic clouds are also likely to be detected at Earth following such solar events. Moderate storms not associated with CMEs are usually caused by Earth passage through the heliospheric current sheet (HCS) and related corotating interaction regions (CIRs). More details about space weather appear in two respective Living Reviews (Schwenn, 2006; Pulkkinen, 2007).
6.2 Unsolved problems
Several enigmatic or outstanding problems remain regarding the origin, propagation, and heliospheric consequences of CMEs. We conclude this review by discussing several of these that we feel are the most important needing to be resolved.
The CME initiation follows storage of energy in closed magnetic field regions on the Sun over a certain period of time but we do not know what triggers the release of that energy. The stored energy that is released during eruption is the free energy available to be released in the form of CMEs, flares, and other eruptive phenomena. The magnetic source of the CME has to build up the free energy. Identification of the signatures of this energy build-up is a crucial step in deciding whether and when a CME will occur. During the build-up phase, minor energetic events occur, but it is difficult to know whether a pre-eruption energy release is a true precursor or a separate eruption. We also do not know how the free energy is apportioned among the subsequent flare energy and the CME mechanical energy. We do know, however, that flares occur without observed CMEs, just as many CMEs are not always accompanied by flares. Flares accompanying CMEs are generally of lower temperature compared to flares not accompanied by CMEs. This may indicate that the many smaller flares without CMEs may contribute to coronal heating (Yashiro et al., 2006), while CMEs carry away the mass and magnetic field into the heliosphere. Based on the highest mass (1014 kg) and speed (∼ 3500 km s-1) observed one can estimate a maximum kinetic energy of ∼ 6 × 1034 erg. Assuming that only a fraction of the stored energy is released in a single episode and that the CME derives all of its energy from a single active region, we can set a limit of ∼ 1036 erg for the maximum free energy available in a solar active region. This is consistent with the size and magnetic field strengths in solar active regions (Kahler, 2006).
CMEs are subject to propelling and retarding forces in the corona and interplanetary medium (see, e.g., Vršnak et al., 2004). The propelling force is not properly identified yet. Solar gravity and the drag force due to momentum exchange between CMEs and the ambient medium constitute the main retarding forces. The net result is that most CMEs tend to acquire the speed of the ambient solar wind at large distances from the Sun. This can be quantified as an effective interplanetary acceleration (Gopalswamy et al., 2000, 2001). However, CMEs come in all sizes and shapes and the ambient solar wind also is highly variable. The propagation of CMEs is also affected by the presence of preceding CMEs (Lyons and Simnett, 2001), especially during solar maximum years when CMEs occur in quick succession (Gopalswamy, 2004). CMEs may also be deflected by other CMEs and by nearby coronal holes (Gopalswamy et al., 2009a) and the CME itself may contain some intrinsic driving property (Howard et al., 2007). We need a proper quantification of these effects to accurately predict the arrival of a CME at a desired location in the heliosphere, once its launch has been observed and the initial speed measured. Another issue is the true speed with which CMEs propagate toward a location in the heliosphere. Coronagraphs measure speeds in the sky plane, but the travel time prediction needs space speed. For example if we consider CMEs heading towards Earth, we need to de-project the sky-plane speed and re-project it along the Sun-Earth line. There have been several attempts to convert the sky plane speed into Earth-directed speed using cone models with reasonable success, but more work is needed (Xie et al., 2006; Michalek et al., 2006; Howard et al., 2008b).
Even though the fastest CMEs produce energetic particles, we do not fully understand why some seemingly energetic events produce only low levels of SEPs. There are clear indications that particle acceleration is a complex issue with multiple sources (shocks and flares) and multiple factors deciding the acceleration efficiency (Kahler, 2001; Gopalswamy, 2004; Kahler and Vourlidas, 2005). We do not know what the flare and shock contributions are for a given SEP event. We also do not know how the ambient medium consisting of previously ejected CMEs, shocks, and SEPs determines the properties of a subsequent event.
We need to more fully understand how the remotely-sensed CMEs evolve into CMEs observed in-situ in the solar wind. Magnetic clouds observed within CMEs in the solar wind have specific magnetic properties, notably their flux rope structure. But flux rope structures near the Sun can only be inferred, although the three-point views from the STEREOs and LASCO and the continous field of view of SECCHI from the corona into the inner heliosphere have improved our understanding. Prominences are themselves thought to be flux ropes near the Sun, but observations in the interplanetary medium are not compatible with that. Magnetic clouds are observed with high charge states implying high temperature (several million K) at the source, whereas prominences are cooler structures with a temperature of only ∼ 8000 K. Such cool prominence material is rarely observed in-situ, another unsolved problem. Coronal cavities observed in eclipse pictures and inner coronal images in X-rays and EUV are thought to contain flux ropes, but an alternative explanation is that these are highly sheared magnetic structures. Recent quantitative comparison between reconnected flux at the eruption site and the azimuthal flux in flux ropes in the solar wind suggest that the two fluxes are approximately the same (Qiu et al., 2007), implying that the flux ropes are formed during the eruption process rather than present in the pre-eruption state. White-light CME observations mainly provide information on the mass content of the CME, but very little on the magnetic structure. Many related observations (magnetic and other) need to be pooled to try to obtain the magnetic structure of CMEs. Another related issue is whether all CMEs contain flux ropes, and the related question of whether all interplanetary CMEs are magnetic clouds? If they are, that implies a definite magnetic structure, from which one can infer the onset time of geomagnetic storms for space weather purposes. The magnetic cloud structure indicates a definite leading and trailing field orientation, which decides the day-side reconnection with Earth’s magnetic field that ultimately results in the magnetic storm. While flux ropes in the interplanetary medium have a well defined magnetic field strength and structure, the same cannot be said about CMEs near the Sun. At present, we have to infer the nature of interplanetary CMEs based on the magnetic properties of solar active regions at the photospheric or chromospheric levels, but the eruption itself starts in the corona.
High temporal and spatial resolution images are needed to identify and study pre-eruption signatures, which is crucial to predicting the onsets of CMEs. We still lack a quantitative understanding of how the magnetic complexity in a source region relates to CME productivity. Since vector magnetograms provide key information on the free energy available in active regions, they need to be developed and the results assimilated into various models, including MHD. Finally, the developing science of helioseismic subsurface imaging of sunspots and active regions suggests important clues to the build-up of energy in active regions that can lead to large flares and CMEs (e.g., Webb et al., 2011).
References
Akmal, A., Raymond, J.C., Vourlidas, A., Thompson, B., Ciaravella, A., Ko, Y.-K., Uzzo, M. and Wu, R., 2001, “SOHO observations of a coronal mass ejection”, Astrophys. J., 553, 922–934. [DOI] (Cited on page 27.)
Antiochos, S.K., DeVore, C.R. and Klimchuk, J.A., 1999, “A model for solar coronal mass ejections”, Astrophys. J., 510, 485–493. [DOI], [ADS], [arXiv:astro-ph/9807220] (Cited on pages 6, 30, 33, and 46.)
Antunes, A., Thernisien, A. and Yahill, A., 2009, “Hybrid reconstructions to derive 3D height-time evolution for coronal mass ejections”, Solar Phys., 259, 199–212. [DOI] (Cited on page 20.)
Aschwanden, M.J., 2006, “Coronal Mass Ejections (CMEs)”, in Physics of the Solar Corona: An Introduction with Problems and Solutions, chap. 17, pp. 703–738, Springer; Praxis, Berlin; New York; Chichester, 2nd edn. [Google Books] (Cited on pages 8 and 46.)
Aschwanden, M.J., Nitta, N.V., Wülser, J.-P., Lemen, J.R., Sandman, A., Vourlidas, A. and Colaninno, R.C., 2009, “First measurements of the mass of coronal mass ejections from the EUV dimming observed with STEREO EUVI A+B spacecraft”, Astrophys. J., 706, 376–392. [DOI], [ADS] (Cited on pages 23 and 34.)
Attrill, G.D.R., Harra, L.K., van Driel-Gesztelyi, L. and Wills-Davey, M.J., 2010, “Revealing the fine structure of coronal dimmings and associated flows with Hinode/EIS; Implications for understanding the source regions of sustained outflow following CMEs”, Solar Phys., 264, 119–147. [DOI] (Cited on page 35.)
Baker, D.N., Balstad, R., Bodeau, J.M., Cameron, E., Fennell, J.F., Fisher, G.M., Forbes, K.F., Kintner, P.L., Leffler, L.G., Lewis, W.S., Reagan, J.B., Small III, A.A., Stansell, T.A., Strachan Jr, L., Graham, S.J., Fisher, T.M., Swisher, V. and Gruber, C.A., 2008, Severe Space Weather Events - Understanding Societal and Economic Impacts: A Workshop Report, The National Academies Press, Washington DC (Cited on page 5.)
Bastian, T.S., Pick, M., Kerdraon, A., Maia, D. and Vourlidas, A., 2001, “The coronal mass ejection of 1998 April 20: Direct imaging at radio wavelengths”, Astrophys. J. Lett., 558, L65–L69. [DOI] (Cited on page 8.)
Bemporad, A. and Mancuso, S., 2010, “First complete determination of plasma physical parameters across a coronal mass ejection-driven shock”, Astrophys. J., 720, 130–143. [DOI] (Cited on pages 37 and 40.)
Bemporad, A., Mierla, M. and Tripathi, D., 2011, “Rotation of an erupting filament observed by the STEREO EUVI and COR1 instruments”, Astron. Astrophys., 531, A147. [DOI] (Cited on page 33.)
Benz, A.O., 2008, “Flare Observations”, Living Rev. Solar Phys., 5, lrsp-2008-1. [ADS]. URL (accessed 17 August 2011): http://www.livingreviews.org/lrsp-2008-1 (Cited on page 31.)
Biesecker, D.A., Myers, D.C., Thompson, B.J., Hammer, D.M. and Vourlidas, A., 2002, “Solar phenomena associated with ‘EIT Waves”’, Astrophys. J., 569, 1009–1015. [DOI], [ADS] (Cited on page 36.)
Billings, D.E., 1966, A Guide to the Solar Corona, Academic Press, New York; London. [ADS] (Cited on pages 5, 20, and 23.)
Bisi, M.M., Jackson, B.V., Hick, P.P., Buffington, A., Odstrčil, D. and Clover, J.M., 2008, “Threedimensional reconstructions of the early November 2004 Coordinated Data Analysis Workshop geomagnetic storms: Analyses of STELab IPS speed and SMEI density data”, J. Geophys. Res., 113, A00A11. [DOI] (Cited on page 52.)
Boursier, Y., Lamy, P., Llebaria, A., Goudail, F. and Robelus, S., 2009, “The ARTEMIS catalog of LASCO coronal mass ejections. Automatic recognition of transient events and Marseille inventory from synoptic maps”, Solar Phys., .257, 125–147. (Cited on pages 10 and 11.)
Brueckner, G.E., Howard, R.A., Koomen, M.J., Korendyke, C.M., Michels, D.J., Moses, J.D., Socker, D.G., Dere, K.P., Lamy, P.L., Llebaria, A., Bout, M.V., Schwenn, R., Simnett, G.M., Bedford, D.K. and Eyles, C.J., 1995, “The Large Angle Spectroscopic Coronagraph (LASCO)”, Solar Phys., 162, 357–402. [DOI] (Cited on page 5.)
Burkepile, J.T., Hundhausen, A.J., Stanger, A.L., St Cyr, O.C. and Seiden, J.A., 2004, “Role of projection effects on solar coronal mass ejection properties: 1. A study of CMEs associated with limb activity”, J. Geophys. Res., 109, A03103. [DOI], [ADS] (Cited on pages 9 and 28.)
Burlaga, F., Sittler, E., Mariani, F. and Schwenn, R., 1981, “Magnetic loop behind an interplanetary shock: Voyager, Helios, and IMP 8 observations”, J. Geophys. Res., 86, 6673–6684. [DOI], [ADS] (Cited on page 50.)
Byrne, J.P., Gallagher, P.T., McAteer, R.T.J. and Young, C.A., 2009, “The kinematics of coronal mass ejections using multiscale methods”, Astron. Astrophys., 495, 325–334. [DOI] (Cited on page 11.)
Byrne, J.P., Maloney, S.A., McAteer, R.T.J., Refojo, J.M. and Gallagher, P.T., 2010, “Propagation of an Earth-directed coronal mass ejection in three dimensions”, Nature Commun., 1, 74. [DOI] (Cited on page 20.)
Cane, H.V. and Richardson, I.G., 2003, “Interplanetary coronal mass ejections in the near-Earth solar wind during 1996-2002”, J. Geophys. Res., 108(A4), 1156. [DOI], [ADS] (Cited on page 17.)
Cane, H.V., Richardson, I.G. and Wibberenz, G., 1997, “Helios 1 and 2 observations of particle decreases, ejecta, and magnetic clouds”, J. Geophys. Res., 102, 7075–7086. [DOI] (Cited on page 50.)
Cane, H.V., Richardson, I.G. and St Cyr, O.C., 2000, “Coronal mass ejections, interplanetary ejecta and geomagnetic storms”, Geophys. Res. Lett., 27, 3591–3594. [DOI] (Cited on page 17.)
Canfield, R.C., Cheng, C.-C., Dere, K.P., Dulk, G.A., McLean, D.J., Schmahl, E.J., Robinson Jr, R.D. and Schoolman, S.A., 1980, “Radiative energy output of the 5 September 1973 flare”, in Solar flares: A monograph from Skylab Solar Workshop II , (Ed.) Sturrock, P.A., pp. 451–469, Colorado Associated University Press, Boulder, CO (Cited on pages 25 and 27.)
Canfield, R.C., Hudson, H.S. and McKenzie, D.E., 1999, “Sigmoidal morphology and eruptive solar activity”, Geophys. Res. Lett., 26, 627–630. [DOI], [ADS] (Cited on pages 6 and 34.)
Cargill, P.J., 2004, “On the aerodynamic drag force acting on interplanetary coronal mass ejections”, Solar Phys., 221, 135–149. [DOI] (Cited on page 48.)
Chen, J., 1996, “Theory of prominence eruption and propagation: Interplanetary consequences”, J. Geophys. Res., 101, 27,499–27,519. [DOI], [ADS] (Cited on page 49.)
Chen, P.F., 2011, “Coronal Mass Ejections: Models and Their Observational Basis”, Living Rev. Solar Phys., 8, lrsp-2011-1. [ADS]. URL (accessed 17 August 2011): http://www.livingreviews.org/lrsp-2011-1 (Cited on pages 8 and 46.)
Chen, P.F. and Wu, Y., 2011, “First evidence of coexisting EIT wave and coronal moreton wave from SDO/AIA observations”, Astrophys. J. Lett., 732, L20. [DOI] (Cited on page 37.)
Christian, E.R., Kaiser, M.L., Kucera, T.A. and St Cyr, O.C. (Eds.), 2009, STEREO Science Results at Solar Minimum, vol. 256 of Solar Phys. (Special Issue), Springer, Dordrecht. [DOI] (Cited on page 8.)
Ciaravella, A. and Raymond, J.C., 2008, “The current sheet associated with the 2003 November 4 coronal mass ejection: Density, temperature, thickness, and line width”, Astrophys. J., 686, 1372–1382. [DOI] (Cited on page 39.)
Ciaravella, A., Raymond, J.C., Thompson, B.J., van Ballegooijen, A., Strachan, L., Li, J., Gardner, L., O’Neal, R., Antonucci, E., Kohl, J. and Noci, G., 2000, “Solar and Heliospheric Observatory observations of a helical coronal mass ejection”, Astrophys. J., 529, 575–591. [DOI] (Cited on page 27.)
Ciaravella, A., Raymond, J.C., Li, J., Reiser, P., Gardner, L.D., Ko, Y.-K. and Fineschi, S., 2003a, “Elemental abundances and post-coronal mass ejection current sheet in a very hot active region”, Astrophys. J., 575, 1116–1130. [DOI], [ADS] (Cited on page 42.)
Ciaravella, A., Raymond, J.C., van Ballegooijen, A., Strachan, L., Vourlidas, A., Li, J., Chen, J. and Panasyuk, A., 2003b, “Physical parameters of the 2000 February 11 coronal mass ejection: Ultraviolet spectra versus white-light images”, Astrophys. J., 597, 1118–1134. [DOI] (Cited on pages 29 and 39.)
Cliver, E.W. and Hudson, H.S., 2002, “CMEs: How do the puzzle pieces fit together?”, J. Atmos. Sol.-Terr. Phys., 64, 231–252. [DOI], [ADS] (Cited on page 27.)
Cliver, E.W. and Webb, D.F., 1998, “Disappearances of High-Latitude Filaments as Sources of High- Latitude CMEs”, in New Perspectives on Solar Prominences, IAU Colloq. 167, Aussois, France, April 28 -May 4, 1997, (Eds.) Webb, D.F., Schmieder, B., Rust, D.M., vol. 150 of ASP Conference Series, pp. 479–483, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 13.)
Cliver, E.W., Webb, D.F. and Howard, R.A., 1999, “On the origin of solar metric type II bursts”, Solar Phys., 187, 89–114. [DOI], [ADS] (Cited on page 37.)
Cliver, E.W., Laurenza, M., Storini, M. and Thompson, B.J., 2005, “On the origins of solar EIT waves”, Astrophys. J., 631, 604–611. [DOI], [ADS] (Cited on page 36.)
Colaninno, R.C. and Vourlidas, A., 2009, “First Determination of the True Mass of Coronal Mass Ejections: A Novel Approach to Using the Two STEREO Viewpoints”, Astrophys. J., 698, 852–858. [DOI], [arXiv:0903.4344] (Cited on page 24.)
Cremades, H. and Bothmer, V., 2004, “On the three-dimensional configuration of coronal mass ejections”, Astron. Astrophys., 422, 307–322. [DOI], [ADS] (Cited on pages 9 and 33.)
Crifo, F., Picat, J.P. and Cailloux, M., 1983, “Coronal transients: Loop or bubble?”, Solar Phys., 83, 143–152. [DOI] (Cited on page 20.)
Crooker, N., 2002, “Solar-heliospheric group ‘SHINE’ sheds light on murky problems”, Eos Trans. AGU, 83, 24. [DOI] (Cited on page 22.)
Davies, J.A., Harrison, R.A., Rouillard, A.P., Sheeley Jr, N.R., Perry, C.H., Bewsher, D., Davis, C.J., Eyles, C.J., Crothers, S.R. and Brown, D.S., 2009, “A synoptic view of solar transient evolution in the inner heliosphere using the Heliospheric Imagers on STEREO”, Geophys. Res. Lett., 36, L02102. [DOI] (Cited on page 54.)
Davis, C.J., Davies, J.A., Lockwood, M., Rouillard, A.P., Eyles, C.J. and Harrison, R.A., 2009, “Stereoscopic imaging of an Earth-impacting solar coronal mass ejection: A major milestone for the STEREO mission”, Geophys. Res. Lett., 36, L08102. [DOI] (Cited on page 54.)
Davis, C.J., de Koning, C.A., Davies, J.A., Biesecker, D., Millward, G., Dryer, M., Deehr, C.S., Webb, D.F., Schenk, K., Freeland, S.L., Möstl, C., Farrugia, C.J. and Odstrčil, D., 2011, “A comparison of space weather analysis techniques used to predict the arrival of the Earth-directed CME and its shockwave launched on 8 April 2010”, Space Weather, 9, S01005. [DOI] (Cited on page 54
de Koning, C.A. and Pizzo, V.J.,.2011, “Polarimetric localization: A new tool for calculating the CME speed and direction of propagation in near-real time”, Space Weather, 9, S03001. [DOI] (Cited on page 20
de Koning, C.A., Pizzo, V.J. and Biesecker, D.A., 2009, “Geometric localization of CMEs in 3D space using STEREO beacon data: First results”, Solar Phys., 256, 167–181. [DOI] (Cited on pages 20 and 21.)
DeForest, C.E., Howard, T.A. and Tappin, S.J., 2011, “Observations of detailed structure in the solar wind at 1 AU with STEREO/HI-2”, Astrophys. J., 738, 103–115. [DOI] (Cited on pages 54 and 56.)
DeForest, C.E., Howard, T.A. and McComas, D.J., 2012, “Disconnecting open solar magnetic flux”, Astrophys. J., 745, 36–44. [DOI] (Cited on pages 24 and 54.)
Demastus, H.L., Wagner, W.J. and Robinson, R.D.,.1973, “Coronal disturbances. I: Fast transient events observed in the green coronal emission line during the last solar cycle”, Solar Phys., 31, 449–459 (Cited on pages 5 and 43.)
Dere, K.P., Brueckner, G.E., Howard, R.A., Koomen, M.J., Korendyke, C.M., Kreplin, R.W., Michels, D.J., Moses, J.D., Moulton, N.E., Socker, D.G., St Cyr, O.C., Delaboudinière, J.P., Artzner, G.E., Brunaud, J., Gabriel, A.H., Hochedez, J.F., Millier, F., Song, X.Y., Chauvineau, J.P., Marioge, J.P., Defise, J.M., Jamar, C., Rochus, P., Catura, R.C., Lemen, J.R., Gurman, J.B., Neupert, W., Clette, F., Cugnon, P., van Dessel, E.L., Lamy, P.L., Llebaria, A., Schwenn, R. and Simnett, G.M., 1997, “EIT and LASCO Observations of the Initiation of a Coronal Mass Ejection”, Solar Phys., 175, 601–612. [DOI], [ADS] (Cited on page 27.)
Dere, K.P., Wang, D. and Howard, R.A., 2005, “Three-dimensional structure of coronal mass ejections from LASCO polarization measurements”, Astrophys. J., 620, L119–L122. [DOI], [ADS] (Cited on page 20.)
Dodson, H.W. and Hedeman, E.R., 1964, “Problems of differentiation of flares with respect to geophysical effects”, Planet. Space Sci., 12, 393–418. [DOI] (Cited on page 43.)
Dryer, M., 1994, “Interplanetary studies: Propagation of disturbances between the Sun and the magnetosphere”, Space Sci. Rev., 67, 363–419. [DOI] (Cited on pages 48 and 50.)
Dryer, M. and Smart, D.F., 1984, “Dynamical models of coronal transients and interplanetary disturbances”, Adv. Space Res., 4, 291–301. [DOI] (Cited on page 48.)
Emslie, A.G., Kucharek, H., Dennis, B.R., Gopalswamy, N., Holman, G.D., Share, G.H., Vourlidas, A., Forbes, T.G., Gallagher, P.T., Mason, G.M., Metcalf, T.R., Mewaldt, R.A., Murphy, R.J., Schwartz, R.A. and Zurbuchen, T.H., 2004, “Energy partition in two solar flare/CME events”, J. Geophys. Res., 109, A10104. [DOI], [ADS] (Cited on pages 6, 25, 27, and 38.)
Emslie, A.G., Dennis, B.R., Holman, G.D. and Hudson, H.S., 2005, “Refinements to flare energy estimates: A followup to ‘Energy partition in two solar flare/CME events’ by A.G. Emslie et al.”, J. Geophys. Res., 110, A11103. [DOI], [ADS] (Cited on page 27.)
Eyles, C.J., Harrison, R.A., Davis, C.J., Waltham, N.R., Shaughnessy, B.M., Mapson-Menard, H.C.A., Bewsher, D., Crothers, S.R., Davies, J.A., Simnett, G.M., Howard, R.A., Moses, J.D., Newmark, J.S., Socker, D.G., Halain, J.-P., Defise, J.-M., Mazy, E. and Rochus, P., 2009, “The Heliospheric Imagers onboard the STEREO mission”, Solar Phys., 254, 387–445. [DOI] (Cited on page 52.)
Fan, Y., 2005, “Coronal Mass Ejections as Loss of Confinement of Kinked Magnetic Flux Ropes”, Astrophys. J., 630, 543–551. [DOI], [ADS] (Cited on page 47.)
Fan, Y. and Gibson, S.E., 2003, “The emergence of a twisted magnetic flux tube into a preexisting coronal arcade”, Astrophys. J., 589, L105–L108. [DOI], [ADS] (Cited on page 6.)
Fan, Y. and Gibson, S.E., 2004, “Numerical simulations of three-dimensional coronal magnetic fields resulting from the emergence of twisted magnetic flux tubes”, Astrophys. J., 609, 1123–1133. [DOI], [ADS] (Cited on page 46.)
Feng, L., Inhester, B., Wei, Y., Gan, W.Q., Zhang, T.L. and Wang, M.Y., 2012, “Morphological Evolution of a Three-dimensional Coronal Mass Ejection Cloud Reconstructed from Three Viewpoints”, Astrophys. J., 751, 18. [DOI], [ADS], [1203.3261] (Cited on page 20.)
Feynman, J. and Hundhausen, A.J., 1994, “Coronal mass ejections and major solar flares: The great active center of March 1989”, J. Geophys. Res., 99, 8451–8464. [DOI] (Cited on page 6.)
Fisher, R.R., Lee, R.H., MacQueen, R.M. and Poland, A.I., 1981, “New Mauna Loa Coronagraph Systems”, Appl. Opt., 20, 330. [DOI] (Cited on page 5.)
Forbes, T.G. and Acton, L.W., 1996, “Reconnection and field line shrinkage in solar flares”, Astrophys. J., 459, 330. [DOI], [ADS] (Cited on page 32.)
Forbes, T.G., Linker, J.A., Chen, J., Cid, C., Kóta, J., Lee, M.A., Mann, G., Mikić, Z., Potgieter, M.S., Schmidt, J.M., Siscoe, G.L., Vainio, R., Antiochos, S.K. and Riley, P., 2006, “CME Theory and Models”, Space Sci. Rev., 123, 251–302. [DOI], [ADS] (Cited on pages 6 and 46.)
Forbush, S.E., 1946, “Three unusual cosmic-ray increases possibly due to charged particles from the Sun”, Phys. Rev., 70, 771–772. [DOI] (Cited on pages 5 and 38.)
Forsyth, R.J., Bothmer, V., Cid, C., Crooker, N.U., Horbury, T.S., Kecskemety, K., Klecker, B., Linker, J.A., Odstrčil, D., Reiner, M.J., Richardson, I.G., Rodriguez-Pacheco, J., Schmidt, J.M. and Wimmer-Schweingruber, R.F., 2006, “ICMEs in the inner heliosphere: Origin, evolution and propagation effects”, Space Sci. Rev., 123, 383–416. [DOI] (Cited on page 50.)
Fry, C.D., Sun, W., Deehr, C.S., Dryer, M., Smith, Z., Akasofu, S.-I., Tokumaru, M. and Kojima, M., 2001, “Improvements to the HAF solar wind model for space weather predictions”, J. Geophys. Res., 106, 20,985–21,001. [DOI] (Cited on page 48.)
Fuller, J., Gibson, S.E., de Toma, G. and Fan, Y., 2008, “Observing the unobservable? Modeling coronal cavity densities”, Astrophys. J., 678, 515–530. [DOI] (Cited on page 50.)
Gallagher, P.T. and Long, D.M., 2011, “Large-scale Bright Fronts in the Solar Corona: A Review of ‘EIT waves’”, Space Sci. Rev., 158, 365–396. [DOI], [ADS], [arXiv:1006.0140] (Cited on page 36.)
Gallagher, P.T., Lawrence, G.R. and Dennis, B.R., 2003, “Rapid acceleration of a coronal mass ejection in the low corona and implications for propagation”, Astrophys. J., .588, L53–L56. [DOI] (Cited on page 22.)
Gloeckler, G., Geiss, J., Roelof, E.C., Fisk, L.A., Ipavich, F.M., Ogilvie, K.W., Lanzerotti, L.J., von Steiger, R. and Wilken, B., 1994, “Acceleration of interstellar pickup ions in the disturbed solar wind observed on ULYSSES”, J. Geophys. Res., 99, 17,637–17,643. [DOI] (Cited on page 37.)
Gopalswamy, N., 2004, “A Global Picture of CMEs in the Inner Heliosphere”, in The Sun and the Heliosphere as an Integrated System, (Eds.) Poletto, G., Suess, S.T., vol. 317 of Astrophysics and Space Science Library, pp. 201–251, Kluwer, Dordrecht; Boston. [Google Books] (Cited on pages 8, 9, 14, 17, 18, 22, 27, and 58.)
Gopalswamy, N., 2010a, “The CME link to geomagnetic storms”, in Solar and Stellar Variability: Impact on Earth and Planets, Brazil, 3–7 August 2009, (Eds.) Kosovichev, A.G., Andrei, A.H., Roelot, J.-P., vol. 264 of IAU Symposia, pp. 326–335, Cambridge University Press, Cambridge; New York. [DOI] (Cited on page 17.)
Gopalswamy, N., 2010b, “Coronal mass ejections: A summary of recent results”, in Proceedings of the 20th National Solar Physics Meeting, Papradno, Slovakia, 31 May–4 June 2010, (Ed.) Dorotovič, I., pp. 108–130, Slovak Central Observatory, Hurbanovo. [ADS] (Cited on pages 9, 13, 21, 27, and 38.)
Gopalswamy, N. and Kundu, M.R., 1992, “Estimation of the mass of a coronal mass ejection from radio observations”, Astrophys. J., 390, L37–L39. [DOI], [ADS] (Cited on page 6.)
Gopalswamy, N. and Kundu, M.R., 1993, “Structure of a fast coronal mass ejection from radio observations”, Adv. Space Res., 13, 75–78. [DOI] (Cited on page 23.)
Gopalswamy, N., Lara, A., Lepping, R.P., Kaiser, M., Berdichevsky, D. and St Cyr, O.C., 2000, “Interplanetary acceleration of coronal mass ejections”, Geophys. Res. Lett., 27, 145–148. [DOI], [ADS] (Cited on page 58.)
Gopalswamy, N., Lara, A., Yashiro, S., Kaiser, M. and Howard, R.A., 2001, “Predicting the 1-AU arrival times of coronal mass ejections”, J. Geophys. Res., 106(A12), 29,207–29,217. [DOI], [ADS] (Cited on page 58.)
Gopalswamy, N., Lara, A., Yashiro, S., Nunes, S. and Howard, R.A., 2003a, “Coronal Mass Ejection Activity During Solar Cycle 23”, in Solar Variability as an Input to the Earth’s Environment (ISCS 2003), Proceedings of the Symposium, Tatranská Lomnica, Slovak Republic, 23–28 June 2003, (Ed.) Wilson, A., vol. SP-535 of ESA Special Publication, pp. 403–414, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 10 and 33.)
Gopalswamy, N., Shimojo, M., Yashiro, S. and Howard, R.A., 2003b, “Prominence eruptions and coronal mass ejection: A statistical study using microwave observations”, Astrophys. J., 586, 562–578. [DOI] (Cited on pages 13 and 31.)
Gopalswamy, N., Shimojo, M., Lu, W., Yashiro, S., Shibasaki, K. and Howard, R.A., 2004a, “On coronal streamer changes”, Adv. Space Res., 33, 676–680. [DOI] (Cited on page 28.)
Gopalswamy, N., Yashiro, S., Krucker, S., Stenborg, G. and Howard, R.A., 2004b, “Intensity variation of large solar energetic particle events associated with coronal mass ejections”, J. Geophys. Res., 109, A12105. [DOI] (Cited on page 38.)
Gopalswamy, N., Xie, H., Yashiro, S. and Usoskin, I.G., 2005, “Coronal mass ejections and ground level enhancements”, in Proceedings of the 29th International Cosmic Ray Conference, August 3–10, 2005, Pune, India, (Ed.) Sripathi Acharya, B. et al., vol. 1, pp. 169–172, Tata Institute of Fundamental Research, Mumbai. [ADS] (Cited on pages 9, 13, and 37.)
Gopalswamy, N., Mewaldt, R. and Torsti, J. (Eds.), 2006a, Solar Eruptions and Energetic Particles, AGU Chapman Conference ‘Solar Energetic Plasmas and Particles’, held at the University of Turku, Finland, August 2 - 6, 2004, vol. 165 of Geophysical Monograph, American Geophysical Union, Washington, DC. [DOI] (Cited on page 8.)
Gopalswamy, N., Mikić, Z., Maia, D., Alexander, D., Cremades, H., Kaufmann, P., Tripathi, D. and Wang, Y.-M., 2006b, “The pre-CME Sun”, Space Sci. Rev., 123, 303–339. [DOI], [ADS] (Cited on pages 8, 9, 13, 21, and 43.)
Gopalswamy, N., Yashiro, S. and Akiyama, S., 2007, “Geoeffectiveness of halo coronal mass ejections”, J. Geophys. Res., 112, A06112. [DOI] (Cited on pages 17 and 31.)
Gopalswamy, N., Yashiro, S., Akiyama, S., Mäkelä, P., Xie, H., Kaiser, M.L., Howard, R.A. and Bougeret, J.-L., 2008, “Coronal mass ejections, type II radio bursts, and solar energetic particle events in the SOHO era”, Ann. Geophys., 26, 1–15. [DOI] (Cited on page 38.)
Gopalswamy, N., Makela, P., Xie, H., Akiyama, S. and Yashiro, S., 2009a, “CME interactions with coronal holes and their interplanetary consequences”, J. Geophys. Res., 114, A00A22. [DOI] (Cited on page 58.)
Gopalswamy, N., Yashiro, S., Michalek, G., Stenborg, G., Vourlidas, A., Freeland, S. and Howard, R., 2009b, “The SOHO/LASCO CME catalog”, Earth Moon Planets, 104, 295–313. [DOI] (Cited on pages 5 and 10.)
Gopalswamy, N., Yashiro, S., Temmer, M., Davila, J., Thompson, W.T., Jones, S., McAteer, R.T.J., Wülser, J.-P., Freeland, S. and Howard, R.A., 2009c, “EUV wave reflection from a coronal hole”, Astrophys. J., 691, L123–L127. [DOI], [ADS] (Cited on page 36.)
Gopalswamy, N., Akiyama, S., Yashiro, S. and Makela, P., 2010a, “Coronal mass ejections from sunspot and non-sunspot regions”, in Magnetic Coupling between the Interior and the Atmosphere of the Sun, (Eds.) Hasan, S.S., Rutten, R.J., Astrophysics and Space Science Proceedings, pp. 289–307, Springer, Berlin; Heidelberg (Cited on pages 13, 17, 18, and 19.)
Gopalswamy, N., Yashiro, S., Michalek, G., Xie, H., Mäkelä, P., Vourlidas, A. and Howard, R.A., 2010b, “A catalog of halo coronal mass ejections from SOHO”, Sun and Geosphere, 5, 7–16. [ADS] (Cited on pages 12 and 17.)
Gopalswamy, N., Shimojo, M., Lu, W., Yashiro, S., Shibasaki, K. and Howard, R.A., 2012, “Coronal magnetic field measurement from EUV images made by the Solar Dynamics Observatory”, Astrophys. J., 744, 72–78. [DOI] (Cited on page 36.)
Gosling, J.T., 1993, “The solar flare myth”, J. Geophys. Res., 98, 18,937–18,949. [DOI], [ADS] (Cited on pages 6, 29, 46, and 50.)
Gosling, J.T., Hildner, E., MacQueen, R.M., Munro, R.H., Poland, A.I. and Ross, C.L., 1976, “The speeds of coronal mass ejection events”, Solar Phys., 48, 389–397. [DOI], [ADS] (Cited on page 22.)
Gosling, J.T., McComas, D.J., Phillips, J.L. and Bame, S.J., 1991, “Geomagnetic activity associated with earth passage of interplanetary shock disturbances and coronal mass ejections”, J. Geophys. Res., 96, 7831–7839. [DOI] (Cited on page 50.)
Hakamada, K. and Akasofu, S.-I., 1982, “Simulation of three-dimensional solar wind disturbances and resulting geomagnetic storms”, Space Sci. Rev., 31, 3–70. [DOI] (Cited on page 48.)
Hanaoka, Y., Kurokawa, H., Enome, S., Nakajima, H., Shibasaki, K., Nishio, M., Takano, T., Torii, C., Sekiguchi, H., Kawashima, S., Bushimata, T., Shinohara, N., Irimajiri, Y., Koshiishi, H., Shiomi, Y., Nakai, Y., Funakoshi, Y., Kitai, R., Ishiura, K. and Kimura, G., 1994, “Simultaneous Observations of a Prominence Eruption Followed by a Coronal Arcade Formation in Radio, Soft X-Rays, and Hα”, Publ. Astron. Soc. Japan, 46, 205–216. [ADS] (Cited on pages 6 and 34.)
Harrison, R.A., 1986, “Solar coronal mass ejections and flares”, Astron. Astrophys., 162, 283–291. [ADS] (Cited on page 31.)
Harrison, R.A., 1991, “Coronal transients and their relation to solar flares”, Adv. Space Res., 11, 25–36. [DOI] (Cited on page 44.)
Harrison, R.A. and Lyons, M., 2000, “A spectroscopic study of coronal dimming associated with a coronal mass ejection”, Astron. Astrophys., 358, 1097–1108. [ADS] (Cited on page 34.)
Harrison, R.A., Hildner, E., Hundhausen, A.J., Sime, D.G. and Simnett, G.M., 1990, “The launch of solar coronal mass ejections: Results from the coronal mass ejection onset program”, J. Geophys. Res., 95, 917–937. [DOI] (Cited on page 44.)
Harrison, R.A., Bryans, P., Simnett, G.M. and Lyons, M., 2003, “Coronal dimming and the coronal mass ejection onset”, Astron. Astrophys., 400, 1071–1083. [DOI] (Cited on pages 23 and 34.)
Harrison, R.A., Davis, C.J., Eyles, C.J., Bewsher, D., Crothers, S.R., Davies, J.A., Howard, R.A., Moses, D.J., Socker, D.G., Newmark, J.S., Halain, J.-P., Defise, J.-M., Mazy, E., Rochus, P., Webb, D.F. and Simnett, G.M., 2008, “First Imaging of Coronal Mass Ejections in the Heliosphere Viewed from Outside the Sun-Earth Line”, Solar Phys., 247, 171–193. [DOI] (Cited on page 54.)
Hathaway, D.H., 2010, “Does the Current Minimum Validate (or Invalidate) Cycle Prediction Methods?”, in SOHO-23: Understanding a Peculiar Solar Minimum, Proceedings of a Workshop held at Asticou Inn, Northeast Harbor, Maine, USA 21–25 September 2009, (Eds.) Cranmer, S.R., J.T., Hoeksema, Kohl, J.L., vol. 428 of ASP Conference Series, pp. 307–314, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:1003.4208] (Cited on page 13.)
Hewish, A., Scott, P.F. and Wills, D., 1964, “Interplanetary scintillation of small diameter radio sources”, Nature, 203, 1214–1217. [DOI] (Cited on page 5.)
Hiei, E., Hundhausen, A.J. and Sime, D.G., 1993, “Reformation of a coronal helmet streamer by magnetic reconnection after a coronal mass ejection”, Geophys. Res. Lett., 20, 2785–2788. [DOI], [ADS] (Cited on page 46.)
Hirayama, T. and Nakagomi, Y., 1974, “Observations of Prominences in He II with a New 25 cm coronagraph”, Publ. Astron. Soc. Japan, 26, 53–56. [ADS] (Cited on page 5.)
Houminer, Z. and Hewish, A., 1974, “Correlation of interplanetary scintillation and spacecraft plasma density measurements”, Planet. Space Sci., 22, 1041–1042. [DOI] (Cited on page 5.)
Howard, R.A., Michels, D.J., Sheeley Jr, N.R. and Koomen, M.J., 1982, “The observation of a coronal transient directed at Earth”, Astrophys. J., 263, L101–L104. [DOI], [ADS] (Cited on page 9.)
Howard, R.A., Sheeley Jr, N.R., Koomen, M.J. and Michels, D.J., 1985, “Coronal Mass Ejections: 1979- 1981”, J. Geophys. Res., 90, 8173–8191. [DOI], [ADS] (Cited on pages 9, 13, 19, and 28.)
Howard, R.A., Sheeley Jr, N.R., Michels, D.J. and Koomen, M.J., 1986, “The solar cycle dependence of coronal mass ejections”, in The Sun and the Heliosphere in Three Dimensions, Proceedings of the XIXth ESLAB Symposium, held in Les Diablerets, Switzerland, 4–6 June 1985, (Ed.) Marsden, R.G., vol. 133 of Astrophysics and Space Science Library, pp. 107–111, D. Reidel, Dordrecht; Boston (Cited on page 21.)
Howard, R.A., Moses, J.D., Vourlidas, A., Newmark, J.S., Socker, D.G., Plunkett, S.P., Korendyke, C.M., Cook, J.W., Hurley, A., Davila, J.M., Thompson, W.T., St Cyr, O.C., Mentzell, E., Mehalick, K., Lemen, J.R., Wülser, J.-P., Duncan, D.W., Tarbell, T.D., Wolfson, C.J., Moore, A., Harrison, R.A., Waltham, N.R., Lang, J., Davis, C.J., Eyles, C.J., Mapson-Menard, H., Simnett, G.M., Halain, J.P., Defise, J.M., Mazy, E., Rochus, P., Mercier, R., Ravet, M.F., Delmotte, F., Auchere, F., Delaboudinière, J.-P., Bothmer, V., Deutsch, W., Wang, D., Rich, N., Cooper, S., Stephens, V., Maahs, G., Baugh, R., McMullin, D. and Carter, T., 2008a, “Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI)”, Space Sci. Rev., 136, 67–115. [DOI], [ADS] (Cited on pages 5 and 52.)
Howard, T.A., 2011a, “Three-dimensional reconstruction of coronal mass ejections using heliospheric imager data”, J. Atmos. Sol.-Terr. Phys., 73, 1242–1253. [DOI] (Cited on pages 25 and 56.)
Howard, T.A., 2011b, Coronal Mass Ejections: An Introduction, Astrophysics and Space Science Library, Springer, New York. [DOI], [Google Books] (Cited on pages 6, 8, 23, and 27.)
Howard, T.A. and DeForest, C.E., 2012a, “Inner flux rope evolution via imaging of coronal mass ejections”, Astrophys. J., 746, 64–75. [DOI] (Cited on pages 12, 50, and 54.)
Howard, T.A. and DeForest, C.E., 2012b, “The Thomson surface: I. Reality and myth”, Astrophys. J., 752, 130. [DOI] (Cited on pages 23 and 25.)
Howard, T.A. and Harrison, R.A., 2012, “Stealth coronal mass ejections: A perspective”, Solar Phys., accepted (Cited on pages 23 and 43.)
Howard, T.A. and Simnett, G.M., 2008, “Interplanetary coronal mass ejections that are undetected by solar coronagraphs”, J. Geophys. Res., 113, A08102. [DOI] (Cited on pages 5, 17, and 52.)
Howard, T.A. and Tappin, S.J., 2005, “Earthbound interplanetary interplanetary shocks, associated coronal mass ejections and their space weather consequences”, Astron. Astrophys., 440, 373–383. [DOI] (Cited on page 17.)
Howard, T.A. and Tappin, S.J., 2008, “Three-dimensional reconstruction of two solar coronal mass ejections using the STEREO spacecraft”, Solar Phys., 252, 373–383. [DOI] (Cited on pages 6, 17, and 20.)
Howard, T.A. and Tappin, S.J., 2009, “Interplanetary coronal mass ejections observed in the heliosphere: 1. Review of theory”, Space Sci. Rev., 147, 31–54. [DOI], [ADS] (Cited on pages 5, 20, 23, 25, and 56.)
Howard, T.A. and Tappin, S.J., 2010, “Application of a new phenomenological coronal mass ejection model to space weather forecasting”, Space Weather, 8, S07004. [DOI] (Cited on pages 52 and 56.)
Howard, T.A., Webb, D.F., Tappin, S.J., Mizuno, D.R. and Johnston, J.C., 2006, “Tracking halo coronal mass ejections from 0-1 AU and space weather forecasting using the Solar Mass Ejection Imager (SMEI)”, J. Geophys. Res., 111, A04105. [DOI] (Cited on page 52.)
Howard, T.A., Fry, C.D., Johnston, J.C. and Webb, D.F., 2007, “On the evolution of coronal mass ejections in the interplanetary medium”, Astrophys. J., 667, 610–626. [DOI] (Cited on pages 9, 52, and 58.)
Howard, T.A., Nandy, D. and Koepke, A.C., 2008b, “Kinematic properties of solar coronal mass ejections: Correction for projection effects in spacecraft coronagraph measurements”, J. Geophys. Res., 113, A01104. [DOI] (Cited on pages 9 and 58.)
Hu, Q. and Sonnerup, B.U. Ö., 2001, “Reconstruction of magnetic flux ropes in the solar wind”, Geophys. Res. Lett., 28, 467–470. [DOI] (Cited on page 50.)
Hudson, H.S., 1991, “Solar flares, microflares, nanoflares, and coronal heating”, Solar Phys., 133, 357–369. [DOI], [ADS] (Cited on page 23.)
Hudson, H.S. and Cliver, E.W., 2001, “Observing coronal mass ejections without coronagraphs”, J. Geophys. Res., 106(A11), 25,199–25,213. [DOI], [ADS] (Cited on pages 6 and 27.)
Hudson, H.S. and Webb, D.F., 1997, “Soft X-ray signatures of coronal ejections”, in Coronal Mass Ejections, (Eds.) Crooker, N., Joselyn, J.A., Feynman, J., vol. 99 of Geophysical Monograph, pp. 27–38, American Geophysical Union, Washington, DC (Cited on pages 6, 23, and 34.)
Hudson, H.S., Haisch, B. and Strong, K.T., 1995, “Comment on ‘The solar flare myth’ by J. T. Gosling”, J. Geophys. Res., 100, 3473–3477. [DOI], [ADS] (Cited on page 29.)
Hundhausen, A.J., 1972, Coronal Expansion and Solar Wind, vol. 5 of Physics and Chemistry in Space, Springer, Berlin; New York (Cited on page 9.)
Hundhausen, A.J., 1988, “The Origin and Propagation of Coronal Mass Ejections (R)”, in Solar Wind Six, Proceedings of the Sixth International Solar Wind Conference held 23–28 August, 1987 at YMCA of the Rockies, Estes Park, Colorado, (Eds.) Pizzo, V.J., Holzer, T., Sime, D.G., NCAR Technical Notes, p. 181, Natl. Cent. for Atmos. Res., Boulder, CO. [ADS] (Cited on page 33.)
Hundhausen, A.J., 1993, “Sizes and Locations of Coronal Mass Ejections: SMM Observations From 1980 and 1984-1989”, J. Geophys. Res., 98(A8), 13,177–13,200. [DOI], [ADS] (Cited on pages 18, 19, 28, 44, and 45.)
Hundhausen, A.J., 1997, “Coronal mass ejections”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonnett, C.P., Giampapa, M.S., Space Science Series, pp. 259–296, The University of Arizona Press, Tucson. [Google Books] (Cited on page 6.)
Hundhausen, A.J., 1999, “Coronal mass ejections”, in The Many Faces of the Sun: A Summary of the Results from NASA’s Solar Maximum Mission, (Eds.) Strong, K.T., Saba, J.L.R., Haisch, B.M., Schmelz, J.T., p. 143, Springer, New York. [ADS] (Cited on pages 5, 6, and 34.)
Hundhausen, A.J., Burkepile, J.T. and St Cyr, O.C., 1994, “Speeds of coronal mass ejections: SMM observations from 1980 and 1984-1989”, J. Geophys. Res., 99, 6543–6552. [DOI], [ADS] (Cited on pages 21 and 48.)
Illing, R.M.E. and Athay, G., 1986, “Physical conditions in eruptive prominences at several solar radii”, Solar Phys., 105, 173–190. [DOI] (Cited on page 28.)
Illing, R.M.E. and Hundhausen, A.J., 1985, “Observation of a coronal transient from 1.2 to 6 solar radii”, J. Geophys. Res., 90, 275–282. [DOI], [ADS] (Cited on page 9.)
Illing, R.M.E. and Hundhausen, A.J., 1986, “Disruption of a coronal streamer by an eruptive prominence and coronal mass ejection”, J. Geophys. Res., 91, 10,951–10,960. [DOI], [ADS] (Cited on pages 28 and 44.)
Jackson, B.V., 1981, “Forerunners: Early coronal manifestations of solar mass ejection events”, Solar Phys., 73, 133–144. [DOI] (Cited on page 43.)
Jackson, B.V., 1985, “Imaging of coronal mass ejections by the HELIOS spacecraft”, Solar Phys., 100, 563–574. [DOI], [ADS] (Cited on pages 5 and 52.)
Jackson, B.V., 1992, “Remote sensing observations of mass ejections and shocks in interplanetary space”, in Eruptive Solar Flares, Proceedings of Colloquium No. 133 of the International Astronomical Union, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V., Machado, M.E., vol. 399 of Lecture Notes in Physics, pp. 248–257, Springer, Berlin; New York. [DOI], [ADS] (Cited on page 51.)
Jackson, B.V. and Hildner, E., 1978, “Forerunners: Outer rims of solar coronal transients”, Solar Phys., 60, 155–170. [DOI] (Cited on page 43.)
Jackson, B.V., Sheridan, K.V., Dulk, G.A. and McLean, D.J., 1978, “A possible association of solar type III bursts and white light transients”, Proc. Astron. Soc. Australia, 3, 241. [ADS] (Cited on page 44.)
Jackson, B.V., Bisi, M.M., Hick, P.P., Buffington, A., Clover, J.M. and Sun, W., 2008a, “Solar Mass Ejection Imager 3-D reconstruction of the 27-28 May 2003 coronal mass ejection sequence”, J. Geophys. Res., 113, A00A15. [DOI] (Cited on page 24.)
Jackson, B.V., Hick, P.P., Buffington, A., Bisi, M.M., Clover, J.M. and Tokumaru, M., 2008b, “Solar Mass Ejection Imager (SMEI) and interplanetary scintillation (IPS) 3D-reconstructions of the inner heliosphere”, Adv. Geosci., 21, 339–365 (Cited on page 52.)
Jackson, B.V., Buffington, A., Hick, P.P., Clover, J.M., Bisi, M.M. and Webb, D.F., 2010a, “SMEI 3-D reconstruction of a coronal mass ejection interacting with a corotating solar wind density enhancement: The 2008 April 26 CME”, Astrophys. J., 724, 829–834. [DOI] (Cited on page 24.)
Jackson, B.V., Hick, P.P., Buffington, A., Bisi, M.M., Clover, J.M., Tokumaru, M., Kojima, M. and Fujiki, K., 2010b, “Three-dimensional reconstruction of heliospheric structure using iterative tomography: a review”, J. Atmos. Sol.-Terr. Phys., 73, 1214–1227 (Cited on page 52.)
Jackson, B.V., Hick, P.P., Buffington, A., Oberoi, D. and Matthews, L.D., 2010c, “Type III metric radiowave activity prior to and during active region flaring and CMEs”, Eos Trans. AGU, 91, SH54D–03 (Cited on page 44.)
Jing, J., Qiu, J., Lin, J., Qu, M., Xu, Y. and Wang, H., 2005, “Magnetic Reconnection Rate and Flux-Rope Acceleration of Two-Ribbon Flares”, Astrophys. J., 620, 1085–1091. [DOI] (Cited on page 48.)
Jones, R.A., Breen, A.R., Fallows, R.A., Canals, A., Bisi, M.M. and Lawrence, G., 2007, “Interaction between coronal mass ejections and the solar wind”, J. Geophys. Res., 112, A08107. [DOI] (Cited on page 52.)
Joshi, A.D. and Srivastava, N., 2011, “Kinematics of two eruptive prominences observed by EUVI/STEREO”, Astrophys. J., 730, 104–114. [DOI] (Cited on page 33.)
Kahler, S.W., 1977, “The morphological and statistical properties of solar X-ray events with long decay times”, Astrophys. J., 214, 891–897. [DOI] (Cited on page 34.)
Kahler, S.W., 1992, “Solar flares and coronal mass ejections”, Annu. Rev. Astron. Astrophys., 30, 113–141. [DOI], [ADS] (Cited on pages 6, 9, and 46.)
Kahler, S.W., 2001, “The correlation between solar energetic particle peak intensities and speeds of coronal mass ejections: Effects of ambient particle intensities and energy spectra”, J. Geophys. Res., 106, 20,947–20,956. [DOI], [ADS] (Cited on page 58.)
Kahler, S.W., 2006, “Observational properties of coronal mass ejections”, in Solar Eruptions and Energetic Particles, (Eds.) Gopalswamy, N., Mewaldt, R., Torsti, J., vol. 165 of Geophysical Monograph, pp. 21–32, American Geophysical Union, Washington, DC. [DOI] (Cited on pages 6, 9, 23, 27, and 58.)
Kahler, S.W. and Hundhausen, A.J., 1992, “The magnetic topology of solar coronal structures following mass ejections”, J. Geophys. Res., 97, 1619–1631. [DOI] (Cited on pages 44 and 46.)
Kahler, S.W. and Vourlidas, A., 2005, “Fast coronal mass ejection environments and the production of solar energetic particle events”, J. Geophys. Res., 110, A12S01. [DOI] (Cited on page 58.)
Kahler, S.W., Moore, R.L., Kane, S.R. and Zirin, H., 1988, “Filament eruptions and the impulsive phase of solar flares”, Astrophys. J., 328, 824–829. [DOI], [ADS] (Cited on page 44.)
Karpen, J.T. and Howard, R.A., 1987, “A search for forerunner activity associated with coronal mass ejections”, J. Geophys. Res., 92, 7227–7234. [DOI] (Cited on page 43.)
Ko, Y.-K., Raymond, J., Lin, J., Lawrence, G., Li, J. and Fludra, A., 2003, “Dynamical and physical properties of a post-coronal mass ejection current sheet”, Astrophys. J., 594, 1068–1084. [DOI] (Cited on page 39.)
Kohl, J.L., Noci, G., Cranmer, S.R. and Raymond, J.C., 2006, “Ultraviolet spectroscopy of the extended solar corona”, Astron. Astrophys. Rev., 13, 31–157. [DOI], [ADS] (Cited on pages 6, 27, 28, 29, and 37.)
Koomen, M., Howard, R., Hansen, R. and Hansen, S., 1974, “The coronal transient of 16 June 1972”, Solar Phys., 34, 447–452. [DOI] (Cited on page 5.)
Kunow, H., Crooker, N.U., Linker, J.A., R., Schwenn and von Steiger, R. (Eds.), 2006, Coronal Mass Ejections, vol. 123 of Space Sci. Rev. (Special Issue), Springer, Dordrecht. [DOI] (Cited on page 8.)
Landi, E., Miralles, M.P., Curdt, W. and Hara, H., 2009, “Physical properties of cooling plasma in quiescent active region loops”, Astrophys. J., 695, 221–237. [DOI], [ADS] (Cited on page 27.)
Landi, E., Raymond, J.C., Miralles, M.P. and Hara, H., 2010, “Physical conditions in a coronal mass ejection from Hinode, Stereo, and SOHO observations”, Astrophys. J., 711, 75–98. [DOI], [ADS] (Cited on pages 27 and 29.)
Leinert, C., Link, H., Pitz, E., Salm, N. and Knueppelberg, D., 1975, “The Helios zodiacal light experiment E9”, Raumfahrtforschung, 19, 264–267 (Cited on page 52.)
Lepping, R.P., Burlaga, L.F. and Jones, J.A., 1990, “Magnetic field structure of interplanetary magnetic clouds at 1 AU”, J. Geophys. Res., 95, 11,957–11,965. [DOI] (Cited on page 50.)
Liewer, P.C., de Jong, E.M., Hall, J.R., Howard, R.A., Thompson, W.T., Culhane, J.L., Bone, L. and van Driel-Gesztelyi, L., 2009, “Stereoscopic analysis of the 19 May 2007 erupting filament”, Solar Phys., 256, 57–72. [DOI], [ADS], [arXiv:0904.1055] (Cited on page 20.)
Lin, J., 2004, “CME-flare association deduced From catastrophic model of CMEs”, Solar Phys., 219, 169–196. [DOI], [ADS] (Cited on pages 30, 32, and 48.)
Lin, J. and Forbes, T.G., 2000, “Effects of reconnection on the coronal mass ejection process”, J. Geophys. Res., 105, 2375–2392. [DOI], [ADS] (Cited on pages 30, 32, and 48.)
Lin, J., Ko, Y.-K., Sui, L., Raymond, J.C., Stenborg, G.A., Jiang, Y., Zhao, S. and Mancuso, S., 2005, “Direct observations of the magnetic reconnection site of an eruption on 2003 November 18”, Astrophys. J., 622, 1251–1264. [DOI], [ADS] (Cited on pages 39 and 41.)
Lin, J., Li, J., Ko, Y.-K. and Raymond, J.C., 2009, “Investigation of thickness and electrical resistivity of the current sheets in solar eruptions”, Astrophys. J., 693, 1666–1677. [DOI] (Cited on page 40.)
Liu, W., Nitta, N.V., Schrijver, C.J., Title, A.M. and Tarbell, T.D., 2010, “First SDO AIA observations of a global coronal EUV ‘wave’: Multiple components and ‘Ripples’”, Astrophys. J. Lett., 723, L53–L59. [DOI] (Cited on page 36.)
Liu, Y., Luhmann, J.G., Bale, S.D. and Lin, R.P., 2011, “Solar source and heliospheric consequences of the 2010 April 3 coronal mass ejection: A comprehensive view”, Astrophys. J., .734, 84. [DOI], [ADS] (Cited on page 22.)
Long, D.M., Gallagher, P.T., McAteer, R.T.J. and Bloomfield, D.S., 2008, “The kinematics of a globally propagating disturbance in the solar corona”, Astrophys. J., 680, L81–L84. [DOI], [ADS], [arXiv:0805.2023] (Cited on page 36.)
Low, B.C., 1996, “Solar activity and the corona”, Solar Phys., 167, 217–265. [DOI], [ADS] (Cited on page 5.)
Low, B.C., 1997, “Solar activity from the coronal perspective”, in Solar Magnetic Fields, Proceedings of the Mini-Workshop, (Ed.) Hansteen, V.H., pp. 1–2, University of Oslo, Oslo (Cited on page 6.)
Low, B.C. and Zhang, M., 2002, “The hydromagnetic origin of the two dynamical types of solar coronal mass ejections”, Astrophys. J., 564, L53–L56. [DOI], [ADS] (Cited on page 22.)
Lugaz, N., Vourlidas, A. and Roussev, I.I., 2009, “Deriving the radial distances of wide coronal mass ejections from elongation measurements in the heliosphere - application to CME-CME interaction”, Ann. Geophys., 27, 3479–3488. [DOI] (Cited on page 56.)
Lugaz, N., Hernandez-Charpak, J.N., Roussev, I.I., Davis, C.J., Vourlidas, A. and Davies, J.A., 2010, “Determining the azimuthal properties of coronal mass ejections from multi-spacecraft remote-sensing observations with STEREO SECCHI”, Astrophys. J., 715, 493–499. [DOI] (Cited on page 56.)
Lynch, B.J., Gruesbeck, J.R., Zurbuchen, T.H. and Antiochos, S.K., 2005, “Solar cycle-dependent helicity transport by magnetic clouds”, J. Geophys. Res., 110, A08107. [DOI] (Cited on pages 6 and 50.)
Lynch, B.J., Antiochos, S.K., DeVore, C.R., Luhmann, J.G. and Zurbuchen, T.H., 2008, “Topological evolution of a fast magnetic breakout CME in three dimensions”, Astrophys. J., 683, 1192–1206. [DOI] (Cited on page 46.)
Lyons, M.A. and Simnett, G.M., 2001, “Erupting magnetic structures observed with SOHO/LASCO”, Solar Phys., 200, 203–211. [DOI] (Cited on page 58.)
Ma, S., Attril, G.D.R., Golub, L. and Lin, J., 2010, “Statistical study of coronal mass ejections with and without distinct low coronal signatures”, Astrophys. J., 722, 289–301. [DOI], [ADS] (Cited on page 43.)
Ma, S., Raymond, J.C., Golub, L., Lin, J., Chen, H., Grigis, P., Testa, P. and Long, D., 2011, “Observations and interpretation of a low coronal shock wave observed in the EUV by the SDO/AIA”, Astrophys. J., 738, 160. [DOI] (Cited on page 37.)
MacQueen, R.M. and Fisher, R.R., 1983, “The kinematics of solar inner coronal transients”, Solar Phys., 89, 89–102. [DOI], [ADS] (Cited on page 22.)
MacQueen, R.M., Csoeke-Poeckh, A., Hildner, E., House, L., Reynolds, R., Stanger, A., Tepoel, H. and Wagner, W., 1980, “The High Altitude Observatory Coronagraph/Polarimeter on the Solar Maximum Mission”, Solar Phys., 65, 91–107. [DOI] (Cited on page 5.)
MacQueen, R.M., Burkepile, J.T., Holzer, T.E., Stanger, A.L. and Spence, K.E., 2001, “Solar coronal brightness changes and mass ejections during solar cycle 22”, Astrophys. J., 549, 1175–1182. [DOI] (Cited on page 24.)
Manchester IV, W.B., Gombosi, T.I., De Zeeuw, D.L., Sokolov, I.V., Roussev, I.I., Powell, K.G., Kóta, J., Tóth, G. and Zurbuchen, T.H., 2005, “Coronal mass ejection shock and sheath structures relevant to particle acceleration”, Astrophys. J., 622, 1225–1239. [DOI] (Cited on page 49.)
Manoharan, P.K., 2010, “Ooty interplanetary scintillation - Remote-sensing observations and analysis of coronal mass ejections in the heliosphere”, Solar Phys., 265, 137–157. [DOI] (Cited on page 52.)
Martin, S.F., 1980, “Preflare conditions, changes and events”, Solar Phys., 68, 217–236. [DOI], [ADS] (Cited on page 44.)
Martin, S.F. and Livi, S.H.B., 1992, “The role of cancelling magnetic fields in the buildup to erupting filaments and flares”, in Eruptive Solar Flares, Proceedings of Colloquium No. 133 of the International Astronomical Union, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V. Machado, M.E., vol. 399 of Lecture Notes in Physics, pp. 33–45, Springer, Berlin; New York. [DOI], [ADS] (Cited on page 44.)
McAllister, A.H., Dryer, M., McIntosh, P., Singer, H. and Weiss, L., 1996, “A large polar crown CME and a ‘problem’ geomagnetic storm: April 14-23, 1994”, J. Geophys. Res., 101, 13,497–13,516. [DOI] (Cited on pages 34 and 43.)
McAllister, A.H., Mackay, D.H. and Martin, S.F., 2002, “The skew of high-latitude X-ray arcades in the declining phase of Cycle 22”, Solar Phys., 211, 155–163 (Cited on page 33.)
McIntosh, S.W., Leamon, R.J., Davey, A.R. and Wills-Davey, M.J., 2007, “The posteruptive evolution of a coronal dimming”, Astrophys. J., 660, 1653–1659. [DOI] (Cited on page 34.)
McKenzie, D.E. and Canfield, R.C., 2008, “Hinode XRT observations of a long-lasting coronal sigmoid”, Astron. Astrophys., 481, L65–L68. [DOI], [ADS] (Cited on page 34.)
McKenzie, D.E. and Hudson, H.S., 1999, “X-ray observations of motions and structure above a solar flare arcade”, Astrophys. J., 519, L93–L96. [DOI], [ADS] (Cited on page 39.)
McKenzie, D.E. and Hudson, H.S., 2001, “Downflows and structure above LDE arcades: Possible signatures of reconnection?”, Earth Planets Space, 53, 577–580 (Cited on page 39.)
Mewaldt, R.A., 2006, “Solar energetic particle composition, energy spectra, and space weather”, Space Sci. Rev., 124, 303–316. [DOI], [ADS] (Cited on page 38.)
Michalek, G., Gopalswamy, N., Lara, A. and Yashiro, S., 2006, “Properties and geoeffectiveness of halo coronal mass ejections”, Space Weather, 4, S10003. [DOI] (Cited on page 58.)
Mierla, M., Inhester, B., Marqué, C., Rodriguez, L., Gissot, S., Zhukov, A.N., Berghmans, D. and Davila, J., 2009, “On 3D reconstruction of coronal mass ejections using SECCHI-COR data”, in EGU General Assembly 2009, Vienna, Austria, 19–24 April 2009, vol. 11 of Geophysical Research Abstracts, Copernicus, Göttingen. [ADS] (Cited on page 20.)
Mierla, M., Inhester, B., Antunes, A., Boursier, Y., Byrne, J.P., Colaninno, R., Davila, J., de Koning, C.A., Gallagher, P.T., Gissot, S., Howard, R.A., Howard, T.A., Kramar, M., Lamy, P., Liewer, P.C., Maloney, S., Marqué, C., McAteer, R.T.J., Moran, T., Rodriguez, L., Srivastava, N., St Cyr, O.C., Stenborg, G., Temmer, M., Thernisien, A., Vourlidas, A., West, M.J., Wood, B.E. and Zhukov, A.N., 2010, “On the 3-D reconstruction of coronal mass ejections using coronagraph data”, Ann. Geophys., 28, 203–215. [DOI], [ADS] (Cited on pages 9 and 20.)
Mierla, M., Srivastava, N. and Rodriguez, L. (Eds.), 2011, Three dimensional aspects of CMEs, their source regions and interplanetary manifestations, vol. 73 of J. Atmos. Sol.-Terr. Phys. (Special Issue), Elsevier, Amstderdam (Cited on page 8.)
Mikić, Z. and Linker, J.A., 1994, “Disruption of coronal magnetic field arcades”, Astrophys. J., 430, 898–912. [DOI], [ADS] (Cited on page 48.)
Minneart, M., 1930, “On the continuous spectrum of the corona and its polarization”, Z. Astrophys., .1, 209–235. [ADS] (Cited on page 25.)
Moore, R.L. and Roumeliotis, G., 1992, “Triggering of eruptive flares: Destabilization of the preflare magnetic field configuration”, in Eruptive Solar Flares, Proceedings of Colloquium No. 133 of the International Astronomical Union, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V., Machao, M.E., vol. 399 of Lecture Notes in Physics, pp. 69–78, Springer, Berlin; New York. [DOI], [ADS] (Cited on pages 6 and 46.)
Moran, T.G. and Davila, J.M., 2004, “Three-dimensional polarimetric imaging of coronal mass ejections”, Science, 305, 66–71. [DOI], [ADS] (Cited on page 20.)
Moran, T.G., Davila, J.M. and Thompson, W.T., 2010, “Three-dimensional polarimetric coronal mass ejection localization tested through triangulation”, Astrophys. J., 712, 453–458. [DOI], [ADS] (Cited on page 20.)
Morrison, P., 1954, “Solar-connection variations of the cosmic rays”, Phys. Rev., 95, 646 (Cited on page 50.)
Möstl, C., Farrugia, C.J., Temmer, M., Miklenic, C., Veronig, A.M., Galvin, A.B., Leitner, M. and Biernat, H.K., 2009, “Linking remote imagery of a coronal mass ejection to its in-situ signatures at 1 AU”, Astrophys. J., 705, L180–L185 (Cited on page 17.)
Möstl, C., Temmer, M., Rollett, T., Farrugia, C.J., Liu, Y., Veronig, A.M., Leitner, M., Galvin, A.B. and Biernat, H.K., 2010, “STEREO and Wind observations of a fast ICME flank triggering a prolonged geomagnetic storm on 5 - 7 April 2010”, Geophys. Res. Lett., 37, L24 103. [DOI] (Cited on pages 17 and 54.)
Munro, R.H., Gosling, J.T., Hildner, E., MacQueen, R.M., Poland, A.I. and Ross, C.L., 1979, “The association of coronal mass ejection transients with other forms of solar activity”, Solar Phys., 61, 201–215. [DOI], [ADS] (Cited on pages 31 and 43.)
Nitta, N. and Akiyama, S., 1999, “Relation between flare-associated X-ray ejections and coronal mass ejections”, Astrophys. J., 525, L57–L60. [DOI] (Cited on page 31.)
Odstrčil, D., 2003, “Modeling 3-D solar wind structure”, Adv. Space Res., 32, 497–506. [DOI] (Cited on page 48.)
Olmedo, O., Zhang, J., Wechsler, H., Poland, A. and Borne, K., 2008, “Automatic detection and tracking of coronal mass ejections in coronagraph time series”, Solar Phys., 248, 485–499. [DOI] (Cited on page 11.)
Ontiveros, V. and Vourlidas, A., 2009, “Quantitative measurements of coronal mass ejection-driven shocks from LASCO observations”, Astrophys. J., 693, 267–275. [DOI] (Cited on page 37.)
Patsourakos, S. and Vourlidas, A., 2009, “‘Extreme ultraviolet waves’ are waves: First quadrature observations of an extreme unltraviolet wave from STEREO”, Astrophys. J., 700, L182–L186. [DOI], [ADS], [arXiv:0905.2164] (Cited on pages 17 and 36.)
Patsourakos, S., Vourlidas, A. and Kliem, B., 2010a, “Toward understanding the early stages of an impulsively accelerated coronal mass ejection SECCHI observations”, Astron. Astrophys., 522, A100. [DOI], [ADS], [arXiv:1008.1171] (Cited on pages 22 and 27.)
Patsourakos, S., Vourlidas, A. and Stenborg, G., 2010b, “The genesis of an impulsive coronal mass ejection observed at ultra-high cadence by AIA on SDO”, Astrophys. J. Lett., 724, L188–L193. [DOI] (Cited on pages 22 and 27.)
Petschek, H.E., 1964, “Magnetic field annihilation”, in The Physics of Solar Flares, Proceedings of the AAS-NASA Symposium held 28–30 October, 1963 at the Goddard Space Flight Center, Greenbelt, MD, (Ed.) Hess, W.N., vol. SP-50 of NASA Special Publications, pp. 425–439, NASA Science and Technical Information Division, Washington, DC. [ADS] (Cited on page 40.)
Pick, M., Démoulin, P., Krucker, S., Malandraki, O. and Maia, D., 2005, “Radio and X-ray signatures of magnetic reconnection behind an ejected flux rope”, Astrophys. J., 625, 1019–1026. [DOI] (Cited on page 48.)
Plunkett, S.P., Vourlidas, A., Šimberová, S., Karlický, M., Kotrč, P., Heinzel, P., Kupryakov, Y.A., Guo, W.P. and Wu, S.T., 2000, “Simultaneous SOHO and ground-based observations of a large eruptive prominence and coronal mass ejection”, Solar Phys., 194, 371–391. [DOI] (Cited on page 7.)
Plunkett, S.P., Michels, D.J., Howard, R.A., Brueckner, G.E., St Cyr, O.C., Thompson, B.J., Simnett, G.M., Schwenn, R. and Lamy, P., 2002, “New insights on the onsets of coronal mass ejections from SOHO”, Adv. Space Res., 29, 1473–1488. [DOI] (Cited on page 31.)
Pulkkinen, T., 2007, “Space Weather: Terrestrial Perspective”, Living Rev. Solar Phys., 4, lrsp–2007–1. URL (accessed 17 August 2011): http://www.livingreviews.org/lrsp-2007-1 (Cited on page 57.)
Qiu, J., Hu, Q., Howard, T.A. and Yurchyshyn, V.B., 2007, “On the magnetic flux budget in low-corona magnetic reconnection and interplanetary coronal mass ejections”, Astrophys. J., 659, 758–772. [DOI] (Cited on page 59.)
Rachmeler, L.A., DeForest, C.E. and Kankelborg, C.C., 2009, “Reconnectionless CME eruption: Putting the Aly-Sturrock conjecture to rest”, Astrophys. J., 693, 1431–1435. [DOI], [ADS], [arXiv:0812.3199] (Cited on page 46.)
Ramesh, R., Kathiravan, C. and Sastry, C.V., 2003, “Metric radio observations of the evolution of a ‘halo’ coronal mass ejection close to the Sun”, Astrophys. J., 591, L163–L166. [DOI] (Cited on page 23.)
Ravindra, B. and Howard, T.A., 2010, “Comparison of energies between eruptive phenomena and magnetic field in AR 10930”, Bull. Astron. Soc. India, 38, 147–163 (Cited on pages 25 and 27.)
Raymond, J.C., 2002, “Spectroscopic diagnostics of CME material”, in From Solar Min to Max: Half a Solar Cycle with SOHO, Proceedings of the SOHO 11 Symposium, 1–15 March 2002, Davos, Switzerland. A symposium dedicated to Roger M. Bonnet, (Ed.) Wilson, A., vol. SP-508 of ESA Special Publication, pp. 421–430, ESA Publications Division, Noordwijk. [ADS] (Cited on page 27.)
Raymond, J.C., Ciaravella, A., Dobrzycka, D., Strachan, L., Ko, Y.-K., Uzzo, M. and Raouafi, N.-E., 2003, “Far-ultraviolet spectra of fast coronal mass ejections associated with X-class flares”, Astrophys. J., 597, 1106–1117. [DOI] (Cited on page 27.)
Reames, D.V., 1999, “Quiet-time spectra and abundances of energetic particles during the 1996 solar minimum”, Astrophys. J., 518, 473–479. [DOI] (Cited on page 37.)
Reeves, K.K. and Golub, L., 2011, “Atmospheric Imaging Assembly observations of hot flare plasma”, Astrophys. J. Lett., 727, L52–L56. [DOI] (Cited on page 34.)
Reeves, K.K. and Moats, S., 2010, “Relating coronal mass ejection kinematics and thermal energy release to flare emissions using a model of solar eruptions”, Astrophys. J., 712, 429–434. [DOI] (Cited on pages 34 and 48.)
Reeves, K.K., Linker, J.A., Mikić, Ž. and Forbes, T.G., 2010, “Current sheet energetics, flare emissions, and energy partition in a simulated solar eruption”, Astrophys. J., 721, 1547–1558. [DOI] (Cited on page 34.)
Reinard, A.A. and Biesecker, D.A., 2008, “Coronal Mass Ejection-Associated Coronal Dimmings”, Astrophys. J., 674, 576–585 (Cited on pages 34 and 35.)
Richardson, I.G. and Cane, H.V., 2010, “Near-Earth interplanetary coronal mass ejections during solar Cycle 23 (1996-2009): Catalog and summary of properties”, Solar Phys., 264, 189–237. [DOI] (Cited on page 51.)
Richter, I., Leinert, C. and Planck, B., 1982, “Search for short term variations of zodical light and optical detection of interplanetary plasma clouds”, Astron. Astrophys., 110, 115–120 (Cited on page 5.)
Riley, P., Lionello, R., Mikić, Z., Linker, J., Clark, E., Lin, J and Ko, Y.-K., 2007, “‘Bursty’ reconnection following solar eruptions: MHD simulations and comparison with observations”, Astrophys. J., 655, 591–597. [DOI] (Cited on page 39.)
Robbrecht, E., Berghmans, D. and van der Linden, R.A.M., 2009a, “Automated LASCO CME catalog for solar cycle 23: Are CMEs scale invariant?”, Astrophys. J., 691, 1222–1234. [DOI], [ADS], [arXiv:0810.1252] (Cited on pages 6, 11, 12, 13, 16, 20, and 43.)
Robbrecht, E., Patsourakos, S. and Vourlidas, A., 2009b, “No trace left behind: STEREO observation of a coronal mass ejection without low coronal signatures”, Astrophys. J., 701, 283–291. [DOI], [ADS], [arXiv:0905.2583] (Cited on pages 17 and 19.)
Rouillard, A.P., Davies, J.A., Forsyth, R.J., Rees, A., Davis, C.J., Harrison, R.A., Lockwood, M., Bewsher, D., Crothers, S.R., Eyles, C.J., Hapgood, M. and Perry, C.H., 2008, “First imaging of corotating interaction regions using the STEREO spacecraft”, Geophys. Res. Lett., 35, L10110. [DOI] (Cited on page 54.)
Rouillard, A.P., Davies, J.A., Lavraud, B., Forsyth, R.J., Savani, N.P., Bewsher, D., Brown, D.S., Sheeley Jr, N.R., Davis, C.J., Harrison, R.A., Howard, R.A., Vourlidas, A., Lockwood, M., Crothers, S.R. and Eyles, C.J., 2010, “Intermittent release of transients in the slow solar wind: 1. Remote sensing observations”, J. Geophys. Res., 115, A04103. [DOI] (Cited on page 54.)
Rust, D.M. and Hildner, E., 1976, “Expansion of an X-ray coronal arch into the outer corona”, Solar Phys., 48, 381–387. [DOI] (Cited on page 23.)
Rust, D.M. and Webb, D.F., 1977, “Soft X-ray observations of large-scale coronal active region brightenings”, Solar Phys., 54, 403–417. [DOI] (Cited on page 31.)
Saint-Hilaire, P., Krucker, S. and Lin, R.P., 2009, “X-ray emission from the base of a current sheet in the wake of a coronal mass ejection”, Astrophys. J., 699, 245–253. [DOI] (Cited on page 39.)
Savage, S.L., McKenzie, D.E., Reeves, K.K., Forbes, T.G. and Longcope, D.W., 2010, “Reconnection outflows and current sheet observed with Hinode/XRT in the 2008 April 9 ‘Cartwheel CME’ Flare”, Astrophys. J., 722, 329–342. [DOI] (Cited on page 39.)
Schrijver, C.J. and Title, A.M., 2011, “Long-range magnetic couplings between solar flares and coronal mass ejections observed by SDO and STEREO”, J. Geophys. Res., 116, A04108. [DOI], [ADS] (Cited on page 35.)
Schuster, A., 1879, “On the polarization of the solar corona”, Mon. Not. R. Astron. Soc., 40, 35–57 (Cited on page 25.)
Schwenn, R., 2006, “Space Weather: The Solar Perspective”, Living Rev. Solar Phys., 3, lrsp–2006–2. URL (accessed 17 August 2011): http://www.livingreviews.org/lrsp-2006-2 (Cited on pages 8, 37, 38, 51, and 57.)
Sheeley Jr, N.R. and Rouillard, A.P., 2010, “Tracking streamer blobs into the heliosphere”, Astrophys. J., 715, 300–309. [DOI], [ADS], [arXiv:1006.5379] (Cited on page 54.)
Sheeley Jr, N.R. and Wang, Y.-M., 2007, “In/out pairs and the detachment of coronal streamers”, Astrophys. J., 655, 1142–1156. [DOI] (Cited on page 39.)
Sheeley Jr, N.R., Michels, D.J., Howard, R.A. and Koomen, M.J., 1980, “Initial observations with the Solwind coronagraph”, Astrophys. J., 237, L99–L101. [DOI] (Cited on pages 5 and 20.)
Sheeley Jr, N.R., Howard, R.A., Koomen, M.J., Michels, D.J., Harvey, J.W. and Harvey, K.L., 1982, “Observations of coronal structure during sunspot maximum”, Space Sci. Rev., 33, 219–231. [DOI] (Cited on page 44.)
Sheeley Jr, N.R., Howard, R.A., Koomen, M.J. and Michels, D.M., 1983, “Associations between coronal mass ejections and soft X-ray events”, Astrophys. J., 272, 349–354. [DOI] (Cited on page 31.)
Sheeley Jr, N.R., Walters, J.H., Wang, Y.-M. and Howard, R.A., 1999, “Continuous tracking of coronal outflows: Two kinds of coronal mass ejections”, J. Geophys. Res., 104, 24,739–24,768. [DOI], [ADS] (Cited on page 22.)
Sheeley Jr, N.R., Warren, H.P. and Wang, Y.-M., 2004, “The origin of postflare loops”, Astrophys. J., 616, 1224–1231. [DOI], [ADS] (Cited on page 39.)
Sheeley Jr, N.R., Herbst, A.D., Palatchi, C.A., Wang, Y.-M., Howard, R.A., Moses, J.D., Vourlidas, A., Newmark, J.S., Socker, D.G., Plunkett, S.P., Korendyke, C.M., Burlaga, L.F., Davila, J.M., Thompson, W.T., St Cyr, O.C., Harrison, R.A., Davis, C.J., Eyles, C.J., Halain, J.-P., Wang, D., Rich, N.B., Battams, K., Esfandiari, E. and Stenborg, G., 2008, “Heliospheric images of the solar wind at Earth”, Astrophys. J., 675, 853–862. [DOI] (Cited on page 54.)
Sheeley Jr, N.R., Lee, D.D.-H., Casto, K.P., Wang, Y.-M. and Rich, N.B., 2009, “The structure of streamer blobs”, Astrophys. J., 694, 1471–1480. [DOI], [ADS] (Cited on page 54.)
Shibata, K., 1999, “Evidence of magnetic reconnection in solar flares and a unified model of flares”, Astrophys. Space Sci., 264, 129–144. [ADS] (Cited on page 39.)
Shibata, K., Masuda, S., Shimojo, M., Hara, H., Yokoyama, T., Tsuneta, S., Kosugi, T. and Ogawara, Y., 1995, “Hot-plasma ejections associated with compact-loop solar flares”, Astrophys. J., 451, L83–L85. [DOI], [ADS] (Cited on page 30.)
Simnett, G.M., 2000, “The relationship between prominence eruptions and coronal mass ejections”, J. Atmos. Terr. Phys., 62, 1479–1487. [DOI], [ADS] (Cited on pages 28 and 33.)
Simnett, G.M., 2004, “Evidence for magnetic reconnection in the high corona”, Astron. Astrophys., 416, 759–764. [DOI], [ADS] (Cited on page 39.)
Simnett, G.M. and Harrison, R.A., 1984, “The relationship between coronal mass ejections and solar flares”, Adv. Space Res., 4, 279–282. [DOI] (Cited on page 31.)
Simnett, G.M. and Harrison, R.A., 1985, “The onset of coronal mass ejections”, Solar Phys., 99, 291–311. [DOI], [ADS] (Cited on page 31.)
Simnett, G.M., Tappin, S.J., Plunkett, S.P., Bedford, D.K., Eyles, C.J., St Cyr, O.C., Howard, R.A., Brueckner, G.E., Michels, D.J., Moses, J.D., Socker, D., Dere, K.P., Korendyke, C.M., Paswaters, S.E., Wang, D., Schwenn, R., Lamy, P., Llebaria, A. and Bout, M.V., 1997, “LASCO observations of disconnected magnetic structures out to beyond 28 solar radii during coronal mass ejections”, Solar Phys., 175, 685–698. [DOI] (Cited on page 39.)
Smith, Z. and Dryer, M., 1990, “MHD study of temporal and spatial evolution of simulated interplanetary shocks in the ecliptic plane within 1 AU”, Solar Phys., 387-405, 129. [DOI] (Cited on page 48.)
Sonnett, C.P., Colburn, D.S., Davis Jr, L., Smith, E.J. and Coleman Jr, P.J., 1964, “Evidence for a collisionfree magnetohydrodynamic shock in interplanetary space”, Phys. Rev. Lett., 13, 153–156. [DOI], [ADS] (Cited on pages 5 and 29.)
Srivastava, N., Schwenn, R., Inhester, B., Stenborg, G. and Podlipnik, B., 1999, “Measurements of flow speeds and acceleration in gradually evolving solar mass ejections as observed by LASCO”, in Solar Wind Nine, Proceedings of the Ninth International Solar Wind Conference, Nantucket, MA, 5–9 October 1998, (Eds.) Habbal, S.R., Halas, C.D., vol. 471 of AIP Conference Proceedings, pp. 115–118, American Institute of Physics, Woodbury, NY. [DOI], [ADS] (Cited on page 22.)
St Cyr, O.C., Burkepile, J.T., Hundhausen, A.J. and Lecinski, A.R., 1999, “A comparison of groundbased and spacecraft observations of coronal mass ejections from 1980-1989”, J. Geophys. Res., 104, 12,493–12,506. [DOI], [ADS] (Cited on page 21.)
St Cyr, O.C., Plunkett, S.P., Michels, D.J., Paswaters, S.E., Koomen, M.J., Simnett, G.M., Thompson, B.J., Gurman, J.B., Schwenn, R., Webb, D.F., Hildner, E. and Lamy, P.L., 2000, “Properties of coronal mass ejections: SOHO LASCO observations from January 1996 to June 1998”, J. Geophys. Res., 105 (A8), 18,169–18,185. [DOI], [ADS] (Cited on pages 6, 9, 13, 19, 21, and 39.)
Sterling, A.C. and Hudson, H.S., 1997, “YOHKOH SXT observations of X-Ray ‘Dimming’ associated with a halo coronal mass ejection”, Astrophys. J., 491, L55. [DOI], [ADS] (Cited on page 6.)
Sterling, A.C., Hudson, H.S., Thompson, B.J. and Zarro, D.M., 2000, “Yohkoh SXT and SOHO EIT observations of sigmoid-to-arcade evolution of structures associated with halo coronal mass ejections”, Astrophys. J., 532, 628–647. [DOI] (Cited on page 34.)
Sui, L. and Holman, G.D., 2003, “Evidence for the formation of a large-scale current sheet in a solar flare”, Astrophys. J., 596, L251–L254. [DOI], [ADS] (Cited on page 39.)
Sui, L., Holman, G.D., White, S.M. and Zhang, J., 2005, “Multiwavelength analyses of a solar flare on 2002 April 15”, Astrophys. J., 633, 1175–1186. [DOI] (Cited on page 39.)
Švestka, Z. and Cliver, E.W., 1992, “History and basic characteristics of eruptive flares”, in Eruptive Solar Flares, Proceedings of Colloquium No. 133 of the International Astronomical Union, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V., Machao, M.E., vol. 399 of Lecture Notes in Physics, pp. 1–11, Springer, Berlin; New York. [DOI], [ADS] (Cited on pages 30, 46, and 48.)
Tappin, S.J., 2006, “The deceleration of an interplanetary transient from the Sun to 5 AU”, Solar Phys., 233, 233–248. [DOI] (Cited on pages 48 and 52.)
Tappin, S.J. and Howard, T.A., 2009, “Interplanetary coronal mass ejections observed in the heliosphere: 2. Model and data comparisons”, Space Sci. Rev., 147, 55–87. [DOI], [ADS] (Cited on pages 52 and 54.)
Tappin, S.J. and Howard, T.A., 2010, “Reconstructing CME structures from IPS observations using a phenomenological model”, Solar Phys., 265, 159–186. [DOI] (Cited on page 52.)
Tappin, S.J., Buffington, A., Cooke, M.P., Eyles, C.J., Hick, P.P., Holladay, P.E., Jackson, B.V., Johnston, J.C., Kuchar, T., Mizuno, D., Mozer, J.B., Price, S., Radick, R.R., Simnett, G.M., Sinclair, D.,Waltham, N.R. and Webb, D.F., 2004, “Tracking a major interplanetary disturbance with SMEI”, Geophys. Res. Lett., 31, L02802. [DOI] (Cited on page 52.)
Temmer, M., Preiss, S. and Veronig, A.M., 2009, “CME projection effects studied with STEREO/COR and SOHO/LASCO”, Solar Phys., 256, 183–199. [DOI] (Cited on page 20.)
Temmer, M., Veronig, A.M., Kontar, E.P., Krucker, S. and Vršnak, B., 2010, “Combined Stereo/RHESSI study of coronal mass ejection acceleration and particle acceleration in solar flares”, Astrophys. J., 712, 1410–1420. [DOI], [ADS], [arXiv:1002.3080] (Cited on page 22.)
Thernisien, A.F.R., Howard, R.A. and Vourlidas, A., 2006, “Modeling of flux rope coronal mass ejections”, Astrophys. J., 652, 763–773. [DOI] (Cited on page 20.)
Thompson, B.J. and Myers, D.C., 2009, “A catalog of coronal ‘EIT wave’ transients”, Astrophys. J. Suppl. Ser., 183, 225–243. [DOI], [ADS] (Cited on page 36.)
Thompson, B.J., Plunkett, S.P., Gurman, J.B., Newmark, J.S., St Cyr, O.C. and Michels, D.J., 1998, “SOHO/EIT observations of an Earth-directed coronal mass ejection on May 12, 1997”, Geophys. Res. Lett., 25, 2465–2468. [DOI], [ADS] (Cited on page 35.)
Thompson, B.J., Gurman, J.B., Neupert, W.M., Newmark, J.S., Delaboudinière, J.-P., St Cyr, O.C., Stezelberger, S., Dere, K.P., Howard, R.A. and Michels, D.J., 1999, “SOHO/EIT observations of the 1997 April 7 coronal transient: Possible evidence of coronal moreton waves”, Astrophys. J., 517, L151–L154. [DOI], [ADS] (Cited on page 6.)
Thompson, B.J., Cliver, E.W., Nitta, N., Delannée, C. and Delaboudinière, J.-P., 2000, “Coronal dimmings and energetic CMEs in April-May 1998”, Geophys. Res. Lett., 27, 1431–1434. [DOI], [ADS] (Cited on page 34.)
Török, T. and Kleim, B., 2003, “The evolution of twisting coronal magnetic flux tubes”, Astron. Astrophys., 406, 1043–1059 (Cited on page 46.)
Török, T. and Kliem, B., 2005, “Confined and ejective eruptions of kink-unstable flux ropes”, Astrophys. J. Lett., 630, L97–L100. [DOI], [ADS] (Cited on page 46.)
Tousey, R., 1973, “The solar corona”, in Space Research XIII, Proceedings of open meetings of working groups on physical sciences of the 15th plenary meeting of COSPAR, Madrid, Spain, 10–24 May, 1972, (Eds.) Rycroft, M.J., Runcorn, S.K., pp. 713–730, Akademie-Verlag, Berlin. [ADS] (Cited on page 5.)
Tripathi, D., Bothmer, V. and Cremades, H., 2004, “The basic characteristics of EUV post-eruptive arcades and their role as tracers of coronal mass ejection source regions”, Astron. Astrophys., 422, 337–349. [DOI], [arXiv:astro-ph/0507662] (Cited on pages 17, 34, 35, 36, and 48.)
Tripathi, D., Solanki, S.K., Mason, H.E. and Webb, D.F., 2007, “A bright coronal downflow seen in multiwavelength observations: Evidence of a bifurcating flux-rope?”, Astron. Astrophys., 472, 633–642. [DOI] (Cited on page 23.)
Uchida, Y., 1968, “Propagation of hydromagnetic disturbances in the solar corona and Moreton’s wave phenomenon”, Solar Phys., 4, 30–44. [DOI], [ADS] (Cited on page 35.)
van Houten, C.J., 1950, “The form of Fraunhofer lines in the inner corona”, Bull. Astron. Inst. Neth., 11, 160–163 (Cited on page 25.)
Veronig, A.M., Muhr, N., Kienreich, I.W., Temmer, M. and Vršnak, B., 2010, “First observations of a dome-shaped large-scale coronal extreme-ultraviolet wave”, Astrophys. J. Lett., 716, L57–L62. [DOI], [ADS], [arXiv:1005.2060] (Cited on page 36.)
Vlasov, V.I., 1981, “Possibility of predicting geophysical activity on the basis of the interplanetary scintillation of radio sources”, Geomagn. Aeron., 21, 441–444. [ADS] (Cited on page 5.)
Vourlidas, A. and Howard, R.A., 2006, “The proper treatment of coronal mass ejection brightness: A new methodology and implications for observations”, Astrophys. J., 642, 1216–1221. [DOI], [ADS] (Cited on page 5.)
Vourlidas, A. and Ontiveros, V., 2009, “A review of coronagraphic observations of shocks driven by coronal mass ejections”, in Shock Waves in Space and Astrophysical Environments, 8th Annual International Astrophysics Conference, Kona, Hawaii, 1–7 May 2009, (Eds.) Ao, X., Zank, G., Burrows, R., vol. 1183 of AIP Conference Proceedings, pp. 139–146, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on page 37.)
Vourlidas, A., Subramanian, P., Dere, K.P. and Howard, R.A., 2000, “Large-angle spectrometric coronagraph measurements of the energetics of coronal mass ejections”, Astrophys. J., 534, 456–467. [DOI], [ADS] (Cited on page 23.)
Vourlidas, A., Buzasi, D., Howard, R.A. and Esfandiari, E., 2002a, “Mass and energy properties of LASCO CMEs”, in Solar Variability: From Core to Outer Frontiers, Proceedings of the 10th European Solar Physics Meeting, Prague, Czech Republic, 9–14 September 2002, (Ed.) Wilson, A., vol. SP-506 of ESA Conference Proceedings, pp. 91–94, ESA, Noordwijk. [ADS] (Cited on pages 9 and 23.)
Vourlidas, A., Howard, R.A., Morill, J.S. and Munz, S., 2002b, “Analysis of LASCO streamer blowout events”, in Solar-Terrestrial Magnetic Activity and Space Environment, Proceedings of the COSPAR Colloquium held in the NAOC in Beijing, China, September 10–12, 2001, (Eds.) Wang, H., Xu, R.L., vol. 14 of COSPAR Colloquia Series, pp. 201–208, Pergamon, Amsterdam; Boston. [DOI], [Google Books] (Cited on page 44.)
Vourlidas, A., Wu, S.T., Wang, A.H., Subramanian, P. and Howard, R.A., 2003, “Direct detection of a coronal mass ejection-associated shock in large angle and spectrometric coronagraph experiment white-light images”, Astrophys. J., 598, 1392–1402. [DOI], [ADS], [arXiv:astro-ph/0308367] (Cited on page 37.)
Vourlidas, A., Howard, R.A., Esfandiari, E., Patsourakos, S., Yashiro, S. and Michalek, G., 2010, “Comprehensive analysis of coronal mass ejection mass and energy properties over a full solar cycle”, Astrophys. J., 722, 1522–1538. [DOI], [ADS], [arXiv:1008.3737] (Cited on pages 9, 23, 24, 25, and 26.)
Vourlidas, A., Colaninno, R., Nieves-Chinchilla, T. and Stenborg, G., 2011a, “The first observation of a rapidly rotating coronal mass ejection in the middle corona”, Astrophys. J., 733, L23. [DOI] (Cited on page 33.)
Vourlidas, A., Howard, R.A., Esfandiari, E., Patsourakos, S., Yashiro, S. and Michalek, G., 2011b, “Erratum: ‘Comprehensive analysis of coronal mass ejection mass and energy properties over a full solar cycle’”, Astrophys. J., 730, 59. [DOI], [ADS] (Cited on pages 9, 23, 24, 25, and 26.)
Vourlidas, A., Syntelis, P. and Tsinganos, K., 2012, “Uncovering the Birth of a Coronal Mass Ejection from Two-Viewpoint SECCHI Observations”, Solar Phys., 280, 509–523. [DOI], [ADS], [arXiv:1201.0162 [astro-ph.SR]] (Cited on page 27.)
Vršnak, B. and Cliver, E.W., 2008, “Origin of coronal shock waves”, Solar Phys., 253, 215–235 (Cited on page 36.)
Vršnak, B., Ruždjak, D., Sudar, D. and Gopalswamy, N., 2004, “Kinematics of coronal mass ejections between 2 and 30 solar radii: What can be learned about forces governing the eruption?”, Astron. Astrophys., 423, 717–728. [DOI], [ADS] (Cited on page 58.)
Vršnak, B., Sudar, D. and Ruždjak, D., 2005, “The CME-flare relationship: Are there really two types of CMEs?”, Astron. Astrophys., 435, 1149–1157. [DOI], [ADS] (Cited on page 23.)
Vršnak, B., Poletto, G., Vujić, E., Vourlidas, A., Ko, Y.-K., Raymond, J.C., Ciaravella, A., Žic, T., Webb, D.F., Bemporad, A., Landini, F., Schettino, G., Jacobs, C. and Suess, S.T., 2009, “Morphology and density structure of post-CME current sheets”, Astron. Astrophys., 499, 905–916. [DOI], [ADS] (Cited on page 39.)
Wang, Y.-M. and Sheeley Jr, N.R., 2002, “Observations of core fallback during coronal mass ejections”, Astrophys. J., 567, 1211–1224. [DOI] (Cited on page 34.)
Warmuth, A., 2007, “Large-scale Waves and Shocks in the Solar Corona”, in The High Energy Solar Corona: Waves, Eruptions, Particles, CESRA Workshop 2004, (Eds.) Klein, K.-L., MacKinnon, A.L., vol. 725 of Lecture Notes in Physics, pp. 107–138, Springer, Berlin; New York. [DOI], [ADS], [Google Books] (Cited on page 36.)
Webb, D.F., 1988, “Erupting prominences and the geometry of coronal mass ejections”, J. Geophys. Res., 93, 1749–1758. [DOI] (Cited on page 33.)
Webb, D.F., 1992, “The solar sources of coronal mass ejections”, in Eruptive Solar Flares, Proceedings of Colloquium No. 133 of the International Astronomical Union, held at Iguazú, Argentina, 2–6 August 1991, (Eds.) Švestka, Z., Jackson, B.V., Machado, M.E., vol. 399 of Lecture Notes in Physics, pp. 234–247, Springer, Berlin; New York. [DOI], [ADS] (Cited on pages 33 and 43.)
Webb, D.F., 2002, “CMEs and the solar cycle variation in their geoeffectiveness”, in From Solar Min to Max: Half a Solar Cycle with SOHO, Proceedings of the SOHO 11 Symposium, 1–15 March 2002, Davos, Switzerland. A symposium dedicated to Roger M. Bonnet, (Ed.) Wilson, A., vol. SP-508 of ESA Special Publications, pp. 409–419, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 6, 9, 17, 27, 31, 33, 35, and 36.)
Webb, D.F., 2004, “CMEs observed in the heliosphere by the Solar Mass Ejection Imager (SMEI)”, Eos Trans. AGU, 85, SH11A–03. [ADS] (Cited on pages 5 and 6.)
Webb, D.F. and Cliver, E.W., 1995, “Evidence for Magnetic Disconnection of Mass Ejections in the Corona”, J. Geophys. Res., 100, 5853–5870. [DOI] (Cited on page 39.)
Webb, D.F. and Howard, R.A., 1994, “The solar cycle variation of coronal mass ejections and the solar wind mass flux”, J. Geophys. Res., 99(A3), 4201–4220. [DOI], [ADS] (Cited on pages 12, 13, and 16.)
Webb, D.F. and Hundhausen, A.J., 1987, “Activity associated with the solar origin of coronal mass ejections”, Solar Phys., 108, 383–401. [DOI], [ADS] (Cited on pages 12, 43, and 44.)
Webb, D.F. and Jackson, B.V., 1981, “Kinematical analysis of flare spray ejecta observed in the corona”, Solar Phys., 73, 341–361. [DOI] (Cited on page 28.)
Webb, D.F. and Jackson, B.V., 1990, “The identification and characteristics of solar mass ejections observed in the heliosphere by the HELIOS 2 photometers”, J. Geophys. Res., 95, 20,641–20,661. [DOI] (Cited on page 52.)
Webb, D.F., Cheng, C.-C., Dulk, G.A., Martin, S.F., McKenna-Lawlor, S., McLean, D.J. and Edberg, S.J., 1980, “Mechanical energy output of the 5 September 1973 flare”, in Solar flares: A monograph from Skylab Solar Workshop II, (Ed.) Sturrock, P.A., pp. 471–499, Colorado Associated University Press, Boulder, CO (Cited on pages 25 and 27.)
Webb, D.F., Howard, R.A. and Jackson, B.V., 1996, “Comparison of CME masses and kinetic energies near the sun and in the inner heliosphere”, in Solar Wind Eight, Proceedings of the Eighth International Solar Wind Conference, Dana Point, California, USA, 25–30 June 1995, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., vol. 382 of AIP Conference Proceedings, pp. 540–543, American Institute of Physics, Woodbury, NY. [DOI] (Cited on pages 6 and 23.)
Webb, D.F., Kahler, S., McIntosh, P. and Klimchuk, J., 1997, “Large-scale structures and multiple neutral lines associated with coronal mass ejections”, J. Geophys. Res., 102, 24,161–24,174. [DOI] (Cited on pages 31 and 33.)
Webb, D.F., Cliver, E.W., Crooker, N.U., St Cyr, O.C. and Thompson, B.J., 2000a, “Relationship of halo coronal mass ejections, magnetic clouds, and magnetic storms”, J. Geophys. Res., 105, 7491–7508. [DOI] (Cited on page 34.)
Webb, D.F., Lepping, R.P., Burlaga, L.F., DeForest, C.E., Larson, D.E., Martin, S.F., Plunkett, S.P. and Rust, D.M., 2000b, “The origin and development of the May 1997 magnetic cloud”, J. Geophys. Res., 105, 27,251–27,260. [DOI] (Cited on pages 43 and 51.)
Webb, D.F., Burkepile, J., Forbes, T.G. and Riley, P., 2004, “Observational evidence of new current sheets trailing coronal mass ejections”, J. Geophys. Res., 108, 1440. [DOI] (Cited on page 39.)
Webb, D.F., Mizuno, D.R., Buffington, A., Cooke, M.P., Eyles, C.J., Fry, C.D., Gentile, L.C., Hick, P.P., Holladay, P.E., Howard, T.A., Hewitt, J.G., Jackson, B.V., Johnston, J.C., Kuchar, T.A., Mozer, J.B., Price, S., Radick, R.R., Simnett, G.M. and Tappin, S.J., 2006, “Solar Mass Ejection Imager (SMEI) observations of coronal mass ejections (CMEs) in the heliosphere”, J. Geophys. Res., 111, A12101. [DOI] (Cited on pages 5, 52, and 53.)
Webb, D.F., Howard, T.A., Fry, C.D., Kuchar, T.A., Mizuno, D.R., Johnston, J.C. and Jackson, B.V., 2009, “Studying geoeffective interplanetary coronal mass ejections between the Sun and Earth: Space weather implications of Solar Mass Ejection Imager observations”, Space Weather, 7, S05002. [DOI] (Cited on page 52.)
Webb, D.F., Cremades, H., Sterling, A.C., Mandrini, C.H., Dasso, S., Gibson, S.E., Haber, D.A., Komm, R.W., Petrie, G.J.D., McIntosh, P.S., Welsch, B.T. and Plunkett, S.P., 2011, “The global context of solar activity during the Whole Heliosphere Interval campaign”, Solar Phys., 274, 57–86. [DOI] (Cited on page 59.)
Wild, J.P., Murray, J.D. and Rowe, W.C., 1954, “Harmonics in the spectra of solar radio disturbances”, Aust. J. Phys., 7, 439–459. [DOI] (Cited on page 5.)
Wild, J.P., Smerd, S.F. and Weiss, A.A., 1963, “Solar bursts”, Annu. Rev. Astron. Astrophys., 1, 291–366. [DOI] (Cited on page 37.)
Wills-Davey, M.J. and Attrill, G.D.R., 2009, “EIT waves: A changing understanding over a solar cycle”, Space Sci. Rev., 149, 325–353. [DOI], [ADS] (Cited on page 36.)
Wolfson, R. and Low, B.C., 1992, “Energy buildup in sheared force-free magnetic fields”, Astrophys. J., 391, 353–358. [DOI], [ADS] (Cited on page 48.)
Wood, B.E. and Howard, R.A., 2009, “An empirical reconstruction of the 2008 April 26 coronal mass ejection”, Astrophys. J., 702, 901–910. [DOI] (Cited on pages 17 and 56.)
Wood, B.E., Howard, R.A., Thernisien, A., Plunkett, S.P. and Socker, D.G., 2009, “Reconstructing the 3D morphology of the 17 May 2008 CME”, Solar Phys., 259, 163–178. [DOI] (Cited on page 20.)
Xie, H., Gopalswamy, N., Ofman, L., St Cyr, O.C., Michalek, G., Lara, A. and Yashiro, S., 2006, “Improved input to the empirical coronal mass ejection (CME) driven shock arrival model from CME cone models”, Space Weather, 4, S10002. [DOI] (Cited on page 58.)
Yashiro, S., Gopalswamy, N., Michalek, G., St Cyr, O.C., Plunkett, S.P., Rich, N.B. and Howard, R.A., 2004, “A catalog of white light coronal mass ejections observed by the SOHO spacecraft”, J. Geophys. Res., 109, A07105. [DOI], [ADS] (Cited on pages 5, 9, 19, 21, and 22.)
Yashiro, S., Gopalswamy, N., Akiyama, S., Michalek, G. and Howard, R.A., 2005, “Visibility of coronal mass ejections as a function of flare location and intensity”, J. Geophys. Res., 110, A12S05. [DOI], [ADS] (Cited on page 31.)
Yashiro, S., Akiyama, S., Gopalswamy, N. and Howard, R.A., 2006, “Different power-law indices in the frequency distributions of flares with and without coronal mass ejections”, Astrophys. J., 650, L143–L146. [DOI] (Cited on pages 23 and 58.)
Yashiro, S., Michalek, G., Akiyama, S., Gopalswamy, N. and Howard, R.A., 2008a, “Spatial relationship between solar flares and coronal mass ejections”, Astrophys. J., 673, 1174–1180. [DOI] (Cited on pages 31 and 44.)
Yashiro, S., Michalek, G. and Gopalswamy, N., 2008b, “A comparison of coronal mass ejections identified by manual and automatic methods”, Ann. Geophys., 26, 3103–3112. [DOI] (Cited on pages 11 and 38.)
Yokoyama, T., Akita, K., Morimoto, T., Inoue, K. and Newmark, J., 2001, “Clear evidence of reconnection inflow of a solar flare”, Astrophys. J., 546, L69–L72. [DOI], [ADS] (Cited on page 39.)
Yurchyshyn, V., Yashiro, S., Abramenko, V., Wang, H. and Gopalswamy, N., 2005, “Statistical distributions of speeds of coronal mass ejections”, Astrophys. J., 619, 599–603. [DOI], [ADS] (Cited on page 23.)
Zhang, J., Dere, K.P., Howard, R.A., Kundu, M.R. and White, S.M., 2001, “On the temporal relationship between coronal mass ejections and flares”, Astrophys. J., 559, 452–462. [DOI], [ADS] (Cited on page 21.)
Zhang, J., Dere, K.P., Howard, R.A. and Vourlidas, A., 2004, “A study of the kinematic evolution of coronal mass ejections”, Astrophys. J., 604, 420–432. [DOI], [ADS] (Cited on page 21.)
Zhang, J., Cheng, X. and Ding, M., 2012, “Observation of an evolving magnetic flux rope before and during a solar eruption”, Nature Commun., 3, 747. [DOI] (Cited on page 22.)
Zhao, X.P. and Webb, D.F., 2003, “Source regions and storm effectiveness of frontside full halo coronal mass ejections”, J. Geophys. Res., 108, 1234. [DOI] (Cited on page 50.)
Zurbuchen, T.H. and Richardson, I.G., 2006, “In-situ solar wind and magnetic field signatures of interplanetary coronal mass ejections”, Space Sci. Rev., 123, 31–43. [DOI] (Cited on page 51.)
Acknowledgments
We thank the editors of Living Reviews in Solar Physics, especially R. Schwenn who solicited this article and helped in its preparation. We benefitted from data from the SOHO mission, which is an international collaboration between NASA and ESA, and also from the SOHO/LASCO CME catalog, generated and maintained by the Center for Solar Physics and Space Weather, The Catholic University of America in cooperation with NRL and NASA. We thank N. Gopalswamy and S. Yashiro for helping us with their group’s latest LASCO CME results. We also thank A. Vourlidas, S. Kahler, and J. Raymond for providing material for this article. The Solar Mass Ejection Imager (SMEI) instrument is a collaborative project of the U.S. Air Force Research Laboratory, NASA, the University of California at San Diego, the University of Birmingham, UK., Boston College, and Boston University. The STEREO SECCHI Heliospheric Imager (HI) instrument was developed by a collaboration that included the Rutherford Appleton Laboratory and the University of Birmingham, both in the United Kingdom, the Centre Spatial de Li`ege (CSL), Belgium, and the US Naval Research Laboratory (NRL), Washington DC, USA. The SECCHI project is an international consortium of the Naval Research Laboratory, Lockheed Martin Solar and Astrophysics Lab, NASA Goddard Space Flight Center, Rutherford Appleton Laboratory, University of Birmingham, Max-Planck-Institut für Sonnensystemforschung, Centre Spatial de Li`ege, Institut d’Optique Théorique et Appliquée, and Institut d’Astrophysique Spatiale. This work was supported at Boston College by Air Force contracts AF19628-00-K-0073 and FA8718- 04-C-0006 and by NASA grant NNGO5GF98G. TAH is funded in part by SHINE Competition grant no. ATM-0849916 and NASA SHP grant no. NNX10AC05G.
All figures from Astronomy and Astrophysics reproduced with permission ©ESO; from The Astrophysical Journal and The Astrophysical Journal Letters reproduced by permission of the AAS; from ESA Special Publications reproduced with permission by ESA; from Journal of Geophysical Research reproduced with permission ©AGU; from Astrophysics and Space Science Library, Astrophysics and Space Science Proceedings, and Solar Physics reproduced with kind permission from Springer Science+Business Media B.V.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2016_3_MOESM1_ESM.mpeg
mpg-Movie (455.255859375 KB) Still from a movie showing LASCO C3 images of lightbulb shaped CME on 27 February 2000. Classic three-part structure with outer shell, void and inner bright structure, in this case an erupting prominence. From SOHO online movie gallery: http://sohowww.nascom.nasa.gov/gallery/Movies/flares.html.
41116_2016_3_MOESM2_ESM.avi
mpg-Movie (10681.5 KB) Still from a movie showing Orbit difference images of an Earthward halo from SMEI. Halo was visible as an arc over ≥ 150° of sky (arrows). Blacked-out areas are due to shuttering of bright sunlight and CCD noise from particles in Coriolis’ 840 km circular Earth orbit.
41116_2016_3_MOESM3_ESM.mpeg
mpg-Movie (28363.8935547 KB) Still from a movie showing Combined views from all of the STEREO SECCHI telescopes during a series of CMEs in early April 2010. The bottom panels show the ST-B and ST-A views of the EUVI disk, COR1 and COR2 imagers out to 15R⊙, and the upper set shows the HI-1 and -2 fields viewing east (left, HI-A) and west (right, HI-B) of the Sun beyond the EUVI, COR1, COR2 set shown to scale. From the online data at: http://secchi.nrl.navy.mil/index.php?p=movies.
41116_2016_3_MOESM4_ESM.avi
mpg-Movie (70268.6445312 KB)Still from a movie showing STEREO/HI2-A images following the latest data processing pipeline for SECCHI (DeForest et al., 2011).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Webb, D.F., Howard, T.A. Coronal Mass Ejections: Observations. Living Rev. Sol. Phys. 9, 3 (2012). https://doi.org/10.12942/lrsp-2012-3
Published:
DOI: https://doi.org/10.12942/lrsp-2012-3