Solar Adaptive Optics

Rimmele, Thomas R.; Marino, Jose

doi:10.12942/lrsp-2011-2

Review Article
Open Access
Published: 10 June 2011

Solar Adaptive Optics

Thomas R. Rimmele¹ &
Jose Marino²

Living Reviews in Solar Physics volume 8, Article number: 2 (2011) Cite this article

7351 Accesses
73 Citations
3 Altmetric
Metrics details

Abstract

Adaptive optics (AO) has become an indispensable tool at ground-based solar telescopes. AO enables the ground-based observer to overcome the adverse effects of atmospheric seeing and obtain diffraction limited observations. Over the last decade adaptive optics systems have been deployed at major ground-based solar telescopes and revitalized ground-based solar astronomy. The relatively small aperture of solar telescopes and the bright source make solar AO possible for visible wavelengths where the majority of solar observations are still performed. Solar AO systems enable diffraction limited observations of the Sun for a significant fraction of the available observing time at ground-based solar telescopes, which often have a larger aperture than equivalent space based observatories, such as HINODE. New ground breaking scientific results have been achieved with solar adaptive optics and this trend continues. New large aperture telescopes are currently being deployed or are under construction. With the aid of solar AO these telescopes will obtain observations of the highly structured and dynamic solar atmosphere with unprecedented resolution. This paper reviews solar adaptive optics techniques and summarizes the recent progress in the field of solar adaptive optics. An outlook to future solar AO developments, including a discussion of Multi-Conjugate AO (MCAO) and Ground-Layer AO (GLAO) will be given.

Introduction

Driven by the quest for ever higher spatial resolution observations of the Sun, the development of solar adaptive optics has excelled tremendously during the last 5–10 years. Several solar AO systems have been deployed at major ground-based solar telescopes and are now routinely operated. These AO systems have facilitated observations of structure in the solar atmosphere at a resolution that is at or near the diffraction limit of those telescopes. It is worthwhile to briefly summarize the main scientific drivers for observations of the Sun at the highest possible resolution and motivate the need for solar adaptive optics. The solar atmosphere is highly structured and dynamic. Understanding the physics of the small scale structure observed on the Sun in many cases is crucial to understanding important scientific questions such as:

What causes solar luminosity variations that affect the climate on Earth?
How are magnetic fields generated by dynamo processes?
How are magnetic fields transported and how is magnetic energy transported and dissipated?
How is magnetic energy stored and what triggers its release as flares and coronal mass ejections?

The two important scales that determine the structuring of the solar atmosphere are the pressure scale height and the photon mean free path. Both are of order 70 km or 0.1” in the solar photosphere and quickly become even smaller at deeper layers of the atmosphere. An angular resolution of better than 0.1” is required to resolve these fundamental scales. Structures as small as a few tens of kilometers on the solar surface corresponding to a few tens of milli-arcseconds on the sky have been predicted by sophisticated MHD models of the solar atmosphere (Cattaneo et al., 2003; Vögler and Schüssler, 2007; Nordlund and Stein, 2009; Nordlund et al., 2009).

Current high-resolution solar telescopes, such as the Dunn Solar Telescope (DST), the Swedish Solar Telescope (SST), the Vacuum Tower Telescope (VTT) are in the one-meter class and utilize AO up to > 95% of the observing time to achieve the diffraction limit at visible and NIR wavelengths. Solar AO has revitalized ground-based solar astronomy at existing telescopes.

Figure 1 shows a sunspot image obtained at the DST using AO and a fast imaging camera that takes short exposure images in rapid sequence. The sequence of images has been post processed with a speckle reconstruction algorithm that compensates for the effects of residual wavefront errors that the AO was not able to correct. The images were recorded with a g-band filter with a passband centered at 430 nm. At this short wavelength, AO becomes very challenging and postfacto reconstruction becomes a necessity. Figure 1 illustrates the degree of fine-scale structuring of the solar atmosphere. Structures, such as penumbral filaments and g-band bright points that mark the sites of magnetic fields are seen at scales of about 0.12”. The apparent size of these structures is near the diffraction limit of the telescope and the granulation pattern that is visible in the photosphere and covers the entire surface of the Sun is seen.

Figure 2 shows several g-band images of sunspot fine-structure obtained at the 97 cm Swedish Solar Telescope (SST) on La Palma (Scharmer et al., 2007). Adaptive optics and post-processing techniques were used to reach a resolution that again is near the diffraction limit. Due to the larger aperture, the diffraction limit of the SST at the wavelength of g-band is 0.1” or about 70 km on the Sun, i.e., the resolution is higher than that of the DST. With this increase in aperture and, hence, resolution Scharmer et al. (2002) were able to clearly identify dark cores in penumbral filaments. This discovery of dark cores has contributed significantly to the development of a better physical understanding of penumbral fine-structure and sunspots in general. Close inspection of Figure 1 shows that penumbral dark cores are visible in this image as well, but only the increase in resolution provided by the larger aperture of the SST enabled the discovery of dark cores as a feature with significance to sunspot physics and magneto-convection in general. The fact that ever more details that allow us to advance our physical understanding of solar magnetic fields are revealed with even modestly increased resolution demonstrates the importance of fully resolving solar features. The measured sizes of many small-scale magnetic features are close to the limit set by diffraction, implying they are not adequately resolved by present solar telescopes.

What kind of resolution is needed to fully resolve the important physical processes? Sophisticated theoretical models and simulations, including radiative energy exchange and cooling, provide fundamental insights. Figure 3 shows simulated observations with a 4 m aperture telescope used by the ATST project science team in order to define imaging requirements for the Telescope-AO system (Rimmele, 2005). The numerical simulation of granular convection (Nordlund and Stein, 2009) is coupled with radiative transfer calculations for the Fe I line 630.2 nm. narrow-band intensity maps and line-of-sight magnetograms are shown over a 8” × 8” FOV. The magnetic fields generated by dynamo action near the surface are small scale, mixed-polarity fields. In order to simulate AO observations of these features the data were convolved with an AO Point Spread Function (PSF). The performance of an AO system varies with seeing conditions. The Strehl ratio measures how close the imaging performance provided by the AO is to that of the ideal diffraction limited telescope. The theoretical diffraction limited PSF has a Strehl of S = 1 and can not be achieved in practice. This performance measure will be discussed in detail in Section 6. In this simulation the Strehl ratio varies from S = 0.001 (seeing limited, virtually no AO correction) to S = 0.55 (good AO correction). These realistic simulations clearly demonstrate that large aperture telescopes with a high performance AO system that obtains high Strehl ratios are required in order to obtain meaningful measurements.

It is this iterative interaction between theoretical modeling and observations with a resolution that is comparable to that of the models (order 10 km) that is vital in arriving at a physical understanding of the fundamental astrophysical processes observed on the Sun. New large aperture telescopes are needed to resolve these features and put models to the test. The development of highorder solar AO that is capable of delivering high Strehl in the visible will be absolutely essential for next generation solar telescopes.

Several new solar telescope efforts are currently under way. Telescopes of the 1.5 m class such as the 1.5 m aperture GREGOR (Volkmer et al., 2003, 2006; Volkmer, 2008; Volkmer et al., 2010) on Tenerife and the 1.6 m aperture New Solar Telescope (NST) (Goode, 2006; Goode et al., 2010) are currently in their commissioning phase. The 4 m Advanced Technology Solar Telescope (ATST) (Rimmele et al., 2006a; Wagner et al., 2008; Rimmele et al., 2010b) is in its construction phase and is expected to be fully commissioned in 2018. In order for these telescopes to achieve their scientific goals complex adaptive optics systems are an essential and integral component of the optical system that feeds the solar instrumentation.

Accurate and precise measurements of physical parameters, such as magnetic field strength and direction or plasma velocity, require spectroscopy and polarimetry at high spatial, but also high spectral (R > 300000), resolution and high polarimetric sensitivity. A sufficient number of photons has to be collected to achieve the required sensitivity, which leads to long exposure times since even the Sun turns into a faint object when observed at this ultra high spectral and spatial resolution. Short exposure observations that allow to fully freeze the seeing and, thus, retain diffraction limited information in many but not all cases are limited to broad-band imaging and are of somewhat limited utility for the precise quantitative scientific analysis mentioned above. However, with highly efficient telescope systems and instrumentation (e.g., CRISP; Scharmer et al., 2008) that have high throughput, and use slightly compromised spectral resolution, sufficiently short exposures can be achieved to allow at least partially if not fully freeze the seeing and, thus, provide short exposure, narrow-band observations. This type of approach is particularly useful at the red end of the visible spectrum and at near infrared wavelengths where the seeing time constant is longer. Frame selection and post-facto image processing can be applied to short exposure, narrow-band images leading to impressive results. High signal-to-noise ratio can in principle be achieved by accumulating post-processed short exposure filtergrams, although a very high duty cycle is required to ensure the required temporal resolution.

Even for short exposure imaging applications AO correction provides a significant advantage in that only small, residual wavefront errors have to be post-facto corrected, which leads to much higher signal-to-noise of the reconstructed images.

Solar adaptive optics can also provide diffraction limited long exposure spectroscopic and polarimetric observations of the solar atmosphere. With a well designed and optimized AO system the exposure time can be chosen to provide optimal sensitivity of the measurement and does no longer have to be limited by the desire to freeze the seeing. It should be mentioned that evolution of the solar structures also limits the length of the exposure interval. The optimal choice of method and observing parameters will always have to be made based on the specific scientific problem at hand and the instrumentation available.

This review paper summarizes the current state of solar AO technology and attempts to give a sense of the impact of AO on the field of high resolution solar astronomy. Section 2 summarizes basic AO principles. In order to understand AO technology a basic understanding of the problem — atmospheric turbulence — is pre-requisite. Many of the challenges of solar AO are common to astronomical AO in general. Section 2.3 discusses the solar AO specific challenges in comparison to night-time adaptive optics systems. The long and difficult path toward developing operational and scientifically productive solar AO systems is summarized in Section 3. The vital role the development of the correlating Shack-Hartmann wavefront sensor played in making solar AO a successful technology is described in Section 4. A number of highly successful solar AO systems are now operated at major solar telescopes. Due to the author’s bias, the DST solar AO system was selected as an example to discuss implementation details (Section 5). In using AO and interpreting AO data it is important to understand the limitations of solar AO or AO in general. AO performance is not perfect as is the case for many optical systems, including space borne telescopes. Section 6 details performance limitations of adaptive optics in the context of developing an AO residual wavefront error budget. Error budgets provide important guidance for the design of an AO system. Performance limitations can be overcome to some extent by estimating the AO PSF and subsequent application of post-facto deconvolution techniques (Section 7). An overview of operational solar AO systems is given in Section 8. Future solar AO developments, including the development of Multi-conjugate AO are discussed in Section 9.

Adaptive Optics Basics

This section briefly summarizes the basic principles of AO. An extensive body of AO literature already exists and includes textbooks (Hardy, 1998; Roddier, 1999; Tyson, 2011), review articles (Beckers, 1993a), and a large collection of conference and workshop proceedings. AO tutorials are also available at various web sites. The web site of the Center for Adaptive Optics (http://cfao.ucolick.org/) contains a large number of links to additional AO web sites and several AO tutorials. It is not the objective of this section to provide a comprehensive summary of AO concepts and principles, but to simply recall the important concepts and definitions and set the stage for the discussion of the solar AO specific problems and their solutions.

Atmospheric turbulence

The task of an AO system is to correct wavefront aberrations introduced by the turbulent atmosphere above the telescope. Turbulent motions in the atmosphere mix eddies with different temperatures and thus different densities. As a consequence light propagating along different paths through a turbulent medium experiences a different refractive index. The result is an optical path difference, which in turn leads to deformations of the incoming wavefronts.

A good understanding of the atmospheric properties above the telescope site and the resulting wavefront aberrations is crucial for the design and operation of an AO system. The importance of site survey and site characterization efforts cannot be overemphasized in this context. Key atmospheric parameters that determine the design and performance of an AO system include the Fried parameter r₀, the Greenwood frequency f_c, and the atmospheric turbulence profile Cn²(h). Cn² is the refractive index (n = refractive index) structure constant, which will be defined and discussed below. By using turbulence theory, these properties can be used to design AO systems and predict their performance. The most widely used model to describe atmospheric turbulence is the Kolmogorov model (Kolmogorov, 1941, 1991). Energy is introduced into the system by wind flows at a large scale (the outer scale) and cascades down to ever smaller scales until, finally, energy is dissipated at molecular scales (the inner scale). The inertial range is bound by the outer and the inner scale and marks the regime where the turbulent power of the temperature fluctuations Φ_T as a function of spatial wave number κ = 2π/l can be expressed by a power law:

$\Phi _T (\kappa ) \propto \kappa ^{ - 5/3} .$

((1))

Similar power laws can be derived for other quantities such as the refractive index power spectral density in one dimension (Hardy, 1998; Tatarskii, 1967):

$$\Phi _N (\kappa ) = \frac{{\Gamma (\tfrac{5} {3})\sin (\tfrac{\pi } {3})}} {{(2\pi )^{5/3} }}C_n^2 \kappa ^{ - 5/3} = 0.0365 C_n^2 \kappa ^{ - 5/3} .$$

((2))

The equivalent in three dimensions leads to the well known κ^-11/3 power law (Roggemann and Welsh, 1996; Quirrenbach, 2002):

$3D_{\Phi _T (\kappa )} = \frac{{\Gamma \left( {\tfrac{8} {3}} \right)\sin \left( {\tfrac{\pi } {3}} \right)}} {{4\pi ^2 }}C_n^2 \kappa ^{ - 11/3} = 0.033C_n^2 \kappa ^{ - 11/3} . $

((3))

The refractive index structure constant $C_n^2 $ is a measure for the strength of the turbulence and is related to the temperature structure constant $C_T^2 $ by: $C_n = \delta n/\delta TC_T $.

At this point it is convenient to discuss the concept of the structure function, which was introduced by Kolmogorov to describe non stationary random processes such as turbulence. In general, structure functions are very useful in assessing the impact of turbulence on the image quality provided by an imaging system, independent of whether the aberrations are caused by atmospheric turbulence or optical imperfections. Today, structure functions are used to, for example, specify optical polishing tolerances.

In the context of atmospheric turbulence the refractive index structure function is assumed to be isotropic and is defined as:

$D_n (\rho ) = \left\langle {\left| {n(\vec r) - n(\vec r + \vec p)^2 } \right|} \right\rangle = C_n^2 \rho ^{2/3} .$

((4))

The angled brackets 〈...〉 indicate an ensemble average and $\vec \rho $ defines a spatial separation, for example in the pupil plane of a telescope. The refractive index structure function can be related to the phase structure function, which is essential in determining the performance of an imaging system in the presence of turbulence. The phase structure function produced by a layer of thickness δh is given by Hardy (1998), Roggemann and Welsh (1996), and Quirrenbach (2002):

$D_\phi (\rho ,h) = 2.914k^2 \delta hC_{n_i }^2 (h)\rho ^{5/3} .$

((5))

The wavenumber $k = \frac{{2\pi }} {\lambda } $, where λ is the wavelength. It should be noted that the phase shift introduced can be related to the refractive index fluctuations along the optical path by Φ = ∫n(h)dh.

Hence, if multiple turbulence layers (or a continuum) are present, Equation (5) has to be integrated along the line-of-sight. The zenith angle γ is introduced to account for changes in the length of the line-of-sight travel path with observing angle:

$D_\phi (\rho ) = 2.914k^2 (\sec \gamma )\rho ^{5/3} \int {C_n^2 (h)dh} .$

((6))

The Fried parameter r₀ is a measure for the strength of the turbulence and is defined as (Fried, 1966a,b):

$r_0 \equiv \left[ {0.423k^2 (\sec \gamma )\int {C_n^2 (h)dh} } \right]^{ - 3/5} .$

((7))

The Fried parameter gives the diameter of a patch in the aperture plane over which the wavefront can be regarded as flat. More precisely, flat in this case means the wavefront variance is less than 1 rad². In that sense the Fried parameter can be interpreted as the smallest AO relevant scale of turbulence. Of course, the turbulent spectrum contains much smaller spatial scales. The Fried parameter is often used to quantify the seeing quality at an astronomical site. The statistical distribution as well as the temporal evolution of the Fried parameter ultimately determines the performance of an AO system at the site. The value of the Fried parameter depends on wavelength according to $r_0 \propto \lambda ^{6/5} $. This means r₀ has to be specified at a certain wavelength, typically 500 nm. The Fried parameter r₀ is larger for longer wavelengths, which means the seeing is significantly better at infrared wavelengths. Hence, correcting the seeing with AO becomes easier at longer wavelengths.

The phase structure function can be expressed in terms of the Fried parameter resulting in a much simpler form of D_ϕ(ρ):

$D_{long} (\rho ) = 6.88\left( {\frac{\rho } {{r_0 }}} \right)^{5/3} . $

((8))

This phase structure function describes the performance of imaging systems in the presence of turbulence. Equation 8 is often referred to as the uncorrected, long exposure phase structure function. This simple form for the structure function is valid only in a statistical sense, i.e., when averaged over a sufficient amount of independent realizations of the atmospheric turbulence. Marino (2007) showed that, for daytime observations, exposures of only a few seconds can be regarded as long exposures. Solar astronomers tend to use such long exposure times when performing precision polarimetric measurements. High resolution spectroscopy sometimes requires exposure times of similar length. However, broad-band solar imaging is typically performed with very short exposures on the order of a few milliseconds with the intention to freeze the seeing. Image motion (tip and tilt) can essentially be removed in this way and the images contain speckle, i.e., structure with width of the diffraction limit $\frac{\lambda } {D} $. The fact that diffraction limited information is contained in the short exposure images can then be used to restore the true image by applying post-facto image reconstruction techniques. Löfdahl et al. (2007) give a review of various post-facto reconstruction in solar astronomy.

An analytical expression for the short exposure structure function can also be given (see, e.g., Hardy, 1998, p. 92):

$D_{short} (\rho ) = 6.88\left( {\frac{\rho } {{r_0 }}} \right)^{5/3} \left( {1 - \left( {\frac{\rho } {D}} \right)^{1/3} } \right). $

((9))

The negative impact of atmospheric turbulence on imaging systems has been described in detail in textbooks (e.g., Hardy, 1998, Section 3). It is the de-correlation of the phase over distances larger than r₀ that results in blurred images where the typical width of the blurred long exposure image is $\frac{\lambda } {{r_0 }} $, i.e., the resolution is seeing limited.

The long exposure Optical Transfer Function (OTF) is defined as the ensemble average of the instantaneous OTFs over the entire exposure:

$\begin{gathered} OTF(\vec \rho /\lambda ) = \left\langle {OTF(\vec \rho /\lambda ,t)} \right\rangle = \hfill \\ = \frac{1} {S}\int {P(\vec x)P*(\vec x + \vec \rho )\left\langle {\exp [i\phi (\vec x,t) - i\phi (\vec x + \vec \rho ,t)]} \right\rangle d\vec x} , \hfill \\ \end{gathered} $

((10))

where $P(\vec x)$ is the pupil function and S, the surface area of the pupil, normalizes the energy contained of the PSF to unity. Using the definition of the structure function the long exposure OTF can be simplified to:

$OTF(\vec \rho /\lambda ) = \frac{1} {S}\int {P(\vec x)P*(\vec x + \vec \rho )} \exp \left[ { - \frac{1} {2}D_\phi (\vec x,\vec \rho )} \right]d\vec x, $

((11))

which leads directly to:

$OTF_{atm} (\vec \rho /\lambda ) = \exp \left[ { - 3.44\left( {\frac{\rho } {{r_0 }}} \right)^{5/3} } \right]. $

((12))

The OTF and the PSF are related through a Fourier transform. Figure 4 shows the OTFs and PSFs of the seeing limited long exposure (Equation 12), the aberration free, diffraction limited telescope and a typical AO corrected case. The seeing limited OTF does not transfer high spatial frequency information. The AO system is able to retain high spatial resolution information potentially up to the diffraction limit. However, the amplitudes are attenuated in particular, for high spatial frequencies where, depending on the particular observation, noise may begin to dominate before the theoretical diffraction limit.

The AO corrected PSF consists of two parts. A diffraction limited core and a seeing limited halo. The width of the core is $\frac{\lambda } {D} $, while the width of the halo is $\frac{\lambda } {{r_0 }} $. The Strehl, which is defined as the ratio of the peak intensity of the observed PSF compared to the peak intensity of the ideal telescope PSF, of the AO corrected PSF shown in Figure 4 is S = 0.6. The Strehl ratio is also a measure for the energy contained in the core vs. energy in the halo. The AO corrected long exposure phase structure function will be revisited in detail in Section 6.3.

The time τ₀ after which wavefront aberrations change significantly is another important parameter that determines and limits the performance of solar AO and also defines the meaning of a short or long exposure. Using the Taylor hypothesis of frozen in turbulence one can easily derive an estimate for τ₀. The assumption is that a turbulence screen is carried across the telescope aperture by wind at time scales much faster than the intrinsic evolution of the turbulence. This assumption has been experimentally verified (Poyneer et al., 2009) and can be used to implement predictive control of AO systems (e.g., Dessenne et al., 1998, 1999; Poyneer and Véran, 2008; Johnson et al., 2008) in order to improve performance. With this assumption the turbulence or seeing time constant τ₀ can be estimated by the simple equation:

$\tau _0 \equiv r_0 /v,$

((13))

where v is the wind speed of the dominant turbulence layer. For visible wavelengths typical values for r₀ ∼ 10 cm and v ∼ 10 m/s result in a τ₀ ∼ of 10 ms. The wavelengths dependence of τ₀ is the same as for $r_0 \sim \lambda ^{\tfrac{6} {5}} $. Thus the bandwidth requirements for AO can be relaxed in the infrared.

Design of an AO system

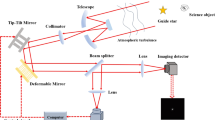
The task of the AO system is to restore and maintain sufficient phase coherence across the telescope aperture to enable formation of a diffraction limited core. The goal is to design a well performing AO system that achieves high Strehl and, hence, approaches the performance of the ideal telescope. Figure 5 shows arrangement of the basic components of an AO system, which are:

a wavefront sensor (WFS) that measures the wavefront aberrations. The wavefront is typically sensed indirectly by, e.g., measuring wavefront gradients at a number of positions in a pupil plane. An example of such a WFS is the Shack-Hartmann WFS (SHWFS), which is shown in Figure 5 and will be explained in detail in Section 4.
a wavefront corrector, such as a deformable mirror (DM) that corrects phase aberrations by introducing the correct, compensating optical path difference. The mirror surface is deformed by actuators located at the back of the thin mirror substrate also referred to as faceplate.
a reconstructor, or more generally, a processing unit that computes actuator commands (e.g., voltages) from the WFS information. The processor unit typically also implements a closed-loop servo algorithm for driving the DM in the most effective way.

Different approaches to solar wavefront sensing and different implementations for wavefront correctors will be discussed briefly in Section 3 in the context of the history of solar AO development. More information can be found in textbooks and other relevant literature (e.g., Proc. SPIE). As a general comment it is noted that the desire to achieve high Strehl ratio leads directly to a requirement for high order correction, meaning that the wavefront aberrations have to be sampled with high density. A similarly large number of DM actuators is required to fit the incoming wavefront with high fidelity. Furthermore, the temporal bandwidth of the AO system has to be sufficient with respect to the seeing time constant. The number of corrective elements or degrees-of-freedom (DOF) of an AO system is roughly $DOF \approx \left( {\frac{D} {{r_0 }}} \right)^2 $. A more detailed analysis will be performed in the context of developing an wavefront error budget (Section 6).

Solar AO challenges: difference between night and day

In basic design solar AO systems are quite similar to night-time AO systems. However, compared to night-time AO, solar AO faces a number of different challenges and solar AO systems are in some aspects technically more challenging than night-time AO (Rimmele, 2004a). The main challenges are the poor and time varying daytime seeing, the fact that solar astronomers mostly observe at visible wavelengths (down to 380 nm), and the solar wavefront sensor, which has to work on lowcontrast, extended, time-varying objects such as solar granulation. Due to heating of the ground by direct sunlight, the near-ground turbulence layer is much stronger during the day and typical Fried parameters are of order 10 cm (500 nm) at an excellent site and at a typical telescope height of 20–40 m above ground. The entrance aperture of the Dunn Solar Telescope at Sacramento Peak, NM was placed at a height of 40 m in order to get above a large fraction of the near-ground turbulence. Nevertheless, the Fried parameter fluctuates significantly on short time scales (seconds) and often drops to values of just a few centimeters (Figure 6). In comparison, night-time seeing conditions generally provide significantly larger and less fluctuating Fried parameters. In addition, most night-time AO systems operating on large aperture night-time telescopes operate at infrared wavelengths where the Fried parameter is again larger. Although some night-time AO systems are already operating at visible wavelengths (Fugate, 2003) and efforts to implement visible AO at large aperture night-time telescopes are in progress (Bouchez et al., 2010).

Due to the worse daytime seeing conditions and the fact that much of the science is done at visible wavelengths, solar AO systems require a large number of corrective elements in spite of the so-far relatively small (compared to night-time telescopes) apertures of solar telescopes. New generation solar telescopes such as the 4 m ATST require a much larger number of DOF, and the AO systems for the ATST and EST approach the complexity of what is referred to as extreme AO. In addition, the corrected FOV of a high order solar AO system implemented at a 4 m telescope is significantly smaller than what solar astronomers are accustomed to from their experience with AO at smaller existing telescopes. This issue will be addressed in much more detail in Section 6.1.3.

The small value of r₀ at visible wavelengths and with daytime seeing conditions require solar AO systems to achieve a very high closed loop bandwidth. The incoming wavefront varies rapidly in time. Figure 7 plots as a function of temporal frequency the Power Spectral Density (PSD) of Zernike coefficient Z4 (astigmatism) and Z24 as measured with the low order NSO AO system (Rimmele, 2000). A break point in the PSD occurs at about 10 Hz for Z4 and 20 Hz for Z24. The frequency at which the break occurs is the Greenwood frequency and increases with the radial mode number. This demonstrates the well known fact that higher order systems require higher bandwidth as well. The spectrum contains signal power out to at least 200 Hz at which point noise becomes dominant. The high Greenwood frequency or more accurately the high temporal frequency content of the wavefront fluctuations leads to required sampling rates of > 2 kHz and closed loop bandwidths for high order solar AO systems in excess of 100 Hz (Rimmele, 2004a).

A major challenge for solar AO was the development of a suitable wavefront sensor. Wavefront sensors used for night-time AO system cannot be directly used for solar AO systems because point sources that are used as guide stars (natural or laser) for night-time AO systems are not available when observing the Sun. A solar AO system has to be able to lock on extended targets such as pores, sunspots or a substructure of a sunspot and solar granulation. Solar granulation, in particular, is a challenging target to track on since the granulation pattern is of low contrast and changes on time scales of about 1 min.

Laser guide stars are not a practical solution for solar AO since either extremely bright lasers would be needed to project a laser spot against the bright background of the solar disk or very special narrow-band filters (e.g., magneto-optical filters for sodium) would have to be used (Beckers, 2008). The complexity and cost of this approach has so far prevented any serious efforts in this direction. A possible application for laser guide stars in solar astronomy may be observations of the very faint corona. The brightness of the corona is only a few millionths of the disk brightness and natural guide stars, i.e., coronal structure bright enough to track are not available. The future use of laser guide star AO may therefore be considered for coronal observations to be performed with the 4 m Advanced Technology Solar Telescope.

A Brief History of Solar AO

The first adaptive optics experiments with the Sun were performed at the Dunn Solar Telescope by Hardy in 1979–1980 (Hardy, 1980). Hardy used a shearing interferometer for a wavefront sensor and a 21 actuator continuous faceplate DM. Wavefront sensing targets were stars and sunspots. This was one of the first on-sky adaptive optics experiments and success was limited.

The National Solar Observatory AO program aimed to develop a solar AO system for the DST (Dunn, 1987; Dunn et al., 1989; Dunn, 1990) using an in-house built 61 actuator continuous faceplate DM (Dunn et al., 1992) and a focal plane LCD mask WFS (von der Lühe, 1988). This wavefront sensor concept can be traced back to the well known Focault knife-edge test (Darvann and Dunn, 1987), which also places a mask (knife-edge) in a focal plane and visualizes phase aberrations as intensity fluctuations in a pupil plane. The sensor measures wavefront gradients, and for small wavefront errors its output has been shown to be equivalent to that of the Shack-Hartmann sensor (Rimmele and Radick, 1998). For high contrast objects that are limited in spatial extent (star, pore, small sunspot, planet) a straight knife edge can be used as focal plane mask as is demonstrated with Figure 8.

Granulation, however, requires a rather complicated focal plane mask, an example of which is shown in Figure 9. The mask is derived from the following equation:

$M(\vec x) = A + B[I(\vec x) - \vec \Delta ) - I(\vec x + \vec \Delta )],$

((14))

where A and B are constants that limit the transmission of the mask between 0 and 1 and Δ is an image displacement comparable to the spatial scale of, e.g., granulation. By placing this “derivative mask” in an image plane wavefront errors are encoded as intensity fluctuations that can be measured in a pupil plane.

Since granulation evolves on time scales of minutes the mask has to be continuously updated; this can be implemented using a programmable LCD screen. Such a sensor was implemented at the DST but, in particular when used on granulation, had serious signal-to-noise issues. This approach does not divide the pupil into subapertures and therefore does not suffer from the limitations such as subaperture diffraction. However, the focal plane mask introduces diffraction effects in the pupil plane and in this way limits the resolution with which the wavefront can be resolved. The concept was recently investigated further with a laboratory setup (Schmidt and von der Lühe, 2007) but so far has not been successfully implemented at a solar telescope.

A Shack-Hartmann based solar AO system was developed by Lockheed (Acton and Smithson, 1992; Acton and Dunn, 1993) and tested at the DST. The system was based on a custom built 19 element segmented mirror combined with a Shack-Hartmann sensor. The SHWFS used analog quad-cell detectors to sense image shifts, which limited its application to small high contrast objects, i.e., solar pores and thus severely limited the system’s scientific use. In addition, due to the complexity of the system, it could be characterized as an optical experiment rather than a science instrument. Figure 10 shows the segmented DM and the quad-cell SHWFS of the Lockheed AO system. A particular challenge of the segmented mirror approach is phasing the segments. Expertise developed for the Lockheed AO system has since been useful to segmented mirror telescope projects such as Keck and JWST.

These early solar AO efforts were forced to custom-develop all components, such as DM, reconstructor and control hardware, and WFS. Many of these components were not available commercially, and development (either in-house or through development contracts) was extremely expensive, time consuming and plagued by frequent setbacks. A viable and practical solution to the solar wavefront sensor problem was also lacking. A breakthrough in solar AO came with the development of the correlating Shack-Hartmann wavefront sensor and its implementation in the NSO low-order adaptive optics system. The NSO low-order solar AO system was the first fully operational solar AO system that was also capable of tracking on granulation. The design of this 24 subaperture solar AO system is described in detail by Rimmele and Radick (1998) and Rimmele (2000).

This system was successfully tested in 1998 at the DST and was operated on a routine basis at the DST for a number of years. The low-order solar AO system achieved diffraction limited imaging with high Strehl ratios (up to 0.6) in good seeing conditions (r₀ (500 nm) > 12 cm). The success was made possible by rapid development of computer technology that allowed the implementation of the compute and data transfer intensive correlation algorithm described in more detail in Section 4.

The NSO low-order AO system made use of components that at the time had just become commercially available. An off-the-shelf XINETICS DM with 97 (Ealey and Wellman, 1994) actuators and sophisticated control electronics could be implemented. A correlating Shack-Hartmann wavefront sensor with 24 subapertures was developed based on Digital Signal Processor (DSP) technology. The correlating Shack-Hartmann wavefront sensor uses the same principle that had been used for quite some time to provide tip/tilt correction at solar telescopes with a device called Correlation Tracker (von der Lühe et al., 1989). The challenge for low-order AO system development was implementing 24 correlation tracker channels running in parallel, at high update rates and with low latency. In 1998 the NSO low-order solar AO was the first system to demonstrate that AO can work on granulation and represented an important and timely milestone in making a compelling case for the ATST through the US decadel review process. A solar AO system was installed at the 50 cm Swedish Solar Telescope in 1999 (Scharmer et al., 2000, 2003). Following the successful implementation of these systems other solar AO systems were developed at major solar telescopes (von der Lühe et al., 2003; Scharmer et al., 2003; Keller et al., 2003) some of which are still in operation. All solar AO systems currently in operation are based on the correlating Shack-Hartmann wavefront sensor. Section 8 summarizes the characteristics of these systems.

The NSO low-order AO system was the first to demonstrate adaptive optics on granulation and scientific utility of solar AO. Hence, some early results from this system are shown here, even though, this system has since been surpassed by higher performing systems installed at solar telescopes such as the SST on La Palma, the German VTT on Tenerife, and the DST in New Mexico.

Figure 11 shows observations of a sunspot obtained with the low-order adaptive optics system at the DST. The observations were performed using a CCD camera behind the Universal Birefringent Filter (UBF), which has a passband of about 250 mÅ. The images shown were obtained by coadding 12 individual 1.5 s exposures resulting in a 18 s effective exposure time. The top row images show a narrow-band filtergram and the corresponding line-of-sight magnetic field map obtained by analyzing the circular polarization states. As expected, the bright points surrounding the sunspot seen in the intensity map are co-located with magnetic field elements. The size of these bright points is on the order of the diffraction limit of 0.2” at 630 nm: demonstrating that diffraction limited resolution has been achieved in these long exposure data. Similarly, diffraction limited resolution is achieved in the intensity (bottom left) and velocity (bottom right — bright: upflow; dark: downflow) map, respectively, taken with the UBF tuned to the wings of an Fe I line at 557.6 nm.

In the above examples the high contrast sunspot structure was used as a wavefront sensing target. However as discussed above, the noise of a correlating Shack-Hartmann wavefront sensor increases as the image contrast of the object decreases. Figure 12 shows a narrow-band filtergram of solar granulation recorded with an effective exposure time of 30 s. The AO was locked on a 10” × 10” FOV in the center of the image. These images demonstrate that the diffraction limit is still achieved when the low contrast granulation is used as a wavefront sensor target.

The low-order AO system has produced a number of impressive results. However, the low-order system was not well matched to median seeing conditions at Sacramento Peak. An early site survey determined that the median seeing at Sac Peak is r₀ (500 nm) = 8.7 cm (Brandt et al., 1987). The ATST site survey (Hill et al., 2004, 2006) performed a much more extensive and systematic measurement of the Fried parameter at Sac Peak and determined a lower median r₀ of less than 5 cm for the Sac Peak daytime seeing. The Fried parameter fluctuates on time scales of seconds during the highly variable daytime seeing conditions. This results in large variations in the Strehl ratio, which are mostly due to the wavefront errors in the uncorrected higher order modes (see Figure 13).

The variations in Strehl ratio also make the interpretation of spectral and polarimetric data very difficult. Difference images are often used to produce magnetograms (left circular — right circular polarization) or dopplergrams (blue wing — red wing of a spectral line), examples of which are seen in Figure 11. In general, those images are not taken simultaneously and variations in Strehl between the, e.g., LCP and RCP images result in spurious magnetic signals. For many science applications time sequences of high resolution images or spectra a needed in order to study the highly dynamic solar atmosphere. For these applications consistent and good image quality is needed for all images/spectra in the time sequence. Correcting more spatial modes mitigates this problem to some extent. Provided that seeing fluctuations are not too severe a high order AO system is more likely to provide sustained high Strehl ratios in variable daytime seeing conditions (see Figure 13). This motivated the development of a high order solar AO system — the AO76 system — for the DST, which is discussed in Section 5.

For completeness it should be mentioned that curvature wavefront sensors that have been implemented with great success in night-time AO systems (Roddier, 1988, 1990, 1991; Roddier et al., 1992; Graves et al., 1998) have also been proposed for solar AO. Although some effort has gone into the development of curvature sensing techniques for solar adaptive optics application (Kupke et al., 1994, 1998; Molodij et al., 2002) those efforts have not yet led to practical implementation of this concept, which is likely due to fundamental signal-to-noise problems with this approach when applied to an extended object like solar granulation (Fienup et al., 1998).

The Correlating Shack-Hartmann Wavefront Sensor

The previous section summarized the vital role of the correlating SHWFS for solar adaptive optics. The principle of a correlating SHWFS is quite simple and is shown in Figure 14. The telescope aperture is sampled by an array of lenslets, which in turn forms an array of images of the object. In this case the object is solar granulation and typically 20 × 20 pixels are used to image a field of view of about 10” × 10” or less. The field can not be much larger to avoid averaging of wavefront information, in particular, from high turbulence layers. On the other hand, the FOV has to be large enough to contain a sufficient number of granules for the correlation algorithm to work in a robust manner (von der Lühe, 1983). As will be discussed in Section 6 depending on the severity of turbulence at high altitudes in the atmosphere and the zenith angle a WFS FOV of 10” × 10” can already severely limit the Strehl performance when compared to a point source WFS that is not subject to the directional averaging effect. The main challenge is to compute cross correlations in real-time between subaperture-images and a randomly selected subaperture-image, which serves as reference. The cross correlations are computed using:

$CC(\vec \Delta _i ) = \sum {\sum {I_M (\vec x) \times I_R (\vec x + \vec \Delta _i )} } ,$

((15))

where $I_M (\vec x)$ is the subaperture image, $I_R (\vec x)$ is the reference image, and $\vec \Delta _i $ is the pixel shift between image and reference. The number of shifts between reference and image can be limited to just a few pixels in either direction, assuming the local tilts are small, i.e., the number of sums that have to be computed can be limited to a small number. Typically, computing the cross correlation on a pixel array of 5 × 5 pixels is sufficient, in particular once the control loop is closed. Alternatively the cross correlations can be computed using Fourier Transforms (FT) (von der Lühe et al., 1989). Using the FT approach may be of advantage on some processor platforms and provides the cross correlation for the entire FOV.

Variations of the classical cross-correlation algorithm have been proposed and are used in some solar AO systems (e.g., Shand et al., 1999; Scharmer et al., 2003). Computing the Square Difference function or the Absolute Difference Function Squared may actually have slightly better performance (Löfdahl, 2010). The Absolute Difference Squared algorithm can be efficiently implemented on general purpose microprocessors using multimedia instruction set extensions (Shand et al., 1999).

The full field cross correlations are shown in Figure 14, upper right. By locating the maximum of the cross correlation the displacement of the images with respect to the reference is determined, thereby measuring the local wavefront gradients or tilts. Image displacements are computed to subpixel precision by fitting a parabola to the correlation peak using and interpolating between pixels. Alternatively, a centroiding algorithm, commonly used for tracking point sources, can be used to track the correlation peaks since those closely resemble point sources. A tilt map is shown in the lower right corner of Figure 14. From the tilt vector map an estimate of the wavefront distortions is derived, i.e., the drive signals for the actuators of the deformable mirror using the same modal or zonal reconstruction schemes used for night-time AO systems (Hardy, 1998; Roddier, 1999; Tyson, 2011) are computed. Therefore, the main difference when compared to the night-time, SHWFS is the additional step required to compute the cross correlations, which adds significant computational expense.

Computing the cross correlations for a large number of subapertures requires not only substantial processing but also significant I/O capabilities. At the time when the first solar AO efforts were undertaken these capabilities were just not available. However, with the advances in the development of computer technology of recent years the processing power and I/O bandwidth are now readily available, for the most part as off-the-shelf products. The correlating Shack-Hartmann WFS is also of interest for tracking extended (elongated) “spots” produced by laser guide stars (e.g., Gratadour et al., 2010). It is interesting to note that images of the retina of the human eye with its cone structure look very similar to images of granulation, which in principle would make this wavefront sensor approach also interesting for vision science applications (Williams, 2000; Carroll et al., 2004). However, sufficient illumination of the retina is a problem and, hence, vision science AO systems project laser point sources onto the retina as wavefront sensing targets.

The subaperture size of Figure 14 is 7 cm and diffraction at this small aperture limits the rms contrast of the granulation images to 1–3%, depending on the seeing conditions (Berkefeld and Soltau, 2010). This compares to typically 6–8% when imaged through the full aperture of the DST and an intrinsic contrast of about 13%. The low rms image contrast limits the sensitivity and ability to maintain lock of a correlating Shack-Hartmann wavefront sensor.

Potential alternatives to the correlating SHWFS

In the near future phase diversity (PD) might become an alternative to a correlating SHWFS, which currently appears to be the only viable choice for solar AO. Phase diversity has been used as a post-facto image reconstruction technique for solar high resolution imaging (Löfdahl and Scharmer, 1994). The implementation of real-time PD (Georges III et al., 2007; Warmuth et al., 2008) has made significant progress in recent years. Paxman et al. (2007) summarizes the current state and future prospects of real time PD and specifically compares performance and information content of PD and correlating SHWFS. Currently existing laboratory PD systems achieve 100 Hz frame rates, which is insufficient for solar AO applications. However, a number of speed-up factors may result in update rates for real time PD systems of 450 Hz to 5.4 kHz with a PD WFS sampling of 128 × 128 pixels or 1.6 to 20 kHz with sampling of 64 × 64 pixels and, thus, promises to provide a high performance alternative to the, by now, conventional correlating SHWFS approach.

AO System Implementation

DST AO system: an example

The DST high order AO76 system (Rimmele, 2004a) will be used as an example to describe common implementation aspects of solar AO. Two of these systems are operated at the DST and a copy of this system was operated at the BBSO 60 cm telescope until the removal of the telescope. With the recent commissioning of the 1.6 m NST the AO76 is now (2010) reinstalled at the NST. This high-order solar AO system is able to correct seeing during median seeing conditions at the DST site. The high-order system design uses a parallel processing approach with mostly off-the-shelf components. The problem of computing cross correlations for a large number of images (76 in this case, hence the name AO76) is well suited for parallel processing and the use of DSPs.

Figure 16 shows a picture of the high order AO76 system at the DST (Rimmele, 2004a). Since the DST was retrofitted with AO, integration of the DM and tip/tilt mirror into the main telescope optics was not possible. Instead an AO bench had to be inserted between prime focus and the instruments. Since the DST has two instrument stations, two identical AO benches were installed that feed the diverse instrumentation. Figure 15 shows a comparison of a long exposure (3 s) image of granulation obtained with the AO76 operating (top) and with just tip/tilt compensation (bottom).

Calibration of the AO system is extremely important to obtain optimal performance. Hence calibration tools are an integral part of the AO setup. A motorized aperture wheel placed at prime focus holds field-stops, a resolution target, a calibration pinhole, and a small mirror, which optionally feeds light from a single-mode fiber into the setup. The pinhole serves as artificial object for alignment of actuator and wavefront sensor grids. The pinhole also can be used to flatten the DM and co-align the focal plane of the WFS and prime focus. The laser feed is used to test and align the AO optics and to flatten the DM to very high precision using a interferometer (Ren et al., 2003). The laser interferometer can be placed at or near a instrument detector focal plane. Non-common path optical aberrations can be measured and calibrated out in this way.

A spherical collimator mirror follows prime focus and forms an image of the pupil on the 30 mm tip/tilt mirror. The tip/tilt mirror is mounted at a 45-degree angle and directs the light into the horizontal axis, i.e., onto the AO bench. Two off-axis parabolas (OAP) serve as collimator and camera mirrors, respectively. The collimator forms a 77 mm image of the pupil on the deformable mirror. The camera parabola forms an image of the Sun. This is a very common approach to implementing AO into the optical path between telescope and instruments. A cube beam splitter near the focal plane of OAP2 transmits about 5% of the light to the WFS assembly. The rest of the light is reflected to the science instrumentation.

Separate pupil imaging for tip/tilt and deformable mirrors is implemented to allow a significantly smaller tip/tilt device that achieves high bandwidth. The importance of high bandwidth tip/tilt correction has been pointed out by Conan et al. (1995). Because of the large variance contained in the tip and tilt modes it is extremely important to correct these modes efficiently with high gain and high bandwidth. For example, if a reduction of tip/tilt variance by a factor of ten is achieved, the residual tip/tilt variance is still of the same order as the variance in all the higher modes combined. A small tip/tilt device is also favorable in terms of cost.

The small fraction of light directed to the wavefront sensor path is split further by additional 5% cube beam-splitters to provide light for a video camera for visual performance control and target selection, and for the detector of the stand alone tip/tilt compensation system (correlation tracker (von der Lühe et al., 1989) that is implemented as an option in the AO system. A tip/tilt measurement can also be directly derived from the AO76 wavefront sensor.

Wavefront sensor

The wavefront sensor is a correlating Shack-Hartmann Wavefront Sensor (SHWFS). The SHWFS processes 76 subaperture images of 20 × 20 pixels. The 76 cm telescope aperture is sampled with 10 subapertures across the pupil resulting in d = 7.5 cm per subaperture. It has been demonstrated that a subaperture of about 8 cm is the smallest allowable subaperture size that delivers a theoretical granulation contrast of a few percent (Berkefeld et al., 2010). In comparison the photon noise on the subaperture images for a typical SHWFS detector is of order 0.5%. The wavefront sensor noise is discussed in more detail in Section 6.1.5. The condition r₀ ≤ d results in additional wavefront sensor noise due to anisoplanatism effects within the SHWFS FOV (Section 6.1.6).

The optical design of the correlating SHWFS is also simple. Figure 17 from Richards et al. (2010) shows the main components of a SHWFS assembly. An adjustable square field stop is placed at the WFS focal plane. A lens is used to collimate the field and at the same time image the pupil onto the lenslet array. The lenslet forms the array of subimages. Lenslet arrays of different focal length can be used to vary the size of the WFS FOV. A typical FOV is 10” × 10”. The square field stop is needed to prevent overlap of the subfields in the focal plane of the lenslet array. Inaddition the stop contains a motorized pinhole mask that can be inserted at the WFS entrance in order to calibrate out aberrations internal to the WFS.

The WFS camera might be placed directly into the focal plane of the lenslet array. However, the subimages have to be matched in size and location to a fixed pixel pattern on the WFS detector. This is achieved by adding a re-imaging optical zoom system.

The relatively high read noise of about 60 electrons of the CMOS WFS camera is not an issue for the solar wavefront sensor since the noise is dominated by shot noise. The camera achieves a frame rate of 2500 fps for a 200 × 200 pixels imaging area. The camera is highly configurable. In its nominal configuration the AO camera reads out 76 subapertures, 20 × 20 pixel each. The 76 20 × 20 pixel subaperture images are processed by 40 DSPs. Ten parallel output ports of the camera, one for each cluster of DSPs, allow fast readout. The camera is programmable to accommodate different formats and frame rates and, thus, is usable for a variety of applications, including Multi-Conjugate AO (MCAO). The camera for the AO76 system is only one implementation example that was driven by the available technology at the time the system was developed. With the steady progression of detector development many off-the-shelf WFS camera options have become available, including interfaces to various processing platforms.

Wavefront sensor and reconstructor processor unit

The DST AO76 uses a DSP system to perform all computations for sensing and reconstructing the wavefront. The processing unit (Figure 18) is built from off-the-shelf components based on the ADSP-21160 SHARC DSP. Newer generation DSPs with much higher performance are of course available now. In addition, CPUs and GPUs in the meantime have enough processing power to perform the processing functions at the high update rates required and several solar AO systems currently operating use either a high-end PC (Shand et al., 1999; Scharmer et al., 2000, 2003) or high-end workstations (von der Lühe et al., 2003) to perform this function.

The real time processing functions includes the following (see also Berkefeld, 2007):

Reading the subaperture images into the processors.
Apply flat and dark field corrections to the subimages.
Optionally, an intensity gradient can be removed from each subaperture image using a bilinear fit when the lock-target is, e.g., near the solar limb. This avoids a systematic bias in the shift measurements as was described by von der Lühe (1983).
The cross correlation between its two subapertures and a reference subaperture. The reference subaperture in principle can be picked at random from the set of 76 subapertures. However, apertures near the edge of the pupil that are occasionally vignetted are avoided. Partially illuminated apertures are also avoided.
The maximum of each cross correlation is located to subpixel precision by fitting a parabola around the maximum pixel.
Calibration offsets are removed from the x/y shifts.
Global tilt is computed and removed from the x/y shifts. The global tilt measurements determined in this way are used to drive the tip/tilt mirror.
The x/y shifts are multiplied with the predetermined reconstruction matrix to compute actuator commands. After applying a PI servo algorithm and gain and offset corrections for each actuator the actuator commands are sent to the DM drive electronics.

The host computer serves as user interface and is not involved in any of the real time processing.

Deformable mirror

The 97 actuator deformable mirror system used is a commercially available unit (Ealey and Wellman, 1994) and has been successfully operated as part of the NSO low order AO system. The continuous facesheet, stacked actuator mirror has very localized influence functions with only 10% crosstalk between adjacent actuators. It has been argued that a larger crosstalk may actually be of advantage (Fusco et al., 2006a,b). The DM system has proven to be very robust.

AO76 System Performance and Wavefront Error Budget

Nothing is perfect! AO systems in general provide partial correction only. Residual wavefront errors from various sources prevent the AO system from providing the ideal telescope performance, i.e., the achieved Strehl is less than S = 1. In this context it should be emphasized that no optical system, whether on the ground or in space, provides the theoretically possible performance. The Solar Optical Telescope onboard the HINODE satellite achieves a Strehl of about S = 0.7 (Suematsu et al., 2007). How closely can ground-based solar telescopes with AO match this kind of performance? This question can be answered by developing a budget of the residual wavefront errors of the solar AO.

Predicted performance based on error budget

The development of an error budget for solar AO is exactly the same as for a night-time AO system with the exception of the noise sources related to the wavefront sensor. Hence the solar AO specific wavefront sensor error budget terms will be discussed in some detail while other contributors will be briefly summarized only since those are discussed at length in textbooks (see, e.g., Hardy, 1998).

The following sources of residual wavefront errors have to be considered:

Wavefront fitting error

The fitting error term is due to the limited number of actuators, which leads to an imperfect fit of the incoming wavefront by the DM and depends on the ration $\frac{d} {{r_0 }} $:

$\sigma _F^2 = a\left( {\frac{d} {{r_0 }}} \right)^{5/3} . $

((16))

The coefficient a is DM specific. For a continuous deformable mirror a = 0.28.

Aliasing error

The aliasing error term is due to the limited spatial sampling of the wavefront by the wavefront sensor. High-order modes can alias into low-order modes and, thus, contribute noise to those modes. The aliasing term is typically of order 30% of the fitting error variance:

$\sigma _F^2 = 0.08\left( {\frac{d} {{r_0 }}} \right)^{5/3} . $

((17))

Angular anisoplanatism error

A conventional adaptive optics system with the DM typically conjugated to the pupil plane provides optimal correction in one direction on the sky only. The wavefront sensor is measuring the wavefront aberrations typically for the center of the extended FOV. For field points offset from the center the light waves travel from different field directions and, hence, sample different turbulent volumes of the atmosphere. For that reason the wavefront sensor measurement and, thus, the AO correction becomes increasingly invalid as the separation from the lock center increases. For an extended object such as the Sun this effect can be and, in many cases, is a severe limitation. The error that is introduced when measuring the wavefront at an off-axis point can be derived from the phase structure function. For the condition D ≫ r₀ the anisoplanatic error variance at angular distance θ can be expressed as (see Hardy, 1998; Quirrenbach, 2002):

$\left\langle {\sigma _\theta ^2 } \right\rangle = 2.914k^2 (\sec z)^{8/3} \theta ^{5/3} \int {C_N^2 (h)h^{5/3} dh} .$

((18))

The condition D k r₀ is typically valid for large aperture astronomical telescopes but may not hold for small aperture solar telescopes during excellent seeing conditions.

The isoplantic angle θ₀ can be defined as the angular distance for which the anisoplanatic error variance is $\sigma (\theta )^2 \leqslant 1rad^2 $. A wavefront that has a variance ≤ 1 rad² is sometimes referred to as “flat”. With this definition the isoplanatic angle θ₀ can be expressed as (see Hardy, 1998):

$\theta _0 = \left[ {2.914k^2 (\sec \gamma )^{8/3} \int {C_N^2 (h)h^{5/3} dh} } \right]^{ - 3/5} .$

((19))

The anisoplanatism error then becomes simply:

$\sigma _\theta ^2 = \left( {\frac{\theta } {{\theta _0 }}} \right)^{5/3} . $

((20))

The wavelength dependence of θ₀ again derives from the wavelength dependence of r₀ and is $\theta _0 \propto \lambda ^{\frac{6} {5}} $, i.e., the isoplanatic angle increases significantly towards infrared wavelengths.

With the above definition of the isoplanatic angle the residual wavefront variance amounts to ∼ 1 rad² at an angular separation of θ₀, corresponding to a Strehl ratio of S = 0.37. The isoplanatic angle can be quite small in this case if $\frac{D} {{r_0 }} $ for the high altitude turbulence is large. For current small aperture solar telescopes, however, $\frac{D} {{r_0 }} $ (for the upper atmosphere) at a good site can be of order one. In this case the aberrations contributed by the upper atmosphere are dominated by low orders, which de-correlate less rapidly than the high order modes as we move away from the lock center. Similarly, if only a limited number of modes is corrected by the AO system the AO performance, in a relative sense, deteriorates less rapidly with angular separation because of the slower de-correlation of low order modes. Normalized modal correlation functions can be defined to quantify the de-correlation as a function of angular separation for individual modes, e.g., Zernikes (Valley and Wandzura, 1979; Fusco and Conan, 2004). If the correlation for a given mode falls below 0.5, adaptive correction for that mode degrades the phase as much as correcting it. Depending on the application and, in particular, the FOV requirements it may make sense to restrict the number of corrected modes in order to optimize correction over a larger FOV. The extreme case is tip/tilt correction only. The isoplanatic angle for tip/tilt, sometimes also referred to as isokinetic angle (Beckers, 1993a), can be many tens of arc seconds.

The size of the isoplanatic patch is determined by a height weighted (h^5/3) integral over Cn(h)². If strong turbulence is located high in the atmosphere the isoplanatic patch can become quite small as $\frac{D} {{r_0 }} $ of the upper atmosphere becomes large. For example, at the DST site the jet stream occasionally moves far enough south and above the DST causing severe high altitude seeing. Although a Cn²(h) meter is not installed at the DST the presence of high altitude seeing is usually quite easy to identify by assessing the real time video image and comparing the visual seeing to the readings of the Seykora seeing meter (Seykora, 1993). This seeing meter measures scintillation of an extended object (the solar disk) and, hence, provides a measure of the turbulence heavily weighted towards seeing layers close to the ground (Beckers, 1993b). Conditions where the video image indicates bad seeing but at the same time the Seykora meter reading indicates relatively good seeing are a clear indication of strong high altitude seeing.

In these conditions the dominant seeing layer produced by the jet stream shear layer is at about h = 10 km and the isoplanatic patch is only of order a few arcsec. This can be seen in Figure 19, left, which shows a long exposure image of solar granulation with the AO locked on the center of the field. The optimally corrected FOV is of order 5–10”, while the surrounding FOV is significantly blurred. The high zenith angle γ under which solar observations are generally performed to take advantage of the best seeing in the early morning hours adversely affects the isoplanatic patch size. Fortunately, these conditions are the exception and the jet stream usually passes north of the DST site (a reason for selecting sites in the south). In this case the seeing is generally dominated by ground layer turbulence caused by heating of the ground layer and the majority of the turbulence is located close to the telescope aperture. The isoplanatic patch for a small aperture telescope as the DST appears to be quite large under these conditions, which is shown in Figure 19, right.

This somewhat qualitative picture is based on observing experience and might be considered anecdotal. Nevertheless, this experience based knowledge can be helpful when trying to predict observing conditions in order to optimize observing programs ahead of time. More sophisticated prediction of seeing conditions use detailed and comprehensive atmospheric modeling (Vernin et al., 1998; Masciadri et al., 2001; Cherubini et al., 2008a,b, 2009).

The limiting effect of anisoplanatism can be pursued in more depth and more quantitatively with simulations that consider different turbulence profiles as well as the effect of aperture size (Marino and Rimmele, 2011). Results for current small aperture solar telescopes can be related to the observations shown in Figure 19.

Two atmospheric turbulence profiles are considered by Marino and Rimmele (2011) and are shown in Table 1. The first turbulence profile used represents realistic good, daytime conditions at the ATST site on Haleakala (see Rimmele et al., 2006c). The second model is built from measurements above Mt. Graham and Mt. Hopkins in Arizona (Milton et al., 2003; McKenna et al., 2003).

The Haleakala profile represents a case of relatively weak turbulence at high altitude with just 5% of the power above 6 km. If an total r₀ of 10 cm is assumed this profile produces a layer r0 at an altitude of 13.5 km of 1.5 m. The Mt. Graham profile is measured at night-time, i.e., the represented case has a much stronger higher atmosphere with 40% of the power above 6 km.

The intention here is not to compare sites but to illustrate the impact of the Cn² profile on the solar AO Strehl ratio and the isoplanatic angle. For each turbulence profile two seeing cases are modeled by setting the overall r₀ to 10 cm (good seeing) and 20 cm (excellent seeing), respectively.

In order to model an existing, small aperture solar telescope Marino and Rimmele (2011) (virtually) place the DST and its high order AO system on Haleakala and the AO76 performance in terms of Strehl is modeled as a function of field angle and with zenith angle and number of corrected modes as parameters. The adaptive optics performance is modeled using a large number of phase screens that obey Kolmogorov statistics at each of the turbulence layers. The fractional distribution of turbulent power and the corresponding layer r0 are shown in Table 1. The turbulence screens are projected onto the extended wavefront sensor with a FOV of 10” × 10”. This ensures that anisoplanatic effects are accurately taken into account also in modeling the extended field wavefront sensor measurement (see Section 6.1.6). Drive signals for the DM, which is modeled using realistic influence functions, are derived from the extended WFS FOV. The model assumes correction of 80 KL modes and also includes a realistic implementation of the servo loop.

Results are shown in Figures 20 and 21. Several interesting points can be made. The Strehl ratio at the lock point drops significantly for high zenith angle observations. Whereas the Strehl at the lock-point would be independent of zenith angle (r₀ is assumed to be the same for each zenith distance in this model calculation) if a point-source WFS is used, the extended source WFS averages wavefront information from many different sky directions. In the extreme case of a very large WFS FOV a ground-layer AO is realized, i.e., the upper atmospheric turbulence is not corrected at all (see Section 9.3). This effect is more pronounced at high zenith angles and worse high altitude seeing due to the geometric projection of the turbulent phase screens. In addition to the high airmass solar AO therefore faces this additional disadvantage in achieving high Strehl in the early morning hours (zenith angle > 70°). Where a WFS FOV of 10” × 10”v” may be adequate for r₀ of 20 cm Figures 20 and, in particular, Figure 21 indicate that for worse seeing conditions a smaller WFS FOV would be of advantage if high Strehl is the objective. For excellent seeing, reasonably low zenith angle and low altitude turbulence the isoplanatic patch size can be quite large. For the most ideal and, thus, rare case (Figure 20, r₀ = 20 cm, vertical pointing) the Strehl dropps to 0.37 at an off-axis angle of about 30”; the isoplanatic patch size is 60”. Reasonably high Strehl is observed over an even larger FOV. It is also obvious that under less ideal conditions the isoplanatic patch size rapidly becomes smaller. Substantial high altitude turbulence leads to significantly reduced Strehl performance and a small isoplanatic patch as can be seen in Figure 21, right. A site with low high altitude turbulence is clearly preferable from the solar AO point of view and this was an important factor in the selection of the ATST site.

The equivalent and very important simulation results for future large aperture telescopes will be presented in Section 9 where it is demonstrated that anisoplanatism is even more of a challenge.

Bandwidth error

The bandwidth error is due to the limited correcting bandwidth of the AO system. The bandwidth error is proportional to the ratio between the frequency of the turbulence, quantified by the Greenwood frequency f_G (Greenwood, 1977), and the bandwidth f_S of the AO system (e.g., Hardy, 1998):

$\sigma _{BW}^2 = \left( {\frac{{f_G }} {{f_S }}} \right)^{5/3} . $

((21))

In the special case of a single turbulent layer moving at a speed v, the Greenwood frequency f_G can be written as (Hardy, 1998; Tyson, 2011):

$f_G = 0.427\frac{v} {{r_0 }}. $

((22))

As discussed in Section 2.3, closed loop bandwidths in excess of 100 Hz are required for solar AO systems.

Closed loop bandwidth should not be confused with sampling rate and using a meaningful definition of closed loop bandwidth is similarly important (Madec, 1999). A reasonable and conservative measure of closed-loop bandwidth is given by the 0 dB error rejection crossover frequency, which for the DST AO76 system is about 120 Hz. As pointed out in Madec (1999) it is of critical importance to minimize compute and other latencies in order to obtain high closed-loop bandwidth. Equation 21 provides an estimate of the bandwidth error. A more accurate value for $\sigma _{BW}^2 $ can be computed if the closed loop error rejection transfer function can be measured or modeled and the PSD of the wavefront aberrations is known.

Often the incoming wavefront is decomposed into the well known Zernike modes (Noll, 1976). The Greenwood frequency depends on the radial mode number in the following way:

$f_G (n) \propto 0.3(n + 1)v/D,$

((23))

where n is the radial degree of the mode, v is the wind speed, and D is the telescope aperture. This modal dependence of f_G can be inferred from Figure 7, which shows modal PSDs for two Zernike modes. The Greenwood frequency for Z4 (astigmatism) is of order 5 Hz, while f_G for Z21 is about 20 Hz. This means that the higher the order of correction, the more bandwidth will be required. Therefore, low-order systems require less bandwidth. Figure 7 also plots the corrected or residual wavefront error PSD, from which the residual wavefront error as a function of mode can be computed. This information can in principle be used to derive or optimize mode dependent servo gain factors as is done for some night-time AO systems (Gendron and Léna, 1994, 1995). However, because of the low wavefront sensor noise of the solar correlating SHWFS the advantage of setting individual signal-to-noise dependent gains for the modes may not be as convincing as it is for a photon starved night-time WFS.

Wavefront sensor measuring error

The WFS noise for a correlating Shack-Hartmann WFS has been studied by Michau et al. (1993, 2006). Michau et al. (1993) derived the following equation for the variance of the image position measurement by tracking the center-of-gravity of the cross-correlation peak:

$\sigma _x^2 = \frac{{5m^2 \sigma _b^2 }} {{4n_r^2 \sigma _i^2 }}(waves^2 ), $

((24))

where $\sigma _b^2 $ is the background noise variance, $n_r^2 $ is the subimage size in pixels (typically 16 × 16 pixels), and $n_r^2 \sigma _i^2 $ is the total “energy” in the image, i.e., σ_i/I_mean is the rms image contrast. Nyquist sampling of the image is assumed. A quantitative analysis of the wavefront sensor noise of a correlating Shack.Hartmann wavefront sensor was given by Poyneer (2003). Equation 24 indicates that the WFS S/N ratio is fundamentally given by the ratio of background noise to image contrast. It is of advantage to use more pixels per subaperture in order to reduce the WFS noise (Berkefeld, 2007).

It is important to realize that in the case of a solar wavefront sensor a large number of photons are available in the wavefront sensor path since the WFS can work with broad-band light (interference filters that can be several 100 A wide or simple color glass can be used). In praxis the number of photons that can be collected by the correlating SH wavefront sensor is limited by the well depth of the detector used. A typical well depth of a CCD is of order 50 ke-. This means that the shot noise completely dominates the background noise even if relatively noisy CCD detectors or CMOS devices with read-noise levels of order 50 e- are used. The low noise (∼ 1e-) wavefront sensor detectors needed for tracking faint guide stars in the night sky are not needed for the solar application. However, because of the extended FOV (∼ 20 × 20 pixels/subaperture) the correlating SHWFS requires large format detectors and in order to achieve the required high bandwidths, the frame rates have to be very high (> 2 kHz). This means that detectors for the solar wavefront sensor typically need to have some sort of parallel readout. The signal to noise ratio might be improved by collecting more photons, which has to be achieved within an update rate time of typically 400 μs. A deep well detector or averaging multiple exposures of a extremely fast framing camera could potentially be used to achieve this and, thus, potentially allow smaller subapertures.

It should be noted that the wavefront sensor noise is object dependent in the sense that high signal to noise ratios can be achieved for high contrast objects, such as sunspots, whereas the S/N ratio for tracking the low contrast granulation is much lower. This is true, in particular, near the solar limb where the granulation contrast is even lower. Bright faculae near the limb can be used to lock the correlating SHWFS. The contrast of granulation imaged through a subaperture drops as the size of the subaperture becomes smaller. Granulation has a typical spatial scale of about 1”. This means that granulation will be “smeared out” by diffraction if a subaperture size much smaller than 10 cm is used. There is a “limiting image contrast” below which a correlating SHWFS will not work anymore. According to practical experience with existing systems the limiting contrast is between 1.5–2%. The limiting contrast can be compared to the “limiting magnitude” that exists for the photon starved night-time AO. Because of the dependence of the wavefront sensor noise on image contrast and the limiting contrast the seeing at the site is extremely important for the performance of a solar AO systems. Matching a small Fried parameter at a bad site with a smaller and smaller subaperture size is not possible if granulation is to be used as tracking target.

One could consider substantially increasing the FOV of the subaperture images in order to be able to track on large-scale intensity structures on the Sun. It has been demonstrated in the context of active optics wavefront sensing for large solar telescopes that a larger FOV can provide more robust tracking performance of the cross correlation algorithm (Owner-Petersen et al., 1993). However, in this case the wavefront sensor averages over many isoplanatic patches and essentially only the near ground turbulence can be corrected in this way. Although Ground-Layer AO (GLAO) may be an attractive option for some solar applications (Rimmele, 2000; Rimmele et al., 2010c) the general conclusion is that scientific productivity of solar AO depends critically on the site performance.

Michau (2002) argued that Equation 24 overestimates the noise by a factor of two. Cain (2004) studied an image projection approach to the extended source wavefront sensor problem and found close agreement with the noise estimates from Equation 24 and his own wavefront sensor noise estimates. Figure 22 shows the subaperture tilt noise estimates based on Equation 24 as a function of number of photons collected by the wavefront sensor camera. Nyquist sampling (0.5”/pix) and 20 pixels across the subaperture are assumed. The number of photons collected during an exposure is only limited by the well depth of the CCD or CMOS device used. For example, the DST AO systems wavefront sensor camera uses a CMOS camera with well depth of 70 ke-, i.e., the shot noise is 264 e- compared to the camera read noise of about 50 e-, leading to a total noise of 268 e-. The different curves in Figure 22 are for subaperture contrasts of 0.015 (granulation, r₀ = 5 cm), 0.025 (granulation, r₀ > 10 cm), 0.05 (pore, r₀ = 7 cm), and 0.1 (sunspot umbra, r₀ = 7 cm) and, thus, give the range of typical observing targets and observing conditions considered in developing error budgets. It is obvious from Figure 22 that a detector with deep wells is desired. However, exceeding a well depth of about 40 ke- results in insignificant gains in performance.

The DST AO system was used to verify the noise levels predicted by Equation 24. Openloop subaperture tilt PSDs with a sampling rate of 2500 Hz were collected. The example PSD of Figure 23 clearly shows a flat noise tail that, assuming white noise, can be used to directly determine the noise of the subaperture tilt measurements. The following subaperture tilt noise levels for different observing targets and seeing conditions were obtained:

Sunspot, median to good seeing conditions: 5–8 nm
Granulation, good to excellent seeing conditions: 15–25 nm.

The DST AO camera is operated at about 75% of its well depth or 52 ke- for granulation. If a sunspot is tracked the number of photons collected per exposure can be as low as 30 ke-. Comparing the measurements with the predicted noise levels one finds that Equation 24 seems to slightly overestimate the WFS noise. The WFS noise is propagated onto the actuator commands by the reconstruction process. The details of this noise propagation are again discussed in textbooks (Hardy, 1998; Roddier, 1999; Tyson, 2011). If B is the reconstruction matrix that converts wavefront sensor slope measurements into actuator commands, then the mean wavefront error over the aperture after the reconstruction is (Southwell, 1980):

$\sigma _{wavefront}^2 = \frac{1} {N}trace(BB^t )\sigma _{wfs}^2 . $

((25))

The simplifying assumption has been made that the noise covariance matrix is diagonal, i.e., the noise is uncorrelated. The important point is that the error propagation coefficient $\frac{1} {N} $ trace(BB^t) is of order one or less.

Wavefront sensor anisoplanatism noise

The wavefront sensor noise due to anisoplanatism within the extended FOV of the SHWFS can be an important term that highly depends on seeing conditions and the size of the WFS FOV. Equation 24 was developed with the assumption that the correlated reference and live images are shifted copies of each other. However, reference and live image are taken at different times or from different subapertures. Distortion of the images due to anisoplanatism within the extended subimage is not considered. The subimage size of the reference and live image of the solar feature is typically between 5” × 5” to 10” × 10”. Depending on the seeing conditions and wavelength larger FOVs may contain several isoplanatic patches, which will compromise Strehl due to the already discussed field averaging effect. If the highest possible Strehl at or near the lock point is the objective a smaller WFS FOV is needed. Unfortunately, the field size can not be smaller than about 5” × 5” since a minimum number of granules are required within the FOV to obtain a distinct correlation peak that can provide an accurate tracking signal (von der Lühe, 1983).

It has been pointed out by Robert et al. (2006) and Védrenne et al. (2007) that anisoplanatism effects result in an additional noise term from the WFS. This noise term originates from a broadening of the PSF, which is an average over many different directions in the sky. Equivalently the cross-correlation function is broadened, which lead to a less precise determination of the maximum position. Scintillation effects and cross-coupling between anisoplanatic and scintillation effects may produce yet another WFS noise terms of significant magnitude. Wöger and Rimmele (2009) performed a study to evaluate the effects of phase aberrations and scintillation within a subaperture of a correlating Shack-Hartmann wavefront sensor and compared the contribution of these effects to the wavefront sensor noise for both isoplanatic and anisoplanatic imaging. Realistic representations of the object, i.e., solar structure, and a close approximatation for a typical $C_n^2 (h)$-profile were used in these simulations. Wöger and Rimmele (2009) found that anisoplanatism in wavefront sensor subapertures can increase the measurement error of Equation 24 by 50% or more depending on the specifics of the WFS, such as pixel sampling and FOV. They also found that the effect of scintillation can be neglected in the solar AO case. The anisoplanatism can only be avoided by making the WFS FOV small enough to only cover one isoplanatic patch, which for practical purposes is not always possible.

Non-common path error

The WFS and the science instrument in most cases do not share the entire optical path. In the simplest case the only difference is a beamsplitter. The science camera might be placed in the focal plane produced by the beam passing through the beamsplitter while the WFS is placed in the focal plan reflected off the beamsplitter. The aberrations introduced by the beamsplitter are different for transmitted and reflected beams and, in this example, the AO will correct what is introduced into the reflected beam and, in turn, add the aberration to the transmitted beam. In general, with more complex science instruments many more optical elements are non-common. Since the instrument and WFS optical paths in the laboratory style environment typical for solar telescopes are through air, bench seeing adds to the non-common path errors. In a well controlled lab environment local seeing can add 0.5–1 nm of wavefront error per meter optical path lengths (Biérent et al., 2008). Optical non-common path errors can be calibrated out as described in Section 5.2.

Tip/tilt error

Residual tip/tilt errors can severely lower the Strehl and degrade resolution. Residual image motion broadens the otherwise diffraction limited core of the PSF. Details can again be found in textbooks (Hardy, 1998). A separate tip/tilt error budget that considers most if not all terms discussed in this section should be developed, in particular, if a a separate tip/tilt system (e.g., correlation tracker (CT)) is used. The WFS noise of the CT sensor, the bandwidth and other terms may be different for the tip/tilt system.

Total error

Assuming statistical independence, which is usually a valid assumption in this case, the overall residual wavefront error can be computed as the Root-Sum-Squared (RSS) of the individual error terms:

$\sigma _{tot}^2 = \sigma _{BW}^2 + \sigma _\theta ^2 + \sigma _{fit}^2 + \sigma _{aliasing}^2 + \sigma _{wfs}^2 + \sigma _{wfs_a niso}^2 + \sigma _{ncp}^2 + \sigma _{T/T}^2 + \sigma _{other}^2 ,$

((26))

$\sigma _{other}^2 $ may, for example, include optical and seeing aberrations within the instrument, if not already accounted for in the non-common path term.

Obviously the goal is to minimize the residual wavefront variance. This is a difficult task, in particular, for visible AO systems, which most solar AO systems are. At a wavelength of 500 nm the total allowable error $\sigma _{tot}^2 $ is less than 50 nm if a Strehl of S = 0.7 is to be achieved. A Strehl of 0.7 in some textbooks is referred to a diffraction limited performance.

A careful error budget analysis during the design phase and careful attention to each of the error budget terms while building the AO system followed by a detailed evaluation of the actual performance are essential steps in ensuring that optimal performance is achieved. During the design a general goal of systems engineering is to produce a well balanced error budget, i.e., all terms should be of about equal magnitude. It does not pay to devote significant effort and expense to reduce one particular error term while other terms remain significantly larger.

Measured performance of AO

Figures of merit for AO system performance include the achieved Strehl ratio and the residual wavefront error. However, it is most desirable to have knowledge of the AO corrected PSF because the most detailed AO performance analysis and optimization of the system can be performed. Furthermore, if the PSF is known, image reconstruction techniques can be deployed to further improve the AO corrected images. Solar AO is at a distinct disadvantage here because estimation of the PSF is not straightforward. For night-time AO the observed object is often a point source or a point source can be found nearby. The PSF can be estimated directly from the corrected image of the point source (Roberts Jr et al., 2004). For solar images one could deploy post-facto PSF estimation techniques such as phase diversity. However, for estimating the long exposure PSF provided by the AO system as a function of r0 it is convenient and efficient to use the information the AO system itself can provide. Some post-facto reconstruction techniques, such as speckle interferometry (Wöger et al., 2008) that work with short exposure imaging also require this AO telemetry information.

Long exposure PSF estimation from AO telemetry

This section explains in some detail the shape of the typical AO corrected long exposure PSF already shown in Section 2. In particular, it will become clear why the PSF has two components — a diffraction limited core and a seeing limited halo. In order to derive an estimate for the solar AO corrected PSF (or equivalently the OTF) the AO structure function needs to be determined (Marino, 2007; Marino and Rimmele, 2010). The phase structure function produced by isotropic and uniform Kolmogorov turbulence depends on the separation parameter ρ only. This is no longer true once AO correction has been applied and the phase structure function now depends on separation $\vec \rho $ and position $\vec x$ in the pupil plane: $D_{\phi _\varepsilon } (\vec x,\vec \rho )$. It should be noted that the fact that the residual phase structure function no longer can be described with Kolmogorov statistics complicates post-facto image reconstruction of AO corrected images. Speckle interferometry algorithms have to be adapted to account for the field dependent AO correction (Wöger et al., 2008). Phase-diversity and MOMFBD, in principle, do not rely on atmospheric model information. However, as pointed out by Scharmer et al. (2010) in order to correct for stray-light from high order atmospheric aberrations that remain uncompensated by these methods, statistical estimation of the average effect of high order modes is required, which again relies on Kolmogorov statistics.

The AO system corrects a limited number of aberration modes. In the case of AO76 the system is typically able to correct between 65–80 Karhunen-Loève (KL) or Zernike modes. Higher order modes remain uncorrected. Hence, the AO system acts as an imperfect high pass filter. The corrected modes are not corrected perfectly, as was discussed in Section 6, and a residual variance remains for each corrected mode. The magnitude of the residual variance is mode dependent.

Closely following Veran et al. (1997), Marino (2007), and Marino and Rimmele (2010), the residual phase after correction can then be expressed as:

((27))

where $\phi _{\varepsilon \parallel } $ is the residual phase of the corrected modes and $\phi _{atm \bot } $ for the uncorrected, respectively. The phase structure function can then be written as:

$\bar D_{\phi _\varepsilon } (\vec \rho ) \approx \bar D_{\phi _{\varepsilon \parallel } } (\vec \rho ) + \bar D_{\phi _{atm \bot } } (\vec \rho ),$

((28))

where cross terms have been assumed to be negligible (Veran et al., 1997). $D_{\phi _{atm \bot } } $ is a function of $\vec \rho $ only since the uncorrected atmospheric phase errors in a statistical sense (long exposure) are homogeneous and isotropic. Hence, $D_{\phi _{atm \bot } } $ can be placed in front of the integral in Equation 11 resulting in a long exposure OTF that can be written as the product of three independent terms:

$OTF_{ao} (\vec \rho /\lambda ) = OTF_{\varphi \varepsilon \parallel } (\vec \rho /\lambda )OTF_{\varphi \varepsilon \bot } (\vec \rho /\lambda )OTF_{tel} (\vec \rho /\lambda ),$

((29))

where

$OTF_{\varphi \varepsilon \parallel } (\vec \rho /\lambda )\exp \left[ { - \frac{1} {2}D_{\phi \varepsilon \parallel } (\vec \rho )} \right] $

((30))

where

$OTF_{\varphi \varepsilon \bot } (\vec \rho /\lambda )\exp \left[ { - \frac{1} {2}D_{\phi atm \bot } (\vec \rho )} \right]. $

((31))

$OTF_{\varphi \varepsilon \parallel } $ is the contribution from the residual variance of the corrected modes and can be derived from the residual wavefront errors measured by the WFS with the AO in closed loop. $OTF_{\varphi \varepsilon \bot } $ derives from the high order modes that the AO system cannot correct. OTF_tel is simply the diffraction limited telescope OTF. $OTF_{\varphi \varepsilon \bot } $ is the main contributor to the seeing halo of the PSF, while the core of the PSF is formed by the other two terms.

$\phi _{\varepsilon \parallel } $ can be extracted from the WFS measurements after accounting for various noise terms, such as the WFS noise described above and aliasing noise (Herrmann, 1981; Dai, 1996). A detailed description of this process and the calibration procedures involved is given by Veran et al. (1997) and Marino (2007).

The residual wavefront variance after correction $\phi _{\varepsilon \parallel } $ can be expressed as:

$\begin{gathered} \phi _{\varepsilon \parallel } (\vec x,t) = \sum\limits_{i = 1}^N {[a_i (t) - k_i (t)]K_i (\vec x)} \hfill \\ = \sum\limits_{i = 1}^N {\varepsilon _i (t)K_i (\vec x)} , \hfill \\ \end{gathered} $

((32))

where a_i are the coefficients KL modes K_i of the uncorrected phase, k_i are the KL coefficients of the applied correction, and the ∈_i are the noise free residual KL coefficients. The phase structure function of the residual corrected phase becomes:

$D_{\phi _{\varepsilon \parallel } } (\vec x,\vec \rho ) = \left\langle {\left| {\phi _{\varepsilon \parallel } (\vec x,t) - \phi _{\varepsilon \parallel } (\vec x + \vec \rho ,t)} \right|^2 } \right\rangle $

((33))

and using Equation (32):

$D_{\phi _{\varepsilon \parallel } } (\vec x,\vec \rho ) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left\langle {\varepsilon _i \varepsilon _j } \right\rangle [K_i (\vec x + \vec \rho )][K_j (\vec x) - K_j (\vec x + \vec \rho )]} } .$

((34))

Due to the isotropy assumption mentioned above computing the mean phase structure function of the residuals averaged over the pupil is sufficient in this case:

$\bar D_{\phi _{\varepsilon \parallel } } (\vec \rho ) = \frac{{\int {P(\vec x)P(\vec x + \vec \rho )D_{\phi _{\varepsilon \parallel } } (\vec x,\vec \rho )d\vec x} }} {{\int {P(\vec x)P(\vec x + \vec \rho )d\vec x} }}, $

((35))

where P is the pupil function. Combining Equations (34) and (35) leads to:

$\bar D_{\phi _{\varepsilon \parallel } } (\vec \rho ) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left\langle {\varepsilon _i \varepsilon _j } \right\rangle U_{ij} (\vec \rho )} } ,$

((36))

where the U_ij functions are defined as:

$U_{ij} (\vec \rho ) = \frac{{\int {P(\vec x)P(\vec x + \vec \rho )} [K_i (\vec x + \vec \rho )][K_j (\vec x) - K_j (\vec x + \vec \rho )]d\vec x}} {{\int {P(\vec x)P(\vec x + \vec \rho )} d\vec x}}. $

((37))

The important conclusion is that the information, which the AO telemetry has to deliver is the covariance of the noise free residual KL coefficients: 〈∈_i∈_j〉. The U_ij functions can be pre-computed and stored. The computation of the covariance for the exposure interval can be performed within the AO system, which reduces the telemetry data rates and storage requirements significantly. The computation of the covariance is typically initiated and terminated by an external trigger signal from the science camera.

The term $\phi _{atm \bot } $ in Equation 31 can be derived from the Kolmogorov model (Kolmogorov, 1941, 1991) if the Fried parameter r₀ is known. The residual uncorrected phase after correction of N KL modes can be expressed in terms of KL modes:

$\phi _{atm \bot } (\vec x,t) = \sum\limits_{i = N + 1}^{N_\infty } {a_i (t)K_i (\vec x)} .$

((38))

Using the definition of the phase structure function the residual uncorrected phase structure function can be expressed as:

$\begin{gathered} D_{\phi \bot } (\vec x,\vec \rho ) = \left\langle {\left| {\phi _{atm \bot } (\vec x,t) - \phi _{atm \bot } (\vec x + \vec \rho ,t)} \right|^2 } \right\rangle \hfill \\ = \sum\limits_{i,j = N + 1}^{N_\infty } {\left\langle {a_i a_j [K_i (\vec x) - K_i (\vec x + \vec \rho )][K_j (\vec x) - K_j (\vec x + \vec \rho )]} \right\rangle } . \hfill \\ \end{gathered} $

((39))

The covariances 〈a_ia_j〉 for Zernike modes was given by Noll (1976) and scales with (D/r₀)^5/3, where D is the aperture size of the telescope. A similar scaling law for the KL covariances can be derived. Only r₀ needs to be determined, which can be estimated from the actuator commands. The modal variance of the DM actuator commands is compared in a least squares sense to the modal variance predicted by the Kolmogorov model in order to derive an estimation of the Fried parameter (r₀).

Figure 24 summarizes the major steps of the PSF estimation method.

Measured AO system performance

The PSF estimation method described in the previous section can be used to measure and optimize the performance of an AO system with the caveat that non-common path errors are not detected. The performance is estimated at the WFS focal plane. Since the PSF is measured indirectly by this method it is desirable to verify its results in some independent fashion. This was done by Marino (2007) and Marino and Rimmele (2010) who modified the AO76 at the DST to enable the system to lock on bright stars (e.g., Sirius), albeit with significantly reduced AO performance due to S/N issues. Figure 25, from Marino and Rimmele (2010), shows several comparisons between estimated PSF and the actual PSF (the Sirius image). In spite of the low Strehl achieved with the solar AO running in night-time mode the agreement between actual and estimated PSF is excellent. Significant deviation is visible only for the images with lowest Strehl and tends to affect the residual seeing halo more than the core of the PSF.

With some confidence the PSF estimation can now be applied to solar AO. Figure 26 plots Strehl ratio versus the Fried parameter r₀. Both Strehl ratio and r₀ were estimated from the AO telemetry data as part of the PSF estimation algorithm. A Strehl of S = 0.9 or greater achieved for excellent seeing conditions of r₀ = 20 cm. A Strehl of S = 0.3 is achieved for an r₀ of about 4 cm.

The solid line follows the Strehl ratio expected from the wavefront error variances that include the most significant AO error sources: fitting error, aliasing error, bandwidth error, and wavefront sensor noise error. The agreement between the model expectation and the actual performance is remarkably good, indicating that the error budget of the AO76 system is in general well understood and that close to theoretical performance is achieved.

The second solid line traces a branch where apparently non-optimal AO performance was achieved. This branch can be modeled by adding a constant noise term. The source of this additional noise term is not yet well understood. Possible candidates are misalignment due to pupil wobble, which the DST is prone to, or wavefront sensor noise due to strong anisoplanatism (Wöger and Rimmele, 2009).

Reconstruction of solar imagery using estimated long exposure PSFs will be discussed in Section 7. It should be mentioned that in spite of the encouraging agreement shown in Figure 25 the contrast of reconstructed solar images appears to be consistently too low when compared to model predictions. Entering this ongoing scientific debate would be beyond the scope of this article. Stray-light from uncorrected high order modes (Scharmer et al., 2010) or other stray-light sources is one possible explanation for this discrepancy.

The Case for Post-Facto Processing

Short exposure

Adaptive optics provides only partial correction and the correction becomes increasingly worse when science observations are performed at short wavelengths (e.g., g-band, Ca II K). In addition, for conventional AO the correction is optimal only within the isoplanatic patch and deteriorates as one moves away from the AO lock point. Post-processing can correct for residual phase aberrations and, in principle, restore the correct amplitudes. Furthermore, post processing can provide uniform image quality across the entire FOV. It is beyond the scope of this article to review the various techniques used to reconstruct short exposure AO images. The reader is referred to Löfdahl et al. (2007) for an in-depth discussion of post-facto reconstruction techniques used in solar astronomy. In addition, individual methods are discussed by: speckle interferometry (Wöger et al., 2008; Wöger and von der Lühe, 2008), phase-diversity and phase-diverse speckle (Löfdahl and Scharmer, 1994; Seldin and Paxman, 1994; Paxman et al., 1996; Seldin et al., 1999; Löfdahl et al., 2007; Valenzuela et al., 2010), multi-frame-blind-deconvolution (MFBD) (van Kampen and Paxman, 1998; Löfdahl, 2007; Scharmer et al., 2010), and Multi-Object-Multi-Frame-Blind Deconvolution (MOMFBD) (van Noort et al., 2005).

The power of these techniques, in particular when combined with AO, is exemplified by just a few images and movies. Figure 27 shows a speckle reconstructed (Wöger and von der Lühe, 2008) time sequence of g-band images of a plage region observed near the limb. Uniform diffraction limited resolution is achieved over a 2’ × 2’ FOV. The algorithm takes into account the adaptive optics correction by utilizing the AO telemetry data in order to achieve high precision photometry (Wöger et al., 2008). Some nice examples of MOMFBD reconstructed images and movies can be downloaded from http://www.iac.es/galeria/svargas/movies.html (see also Vargas Domínguez et al., 2008). The movie shown in Figure 28 shows evolution of a pore that develops a penumbra (Schlichenmaier et al., 2010). This speckle reconstructed sequence covers a period of 4 hours and 40 minutes with occasional gaps. This movie is a nice case study of penumbra formation. Figure 29 shows a MOMFBD processed movie of chromospheric structure and is an impressive example of highly dynamic chromospheric fibrils seen in Hα (image and movie from van Noort and Rouppe van der Voort, 2006).

These are just a few examples of many that can be found in the literature that demonstrate how new scientific results can be achieved from a combination of AO and post-facto processing. Real-time instead of post-facto processing of the AO data is of advantage and is now considered for implementation at the ATST (Wöger et al., 2010). Using GLAO, once operational, instead of conventional AO may be the better choice for some of these reconstruction methods since GLAO provides uniform and potentially subarcsec seeing across the FOV, i.e., there is no field dependence of AO performance which complicates the reconstruction algorithm.

The MOMFBD reconstructed movie of chromospheric Hα structure of Figure 29 has been obtained with a relatively narrow filter passband of 12.8 pm and an exposure time of 15 ms. At red, and in particular infrared wavelengths, the longer seeing time constant allows for increasing the maximum exposure time the still freezes the seeing. With efficient instrumentation such as IBIS (Cavallini, 2002; Righini et al., 2010), CRISP (Scharmer et al., 2008), and the GREGOR Fabry-Pérot interferometer (GFPI) (Denker et al., 2010) reconstruction techniques can be applied to very narrow-band images. A recent example is shown with Figure 30, which displays speckle reconstructions of a sunspot region observed with the IBIS instrument tuned to the core of the Ca II 8542 Å line. The passband at this wavelengths is about 4 pm and the exposure time was 30 ms. The large FOV of 240” × 240” was constructed by mosaicing the 90” × 90” FOV of the IBIS. This example demonstrates that, in principle, reconstruction techniques that are typically associated with broad-band imaging can be used to perform spectroscopy with high spectral resolution. Cadence, i.e., temporal resolution becomes the issue since multiple (50 in the example presented here) exposures are required at each spectral position the filter is tuned to. If polarimetry is performed even more images have to be collected. In principle, adding many short exposures is equivalent to a single long exposure in terms of S/N as long a the photon noise dominates over read noise for each exposure, and the read-out time is small relative to the exposure time. This means that with appropriate detectors this potential drawback can be overcome. Remaining issues the high data storage and processing requirements. However, given the rapid and continuous advances with these technologies these issues are not expected to be a limitation. Nevertheless, the capability to post-process and improve long exposure AO images may also be of interest for some applications.

Long exposure

Besides aiding in understanding and optimizing the AO performance estimates of the AO PSF can be used to post-facto deconvolve long exposure images. The advantage of applying post-facto deconvolution techniques was clearly demonstrated by Marino and Rimmele (2010). Accurate photometry, for example, requires that the PSF is well known. Measurements of physical parameters often are performed by computing difference images. A dopplergram that measures flows on the solar surface is essentially computed by subtracting the images taken in the red and blue wing of a spectral line. If the red and blue wing images are recorded sequentially the impact of varying seeing conditions and the resulting variations in AO Strehl on the quantitative velocity measurements can be so severe that the scientific interpretation becomes impossible. Most notably, wing images with significantly different Strehl produce dopplergrams that display residual intensity signal. This is referred to as intensity-velocity cross talk that in severe cases can render the velocity measurement completely useless. The same issue exists when polarimetric measurements are performed. PSF estimation and subsequent deconvolution of line wing images can restore the relevant information to a large extent and, thus, lead to useful scientific results.

Figure 31 shows a sample pair of long exposure images, which compare images before and after deconvolution. The top row shows the AO corrected red wing images captured within a few seconds of each other but during vastly different seeing conditions. The image on the right was recorded with a Fried parameter r₀ = 16.5 cm and a Strehl of S = 0.88. The image on the left has a significantly lower Strehl of S = 0.46 and was recorded at r₀ = 5.4 cm. The high spatial frequency information is still present in the poor seeing image on the left but the contrast is reduced significantly and the image appears “soft”. The corresponding deconvolved images are displayed at the bottom row of Figure 31. The deconvolution process clearly enhances the contrast of the poor seeing image close to the level of the restored high Strehl image. The power spectra of these images are shown in Figure 32. The restored PSDs closely match each other throughout the frequency range.

The top row of Figure 33 displays the velocity maps obtained from the two sets of unprocessed blue and red wing pairs, the first (left) captured during different seeing conditions and the second (right) set during very good seeing conditions. The bottom row of the figure displays the velocity maps obtained from the deconvolved wing images. The dopplergram produced from raw filtergrams exhibits severe intensity-velocity crosstalk. In particular, velocities measured in the sunspot umbra display the resulting artifacts and spurious velocities. Deconvolution of the wing images significantly reduces intensity-velocity crosstalk.

Rimmele and Marino (2006) give an example of science results achieved by deploying PSF estimation and post-facto deconvolution. In general, quantitative analysis of AO data can be significantly improved by applying post-facto deconvolution techniques even in the case of long exposures. At present, solar astronomers are very familiar with and heavily apply post-facto reconstruction to short exposure images and do so with much success.

Overview of Operational Solar AO Systems

The DST AO system was already described in some detail in the previous sections. A copy of AO76 is now operating at the NST integrated with an optical system designed and optimized for the NST (Cao et al., 2010). Several other AO systems are successfully operating at solar telescopes and have significantly increased the scientific productivity of these facilities. Without claiming completeness a few of these systems, which arguably might be considered scientifically most productive, are described in the following sections.

The Swedish Solar Telecope (SST) AO system

The SST is a 97 cm aperture vacuum telescope located on La Palma, Spain (Scharmer et al., 2003). Adaptive optics is an essential component of the telescope. The SST was built after the power of solar AO had been demonstrated and consequently the DM is integrated into the optical path that feeds the instrumentation. A separate correlation tracker is used to measure the tip/tilt component, which is corrected by a tip/tilt stage located close to the DM. The optical layout of the system is very simple, compact, and efficient (Scharmer et al., 2000). The 37-element bimorph mirror is combined with a 37 subaperture correlating Shack-Hartmann wavefront sensor. The system corrects about 35 modes. The lenslet array with a hexagonal arrangement provides a subaperture size of d = 13.8 cm. The off-the-shelf CCD camera reads the Shack-Hartmann images with a frame rate of 955 fps, which limit the bandwidth of the system to about 65 Hz (0 dB crossover of error rejection). The data is processed by an off-the-shelf general purpose computer. Processing of subapertures, reconstruction, and servo control, as well as other control tasks, are all performed by this commercially available computer, which allows for easy upgrade of hardware since the software can be easily ported to faster computers as they become available.

The large aperture of the NSST combined with the 37-element AO system and post-facto processing techniques have produced many of the highest resolution images and movies of the Sun so far, a few examples of which were shown in previous sections. However, the 35 mode correction provided by the SST AO system has to be considered a low order correction that provides good results under excellent seeing conditions. An upgrade of the SST AO system to a 85-element bimorph DM is already in progress and will enable diffraction limited observations for a wider range of seeing conditions and, thus, further increase the scientific productivity of the SST.

Kiepenheuer Institute Adaptive Optics System (KAOS)

The Kiepenheuer Institute Adaptive Optics System has been operating at the 70 cm Vacuum Tower Telescope (VTT) on Tenerife, Spain, since 2002 (von der Lühe et al., 2003). The system is very similar in design and implementation to the SST system in that it uses a correlating SHWFS with 36 subapertures (d = 10 cm) with a hexagonal arrangement and a 35 element bimorph mirror. The FOV of the subaperture images is 12” × 12” sampled with 24 × 24 pixels. Using more pixels per subaperture increases the tracking stability (Berkefeld, 2007). Significant effort has been spent to automate many system calibration functions, which is essential for making the system operational to the non-expert user and enabling remote system support. The system frame rate was increased in 2006 in order to increase the system bandwidth to approximately 100 Hz. The minimum seeing needed to achieve diffraction limited observations is 0.8”. The processor unit is a general purpose Sun Fire V880. Figure 34 shows the optical implementation of KAOS into the German VTT on Tenerife. Figure 35 (left) shows quantitatively what level of correction can be achieved with KAOS as a function of the Fried parameter. The uncorrected and corrected power spectral density is plotted as well in Figure 35 (right) and indicates that a bandwidth of about 100 Hz is achieved. The residual rms wavefront error is 0.1 waves and a Strehl of S = 0.7 is achieved for seeing of about r₀ = 20 cm. In comparison, the high order DST AO76 system achieves a Strehl of S = 0.7 for seeing of r₀ = 8 cm. Figures 36 and 37 show uncorrected and corrected granulation movies, respectively, that demonstrate the ability of KAOS to compensate for atmospheric turbulence and fixed aberrations of the optical system.

Adaptive optics for the infrared at the McMath-Pierce Telescope

Due to the increased Fried parameter in the infrared low cost AO systems specifically designed for the infrared are an option. A low-cost adaptive optics system with a 37 actuator electrostatic membrane deformable mirror and a fast tip/tilt mirror was developed for the 1.5 m McMath-Pierce main telescope (Keller et al., 2003) and has been operating for a number of years. The system uses a general purpose PC to accomplish all processing tasks. Up to 200 8 × 8 pixel subapertures can be processed at a 1 kHz rate. The number of subapertures does not seem to be well matched to the number of degrees of freedom on the DM, leaving room for upgrading the system to higher order. The system works on sunspots and pores and can also track on the solar limb.

Systems under development

AO systems currently under development to upgrade existing solar telescopes include AO for the 60 cm Hida Observatory in Japan (Miura et al., 2008a, 2009, 2010, 2008b), AO at the CSUN, Northridge (Ren et al., 2009), and an AO upgrade of THEMIS, Tenerife. Themis is building a solar AO system with the goal to improve the output of the polarimetric spectro-imaging instruments that are being built and tested as part of the EST project. The system uses a 66 subaperture Shack-Hartmann (d = 9 cm) working at 1000 fps (goal: 1500 Hz), and a 59 actuator Micro Machined DM mirror from OKOTECH. Modal control is implemented on a low cost Intel Core 2 Quad core processor (López Ariste, 2010).

Future Developments

Solar AO, of course, is a continually developing field. The two major areas of development are AO for large aperture solar telescopes and MCAO. Where building larger conventional AO systems can be regarded as a increase in system size of a, by now, well understood technology, MCAO at this point must be considered as a development effort for a new, significantly more complex technology. MCAO is considered a vital technology for large aperture solar telescopes. As has been shown in Section 6.1.3, classical AO can provide a reasonable correction over a large FOV for current small aperture solar telescopes. Post-facto processing techniques can be used efficiently to obtain diffraction limited data over large FOVs. Achieving this for a 4 m class solar telescope will be much more challenging, as will be discussed in detail in Section 9.1.3.

AO for large aperture solar telescopes

Several new, large aperture telescopes are currently under development. Those include the 1.5 m GREGOR telescope on Tenerife and the 1.6 m New Solar Telescope (NST) at BBSO. Both of these telescopes are currently in the commissioning phase. Since the aperture of GREGOR and NST is roughly twice that of the DST the AO systems needed for these telescopes require four times the number of actuators (order 300–400). The 2–4 m aperture solar telescopes of the future include the proposed 2 m class National Large Solar Telescope (NLST) by Indian Institute of Astrophysics (Hasan, 2010), the 4 m Advanced Technology Solar Telescope currently under construction at the US National Solar Observatory and its partners, and the 4 m European Solar Telescope (EST) (Zuccarello, 2009), which is currently in its design phase. The 4 m telescopes require AO systems of order 1500–2000 DOF, i.e., more than an order of magnitude in size over currently existing solar AO systems but well within the realm of already operating night-time AO systems.

GREGOR and NST conventional AO

Initially, the 1.5 m GREGOR and the 1.6 m NST will be outfitted with high order conventional AO systems. The main parameters that describe these systems are listed in Table 2.

Both systems plan to operate with a correlating SHWFS and use stacked actuator, continuous facesheet DMs. The NST system is designed as a scaled up version of the DST AO76 and utilizes a new generation of DSPs (TIGERSHARC) while the GREGOR is based on the KAOS heritage and uses general purpose processing.

Predictions of the Strehl ratio achieved in the detector plane of post-focus instruments of the NST can be derived from detailed performance modeling as described in Section 6. The analysis uses the ATST site survey data and is partially based on the extensive error budget modeling that was done for the ATST since both NST and ATST are similar off-axis designs with ventilated enclosures and face similar non-common path issues. The results are shown in Figure 38 in the form of histograms of the predicted Strehl at visible and NIR wavelengths. This figure compares the Strehl performance of the AO76 currently operating at the NST with the predicted performance of the high order 357 actuator system. The conclusion is that with the NST and AO76 diffraction limited observations of reasonable Strehl at visible wavelengths are only possible for the most extraordinary seeing conditions. In comparison, the high order 357 actuator system is expected to provide reasonable Strehl in the visible for a significant fraction of the observing time. Figure 38 clearly demonstrates the need for an upgrade to a high order AO system for the NST. GREGOR will have a similar high order system. These systems will be essential to realize full scientific benefit from these 1.5 m class aperture telescopes.

These conventional high order AO systems should be regarded as intermediate steps toward the implementation of MCAO systems at both GREGOR and NST (see Section 9.2).

High order AO for the ATST

As an example of an extremely high order solar AO system this section summarizes the design characteristics of the ATST conventional AO system, which is the centerpiece of the ATST wavefront correction system (Rimmele et al., 2006a). The AO system planned for the 4 m EST will be discussed in Section 9.2 in the broader context of MCAO since both ATST and EST plan to implement MCAO systems as soon as the technology has been demonstrated at the 1.5 m class solar telescopes.

The ATST wavefront correction system is required to achieve the high Strehl requirements at visible and infrared wavelengths called for in the Science Requirements Document (Rimmele, 2005).

The ATST uses a comprehensive wavefront correction strategy with several correctors and wavefront sensors including:

Quasi-static alignment (QSA) for keeping the entire optical path — most importantly M1 and M2 — aligned in closed-loop. Decenter and tilt of M2 are used to correct coma and astigmatism. Due to the off-axis design coma is actually not the dominant aberration introduced (or compensated) by decenter/tilt of M2.
Active optics (aO), the main function of which is to keep the figure of M1 within specified tolerances. M1 compensates for deformation due to gravitational and thermal distortions.
Tip/tilt devices for image stabilization used for seeing limited on disk observations and diffraction limited AO observations
Hgh order adaptive optics (HOAO) as the centerpiece of the WFC system. Details about the functions of the various ATST WFC subsystems and their design can be found at Rimmele et al. (2006c) and Richards et al. (2010). This section focuses on the HOAO.

The HOAO system of the ATST has been integrated into the ATST’s optical path from the start and will correct atmospheric seeing and any internal seeing and optical aberrations along the optical path to the WFS. The top-level science requirements that drive the ATST AO design are:

Strehl > 0.3 for r₀ (500 nm) > 7 cm. This requirement defines the ATST imaging performance for seeing conditions for which the solar AO will function effectively. According to the ATST site survey r₀ (500 nm) > 7 cm describes seeing conditions slightly better than median seeing at the Haleakala site (Beckers, 2004).
Strehl > 0.6 for r₀ (630 nm) > 20 cm. This requirement defines the ATST imaging performance for excellent seeing conditions, during which high-priority science objectives will be achieved.

The original baseline design used a 1313 actuator DM and a correlating SHWFS with 1280 subapertures operating at > 2 kHz rates. It is interesting to note that with the ATST entering construction and further refinement of error budgets the system size has now been increased to about 1700 actuators in order to accommodate pressures on the error budget exerted by various subsystems including instrumentation (Richards et al., 2010). This clearly demonstrated the importance of careful and continuously updated error budget analysis and systems engineering approach in general. To further illustrate this point Figure 39 plots predicted Strehl histograms for the ATST baseline HOAO design at visible and near infrared wavelengths. Considering the atmospheric fitting error only, which unfortunately sometimes is done to provide crude performance predictions, results in an overly optimistic performance estimate (visible histogram, dashed line). The dotted line is produced by including atmospheric fitting error, aliasing error, bandwidth error, and WFS measurement error, which sometimes are referred to as the AO system errors. However, a realistic error budget has to include all possible error sources (visible histogram, solid line). The science instrument, for example a spectrograph, introduces wavefront errors that are not sensed by the AO wavefront sensor and, therefore, are not corrected. It is not always possible to calibrate out these non-common path errors. In particular, in a multi-instrument experiment calibration of non-common path wavefront errors of one instrument results in adding these errors to all other instruments involved in the experiment. Multi-instrument experiments are becoming the norm in solar observations. The imaging performance of AO instrumentation, in particular in the visible, is driven to much higher imaging quality standards than used to be the case for seeing limited instruments. The NIR (1.6 μm) wavelengths Strehl histogram indicates that with the ATST Strehl ratios of S ≥ 0.6 might be achieved for most of the clear time, i.e., space quality observations with a resolution of ≤ 0.1” will be possible for the majority of the available observing hours.

The real time control (RTC) system of the HOAO system is modeled after the AO76. A top level block diagram that details the functionality was described by (Rimmele et al., 2006c; Richards et al., 2010). This unit performs the cross correlations of the 1232 subapertures as well as the reconstruction. Servo algorithms for the DM and tip/tilt mirrors are also implemented on the RTC unit. Telemetry data is collected and streamed to a local disk via the auxiliary PCs. The size and complexity of the significantly higher order ATST HOAO RTC is not much increased compared to the RTC of the AO76. This is due to advances in processing hardware (Moore’s law) (Rimmele et al., 2006c).

Figure 40 shows the layout of the ATST HOAO system in the ATST coude instrument lab (Richards et al., 2010). The HOAO is highly integrated with the instrumentation and feeds a number of first light facility instruments that will be used from visible to infrared wavelengths. The long instrument feed optical paths can result in significant non-common path local seeing errors (Biérent et al., 2008). The ATST mitigates this by careful thermal control of the entire instrument laboratory (Phelps et al., 2010).

With a 4 m collecting area thermal control of the corrective optical elements such as the DM and the tip/tilt devices becomes essential. These devices are typically kept small for performance (bandwidth) and optical packaging reasons. With a diameter of the device of 200 mm and a FOV of 2.83’ circular the absorbed heat flux is about 100 W/m² assuming a high reflection silver coating. Without active cooling the surface of the DM or tip/tilt device could heat up by tens of degrees C above ambient causing serious local seeing degradation. Active cooling is required to keep the mirror surface temperature with 0 °C to -2 °C, which is the allowable range where local seeing can be avoided. Air cross flows could also be used to mitigate image degradation (Hubbard et al., 2006). However, actuator drifts, time dependent changes of actuator characteristics, and thermal deformations of the assembly due to a changing heat load are problems that also need to be dealt with if no thermal control is applied. Figure 41 shows, as an example for the potential added complexity of thermal control, an air cooled tip/tilt device envisioned for implementation at the ATST.

Angular anisoplanatism: a serious challenge for large aperture solar telescopes

In addition to the technical challenges involved in building high order solar AO systems for 4 m class telescopes anisoplanatism poses a much more serious challenge at these larger telescopes. As was shown in Section 6.1.3 the residual wavefront errors introduced by anisopanatism limit the size of the AO corrected FOV. For current small solar telescopes and under certain conditions $\frac{D} {{r_0 }} $ can be small and acceptable AO performance can be achieved over a FOV of tens of arcsec (see Figure 20). Reasonable or useful Strehl ratios (in terms of being able to apply post-facto reconstruction methods) can be achieved over even larger FOVs. For large aperture telescopes, however, even during excellent seeing conditions $\frac{D} {{r_0 }} $ is generally large also for the upper atmosphere. Figure 42 (Marino and Rimmele, 2011) shows the result of repeating the simulations presented in Section 6.1.3 but for a 4 m aperture telescope with an AO system that has about 1300 actuators. These parameters closely match the ATST AO system and, therefore, predict anisoplanatic behavior expected for the ATST.

The isoplanatic angle for a best case scenario of vertical pointing and r₀ of 20 cm is now only about 10 arcsec for the Haleakala profile (Figure 42, right) and 2–3 arcsec for the Mt. Graham profile (Figure 43, right). The Strehl drops quickly away from the lock center and for near horizon pointing. The Haleakala profile yields an isoplanatic angle of about 3” and about 10” away from the lock center the Strehl is virtually zero. The Mt. Graham profile does not yield satisfactory Strehl for near horizon pointing even if excellent seeing (r₀ = 20 cm) is assumed. For more common seeing conditions (r₀ = 10 cm) only the Haleakala profile leads to good Strehl performance and reasonable corrected FOV.

The impact of using an extended FOV of 8” × 8”, that is required for the correlating Shack-Hartmann wavefront sensor, is clearly revealed in Figure 43. Even for vertical pointing the directional averaging effect is significant as can be inferred by comparing Figures 42 (left) and 43 (left). For near horizon pointing averaging wavefront sensor information from different directions is devastating and leads to substantial Strehl reduction. The early morning hours are, of course, exactly when conditions for solar observations are considered best because the strong ground layer turbulence has not formed yet. Hence, high resolution solar observations are generally performed at fairly high zenith angles. These results emphasize the relative importance of MCAO for large aperture telescopes in comparison to the small aperture current solar telescopes. It is important to note that the negative impact of anisoplanatism makes post-facto processing of conventional solar AO imagery a necessity for many applications. As a side note it should be mentioned that the dominance of the ground layer seeing during the daytime might make Ground-Layer AO (GLAO) an attractive option for solar telescopes and for some scientific applications.

As pointed out in a previous section at near infrared wavelengths high Strehl AO performance can be expected for a considerable fraction of the available observing time. In addition, the isoplanatic angle increases with $\lambda ^{\frac{6} {5}} $ and, thus, one might expect roughly a factor of four increase in isoplanatic patch size when near infrared instead of visible observations are performed. Figures 44 and 45 show the equivalent plots to what was shown in Figures 42 and 43 but for 1.6 micron instead of visible. These plots confirm that the isoplanatic angle (patch) is indeed about 4 times larger at near infrared wavelengths compared to visible wavelengths. The Haleakala profile yields an isoplanatic angle of about 17 arcsec (isoplanatic patch = 34 arcsec) for r₀ = 10 cm and zenith angle of 45°, i.e., the isoplanatic patch covers the size of a small sunspot. These results indicate that with the development of 4 m solar telescopes infrared observations are likely to gain in importance. A 4 m aperture will provide better than 0.1 arcsec diffraction limited resolution at a wavelength of 1.6 microns.

Chromatic ansisoplanatism

Another form of anisoplanatism that effects and limits solar AO performance is chromatic anisoplanatism. A detailed discussion of chromatic anisoplanatism is given by Hardy (1998, Section 9.3). Due to atmospheric dispersion light of different wavelength propagates through different parts of the atmosphere and, thus, samples different turbulence volumes. Atmospheric dispersion becomes a limiting factor for large zenith angle observations, which solar observations usually are.

The most significant error caused by chromatic anisoplanatism is the multi-spectral error. The vast majority solar observations are multi-spectral typically covering wavelengths that range from UV to near infrared. The wavefront sensor of existing solar AO systems operates at a particular visible wavelengths with a fairly narrow passband. For example, the atmospheric dispersion between 430 nm, the observing wavelength of the science camera, and 500 nm, the wavefront sensor wavelength, is about 1 arcsec. For early morning observations with the Sun at 20° elevation (zenith angle = 80°) and with a single turbulence layer at 10 km the 430 nm phase screen that needs to be corrected by the AO is shifted by about 0.14 m with respect to the 500 nm phase screen that is actually measured by the AO wavefront sensor. This simple estimate gives the order of magnitude of the effect. The exact equations for calculating the ray displacement can again be found in Hardy (1998, Section 9.3).

This misregistration of the science beam wavefront and the sensor beam wavefront can be of order r₀, which results in significant reduction of Strehl when compared to an AO system that senses at the same wavelength as the science detector. This is demonstrated with Figure 46, which plots the Strehl ratio as a function of elevation for a number of wavelengths. This simulation again models the four layer Haleakala turbulence profile and the ATST 1300 actuator AO system. The r₀ is assumed to be 10 cm in all cases. The dotted, solid, dashed, and dashed-dotted lines represent the expected Strehl performance for the ideal mono-chromatic AO system, which senses at 430 nm, 500 nm, 630 nm, and 1600 nm, respectively, and observations are performed at these same wavelengths. The same lines with over-plotted symbols show the performance of the multispectral AO, which senses the wavefront errors at 500 nm but the correction is evaluated at 430 nm (diamonds), 630 nm (stars), and 1600 nm (circles), respectively. For elevation angles smaller than 30° (zenith angle ≤ 70°) the curves diverge with significantly reduced Strehl for the multi-spectral AO. Figure 46 suggests that solar multi-spectral observations could gain form careful selection of the WFS wavelength taking into account the primary wavelengths, science priorities of the multispectral experiment and the possibility of performing post-facto reconstruction of some instruments that might not exist for other participating instruments. For example, post-facto reconstruction is more difficult for spectrograph instruments than it is for imaging devices. One might, therefore, in some cases, decide to optimize the AO performance for 630.2 nm polarimetry and accept a performance hit with the secondary instrument, the g-band imager, since the g-band images will be post-fact reconstructed (e.g., speckle). A WFS that can operate at different, user-selectable wavelengths would be of advantage.

Solar AO has the luxury of using a relatively narrow bandpass WFS. Science observations are usually performed within a very limited wavelengths range as well. In this way other error sources that would have to be considered for broad-band WFS and broad-band science observations, such as the angular dispersion error and the dispersion displacement error can be largely neglected. It should be noted that solar astronomers often use the term broad-band to describe filtergraph observations with passbands of 10 nm or even less. In the context of atmospheric dispersion such passbands would still be considered narrow-band.

Multi-Conjugate Adaptive Optics (MCAO)

A severe limitation of conventional AO is its ability to fully correct only the seeing aberrations within the isoplanatic patch. Anisoplanatism causes the quality of the AO correction to gradually decline away from the diffraction limit with distance from the chosen lock center and as a consequence, the Strehl ratio decreases. In the visible, conventional AO limits the corrected FOV to a few arcseconds diameter or less (Equation 20). At near infrared wavelengths, where r₀ is larger, a corrected FOV of a few tens of arcseconds might be achieved (Rimmele et al., 2006c). As was shown in Sections 6.1.3 and 9.1.3 the actual size of the isoplanatic patch depends strongly on telescope aperture size, the Fried parameter, wavelength, and, of course, the particular turbulence profile.

A sunspot or active region extends typically over 1–2’. Flares can occur “unannounced” anywhere in the extended FOV. Flare trigger mechanisms operate rapidly and on the smallest spatial scales and their location within the FOV is difficult to predict. Diffraction limited resolution over a FOV of 1–2’ is required in these cases.

MCAO is a technique that can provide real-time diffraction limited imaging over an extended FOV of 1–2’ (Beckers, 1988; Rigaut et al., 2000). Figure 47 illustrates the basic principle is tomography. Guide stars in different sky directions are used to probe the turbulent volume above the telescope. Two or more DMs are placed at conjugates of the main turbulence layers and provide correction over an extended FOV as is illustrated with Figure 48. The operation of multiple DMs poses a challenging controls problem.

Night-time MCAO development has progressed to a point where scientific results with MCAO have been obtained. The ESO MAD system (Marchetti et al., 2003, 2008), which uses natural guide stars, demonstrated the power of MCAO for scientific discovery even with a demonstrator system. Wavefront sensing in night-time MCAO is difficult because for general use, multiple laser guide stars (LGSs) are needed for tomographic wavefront reconstruction. Thus, to accurately reconstruct 3-D turbulence, generally a number of laser guide stars are needed. The Sun, on the other hand, is an ideal target for MCAO. Any number and any configuration of “guide stars” can in principle be created from the omni-present granulation the same but multiple correlating SHWFS used for conventional AO. Implementing operational solar MCAO is an essential, but challenging task that faces the NST, GREGOR, ATST, and EST.

A number of successful on-the-sky MCAO experiments were performed at the DST and at the German VTT (Vacuum Tower Telescope) on the Canary Islands (Berkefeld et al., 2003; Langlois et al., 2004; Berkefeld et al., 2005; von der Lühe et al., 2005; Rimmele et al., 2009). As an example the KIS MCAO approach is shown in Figure 49. A common theme of the solar MCAO experiments is the two stage approach, which uses the high order conventional AO to provide a good correction of the ground layer, and a second, low-order MCAO stage with multiple off-axis, extended “guide fields”, which are equivalent to the night-time MCAO guide stars. Figure 50 shows results from solar MCAO experiments performed at the VTT, Tenerife (von der Lühe et al., 2005) and at the DST (Rimmele et al., 2010a,c). Both examples clearly demonstrate the MCAO’s ability to extend the corrected FOV significantly beyond the conventional AO FOV.

As an example of a typical MCAO optical implementation Figure 51 shows the MCAO optical path of GREGOR (Berkefeld et al., 2006). The collimator M12 images the entrance pupil onto the tip/tilt mirror M13 which is followed by the pupil plane DM1. The combination of M15MCAO and M16 produce 25 km and 8 km conjugate images at a convenient beam size in order to accommodate the MCAO DMs. The DMs can easily be moved to adjust the conjugate heights. M19 produces the final image at f/37.

The 1.5 m GREGOR telescope project is planning to implement a MCAO system shortly after first light (Berkefeld et al., 2006). The system is currently being tested in the lab. Further development is progressing at the DST with the goal to provide the ground work for operational solar MCAO at the BBSO NST. The optical path of the 4 m ATST, currently under construction, is designed to allow the high order conventional AO system to be easily upgraded to high order MCAO once the solar MCAO technology is mature (Rimmele et al., 2006b). The EST project is considering MCAO as a first light capability (Berkefeld et al., 2010; Soltau et al., 2010).

The EST MCAO goals are quite ambitious (Berkefeld et al., 2010). The requirement to achieve a Strehl ratio of S = 0.3 for r₀ = 7 cm and S = 0.6 at r₀ = 20 cm across a corrected FOV of 1’ at visible wavelengths is extremely challenging. The design uses a large number of DMs and off-axis WFS. In addition to the tip/tilt device there are five (5) DMs at conjugate heights of 0, 5, 9, 15, and 30 km as shown in Figure 52. The science FOV envisioned is 60” square. Performance modeling of such a system was presented by Berkefeld et al. (2010) and illustrates the difficult issues facing solar MCAO. The best seeing conditions at solar telescopes are generally in the morning hours when ground layer turbulence due to ground heating is minimal. On the other hand the zenith angle is large and, consequently, the air mass through which the Sun is observed is multiple times that of observations performed at near zenith pointing.

The impact of zenith angle on MCAO field performance is seen in Figure 53. The achievable maximum Strehl drops drastically with increasing zenith angle. The simulation indicates that even with a 5 DM MCAO system the Strehl does not exceed S = 0.2 once the zenith angle is 60 degrees or larger. In comparison, for zenith pointing high Strehl can be achieved with only four DMs. if the MCAO performance is optimized for a reduced FOV of 30” diameter good Strehl performance can be achieved at large zenith angles (Figure 53, right).

These results point to fundamental issues with the implementation of solar MCAO. Tradeoffs will have to be performed in order to optimize the MCAO performance toward specific science experiments. The FOV over which diffraction limited observations have to be performed to achieve scientific goals as well as the desired Strehl will drive the complexity of the MCAO and the zenith distance for which the observations are possible. Achieving a high visible Strehl over a large (≥ 2’) FOV does not appear to be practical during the typical prime solar observing hours. The probability of obtaining large corrected FOVs with MCAO in the infrared is much higher because of the $\lambda ^{\frac{6} {5}} $ dependence of key atmospheric parameters, such as the Fried parameter and the isoplanatic angle. MCAO observations are best performed for near zenith pointing. However, the build up of ground turbulence will increasingly stress the ground layer DM and drive it toward the highest possible order of correction. As was noted above the minimum subaperture size of the correlating SHWFS is around 7–8 cm. The order of the ground-layer DM can not be increased much beyond this limit unless ways to significantly improve the SNR performance of this WFS approach can be found (see Section 6.1.5) or different WFS approaches that do not have this limitation can be developed for solar AO application. The phase diversity approach (Paxman et al., 2007) to the solar WFS appears to be the most promising in this regard since it deploys full aperture WFS and, thus, is not limited by subaperture diffraction. The information content of the PD sensor is higher compared to the correlating SHWFS.

Ground-Layer Adaptive Optics (GLAO)

Ground-Layer Adaptive Optics is an attractive option for solar AO (Rimmele et al., 2010c). During the daytime most of the turbulence is located near the ground. Up to 90% of the turbulence can be located within the first 100–200 m while the r₀ of the upper atmosphere can be rather large. Fried parameters of 20–40 cm are possible at those higher layers. Excluding the ground layer and assuming an overall r₀ in the visible of 10 cm (20 cm) the Haleakala turbulence profile shown in Table 1 would yield an effective r0 for all higher layers of 22 cm (42 cm). Because of the $\lambda ^{\frac{{ - 6}} {5}} $ dependence of r₀ the best utility of GLAO at large aperture telescopes may be at near infrared wavelengths. This means that with a simple high order ground layer correction it is theoretically possible to achieve subarcsecond resolution over a very wide field. A number of science objectives can be addressed with a resolution of 0.25–0.5” that potentially might be provided by GLAO. At this reduced resolution (with GLAO the diffraction limit can not be reached at visible wavelengths) a large aperture solar telescope, such as the 4 m ATST, would provide a tremendous photon flux and, thus, a significant cadence and/or sensitivity advantage. Sensitive vector magnetic field measurements of active regions that currently take on the order of an hour and, hence, miss much of the very dynamic nature of active region evolution could be performed in a few minutes provided efficient instrumentation is used.

Experiments with the goal to provide a ground layer correction by using a wide field SHWFS were performed at the DST (Rimmele et al., 2010c). Modeling of wide field SHWFS was performed by Wöger and Rimmele (2009). As the WFS FOV is increased from the small field of the conventional AO to larger and larger field size the correction applied with the DM is an average over an increasingly larger number of field directions, i.e., a large number of isoplanatic patches. The field averaging of wavefront information is essentially done optically and by the correlation algorithm. However, this simple implementation of GLAO has its limitations as is seen in Figure 54, which shows the variance of residual image motion overlaid on the speckle reconstructed granulation. The WFS FOV was 42” × 42”. The residual image motion variance is fairly uniform across the field but residual field dependence is still visible.

It has been demonstrated that a wide field WFS can increase the sensitivity of the correlating WFS and, thus, is expected to work for worse seeing conditions (Owner-Petersen et al., 1993). As pointed out by Rimmele et al. (2010c) GLAO may be a tool to improve telescope efficiency. Bad seeing periods during which conventional AO provides very low Strehl or simply does not work at all can still be utilized for certain science projects that require subarcsecond but not diffraction limited resolution. Such observations would gain from the available photon flux of a large aperture. In particular, in the near infrared a modestly sized GLAO system could potentially open up a new window for high cadence polarimetry.

GLAO might also be an attractive option for synoptic solar telescopes such as SOLIS and a future larger aperture GONG network. Depending on the site characteristics the 50 cm SOLIS telescope could potentially operate close to its diffraction limit for the full solar disk with a relatively modest GLAO system.

Summary

Solar adaptive optics has to be considered a success story. The success of solar AO can be measured not only by the impressive imagery obtained with AO but most importantly by new scientific results, the use-rate of solar AO and the numerous scientific publications that were enabled by AO. Ground-based solar astronomy is experiencing a renaissance. New large aperture adaptive optics telescopes such as the ATST are currently under construction and will provide observations of the Sun with unprecedented resolution. These observations will allow us to put to the test and guide theoretical models and simulations and, thus, advance tremendously our physical understanding of solar phenomena. The successful development of solar AO and the demonstration of its scientific potential contributed in no small part to the community’s success in making the case for funding of large aperture ground-based solar telescopes.

This article summarized the difficult path that led to the successful implementation of solar AO at ground-based solar telescopes. It is fair to say that the rapid development of fast computer technology needed for the implementation of the correlating SHWFS as well as the commercial availability of deformable mirrors were major prerequisites in bring solar adaptive optics to fruition. As with any instrument a good understanding of potential error sources is crucial for estimating and optimizing the systems performance and, in turn, maximizing scientific productivity. The combination of AO and post facto image processing provides ground-based solar astronomers with a powerful tool that can rival or even surpass space based observations. AO enables diffraction limited observing at large aperture telescopes where similar size aperture telescopes from space are likely cost prohibitive.

New developments in the field of solar AO include the construction of extreme solar AO systems with thousands of actuators for the 4 m class telescopes, the very challenging development of MCAO and the possible use of GLAO. MCAO will mitigate one of the major limitations of conventional AO — the small corrected FOV. Compared to current small aperture solar telescopes the isoplanatic patch will be significantly smaller at 4 m solar telescopes. Some level of partial correction can be achieved over wide fields at small aperture solar telescopes with conventional AO. The correction level is sufficient to facilitate post-facto processing and diffraction limited imaging can be obtained over sizable FOVs even at visible wavelengths. This will be extremely challenging at 4 m solar telescopes. MCAO is, therefore, considered a vital technology for these next generation telescopes. The large 4 m aperture, in principle, provides 0.1” diffraction limited resolution at near infrared wavelengths. Because of the $\lambda ^{\frac{6} {5}} $ dependence of the Fried parameter the size of r₀ increases by about a factor of four (4) for observations in the near infrared (1.6 μ). This means that the $\frac{D} {{r_0 }} $ for a 4 m telescope and for near infrared wavelengths is roughly the same ratio as for a 1 m telescope operating at visible wavelengths and conventional AO performance is expected to be comparable. This may lead to more focus being placed on infrared instrumentation at these larger telescopes at least initially and until MCAO is fully operational at a level comparable to current conventional solar AO systems.

The implementation of MCAO at solar telescopes is aided by the fact that the multiple “guide stars” required to perform tomography of the turbulent volume are provided by the Sun’s omnipresent granulation pattern. The complexity of multiple laser guide stars needed for night-time MCAO is avoided. The initial success achieved with solar MCAO development is encouraging. Nevertheless, much work remains to be done before fully operational MCAO will be available at solar telescopes. GREGOR and NST will soon allow us to gain operational experience with solar MCAO. The use of GLAO may be of advantage for certain applications where sub-arcsec (but not diffraction limited resolution) and high photon flux is required. GLAO can be used in combination with post-facto reconstruction techniques, although at 4 m telescopes and at visible wavelengths achieving large, well corrected FOVs will be a serious challenge. GLAO also seems to be an attractive option for synoptic telescopes of moderate aperture (e.g., SOLIS).

References

Acton, D.S. and Dunn, R.B., 1993, “Solar imaging at National Solar Observatory using a segmented adaptive optics system”, in Active and Adaptive Optical Components and Systems II, Albuquerque, NM, USA, 1 February 1993, (Ed.) Ealey, M.A., vol. 1920 of Proc. SPIE, pp. 348–352, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 20.)
ADS Article Google Scholar
Acton, D.S. and Smithson, R.C., 1992, “Solar imaging with a segmented adaptive mirror”, Appl. Opt., 31, 3161–3169. [DOI], [ADS] (Cited on pages 20 and 21.)
ADS Article Google Scholar
Beckers, J.M., 1988, “Increasing the size of the isoplanatic patch with multiconjugate adaptive optics”, in Very Large Telescopes and their Instrumentation, Vol. 2, Proceedings of the ESO Conference held in Garching, March 21–24, 1988, (Ed.) Ulrich, M.-H., vol. 30 of ESO Conference and Workshop Proceedings, pp. 693–703, ESO, Garching. [ADS] (Cited on page 68.)
ADS Google Scholar
Beckers, J.M., 1993a, “Adaptive optics for astronomy: Principles, performance, and applications”, Annu. Rev. Astron. Astrophys., 31, 13–62. [DOI], [ADS] (Cited on pages 11 and 34.)
ADS MathSciNet Article Google Scholar
Beckers, J.M., 1993b, “On the relation between scintillation and seeing observations of extended objects”, Solar Phys., 145, 399–402. [DOI], [ADS] (Cited on page 34.)
ADS Article Google Scholar
Beckers, J.M., 2008, “Laser guide stars for daytime thermal IR observations”, in Extremely Large Telescopes: Which Wavelengths? Retirement Symposium for Arne Ardeberg, Lund, Sweden, 29–30 November 2007, (Ed.) Andersen, T.E., vol. 6986 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 18.)
Beckers, J.M. et al. [ATST Site Survey Working Group], 2004, ATST Site Survey Working Group Final Report, RPT-0021, ATST, Tucson, AZ. URL (accessed 16 May 2011): http://atst.nso.edu/files/docs/RPT-0021.pdf (Cited on page 61.)
Google Scholar
Berkefeld, T., 2007, “Solar adaptive optics”, in Modern Solar Facilities — Advanced Solar Science, Proceedings of a Workshop held at Göttingen, Germany, September, 27–29, 2006, (Eds.) Kneer, F., Puschmann, K.G., Wittmann, A.D., pp. 107–113, Universitätsverlag, Göttingen. [ADS], [Google Books]. Online version (accessed 19 April 2011): http://webdoc.sub.gwdg.de/univerlag/2007/solar_science_book.pdf (Cited on pages 31, 39, 55, 56, and 72.)
Google Scholar
Berkefeld, T. and Soltau, D., 2010, “EST adaptive optics performance estimations”, Astron. Nachr., 331, 640. [DOI], [ADS] (Cited on page 27.)
ADS Article Google Scholar
Berkefeld, T., Soltau, D. and von der Lühe, O., 2003, “Multi-conjugate Adaptive Optics at the Vacuum Tower Telescope, Tenerife”, in Adaptive Optical System Technologies II, Waikoloa, HI, USA, 22 August 2002, (Eds.) Wizinowich, P.L., Bonaccini, D., vol. 4839 of Proc. SPIE, pp. 544–553, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 69.)
ADS Article Google Scholar
Berkefeld, T., Soltau, D. and von der Lühe, O., 2005, “Results of the multi-conjugate adaptive optics system at the German solar telescope, Tenerife”, in Astronomical Adaptive Optics Systems and Applications II, San Diego, CA, USA, 3 August 2005, (Eds.) Tyson, R.K., Lloyd-Hart, M., vol. 5903 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 69.)
Berkefeld, T., Soltau, D. and von der Lühe, O., 2006, “Multi-conjugate solar adaptive optics with the VTT and GREGOR”, in Advances in Adaptive Optics II, Orlando, FL, USA, 24 May 2006, (Eds.) Ellerbroek, B.L., Bonaccini Calia, D., vol. 6272 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 69 and 70.)
Berkefeld, T., Soltau, D. and von der Lühe, O., 2007, The Kiepenheuer Institute Adaptive Optics System at the Vacuum Tower Telescope, KIS internal report, Kiepenheuer Institute for Solar Physics, Freiburg (Cited on page 56.)
Google Scholar
Berkefeld, T., Soltau, D., del Moro, D. and Löfdahl, M.G., 2010, “Wavefront sensing and wavefront reconstruction for the 4m European Solar Telescope EST”, in Adaptive Optics Systems II, 27 June 2010–2 July, San Diego, California, USA, (Eds.) Ellerbroek, B.L., Hart, M., Hubin, N., Wizinowich, P.L., vol. 7736 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on pages 30, 73, and 74.)
Biérent, R., Rimmele, T.R. and Marino, J., 2008, “Assessment of local seeing within a telescope lab environment”, in Ground-based and Airborne Telescopes II, Marseille, France, 23 June 2008, (Eds.) Stepp, L.M., Gilmozzi, R., vol. 7012 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 43 and 62.)
Bouchez, A.H., Dekany, R.G., Roberts, J.E., Angione, J.R., Baranec, C., Bui, K., Burruss, R.S., Croner, E.E., Guiwits, S.R., Hale, D.D.S., Henning, J.R., Palmer, D., Shelton, J.C., Troy, M., Truong, T.N., Wallace, J.K. and Zolkower, J., 2010, “Status of the PALM-3000 high-order adaptive optics system”, in Adaptive Optics Systems II, San Diego, CA, USA, 27 June 2010, (Eds.) Ellerbroek, B.L., Hart, M., Hubin, N., Wizinowich, P.L., vol. 7736 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 16.)
Brandt, P.N., Mauter, H.A. and Smartt, R., 1987, “Day-time seeing statistics at Sacramento Peak Observatory”, Astron. Astrophys., 188, 163–168. [ADS] (Cited on page 22.)
ADS Google Scholar
Cain, S.C., 2004, “Design of an image projection correlating wavefront sensor for adaptive optics”, Opt. Eng., 43, 1670–1681. [DOI], [ADS] (Cited on page 40.)
ADS Article Google Scholar
Cao, W., Gorceix, N., Coulter, R., Coulter, A. and Goode, P., 2010, “First light of the 1.6 meter off-axis New Solar Telescope at Big Bear Solar Observatory”, in Ground-based and Airborne Telescopes III, 27 June–2 July 2010, San Diego, California, USA, (Eds.) Stepp, L.M., Gilmozzi, R., Hall, H.J., vol. 7733 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on page 55.)
Carroll, J., Gray, D.C., Roorda, A. and Williams, D.R., 2004, “Recent Advances in Retinal Imaging With Adaptive Optics”, Opt. Photon. News, 16, 36. [DOI], [ADS] (Cited on page 27.)
ADS Article Google Scholar
Cattaneo, F., Emonet, T. and Weiss, N., 2003, “On the Interaction between Convection and Magnetic Fields”, Astrophys. J., 588, 1183–1198. [DOI], [ADS] (Cited on page 5.)
ADS Article Google Scholar
Cavallini, F., 2002, “IBIS (Interferometric BIdimensional Spectrometer)”, in Solspa 2001, Proceedings of the Second Solar Cycle and Space Weather Euroconference, 24–29 September 2001, Vico Equense, Italy, (Ed.) Sawaya-Lacoste, H., vol. SP-477 of ESA Conference Proceedings, pp. 585–587, ESA Publications Division, Noordwijk. [ADS] (Cited on page 50.)
Google Scholar
Cherubini, T., Businger, S. and Lyman, R., 2008a, “Modeling Optical Turbulence and Seeing over Mauna Kea: Verification and Algorithm Refinement”, J. Appl. Meteor. Climatol., 47, 3033–3043. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
Cherubini, T., Businger, S., Lyman, R. and Chun, M., 2008b, “Modeling Optical Turbulence and Seeing over Mauna Kea”, J. Appl. Meteor. Climatol., 47, 1140–1155. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
Cherubini, T., Businger, S. and Lyman, R., 2009, “Modeling Optical Turbulence on Mauna Kea: An Operational Challange”, Eos Trans. AGU, 90, A13I–0386. [ADS] (Cited on page 36.)
Google Scholar
Conan, J.-M., Rousset, G. and Madec, P.-Y., 1995, “Wave-front temporal spectra in high-resolution imaging through turbulence”, J. Opt. Soc. Am. A, 12, 1559–1570. [DOI], [ADS] (Cited on page 28.)
ADS Article Google Scholar
Dai, G.-M., 1996, “Modal wave-front reconstruction with Zernike polynomials and Karhunen-Loève functions”, J. Opt. Soc. Am. A, 13(6), 1218–1225. [DOI], [ADS] (Cited on page 45.)
ADS Article Google Scholar
Darvann, T.A. and Dunn, R.B., 1987, The Foucault Test for Solar Telescopes, LEST Technical Report 26, LEST Foundation, Stockholm. [ADS] (Cited on page 19.)
Google Scholar
Denker, C., Balthasar, H., Hofmann, A., Bello González, N. and Volkmer, R., 2010, “The GREGOR Fabry-Perot interferometer: a new instrument for high-resolution solar observations”, in Groundbased and Airborne Instrumentation for Astronomy III, San Diego, CA, USA, 27 June 2010, (Eds.) McLean, I.S., Ramsay, S.K., Takami, H., vol. 7735 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 50.)
Dessenne, C., Madec, P.-Y. and Rousset, G., 1998, “Optimization of a predictive controller for closed-loop adaptive optics”, Appl. Opt., 37, 4623–4633. [DOI], [ADS] (Cited on page 14.)
ADS Article Google Scholar
Dessenne, C., Madec, P.-Y. and Rousset, G., 1999, “Sky implementation of modal predictive control in adaptive optics”, Opt. Lett., 24, 339–341. [DOI], [ADS] (Cited on page 14.)
ADS Article Google Scholar
Dunn, R.B., 1990, “NSO/SP adaptive optics program”, in Adaptive Optics and Optical Structures, The Hague, Netherlands, 12 March 1990, (Eds.) Tyson, R.K., Schulte-in-den Baeumen, J.J., vol. 1271 of Proc. SPIE, pp. 216–231, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 19.)
ADS Article Google Scholar
Dunn, R.B., Streander, G. and von der Lühe, O., 1989, “Adaptive optical system at Sac Peak: a progress update”, in High spatial resolution solar observations, Proceedings of the 10th Sacramento Peak Summer Workshop, Sunspot, New Mexico, August 22–26, 1988, (Ed.) von der Lühe, O., p. 53, NSO, Sunspot. [ADS] (Cited on page 19.)
Google Scholar
Dunn, R.B., Streander, G.W., Hull, W. and Wilkins, L., 1992, “The NSO/Sac Peak continuousface-plate adaptive mirror”, in Active and Adaptive Optical Components, San Diego, CA, USA, 24 July 1991, (Ed.) Ealey, M.A., vol. 1543 of Proc. SPIE, pp. 88–100, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 19.)
ADS Article Google Scholar
Dunn, R.R., 1987, Adaptive Optical System at NSO/Sac Peak, LEST Technical Report 28, LEST Foundation, Stockholm. [ADS] (Cited on page 19.)
Google Scholar
Ealey, M.A. and Wellman, J.A., 1994, “Xinetics low-cost deformable mirrors with actuator replacement cartridges”, in Adaptive Optics in Astronomy, Kailua, Kona, HI, USA, 17 March 1994, (Eds.) Ealey, M.A., Merkle, F., vol. 2201 of Proc. SPIE, pp. 680–687, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 22 and 32.)
ADS Article Google Scholar
Fienup, J.R., Thelen, B.J., Paxman, R.G. and Carrara, D.A., 1998, “Comparison of phase diversity and curvature wavefront sensing”, in Adaptive Optical System Technologies, Kona, HI, USA, 23 March 1998, (Eds.) Bonaccini, D., Tyson, R.K., vol. 3353 of Proc. SPIE, pp. 930–940, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Fried, D.L., 1966a, “Limiting Resolution Looking Down Through the Atmosphere”, J. Opt. Soc. Am., 56, 1380–1384. [DOI], [ADS] (Cited on page 12.)
ADS Article Google Scholar
Fried, D.L., 1966b, “Optical Resolution Through a Randomly Inhomogeneous Medium for Very Long and Very Short Exposures”, J. Opt. Soc. Am., 56, 1372–1379. [DOI], [ADS] (Cited on page 12.)
ADS Article Google Scholar
Fugate, R.Q., 2003, “The Starfire Optical Range 3.5-m Adaptive Optical Telescope”, in Large Ground-based Telescopes, Waikoloa, HI, USA, 22 August 2002, (Eds.) Oschmann, J.M., Stepp, L.M., vol. 4837 of Proc. SPIE, pp. 934–943, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 16.)
ADS Article Google Scholar
Fusco, T. and Conan, J.-M., 2004, “On- and off-axis statistical behavior of adaptive-opticscorrected short-exposure Strehl ratio”, J. Opt. Soc. Am. A, 21, 1277–1289. [DOI], [ADS] (Cited on page 34.)
ADS MathSciNet Article Google Scholar
Fusco, T., Petit, C., Rousset, G., Sauvage, J.-F., Dohlen, K., Mouillet, D., Charton, J., Baudoz, P., Kasper, M., Fedrigo, E., Rabou, P., Feautrier, P., Downing, M., Gigan, P., Conan, J.-M., Beuzit, J.-L., Hubin, N., Wildi, F. and Puget, P., 2006a, “Design of the extreme AO system for SPHERE, the planet finder instrument of the VLT”, in Advances in Adaptive Optics II, Orlando, FL, USA, 24 May 2006, (Eds.) Ellerbroek, B.L., Bonaccini Calia, D., vol. 6272 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 32.)
Fusco, T., Rousset, G., Sauvage, J.-F., Petit, C., Beuzit, J.-L., Dohlen, K., Mouillet, D., Charton, J., Nicolle, M., Kasper, M., Baudoz, P. and Puget, P., 2006b, “High-order adaptive optics requirements for direct detection of extrasolar planets: Application to the SPHERE instrument”, Opt. Express, 14, 7515. [DOI], [ADS] (Cited on page 32.)
ADS Article Google Scholar
Gendron, E. and Léna, P., 1994, “Astronomical adaptive optics I. Modal control optimization”, Astron. Astrophys., 291, 337–347. [ADS] (Cited on page 39.)
ADS Google Scholar
Gendron, E. and Léna, P., 1995, “Astronomical adaptive optics. II. Experimental results of an optimized modal control”, Astron. Astrophys. Suppl., 111, 153. [ADS] (Cited on page 39.)
ADS Google Scholar
Georges III, J.A., Dorrance, P., Gleichman, K., Jonik, J., Liskow, D., Lapprich, H., Naik, V., Parker, S., Paxman, R., Warmuth, M., Wilson, A. and Zaugg, T., 2007, “High-speed closedloop dual deformable-mirror phase-diversity testbed”, in Advanced Wavefront Control: Methods, Devices, and Applications V, San Diego, CA, USA, 29 August 2007, (Eds.) Carreras, R.A., Gonglewski, J.D., Rhoadarmer, T.A., vol. 6711 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 27.)
Goode, P., 2006, “The High Resolution 1.6 m Off-Axis Solar Telescope for BBSO — The NST”, 36th COSPAR Scientific Assembly, Beijing, China, 16–23 July 2006, conference paper. [ADS] (Cited on page 9.)
Google Scholar
Goode, P.R., Coulter, R., Gorceix, N., Yurchyshyn, V. and Cao, W., 2010, “The NST: First results and some lessons for ATST and EST”, Astron. Nachr., 331, 620. [DOI], [ADS] (Cited on page 9.)
ADS Article Google Scholar
Gratadour, D., Gendron, E. and Rousset, G., 2010, “Intrinsic limitations of Shack-Hartmann wavefront sensing on an extended laser guide source”, J. Opt. Soc. Am. A, 27, A171–A181. [DOI] (Cited on page 27.)
ADS Article Google Scholar
Graves, J.E., Northcott, M.J., Roddier, F.J., Roddier, C.A. and Close, L.M., 1998, “First light for Hokupa'a: 36-element curvature AO system at UH”, in Adaptive Optical System Technologies, Kona, HI, USA, 23 March 1998, (Eds.) Bonaccini, D., Tyson, R.K., vol. 3353 of Proc. SPIE, pp. 34–43, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Greenwood, D.P., 1977, “Bandwidth specification for adaptive optics systems”, J. Opt. Soc. Am., 67, 390–393. [DOI], [ADS] (Cited on page 38.)
ADS Article Google Scholar
Hardy, J.W., 1980, Solar Imaging Experiment: Final Report, Feb. 1979–Jun. 1980, AFGL-TR80-0338, Air Force Geophysics Laboratory, Hanscom AFB, Lexington, MA. [ADS] (Cited on page 19.)
Google Scholar
Hardy, J.W., 1998, Adaptive Optics for Astronomical Telescopes, vol. 16 of Oxford Series in Optical and Imaging Sciences, Oxford University Press, Oxford; New York (Cited on pages 11, 12, 13, 26, 33, 34, 38, 42, 43, 65, and 67.)
Hasan, S.S., 2010, “The Indian National Large Solar Telescope (NLST)”, in Solar and Stellar Variability: Impact on Earth and Planets, Brazil, 3–7 August 2009, (Eds.) Kosovichev, A.G., Andrei, A.H., Roelot, J.-P., vol. 264 of IAU Symposia, pp. 499–504, Cambridge University Press, Cambridge; New York. [DOI], [ADS] (Cited on page 59.
ADS Google Scholar
Herrmann, J., 1981, “Cross coupling and aliasing in modal wave-front estimation”, J. Opt. Soc. Am., 71, 989–992. [DOI], [ADS] (Cited on page 45.)
ADS Article Google Scholar
Hill, F., Beckers, J.M., Brandt, P., Briggs, J., Brown, T., Brown, W., Collados, M., Denker, C., Fletcher, S., Hegwer, S., Horst, T., Komsa, M., Kuhn, J.R., Lecinski, A., Lin, H., Oncley, S., Penn, M., Rimmele, T.R., Socas-Navarro, H. and Streander, K., 2004, “Solar site testing for the Advanced Technology Solar Telescope”, in Ground-based Telescopes, Glasgow, Scotland, UK, 21 June 2004, (Ed.) Oschmann Jr, J.M., vol. 5489 of Proc. SPIE, pp. 122–129, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 22.)
ADS Article Google Scholar
Hill, F., Beckers, J.M., Brandt, P., Briggs, J., Brown, T., Brown, W., Collados, M., Denker, C., Fletcher, S., Hegwer, S., Horst, T., Komsa, M., Kuhn, J.R., Lecinski, A.R, Lin, H., Oncley, S., Penn, M., Radick, R., Rimmele, T.R., Socas-Navarro, H. and Streander, K., 2006, “Site testing for the Advanced Technology Solar Telescope”, in Ground-based and Airborne Telescopes, Orlando, FL, USA, 24 May 2006, (Ed.) Stepp, L.M., vol. 6267 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 22.)
Hubbard, R.P., Rimmele, T.R., Schoening, W., Dalrymple, N., Poczulp, G. and Warner, M., 2006, “Controlling wavefront distortions across a thermal boundary”, in Ground-based and Airborne Telescopes, Orlando, FL, USA, 24 May 2006, (Ed.) Stepp, L.M., vol. 6267 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 62.)
Johnson, L.C., Gavel, D.T., Reinig, M. and Wiberg, D.M., 2008, “Wind estimation and prediction for adaptive optics control systems”, in Adaptive Optics Systems, Marseille, France, 23 June 2008, (Eds.) Hubin, N., Max, C.E., Wizinowich, P.L., vol. 7015 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 14.)
Keller, C.U., Plymate, C. and Ammons, S.M., 2003, “Low-cost solar adaptive optics in the infrared”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, HI, USA, 24 August 2002, (Eds.) Keil, S.L., Avakyan, S.V., vol. 4853 of Proc. SPIE, pp. 351–359, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 22 and 58.)
ADS Article Google Scholar
Kolmogorov, A., 1941, “The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers”, Dokl. Akad. Nauk. SSSR, 30, 301–305. [ADS] (Cited on pages 11 and 46.)
ADS MathSciNet Google Scholar
Kolmogorov, A.N., 1991, “The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers”, Proc. R. Soc. London, Ser. A, 434, 9–13. [ADS] (Cited on pages 11 and 46.)
ADS MathSciNet MATH Google Scholar
Kupke, R., Roddier, F.J. and Mickey, D., 1994, “Curvature-based wavefront sensor for use on extended patterns”, in Adaptive Optics in Astronomy, Kailua, Kona, HI, USA, 17 March 1994, (Eds.) Ealey, M.A., Merkle, F., vol. 2201 of Proc. SPIE, pp. 519–527, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Kupke, R., Roddier, F.J. and Mickey, D.L., 1998, “Wavefront curvature sensing on extended arbitrary scenes: simulation results”, in Adaptive Optical System Technologies, Kona, HI, USA, 23 March 1998, (Eds.) Bonaccini, D., Tyson, R.K., vol. 3353 of Proc. SPIE, pp. 918–929, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Langlois, M., Moretto, G., Richards, K., Hegwer, S. and Rimmele, T.R., 2004, “Solar multiconjugate adaptive optics at the Dunn Solar Telescope: preliminary results”, in Advancements in Adaptive Optics, Glasgow, Scotland, United Kingdom, 21 June 2004, (Eds.) Bonaccini Calia, D., Ellerbroek, B.L., Ragazzoni, R., vol. 5490 of Proc. SPIE, pp. 59–66, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 69.)
ADS Article Google Scholar
Löfdahl, M.G., 2007, “Multiframe deconvolution with space-variant point-spread functions by use of inverse filtering and fast Fourier transform”, Appl. Opt., 46, 4686–4693. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Löfdahl, M.G., 2010, “Evaluation of image shift measurement algorithms for solar Shack-Hartmann wavefront sensors”, Astron. Astrophys., 524, A90. [DOI], [arXiv:1009.3401] (Cited on page 26.)
Article Google Scholar
Löfdahl, M.G. and Scharmer, G.B., 1994, “Wavefront sensing and image restoration from focused and defocused solar images”, Astron. Astrophys. Suppl., 107, 243–264. [ADS] (Cited on pages 27 and 49.)
ADS Google Scholar
Löfdahl, M.G., van Noort, M.J. and Denker, C., 2007, “Solar image restoration”, in Modern Solar Facilities — Advanced Solar Science, Proceedings of a Workshop held at Göttingen, Germany, September, 27–29, 2006, (Eds.) Kneer, F., Puschmann, K.G., Wittmann, A.D., pp. 119–126, Universitätsverlag, Göttingen. [ADS], [Google Books] (Cited on pages 13 and 49.)
Google Scholar
López Ariste, A., 2010, “Themis Adaptive Optics”, personal communication (Cited on page 58.)
Google Scholar
Madec, P.-Y., 1999, “Control techniques”, in Adaptive Optics in Astronomy, (Ed.) Roddier, F., pp. 131–154, Cambridge University Press, Cambridge; New York. [ADS], [Google Books] (Cited on page 38.)
Chapter Google Scholar
Marchetti, E., Hubin, N.N., Fedrigo, E., Brynnel, J., Delabre, B., Donaldson, R., Franza, F., Conan, R., Le Louarn, M., Cavadore, C., Balestra, A., Baade, D., Lizon, J.-L., Gilmozzi, R., Monnet, G.J., Ragazzoni, R., Arcidiacono, C., Baruffolo, A., Diolaiti, E., Farinato, J., Vernet-Viard, E., Butler, D.J., Hippler, S. and Amorin, A., 2003, “MAD the ESO multi-conjugate adaptive optics demonstrator”, in Adaptive Optical System Technologies II, Waikoloa, HI, USA, 22 August 2002, (Eds.) Wizinowich, P.L., Bonaccini, D., vol. 4839 of Proc. SPIE, pp. 317–328, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 68.)
ADS Article Google Scholar
Marchetti, E., Brast, R., Delabre, B., Donaldson, R., Fedrigo, E., Frank, C., Hubin, N., Kolb, J., Lizon, J.-L., Marchesi, M., Oberti, S., Reiss, R., Soenke, C., Tordo, S., Baruffolo, A., Bagnara, P., Amorim, A. and Lima, J., 2008, “MAD on sky results in star oriented mode”, in Adaptive Optics Systems, Marseille, France, 23 June 2008, (Eds.) Hubin, N., Max, C.E., Wizinowich, P.L., vol. 7015 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 68.)
Marino, J., 2007, Long Exposure Point Spread Function Estimation from Solar Adaptive Optics Loop Data, Ph.D. Thesis, New Jersey Institute of Technology, Newark, NJ. [ADS]. Online version (accessed 2 February 2011): http://library1.njit.edu/etd/2000s/2007/njit-etd2007-048/njit-etd2007-048.html (Cited on pages 13, 44, 45, 46, and 47.)
Google Scholar
Marino, J. and Rimmele, T., 2010, “Estimation and application of the solar adaptive optics corrected long-exposure point spread function”, Appl. Opt., 49, G95–G104. [DOI] (Cited on pages 44, 47, 48, and 51.)
Article Google Scholar
Marino, J. and Rimmele, T., 2011, “Modeling the isoplanatic patch of solar Adaptive Optics”, in preparation (Cited on pages 36, 37, 38, 64, 65, 66, and 67.)
Google Scholar
Marino, J., Rimmele, T.R. and Christou, J.C., 2004, “Long-exposure point spread function estimation from adaptive optics loop data”, in Advancements in Adaptive Optics, Glasgow, Scotland, United Kingdom, 21 June 2004, (Eds.) Bonaccini Calia, D., Ellerbroek, B.L., Ragazzoni, R., vol. 5490 of Proc. SPIE, pp. 184–194, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 16.)
ADS Article Google Scholar
Masciadri, E., Vernin, J. and Bougeault, P., 2001, “3D numerical simulations of optical turbulence at the Roque de Los Muchachos Observatory using the atmospherical model Meso-Nh”, Astron. Astrophys., 365, 699–708. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
McKenna, D.L., Avila, R., Hill, J.M., Hippler, S., Salinari, P., Stanton, P.C. and Weiss, R., 2003, “LBT facility SCIDAR: recent results”, in Adaptive Optical System Technologies II, Waikoloa, HI, USA, 22 August 2002, (Eds.) Wizinowich, P.L., Bonaccini, D., vol. 4839 of Proc. SPIE, pp. 825–836, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
Michau, V., 2002, Calcul de la précision de mesure d’un analyseur de Shack-Hartmann fonctionnant avec une source étendue, Internal ONERA Report, ONERA, France (Cited on page 40.)
Google Scholar
Michau, V., Rousset, G. and Fontanella, J.C., 1993, “Wavefront Sensing from Extended Sources”, in Real Time and Post Facto Solar Image Correction, Proceedings of 13th NSO/SP Summer Workshop, Sunspot, New Mexico, 15–18 September 1992, (Ed.) Radick, R., vol. 13, pp. 124–128, NSO, Tucson, AZ (Cited on page 39.)
ADS Google Scholar
Michau, V., Conan, J.-M., Fusco, T., Nicolle, M., Robert, C., Velluet, M.-T. and Piganeau, E., 2006, “Shack-Hartmann wavefront sensing with extended sources”, in Atmospheric Optical Modeling, Measurement, and Simulation II, San Diego, CA, USA, 15 August 2006, (Eds.) Hammel, S.M., Kohnle, A., vol. 6303 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 39.)
Milton, N.M., Lloyd-Hart, M., Cheng, A., Georges III, J.A. and Angel, J.R.P., 2003, “Design and expected performance of an MCAO system for the Giant Magellan Telescope”, in Astronomical Adaptive Optics Systems and Applications, San Diego, CA, USA, 03 August 2003, (Eds.) Tyson, R.K., Lloyd-Hart, M., vol. 5169 of Proc. SPIE, pp. 238–249, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
Miura, N., Noto, Y., Kato, S., Kuwamura, S., Baba, N., Hanaoka, Y., Nagata, S., Ueno, S., Kitai, R. and Takami, H., 2008a, “Solar adaptive optics system at the Hida Observatory”, in Adaptive Optics Systems, Marseille, France, 23 June 2008, (Eds.) Hubin, N., Max, C.E., Wizinowich, P.L., vol. 7015 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 58.)
Miura, N., Yokoyama, F., Nefu, M., Kuwamura, S., Baba, N., Hanaoka, Y., Ueno, S., Nakatani, Y., Nagata, S., Kitai, R., Ichimoto, K. and Takami, H., 2008b, “Solar adaptive optics system at the Hida Observatory”, in Adaptive Optics Systems, 23–28 June 2008, Marseille, France, (Eds.) Hubin, N., Max, C.E., Wizinowich, P.L., vol. 7015 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 58.)
Miura, N., Noto, Y., Kato, S., Yokoyama, F., Kuwamura, S., Baba, N., Hanaoka, Y., Nagata, S., Ueno, S., Kitai, R., Ichimoto, K. and Takami, H., 2009, “Advances in solar adaptive optics system at the domeless solar telescope of the Hida Observatory”, in Astronomical and Space Optical Systems, San Diego, CA, USA, 2–3 August 2009, (Eds.) Warren, P.G., Marshall, C.J., Tyson, R.K., Lloyd-Hart, M., Heaney, J.B., Kvamme, E.T., vol. 7439 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 58.)
Miura, N., Noto, Y., Kato, S., Yokoyama, F., Kuwamura, S., Baba, N., Hanaoka, Y., Nagata, S., Ueno, S., Kitai, R., Ichimoto, K. and Takami, H., 2010, “Solar adaptive optics system using an electromagnetic deformable mirror”, Opt. Rev., 16, 558–561. [DOI], [ADS] (Cited on page 58.)
Article Google Scholar
Molodij, G., Roddier, F., Kupke, R. and Mickey, D.L., 2002, “Curvature Wavefront Sensor For Solar Adaptive Optics”, Solar Phys., 206, 189–207. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Noll, R.J., 1976, “Zernike polynomials and atmospheric turbulence”, J. Opt. Soc. Am., 66, 207–211. [DOI], [ADS] (Cited on pages 17, 38, and 46.)
ADS Article Google Scholar
Nordlund, Å. and Stein, R.F., 2009, “Accurate Radiation Hydrodynamics and MHD Modeling of 3-D Stellar Atmospheres”, in Recent Directions in Astrophysical Quantitative Spectroscopy and Radiation Hydrodynamics, Proceedings of the International Conference in Honor of Dimitri Mihalas for His Lifetime Scientific Contributions on the Occasion of His 70th Birthday, Boulder, Colorado, March 30–April 3, 2009, (Eds.) Hubeny, I., Stone, J.M., MacGregor, K., Werner, K., vol. 1171 of AIP Conf. Proc., pp. 242–259, American Institute of Physics, Melville, NY. [DOI], [ADS] (Cited on pages 5 and 6.) Nordlund, Å., Stein, R.F. and Asplund, M., 2009, “Solar Surface Convection”, Living Rev. Solar Phys., 6, lrsp-2009-2. [ADS]. URL (accessed 1 October 2010): http://www.livingreviews.org/lrsp-2009-2 (Cited on page 5.)
Google Scholar
Nordlund, Å, Stein, R.F. and Asplund, M., 2009, “Solar Surface Convection”, Living Rev. Solar Phys., 6, lrsp-2009-2. [ADS]. URL (accessed 1 October 2010): http://www.livingreviews.org/lrsp-2009-2 (Cited on page 5.)
Owner-Petersen, M., Darvann, T.A. and Engvold, O., 1993, “Design of the slow LEST wavefront sensor”, in Real Time and Post Facto Solar Image Correction, Proceedings of the 13th NSO/Sac Peak Summer Workshop, Sunspot, New Mexico, 15–18 September 1992, (Ed.) Radick, R., vol. 63–76 of NSO Conference Proceedings, NSO, Tucson, AZ (Cited on pages 40 and 75.)
Paxman, R.G., Seldin, J.H., Löfdahl, M.G., Scharmer, G.B. and Keller, C.U., 1996, “Evaluation of Phase-Diversity Techniques for Solar-Image Restoration”, Astrophys. J., 466, 1087. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Paxman, R.G., Thelen, B.J., Murphy, R.J., Gleichman, K.W. and Georges III, J.A., 2007, “Phasediverse adaptive optics for future telescopes”, in Advanced Wavefront Control: Methods, Devices, and Applications V, San Diego, CA, USA, 29 August 2007, (Eds.) Carreras, R.A., Gonglewski, J.D., Rhoadarmer, T.A., vol. 6711 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 27 and 73.)
Phelps, L., Rimmele, T.R., Hubbard, R.P. and Elmore, D., 2010, “The Advanced Technology Solar Telescope coudé lab thermal environment”, in Ground-based and Airborne Telescopes III, 27 June–2 July 2010, San Diego, California, USA, (Eds.) Stepp, L.M., Gilmozzi, R., Hall, H.J., vol. 7733 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on page 62.)
Poyneer, L. and Véran, J.-P., 2008, “Predictive wavefront control for adaptive optics with arbitrary control loop delays”, J. Opt. Soc. Am. A, 25, 1486. [DOI], [ADS] (Cited on page 14.)
ADS MathSciNet Article Google Scholar
Poyneer, L., van Dam, M. and Véran, J.-P., 2009, “Experimental verification of the frozen flow atmospheric turbulence assumption with use of astronomical adaptive optics telemetry”, J. Opt. Soc. Am. A, 26, 833. [DOI], [ADS] (Cited on page 14.)
ADS Article Google Scholar
Poyneer, L.A., 2003, “Scene-based Shack-Hartmann wave-front sensing: analysis and simulation”, Appl. Opt., 42, 5807–5815. [DOI], [ADS] (Cited on page 39.)
ADS Article Google Scholar
Quirrenbach, A., 2002, “Atmospheric turbulence”, CfAO Summer School, University of California in Santa Cruz, 3–9 August 2002, conference paper (Cited on pages 11, 12, and 33.)
Google Scholar
Ren, D., Rimmele, T.R., Hegwer, S. and Murray, L., 2003, “A Single-Mode Fiber Interferometer for the Adaptive Optics Wave-Front Test”, Publ. Astron. Soc. Pac., 115, 355–361. [DOI], [ADS] (Cited on page 28.)
ADS Article Google Scholar
Ren, D., Penn, M., Wang, H., Chapman, G. and Plymate, C., 2009, “A portable solar adaptive optics system”, in Solar Physics and Space Weather Instrumentation III, 4–6 August 2009, San Diego, CA, USA, (Eds.) Fineschi, S., Fennelly, J.A., vol. 7438 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 58.)
Richards, K., Rimmele, T.R., Hegwer, S.L., Upton, R.S., Marino, J., Gregory, S. and Goodrich, B., 2010, “The adaptive optics and wavefront correction systems for the Advanced Technology Solar Telescope”, in Adaptive Optics Systems II, 27 June 2010–2 July, San Diego, California, USA, (Eds.) Ellerbroek, B.L., Hart, M., Hubin, N., Wizinowich, P.L., vol. 7736 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on pages 30, 31, 61, and 62.)
Rigaut, F.J., Ellerbroek, B.L. and Flicker, R., 2000, “Principles, limitations, and performance of multiconjugate adaptive optics”, in Adaptive Optical Systems Technology, Munich, Germany, 29 March 2000, (Ed.) Wizinowich, P.L., vol. 4007 of Proc. SPIE, pp. 1022–1031, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 68.)
ADS Article Google Scholar
Righini, A., Cavallini, F. and Reardon, K.P., 2010, “Imaging performance of multi-etalon bidimensional spectrometers”, Astron. Astrophys., 515, A85. [DOI], [ADS] (Cited on page 50.)
ADS Article Google Scholar
Rimmele, T.R., 2000, “Solar adaptive optics”, in Adaptive Optical Systems Technology, Munich, Germany, 29 March 2000, (Ed.) Wizinowich, P.L., vol. 4007 of Proc. SPIE, pp. 218–231, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 16, 17, 20, and 40.)
ADS Article Google Scholar
Rimmele, T.R., 2004a, “Recent advances in solar adaptive optics”, in Advancements in Adaptive Optics, Glasgow, Scotland, United Kingdom, 21 June 2004, (Eds.) Bonaccini Calia, D., Ellerbroek, B.L., Ragazzoni, R., vol. 5490 of Proc. SPIE, pp. 34–46, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 15, 16, 28, and 56.)
ADS Article Google Scholar
Rimmele, T.R., 2004b, “Plasma Flows Observed in Magnetic Flux Concentrations and Sunspot Fine Structure Using Adaptive Optics”, Astrophys. J., 604, 906–923. [DOI], [ADS] (Cited on page 23.)
ADS Article Google Scholar
Rimmele, T.R. [ATST Science Team], 2005, ATST Science Requirements Document, SPEC-0001, ATST, Tucson, AZ. URL (accessed 1 October 2010): http://atst.nso.edu/files/docs/SPEC-0001.pdf (Cited on pages 6 and 60.)
Google Scholar
Rimmele, T.R. and Marino, J., 2006, “The Evershed Flow: Flow Geometry and Its Temporal Evolution”, Astrophys. J., 646, 593–604. [DOI], [ADS] (Cited on page 54.)
ADS Article Google Scholar
Rimmele, T.R. and Radick, R.R., 1998, “Solar adaptive optics at the National Solar Observatory”, in Adaptive Optical System Technologies, Kona, HI, USA, 23 March 1998, (Eds.) Bonaccini, D., Tyson, R.K., vol. 3353 of Proc. SPIE, pp. 72–81, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 19, 20, and 26.)
ADS Article Google Scholar
Rimmele, T.R., Richards, K., Hegwer, S., Fletcher, S., Gregory, S., Moretto, G., Didkovsky, L.V., Denker, C.J., Dolgushin, A., Goode, P.R., Langlois, M., Marino, J. and Marquette, W., 2004, “First results from the NSO/NJIT solar adaptive optics system”, in Telescopes and Instrumentation for Solar Astrophysic, San Diego, CA, USA, 7 August 2003, (Eds.) Fineschi, S., Gummin, M.A., vol. 5171 of Proc. SPIE, pp. 179–186, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 32.)
ADS Article Google Scholar
Rimmele, T.R., Keil, S. and Wagner, J., 2006a, “The unique scientific capabilities of the Advanced Technology Solar Telescope”, 36th COSPAR Scientific Assembly, Beijing, China, 16–23 July 2006, conference paper. [ADS] (Cited on pages 9 and 60.)
Google Scholar
Rimmele, T.R., Richards, K., Roche, J., Hegwer, S. and Tritschler, A., 2006b, “Progress with solar multi-conjugate adaptive optics at NSO”, in Advances in Adaptive Optics II, 24 May 2006, Orlando, FL, USA, (Eds.) Ellerbroek, B.L., Bonaccini Calia, D., vol. 6272 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 73.)
Rimmele, T.R., Richards, K., Roche, J.M., Hegwer, S.L., Hubbard, R.P., Hansen, E.R., Goodrich, B. and Upton, R.S., 2006c, “The wavefront correction system for the Advanced Technology Solar Telescope”, in Advances in Adaptive Optics II, 24 May 2006, Orlando, FL, USA, (Eds.) Ellerbroek, B.L., Bonaccini Calia, D., vol. 6272 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 36, 61, 62, and 68.)
Rimmele, T.R., Hegwer, S., Richards, K., Wöger, F., Marino, J., Schmidt, D. and Waldmann, T., 2009, “Solar Multi-Conjugate Adaptive Optics at the Dunn Solar Telescope”, in Advanced Maui Optical and Space Surveillance Technologies Conference, Wailea, Maui, HI, September 16–19, 2008, Curran Associates, Red Hook, NY. [ADS]. Online version (accessed 2 December 2010): http://www.amostech.com/TechnicalPapers/2008.cfm (Cited on page 69.)
Google Scholar
Rimmele, T.R., Hegwer, S., Marino, J., Richards, K., Schmidt, D., Waldmann, T. and Wöger, F., 2010a, “Solar Multi-Conjugate Adaptive Optics at the Dunn Solar Telescope”, in Adaptative Optics for Extremely Large Telescopes (AO4ELT), Paris, France, 22–26 June 2009, (Eds.) Clénet, Y., Conan, J.-M., Fusco, T., Rousset, G., EDP Sciences, Les Ulis. [DOI], [ADS] (Cited on page 69.)
Google Scholar
Rimmele, T.R., Wagner, J., Keil, S., Elmore, D., Hubbard, R.P., Hansen, E., Warner, M., Jeffers, P., Phelps, L., Marshall, H., Goodrich, B., Richards, K., Hegwer, S., Kneale, R. and Ditsler, J., 2010b, “The Advanced Technology Solar Telescope: beginning construction of the world’s largest telescope”, in Ground-based and Airborne Telescopes III, 27 June–2 July 2010, San Diego, California, USA, (Eds.) Stepp, L.M., Gilmozzi, R., Hall, H.J., vol. 7733 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on page 9.)
Rimmele, T.R., Wöger, F., Marino, J., Richards, K., Hegwer, S., Berkefeld, T., Soltau, D., Schmidt, D. and Waldmann, T., 2010c, “Solar multi-conjugate adaptive optics at the Dunn Solar Telescope”, in Adaptive Optics Systems II, 27 June 2010–2 July, San Diego, California, USA, (Eds.) Ellerbroek, B.L., Hart, M., Hubin, N., Wizinowich, P.L., vol. 7736 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on pages 40, 69, 71, 73, and 75.)
Robert, C., Conan, J.-M., Michau, V., Fusco, T. and Vedrenne, N., 2006, “Scintillation and phase anisoplanatism in Shack-Hartmann wavefront sensing”, J. Opt. Soc. Am. A, 23, 613–624. [DOI], [ADS] (Cited on page 42.)
ADS Article Google Scholar
Roberts Jr, L.C., Perrin, M.D., Marchis, F., Sivaramakrishnan, A., Makidon, R.B., Christou, J.C., Macintosh, B.A., Poyneer, L.A., van Dam, M.A. and Troy, M., 2004, “Is that really your Strehl ratio?”, in Advancements in Adaptive Optics, Glasgow, Scotland, UK, 21 June 2004, (Eds.) Bonaccini Calia, D., Ellerbroek, B.L., Ragazzoni, R., vol. 5490 of Proc. SPIE, pp. 504–515, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 44.)
ADS Article Google Scholar
Roddier, F., 1988, “Curvature sensing and compensation: a new concept in adaptive optics”, Appl. Opt., 27, 1223–1225. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Roddier, F., 1990, “Wavefront sensing and the irradiance transport equation”, Appl. Opt., 29, 1402–1403. [DOI], [ADS] (Cited on page 24.)
ADS Article Google Scholar
Roddier, F. (Ed.), 1999, Adaptive Optics in Astronomy, Cambridge University Press, Cambridge; New York. [ADS], [Google Books] (Cited on pages 11, 26, and 42.)
Google Scholar
Roddier, F., Graves, J.E., McKenna, D.L. and Northcott, M.J., 1992, “The UH (University of Hawaii) wavefront curvature sensor”, in Adaptive Optics for Large Telescopes, Summaries of papers presented at the Topical Meeting, August 17–21, 1992, Lahaina, Maui, Hawaii, vol. 19 of Technical Digest, pp. 170–172, Optical Society of America, Washington, DC. [ADS] (Cited on page 24.)
ADS Google Scholar
Roddier, F.J., 1991, “Wavefront curvature sensing and compensation methods in adaptive optics”, in Propagation Engineering: Fourth in a Series, Orlando, FL, USA, 3 April 1991, (Eds.) Bissonnette, L.R., Miller, W.B., vol. 1487 of Proc. SPIE, pp. 123–128, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 24.)
ADS Google Scholar
Roggemann, M.C. and Welsh, B., 1996, Imaging Through Turbulence, CRC Press, Boca Raton, FL (Cited on pages 11 and 12.)
Google Scholar
Scharmer, G.B., Shand, M., Löfdahl, M.G., Dettori, P.M. and Wei, W., 2000, “Workstation-based solar/stellar adaptive optics system”, in Adaptive Optical Systems Technology, Munich, Germany, 29 March 2000, (Ed.) Wizinowich, P.L., vol. 4007 of Proc. SPIE, pp. 239–250, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 22, 31, and 55.)
ADS Article Google Scholar
Scharmer, G.B., Gudiksen, B.V., Kiselman, D., Löfdahl, M.G. and Rouppe van der Voort, L.H.M., 2002, “Dark cores in sunspot penumbral filaments”, Nature, 420, 151–153. [DOI], [ADS] (Cited on pages 5 and 7.)
ADS Article Google Scholar
Scharmer, G.B., Bjelksjo, K., Korhonen, T.K., Lindberg, B. and Petterson, B., 2003, “The 1-meter Swedish solar telescope”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, HI, USA, 24 August 2002, (Eds.) Keil, S.L., Avakyan, S.V., vol. 4853 of Proc. SPIE, pp. 341–350, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 22, 25, 31, and 55.)
ADS Article Google Scholar
Scharmer, G.B., Langhans, K., Kiselman, D. and Löfdahl, M.G., 2007, “Recent High Resolution Observations and Interpretations of Sunspot Fine Structure”, in New Solar Physics with Solar-B Mission, (Eds.) Shibata, K., Nagata, S., Sakurai, T., vol. 369 of ASP Conference Series, p. 71, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 5.)
ADS Google Scholar
Scharmer, G.B., Narayan, G., Hillberg, T., de la Cruz Rodriguez, J., Löfdahl, M.G., Kiselman, D., Sütterlin, P., van Noort, M.J. and Lagg, A., 2008, “CRISP Spectropolarimetric Imaging of Penumbral Fine Structure”, Astrophys. J. Lett., 689, L69–L72. [DOI], [ADS], [arXiv:0806.1638 [astro-ph]] (Cited on pages 9 and 50.)
ADS Article Google Scholar
Scharmer, G.B., Löfdahl, M.G., van Werkhoven, T.I.M. and de la Cruz Rodriguez, J., 2010, “Highorder aberration compensation with Multi-frame Blind Deconvolution and Phase Diversity image restoration techniques”, arXiv e-print. [ADS], [arXiv:1007.1236] (Cited on pages 44, 48, and 49.)
Google Scholar
Schlichenmaier, R., Rezaei, R., Bello González, N. and Waldmann, T.A., 2010, “The formation of a sunspot penumbra”, Astron. Astrophys., 512, L1. [DOI], [ADS] (Cited on page 50.)
ADS Article Google Scholar
Schmidt, D. and von der Lühe, O., 2007, “Optical wavefront differentiation: wavefront sensing for solar adaptive optics based on a LCD”, in Adaptive Optics for Laser Systems and Other Applications, Prague, Czech Republic, 18 April 2007, (Eds.) Cheriaux, G., Hooker, C.J., Stupka, M., vol. 6584 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 20.)
Seldin, J.H. and Paxman, R.G., 1994, “Phase-diverse speckle reconstruction of solar data”, in Image Reconstruction and Restoration, San Diego, CA, USA, 26 July 1994, (Eds.) Schulz, T.J., Snyder, D.L., vol. 2302 of Proc. SPIE, pp. 268–280, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Seldin, J.H., Paxman, R.G., Carrara, D.A., Keller, C.U. and Rimmele, T.R., 1999, “Deconvolution of narrowband solar images using aberrations estimated from phase-diverse imagery”, in Digital Image Recovery and Synthesis IV, Denver, CO, USA, 20 July 1999, (Eds.) Schulz, T.J., Idell, P.S., vol. 3815 of Proc. SPIE, pp. 155–163, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Seykora, E.J., 1993, “Solar scintillation and the monitoring of solar seeing”, Solar Phys., 145, 389–397. [DOI], [ADS] (Cited on page 34.)
ADS Article Google Scholar
Shand, M., Scharmer, G.B. and Wei, W., 1999, “Correlation Tracking and Adaptive Optics Control Using Off-The-Shelf Workstation Technology”, in High Resolution Solar Physics: Theory, Observations, and Techniques, Proceedings of the 19th NSO/Sac Peak Summer Workshop, Sunspot, New Mexico, USA, 28 September-2 October 1998, (Eds.) Rimmele, T.R., Balasubramaniam, K.S., Radick, R.R., vol. 183 of ASP Conference Series, pp. 231–238, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on pages 25, 26, and 31.)
ADS Google Scholar
Soltau, D., Berkefeld, T., Sánchez Capuchino, J., Collados Vera, M., Del Moro, D., Löfdahl, M.G. and Scharmer, G.B., 2010, “Adaptive optics and MCAO for the 4-m European Solar Telescope EST”, in Adaptive Optics Systems II, 27 June 2010–2 July, San Diego, California, USA, (Eds.) Ellerbroek, B.L., Hart, M., Hubin, N., Wizinowich, P.L., vol. 7736 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 73.)
Southwell, W.H., 1980, “Wave-front estimation from wave-front slope measurements”, J. Opt. Soc. Am., 70, 998–1006. [DOI], [ADS] (Cited on page 42.)
ADS Article Google Scholar
Suematsu, Y., Ichimoto, K., Katsukawa, Y., Otsubo, M., Tsuneta, S., Nakagiri, M., Noguchi, M., Tamura, T., Kato, Y., Hara, H., Miyashita, M., Shimizu, T., Kubo, M. and Sakamoto, Y., 2007, “Optical Performance of the Solar Optical Telescope aboard HINODE”, Bull. Am. Astron. Soc., 38, 217. [ADS] (Cited on page 33.)
Google Scholar
Tatarskii, V.I., 1967, “Ray trajectories in a medium with weak random fluctuations of refractive index”, Radiophys. Quantum Electron., 10, 121–125. [DOI], [ADS] (Cited on page 11.)
ADS Article Google Scholar
Tyson, R.K., 2011, Principles of Adaptive Optics, Series in Optics and Optoelectronics, CRC Press, Boca Raton, FL, 3rd edn. [Google Books] (Cited on pages 11, 26, 38, and 42.)
Google Scholar
Valenzuela, J.R., Fessler, J.A. and Paxman, R.G., 2010, “Joint estimation of Stokes images and aberrations from phase-diverse polarimetric measurements”, J. Opt. Soc. Am. A, 27, 1185. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Valley, G.C. and Wandzura, S.M., 1979, “Spatial correlation of phase-expansion coefficients for propagation through atmospheric turbulence”, J. Opt. Soc. Am., 69, 712–717. [DOI], [ADS] (Cited on page 34.)
ADS Article Google Scholar
van Kampen, W.C. and Paxman, R.G., 1998, “Multiframe blind deconvolution of infinite-extent objects”, in Propagation and Imaging through the Atmosphere II, San Diego, CA, USA, 22 July 1998, (Ed.) Bissonnette, L.R., vol. 3433 of Proc. SPIE, pp. 296–307, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
van Noort, M.J. and Rouppe van der Voort, L.H.M., 2006, “High-Resolution Observations of Fast Events in the Solar Chromosphere”, Astrophys. J. Lett., 648, L67–L70. [DOI], [ADS] (Cited on pages 50 and 51.)
ADS Article Google Scholar
van Noort, M.J., Rouppe van der Voort, L. and Löfdahl, M.G., 2005, “Solar Image Restoration By Use Of Multi-frame Blind De-convolution With Multiple Objects And Phase Diversity”, Solar Phys., 228, 191–215. [DOI], [ADS] (Cited on page 49.)
ADS Article Google Scholar
Vargas Domínguez, S., Rouppe van der Voort, L., Bonet, J.A., Martínez Pillet, V., van Noort, M.J. and Katsukawa, Y., 2008, “Moat Flow in the Vicinity of Sunspots for Various Penumbral Configurations”, Astrophys. J., 679, 900–909. [DOI], [ADS], [arXiv:0802.1457] (Cited on page 50.)
ADS Article Google Scholar
Védrenne, N., Michau, V., Robert, C. and Conan, J.-M., 2007, “Shack-Hartmann wavefront estimation with extended sources: anisoplanatism influence”, J. Opt. Soc. Am. A, 24, 2980–2993. [DOI], [ADS] (Cited on page 42.)
ADS Article Google Scholar
Veran, J.-P., Rigaut, F., Maitre, H. and Rouan, D., 1997, “Estimation of the adaptive optics longexposure point-spread function using control loop data”, J. Opt. Soc. Am. A, 14, 3057–3069. [DOI], [ADS] (Cited on pages 44 and 45.)
ADS Article Google Scholar
Vernin, J., Masciadri, E. and Avila, R., 1998, “New approaches in atmospheric optics: generalized scidar and seeing prediction”, New Astron. Rev., 42, 405–408. [DOI], [ADS] (Cited on page 36.)
ADS Article Google Scholar
Vögler, A. and Schüssler, M., 2007, “A solar surface dynamo”, Astron. Astrophys., 465, L43–L46. [DOI], [ADS], [arXiv:astro-ph/0702681] (Cited on page 5.)
Article Google Scholar
Volkmer, R., 2008, “The Solar Telescope GREGOR”, in 12th European Solar Physics Meeting, Freiburg, Germany, 8–12 September 2008, (Ed.) Peter, H., KIS, Freiburg. [ADS]. Online version (accessed 1 October 2010): http://espm.kis.uni-freiburg.de/ (Cited on page 9.)
Google Scholar
Volkmer, R., von der Lühe, O., Kneer, F., Staude, J., Hofmann, A., Schmidt, W., Sobotka, M., Soltau, D., Wiehr, E., Wittmann, A. and Berkefeld, T., 2003, “GREGOR: the new 1.5m solar telescope on Tenerife”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, HI, USA, 24 August 2002, (Eds.) Keil, S.L., Avakyan, S.V., vol. 4853 of Proc. SPIE, pp. 360–369, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 9.)
ADS Article Google Scholar
Volkmer, R., von der Lühe, O., Kneer, F., Staude, J., Berkefeld, T., Caligari, P., Halbgewachs, C., Heidecke, F., Schmidt, W., Soltau, D., Nicklas, H., Wittmann, A., Balthasar, H., Hofmann, A., Strassmeier, K., Sobotka, M., Klvaňa, M. and Collados, M., 2006, “The new 1.5m solar telescope GREGOR: first light and start of commissioning”, in Ground-based and Airborne Telescopes, (Ed.) Stepp, L.M., vol. 6267 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 9.)
Volkmer, R., von der Lühe, O., Denker, C., Solanki, S.K., Balthasar, H., Berkefeld, T., Caligari, P., Collados, M., Fischer, A., Halbgewachs, C., Heidecke, F., Hofmann, A., Klvaňa, M., Kneer, F., Lagg, A., Popow, E., Schmidt, D., Schmidt, W., Sobotka, M., Soltau, D. and Strassmeier, K.G., 2010, “GREGOR solar telescope: Design and status”, Astron. Nachr., 331, 624. [DOI], [ADS] (Cited on page 9.)
ADS Article Google Scholar
von der Lühe, O., 1983, “A study of a correlation tracking method to improve imaging quality of ground-based solar telescopes”, Astron. Astrophys., 119, 85–94. [ADS] (Cited on pages 25, 31, and 42.)
ADS Google Scholar
von der Lühe, O., 1988, “Wavefront error measurement technique using extended, incoherent light sources”, Opt. Eng., 27, 1078–1087. [ADS] (Cited on pages 19 and 20.)
ADS Article Google Scholar
von der Lühe, O., Widener, A.L., Rimmele, T.R., Spence, G. and Dunn, R.B., 1989, “Solar feature correlation tracker for ground-based telescopes”, Astron. Astrophys., 224, 351–360. [ADS] (Cited on pages 22, 25, and 28.)
ADS Google Scholar
von der Lühe, O., Soltau, D., Berkefeld, T. and Schelenz, T., 2003, “KAOS: Adaptive optics system for the Vacuum Tower Telescope at Teide Observatory”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, HI, USA, 24 August 2002, (Eds.) Keil, S.L., Avakyan, S.V., vol. 4853 of Proc. SPIE, pp. 187–193, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on pages 22, 31, and 55.)
ADS Article Google Scholar
von der Lühe, O., Berkefeld, T. and Soltau, D., 2005, “Multi-conjugate solar adaptive optics at the Vacuum Tower Telescope on Tenerife”, C. R. Physique, 6, 1139–1147. [DOI], [ADS] (Cited on pages 69, 70, and 71.)
ADS Article Google Scholar
Wagner, J., Rimmele, T.R., Keil, S., Hubbard, R.P., Hansen, E., Phelps, L., Warner, M., Goodrich, B., Richards, K., Hegwer, S., Kneale, R. and Ditsler, J., 2008, “Advanced Technology Solar Telescope: a progress report”, in Ground-based and Airborne Telescopes II, (Eds.) Stepp, L.M., Gilmozzi, R., vol. 7012 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 9.)
Warmuth, M.W., Parker, S.W., Wilson, A.J., Gleichman, K.W., Paxman, R.G., Thelen, B.J., Murphy, R.J., Hunt, J.D. and LeBlanc, J.W., 2008, “Operation of phase-diverse adaptive-optics with extended scenes”, in Advanced Wavefront Control: Methods, Devices, and Applications VI, San Diego, CA, USA, 14 August 2008, (Eds.) Gonglewski, J.D., Carreras, R.A., Rhoadarmer, T.A., vol. 7093 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 27.)
Williams, D.R., 2000, “Adaptive Optics for the Human Eye”, Bull. Am. Astron. Soc., 32, 750. [ADS] (Cited on page 27.)
ADS Google Scholar
Wöger, F. and Rimmele, T., 2009, “Effect of anisoplanatism on the measurement accuracy of an extended-source Hartmann-Shack wavefront sensor”, Appl. Opt., 48, A35–A46. [DOI], [ADS] (Cited on pages 42, 48, and 75.)
ADS Article Google Scholar
Wöger, F. and von der Lühe, O., 2008, “KISIP: a software package for speckle interferometry of adaptive optics corrected solar data”, in Advanced Software and Control for Astronomy II, Marseille, France, 26 June 2008, (Eds.) Bridger, A., Radziwill, N.M., vol. 7019 of Proc. SPIE, SPIE, Bellingham, WA. [DOI], [ADS] (Cited on page 49.)
Wöger, F., von der Lühe, O. and Reardon, K., 2008, “Speckle interferometry with adaptive optics corrected solar data”, Astron. Astrophys., 488, 375–381. [DOI], [ADS] (Cited on pages 44, 49, and 50.)
ADS Article Google Scholar
Wöger, F., Uitenbroek, H., Tritschler, A., McBride, W., Elmore, D., Rimmele, T.R., Cowan, B., Wampler, S. and Goodrich, B., 2010, “The ATST Visible Broadband Imager: A Case Study For Real-time Image Reconstruction and Optimal Data Handling”, in Ground-based and Airborne Instrumentation for Astronomy III, 27 June 2010-2 July, San Diego, California, USA, (Eds.) McLean, I.S., Ramsay, S.K., Takami, H., vol. 7735 of Proc. SPIE, SPIE, Bellingham, WA. [DOI] (Cited on page 50.)
Zuccarello, F. [EST Team], 2009, “EST: the European future of solar ground-based observations”, Mem. Soc. Astron. Ital., 80, 243. [ADS] (Cited on page 59.)
ADS Google Scholar

Download references

Acknowledgments

I am grateful to my adaptive optics colleagues whose work this article is based on and to the referees for many valuable comments. Many thanks to Simon Rimmele for his assistance with LATEX formatting and the bibliography. Friedrich Wöger provided valuable comments to the manuscript. My thanks to the Living Reviews Back Office for their patience.

Author information

Affiliations

National Solar Observatory, 62, Sunspot, 88340, NM, USA
Thomas R. Rimmele
National Solar Observatory, 62, Sunspot, 88340, NM, USA
Jose Marino

Authors

Thomas R. Rimmele
View author publications
You can also search for this author in PubMed Google Scholar
Jose Marino
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas R. Rimmele.

Electronic supplementary material

41116_2011_2_MOESM1_ESM.mpg

mpg-Movie (229.625 KB) Still from a movie showing Focault knife-edge wavefront sensor applied to the planet Venus. A beam splitter arrangement images four images of Venus onto pairs of orthogonal knife edges. This knife edge configuration encodes wavefront gradients as intensity fluctuations in the pupil plane. The movie shows the temporal evolution of these patterns and clearly shows how wavefront aberrations are carried across the telescope aperture by the wind.

Electronic supplementary material

41116_2011_2_MOESM2_ESM.mpg

mpg-Movie (782.873046875 KB) Still from a movie showing Principle of correlating Shack-Hartmann wavefront sensor. Crosscorrelation techniques are used to track the low contrast granulation images or any other extended object of sufficient contrast (Rimmele and Radick, 1998). The movie shows a time sequence of wavefront sensor camera images with 12 subapertures across the pupil of the DST. The cross-correlation functions of the subaperture images of granulation are shown on the right.

Electronic supplementary material

41116_2011_2_MOESM3_ESM.mpg

mpg-Movie (5807.69238281 KB) Still from a movie showing Long exposure (3 s) granulation image recorded with AO76 (top) and with just tip/tilt correction applied (bottom). The movie shows the real time video sequence obtained during first light with AO76. The system is locked on a small pore. The AO is turned off several time during the sequence to show the uncorrected image quality delivered by the DST.

Electronic supplementary material

41116_2011_2_MOESM4_ESM.mpg

mpg-Movie (6274.92773438 KB) Still from a movie showing Speckle reconstructed g-band movie of granulation and g-band bright points near the solar limb. The FOV is 2’ × 2’. The lower left corner zooms in on an area with magnetic bright points (courtesy of F. Wöger, NSO).

Electronic supplementary material

41116_2011_2_MOESM5_ESM.mpg

mpg-Movie (13828.90625 KB) Still from a movie showing Speckle reconstructed g-band image sequence that captures the formation of a sunspot penumbra (from Schlichenmaier et al., 2010).

Electronic supplementary material

41116_2011_2_MOESM6_ESM.mpg

mpg-Movie (12914.0039062 KB) Still from a movie showing MOMFBD reconstructed image and movie of chromospheric Hα fine structure (from van Noort and Rouppe van der Voort, 2006).

Electronic supplementary material

41116_2011_2_MOESM7_ESM.mpg

mpg-Movie (1536.15917969 KB) Still from a movie showing KAOS: uncorrected granulation movie (courtesy of T. Berkefeld, KIS).

Electronic supplementary material

41116_2011_2_MOESM8_ESM.mpg

mpg-Movie (2162.17773438 KB)Still from a movie showing KAOS: corrected granulation movie (courtesy of T. Berkefeld, KIS). (For video see appendix)

Rights and permissions

Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Reprints and Permissions

About this article

Cite this article

Rimmele, T.R., Marino, J. Solar Adaptive Optics. Living Rev. Sol. Phys. 8, 2 (2011). https://doi.org/10.12942/lrsp-2011-2

Download citation

Published: 10 June 2011
DOI: https://doi.org/10.12942/lrsp-2011-2

Keywords

Point Spread Function
Adaptive Optic
Solar Telescope
Adaptive Optic System
Deformable Mirror

Abstract

Introduction

Adaptive Optics Basics

Atmospheric turbulence

Design of an AO system

Solar AO challenges: difference between night and day

A Brief History of Solar AO

The Correlating Shack-Hartmann Wavefront Sensor

Potential alternatives to the correlating SHWFS

AO System Implementation

DST AO system: an example

Wavefront sensor

Wavefront sensor and reconstructor processor unit

Deformable mirror

AO76 System Performance and Wavefront Error Budget

Predicted performance based on error budget

Wavefront fitting error

Aliasing error

Angular anisoplanatism error

Bandwidth error

Wavefront sensor measuring error

Wavefront sensor anisoplanatism noise

Non-common path error

Tip/tilt error

Total error

Measured performance of AO

Long exposure PSF estimation from AO telemetry

Measured AO system performance

The Case for Post-Facto Processing

Short exposure

Long exposure

Overview of Operational Solar AO Systems

The Swedish Solar Telecope (SST) AO system

Kiepenheuer Institute Adaptive Optics System (KAOS)

Adaptive optics for the infrared at the McMath-Pierce Telescope

Systems under development

Future Developments

AO for large aperture solar telescopes

GREGOR and NST conventional AO

High order AO for the ATST

Angular anisoplanatism: a serious challenge for large aperture solar telescopes

Chromatic ansisoplanatism

Multi-Conjugate Adaptive Optics (MCAO)

Ground-Layer Adaptive Optics (GLAO)

Summary

References

Acknowledgments

Author information

Affiliations

Corresponding author

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Electronic supplementary material

Rights and permissions

About this article

Cite this article

Share this article

Keywords