Abstract
Kinetic plasma physics of the solar corona and solar wind are reviewed with emphasis on the theoretical understanding of the in situ measurements of solar wind particles and waves, as well as on the remote-sensing observations of the solar corona made by means of ultraviolet spectroscopy and imaging. In order to explain coronal and interplanetary heating, the micro-physics of the dissipation of various forms of mechanical, electric and magnetic energy at small scales (e.g., contained in plasma waves, turbulences or non-uniform flows) must be addressed. We therefore scrutinise the basic assumptions underlying the classical transport theory and the related collisional heating rates, and also describe alternatives associated with wave-particle interactions. We elucidate the kinetic aspects of heating the solar corona and interplanetary plasma through Landau- and cyclotron-resonant damping of plasma waves, and analyse in detail wave absorption and micro instabilities. Important aspects (virtues and limitations) of fluid models, either single- and multi-species or magnetohydrodynamic and multi-moment models, for coronal heating and solar wind acceleration are critically discussed. Also, kinetic model results which were recently obtained by numerically solving the Vlasov-Boltzmann equation in a coronal funnel and hole are presented. Promising areas and perspectives for future research are outlined finally.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Scope of the article and previous reviews
The kinetic physics of the solar corona and solar wind is reviewed, whereby emphasis is placed on the progress made in the theoretical understanding of the properties of thermal particles and plasma waves as measured in situ in the solar wind. Also, new results on the kinetic state of the corona will be addressed, which were obtained through remote-sensing solar observations and by means of visible-light and VUV/EUV (Vacuum/Extreme Ultraviolet) spectroscopy and imaging, capabilities provided especially by the optical instruments on SOHO (Solar and Heliospheric Observatory). Measurements, theories and numerical simulations will be discussed.
Several books and reviews (Hundhausen, 1970; Hollweg, 1975, 1978; Schwartz, 1980; Marsch, 1991a, b; Feldman and Marsch, 1997) were written in the past, which partly covered kinetic aspects of solar wind and coronal physics. Some of them were even fully devoted to this subject. Here, some previous material is cursorily covered, however, selected key results, and theories which are still valid or relevant, will anew be discussed if the scientific context requires that. The many solar and heliospheric missions of the past decades have greatly enhanced our knowledge and understanding, as compared with the early days of solar wind physics, the state of which then was reviewed by Parker (1963) and Hundhausen (1972) in their classical monographs. An early review of kinetic and exospheric physics was provided by Fahr and Shizgal (1983). A comprehensive account of solar wind phenomenology and the properties of the interplanetary medium was given by Schwenn (1990) after completion of the Helios mission.
In coronal physics, kinetic processes have always played a major role in the interpretation of the non-thermal radio and X-ray emissions, in particular during flares in association with suprathermal ions and electrons. The corresponding literature is very comprehensive. We cannot address the related physics issues here, but must refer the reader to the books of Benz (1993) and Aschwanden (2002), or the modern textbook of Aschwanden (2004) and the many references therein. In this review, we will concentrate on the thermal and suprathermal particles that constitute the bulk and beam populations of the coronal and solar wind plasma, and on the various plasma waves occurring in the kinetic domain at the natural scales of a warm plasma.
Waves in the solar corona and solar wind is a rather wide and mature research field. Because of the lack of space and size of this subject, here we cannot deal with magnetohydrodynamic waves (and turbulence), but must at the outset of this article refer to the existing reviews for the details and in depth discussions. MHD structures, waves and turbulence in the solar wind, including observations and models, have in the past been reviewed extensively by Marsch (1991b), Mangeney et al. (1991) and Tu and Marsch (1995), with emphasis on the Helios observations in the ecliptic plane and inner heliosphere. The Ulysses observations at high latitudes and radial distances between 1 AU and about 5 AU are described by Horbury and Tsurutani (2001), and observations made in the outer heliosphere mostly by the Voyagers are contained in the book of Burlaga (1995) and the review of Goldstein et al. (1997), which also includes some numerical simulation results.
Recently in this journal, two modern and comprehensive reviews have become available, by Bruno and Carbone (2005) on the solar wind as a turbulence laboratory, an article which partly covers kinetic issues as well, and by Nakariakov and Verwichte (2005) on the novel subject of coronal waves and oscillations.
1.2 The importance of kinetic physics
Kinetic processes prevail in the solar corona and solar wind. Since the plasma is tenuous, multi-component, non-uniform, and mostly not at LTE (Local Thermodynamic Equilibrium) or collisional equilibrium conditions, multi-fluid theories or kinetic physics are required for an adequate description of many coronal and solar wind phenomena. The coronal plasma is stratified and turbulent, and strongly driven by the underlying photospheric magnetoconvection, which is continuously pushing around the magnetic field lines reaching out into the corona. Thus the field contains ample free energy for driving plasma macro- and micro-instabilities. Consequently, magnetohydrodynamic as well as kinetic plasma waves and associated wave-particle interactions are expected to play a major role.
Certainly, Coulomb collisions also matter, which are kinetically described by the Fokker-Planck operator (see, e.g., Montgomery and Tidman, 1964). However, excitation, scattering and absorption of waves, either of fluid or kinetic type, will dominate over collision effects. The consequences for the velocity distribution function (VDFs) are often described by a quasilinear diffusion operator involving the wave spectra. The key problem then is to understand the transport properties of the weakly collisional corona (and solar wind), which requires consideration of multiple scales, spatial non-uniformity and most likely also temporal variability.
The solar wind consists of electrons, protons, alpha particles and heavy ions. Kinetic plasma physics deals with their collective behaviour as a statistical ensemble. Space-borne particle spectrometers enable us to measure the composition and three-dimensional velocity distribution functions (VDFs) of the particles. The Vlasov/Boltzmann kinetic plasma theory provides the adequate means for their theoretical description. Key issues of kinetic physics are to address the coronal origin and acceleration of the wind and the spatial and temporal evolution of the particles’ VDFs. They are shaped through the forces of the Sun’s gravitational field, the average-macroscale and fluctuating-mesoscale electric and magnetic fields of interplanetary space, and through multiple microscale kinetic processes like binary Coulomb collisions and collective wave-particle interactions. Although, coronal expansion is irreversible, the solar wind microstate carries distinct information about the coronal plasma state in the source region, and thus in situ measurements allow for inferences and provide a kind of remote-sensing diagnosis of the coronal plasma.
1.3 Main types and solar sources of the solar wind
As is well known, the solar wind is the continuous outflow of completely-ionised gas from the solar corona (Parker, 1958, 1963). It consists of protons and electrons, with an admixture of a few percent alpha particles and much less abundant heavy ions in different ionization stages. The hot corona typically has electron and proton temperatures of 1 to 2 MK and expands radially outward into interplanetary space, with the flow becoming supersonic within a few solar radii. Because the solar wind plasma is highly electrically conductive, the solar magnetic field lines are dragged away by the flow, and due to solar rotation are wound into spirals. The wind attains a constant terminal speed, and its density then decreases radially in proportion to the square of the radial distance.
Space missions have revealed that there are three major types of solar wind flows: first, the steady fast wind which originates on open magnetic field lines in coronal holes; second, the unsteady slow wind coming from the tips and edges of temporarily open streamers or from opening loops and active regions; and third, the transient wind in the form of coronal mass ejections (CMEs) prevailing during solar maximum. Models for these types of wind have been developed to different levels of sophistication. Subsequently, we discuss the empirical constraints (Marsch, 1999) imposed on the models mainly by Helios (in-ecliptic) and Ulysses (high-latitude) interplanetary in situ measurements, and by the solar remote-sensing observations of the corona made by SOHO.
These observations indicate that the fast solar wind seems to emanate in the polar coronal holes directly from the chromospheric magnetic network (boundaries) (Hassler et al., 1999; Wilhelm et al., 2000; Xia et al., 2004; Wiegelmann et al., 2005; Aiouaz et al., 2005), with outward initial speeds of up to 10 km s−1. The open coronal magnetic field (of about 10 G) is anchored in the supergranular network, which occupies merely 10% of the coronal base area. The strong network field (with an average of about 10–100 G) is rooted in the photosphere in small, kG-field flux tubes (about 100 km in size). The field in the shape of coronal funnels rapidly expands with height in the transition region and ultimately fills the entire overlying corona. That the solar wind originates in these coronal funnels was recently found by Tu et al. (2005), who identified, by means of correlations between Doppler shifts and the coronal magnetic field as obtained by extrapolation from photospheric magnetogrammes, the source regions of the plasma outflow. The origin of the slow solar wind remains less clear (Schwadron and McComas, 2003), but most likely involves magnetic reconnection, which may lead to transient openings of coronal loops feeding plasma to the slow wind.
2 Particle Velocity Distributions
2.1 General considerations
The solar wind is the classical paradigm of a collisionless plasma. Detailed in situ measurements have been carried out over about four decades in the solar wind, and therefore its state is well known over a wide range of distances from the Sun, essentially from the corona to the heliopause, and over the entire range of heliospheric latitudes and longitudes. For comprehensive reviews of its microstate see the introduction section, in particular the reviews of Marsch (1991a) and more recently Feldman and Marsch (1997). We refer the reader to these works and the many references therein, to avoid unnecessary repetitions. For a recent reviews of solar wind theory see, e.g., the book article of Marsch et al. (2003) or the concise paper of Hansteen et al. (1999).
The solar wind is known to originate in three basic types from the solar corona, whose open fields yield steady fast flows, the transiently open fields unsteady slow flows, and active fields sometimes very fast ejections of mass and magnetic flux. The solar wind microstate still carries remnants from its origin and information about the plasma state in the coronal source regions, which thus become remotely accessible through interplanetary solar wind measurements.
Kinetic processes prevail in the solar corona and solar wind, because the plasma is tenuous, multi-component and non-uniform. As a result of this, and owing to the macroscopic forces, significant deviations from LTE are bound to arise, and complexity is caused in particle phase space. These effects are signaled by strong distortions of the VDFs in the thermal regime, as well as by the occurrence of suprathermal particles, e.g., the electron strahl or non-thermal ion beams and heavy ion differential streaming. Because of the weak collisionality, there is a lasting influence of the boundary conditions in the corona on the interplanetary characteristics of the solar wind.
The Sun’s magnetic field varies over the solar cycle, and the solar wind varies correspondingly in response to solar activity (see, e.g., the review of Marsch, 2005). The global coronal field always consists of three major components: long-term open coronal holes (CHs), closed streamers and transiently open or closed loops. These components are respectively associated with uniform fast solar wind, filamentary slow wind, and transient variable-speed wind that is related with coronal mass ejections. The three basic types of wind differ substantially in their kinetic properties, because of different solar boundary conditions and interplanetary plasma dynamics. The radial evolution of the internal state of the wind thus resembles a complicated relaxation process, in which the particles’ free energy (as compared to energy bound by kinetic and magnetohydrodynamic equilibrium conditions) is converted to thermal and wave energy distributed over a range of scales.
2.2 Solar wind electrons
Because of their small masses, electrons are less important than ions for the solar wind dynamics. Yet, they ensure quasineutrality, constitute an electric field through their thermal pressure gradient and carry heat in the skewness of the thermal bulk and the suprathermal tail of their VDFs, which are determined mainly by the large-scale interplanetary magnetic field and the self-generated electrostatic potential, by Coulomb collisions in the thermal energy range at a few 10 eV, and by various kinds of wave-particle interactions. The electrons are subsonic, i.e. their mean thermal speed considerably exceeds the solar wind (ion) bulk speed. Suprathermal electrons (at several 100 eV) may be considered as test particles that quickly explore the global structure of the heliospheric magnetic field, which consists usually of open field lines mostly anchored in coronal holes (CHs), but may temporarily attain the shape of magnetic bottles or closed loops.
Figure 1 shows in the upper frame a typical solar wind electron VDF measured in a fast stream at 1 AU, after Pilipp et al. (1987a). A strong heat flux tail is clearly visible as a distinct bulge (the “Strahl”, Rosenbauer et al., 1977) in the VDF along the magnetic field direction (indicated by a dashed line). The main colder core population is surrounded by hotter halo electrons that amount to a few (typically four) percent in relative number density. The lower frame of Figure 1 after Maksimovic et al. (2005) indicates that the strahl is declining with radial distance from the Sun, whereas the halo is relatively increasing, perhaps by scattering of strahl electrons.
Top: Electron velocity distribution function in the solar wind as measured by the plasma instrument on the Helios spacecraft at 1 AU. Note the distinct bulge along the magnetic field, which is the so-called strahl, a suprathermal population carrying the heat flux together with the halo, the hotter isotropic component which is slightly displaced with respect to the maximum of the core part (indicated in red) (after Pilipp et al., 1987b). Below: Radial decline (increase) of the number of strahl (halo) electrons with heliocentric distance from the Sun according to the Helios, WIND and Ulysses measurements (after Maksimovic et al., 2005).
The collisional free path λc is according to Table 1 much larger than the temperature gradient scale height L. A polynomial expansion of the electron VDF about a local Maxwellian is found to badly converge (see also Dum et al., 1980), and thus an expansion like in the subsequent Equations (23) or (26) is certainly not appropriate for solar wind electrons. The reason is that they are global players and reflect, as is obvious from their strongly skewed VDF, the large-scale inhomogeneity of the solar wind and coronal boundary conditions, as well as local collisional processes that shape the central part of their VDF. This was emphasised long time ago by Scudder and Olbert (1979a, b) in analytical model calculations.
In detailed kinetic simulations, Lie-Svendsen et al. (1997) numerically integrated an approximate kinetic equation derived from the basic Boltzmann Equation (9) to be discussed later, and could reproduce essential features of the observed VDFs. They concluded that electrons do not matter dynamically in solar wind acceleration. The radial evolution of thermal electrons due to expansion and collisions was studied in the fluid picture by Phillips and Gosling (1990). As we will discuss below, Landi and Pantellini (2001) recently carried out fully kinetic simulations of electrons in a coronal hole and the associated solar wind. We come back to these theoretical issues in Section 7, where kinetic models for the corona and solar wind are discussed.
The magnetic field topology has a strong influence on the shapes of the velocity distributions, which can observationally be considered to be composed of three main components, a cold and almost isotropic collisional core, a hot variably-skewed halo population, and in fast solar wind often a narrow field-aligned strahl. The basic electron characteristics were first measured and described by Feldman et al. (1975). A comprehensive modern review was given by Feldman and Marsch (1997). The VFDs have often been modelled by only two convecting bi-Maxwellians as illustrated in the top part of Figure 2, taken from the Helios observations published by Pilipp et al. (1987a). On open field lines in the fast wind, the VDF usually develops a high-energy extension with a very narrow pitch-angle distribution only 10–20 degrees wide. This electron strahl population responds sensitively to the local magnetic field orientation.
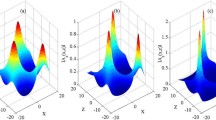
Electron velocity distribution functions as energy spectra (top) and velocity space contours (bottom) for fast (left), intermediate (middle) and slow (right) solar wind. Isodensity contours are in steps by a factor of 10. Note the core-halo structure and the strahl of suprathermal electrons in fast solar wind (after Pilipp et al., 1987a).
Common observations of the same plasma parcel of the wind by instruments on different spacecrafts, when being radially aligned, allows one to characterise the radial gradients of electron thermal parameters. The core temperature is found to vary widely between isothermal and adiabatic, while the halo temperature behaves more isothermally. The halo density falls off more steeply in dense plasma. Electron parameters have been studied by Ulysses in the distance range from 1 to 4 AU (McComas et al., 1992), where the halo is found to represent always about 4% of the total electron number. Since there is no reason for this ratio to be constant if the halo and core particles were completely separated, it appears that halo particles are not entirely decoupled from the core.
Solar wind electron parameters, in comparison with other measurements made on Ulysses, have also been derived from quasi-thermal noise spectroscopy, a novel method which was introduced by Meyer-Vernet and Perche (1989) and then exploited by Maksimovic et al. (1995) and Issautier et al. (1996).
Solar cycle variations in the electron heat flux have been studied by Scime et al. (2001), who did not find any significant dependence of the heat flux on the cycle or heliographic latitude. On average, the heat flux radially varies according to a power-law scaling, qe ∼ R−2.9, but there is no significant correlation of its magnitude with the solar wind speed. Concerning the electron temperature in the ambient solar wind, typical values and a lower bound were inferred from ISEE data at 1 AU in a paper by Newbury et al. (1998). In particular, the temperature ratio, Te/Tp was investigated and found to depend systematically on the wind speed. The average ratio declines from about 4 at 300 km s−1 to about 0.5 at 700 km s−1.
The break-point energy in the electron spectra of Figure 2 scales on average like seven times the core temperature, a result which was predicted by a kinetic theory for the electrons when being mediated by Coulomb collisions alone (Scudder and Olbert, 1979a, b). Such value of the break-point energy is also consistent with its interpretation as being equal to the electrostatic interplanetary potential that traps thermal electrons. Typical values of the interplanetary potential Φe at 1 AU are 50–100 eV (Pilipp et al., 1987a, b). For the importance of Φe(r) see the following Subsection 3.3 and the discussion in the paper by Maksimovic et al. (2001). Concerning the radial profile of the mean electron temperature, Meyer-Vernet and Issautier (1998) presented a kinetic model to obtain what they called the generic radial temperature variation derived from collisionless kinetics. Empirically (Marsch, 1991a), the temperature varies between almost isothermal and adiabatic behaviour (that implies r−4/3 scaling with distance r).
2.3 Solar wind protons and alpha particles
Solar wind ions, once being beyond the sonic critical point and detached from the Sun, behave very differently than electrons. Their VDFs are, due to weak collisionality, prone to sizable distortions in phase space, and strongly shaped in response to wave-particle interactions in the turbulent wind. For a comprehensive discussion of the phenomenology of solar wind ion VDFs we refer to the reviews by Marsch (1991a, b) and Feldman and Marsch (1997), and the many references therein.
Here we keep the discussion short and focus on the salient kinetic features. Four typical examples of proton VDFs in fast solar wind are given in Figure 3, after Marsch et al. (1982c), which shows isodensity contours in velocity space from the maximum down to the 1% level. The pertinent traits are the proton core temperature anisotropy and the proton beam travelling at about 1.5VA. The origin of these features in the outer corona is still unclear. Two recent papers by Marsch et al. (2004) and Tu et al. (2004) address some of the kinetic physics issues, to which we will turn in Section 6.
Proton velocity distribution functions in the fast solar wind as measured by Helios at 0.5 AU (top left), 0.54 AU (top right), 0.4 AU (bottom left) and 0.3 AU (bottom right). Note in the lower VDFs a distinct temperature anisotropy in the core and the strong beam (after Marsch et al., 1982c).
Obviously, the observed distributions of ions and electrons exhibit various shapes and change widely with the local in situ conditions, heliographic coordinates and the phase of the solar cycle. The proton VDFs range from Maxwellians in slow wind, embedding the heliospheric current sheet (HCS), to highly non-thermal ones in fast streams that emanate from CHs. In fast solar wind the proton temperatures are anisotropic, with Tp⊥ > Tp∥, whereas in slow wind the anisotropy is opposite, with Tp⊥ < Tp∥. Frequently, and in both types of streams, strong field-aligned proton beams occur with drift speeds larger than the local Alfvén speed.
The electrons are cooler than the protons in fast wind (Te = 0.1–0.2 MK and Tp = 0.5–0.8 MK at 0. 3 AU), but hotter in slow wind, which is more variable in abundance, more compressive and comparatively cold, with all particle temperatures becoming minimal at the HCS (Tp = 5 × 104 K at 1 AU). The fast wind is permeated by Alfvén waves, which are broad-band in frequency and believed to play a main role, through their dissipation, in maintaining the ion temperatures above the level expected for adiabatic cooling. Whereas high-energy extensions are a universal property of the protons, they are less frequently seen in the alpha particles (Marsch et al., 1982b).
Evidence for local perpendicular proton heating in solar wind high-speed streams was first provided by Bame et al. (1975) from observations at Earth orbit. Some typical proton distributions as measured by Helios in fast wind are presented in Figure 4, together with the radial profile of the average magnetic moment, μp = Tp⊥/B, of the protons, which is displayed as a function of radial distance from the Sun. That μp radially increases, indicates continuous ion heating perpendicular to the magnetic field must occur. The solid line in the top frame of Figure 4, which is drawn through the measured points carrying standard-deviation bars, shows proton magnetic moment (temperature) resulting from a model after Tu (1988), which explains the inferred interplanetary heating by Alfvén wave damping.
Top: The proton magnetic moment is observed to increase with heliocentric distance and indicates through its non-conservation proton heating. Bottom: Selected velocity distribution functions measured in high-speed wind. The solid isodensity contours correspond to 20% steps of the maximum, and the last broken contour is at 0.1%. Note the large temperature anisotropy in the core and the tails along the magnetic field direction (after Marsch, 1991a).
2.4 Solar wind heavy ions
Other than for protons and alpha particles, for solar wind heavy ions the three-dimensional VDF have not been measured. There are many results from in situ measurements of modern ion spectrometers flown on various spacecraft. However, the main objectives of those measurements usually were to analyse the chemical composition and ionization state (von Steiger et al., 1997) of the solar wind, and not the kinetic properties (other than simple energy spectra) of the heavy ions. They usually come in various ionization stages and have about coronal abundances in fast wind, but show distinct element fractionation in slow wind (for a review see, e.g., the paper of Peter, 1998). Helium is always an exception Neugebauer (1981), in that its sizable relative abundance of about 3–5% on average differentiates it from a minor constituent. In slow wind and the current sheet, the higher density and lower temperature there may enforce a state in which all ions are near collisional equilibrium. The composition of the solar wind and the abundances of heavy ions, and their variation with the wind stream structure, was extensively discussed by von Steiger et al. (1997). Many important solar and heliospheric processes can be inferred from solar wind composition measurements, as was demonstrated by Geiss et al. (1994).
The energy requirements on heavy ions are tough, given the notion that Coulomb friction (Geiss, 1982) in the dilute, hot corona is usually too weak to couple the ions together tightly. It appears rather difficult to drag out such heavy ions as He+, or He2+, or multiply-charged ions of any heavier element, against the Sun’s gravitational attraction. To achieve equal proton and heavy-ion bulk speeds in the distant wind (Ryan and Axford, 1975), their coronal velocity distributions should overlap sufficiently, which roughly requires about equal effective thermal speeds of a proton-electron pair and a heavy ion dressed by its electron cloud, and which means we must require that
where Z is the charge and A i the atomic mass number of ion species i. This relation implies that T i > A i Tp. Since Coulomb collisions would make T i → Tp and V i → Vp, wave heating must play a crucial role in lifting the heavy species out of the corona, with low heat transfer occurring in the wave dissipation region. The corresponding unknown minor ion heating rate, Q i , should reflect this requirement, i.e., Q i > A i Qp. Concerning the overall energy budget of solar wind minor ions and their temperatures and abundances in the corona, Lie-Svendsen and Esser (2005) have recently modelled these features by treating the heavy ions as test particles in a prescribed collisional proton-electron solar wind. They found that minor ions are always hotter than protons, even with lower heating rates per ion than proton. However, to avoid too large abundances and obtain faster flows of the heavy ions, preferential heating is necessary.
The heavy minor ions seem to act as ideal tracers of wave effects in the wind. There is ample evidence that waves do preferentially heat heavy ions in interplanetary fast streams as observed by Helios (Marsch, 1991a) and Ulysses (von Steiger et al., 1995). They also stream faster than protons (Asbridge et al., 1976) by a fraction of the local Alfvén velocity, V i ≤ Vp + VA (Marsch et al., 1981, 1982b; Neugebauer et al., 1994), and are sometimes found to surf on the ubiquitous Alfvén waves without participating in the wave motion (Marsch et al., 1981). This differential streaming presumably originates in the outer corona and is observed by Helios to fade away with increasing heliocentric distance. Smaller speed differences between protons and alpha particles are seen also by Ulysses beyond 1 AU (Neugebauer et al., 1996; Reisenfeld et al., 2001), and sometimes appear to be generated locally at shocks and stream interaction regions. In fast solar wind streams, heavy ions have a high kinetic temperature, with T i ≥ A i Tp (von Steiger et al., 1995). In the past years, new and more detailed observations became available (von Steiger et al., 1995; Steinberg et al., 1996; Hefti et al., 1998), and thus new theoretical work on an old subject was stimulated.
One of the interesting salient features, detected by modern ion spectrometers in the suprathermal domain of the heavy-ion energy spectra in the solar wind, are the extended tails which link the thermal keV-energy range of the solar wind with the energetic particle range with MeV energies and beyond. Figure 5 shows the speed (energy) distribution functions of helium, oxygen and neon in the solar wind, after measurements from the WIND spacecraft at 1 AU according to a paper by Collier et al. (1996). This paper also gives the relative abundances and the temperature ratios of these three species. Note the pronounced suprathermal tails appearing in the energy (speed) distributions, which are well fitted by a convected kappa function after Equation (6), with κ ranging here between 2.5 and 4. Remember in this context that in their exospheric model Pierrard et al. (2004) assumed that such non-thermal VDS of heavy ions already prevailed in the solar corona, in which case, as they showed, the heavy ions were driven even faster than the protons out of CHs.
Velocity distribution functions of helium (top), oxygen (intermediate) and neon (bottom curves) ions as measured by the ion mass spectrometer on the WIND spacecraft for various solar wind speeds. Note the extended power-law tails in the VDFs which are fitted well by kappa functions, in particular for helium (after Gloeckler et al., 2001).
The kinetic features and speed distributions of heavy interplanetary ions are not the subject of this article. But for the interested reader we refer to the review of Gloeckler et al. (2001), who discuss at length the heliospheric and interstellar phenomena revealed from observations of pick-up ions. Heavy ions in the solar wind may not only originate from the corona but for example as pick-up ions from cometary dust and various other sources in the inner heliosphere.
3 Kinetic Description of Corona and Solar Wind
3.1 Basic energetics of coronal expansion
The majority of the models have been concerned with the fast solar wind which, at least during solar minimum, appears to be the basic or equilibrium mode of flow. Its properties can be reproduced by using (single- or multi-) fluid models involving waves. Such studies show that electrons may remain hot because of their high heat conduction. Although protons (and other ions) can be accelerated by magnetohydrodynamic wave pressure, it is necessary that they are heated preferentially in the corona. This can be concluded from a simple consideration of the energetics of a polytropic model of coronal expansion, in which the sum of the specific enthalpy, binding gravitational energy and kinetic energy is conserved (Bernoulli’s equation). This conservation law takes the simple form:
where kB is Boltzmann’s constant, G Newton’s gravitational constant, mp the proton mass, M⊙ the Sun’s mass, R⊙ its radius, V the terminal wind speed, and TC the coronal temperature. The escape speed from the solar surface is V∞ = (2GM⊙/R⊙)1/2, giving 618 km s−1.
The above constraint requires a coronal energy per proton-electron pair of about 5 keV, to release the fast wind from the Sun’s gravitational potential well and attain its high asymptotic speed. If γ = 5/3, there is no critical point, so that if TC = 1 MK the corona appears gravitationally bound. To obtain a fast flow according to Equation (2), an average temperature of about TC = 10 MK is needed for V = 700 km and γ = 5/3. However, isothermal models, for which γ → 1, require an infinite amount of internal energy, since formally their enthalpy diverges. Anyway, the key issue of coronal heating is not even addressed in a polytropic model. However, one has to deal with the thermodynamics of the weakly collisional and turbulent corona and wind, a complex problem which requires the kinetic approach. Apparently, in the single-fluid description the coronal temperature profile entirely determines the coronal expansion and solar wind outflow, which is a natural consequence of a hot corona. Here we do not want to address fluid-modelling issues, but refer the reader to the book chapter by Marsch et al. (2003) and further references therein.
3.2 Collisional conditions in the corona and solar wind
The corona still is weakly collisional but strongly magnetised, which means that the particle gyroradius is much smaller than the collisional free path, ri,e ≪ λi,e, and the gyrofrequency much larger than the collision frequency, Ωi,e ≫ νi,e. Numerical values of the Coulomb collision rate, νi,e, of the electrons and protons can, for example, be found in Braginskii (1965).
In dilute space plasmas, such as the solar corona and solar wind, collisions are generally rare (see Table 1). Therefore, solar wind electrons and ions strongly violate the requirements of classical transport, which is to say that their collisional free paths are large against any fluid scale, or their collision time much longer than their transit time through 1 AU. To determine the collisionality of the interplanetary medium, Livi et al. (1986) investigated different types of solar wind streams and empirically defined the collisional domains. In a simple black-and-white picture one may say that the fast wind from coronal holes is collisionless and the slow wind from the streamer belt and transiently open coronal loops or small holes is weakly collisional. It is only in the dense and cold heliospheric current sheet, where even at 1 AU sometimes collisions may suffice to equilibrate particle temperatures or ion differential speeds (Borrini et al., 1981), or even produce Maxwellian protons (Marsch and Goldstein, 1983), however never Maxwellian but often fairly isotropic electrons (Pilipp et al., 1987a, b).
3.3 The exospheric paradigm and related models
As the consequence of rare collisions, the idea has been around since the early days of solar wind modelling to describe coronal expansion as a collisionless process, in which the corona kind of evaporates from an assumed exosphere. This exospheric model is based on the simplest approach that could be thought of to model analytically the solar wind: Consider neither collisions nor waves but only free protons and electrons that move in the gravitational field and interplanetary electric field, while being guided by the magnetic field. The work of Jockers (1970) and Lemaire and Scherer (1971a, b) are classic references for this topic. In these kinetic exospheric models the exobase is defined as the altitude where the mean free paths of the coronal ions and electrons become larger than the barometric scale height. In reality, this transition is of course continuous, and thus the exosphere empirically is badly defined. After Parker’s work (Parker, 1963), these models ran out of fashion. Yet in the recent past, they became fashionable again, although the importance of collisions and wave-particle interactions in the solar corona and solar wind is out of question more than ever. Certainly, the exospheric model contains some of the basic kinetic physics and only makes a few fundamental assumptions (for example about the VDFs at the exobase of the corona). It works well in predicting a supersonic solar wind. We give a short review of the exospheric paradigm to do justice to the existing literature. The reader who wants to know more is referred to Lemaire and Pierrard (2003) for a concise modern account of exospheric theory and the references therein.
In the old models, the exobase was usually located at a distance beyond 5–10 R⊙. However, since the number density is lower in open coronal holes than closed regions of the magnetised solar atmosphere, the exobase has to be lower in coronal holes, more realistically perhaps at about 1.1–5 R⊙. At such distances, gravitational attraction is still larger than electric repulsion for protons. In the recent exospheric models (Lamy et al., 2003; Zouganelis et al., 2003, 2004) a non-monotonic total potential energy for the protons was therefore assumed (as Jockers (1970) did already), and by lowering the altitude of the exobase below the maximum of the potential energy, an acceleration of the solar wind to high velocities was obtained. The profile with radial distance, r, of the accelerating mean electric field, (which is to say of the electron partial pressure gradient) is the key ingredient of the models, besides the coronal magnetic field, guiding the particle motion through its Lorentz force. Yet, the essential characteristic of the new exospheric models is that it provides a driving mechanism for the fast solar wind through a strong electric field, which is largely set up by the suprathermal electrons in the VDF, fe(r0, v) (assumed at the exobase with radius r0), from which the interplanetary VDF can by means of Liouville’s theorem be constructed everywhere. Direct observational evidence for the existence of suprathermal electrons in the corona is still lacking.
Kinetic exospheric models assume that the charged particles move without collisions in the Sun’s gravitational field, the mean electric field, E(r), and the solar and interplanetary magnetic field, B(r), along trajectories that are determined by their total energy, E, and pitch angle or magnetic moment, μ. When accounting for a spiral field, the two basic conserved quantities therefore are:
where for simplicity a radial dependence on r only was assumed. Here Φe(r) is the selfconsistent electric potential, Φg(r) = −GM⊙/r, the Sun’s gravitational potential, and λ the heliographic latitude. The particle mass is m and charge q. The first term contributing to the constant E in Equation (3) is the kinetic energy in the rotating frame and the second the centrifugal energy. Solar rotation at a frequency Ω⊙ at the equator leads to a co-rotation speed of Ω⊙R⊙ = 2 km s−1. Further details of a collisionless solar wind model in a simple spiral magnetic field are discussed by Pierrard et al. (2001).
Even including the field curvature does not heal a main problem of exospheric theory, which is that the thermal anisotropies of ions and electrons come out too large, inconsistent with in situ measurements, which for their explanation require ion scattering by waves and collisions (as discussed in subsequent sections). For the magnetic field model a simple Parker spiral of the form
may be assumed. Then the effective potential,
which corresponds to the magnetic mirror force, the gravitational attraction and the attraction (for electrons) or repulsion (for positive ions) due to the ambipolar electrostatic potential, is the key quantity in (steady state) exospheric theory and fully determines the energetics of the coronal expansion and solar wind, together with the VDF at the exobase, f(r0, v). The model VDF is assumed to be given at the exobase at r0, and is then according to Liouville’s theorem determined everywhere in corona and heliosphere. In the exospheric paradigm, it is the electric field that drives the expansion and drags out the ions against gravity.
The electric potential and the force ratio are plotted versus distance from the Sun in Figure 6, which was taken from the model of Lamy et al. (2003) and Pierrard et al. (2004). According to simple fluid theory, when fully neglecting all terms of the order of the electron mass, one finds that −e0neE(r) = −d/dr(ne(r)kBTe(r)) (with the electric charge unit e0). The ambipolar electric field is given by the electron partial-pressure gradient, which can be made large either by very hot bulk electrons (for which however there is no observational evidence, see David et al., 1998), or by sizable tails of suprathermal electrons (for which there is indirect evidence from the deviation from ionization equilibrium see, e.g., Esser and Edgar, 2000). The existence of such VDF was first proposed by Scudder (1992a, b), to explain merely by collisionless electron kinetics the high temperature of the corona. These extended electron tails are required to set up a sufficiently strong electrostatic potential in the corona.
Left: Electrostatic interplanetary potential from the exobase (at 2 R⊙) out to 215 R⊙ in an exospheric model with kappa VDFs of the solar wind consisting of protons and electrons, with base temperature, Te(r0) = Tp(r0) = 106 K and κe = 2.5. Right: Module of the ratio of outward directed electric force, qE(r), and inward directed gravity, mpg(r), acting on a proton. This ratio in the solar wind is plotted versus radial distance (after Pierrard et al., 2004).
Such VDFs can be described as κ-functions or generalised Lorentzians, and are a key property of the modern exospheric model VDFs that are assumed to exist at the exobase, which was assumed to be located at r0 = 2 R⊙ in the recent models, e.g., Pierrard and Lemaire (1996). The non-thermal K-VDF (see the paper of Maksimovic et al., 1997a) reads as a function of the particle speed υ as follows:
with the equivalent thermal speed υ κ . The temperature is as usually calculated as the second moment of the VDF (with number density n) and reads: kBT κ = m < υ2 > /3. The symbol Γ(x) denotes the gamma function. For κ → ∞ one retains a Maxwellian. The value of κ determines the slope of the energy spectrum of the suprathermal particles, and gives the exponent of the power-law tail for υ ≫ υ κ , where f(υ) ∼ υ−2(k+1). Small κ values (e.g., smaller than 3) mean a hard spectrum.
Figure 7 shows various examples of kappa functions that are plotted in the left frame (and are extracted from the paper by Maksimovic et al., 1997a). The logarithm of the VDF is given so that a Maxwellian appears as a parabola. One can see the appearance of extended high-energy tails for low values of κ. In the right frame a classical electron VDF as measured in the solar wind is shown after Feldman et al. (1975). The diamonds represent the measurements, while the dashed lines represent a double-Maxwellian core/halo model fit, which will be explained in more detail below. The continuous line represents the VDF according to Equation (6) for κ = 4. Note, however, that the detailed pitch-angle distributions observed in situ often reveal distinct anisotropies which are not well described by κ-functions. Some typical examples of measured electron VDF are given in Figure 2 in Section 2, where it is also shown that the suprathermal electrons in fast solar wind are best represented by an isotropic halo and a highly anisotropic strahl which is the primary carrier of the heat flux.
Left: Different examples of κ-functions (after Maksimovic et al., 1997a), all normalised to unity at υ = 0. Obviously, in the limit κ → ∞, these functions transform into a Maxwellian or Gaussian (solid line). Right: Measured electron VDF (after Feldman et al., 1975) in the solar wind (diamonds). The dashed lines correspond to the classical model VDF, being composed of two Maxwellians: a core with nc = 30.8 cm−3 and Tc = 1.6 × 105 K, and a halo with nh = 2.2 cm−3 and Th = 8.9 × 105 K. The full line represents the κ-VDF model fit with n = 33.9 cm−3, T κ = 1.9 × 105 K and κ = 4.
The restriction to isotropy is particularly questionable for the weakly collisional coronal electrons that are moving in the non-uniform, mirror-type or flux-tube-like, configurations of the coronal magnetic field. Furthermore, an obvious yet unanswered question is what physical process generates in the low corona or at the exospheric base a κ-function in the first place? Several authors, such as Collier (1993), Roberts and Miller (1998), Viñas et al. (2000), and Leubner (2002) have made proposals for kinetic processes that could produce such distributions in the chromosphere and corona.
Taking these functions for granted, exospheric models based on them were in the past years developed. The results presented by Maksimovic et al. (1997a, b) indicated that basic features of the fast solar wind can indeed be explained, if the exospheric electron VDFs in coronal holes have enhanced tails, which result in a sufficiently strong electric field accelerating the protons (see Figure 6 again). Quantitatively speaking, for an electron base temperature of Te(r0) = 2 × 106 K, the bulk speed at 1 AU is about 400, 500, and 800 km s−1 for assumed kappa-values of 6, 3, and 2, the latter value corresponding to a huge, presumably unrealistic reservoir of suprathermal electron energy in the lower corona.
Pierrard et al. (2004) recently investigated also the acceleration of heavy solar ions on the basis of an exospheric Lorentzian model and showed that heavy ions can flow faster than protons if their temperatures in the corona are more than proportional to their masses. The κ-function kinetic exospheric model (Pierrard and Lemaire, 1996), initially developed only for electrons and protons, was generalised to the case of a non-monotonic effective potential energy, Ψ(r), for heavy coronal ions and solar wind ions (see Figure 6 for the relevant radial profiles).
Pierrard et al. (2004) showed that the ion velocity filtration effect can lead to very hot ions in the solar corona, given the ion VDF had enhanced suprathermal tails in the low corona. For sufficiently high ion temperatures at the exobase, located at 2 R⊙, their exospheric model could account for the high bulk speeds of the heavy ions in fast solar wind ions at 1 AU. The assumed κ-value was 2.1, resulting in very high coronal kinetic temperatures, ranging in MK units between from about 60 for He2+, to 250 for O6+, and up to 950 for Fe12+. These are very high ion temperatures, way beyond what was typically inferred from spectroscopic data obtained by SOHO. Inspection of the simple energy constraint (2) shows that (for γ = 5/3, as it should be for a monoatomic gas) a heavy ion of species i must have an effective coronal temperature scaling, such that TC ∼ m i , because only then its coronal thermal speed is of the order of or larger than the escape speed of 618 km s−1 from the solar surface.
The new exospheric kinetic models claim to predict the fast solar wind without assuming an unreasonably large TC, and without additional heating of the outer region of the corona, as it is needed in hydrodynamic models to achieve the same solar wind speed through pressure gradient forces. However, the problem of coronal heating has only been circumvented, and it severely reemerges at the exospheric boundary in the new guise of the unknown origin of the crucial suprathermal particles. In their recent collisionless transonic model of the solar wind Zouganelis et al. (2003, 2004) presented parametric studies showing that a high terminal wind speed does not depend on the details of the non-thermal electron VDF, but is claimed to be a robust outcome of a sufficient number of suprathermal electrons. For example, a core-halo electron VDF as occurring in interplanetary space (shown previously in the right frame of Figure 7) was assumed to exist in the low corona.
The left frame of Figure 8 from the paper of Zouganelis et al. (2004) shows that low values of κ yield enhanced coronal electron temperatures reaching a maximum of 7 × 106 K within a few solar radii. This maximum gets smaller for larger values of κ. This temperature increase is a direct consequence of the velocity filtration effect (Scudder, 1992a, b), but is not observed, which suggests that κ-VDFs with strong suprathermal tails are not adequate for the corona. One may take double-Maxwellian instead, as was done by Zouganelis et al. (2004), with the exobase being located at the Sun’s surface, r0 = R⊙. The right frame of Figure 8 shows their model results for a sum of two Maxwellians, core and halo. The diagram gives contours of the terminal solar wind speed as function of α0 = nh(r0)/nc(r0) and τ0 = Th(r0)/Tc(r0). One can see that this kind of non-thermal VDF can explain the fast solar wind (700–800 km s−1) for a dense and hot enough halo, corresponding to substantial number of suprathermal coronal electrons. If the empirical in situ values of α = 0.04 and τ = 7, as observed by Ulysses (McComas et al., 1992), also prevail in the lower corona, one must come to the conclusion that the resulting electron tails are too weak to accelerate the solar wind to the observed high speeds.
Left: Electron temperature profile in the corona in an exospheric model with kappa function tails of the VDF. The kappa values are indicated at the different lines. The dashed vertical line corresponds to 1 AU. Only κ larger than about 5 is compatible with empirical constraints. Right: Contours of the terminal (at 1 AU) solar wind speed in km s−1 for an electron VDF composed of core and halo Maxwellians. The contours are shown as a function of the relative density, α0 = nh(r0)/nc(r0), and the temperature ratio, τ0 = Th(r0)/Tc(r0), of the electron core and halo at the exobase, being located on the solar surface, r0 = R⊙ (after Zouganelis et al., 2004).
Finally, we would like to mention the recent work by Zouganelis et al. (2005) who demonstrated that both approaches, the exospheric and collisional (modelled by direct particle simulation), yield a similar variation of the wind speed with the basic model parameters. In other words, a proper inclusion of collisions in an exospheric approach does not change the effects that suprathermal particles may have on solar wind acceleration.
The new exospheric models, implying the acceleration of coronal ions through the average ambipolar electric field set up by suprathermal electrons, work in principle but seem to fail in providing the high terminal speeds observed in fast streams. To achieve this end requires, as is illustrated in Figure 8, unrealistically large tails in the VDFs and/or high electron coronal temperatures, which are not consistent with known empirical constraints (Marsch, 1999). The consequence therefore has been to look for a direct acceleration of the ions through either their partial pressure gradient force (set up, e.g., by wave heating) when speaking in fluid terms, or kinetically and directly through wave-particle interaction forces, i.e., ultimately by micro-turbulent or coherent-wave electromagnetic fields, yielding the proper Lorentz force in the particles’ frame. This way seems to be the most promising remaining alternative.
3.4 The failure to heat chromosphere or corona by collisions
The coronal heating problem as formulated in the literature encompasses three main topics: The generation and release of energy in the photosphere, its transport and propagation into the corona, and its conversion and dissipation at different heights in various coronal magnetic structures. The ultimate energy source is magnetoconvection and flux emergence that render the coronal magnetic field dynamic and energetic. Coronal MHD waves and oscillations are assumed to be the main carrier of the energy (Nakariakov and Verwichte, 2005). Conventionally, ohmic, conductive, and viscous heating is supposed to provide the heating in the transition region and corona. However, the problems already start at low heights, since even in the chromosphere the collisional heating rates are much too small. Therefore, shock heating is presently favoured there (see, e.g., Ulmschneider and Kalkofen, 2003). Can fluid modes and kinetic plasma waves then provide the heating of the transition region and the corona? What is the microphysics of their dissipation? Ideas and heating scenarios abound, but these basic questions until today remain unanswered.
Let us estimate the collisional heating rates in the upper chromosphere, where the problems already occur. Typical parameters may be for the density, n = 1010 cm−3, and barometric scale height, hG = 400 km. The assumed perturbation values are: L = 200 km, ΔB = 1 G, ΔV = 1 km s−1, ΔT = 1000 K. With these reasonable parameters the dissipation rates are (in cgs units) as follows: Through viscous shear, QV = η(ΔV/ΔL)2 = 2 × 10−8, through thermal conduction, Q c = κ(ΔT/ΔL)2 = 3×10−7, and through Ohmic resistance, QJ = j2/σ = (c/4π)2(ΔB/ΔL)2/σ = 7 × 10−7. Here j is the plasma current density, and the transport coefficients are viscosity, η, heat conductivity, κ, and electrical conductivity, σ, for which values can be found in Braginskii (1965).
These numbers ought to be confronted with the losses due to radiative cooling, which amount to QR = n2Λ(T) = 10−1 erg cm−3 s−1, with the radiative loss functions Λ, for references see the book of Mariska (1992). QR is a factor of 106 or more larger than QV,C,J. Consequently a much smaller than the assumed scale, for instant L = 200 m, is required to match heating to cooling. Note, however, that then the assumption stated in the following Equation (27), which is implicit in the derivation of η, κ and σ from the subsequent Equation (23), seriously breaks down, since λc = 1–10 km is larger than this L in the chromosphere.
The situation is no better under coronal conditions, where classical dissipation rates have to be grossly enhanced, by more than six orders of magnitude, to match the empirical damping of loop oscillations (Nakariakov et al., 1999), or dissipation of propagating waves (Ofman et al., 1999). This problem, however, cannot be healed by simply claiming anomalously high transport coefficients or correspondingly low Reynolds numbers, but only by revising the classical transport scheme and developing a new kinetic paradigm for coronal transport. This is even more so needed as the functional dependencies on local gradients of fluid parameters as employed in the subsequent Equations (23), (24) and (25) are not self-evident for a collisionless plasma, and may become meaningless in the corona, where global boundary effects superpose local processes.
3.5 Dissipation of plasma waves in solar corona and solar wind
It is now widely recognised that in the solar corona and solar wind plasma waves play a role similar to collisions in ordinary fluids. In the expanding inhomogeneous solar wind particle distributions will develop velocity-space gradients and strong deviations from Maxwellians, which may drive all kinds of plasma instabilities, and thus lead to wave growth or damping. The kinetic wave modes of primary importance are the ion-cyclotron, ion-acoustic and whistler-mode waves, which are the high-frequency extensions of such fluid modes as the Alfvén, slow and fast magnetoacoustic waves. They will in much detail be discussed later.
Unfortunately, we know nothing about plasma wave spectra in the corona. Therefore, in kinetic models assumptions have to be made about the spectrum of the waves injected at the coronal base. A power-law is often assumed, the intensity of which is then constrained by extrapolation of the in situ measurements (Tu and Marsch, 1995) to the corona. Furthermore, the important questions of cascading — oblique as well as parallel — remains an open problem (Cranmer and van Ballegooijen, 2003). Large-scale MHD structures may preferentially excite perpendicular short-scale fluctuations Leamon et al. (2000), the dissipation of which may involve strong Landau damping coupled to kinetic processes acting on oblique wavevectors.
The relevant typical wavenumber, kd, for collisionless dissipation was estimated by Gary (1999), who defined it to be the minimum value at which kinetic damping becomes significant, and determined kd from linear Vlasov theory for the Alfvén-cyclotron and magnetosonic wave branches. Essentially, the dissipation scale is set by the ion inertial length, whereby a scaling law was found to apply as follows:
Here S k and α k are fitting parameters, with S k being of order unity, respectively, α k ranges between 0.3 (Alfvén wave) and 0.8 (magnetosonic mode). The cyclotron damping of Alfvén-cyclotron fluctuations increases monotonically with increasing βp, whereas proton cyclotron damping of magnetosonic fluctuations is essentially zero at low βp and becomes significant only at βp > 1. Concerning the spectral index of magnetic fluctuations in the solar wind, Li et al. (2001) argued that collisionless dissipation, because of its exponential dependence of the damping rate on kd, cannot be the main mechanism for spectral steepening; rather, damped power spectra should decrease more rapidly than any power law as the wavenumber increases. They obtained an analytic expression for the damping rate of the form (with fit parameter, a i , i = 1, 2, 3):
The three fit parameters depend upon and vary with the propagation angle of the waves and different values of the plasma beta.
For the subsequent theoretical sections of this review, we provide some frequently used definitions. The density of species j is n j , its mass m j , and its plasma frequency is denoted as \(\omega_{j}^{2}=(4\pi e_{j}^{2}n_{j})/m_{j}\). The particle’s gyrofrequency, carrying the sign of the charge, reads Ω j = (e j B0)/(m j c), for a background magnetic field of magnitude B0. The mean thermal speed is υ j = (kBT j /m j )1/2, with the temperature T j . The plasma beta of species j is defined as \(\beta_{j}=8\pi n_{j}k_{{\rm B}}T_{j}/B_{0}^{2}\). The mass density is ρ j = n j m j , and fractional mass density, \(\hat{\rho}_{j}=\rho_{j}/\rho\), with the total mass density being ρ = ∑ ℓ nℓmℓ. We will also make use of the relation \(\hat{\rho}_{j}\Omega_{j}^{2}=\omega_{j}^{2}(V_{{\rm A}}/c)^{2}\), where the Alfvén speed is based on the total mass density and as usually defined by \(V_{{\rm A}}^{2}=B_{0}^{2}/(4\pi\rho)\).
Whatever the wave dissipation process heating the particles may be, it certainly must be more effective for heavy ions than for protons (and electrons), because, as we previously discussed, the minor heavy ions are much hotter than the protons in coronal holes and the fast solar wind (Marsch, 1991a, b; von Steiger et al., 1995). Before we can address wave-particle interactions in more detail, the basics of kinetic theory first need to be discussed. We return to the topic of plasma waves at a later stage of this review in Section 5.
3.6 Basics of Vlasov-Boltzmann theory
The coronal expansion and solar wind acceleration are a complex processes, which require a kinetic description if the detailed particle velocity distributions are to be evaluated. The coronal magnetic field guides the outflow of plasma out to the Alfvénic critical surface, where the ram pressure of the wind starts exceeding the magnetic pressure of the coronal field, and where thus the solar wind is ultimately released from the Sun. The subsequent almost spherical expansion and the large-scale inhomogeneity continuously compel the solar wind plasma to attain a variable state of dynamic statistical equilibrium between the particles and electromagnetic field fluctuations. In principle, all these kinetic processes are fully described by the Boltzmann-Vlasov equation for the phase-space distribution for each species, f j (x, t, v), which is a measure of the number of particles at time t in a volume surrounding position x and with velocities in a certain range around v. The kinetic equation reads:
with the interplanetary magnetic field, B(x, t), electric field, E(x, t), and the Sun’s gravitational acceleration, g(x). Coulomb collisions or wave-particle interactions are also included and described by the Fokker-Planck collision integral or the quasilinear diffusion operator on the right hand side of Equation (9). Here the particle charge is e j , its mass m j , speed v, and space coordinate x. The speed of light in vacuo is c. In addition to Equation (9), Maxwell’s equations have to be solved with the self-consistent current density and charge density of the multi-component plasma of the solar corona and wind, which are calculated from the velocity moments of Equation (9). This complex problem has not been solved for the corona, but solutions of simplified versions of this problem, restricted to a single particle species and special geometries, do exist, and will be discussed in Section 7.
3.7 Vlasov-Boltzmann equation and fluid theory
The standard fluid MHD theory is described in any text book (e.g., Montgomery and Tidman, 1964 or Stix, 1992) of plasma physics and will not be discussed here, however the basic fluid equations are derived from the moments of the Vlasov/Boltzmann kinetic equation below. Here we concentrate instead on the assumptions underlying classical transport theory of plasma with emphasis on basic kinetic concepts and perturbation analysis. Transport theory in a plasma is based on approximate solutions of Equation (9) for weakly non-uniform media. In our discussion of space plasmas, we will closely follow the article of Dum (1990). The complete and most detailed description of a plasma is in terms of the particle velocity distribution function (VDF), denoted by f = f(x, t, w), the evolution of which in phase space is generally described by the kinetic Vlasov-Boltzmann Equation (9), in which we now omit the index. It can also be written in the non-standard form:
Here a single dot means the scalar product of vectors, and a double dot the dyadic contraction of tensors. The Coulomb collisions and/or wave-particle interactions are included in this equation via the collision term that involves the acceleration, A, and the diffusion tensor, \({\cal D}\). We introduced the relative or random velocity w = v − u(x, t), with respect to the mean (or bulk) velocity u(x, t), and v is the particle’s velocity in the inertial frame. We also defined the vector gyrofrequency, Ω = qB/mc, with q being the charge and m the mass of any particle species. The electric field in the moving frame is denoted as E′ and according to the Lorentz transformation given by:
As usually, the advective derivative (time change in the moving frame) is given by
The collision operator, which is here understood to describe either binary Coulomb collisions or wave-particle interactions, reads as follows:
It can be written as a velocity divergence of a flux density associated with friction and diffusion, see, e.g., the textbooks of Melrose and McPhedran (1991) and Montgomery and Tidman (1964).
If for Coulomb collisions the so-called Rosenbluth potentials,
are exploited (Rosenbluth et al., 1957), the related frictional acceleration and diffusion terms can concisely be written as:
Only here we used two indices to indicate the two species involved in the binary collision. The gamma factor is defined as \(\Gamma_{ij}=4\pi e_{i}^{2}e_{j}^{2}/m_{i}^{2}\ln \Lambda\), with the Coulomb logarithm being given via the plasma parameter (i.e., number of particles in the Debye sphere) through \(\Lambda=12\pi n\lambda_{\rm D}^{3}\), with the total particle density n = ∑ j n j . The Debye shielding length is given by
with the individual species Debye length defined as λ j = υ j /ω j . As one can see in Equation (15), the collision frequency is defined as the negative velocity gradient of the Rosenbluth potential. Hernandez and Marsch (1985) evaluated the collisional times scale for temperature and velocity exchange between drifting bi-Maxwellians, and Livi and Marsch (1986) and Marsch and Livi (1985a, b) calculated the collisional relaxation process and the associated rates for non-thermal solar wind VDFs and self-similar and kappa VFDs. This issue is also addressed in a previous review by Marsch (1991a). In the case of ion-electron collisions with electron thermal speed obeying υe ≫ υ i , we have the collision frequency \(\nu_{ei}=2\Gamma_{ei}n_{i}v_{\rm e}^{-3}\), showing the well-known strong speed dependence of the collisional friction on the relative speed of the colliding partners.
In multi-fluid theory, the dynamic equations for each species are separately obtained (we suppress an index labelling the species) by taking the zeroth, first, second, etc., moment of Equation (10). The zeroth order moment gives the continuity equation for the density, n, which reads:
Note that collisions do not change the particle number, i.e. \(< {\cal C}f > = 0\), which is obvious from the form of Equation (13). Here the angular brackets indicate velocity space integration. Similarly, the momentum equation can be written:
The couplings between the particles appear through the collisional (or wave-particle) momentum transfer rate, which is given by the first moment of the collision operator, \({\bf{R}}=m < {\bf{w}}{\cal C}f >\). By taking the other moments of the velocity distribution function, one obtains the zero mean random velocity, the pressure (or stress) tensor, and the heat flux vector:
The thermal pressure p (and kinetic temperature T), and the thermal stress tensor Π are derived as follows:
Here Tr denotes the trace, \({\cal I}\) is the unit tensor, and kB is Boltzmann’s constant. By definition the trace of Π vanishes. In terms of these quantities the internal energy or temperature equation is written as:
The left side contains the adiabatic changes (of the entropy) owing to advection, and the right side the dissipation terms related with velocity shear (viscosity), heat conduction and collisional friction (Ohmic heating) at a volumetric rate Q, with \(Q = {\textstyle{m \over 2}} < {w^2}{\cal C}f >\).
In principle, one can continue this scheme, by taking ever higher moments of (10), which will lead to an infinite chain. For practical purposes, this chain must be terminated, and a way of closure be found. Transport theory is expected to provide this closure, yielding transport coefficients that link the unknown moments q, Π, R and Q with the fluid variables n, T, and u and their spatio-temporal variations. Transport relations providing closure are explicitly given in the review of Dum (1990). The general closure problem of the Vlasov-Boltzmann equation was recently revisited by Chust and Belmont (2006), with emphasis on the behaviour of a collisionless plasma. Yet, the potential relevance of this work for the solar wind remains to be demonstrated.
4 Transport in Solar Corona and Solar Wind
4.1 Transport theory in collisional plasma
The conventional way to solar wind modelling of course is the fluid approach, following the early work of Parker (1963). Here we shall review possible ways to remedy the shortcomings of the standard fluid description, e.g., by considering multi-species fluids either, or for a single species, by accounting for higher-order moments of the VDF. The advances made in this respect in modelling the fast solar wind were briefly reviewed by Hansteen et al. (1999). The intention here is not to discuss the existing fluid models of the solar wind themselves, but from the kinetic perspective to identify the weak and questionable points of transport theory in the solar wind and corona, and then to indicate possible physical remedies.
The basic assumption of classical transport theory is that collisions are strong and only permit very small deviations from collisional equilibrium. As a consequence, the particle VDFs can be expanded about a local Maxwellian (LTE, local thermal equilibrium), in which a dependence upon space and time occurs only through the fluid moments,
This approach following Chapman, Enskog, Cowling, Grad and others (see Dum, 1990 for further references), typically leads to polynomial expansions in the velocity variable w (we suppress the variables x and t for simplicity) of the form:
where the higher order terms are proportional to the spatial gradients of the first few moments, such that the linear corrections scale like \({\bf{F}}_{1}\sim{\cal T},{\cal N},{\bf{R}}\), and the quadratic ones relating to the velocity shear as \({\cal F}_{2}\sim {\cal U}\). The deviation from the local Maxwellian describe heat conduction, particle diffusion, electrical resistivity, and viscosity, where the symbols mean:
The superscript T denotes the transposed tensor. Taking the appropriate moments of the VDF (23), yields the sought for transport relations, such that \({\bf{\Pi}}\sim {\cal U}\) and \({\bf{q}}\sim{\cal T}\), or a drift velocity \(\Delta {\bf{u}}\sim{\cal N}\).
The transport coefficients are calculated by means of a kinetic perturbation theory, where the effects of collisions are included in an approximate solution of the Boltzmann equation, an approach leading to a series expansion that can in lowest order be expressed as:
It is important to note here, that to ensure rapid convergence of such series one requires a smallness parameter, ε, to exist, so that the higher order terms in Equation (26) can safely be neglected. The small parameter usually is the ratio, ε = λc/L, of the collisional free path, λc, over the gradient scale, L, of the fluid parameters.
The collision term is characterised by the mean time between collisions, τc, and scales as follows: \({\cal C}f\sim f/\tau_{{\rm c}}\). Therefore, to guarantee small non-uniformity, or to obtain weak deviations from LTE, the following inequalities must be fulfilled:
The lowest-order (of order ε0) uniform and stationary solution of the basic Equation (10) must therefore obey:
If the background magnetic field is only weak, the left hand side of Equation (28) may also be omitted, and then one simply has, \({\cal C}f_{0}=0\), a result which directly leads to a Maxwellian that is known to annihilate the collision operator (13). Expansions such as in Equation (23), even when going to much higher order in w or in the cosine of the pitch angle, do in the solar wind hardly converge (see Dum et al., 1980 and Marsch, 1991a). Consequently, a non-perturbative kinetic treatment suggests itself, since using the classical transport coefficients of Braginskii (1965) in fluid equations for space plasmas becomes questionable, and will often lead to spurious results.
As in the fast solar wind usually N < 1, with the number of collisions being \(N = {({\tau _{\rm{c}}}{\textstyle{d \over {dt}}})^{- 1}}\), Coulomb collisions certainly require a kinetic treatment. However, as shown in numerical model calculations for the solar wind by Livi and Marsch (1987), only very few collisions may already suffice to remove the otherwise extreme exospheric anisotropies in the VDFs. In the slow wind one has N > 5 for only about 10% of the time, but N > 1 for about 30–40% of the time. When seeking the lowest order solution of Equation (28) in the strongly magnetised corona, one obtains a gyrotropic distribution, from which strongly anisotropic transport coefficients may result, which can differ substantially along and transverse to the magnetic field.
4.2 Validity of classical electron heat flux in the transition region
Proton and more so electron heat conduction reduce the maximal corona temperature, and consequently the initial solar wind acceleration. However, high temperatures also yield a long Coulomb mean free path, thus bringing into question the application of the classical heat flux law, particularly in the presence of strong waves which can affect the ions on much shorter scales. Whereas this problem of a possible breakdown of classical collision-dominated transport in the solar corona has found not much attention as far as protons, alpha particles and minor ions are concerned, there has for a long time been a debate about the validity of the Spitzer-Härm electron heat conduction (Spitzer and Härm, 1953), or the validity of Fourier’s law according to which heat flows down the temperature gradient.
Lie-Svendsen et al. (1999) studied the transport of thermal energy in the solar transition region (TR), to find out if there the classical description,
of electron heat conduction is applicable. Here Te is the electron temperature, and κe the heat conductivity. Using an approximation in which test electrons moved in a prescribed Maxwellian electron-proton plasma, they validated this approach by a comparison of their with known results (Spitzer and Härm, 1953) in the collision-dominated regime, where the Spitzer-Härm relation (29) applied. They obtained electron VDFs in good agreement with that theory, showing that classical theory is sufficient to describe heat transport in the TR. Only when the pressure (density) was reduced to unrealistically low values, while the temperature profile remained unchanged, a significant fraction of the heat flux was carried by suprathermal electrons from the corona. But even then the total heat flux was never found to exceed the classical value.
However, this conclusion is in striking disagreement with other more recent results described in the subsequent section, but also the older results obtained by Shoub (1983), who solved numerically the Landau-Fokker-Planck equation for a kinetic transition region model and found that sizable high-energy tails developed in the electron distribution even for very low Knudsen number, ε = 10−3. This result was affirmed by Landi and Pantellini (2001) and Dorelli and Scudder (2003), who emphasised the importance of suprathermal electrons in coronal plasma conditions.
4.3 Breakdown of classical electron transport in the corona
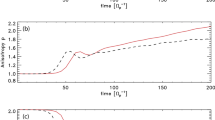
As was shown by Dorelli and Scudder (2003), the deceleration of suprathermal electrons in the coronal polarization electric field may even allow electron heat to flow radially outward against the local coronal temperature gradient, in contrast to the LTE relation (29), in which heat is constrained to flow down the local temperature gradient. The reason being, that the Sun’s gravitational field and the electric polarization field in the transition region cause a trapping of thermal electrons, but cannot prevent runaway of suprathermals, which can thus carry heat radially outward below the temperature maximum. This is illustrated in Figure 9, which shows the normalised value, θ = qe/qsat, with the saturation heat flux, being \(q_{{\rm sat}}=\rho_{{\rm e}}V_{{\rm e}}^{3}\), versus the kappa index. For κ ≈ 10, the heat flux direction reverses.
Electron heat flux in transition region as calculated for a kappa VDF at the chromospheric lower boundary. The horizontal dash-dot line (left frame) and dashed line (right) are the Spitzer and Härm (1953) predictions drawn for reference. Left: The squares show the predicted normalised heat flux from the kappa-function model equation. The vertical dashed line shows the value of κ for which the electron heat flux vector changes sign. Positive values of θ correspond to heat flowing up the temperature gradient (antiSunward) for strong tails (κ < 10). Negative values of θ = q/qsat correspond to heat flowing down the temperature (Sunward) gradient (after Dorelli and Scudder, 1999). Right: Similar plot, but for a full numerical solution obtained by solving the kinetic problem according to Fokker-Planck diffusion. Note that here non-classical conduction occurs only for strong suprathermal tails, κ < 5, assumed to prevail at the lower boundary (after Landi and Pantellini, 2001).
Dorelli and Scudder (1999) modelled this effect, while describing the zeroth-order local electron VDF by a kappa function with exponent κ, and retaining only the linear terms in an expansion in terms of the pitch angle variable μ = cosϑ. This linearization badly fails in the distant solar wind, as was shown by Dum et al. (1980), and was also criticised for its application to the lower corona by Landi and Pantellini (2001), both authors arguing that higher-order polynomials must be retained to model the collisional energy exchange between the thermal core electrons and suprathermal halo electrons. Also some time ago, Anderson (1994) criticised the exospheric velocity filtration model and argued that a collisional treatment of this effect is needed.
According to Dorelli and Scudder (1999), if one considers in the electron VDF power-law suprathermal tails (kappa function) and then accounts for the associated velocity filtration effect, one gets a corrected energy balance for a steady-state transition region (for a general review of the classical approach see the book of Mariska, 1992 about the TR), reading:
where K1 and K2 are positive constants depending on the κ-exponent, and Fe denotes the combined external force related to the gravitational and electric potential. Here z is the altitude, and R and H are the radiative loss function, respectively local heating function. If the net force is attractive (Fe < 0), then the last term represents a heating source adding to H. In conclusion, non-local electron heat flow coupled to the force Fe through velocity filtration must be taken into account in the internal energy balance in the TR.
This result is a kinetic consequence of heat flow in a weakly collisional and a non-uniform medium such as the corona, and will likely remain valid in any realistic future model. Landi and Pantellini (2001) have already demonstrated this with their more refined kinetic model of electron heat conduction. In the solar corona the collisional mean free path for a thermal particle (electrons or protons) is small, of the order of 10−2 to 10−3 times the typical scale height, h, of macroscopic fluid quantities like density or temperature. Despite this relative smallness of λc/h, the coronal plasma cannot be described satisfactorily by theories supposing that the local VDFs are close to Maxwellians (see our previous discussion again).
It was shown in particular that if the electron VDFs at the base of the corona have sufficiently strong suprathermal power-law tails, the heat flux may indeed flow upwards, i.e., in the direction of increasing temperature. Using kappa functions as prototypes for non-thermal VDFs at the base, they found that heat conduction can only be adequately described by the classical law provided that κ > 5. This value is much smaller than the one found by Dorelli and Scudder (1999). The results from both groups are illustrated and compared in Figure 9. Landi and Pantellini (2001) further showed that, unless extremely strong electron tails are assumed near the base of the corona (κ < 4), a local heating mechanism (most likely by waves) is needed to sustain the steep temperature gradient between the base of the corona and the location of its temperature maximum.
4.4 Higher-order gyrotropic multi-fluid equations
In previous sections we discussed the assumptions and limitations of transport theory based on Coulomb collisions, and studied the validity and breakdown of the classical (Spitzer and Härm, 1953; Braginskii, 1965) theory in the solar corona and wind. For modelling the polar wind in the Earth polar magnetosphere, Demars and Schunk (1979) developed a set of transport equations in terms of a polynomial expansion (up to the first three orders in speed) about a local bi-Maxwellian. This set includes sixteen relevant moments and the corresponding fluid-type differential equations. The momentum and energy exchange collision terms based on the Coulomb operator (13) were for interpenetrating bi-Maxwellian gases calculated by Barakat and Schunk (1981). This set was used by Lie-Svendsen et al. (2001) to define a 16-moment solar wind model, which was applied from the chromosphere through the corona into the distant solar wind out to 1 AU. The flux conservation of the radial component of the magnetic field, B(r), for one spatial variable, the radius r, implies that
which means that the area of the flux or flow tube scales like: A(r) ∝ 1/B(r). Subsequently, the index s refers to particle species s, with mass ms, density, ns, parallel and perpendicular temperatures, Ts∥ and Ts⊥, respectively, heat fluxes, qs∥ and qs⊥. For completeness, and since they have been used by various authors (Olsen and Leer, 1999; Li, 1999; Lie-Svendsen et al., 2001), we explicitly quote these anisotropic, gyrotropic higher-order fluid equations:
The symbol E is the electric field, and the solar gravity force term is in standard notation. The respective rightmost terms refer to the volumetric transfer rates of particle, momentum, internal energy, and heat flow, which all still have to be specified. They are assumed to include internal exchange, among the species and degrees of freedom, and external exchange, for example of momentum transferred to the bulk flow by an Alfvén wave pressure. Without exchanges the set forms a closed system. The equations are still fairly general. However, to evaluate the exchange terms crucial assumptions have to be made about the form of the VDFs of the species involved. A large variety of VDFs will yield the same moments, and therefore the choice is not unique. The standard procedure, as quoted for example in the paper of Barakat and Schunk (1982), assumes for species s in its rest frame a VDF that takes the following convenient form:
with the thermal speeds: \({V_{{\rm{s}}\parallel}} = \sqrt {2{k_{\rm{B}}}{T_{{\rm{s}}\parallel}}/{m_{\rm{s}}}}\), and \({V_{{\rm{s}} \bot}} = \sqrt {2{k_{\rm{B}}}{T_{{\rm{s}} \bot}}/{m_{\rm{s}}}}\). The correction function, Φs(w), is a polynomial and depends on the four scalar velocity moments appearing in the stress and heat flux tensor, and its evaluation requires further calculations. Barakat and Schunk (1982) gave examples for various multi-moment approximations, and presented a discussion of the related model VDFs. We recall the discussion in Subsection 4.1, in which it was emphasised that Φs has to be small against unity for the expansion of the VDF to converge and stay positive definite.
In applications of the moment Equations (32)–(37) to the modelling of coronal expansion and wind acceleration, the exchange rates on the right sides of the set must be specified. Given model VDFs such as (38), one can evaluate the self-collision integral (13), or the wave-particle exchange terms (63), and thus obtain the rates requested for closure of the set. Examples for Coulomb collisions are given in the 16-moment fluid model with Alfvén-cyclotron wave heating by Li (1999) and Lie-Svendsen et al. (2001). With respect to wave-particle interactions, the heating and acceleration rates after (63) were, for bi-Maxwellians and power-law wave ESDs, calculated by many authors (Marsch et al., 1982a; Isenberg, 1984a; Li and Habbal, 1999; Li, 1999; Marsch and Tu, 2001a).
The standard VDF, resulting from the procedure used by Demars and Schunk (1979) and Li (1999), implies the following third-order-polynomial correction function:
What they called improved transport equations for fully ionised gases were recently proposed by Killie et al. (2004) to improve the description of Coulomb collisions, for which the transfer rates for momentum, energy, and heat flux were anew calculated within the eight-moment fluid equations. They found transport coefficients that deviate by less than 20% from the rigorous values (Spitzer and Härm, 1953) obtained from solving the Fokker-Planck equation.
Presently, there is no basic kinetic model of the solar corona and solar wind. The various forms of the multi-moment multi-species fluid equations were used to study different physical process and such characteristics as the dependence of solar wind parameters on variations in the coronal heating function (Olsen et al., 1998), the acceleration of the wind when being based on the above gyrotropic transport equations (Olsen and Leer, 1999), the heating and cooling of protons by turbulence-driven ion-cyclotron waves in fast solar wind (Li et al., 1999), the effect of transition region heating on the generation of the solar wind from coronal holes (Lie-Svendsen et al., 2002), and the coronal energy budget, abundances and temperatures of solar wind minor ions (Lie-Svendsen and Esser, 2005). In their 16-moment model, Lie-Svendsen et al. (2001) also included the heat-flux moment equation explicitly, and integrated the fluid Equations (32)–(37) all the way out from the chromosphere, through the corona into the inner heliosphere.
4.5 Model velocity distributions from moment expansions
Apparently, proton model VDFs that obey the multi-moment fluid Equations (32)–(37) can be constructed on the basis of the 16-moment expansion (38) and (39), where in addition terms related to viscosity may be included. Demars and Schunk (1990) used this expansion to model such measured VDFs as shown in Figure 3 and Figure 4. By comparison and visual inspection of the measured and modelled velocity space contours they concluded that many features of the VDFs could be reproduced, even a possible secondary peak, as long as the beam relative density stayed between 0. 1 and 0. 4, which is to say massive beams cannot be described properly, and dilute beams with drift speed of several thermal speeds either. A double beam is better represented by a two-Maxwellian (double-humped) VDF in the first place. They found that the components of the stress tensor were not required, but the four parameters, Vs∥, Vs⊥, qs∥, qs⊥, mostly were sufficient to characterise the shape of the distributions published by Marsch et al. (1982c).
However, spherical-harmonics or Legendre expansions (Dum et al., 1980) previously had indicated that the polynomial Φs must often be of order up to ten, as to obtain credible representations of fs(w) in the presence of an extended tail or a strong beam, for example, or a distinct thermal core anisotropy. A more recent comparison of proton model VDFs by Li (1999) and Olsen and Leer (1999) with the ones measured in the solar wind indicated that a lower-order moment expansion badly failed in reproducing the key features of those observed proton VDFs that were shown in previous figures. Some model results of Li (1999) for solar wind protons are reproduced in Figure 10, which clearly illustrates the problem with and inadequacy of the moment expansion for ions. The model includes perpendicular wave heating that leads to the exaggerated ion conic-like VDFs. The overall tendency for magnetic moment conservation in the magnetic field mirror is also obvious, which leads to pitch-angle focussing such that the distribution at 215 R⊙ reveals Tp∥ > T⊥.
Two-dimensional contours of gyrotropic model VDFs of protons at various solar distances in the solar wind frame (with speed components c∥ and c⊥). The VDF is normalised to unity, and contours (from outside to maximum) correspond to fractions of 0.01, 0.03, 0.05, 0.2, 0.4, 0.6, and 0.8 of the maximum. Note the unphysical negative values (−0.005) indicated by the dotted contour. The positive parallel speed points away from the Sun along the local magnetic field direction (after Li, 1999).
In parallel to the activities described in Subsection 4.4, Leblanc and Hubert (1997, 1998) and Leblanc et al. (2000) in a series of three papers also developed a generalised multi-moment fluid model, in which solar wind proton VDFs were constructed by expansions to higher-order moments. However, instead of using a zeroth-order background single Maxwellian or bi-Maxwellian, which are distinguished by the fact that they describe local thermal equilibrium, a non-thermal Fs(w) was chosen at the outset. It was constructed such as to be closer to the true (though unknown) solution of the non-uniform Vlasov-Boltzmann Equation (9), and thus to ensure more rapid convergence than the series (38) and (39).
The impasse to which all such expansions about an assumed background (weight) function leads is illustrated in Figure 11 taken from Leblanc and Hubert (1997), in which a VDF with a beam and its model representations (left a bi-Maxwellian and right a skewed weight function Fs) are displayed as one-dimensional cuts in the field direction of the normalised VDF (velocity component c∥), with crosses indicating the measurements from Marsch et al. (1982c) and lines the various fits. The general slowness of the convergence is obvious in either case. While only if Φs(c∥, c⊥) is a higher-order polynomial (up to 7) the convergence is acceptable (see left bottom frame), it is worse for a skewed background VDF, that was intended to account for the beam in the first place (see right bottom frame of Figure 11). Also, the core density is much better fitted by a bi-Maxwellian.
Comparison of a measured proton VDF in the solar wind (1-D cut along the field of the normalised VDF indicated by crosses) with various models. Left frames: Bi-Maxwellian (continuous line) background and expansions in c∥,⊥ up to order 3 (dashed) and 4 (dotted line) in the top panel, and up to order 5 (dashed) and 7 (dotted line) in the bottom panel. Right fames: Same format but now for a skewed weight function as zeroth-order solution, which better interpolates the beam (after Leblanc and Hubert, 1997).
For their generalised model Leblanc and Hubert (1998) derived the associated transport equation, which are substantially more involved than the set (32)–(37). The related collisional exchange terms were provided in the work of Leblanc et al. (2000). The background function Fs(w∥, w⊥) has to be estimated well and calculated such that essential aspects (such as the electrostatic field or mirror force producing skewness) are incorporated in this zeroth-order solution. Formally, after (Leblanc and Hubert, 1997) we may write their VDF as:
where the new function Ψs(w∥) is normalised to unity and of the same order than the perpendicular Gaussian. It essentially describes heat conduction and thus is a skewed distribution in the parallel velocity. The small function ϒs(w) is an appropriate polynomial correction. To obtain Ψs(w∥) already requires to solve a kinetic equation. The advantage is the intrinsic asymmetry, representing a possible suprathermal tail. Then the heat flux qs∥ is not involved in the construction of the polynomial part ϒs(w), according to Leblanc and Hubert (1997).
5 Plasma Waves and Microinstabilities
5.1 Plasma waves in the solar corona and solar wind
In addition to the unavoidable, though with solar distance highly variable Coulomb collisions, kinetic plasma waves play an important role in shaping the VDFs of plasma particles in the corona and solar wind. The interactions of the waves with the particles, especially near their gyrofrequencies, may lead to inelastic pitch-angle scattering and thus to heating or cooling of the particles in association with wave absorption or emission, as discussed in detail in Subsections 6.1 and 6.9.
In briefly summarizing our present understanding of the role of plasma waves and microinstabilities in the solar wind, we can generally state that most VDFs are found to be stable or marginally stable. However, comparatively many proton VDFs are prone to the core temperature anisotropy instability. The four salient wave modes (and free energy sources) are: (1) ion acoustic wave (ion beam, electron heat flux); (2) electromagnetic ion Alfvén-cyclotron wave (proton beam and core temperature anisotropy); (3) magnetosonic wave (proton beam, ion differential streaming); (4) whistler-mode and lower-hybrid wave (core-halo drift, electron heat flux). The quasilinear evolution of these waves and instabilities, let alone their non-linear evolution or possible saturation, and the associated spatial evolution of the VDFs in the non-uniform corona and interplanetary medium have not yet been explored.
High-frequency plasma waves (most likely in the Alfvén/ion-cyclotron mode) have been suggested to heat the corona through rapid dissipation within a fraction of a solar radius. This idea of Axford and McKenzie (1992) was corroborated in a two-fluid turbulence model (Tu and Marsch, 1997), including parametric studies of the wind properties (Marsch and Tu, 1997) in dependence on the average wave amplitude at the coronal base. Resonant cyclotron-wave absorption was already shown by Marsch et al. (1982a) to heat the interplanetary solar wind. It is now generally believed, that high-frequency Alfvén waves may through reconnection (Axford and McKenzie, 1997) originate from the flaring magnetic network in the lower solar transition region. A key feature of this scenario is that the damping at the cyclotron frequency of Alfvén waves propagating in a rapidly declining magnetic field will through the frequency sweeping mechanism provide strong heating close to the Sun.
In an empirical model (Cranmer et al., 1999) of a polar coronal hole, spectroscopic constraints were placed on the cyclotron-resonance heating. Cranmer (2000) further investigated the ion-cyclotron wave dissipation in the solar corona by a consideration of the summed effect of more than 2000 ion species. There is an increasing awareness that cyclotron resonance may play an important role in heating all ions in coronal holes and the fast solar wind. For a recent review see Hollweg and Isenberg (2002). Most work on cyclotron-resonant interactions published so far has concentrated on the perhaps unrealistic case of wave propagation along the ambient magnetic field. However, a paper by Hollweg and Markovskii (2002) offers a comprehensive discussion of how an ion in cyclotron resonance will behave for oblique wave propagation. In particular it is shown how the resonances at harmonics of the cyclotron frequency come about. The linear-theory result of Gary and Borovsky (2004), who showed that proton cyclotron damping is essentially independent of k⊥, implies that the consequences of cyclotron damping should be similar for both parallel and obliquely propagating fluctuations. Because of the great analytical simplification that parallel wave propagation gives us, we subsequently concentrate on this transparent situation.
5.2 Dispersion relations and Landau and cyclotron resonance
Usually, a (warm and multi-component) plasma is analysed for stability by Fourier decomposing the linear fluctuations of the electromagnetic fields into plane waves with a given wave vector k. Each species contributes a distinct dispersion branch of kinetic waves, which are weakly damped normal modes or unstable in the presence of free energy. For the general dispersion relation we refer to the standard text book literature, e.g., Stix (1992), Melrose and McPhedran (1991), or Baumjohann and Treumann (1996). As an important example, we present the dispersion equation for parallel propagating left (∞ sign) and right (+ sign) handed circularly polarised electromagnetic waves with wave vector component k∥ along the background magnetic field, B0. This dispersion equation can be written as:
where the fractional mass density, \(\hat{\rho}_{j}\), has been used. For the low-frequency ion wave modes below Ωp the displacement current term can be neglected, since usually VA ≪ c. On the other hand without plasma, i.e., for \(\hat{\rho}_{j}=0\), we obtain the free-space electromagnetic wave. In the gyrofrequency domain, i.e. for ω ≈ Ω j , the typical wave length is just of the order of the gyroradius, r j = VA/Ω j , of the species that dominates in mass. The gyroradius is based on the Alfvén speed as defined by the total mass density, \(V_{\rm{A}}^2 = B_0^2/(4\pi \rho)\), which is most appropriate to normalise any phase speed.
For a given parallel wave vector, k∥, solutions of Equation (41) in terms of the complex frequency \(\tilde \omega ({k_\parallel}) = \omega ({k_\parallel}) + i\gamma ({k_\parallel})\) are sought, whereby a positive γ(k∥) signifies the growth of a plasma microinstability. The dielectric constant involves a resonance integral over the velocity-space derivative of the VDF, corresponding to the pitch-angle gradient of a particle in the wave frame as defined by the phase speed, and reads as follows:
The symbols w⊥,∥ refer to the random velocity components perpendicular and parallel to \(\hat{{\bf{B}}}_{0}\) in the species j proper frame, whereby \({\bf{w}}={\bf{v}}-U_{j}\hat{{\bf{B}}}_{0}\). The prime at \(\tilde \omega ({k_\parallel})\) indicates a Doppler shift into the rest frame of species j, drifting at bulk speed U j , i.e. \({\tilde \omega ^{\prime}}({k_\parallel}) = \tilde \omega ({k_\parallel}) - {k_\parallel}{U_j}\). The VDF is here understood to be normalised to the particle number density n j . Numerical investigations of Equation (41) have been carried out in the literature under various conditions. The monograph on space plasma instabilities Gary (1993) contains many relevant results for the solar wind and other space plasmas. The multi-component solar wind plasma is usually stable but sometimes close to the margin of a microscopic instability.
When interacting with a wave, a particle sees a stationary electric field if its velocity meets the condition for cyclotron resonance, where \({w_\parallel} = w_j^ \pm = ({\tilde \omega ^{\prime}}({k_\parallel}) \pm {\Omega _j})/{k_\parallel}\). Energy and momentum between particle and wave are exchanged as a result of this wave-particle interaction. The velocity distributions are reshaped, until the free energy in the form of temperature anisotropy, beam drift or ion differential motion, and skewness or heat flux is reduced or removed. These processes are analytically described by quasilinear theory, based on Equation (9) with the fields being decomposed into means and fluctuations, or fully calculated and visualised by direct numerical simulations.
In addition to electromagnetic modes, electrostatic waves frequently occur with variable intensity in different regions of the heliosphere (see the reviews by Gurnett, 1991 and MacDowall and Kellog, 2001). Below the proton plasma frequency one has the ion acoustic modes and above the electron plasma frequency the electrostatic Langmuir oscillations and the free-space electromagnetic waves. These prevailing waves are derived from the simple electrostatic dispersion equation:
where k j is the Debye wave number of species j, given by k j = ω j /υ j . We recall that the thermal speed is υ j = (kBT j /m j )1/2. The dielectric function involves the Landau-resonance integral over the derivative of the VDF in the k-direction. The dispersion relation (43) gives the wave vector k in dependence on the propagation direction \(\hat{{\bf{k}}}\) and phase speed \(\tilde \omega ({\bf{k}})/k\). Here \(\tilde \omega ({\bf{k}}) = \omega ({\bf{k}}) + i\gamma ({\bf{k}})\) is the complex frequency as a function of k. The wavelength may vary between infinity and the very short electron Debye length \({\lambda _{\rm{e}}} = k_{\rm{e}}^{- 1}\). Observationally, the occurrence of ion acoustic waves was found (Gurnett, 1991) to be correlated with the electron to proton temperature ratio, Te/Tp, and the magnetic field direction. Highest wave intensities are observed around the heliospheric current sheet (MacDowall and Kellog, 2001), where usually Te/Tp > 1, implying weak Landau damping.
5.3 Resonant wave-particle interactions
For the solar wind, the dispersion relations like (43) or (41) can be evaluated by using VDFs obtained from either measurements or models. The involved dielectric constants are functionals of f(w), which might, for example when being non-Maxwellian, contain free energy for wave excitation. If the growth rate γ(k) > 0, then a micro-instability occurs. Differently shaped VDFs can thus lead to wave emission and absorption, and as a result to a depletion or growth of the electromagnetic field.
In this process the fluctuations will be excited or damped through resonant particles, which may be either in Landau resonance, ω(k) − k · v = 0, or in cyclotron resonance, with ω(k) − k · v = ±Ω j , in which the Doppler-shifted frequency matches the particle’s gyrofrequency. For general considerations see the books of Stix (1992) and Gary (1993). A plasma composed of non-drifting Maxwellian VDFs will always lead to wave damping and absorption. Free energy for wave excitation requires thermal anisotropies, beams, differential motions, or skewed VDFs. Most of the stability analyses which were carried out for the solar wind were based on idealised model distributions, such as drifting bi-Maxwellians or Lorentzians with high-energy tails. However, sometimes also the measured VDFs were implemented, e.g., by Dum et al. (1980) or Leubner and Viñas (1986), in the numerical dispersion codes to diagnose the stability of the measured VDFs and predict the possible wave activity caused by the non-thermal features.
Resonant wave-particle processes in the inhomogeneous corona, as compared to the locally uniform solar wind, are complicated by the non-uniformity of the coronal magnetic field and radial variation of other plasma parameters. In a series of papers Hollweg (1999a, b, c) looked into these complications and did some detailed kinetic studies of ion resonances with cyclotron waves in coronal holes. In addition, Hollweg and Markovskii (2002) discussed the behaviour of cyclotron resonances when the waves propagate obliquely to the magnetic field.
5.4 Alfvén-cyclotron waves and kinetic Alfvén waves
Waves that interact with the thermal ions are of primary importance for the transport of thermal energy in the solar corona and wind. At wavelengths near the thermal proton gyroradius, rp = υp/Ωp, or of the order of the proton inertial length, lp = c/ωp = VA/Ωp, there are three prominent normal wave modes: the Alfvén-cyclotron wave, the magnetosonic-whistler wave, and the ion-acoustic wave (Gary, 1993). For the solar wind and corona the wave properties and dispersion of course depend on the plasma β, with the parameter range 0. 005 < β < 2 being especially important. Recently, detailed numerical studies were carried out with respect to the parametric dependence on β, and on the ion temperature anisotropies and drifts. The onset of Landau or cyclotron damping in particular depends sensitively on β. Gary and Borovsky (2004) derived for parallel propagation a typical wavenumber kd at which strong resonant dissipation sets in. It is roughly given by kdlp = 0.1 for β = 1. The detailed dependence on the proton βp is for a Maxwellian plasma shown in Figure 12, which was derived by solving the kinetic dispersion relation (41). Gary and Borovsky (2004) obtained three distinct damping regimes. Their results are summarised in Table 2. The dissipation of solar wind magnetic fluctuation spectra was also studied with respect to a comparison of dispersion versus damping by Stawicki et al. (2001).
Left: The proton cyclotron dissipation wave number for parallel Alfvén-cyclotron waves as a function of βp. The solid line represents kdlp, and the dashed line represents kdrp, where the thermal proton gyroradius, rp = υp/Ωp, and the proton inertial length, lp = c/ωp = VA/Ωp, are used for normalization, and kd is the dissipation wave vector. Right: The damping rate divided by the real frequency, γ/ω, of the oblique Alfvén-cyclotron waves as a function of the perpendicular wave number for three values of the electron βe as labelled. Here k∥ = kd/3 and −0.01 ≤ γ/Ωp ≤ 0. Note the increasing damping, leading to oblique wave dissipation, with growing electron temperature, i.e. with increasing βe (after Gary and Borovsky, 2004).
The work of Gary and Borovsky (2004) showed that parallel Alfvén-cyclotron fluctuations of sufficiently short wavelength lead to strong proton cyclotron resonance. Yet as the wavevector component k∥ decreases, the proton cyclotron interaction ceases, and the electron Landau resonance may become effective at oblique propagation. Gary and Nishimura (2004) investigated the dispersion and damping properties of Alfvén-cyclotron waves associated with the transition from the proton-cyclotron to the electron-Landau resonance regime.
If the wavevector component, k∥, of an Alfvén-cyclotron waves becomes smaller, the resonant ion-wave interactions gradually decreases. However, if k⊥ concurrently becomes substantial, then Landau resonance will play an increasingly important role. The waves with propagation strongly oblique to the field are called “kinetic Alfvén waves” (KAW). They have been studied by many authors, e.g., Hollweg (1999d) (and references therein) who calculates their approximate dispersion relation for an electron-proton plasma:
where the effective sound speed is given by \({C_{\rm{s}}} = \sqrt {({\gamma _{\rm{e}}}{k_{\rm{B}}}{T_{\rm{e}}} + {\gamma _{\rm{p}}}{k_{\rm{B}}}{T_{\rm{p}}})/{m_{\rm{p}}}}\), and \({\gamma _{{\rm{e}},{\rm{p}}}}\) corresponds to the ratio of specific heats, i.e., is equal to 5/3 for a simple hydrogen plasma. Note that the Alfvén wave dispersion is, via the perpendicular wave vector, modified and for KAW also depends on the electron inertial length and the effective gyroradius that is based on the ion and electron temperatures. Equation (44) contains various limiting cases discussed in the literature and explained by Hollweg (1999d). The complete kinetic dispersion properties were calculated with the Vlasov theory for Maxwellian particles. Selected results for βp = 0.01 are presented in Figure 13 (after Gary and Nishimura, 2004) and shown in dependence on such key wave parameters as propagation angle θ and electron to proton temperature ratio, Te/Tp, which quantifies the relative importance of electron versus ion Landau damping.
The dispersion relation of kinetic Alfvén waves for βp = 0.01 versus k∥lp. The solid and dashed lines represent the real frequency, and the dotted chains represent the corresponding damping rates after Gary and Nishimura (2004). Left: Dispersion results for parallel and very oblique propagation. Right: Three dispersion curves relating to different temperature ratios.
Gary and Nishimura (2004) also used particle-in-cell simulations (for earlier simulations see references therein) to examine the electron kinetic response to the waves being subject to electron Landau damping. Their computations show heating of the electrons in the parallel direction and formation of a field-aligned electron beam.
5.5 Non-Linear wave couplings and decays
Kinetic Alfvén waves may also prevail in the solar corona, for observations indicate them to exist, with nearly transverse wavevectors with respect to the back-ground magnetic field, in the solar wind (Matthaeus et al., 1990). Leamon et al. (1998) have argued that at shorter wavelengths very obliquely propagating Alfvén-cyclotron waves are consistent with the measured solar wind fluctuations at scales comparable to lp. Cranmer and van Ballegooijen (2003) discussed in detail a coronal wave-turbulence cascading scenario in which the cross-field small scales play a prominent role in the predominantly perpendicular cascade. Voitenko and Goossens (2005a, b) discussed in mathematical detail the non-linear coupling of Alfvén waves with widely different cross-field wavelengths in space plasmas.
Multi-scale solar magnetic activity and the resulting generation (Axford and McKenzie, 1997) and dissipation of Alfvén waves may play an important role in coronal heating. The popular cascading approach assumes a gradual evolution of the wave energy to the small dissipative scale of the order of lp = c/ωp by local non-linear interactions among MHD waves. Voitenko and Goossens (2005a, b) investigated an alternative non-local transfer of Alfvén wave energy from the large MHD length scales directly into the small dissipation-range scales, which are naturally associated with kinetic Alfvén waves (KAWs). As discussed in Subsection 5.4, these waves have very short wavelengths across the magnetic field, irrespectively of the frequency which their dispersion relation (44) contains.
A non-linear mechanism for the excitation of KAWs is via the resonant decay of a pump low-frequency Alfvén wave: AW → KAW1 + KAW2. The decay is still efficient for the amplitudes expected for coronal Alfvén waves, which thus will, through the non-linearly driven KAWs, suffer significant dissipation. Therefore, the cross-scale non-linear coupling of Alfvén waves can provide a mechanism for the replenishment of the energy in the dissipation domain, and consequently may lead to heating of the corona and fast solar wind. The maximal non-linear growth rate, γNL, of the KAWs may reach the order of the lower-hybrid frequency, and is given by an expression that only involves the relative pump-wave amplitude but has a sensitive parametric dependence on the plasma β via a dimensionless function Γ(β), such that
The function Γ ranges between about zero and unity. Therefore, the decay can be very fast by MHD standards. A detailed quantitative discussion is provided in the original references.
Given the existence of low-frequency KAW or other small-scale turbulence in the corona, Voitenko and Goossens (2004) studied the possible cross-field heating of coronal ions by these waves or turbulence. They showed that test ions moving in the electromagnetic field of a KAW may get locally detached from cyclotron motion in the demagnetizing phase of the wave field, and thereby undergo strong cross-field heating. In particular, heavy O5+ ions were found to enhance their perpendicular energy by up to two orders of magnitude. The required small perpendicular wavelength, being of the order of r i = Ω i /V i , may for example be produced by phase mixing of MHD Alfvén waves, or could result from the above discussed decay process.
Continuing the discussion of kinetic wave dissipation, we mention that besides linear wave damping also non-linear mechanisms have recently been considered. Voitenko and Goossens (2002a) studied the non-linear excitation of kinetic Alfvén waves (KAWs) by fast magnetoacoustic waves in the solar atmosphere. Since these waves have very small wavelengths in the direction perpendicular to the background magnetic field, they are very efficient in exchanging energy with kinetic plasma waves or MHD waves. It was shown that the non-linear supply of energy by the finite-amplitude fast-mode pump wave to the small-scale KAWs can be much faster than dissipation mechanisms such as viscous damping and Landau damping. Transient heating events observed by Yohkoh and SOHO may thus be produced by KAWs which are excited by parametric decay of fast waves originating from reconnection sites.
Turbulence simulations generally show that the MHD cascade process transfers fluctuation energy from long to short wavelengths in directions predominantly perpendicular to the background magnetic field. If the resulting fluctuations are kinetic Alfvén waves, then the Gary and Borovsky (2004) results indicate that (in the low-beta solar corona) electron Landau damping is the most likely consequence. Computer simulations of KAWs clearly show electron heating, and therefore MHD turbulence in the corona may not easily result in heating or acceleration of the ions. On the other hand, several different hybrid simulations (Liewer et al., 2001; Ofman et al., 2002; Xie et al., 2004) already demonstrated that Alfvén-cyclotron waves at parallel propagation can provide strong perpendicular heating of the protons and heavy ions in association with the frequency sweeping mechanism. The differences between the turbulent cascade model and the frequency sweeping scenario deserve further discussion and detailed evaluation which is beyond the scope of this review. For further reading we therefore refer to the recent comprehensive articles by Cranmer and van Ballegooijen (2003, 2005), who presented a model of magnetohydrodynamic Alfvénic turbulence in the extended solar corona, which contains collisionless dissipation and anisotropic particle heating, and discussed the global properties of Alfvén waves in the solar atmosphere and fast solar wind.
6 Wave-Particle Interactions
6.1 Inelastic pitch-angle diffusion of ions in resonance with waves
The response of particles to turbulent electromagnetic wave fields has traditionally been described by the paradigm of inelastic pitch-angle diffusion. The corresponding Quasilinear Theory (QLT) was in parallel developed by several authors (Shapiro and Shevchenko, 1962, Rowlands et al., 1966, and Kennel and Engelmann), 1966), and then described in many other articles. Here we mainly refer to the excellent textbooks by Melrose and McPhedran (1991) and Stix (1992). QLT is quadratically non-linear in the coupling terms between the fluctuations of the VDFs and electromagnetic fields. But it is still linear (hence its name) in the sense that both kinds of fluctuations enter only linearly in the quadratic product terms of the perturbed second-order Vlasov equation. The wave properties, such as dispersion and polarization, are still evaluated from linear theory with slowly time-varying VDFs and power spectral density (PSD), implying weak wave growth or dissipation.
In QLT it is assumed that the electromagnetic wave fields can generally be Fourier-decomposed in plane waves with the frequency, ω = ωM(k), and growth rate, γM(k), for a particular wave mode (index M) and a given real wave vector k, which is assumed here to be directed arbitrarily with respect to the constant background field, B0. The full dispersion equation for any linear plasma wave mode M in a multi-component plasma can for instance be found in Stix (1992). Mann et al. (1997) have studied in much detail the polarization properties of waves in a multi-component plasma. Ofman et al. (2005) recently discussed the possible observational implications of high-frequency Alfvén waves in a multi-ion corona. In the previous sections we have already given special, but for the solar wind particularly relevant, examples for dispersion relations in Equations (41) and (43).
QLT assumes the validity of the random-phase approximation, which ensures that no constructive interference occurs between the different waves modes, and thus these modes can be simply superposed linearly. Therefore, we can write the Fourier-transformed total electric field as a sum over the various modes as
Thus the Fourier components of the electric field vector can be expressed in terms of the wave amplitude, EM(k), and the unimodular polarization vector, eM(k). The magnetic field, \({{\bf{\tilde B}}_{\rm{M}}}({\bf{k}})\), can through the induction equation be calculated as
The wave growth rate, γM(k), or damping rate if it is negative, together with the real frequency, ωM(k), may be combined to a complex frequency, \({\tilde \omega _{\rm{M}}}({\bf{k}}) = {\omega _{\rm{M}}}({\bf{k}}) + i{\gamma _{\rm{M}}}({\bf{k}})\). The spectral energy density of the magnetic field of mode M is given by \({{\cal B}_{\rm{M}}}({\bf{k}}) = \vert{{\bf{\tilde B}}_{\rm{M}}}({\bf{k}}){\vert^2}/(8\pi V)\), with arbitrarily large integration volume V, and evolves according to a simple exponential equation:
which follows from the Fourier decomposition
where x is the spatial coordinate and t is the time. One has \({\bf{\tilde B}}_{\rm{M}}^{\ast}({\bf{k}}) = {{\bf{\tilde B}}_{\rm{M}}}(- {\bf{k}})\), since the magnetic field in Equation (49) must be real. Therefore, \({{\cal B}_{\rm{M}}}({\bf{k}}) = {{\cal B}_{\rm{M}}}(- {\bf{k}})\) by definition. The asterisk indicates the complex conjugate number. It is often convenient to use the Doppler-shifted frequency denoted by a prime, \(\tilde \omega _{\rm{M}}^{\prime}({\bf{k}}) = {\omega _{\rm{M}}}({\bf{k}}) - {k_\parallel}{U_j}\), as measured in a frame of reference moving with the bulk speed component, U j , of species j along B0. The background electric field is taken to be zero, and the background plasma may be multi-component but is assumed to bear zero current and be quasi-neutral.
The quasilinear diffusion equation describes the evolution of the velocity distribution function, f j (υ∥, υ⊥, t), of any particle species j in an inertial frame of reference, in which the particles and waves are assumed to propagate. We will in this section of the paper assume that the VDF is normalised to a density of unity. The diffusion equation was originally derived by Shapiro and Shevchenko (1962) and is calculated in a transparent way by Stix (1992). It can generally be written as
where the pitch-angle gradient in the wave reference frame (defined by the phase speed υM(k) = ωM(k)/k∥, which for Alfvén waves would be equal to the Alfvén speed, VA) was introduced. It is given by the velocity derivative
The magnetic field fluctuation spectrum is normalised to the background-field energy density. We find:
The term in the denominator comes from the replacement of the electric field by the magnetic field. It turns out to be physically meaningful to introduce what we may call an ion-wave relaxation or scattering rate. It is defined as
Note that this positive quantity has indeed the dimension of an inverse time or rate. Here we also introduced the s-order resonance speed and made use of the Bessel function (with index s):
The circular components of the wave polarization vector are defined as
The fundamental Equation (50) is quoted here without derivation as the starting point of our discussion on quasilinear diffusion. We have only slightly rewritten it in a form most appropriate for our subsequent purposes. Note that the famous quasilinear plateau in the VDF, to be discussed below, results for a vanishing pitch-angle gradient, meaning that ∂/∂α = 0, in which case wave absorption or emission ceases. The wave absorption coefficient can be calculated in QLT and is discussed below in Subsection 6.9.
6.2 Evidence for wave scattering effects on protons
The diffusion in velocity space of plasma ions being in resonance with waves is an old subject (Kennel and Engelmann, 1966) of plasma physics and has been studied in the literature in very much detail. Yet only recently have Galinsky and Shevchenko (2000), Isenberg et al. (2000), Isenberg et al. (2001), Cranmer (2001), Vocks and Marsch (2001), Vocks and Marsch (2002) and Vocks and Mann (2003) applied QLT also to the solar corona and solar wind (see the subsequent Section 7). QLT predicts that ions in resonance with transverse ion-cyclotron waves, propagating parallel to the magnetic field, undergo merely pitch-angle diffusion, while conserving their total kinetic energy in a frame moving with the wave phase speed υM (k). If the wave growth rate remains small, the slowly varying part of the ion VDF is controlled by diffusion. Its time evolution will, if the wave power is large enough, lead to a time-asymptotic state given by
where υ∥ 0 and υ⊥ 0 are the initial values, and whereby υ∥ has to satisfy the resonance condition, ω(k∥) − k∥υ∥ − Ω j . Here k∥ is the parallel wave-vector component, and ω(k∥) the frequency in the inertial frame where the waves are assumed to propagate. In the case of plateau formation, the particles conserve their energy in this wave frame.
Observational evidence from Helios plasma data has been obtained for the occurrence of proton pitch-angle diffusion (Marsch and Tu, 2001b). A comparison of the cyclotron-wave diffusion plateau, as it is predicted by using the cold plasma dispersion relation in the plateau condition of Equation (56), with the Helios observations is shown in Figure 14. The VDFs in the left and right frames show the plateaus defined by vanishing pitch-angle gradients (also implying marginal plasma stability). Parts of the isodensity contours in velocity space shown in Figure 14 are outlined well by a sequence of segments of circles centered at the respective phase speeds (bold dots indicate its location), which are assumed to vary slightly, and due to dispersion are smaller than the local Alfvén speed. For the contours between 0.2 and 0.4 of the maximum density, the plateau can be as wide as 70 degrees in pitch angle as calculated in the wave frame. The horizontal axis refers to the parallel proton velocity component, whereby an outward velocity has a positive value. The dotted lines show the density contours observed by Helios at 0.3 AU in a high-speed wind. In the right frame, R = 0.3 AU, Vsw = 678 km s−1, and VA = 184 km s−1. The diffusion plateaus of protons in resonance with left hand polarised cyclotron waves are shown by the solid lines. For υ∥ < 0, a proton is in resonance with outward waves, and for υ∥ > 0 with inward propagating waves. The solid lines are the numerical solutions of Equation (56).
Left: Comparison of measured proton velocity contours with the quasilinear plateau. The horizontal axis gives υ∥ and the vertical υ⊥ (in units of km s−1). The measured contours correspond to fractions of 0.8, 0.6, 0.4, 0.2 of the maximum. The dotted lines (circular arcs) delineate the theoretical contours shaped by diffusion Marsch and Tu (after 2001b). Right: Another comparison of the cyclotron diffusion plateau in velocity space with proton observations. The solid lines on the left hand (right hand) side of the vertical axis represent the theoretical contours (for zero pitch-angle gradient) formed by the cyclotron resonance of protons with outward propagating (inward) left hand circularly polarised cyclotron waves. The dotted contours are measured and correspond to fractions 0.8, 0.6, 0.4, 0.2, 0.1, of the maximum of the VDF, respectively. The dispersion relation of a cold plasma with protons and electrons was used to calculate the phase speed. The Alfvén speed is 184 km s−1 Tu and Marsch (after 2002).
The observations shown in Figure 14 suggest that Alfvén-cyclotron fluctuations propagating parallel or antiparallel to the background magnetic field influence the shape of the ion VDFs. The waves may be generated at low, non-resonant frequencies and, by propagation through the inhomogeneous coronal plasma, approach the ion-cyclotron resonances and by proton scattering cause their anisotropy. In turn, ion thermal anisotropies of sufficient magnitude can lead to growth of ion-cyclotron instabilities. The resulting enhanced Alfvén-cyclotron fluctuations scatter the ions and thereby reduce their original anisotropy.
Gary and Saito (2003) have carried out particle-in-cell simulations of Alfvén-wave-scattering of protons in a magnetised, homogeneous, collisionless model plasma of electrons and one ion species to study the evolution of the VDFs in response to these scattering processes. A solar wind simulation with a spectrum of right-travelling Alfvén-cyclotron fluctuations initially imposed leads according to Gary and Saito (2003) to highly non-Maxwellian proton VDFs. Their computations are illustrated in Figure 15 and show that the pitch-angle scattering of left-travelling (with υ∥ < 0) ions becomes weaker, as their parallel speed becomes less negative, but also that such scattering can even transport ions across the line at υ∥ = 0. This important numerical result confirms the basic observational features.
Numerical simulation of the proton velocity distribution fp(υ∥, υ y ) at tΩp = 56. The phase speeds, ω/k∥, are for five left hand polarised wave modes indicated on the right hand side by the five dots at the locations with υ⊥ = 0 and υ∥ > 0. The five dots on the left axis represent the corresponding cyclotron resonant velocities. The related solutions of the plateau Equation (56) are indicated by the five heavy solid lines. Note that the diffusion can even render the ions cross the υ∥ = 0 line (after Gary and Saito, 2003).
6.3 The kinetic shell model
In a series of papers, Isenberg (2001a, b), Isenberg et al. (2001), and Isenberg (2004) developed their so-called kinetic shell model, which seeks to test the collisionless response of protons in the solar corona and solar wind to the resonant dissipation of ion cyclotron waves propagating outwardly from the Sun. As reviewed by Hollweg and Isenberg (2002), this wave-particle mechanism is often invoked as responsible for generating the fast solar wind.
In the kinetic shell (or bi-shell) model, the approximation is made that the resonant cyclotron interaction proceeds much faster than any other process affecting the protons, which is consistent with the size of the relaxation rate as defined in Equation (53). In addition, it is assumed that the resonant portions of the VDF are kept in a state of marginal stability, such that resonant protons are organised on nested shells of constant density in velocity space, defined by the condition that the proton energy is conserved in the rest frame moving with the phase speed of the resonant wave, according to the plateau condition, ∂/∂α = 0, as derived from Equation (50) is assumption is to some extent supported by the shape of the middle parts of the observed fast proton VDFs, which were shown in Figure 14 and appeared to obey Equation (56). Note however, that most VDFs in their innermost cores, where the strongest resonance due to the highest proton density will take place, hardly reveal a rigid bi-shell shape (see, e.g., the previous Figure 3).
The fixed shells in the model are argued to evolve on the large non-resonant timescale (expansion time), corresponding to the shell-averaged forces of gravity, charge-separation electric field, and magnetic mirror, which all are contained in Equation (9). The crucial assumption then made is that these kinetic shell VDFs are held in a marginally stable state, in which they cannot exchange any more energy with the waves. Isenberg (2004) claims that in this state the evolution of the shells corresponds to the effect of the maximum possible dissipation of the waves.
The earlier work was expanded to include Sunward propagating waves and improved to treat also anti-Sunward protons. These changes in the model yielded more plausible proton speeds and temperatures than obtained previously. Also, the important effects of ion-cyclotron wave dispersion were incorporated into the model. Dispersion created broader resonant shells, consistent with the in situ observations (Marsch and Tu, 2002; Tu and Marsch, 2002).
In this way Isenberg (2004) found that the non-resonant forces acting on dispersive-shell VDFs invariably produced only weak acceleration, and surprisingly perpendicular cooling rather than the observed heating. These model effects were attributed to the weaker inertial force on the Sunward dispersive shells. Since according to the authors the model describes the maximal wave dissipation, it was concluded that heating and acceleration of protons in coronal holes are not caused by the dissipation of parallel propagating ion-cyclotron waves. Relaxing the extreme kinetic shell assumption will not change this negative result, Isenberg (2004) stated and concluded that “…with a less instantaneous interaction, the resonant shells will not be completely filled, but then the dissipation will provide even less proton heating than in our model…”. Apparently, more work needs to be done, and certainly other wave modes, like kinetic Alfvén waves propagating obliquely, should be considered.
One reason for the negative conclusion of Isenberg (2004) is his invalid assumption that Alfvén-cyclotron waves cannot scatter protons through the condition υ∥ = 0. However, as noted in Subsection 6.2, the simulation of Gary and Saito (2003) showed that such scattering can indeed take place. Of course, their simulations were based on different approximations, and thus it remains to be consistently determined whether protons can be scattered appreciably by Alfvén-cyclotron fluctuations.
Such future research should be conducted in the framework defined by the work of Cranmer (2000, 2001) and Vocks and Marsch (2002). If ion heating is due primarily to Alfvén-cyclotron wave scattering, and frequency sweeping is the mechanism transferring fluctuation energy from longer to shorter wavelengths, do the heavy ions absorb all the fluctuation energy and leave nothing for the protons? Kinetic modelling of ions in the corona seems to show that heavy-ion wave scattering might saturate in a way allowing wave energy to progress to the shorter proton cyclotron wavelengths. This issue will be resumed and further discussed in Subsection 7.2.
Galinsky and Shevchenko (2000) did not make the rigid bi-shell assumption in their model, but started from the full quasilinear Equation (50) for wave-particle interactions in the solar wind with a weakly non-uniform magnetic field. Their method was also based on a scale separation between the length scales of quasilinear diffusion and magnetic-field inhomogeneity, thus allowing them to obtain large-scale kinetic solutions for both the VDF and wave energy spectrum density, without the need to consider the details of the small-scale relaxation process. The numerical solution of their equations illustrated the importance of the diffusion plateaus and indicated the possible existence of a secondary plasma instability for an initially stable proton VDF. Tam and Chang (1999, 2001) also solved the diffusion equations of QLT in a non-uniform model solar wind for electrons and protons and reproduced some observational trends, however, obtained VDFs that hardly resembled the measured ones.
6.4 Regulation of the proton core temperature anisotropy
We now return to the observed characteristics of the proton VDFs in the solar wind. Their core parts often show a distinct thermal anisotropy (illustrated before in Figure 3), which was first discovered in the early days of space observations near 1 AU (Feldman et al., 1974). Subsequently, the Helios observations also indicated that the proton core temperature ratio, T∥c/T⊥c, was relatively high and found to range from about 2 to 3 in the high-speed streams measured in situ near 0.3 AU (Marsch et al., 1982c). An example is shown in Figure 16. Schwartz et al. (1981) provided an early explanation of the coupling between the core anisotropy and the beam component of the protons. More recently, similar pronounced anisotropies were also found in the solar wind proton data, including the entire velocity distribution, from the Ulysses SWOOPS instrument (Gary et al., 2002) and near 1 AU from the Advanced Composition Explorer (ACE) satellite (Gary et al., 2001c) and the WIND spacecraft (Kasper et al., 2003). When the beam in the proton VFD is sufficiently tenuous, a simple two-parameter description determined by the parameters anisotropy, A = T⊥/T∥ − 1, and proton plasma beta, βp, usually provides a good characterization of the instability consequences of the thermal anisotropy.
A highly anisotropic proton VDF with a large core-temperature anisotropy as measured by Helios 2 in fast solar wind near 0.3 AU. The data were taken in the year 1976 on day 107, during the time span from 01:24:38 to 01:25:18. The proton fluid speed is 729 km s−1. The contour lines correspond to fractions 0.8, 0. 6, 0. 4, 0.2 of the maximum located at the central point (continuous lines), and to fractions 0.1, 0.032, (dashed lines) and 0.01, 0.0032, 0.001 (dotted lines). The velocity plane is determined by the unit vectors in the direction of the proton fluid velocity (x-axis) and the magnetic field (straight solid line) and centered at the maximum. Apparently, the symmetry axis is well defined by the magnetic field direction that represents the axis of gyrotropy. The distribution also reveals a hot tail travelling along the field (after Tu and Marsch, 2002).
Following the basic rationale of collisionless kinetic plasma theory, according to which enhanced wave-particle interactions induced by a kinetic instability would limit and regulate possible free energy sources, some early simulations were carried out by Gary et al. (1997, 1998). They predicted that anisotropy-beta relations which represent proton anisotropy constraints should exist. Subsequently, solar wind observations (the last three citations in the first paragraph) presented experimental confirmation of these predictions. Gary et al. (2000b) further investigated the proton cyclotron anisotropy instability and derived scattering rates, or temperature anisotropy relaxation rates, from numerical hybrid simulations. The threshold anisotropy estimated from theory can be written as:
where Sp (of order unity) and αp (≈ 0.4) are fitting parameters derived from various growth rates, and \({\beta _{\parallel {\rm{p}}}} = 8\pi {n_{\rm{p}}}{k_{\rm{B}}}{T_{\parallel {\rm{p}}}}/B_0^2\). Equation (57) completely determines the properties of the instability in space plasma conditions. Computer simulations allow one to infer scaling relations that describe the non-linear saturation of this instability. Defining the variable \({x_{\rm{p}}} = \beta _{\parallel {\rm{p}}}^{0.4}({T_{\bot {\rm{p}}}}/{T_{\bot {\rm{p}}}} - 1)\), permits one to write the maximum proton scattering rate, \({\tilde \nu _{\rm{p}}}\), as follows:
which shows that scattering in its non-linear phase sensitively depends on the proton anisotropy and effectively ceases when isotropy is reached. Further hybrid simulations were carried out by Gary et al. (2003) on the proton and alpha-particle anisotropies. They show a clear tendency of the fluctuations to reduce the temperature anisotropies (consistent with the linear constraint of Equation (57)), and also reduce the initial differential speed that was assumed to be at a sizable fraction of the Alfvén speed. The numerical results were found to be consistent with Ulysses observations.
Kasper et al. (2002) also evaluated the total proton thermal anisotropy and investigated the firehose instability, which may arise in the solar wind. They demonstrated, with a large data set of more than seven years, that the observed limit to the proton temperature anisotropy for T∥/T⊥ > 0 was in agreement with constraints posed by theory and simulations on the firehose instability (Gary et al., 1997, 1998, 2000a). This constraint is analogous to the anisotropy limit obtained by theoretical and computational methods for the electromagnetic cyclotron instability driven by T∥/T⊥ > 1 (see Gary et al., 2001b and references therein). Matteini et al. (2005) demonstrated that the proton fire hose instability, which can develop when T∥ > T⊥, is able to counteract and limit the growth of the anisotropy as naturally caused by adiabatic expansion.
Concerning other recent theoretical interpretations of the measured anisotropies, Araneda et al. (2002) studied the proton core temperature effects on the relative drift and anisotropy evolution of the ion beam instability in the fast solar wind, and Gary and Saito (2003) presented theoretical evidence obtained through numerical simulations for the regulation of the core anisotropy in association with plateau formation through pitch-angle diffusion of protons in cyclotron resonance.
Tu and Marsch (2002) analysed proton VDFs in the solar wind with respect to the dependence of the temperature anisotropy on the plasma beta and established an empirical relationship and theoretical explanation of their result on the basis of resonant diffusion of the protons by dispersive cyclotron waves. Marsch et al. (2004) provided solid statistical evidence on the relation between the anisotropy and the proton plasma beta, parameters that are believed to play a key role in the wave regulation of the shape of the core VDF. They found a clear linear correlation between T⊥/T∥ and the plasma beta β, and used these data to make a least-squares-fit analysis and to compare the resulting empirical fit with theoretical predictions.
These results are shown in Figure 17. The black isolated dots represent the mean values of the observed Helios data points, with the data binned in various β intervals. The whole β range extends from log(0.06) to log(1.0) and is divided into 36 bins. The vertical bars give the corresponding standard deviations, respectively. The thick solid line shows the result of a least-squares fit to the data points. The light-dotted line shows the temperature ratio resulting from quasi-linear diffusion caused by dispersive cyclotron waves, which obey the cold plasma dispersion relation Tu and Marsch (2002). The dotted-dashed line shows the function A = 0.65β−0.40, which is the anisotropy instability threshold as inferred from numerical simulations for a limiting growth rate γ/Ωp = 0.01 (Gary et al., 2001c).
Comparison of the measured proton core temperature ratio, A + 1 = T⊥c/T∥c, with theoretical predictions. This empirical ratio is plotted versus the plasma beta based on the core VDF only. A least-squares fit to the binned data with variance bars is also given, together with other lines indicating the A-β-relations derived from various sources in the literature (after Tu and Marsch, 2002).
The least-squares fit presented in Figure 17 involves a large number of data points: 25439. The fit gives the functional relation A = eaβb − 1, with the coefficients a = 1.505 × 10−1 ± 4.358 × 10−3 and b = −5.533 × 10−1 ± 2.809 × 10−3. This correlation with a coefficient of 0.78 indicates that in high-speed wind there exists an empirical relation between the proton core anisotropy and plasma beta determined by the proton core parallel temperature.
Large heavy-ion thermal anisotropies were also detected in the solar corona. The Ultraviolet Coronagraph and Spectrograph (UVCS) on SOHO measured the Ovi line widths and inferred that very high temperature anisotropies of the O5+ ions must exist in the Sun’s polar corona hole (Kohl et al., 1998). According to these remote-sensing observations, T⊥o/T∥o, may become higher than 100. However, Ofman et al. (2001) have shown by numerical simulations that the ion-cyclotron instability constrains the anisotropy of the O5+ ions that can be sustained in the corona. Maximum growth is obtained for parallel wave propagation. Using the linear dispersion relation after Gary and Lee (1994), the exact numerical solution of the dispersion equation allows one to derive for any heavy ion species i a threshold condition involving the parallel plasma beta, β∥i, such that the limiting anisotropy for maximal growth rate reads as follows:
where S i is of order unity, and for the exponent one obtains α i ≈ 0.4. Hybrid numerical simulations were performed by Gary et al. (2001c), which carried the instability to its non-linear saturation. The simulation results are in general agreement with the instability threshold scaling of Equation (59), however the best description of the non-linear stage yields higher S i values, with 1 < S ≤ 10. There were limitations in this work in so far as no relative flows between protons and heavy ions were considered. The effective wave-ion scattering rate turned out to be about of the order the ion gyrofrequency and rather independent of the plasma beta, with \({\tilde \nu _i} \approx 0.3\;{\Omega _i}\).
It is now widely believed that the observed large ion temperature anisotropies indicate the physical mechanism by which the solar corona and solar wind are heated (see the review by Hollweg and Isenberg, 2002). Recently, Li and Habbal (2005) have also carried out hybrid simulation of the ion-cyclotron resonance in the solar wind and studied the evolution of velocity distribution functions. However, the coronal and interplanetary origin of the strong perpendicular ion heating is still not well understood.
6.5 Origin and regulation of proton beams
In addition to the anisotropic core discussed above, a secondary proton component was often observed as a salient feature of the VDFs in fast solar wind. The beams were already found in the early era of space in situ explorations (Feldman et al., 1973, 1974; Goodrich and Lazarus, 1976; Marsch et al., 1981, 1982c, b; Feldman et al., 1993; Goldstein et al., 2000), and were extensively described in the review by Feldman and Marsch (1997). In Figure 3 several beams from Helios are shown, and another typical example is shown in Figure 18. These double-beam distributions carry important information about the kinetic state of the solar wind plasma and on the interplanetary dynamic processes. However, the origin (either in the corona and/or interplanetary medium) of the proton beams and their spatial and temporal evolution has not yet been fully understood.
Left: This panel shows 2-D contours of a typical proton beam VDF, based on a 3-D interpolation of the data obtained by Helios 2 at 09:08:33 on day 70 in 1976 after Tu et al. (2004). The horizontal axis gives the velocity component parallel (υ∥) and the vertical perpendicular (υ x ) to the magnetic field. The solid, dashed and dotted curves, respectively, show the contours of the VDF relative to its maximum value which is located at υ∥ = 0 and υx = 0. The respective values of the contours from the center correspond to 0.8, 0.6, 0.4, 0.2, 0.1, 0.032, 0.01, 0.0032, and 0.001 of the maximum. Right: This panel shows a 1-D reduced VDF, ΔF(υ∥), obtained by integration along the vertical υ x -direction indicated in the left panel. The VDF is normalised to its maximum value. The horizontal axis gives the velocity component υ∥ in km s−1.
Feldman et al. (1974, 1996) argued that proton beams originally might stem from proton injections into the nascent solar wind at the base of the expanding solar corona. On the contrary, Livi and Marsch (1987) suggested that the solar wind proton double beams may be generated and shaped by coronal and interplanetary Coulomb collisions, which are insufficient to prevent proton runaway or pitch-angle focusing in the mirror field configuration. Montgomery et al. (1976), Daughton and Gary (1998) and Daughton et al. (1999) provided arguments from instability calculations and direct numerical simulations that the velocity of the proton beam is regulated by electromagnetic instabilities driven by the beam kinetic energy. Dum et al. (1980) found evidence for wave growth from the measured distributions, and so did Leubner and Viñas (1986) for some selected double-peaked proton VDFs.
A basic hypothesis in collisionless plasma theory is that wave-particle scattering by enhanced fluctuations stemming from a kinetic instability should constrain the source of free energy that drives the unstable wave. This idea implies that the stability threshold derived from linear theory should place observable bounds on the parameters that characterise a growing mode. Goldstein et al. (2000) found that the proton measurements obtained from the plasma instrument on Ulysses support this notion, as they indicated that linear plasma instabilities constrain the relative streaming of the two proton components. Their results are illustrated in the right frame of Figure 19. The four lines shown represent the threshold conditions for two proton-proton instabilities as calculated in Daughton and Gary (1998). The upper and lower solid lines represent the thresholds of the magnetosonic instability at β∥c = 0.2 and 1.0, respectively, whereas the upper and lower dashed lines display the thresholds of the Alfvén instability at β∥c = 1.0 and 0.2, respectively. Apparently, the proton beams in the solar wind as measured by Ulysses are practically stable.
Left: The normalised beam drift speed is plotted versus the plasma beta after Tu et al. (2004). Each cross point represents a single Helios plasma measurement of the proton beam drift speed plotted against the core plasma beta, β∥c. The dash-dot line shows the result of a linear least-squares fit to the logarithm of the observed data points. The dotted line and the dashed line show the threshold of the Alfvén I instability after Daughton and Gary (1998) with a constant ratio of the proton beam density, nb, to the electron density, ne. The values of their ratio, nb/ne, are 0.05 (upper line) and 0.2 (lower line). The maximum instability growth rate at the threshold is γm/Ωp = 0.01. The diamonds show the few data points for which the VDFs are found to be unstable. Right: The normalised proton-proton relative drift speed is shown versus the relative beam density. Individual data points as measured by Ulysses are given after Goldstein et al. (2000). The four lines represent threshold conditions for two proton-proton instabilities as shown in Daughton and Gary (1998). The upper and lower solid lines represent the thresholds of the magnetosonic instability at β∥c = 0. 2 and 1. 0, respectively, whereas the upper and lower dashed lines display the thresholds of the Alfvén instability at β∥c = 1.0 and 0.2, respectively.
In addition to linear beam instabilities, Tu et al. (2002, 2003) suggested that the proton beams (running faster than the core) could also be shaped by quasi-linear diffusion caused by cyclotron waves, which follow a second branch of the dispersion relation owing its existence to the ubiquitous alpha particles in the solar wind. Whether this branch is populated by waves in the real solar wind remains unclear.
More recently, Leubner (2004a) newly interpreted proton beam distribution functions as a natural equilibrium state in generalised thermo-statistics. Leubner (2004b) also fitted the VDFs by two superposed kappa functions for the proton core and beam, and discussed fundamental issues of such kappa distributions for interplanetary protons. In these papers the core-beam distributions are theoretically derived from a non-extensive entropy generalization and then tested on twelve measured Helios VDFs, where the core-beam separation scale is found to obey a condition of maximal entropy.
Tu et al. (2004) again analysed the Helios data with respect to the proton beam instability. Their statistical results from a large data set are shown in Figure 19, giving in the left frame a scatter plot of the measured beam drifts versus the core β∥c. The crosses represent the observed beam drift speed along the magnetic field, which is normalised to the local Alfvén speed, i.e., the ratio υd/VA. From this plot we can see that the two parameters are surprisingly well correlated. The correlation coefficient between lg(β∥c) and lg(υd/VA) is 0.82. By using a linear fit to represent the data, one finds a simple empirical relation, which may (including the standard deviations) be written as:
This relation is plotted in Figure 19 as the dashed-dotted line, which fits the data points well, especially for the plasma beta range: β∥c = 0.1–0.6. There are two additional curves in Figure 19. The dotted line and the dashed line refer to theoretical results. They give the threshold values of the Alfvén I instability according to Daughton and Gary (1998). Their threshold curve was regular enough that they could fit it by the simple relation:
where \({\Delta _1} \cong 1.65\beta _{\parallel {\rm{c}}}^{0.06}\), and Δ2 = 5.1 + 1.9β∥c. This theoretical curves is shown for a constant relative beam density, having the values: nb/ne = 0.05, respectively 0.2. From Figure 19 we can see that the majority of the data points correspond to relative beam densities ranging between 0. 05 and 0. 2. This plot clearly indicates that most of the measured proton beam distributions that qualified for our data set are stable against the oblique electromagnetic Alfvén I beam instability, since we see that the majority of the data points are distributed below (outside of) the regions delineated by the dashed and dotted lines.
Although the stability boundary for the Alfvén I instability has been parameterised in terms of drift speed and plasma beta in Equation (61), it is worth mentioning that this instability is actually a good deal more complicated than can be represented in a two parameter fit. Equation (61) was derived assuming a bi-Maxwellian, with isotropic beam, isotropic core, isotropic electrons, and beam temperature equal to core temperature. In reality, the growth rate of the Alfvén I instability has a significant dependence on all four of these additional complications as shown in Figures 3 to 6 of Daughton and Gary (1998). So the true stability boundary (assuming a bi-Maxwellian) is a function of six parameters and thus too complicated to fit in a simple relation.
There are only 10 data points, indicated by diamonds in the right upper corner of Figure 19, which correspond to VDFs that are unstable against the Alfvén I instability, according to the results presented by and Daughton et al. (1999) and Daughton and Gary (1998). Their equation (1) was used to calculate the theoretical instability-threshold value of υd/VA. If this is smaller than the observed value, υd/VA, for a measured VDF, the corresponding data points are indicated by diamonds.
Marsch and Livi (1987) some time ago analysed solar wind ion beams and found observational evidence for marginal stability of many proton beams having υd/VA ≥ 2, values which one hardly finds in Figure 19. Marsch and Livi (1987) were mostly looking for right hand polarised magnetosonic waves driven unstable by resonant protons at the high-energy flanks of the beam, and found about 20% of their fast beams to be weakly unstable. They concluded that this instability was important in regulating the proton beam and heat flux. Clear single examples for this were found before by Dum et al. (1980) from a stability analysis based on the full measured VDFs, as well as on several modelled VDFs by Leubner and Viñas (1986). According to the data in Figure 19, one comes to a more moderate conclusion, although on the basis of a different, and more restrictively and by visual inspection selected, data set of about 600 proton beams in fast solar wind of which one is shown in Figure 18. It turns out that most of the low-density (nb/ne ≤ 0.05), high-speed (υd/VA ≥ 2) proton beams obtained in the previous study by Marsch and Livi (1987) were perhaps spurious, and their identification severely suffered from low, unreliable counting statistics.
Voitenko and Goossens (2002b) studied kinetic excitation of high-frequency ion-cyclotron kinetic Alfvén waves (ICKAWs) by ion beams produced by magnetic reconnection in the solar corona. Plasma outflowing from a reconnection site may set up a neutralised proton beam, providing free energy for wave excitation. High growth rates of the order of γ ≈ 104 s−1 were found for typical plasma conditions in the low corona. These ICKAWs can undergo Cerenkov resonances with both super- and sub-Alfvénic particles. The waves were found to be damped mainly by wave-particle interactions, with ions at the cyclotron resonance and electrons at the Landau resonance. Therefore, ICKAWs can heat all plasma species in the corona, and may also give rise to anisotropic ion heating.
As we have discussed, ion beams are permanently present in the solar wind, and their stability has been investigated for quite some time (see, e.g., the review of Gary, 1991). Some of the more recent studies within the framework of linear theory were carried out by Gomberoff and Elgueta (1991), Gnavi et al. (1996), Gomberoff and Astudillo (1998), Gomberoff and Astudillo (1999), Gomberoff et al. (2000). The non-linear behaviour of circularly polarised electromagnetic waves and parametric instabilities in a plasma with ion beams were studied by many authors (Hollweg et al., 1993; Gomberoff et al., 1994; Jayanti and Hollweg, 1993a, b, 1994; Gomberoff, 2000; Gomberoff et al., 2001, 2002, 2003). The influence of ion kinetics on the non-linear behaviour of the waves was also investigated by means of the drift-kinetic approach (Inhester, 1990), hybrid simulation (Daughton et al., 1999; Araneda et al., 2002), and quasi-linear theory (Tu et al., 2002; Tu and Marsch, 2002). A simulation study of the role of ion kinetics in low frequency wave-train evolution was carried out by Vasquez (1995). It is only recently that it was realised that in the presence of an ambient large-amplitude Alfvén wave the nature and threshold of the proton beam instability can be substantially modified.
6.6 Effects of wave couplings on linear beam instabilities
A non-uniform background plasma can strongly change the linear properties of common plasma instabilities. For example, Gomberoff (2003) showed that in the presence of large-amplitude Alfvén-cyclotron waves, the beam-driven instability of linear right hand polarised waves could be stabilised. Recently, Araneda and Gomberoff (2004) demonstrated by direct numerical simulation with a one-dimensional hybrid code (Winske and Leroy, 1984) that, if the non-linear wave amplitude exceeded a certain threshold value, the linear instability was completely stabilised. We present some results from these simulations in Figure 20, which shows the spectral density of the waves in the frequency-wavevector plane, such that the dispersion curves become clearly recognizable. The wave power is given in grey coding.
Power spectrum arranged according to the dispersion relation of transverse magnetic field fluctuations propagating along the field, for the case of zero background-wave amplitude, A = 0, on the upper (a) and large amplitude, A = 0.3, on the lower panel (b). The bottom gray codes correspond to the logarithms of the wave power. A strong beam is present, but the original beam instability (a) is highly suppressed in the presence of the ambient wave (b) (after Araneda and Gomberoff, 2004).
As Figure 20 demonstrates, that in the presence of a large-amplitude Alfvén-cyclotron wave the power of the waves corresponding to the linear instability strongly decreases (see the fading of the left grey bar with the relative amplitude A, rising from 0.0 to 0.2). There is low wave activity in the third quadrant, except for the power at k∥VA/Ωp = −0.35, which may be due to a parametric decay. This region would be expected to be stable in a linear system with A = 0. These properties show that there is a stabilization of the linear instability (Gomberoff, 2003), due to the presence of the large amplitude wave that is visible as dark bar in the lower frame (b) at k∥VA/Ωp = 0.4. The beam drift is large, U = 2.1 VA, and the beam density sizable, nb/ne = 0.15, with ne = nb + np. Finally, note that the beam-modified linear dispersion relation is nicely outlined by the two curves crossing at the origin. On these lines the fluctuation level clearly appears to be enhanced.
These simulation findings are particularly important in the light of the results presented in the previous section, in which the observed proton double beams in the fast solar wind were found to be largely stable. However, in the standard linear stability analyses (as discussed in the previous section) the presence of the large-amplitude Alfvénic turbulence, which is ubiquitous in the fast solar wind (Tu and Marsch, 1995), was not accounted for. But Kaghashvili et al. (2004) showed that the relative streaming between proton components decelerated among non-linear low-frequency Alfvén waves. Some of their results are shown in Figure 21, which gives the normalised proton beam drift versus time in gyroperiods for various ambient Alfvén wave amplitudes.
Left: Time evolution of the average differential streaming speed U pp for a relative beam density nb = 0. 25. Initially, the main and beam protons are isotropic and have the same temperatures. Curves for five values of the starting speed are plotted, each for the case without waves (dotted lines) and with initial waves (solid lines). Only the fast initial beams show significant deceleration in the presence of waves. Right: Time evolution (extending to 3000 cyclotron periods) of U pp for a strong beam with nb = 0.5 and starting speed 1.57 VA. The case without waves is given by the dotted line, and the cases with waves are indicated by solid lines for different relative wave amplitudes, A. All cases show speeds saturating well below VA. The maximum deceleration rate (for A = 0.0, 0.1, 0.25, and 0.5) is 1.13, 1.31, 2.04, and 2.53, respectively, in units of 10−3VAΩp (after Kaghashvili et al., 2004).
The evolution of streaming minor ions in the presence of large-amplitude Alfvén waves is similar to weak proton beam deceleration. Kaghashvili et al. (2003) showed that minor ion deceleration is associated with the development of a compressional wave component. But they did not relate this with instability, and their simulation results show that minor ion deceleration only begins after an onset time. Therefore, minor ion deceleration may be related with an effective beam instability.
To summarise, Gomberoff (2003), Gomberoff et al. (2003), Araneda and Gomberoff (2004) and Kaghashvili et al. (2004) all have clearly shown that finite-amplitude Alfvén waves have a parametric (often stabilizing) effect on parallel-propagating magnetosonic waves that are generated by a beam instability. Similarly, we may conclude that the obliquely-propagating proton-proton Alfvén cyclotron waves generated by a beam instability are altered by finite-amplitude Alfvén waves. To verify all these theoretical findings by an analysis of measured wave and particle data is an important future task.
Dubinin et al. (2005) analysed the non-linear evolution of differential ion streaming with the non-linear multifluid MHD equations and showed that the cold ion beam-plasma system possesses an equilibrium with a remnant of differential streaming. The plasma may, through the non-linear action of the hydromagnetic waves, attain such a dynamic equilibrium state. It is shown that at zero plasma beta the differential speed between the alphas and protons can range between 0.8 and 1.5VA, and for a proton double beam between 0.3 and 1.5VA. The waves involved are either the Alfvén or magnetosonic modes, depending upon the beam speed, whereby Alfvén waves enable larger differential speeds.
6.7 Regulation of the ion differential motion
As we have seen in Subsections 6.1 and 6.2, theory and simulations predict that Alfvén-cyclotron fluctuations of short wavelength can, when propagating approximately parallel or antiparallel to B, effectively scatter protons so that their perpendicular temperature increases. Moreover, Gary et al. (2005) using the linear Vlasov theory for a uniform, isotropic solar wind plasma consisting of electrons, protons, and alpha particles have recently shown that alpha-particle-cyclotron resonance and proton-cyclotron damping of such fluctuations do sensitively depend on the ion relative velocity, ΔVαp = V α − Vp. The associated ion pitch-angle scattering implies observable correlations between the ion anisotropies and drifts, which were statistically tested and confirmed with plasma data from the ACE mission.
Theoretical investigations of ion differential streaming in the solar wind have been done for a long time. McKenzie et al. (1979), McKenzie and Marsch (1982), and Isenberg and Hollweg (1983) described a mechanism for ion acceleration by waves, and Marsch et al. (1982a) developed the first semi-kinetic models to explain these phenomena. Isenberg (1984a, b) first studied the thermal effects on the cyclotron-wave dispersion relation in a proton-alpha-particle plasma. McKenzie (1994) investigated the interaction between Alfvén waves and a multi-component plasma, including ion differential streaming. More recently, Gomberoff et al. (1996a, b, c) investigated in detail the subtleties of the dispersion relations of ion-cyclotron waves in a multi-component solar wind containing minor ions.
The preferential heating and acceleration of minor ions in the solar wind is an issue of ongoing research, in particular through theory and simulation. Ion resonant acceleration and heating by dispersive ion cyclotron waves was studied by Hu and Habbal (1999). Gary et al. (2000c) and Li and Habbal (2000) investigated the alpha/proton magnetosonic instability in the fast solar wind. Helium ion acceleration and heating by Alfvén/cyclotron fluctuations in the solar wind was studied by Gary et al. (2001a). Facing new SOHO observations, the resonant heating and acceleration of heavy ions in coronal holes driven by cyclotron resonant spectra was addressed and simulated by Ofman et al. (2002). Gary et al. (2003) looked into the consequences of proton and alpha anisotropies in the solar wind by means of numerical hybrid simulations, following earlier work by Winske and Omidi (1992) on the electromagnetic ion/ion cyclotron instability. Dubinin et al. (2005) showed that the ion differential speed can be understood as the result of a non-linear ion-wave equilibrium.
Electromagnetic heavy-ion/proton instabilities driven by the relative velocity of two distinct ion components were generally studied by means of linear theory and non-linear numerical hybrid simulation by Wang et al. (1999). Linear dispersion theory (see again the discussion in the previous Subsection 6.5) predicts that the fastest growing mode is the right hand polarised proton beam instability. The simulations provided scaling relations for the magnetic field fluctuation level at saturation and the maximum growth rate, results which are also relevant for the solar corona and solar wind. Alpha/proton streaming instabilities in the solar wind were further studied by Gary et al. (2000d) by help of bydrid simulations, which allowed them to derive wave-particle scattering rates of the two components. This scattering reduces and limits the differential speed and heats the alpha particles more strongly than the protons perpendicular to the field.
6.8 Regulation of the electron heat flux
Significant progress, on the basis of Ulysses electron measurements (Scime et al., 1994), was made in the understanding of the electron heat flux regulation. The empirical heat conduction law suggested long time ago by Feldman et al. (1975) gives for the heat flux value, q∥e, the following empirical scaling relation with the parallel and perpendicular core and halo temperatures:
which shows that the heat flux is carried mainly by the halo electrons (including the then still unresolved strahl), and essentially scales like the halo particle flux times the halo thermal energy. This dependence has experimentally been verified, demonstrating that solar wind heat conduction has nothing to do with the local temperature gradient but with the thermal energy convected by halo electrons. Empirically, the heat flux scales with radial distance, R in units of AU, from the Sun according to the formula: q∥ e = 12.7 R−31μ Wm−2, which describes the average observations in full agreement with Equation (62). This scaling with distance gives values of q∥ e being much larger than predicted by the collisional Spitzer-Härm theory that was discussed in previous sections.
The heat flux regulation mechanism enters formula (62) through the zero-current condition for the combined core and halo drifts, which reads nH∆VH + nC∆VC = 0, whereby quasineutrality of courserequires that nH + nC = ne, and through the fact that VH ∼ VA, which is in proportion to the magnetic field magnitude B. One also finds the relation TH ≈ 7 TC, which was however predicted by collisional transport theory Scudder and Olbert (1979a, b) and is not easily explained by wave effects. From the work of Maksimovic et al. (2005) it appears that the strahl electron density is comparable to the halo density at heliospheric distances below 0. 5 AU. Therefore, in a future study it should be investigated if the strahl electrons play a role in the zero current condition closer to the Sun.
That the halo drift speed was observationally found to be closely tied to the Alfvén velocity, supports a regulation of the heat flux by Whistler-mode waves. This correlation is shown in Figure 22 after Scime et al. (1994), where on the left the halo flux density and total heat flux density are displayed, and on the right the halo flux density and B. Both plots illustrate the similar course versus time of the compared quantities, thus confirming that electron heat conduction in the distant solar wind is due to convection of differential heat (between halo and core electrons) at the halo speed, and that it follows closely the Alfvén speed.
Left: Correlation of the total electron heat flux with the halo particle flux from 2 to 2.3 AU. VH is the halo drift speed in the Sun’s (inertial) frame of reference. Similar correlations are seen over the whole distance range from 1 to 5 AU. Right: The electron heat flux and the local magnetic field magnitude show a clear and lasting correlation (after Scime et al., 1994).
The results in Figure 22 indicate that the halo electrons (a strahl could not be resolved in those measurements) carry the electron heat flux which is observed to vary with B or VA. This points to the importance of waves regulating the halo drift. Gary et al. (1994) studied in detail the possible whistler regulation of the electron heat flux, within the electron model VDF of two drifting anisotropic bi-Maxwellians. They considered models of local and global scalings of the heat flux with plasma parameters. The global model yields a heat flux at the threshold of the whistler instability, which scales with distance in the same way as the average observed heat flux from Ulysses and provides an upper bound. A closure relation was also suggested. Gary and Li (2000) provide further parametric studies for the instability over a wide range of the electron plasma beta.
The “maximal” heat flux is globally given as a function of radial distance by the empirical relation qmax = 22.85 R−3.19μ Wm−2 after Scime et al. (1994), whereby the local values can substantially fluctuate about this mean value. This maximum is defined by the flux that is carried by all electrons, when having the core thermal energy, and that is convected at the core thermal speed, i.e., \({q_{\max}} = 3/2{n_{\rm{e}}}{m_{\rm{e}}}V_{\rm{c}}^3\), where the core thermal speed is given by \({V_{\rm{c}}} = \sqrt {{k_{\rm{B}}}{T_{\rm{C}}}/{m_{\rm{e}}}}\). The dimensionless heat flux in units of qmax at the threshold of the whistler instability is for two growth rates plotted versus radial distance in units of 1 AU in Figure 24. Apparently, the observed value of qe stays well below the threshold, suggesting the heat flux may be controlled and regulated by the whistler mode instability. However, Scime et al. (2001) then concluded from a large statistical study that the whistler heat flux instability does on average not provide the observed constraint on the measured qe. For its latitudinal variation see Scime et al. (1995).
In contrast to these statistical results, Dum et al. (1980) found individual measured electron VDFs to be at the margin of the whistler instability. We recall the quasilinear diffusion scenario that was discussed previously for the ions interacting with cyclotron waves. A similar interaction takes place between electrons and the right hand polarised whistler mode waves, which pitch-angle scatter the electrons to the effect that their thermal energy perpendicular to the field will increase. Since the fluctuation level of whistlers (Gurnett, 1991) is usually low in the solar wind, the net resulting heating may be weak. However, by elastic scattering the influence of waves on the shape of the halo and the broadening of the strahl may be substantial.
That the halo shape varies with radial distance was recently demonstrated with Helios, WIND and Ulysses observations by Maksimovic et al. (2005), who used a mixed model for the electron VDF, taking the fact into account that the VDF at high speeds varies more like a power law rather than a Maxwellian. The simplified model VDF (neglecting the strahl), which would correspond to a pure energy distribution as obtained by pitch-angle averaging, is assumed to be composed of two Maxwellians (Feldman et al., 1975; Pilipp et al., 1987a, b; McComas et al., 1992), one for the core and one for the halo (see the previous Figure 2). However, Maksimovic et al. (1997a, b) modelled the Ulysses VDF as a generalised Lorentzian or kappa function, as in our Equation (6). After a careful analysis of their data, Maksimovic et al. (2005) used as the best fit an anisotropic sum of a bi-Maxwellian for the core and a bi-kappa for the halo.
Some of their results are shown in Figure 23, where the VDF is plotted versus υ⊥. Obviously, the normalised core component remains unchanged at all radial distances, and thus the relative importance of the halo component is increasing with radial distance. This enhancement would qualitatively be consistent with enhanced pitch-angle scattering in a background whistler mode field. Also, scattering or mirroring by meso-scale field fluctuations might be a possible cause.
The normalised VDFs are plotted as a function of υ⊥/Vc, for different radial distances (0.3–0.41, 0.48–0.53, 0.7–0.75, 1, 1.35–1.50 AU, in black, red, blue, green, and magenta, respectively). As one can see, the normalised core component remains unchanged at all radial distances but the relative number of halo electrons, as compared to the ones of the core, increases with radial distance (after Maksimovic et al., 2005).
The dimensionless heat flux at threshold of the whistler instability versus radial distance in units of 1 AU. Open squares (triangles) correspond to γm/Ωp = 0.1(0.01). The continuous line gives qe/qmax = 1.78 R0.16, respectively the broken one qe/qmax = 1.68 R0.19. Obviously, the measured heat flux is, on average and everywhere, clearly below the threshold for the whistler instability, which provides an upper bound on qe (after Gary et al. (1994)).
Certainly, Coulomb collision would be insufficient to modify the VDF to the observed degree. However, they seem to matter according to WIND observations made at 1 AU by Salem et al. (2003), who could show that the electron temperature anisotropy, Te∥/Te⊥, which seems to depend mainly on the solar wind speed, Vsw, and electron density, ne, and heliocentric distance, R, actually depends on the number of Coulomb collisions through what they called the electron collisional age, Ae ∼ νeeR/Vsw. It is the number of transverse collisions, at a rate νee, suffered by a thermal electron during the expansion time of the wind over the density-gradient scale. The age Ae also depends on the spatial coordinates, like R, and it may change considerably at stream-interface crossings. Salem et al. (2003) demonstrated that Te∥/Te⊥ was strongly correlated with νee, and they also found that the normalised heat flux Qn = Qe/q0 displays an upper bound inversely proportional to the collisional age, a result being in favour of an overall regulation of the heat flux by Coulomb collisions. Here the free streaming heat flux for the entire VDF is defined as q0 = 3/2nekBTeVe, where the mean thermal speed is given by \({V_{\rm{e}}} = \sqrt {2{k_{\rm{B}}}{T_{\rm{e}}}/{m_{\rm{e}}}}\). The classical Spitzer-Härm value of Qn, which was given in Equation (29) and linearly increases with the free path, represents an upper limit to the observations. Apparently, other than collisional friction keeps Qn constrained. The results of the correlation analysis are shown in the two frames of Figure 25.
WIND electron data from 50 consecutive days after Salem et al. (2003). Left: Scatter plot of 11-minute averages of the electron temperature anisotropy as a function of the inverse of the collisional age, 1/Ae. Right: Scatter plot of 11-minute averages of the normalised heat flux Qn = Qe/q0 in the solar wind as a function of the ratio between the electron mean free path, Lfp = Ve/νee, and the scale of the temperature gradient LT = (dTe/dR)−1 ∼ R. The classical Spitzer-Härm value of Qn (given by the straight line indicated SH) represents an upper limit to the observations.
In summarizing this section, one must conclude that the electron heat flux appears to be regulated by a variety of processes, in which local wave-particle interactions as well as collisions act in combination with global ballistic effects (on the almost collision-free suprathermal electrons), so as to produce and regulate together the observed features like core-halo structure, heat-flux tail, and skewness and thermal anisotropy in the thermal range of the VDFs. Note that all electrons are locally coupled to the ions by the quasineutrality condition, violations of which lead immediately (on the fast scale of the ion or electron plasma period, which is to say within a few milliseconds at 1 AU) to strong electrostatic couplings, which tend to equilibrate ion and electron charge densities.
Finally, a note of caution is in order concerning the measured electron VDF. The Helios electron measurements (Rosenbauer et al., 1977) first showed the presence of a narrow strahl in the electron velocity distribution. A more recent paper Gosling et al. (2001) states that the suprathermal electrons consist of two separable components: a relatively isotropic halo and a narrow strahl which carries the heat flux. Therefore, future electron measurements at higher pitch-angle resolution will hopefully allow us to better understand the still open problem of solar wind heat conduction.
6.9 Plasma heating (cooling) by wave absorption (emission)
In the previous sections we have extensively discussed the various non-thermal features of particle VDFs in the solar wind and the associated linear instabilities and non-linear effects. The coronal origin of the proton beam, thermal core anisotropy or ion differential streaming still remains unclear. The ion core temperature anisotropy (as illustrated in Figure 3 and Figure 16) is commonly believed to be generated by cyclotron resonance through Alfvén-cyclotron wave absorption, a process that presumably takes place in the corona and solar wind. The ion beams may originally come from coronal sources, such as reconnection jets (Feldman et al., 1996) and explosive events, or they may be produced in situ, either by plasma wave absorption and scattering or cumulative collisions (Livi and Marsch, 1987). Also, an electric current, e.g., due to an ion-electron cross-field drift, may produce cyclotron waves (Markovskii and Hollweg, 2002) that in turn could generate the core temperature anisotropy.
Markovskii (2001) argued that ion-cyclotron waves might be generated in coronal holes by a global resonant magnetohydrodynamic wave mode. Particle loss-cone distributions might originate in coronal magnetic mirrors, as represented by expanding coronal funnels (Vocks and Mann, 2003). Parametric decay of large-amplitude Alfvén waves (Gomberoff et al., 2002; Araneda et al., 2002; Gomberoff et al., 2003) may also lead to cyclotron daughter waves. Inhomogeneity of the field will cause frequency sweeping (Tu and Marsch, 1997) of a primordial spectrum via the radial decline of Ωi,e(r) with solar distance r. Do all these processes operate in the corona? We do not know yet, but it seems likely. Hollweg and Isenberg (2002) provide a comprehensive review of the cyclotron heating mechanism.
Whatever the wave-particle interaction is, according to quasilinear theory the heating due to plasma wave absorption can readily be calculated by taking appropriate moments of the fundamental kinetic Equation (50), which describes the evolution of the VDF in the wave field. The corresponding rates are equivalent to the work done by the rest-frame electric field on the current density. In their book, Melrose and McPhedran (1991) give a lucid general account of particle heating by electromagnetic fluctuations. Energy and momentum will, as the result of wave-particle interactions, be exchanged between fields and particles. Quasilinear relaxation of f j (v) will be the consequence, at the expense of the available free energy. The resulting heating rates (Q j ∥, Q j ⊥) and acceleration or momentum transfer rate (R j ) for any species were calculated by Marsch and Tu (2001a), and can be written as follows:
Equation (63) expresses the wave heating rates and acceleration in terms of an integral over the normalised magnetic PSD and sums over the mode number, M, and resonance-order number, s, which denotes the order of the involved Bessel function. The normalised spectral density \({\hat {\cal B}_{\rm{M}}}({\bf{k}})\) was before defined in Equation (52). The resonant speed was already defined by the expression (54). The resonance function or wave absorption coefficient, \({\cal R}_{j}({\bf{k}},s)\), is a functional of the particle distribution function, f j (υ∥, υ⊥) and essentially involves the negative pitch-angle derivative, which is evaluated in the respective wave frame at the Landau resonance (s = 0) or at the cyclotron resonance, for any integer Bessel function index (s = ±1, ±2,..). This dimensionless coefficient is given by the following expression:
It corresponds to the velocity average of the relaxation rate given in Equation (53), which is weighted by the pitch-angle gradient at the resonance. As in the case of parallel propagation, for oblique wave propagation the coefficient \({\cal R}_{j}\) can be entirely expressed in terms of reduced VDFs, see, e.g., Marsch (2002), if the dependence of (64) on υ⊥ is smoothed out by replacing this variable in the Bessel functions by the thermal speed V j ⊥. Wave absorption vanishes when the pitch-angle gradient is zero and a plateau is formed, i.e. for df j /∂α = 0. Explicit expressions for \({\cal R}_{j}\), e.g. for a bi-Maxwellian, were given in the paper of Marsch and Tu (2001a).
Of course, the full rates in Equation (63) can only be evaluated once the VDF, f j (υ∥, υ⊥), for all particle species and the wave power spectral density (PSD), \({\hat {\cal B}_{\rm{M}}}({k_\parallel},{k_ \bot})\), of all wave modes involved are known. This complexity is an unavoidable feature of kinetic theory as compared with fluid theory, in which only velocity averages and mean wave amplitudes are considered. Note that \({\cal R}_{j}\) plays the role of a “wave opacity”, using a term from radiation transfer theory. The wave PSD in the kinetic domain are not well known for the solar wind (not to speak of the corona), and in particular the electric field near the ion gyrofrequency is notoriously difficult to measure from spacecraft. It was only more recently (Kellogg, 2000; Kellogg et al., 2001), that with wave instruments on the modern Cassini and Cluster spacecraft such measurements became possible. As plasma waves and fluctuations, by inelastic pitch-angle scattering according to the diffusion operator (50), randomise the particle VDFs, the knowledge of the wave PSD is of paramount importance to understand the kinetic evolution of the VDFs, or the possible wave-particle equilibrium.
Given reasonable wave fluctuation levels in the corona, see for example the numbers quoted in Marsch (1992) or in Shukla et al. (1999), these micro-turbulent rates might provide sufficient ion and electron heating, and perhaps acceleration as well. The spectra of the plasma waves, as well as of the VDFs, are of course crucial, yet unknown in the corona. The lack of empirical knowledge forces one to make either assumptions, or to calculate ab initio a wave PSD for each wave mode and particle VDF for each species by help of the kinetic Equation (9) and the wave transfer equation, which was for example derived in Melrose and McPhedran (1991). Both equations may then be applied to a specific magnetic field structure in the corona, such as to coronal loops or a coronal hole. Limited reduced cases of Equation (63) were discussed in the literature. For example, heating by high-frequency dispersive Alfvén waves was considered by Shukla et al. (1999), and kinetic aspects of coronal heating were discussed recently by Bingham and Shukla (2004), who specifically investigated lower-hybrid drift modes.
7 Kinetic Modelling of Coronal Expansion
7.1 Kinetics models of solar wind electrons and protons
Given the complexity of the particle VDFs in the solar wind as described in Section 2, it is not surprising that an adequate description of the ion and electron VDFs in the non-uniform solar corona and interplanetary space requires to consider the full kinetic Vlasov-Boltzmann Equation (9) or its reduced variants. Some time ago, Williams (1994) proposed a model of the proton heat flux in collisionless space plasmas, in which he used a simple relaxation-time collision operator in the Boltzmann equation. Observationally, it seems clear that weak collisions and strong wave-particle interactions together with global forces shape the particle VDFs, and can thus cause substantial deviations from local Maxwellians. As the comparisons in Subsection 4.5 demonstrated, moment expansions do not provide a satisfying description of the transport.
To develop better kinetic models requires substantial numerical and algebraic efforts. The starting point again is, as for any kinetic model, the full Boltzmann Equation (9). Since this equation depends on time and on three spatial and three velocity coordinates, the numerical effort in solving it is considerable, and therefore simplifications have to be made. For example, in the solar corona and solar wind, all characteristic time scales are small compared to the ion (and of course even more so the electron) gyroperiod. Thus, it is reasonable to assume a gyrotropic VDF. This reduces the number of velocity coordinates from three to two, instead of the full vector v we may just consider the components υ∥ and υ⊥ (with respect to the local magnetic field direction).
Concerning the electrons, some authors (Maksimovic et al., 1997a) have proposed a solar wind model that relies entirely on suprathermal electrons (represented by a kappa velocity distribution) in the corona to accelerate the fast solar wind ions through the ambipolar electric field. However, their model does not explain two major features of coronal holes, namely hot ions and cold electrons, and makes perhaps unrealistic assumptions at the coronal base. Pierrard et al. (1999) developed a test-particle model of electrons, including Coulomb collisions via the Fokker-Planck operator, and solved their kinetic equations according to boundary conditions posed at 1 AU, in order to construct the corresponding consistent VDF in the corona. They conclude that to match the in situ observations suprathermal electrons have to present in the corona.
Some progress in kinetic modelling of solar wind electrons has also been made by Lie-Svendsen et al. (1997) and Lie-Svendsen and Leer (2000), who were able to partly reproduce the core-strahl structure of the electrons, by using only the Fokker-Planck equation for Coulomb collisions (also including the effects of protons) while starting with Maxwellian electrons at the coronal base. They used a test particle approach, in which test electrons were injected into a prescribed background solar wind, the properties of which were calculated by means of the usual fluid equations. Yet, their model does not give the basic core-halo shape of the velocity distributions as measured in situ. Their electron pitch-angle distributions look realistic, yet show an agreement only for the strahl but not the halo (Pilipp et al., 1987a, b).
Lie-Svendsen and Leer (2000) found that the velocity filtration effect (see again Subsection 4.3) was rather small and not capable of producing sizable electron beams. The drift speed and heat flux were solely carried by the tail that is able to escape from the potential. These results essentially confirm the standard empirical (and exospheric) picture already described by Feldman et al. (1975) and later by Pilipp et al. (1987a, b). Some of their model results are presented in Figure 26, which shows on the left side three isocontours of the VDF, and on the right side cuts through these VDF, which illustrate the formation of electron collisional run-away tails and the missing of electrons on the Sunward side (left) at speeds below the escape speed (11000 km s−1 in this case). Remarkably, the electron pitch-angle distributions resemble very much the measured ones from Helios (see Pilipp et al., 1987a), in particular the narrow electron strahl also occurs at energies beyond about 100 eV. These main kinetic features arise from self-collisions alone. Adding collisions with protons only leads to stronger isotropization (Lie-Svendsen and Leer, 2000).
Model electron VDFs at a distance of 1, 7.5, and 14.8 R⊙ from the Sun (from bottom to top). In the left column we see isocontours, and in the right column cuts through the VDF (logarithmically displayed) along the magnetic field (continuous line) and perpendicular to it (dashed line). The dotted line is the equivalent Maxwellian. In the top panels the escape speed of 11000 km s−1 is indicated by dotted vertical lines. Note the occurrence of a pronounced skewness, equivalent to the electron strahl, and the evolution of a slight temperature anisotropy, with Te∥ > Te⊥, for increasing solar distance (after Lie-Svendsen et al., 1997).
Kinetic solutions of the Fokker-Planck equation were also obtained by Pierrard et al. (1999). Their model mainly differs from the one of Lie-Svendsen and Leer (2000) in the boundary VDF in the corona and the background electron distributions, which were determined from in situ WIND measurements without the artifacts introduced by an exospheric-type cut off, but the conclusions obtained are essentially the same. The core-halo electron VDF may therefore be produced by Coulomb collisions and the large-scale electric and gravitational forces (in this context see again the exospheric model in Subsection 3.3).
What role whistler-mode waves have to play in such a scenario (see again the clear evidence for wave effects provided in Subsection 6.8) has to remain an open issue. However, we want to mention the work of Chen et al. (2003), who numerically modelled the halo and core electrons by a two-fluid model, and found that the drift between them was not effectively enough regulated by Coulomb collisions. To reconcile their model with the observations, they concluded that enhanced friction by wave-particle interaction is required, beyond about 20 R⊙ say, from where on it becomes the dominant factor limiting the skewness.
Concerning solar wind protons, Tam and Chang (1999) first investigated the kinetic effects of wave-particle interactions by using a global hybrid model, which follows the evolution of the particle VDFs along an inhomogeneous field line. By considering diffusion in the wave field, the ambipolar interplanetary electric field and Coulomb collisions, the model corresponds to solving a simplified and approximate variant of the basic Equations (9, 10). This model could qualitatively account for the bulk proton acceleration, preferential heating of heavy ions, as well as double-beam formation (by a mechanism similar to the collisional runaway in the model of Livi and Marsch, 1987). It thus represented an instructive global evolutionary study of the solar wind that took into account these kinetic effects. However, quantitatively the details of the VDFs are poorly reproduced when being compared with the observations shown previously in Subsection 2.3.
The authors extended their study (Tam and Chang, 2001) and also considered cyclotron-resonant heating of the electrons, which did not change qualitatively the features obtained in their previous solar wind model. However, the electron heating increased the electric field, which is to say the electron partial pressure gradient, and thereby enhanced the terminal wind velocity. In a further kinetic study, Tam and Chang (2002) have compared the effects on the solar wind velocity of wave-proton interactions with those of suprathermal electrons. Besides Coulomb self-collisions, they considered no other process affecting the shape of the electron VDFs.
Therefore, the essential kinetic effect on the suprathermal electrons was velocity filtration, which arises from weak Coulomb collisions together with the globally kinetic nature of the solar wind. Their model results showed that in the presence of cyclotron-resonant heating of protons and alpha particles, the electron velocity filtration is relatively insignificant for the acceleration of the fast solar wind. They concluded, however, that when there are wave-cyclotron resonances that also affect the suprathermal electrons strongly, then kinetic effects on the suprathermals may no longer be negligible.
7.2 Kinetic model of coronal ions
Besides the study of Tam and Chang (1999), no attempt was made to directly solve the full Vlasov-Boltzmann equation for solar wind ions. A study of solar wind acceleration based on gyrotropic transport equations (an approach which allows one to construct the particle VDFs from the moments, as we discussed before in Subsection 4.5), including the Alfvén-wave pressure and coronal heating functions, was performed by Olsen and Leer (1999). Their proton VDF closely resemble the model VDFs shown in Figure 10, but they are also missing the ubiquitous proton beam or heat flux and reveal some artificial conic features. Similarly, their electron model VDFs are overally too isotropic and do neither clearly reveal the core-halo structure nor a strahl. Therefore, more complete kinetic models are required to describe the measured VDFs appropriately for realistic coronal and interplanetary magnetic field geometries.
A less ambitious approach was taken by (Vocks and Marsch, 2002) who have shown that it may be meaningful to simplify the full problem and reduce the kinetic VDF further by an integration over υ⊥. This procedure, used before by Dum et al. (1980) to solve dispersion relations, yields two reduced VDFs which are defined as follows:
where a negative υ∥ points in the Sunward direction. The evolution equations for these reduced VDFs are obtained by taking the corresponding moments of the Boltzmann Equation (9) and using the methods of Vocks (2002). To break the chain of higher-order moments appearing in the original diffusion equation we make the Gaussian approximation (Marsch, 1998), which reads:
This relation would be exact for a bi-Maxwellian. Of course, this does not imply that F j ⊥ is Gaussian itself. Empirical motivation for the factorization (66) stems from the solar wind in situ observations, yielding that at any parallel speed the protons perpendicular speeds are distributed as a Gaussian (Marsch and Goldstein, 1983), despite the fact that the VDFs can be skewed, and that there may be proton beams drifting along the mean field.
Using the reduced VDFs, one can construct a gyrotropic, 2-D model VDF by introducing the effective perpendicular thermal speed, which leads with the Gaussian approximation to a convenient model VDF based solely on the reduced VDFs:
Making use of such reduced VDFs for protons and minor ions in the solar corona and solar wind, Vocks and Marsch (2001) first developed a semi-kinetic hybrid model for solar wind expansion in coronal funnels. We quote the pair of reduced Boltzmann equations, which according to the work of Vocks (2002) and Vocks and Marsch (2001) have the form:
Here the symbol A(r) again denotes the cross-sectional area of the magnetic flux tube considered in Equation (31). The last term on the left hand side is related to the expansion of the flux tube and corresponds to the mirror force a charged particle experiences in an inhomogeneous magnetic field. The terms on the right hand side denote the wave-particle interactions and Coulomb collisions, which are not quoted here explicitly. To calculate them for the reduced distribution functions is a tedious task, algebraically as well as numerically, and requires to take partial moments of the wave diffusion operator (50), respectively, of the collision operator (13). This lengthy procedure is described in detail by Vocks (2002).
The semi-kinetic model has been applied by Vocks and Marsch (2001) and Vocks and Marsch (2002) to calculate the plasma dynamics and VDFs of heavy ions in the solar corona. The numerical model includes ion-cyclotron wave-particle interactions and Coulomb collisions as calculated by use of the Landau collision integral. The reduced ion VDFs only depend on the height coordinate r, ion speed υ∥ and time t, and can numerically be solved with reasonable effort for a coronal funnel with an expanding magnetic field (mirror geometry).
The numerical results obtained for heavy ions in a coronal funnel show good agreement with SOHO observations and yield strong heating of the heavy ions. This is illustrated in the Figure 27. It was found that the heavy ions are heated preferentially with respect to the protons, and that sizable temperature anisotropies and ion beams or heat fluxes form, qualitatively similar than the weak-tail solar wind proton VDFs shown in Figure 3. The reduced model VDFs of the heavy ions develop distinct deviations from a Maxwellian, which tend to increase with height owing to the declining efficiency of Coulomb collisions. The wave damping/growth rate γ indicates that the VDFs can reach a limit of marginal stability over a wide range of resonance speeds, where wave emission or absorption gets weak. Wave growth or damping completely vanishes for particles being on the quasilinear plateau, where the pitch-angle gradient is zero in the wave frame. Then the resonance function \({\cal R}\) defined in Equation (64) is by definition equal to zero.
Two-dimensional gyrotropic model VDF of the heavy coronal ion O5+ at 0.44 R⊙ (left) and 0.73 R⊙ (right). The left gyrotropic VDF shows plateau formation leading to marginal stability at the Sunward side. Note on the left the contours with a large perpendicular temperature anisotropy, and on the right the skewness developing along the magnetic field with increasing distance (after Vocks and Marsch, 2002).
Similar results were recently found in direct numerical simulation by Hellinger et al. (2005), who used the so-called expanding box model for the non-uniform solar wind (Hellinger et al., 2003) and presented kinetic hybrid simulations of the interaction of left handed outward propagating Alfvén waves with protons, alpha particles and a tenuous population of oxygen O5+ ions. The Alfvén waves were initially non-resonant with all the ions. Then radial expansion brings the ions to local cyclotron resonance (through the frequency sweeping mechanism suggested by Tu and Marsch, 1997), first the O5+ ions, then alpha particles, and finally protons. These simulations show that oxygen ions are efficiently heated in the direction perpendicular to the background field, but are only slightly accelerated. Oxygen scattering lasts for a finite time span but then saturates, mainly due to the marginal stabilization with respect to the oxygen-cyclotron instability that is generated by the temperature anisotropy. During their scattering the oxygen ions can only absorb a limited amount of the available wave energy.
Liewer et al. (2001) also simulated the Alfvén wave propagation and ion-cyclotron interactions in the expanding solar wind. Recently, Xie et al. (2004) carried out hybrid simulations of heavy ions to analyse the multiple ions resonant heating and acceleration by Alfvén-cyclotron waves in the corona and solar wind. For the solar wind parameters used by Hellinger et al. (2005) in their simulations, the presence of minor heavy ions had a minimal influence on the major species. These simulations do not support the claim made by Cranmer (2000) that minor ions would effectively prevent the cyclotron-wave absorption of alpha particles and protons.
Resonant heating and acceleration of ions in coronal holes driven by cyclotron resonant waves were also studied by Ofman et al. (2002) in one-dimensional hybrid simulations of an initially homogeneous, collisionless plasma. They used a model of corona including kinetic protons, a tenuous component of oxygen ions, and massless fluid electrons. Spectra of ion-cyclotron resonant Alfvén waves were imposed, and the effects of various power-law spectra scaling like f−1 or f−5/3 were analysed. The resulting ion heating was found to strongly depend on the power contained in the ion resonance frequency range. Usually, the minor O5+ ions were easily heated and became anisotropic, however the protons remained nearly isotropic and were mostly heated weakly. For the parameters used, the oxygen temperature ratio, T⊥o/T∥o, reached values of up to ten within several thousand proton cyclotron periods. Whereas shell-like VDFs were transiently present, the long-term shape was more that of a bi-Maxwellian.
7.3 Kinetic model of coronal electrons
The observations shown in Figure 2 reveal pronounced deviations from a Maxwellian, a fact that reflects the local as well as global kinetic nature of solar wind electrons. To model these features certainly requires a kinetic approach. We discussed in Subsection 7.1 the model results for the solar wind. Only Tam and Chang (2001) investigated the kinetic effects of electron cyclotron-resonant heating on the evolution and acceleration of the fast solar wind. Their model followed the evolution of the electron VDFs along a non-uniform magnetic field line under the influence of resonant wave heating, Coulomb collisions, and the electric field consistent with the VDFs themselves.
As discussed in previous sections, there is a distinct tail in the observed electron VDFs in the solar wind. This skewness along the magnetic field due to suprathermal electrons may contribute substantially to the ambipolar electric field, which was also discussed in Subsection 3.3 on exospheric models. To include wave effects as well, a three-dimensional (in velocity space) kinetic model has been developed by Vocks and Mann (2003). In this model, it was shown that a suprathermal tail in the electron VDF can directly originate from coronal plasma processes. Their model describes the kinetics of coronal electrons, including their Coulomb collisions and diffusion in a field of outward propagating whistler waves.
The coronal source of these waves is unclear. However, an electron temperature with T⊥ e/T∥ e > 1 is known to drive whistler waves unstable, which then may lead to enhanced wave-electron scattering. For example, Nishimura et al. (2002) have shown this by particle-in-cell simulation, and thus estimated the maximum scattering rate. They found a numerical constraint which reads:
where Se = 0.7 and αe = 0.55 are fitting parameters derived from the simulation, and \({\beta _{\parallel \;{\rm{e}}}} = 8\pi {n_{\rm{e}}}{k_{\rm{B}}}{T_{\parallel \;{\rm{e}}}}/B_0^2\). Equation (70) defines a theoretical bound for the measured electron temperature anisotropy. The effective temperature isotropization rate \({\tilde \nu _{\rm{e}}}\) is found to be high, of the order of a tenth of the maximal instability growth rate, and thus \({\tilde \nu _{\rm{e}}}/\vert{\Omega _{\rm{e}}}\vert\) may vary between 0.01 and 0.1.
Quasi-linear theory according to Equation (50) describes the wave-electron interaction as pitch-angle diffusion in the reference frame of the whistler waves. They are assumed to be generated below the coronal base and to propagate antiSunward through the corona. For high whistler-wave phase speeds, the resonant interaction causes electrons to be accelerated from relatively small Sunward velocities parallel to the background magnetic field to high speeds perpendicular to the magnetic field. As Vocks and Mann (2003) showed, suprathermal coronal electrons can in this way be generated by wave-particle interactions, a result that is illustrated in Figure 28.
Contours of gyrotropic model VDF of coronal electrons after Vocks and Mann (2003). Left: Contours (at 1.014 R⊙) displaying a perpendicular temperature anisotropy and resonant plateaus (indicated by dotted circular lines) on the Sunward left side. Right: Contours (at 6.5 R⊙) showing a sizable skewness (non-classical heat flux) along the field away from the Sun on the right.
In the paper by Vocks and Mann (2003) a simplified Boltzmann-type equation is numerically solved, which specifically can be written as
In this kinetic equation, g∥ is the gravitational acceleration along the field. The collision terms describe binary collisions and electron pitch-angle scattering by waves. They produce resonant shells on the Sunward side, and subsequent focusing that leads to an anti-Sunward strahl. The electron model VDFs reveals deviations from a Maxwellian, in accord with theoretical expectations and qualitatively similar than the observed electron VDFs shown in Figure 1.
The kinetic model enables one to study electron acceleration and the evolution of the electron VDF from the coronal base into interplanetary space. It includes not only the resonant interaction with whistler waves but also Coulomb collisions and the mirror force that electrons experience in the opening magnetic structure of a coronal funnel. Moreover, wave absorption of the electrons is accounted for to guarantee energy conservation. Apparently, whistler waves can generate suprathermal electrons. Towards interplanetary space, the mirror force focuses the electrons into a narrow field-aligned strahl.
8 Summary and Conclusions
8.1 Summary
This article started out with a definition of its scope and relation with previous reviews. From what we have discussed, the importance of kinetic physics has become clearly evident. A comprehensive theoretical description of the solar corona and solar wind is required, which should rely on the theory of anisotropic and multi-species fluids, and must in many cases invoke full kinetic theory, in particular to evaluate the exchange of energy and momentum. In the weakly collisional corona, waves and particles appear to be intimately linked through plasma instabilities and wave-particle interactions. These processes involve plasma waves at frequencies (up to the MHz range), much higher than the frequencies of MHD waves, which mostly have been considered in conventional fluid models.
We briefly described the main types and solar sources of the solar wind, and then addressed key issues of a kinetic description of coronal expansion and of the associated solar wind transport theory, such as the basic energetics of coronal expansion, including kinetic parameters and plasma conditions in the corona, or the exospheric paradigm and related models. The failure to heat chromosphere or corona only by collisions was discussed. After an introduction to the basics of the Vlasov-Boltzmann theory, the kinetic concepts and various fluid theories were presented, and the transport theory in a collisional plasma was outlined. New work related to the validity of the classical electron heat flux in the transition region, and to the breakdown of classical heat conduction in the corona was discussed.
Then the in situ measured particle velocity distributions were considered, in particular for solar wind electrons, protons and alpha particles, and heavy ions. In addition to the particles, plasma waves and their microinstabilities constitute the main ingredients of space plasmas. Relevant plasma waves in the solar corona and solar wind, their dispersion relations and associated Landau and cyclotron resonances were presented. Resonant wave-particle interactions, for example with Alfvén-cyclotron waves and kinetic Alfvén waves, were identified and shown to play a central role in transport phenomena.
A whole section was devoted to wave-particle interactions, and their manifestations in the VDFs through inelastic pitch-angle diffusion of ions in resonance with waves. Evidence for wave effects on protons and the kinetic shell model were discussed. The origin and regulation of proton beams, the effects of non-linear wave couplings on linear beam instabilities, the regulations of the proton core temperature anisotropy and of the electron heat flux were analysed, and plasma heating (cooling) by wave absorption (emission) was evaluated.
Subsequently, kinetic transport in the solar corona and solar wind was described in terms of higher-order, gyrotropic multi-fluid equations. The model velocity distributions derived from such moment expansions were analysed. From their defects a dire need was stated for a consistent kinetic modelling of coronal expansion. Numerical results from such kinetic models of the solar wind and for the VDFs of coronal electrons, protons and ions were presented. A summary and conclusion section rounds the review off, together with some future research perspectives that we present now.
8.2 Conclusions and perspectives
We have discussed the kinetic physics of the solar corona and solar wind. Modern in situ solar wind plasma measurements and coronal plasma observations, remotely through imaging and spectroscopy, indicate significant deviations of the plasma from thermal equilibrium. The existing ample evidence asks for a substantial revision of the conventional transport paradigm. We conclude that understanding the thermodynamics (heating) of the solar corona and the dynamics (acceleration) of the solar wind will ultimately require to consider kinetic issues and to go beyond a fluid description. In the following we define promising central areas for future research:
-
New multi-fluid or kinetic models involving plasma particles and waves need to be developed, allowing us to understand better the thermal kinetics and plasma dynamics of the Sun’s corona and the solar wind.
-
Novel kinetic concepts, capable of describing the self-consistent evolution of wave spectra and particle VDFs and their spatial and spectral transfer and coupling, are required to obtain a deeper physical insight into the coronal heating mechanism.
-
Small-scale dissipation processes of waves and fluctuations should be studied in depth, because turbulent wave energy transport, as well as cascading and dissipation in the kinetic domain, are expected to play a key role in the thermodynamics of tenuous space plasmas.
In the case of the solar corona and wind we are dealing with a complex kinetic system, which to understand requires a multiple-scale analysis and multiple-species description (electrons, protons, and heavy ions). They all have to be considered, since each species has a unique and prominent role to play, like electrons in heat conduction, protons and alpha particles in mass and momentum transport, and heavy ions in radiative cooling and wave-induced preferential heating. This heat is then gradually shared with protons and electrons by weak but unavoidable Coulomb collisions.
Therefore, it is time to develop a novel wave-based plasma transport scheme, which will enable us to achieve a new type of fluid closure, or to obtain the appropriate transport coefficients. They will complement or replace the ones presently available and in use for Coulomb-collision mediated transport.
Finally, it is worth stressing that theoretical progress will require adequate observations and new data. Up to now, the solar wind was only observed in situ at heliocentric distances larger than 0. 3 AU (Helios perihelion). This is far away from the inner corona where the solar wind originates. Furthermore, even the present-day remote-sensing observations (such as made by SOHO and TRACE) of the solar corona do not provide the needed comprehensive diagnostics of the coronal plasma state. We can still not fully probe those regions where the corona is heated and the wind becomes supersonic. Therefore, novel observational strategies, including in situ measurements to be made at the closest possible (Solar Probe) distances from the solar surface, are required to make progress in the empirical phenomenology and physical understanding of coronal heating and solar wind acceleration.
References
Aiouaz, T., Peter, H., Lemaire, P., 2005, “The correlation between coronal Doppler shifts and the supergranular network”, Astron. Astrophys., 435, 713–721. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005A%26A...435..713A.
Anderson, S., 1994, “Coulomb collisions and coronal heating by velocity filtration”, Astrophys. J., 437, 860–866. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994ApJ...437..860A.
Araneda, J.A., Gomberoff, L., 2004, “Stabilization of right-hand polarized beam plasma instabilities due to a large-amplitude left-hand polarized wave: A simulation study”, J. Geophys. Res., 109, A01106. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10901106A.
Araneda, J.A., Viñas, A.F., Astudillo, H.F., 2002, “Proton core temperature effects on the relative drift and anisotropy evolution of the ion beam instability in the fast solar wind” J. Geophys. Res., 107, 1453. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107l.SSH8A.
Asbridge, J.R., Bame, S.J., Feldman, W.C., Montgomery, M.D., 1976, “Helium and hydrogen velocity differences in the solar wind”, J. Geophys. Res., 81, 2719–2727. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1976JGR...81.2719A.
Aschwanden, M.J., 2002, Particle Acceleration and Kinematics in Solar Flares: A Synthesis of Recent Observations and Theoretical Concepts, Kluwer Academic Publishers, Dordrecht, Netherlands; Boston, U.S.A. Reprinted from Space Science Reviews, volume 101, nos. 1–2, 2002.
Aschwanden, M.J., 2004, Physics of the Solar Corona: An Introduction, Springer-Praxis Books in Geophysical Sciences, Springer; Praxis, Berlin, Germany; New York, U.S.A.; Chichester, U.K.
Axford, W.I., McKenzie, J.F., 1992, “The origin of high speed solar wind streams”, in Solar Wind Seven, (Eds.) Marsch, E., Schwenn, R., Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, vol. 3 of COSPAR Colloquia Series, pp. 1–5, Pergamon Press, Oxford, U.K.; New York, U.S.A.
Axford, W.I., McKenzie, J.F., 1997, “The Solar Wind”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 31–66, Arizona University Press, Tucson, U.S.A.
Bame, S.J., Asbridge, J.R., Feldman, W.C., Gary, S.P., Montgomery, M.D., 1975, “Evidence for local ion heating in solar wind high speed streams”, Geophys. Res. Lett., 2, 373–375. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1975GeoRL...2..373B.
Barakat, A.R., Schunk, R.W., 1981, “Momentum and energy exchange collision terms for interpenetrating bi-Maxwellian gases”, J. Phys. D, 14, 421–438. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1981JPhD...14..421B.
Barakat, A.R., Schunk, R.W., 1982, “Comparison of transport equations based on Maxwellian and bi-Maxwellian distributions for anisotropic plasma”, J. Phys. D, 15, 1195–1216. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982JPhD...15.1195B.
Baumjohann, W., Treumann, R.A., 1996, Basic Space Plasma Physics, Imperial College Press; World Scientific, London, U.K.; River Edge, U.S.A.
Benz, A.O., 1993, Plasma Astrophysics: Kinetic Processes in Solar and Stellar Coronae, vol. 184 of Astrophysics and Space Science Library, Kluwer Academic Publishers, Dordrecht, Netherlands; Boston, U.S.A.
Bingham, R., Shukla, P.K., 2004, “Kinetic Aspects of Solar Coronal Heating”, in Proceedings of the SOHO 15 Workshop: Coronal Heating, 6–9 September 2004, St. Andrews, Scotland, UK, (Eds.) Walsh, R.W., Ireland, J., Danesy, D., Fleck, B., vol. SP-575 of ESA Conference Proceedings, pp. 180–185, ESA Publications Division, Noordwijk, Netherlands. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004soho...15..180B.
Borrini, G., Gosling, J.T., Bame, S.J., Feldman, W.C., Wilcox, J.M., 1981, “Solar wind helium and hydrogen structure near the heliospheric current sheet”, J. Geophys. Res., 86, 4565–4573. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1981JGR....86.4565B.
Braginskii, S.I., 1965, “Transport processes in plasma”, in Review of Plasma Physics, (Ed.) Leontovich, M.A., vol. 1 of Review of Plasma Physics, pp. 201–311, Consultants Bureau, New York, U.S.A.
Bruno, R., Carbone, V., 2005, “The Solar Wind as a Turbulence Laboratory”, Living Rev. Solar Phys., 2, lrsp-2005-4. URL (cited on 4 October 2005): http://www.livingreviews.org/lrsp-2005-4.
Burlaga, L.F., 1995, Interplanetary Magnetohydrodynamics, vol. 3 of International Series on Astronomy and Astrophysics, Oxford University Press, New York, U.S.A.
Chen, Y., Esser, R., Hu, Y.Q., 2003, “Numerical modelling of the halo electrons in the fast solar wind” J. Geophys. Res., 108, 1371. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108j.SSH7C.
Chust, T., Belmont, G., 2006, “Closure of fluid equations in collisionless magnetoplasmas”, Phys. Plasmas, 13, 012 506.
Collier, M.R., 1993, “On generating kappa-like distribution functions using velocity space Lévy flights”, Geophys. Res. Lett., 20, 1531–1534. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/1993GeoRL..20.1531C.
Collier, M.R., Hamilton, D.C., Gloeckler, G., Bochsler, P., Sheldon, R.B., 1996, “Neon-20, Oxygen-16, and Helium-4 densities, temperatures, and suprathermal tails in the solar wind determined with WIND/MASS”, Geophys. Res. Lett., 23, 1191–1194. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996GeoRL..23.1191C.
Cranmer, S.R., 2000, “Ion Cyclotron Wave Dissipation in the Solar Corona: The Summed Effect of more than 2000 Ion Species”, Astrophys. J., 532, 1197–1208. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...532.1197C.
Cranmer, S.R., 2001, “Ion cyclotron diffusion of velocity distributions in the extended solar corona”, J. Geophys. Res., 106, 24,937–24,954. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...10624937C.
Cranmer, S.R., van Ballegooijen, A.A., 2003, “Alfvénic turbulence in the extended solar corona: kinetic effects and proton heating”, Astrophys. J., 594, 573–591. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003ApJ...594..573C.
Cranmer, S.R., van Ballegooijen, A.A., 2005, “On the generation, propagation, and reflection of Alfvén waves from the solar photosphere to the distant heliosphere”, Astrophys. J. Suppl. Ser., 156, 265–293. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2005ApJS..156..265C.
Cranmer, S.R., Field, G.B., Kohl, J.L., 1999, “Spectroscopic constraints on models of ion cyclotron resonance heating in the polar solar corona and high-speed solar wind”, Astrophys. J., 518, 937–947. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999ApJ...518..937C.
Daughton, W., Gary, S.P., 1998, “Electromagnetic proton/proton instabilities in the solar wind”, J. Geophys. Res., 103, 20,613–20,620. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998JGR...10320613D.
Daughton, W., Gary, S.P., Winske, D., 1999, “Electromagnetic proton/proton instabilities in the solar wind: Simulations”, J. Geophys. Res., 104, 4657–4668. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...104.4657D.
David, C., Gabriel, A.H., Bely-Dubau, F., Fludra, A., Lemaire, P., Wilhelm, K., 1998, “Measurement of the electron temperature gradient in solar coronal holes”, Astron. Astrophys., 336, L90–L94. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998A%26A...336L..90D.
Demars, H.G., Schunk, R.W., 1979, “Transport equations for multispecies plasmas based on individual bi-Maxwellian distributions”, J. Phys. D, 12, 1051–1077. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1979JPhD...12.1051D.
Demars, H.G., Schunk, R.W., 1990, “Solar wind proton velocity distributions: comparison of the bi-Maxwellian based 16-moment expansion with observations”, Planet. Space Sci., 38, 1091–1103. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1990P%26SS...38.1091D.
Dorelli, J.C., Scudder, J.D., 1999, “Electron heat flow carried by kappa distributions in the solar corona”, Geophys. Res. Lett., 26, 3537–3540. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999GeoRL..26.3537D.
Dorelli, J.C., Scudder, J.D., 2003, “Electron heat flow in the solar corona: Implications of non-Maxwellian velocity distributions, the solar garvitational field, and Coulomb collisions” J. Geophys. Res., 108, 1294. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108g.SSH7D.
Dubinin, E., Sauer, K., McKenzie, J.F., 2005, “Differential ion streaming in the solar wind as an equilibrium state”, J. Geophys. Res., 110, A07 101. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005JGRA..11007101D.
Dum, C.T., 1990, “Classical Transport Properties of Plasmas”, in Physical Processes in Hot Cosmic Plasmas, (Eds.) Brinkmann, W., Fabian, A.C., Giovannelli, F., Proceedings of the NATO Advanced Research Workshop, Vulcano, Sicily, Italy, May 29–June 2, 1989, vol. 305 of NATO ASI Series C, pp. 157–180, Kluwer Academic Publishers, Dordrecht, Netherlands; Boston, U.S.A. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1990pphc.proc..157D.
Dum, C.T., Marsch, E., Pilipp, W.G., 1980, “Determination of wave growth from measured distribution functions and transport theory”, J. Plasma Phys., 23, 91–113.
Esser, R., Edgar, R.J., 2000, “Reconciling Spectroscopic Electron Temperature Measurements in the Solar Corona with In Situ Charge State Observations”, Astrophys. J., 532, L71–L74. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...532L..71E.
Fahr, H.J., Shizgal, B., 1983, “Modern Exospheric Theories and Their Observational Relevance”, Rev. Geophys. Space Phys., 21, 75–124. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1983RvGSP..21...75F.
Feldman, W.C., Marsch, E., 1997, “Kinetic Phenomena in the Solar Wind”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 615–676, Arizona University Press, Tucson, U.S.A.
Feldman, W.C., Asbridge, J.A., Bame, S.J., Montgomery, M.D., 1973, “Double ion streams in the solar wind”, J. Geophys. Res., 78, 2017–2027.
Feldman, W.C., Asbridge, J.A., Bame, S.J., Montgomery, M.D., 1974, “Interpenetrating solar wind streams”, Rev. Geophys. Space Phys., 12, 715–723. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1974RvGSP..12..715F.
Feldman, W.C., Asbridge, J.R., Bame, S.J., Montgomery, M.D., Gary, S.P., 1975, “Solar wind electrons”, J. Geophys. Res., 80, 4181–4196. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1975JGR....80.4181F.
Feldman, W.C., Gosling, J.T., McComas, D.J., Phillips, J.L., 1993, “Evidence for ion jets in the high-speed solar wind”, J. Geophys. Res., 98, 5593–5605. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1993JGR....98.5593F.
Feldman, W.C., Barraclough, B.L., Phillips, J.L., Wang, Y.-M., 1996, “Constraints on high-speed solar wind structure near its coronal base: a Ulysses perspective”, Astron. Astrophys., 316, 355–367. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996A%26A...316..355F.
Galinsky, V.L., Shevchenko, V.I., 2000, “Nonlinear Cyclotron Resonant Wave-Particle Interaction in a Nonuniform Magnetic Field”, Phys. Rev. Lett., 85, 90–93. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000PhRvL..85...90G.
Gary, S.P., 1991, “Electromagnetic ion/ion instabilities and their consequences in space plasmas: A review”, Space Sci. Rev., 56, 373–415. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1991SSRv...56..373G.
Gary, S.P., 1993, Theory of Space Plasma Microinstabilities, Cambridge Atmospheric and Space Science Series, Cambridge University Press, Cambridge, U.K., New York, U.S.A.
Gary, S.P., 1999, “Collisionless dissipation wave number: Linear theory”, J. Geophys. Res., 104, 6759–6762. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...104.6759G.
Gary, S.P., Borovsky, J.E., 2004, “Alfvén-cyclotron fluctuations: Linear Vlasov theory”, J. Geophys. Res., 109, A06 105. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10906105G.
Gary, S.P., Lee, M.A., 1994, “The ion cyclotron anisotropy instability and the inverse correlation between proton anisotropy and proton beta”, J. Geophys. Res., 99, 11 297–11 302. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....9911297G.
Gary, S.P., Li, H., 2000, “Whistler heat flux instability at high beta”, Astrophys. J., 529, 1131–1135. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...529.1131G.
Gary, S.P., Nishimura, K., 2004, “Kinetic Alfvén waves: Linear theory and a particle-in-cell simulation”, J. Geophys. Res., 109, A02 109. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10902109G.
Gary, S.P., Saito, S., 2003, “Particle-in-cell simulations of Alfvén-cyclotron wave scattering: Proton velocity distributions” J. Geophys. Res., 108, 1194. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108e.SSH6G.
Gary, S.P., Scime, E.E., Phillips, J.L., Feldman, W.C., 1994, “The whistler heat flux instability: Threshold conditions in the solar wind”, J. Geophys. Res., 99, 23,391–23,399. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....9923391G.
Gary, S.P., Wang, J., Winske, D., Fuselier, S.A., 1997, “Proton temperature anisotropy upper bound”, J. Geophys. Res., 102, 27,159–27,170. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/1997JGR...10227159G.
Gary, S.P., Li, H., O’Rourke, S., Winske, D., 1998, “Proton resonant firehose instability: Temperature anisotropy and fluctuating field constraints”, J. Geophys. Res., 103, 14,567–14,575. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/1998JGR...10314567G.
Gary, S.P., Yin, L., Winske, D., 2000a, “Electromagnetic proton cyclotron anisotropy instability: Wave-particle scattering rate”, Geophys. Res. Lett., 27, 2457–2460. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2000GeoRL..27.2457G.
Gary, S.P., Yin, L., Winske, D., 2000b, “Electromagnetic proton cyclotron anisotropy instability: Wave-particle scattering rate”, Geophys. Res. Lett., 27, 2457–2460. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000GeoRL..27.2457G.
Gary, S.P., Yin, L., Winske, D., Reisenfeld, D.B., 2000c, “Alpha/proton magnetosonic instability in the solar wind”, J. Geophys. Res., 105, 20 989–20 996. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000JGR...10520989G.
Gary, S.P., Yin, L., Winske, D., Reisenfeld, D.B., 2000d, “Electromagnetic alpha/proton instabilities in the solar wind”, Geophys. Res. Lett., 27, 1355–1358. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000GeoRL..27.1355G.
Gary, S.P., Goldstein, B.E., Steinberg, J.T., 2001a, “Helium ion acceleration and heating by Alfvén/cyclotron fluctuations in the solar wind”, J. Geophys. Res., 106, 24 955–24 964. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...10624955G.
Gary, S.P., Skoug, R.M., Steinberg, J.T., Smith, C.W., 2001b, “Proton temperature anisotropy constraint in the solar wind: ACE observations”, Geophys. Res. Lett., 28, 2759–2762. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2001GeoRL..28.2759G.
Gary, S.P., Skoug, R.M., Steinberg, J.T., Smith, C.W., 2001c, “Proton temperature anisotropy constraint in the solar wind: ACE observations”, Geophys. Res. Lett., 28, 2759–2762. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28.2759G.
Gary, S.P., Goldstein, B.E., Neugebauer, M., 2002, “Signatures of wave-ion intercations in the solar wind: Ulysses observations” J. Geophys. Res., 107, 1169. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107h.SSH4G.
Gary, S.P., Yin, L., Winske, D., Ofman, L., Goldstein, B.E., Neugebauer, M., 2003, “Consequence of proton and alpha anisotropies in the solar wind: Hybrid simulations” J. Geophys. Res., 108, 1068. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108b.SSH3G.
Gary, S.P., Smith, C.W., Skoug, R.M., 2005, “Signatures of Alfvén-cyclotron wave-ion scattering: Advanced Composition Explorer (ACE) solar wind observations”, J. Geophys. Res., 110, A07 108. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005JGRA..11007108G.
Geiss, J., 1982, “Processes affecting abundances in the solar wind”, Space Sci. Rev., 33, 201–217. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982SSRv...33..201G.
Geiss, J., Gloeckner, G., von Steiger, R., 1994, “Solar and heliospheric processes from solar wind composition measurements”, Philos. Trans. R. Soc. London, Ser. A, 349, 213–226.
Gloeckler, G., Geiss, J., Fisk, L.A., 2001, “Heliospheric and interstellar phenomena revealed from observations of pickup ions”, in The Heliosphere Near Solar Minimum: The Ulysses perspective, (Eds.) Balogh, A., Marsden, R.G., Smith, E.J., Springer-Praxis Books in Astronomy and Space Sciences, pp. 287–326, Springer; Praxis, Berlin, Germany; New York, U.S.A.; Chichester, U.K.
Gnavi, G., Gomberoff, L., Gratton, F.T., Galvaõ, R.M.O., 1996, “Electromagnetic ion-beam instabilities in a cold plasma”, J. Plasma Phys., 55, 77–86.
Goldstein, B., Neugebauer, M., Zhang, L.D., Gary, S.P., 2000, “Observed constraints on proton-proton relative velocities in the solar wind”, Geophys. Res. Lett., 27, 53–56. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000GeoRL..27...53G.
Goldstein, M.L., Roberts, D.A., Matthaeus, W.H., 1997, “Magnetohydrodynamic Turbulence in Cosmic Winds”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 521–580, University of Arizona Press, Tucson, U.S.A.
Gomberoff, K., Gomberoff, L., Astudillo, H.F., 2000, “Ion-beam plasma electromagnetic instabilities”, J. Plasma Phys., 64, 75–87. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000JPlPh..64...75G.
Gomberoff, L., 2000, “Ion acoustic damping effects on parametric decays of Alfvén waves”, J. Geophys. Res., 105, 10,509–10,518. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000JGR...10510509G.
Gomberoff, L., 2003, “Stabilization of linear ion beam right-hand polarized instabilities by nonlinear Alfvén/ion-cyclotron waves”J. Geophys. Res., 108, 1261. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108f.SSH8G.
Gomberoff, L., Astudillo, H., 1999, “Ion heating and acceleration in the solar wind”, in Solar Wind Nine, (Eds.) Habbal, S.R., Hollweg, J.V., Isenberg, P.A., Proceedings of the Ninth International Solar Wind Conference, Nantucket, Massachusetts, October, 1998, vol. 471 of AIP Conference Proceedings, pp. 461–464, American Institute of Physics, Woodbury, U.S.A.
Gomberoff, L., Astudillo, H.F., 1998, “Electromagnetic ion-beam plasma instabilities”, Planet. Space Sci., 46, 1683–1687. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999AIPC..471..457A.
Gomberoff, L., Elgueta, R., 1991, “Resonant acceleration of alpha particles by ion-cyclotron waves in the solar wind”, J. Geophys. Res., 96, 9801–9804. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1991JGR....96.9801G.
Gomberoff, L., Gratton, F.T., Gnavi, G., 1994, “Excitation and parametric decay of electromagnetic ion cyclotron waves in high speed solar wind streams”, J. Geophys. Res., 99, 14,717–14,727. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....9914717G.
Gomberoff, L., Gnavi, G., Gratton, F.T., 1996a, “Minor heavy ions beam plasma interactions in the solar wind”, J. Geophys. Res., 101, 13,517–13,522. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996JGR...10113517G.
Gomberoff, L., Gratton, F.T., Gnavi, G., 1996b, “Acceleration and heating of heavy ions in high speed solar wind streams”, in Solar Wind Eight, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., Proceedings of the Eighth International Solar Wind Conference, Dana Point, CA 1995, vol. 382 of AIP Conference Proceedings, pp. 319–322, American Institute of Physics, Woodbury, U.S.A.
Gomberoff, L., Gratton, F.T., Gnavi, G., 1996c, “Acceleration and heating of heavy ions by circularly polarized Alfvén waves”, J. Geophys. Res., 101, 15,661–15,666. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996JGR...10115661G.
Gomberoff, L., Gomberoff, K., Brinca, A.L., 2001, “Ion acoustic damping effects on parametric decays of Alfvén waves: Right-hand polarization”, J. Geophys. Res., 106, 18,713–18,720. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...10618713G.
Gomberoff, L., Gomberoff, K., Brinca, A.L., 2002, “New parametric decays of proton beam-plasma electromagnetic waves” J. Geophys. Res., 107, 1123. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107g.SSH5G.
Gomberoff, L., Hoyos, J., Brinca, A.L., 2003, “The effect of a large-amplitude circularly polarized wave on linear beam-plasma electromagnetic instabilities” J. Geophys. Res., 108, 1472. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108lSSH10G.
Goodrich, C.C., Lazarus, A.J., 1976, “Suprathermal protons in the interplanetary solar wind”, J. Geophys. Res., 81, 2750–2754. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1976JGR....81.2750G.
Gosling, J.T., Skoug, R.M., Feldman, W.C., 2001, “Solar wind electron halo depletions at 90circ pitch angle”, Geophys. Res. Lett., 28, 4155–4158. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2001GeoRL..28.4155G.
Gurnett, D.A., 1991, “Waves and Instabilities”, in Physics of the Inner Heliosphere, Vol. 2: Particles, Waves, and Turbulence, (Eds.) Schwenn, R., Marsch, E., vol. 20 of Physics and Chemistry in Space, pp. 135–157, Springer, Berlin, Germany; New York, U.S.A.
Hansteen, V.H., Leer, E., Lie-Svendsen, Ø., 1999, “Advances in modelling the fast solar wind”, in Magnetic Fields and Solar Processes, (Ed.) Wilson, A., The 9th European Meeting on Solar Physics, held 12–18 September, 1999, in Florence, Italy, vol. SP-448 of ESA Conference Proceedings, pp. 1091–1100, ESA Publications Division, Noordwijk, Netherlands. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999mfsp.conf.1091H.
Hassler, D.M., Dammasch, I.E., Lemaire, P., Brekke, P., Curdt, W., Mason, H.E., Vial, J.-C., Wilhelm, K., 1999, “Solar Wind Outflow and the Chromospheric Magnetic Network”, Science, 283, 810–813. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999Sci...283..810H.
Hefti, S., Grünwaldt, H., Ipavich, F.M., Bochsler, P., Hovestadt, D., Aellig, M.R., Hilchenbach, M., Kallenbach, R., Galvin, A.B., Geiss, J., Gliem, F., Gloeckler, G., Klecker, B., Marsch, E., Möobius, E., Neugebauer, M., Wurz, P., 1998, “Kinetic properties of solar wind minor ions and protons measured with SOHO/CELIAS”, J. Geophys. Res., 103, 29,697–29,704. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998JGR...10329697H.
Hellinger, P., Trávníček, P., Mangeney, A., Grappin, R., 2003, “Hybrid simulations of the expanding solar wind: Temperatures and drift velocities” Geophys. Res. Lett., 30, 1211. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003GeoRL..30e..15H.
Hellinger, P., Velli, M., Trávníček, P., Gary, S.P., Goldstein, B.E., Liewer, P.C., 2005, “Alfvén wave heating of heavy ions in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 110, A12109. Related online version (cited on 3 July 2006): http://adsabs.harvard.edu/abs/2005JGRA..11012109H.
Hernandez, R., Marsch, E., 1985, “Collisional time scales for temperature and velocity exchange between drifting Maxwellians”, J. Geophys. Res., 90, 11,062–11,066. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1985JGR....9011062H.
Hollweg, J.V., 1975, “Waves and instabilities in the solar wind”, Rev. Geophys. Space Phys., 13, 263–289. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1975RvGSP..13..263H.
Hollweg, J.V., 1978, “Some physical processes in the solar wind”, Rev. Geophys. Space Phys., 16, 689–720. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1978RvGSP..16..689H.
Hollweg, J.V., 1999a, “Potential wells, the cyclotron resonance, and ion heating in coronal holes”, J. Geophys. Res., 104, 505–520. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...104..505H.
Hollweg, J.V., 1999b, “The cyclotron resonance in coronal holes, 1, Heating and acceleration of protons, O5+, and Mg9+”, J. Geophys. Res., 104, 24 781–24 792. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10424781H.
Hollweg, J.V., 1999c, “The cyclotron resonance in coronal holes, 2, A two-proton description”, J. Geophys. Res., 104, 24 793–24 806. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10424793H.
Hollweg, J.V., 1999d, “Kinetic Alfvén wave revisited”, J. Geophys. Res., 104, 14,811–14,820. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10414811H.
Hollweg, J.V., Isenberg, P.A., 2002, “Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction” J. Geophys. Res., 107, 1147. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107gSSH12H.
Hollweg, J.V., Markovskii, S.A., 2002, “Cyclotron resonances of ions with obliquely propagating waves in coronal holes and the fast solar wind” J. Geophys. Res., 107, 1080. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107f.SSH1H.
Hollweg, J.V., Esser, R., Jayanti, V., 1993, “Modulational and decay instabilities of Alfvén waves: Effect of streaming He++”, J. Geophys. Res., 98, 3491–3500. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1993JGR....98.3491H.
Horbury, T.S., Tsurutani, B., 2001, “Ulysses measurements of waves, turbulence and discontinuities”, in The Heliosphere Near Solar Minimum: The Ulysses perspective, (Eds.) Balogh, A., Marsden, R.G., Smith, E.J., Springer-Praxis Books in Astronomy and Space Sciences, pp. 167–227, Springer; Praxis, Berlin, Germany; New York, U.S.A.; Chichester, U.K. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001hnsm.book..167H.
Hu, Y.Q., Habbal, S.R., 1999, “Resonant acceleration and heating of solar wind ions by dispersive ion cyclotron waves”, J. Geophys. Res., 104, 17045–17056. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10417045H.
Hundhausen, A.J., 1970, “Composition and dynamics of the solar wind plasma”, Rev. Geophys. Space Phys., 8, 729–811.
Hundhausen, A.J., 1972, Coronal Expansion and the Solar Wind, vol. 5 of Physics and Chemistry in Space, Springer, Berlin, Germany; New York, U.S.A.
Inhester, B., 1990, “A drift-kinetic treatment of the parametric decay of large-amplitude waves”, J. Geophys. Res., 95, 10 525–10 539. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1990JGR....9510525I.
Isenberg, P.A., 1984a, “The ion-cyclotron dispersion relation in a proton alpha solar wind”, J. Geophys. Res., 89, 2133–2141. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1984JGR....89.2133I.
Isenberg, P.A., 1984b, “Resonant acceleration and heating of solar wind ions: anisotropy and dispersion”, J. Geophys. Res., 89, 6613–6622. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1984JGR....89.6613I.
Isenberg, P.A., 2001a, “Heating of coronal holes and generation of the solar wind by ion-cyclotron resonance”, Space Sci. Rev., 95, 119–131. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001SSRv...95..119I.
Isenberg, P.A., 2001b, “The kinetic shell model of coronal heating and acceleration by ion cyclotron waves 2. Inward and outward propagating waves”, J. Geophys. Res., 106, 29 249–29 260. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...10629249I.
Isenberg, P.A., 2004, “The kinetic shell model of coronal heating and acceleration by ion cyclotron waves: 3. The proton halo and dispersive waves”, J. Geophys. Res., 109, A03 101. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10903101I.
Isenberg, P.A., Hollweg, J.V., 1983, “On the preferential acceleration and heating of solar wind heavy ions”, J. Geophys. Res., 88, 3923–3935. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1983JGR....88.3923I.
Isenberg, P.A., Lee, M.A., Hollweg, J.V., 2000, “A kinetic model of coronal heating and acceleration by ion-cyclotron waves: Preliminary results”, Solar Phys., 193, 247–257. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000SoPh..193..247I.
Isenberg, P.A., Lee, M.A., Hollweg, J.V., 2001, “The kinetic shell model of coronal heating and acceleration by ion-cyclotron waves: 1. Outward propagating waves”, J. Geophys. Res., 106, 5649–5660. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106.5649I.
Issautier, K., Meyer-Vernet, N., Moncuquet, M., Hoang, S., 1996, “A novel method to measure the solar wind speed”, Geophys. Res. Lett., 23, 1649–1652. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996GeoRL..23.1649I.
Jayanti, V., Hollweg, J.V., 1993a, “Parametric instabilities of parallel propagating Alfvén waves: Some analytical results”, J. Geophys. Res., 98, 19,049–19,063. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1993JGR....9819049J.
Jayanti, V., Hollweg, J.V., 1993b, “On the dispersion relation for parametric instabilities of parallel propagating Alfvén waves”, J. Geophys. Res., 98, 13 247–13 252. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1993JGR....9813247J.
Jayanti, V., Hollweg, J.V., 1994, “Growth rates of new parametric instabilities occurring in a plasma with streaming He++”, J. Geophys. Res., 99, 23,449–23,459. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....9923449J.
Jockers, K., 1970, “Solar wind models based on exospheric theory”, Astron. Astrophys., 6, 219–239. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1970A%26A....6..219J.
Kaghashvili, E.K., Vasquez, B.J., Hollweg, J.V., 2003, “Deceleration of streaming alpha particles interacting with waves and imbedded rotational discontinuities” J. Geophys. Res., 108, 1036. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003JGRA.108a.SSH8K.
Kaghashvili, E.K., Vasquez, B.J., Zank, G.P., Hollweg, J.V., 2004, “Deceleration of relative streaming between proton components among nonlinear low-frequency Alfvén waves”, J. Geophys. Res., 109, 10.1029/2004JA010382. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10912101K.
Kasper, J.C., Lazarus, A.J., Gary, S.P., 2002, “Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy” Geophys. Res. Lett., 29, 1839. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2002GeoRL..29q..20K.
Kasper, J.C., Lazarus, A.J., Gary, S.P., Szabo, A., 2003, “Solar Wind Temperature Anisotropies”, in Solar Wind Ten, (Eds.) Velli, M., Bruno, R., Malara, F., Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, vol. 679 of AIP Conference Proceedings, pp. 538–541, American Institute of Physics, Melville, U.S.A. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003AIPC..679..538K.
Kellogg, P.J., 2000, “Fluctuations and ion isotropy in the solar wind”, Astrophys. J., 528, 480–485. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...528..480K.
Kellogg, P.J., Gurnett, D.A., Hospodarsky, G.B., Kurth, W.S., 2001, “Ion isotropy and ion resonant waves in the solar wind: Cassini observations”, Geophys. Res. Lett., 28, 87–90. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28...87K.
Kennel, C.F., Engelmann, F., 1966, “Velocity space diffusion from weak plasma turbulence in a magnetic field”, Phys. Fluids, 9, 2377–2388.
Killie, M.A., Janse, A.M., Lie-Svendsen, Ø., Leer, E., 2004, “Improved transport equations for fully ionized gases”, Astrophys. J., 604, 842–849. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004ApJ...604..842K.
Kohl, J.L., Noci, G., Antonucci, E., Tondello, G., Huber, M.C.E., Cranmer, S.R., Strachan, L., Panasyuk, A.V., Gardner, L.D., Romoli, M., Fineschi, S., Dobrzycka, D., Raymond, J.C., Nicolosi, P., Siegmund, O.H.W., Spadaro, D., Benna, C., Ciaravella, A., Giordano, S., Habbal, S.R., Karovska, M., Li, X., Martin, R., Michels, J.G., Modigliani, A., Naletto, G., O’Neal, R.H., Pernechele, C., Poletto, G., Smith, P.L., Suleiman, R.M., 1998, “UVCS/SOHO empirical determinations of anisotropic velocity distributions in the solar corona”, Astrophys. J. Lett., 501, L127–L131. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998ApJ...501L.127K.
Lamy, H., Pierrard, V., Maksimovic, M., Lemaire, J.F., 2003, “A kinetic exospheric model of the solar wind with a nonmonotonic potential energy for the protons” J. Geophys. Res., 108, 1047. Related online version (cited on 4 October 2005):http://adsabs.harvard.edu/abs/2003JGRA.108aSSH13L.
Landi, S., Pantellini, F.G.E., 2001, “On the temperature profile and heat flux in the solar corona: Kinetic simulations”, Astron. Astrophys., 372, 686–701. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001A%26A...372..686L.
Leamon, R.J., Smith, C.W., Ness, N.F., Matthaeus, W.H., Wong, H.K., 1998, “Observational constraints on the dynamics of the interplanetary magnetic field dissipation range”, J. Geophys. Res., 103, 4775–4787. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998JGR...103.4775L.
Leamon, R.J., Matthaeus, W.H., Smith, C.W., Zank, G.P., Mullan, D.J., Oughton, S., 2000, “MHD-driven kinetic dissipation in the solar wind and corona”, Astrophys. J., 537, 1054–1062. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...537.1054L.
Leblanc, F., Hubert, D., 1997, “A generalised model for the proton expansion in astrophysical winds. I. The velocity distribution function representation”, Astrophys. J., 483, 464–474. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997ApJ...483..464L.
Leblanc, F., Hubert, D., 1998, “A generalised model for the proton expansion in astrophysical winds. II. The asociated set of transport equations”, Astrophys. J., 501, 375–385. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998ApJ...501..375L.
Leblanc, F., Hubert, D., Blelly, P.-L., 2000, “A generalized model for the proton expansion in astrophysical winds. III. The collisional transfers and their properties”, Astrophys. J., 530, 478–490. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000ApJ...530..478L.
Lemaire, J., Scherer, M., 1971a, “Kinetic models of the solar wind”, J. Geophys. Res., 76, 7479–7490.
Lemaire, J., Scherer, M., 1971b, “Simple model for an ion-exosphere in an open magnetic field”, Phys. Fluids, 14, 1683–1694.
Lemaire, J.F., Pierrard, V., 2003, “The Kinetic Treatment of Space Plasmas”, in Rarefied Gas Dynamics, (Eds.) Ketsdever, A.D., Muntz, E.P., Proceedings of the 23rd International Symposium, Whistler, British Columbia, Canada, 20–25 July, 2002, vol. 663 of AIP Conference Proceedings, pp. 857–864, American Institute of Physics, Melville, U.S.A. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003AIPC..663..857L.
Leubner, M.P., 2002, “A Nonextensive Entropy Approach to Kappa-Distributions”, Astrophys. Space Sci., 282, 573. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2002Ap%26SS.282..573L.
Leubner, M.P., 2004a, “Core-Halo distribution functions: A natural equilibrium state in generalized thermostatistics”, Astrophys. J., 604, 469–478. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004ApJ...604..469L.
Leubner, M.P., 2004b, “Fundamental issues on kappa-distributions in space plasmas and interplanetary proton distributions”, Phys. Plasmas, 11, 1308–1316.
Leubner, M.P., Viñas, A.F., 1986, “Stability analysis of double-peaked proton distribution functions in the solar wind”, J. Geophys. Res., 91, 13,366–13,372. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1986JGR....9113366L.
Li, H., Gary, S.P., Stawicki, O., 2001, “On the dissipation of magnetic fluctuations in the solar wind”, Geophys. Res. Lett., 28, 1347–1350. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28.1347L.
Li, X., 1999, “Proton temperature anisotropy in the fast solar wind: A 16-moment bi-Maxwellian model”, J. Geophys. Res., 104, 19 773–19 785. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10419773L.
Li, X., Habbal, S.R., 1999, “Ion cyclotron waves, instabilities and solar wind heating”, Solar Phys., 190, 485–497. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999SoPh..190..485L.
Li, X., Habbal, S.R., 2000, “Proton/alpha magnetosonic instability in the fast solar wind”, J. Geophys. Res., 105, 7483–7490. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000JGR...105.7483L.
Li, X., Habbal, S.R., 2005, “Hybrid simulation of ion cyclotron resonance in the solar wind: Evolution of velocity distribution functions”, J. Geophys. Res., 110, A10 109. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2005JGRA..11010109L.
Li, X., Habbal, S.R., Hollweg, J.V., Esser, R., 1999, “Heating and cooling of protons by turbulence-driven ion-cyclotron waves in the fast solar wind”, J. Geophys. Res., 104, 2521–2535. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...104.2521L.
Lie-Svendsen, Ø., Esser, R., 2005, “Modelling the energy budget of solar wind minor ions: Implications for temperatures and abundances”, Astrophys. J., 618, 1057–1073. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005ApJ...618.1057L.
Lie-Svendsen, Ø., Leer, E., 2000, “The electron velocity distributions in the high-speed solar wind: Modelling the effects of protons”, J. Geophys. Res., 105, 35–46. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000JGR...105...35L.
Lie-Svendsen, Ø., Hansteen, V.H., Leer, E., 1997, “Kinetic electrons in high-speed solar wind streams: Formation of high-energy tails”, J. Geophys. Res., 102, 4701–4718. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997JGR...102.4701L.
Lie-Svendsen, Ø., Holzer, T.E., Leer, E., 1999, “Electron heat conduction in the solar transition region: Validity of the classical description”, Astrophys. J., 525, 1056–1065. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999ApJ...525.1056L.
Lie-Svendsen, Ø., Leer, E., Hansteen, V.H., 2001, “A 16-moment solar wind model: From the chromosphere to 1 AU”, J. Geophys. Res., 106, 8217–8232. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106.8217L.
Lie-Svendsen, Ø., Hansteen, V.H., Leer, E., Holzer, T.E., 2002, “The effect of transition region heating on the solar wind from coronal holes”, Astrophys. J., 566, 562–576. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002ApJ...566..562L.
Liewer, P.C., Velli, M., Goldstein, B.E., 2001, “Alfvén wave propagation and ion-cyclotron interactions in the expanding solar wind: One-dimensional hybrid simulations”, J. Geophys. Res., 106, 29 261–29 282. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...10629261L.
Livi, S., Marsch, E., 1986, “On the collisional relaxation of solar wind velocity distributions”, Ann. Geophys. A, 4, 333–340. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1986AnGeo...4..333L.
Livi, S., Marsch, E., 1987, “Generation of solar wind proton tails and double beams by Coulomb collisions”, J. Geophys. Res., 92, 7255–7261. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1987JGR....92.7255L.
Livi, S., Marsch, E., Rosenbauer, H., 1986, “Coulomb collisional domains in the solar wind”, J. Geophys. Res., 91, 8045–8050. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1986JGR....91.8045L.
MacDowall, R.J., Kellog, P.J., 2001, “Waves and instabilities in the three-dimensional heliosphere”, in The Heliosphere Near Solar Minimum: The Ulysses perspective, (Eds.) Balogh, A., Marsden, R.G., Smith, E.J., Springer-Praxis Books in Astronomy and Space Sciences, pp. 229–258, Springer; Praxis, Berlin, Germany; New York, U.S.A.; Chichester, U.K. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001hnsm.book..229M.
Maksimovic, M., Hoang, S., Meyer-Vernet, N., Moncuquet, M., Bougeret, J.-L., Phillips, J.L., Canu, P., 1995, “Solar wind electron parameters from quasi-thermal noise spectroscopy and comparison with other measurements on Ulysses”, J. Geophys. Res., 100, 19,881–19,892. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1995JGR...10019881M.
Maksimovic, M., Pierrard, V., Lemaire, J.F., 1997a, “A kinetic model of the solar wind with Kappa distribution functions in the corona”, Astron. Astrophys., 324, 725–734. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997A7.26A...324..725M.
Maksimovic, M., Pierrard, V., Riley, P., 1997b, “Ulysses electron distributions fitted with Kappa functions”, Geophys. Res. Lett., 24, 1151–1154. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997GeoRL..24.1151M.
Maksimovic, M., Pierrard, V., Lemaire, J.F., 2001, “On the Exospheric Approach for the Solar Wind Acceleration”, Astrophys. Space Sci., 277, 181–187. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001Ap726SS.277..181M.
Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E.E., Littleton, J.E., Marsch, E., McComas, D.J., Salem, C., Lin, R.P., Elliott, H., 2005, “Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU”, J. Geophys. Res., 110, A09 104. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2005JGRA..11009104M.
Mangeney, A., Grappin, R., Velli, M., 1991, “MHD turbulence in the solar wind”, in Advances in Solar System Magnetohydrodynamics, (Eds.) Priest, E.R., Hood, A.W., pp. 327–356, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Mann, G., Hackenberg, P., Marsch, E., 1997, “Linear mode analysis in multi-ion plasmas”, J. Plasma Phys., 58, 205–211.
Mariska, J.T., 1992, The Solar Transition Region, vol. 23 of Cambridge Astrophysics Series, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Markovskii, S.A., 2001, “Generation of ion-cyclotron waves in coronal holes by a global resonant magnetohydrodynamic mode”, Astrophys. J., 557, 337–342. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001ApJ...557..337M.
Markovskii, S.A., Hollweg, J.V., 2002, “Parametric cross-field current instability in solar coronal holes” J. Geophys. Res., 107, 1329. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107jSSH21M.
Marsch, E., 1991a, “Kinetic Physics of the Solar Wind Plasma”, in Physics of the Inner Heliosphere, Vol. 2: Particles, Waves and Turbulence, (Eds.) Schwenn, R., Marsch, E., vol. 20 of Physics and Chemistry in Space, pp. 45–133, Springer, Berlin, Germany; New York, U.S.A.
Marsch, E., 1991b, “MHD Turbulence in the Solar Wind”, in Physics of the Inner Heliosphere, Vol. 2: Particles, Waves and Turbulence, (Eds.) Schwenn, R., Marsch, E., vol. 20 of Physics and Chemistry in Space, pp. 159–241, Springer, Berlin, Germany; New York, U.S.A.
Marsch, E., 1992, “On the possible role of plasma waves in the heating of chromosphere and corona”, in Solar Wind Seven, (Eds.) Marsch, E., Schwenn, R., Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, vol. 3 of COSPAR Colloquia Series, pp. 65–68, Pergamon Press, Oxford, U.K.; New York, U.S.A. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1992sws..coll...65M.
Marsch, E., 1998, “Closure of multifluid and kinetic equations for cyclotron-resonant interactions of solar wind ions with Alfvén waves”, Nonlinear Proc. Geophys., 5, 111–116.
Marsch, E., 1999, “Solar wind models from the sun to 1 AU: Constraints by in situ and remote sensing measurements”, Space Sci. Rev., 87, 1–24. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999SSRv...87....1M.
Marsch, E., 2002, “On resonant interactions of ions with plasma waves in a reduced quasi-linear theory”, Nonlinear Proc. Geophys., 6, 1–6.
Marsch, E., 2005, “Solar wind responses to the solar activity cycle”, Adv. Space Res., accepted.
Marsch, E., Goldstein, H., 1983, “The effects of Coulomb collisions on solar wind ion velocity distributions”, J. Geophys. Res., 88, 9933–9940. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1983JGR....88.9933M.
Marsch, E., Livi, S., 1985a, “Coulomb collision rates for the self-similar and kappa distributions”, Phys. Fluids, 28, 1379–1386. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1985PhFl...28.1379M.
Marsch, E., Livi, S., 1985b, “Coulomb collision frequencies for nonthermal velocity distributions in the solar wind”, Ann. Geophys., 3, 545–555. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1985AnGeo...3..545M.
Marsch, E., Livi, S., 1987, “Observational evidence for marginal stability of solar wind ion beams”, J. Geophys. Res., 92, 7263–7268. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1987JGR....92.7263M.
Marsch, E., Tu, C.-Y., 1997, “The effects of high-frequency Alfvén waves on coronal heating and solar wind acceleration”, Astron. Astrophys., 319, L17–L20. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997A7.26A...319L..17M.
Marsch, E., Tu, C.-Y., 2001a, “Heating and acceleration of coronal ions interacting with plasma waves through cyclotron and Landau resonance”, J. Geophys. Res., 106, 227–238. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106..227M.
Marsch, E., Tu, C.-Y., 2001b, “Evidence for pitch angle diffusion of solar wind protons in resonance with cyclotron waves”, J. Geophys. Res., 106, 8357–8362. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106.8357M.
Marsch, E., Tu, C.-Y., 2002, “Anisotropy regulation and plateau formation through pitch angle diffusion of solar wind protons in resonance with cyclotron waves”J. Geophys. Res., 107, 1249. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107i.SSH7T.
Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., Denskat, K.U., 1981, “Pronounced proton core temperature anisotropy, ion differential speed and simultaneous Alfvén activity in slow solar wind”, J. Geophys. Res., 86, 9199–9203. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1981JGR....86.9199M.
Marsch, E., Goertz, C.K., Richter, K., 1982a, “Wave heating and acceleration of solar wind ions by cyclotron resonance”, J. Geophys. Res., 87, 5030–5044. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982JGR....87.5030M.
Marsch, E., Muühlhüauser, K.-H., Rosenbauer, H., Schwenn, R., Neubauer, F.M., 1982b, “Solar wind helium ions: observations of the Helios solar probes between 0.3 and 1 AU”, J. Geophys. Res., 87, 35–51. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982JGR....87...35M.
Marsch, E., Muühlhäauser, K.-H., Schwenn, R., Rosenbauer, H., Pilipp, W.G., Neubauer, F.M., 1982c, “Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 AU”, J. Geophys. Res., 87, 52–72. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982JGR....87...52M.
Marsch, E., Axford, W.I., McKenzie, J.M., 2003, “Solar wind”, in Dynamic Sun, (Ed.) Dwivedi, B.N., pp. 374–402, Cambridge University Press, Cambridge, U.K.; New York, U.S.A. Contents.
Marsch, E., Ao, X.-Z., Tu, C.-Y., 2004, “On the temperature anisotropy of the core part of the proton velocity distribution function in the solar wind”, J. Geophys. Res., 109, A04 102. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10904102M.
Matteini, L., Landi, S., Hellinger, P. et al., 2005, “Proton Fire Hose Instability in the Expanding Solar Wind”, in Connecting Sun and Heliosphere, (Ed.) Lacoste, H., Proceedings of Solar Wind 11 / SOHO 16, 12–17 June 2005, Whistler, Canada, vol. SP-592 of ESA Conference Proceedings, pp. 503–506, ESA Publications Division, Noordwijk, Netherlands.
Matthaeus, W.H., Goldstein, M.L., Roberts, D.A., 1990, “Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind”, J. Geophys. Res., 95, 20 673–20 683. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1990JGR....9520673M.
McComas, D.J., Bame, S.J., Feldman, W.C., Gosling, J.T., Phillips, J.L., 1992, “Solar wind halo electrons from 1–4 AU”, Geophys. Res. Lett., 19, 1291–1294. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1992GeoRL..19.1291M.
McKenzie, J.F., 1994, “Interaction between Alfvén waves and a multicomponent plasma with differential ion streaming”, J. Geophys. Res., 99, 4193–4200. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....99.4193M.
McKenzie, J.F., Marsch, E., 1982, “Resonant wave acceleration of minor ions in the solar wind”, Astrophys. Space Sci., 81, 295–314. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1982Ap726SS..81..295M.
McKenzie, J.F., Ip, W.-H., Axford, W.I., 1979, “The acceleration of minor ion species in the solar wind”, Astrophys. Space Sci., 64, 183–211.
Melrose, D.B., McPhedran, R.C., 1991, Electromagnetic Processes in Dispersive Media: A Treatment Based on the Dielectric Tensor, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Meyer-Vernet, N., Issautier, K., 1998, “Electron temperature in the solar wind: Generic radial variation from kinetic collisionless models”, J. Geophys. Res., 103, 29 705–29 718. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998JGR...10329705M.
Meyer-Vernet, N., Perche, C., 1989, “Tool kit for antennae and thermal noise near the plasma frequency”, J. Geophys. Res., 94, 2405–2415. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/1989JGR....94.2405M.
Montgomery, D.C., Tidman, D.A., 1964, Plasma Kinetic Theory, McGraw-Hill, New York, U.S.A.
Montgomery, M.D., Gary, S.P., Feldman, W.C., Forslund, D.W., 1976, “Electromagnetic instabilities driven by unequal proton beam in the solar wind”, J. Geophys. Res., 81, 2743–2749. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1976JGR....81.2743M.
Nakariakov, V.M., Verwichte, E., 2005, “Coronal Waves and Oscillations”, Living Rev. Solar Phys., 2, lrsp-2005-3. URL (cited on 4 October 2005): http://www.livingreviews.org/lrsp-2005-3.
Nakariakov, V.M., Ofman, L., DeLuca, E.E., Roberts, B., Davila, J.M., 1999, “TRACE observation of damped coronal loop oscillations: Implications for coronal heating”, Science, 285, 862–864.
Neugebauer, M., 1981, “Observations of solar wind helium”, Fundam. Cosmic Phys., 7, 131–199. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1981FCPh....7..131N.
Neugebauer, M., Goldstein, B.E., Bame, S.J., Feldman, W.C., 1994, “Ulysses near-ecliptic observations of differential flow between proton and alphas in the solar wind”, J. Geophys. Res., 99, 2505–2511. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....99.2505N.
Neugebauer, M., Goldstein, B.E., Smith, E.J., Feldman, W.C., 1996, “Ulysses observations of differential alpha-proton streaming in the solar wind”, J. Geophys. Res., 101, 17,047–17,056. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996JGR...10117047N.
Newbury, J.A., Russell, C.T., Phillips, J.L., Gary, S.P., 1998, “Electron temperature in the ambient solar wind: Typical properties and a lower bound at 1 AU”, J. Geophys. Res., 103, 9553–9566. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998JGR...103.9553N.
Nishimura, K., Gary, S.P., Li, H., 2002, “Whistler anisotropy instability: Wave-particle scattering rate” J. Geophys. Res., 107, 1375. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107kSMP18N.
Ofman, L., Nakariakov, V.M., DeForest, C.E., 1999, “Slow Magnetosonic Waves in Coronal Plumes”, Astrophys. J., 514, 441–447. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999ApJ...514..4410.
Ofman, L., Viñas, A.F., Gary, S.P., 2001, “Constraints on the O5+ anisotropy in the solar corona”, Astrophys. J. Lett., 547, L175–L178. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001ApJ...547L.1750.
Ofman, L., Gary, S.P., Viñas, A., 2002, “Resonant heating and acceleration of ions in coronal holes driven by cyclotron resonant spectra” J. Geophys. Res., 107, 1461. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107l.SSH90.
Ofman, L., Davila, J.M., Nakariakov, V.M., Viñas, A., 2005, “High-frequency Alfvén waves in multi-ion coronal plasma: Observational implications”, J. Geophys. Res., 110, A09 102. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005JGRA..110091020.
Olsen, E.L., Leer, E., 1999, “A study of solar wind acceleration based on gyrotropic transport equations”, J. Geophys. Res., 104, 9963–9973. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...104.99630.
Olsen, E.L., Leer, E., Lie-Svendsen, Ø., 1998, “An eight-moment model parameter study of the solar wind: dependence in variations in coronal heating”, Astron. Astrophys., 338, 747–755. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998A726A...338..7470.
Parker, E.N., 1958, “Dynamics of the interplanetary gas and magnetic field”, Astrophys. J., 128, 664–676. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1958ApJ...128..664P.
Parker, E.N., 1963, Interplanetary Dynamical Processes, vol. 8 of Interscience Monographs and Texts in Physics and Astronomy, Interscience Publishers, New York, U.S.A.
Peter, H., 1998, “Element fractionation in the solar chromosphere driven by ionization-diffusion processes”, Astron. Astrophys., 335, 691–702. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1998A726A...335..691P.
Phillips, J.L., Gosling, J.T., 1990, “Radial evolution of solar wind thermal electron distributions due to expansion and collisions”, J. Geophys. Res., 95, 4217–4228. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1990JGR....95.4217P.
Pierrard, V., Lemaire, J., 1996, “Lorentzian ion exosphere model”, J. Geophys. Res., 101, 7923–7934. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996JGR...101.7923P.
Pierrard, V., Maksimovic, M., Lemaire, J., 1999, “Electron velocity distribution functions from the solar wind to the corona”, J. Geophys. Res., 104, 17 021–17 032. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10417021P.
Pierrard, V., Issautier, K., Meyer-Vernet, N., Lemaire, J., 2001, “Collisionless model of the solar wind in a spiral magnetic field”, Geophys. Res. Lett., 28, 223–226. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28..223P.
Pierrard, V., Lamy, H., Lemaire, J., 2004, “Exospheric distributions of minor ions in the solar wind”, J. Geophys. Res., 109, A02 118. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10902118P.
Pilipp, W.G., Miggenrieder, H., Montgomery, M.D., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., 1987a, “Characteristics of electron velocity distribution functions in the solar wind derived from the HELIOS plasma experiment”, J. Geophys. Res., 92, 1075–1092. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1987JGR....92.1075P.
Pilipp, W.G., Miggenrieder, H., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., Neubauer, F.M., 1987b, “Variations of electron distribution functions in the solar wind”, J. Geophys. Res., 92, 1103–1118. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1987JGR....92.1103P.
Reisenfeld, D.B., Gary, S.P., Gosling, J.T., Steinberg, J.T., McComas, D.J., Goldstein, B.E., Neugebauer, M., 2001, “Helium energetics in the high-latitude solar wind: Ulysses observations”, J. Geophys. Res., 106, 5693–5708. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106.5693R.
Roberts, D.A., Miller, J.A., 1998, “Generation of nonthermal electron distributions by turbulent waves near the Sun”, Geophys. Res. Lett., 25, 607.
Rosenbauer, H., Schwenn, R., Marsch, E., Meyer, B., Miggenrieder, H., Montgomery, M.D., Muühlhäauser, K.-H., Pillip, W., Voges, W., Zink, S.M., 1977, “A survey of initial results of the Helios plasma experiment”, J. Geophys., 42, 561–580. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1977JGZG...42..561R.
Rosenbluth, M.N., McDonald, M.W., Judd, D.L., 1957, “Fokker-Planck equation for an inverse-square force”, Phys. Rev., 107, 1–6. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1957PhRv..107....1R.
Rowlands, J., Shapiro, V.D., Shevchenko, V.I., 1966, “Quasilinear theory of plasma cyclotron instability”, Sov. Phys. JETP, 23, 651–660.
Ryan, J.M., Axford, W.I., 1975, “The behaviour of minor species in the solar wind”, Z. Geophysik, 41, 221–232. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1975ZGeo...41..221R.
Salem, C., Hubert, D., Lacombe, C., Bale, S.D., Mangeney, A., Larson, O.E., Lin, R.P., 2003, “Electron properties and Coulomb collisions in the solar wind at 1 AU: WIND observations”, Astrophys. J., 585, 1147–1157. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003ApJ...585.1147S.
Schwadron, N.A., McComas, D.J., 2003, “Solar wind scaling law”, Astrophys. J., 599, 1395–1403. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003ApJ...599.1395S.
Schwartz, S.J., 1980, “Plasma instabilities in the solar wind: A theoretical review”, Rev. Geophys. Space Phys., 18, 313–336. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1980RvGSP..18..313S.
Schwartz, S.J., Feldman, W.C., Gary, S.P., 1981, “The source of proton anisotropy in the high-speed solar wind”, J. Geophys. Res., 86, 541–546. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1981JGR....86..541S.
Schwenn, R., 1990, “Large-scale structure of the interplanetary medium”, in Physics of the Inner Heliosphere, Vol. 1: Large-Scale Phenomena, (Eds.) Schwenn, R., Marsch, E., vol. 20 of Physics and Chemistry in Space, pp. 99–181, Springer, Berlin, Germany; New York, U.S.A.
Scime, E.E., Bame, S.J., Feldman, W.C., Gary, S.P., Philips, J.A., Balogh, A., 1994, “Regulation of the solar wind electron heat flux from 1 to 5 AU: Ulysses observations”, J. Geophys. Res., 99, 23,401–23,410. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994JGR....9923401S.
Scime, E.E., Bame, S.J., Phillips, J.L., Balogh, A., 1995, “Latitudinal variations in the electron heat flux”, Space Sci. Rev., 72, 105–108. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1995SSRv...72..105S.
Scime, E.E., Littleton, J.E., Gary, S.P., Skoug, R.M., Lin, N., 2001, “Solar cycle variations in the electron heat flux: Ulysses observations”, Geophys. Res. Lett., 28, 2169–2172. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28.2169S.
Scudder, J.D., 1992a, “Why all stars should posses circumstellar temperature inversions”, Astrophys. J., 398, 319–349. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1992ApJ...398..319S.
Scudder, J.D., 1992b, “On the causes of temperature change in inhomogenous low-density astrophysical plasmas”, Astrophys. J., 398, 299–318. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1992ApJ...398..299S.
Scudder, J.D., Olbert, S., 1979a, “A theory of local and global processes which affect solar wind electrons, 1. The origin of typical 1 AU velocity distribution functions — Steady state theory”, J. Geophys. Res., 84, 2755–2772. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1979JGR....84.2755S.
Scudder, J.D., Olbert, S., 1979b, “A theory of local and global processes which affect solar wind electrons, 2. Experimental support”, J. Geophys. Res., 84, 6603–6620. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1979JGR....84.6603S.
Shapiro, V.D., Shevchenko, V.I., 1962, “The nonlinear theory of intercation between charged particle beams and a plasma in a magnetic field”, Sov. Phys. JETP, 15, 1053–1061.
Shoub, E.C., 1983, “Invalidity of local thermodynamic equilibrium for electrons in the solar transition region. I. Fokker-Planck results”, Astrophys. J., 266, 339–369. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/1983ApJ...266..339S.
Shukla, P.K., Bingham, R., McKenzie, J.F., Axford, W.I., 1999, “Solar coronal heating by high-frequency dispersive Alfvén waves”, Solar Phys., 186, 61–66. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999SoPh..186...61S.
Spitzer, L., Härm, R., 1953, “Transport phenomena in a completely ionized gas”, Phys. Rev., 89, 977–981. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1953PhRv...89..977S.
Stawicki, O., Gary, S.P., Li, H., 2001, “Solar wind magnetic fluctuation spectra: Dispersion versus damping”, J. Geophys. Res., 106, 8273–8282. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001JGR...106.8273S.
Steinberg, J.T., Lazarus, A.J., Ogilvie, K.W., Lepping, R., Byrnes, J., 1996, “Differential flow between solar wind protons and alpha particles: First WIND observations”, Geophys. Res. Lett., 23, 1183–1186. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1996GeoRL..23.1183S.
Stix, T.H., 1992, Waves in Plasmas, American Institute of Physics, New York, U.S.A., rev. edn.
Tam, S.W.Y., Chang, T., 1999, “Kinetic evolution and acceleration of the solar wind”, Geophys. Res. Lett., 26, 3189–3192. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999GeoRL..26.3189T.
Tam, S.W.Y., Chang, T., 2001, “Effect of electron resonant heating on the kinetic evolution and acceleration of the solar wind”, Geophys. Res. Lett., 28, 1351–1354. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28.1351T.
Tam, S.W.Y., Chang, T., 2002, “Comparison of the effects of wave-particle interactions and the kinetic suprathermal electron population on the acceleration of the solar wind”, Astron. Astrophys., 395, 1001–1012. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002A726A...395.1001T.
Tu, C.-Y., 1988, “The damping of interplanetary Alfvénic fluctuations and the heating of the solar wind”, J. Geophys. Res., 93, 7–20. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1988JGR....93....7T.
Tu, C.-Y., Marsch, E., 1995, “MHD Structures, Waves and Turbulence in the Solar Wind: Observations and Theories”, Space Sci. Rev., 73, 1–210. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1995SSRv...73....1T.
Tu, C.-Y., Marsch, E., 1997, “Two-fluid model for heating of the solar corona and acceleration of the solar wind by high-frequency Alfvén waves”, Solar Phys., 171, 363–391. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1997SoPh..171..363T.
Tu, C.-Y., Marsch, E., 2002, “Anisotropy regulation and plateau formation through pitch angle diffusion of solar wind protons in resonance with cyclotron waves”, J. Geophys. Res., 107, 1249. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107i.SSH7T.
Tu, C.-Y., Wang, L.-H., Marsch, E., 2002, “Formation of the proton beam distribution in high-speed solar wind”, J. Geophys. Res., 107, 1291. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002JGRA.107j.SSH8T.
Tu, C.-Y., Marsch, E., Wang, L.-H., 2003, “Cyclotron-resonant diffusion regulating the core and beam of solar wind proton distributions”, in Solar Wind Ten, (Eds.) Velli, M., Bruno, R., Malara, F., Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, vol. 679 of AIP Conference Proceedings, pp. 389–392, American Institute of Physics, Melville, U.S.A. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003AIPC..679..389T.
Tu, C.-Y., Marsch, E., Qin, Z.-R., 2004, “Dependence of the proton beam drift velocity on the proton core plasma beta in the solar wind”, J. Geophys. Res., 109, A05101. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10905101T.
Tu, C.-Y., Zhou, C., Marsch, E., Xia, L.-D., Zhao, L., Wang, J.-X., Wilhelm, K., 2005, “Solar wind origin in coronal funnels”, Science, 308, 519–523. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005Sci...308..519T.
Ulmschneider, P., Kalkofen, W., 2003, “Heating of the solar chromosphere”, in Dynamic Sun, (Ed.) Dwivedi, B.N., pp. 181–195, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Vasquez, B.J., 1995, “Simulation study of the role of ion kinetics in lowfrequency wave train evolution”, J. Geophys. Res., 100, 1779–1792. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1995JGR...100.1779V.
Viñas, A.F., Wong, H.K., Klimas, A.J., 2000, “Generation of Electron Suprathermal Tails in the Upper Solar Atmosphere: Implications for Coronal Heating”, Astrophys. J., 528, 509–523. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2000ApJ...528..509V.
Vocks, C., 2002, “A kinetic model for ions in the solar corona including wave-particle interactions and Coulomb collisions”, Astrophys. J., 568, 1017–1029. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002ApJ...568.1017V.
Vocks, C., Mann, G., 2003, “Generation of Suprathermal Electrons by Resonant Wave-Particle Interaction in the Solar Corona and Wind”, Astrophys. J., 593, 1134–1145. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2003ApJ...593.1134V.
Vocks, C., Marsch, E., 2001, “A semi-kinetic model of wave-ion interaction in the solar corona”, Geophys. Res. Lett., 28, 1917–1920. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2001GeoRL..28.1917V.
Vocks, C., Marsch, E., 2002, “Kinetic Results for Ions in the Solar Corona with Wave-Particle Interactions and Coulomb Collisions”, Astrophys. J., 568, 1030–1042. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002ApJ...568.1030V.
Voitenko, Y.M., Goossens, M., 2002a, “Excitation of high-frequency Alfvén waves by plasma outflows from coronal reconnection events”, Solar Phys., 206, 285–313. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002SoPh..206..285V.
Voitenko, Y.M., Goossens, M., 2002b, “Nonlinear excitation of small-scale Alfvén waves by fast waves and plasma heating in the solar atmosphere”, Solar Phys., 209, 37–60. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2002SoPh..209...37V.
Voitenko, Y.M., Goossens, M., 2004, “Cross-Field Heating of Coronal Ions by Low-Frequency Kinetic Alfvén Waves”, Astrophys. J. Lett., 605, L149–L152. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004ApJ...605L.149V.
Voitenko, Y.M., Goossens, M., 2005a, “Nonlinear coupling of Alfvén waves with widely different cross-field wavelengths in space plasmas”, J. Geophys. Res., 110, A10S01. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005JGRA..11010S01V.
Voitenko, Y.M., Goossens, M., 2005b, “Cross-scale nonlinear coupling and plasma energization by Alfvén waves”, Phys. Rev. Lett., 94, 135 003. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005PhRvL..94m5003V.
von Steiger, R., Geiss, J., Gloeckler, G., Galvin, A.B., 1995, “Kinetic properties of heavy ions in the solar wind from SWICS/Ulysses”, Space Sci. Rev., 72, 71–76. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1995SSRv...72...71V.
von Steiger, R., Geiss, J., Gloeckler, G., 1997, “Composition of the solar wind”, in Cosmic Winds and the Heliosphere, (Eds.) Jokipii, J.R., Sonett, C.P., Giampapa, M.S., Space Science Series, pp. 581–616, Arizona University Press, Tucson, U.S.A.
Wang, J.J., Gary, S.P., Liewer, P.C., 1999, “Electromagnetic heavy-ion/proton instabilities”, J. Geophys. Res., 104, 24 807–24 818. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1999JGR...10424807W.
Wiegelmann, T., Xia, L.-D., Marsch, E., 2005, “Links between magnetic fields and plasma flows in a coronal hole”, Astron. Astrophys., 432, L1–L4. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2005A726A...432L...1W.
Wilhelm, K., Dammasch, I.E., Marsch, E., Hassler, D.M., 2000, “On the source regions of the fast solar wind in polar coronal holes”, Astron. Astrophys., 353, 749–756. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2000A726A...353..749W.
Williams, L.L., 1994, “A model of the proton heat flux appropriate for collisionless plasmas”, Astrophys. J. Lett., 424, L143–L146. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1994ApJ...424L.143W.
Winske, D., Leroy, M.M., 1984, “Diffuse ions produced by electromagnetic ion beam instabilities”, J. Geophys. Res., 89, 2673–2688. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1984JGR....89.2673W.
Winske, D., Omidi, N., 1992, “Electromagnetic ion/ion cyclotron instability: Theory and simulations”, J. Geophys. Res., 97, 14,779–14,799. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/1992JGR....9714779W.
Xia, L.-D., Marsch, E., Wilhelm, K., 2004, “On the network structures in solar equatorial coronal holes — Observations of SUMER and MDI on SOHO”, Astron. Astrophys., 424, 1025–1037. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004A726A...424.1025X.
Xie, H., Ofman, L., Vinfas, A., 2004, “Multiple ions resonant heating and acceleration by Alfvén/cyclotron fluctuations in the corona and the solar wind”, J. Geophys. Res., 109, A08 103. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004JGRA..10908103X.5.5
Zouganelis, I., Maksimovic, M., Meyer-Vernet, N., Lamy, H., Pierrard, V., 2003, “A new exospheric model of the solar wind acceleration: The transsonic solutions”, in Solar Wind Ten, (Eds.) Velli, M., Bruno, R., Malara, F., Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, vol. 679 of AIP Conference Proceedings, p. 315, American Institute of Physics, Melville, U.S.A.
Zouganelis, I., Maksimovic, M., Meyer-Vernet, N., Lamy, H., Issautier, K., 2004, “A transonic collisionless model of the solar wind”, Astrophys. J., 606, 542–554. Related online version (cited on 4 October 2005): http://adsabs.harvard.edu/abs/2004ApJ...606..542Z.
Zouganelis, I., Meyer-Vernet, N., Landi, S., Maksimovic, M., Pantellini, F.G.E., 2005, “Acceleration of Weakly Collisional Solar-Type Winds”, Astrophys. J. Lett., 626, L117–L120. Related online version (cited on 18 June 2006): http://adsabs.harvard.edu/abs/2005ApJ...626L.117Z.
Acknowledgements
Sincere thanks go to the two referees for their critical but constructive reading of this rather long paper, and for their thoughtful comments and valuable suggestions, which lead to a significant improvement of the revised version of this review.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Marsch, E. Kinetic Physics of the Solar Corona and Solar Wind. Living Rev. Sol. Phys. 3, 1 (2006). https://doi.org/10.12942/lrsp-2006-1
Published:
DOI: https://doi.org/10.12942/lrsp-2006-1