Introduction

Item response theory (IRT) is a statistical methodology that can be used to analyze clinical outcome assessments which are often in a form of a questionnaire that describe or reflect how a patient feels or functions. Such assessments include patient-, observer-, and clinician-reported outcomes as well as performance outcomes related to a standardized set of tests. IRT describes the relationship between a subject-specific unobserved latent variable (Ψi), representing disease severity, and the probability of a response for each item through item characteristic functions (ICF) estimated from data. A particular feature of IRT models is the large number of parameters utilized to parametrize the ICF. In addition to effectively defining the ICF, selection of an appropriate approach to incorporation of longitudinal aspects to characterize the time-course of the latent variable should also be considered when applying IRT within a pharmacometrics (i.e., longitudinal) framework. Handling of the longitudinal data is a critical component of model development, as each of these may have implications on model fit, stability, and resulting impact on parameter precision and power.

The earliest application of IRT within a pharmacometrics framework utilized the Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog). The ICF parameters were defined using only baseline data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) aggregate study database. The ICF parameters were then fixed, and subsequently, the longitudinal parameters were modeled [1]

The evolution of knowledge in the field has led to the development of alternative approaches to defining the ICF parameters in order to address unique analytical challenges and optimize use of the available data. One such approach simultaneously estimates ICF parameters (i.e., fixed effects) and latent variable parameters (e.g., progression rate, drug effect, covariates) through fixed and random effects with the assumption that the latent variable for a reference condition follows a given, typically normal, distribution. In analyses of clinical trial data, the reference condition is often the baseline data [2, 3]. This approach may be more complicated to implement due to joint estimation of all parameters which could result in challenges with model convergence. Also, re-estimation of all parameters with each new model evaluation can result in longer model run-times.

Another method that can be leveraged utilizes a sequential process [4,5,6] and ultimately models the latent variable directly. In the first step, which is focused on estimating the ICF parameters, separate latent variables are estimated for each time point observation. In this method, as in the simultaneous method, the baseline is typically taken to be the reference condition. For timepoints after baseline, a separate fixed and random effect is estimated, but also, these observations contribute to the estimation of ICFs. This first step is easy to implement and less computing resource intensive. In the second step, the estimated latent variable values are treated as data (i.e., dependent variable) and then the estimation of progression rate, covariate testing, drug effect modeling etc., takes place in an accelerated fashion as there is no need to re-estimate the ICF parameters each time.

It has been demonstrated in the literature that pharmacometric IRT models have an increased power to detect drug effect and provide a more precise estimate of these drug effects [7,8,9] compared to traditional methods using a single end of trial endpoint and also longitudinal methods such as disease progression modeling with composite score [1, 10,11,12].

This increase in power can be attributed to the increased precision from the use of all available data, where the relative information content in different items is recognized, together with using a model that respects the discrete, bounded interval, nature of the data. Known factors such as sample size, rate of disease progression, and effect size have an impact on the resulting power and parameter precision. However, how data is handled within each of the analytical methods may also be important.

To date, a direct comparison of the “simultaneous” and “sequential” methodologies described herein has not yet been investigated. While there are some similarities between the estimation methods, each present different considerations when handling longitudinal data. In this manuscript, we investigate the estimation properties and parameter recovery of two approaches for defining ICF and incorporation of longitudinal data to characterize the latent variable.

Methods

Data Generation

The model used for this simulation study was adapted from a published longitudinal unidimensional IRT model of the Movement Disorder Society-Sponsored Revision of the Unified Parkinson’s Disease Rating scale (MDS-UPDRS) motor scale in patients with early Parkinson’s disease [3]. Item parameters were informed by real data; the final estimates from the first 20 items from the motor scale were extracted along with the mean latent variable progression rate (0.017 Ψ/month) and interindividual variability (standard deviation (SD) of 0.0086). The maximum total score based on the items in this truncated scale of 20 ordered categorical items was 44. The maximum individual item score was 3: there were seven 4-category items, ten 3-category items, and three 2-category items, due to item consolidation based on the final publication model [3]. The same item parameters were supplied to each estimation model as initial estimates. These conditions served as the basis for the slow progression rate data scenario, which for the purpose of this study is representative of slow progressing diseases. Monte Carlo simulations were performed with or without a hypothetical disease-modifying drug effect (i.e., 18% reduction in progression rate) to simulate item scores. Replicate trials (n trials =500) were simulated assuming a 12-month, 2-arm (placebo: disease-modifying treatment) parallel trial with 100 subjects per arm.

As a methodological consideration, a secondary scenario was also explored, which employed a mean rapid progression rate of 0.2 Ψ/month (SD 0.1 for interindividual variability) with 250 subjects per arm. This case scenario evaluated model performance under conditions expected to have higher sensitivity to a disease-modifying treatment effect due to steeper progression rate and larger sample size, but would be considered unrealistic in slow-progressing disease such as Parkinson’s disease. However, this scenario is intended to investigate any divergence between the approaches under varying conditions.

All estimations were performed with either simultaneous estimation or the sequential method. In total, there were eight simulation/estimation scenarios. Figure 1 outlines the simulation scenarios and workflow. The same initial estimates (different from the simulation parameters) were provided for the simultaneous and sequential methods to not favor the simultaneous method estimation.

Fig. 1
figure 1

Simulation workflow

Full size image

Longitudinal IRT Model

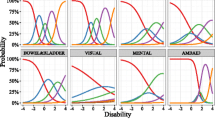
A unidimensional graded response IRT model was used as the simulation model. Disease severity at baseline was assumed to follow a normal distribution on the latent variable (Ψ) scale with a mean of 0 and variance of 1. A linear progression was assumed for the latent variable change over time, with the interindividual variability in progression rate following a normal distribution with pre-specified mean and variance as described above for simulation.

For subject \(i\) and item \(j\), the graded response model describes the probability of achieving a score of at least \(s\) at time point \(k\):

$$P\left({Y}_{ijk}\ge s|{\Psi }_{i,k}\right)=\frac{{e}^{{a}_{j}\left({\Psi }_{i,k}-{b}_{j,s}\right)}}{1+{e}^{{a}_{j}\left({\Psi }_{i,k}-{b}_{j,s}\right)}}$$
(1)

and, consequentially, to achieve a score of exactly \(s\) as

$$P\left({Y}_{ijk}=s|{\Psi }_{ik}\right)=P\left({Y}_{ijk}\ge s|{\Psi }_{ik}\right)-P\left({Y}_{ijk}\ge s+1|{\Psi }_{ik}\right)$$
(2)

where \({\Psi }_{i,k}\) is the subject’s time-dependent latent variable value, \({a}_{j}\) is the item-specific discrimination parameter (later referred to as DIS), and \({b}_{j,s}\) is the threshold parameter (later referred to as DIF(n)) for that specific item and score.

The latent variable time course was evaluated in models with and without drug effect (DMEFF).

A disease-modifying drug effect of 0.18 (fixed effect) was proportionally applied to the disease progression rate after time zero for both progression rate scenarios as shown below:

$${\Psi }_{i,k}={\Psi }_{i}^{0}+{\alpha }_{i}*\left(1-DMEFF\right)*{t}_{k}$$
(3)

\({\Psi }_{i}^{0}\) is the baseline latent variable value, \({\mathrm{\alpha }}_{{\text{i}}}\) is the disease progression rate, DMEFF is assigned 0 at baseline and placebo, and \({t}_{k}\) is time point. DMEFF is fixed to 0 in the model without drug effect.

Sequential Method

In step 1, using the IRT model structure described above, ICF parameters were estimated treating each observation visit as a unique separate individual. Baseline measurements at time zero were assumed to be related to a normal distribution for \(\Psi\) with a mean of zero and variance of 1. A post-baseline shift was estimated for observations after time zero estimating separate fixed and random effects for post baseline timepoints. With this approach, the ICFs are expected to have the same underlying true values for the sequential and simultaneous approach. In step 2, the subject and time-specific \({\Psi }_{i,k}\) (latent variables) were extracted and modeled directly for each original ID. In this procedure, the second step is dependent on the estimated values of \(\Psi\). These estimates may be more or less precise, depending on the underlying \(\Psi\) value. Similar to the approach taken in a publication by Lacroix et al. regarding inclusion of uncertainty on individual PK parameter estimates during sequential population PKPD analysis [13], to account for such differences in precision, the latent variable standard error (\(SE\_{\Psi }_{i,k}\)) was also included as additional parameter information in the longitudinal model of disease progression (Eq. 4) as shown below:

Sequential method (Step 2)

$${Y}_{i,k}={\Psi }_{i}^{0}+{\alpha }_{i}*\left(1-DMEFF\right)*{t}_{k}+SE\_{\Psi }_{i,k}*{\varepsilon }_{i,k}$$
(4)

\({\Psi }_{i}^{0}\) is the baseline latent variable value fixed to zero with an estimated additive random effect, and \({\varepsilon }_{ik}\) is a zero mean random variable; the remaining variables are as earlier defined.

Assessment of Parameter Estimation Accuracy

Parameter recovery in relation to true parameters was evaluated in terms of estimation bias, and precision (SD) for ICF parameters, progression rate, and drug effect for each model scenario \(s\), and replicate n (total replicates trials).

Estimation error:

$${{e}_{j,s,r}=\widehat{\theta }}_{j,s,r}-{\theta }_{j,s,r}$$
(5)

where \({\widehat{\theta }}_{j,s,r}\) is the estimated value, and \({\theta }_{j,s,r}\) is the true parameter.

The bias is represented by mean estimation error and precision is represented by standard deviation. The equation for bias is shown below (Eq.6):

$$Bias_{j,s}=\frac1{n\;trials}\sum\limits_{n=1}^{n\;trials}e_{j,s,r}$$
(6)

Hypothesis Testing

The evaluation of type 1 error and power was performed by stochastic simulation and re-estimation using maximum likelihood framework for hypothesis testing (Fig. 1).

To assess power, simulation was performed with the full model which includes the drug effect parameter, and to assess type 1 error rate, the simulation was performed with the reduced model (without drug effect).

Reduced and full model performance for each of the methods was compared using the log-likelihood ratio (LLR) test statistic to test for frequency of rejecting or accepting the null hypothesis (H0) for each of the replicate trials. The proportion of the replicate trials that met the criteria of significance level (0.05) cutoff for difference in objective function value (∆OFV) defined the type 1 error rate or power.

Log-likelihood ratio test

$$\begin{array}{c}LLR\left(\Theta\right)=L({\widehat\Theta}_{withdrugeffect,full},\;y)-L({\widehat\Theta}_{withoutdrugeffect,reduced},\;y)\\\mathrm\Delta\mathrm O\mathrm F\mathrm V=\mathrm{OFV}\;\mathrm{full}\;\mathrm{model}-\mathrm{OFV}\;\mathrm{reduced}\;\mathrm{model}\\>3.84\;\mathrm{for}\;p<0.05\;\mathrm{and}\;1\;\mathrm{degree}\;\mathrm{of}\;\mathrm{freedom}\end{array}$$
(7)

Estimation and Statistical Analysis

All models were estimated using the Laplacian (second order conditional) estimation method. The simulations and estimations were performed using NONMEM v7.4.3 [14]. For the simultaneous IRT model, the sse command in PsN [15] was leveraged to calculate type 1 error and power. Standard errors of individual random effects were retrieved using the VARCALC option in NONMEM. For other statistical procedures (including sequential method type 1 error and power), R 3.5.2 was used.

Results

Simulated Data and Total Score Trajectory

The maximum total score of the 20-item assessment scale was 44. Representative mean and individual total score trajectory for 20 randomly sampled subjects are shown in Figure 2 to demonstrate the disease progression on the total score scale based on the progression rate and ICF simulation parameters. At the mean level, the total score trajectory appears to be in the middle of the assessment scale. However, at the individual level, it is clear that while the full range of possible scores (i.e., 0–44) is not present in these individuals, there are many observations close to the upper and lower bounds, where information content in data is lower. The latter is evident from the Fisher information for the simulation IRT model (See Online Resource 1).

Fig 2.
figure 2

Mean and individual total score from 20 random sampled individuals showing variability in individual total sore

Full size image

ICF Parameter Estimation

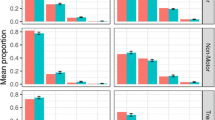
Item characteristic function parameter estimation was evaluated in terms of bias (mean estimation error) and precision (standard deviation), in order to understand the impact that the post baseline data handling approach may have on the ICF parameters. While there are not an equal number of categories across all items, the number of categories will be consistent for a particular item across replicate trials for each method, which allows for direct comparison at the method level. The mean estimation error and standard deviation for each item parameter summarized across replicate trial scenarios, when longitudinal model is correctly specified, are presented in columns 1–4 of Table I. A similar summary at the item level for select representative items is presented in the online resource 2.

Table I Across Item Aggregate Summary Statistics of Item Parameter Estimation Bias and Precision
Full size table

Overall, the simultaneous and sequential methods performed similarly with minimal bias in the estimation of the ICF parameters. A similar magnitude of error was observed between estimation approaches, within the same progression rate scenario. An increase in precision was observed in the scenario with the rapid progression rate and increased sample size, as expected with more informative data across a wider range of latent variable values. As can be seen in Fig. 2, with the slow progression rate, the severe side of the scale is poorly informed. This results in higher imprecision, especially for the higher-response category difficulty (i.e., threshold) parameters DIF2 and DIF3.

A small, but consistently higher precision can be observed for the simultaneous method over the sequential. When the two models estimate ICF parameters, they use the same number of population parameters, but at the individual level, the simultaneous IRT model estimates two random effects (baseline and slope), whereas there are five estimated random effects in the sequential method (one for each observation visit). When the longitudinal model is correctly specified as in the default setting, this results in better informed random effects compared to the sequential method, as evident from Figs. 3 and 4. However, if there is misspecification in the longitudinal model, there is a risk of bias in the ICF parameters. To explore this, we have also evaluated ICF parameter estimation in a model where misspecification in the longitudinal component was introduced intentionally. This is presented in the right-most column in Table I, using the rapid progression rate as an example. There is a clear increase in bias of all the ICF parameters (DIS, DIF1, DIF2, and DIF3).

Fig. 3
figure 3

Representative trial latent variable (Ψ) standard error (SE) time-course

Full size image
Fig. 4
figure 4

Representative trials (n = 10) individual estimated latent variable (Ψ) vs simulated (true) latent variable (Ψ) correlation for the slow progression rate (a, b) and rapid progression rate (c, d) scenarios

Full size image

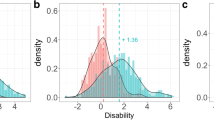
The ICF parameters (DIS and DIFx) were well determined when the model is correctly specified, for both methods. To understand the origin of the slight increase in precision for the simultaneous method, the SEs in individual latent variable (Ψ) values were retrieved for the two methods (Fig. 3). The latent variable uncertainty in the sequential method is consistently ~ 2-fold higher across all timepoints than that of the simultaneous method. This implies that while the ICF parameters are well informed, the latent variable could be less well determined.

This increase in latent variable uncertainty is more pronounced at the upper and lower ends of the latent variable scale where there is less information as illustrated in Fig. 4. When comparing the simulated (true) latent variable to the estimated latent variable for the sequential method, the points begin to deviate more from the line of identity at the upper and lower bounds of the scale. Whereas for the simultaneous method, the agreement between the true value for the latent variable and estimated latent variable consistently aligns across the scale.

Disease Progression Rate and Drug Effect Estimation

The mean estimation error and standard deviation for progression rate and drug effect for the 500 simulated trials is presented in Fig. 5. Overall, the simultaneous and sequential method performed similarly.

Fig 5.
figure 5

Mean estimation error for a progression rate and b disease progression parameters for each progression rate scenario

Full size image

In general, the disease progression rate was estimated with good precision and minimal bias for both methods. The progression rate was estimated more precisely under the slow progression rate conditions than the rapid progression rate. This is likely due to some subjects progressing much quicker and reaching the upper bounds of the score in the rapid progression rate scenario thus a slight increase in uncertainty in the estimation.

While only a small difference, the sequential method appeared to be more biased than the simultaneous in regard to progression rate estimation. In particular for the rapid progression rate scenario, the simultaneous method has negligible (i.e., almost zero) estimation error, while sequential method has negative bias of ~ 0.015 (7% of true value).

In terms of drug effect, both methods had large estimation bias (~ 30–40%) for the drug effect estimate itself in the slow progression rate scenario; with the reduced accuracy mainly driven by imprecision. This imprecision is a result of outliers with negative values for estimated drug effect.

In contrast, in the rapid progression rate scenario, drug effect was estimated with good precision and minimal bias for both methods. This increase in precision is attributed to the increased number of subjects (N = 200 to 500) and the ~10-fold increase in effect size. This trend was observed regardless of the presence of drug effect in the simulation conditions.

Hypothesis Testing

In terms of type 1 error and power, the simultaneous and sequential method performed similarly (Table II). Furthermore, there was no sign of inflation of the type 1 error with either method, when the confidence interval was considered. In the slow progression rate scenario with small sample size, the power to detect drug effect was low; however, this is consistent with the expectation for small sample size coupled with slow progression rate for a small effect size. In the rapid progression rate scenario with two-fold larger sample size, both models achieved almost 100% power, with similar average magnitude for ΔOFV between the full and reduced model of ~ 20 and ~ 21 for simultaneous and sequential method respectively.

Table II Simultaneous and Sequential Model Power and Type 1 Error Comparison
Full size table

Discussion

In this work, we compared two IRT methodologies for handling the ICF parameters, simultaneous estimation method and the sequential method, and evaluated their model performance in terms of parameter estimation and inference. In this section, we will discuss the general benefits and limitations of each of the methods as evaluated through the simulation examples to characterize and assess the evolution of the latent variable over time and define the ICF parameters.

We evaluated the performance of each of these methods under the following conditions (i) slow progression rate with small sample size, (ii) rapid progression rate with large sample size, and (iii) with and without drug effect to assess propensity for type 1 error rate and power. The rationale for selection of the simulation design options for progression rate and sample size was to illustrate the expectations at the extreme ends, acknowledging that a balanced variation between these two options would likely perform in line with known statistical principles (i.e., increase in sample size, observations, yield increased precision)

The results of our evaluation show that overall, the simultaneous and sequential methods performed similarly with relatively accurate estimation for key parameters. In all scenarios, the latent variable was well determined. However, there are some differences observed related to the longitudinal data handling. These will be particularly noticeable when the disease progression is rapid and thereby accounts for much of the variability over time, and/or when the longitudinal model is misspecified.

Item characteristic function parameters were well determined and estimated with low bias and good precision in default scenarios. As described in the “Results” section, the sequential method estimates five random effects at the individual subject level thus defining the ICF parameters independent of time and subject, resulting in larger parameter uncertainty for the latent variable estimation than the simultaneous method (Fig. 3). The simultaneous method allows for a fixed-effects estimation of the latent variable variability resulting from disease progression. However, as demonstrated in Table I, simultaneous estimation of the fixed effects (i.e., ICF parameters) and the longitudinal component of the model can bias both the discrimination and difficulty parameters if the longitudinal components are misspecified. As IRT disease progression models often use a simple linear progression, and in reality, the individual patients’ progression trajectories often more complex, some level of misspecification is likely often present. The sequential method in its determination of ICF parameters is not impacted by the longitudinal component misspecification due to the separate estimation of the ICF and longitudinal parameters.

The two methods performed similarly for the estimation of progression rate in the slow progression rate scenario. The 95% CI for estimation error indicated that this error was not statistically different from zero for the simultaneous IRT and the upper bound of the CI for sequential method was approaching zero (Online Resource 3). However, in the rapid progression rate scenario, a larger estimation bias and increased imprecision was observed for the sequential method compared to the simultaneous IRT. While this difference in bias and precision may be considered negligible relative to the true value, the larger estimation bias with wider 95% CI statistically different from zero points to the sequential method potentially being more influenced by shrinkage. In the sequential method, the increase in number of random effects results in the information content to be distributed across multiple ETAs resulting in less precise estimates for the latent variable as seen in Figs. 3 and 4. This becomes of greater importance at the lower and upper bounds of the scale, and this could impact the estimation of the individual progression rate. Using the rapid progression rate scenario as an example to further elucidate the presence of shrinkage due to imprecision, the individual progression rate estimates were compared across methods (Online Resource 3). The individual progression rate estimates for the simultaneous method range from − 0.16 to 0.57, while the sequential method individual estimates span a smaller range from − 0.11 to 0.46. This, along with the relation between the estimated and simulated latent variable (Ψ) values, (Fig. 4), can explain the bias we see in the progression rate at the trial level.

It is also important to note that Fig. 4 includes data for all subjects and timepoints, but does not reflect time directly. Figures for individual estimated latent variable vs simulated latent variable for both methods stratified by time are presented in online resource 4. Here, the mispredictions at time 0 and 12 months are more evident for the sequential method and are demonstrative of the increased uncertainty shown in Fig. 3. Similarly for the simultaneous method, the slight mispredictions are observed at the timepoints on the extreme end, but at a smaller magnitude.

The drug effect was estimated with minimal bias and good precision in the rapid progression rate scenario. However, for the estimation of drug effect in the slow progression rate scenario, an increase in bias at the drug effect parameter level attributed to imprecision was observed. If we consider the impact of this estimate on the relative scale for such a slow progression rate (0.017Ψ/month), this bias seen in drug effect estimation can be considered minimal.

Inclusion of the standard error term for the latent variable for the sequential method was selected as the default condition as was done by Lyuak et al [4]. It is expected that incorporating the \(SE\_{\Psi }_{i,k}\) would be more important the more variable the values are across individual latent variable estimates. When the sequential method was implemented with and without inclusion of \(SE\_{\Psi }_{i,k}\), a greater benefit of inclusion could be observed for the rapid progression rate compared to the slow (online resource 4). This is in line with the greater heterogeneity across \(SE\_{\Psi }_{i,k}\) for the rapid progression rate (Fig. 3)

Despite the minor differences in parameter estimation observed, both methods performed similarly in terms of type 1 error rate and power under the conditions explored. In addition, the model convergence rate of each of these methods was > 99% under the conditions explored.

We have studied what can be considered two extreme approaches to the estimation of longitudinal IRT models. One could imagine the two being combined, for example if a simultaneous approach is selected, calculating the ICFs also with the first step of the sequential method and compare the two sets of ICFs. Similarity across the ICFs could provide assurance that the ICFs are not impacted by any longitudinal model misspecification of the simultaneous approach. Others have utilized what can be considered an intermediate strategy, estimating ICFs as in the sequential method, but instead of continuing the modeling using the estimate of the latent variable, one would fix the ICFs and continue longitudinal model development using the original item level data [2, 16]. Such a method could retain the advantage of the sequential method with respect to lack of impact from longitudinal misspecification on ICF parameters but avoid the drawback of loss of information through shrinkage of the latent variable of the sequential method. In the cases where estimation of ICF and longitudinal components is performed in two separate steps, an additional step which simultaneously re-estimates all components can be performed [4,5,6, 17] and considered as an additional diagnostic. If ICFs or longitudinal parameters change upon such re-estimation, this is likely a sign of model misspecification.

In terms of model diagnostics, the sequential method allows for the generation of additional diagnostics beyond what is typically done for traditional IRT models. Traditional IRT models require diagnostics that are better suited for categorical data and are mostly simulation based, to diagnose model fit at the item and total score level [18]. In cases where there are different dependencies on different items, it may be more difficult to visualize improper model fit the total score alone may not be as informative. In the sequential method, the dependent variable is now a continuous variable which makes other diagnostics that are more commonly used in pharmacometrics such as residuals (e.g., CWRES), IPRED/PRED vs Observed and VPC of continuous dependent variable accessible. This allows for more thorough investigation of properties of the model, especially for the latent variable itself. Examples of the additional diagnostic plots that can be generated for the sequential method can be found in Online Resource 5 and example model code in Online Resource 6.

Conclusions

The simultaneous method and sequential method performed similarly with respect to bias and precision for key parameters and hypothesis test of drug effects. The simultaneous method has some advantage with respect to precision of the latent variable estimation while the sequential method is more robust towards longitudinal model misspecification and offers practical advantages in model building.