Tumor Static Concentration Curves in Combination Therapy

Abstract

Combination therapies are widely accepted as a cornerstone for treatment of different cancer types. A tumor growth inhibition (TGI) model is developed for combinations of cetuximab and cisplatin obtained from xenograft mice. Unlike traditional TGI models, both natural cell growth and cell death are considered explicitly. The growth rate was estimated to 0.006 h⁻¹ and the natural cell death to 0.0039 h⁻¹ resulting in a tumor doubling time of 14 days. The tumor static concentrations (TSC) are predicted for each individual compound. When the compounds are given as single-agents, the required concentrations were computed to be 506 μg · mL⁻¹ and 56 ng · mL⁻¹ for cetuximab and cisplatin, respectively. A TSC curve is constructed for different combinations of the two drugs, which separates concentration combinations into regions of tumor shrinkage and tumor growth. The more concave the TSC curve is, the lower is the total exposure to test compounds necessary to achieve tumor regression. The TSC curve for cetuximab and cisplatin showed weak concavity. TSC values and TSC curves were estimated that predict tumor regression for 95% of the population by taking between-subject variability into account. The TSC concept is further discussed for different concentration-effect relationships and for combinations of three or more compounds.

INTRODUCTION

Combination therapy plays a significant role in pharmacotherapy (1). One important aspect of combination therapy is the potential for synergistic effects. Other benefits compared to single-agent treatment include higher overall efficacy, lower exposure to the drugs and thereby improved safety, reduced toxicity, and lower risk of developing drug resistances (2–5).

Establishing synergies, finding the most effective anticancer drug combinations, and optimizing dosing schedules are all challenging tasks. Mathematical modeling has proved to be a valuable tool that addresses these challenges and can be used to quantify and predict the impact of drug combinations on tumor growth dynamics (6,7).

Different data-driven tumor models have been suggested (8,9). One of the most commonly applied experimental models is the tumor growth inhibition (TGI) model (10–13). The TGI model balances model complexity with data availability. In particular, the TGI model maintains a semi-mechanistic foundation while having few enough system and drug parameters for the model to still be calibrated using experimental data. A theoretical foundation for the TGI model has also been established by deriving the model from basic probabilistic assumptions in both single-agent and combination therapy settings (14,15).

The TGI model divides cancer cells into two categories: proliferating or damaged. The model consists of a main compartment representing the proliferating cancer cells and a number of damage compartments which cells irreversibly traverse before dying. The drug action of an anticancer compound is said to be cytostatic and/or cytotoxic. Cytostatic drug action acts on the proliferating cells by inhibiting proliferation (cell growth), whereas cytotoxic drug action stimulates cell death by triggering apoptosis. The TGI model can be generalized to combination therapy with two or more cytostatic and/or cytotoxic compounds. There have been several reported successes of this (16–20).

Several general methods have been established to evaluate drug combinations (21–24). A graphical tool is the isobologram (25–28). The isobologram is based on the simplified model of a direct relationship between drug dose and a biomarker response and generates a “curve of additivity” which can be used to distinguish additivity from synergy. A typical isobologram is shown in Fig. 1. Although depicted as such here, isobolographic curve of additivity need not be a straight line (29). The isobologram does not take into account the drug response, nor cancer-specific information that a TGI model can provide.

Fig. 1

The isobolographic curve of additivity (blue). An experimentally observed effect above or below this curve is indicative of a synergistic or antagonistic relationship between the two drugs, respectively

A TGI model is developed for individual exposure to combinations of cetuximab and cisplatin for the treatment of non-small cell lung cancer. These compounds are clinically relevant and have been tested together on various cell lines as well as in the clinic (30,31). The model assumes that the compounds act independently of each another. The model is an extension of the standard TGI models in that it incorporates natural cell death. A consequence of this is that the initial tumor volume should be distributed appropriately among the main and damage compartments. The model is mechanistically attractive, since it discriminates between natural cell death and increased kill rate by means of chemical intervention. We further investigate conditions for tumor stasis based on the model equations for both the single-agent treatments and the combination therapy. This results in the derivation of what is defined as the tumor static concentration (TSC) value and, for combinations of two compounds, the tumor static concentration curve. The TSC value of a single compound is the plasma concentration of that compound required to maintain the tumor in stasis. Such values have been obtained for TGI models (12,32). The TSC curve is a generalization of the TSC value when two compounds are given together (33,34). Instead of a single TSC value, the TSC curve consists of all concentration pairs which give tumor stasis when present simultaneously. Moreover, we show how the curvature of the TSC profile has a large impact on the resulting tumor growth and total exposure to test compounds. In particular, a highly concave¹ (i.e., curving downward) TSC curve will allow for tumor regression even with a reduced total drug exposure. Additionally, by taking between-subject variability into account, we show that it is possible to obtain TSC curves for specific individuals from the experimental data. This also makes it possible to construct a TSC curve of concentration pairs for which a large percentage (e.g., 95%) of the population is predicted to show tumor regression.

METHODS

Experimental Data

Patient-derived xenograft data consisted of 40 tumor-bearing female nude-nu mice used in a combination therapy experiment with the anticancer compounds cetuximab and cisplatin to treat non-small cell lung cancer. These data have previously been published by Amendt et al. (35).

The 40 mice were divided evenly into four treatment arms: vehicle, single-agent treatment with cetuximab, single-agent treatment with cisplatin, and combination treatment with both cetuximab and cisplatin. Treatment was started when tumors became palpable (with sizes around 80–200 mm ³). All treatment arms were given intraperitoneal doses on days 0, 3, 7, 10, and 14 and the doses were always 30 mg/kg for cetuximab and 5 mg/kg for cisplatin. The mice in the combination arm were given doses of both drugs on each day of dosing. Tumors were measured by caliper on days 0, 3, 7, 10, 14, 17, 21, 24, and 28.

Drug Exposure Models

Since there were no available exposure data for either cetuximab or cisplatin, pharmacokinetic models were taken from literature for both compounds. To describe cetuximab exposure, a one-compartment pharmacokinetic model with first-order absorption kinetics was used, with the explicit solution

$$ {\mathrm{C}}_{\mathrm{cetuximab}}=\frac{k_aFD}{V\left({k}_a-{k}_e\right)}\left({e}^{-{k}_et}-{e}^{-{k}_at}\right) $$

(1)

where k _a is the absorption rate, k _e the elimination rate, D the dose of cetuximab, F the bioavailability, and V the distribution volume (36). This model is shown in Fig. 2 (left).

Fig. 2

(left) Pharmacokinetic model for cetuximab with gut and plasma compartments. The parameters k _a and k _e represent the drug absorption and elimination rates, respectively. (right) pharmacokinetic model for cisplatin with gut, plasma, and tissue compartments. The parameter k _a represents the absorption rate and k ₁₂, k ₂₁, and k ₁₀ are the microconstants

To describe total cisplatin exposure, a two-compartment pharmacokinetic model with first-order absorption kinetics was used. The model is described by the following system of differential equations (37). The gut compartment is

$$ \frac{d{A}_g}{dt}=-{k}_a{A}_g $$

(2)

Drug in the central (plasma) and peripheral (tissue) compartments then become

$$ \begin{array}{l}\frac{d{A}_p}{dt}={k}_aF{A}_g-\left({k}_{10}+{k}_{12}\right){A}_p+{k}_{21}{A}_t\hfill \\ {}\frac{d{A}_t}{dt}={k}_{12}{A}_p-{k}_{21}{A}_t\hfill \end{array} $$

(3)

The initial conditions of the gut, central, and peripheral compartments are

$$ \begin{array}{l}{A}_g(0)=D,\kern2.25em {A}_p(0)=0,\kern2.25em {A}_t(0)=0\\ {}\end{array} $$

(4)

where k _a is the absorption rate, D the dose, F the bioavailability, and k ₁₀, k ₁₂, and k ₂₁, the microconstants. Here, A _g , A _p , and A _t denote the amount of cisplatin in the gut, plasma and tissue, respectively. An illustration of this model is shown in Fig. 2 (right). The total plasma concentration of cisplatin is then given by

$$ {\mathrm{C}}_{\mathrm{cisplatin}}=\frac{A_p}{V_C} $$

(5)

where V _C denotes the volume of the central compartment.

Tumor Growth Inhibition Model

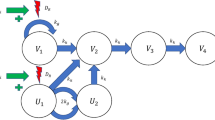
A TGI model with cetuximab as a cytostatic and cisplatin as a cytotoxic drug was used to describe the data in the final model. Modeling of each drug as cytostatic/cytotoxic was tested using both linear and nonlinear functions. The final selection was made based on AIC. Drug action was assumed to be independent. An illustration of this model is given in Fig. 3. The corresponding system of differential equations is

$$ \begin{array}{l}\frac{d{V}_1}{dt}=I\left({\mathrm{C}}_{\mathrm{cetuximab}}\right){k}_g{V}_1-S\left({\mathrm{C}}_{\mathrm{cisplatin}}\right){k}_k{V}_1\hfill \\ {}\frac{d{V}_4}{dt}={k}_k{V}_3-{k}_k{V}_4\hfill \end{array} $$

(6)

Fig. 3

TGI model for combination therapy with independent drug action. Cetuximab (A) inhibits cell proliferation, whereas cisplatin (B) stimulates cell apoptosis. The k _g and k _k parameters represent the natural cell kill and death rates, respectively

Here V ₁ is the main compartment of proliferating cancer cells, V ₂, V ₃, and V ₄ are the damage compartments that cells must go through before dying, k _g is the growth rate, and k _k is the (natural) death rate. The inhibitory drug action, I, of cetuximab was described using an E _max-function and the stimulatory drug action, S, of cisplatin was described using a linear function

$$ \begin{array}{l}I\left({\mathrm{C}}_{\mathrm{cetuximab}}\right)=1-\frac{I_{\max }{\mathrm{C}}_{\mathrm{cetuximab}}}{I{C}_{50}+{\mathrm{C}}_{\mathrm{cetuximab}}}\hfill \\ {}S\left({\mathrm{C}}_{\mathrm{cisplatin}}\right)=1+b\;{\mathrm{C}}_{\mathrm{cisplatin}}\hfill \end{array} $$

(7)

where I _max is the maximum inhibition cetuximab can accomplish, IC ₅₀ is the concentration of cetuximab required to obtain 50% of the maximum inhibition, and b is a pharmacodynamic parameter of cisplatin. The total tumor volume V _total comprises both V ₁ and the compartments representing dying cells.

$$ {V}_{\mathrm{total}}={V}_1+{V}_2+{V}_3+{V}_4 $$

(8)

Initial Conditions for the TGI Model

An important question is how to distribute the initial tumor volume among the different compartments V ₁, V ₂, V ₃, and V ₄. Without natural cell death, the usual thing to do is to put all of the initial volume into the main compartment V ₁. However, with natural cell death included, this would neglect that cells have been dying since before treatment was started and one would therefore expect some cells to be in V ₂ to V ₄.

It is possible to show that, starting from any distribution of the total initial tumor volume into V ₁ and V ₂ to V ₄, the ratio between two neighboring compartments, (i.e., V _i /V _i − 1) will approach a constant. If one assumes that the tumor has already existed for a long time before treatment started, it would make sense to also assume that this stage has been reached. Therefore, a reasonable choice of initial conditions is given by

$$ {V}_1(0) = {V}^0,\ {V}_2(0)={V}^0\left(\frac{k_k}{k_g}\right),\ {V}_3(0)={V}^0{\left(\frac{k_k}{k_g}\right)}^2,\ {V}_4(0)={V}^0{\left(\frac{k_k}{k_g}\right)}^3 $$

(9)

where V ⁰ is the initial volume of V ₁. For a detailed derivation of the initial conditions, see Appendix 1.

Deriving Tumor Static Concentrations

Consider the individuals treated with cetuximab alone. Since tumor regression is often a treatment goal, we would like to determine plasma concentrations resulting in tumor shrinkage. This is done by determining the drug concentration for which the input and output of each compartment is in balance. Plasma concentrations above this level may then be assumed to give tumor shrinkage.² For the cetuximab treatment, this means that each right-hand side in Eq. 6 should be zero, but since V ₂ to V ₄ only act to delay the death process, we only need to consider V ₁. For single-agent treatment with cetuximab it must hold

$$ \left({k}_g\left(1-\frac{I_{\max }{\mathrm{C}}_{\mathrm{cetuximab}}}{I{C}_{50}+{\mathrm{C}}_{\mathrm{cetuximab}}}\right)-{k}_k\right){V}_1=0 $$

(10)

which implies that

$$ {k}_g\left(1-\frac{I_{\max }{\mathrm{C}}_{\mathrm{cetuximab}}}{I{C}_{50}+{\mathrm{C}}_{\mathrm{cetuximab}}}\right)-{k}_k=0 $$

(11)

since the volume of the main compartment V ₁ will not be zero unless the tumor is already eradicated. Equation 11 can be solved for C_cetuximab to obtain

$$ {\mathrm{C}}_{\mathrm{cetuximab}}=\frac{I{C}_{50}\left({k}_g-{k}_k\right)}{k_k-\left(1-{I}_{\max}\right){k}_g} $$

(12)

This concentration is defined as the tumor static concentration (TSC) value of cetuximab. The TSC value holds for any tumor volume and at any point in time. Therefore, to ensure tumor shrinkage over time, plasma exposure above TSC should be established. A TSC value for cisplatin can be derived in a similar manner. When C_cetuximab = 0 the condition for stasis becomes

$$ {k}_g-{k}_k\left(1+b\;{\mathrm{C}}_{\mathrm{cisplatin}}\right)=0 $$

(13)

which can be simplified to

$$ {\mathrm{C}}_{\mathrm{cisplatin}} = \frac{k_g-{k}_k}{b\ {k}_k} $$

(14)

Tumor Static Concentrations for Combinations

An analysis similar to that for the single-agent compounds can be performed for the treatment arm that receives both compounds. For V ₁, it must therefore hold that

$$ {k}_g\left(1-\frac{I_{\max }{\mathrm{C}}_{\mathrm{cetuximab}}}{I{C}_{50}+{\mathrm{C}}_{\mathrm{cetuximab}}}\right)-{k}_k\left(1+b\;{\mathrm{C}}_{\mathrm{cisplatin}}\right)=0 $$

(15)

This equation describes a curve in the concentration plane with C_cetuximab and C_cisplatin along the coordinate axes. In this case one can solve for C_cisplatin to obtain

$$ {\mathrm{C}}_{\mathrm{cisplatin}} = \frac{k_g}{b\ {k}_k}\left(1-\frac{I_{\max }{\mathrm{C}}_{\mathrm{cetuximab}}}{I{C}_{50}+{\mathrm{C}}_{\mathrm{cetuximab}}}\right)-\frac{1}{b} $$

(16)

Equation 16 describes a curve of concentration pairs (C_cetuximab, C_cisplatin). Any concentration pairs located above this curve will give tumor shrinkage, whereas concentration pairs located below the curve will give tumor growth. Equation 16 is therefore introduced as the TSC curve. The points of intersection with the coordinate axes are the TSC values derived for the individual compounds. The TSC curve is valid for any tumor volume and at any time point. To ensure tumor shrinkage over time, dosing should be such that the concentration pair (C_cetuximab, C_cisplatin) is kept above the TSC curve at all times. An illustration of what a TSC curve could look like is given in Fig. 4. How the TSC concept is generalized to three or more compounds is discussed in Appendix 2.

Fig. 4

Schematic of a TSC curve (solid curve) for combination therapy with two compounds A and B. Reference straight line (dashed). Concentration pairs (C _A , C _B ) above the curve (green shaded area) give tumor shrinkage, whereas concentration pairs below (red shaded area) give tumor growth

Computational Methods

Nonlinear mixed-effects modeling of the cetuximab and cisplatin pharmacodynamic data was performed with a first-order conditional estimation (FOCE) method, using a computational framework developed at the Fraunhofer-Chalmers Research Centre for Industrial Mathematics (Gothenburg, Sweden) and implemented in Mathematica 10 (Wolfram Research) (38). The model was evaluated based on individual fit, residual analysis, visualizations of Empirical Bayes Estimates, and the Akaike information criterion.

To validate the assumption of independent drug action, a separate set of parameter estimates were obtained by omitting the combination arm. Then, a visual predictive check (VPC) was performed by using these estimates to simulate n = 5 000 individuals given the combination treatment and comparing the 5th and 95th quantiles to the actual observations.

To generate a TSC curve for which 95% of the population is expected to show tumor regression, a Monte Carlo simulation was performed. The between-subject variability information contained in the covariance matrix Ω was used to simulate TSC curves for 1000 hypothetical individuals. The 95% TSC curve was then selected as the 95th percentile of the simulated curves.

RESULTS

Drug Exposure Models

Parameter estimates for the pharmacokinetic models of cetuximab and cisplatin were taken from the literature (36,37).

The parameter values used for the cetuximab model (Eq. 1) were k _e  = 0.017 h^− 1, k _a  = 0.44 h^− 1, F = 1, and V = 0.094 mL · kg⁻¹. The corresponding exposure profile is shown in Fig. 5 (left).

Fig. 5

(left) Drug exposure for cetuximab. The orange line indicates the IC ₅₀ estimate for cetuximab, and the green line the estimated TSC value for cetuximab. (right) Drug exposure for cisplatin. The orange line indicates the estimated plasma concentration required to double the death rate (given by 1/b), and the green curve the TSC value for cisplatin. Dosing was repeated for both compounds on days 0, 3, 7, 10, and 14

The parameter values used for the cisplatin model (Eqs. 2–4) were k _a  = 42 h^− 1, k ₁₀ = 1.3 h^− 1, k ₁₂ = 3.3 h^− 1, k ₂₁ = 1.12 h^− 1, F = 1, and V _p  = 377 mL ⋅ kg^− 1. The corresponding exposure profile is shown in Fig. 5 (right).

Tumor Growth Inhibition Model

A population pharmacodynamic model was constructed by letting the parameters k _g and V ⁰ have lognormally distributed between-subject variability. A sample of the individual fit for each treatment arm is given in Fig. 6. Visual predictive checks for all for treatment arms can be found in Appendix 3.

Fig. 6

Representative time courses of observed (symbols) tumor volumes (mm³) for each of the four treatment arms. The solid lines represent the tumor volumes fitted by the TGI model

The parameter estimates for the tumor model are shown in Table I. The estimated net growth rate is given by k _g  − k _k  = 0.0021 h^− 1 corresponding to a doubling time of 330 h or 14 days. When the estimated volume of the main compartment of 60 mm ³ is used, the total initial volume is computed to be

$$ {V}_{\mathrm{total}} = \left(1+\left(\frac{k_k}{k_g}\right)+{\left(\frac{k_k}{k_g}\right)}^2+{\left(\frac{k_k}{k_g}\right)}^3\right){V}^0 $$

(17)

which gives an estimate of 140 mm³.

Table I Parameter Estimates for the Model Describing the Cetuximab and Cisplatin Combination Therapy

The parameter value of I _max was set to 1 in the final model. The estimated IC ₅₀ value for cetuximab of 994 μg · mL⁻¹ may be compared to the maximum exposure of 400 μg · mL⁻¹ which corresponds to roughly 30% inhibition of cell proliferation. The estimated pharmacodynamics parameter of cisplatin is 0.0093 mL ⋅ ng^− 1. and could be compared to the maximum cisplatin exposure of 10⁴ ng · mL⁻¹ which increases the kill rate by a factor of 100, although such levels of exposure only occurred during very short time periods (see Fig. 5). The model assumption of independent drug action was validated by a visual predictive check for the combination arm (see Appendix 4).

TSC Curve of Cetuximab-Cisplatin

Recall that from the tumor model, we derived Eq. 16 for the TSC curve. Using the parameter estimates from Table I, the TSC curve was computed, as depicted in Fig. 7. The individual TSC values were computed to be TSC_Cetuximab = 506 μg · mL⁻¹ and TSC_cisplatin = 56 ng · mL⁻¹. The TSC curve shows a slight deviation from a straight line. Individual TSC curves were constructed by taking between-subject variability into account. These are shown in blue in Fig. 8. The dashed red TSC curve, obtained by Monte Carlo simulation, indicates expected concentrations required for 95% of the population to experience tumor shrinkage.

Fig. 7

TSC curve for cetuximab-cisplatin combinations (blue, bold) distinguishing between regions of tumor growth (light red) and tumor shrinkage (light green). Reference straight line connecting the individual TSC values (black, dashed)

Fig. 8

Individual TSC curves (blue) for the cetuximab-cisplatin combination therapy, taking into account between-subject variability in the growth rate k _g . The TSC curve for the median individual from Fig. 7 is shown as a solid red curve. The dashed red line represents a region below which 95% of the population is expected to show tumor regression

Four Cases of TSC Curves for Independent Drug Action

While there are many ways to incorporate drug interaction into a tumor growth model, the number of models with independent action is considerably smaller and therefore easier to investigate. Consider the tumor model in Eq. 6 with two generic compounds A and B. The corresponding equation for the TSC curve reads

$$ I\left({\mathrm{C}}_A\right){k}_g-S\left({\mathrm{C}}_B\right){k}_k=0 $$

(18)

We shall consider four cases depending on how I(C _A ) and S(C _B ) are chosen. In all four cases, the TSC equation can be written in the form

$$ \alpha {\mathrm{C}}_A{\mathrm{C}}_B+\beta {\mathrm{C}}_A+\gamma {\mathrm{C}}_B=\delta $$

(19)

where α, β, γ, and δ are constants which depend on both the drug and the system parameters. The individual TSC values can then be expressed as

$$ {\mathrm{TSC}}_A=\frac{\delta }{\beta },\kern2em {\mathrm{TSC}}_B=\frac{\delta }{\gamma } $$

(20)

Linear Inhibition and Linear Stimulation

When both the cytostatic drug action and the cytotoxic drug action are assumed linear

$$ I\left({\mathrm{C}}_A\right)=1-a\ {\mathrm{C}}_A,\kern1.25em S\left({\mathrm{C}}_B\right)=1+b\;{\mathrm{C}}_B $$

(21)

the resulting TSC curve will also be linear and can be rearranged to

$$ {k}_ga\ {\mathrm{C}}_A+{k}_kb\ {\mathrm{C}}_B={k}_g-{k}_k $$

(22)

which is a straight line passing through the individual TSC values.

Nonlinear Inhibition and Linear Stimulation

In the second scenario, the cytostatic drug action is of E _max-type with unit sigmoidicity and the cytotoxic drug action is linear

$$ I\left({\mathrm{C}}_A\right)=1-\frac{I_{\max }{\mathrm{C}}_A}{I{C}_{50}+{\mathrm{C}}_A},\kern0.75em S\left({\mathrm{C}}_B\right)=1+b\ {\mathrm{C}}_B $$

(23)

The TSC equation can be shown to be

$$ {k}_kb\;{\mathrm{C}}_A{\mathrm{C}}_B+\left({k}_k-\left(1-{I}_{\max}\right){k}_g\right)\kern0.5em {\mathrm{C}}_A+{k}_k bI{C}_{50}{\mathrm{C}}_B=I{C}_{50}\left({k}_g-{k}_k\right) $$

(24)

The first term is nonlinear in C _A and C _B and will provide curvature to the TSC curve. This case was illustrated in the cetuximab-cisplatin example above.

Linear Inhibition and Nonlinear Stimulation

The third case has the roles reversed—the cytostatic drug action is now linear, while the cytotoxic drug action is of E _max-type with unit sigmoidicity

$$ S\left({\mathrm{C}}_A\right)=1-a\ {\mathrm{C}}_A,\kern1.25em S\left({\mathrm{C}}_B\right)=1+\frac{S_{\max }{\mathrm{C}}_B}{S{C}_{50}+{\mathrm{C}}_B} $$

(25)

The corresponding TSC equation becomes

$$ {k}_ga\ {\mathrm{C}}_A{\mathrm{C}}_B+{k}_gaS{C}_{50}{\mathrm{C}}_A+\left({k}_g-\left(1+{S}_{\max}\right){k}_k\right)\;{\mathrm{C}}_B=S{C}_{50}\left({k}_g-{k}_k\right) $$

(26)

Nonlinear Inhibition and Nonlinear Stimulation

Lastly, both the cytostatic drug action and the cytotoxic drug action are assumed to be nonlinear of E _max-type with unit sigmoidicity

$$ S\left({\mathrm{C}}_A\right)=1-\frac{I_{\max }{\mathrm{C}}_A}{I{C}_{50}+{\mathrm{C}}_A},\kern1em S\left({\mathrm{C}}_B\right)=1+\frac{S_{\max }{\mathrm{C}}_B}{S{C}_{50}+{\mathrm{C}}_B} $$

(27)

The corresponding TSC equation is similar to the previous two cases, albeit with slightly more complicated terms

$$ \left(\left(1+{S}_{\max}\right){k}_k-\left(1-{I}_{\max}\right){k}_g\right){\mathrm{C}}_A{\mathrm{C}}_B+S{C}_{50}\left({k}_k-\left(1-{I}_{\max}\right){k}_g\right){\mathrm{C}}_A+I{C}_{50}\left(\left(1+{S}_{\max}\right){k}_k-{k}_g\right){\mathrm{C}}_B=I{C}_{50}S{C}_{50}\left({k}_g-{k}_k\right) $$

(28)

Impact of the TSC Curve on Tumor Growth

To illustrate the impact of different TSC curves, two hypothetical curves with the same individual TSC values but different curvatures were constructed based on the nonlinear-linear TSC equation (Eq. 24). The two curves are depicted in Fig. 9 (left) with their corresponding parameter values listed in Table II. Tumor volume time courses were simulated assuming a constant plasma concentration of each drug at three different levels: (A) 0.3 μg · mL⁻¹, (B) 0.4 μg · mL⁻¹, and (C) 0.5 μg · mL⁻¹. The different time courses are shown in Fig. 9 (right). As expected, the tumor volumes are much lower for the blue curves than for the red, since the corresponding blue TSC curve exhibits much larger curvature than its red counterpart.

Fig. 9

(left) Two different TSC curves (blue and red) and (right) the corresponding growth dynamics assuming a constant drug infusion of each drug at three concentration levels (A, B, and C)

Table II Parameter Values Used to Construct the Two TSC Curves in Fig. 9 (Blue and Red)

DISCUSSION

Drug Exposure Models

Since there were no available exposure data for either cetuximab or cisplatin, models were taken from literature. For this reason, relatively simple models were chosen to give a rough estimate of what the exposure could have looked like. A disadvantage with this approach is that all individuals are assumed to have identical exposure profiles; there is no between-subject variation. This could lead to situations where actual variability in kinetic parameters is falsely attributed to variations in dynamic parameters, e.g., a large-growing tumor that was due to low drug exposure, could instead be falsely explained by the model with an unreasonably large growth rate parameter or low potency drug.

Tumor Growth Inhibition Model

A TGI model with independent drug action between cetuximab and cisplatin proved sufficient to explain the combination arm and no investigation into possible interaction terms was necessary. Since exposure profiles and models were taken solely from the literature, an assumption of no interaction on exposure level was implied. All parameters in Table I except for IC ₅₀ were estimated with acceptable precision and were located within biologically reasonable ranges. The relatively poor precision for IC ₅₀ is due to the estimated value of 994 μg · mL⁻¹ is well above the maximum drug exposure at around 400 μg · mL⁻¹ and the model is therefore insensitive to changes in IC ₅₀. The between-individual variation was large for both the growth rate and initial tumor volume, which is due to the variability between subjects in the vehicle arm. It is also possible that some of the between-subject variability in growth rate is actually due to different levels of epidermal growth factor receptor expression (EGFR), which has been suggested to be associated with the drug effect of cetuximab (35). In the TGI model, individuals with a high EGFR expression would therefore be given a larger growth rate than those with a low EGFR expression. The parameter estimates when the combination arm was removed (Table III) were very similar to before, indicating that the combination arm is well-explained by the zero-interaction model. This is further validated from the visual predictive check in Fig. 10 (Appendix 3) which shows that almost all observations from the combination arm fall within the estimated 90% confidence intervals obtained using Table III.

Table III Parameter Estimates for the Model Describing the Cetuximab and Cisplatin Combination Therapy, Using Only the Vehicle and Single-Agent Treatment Arms

Fig. 10

A VPC for the combination arm using the parameter estimates from Table III. The solid lines indicate the simulated 5th, 50th, and 95th percentiles. Colored dots represent different observed individuals in the combination arm

The TGI model incorporates a natural cell death rate k _k which was successfully estimated. However, it should be noted that the vehicle model alone is not identifiable; one can only determine the net growth rate k _g  − k _k . However, with the presence of a drug, these parameters can be separated and were estimated with good precision. This is made possible by an underlying assumption that the natural and drug-induced death processes are equivalent in a modeling sense, which is consistent with our viewpoint of cisplatin stimulating an already existing death process as opposed to induces a new one.

TSC Curve for Cetuximab-Cisplatin

The TSC curve is visually similar to the well-established isobologram (26,27), but with doses along the coordinate axes replaced with drug plasma concentrations, and the considered effect is when the net growth rate is zero. While the isobologram is typically based on a dose-effect model of E _max-type, the TSC curve is obtained from an exposure-driven growth model.

The TSC curve derived from cetuximab-cisplatin data serves as a practical example. The TSC curve exhibited a slight curvature, indicating that the drug combination effect is weakly synergistic. This is an interesting result given previous claims that EGFR inhibitors should act antagonistically with chemotherapy, although it is here limited to only one study of one specific combination (39). The certainty of the weak synergy is further explored in Appendix 5.

It is possible to derive TSC curves for more complicated growth functions than the exponential one used here. The Gompertz, logistic, and Simeoni growth functions (9,12) all start with an exponential growth phase which slows down as the tumor grows large. A TSC curve can then be derived by assuming that the tumor maintains its initial exponential growth. This is a necessary approximation, since we want the concentration pairs above the TSC curve to give tumor shrinkage for all tumor volumes, including those in the initial exponential phase.

The individual TSC curves in Fig. 8 show that there can be significant variation in which concentrations will be needed for tumor shrinkage. It is necessary to take between-subject variability into account and construct and simulate individual TSC curves. One can then target concentrations above the TSC curve for, e.g., 95% of the population (dashed, red).

In Fig. 8, the individual TSC curves are non-intersecting. This is not true in general and would typically only occur when only one parameter has population variability (in this case k _g ). If two or more parameters have between-subject variability, some of the individual TSC curve would be expected to intersect unless the parameters are highly correlated.

Four Cases of TSC Curves for Independent Drug Action

We outlined four standard cases of independent drug action between a cytotoxic drug and a cytostatic drug. The first important observation is that the case with linear inhibitory drug action and linear stimulatory drug action is the only case where the TSC curve becomes a straight line (signified by α = 0) indicating additivity. This straight line means that the concentration-effect relationship is linear even when the drugs are combined. There are no benefits from combining the drugs. In contrast, when either the inhibition or stimulation is nonlinear, or both are nonlinear, the TSC curve will also be a nonlinear curve falling below the straight line connecting the individual TSC values. It will then be possible to decrease the total exposure levels of both compounds and still obtain tumor shrinkage. Even with two drugs which when given individually each require a concentration of 100 μg · mL⁻¹ to be above the TSC value a sufficiently curved TSC curved may tell us that tumor shrinkage can be obtained with a concentration of 25 μg · mL⁻¹ of each drug when given together. If the TSC curve were a straight line, the required concentrations would instead have been 50 μg · mL⁻¹ of each drug.

None of the four cases studied allow for antagonism, or an outward curving TSC curve. To allow for antagonism, the most common way would be to include an explicit (negative) interaction term added to the TGI model, which would contribute to making the parameter α in Eq. 19 negative and result in an antagonistic TSC curve.

Impact of the TSC Curve on Tumor Growth

We also investigated the relationship between the TSC curve and tumor growth dynamics. We showed in Fig. 9 that even if the individual TSC values are the same, the shape of the TSC curve is very important to how rapidly the tumor volume changes. Since we have assumed that the drugs do not interact, the different growth dynamics shown in Fig. 9 must originate from the nonlinear concentration-response relationship of the inhibitory function I(C_B). In particular, what ultimately decides why the blue TSC curve performs better is how well the drugs perform at exposure levels well below TSC. That the drugs have higher efficacy in the blue curve than in the red curve at concentrations lower than the TSC value is translated into the blue TSC curve exhibiting larger curvature than the red.

Extensions and Future Work

Since we focused on introducing the TSC curve and providing several examples under zero-interaction hypotheses, a natural next step would be to explore how the TSC curve changes with the inclusion of (natural) synergy/antagonism terms. Synergy terms should increase the concavity of the TSC curve, while antagonism should have the opposite effect and make it more convex. Future work will also need to explore the validity and utility of the TSC approach, for example by using independent data sets.

CONCLUSIONS

The concept of a TSC curve for drug combinations in tumor growth models is derived and applied to an in vivo dataset. The TSC curve provides three important pieces of information. First, it gives minimal concentration pairs needed to achieve tumor shrinkage. Second, the shape of the TSC curve indicates how well the compounds work in combination, in the sense that a highly concave TSC curve indicates that it is possible to reduce the total drug exposure and still obtain tumor shrinkage. Third, the TSC curve can be used to optimize dosing regimens by maintaining concentrations above the curve as much and for as long as possible.

Appendices

APPENDIX 1

Consider the unperturbed tumor model incorporating natural cell death, with main compartment V ₁ and damage compartments V ₁, …, V _n , described by the following system of differential equations

$$ \begin{array}{l}\frac{d{V}_1}{dt}={k}_g{V}_1-{k}_k{V}_1\hfill \\ {}\frac{d{V}_2}{dt}={k}_k{V}_1-{k}_k{V}_2\hfill \\ {}\frac{d{V}_i}{dt}={k}_k{V}_{i-1}-{k}_k{V}_i,\kern0.5em 3\le i\le n\hfill \end{array} $$

(29)

This model can also be expressed in matrix form

$$ \frac{d\boldsymbol{v}}{dt}=A\boldsymbol{v} $$

(30)

where v = (V ₁, …, V _n ) is the n-dimensional vector of volumes and the n × n-matrix A is defined by

$$ \left(\begin{array}{lllll}{k}_g-{k}_k\hfill & 0\hfill & \cdots \hfill & 0\hfill & 0\hfill \\ {}{k}_k\hfill & -{k}_k\hfill & \cdots \hfill & 0\hfill & 0\hfill \\ {}\vdots \hfill & \hfill & \hfill & \hfill & \vdots \hfill \\ {}0\hfill & 0\hfill & \cdots \hfill & {k}_k\hfill & -{k}_k\hfill \end{array}\right) $$

(31)

Since A is a triangular matrix, its eigenvalues can be found on the diagonal

$$ {\lambda}_1={k}_g-{k}_k,\kern2.25em {\lambda}_2={\lambda}_3=\dots ={\lambda}_n = -{k}_k $$

(32)

The corresponding eigenvectors are given by

$$ {\boldsymbol{w}}_1=\left(1,\frac{k_k}{k_g},{\left(\frac{k_k}{k_g}\right)}^2,\dots, {\left(\frac{k_k}{k_g}\right)}^3\right),\kern0.28em {\boldsymbol{w}}_2=\left(0,\dots, 0,1\right) $$

(33)

The solution to Eq. 29 is then given by a linear combination of the n independent solutions

$$ {\boldsymbol{w}}_1{e}^{\lambda_1t},\kern0.28em {\boldsymbol{w}}_2{e}^{\lambda_2t} $$

(34)

and

$$ \begin{array}{l}{e}^{\lambda_2t}\left(t{\boldsymbol{w}}_2+{\boldsymbol{w}}_{2,2}\right),{e}^{\lambda_2t}\left(\frac{t^2}{2}{\boldsymbol{w}}_2+t{\boldsymbol{w}}_{2,2}+{\boldsymbol{w}}_{2,3}\right),\dots, \hfill \\ {}{e}^{\lambda_2t}\left(\frac{t^{n-1}}{\left(n-1\right)!}{\boldsymbol{w}}_2+\dots +{\boldsymbol{w}}_{2,n}\right)\hfill \end{array} $$

(35)

where the vectors w _2,k are so-called generalized eigenvectors of the matrix A, which for this particular problem can be shown to be

$$ {\boldsymbol{w}}_{2,2}=\left(0,\ 1,\ 0, \dots,\ 0\right),\ {\boldsymbol{w}}_{2,3}=\left(0,\ 0,\ 1,0, \dots,\ 0\right), \dots, {\boldsymbol{w}}_{2,n}=\left(0,\ 0,\ 0, \dots,\ 1\right) $$

(36)

As t grows large, ${e}^{\lambda_2t}={e}^{-{k}_kt}$ goes to zero. Therefore, for sufficiently large t, the solution to Eq. 29 is described only by the first solution

$$ \boldsymbol{v}(t)={\boldsymbol{w}}_1{e}^{\left({k}_g-{k}_k\right)t} $$

(37)

Hence, the tumor will grow exponentially with rate parameter λ ₁ and a constant proportion between the compartments governed by w ₁.

APPENDIX 2

It is in theory possible to generalize the TSC construction to treatments with three or more compounds by following the same steps. We know that a treatment with a single compound gives a point (the TSC value) in ℝ and a combination of two compounds gives a curve (the TSC curve) in ℝ². Likewise, a combination of three compounds will give a surface (the TSC surface) in ℝ³, and, in general, a combination of n compounds will give an (n − 1)-dimensional hypersurface in ℝⁿ.

To show one higher-dimensional example, imagine a treatment with n independent cytotoxic compounds with concentrations C ₁, …, C _n and each with a linear stimulatory function

$$ {S}_i\left({\mathrm{C}}_i\right)={a}_i{\mathrm{C}}_i,\kern1em 1\le i\le n $$

(38)

with different potency parameters a _i . The differential equation for the proliferating state V ₁ would in such a situation be

$$ \frac{d{V}_1}{dt}={k}_g{V}_1-{\displaystyle \sum_{i=1}^n}{k}_k{S}_i\left({C}_i\right){V}_1 $$

(39)

The condition for tumor stasis is therefore

$$ {k}_g-{\displaystyle \sum_{i=1}^n{k}_k{S}_i\left({C}_i\right)=0} $$

(40)

In particular, for n = 3 this gives an equation on the form

$$ {a}_1{\mathrm{C}}_1+{a}_2{\mathrm{C}}_2+{a}_3{\mathrm{C}}_3=\frac{k_g}{k_k} $$

(41)

which can be recognized as the equation of a plane in ℝ³.

APPENDIX 3

Using the parameter estimates in Table I, a VPC was performed for each of the four treatment arms as shown in Fig. 11. The figure indicates that all treatment arms were adequately predicted by the model.

Fig. 11

A VPC for each of the four treatment arms using the parameter estimates from Table I. The solid lines indicate the simulated 5th, 50th, and 95th percentiles. Colored dots represent different observed individuals in the combination arm

APPENDIX 4

To validate the assumption of independent drug action, a separate set of parameter estimates were obtained by omitting the combination arm (see Table III). Then, a VPC was performed by using these estimates to simulate n = 5000 individuals given the combination treatment and comparing the 5th and 95th quantiles to the actual observations. The resulting VPC is shown in Fig. 10. With approximately 10% of the observations outside the shaded region, the assumption of independent drug action cannot be rejected.

APPENDIX 5

To study the certainty of the weak synergy between cetuximab and cisplatin, a Monte Carlo simulation was performed to construct TSC curves consistent with the relative standard errors reported for the parameters in Table I. To evaluate whether such a curve was sufficiently curved, the ratio between the areas under the TSC curve and the reference line was computed, yielding values ranging from zero to one. If the ratio was below 0.9, the TSC curve was regarded as sufficiently curved to indicate (at least) weak synergy. A total of 99.4% of the simulated TSC curves showed weak synergy, indicating that the claim of weak synergy is well-founded.