A Flexible Nonlinear Feedback System That Captures Diverse Patterns of Adaptation and Rebound

Abstract

An important approach to modeling tolerance and adaptation employs feedback mechanisms in which the response to the drug generates a counter-regulating action which affects the response. In this paper we analyze a family of nonlinear feedback models which has recently proved effective in modeling tolerance phenomena such as have been observed with SSRI’s. We use dynamical systems methods to exhibit typical properties of the response-time course of these nonlinear models, such as overshoot and rebound, establish quantitive bounds and explore how these properties depend on the system and drug parameters. Our analysis is anchored in three specific in vivo data sets which involve different levels of pharmacokinetic complexity. Initial estimates for system (k _in, k _out, k _tol ) and drug (EC ₅₀/IC ₅₀, E _max/I _max, n ) parameters are obtained on the basis of specific properties of the response-time course, identified in the context of exploratory (graphical) data analysis. Our analysis and the application of its results to the three concrete examples demonstrates the flexibility and potential of this family of feedback models.

INTRODUCTION

Clinical tolerance may be associated with the effects of many drugs especially opioids, various central nervous stimulants, and organic nitrates (cf. Goodman and Gilman 1996 (1)). Acute tolerance is also seen in an experimental setting in laboratory animals. Factors like dose rates and frequencies, and diurnal oscillations (Sällström et al. 2005 (2) and Visser et al. 2006 (3)) often manifest themselves as tolerance to the pharmacological activity of the test compound. In our own experience we then see how the rate and extent of an intravenous infusion may impact the onset, intensity and duration of e.g., a cardiovascular response. Therefore, we believe that a parametric characterization of the rate and extent of tolerance development has a practical bearing on design and analyses of pharmacodynamic studies.

Over the years there have been several different approaches to modeling tolerance. We mention time-dependent attenuation of drug constants (cf. Colburn et al. 1994 (4)), effect compartment models (Porchet et al. 1988 (5) and Ouellet and Pollack 1997 (6)), systems analysis (Urquhart and Li 1968 (7) and 1969 (8), Veng-Pedersen et al. 1993 (9)), pool/precursor models (Licko and Ekblad 1992 (10), Bauer and Fung 1994 (11) and Sharma et al. 1998 (12), and feedback turnover models (Ackerman et al. 1964 (13), Resigno and Segre 1961, 1966 (14), Holford et al. 1990 (15), Wakelkamp et al. 1996 (16), Agersø et al. 2001 (17), Zuideveld et al. 2001 (18), Lima et al. 2004 (19), Sällström et al. 2005 (2), Visser et al. 2006 (3), and de Winter et al. 2006 (20)).

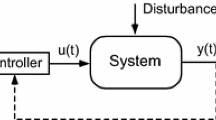
In the present paper we focus on the latter and discuss in detail a family of nonlinear feedback models involving the response R, as well as a Moderator M. One such model has recently been successfully used to model tolerance phenomena in SSRI’s (Bundgaard 2006 (21)). These models are based on the classic turnover Indirect Response models. However, tolerance is modeled through the intervention of a moderator, which acts to diminish the response created by the drug and which is generated by the response (cf. Gabrielsson and Peletier 2007 (22)). The structure of one such model system is sketched in Fig. 1.

Fig. 1

Sketch of the basic feedback model and a typical response versus time course. The response R is governed by the zero-order turnover rate k _in and the first-order fractional turnover rate k _out, and then indirectly also controlled by a separate moderator M. The turnover of the moderator is governed by a single first-order rate constant k _tol. The build-up of the moderator is k _tol·R and loss is k _tol·M. The moderator acts via inhibition of k _in on the production of response (as in the scheme above) or via stimulation of k _out (negative feedback). The solid lines denote flows and the dashed lines denote control action. In the response versus time course we note substantial overshoot and rebound

The class of feedback models we discuss here is nonlinear in that an increase in M will reduce the production of R by a factor 1/M. Thus, the dynamic properties of these models, such as overshoot, rebound and presence of oscillatory behavior, depend on the state of the system, and so change when the system is taken by the drug from the baseline state R ₀ to a higher or a lower pharmacodynamic steady state R _ss. Specifically, this class of models is designed to have the following properties:

• Rapid drug induced changes in the pharmacodynamic steady state yield pronounced overshoot and rebound.

• Inhibition of the loss term which raises the steady state R _ss, causes an overshoot which is larger than the rebound upon the return to the baseline after washout.

• Stimulation of the loss term which lowers the steady state R _ss, causes an overshoot which is smaller than the rebound upon the return to the baseline after washout.

Similar behavior is found when the production term is stimulated or inhibited.

It is the characteristic shape of these response curves: a large overshoot with respect to the new pharmacodynamic steady state when R _ss > R ₀ and a large rebound upon return to the baseline when R _ss < R ₀, and the difference in magnitude of these two, which we want to study in this paper. An important factor in determining the size of overshoot or rebound is the rate of input or removal of the drug in relation to the intrinsic rates of the system. We show how a rapid input or removal tends to cause a large overshoot or rebound, whilst a gradual input or removal tends to suppress overshoot or rebound.

We demonstrate the effectiveness of this class of models by fitting system and drug parameters to data sets obtained for three in vivo experiments (see also Fig. 2).

• (a) A data set displaying a pronounced rebound effect of the response when the exposure to the test compound is abruptly terminated. The pharmacokinetics of this test compound has a 1–3 min half-life (Example I).

• (b) A pharmacodynamic data set derived from constant rate intravenous infusion of an experimental compound displaying both tolerance, drift in the baseline, and no rebound upon return towards baseline (Example II).

• (c) A recently applied in vivo model for serotonin (5-HT) turnover in rat brains during intravenous administration of selective serotonin reuptake inhibitors (SSRI’s) (Bundgaard et al. (21)) (Example III).

Fig. 2

Response versus time courses of the three examples that anchor the analysis. Example I is derived from a compound A that inhibits the production of response of which data were gathered after a regimen of multiple intravenous infusions. Example II represents a test compound X acting via inhibition of k _out after a short constant rate infusion of X followed by washout. Example III represents our extended model fitted to the Bundgaard et. al. (21) data set, where escitalopram acts via inhibition of the loss of R and the moderator compartment is split into two transduction compartments

It will prove very illuminating to study the evolution of the turnover feedback sytem in State Space, which for these models is two-dimensional, the dimensions being the response R and the moderator M. Viewing the evolution of the system as an Orbit in the (R, M)-plane gives valuable insight into the properties of the response versus time curve. Also, we shall see that the structure of the state space immediately reveals some of these properties, such as the tendency of the system towards overshoot when the response jumps to a higher value, whether at onset, when R _ss > R ₀ or at washout when R _ss < R ₀.

The plan of the paper is the following. We begin with an analysis of the main class of feedback models and exhibit a series of characteristic properties such as bounds for R _max, for overshoot and for rebound, and analyze how these characteristic properties depend on the different pharmacodynamic rate constants in the model (system properties). Important mathematical ingredients here will be (i) comparison with simpler systems and (ii) asymptotic methods. Then we use these results to discuss successively the data of the three examples exhibited in Fig. 2. We also apply them to the data of Example II to demonstrate how the pharmacodynamic and kinetic constants in the model can be estimated from the response versus time course. In order to gain a deeper understanding of the system, we then return to the feedback model and present a geometric analysis of the dynamics in state space. We conclude with a discussion of the main results we obtain and the methods we use.

METHODS

In this section we introduce the class of feedback systems and derive analytically a series of characteristic properties of its response versus time curves. In particular we discuss the propensity of these models to show overshoot and rebound. We first give a detailed description of the class of models. Then we analyze the onset and termination of a constant rate infusion with fast kinetics.

Introduction of the Models

We focus on the class of feedback systems sketched in Fig. 1, i.e., systems in which the response generates a moderator, which in turn inhibits the production of the response. They are based on the following system of two coupled differential equations:

$$ \begin{array}{*{20}c} {{\frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {M} - k_{{out}} \cdot R}} \\ {{\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}}} \\ \end{array} $$

(1)

Thus, the production of the response R is here inversely proportional to the strength M of the moderator. In addition, production of response tends to infinity when M drops down to zero and tends to zero when M tends to infinity.

As in the classical four indirect response models (23), the drug may have an impact on the system through either the production term or through the loss term, i.e.,

$$\begin{array}{*{20}c} {{\frac{{dR}}{{dt}} = k_{{in}} \cdot \frac{1}{M} \cdot H_{1} {\left( C \right)} - k_{{out}} \cdot H_{2} {\left( C \right)} \cdot R}} \\ {{\frac{{dM}}{{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}}} \\ \end{array} $$

(2)

where C denotes the plasma concentration of the drug and H ₁(C) and H ₂(C) are drug mechanism functions. Also, the drug may act in fixing a setpoint, as in Zuideveld et al. (18). Since the effect of the drug may be to inhibit or to stimulate the response, H ₁(C) and H ₂(C) may be given by either a stimulatory drug mechanism function such as,

$$S{\left( C \right)} = 1 + S_{{\max }} \frac{{C^{n} }}{{SC^{n}_{{50}} + C^{n} }}$$

(3)

or by an inhibitory drug mechanism function such as,

$$I{\left( C \right)} = 1 - I_{{\max }} \frac{{C^{n} }}{{IC^{n}_{{50}} + C^{n} }}$$

(4)

Thus, we end up with four models.

In Bundgaard et al. (21) and in the study of Compound X (cf. Example II) this model was used to fit the data while the drug was assumed to inhibit the loss term (H ₁ = 1 and H ₂ = I). And in Gabrielsson and Peletier (22) this model was fitted to the data from Urquhart and Li (7), also assuming that loss was inhibited by the drug (H ₁ = 1 and H ₂ = I).

If no drug is present, i.e., when C(t) ≡ 0, then, since H _i (0) = 1 for i = 1, 2, the baseline values R ₀ and M ₀ of, respectively, R and M are given by

$$R_{0} = M_{0} = {\sqrt {\frac{{k_{{in}} }}{{k_{{out}} }}} }$$

(5)

If C(t) ≡ C _ss, then the pharmacodynamic steady state (R _ss, M _ss) of the system 2 is given by

$$R_{{ss}} = M_{{ss}} = R_{0} {\sqrt {\frac{{H_{1} {\left( {C_{{ss}} } \right)}}}{{H_{2} {\left( {C_{{ss}} } \right)}}}} }$$

(6)

It can be shown that the pharmacodynamic steady state is a global attractor (22), i.e., whatever the initial values of the response and the moderator, response and moderator will eventually converge towards the pharmacodynamic steady state i.e.,

$$R{\left( t \right)} \to R_{{ss}} \quad and\quad M{\left( t \right)} \to M_{{ss}} \quad as\quad t \to \infty $$

(7)

The main capability of this family of feedback models is their ability to model substantial overshoot and rebound. In addition, they possess the following general properties and features:

• (a) Overshoot and rebound are biased towards larger response values in that when a drug raises the pharmacodynamic steady state response R _ss, then the overshoot tends to be larger than when the drug depresses the steady state response R _ss. Similarly, when a return to baseline causes the steady state response R _ss to rise, then the overshoot will be larger than when it drops. We shall see that this property can be traced back to the nonlinearity of the system, i.e., to the fact that the moderator acts nonlinearly on the production term. We shall return to this important issue when we give a geometric analysis of the system at the end of the paper.

• (b) It is possible to obtain precise bounds and estimates for overshoot and rebound. In particular the accuracy of these bounds increases as the dimensionless ratio κ=k _tol/k _out tends to zero.

  Let the departure of the response from the baseline value R ₀ reach its maximum value R _max at T _max, i.e., R _max = R(T _max). Then we show that

• (c) R _max is either a decreasing or an increasing function of κ. Specifically:

  • If R _max > R ₀ then R _max decreases as κ increases.

  • If R _max < R ₀ then R _max increases as κ increases.

Since the main characteristics of these four feedback models are similar, we focus here on just one of them in detail, the one in which the loss term is inhibited, i.e., H ₁(C) = 1 and H ₂(C) = I(C), where I(C) is given in Eq. 4. The system 2 then becomes

$$ \begin{aligned} & \frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {M} - k_{{out}} \cdot R \cdot I{\left( C \right)} \\ & \frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)} \\ \end{aligned} $$

(8)

and ${\text{R}}_{{{\text{ss}}}} = M_{{ss}} = {R_{0} } \mathord{\left/ {\vphantom {{R_{0} } {{\sqrt {l{\left( {C_{{ss}} } \right)}} }}}} \right. \kern-\nulldelimiterspace} {{\sqrt {l{\left( {C_{{ss}} } \right)}} }}$ (see Eq. 6).

In this section, we wish to bring out the characteristic properties of the dynamics of the system 8. We therefore assume that the system is subjected to a very simple drug regimen: we assume that at t = 0 a constant rate infusion is initiated and that it is terminated at t = t ₁. We also assume that the pharmacokinetic time scale is short. This will then result in a plasma concentration C(t) given by a step-function:

$$ C{\left( t \right)} = C_{{ss}} {\left\{ {{\rm H}eav{\left( t \right)} - {\rm H}eav{\left( {t - t_{1} } \right)}} \right\}},\quad t_{1} > 0,\quad C_{{ss}} > 0 $$

(9)

where Heav(t) denotes the Heaviside function (Heav(t) =1 if t > 0 and Heav(t) = 0 if t ≤ 0). With such rapid pharmacokinetics, the turnover of the pharmacodynamical system becomes the rate limiting step. In contrast, slow pharmacokinetics may confound the true system (response) behavior in that turnover of the drug now becomes the rate limiting step.

In the sections which deal with the three examples, the drug regimen and the pharmacokinetics are much more complex, and we shall see how the properties found for the simple plasma concentration profile given by Eq. 9 can still be identified and help in fitting the model to the data.

In the following two subsections we study the impact of the above drug regimen and discuss in succession: (i) onset of a constant rate infusion, assuming that t ₁ = ∞, and (ii) washout at t ₁ < ∞.

Onset of Test Compound

We assume that initially, the system is at baseline, i.e., R(0) = R ₀ and M(0) = M ₀, and we follow the response R and the moderator M as they evolve with time.

In order to demonstrate the effect of feedback we follow the response versus time profile as k _tol increases from k _tol = 0 (no feedback) to values of k _tol which are large compared to k _out (strong feedback).

If k _tol = 0, the second equation of the system 8 implies that M(t) ≡ M ₀, and hence the first equation of the system 8 becomes

$$ \frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {{M_{0} }} - k_{{out}} \cdot R \cdot I{\left( C \right)}\quad for\quad t > 0 $$

(10)

This is the well-known Indirect Response Model; its solution, starting from the baseline R ₀, which we denote by $\overline{R} {\left( t \right)}$, can readily be found to be

$$ \overline{R} {\left( t \right)} = \frac{{R_{0} }} {{I{\left( {C_{{ss}} } \right)}}} \cdot {\left\{ {{\text{ }}1 - {\left[ {1 - I{\left( {C_{{ss}} } \right)}} \right]} \cdot e^{{ - k_{{out}} I{\left( {C_{{ss}} } \right)}t}} } \right\}} $$

(11)

Plainly

$$ \overline{R} {\left( t \right)} \to R_{{top}} {\mathop = \limits^{def} }\frac{{R_{0} }} {{I{\left( {C_{{ss}} } \right)}}}\quad \quad {\text{as}}\quad {\text{t}} \to \infty $$

(12)

and $\overline{R} {\left( t \right)}$is an increasing function, so that there is no tolerance. It is shown as the top curve in Fig. 3.

Fig. 3

Simulations of response and moderator versus time for onset of a constant long-lasting infusion (t ₁ = ∞) for k _tol = 0, 0.001, 0.005, 0.01. The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. Solid lines represent the response-time courses and the dashed lines the moderator-time courses

If k _tol > 0, however small, then by Eq. 7,

$$ R{\left( t \right)} \to R_{{ss}} = {R_{o} } \mathord{\left/ {\vphantom {{R_{o} } {{\sqrt {I{\left( {C_{{ss}} } \right)}} }}}} \right. \kern-\nulldelimiterspace} {{\sqrt {I{\left( {C_{{ss}} } \right)}} }}\quad \quad as\quad t \to \infty $$

Since, by a well-known property of ordinary differential equations (24), for any given t > 0

$$ {\left| {R{\left( t \right)} - \overline{R} {\left( t \right)}} \right|} \to 0\quad \quad as\quad k_{{tol}} \to \infty$$

it follows that R _max → R _top as k _tol  → 0. Thus, for small values of k _tol, we have

$$\ \left. {\Delta R} \right|_{{overshoot}} {\mathop = \limits^{def} }R_{{\max }} - R_{{ss}} \approx R_{{top}} - R_{{ss}} = \frac{{R_{0} }} {{I(C_{{ss}} )}}{\left[ {1 - {\sqrt {I{\left( {C_{{ss}} } \right)}} }} \right]} $$

(13)

and the relative overshoot is approximately given by

$$ \frac{{R_{{top}} - R_{0} }} {{R_{{ss}} - R_{0} }} = 1 + \frac{1} {{{\sqrt {I{\left( {C_{{ss}} } \right)}} }}} $$

(14)

As k _tol increases, one can show that R _max decreases (22), and hence, since R _ss remains the same, the overshoot also decreases and eventually disappears for large values of k _tol. In Figs. 3 and 4 we show response and moderator versus time graphs for different values of k _tol whilst k _out remains fixed.

Fig. 4

Simulations of response and moderator versus time for onset of a constant long-lasting infusion (t ₁ = ∞) for k _tol = 0.1, 0.2, 0.5, 2.0 (right). The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. Solid lines represent the response-time courses and the dashed lines the moderator-time courses

We study two extreme cases: (i) k _tol is small and (ii) k _tol is large.

• Case (i) k _tol « k _out : In this case the moderator changes slowly compared to the response. Thus for an initial period M(t) ≈ M ₀ and hence $R{\left( t \right)} \approx \overline{R} {\left( t \right)}$. This means that the response quickly rises to a level that is almost equal to R _top, which is defined as the root of the equation

  $$ k_{{in}} \cdot \frac{1} {{M_{0} }} - k_{{out}} \cdot R \cdot I{\left( {C_{{ss}} } \right)} = 0 $$

  Then, as time progresses, M(t) increases because R > M. However, because of the relatively fast dynamics of the response, any departures from the equality

  $$ k_{{in}} \cdot \frac{1} {{M{\left( t \right)}}} - k_{{out}} \cdot R{\left( t \right)} \cdot I{\left( {C_{{ss}} } \right)} = 0 $$

  (15)

  are quickly corrected. Thus, we may assume that Eq. 15 holds approximately once R has reached its maximum value R _max at time T _max. When we use this relation to eliminate R from the equation for M in Eq. 8 we obtain

  $$ \frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {\frac{{R^{2}_{0} }} {{I{\left( {C_{{ss}} } \right)}}} \cdot \frac{1} {M} - M} \right)} $$

  (16)

  Since the time of maximal response T _max is small and k _tol is small, it follows that approximately M(T _max) = M ₀. The solution of equation Eq. 16 with this value at t = T _max is given by

  $$ M{\left( t \right)} = M_{{ss}} \cdot {\left\{ {1 - {\left[ {1 - I{\left( {C_{{ss}} } \right)}} \right]} \cdot e^{{ - 2k_{{tol}} {\left( {t - T_{{\max }} } \right)}}} } \right\}}^{{1/2}} \quad \quad t > T_{{\max }} $$

  (17)

  so that we obtain for the response,

  $$ R{\left( t \right)} = R_{{ss}} \cdot {\left\{ {1 - {\left[ {1 - I{\left( {C_{{ss}} } \right)}} \right]} \cdot e^{{ - 2k_{{tol}} {\left( {t - T_{{\max }} } \right)}}} } \right\}}^{{ - 1/2}} \quad \quad t > T_{{\max }} $$

  (18)

  Therefore,

  $$ {\left| {R{\left( t \right)} - R_{{ss}} } \right|} = O{\left( {e^{{ - 2k_{{tol}} t}} } \right)}\quad \quad as\quad \quad t \to \infty $$

  i.e., in this extreme case, t _1/2 = ln 2/(2 k _tol). Thus, as k _tol  → 0 it takes longer for the response to settle on its final value R _ss. In Fig. 3 this gradual descent is clearly manifest.

• Case (ii) k _tol » k _out : Now, the dynamics of the moderator is relatively fast and any departures from the equality

  $$ k_{{tol}} {\left\{ {R{\left( t \right)} - M{\left( t \right)}} \right\}} = 0 $$

  (19)

  have soon disappeared. Since R(0) = M(0), we may now assume that Eq. 19 holds approximately for all t  ≥ 0. Using Eq. 19 to eliminate M, we find that the equation for R becomes, approximately,

  $$ \frac{{dR}} {{dt}} = k_{{in}} \frac{1} {R} - k_{{out}} R \cdot I{\left( {C_{{ss}} } \right)} = k_{{out}} I{\left( {C_{{ss}} } \right)} \cdot {\left( {\frac{{R^{2}_{0} }} {{I{\left( {C_{{ss}} } \right)}}} \cdot \frac{1} {R} - R} \right)} $$

  (20)

  This equation is of the same form as Eq. 16; its solution, starting from the baseline R ₀, is given by

  $$ R{\left( t \right)} = R_{{ss}} \cdot {\left\{ {1 - {\left[ {1 - I{\left( {C_{{ss}} } \right)}} \right]} \cdot e^{{ - 2k_{{out}} I{\left( {C_{{ss}} } \right)}t}} } \right\}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} $$

  (21)

  Note that R(t) is now a strictly increasing function. Hence, in the limit as k _tol  →  ∞, there is no tolerance. We see this behavior demonstrated in Fig. 4.

  We also see that

  $$ {\left| {R{\left( t \right)} - R_{{ss}} } \right|} = O{\left( {e^{{ - 2k_{{out}} I{\left( {C_{{ss}} } \right)}t}} } \right)}\quad \quad as\quad t \to \infty $$

  i.e., in this extreme case, t _1/2 = ln 2/(2 k _out I(C _ss )).

  It is interesting to note that since R(t) - M(t) → 0 as k _tol  →  ∞, the graph of M(t) is also increasing in the limit as k _tol  →  ∞. However, we see clearly in Fig. 4 that M overshoots its limiting value M _ss for k _tol = 0.1. In Gabrielsson and Peletier (22) it is shown that there is a range of values of k _tol for which R(t) and M(t) tend to, respectively, R _ss and M _ss through a damped oscillation, whilst outside this range, the approach to R _ss and M _ss is monotone.

Washout of Test Compound

We assume that just prior to washout at t = t ₁, the system is in the pharmacodynamic steady state, i.e., R(t ₁) = R _ss and M(t ₁) = M _ss. If k _tol = 0, then M(t) = M _ss for t > t ₁, and the equation for R becomes

$$ \frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {{M_{{ss}} }} - k_{{out}} \cdot R\quad for\quad t > t_{1} $$

(22)

The solution of this equation, which starts at time t ₁ at R _ss is given by

$$\underline{R} {\left( t \right)} = R_{0} \cdot {\sqrt {I{\left( {C_{{ss}} } \right)}} }{\left\{ {1 + {\left[ {I^{{ - 1}} {\left( {C_{{ss}} } \right)} - 1} \right]} \cdot e^{{ - k_{{tol}} {\left( {t - t_{1} } \right)}}} } \right\}}$$

(23)

We see that R (t) is decreasing and that

$$ \underline{R} {\left( t \right)} \to R_{{bottom}} {\mathop = \limits^{def} }R_{0} {\sqrt {I{\left( {C_{{ss}} } \right)}} }\quad \quad as\quad t \to \infty $$

(24)

In Fig. 5 we show two sets of response and moderator versus time curves of the same system as shown in Figs. 3 and 4 but now with rapid washout after t ₁ = 500 min, respectively 100 min.

Fig. 5

Simulations of response and moderator versus time during constant infusion, and subsequent washout for k _tol = 0.001, 0.005, 0.01 (a) and for k _tol = 0.03, 0.1, 0.3, 1.0 (b). The other parameter values are k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀

If k _tol > 0 one can show that the state returns to baseline (22) i.e., in particular,

$$ R{\left( t \right)} \to R_{0} \quad \quad as\quad t \to \infty $$

(25)

Thus, writing R _min = min{R(t): t > t ₁}, we obtain – as with onset – that R _min → R _bottom as k _tol  → 0, so that for small k _tol,

$$\left. {\Delta R} \right|_{{rebound}} = R_{0} - R_{{\min }} \approx R_{0} - R_{{bottom}} = R_{0} {\left[ {1 - {\sqrt {I{\left( {C_{{ss}} } \right)}} }} \right]} $$

(26)

It follows from Eqs. 13 and 26 that

$$ \left. {\Delta R} \right|_{{overshoot}} \approx \frac{1} {{I{\left( {C_{{ss}} } \right)}}}\left. {\Delta R} \right|_{{rebound}} $$

(27)

This equality implies that when k _tol is small compared to k _out, then overshoot is much larger than rebound.

As with the overshoot at onset, we find that at washout, rebound diminishes monotonically as κ = k _tol/k _out increases and eventually disappears when κ is large enough.

Conclusion

We have demonstrated the following characteristic properties of the main model, Eq. 8, in which the loss term is inhibited:

• 1. Uniform upper and lower bounds for the response: If k _tol > 0, then

  $$\begin{array}{*{20}l} {{R_{0} < R{\left( t \right)} < R_{{top}} \quad \quad after{\text{ }}onset} \hfill} \\ {{R_{{bottom}} < R{\left( t \right)} < R_{{ss}} \quad after{\text{ }}washout} \hfill} \\ \end{array} $$

  (28)

• 2. Bounds for overshoot and rebound of the response: If k _tol > 0, then

  $$ \begin{aligned} & \left. {\Delta R} \right|_{{overshoot}} < \frac{{R_{0} }} {{I(C_{{ss}} )}}{\left[ {1 - {\sqrt {I{\left( {C_{{ss}} } \right)}} }} \right]}\quad and\quad \\ & \left. {\Delta R} \right|_{{rebound}} < R_{0} {\left[ {1 - {\sqrt {I{\left( {C_{{ss}} } \right)}} }} \right]} \\ \end{aligned} $$

  (29)

  so that for κ small,

  $$ \left. {\Delta R} \right|_{{overshoot}} \approx \frac{1} {{I{\left( {C_{{ss}} } \right)}}}\left. { \cdot \Delta R} \right|_{{rebound}} $$

  (30)

• 3. Pharmacodynamic steady state and baseline are “global attractors”: If k _tol > 0 and the infusion is constant for all time, then R(t) → R _ss as t  →  ∞. Similarly, after washout when C = 0 for all time, then R(t) → R ₀ as t  →  ∞.

• 4. Influence of the ratio κ = k _tol/k _out : We have exhibited the pivotal importance of the ratio κ of the rate constants of the two equations: k _tol and k _out. For instance,

  • (a) Overshoot and rebound are greatest when κ is small.

  • (b) As κ increases, both overshoot and rebound become smaller and eventually disappear.

For further properties we refer to Gabrielsson and Peletier (22).

GENERALIZATIONS

The analysis we have presented for the feedback system 8 in which the loss term is inhibited by the drug, and the results we have obtained for that system, easily carry over to the other three types of systems defined in Eq. 2, i.e., the systems in which the loss term is stimulated (H ₁ = 1 and H ₂ = S) or the production term is either stimulated (H ₁ = S and H ₂ = 1) or inhibited (H ₁ = I and H ₂ = 1).

For instance, as another example, if the production term is stimulated, we find that if C = C _ss, then

$$ R_{{ss}} = R_{0} {\sqrt {S{\left( {C_{{ss}} } \right)}} },\quad R_{{top}} = R_{0} S{\left( {C_{{ss}} } \right)}\quad and\quad R_{{bottom}} = \frac{{R_{0} }} {{{\sqrt {S{\left( {C_{{ss}} } \right)}} }}} $$

and

$$ \begin{aligned} & \left. {\Delta R} \right|_{{overshoot}} < R_{0} {\left[ {S{\left( {C_{{ss}} } \right)} - {\sqrt {S{\left( {C_{{ss}} } \right)}} }} \right]} \\ & \left. {\Delta R} \right|_{{rebound}} < R_{0} {\left[ {1 - \frac{1} {{{\sqrt {S{\left( {C_{{ss}} } \right)}} }}}} \right]} \\ \end{aligned} $$

(31)

so that for small values of κ

$$ \left. {\Delta R} \right|_{{overshoot}} \approx S{\left( {C_{{ss}} } \right)} \cdot \Delta \left. R \right|_{{rebound}} $$

(32)

Since S(C _ss) > 1 we find again that for small values of κ, overshoot is larger than rebound.

A nonlinear feedback system that is closely related to the one we have studied above is

$$\begin{array}{*{20}c} {\frac{{dR}}{{dt}} = k_{{in}} - k_{{out}} \cdot R \cdot M} \\ {\frac{{dM}}{{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array}$$

(33)

i.e., the system in which the moderator does not inhibit the production term but instead stimulates the loss term if the drug causes the response rise. When we incorporate the drug mechanism functions H ₁(C) and H ₂(C) as in Eq. 2, we see that the pharmacodynamic steady state is also given by Eq. 6. An analysis along the lines of the one given above now yields results which are very similar, and in some instances even identical, to results we have obtained for the systems 1 and 2. This applies in particular to such results as large time behavior, global bounds, and a bias towards overshoot when R _ss > R ₀ and towards rebound when R _ss < R ₀.

Many of the properties of the response versus time curves which we have sketched above can be explained in a geometrical way by viewing the state (R,M) of the system as moving along a trajectory in state space. We present such an explanation in a special section towards the end of the paper.

EXAMPLE I: INHIBITION OF PRODUCTION OF RESPONSE

Example I is based on an experimental compound A with fast plasma kinetics (t _1/2 = 1–2 min and an elimination rate constant k = 0.22 min⁻¹ ) and a pharmacological response with high k _out (t _1/2 = 3 min) that also displays tolerance and rebound. The data are shown in Fig. 6.

Fig. 6

Response versus time data after a multiple intravenous infusion regimen of compound A, followed by washout. Note the substantial rebound effect shortly after the infusion has been terminated at about 200 min. The infusion pump stopped for a brief period at about 90 min until the next syringe had been loaded. Then there is a rapid return of response towards the baseline and past the baseline. The six gray bars represent six different infusion rates. Response denotes concentration of fatty acids in plasma

Typical features of this data set are (i) overshoot at every sudden increase of the plasma concentration and (ii) a seizable rebound at washout. The dynamics of compound A was characterized by a nonlinear feedback system of the type introduced in Eq. 1, in which the production term is mechanistically inhibited by means of a nonlinear drug mechanism function I(C) of the form given in Eq. 4, however assuming at the outset that I _max = 1 :

$${\matrix{ {{{dR} \over {dt}} = k_{{in}} \cdot {1 \over M} \cdot I{\left( C \right)} - k_{{out}} \cdot R} \cr {{{dM} \over {dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \cr } }$$

(34)

Fitting the model to the data set yields the values given in Table I in which the first order rate constants k _out and k _tol are measured in min⁻¹. In Table I, R ₀ denotes the baseline of the response, k _in = R ₀ ² k _out, and κ = k _tol/k _out. The model prediction for these values is also shown in Fig. 6 (solid line).

Table I Parameter estimates for Example I

The exact start and stop of drug input (infusions) and the exact sampling times of the pharmacological response are particularly important for this system with rapid turnover of both test compound and response. Since the half life of kinetics falls in the range of 1–2 min and half life of response is about 1 min, a 15–30 sec error in sampling times at pivotal occasions will not only impact parameter estimates (accuracy) but also their precision. We will expand on this particular system (response) and test compound in a subsequent series of papers.

EXAMPLE II: INHIBITION OF LOSS OR STIMULATION OF PRODUCTION OF RESPONSE

Example II is based on a test compound X given as a 10 min constant rate intravenous infusion. It displays two-compartment disposition kinetics with a terminal half life of 17 min. Disposition of the test compound is relatively slow in comparison to the system (t _1/2kout = 2–4 min) and becomes the rate limiting step. The data are shown in Fig. 7.

Fig. 7

Response versus time courses of Example II which represents test compound X acting via inhibition of k _out after a 10 min constant rate intravenous infusion of X followed by washout. Note the drift of the baseline over the 260 min observation period. Response denotes EEG effects in experimental animals

Typical features of this data set are (i) a strong overshoot at onset of the infusion and (ii) no rebound upon washout and (iii) a substantial drift in the baseline response. The slow washout confounds rebound (22), as is seen from the simulation shown in Fig. 8 of the same system 35 but with rapid onset at t = 50 min and washout at t = 200 min, and no baseline drift.

Fig. 8

Simulation of response versus time course based on the final parameter estimates in Table 2 (model A) where the exposure profile was given as a square-wave (gray horizontal bar) and no baseline drift was assumed to occur. R ₀, R _max and R _ss denote the baseline value, peak-response in overshoot and steady-state response, respectively

The drug mechanism of the test compound X in this example acts through inhibition of the k _out parameter (I(C) × k _out × R ), as shown in Eq. 35:

$$ {\left( A \right)}\left\{ {\begin{array}{*{20}c} {\frac{{dR}} {{dt}} = k_{{in}} \frac{1} {M} - k_{{out}} \cdot R \cdot I{\left( C \right)}} \\ {\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array} } \right. $$

(35)

Interestingly, a stimulatory function on the turnover rate (S(C) × k _in ) as shown in Eq. 36:

$$ {\left( B \right)}\left\{ {\begin{array}{*{20}c} {\frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {M} \cdot S{\left( C \right)} - k_{{out}} \cdot R} \\ {\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array} } \right. $$

(36)

gave as good a fit as the mechanistically correct inhibition of loss, including high parameter precision in all parameters (Table II). The functions I(C) and S(C) in the systems (A) and (B) are given by, respectively, Eqs. 4 and 3. In both models, baseline drift was described by the linear function

$$ R_{0} {\left( t \right)} = R_{0} {\left( t \right)}{\left( {1 + \alpha t} \right)} $$

(37)

Assuming that k _out remains constant, this means that k _in(t) = k _in(0)(1 + α t)².

Table II Parameter estimates for models (A) and (B)

This suggests that more doses and eventually an extended input (infusion) period are necessary challenges for model discrimination. It was necessary to model the drift in baseline as a linear function, as part of the full model. We would not advocate modeling baseline subtracted response data because the meaning of different parameters would become less transparent.

In future experiments we would suggest a separate control group that captures the unperturbed baseline drift.

An ordinary turnover model (by inhibition of loss), or a pool/precursor model (Stimulation of the loss from the pool compartment) did not adequately capture the upswing, overshoot, roof and decline to the baseline of this data set. For the turnover model, this can be explained by analytical arguments (cf. (25)).

EXAMPLE III: INHIBITION OF LOSS OF RESPONSE

Example III is based on data obtained by Bundgaard et al. (21). Three intravenous infusions lasting for 60 min were given to three different groups of rats. The response corresponds to the change in 5-HT in rat hippocampal brain regions (Fig. 9).

Fig. 9

Response versus time (left) and response versus concentration (right) courses of Example III which represent escitalopram acting via inhibition of k _out after a 60 min constant rate intravenous infusion followed by washout. Symbols represent experimental data and solid lines model fits. The three 60 min constant rate intravenous infusions were 2.5 (filled circles), 5 (filled squares) and 10 (open squares) mg/kg. The small arrows on the right hand plot show the time order of the data. Note how the middle and upper concentration-response curves cut through the lower and middle concentration-response curves, respectively

In a previous study (22) this process was modeled by means of a generalization of the nonlinear feedback system introduced in the “Introduction” section, which involves a sequence of two moderators, M ₁ and M ₂, as shown in Fig. 10.

Fig. 10

Sketch of the extended feedback model involving two moderators M ₁ and M ₂ in sequence. The solid lines denote flows and the dashed lines denote control action

The feedback system described in Fig. 10 leads to the following system of three coupled differential equations:

$$ \begin{aligned} & \frac{{dR}} {{dt}} = \frac{{k_{{in}} }} {{M_{2} }} - k_{{out}} \cdot R \cdot I{\left( C \right)} \\ & \frac{{dM_{1} }} {{dt}} = k_{{tol}} \cdot {\left( {R - M_{1} } \right)} \\ & \frac{{dM_{2} }} {{dt}} = k_{{tol}} \cdot {\left( {M_{1} - M_{2} } \right)} \\ \end{aligned} $$

(38)

Fitting this model to the data we obtain the parameter values listed in Table III:

Table III Parameter estimates for the model Eq. 38

Table IV Critical response levels in Examples I–III

By extending the original Bundgaard et al. (21) analysis to also include a transduction step for the moderator compartment, the parameter precision of k _tol was improved. Increasing k _tol also resulted in a shortening of its corresponding half-life (ln 2/k _tol). All other parameters and their precision remained the same.

This demonstrated the flexibility of this feedback turnover model without increasing the number of model parameters. We will expand on this topic in a subsequent series of papers.

It is not surprising that the model predicts an uptake half-life (t _1/2kout ) of about 3–4 min in light of the rate limiting distribution across the dialysis probe membrane. The true uptake half-life into pre-synaptic vesicles does probably lie in the microsecond to second range, but the equilibrium process across the dialysis probe confounds the more rapid reuptake process.

INITIAL PARAMETER ESTIMATES

To successfully model biological systems, one also needs to be able to derive the initial parameter estimates graphically, directly from the experimental data, and not only via indirect estimation during regression. As an example of how this may be done, we use the data set of Example II shown in Fig. 11.

Fig. 11

Schematic illustration of deriving the initial parameter estimates based on the response-time course of Example II obtained after a 15 min constant rate intravenous infusion of test compound X followed by washout. The slope is mathematically defined by Eq. 42, and Δ = R _ss(t) − R ₀(t) = R _ss(0) − R ₀(0)

The system we will derive initial estimates for is

$$ \begin{aligned} & \begin{array}{*{20}c} {\quad \quad \quad \quad \quad \frac{{dR}} {{dt}} = \frac{{k_{{in}} }} {M} - k_{{out}} \cdot R \cdot I{\left( C \right)}} \\ {\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array} \\ & with \\ & \quad \quad \quad \quad \quad k_{{in}} {\left( t \right)} = k_{{in}} {\left( 0 \right)}{\left( {1 + \alpha t} \right)}^{2} \\ \end{aligned} $$

(39)

where we assume that the drug mechanism function I(C) is given by Eq. 4:

$$ I{\left( C \right)} = 1 - I_{{\max }} \frac{{C^{n} }} {{IC^{n}_{{50}} + C^{n} }} $$

Throughout we assume that C _ss » IC ₅₀. Then I(C _ss) ≈ 1 − I _max, and we need to determine the initial estimates for

$$ k_{{in}} {\left( 0 \right)},\quad \quad k_{{out}} ,\quad \quad k_{{tol}} ,\quad \quad \alpha ,\quad \quad and\quad \quad I_{{\max }} $$

We shall do this by using the following geometric properties of the response versus time graph given in Fig. 11:

• (a) The evolution of the baseline over time, modeled by

  $$ R_{0} {\left( t \right)} = R_{0} {\left( 0 \right)}{\left( {1 + \alpha t} \right)},\quad \quad R_{0} {\left( 0 \right)} = 149,\quad \quad R_{0} {\left( {250} \right)} = 162 $$

  (40)

• (b) The evolution of the pharmacodynamic steady state modeled by

  $$ R_{{ss}} {\left( t \right)} = R_{{ss}} {\left( 0 \right)}{\left( {1 + \alpha t} \right)},\quad \quad R_{{ss}} {\left( 0 \right)} = 220 $$

  (41)

• (c) The slope at onset of infusion (t = t ₀ = 32):

  $$ slope{\mathop = \limits^{def} }\left. {\frac{{dR}} {{dt}}} \right|_{{t = t_{0} }} = 17 $$

  (42)

As a first step we compute I _max from the values of R ₀(0) and R _ss(0) given in (a) and (b). From Eq. 6 we know that

$$ R_{{ss}} {\left( 0 \right)} = R_{0} {\left( 0 \right)}{\sqrt {\frac{1} {{I{\left( {C_{{ss}} } \right)}}}} } = R_{0} {\left( 0 \right)}{\sqrt {\frac{1} {{1 - I_{{\max }} }}} } $$

Hence,

$$ I_{{\max }} = 1 - {\left( {\frac{{R_{0} {\left( 0 \right)}}} {{R_{{ss}} {\left( 0 \right)}}}} \right)}^{2} \approx 0.54 $$

(43)

where we have used Eqs. 40 and 41.

Next, we compute the slope α from the values of R ₀(t) at t = 0 and t = 250. Rewriting the equation for R ₀(t) in Eq. 40 and evaluating the right hand side at t = 250, we obtain

$$ \alpha = \frac{1} {t}\left. {{\left( {\frac{{R_{0} {\left( t \right)}}} {{R_{0} {\left( 0 \right)}}} - 1} \right)}} \right|_{{t = 250}} \approx 0.0004 $$

(44)

We now use the slope of the response versus time curve at onset of the infusion to compute estimates for k _in(0) and k _out. We deduce from the differential equation for R that

$$ \left. {\frac{{dR}} {{dt}}} \right|_{{t = t_{0} }} = \frac{{k_{{in}} {\left( {t_{0} } \right)}}} {{M_{0} {\left( {t_{0} } \right)}}} - k_{{out}} {\left( {1 - I_{{\max }} } \right)}R_{0} {\left( {t_{0} } \right)} $$

(45)

Since, $R_{0} {\left( t \right)} = {\sqrt {k_{{in}} {\left( t \right)}/k_{{out}} } },$ we can write k _out R ₀(t) = k _in(t)/R ₀(t). Hence, because R ₀(t) = M ₀(t), we can write Eq. 45 as

$$ \left. {\frac{{dR}} {{dt}}} \right|_{{t = t_{0} }} = \frac{{k_{{in}} {\left( {t_{0} } \right)}}} {{R_{0} {\left( {t_{0} } \right)}}} \cdot {\left\{ {1 - {\left( {1 - I_{{\max }} } \right)}} \right\}} = \frac{{k_{{in}} {\left( {t_{0} } \right)}}} {{R_{0} {\left( {t_{0} } \right)}}} \cdot I_{{\max }} $$

(46)

Because both k _in and R ₀(t) vary very slowly and t ₀ = 32 is small, we may approximate Eq. 46 by

$$ \left. {\frac{{dR}} {{dt}}} \right|_{{t = t_{0} }} = \frac{{k_{{in}} {\left( 0 \right)}}} {{R_{0} {\left( 0 \right)}}} \cdot I_{{\max }} $$

(47)

Thus, an estimate for k _in(0) can be obtained from the expression

$$ k_{{in}} {\left( 0 \right)} = \frac{{R_{0} {\left( 0 \right)}}} {{I_{{\max }} }} \cdot \left. {\frac{{dR}} {{dt}}} \right|_{{t = t_{0} }} \approx 4700 $$

(48)

Therefore,

$$k_{{out}} = \frac{{k_{{in}} {\left( 0 \right)}}} {{{\left\{ {R_{0} {\left( 0 \right)}} \right\}}^{2} }} \approx 0.2 $$

(49)

where we have used the values for k _in(0) and R ₀(0) obtained in Eqs. 48 and 40.

From the start of infusion to the pharmacodynamic steady state takes about 40 min. If we assume that it takes about 4 × t _1/2ktol for equilibrium to be established we expect k _tol to be given by approximately

$$ k_{{tol}} = \frac{{\ln 2}} {{t_{{1/2k_{{tol}} }} }} = \frac{{\ln 2}} {{10}} \approx 0.07\quad \min ^{{ - 1}} $$

We assume the value of n to be in the neighborhood of 2. This is a valid assumption because in our own experience, n seldom falls outside the range of 1–4. Also, two or more dose levels will further strengthen the estimation of, particularly, the drug parameters IC ₅₀, I _max and n. Obtaining good initial estimates not only shortens the regression time, but also avoids the potential risk of ending up in a local minimum resulting in biased and imprecise parameter estimates.

For convenience we collect some pertinent formulae in Table IV.

THE STATE SPACE—A GEOMETRIC DESCRIPTION OF THE DYNAMICS

The observations made in the “Methods” section can be illustrated and illuminated by a geometrical representation of the dynamics of the system.

$$ \begin{array}{*{20}c} {\frac{{dR}} {{dt}} = k_{{in}} \cdot \frac{1} {M} - k_{{out}} \cdot R \cdot I{\left( {C_{{ss}} } \right)}} \\ {\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array} $$

(50)

The underlying idea is that the state of the system is completely determined by the values of R and M and can be represented by a point in the (R,M) -plane. As the system evolves, the point will trace out an orbit in the (R,M) -plane. It will do so with a speed ν= (dR/dt,dM/dt) which is given in terms of R and M by the system of differential equations.

We point out two important curves in the (R,M) -plane. They are the curve Γ _R on which the tangent to the orbit is parallel to the M -axis, and Γ _M on which the tangent to the orbit is parallel to the R-axis:

$$ \Gamma _{R} = {\left\{ {{\left( {R,M} \right)}:{dR} \mathord{\left/ {\vphantom {{dR} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = 0} \right\}}\quad \quad and\quad \quad \Gamma _{M} = {\left\{ {{\left( {R,M} \right)}:{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-\nulldelimiterspace} {dt} = 0} \right\}} $$

These curves are called the Null Clines of the system. Thus, by Eq. 50

$$ \Gamma _{R} :R = \frac{{R^{2}_{0} }} {{l{\left( {C_{{ss}} } \right)}}}\frac{1} {M}\quad a\;hyperbole\quad \Gamma _{M} :R = M\quad a\;straight\;line $$

Points where Γ _R and Γ _M intersect correspond to equilibrium states. If C = 0, the unique point of intersection is the baseline (R ₀,M ₀), whilst if C = C _ss, the null clines intersect at the pharmacodynamic steady state (R _ss,M _ss).

In Fig. 12 we show two sets of such orbits. In one set (left) we show orbits that correspond to the onset of an infusion, and in the other set we show orbits that correspond to washout. We do this for four values of k _tol keeping k _out fixed. Specifically, we choose k _tol such that κ = k _tol/k _out = 0, 0.01, 0.1 and 1.0.

Fig. 12

Orbits in the (R, M)-plane for onset of infusion (a) and for washout (b). The constants are κ = k _tol/k _out = 0, 0.01, 0.1, 1 and k _in = 0.23, k _out = 0.23 (R ₀ = 1), and I _max = 0.8, C _ss » IC ₅₀. The dashed lines are the null clines through (R ₀,M ₀) and through (R _ss,M _ss)

Below we list a few observations about these orbits.

Onset of response

Since I(C _ss) < 1, the null cline Γ _R shifts upward.

k _tol = 0: Since M(t) = M ₀ along this orbit, it traces out a vertical line until it reaches Γ _R at R=R _top.

k _tol << k _out: Here M(t) grows slowly and the orbit is almost vertical until it reaches Γ _R , crosses it at time T _max, where the response reaches its maximal value R _max. The orbit then follows Γ _R down until it reaches the pharmacodynamic steady state (R _ss, M _ss). Note that R _max ≈ R _top.

k _tol ≈ k _out: Here R(t) and M(t) develop more in tandem and the overshoot is much diminished, i.e. R _max is much lower. Notice the spiral-type behavior near (R _ss,M _ss).

Washout of response

Since I(0) = 1, the null cline Γ _R drops back to the starting position.

k _tol = 0: Since M(t) = M _ss along this orbit, it traces out a vertical line until it reaches Γ _R at R = R _bottom

k _tol << k _out: The orbit drops down and quickly reaches Γ _R . Thereafter, it slowly follows Γ _R back towards the baseline (R ₀,M ₀).

k _tol ≈ k _out: The rebound is now less pronounced and the baseline point (R ₀,M ₀) is approached via a small spiral.

It is evident from the way the orbits must cross the null clines in the phase plane that

• (i) R _max cannot exceed R _top and that R _min cannot drop below R _bottom.

• (ii) Overshoot (R _max - R _ss) as well as rebound (R ₀ - R _min) become smaller as the ratio κ = k _tol/ k _out becomes larger.

It is interesting to compare the nonlinear feedback system 8 with the linear system (19, 26),

$$ \begin{array}{*{20}c} {\frac{{dR}} {{dt}} = k_{{in}} - k_{{out}} M \cdot I{\left( C \right)}} \\ {\frac{{dM}} {{dt}} = k_{{tol}} \cdot {\left( {R - M} \right)}} \\ \end{array} $$

(51)

Plainly, here the baseline is given by R ₀ = M ₀ = k _in/k _out and the pharmacodynamic steady state is R _ss = M _ss = k _in/{k _out I(C _ss)}. As in the nonlinear model, if k _tol > 0, then

$$ \begin{array}{*{20}l} {{R{\left( t \right)} \to R_{{ss}} \quad \quad as\quad \quad t \to \infty \quad after{\text{ }}onset\quad {\left( {t_{1} = \infty } \right)}} \hfill} \\ {{R{\left( t \right)} \to R_{0} \quad \quad as\quad \quad t \to \infty \quad after{\text{ }}washout} \hfill} \\ \end{array} $$

(52)

In Fig. 13a, we show a response versus time course following onset and subsequent washout after t ₁ = 10 minutes. Below, in Fig. 13b, we also show the corresponding orbit in the (R,M)-plane.

Fig. 13

Response versus time plot (a) and the corresponding orbit in the (R,M) -plane for onset (b) of infusion and washout after 10 min. The constants are k _tol = 1, k _in = 10, k _out = 10 and I _max = 0.5 and C _ss » IC ₅₀. The dashed lines are the null clines through, respectively, (R ₀,M ₀) and (R _ss,M _ss)

The null clines in the (R,M) -plane are now given by $\Gamma _{R} = {\left\{ {{\left( {R,M} \right)}:M = {M_{0} } \mathord{\left/ {\vphantom {{M_{0} } {\text{I}}}} \right. \kern-\nulldelimiterspace} {\text{I}}{\left( {C_{{ss}} } \right)}\,} \right\}}\,\,\,\,and\,\,\,\,\Gamma _{M} = {\left\{ {{\left( {R,M} \right)}:R = M} \right\}}$

After onset, Γ _R shifts to the right since I(C _ss) < 1 if C _ss > 0, and it shifts back at washout. We see how the orbit, which starts at the baseline (R ₀, M ₀) = (1,1) spirals towards (R _ss, M _ss) = (2, 2), as predicted by Eq. 52 and after washout spirals back to the baseline.

If k _tol = 0, then M(t) ≡ M ₀ and the equation for R becomes

$$ \frac{{dR}} {{dt}} = k_{{in}} - k_{{out}} M_{0} \cdot I{\left( {C_{{ss}} } \right)} = k_{{in}} {\left\{ {1 - I{\left( {C_{{ss}} } \right)}} \right\}} $$

(53)

Therefore

$$ R{\left( t \right)} = R_{0} + k_{{in}} {\left\{ {1 - I{\left( {C_{{ss}} } \right)}} \right\}}t $$

(54)

Thus, if t ₁ = ∞, then, in contrast to the nonlinear model 8, in the linear model R(t) becomes unbounded, i.e., exceeds any value for t large enough.

If k _tol > 0 the limiting behavior for large time shown in Eq. 52 implies that R _max < ∞. As in system 8, we find that R _max decreases as k _tol/k _out increases. In addition, we conclude from Eq. 54 and an asymptotic analysis that

$$ \begin{array}{*{20}l} {{R_{{\max }} \to \infty \quad \quad as\quad \quad k_{{tol}} \to 0} \hfill} \\ {{R_{{\max }} \to R_{{ss}} \quad \quad if\quad \quad k_{{tol}} \geqslant 4k_{{out}} I{\left( {C_{{ss}} } \right)}} \hfill} \\ \end{array} $$

Therefore, unlike in the nonlinear model, there is no upper bound for R _max, which is independent of k _tol. Similarly, there is no lower bound for R(t) which is independent of k _tol and R _min → - ∞ as k _tol → 0. Therefore, R(t) may become negative for some time interval when k _tol is small enough. We see this happening in Fig. 13a. In the nonlinear model 8, the response is always positive, regardless of the values of the system and drug parameters.

DISCUSSION

Background

From a drug discovery point of view many biological variables including the ones affected by drugs, are subject to adaptation and tolerance. In the description of the time course of the response to drugs, it may therefore be necessary to consider the endogenous feedback control as an intrinsic part of the pharmacodynamics. With still the same system parameters and properties, different drug parameters will result in different response-time courses and consequently different levels of onset, intensity, duration and adaptation.

Does tolerance confound the estimability of system and drug parameters? Yes, particularly with slow drug kinetics relative to kinetics of response, and with a substantial baseline drift, unless data are rich and well-spaced such as in Examples II and III. Since tolerance/adaptation may develop on a totally different (slower) time scale than the primary response (k _out), this may result in unexpected (and unpredictable from acute dosing) responses at pharmacodynamic steady-state. We believe that not only tolerance per se, but tolerance coupled to a substantial rebound effect may jeopardize the clinical outcome of unscheduled drug holidays (missed doses) and temporarily result in clinically harmful rebound effects. Therefore, multiple dosing and continuous tracking of the pharmacodynamic effect will be necessary at two or more dose levels. The kappa parameter (k _tol/k _out) may also serve as an early indicator variable of how slow tolerance develops and therefore how long extended exposure is needed.

In quantitative pharmacology, the physiology and the system need to be (i) condensed into a conceptual (picture) model that captures the main features, including rate limiting step(s). When the mechanism of action has been presented as a conceptual model, the latter then needs to be translated into (ii) equations, i.e., the mathematical model, e.g., of the rate process (quantitative pharmacological), which is implemented into the regression software package. This is the second condensation, because model parameters also need to be identifiable and estimable.

The next step (iii) will be to add the statistical model (error and/or covariate models) to the regression model. This is, of course, of importance in most instances, but it also needs to be balanced against mechanism of action (including the mathematical structure) and supported by a thorough experimental design. We envision more of a focus on mechanistic/mathematical model building including emphasis on experimental design. However, pattern recognition and exploratory data analysis are more related to the art of successful model building than the pure mathematical/statistical regression.

Examples

The analysis in this paper has been anchored in data sets obtained from three examples.

Example I covers rapid test compound kinetics, multiple provocations, washout dynamics, and a value of κ = k _tol/k _out which is less than 1. These combinations reveal the system properties and result in accurate and precise system and drug parameters. The pharmacological response exhibits adaptation and particularly extensive rebound.

Example II covers rapid system kinetics, relatively slow washout of test compound and a substantial drift in the baseline. Again, the value of κ is less than 1. The pharmacological response shows a pronounced overshoot, adaptation and a slow return towards baseline without any indication of a rebound. However, simulations also demonstrate rebound of this system provided rapid kinetics and stable baseline.

Example III covers intravenous infusion at a 4-fold dose (exposure) range, slow washout of test compound and a stable baseline. The pharmacological response shows a rapid onset, superimposing response-time courses for the two highest doses and lack of rebound upon return towards the baseline. This time the value of κ was much less than 1, but the slow pharmacokinetics of the test compound confounded the possibility of a rebound.

The intravenous way of administration avoids confounding absorption processes and first-pass phenomena. In neither of the three examples, pharmacologically active metabolites are known to be involved.

Initial Estimates

Using the data set of Example II we have shown how initial estimates for system and drug parameters can be obtained from just a few critical properties of the response versus time curve, such as baseline, pharmacodynamic steady state and initial slope.

Qualitative Analysis of the Model

Using qualitative methods we have obtained a-priori estimates for the response versus time course, such as upper and lower bounds, rate of convergence to the pharmacodynamic steady state, and to the baseline and insight into the crucial importance of the ratio κ of the rate constants for the moderator k _tol and the response k _out. Viewing the dynamics of the system as an orbit in the state space represented by the (R, M)—plane has yielded valuable insight into the specific properties of the feedback model such as a tendency towards overshoot and rebound, and an “upward bias” in that the tendency towards overshoot tends to be larger if the response jumps up than when it jumps down.

With the a-priori knowledge we have obtained for this class of feedback models it will be easier to assess before hand whether or not a given data set can be fruitfully modeled by a model of this type.

Design

What are study designs generally lacking in situations where we also have feedback, tolerance and adaptation? We advocate several dose levels coupled to different routes and rates of input, multiple dosing, re-dosing during overshoot, pharmacodynamic steady-state or during rebound. Multiple consecutive intravenous infusions were given to the system presented in Example I. This is an example of multiple perturbations of a system, which reveals the system properties nicely. Since adaptation is a time-phenomenon, experimental design also requires repeated provocations (repeated dosing, different rates and routes of administration) of the system that is being studied. There is no generic schedule for this, but multiple provocations for at least 3–4 t _1/2ktol, coupled to washout dynamics with sufficient baseline data, are probably informative. In a subsequent series of papers we will demonstrate how multiple rates and durations of intravenous dosing, coupled to observations of pharmacology during and after the provocations (washout), may help to elucidate the rate limiting steps behind a physiological turnover system exhibiting rapid adaptation.

We also advocate ex vivo plasma protein binding of the test compound for appropriate estimation of unbound exposure, since changes in plasma protein binding have been shown to affect the exponent (Hill coefficient) in the sigmoid E _max model when converting total to unbound concentrations. Ex vivo plasma protein binding has, in our experience, given different results compared to pooled in vitro plasma protein binding experiments. One may also need to consider dosing (infuse) potentially active metabolites if their potencies and/or exposure levels fall in the neighborhood of parent compound. Making model simulations prior to executing the full experiment also helps to set up a strategy for experimental design.

A constant (stable) drug input is probably the least satisfactory design for a feedback experiment. For tolerant physiological systems we believe that the constant 24 hr exposure paradigm may be deleterious in that most physiological systems need to be reset to some extent at some point during each dosing interval for the system to be susceptible to a new dose.

Final Conclusion

We have demonstrated the flexibility of a class of turnover models in their ability to mimic overshoot, pharmacodynamic steady state, return to baseline and rebound. We anchored this analysis to three experimental data sets of varying complexity. Finally, we discuss analytical tools such as phase plane plots and show a strategy as to how to derive initial parameter estimates.