Abstract
Augmented reality (AR) displays, as the next generation platform for spatial computing and digital twins, enable users to view digital images superimposed on real-world environment, fostering a deeper level of human-digital interactions. However, as a critical element in an AR system, optical combiners face unprecedented challenges to match the exceptional performance requirements of human vision system while keeping the headset ultracompact and lightweight. After decades of extensive device and material research efforts, and heavy investment in manufacturing technologies, several promising waveguide combiners have been developed. In this review paper, we focus on the perspectives and challenges of optical waveguide combiners for AR displays. We will begin by introducing the basic device structures and operation principles of different AR architectures, and then delve into different waveguide combiners, including geometric and diffractive waveguide combiners. Some commonly used in-couplers and out-couplers, such as prisms, mirrors, surface relief gratings, volume holographic gratings, polarization volume gratings, and metasurface-based couplers, will be discussed, and their properties analyzed in detail. Additionally, we will explore recent advances in waveguide combiner design and modeling, such as exit pupil expansion, wide field of view, geometric architectures of waveguide couplers, full-color propagation, and brightness and color uniformity optimization. Finally, we will discuss the bottlenecks and future development trends in waveguide combiner technologies. The objective of this review is to provide a comprehensive overview of the current state of waveguide combiner technologies, analyze their pros and cons, and then present the future challenges of AR displays.
Similar content being viewed by others
1 Introduction
After decades of device innovation, vibrant advances in microdisplay technologies and ultracompact imaging optics, together with high-speed digital processors, augmented reality (AR) has evolved from a futuristic concept to a tangible and pervasive technology [1,2,3,4]. By seamlessly blending the projected virtual contents with the real-world scenes, AR enhances our perception and interaction with the environment, opening exciting possibilities for metaverse [5], digital twins [6] and spatial computing [7] that have found widespread applications in smart education and training, smart healthcare, navigation and wayfinding, gaming and entertainment, and smart manufacturing and assembly, etc.
Since the primitive concept proposed in the 1990s, AR has made significant strides, especially the emergence and development of waveguide-based AR display [8, 9], which enables the wearable system to be lightweight and have a slim formfactor, while keeping high optical performance. Essentially, it is a lightguide, encompassing thousands of propagating modes, that possesses the power to fold the optical path and replicate luminosity from a small light source across an expansive area. This interesting idea, initially conceived in realms unrelated to display, such as optical clock broadcasting, brilliantly achieves the replication of a single incoming beam into numerous beams, each with an equal intensity [10]. In essence, it mirrors the process of exit pupil expansion (EPE). Within the domain of display technology, this concept manifests itself splendidly in edge-lit liquid crystal displays (LCDs) [11].
The main objective of this paper is to provide an overview on diverse optical combiners utilized in waveguide-based AR displays. First, we briefly review the present status of light engines for waveguide-based AR displays and introduce various optical combiners because they are the two key components in an AR display. Next, we investigate the operation mechanisms and properties of different waveguide combiner couplers and discuss their technical challenges and possible solutions. Finally, a comprehensive review on waveguide combiner design, including EPE scheme, field of view (FoV) expansion, front geometry design of couplers, full-color displays and uniformity optimization will be provided, and their underlying physical mechanisms analyzed. Besides, we will also discuss the bottlenecks hindering the full potential realization of waveguide combiner design, which in turn may shed light on the areas necessitating further development.
1.1 Metrics of AR displays
Irrespective of the specific combiner technique employed, there are some universal metrics to evaluate the performance of an AR display. They can be broadly categorized into two groups: those pertaining to what the user perceives, and those concerning how others perceive the user when wearing the device. The latter group assumes significance in terms of social acceptance, aesthetic appeal, and overall cosmetics. From the user’s viewpoint, certain metrics lend themselves to straightforward definition. These include image quality, FoV, eyebox, color uniformity, waveguide combiner’s efficiency, ambient contrast ratio (ACR), transmittance of ambient light, ghost images, possible presence of rainbow effects, as well as formfactor and weight.
The quality of the displayed images can be effectively characterized through the utilization of modulation transfer function (MTF). Imperfections introduced during manufacturing process and the presence of stray light can jointly degrade the MTF. Additionally, image artifacts arising from the rainbow effect can also impact the image quality adversely. The ultimate objective is to approach the diffraction limit, striving for optimal visual fidelity.
FoV refers to the angular extent of the image that is observable to the user. Although the waveguide itself might support a certain FoV, vignetting can cause users to perceive it differently from the projection system. Taking a diffractive waveguide combiner as an example, vignetting largely results from the varied diffraction efficiencies of the couplers at different incident angles.
Eyebox [12] on the other hand, represents the spatial volume within which the user can view the displayed image. It is crucial to provide a sufficiently large viewing area within the eyebox to accommodate the natural diameter of the human eye’s pupil. Moreover, the eyebox should also allow for a margin to accommodate normal eye rotations during typical usage. For commercial products, it is essential for the eyebox to accommodate a range of interpupillary distances. The waveguide structure itself can naturally enhance the eyebox size through the EPE process. In addition, gradually ascending outcoupling efficiency plays a key role in achieving a uniform eyebox. When utilizing customized designs for a single user or incorporating eye-tracking technology, it is possible to reduce the eyebox requirement.
Uniformity [13] means the ability of a display to provide consistent color and brightness across the entire FoV and eyebox. Besides, uniformity can be compensated through electronic correction, albeit at the tradeoff of luminance.
The overall efficiency of an AR waveguide display is typically measured in nits per watt, representing the electrical-to-optical efficiency. It quantifies the electrical power required to achieve a specific luminance level in the entire system. This efficiency can be further divided into two parts: the first part is measured in lumens per watt which represents the efficiency of the light engine itself, and the second part focuses on the efficiency of the waveguide combiners and is measured in nits per lumen. This measurement is tied closely to the FoV and eyebox characteristics of the display. The overall efficiency is the product of these two parts. A waveguide combiner’s efficiency can also be expressed as the ratio of photons directed into the eyebox compared to those injected into the waveguide. This metric is often expressed as a percentage, providing insight into the efficiency of directing light to the intended viewing area.
From the optics perspective, the formfactor and weight of a waveguide-based AR display are primarily determined by the thickness of the waveguide and the size and position of the light engine. A thicker waveguide may lower the transmittance of ambient light, but it is beneficial in terms of the EPE process.
From the observer’s perspective, one of the most significant considerations is the occurrence of eye glow, which refers to the unintended light leakage from the display that can be observed by other people in the vicinity. Eye glow can hinder eye contact between the user and others, potentially impacting social interactions and communications.
ACR [2] is a metric for evaluating how ambient lighting affects the contrast of the displayed images. It is determined by the ratio of the perceived luminance in the on-state to that in the off-state. This perceived luminance is a combination of the display’s luminance and the ambient luminance transmitted through the waveguide. To achieve a 10:1 ACR under bright ambient, a high brightness light engine and an efficient waveguide are needed. While a smart dimmer [14] helps lower the brightness requirement, it could compromise the ambient light transmittance.
Indeed, there are tradeoffs between the metrics mentioned above, e.g., efficiency vs. uniformity, and eyebox vs. formfactor. The goal is to achieve a proper balance between these metrics, while simultaneously striving to improve the overall AR performance. Manufacturability is another crucial metric to consider when assessing the mass production potential of waveguide-based AR displays.
2 Optical architecture of AR systems
2.1 Light engines
In an AR system, the employed microdisplays (also called light engines) generate image contents that are overlaid with physical worlds via the optical combiner. Currently, the major competing microdisplay technologies are liquid-crystal-on-silicon (LCoS), digital light processing (DLP), organic light-emitting diode (OLED)-on-silicon, micro-LED (µLED), and laser beam scanning (LBS). LCoS and DLP are light modulation displays. LCoS utilizes the voltage-induced liquid crystal reorientations to modulate the polarization state of the incoming light, while using the pixelated metallic mirrors to reflect the modulated light. Pixelated reflectance can be obtained via converting the phase retardation to amplitude modulation after passing through the analyzer or polarizing beam splitter (PBS) [15]. Different from LCoS, DLP relies on the tilting micromirrors to steer the incident light to two different directions corresponding to the on- and off-states. OLED and µLED are self-emissive displays and thereby exhibit a smaller form factor and higher contrast ratio. In contrast to panel-based microdisplays composed of two-dimensional pixel arrays, each pixel of the LBS microdisplay is formed in a time-sequential manner. Detailed working principles of each microdisplay have been extensively reviewed in previous literatures [2, 16,17,18]. In this review paper, we focus on highlighting the emerging research trends and recent technological advances.
In a waveguide-based AR system with EPE scheme, a small-area in-coupler enables a compact formfactor, which in turn raises stringent requirements for light engines: a smaller panel size and a narrower angular distribution. A smaller panel size helps reduce the light engine’s volume including the collimating optics. To maintain the same FoV, the focal length of the collimating lens should be shortened, and the pixel pitch reduced to keep the same resolution for achieving 60 pixels per degree (PPD). For example, a 3-µm pixel pitch is required to achieve 60 PPD and 50° diagonal FoV if we use a commercial diffractive waveguide combiner (Dispelix DPX 50°) whose etendue is 6.2 mm2 sr, and an f/2 imaging optics [19]. Compound Photonics has demonstrated 3-µm pixel-pitch LCoS panels. The emerging research trend is to achieve 1-µm pixel size to support the ~ 0.1-inch LCoS panel with a ~ 2 K×2 K resolution. On the other hand, the angular distribution of LCoS is determined by the illumination light source. The angular distribution of LED sources can be narrowed by a collimating lens. A more effective solution is to adopt laser sources because of their narrower beam spread than LEDs, if the speckles can be suppressed. Another research trend is to shrink the volume of illumination optics via eliminating the PBS. Many companies such as Himax [20], Magic Leap [14], and Avegant [21] have developed their own versions of compact illumination systems, but how to balance the compactness with efficiency remains to be studied. Lastly, a higher frame rate [22] is desired to eliminate the color breakup when users quickly turn their heads or have a large eye saccade. As another kind of light modulation display, the volume of DLP microdisplays should be shrunk and the pixel size should be further reduced as well.
For µLED microdisplay, it usually exhibits a much larger etendue than LCoS because of the Lambertian angular distribution. To narrow the angular distribution of µLEDs, a straightforward approach is to introduce pixel-level collimating microlens array, but the challenges are twofold: manufacturing process and optical crosstalk. Besides, the emission area of µLEDs should be much smaller than the pixel area to achieve an efficient light collection. Compared with conventional µLED-on-silicon, nanowire LEDs stand out because of their sub-micron diameters and directional angular distribution [23, 24]. To triple the resolution density, a three-panel system using a trichomic prism or vertically stacked µLEDs have been demonstrated. For examples, in 2023, Jade Bird Display demonstrated a µLED prototype with 6350 pixels per inch (ppi) by a trichomic prism, and MIT unveiled vertically stacked µLEDs with 5100 ppi using two-dimensional material-based layer transfer [25]. The challenge for the former is that it requires a high-precision pixel alignment, while the latter reduces the display brightness (due to the blue and green absorbers) and requires the epitaxy of thin RGB LEDs. Another promising self-emission display is OLED-on-silicon. However, its brightness and resolution density are currently the bottlenecks for AR applications.
For a light scanning microdisplay, LBS can eliminate the collimating optics and break the limitation of the combiner etendue at the cost of constrained frame rate and resolution. For this reason, the flicker and image blur (due to raster scan) may be noticeable. High-Q MEMS resonators are beneficial to mitigating those issues. Overall, LCoS with laser backlight is likely to be a strong contender for achieving high-efficiency and high-resolution waveguide-based AR displays. µLED-on-silicon requires further development on directional angular distribution and small full-color pixel size to pave the way for high-brightness and high-resolution AR displays. To compete with LCoS and µLED, LBS needs significant improvements on frame rate and resolution. For a comprehensive reference, Table 1 summarizes the pros and cons of the above discussed five light engines, including their research trend, system efficiency, formfactor, resolution density, frame rate, and contrast ratio.
2.2 Optical combiners
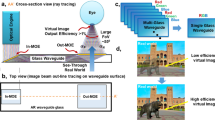
As another crucial optical component in AR displays, optical combiner serves as the interface through which user’s eye directly perceives both digital content and real-world environment. The optical combiners of AR systems can be broadly classified into two types: free space and waveguide combiners. Free space refers to the case when light freely propagates in space, as opposed to a waveguide where light is trapped and guided by the total internal reflection (TIR) process within a waveguide, which can be glass or plastic. Regarding the free space combiner, several configurations have been developed, including a single freeform partial mirror, birdbath optics, Auxiliary freeform lens, and Maxwellian-type systems. Detailed working principles of each free space combiner have been extensively reviewed in previous literatures [2, 3, 16, 26, 27]. Based on the characteristics of couplers, waveguide combiners can be categorized into two types: diffractive and geometric. In a geometric waveguide combiner [9, 28], the in-coupling process of rays is accomplished using a reflective mirror or a refractive prism, and the out-coupling process is achieved by a partial mirror array (Fig. 1a). Regarding a diffractive waveguide combiner (Fig. 1b) [8], the couplers are diffractive optical elements, in most cases, gratings. Four major diffractive couplers have been developed: surface-relief grating (SRG), volume holographic grating (VHG), polarization volume grating (PVG), and metasurface couplers. The first two types have been widely incorporated in commercial AR products, such as HoloLens, Magic Leap, WaveOptics, Dispelix, DigiLens, and so on. The last two kinds of couplers are currently under active development, showing great potential for future products [29, 30].
However, as the desired FoV increases, the optical module of all combiners becomes larger, bulkier, and increasingly difficult to implement due to the etendue conservation. This is a major drawback for near-eye displays, where the headset should be as light and as compact as possible. Furthermore, the eyebox for viewing the images in such designs is small. Hence, the performance of the optical system is very sensitive to an even small movement of the optical module relative to the viewer’s eye and is inconvenient for different users with a different inter-pupil distance (IPD).
Therefore, different kinds of exit pupil expansion and pupil steering methods have been studied and developed, especially for Maxwellian displays [31,32,33,34] and waveguide displays [28, 35, 36]. However, one of the biggest issues of Maxwellian displays remains to be solved is the aberration when the pupil moves to a different eyebox position or when the eye saccades. On the other hand, EPE process is very natural for waveguide display as discussed in Sect. 1. The waveguide combiner can obtain a large FoV while keeping a large eyebox size, featuring a slim formfactor as well. Therefore, in this review paper, we focus on the emerging research trends and recent advances in waveguide-based AR displays.
3 Waveguide couplers
Waveguide combiners are based on TIR to propagate the entire field within an optical guide, effectively functioning as a transparent periscope featuring slim formfactor and large eyebox. These distinctive features originate from the EPE process that effectively enlarges the system etendue. In the EPE process, a portion of the trapped light is repeatedly coupled out of the waveguide upon each TIR. The effective eyebox is therefore enlarged. While the waveguide combiner relies on TIR propagation, which is governed by the refractive index of waveguide, the primary functional components of a waveguide combiner are the couplers since the angular and spectral properties of the couplers will impact the digital images over user’s eyes. In the last few decades, numerous couplers have been developed, such as prisms, mirrors, SRGs, holographic gratings, and metasurfaces, etc. Here, based on different features, they are basically classified into geometric and diffractive waveguide couplers.
3.1 Geometric waveguide couplers
Geometric waveguide coupler mainly consists of refractive and reflective optical elements, such as prisms and mirrors. There is barely chromatic aberration in these optical elements, so they are also called achromatic couplers.
3.1.1 Mirrors
As one of the simplest geometric optical elements, mirrors function very well as an in-coupler or out-coupler. In the early design of geometric waveguide combiner [9, 28], a fully reflective mirror is applied as an in-coupler to reflect the projected light from microdisplay into the waveguide. After a few TIR cycles inside the waveguide, the trapped light reaches the out-coupler, another fully reflective mirror, which couples the light out of the waveguide into the user’s eye. However, the FoV and eyebox are limited by this out-coupler in a thin waveguide [9]. To solve this problem, the cascaded embedded partially reflective mirrors with gradient efficiency work as an out-coupler, which can replicate and couple the light out of the waveguide into user’s eye, as Fig. 1a shows, thereby achieving a large and uniform eyebox. Although this process seems simple, the variation in coating process is tedious and could undermine the overall yield [3] because each mirror is deposited with tens of layers of coatings to generate a different reflection/transmission ratio to assure the output light uniformity across the whole eyebox.
In addition, other mirrors, like curved mirrors in Epson 300T and Zeiss Tooz, pin-mirror array in Optinvent and LetinAR [1], could also be used as the waveguide couplers.
3.1.2 Prisms
Another simple geometric optical element is prism. Prisms are usually utilized as in-couplers to equivalently replace the reflective mirror (to be discussed in next section) [37], but it can also function as an out-coupler to couple the light out by TIR, such as in the Oorym waveguide combiner [38], thus resulting in a limited eyebox. As an in-coupler, the prism may be bounded on top of the waveguide as shown in Fig. 1a, or the waveguide itself can be cut at an angle, to couple the incident light into the waveguide by TIR.
Most of these geometric couplers can also be fabricated using a plastic substrate because they do not require a high refractive index substrate. For example, Zeiss Tooz, Optinvent, and LetinAR are developing plastic geometric waveguide combiners.
3.1.3 Issues induced by geometric couplers
Being an achromatic optical element, a geometric coupler does not suffer from color uniformity issue. But the major problem of the geometric waveguide combiner is the stray light and ghost images caused by the undesired reflections on the couplers, which can severely degrade the image quality, especially when FoV increases in the direction of pupil expansion. Based on previous research [37, 39, 40], stray light is primarily generated in three ways, as illustrated in Fig. 2a–c.
Issues in geometric waveguide combiners. a Stray light generated by two reflections from the in-coupling mirror. b Stray light caused by undesired reflection from the back surface and c from the front surface of out-coupling mirrors. The blue arrows represent the desired light path, red arrows show the unwanted light path, and black circles indicate where the undesired reflection happens. d Stray light elimination on the in-coupler by replacing the mirror with an absorptive prism. The brown dashed lines represent the replaced mirror. Blue dashed arrows and blue arrows represent the beams from light engine when a mirror or an absorptive prism works as the in-coupler. e Eye glow generated by Fresnel reflections. The red dashed arrows represent eye glow towards environment, and blue arrows indicate the desired light path
The first one is caused by the light rays hitting the in-coupling mirror twice, as shown by the circled area in Fig. 2a. In an ideal design, all the light from microdisplay only undergoes a single reflection by the in-coupling reflective mirror as illustrated by the blue arrows. However, the undesired second reflection changes the original direction of the normal light, thus generating stray light, as depicted by the red arrows. To eliminate this type of stray light, an equivalent prism with an absorber layer can be applied to replace the in-coupling mirror, as shown in Fig. 2d [37]. To circumvent the chromatic aberration and distortion caused by incorporating the prism, the angle \({\alpha }_{p}\) of the prism should satisfy that the rays in the waveguide coupled by the prism coincide with those reflected by the replaced mirror drawn as brown dashed lines in Fig. 2d, thus \({\alpha }_{p}=2{\alpha }_{m}\), where \({\alpha }_{m}\) is the slanted angle of the mirror. Otherwise, the exit pupil of projection optics should be decreased to avoid the second reflection [39].
Another two cases occur when the light is incident at the front or back surface of the partially reflective mirrors from an undesired direction, as shown in Fig. 2b, c. In an ideal design, all the light from any unwanted direction should pass through the partial reflectors. However, the coating may not be perfect, thus stray light is produced when these lights are reflected from the front or back of them. Optimizing the angular reflection bandwidth of the coating would help reduce these two kinds of stray lights.
Another issue, eye glow, mainly results from Fresnel reflection at the bottom surface of the waveguide as shown in Fig. 2e, which can be significantly reduced by applying anti-reflection (AR) coating to the bottom surface. Besides, such a reflective waveguide combiner also suffers from the louvre blinds effect.
3.2 Diffractive waveguide couplers
As the name implies, diffractive waveguide combiners employ diffractive optical elements as couplers. Among several diffractive optical elements, gratings are mostly employed. Diffractive grating exhibits a self-repeating diffractive structure, such as surface modulation on an optical component and refractive index modulation within its volume or other phase modulation methods, such as geometric phase modulation and resonance phase tuning. More specifically, diffractive grating couplers are mainly divided into four types: SRGs, VHGs, PVGs and metasurface-based gratings. When the incident light impinges the grating coupler, it is deflected to a predetermined direction. This behavior is described by the following grating equation,
where \({n}_{in}\) and \({n}_{out}\) represent the refractive index of the incident and output media, \({\theta }_{in}\) and \({\theta }_{out}\) are the incident and diffracted angles, \(\lambda\) is the wavelength, \({{\Lambda }}_{x}\) is the grating period, and m is the diffraction order. From Eq. (1), the diffraction angle is wavelength dependent. Consequently, this gives rise to color dispersion. Therefore, the in-coupler (folding coupler) and out-coupler in most cases are both gratings with symmetric \(k\)-vectors (triangular relationship among \(k\)-vectors) to cancel the dispersion induced by diffraction. In addition to diffraction gratings, the in-coupler could also be an off-axis lens, which combines the functions of in-coupling grating and projection lens, while the out-coupler can also be an off-axis lens with a small curvature to generate image with finite depth, such as the out-couplers employed in Magic Leap 1.
3.2.1 Surface relief gratings
When the periodic structure is situated on the surface of an optical component, it is called surface grating. Furthermore, if the periodic structure arises from the modulation directly on the surface itself, it is termed as surface relief grating. An SRG serves as an exemplary instance of a diffractive optical element (DOE). The diffraction behaviors of a SRG are governed by several factors, such as wavelength, grating line spacing, groove depth and slant angle, and the employed materials. An SRG can be engineered to exhibit a single diffraction order, as will be discussed later. The suppression of high diffraction orders relies on the specific SRG configuration. Figure 3a–e portray schematic cross-sectional views of some exemplary SRGs, which are created through surface modulation of optical elements. A 1D SRG can be conceptualized as spatial waveforms intricately embedded within the surface of an optical element. These spatial waveforms can assume shapes such as sinusoidal, square, or triangular waves. On the other hand, a 2D SRG essentially manifests as photonic crystals with lattice structures, exhibiting properties across two dimensions.

(e Is redrawn from [1]. f, g Are adapted with permission from [41] © The Optical Society. h Is adapted with permission from [42] © 2023 DigiLens Inc.)
Structure and fabrication of various SRGs. a Straight binary SRGs. b Slanted binary SRGs. c Triangular (blazed) SRGs. d Multilevel SRGs. The thickness of the arrows indicated the diffracted intensities. e Trapezoidal SRGs. f Replication master and g replicated SRG utilizing nanoimprint lithography. h High aspect ratio SRG based on optical interference lithography
Figure 3a shows a straight binary SRG [43], where the width of the arrow represents the relative diffraction intensity. Such a SRG consists of a series of grooves on the surface, separated by the raised regions called “filling regions,“ “grating lines,“ or simply “lines.“ The SRG possesses a spatial period denoted as \({{\Lambda }}_{x}\), a filling factor represented by f, and a groove depth indicated as h. The filling regions exhibit straight walls and maintain a uniform width (w), which is determined by the product of the filling factor f and the spatial period \({{\Lambda }}_{x}\). Due to the perpendicular orientation of the walls to the surface, the straight binary SRG induces symmetric diffractions when the incident light enters the surface at normal direction. As a result, the transmissive + 1 (\({T}_{+1}\)) and −1 (\({T}_{-1}\)) diffraction orders have the same efficiency, thereby causing the straight binary pattern to solely function as an out-coupler in most cases.
Figure 3b depicts an example of a slanted binary SRG [41, 44], which, like the straight binary SRG, consists of grooves and walls in the filling regions. However, in the slanted binary SRG, the walls are inclined at an angle β relative to the surface normal. This non-zero slant introduces an asymmetry in the diffraction behavior. As a result, the diffracted beams, e.g., the \({T}_{+1}\) order, traveling away from the slant direction exhibit a higher intensity compared to their counterparts, such as the \({T}_{-1}\) order. By increasing the slant angle to an extent, these counterparts can be suppressed to a negligible level. Additionally, the zeroth order diffraction efficiency is also diminished due to the introduced asymmetry. However, it is crucial to note that the suppression and efficiency characteristics may significantly depend on the wavelength and the incident angle of the light.
Different SRG shapes have also been realized. For instance, Fig. 3c showcases an overhanging triangular SRG, also called blazed SRG [45], which has the capability to eliminate both the zeroth order and other diffraction orders, thereby leaving only the desired diffraction order. The above mentioned SRGs can be viewed as special cases of trapezoidal SRGs. As shown in Fig. 3e, the trapezoidal SRGs provide a more general framework that encompasses these various designs and offers a greater flexibility in terms of their geometrical parameters and diffraction properties. Additionally, the employment of multilevel structures, as Fig. 3d depicts, also helps enhance the diffraction efficiency of the desired diffraction order.
Overall, the triangle gratings can achieve a maximum diffraction efficiency in some directions, which is well predicated by the scalar diffraction theory. Multi-level gratings can approximate the triangle gratings, and the diffraction efficiency increases rapidly with the number of phase levels. A four-phase level grating can achieve a diffraction efficiency of 81% and eight levels boost the efficiency to 95%. The slanted binary grating can also achieve a high diffraction efficiency when the grating period is close to the wavelength. In this case, only two diffraction orders are present, and empirically they are determined mainly by the value of the first Fourier harmonic of the grating profile [45]. Various degrees of freedom in the trapezoidal grating can be used to optimize the spectral and angular bandwidths [26].
Besides, the diffraction efficiency of SRGs is markedly influenced by the polarization characteristics of the incident light. For instance, the optimal blazing condition for a reflective triangular SRG configured in the Littrow configuration is exclusively attainable when the incident light exhibits the TM polarization, owing to the presence of a thin metal coating on the grating surface. Consequently, only TM-polarized light can fulfill the requisite boundary conditions pertaining to the electric field at the metallic interface [45]. While blazing conditions may be viable for other incident angles in the TE case, they are inherently incongruent with those observed in the TM scenario. Hence, the diffraction efficiency of the SRG is usually sensitive to the incident polarization. However, the sensitivity can be lowered by operating at a non-blazing condition. For example, Liu et al. [46] proposed a polarization independent double-layer slanted SRG.
The fabrication of an SRG can be accomplished by various methods on glass substrates, including focused ion beam or reactive ion beam etching, electronic beam lithography (EBL) [3] and nanoimprint lithography (NIL) [1, 47]. The first two methods entail employing a suitable microfabrication process, which may involve etching and/or deposition on a substrate to create the desired periodic microstructure, ultimately forming an optical component. This optical component can then serve as a production master, such as a mold, for the NIL process (Fig. 3f, g) [41, 48]. It is important to note that certain etching techniques, like e-beam lithography, can be time-consuming, taking several days to write a single sample. In contrast, NIL offers advantages of high yield and reproducibility for mass production of SRGs, making it a more suitable technique in such scenarios. Nevertheless, the existing NIL technology still falls short of meeting the requirements for mass production of SRGs [49, 50]. The process remains costly, primarily due to the rapid degradation of both the master and soft stamps due to mechanical contact. Also, mechanical contact limits the feasibility for achieving high aspect ratio and large slant angle SRGs, which in turn restricts the ability to reduce eye glow and to enhance the waveguide efficiency.
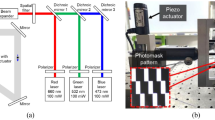
Therefore, a non-NIL replication process is highly desirable to address the limitations of current technologies [49, 51]. Optical interference lithography presents a promising alternative as it eliminates the need for master gratings, thereby avoiding mechanical contact during the process. This method, when coupled with organic dry resist development, allows for the fabrication of large slant angle and high aspect ratio SRGs at a lower cost. For example, DigiLens has fabricated an SRG with a 10:1 aspect ratio using optical interference lithography. Furthermore, by implementing atomic layer deposition (ALD) coating on top of the SRG, the effective index can be increased, leading to an improved performance and reliability of the gratings. This coating technique enhances the functionality of the SRGs and contributes to their overall effectiveness.
3.2.2 Volume holographic gratings
VHGs are a type of holographic optical elements that employ recording materials with sensitivity to the intensity of the interfering field [52]. VHGs can be classified into amplitude and phase holograms. Amplitude holograms transfer the intensity information of interfering lights into transmittance modulation, while phase holograms modulate the wavefront based on the refractive index modulation of the medium [53]. VHGs can be designed as either transmissive or reflective gratings, depending on whether the two interfering beams are on the same side or opposite side with respect to the recording medium.

(a–d Are redrawn from [52])
Schematics of VHGs and PVGs. a structure of a PPVHGs. b structure of an HPDLC. b1 Schematics of local molecular rotation and distribution at zero voltage and b2 at field applied. c Interference of LCP and RCP light to produce a sinusoidal linearly polarized pattern. d Formation of PVGs
Photopolymer-based VHGs (PPVHGs) have garnered significant attention as waveguide couplers due to their advantages in high resolution, low cost, low scattering, and simple fabrication process [54,55,56,57]. The recording process of PPVHGs relies on the light-intensity-dependent polymerization rate and monomer diffusion. When exposed to the high-intensity regions as depicted in Fig. 4a, the monomers undergo polymerization by absorbing photons. This leads to monomer diffusion from dark regions to bright regions, resulting in an increased density and refractive index in the bright areas and then generating index modulation between dark and bright regions, thus forming gratings. Another type of holographic material, called holographic polymer-dispersed liquid crystal (HPDLC), operates on a similar principle of monomer diffusion and polymerization, along with dynamically switchable LCs [58, 59]. During the formation process, the monomers diffuse to bright regions and subsequently polymerize, while the LC molecules migrate to dark regions, forming droplets with random director orientations, as illustrated in Fig. 4b1. This represents the voltage-off state of the grating modulation. Applying a voltage aligns the LC directors inside the droplets along the electric field direction as shown in Fig. 4b2. When the refractive index of the polymer matches the ordinary refractive index of the LC, the entire structure becomes transparent. The utilization of switchable HPDLC gratings as active couplers offers an enhanced design flexibility. Further details on this topic will be discussed in Sect. 4.2. However, haze is a concern of HPDLC [60], which results from the LC droplets. Therefore, decreasing the LC droplet size helps to improve the transparency and uniform modulation. Lately, DigiLens has substantially suppressed the haze with their Reactive Monomer Liquid Crystal Mix [61], and implemented such HPDLC gratings with a large index modulation (0.17) into waveguides as couplers.
Diffraction properties of reflective VHGs and PVGs. Spectral responses at incident angle \(\theta ={0}^{\circ}\) under different sample thickness of a PPVHGs, c HPDLC, and e PVGs. Angular responses at \(\lambda =532 \,\text{nm}\) under different sample thickness of b PPVHGs, d HPDLC, and f PVGs. The index modulation \(\left(\delta n\right)\) used in PPVHGs and HPDLC is 0.02 and 0.07, respectively. The birefringence \(({\Delta }n)\) of PVGs is 0.2
When VHGs are employed as waveguide couplers, their spectral and angular responses play a pivotal role in determining the final waveguide image performance, including field of view, efficiency, and color uniformity. Here, we investigate the spectral and angular responses of PPVHGs and HPDLC gratings using rigorous coupled-wave analysis (RCWA). In our simulation model, the horizontal grating period \({{\Lambda }}_{x}\) is set at 450 nm for both PPVHGs and HPDLC. The index modulation \((\delta n\)) is chosen as 0.02 for PPVHGs and 0.07 for HPDLC gratings, respectively. The input and output media are both glass substrates with a refractive index of 1.58. The spectral and angular responses of the reflective PPVHGs and HPDLC, under different device thickness, are plotted in Fig. 5a–d. In both cases, a thinner device will lead to a broader spectral and angular bandwidth, albeit at the cost of lower diffraction efficiency. Furthermore, a comparison between Fig. 5a, b and Fig. 5c, d reveals that the VHGs with a larger index modulation also exhibit a wider bandwidth. Besides, it is notable that VHGs possess the unique capability of recording multiple holograms into a single film [62], which is usually called phase multiplexing. This feature provides an enhanced design flexibility when utilized as a waveguide coupler. Moreover, VHGs can also be fabricated on a plastic substrate by the roll-to-roll process. The manufacturing process of VHG-based plastic waveguide combiners has been discussed in [3, 63].
3.2.3 Polarization volume gratings
PVG is a polarization-type holographic optical element that records the polarization information of interfering beams composed of righthanded circularly polarized (RCP) and lefthanded circularly polarized (LCP) lights [64,65,66,67,68]. Currently, photoalignment material is widely used for recording the polarization holography [69, 70], and its basic principle is illustrated in Fig. 4c. When RCP and LCP lights interfere, the electric field on the plane exhibits a sinusoidal polarization pattern along the x-axis, duplicating in the y-direction. This patterned photoalignment layer is later used to align the LC material placed on top, resulting in the formation of PVGs as depicted in Fig. 4d. Detailed fabrication process can be found in [3, 52]. PVGs exhibit a slanted cholesteric liquid crystal (CLC) structure, where the LC directors rotate along the helical axis. The gray lines connecting the short axes of the LC directors represent the Bragg surface. Both transmissive and reflective PVGs can be achieved, depending on the slant angle of the Bragg structure, which determines the grating vector (\({k}_{G}\)) in conjunction with the horizonal grating pitch \({\varLambda }_{x}\) [71]. The slant angle (\(\alpha\)) can be regulated by the concentration of the doped chiral dopant, where a higher concentration leads to a smaller slant angle. Reflective PVGs are classified as having an \(\alpha\) angle below 45°, while \(\alpha >45^\circ\) leads to transmissive PVGs. Reflective PVGs are favored in waveguide couplers due to their wider angular bandwidth and simpler fabrication compared to transmissive PVGs. In the following, we will focus on the reflective PVGs and discuss their optical performance and design as waveguide couplers.
Reflective PVGs follow the polarization-selectivity rule of CLC. They selectively respond to the circular polarization state that possesses the same handedness as the helical twist of the CLC, while remaining transparent to the orthogonal polarization state as shown in Fig. 4d. To further investigate the characteristics of PVGs, we simulate their spectral and angular responses by varying the device thickness using RCWA. In our simulation model, the horizontal grating period is set at 450 nm and the birefringence (\({\Delta }n\)) of PVG is set at 0.2. Both input and output media are glass substrates (n = 1.58). Figure 5e, f depicts the spectral and angular responses, respectively, as they depend on the device thickness. Like VHGs, reducing the PVG device thickness results in a broader spectral and angular bandwidth, but at the cost of a lower diffraction efficiency. In addition, a broader bandwidth implies to a more uniform response to a wider range of incident wavelengths and angles. Besides, a higher \({\Delta }n\) LC material will also lead to a wider angular and spectral bandwidth based on the geometric explanation in [72].
3.2.4 Metasurface-based couplers
Similar to conventional diffractive couplers, metasurface-based couplers can also work as both in-coupler and out-coupler, such as metagratings, but with more functionalities and better optical properties due to their superior light modulation capabilities [29]. In metasurfaces, the diffractive nature can be understood through the Huygens principle. Each constituent meta-atom acts as a secondary wave emitter, producing light with specific phase, amplitude, or polarization. By arranging the meta-atoms in a designated array, various functionalities can be achieved through local or nonlocal modulation of the phase of light using the meta-atoms.

(a Is adapted from [73] with permission from AAAS. b Is adapted with permission from Feng et al. [74]. Copyright © 2022, American Chemical Society. c Is adapted from [75] with permission from AAAS. d Is adapted with permission from Sell et al. [76]. Copyright © 2017, American Chemical Society)
Different phase modulation mechanisms in metasurfaces. a Resonant phase modulation. b Propagation phase modulation. c Geometric phase modulation. d Nonlocal phase modulation
Common mechanisms for local phase modulation include resonant phase, propagation phase, and geometric phase as shown in Fig. 6a–c. Resonant phase refers to the phase shift experienced by transmitted or reflected light due to the resonant mode of the meta-atoms when excited by an incident light. Early studies primarily focused on phase modulation using plasmonic resonances [77, 78]. A well-known example is the V-shaped golden resonators in Fig. 6a [73], which support two intrinsic resonant modes for two orthogonal polarization states. The resonant phase can be adjusted by changing the geometrical parameters of these resonators, such as the opening angle and arm lengths, which determine the resonant conditions of the two modes. However, metasurfaces utilizing plasmonic resonances suffer from low efficiency due to ohmic loss and weak interaction with incident light. Alternatively, dielectric meta-atoms based on Mie resonance have been proposed [79]. By controlling the intrinsic properties of electric and magnetic resonances in these meta-atoms, phase modulation can also be achieved. The advantage of using dielectric materials is their lower loss, resulting in significantly higher efficiency. Furthermore, integrated-resonant units have been developed [80, 81], incorporating multiple resonant modes into one supercell. This approach offers an additional design freedom for more sophisticated functionalities.
While resonant phase modulation relies on resonant conditions to alter the output phase, propagation phase refers to the phase shift that occurs when light propagates through a dielectric meta-atom [81,82,83]. In this scenario, the meta-atom is treated as a truncated waveguide (Fig. 6b), and as light passes through it, it accumulates a phase shift as:
where λ is the wavelength of incident light, \({n}_{eff}\) and H are the effective refractive index and the height of the meta-atom, respectively. It is worth noting that the effective refractive index in Eq. (2) is determined by several factors such as the fill-factor, lattice spacing, and constituent material of the meta-atoms. Consequently, phase modulation can be achieved by adjusting the geometrical parameters of the meta-atoms, like the modulation of resonant phase. Propagation phase modulation typically offers a high transmission efficiency when transparent materials are used as constituents. Moreover, it can respond to both polarized and unpolarized light, making it a convenient method for constructing metasurfaces.
Geometric phase, also known as the Pancharatnam–Berry (PB) phase, is a special and widely used phase modulation technique in metasurfaces. It occurs when a circularly polarized light interacts with anisotropic meta-atoms, resulting in an output phase shift that is exactly twice the in-plane rotational angle of the meta-atoms [75, 84]. In this case, metasurfaces can be constructed using an array of anisotropic meta-atoms with the same geometry but different in-plane rotational angles as illustrated in Fig. 6c. Geometric phase-based metasurfaces offer the advantage of high efficiency, but they only respond to circularly polarized input light.
Recently, nonlocal phase modulation mechanisms (Fig. 6d) have introduced new possibilities for light modulation. An example of this is metagratings with nonintuitive nanoscale patterns obtained through inverse design [76]. These metagratings support not only the typical Bloch modes but also many spatially overlapping optical modes. By achieving strong constructive interference between the out-coupled modes in the desired diffraction channel, large angle deflection can be achieved with high efficiency. Another intriguing method is the utilization of quasi-bound states in the continuum (quasi-BIC) geometric phase [85, 86]. This is accomplished by leveraging the collective responses of identical meta-atoms with spatially varying orientation angles. The meta-atoms responsible for this phase modulation usually consist of a pair of anisotropic nanoposts oriented perpendicular to each other. These meta-atoms perturb the symmetry-protected BIC, inducing radiation in free-space or in-plane.

(a Is reprinted with permission from [87] © The Optical Society. b Is adapted with permission from Liu et al. [88]. Copyright © 2021, American Chemical Society. c Is reprinted with permission from [89]. © 2018 SPIE. d Is adapted with permission from Liu et al. [90]. Copyright © 2023, American Chemical Society)
Unique optical properties of metasurfaces applying to waveguide-based AR displays. a High in-coupling efficiency. b Polarization manipulation with geometric phase to generate stereoscopic AR. c Polarization multiplexing to expand FoV in waveguide display. d Wavelength multiplexing to generate holographic images
The versatile methods of phase modulation offer a broader angular bandwidth and higher coupling efficiency [87, 91] for metasurface-based couplers compared to conventional couplers. This improved angular efficiency response of metagratings allows for the FoV expansion in waveguide-based AR systems. It also makes metagratings highly suitable for meeting the efficiency limits (Fig. 7a), thereby opening the possibilities for more efficient waveguide-based AR displays.
In addition, metasurfaces also offer the ability to couple light by manipulating its polarization states. It is easy for a metasurface to control the polarization states since the meta-atoms can be designed to have various anisotropic geometries. This distinct feature allows the metasurfaces to easily achieve unique functionalities by multiplexing polarizations that the conventional optics is difficult to do. For instance, a geometric-phase-based metagrating in-coupler, combined with two surface-relief grating out-couplers, provides a compact platform for creating stereoscopic AR vision (Fig. 7b) [88]. The polarization states can be multiplexed in a metagrating to enlarge the FoV by doubling the channels in a waveguide (Fig. 7c) [89]. Besides, the metasurface-based couplers also offer a unique capability of coupling light by multiplexing wavelengths [90]. The metagrating could be inverse designed to couple two different wavelengths into waveguide with opposite directions (Fig. 7d).
The fabrication of metasurface-based couplers aligns well with microelectronic processes. Electron Beam Lithography (EBL) is extensively employed for its remarkable fabrication precision; however, its time-consuming writing process renders it unsuitable for mass production. In this context, the utilization of Extreme Ultraviolet (EUV) or Deep Ultraviolet (DUV) lithography steppers is strongly recommended for achieving productive and highly accurate fabrication [92]. Additionally, alternative fabrication techniques such as nano-imprint [93] self-assembly [94], and laser writing [95] are also gaining prominence as preferred methods for creating specific designs efficiently.
3.2.5 Issues induced by diffractive waveguide couplers
While diffractive optical elements serve as high-performance couplers for waveguide displays, they also introduce certain challenges, such as rainbow effect, light leakage at in-coupler, light leakage at out-coupler (eye glow), ghost images, and phase distortion, etc. In this section, the mechanisms of these issues will be analyzed, and some possible solutions will be discussed.
Issues induced by diffractive couplers and solutions. a Rainbow effect. b Eye glow. c Top view of a tilted waveguide at wrap angle \(\alpha\). d Side view of a tilted waveguide at pantoscopic angle \(\alpha\), wherein the light engine is hidden
One of the most noticeable issues for users is the diffraction of external light source, usually called rainbow effect, which results in the appearance of a rainbow streak of light in the user’s see-through field of view. Such an external source includes the room light (ceiling light) and the sunlight. This rainbow effect is an unwanted distraction to the user experience in an AR display system. As shown in Fig. 8a, the external sources may be backwardly or forwardly diffracted towards the eye by the out-coupling grating, causing a multicolored glare in a see-through view. The rainbow effect mostly results from an external source having a large incident angle because such light may be diffracted to the eye by the out-coupling grating. To reduce the rainbow effect, a straightforward way is to use a larger grating \(k\)-vector by sacrificing the FoV or using a higher index waveguide substrate [2]. With a higher refractive index, the waveguide could accommodate larger grating \(k\)-vectors. The enlarged \(k\)-vectors would therefore diffract the external sources to a large angle, leading to a decreased rainbow light into the see-through FoV. Alternatively, an optical filter (e.g., angularly selective gratings, or polarizer) could be laminated to the waveguide for suppressing the rainbow effect [97, 98]. Such an optical element may deflect the large incident angle via any suitable mechanisms, such as reflection, diffraction, scattering, or absorption, etc. Besides, a switchable out-coupler also helps suppress the rainbow effect [99].
One of the most serious issues that annoy social interactions of AR users is the light leakage at out-coupler or eye glow effect, which refers to the out-coupled light going outwards to the environment from the microdisplay, as Fig. 8b illustrates. Aside from decreased efficiency, the light leakage also brings an unnatural ‘cyborg’ appearance of the user’s eye and privacy issues, which dramatically impede our interactions with real world [96]. In an SRG-based waveguide combiner, optimization of the grating structure like geometry of SRG may reduce the leakage. For example, when the straight binary SRG is used as an out-coupler, the \({T}_{-1}\) diffraction efficiency is almost equal in magnitude to the desired reflective \(-1\) (\({R}_{-1}\)) diffraction order. Using a slanted structure or extra coatings, this effect can be lessened. When SRGs are operated in the thin grating regime [96], a relatively high diffraction efficiency persists with the \({T}_{-1}\) order, particularly when compared to PVGs and VHGs. For example, Dispelix has reduced the eye glow by 20% and achieved an efficiency over 1000 nits/lm (~ 2.1%) by optimizing the structure of slanted binary SRGs [100]. Alternatively, a pantoscopic or/and wrap tilt waveguide combiner could be used to mitigate the eye-glow effect [96, 101]. As illustrated in Fig. 8c, d, when the waveguide is tilted at a wrap or pantoscopic angle \(\alpha\), the light engine will tilt \(2\alpha\) (the light engine is hidden in Fig. 8d) to make sure the light coming straight into the eye and the eye glow turning towards ground or side by \(2\alpha .\) Besides, Fresnel reflection at the bottom surface of the waveguide also contributes to the eye glow effect in a diffractive waveguide combiner, which can be mitigated by AR coatings.

(a, c Are redrawn from [102], b is reprinted with permission from [87] © The Optical Society, and d is redrawn from [2])
Issues induced by diffractive waveguide couplers and solutions. a Light leakage at in-coupler. b Theoretical in-coupling efficiency after the in-coupler. c Enhanced in-coupling efficiency by QWP. d See-through ghost images generated by the out-coupler
The low efficiency of diffractive waveguide combiners is the major blame. A main reason stems from light leakage at in-coupling grating. When a diffractive grating is used as an in-coupler, the waveguide combiner suffers from significant light loss because of multiple interactions with in-coupling grating, even if the in-coupling grating has a high diffraction efficiency. The reduced brightness decreases the ambient contrast ratio of the virtual images. These multiple interactions at in-coupling gratings are not easy to solve. As shown in Fig. 9a, if the width W of the in-coupling grating is arranged to be larger than \(2dtan\theta\), where \(d\) is the thickness of the waveguide and \(\theta\) is the minimum TIR angle of the light inside of the waveguide, then the in-coupling light may interact with the in-coupling grating two or multiple times. Here, the second interaction of the light with the in-coupling grating is undesirable, because this causes a significant portion of the light to change propagation direction or diffract out the waveguide. In other words, this part of light cannot travel forward inside the waveguide based on the original TIR angle. According to the analysis of recent research [87], the light loss may exceed 71% after in-coupling grating at an extreme FoV as depicted in Fig. 9b. A most straightforward solution is to decrease the width W of in-coupling grating, but this strict demand may be challenging to realize by the light engine, because it would require a small emission cone and a small f-number projection lens to boost the light collecting power. Therefore, it would be highly desirable to have a way around the above-described limitations related to the width W of the in-coupling grating. This issue may be mitigated by a polarization converter and a polarization dependent in-coupling grating, either transmissive or reflective grating [102]. In Fig. 9c, the polarized light (e.g., TE) from light engine interacts with in-coupling grating and diffracted into waveguide. When the diffracted light travels downwards and upwards (or upwards and downwards for transmissive gratings) through the polarization converter layer, its polarization could be totally rotated to an orthogonal one (e.g., TM), so the energy loss may be mitigated at the second interaction by optimizing the polarization response of the in-coupling grating. Besides, a light recycling system in the in-coupling region could also enhance the in-coupling efficiency [103, 104].
Diffractive waveguide combiner also suffers from ghost images. Ghost images typically arise from out-coupling gratings that exhibit higher-order diffractions, but this can be mitigated by utilizing a single-order grating like PVG and VHG, or by optimizing the SRG structure. For multiple layer waveguides, the crosstalk between each layer’s out-coupler may also cause ghost images [1]. Another ghost is the See-through ghost, which is formed by consecutive in-coupling and out-coupling caused by the out-coupling gratings, as sketched in Fig. 9d. After the consecutive interaction with out-coupling grating, a real object with finite depth may produce a ghost image with shift in both FoV and depth. Generally, an out-coupling grating with higher efficiency suffers more see-through ghost. For polarization dependent grating, the ghost image could be suppressed by a polarization filter, such as a reflective polarizer, but such device may decrease the optical transparency of the waveguide combiner.

(a–d Are redrawn from [105])
Phase distortion in SRGs-based waveguide combiner. a Side view of a waveguide with two gratings \({G}_{1}\) and \({G}_{2}.\) b Phase mismatch among grating \({G}_{1}\), \({G}_{2}\) and waveguide. c Side view of a waveguide with two phase matched gratings \({G}_{1}\) and \({G}_{2}\). d Phase match among gratings \({G}_{1}\), \({G}_{2}\) and waveguide
Besides, phase distortion at couplers edge is also a serious issue in diffractive waveguide combiner. Gratings can introduce undesired phase distortions in the light field as it traverses through the waveguide, particularly when the wavefront encounters the edges of the gratings. While gratings may induce amplitude variations due to non-uniform diffraction efficiency, the impact of phase distortion is more severe in terms of image quality. Ideally, light from the same pixel should propagate in a plane-wave manner. However, due to phase distortions, the light may diffract during propagation, leading to a degraded image quality. To better understand this phase distortion, let us take SRGs-based waveguide combiner as an example [105]. Figure 10a portrays a side view of a waveguide showcasing two grating elements, \({G}_{1}\) and \({G}_{2}\), which may serve as in-coupling, folding, or out-coupling gratings, etched onto its surface. These gratings are separated by an unadorned region designated as \(B\), wherein the alteration of phase during TIR diverges among the distinct regions. The phase change within region \(B\) is denoted as \({\varphi }_{0}\), while the phase adjustments on \({G}_{1}\) and \({G}_{2}\) are denoted as \({\varphi }_{1}={\varphi }_{0}-{\Delta }{\varphi }_{1}\) and \({\varphi }_{2}={\varphi }_{0}-{\Delta }{\varphi }_{2}\), respectively. Consequently, the resulting phase distribution of reflected beams within the waveguide exhibits a staircase-like function, as depicted in Fig. 10b. The phase jumps in this distribution can cause unwanted diffraction and result in beam spreading, further exacerbating the effects of phase distortion.
To mitigate the phase discrepancies arising from the reflections at \({G}_{1}\), \({G}_{2}\), and the blank TIR surface B, compensatory adjustments can be made by introducing height offsets, denoted as \(\varDelta {h}_{1}\) and \(\varDelta {h}_{2}\), on \({G}_{1}\) and \({G}_{2}\), respectively, relative to the reference TIR surface. This is illustrated in Fig. 10c, d. Each height offset is carefully chosen to ensure that the additional optical path length introduced by the offset aligns with the phase difference between the reflection from the corresponding grating region and the TIR process. The additional optical path length is determined by the product of the waveguide’s refractive index (n) and the additional distance that light travels due to the height offset. It is important to note that obtaining precise phase matching is not always necessary to achieve acceptable image quality. The phase changes induced by the grating and TIR are dependent on factors such as angle of incidence, wavelength, and polarization, implying that achieving ‘fully’ optimal performance is only possible for specific cases. However, in terms of image quality, a less-than-perfect performance may still be deemed acceptable.
4 Waveguide combiner design
4.1 Exit pupil expansion
Relative to conventional AR systems, waveguide displays offer a significant advantage through the implementation of an EPE scheme, which results in a desired eyebox. This innovative approach allows for an enlarged etendue of the system while maintaining a thin profile.
4.1.1 1D exit pupil expansion
As the horizontal eyebox is often the most crucial factor in accommodating large IPD percentiles, a 1D EPE may be sufficient. In Sect. 3, we have described the basic working principle of 1D EPE. For geometric waveguide combiners, this scheme has been extensively developed and applied in Lumus AR display since it was proposed by Amitai [9]. In Fig. 1a, it only requires one-dimensional cascaded partial mirrors as an out-coupler. On the other hand, such expansion technology is also implemented in diffractive waveguide combiners by 1D gradient efficiency out-coupler as shown in Fig. 1b and Fig. 11a, such as Sony SED 100 A waveguide combiner. In order to obtain a deeper sight of EPE process, it is imperative to introduce the concept of the normalized \(k\)-vector diagram. Within a 3D \(k\)-vector diagram, each point represents a wave vector with components \({k}_{x}\), \({k}_{y}\) and \({k}_{z}\). These components must adhere to the following dispersion relation:
where \({k}_{0}\) is the wave vector in vacuum and \(n\) is the refractive index of the medium. From Eq. (3), we can obtain the full \(k\)-vector information from any arbitrary cross-section diagram of the \(k\) space. For example, the 1D EPE scheme for diffractive waveguide combiner could be completely illustrated by the normalized \({k}_{x}\)–\({k}_{y}\) diagram (normalized \(k\)-vector diagram without specific markings) as shown in Fig. 11b. For the light propagating in air with wavenumber \({k}_{0}\), its possible normalized \(k\) values in x and y directions (\({k}_{x}\)/\({k}_{0}\) and \({k}_{y}/{k}_{0}\)) fall within the circle with radius 1. When the light is trapped into waveguide by TIR, \({k}_{x}/{k}_{0}\) and \({k}_{y}/{k}_{0}\) are outside the circle with radius 1 and inside the circle with radius \(n\), where \(n\) is the refractive index of the substrate. \({k}_{x}/{k}_{0}\) and \({k}_{y}/{k}_{0}\)stay unchanged in the TIR process and are only changed in diffraction processes. The central quasi-rectangular box in Fig. 11b indicates all normalized \(k\) values within the system FoV. After the in-coupler, the \(k\) values are added by the grating \(k\)-vector \({G}_{in}\), shifting the normalized k-value into TIR region. When the light encounters the out-coupling grating, the out-coupling grating then applies a symmetric \(k\)-vector \({G}_{out }\) and shifts the normalized \(k\)-values back to the propagation region in air.

(a Is redrawn from [106])
Schemes of exit pupil expansion. a Schematic of 1D EPE. b Corresponding normalized \(k\)-vector diagram of the 1D EPE scheme, where \({\bar{G}}_{in} \;\text{and}\; {\bar{G}}_{out}\) represent the normalized \(k\)-vectors of the in-coupling grating and out-coupling grating in a, respectively. c Schematic of 2D EPE based on two consecutive 1D EPEs. d Corresponding normalized \(k\)-vector diagram of the 2D EPE scheme, where \({\bar{G}}_{in}, {\bar{G}}_{f}, \; \text{and}\; {\bar{G}}_{out}\) represent the normalized \(k\)-vectors of the in-coupling grating, folding grating, and out-coupling grating in c, respectively. The coral regions in b and d correspond to all normalized \(k\)-vector within the system FoV. Black dashed arrows in b and d indicate the normalized grating vectors
Such an EPE scheme offers high efficiency and good imaging and color uniformity over the eyebox in comparison with 2D EPE. However, to generate a sufficiently large eyebox in the nonexpanded direction, the entrance pupil produced by the light engine needs to be quite large in the unexpanded direction, even larger than the exit pupil in the expansion direction, as shown in Fig. 11a. In many cases, a tall aspect ratio entrance pupil may require a tall aspect ratio emission cone, thus leading to a large projection optics system [1].
4.1.2 2D exit pupil expansion
Drawing from the preceding discussion, it becomes evident that in order to achieve a large eyebox while employing a compact light engine and projection optics system, a 2D EPE emerges as the preferred approach within such a diminutive formfactor architecture. Over the last few decades, various types of 2D EPE have been proposed and developed. The simplest 2D EPE consists of two consecutive 1D EPEs with different directions [28, 35, 36], which has been developed in Lumus Z-Lens, Magic Leap 2, HoloLens 2, etc. In a diffractive waveguide combiner, this EPE method usually includes three regions, an in-coupling grating, a folding grating, and an out-coupling grating [35, 36]. In the scheme sketched in Fig. 11c, the first EPE occurs in the folding grating, where the light is duplicated in x direction and turned into y direction at the same time. The light rays then encounter the out-coupling grating and are expanded in the y direction. To better understand this process, the normalized \(k\)-vector diagram is given in Fig. 11d. Here, the default representation is for a single color, unless otherwise specified or indicated. The coral regions represent the normalized \(k\) vector of system FoV in air or waveguide, the arrows correspond to the size and direction of normalized grating \(k\)-vctors \({\bar{G}}_{in}, {\bar{G}}_{f}, \; \text{and}\; {\bar{G}}_{out}\). However, due to the etendue conservation between field of view and eyebox, the areas of folding grating and out-coupling grating will also increase as the field of view increases. Thus, such a design is relatively bulky and costly.
Scheme of 2D EPE. a Schematic of 2D EPE based on a pair of cross out-coupling gratings. b Corresponding normalized \(k\)-vector diagram of the 2D EPE scheme, where \({\bar{G}}_{in}, {\bar{G}}_{c1} \; \text{and}\; {\bar{G}}_{c2}\) represent the normalized \(k\)-vectors of the in-coupling grating, cross out-coupling grating 1 and cross out-coupling grating 2 in a, respectively. c Schematic of butterfly 2D EPE. d Corresponding normalized \(k\)-vector diagram of the butterfly 2D EPE scheme, where \({\bar{G}}_{in1}, {\bar{G}}_{in2},{\bar{G}}_{f1}, {\bar{G}}_{f2} \;\text{and}\; {\bar{G}}_{out}\) represent the normalized \(k\)-vectors of the in-coupling grating 1, in-coupling grating 2, folding grating 1, folding grating 2, and out-coupling grating in c, respectively. The coral regions in b and d correspond to all normalized \(k\)-vector within the system FoV. Black dashed arrows in b and d indicate the normalized grating vectors
To overcome the above-mentioned drawbacks, WaveOptics [107] proposed a 2D EPE scheme with two crossed 1D gratings overlaid on waveguide as shown in Fig. 12a. This optical scheme combines the functions of folding and out-coupling gratings to provide simultaneous vertical and horizontal expansion, and light extraction while reducing the grating real estate. Such a scheme can allow more efficient use of space in an optical device because 2D expansion can be provided within the same area of the waveguide. Thus, this approach helps reduce the manufacture cost. In the overlaid cross-gratings, one of them directs received light rays from the in-coupling grating towards the other grating in the overlaid pair. The other grating can then couple light out of the waveguide and into the user eye. Preferably, this is a symmetrical arrangement so that each of the overlaid gratings can direct received light towards the other for outward coupling, which is better described in normalized \(k\)-diagram in Fig. 12b, where coral regions represent the normalized \(k\)-vector of system FoV in air or waveguide, the black, green and red arrows separately correspond to the normalized grating \(k\)-vctors, \({\bar{G}}_{in}\), \({\bar{G}}_{c1}\) and \({\bar{G}}_{c2}\). Likewise, the utilization of a 2D grating as an out-coupler presents a viable means to attain a comparable outcome [107].
In the above two 2D EPE designs, the first EPE coupler typically limits the diagonal FoV that can be supported by an optical waveguide combiner, as will be discussed in next section. To enlarge FoV, Microsoft introduced a butterfly scheme [108] in HoloLens 2, as depicted in Fig. 12c. The apparatus comprises an in-coupling grating, first and second folding gratings, and an out-coupling grating. The in-coupling region, composed of two gratings with symmetric \(k\)-vector \({G}_{in1}\) and \({G}_{in2}\) on both surfaces of waveguide, is configured to couple light with a corresponding FoV into the waveguide and split the FoV into the first and second portions. The first portion, corresponding to the first portion of FoV, is diffracted toward the first folding gratings with \(k\)-vecor \({G}_{f1}\), and the second portion of light, representing the second portion of FoV of image, is diffracted toward the second folding grating with \(k\)-vector \({G}_{f2}\). The two folding gratings are configured to diffract these two parts of FoV toward out-coupling grating with \(k\)-vecor \({G}_{out}\) and realize pupil expansion at certain directions. Finally, the out-coupling grating combines the light corresponding to the first and second portions of the FoV and couples the light out of the waveguide to user’s eye. Beneficially, the combined FoV is greater than a maximum FoV that each of the folding grating can support on their own, which could be better understood in normalized \(k\)-vector diagram in Fig. 12d, where the coral regions represent the normalized \(k\)-vector of system FoV in air or waveguide, the arrows correspond to the normalized grating \(k\)-vctors \({\bar{G}}_{in1}, {\bar{G}}_{in2},{\bar{G}}_{f1}, {\bar{G}}_{f2}\), and \({\bar{G}}_{out}\).
Scheme of 2D EPE. a Schematic of IDA 2D EPE. b Corresponding normalized \(k\)-vector diagram of the IDA 2D EPE scheme, where \({\bar{G}}_{in}, {\bar{G}}_{f1} \; \text{and}\; {\bar{G}}_{f2}\) represent the normalized \(k\)-vector of the in-coupling grating, folding grating 1, and folding grating 2, respectively. (c) Schematic of 2D EPE utilizing four grating sequences. d Schematic of the first 2D EPE and FoV expansion in c. e Schematic of the second 2D EPE and FoV expansion in c. Corresponding normalized \(k\)-vector diagram of the f first and g second 2D EPE scheme and FoV expansion. Black dashed arrows in b, f and g correspond to the normalized grating \(k\)-vector. The coral regions in b, f and g correspond to all normalized \(k\)-vector within the system FoV
While the butterfly design could achieve a larger FoV, it occupies too much waveguide real estate because it includes more grating regions. To reduce the oversize of the waveguide combiner while keeping a large FoV, DigiLens released its integrated dual axis (IDA) waveguide architecture which combines the technologies from HoloLens’ butterfly and WaveOptics’ cross-gratings [109]. As shown in Fig. 13a, the pupil expansion and light extraction are accomplished using a pair of crossed folding gratings with \(k\)-vecor \({G}_{f1}\) and \({G}_{f2}\) (referred to as Multiplexed Grating 1 and Multiplexed Grating 2). A leftward propagating portion of FoV injected into the waveguide by the in-coupling grating is folded and expanded horizontally by Multiplexed Grating 1 while Multiplexed Grating 2 expands the beam vertically and extracts it from the waveguide to the eyebox. The rightward propagating portion of the FoV is handled in a similar fashion with Multiplexed Grating 2 now folding and expanding the beam horizontally and Multiplexed Grating 1 expanding the beam vertically and extracting it to the eyebox. An important benefit of IDA architectures is the large achievable FoV according to normalized \(k\)-vector diagram in Fig. 13b, where coral regions represent the normalized \(k\)-vector of system FoV in air or waveguide, the black, red and green arrows separately correspond to the normalized grating \(k\)-vctors \({\bar{G}}_{in}, {\bar{G}}_{f1}\) and \({\bar{G}}_{f2}\).
The butterfly and IDA configurations can give the AR display a helmet-like appearance since the in-coupler is always at the top center of the waveguide combiner. Alternatively, by rotating the above two designs \(90^\circ\), light is in-coupled from the side, resulting in a more compact glasses-like design. However, the user perceives an expanded vertical FoV, which is typically less preferred for human perception.
When combing these two designs together, i.e., utilizing four grating sequences [110], it is possible to expand the FoV in both horizontal and vertical directions. An example of this configuration is depicted in Fig. 13c. While the grating layout may resemble the first option of the butterfly design, it can be decomposed into one butterfly design and one IDA design as shown in Fig. 13d, e, each expanding the FoV in the vertical direction. Each of them could also be better understood in \(k\)-vector diagram as shown in Fig. 13f, g, respectively. Finally, by combining the FoV of each individual design, the overall FoV is then expanded in the horizontal direction.
Working principle of 2D EPE for geometric waveguide combiner. Normalized \(k\)-vector diagram in the \({k}_{z}\)–\({k}_{x}\), \({k}_{x}\)–\({k}_{y}\), and \({k}_{z}\)–\({k}_{y}\) planes a after the initial refraction from air to the waveguide, b reflection at the in-coupling mirror, c reflection at the folding mirror and d reflection at the out-coupling mirror. Light paths before and after reflection on e in-coupling mirror, f folding mirror array, and g out-coupling mirror array in a geometric waveguide combiner with 2D EPE at normal incidence. Once the reflection happens, the coordinate will be rotate \({180}^{\circ}\). The dashed black lines represent the reflection symmetric axes (normal to the mirror’s surface). The dashed blue boxes correspond to the planes where the reflection takes place. Blue arrows represent light path in waveguide
Instead of gratings, the 2D EPE scheme in geometric waveguide combiners is achieved through two cascaded partially reflective mirror arrays with different expansion directions [28]. Similarly, this could also be explained by the \(k\)-vector diagram. However, in contrast to the \(k\)-vector diagrams in diffractive waveguide combiners, the shape of FoV area in that of geometric waveguide combiners does not remain constant during reflection process on mirrors. Because reflections can occur in the \(x\)–\(y\), \(x\)–\(z\) or, \(y\)–\(z\) planes, the k vectors are not constrained within an annular region in the \({k}_{x}\)–\({k}_{y}\) diagram. Besides, the impact of mirrors will be visualized using a symmetric axis in the \(k\)-vector diagram instead of arrows representing gratings \(k\) vectors. While a single cross-section \(k\)-vector diagram contains complete vector information, the symmetric axis can lie in any plane. Consequently, \(k\)-vector diagrams in the \({k}_{x}\)–\({k}_{z}\), \({k}_{x}\)–\({k}_{y}\), and \({k}_{y}\)–\({k}_{z}\) planes are all necessary to visualize the 2D EPE process. As illustrated in Fig. 14, for the sake of simplicity, only one central FoV point and four corner FoV points are plotted. Figure 14a represents the k vector states after the initial refraction from air to the waveguide. The three subsequent reflections on in-coupler, folding coupler and out-coupler occur sequentially in the \(x\)–\(z\), \(x\)–\(y\) and \(y\)–\(z\) planes, as shown in Fig. 14e–g, which correspond the \({k}_{x}\)–\({k}_{z}\), \({k}_{x}\)–\({k}_{y}\), and \({k}_{y}\)–\({k}_{z}\) planes, as illustrated by the dashed blue box in Fig. 14a–d. The symmetric axes in reflections on the in-coupler and out-coupler are complementary to each other. Additionally, the aspect ratio of FoV is flipped due to a 45° symmetry axis in the reflection on folding coupler. These successive reflections and the corresponding symmetric axes play a crucial role in determining the behavior of the \(k\) vectors and the resulting FoV in geometric waveguide combiners, facilitating a comprehensive understanding of the EPE process.
4.2 Enlarging field of view
As one of the most intuitive optical parameters for users, FoV shows how large the image is displayed in front of users’ eye. In a waveguide combiner, FoV is mainly limited by two aspects. The first one stems from the refractive index of waveguide substrate, which is the essential cause of limited FoV in either geometric or diffractive waveguide combiners. A waveguide display relies on TIR propagation inside waveguide, in which the minimum TIR angle depends on the refractive index \(n\) of waveguide as follows:
From Eq. (4), a higher refractive index leads to a wider range of TIR angles to propagate the light inside the waveguide, which in turn expands the FoV. For diffractive waveguide combiners, this can also be explained by the normalized \(k\)-vector diagram, shown in Fig. 11b, where the radius of outer circle is refractive index \(n\). The size of quasi-rectangular region (FoV) is mainly limited by the width of TIR region. To accommodate a larger FoV, the outer circle of TIR region needs to be expanded, which corresponds to an increased \(n\). Although the theoretical maximum
Analysis of FoV limit in diffractive and geometric waveguide combiners. a Eyebox discontinuity in waveguide display. The \(k\)-vector diagram in the \({k}_{z}\)–\({k}_{x}\) plane b before diffraction or reflection, c after diffraction in diffractive waveguide combiner or d after reflection in geometric waveguide combiner. e Relationship between diagonal FoV limit and waveguide refractive index at single wavelength for butterfly design at aspect ratio 16:9 and traditional 2D EPE design at aspect ratio 1:1, respectively. The maximum TIR angle in these two designs is \(75^\circ\)
TIR angle is \(90^\circ\), in practice, it can only reach about \(70^\circ\) because of eyebox discontinuity as shown in Fig. 15a. To keep the eyebox continuous, the distance between two consecutive TIR should be smaller than the sum of the pupil size \({D}_{pupil}\) and beam size (entrance pupil size) \({D}_{in}\) as explained in Eq. (5):
where \({\theta }_{max}\) stands for the maximum TIR angle. Both geometric and diffractive waveguide combiners rely on TIR propagation, but their FoV limits are different because their couplers are based on refraction and reflection for the former, and diffraction effect for the latter. Diffraction usually causes spectral dispersion following the grating diffraction equation (Eq. 1), which dramatically decreases the FoV of diffractive waveguide combiner.
To widen the FoV of diffractive waveguide combiner, multiple approaches have been developed. For example, directing RGB colors into three waveguides. Details of the full-color waveguide display will be discussed in Sect. 4.4. In contrast to diffractive waveguide display, there is almost no spectral spread (dispersion) in geometric waveguide combiner, which can accommodate RGB colors in one waveguide. However, if both waveguide combiners have the same refractive index n, then the FoV of the geometric waveguide combiner will be generally larger than that of the diffractive waveguide combiner, even for a single-color waveguide display. This is because the occupied k space can be compressed during the reflection process on mirrors in a geometric waveguide combiner. Figure 15b represents the \(k\)-vector diagram in the \({k}_{z}\)–\({k}_{x}\) plane, where the central FoV point (represented by the red vector) is designed to maintain the same angle after both reflection and diffraction. In Fig. 15b, the FoV occupies a length h in the \({k}_{x}\) direction before EPE. Diffraction does not change this length as Fig. 15c shows, but reflection can compress the length to \(h\)/2 when the angle \(\beta\) (\(\beta =2\alpha ,\) where \(\alpha\) is the slanted angle of the in-coupling mirror in a geometric waveguide combiner) is 60° as depicted in Fig. 15d, suggesting that the FoV can be doubled in a geometric waveguide combiner. This conclusion can also be understood from the angular space. In a geometric waveguide combiner, the angles before and after reflection are directly mapped to each other by symmetry. However, in a diffractive waveguide combiner, only the tangential component of the \(k\) vector is conserved. By considering the first two terms in the Taylor’s expansion of the sine function at middle point, the grating equation leads to:
In Eq. (6), \({\theta }_{1}\) and \({\theta }_{2}\) represent the angles before and after diffraction, and \({\theta }_{1,avg}\) and \({\theta }_{2,avg}\) are the average angles of \({\theta }_{1}\) and \({\theta }_{2}\), respectively. Taking the example of in-coupling light with \({\theta }_{1,avg}={0}^{o}\) and \({\theta }_{2,avg}=60^\circ\), we find that \(\varDelta {\theta }_{1}=\varDelta {\theta }_{2}/2\). This implies that the FoV is compressed by a factor of 2. Thus, the FoV of a geometric waveguide combiner is approximately twice as large as that of a diffractive waveguide combiner with the same refractive index. Without any special design, a geometric waveguide combiner can achieve \(50^\circ\) FoV if the refractive index is 1.6 [111, 112]. In comparison, the diffractive waveguide combiner can only realize \(70^\circ\) even the waveguide index is as high as 2.0 (Magic Leap 2).
Besides, some special designs can also enlarge the FoV of the system, such as butterfly architecture [108] and IDA architecture [61]. In accordance with the normalized k-vector diagram, both methods rely on achieving a large FoV through top-down pupil expansion while also splitting the FoV in the horizontal direction. Here, let us take the butterfly design in Fig. 12c as an example. Compared to traditional 2D EPE scheme in Fig. 11c, the butterfly design possesses a much larger FoV limit at 16:9 aspect ratio, compared to conventional two consecutive 1D EPE scheme at aspect ratio 1:1, as illustrated in Fig. 15e. As the aspect ratio increases, the FoV limit of the butterfly design will also increase.
Although the FoV limit is contingent to the refractive index of the waveguide, another crucial factor restricting the practical FoV is the angular response of the couplers. Therefore, another method to enlarge FoV is to expand the angular bandwidth of the waveguide couplers. As discussed in Sect. 3, different couplers exhibit distinct optical properties. Consequently, it is essential to examine the methods for expanding the angular response of couplers individually.
In an SRG-based diffractive waveguide combiner, due to the high freedom of SRGs’ geometry as shown in Fig. 3e, the angular bandwidth of the SRG coupler can be expanded by the grating structure [1]. These parameters include the front and back slant angles, grating fill factor, potential coatings, grating depth, and period. Moreover, the refractive index of the grating structure, grating base, grating coating, and grating top layer are additional material parameters contributing to the device optimization. For instance, increasing the refractive index of the grating while simultaneously reducing the back slant angle and increasing the front slant angle can lead to a wider angular response. Further optimizations across an extended section of the grating can be implemented, such as depth modulations, slant modulations, or duty cycle modulations. These techniques aim to achieve an expanded angular bandwidth over a large and uniform eyebox.
Methodology of expanding angular bandwidth for VHGs and PVGs. a Spatial invariant (traditional) in-coupler design and its diffraction property. b Rolled \(k\)-vector in-coupler design and its corresponding diffraction property. c Two-layer structure of PVGs. d Diffraction properties for single-layer PVGs with slanted angle \(26.7^\circ\), \(24.2^\circ\) and two-layer PVG at horizontal period \(450\,\text{nm}\)
In an VHG-based diffractive waveguide combiner, which is also called holographic waveguide combiner, the angular bandwidth of an VHG coupler usually relies on the index modulation \(({\updelta }n)\) as discussed in Sect. 3.2.2. A straightforward method is to use a material with a larger index modulation \(\left({\updelta }n\right)\), for example, using a higher effective refractive index of liquid crystal in HPDLC. Moreover, a fundamental property of any phase grating is that for a given index modulation, a thinner grating has a larger angular bandwidth (this works for PVGs too), except its lower efficiency, as Fig. 5b, d depict. Another way to increase the angular bandwidth of the VHG coupler is the rolled \(k\)-vector of gratings [56, 113] (this also works for SRG and PVG), as shown in Fig. 16. Usually, all the light from different directions will be injected onto the in-coupling grating with only one Bragg plane, which corresponds to a single angular bandwidth as shown in Fig. 16a. However, if the light from different directions is configured to incident on different positions of the in-coupling grating (which is natural for LBS), then the grating could be configured to have a continuously varying slant angle as a function of spatial positions, while the surface period of the grating is held constant. Because the Bragg diffraction efficiency changes with the slant angle according to Eq. (7), the angular bandwidth is thereby expanded effectively as shown in Fig. 16b:
where \({n}_{eff}\) represents the effective refractive index of the medium, \({{\Lambda }}_{B}\) is the Bragg period, \({\lambda }_{b}\) is the Bragg wavelength, \(\theta\) is the incident angle, and φ is the slant angle of the Bragg plane.
In a PVG-based diffractive waveguide combiner, the angular bandwidth is proportional to the employed birefringence \(({\Delta }n)\). Thus, choosing a large \({\Delta }n\) LC material would increase the angular bandwidth. Besides, owing to the self-assembly of liquid crystals, multi-layer structure of PVGs is also feasible to enlarge the angular response [114,115,116]. As depicted in Fig. 16c, each layer of the PVG has the same horizontal period, but with different slanted angles, leading to different response bands, like the blue and red bands in Fig. 16d. The green band represents the expanded angular response of a two-layer PVG. Besides, polarization multiplexing also helps to expand the FoV because the PVG is polarization dependent [117, 118] (this also works for metagratings [89]).
In a metasurface-based diffractive waveguide combiner, metasurfaces share a very similar diffraction nature to expand the angular bandwidth. However, since the metasurfaces have a higher flexibility and versatility of wavefront modulation, a large angular bandwidth with high efficiency can be achieved more easily. As discussed in Sect. 3.2.4, the metagratings with nonintuitive nanoscale patterns not only induces the local modes for basic modulation of phase, but also excites the nonlocally interplaying modes for coupling light into the designated diffraction channels [76]. In this case, the diffraction efficiency maintains high and uniform across a wide range of deflection angles, leading to a large enough angular bandwidth. Although nonlocal optical modes are difficult to precisely design, the topological optimization could offer great convenience to design these metasurfaces [119]. Based on the aforementioned principles and algorithms, both 2D metagratings [91] and slanted titanium dioxide (TiO2) metagratings [120] have been reported to exhibit a broad angular bandwidth and high efficiency, which is promising for expanding the FoV of AR couplers.
In addition to the flexible manipulating of optical modes, by incorporating the modulation of polarization states, the FoV can be further expanded by metagratings as shown in Fig. 7c. For example, the polarization-dependent metagratings capable of encoding the left and right halves of the FoV into two orthogonal polarization channels with minimal crosstalk [89]. The meta-atoms in these metagratings are carefully designed with different slanted angles, heights, and refractive indices, allowing them to selectively diffract transverse electric (TE) and transverse magnetic (TM) polarized light to their corresponding halves of the FoV. As a result, an overall horizontal FoV of \(67^\circ\) at λ = 460 nm is achieved.
In a geometric waveguide combiner, the FoV limit is naturally large (almost doubled) compared to a diffractive waveguide combiner. Therefore, the practical FoV may strongly depend on the couplers. Since the key coupler element is the partially reflective mirrors with certain reflective and transmissive angular bandwidth, using a better coating material or optimizing the angular bandwidth of coatings on these partial mirrors helps enlarge the FoV.
Besides, electrically switchable couplers like LC-based PVG [99], HPDLC [61, 121], LC-infiltrated SRGs [122, 123], and LC-filled metasurface [124] can also be employed to expand the FoV. For instance, one approach is to increase the FoV through temporal sub-FoV stitching at a doubled refresh rate [121].
4.3 Front geometry of waveguide couplers
Unlike other optical combiner architectures, waveguide combiners are desirable since their thickness is barely impacted by the FoV. However, the frontal dimensions of waveguide couplers are closely related to the size of the FoV and the eyebox. To determine the couplers layout, especially diffractive waveguide couplers, the light incident from an extreme angle is considered, visualized with the normalized \(k\)-vector diagram, where the normalized \(k\)-vectors represent the propagation direction of the lights in air or waveguide. Here, we take the 2D EPE design in Fig. 11c as an example. The largest coupler area requirement is usually the out-coupler element, aiming at processing all FoV and building up the entire eyebox. Figure 17a shows how the layout of the out-coupler is dictated by the FoV and eyebox. As FoV and eyebox increase, the out-coupler region will get larger, but the efficiency of waveguide combiner decreases due to the stronger pupil expansion.
Owing to the 2D EPE, the in-coupler area (entrance pupil) is relatively small as discussed in Sect. 4.1. It is mainly dictated by the light engine (microdisplay) and the projection optics, as sketched in Fig. 17b, where the entrance pupil of the waveguide usually matches the exit pupil of the light engine and the projection lens. If the light engine is an LBS, the work distance and FoV will jointly determine the size of the in-coupler, as illustrated in Fig. 17c. As discussed in Sect. 3.2.4, the entrance pupil should be small enough to avoid multiple interactions between the coupled lights and the in-coupler, which helps increase the in-coupling efficiency. Moreover, further reducing the in-coupler size also helps to decrease the waveguide thickness.
Once the relative position and size of the in-coupler and out-coupler is established, the layout of the folding region can be determined [125]. For example, based on the normalized \(k\)-vector diagram in Fig. 17d, the light \({k}_{1}/{k}_{0}\) coming from the in-coupling grating and the light \({k}_{2}/{k}_{0}\) exiting to the out-coupling gratings form a parallelogram overlapping region on the folding grating, as shown in Fig. 17e. Combing all the light from the overlapping region for an extreme incident angle, the boundary of the folding grating can be traced out as depicted in Fig. 17e. Moreover, the gradient efficiency design for the folding grating and the out-coupling grating could also be determined by this ray tracing process. One may observe in Fig. 17e that some pupil expansion in the folding and the out-coupling regions will never be coupled to the user’s eye, thus decreasing the waveguide combiner’s efficiency. While this ray tracing process is for 2D EPE design in Fig. 11c, it works equally well for the diffractive waveguide combiners.
Working principle of waveguide couplers shape design. a Relationship of eyebox, FoV and out-coupler size. b Relationship of microdisplay, projection lens and in-coupler size. c Relationship of LBS and in-coupler size. d Normalized \(k\)-vector diagram of the 2D EPE based on two consecutive 1D EPE, where the black arrows \({k}_{1}/{k}_{0}\) and \({k}_{2}/{k}_{0}\) represent the propagation directions of a certain FoV angle inside waveguide. e Corresponding ray tracing process of the certain FoV angle inside waveguide, where deep blue, orange and green regions represent the effective pupil expansion regions for this FoV angle
4.4 Full-color waveguide displays
In a geometric waveguide combiner, since all the couplers are either refractive or reflective elements, there is almost no spectral spread (except material dispersion) when the incident RGB colors interact with the couplers. As a result, a single waveguide can accommodate both RGB colors simultaneously. However, as discussed in Sect. 3.2, spectral spread (dispersion) takes place when a diffractive optical coupler is employed. To compensate for the spectral spread induced by diffraction, a straightforward method is to use a symmetric in-coupler and out-coupler configuration or couplers with \(k\)-vectors satisfying the triangular relationship.
Schematics of spectral spread in diffractive waveguide combiner. a Spectral spread in single diffractive waveguide scheme. b Boundary condition of FoV for full-color display in this scheme. c Relationship between FoV limit in pupil expansion direction and refractive index \({n}_{g}\) under different maximum TIR angles for this scheme. d Top-down 1D EPE scheme and e right–left 1D EPE scheme under 16:9 aspect ratio
Although the spectral spread can be compensated by the symmetric grating configuration, it is evident from Fig. 18a that the light of different wavelengths is spatially displaced at the out-coupler, which will induce a strong color nonuniformity over the eyebox. Thus, strong exit pupil replication, such as decreasing the distance between two consecutive TIR by reducing the waveguide thickness or decreasing the maximum TIR angle, is required to smoothen out the color nonuniformity. However, this may reduce the FoV over which all the RGB colors can propagate by TIR [126]. When the RGB colors propagate in one waveguide, like in Fig. 18b, the FoV in the pupil expansion direction is usually bounded by the maximum and minimum TIR angles (\({\theta }_{max}; {\theta }_{min}\)), and the refractive index (\({n}_{g}\)) of the waveguide medium as follows:
In Eq. (8), \({n}_{air}\) is the refractive index of air, and \({\lambda }_{min}\) and \({\lambda }_{\max}\) represent the minimum and maximum wavelength guided in the waveguide. The minimum TIR angle \({\theta }_{min}\) can be the critical TIR angle as shown in Eq. (4). Here, let us take R = 630 nm, G = 532 nm, and B = 457 nm as an example, the FoV at the pupil expanded direction can reach 30.3o for \({n}_{g}=2.0\) and \({ \theta }_{max}=90^\circ\), as shown in Fig. 18c. However, considering the eyebox continuity discussed in Sect. 4.2, \({\theta }_{max}\) should be kept at about \(70^\circ\), thus the FoV is only about \(25^\circ\). Although the FoV in the pupil expansion direction is small, a larger diagonal FoV (or FoV at pupil unexpanded direction) could be achieved if the top-down pupil expansion is applied, because the aspect ratio of the microdisplay panel is usually larger than 1:1. For instance, if a 16:9 aspect ratio is applied, the diagonal FoV can reach \(50^\circ\) at the top-down pupil expansion. This phenomenon can be understood from the normalized \(k\)-vector diagram shown in Fig. 18d, e, which also explains why the butterfly and IDA architectures can realize a large FoV [127]. However, this approach requires the gratings to be efficient over a large spectral band and angular band to cover the entire RGB colors.

(a–d Are redrawn from [1])
Full-color display in multiple diffractive waveguides. a Full-color display with three waveguides. b Full-color display with two waveguides, where green light propagates in both waveguides but with a different FoV, blue and red light is guided in two waveguides separately. The normalized \(k\)-vector diagram of the two-waveguide combiner for c top waveguide and d bottom waveguide. The in-coupler and out-coupler can be a diffractive coupler
To overcome the spectral spread and maximize the RGB FoV in a diffractive waveguide combiner, a common solution is to use three stacked waveguides with a proper air gap, e.g., Magic Leap and HoloLens, as sketched in Fig. 19a, where the RGB lights are guided by three different waveguides, respectively. Therefore, each waveguide coupler needs to be specifically designed and optimized for a single color to achieve a large FoV, which means the FoV limit can be the same as the single-color waveguide display discussed in Sect. 4.2. To better understand this architecture, one can observe from Fig. 19a that RGB colors propagate inside the waveguide at same TIR angle, which means three colors have exact same normalized \(k\)-vector diagram. Besides, it is also noticed that an air gap between all plates is required to produce the TIR condition.
Reducing the number of waveguides without deteriorating the image quality while propagating at the maximum FoV is highly desirable because it reduces the weight, size and complexity of the combiner and make it also less prone to MTF reductions due to waveguide misalignments [1]. Both lateral and longitudinal waveguide misalignments, and waveguide surface roughness will degrade the MTF established by the light engine.
Therefore, a simple two waveguides architecture is proposed [128]. In such a scheme, one waveguide supports the whole FoV of red light while the blue and green lights are guided in another waveguide because blue is closer to green in terms of wavelength. While this two-waveguide combiner configuration reduces one-third the weight and size of the traditional three-waveguide combiner, its FoV is narrower. In [1, 126], another two-waveguide combiner has been investigated to realize the same FoV limit of three stacked waveguides as shown in Fig. 19b, where the green FoV is shared between the top and bottom layers. Specifically, one waveguide supports the entire FoV for the blue light and a portion of FoV for the green light, while the bottom waveguide propagates the whole FoV for the red light and remaining part of FoV for the green light. We can have a better understanding of this scheme based on the normalized \(k\)-vector diagram in Fig. 19c, d. However, achieving good color uniformity when combining the green light over the out-coupler necessitates a precise efficiency control at two waveguides to seamlessly merge these two parts of the FoV. Moreover, it is important to address the potential overlap between the two FoV parts, as it can result in a poor field uniformity at the stitching region.

(a Is redrawn from [129], b, c are reprinted with permission from [130] © The Optical Society, and d is reprinted with permission from [131] © SPIE)
Schematics of achromatic display in a single diffractive waveguide. a Achromatic waveguide display using phase multiplexing VHGs. b Diffraction property and structure of nine-layer achromatic metagratings made of \(\text{TiO}_{2}\) and \(\text{SiO}_{2}\). c FDTD simulation result of such achromatic metagratings. d Structure of achromatic metagratings made of Al, Ag, and Au
An alternative approach to avoid the issues induced by a multiple-waveguide display is to use the multiplexing ability of VHG [129, 132] or stacking multiple VHG layers together [133]. For example, three different periods, corresponding to RGB, can be multiplexed onto a single waveguide, as shown in Fig. 20a, but it needs to optimize the coupler parameters to avoid the ghost images induced by crosstalk. To reduce the crosstalk, one waveguide could be multiplexed for blue and red colors while another waveguide works for green color [129]. Besides, the disadvantage of phase multiplexing is its low efficiency.
In a metasurface-based waveguide coupler, the above stacked waveguide strategies could be used as well. However, owing to the high design freedom of metasurface couplers, it becomes possible to realize achromatic couplers. In metasurfaces, chromatic aberration arises from the dispersive nature of meta-atoms and the rapid phase wrapping, causing inherent diffractive dispersion. The dispersion can be quantitatively characterized using a Taylor expansion of the phase response, which can be expressed as follows:
In Eq. (9), the first term on the right side represents the phase response of the meta-atoms at the designed frequency \({\omega }_{0}\), which can be controlled using various methods such as propagation phase [134, 135], geometric phase [136, 137], and resonant phase [138, 139]. The derivatives in the second and third terms represent the group delay and group delay dispersion, respectively, which govern the dispersive response of the meta-atoms. To correct chromatic aberration, the group delay needs to vary as the frequency deviates from \({\omega }_{0}\) to compensate for the difference in wave packet arrival time, while the group delay dispersion ensures that the outgoing wave packets are identical.
Based on this principle, broadband achromatic metasurface-based devices have been designed and fabricated by using coupled waveguides as phase-shift elements, which exhibit linear structural dispersion through the visible spectrum, and incorporating the geometric phase through the rotation of the structure to tailor the wavefront [140,141,142]. Especially, Shrestha et al. analyzed that the achromatic bandwidth, maximum radius of the metalens, numerical aperture, and other optical properties are trading off with each other, as they are limited by the range of phase dispersion covered by the meta-atoms [142]. This conclusion is generally applicable to other metasurface-based devices, indicating that achieving a broadband achromatic meta-device is often constrained by its size. For instance, an achromatic metasurface-based coupler with large-angle coupling covering the full visible spectrum would be limited to a few hundred micrometers in size, which is too small to be applicable for AR display.
However, achieving broadband achromatism is not necessary for AR displays, because the light engines are primarily tricolors. Thus, it is adequate to correct the chromatic aberration at these specific wavelengths. This approach is referred to as “multi-wavelength achromatic” or “RGB achromatic”. By considering the central wavelengths \(({\lambda }_{R}, {\lambda }_{G}, {\lambda }_{B})\) emitted from a light engine and their corresponding bandwidths (\({{\Delta }\lambda }_{R}, {\Delta }{\lambda }_{G}, {\Delta }{\lambda }_{B}\)), the total achromatic bandwidth can be obtained by summing up these individual bandwidths. This strategy is applicable to AR displays that utilize a wide color-gamut light engine based on LEDs, OLEDs, lasers, or other sources with narrow bandwidths. Since the total achromatic bandwidth is much smaller than the entire visible spectrum, it enables a sufficiently large-size waveguide coupler to be fabricated, while still effectively correcting the chromatic aberrations.
Based on the above strategy, several attempts have been made to develop multicolor-achromatic metagrating-based waveguides. One example is a metagrating-based coupler constructed with stacked layers, employing precisely designed nanoridges of titanium dioxide (\(\text{TiO}_{2}\)) and silicon dioxide (\(\text{SiO}_{2}\)) [139] as depicted in Fig. 20b. These couplers are designed in an inverse manner using physics-driven deep neural networks to ensure high coupling and decoupling efficiencies. The simulated outcome is shown in Fig. 20c. Another approach [131] is to streamline the fabrication process by reducing the metastructure to three layers composed of aluminum (Al), silver (Ag), and gold (Au), as shown in Fig. 20d.
Both above instances rely on the multi-layered structures to deflect the RGB beams at angles surpassing the TIR threshold. Nonetheless, fabricating such multi-layered dielectric metagratings remains quite challenging. Recently, dispersion-engineered metagratings is introduced, which is capable of concurrently achieving broadband and polarization-insensitive properties, resulting in a remarkable diffraction efficiency up to 90% [143]. This advancement offers a potential for producing achromatic metasurface-based couplers on a single layer, circumventing the need for resource-intensive simulations and intricate fabrication procedures.
4.5 Uniformity optimization
In a waveguide-based AR display, good image uniformity in the eyebox can be achieved by varying the diffraction efficiency of folding couplers and out-couplers spatially, e.g., changing the height and the duty cycle of SRGs, modulating the slanted angle of VHGs, and adjusting the polarization state in PVGs, etc. [2]. Based on the metrics of AR display described in Sect. 1, there are two types of uniformity issues: color uniformity and brightness uniformity. The former indicates the color reproduction accuracy of an AR display across the FoV and the eyebox. Reflective waveguide combiners barely have the color nonuniformity issue with glass substrate because they are based on refraction and reflection. Recently, Lumus reported the color uniformity of their Maximus waveguide combiner; the color shift Δu′Δv′ < 0.02 around the D65 white point across the entire 50° FoV, which is indistinguishable by human eye [144]. On the other hand, in a diffractive waveguide combiner, the diffraction optical component, such as SRG, causes a strong angular spread and spectral dispersion, which in turn leads to a degraded color uniformity across the entire FoV and the eyebox. Therefore, the three-waveguide approach (one for each color) is commonly used; each layer having its own grating parameters optimized for a specific color. This reduces the color nonuniformity across the eyebox. However, when RGB LEDs are used in the light engine, each emission band has its own full width at half maximum (FWHM ≈ 30 nm). Thus, the color nonuniformity can be minimized by the optimization process but cannot be eliminated completely. As a result, geometric waveguide combiners should exhibit a significantly better color uniformity than diffractive waveguide combiners. Although the color uniformity of a diffractive waveguide combiner can be improved by electronic correction, the tradeoff is the compromised optical efficiency [145].
Besides, brightness uniformity over the entire FoV and eyebox is also difficult to achieve due to the strict manipulation of diffraction (or reflection) efficiency and bandwidth in the folding couplers and out-couplers [146, 147]. It can also be mitigated through electronic correction with a slightly compromised optical efficiency. The detailed brightness uniformity comparison between geometric waveguide and diffractive waveguide remains to be investigated.
5 Conclusions and perspectives
In this review, we investigate recent advances in waveguide-based AR displays and discuss the prospects of two existing geometric and diffractive waveguide combiners. In Table 2, we summarize their key optical performances. Generally, geometric waveguide combiners exhibit advantages in potentially large FoV (e.g., \(50^\circ \; \text{at}\; {n}_{g}=1.6\) [111, 112]), good uniformity, negligible eye glow, and high efficiency (5% for 2D EPE and \(50^\circ\) FoV [111, 112]), but with more complicated fabrication process and low yield. Therefore, high quality coating technology should be developed. In contrast, diffractive waveguide combiners have a relatively low efficiency (up to ~ 2.1% for \(30^\circ\) FoV [100]), a smaller FoV (e.g., \(70^\circ \;{ \text{at}\; n}_{g}=2 \left[14\right]\)), and they also suffer from other issues, such as color nonuniformity, eye glow, and rainbow effect. All these issues remain to be overcome. Particularly, color uniformity and optical efficiency are two major challenges in a diffractive waveguide combiner. Therefore, how to improve diffractive waveguide efficiency while keeping a reasonably good uniformity will be the most important task in the future. The rapid development of various EPE designs, fabrication methods, and materials performance of diffractive couplers, like optical interference lithography for SRGs and HPDLC with a large index modulation, could improve the performance of diffractive waveguide combiners to be comparable to that of geometric waveguide combiners. However, current index modulation of VHGs is still inadequate to extend the FoV beyond \(50^\circ\). Low-cost and high-quality manufacture process remains to be developed for SRGs. Besides, a novel diffractive coupler, PVG, offers distinct features such as dynamic modulation ability, to increase the functionality of waveguide-based AR displays. At the same time, emerging metasurface-based couplers provide extensive design freedoms, thus enabling novel functionalities, like the achromatic characteristics. Further advances in device engineering and manufacturing process are expected to boost the performance of PVGs and metasurface-based couplers for AR displays.
Availability of data and materials
All data and materials needed to evaluate the conclusions in the paper are present in the paper. Additional data related to this paper may be requested from the authors.
Change history
04 January 2024
A Correction to this paper has been published: https://doi.org/10.1186/s43593-023-00060-4
References
B.C. Kress, I. Chatterjee, Waveguide combiners for mixed reality headsets: a nanophotonics design perspective. Nanophotonics 10(1), 41–74 (2021)
J. Xiong, E.L. Hsiang, Z. He, T. Zhan, S.T. Wu, Augmented reality and virtual reality displays: emerging technologies and future perspectives. Light Sci. Appl. 10, 216 (2021)
D. Cheng, Q. Wang, Y. Liu, H. Chen, D. Ni, X. Wang, C. Yao, Q. Hou, W. Hou, G. Luo, Y. Wang, Design and manufacture AR head-mounted displays: a review and outlook. Light Adv. Manuf. 2(3), 350–369 (2021)
A. Bauer, J.P. Rolland, The optics of augmented reality displays, in Springer Handbook of Augmented Reality. ed. by A.Y.C. Nee, S.K. Ong (Springer International Publishing, Cham, 2023), pp.187–209
S. Mystakidis, Metaverse. Encyclopedia 2(1), 486–497 (2022)
M. Grieves, J. Vickers, Digital twin: mitigating unpredictable, undesirable emergent behavior in complex systems, in Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches. ed. by F.-J. Kahlen, S. Flumerfelt, A. Alves (Springer International Publishing, Cham, 2017), pp.85–113
S. Greenwold, Spatial computing, Master, Massachusetts Institute of Technology, 2003
Y. Amitai, S. Reinhorn, A.A. Friesem, Visor-display design based on planar holographic optics. Appl. Opt. 34(8), 1352–1356 (1995)
Y. Amitai, P-21: extremely compact high-performance hmds based on substrate-guided optical element. SID Symp. Digest 35(1), 310–313 (2004)
S.J. Walker, J. Jahns, Optical clock distribution using integrated free-space optics. Opt. Commun. 90(4–6), 359–371 (1992)
J. Yan, Q. Wang, D. Li, J. Zhang, Edge-lighting light guide plate based on micro-prism for liquid crystal display. J. Disp. Technol. 5(9), 355–357 (2009)
S.A. Cholewiak, Z. Başgöze, O. Cakmakci, D.M. Hoffman, E.A. Cooper, A perceptual eyebox for near-eye displays. Opt. Express 28(25), 38008–38028 (2020)
International Committee for Display Metrology, Information Display Measurements Standard (Society for Information Display (SID), 2023)
K.R. Curtis, Unveiling magic leap 2’s advanced ar platform and revolutionary optics. Proc. SPIE 11932, 119320P (2022)
K.Y. Chen, Y.W. Li, K.H. Fan-Chiang, H.C. Kuo, H.C. Tsai, P-181L: late-news poster: color sequential front-lit LCOS for wearable displays. SID Symp. Digest 46(1), 1737–1740 (2015)
K. Yin, E.-L. Hsiang, J. Zou, Y. Li, Z. Yang, Q. Yang, P.C. Lai, C.L. Lin, S.T. Wu, Advanced liquid crystal devices for augmented reality and virtual reality displays: principles and applications. Light Sci. Appl. 11, 161 (2022)
E.L. Hsiang, Z. Yang, Q. Yang, P.C. Lai, C.L. Lin, S.T. Wu, AR/VR light engines: perspectives and challenges. Adv. Opt. Photonics 14(4), 783–861 (2022)
K. Blankenbach, Q. Yan, R.J. Obrien, Handbook of Visual Display Technology (Springer, Cham, 2020)
N.W. Melena, J.T. Wiersma, Pixel size requirements for AR/MR. Proc. SPIE 11765, 1176505 (2021)
Y.W. Li, C.W. Lin, K.Y. Chen, K.H. Fan-Chiang, H.C. Kuo, H.C. Tsai, 18.5L: late-news paper: front-lit LCOS for wearable applications. SID Symp. Digest 45(1), 234–236 (2014)
E. Tang, The smallest LCoS engine: introducing the AG-30L2. Proc. SPIE 12450, 124500O (2023)
Y. Zhao, S. Pan, Y. Li, Z. Sun, Z. Yuan, Y. Huo, M.C. Tseng, L. Lu, V. Vashchenko, A.K. Srivastava, H.S. Kwok, X. Chen, X. Zhang, S. Zhang, L. Chen, High contrast ratio and fast response ferroelectric liquid crystal displays based on alignment optimization. Opt. Mater. 143, 114257 (2023)
A. Pandey, Y. Xiao, M. Reddeppa, Y. Malhotra, J. Liu, J. Min, Y. Wu, Z. Mi, A red-emitting micrometer scale LED with external quantum efficiency > 8%. Appl. Phys. Lett. 122(15), 151103 (2023)
Y. Qian, Z. Yang, Y.H. Huang, K.H. Lin, S.T. Wu, Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays. Opto-Electron. Sci. 1, 220021 (2022)
J. Shin, H. Kim, S. Sundaram, J. Jeong, B.-I. Park, C.S. Chang, J. Choi, T. Kim, M. Saravanapavanantham, K. Lu, S. Kim, J.M. Suh, K.S. Kim, M.-K. Song, Y. Liu, K. Qiao, J.H. Kim, Y. Kim, J.-H. Kang, J. Kim, D. Lee, J. Lee, J.S. Kim, H.E. Lee, H. Yeon, H.S. Kum, S.-H. Bae, V. Bulovic, K.J. Yu, K. Lee, K. Chung, Y.J. Hong, A. Ougazzaden, J. Kim, Vertical full-colour micro-LEDs via 2D materials-based layer transfer. Nature 614, 81–87 (2023)
B.C. Kress, Optical Architectures for Augmented-, Virtual-, and Mixed-Reality Headsets (SPIE, 2020).
O. Cakmakci, J. Rolland, Head-worn displays: a review. J. Disp. Technol. 2(3), 199–216 (2006)
Y. Amitai, P-27: a two-dimensional aperture expander for ultra-compact, high-performance head-worn displays. SID Symp. Digest 36(1), 360–363 (2005)
Z. Liu, D. Wang, H. Gao, M. Li, H. Zhou, C. Zhang, Metasurface-enabled augmented reality display: a review. Adv. Photonics 5(3), 034001 (2023)
X. Feng, J. Wang, Z. Zhao, S. Choi, M. Wang, M. Hu, L. Lu, B. Silverstein, Liquid crystal photonic technology in AR application (conference presentation). Proc. SPIE PC12442, PC1244201 (2023)
S.B. Kim, J.H. Park, Optical see-through Maxwellian near-to-eye display with an enlarged eyebox. Opt. Lett. 43(4), 767–770 (2018)
M.H. Choi, Y.G. Ju, J.H. Park, Holographic near-eye display with continuously expanded eyebox using two-dimensional replication and angular spectrum wrapping. Opt. Express 28(1), 533–547 (2020)
J. Zou, L. Li, S.T. Wu, Gaze-matched pupil steering Maxwellian-view augmented reality display with large angle diffractive liquid crystal lenses. Adv. Photonics Res. 3(5), 2100362 (2022)
J. Xiong, Y. Li, K. Li, S.T. Wu, Aberration-free pupil steerable Maxwellian display for augmented reality with cholesteric liquid crystal holographic lenses. Opt. Lett. 46(7), 1760–1763 (2021)
R. Shechter, Y. Amitai, A.A. Friesem, Compact beam expander with linear gratings. Appl. Opt. 41(7), 1236–1240 (2002)
T. Levola, Diffractive optics for virtual reality displays. J. Soc. Inf. Disp. 14(5), 467–475 (2006)
L. Gu, D. Cheng, Q. Wang, Q. Hou, Y. Wang, Design of a two-dimensional stray-light-free geometrical waveguide head-up display. Appl. Opt. 57(31), 9246–9256 (2018)
Y. Amitai, N. Amitai, Compact head-mounted display system, United States patent US20200124854A1, 23 Apr 2020
D. Cheng, Y. Wang, C. Xu, W. Song, G. Jin, Design of an ultra-thin near-eye display with geometrical waveguide and freeform optics. Opt. Express 22(17), 20705–20719 (2014)
Y. Zhou, J. Zhang, F. Fang, Design of a large field-of-view two-dimensional geometrical waveguide. Results Opt. 5, 100147 (2021)
T. Levola, P. Laakkonen, Replicated slanted gratings with a high refractive index material for in and outcoupling of light. Opt. Express 15(5), 2067–2074 (2007)
DigiLens, DigiLens Announces Launch of SRG+ (DigiLens Inc., Sunnyvale, 2023)
M.G. Moharam, T.K. Gaylord, Diffraction analysis of dielectric surface-relief gratings. J. Opt. Soc. Am. 72(10), 1385–1392 (1982)
J.M. Miller, N. de Beaucoudrey, P. Chavel, J. Turunen, E. Cambril, Design and fabrication of binary slanted surface-relief gratings for a planar optical interconnection. Appl. Opt. 36(23), 5717–5727 (1997)
E.G. Loewen, E. Popov, Diffraction Gratings and Applications (CRC Press, New York, 2018)
W.C. Liu, G. Jin, Y.F. Xie, P. Sun, B. Zhou, W. Jia, J. Wang, C. Zhou, Broadband high-efficiency polarization-independent double-layer slanted grating for RGB colors. Opt. Commun. 488, 126864 (2021)
S.Y. Chou, P.R. Krauss, P.J. Renstrom, Nanoimprint lithography. J. Vacuum Sci. Technol. B Microelectron. Nanometer. Struct. Process. Meas. Phenom. 14(6), 4129–4133 (1996)
C. Thanner, Nanoimprint (lithography): small impressions with huge impact. Proc. SPIE 12450, 124500W (2023)
B.C. Kress, Venturing beyond the limits of nano-imprint lithography for immersive displays. Proc. SPIE PC12497, PC1249701 (2023)
H.J. Lee, H.W. Ro, C.L. Soles, R.L. Jones, E.K. Lin, W. Wu, D.R. Hines, Effect of initial resist thickness on residual layer thickness of nanoimprinted structures. J. Vacuum Sci. Technol. B Microelectron. Nanometer. Struct. Process. Meas. Phenom. 23(6), 3023–3027 (2005)
B.C. Kress, M. Pace, Holographic optics in planar optical systems for next generation small form factor mixed reality headsets. Light Adv. Manuf. 3(4), 771–801 (2022)
J. Xiong, K. Yin, K. Li, S.T. Wu, Holographic optical elements for augmented reality: principles, present status, and future perspectives. Adv. Photonics Res. 2(1), 2000049 (2021)
M.A. Ferrara, V. Striano, G. Coppola, Volume holographic optical elements as Solar concentrators: an overview. Appl. Sci. 9(1), 193 (2019)
D. Ni, D. Cheng, Y. Wang, T. Yang, X. Wang, C. Chi, Y. Wang, Design and fabrication method of holographic waveguide near-eye display with 2D eye box expansion. Opt. Express 31(7), 11019–11040 (2023)
Z. Shen, Y. Zhang, Y. Weng, X. Li, Characterization and optimization of field of view in a holographic waveguide display. IEEE Photonics J. 9(6), 1–11 (2017)
C. Yu, Y. Peng, Q. Zhao, H. Li, X. Liu, Highly efficient waveguide display with space-variant volume holographic gratings. Appl. Opt. 56(34), 9390–9397 (2017)
A. Liu, Y. Zhang, Y. Weng, Z. Shen, B. Wang, Diffraction efficiency distribution of output grating in holographic waveguide display system. IEEE Photonics J. 10(4), 1–10 (2018)
L.V. Natarajan, C.K. Shepherd, D.M. Brandelik, R.L. Sutherland, S. Chandra, V.P. Tondiglia, D. Tomlin, T.J. Bunning, Switchable holographic polymer-dispersed liquid crystal reflection gratings based on thiolene photopolymerization. Chem. Mater. 15(12), 2477–2484 (2003)
Y.J. Liu, X.W. Sun, Holographic polymer-dispersed liquid crystals: materials, formation, and applications. Adv. OptoElectron. 2008, 684349 (2008)
T.J. Bunning, L.V. Natarajan, V.P. Tondiglia, R.L. Sutherland, Holographic polymer-dispersed liquid crystals (H-PDLCs). Annu. Rev. Mater. Sci. 30(1), 83–115 (2000)
J.D. Waldern, S. Abraham, M.M. Popovich, DigiLens holographic photopolymers for wide angle AR waveguides. Proc. SPIE 11367, 113670O (2020)
C.C. Bowley, A.K. Fontecchio, G.P. Crawford, J.J. Lin, L. Li, S. Faris, Multiple gratings simultaneously formed in holographic polymer-dispersed liquid-crystal displays. Appl. Phys. Lett. 76(5), 523–525 (2000)
T. Yoshida, K. Tokuyama, Y. Takai, D. Tsukuda, T. Kaneko, N. Suzuki, T. Anzai, A. Yoshikaie, K. Akutsu, A. Machida, A plastic holographic waveguide combiner for light-weight and highly-transparent augmented reality glasses. J. Soc. Inform. Disp. 26(5), 280–286 (2018)
Y.H. Lee, K. Yin, S.T. Wu, Reflective polarization volume gratings for high efficiency waveguide-coupling augmented reality displays. Opt. Express 25(22), 27008–27014 (2017)
O. Sakhno, Y. Gritsai, H. Sahm, J. Stumpe, Fabrication and performance of efficient thin circular polarization gratings with Bragg properties using bulk photo-alignment of a liquid crystalline polymer. Appl. Phys. B 124, 52 (2018)
V.G. Chigrinov, V.M. Kozenkov, H.-S. Kwok, Photoalignment of Liquid Crystalline Materials: Physics and Applications (Wiley, Chichester, 2008)
O. Yaroshchuk, Y. Reznikov, Photoalignment of liquid crystals: basics and current trends. J. Mater. Chem. 22(2), 286–300 (2012)
J. Xiong, S.T. Wu, Planar liquid crystal polarization optics for augmented reality and virtual reality: from fundamentals to applications. eLight 1, 3 (2021)
A.G.-S. Chen, D.J. Brady, Surface-stabilized holography in an azo-dye-doped liquid crystal. Opt. Lett. 17(17), 1231–1233 (1992)
L. Nikolova, T. Todorov, M. Ivanov, F. Andruzzi, S. Hvilsted, P.S. Ramanujam, Polarization holographic gratings in side-chain azobenzene polyesters with linear and circular photoanisotropy. Appl. Opt. 35(20), 3835–3840 (1996)
Y. Weng, D. Xu, Y. Zhang, X. Li, S.T. Wu, Polarization volume grating with high efficiency and large diffraction angle. Opt. Express 24(16), 17746–17759 (2016)
R. Ozaki, K. Saiki, S. Hashimura, K. Kadowaki, H. Yoshida, M. Ozaki, Geometrical optics analysis of diffraction in patterned cholesteric liquid crystals. ACS Appl. Opt. Mater. (2023). https://doi.org/10.1021/acsaom.3c00093
N. Yu, P. Genevet, M.A. Kats, F. Aieta, J.P. Tetienne, F. Capasso, Z. Gaburro, Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334(6054), 333–337 (2011)
W. Feng, J. Zhang, Q. Wu, A. Martins, Q. Sun, Z. Liu, Y. Long, E.R. Martins, J. Li, H. Liang, RGB achromatic metalens doublet for digital imaging. Nano Lett. 22(10), 3969–3975 (2022)
M. Khorasaninejad, W.T. Chen, R.C. Devlin, J. Oh, A.Y. Zhu, F. Capasso, Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352(6290), 1190–1194 (2016)
D. Sell, J. Yang, S. Doshay, R. Yang, J.A. Fan, Large-angle, multifunctional metagratings based on freeform multimode geometries. Nano Lett. 17(6), 3752–3757 (2017)
X. Ni, N.K. Emani, A.V. Kildishev, A. Boltasseva, V.M. Shalaev, Broadband light bending with plasmonic nanoantennas. Science. 335(6067), 427–427 (2012)
S. Sun, K.-Y. Yang, C.-M. Wang, T.-K. Juan, W.T. Chen, C.Y. Liao, Q. He, S. Xiao, W.-T. Kung, G.-Y. Guo, L. Zhou, D.P. Tsai, High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 12(12), 6223–6229 (2012)
Q. Yang, S. Kruk, Y. Xu, Q. Wang, Y.K. Srivastava, K. Koshelev, I. Kravchenko, R. Singh, J. Han, Y. Kivshar, I. Shadrivov, Mie-resonant membrane Huygens’ metasurfaces. Adv. Funct. Mater. 30(4), 1906851 (2020)
S. Wang, P.C. Wu, V.C. Su, Y.-C. Lai, C. Hung Chu, J.W. Chen, S.H. Lu, J. Chen, B. Xu, C.H. Kuan, T. Li, S. Zhu, D.P. Tsai, Broadband achromatic optical metasurface devices. Nat. Commun. 8, 187 (2017)
J. Yao, R. Lin, M.K. Chen, D.P. Tsai, Integrated-resonant metadevices: a review. Adv. Photonics 5(2), 024001 (2023)
P. Lalanne, S. Astilean, P. Chavel, E. Cambril, H. Launois, Blazed binary subwavelength gratings with efficiencies larger than those of conventional échelette gratings. Opt. Lett. 23(14), 1081–1083 (1998)
C. Zhang, S. Divitt, Q. Fan, W. Zhu, A. Agrawal, Y. Lu, T. Xu, H.J. Lezec, Low-loss metasurface optics down to the deep ultraviolet region. Light Sci. Appl. 9, 55 (2020)
H. Liang, Q. Lin, X. Xie, Q. Sun, Y. Wang, L. Zhou, L. Liu, X. Yu, J. Zhou, T.F. Krauss, J. Li, Ultrahigh numerical aperture metalens at visible wavelengths. Nano Lett. 18(7), 4460–4466 (2018)
S.C. Malek, A.C. Overvig, A. Alù, N. Yu, Multifunctional resonant wavefront-shaping meta-optics based on multilayer and multi-perturbation nonlocal metasurfaces. Light Sci. Appl. 11, 246 (2022)
H. Huang, A.C. Overvig, Y. Xu, S.C. Malek, C.C. Tsai, A. Alù, N. Yu, Leaky-wave metasurfaces for integrated photonics. Nat. Nanotechnol. 18, 580–588 (2023)
J. Goodsell, P. Xiong, D.K. Nikolov, A.N. Vamivakas, J.P. Rolland, Metagrating meets the geometry-based efficiency limit for AR waveguide in-couplers. Opt. Express 31(3), 4599–4614 (2023)
Z. Liu, C. Zhang, W. Zhu, Z. Huang, H.J. Lezec, A. Agrawal, L.J. Guo, Compact stereo waveguide display based on a unidirectional polarization-multiplexed metagrating in-coupler. ACS Photonics 8(4), 1112–1119 (2021)
Z. Shi, W.T. Chen, F. Capasso, Wide field-of-view waveguide displays enabled by polarization-dependent metagratings. Proc. SPIE 10676, 1067615 (2018)
Y. Liu, Y. Shi, Z. Wang, Z. Li, On-chip integrated metasystem with inverse-design wavelength demultiplexing for augmented reality. ACS Photonics 10(5), 1268–1274 (2023)
C. Choi, T. Choi, J.G. Yun, C. Yoo, B. Lee, Two-dimensional angular bandwidth broadening of metasurface grating. Adv. Photonics Res. 3(12), 2200158 (2022)
J.-S. Park, S. Zhang, A. She, W.T. Chen, P. Lin, K.M.A. Yousef, J.X. Cheng, F. Capasso, All-glass, large metalens at visible wavelength using deep-ultraviolet projection lithography. Nano Lett. 19(12), 8673–8682 (2019)
H. Kang, D. Lee, Y. Yang, D.K. Oh, J. Seong, J. Kim, N. Jeon, D. Kang, J. Rho, Emerging low-cost, large-scale photonic platforms with soft lithography and self-assembly. Photonics Insights 2(2), R04 (2023)
C. Zhang, H. Subbaraman, Q. Li, Z. Pan, J.G. Ok, T. Ling, C.-J. Chung, X. Zhang, X. Lin, R.T. Chen, L. JayGuo, Printed photonic elements: nanoimprinting and beyond. J. Mater. Chem. C 4(23), 5133–5153 (2016)
X. Xiao, Y. Zhao, X. Ye, C. Chen, X. Lu, Y. Rong, J. Deng, G. Li, S. Zhu, T. Li, Large-scale achromatic flat lens by light frequency-domain coherence optimization. Light Sci. Appl. 11(1), 323 (2022)
A.J. Grant, Social acceptability in AR/MR waveguide displays. Proc. SPIE 11932, 119321T (2022)
H.Y. Lee, N. Huang, E. Fest, P. Saarikko, E. Shipton, G. Calafiore, Rainbow reduction in waveguide displays, United States patent US10761330B2, 1 Sept 2020
X. Feng, Y.H. Lee, B. Amirsolaimani, M. Wang, J. Wang, L. Lu, Liquid crystal polarization hologram element for reducing rainbow effects, United States patent US20230080580A1, 16 Mar 2023
Y. Li, J. Semmen, Q. Yang, S.T. Wu, Switchable polarization volume gratings for augmented reality waveguide displays. J. Soc. Inform. Disp. 31(5), 328–335 (2023)
I.J. Vartiainen, A. Sunnari, The unseen simplicity: design vision for XR waveguide combiners. Proc. SPIE 12450, 124500E (2023)
A. Sunnari, Dispelix: waveguide displays for AR. Proc. SPIE 11764, 117640D (2021)
T. Levola, Method and optical system for coupling light into a waveguide, United States patent US20050002611A1, 6 Jan 2005
Y. Lin, H. Xu, R. Shi, L. Lu, S.T. Zhang, D. Li, Enhanced diffraction efficiency with angular selectivity by inserting an optical interlayer into a diffractive waveguide for augmented reality displays. Opt. Express 30(17), 31244–31255 (2022)
J. Olkkonen, P. Myöhänen, Diffractive display element with grating mirror, United States patent US20210215942A1, 15 July 2021
P. Saarikko, P. Kostamo, Waveguide, United States patent US20160231568A1, 11 Aug 2016
Y. Weng, Y. Zhang, W. Wang, Y. Gu, C. Wang, R. Wei, L. Zhang, B. Wang, High-efficiency and compact two-dimensional exit pupil expansion design for diffractive waveguide based on polarization volume grating. Opt. Express 31(4), 6601–6614 (2023)
D. Grey, S. Talukdar, Exit pupil expanding diffractive optical waveguiding device, United States patent US10359635B2, 23 July 2019
T. Vallius, J. Tervo, Waveguides with extended field of view, United States patent US9791703B1, 17 Oct 2017
J.D. Waldern, A.J. Grant, M.M. Popovich, Wide field of view multiplexed photopolymer consumer AR displays. Proc. SPIE 11310, 113100I (2020)
V.N. Borisov, N.V. Muravyev, R.A. Okun, A.E. Angervaks, G.N. Vostrikov, M.V. Popov, A DOE-based waveguide architecture of wide field of view display for augmented reality eyewear. Proc. SPIE 11765, 117650B (2021)
Z. Bouhamri, Diffractive vs holographic vs reflective waveguides: what should the industry target? Proc. SPIE 12450, 124500L (2023)
A. Frommer, 2D reflective waveguide-based near to eye displays for consumer AR glasses. Proc. SPIE 12450, 124500I (2023)
J.D. Waldern, A.J. Grant, M.M. Popovich, 17-4: DigiLens AR HUD waveguide technology. SID Symp. Digest 49(1), 204–207 (2018)
Y. Gu, Y. Weng, R. Wei, Z. Shen, C. Wang, L. Zhang, Y. Zhang, Holographic waveguide display with large field of view and high light efficiency based on polarized volume holographic grating. IEEE Photonics J. 14(1), 1–7 (2022)
K. Yin, H.Y. Lin, S.T. Wu, Chirped polarization volume grating with ultra-wide angular bandwidth and high efficiency for see-through near-eye displays. Opt. Express 27(24), 35895–35902 (2019)
X. Xiang, J. Kim, M.J. Escuti, Bragg polarization gratings for wide angular bandwidth and high efficiency at steep deflection angles. Sci. Rep. 8, 7202 (2018)
C. Yoo, K. Bang, M. Chae, B. Lee, Extended-viewing-angle waveguide near-eye display with a polarization-dependent steering combiner. Opt. Lett. 45(10), 2870–2873 (2020)
C.P. Chen, Y. Cui, Y. Ye, F. Yin, H. Shao, Y. Lu, G. Li, Wide-field-of-view near-eye display with dual-channel waveguide. Photonics 8(12), 557 (2021)
J. Jiang, M. Chen, J.A. Fan, Deep neural networks for the evaluation and design of photonic devices. Nat. Rev. Mater. 6, 679–700 (2021)
Y. Liu, G. Qu, X. Jiang, J. Han, Z. Ji, Z. Liu, Q. Song, S. Yu, S. Xiao, Slanted TiO2 metagratings for large-angle, high-efficiency anomalous refraction in the visible. Laser Photonics Rev. 17(6), 2200712(2023)
J.D. Waldern, A.J. Grant, M.M. Popovich, DigiLens switchable Bragg grating waveguide optics for augmented reality applications. Proc. SPIE 10676, 106760G (2018)
S. Toubi, M. Colard, Y. Lee, B. Racine, A. Suhm, D. Grosso, B. Kerzabi, C. Martinez, Study and validation of switchable grating using liquid crystal for active waveguide addressing. Proc. SPIE 12442, 124420B (2023)
A. Héliot, S. Pelloquin, O. Gauthier-Lafaye, A. Monmayrant, H. Camon, T. Gacoin, K. Lahlil, L. Martinelli, C. Biver, S. Archambeau, Characterization of liquid crystals impregnated micrometric diffraction gratings for an active near-IR light extraction control. Microsyst. Technol. 28, 1535–1543 (2022)
D. Franklin, Y. Chen, A. Vazquez-Guardado, S. Modak, J. Boroumand, D. Xu, S.T. Wu, D. Chanda, Polarization-independent actively tunable colour generation on imprinted plasmonic surfaces. Nat. Commun. 6, 7337 (2015)
P.H. Chiu, T.W. Huang, Y.S. Hsu, B.K. Zhang, S.-T. Chien, W.C. Hung, C.Y. Huang, Y.C. Cheng, Compact design principle for diffractive exit-pupil expander in AR near-eye system. Proc. SPIE 11931, 119310C (2022)
Y. Ding, Y. Li, Q. Yang, S.T. Wu, Design optimization of polarization volume gratings for full-color waveguide-based augmented reality displays. J. Soc. Inform. Disp. 31, 380–386 (2023)
J. Olkkonen, Diffractive outlet pupil dilator for display applications, U.S. patent FI129306B, 30 Nov 2021
Y. Weng, Y. Zhang, J. Cui, A. Liu, Z. Shen, X. Li, B. Wang, Liquid-crystal-based polarization volume grating applied for full-color waveguide displays. Opt. Lett. 43(23), 5773–5776 (2018)
H. Mukawa, K. Akutsu, I. Matsumura, S. Nakano, T. Yoshida, M. Kuwahara, K. Aiki, A full-color eyewear display using planar waveguides with reflection volume holograms. J. Soc. Inform. Disp. 17(3), 185–193 (2009)
W.Q. Chen, D.S. Zhang, S.Y. Long, Z.Z. Liu, J.J. Xiao, Nearly dispersionless multicolor metasurface beam deflector for near eye display designed by a physics-driven deep neural network. Appl. Opt. 60(13), 3947–3953 (2021)
R. Ditcovski, O. Avayu, T. Ellenbogen, Full-color optical combiner based on multilayered metasurface design. Proc. SPIE 10942, 109420S (2019)
T. Utsugi, M. Sasaki, K. Ono, Y. Tada, Volume holographic waveguide using multiplex recording for head-mounted display. ITE Trans. Media Technol. Appl. 8(4), 238–244 (2020)
J.A. Piao, G. Li, M.L. Piao, N. Kim, Full color holographic optical element fabrication for waveguide-type head mounted display using photopolymer. J. Opt. Soc. Korea 17(3), 242–248 (2013)
Z. Zhou, J. Li, R. Su, B. Yao, H. Fang, K. Li, L. Zhou, J. Liu, D. Stellinga, C.P. Reardon, T.F. Krauss, X. Wang, Efficient silicon metasurfaces for visible light. ACS Photonics. 4(3), 544–551 (2017)
M. Khorasaninejad, A.Y. Zhu, C. Roques-Carmes, W.T. Chen, J. Oh, I. Mishra, R.C. Devlin, F. Capasso, Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 16(11), 7229–7234 (2016)
R.C. Devlin, M. Khorasaninejad, W.T. Chen, J. Oh, F. Capasso, Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc. Natl. Acad. Sci. 113(38), 10473–10478 (2016)
B.H. Chen, P.C. Wu, V.C. Su, Y.C. Lai, C.H. Chu, I.C. Lee, J.W. Chen, Y.H. Chen, Y.C. Lan, C.H. Kuan, D.P. Tsai, GaN metalens for pixel-level full-color routing at visible light. Nano Lett. 17(10), 6345–6352 (2017)
M. Decker, I. Staude, M. Falkner, J. Dominguez, D.N. Neshev, I. Brener, T. Pertsch, Y.S. Kivshar, High-efficiency dielectric Huygens’ surfaces. Adv. Opt. Mater. 3(6), 813–820 (2015)
L. Zhang, J. Ding, H. Zheng, S. An, H. Lin, B. Zheng, Q. Du, G. Yin, J. Michon, Y. Zhang, Z. Fang, M.Y. Shalaginov, L. Deng, T. Gu, H. Zhang, J. Hu, Ultra-thin high-efficiency mid-infrared transmissive Huygens meta-optics. Nat. Commun. 9, 1481 (2018)
W.T. Chen, A.Y. Zhu, V. Sanjeev, M. Khorasaninejad, Z. Shi, E. Lee, F. Capasso, A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 13, 220–226 (2018)
S. Wang, P.C. Wu, V.C. Su, Y.C. Lai, M.-K. Chen, H.Y. Kuo, B.H. Chen, Y.H. Chen, T.T. Huang, J.H. Wang, R.M. Lin, C.H. Kuan, T. Li, Z. Wang, S. Zhu, D.P. Tsai, A broadband achromatic metalens in the visible. Nat. Nanotechnol. 13, 227–232 (2018)
S. Shrestha, A.C. Overvig, M. Lu, A. Stein, N. Yu, Broadband achromatic dielectric metalenses. Light Sci. Appl. 7, 85 (2018)
W.T. Chen, J.S. Park, J. Marchioni, S. Millay, K.M.A. Yousef, F. Capasso, Dispersion-engineered metasurfaces reaching broadband 90% relative diffraction efficiency. Nat. Commun. 14, 2544 (2023)
A. Frommer, Reflective waveguides near to eye displays for consumer AR glasses. Proc. SPIE 11932, 119321R (2022)
P.A. Greenhalgh, Diffractive and reflective waveguides: a game of trade-offs (conference presentation). Proc. SPIE 11310, 113102F (2020)
D. Ni, D. Cheng, Y. Liu, X. Wang, C. Yao, T. Yang, C. Chi, Y. Wang, Uniformity improvement of two-dimensional surface relief grating waveguide display using particle swarm optimization. Opt. Express 30(14), 24523–24543 (2022)
S. Yan, E. Zhang, J. Guo, P. Jia, K. Yang, L. Kong, Eyebox uniformity optimization over the full field of view for optical waveguide displays based on linked list processing. Opt. Express 30(21), 38139–38151 (2022)
Funding
Goertek Electronics.
Author information
Authors and Affiliations
Contributions
YD proposed the idea and initiated the project. YD, QY, YL, ZY and ZW conducted the experiment and simulation and wrote the manuscript. HL and S-TW supervised the project and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
The original online version of this article was revised: The author name is changed from Yuqian Ding to Yuqiang Ding.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, Y., Yang, Q., Li, Y. et al. Waveguide-based augmented reality displays: perspectives and challenges. eLight 3, 24 (2023). https://doi.org/10.1186/s43593-023-00057-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43593-023-00057-z