Abstract
Background
The buckling load as well as the natural frequency under axial load for non-prismatic beam is a changeling problem. Determination of buckling load, natural frequency, and elastic deflection is very important in civil applications. The current paper used both perturbation method (PM), analytic method, and differential quadrature method (DQM), numerical method, to find buckling load and natural frequency with different end supports. The deflection of the beam resting on an elastic foundation under transverse distributed and axial loads is also obtained. Both PM and DQM are used for non-prismatic beams with rectangular and circular cross sections in the vibration analysis. The comparisons of results obtained from both PM and DQM showed perfect agreement with analytical solution for uniform beams with different end supports. The PM and DQM succeeded powerfully for investigating the buckling load as well as the natural frequency for non-prismatic beam.
Results
The percentage of relative error between DQM and PM doesn’t exceed than 5% if the gradient of rectangular section height and the gradient of circular section radius are less than 0.6. As the gradient of height and radius increase, the maximum deflection decreases and the location of maximum deflection displaced toward the smaller moment of inertia.
Conclusions
The PM has not been used for solving the problem of non-prismatic beams resting on elastic foundations subjected to transverse distributed and axial loads. The current research proved the good ability of PM as an analytical solution for a complicated problem and defined its range of accuracy as compared to DQM. Also, it introduced accurate empirical formulae to find both natural frequency and buckling load of non-prismatic beams. These empirical formulae represent a good achievement in vibration analysis of non-prismatic beams.
Similar content being viewed by others
1 Background
The DQM is a numerical technique for initial and/or boundary value problems. It was developed by the late Richard Bellman and his associates in the early 70 s and, since then, the method has been successfully employed in a variety of problems in physical and engineering sciences. The DQM has been projected by its proponents as a potential alternative to the conventional numerical solution techniques such as the finite difference and finite element methods [1]. Non-prismatic beams resting on elastic foundations are important structural elements. The dynamic characteristics of such non-prismatic beams are of considerable importance in many designs. The vibration of non-prismatic beams is formulated as a fourth-order differential equation of variable coefficients; it is possible to determine their exact solutions [2, 3], using homotopy analysis [2] or the Green's functions method [3]. However, in most cases, the solution is obtained by approximate methods such as finite difference [4], DQM [5], boundary element method [6], the power series [7, 8], Lagrange multiplier formulation [9], coupled displacement field method [10]. Sato [11] reported the transverse vibration of linearly tapered beams using Ritz method. He studied the effect of end restraints and axial load on the natural frequencies.
The PM is a method which relies on there being a dimensionless parameter in the problem that is relatively small: ε < < 1. The PM is used to analyze the nonlinear vibration behavior of imperfect general structures under static load. The effects on the linearized and nonlinear vibrations caused by geometric imperfections, a static fundamental state, and a nontrivial static state are included in the perturbation procedure. The theory is applied in the nonlinear vibration analysis of cylindrical shells [12]. However, the PM has not been used for solving the problem of non-uniform beams resting on elastic foundations under the action of transverse distributed load and axial load. In this paper, the PM is used to obtain the non-dimensional frequencies and buckling loads for a non-prismatic beam resting on elastic foundations. Also, the deflected shape can be obtained by PM.
In the present paper, the concepts of both DQM and PM are presented for the vibration analysis of non-prismatic Euler–Bernoulli beam. The DQM was widely used in vibration analysis of non-prismatic beams. In this paper, we used it again to solve the same problem to investigate accuracy of PM in analysis of vibration of non-prismatic beams. The generated PM results for non-prismatic beam also verified with Dua [13]. From the comparison between PM and DQM, an empirical formula is investigated to find natural frequency and buckling load of non-prismatic beams. These empirical formulae represent a good achievement in vibration analysis of non-prismatic beams. A full parametric study is then performed.
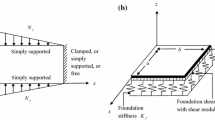
Figure 1 shows the schematic diagram for non-prismatic beam on elastic foundation subjected to axial load “n” and transverse uniform load \(p\left( x \right)\). The free vibration of a non-uniform beam is governed by the following equation
Using the non-dimensional parameters: \(W = \frac{Y}{L}\), \(X = \frac{x}{L}\), \(Q = \frac{{nL^{2} }}{{{\text{EI}}_{0} }}\), \(K = \frac{{kL^{4} }}{{{\text{EI}}_{0} }}\), \(P = \frac{{p(x)L^{2} }}{{{\text{EI}}_{0} }}\),\(\Omega^{4} = \frac{{\rho A(x)L^{4} \omega^{2} }}{{EI_{0} }}\), and \(S(X) = \frac{{{\text{EI}}(x)}}{{{\text{EI}}_{0} }}\).
Equation (1) by direct substitution will be reduced to
where \(W\) is non-dimensional transverse deflection, \(X\) is non-dimensional position along beam length, \(Q\) is non-dimensional axial load parameter, \(K\) is linear non-dimensional stiffness of elastic foundation parameter, \(P\) is non-dimensional transverse distributed load, \(\Omega\) is non-dimensional frequency parameter, \(I_{0}\) is the base mass moment of inertia, and S(X) is non-dimensional stiffness parameter of the beam.
In the current paper, the beam has a rectangular cross section of linear variable height and constant width. The height is \(h_{{\text{o}}}\) at the base and \(h_{1}\) at the end. The equations of non-dimensional height, non-dimensional cross section, and non-dimensional stiffness parameters are:
Another case is considered for a beam of circular cross section of linear variable radius. The equations of non-dimensional radius, non-dimensional cross section, and non-dimensional stiffness parameters are:
2 Methods
2.1 Perturbation method (PM)
The PM is employed for rectangular cross section as:
By substituting Eqs. (5, 6) in Eq. (2) and considering \(\gamma\) as perturbation parameter \(\varepsilon\)
where \(0 \le \varepsilon \le 1\).
The solution will be presented for non-uniform rectangular cross section; for zero-order perturbation,
For first-order perturbation,
For second-order perturbation,
For third-order perturbation,
The left-hand side of Eqs. (8–12) is the same ordinary differential equation and its complementary solution is:
where \(C_{i1} ,C_{i2} ,C_{i3} ,C_{i4}\) are constants, \(i = 0,1,2,3\) and
Assuming that the transverse load is a sine load across the beam length, the particular solutions for zero and first order are:
where
where
The total non-dimensional lateral deflection is:
The natural frequency and buckling load can be calculated as:
For a free non-prismatic beam on elastic foundation:
For a non-prismatic beam subjected to axial load:
Applying the boundary conditions to obtain four linear equations in the constants \(C_{i1} ,C_{i2} ,C_{i3} ,C_{i4}\) in the form of:
To have a non-trivial solution of Eq. (20), determinant of \(\left[ G \right]_{4*4}\) must be equal to zero. This will lead the critical value of \(\beta,\) and then, we can find the non-dimensional frequency and buckling load parameters for non-prismatic beam as
where \(\Omega _{{\text{o}}} \;{\text{and}}\;Q_{{\text{o}}}\) are the non-dimensional frequency and buckling load parameters for uniform beam.
2.2 Differential quadrature method (DQM)
The DQM requires to divide the domain of the problem into N pointes. Then, the derivatives at any point are approximated by a weighted linear summation of all the functional values along the domain, as follows [14,15,16]:
where Aij represented the weighting coefficient and N is the number of grid points in the whole domain. The weighting coefficient can be determined by making use of Lagrange formula as follows:
where
By applying Eq. (28) at N grid points, the following algebraic formulations to compute the weighting coefficients Aij can be obtained.
For calculating the weighting coefficients of mth order
The accuracy of DQM is affected by choosing of the number, N, and type of the sampling points, xi. The optimal selection of the sampling points in the vibration problems, is the normalized Gauss–Chebyshev–Lobatto points [12, 13],
Applying the DQM scheme to the non-dimensional governing Eq. (8) yields:
where \(W_{i}\) is the functional value at the grid points \(X_{i}\), \(C_{ij}^{\left( 2 \right)}\),\(C_{ij}^{\left( 3 \right)}\) and \(C_{ij}^{\left( 4 \right)}\) are the weighting coefficient matrices of the second-, third- and fourth-order derivatives. The result is a linear system of equations of N unknowns that can be written in a matrix form as
Four boundary conditions are needed to solve the problem. For clamped and simply supported end conditions, the discrete boundary conditions using the DQM can be written as:
where n0, n1 may be taken either 1 or 2; value of 1 represents simply supported and value of 2 represents clamped end. the boundary condition can be written in a matrix form as
Combining governing Eqs. (33) and boundary conditions (34), we get
; introducing the Lagrange multiplier approach [17], Eq. (40) can be modified to square matrix as
where \(l\) is the Lagrange multiplier and \(\upsilon\) is the Eigen-value to be obtained. Rewrite Eq. (41) in the form
Solve the Eigen-value problem in Eq. (42) to find non-dimensional frequency parameter and non-dimensional buckling load parameter. This approach can be used to easily implement any boundary condition without modifying weighting coefficients of the DQM.
3 Results
3.1 Verification for prismatic beams
The present PM and DQM results for uniform beam with different end support, listed in Table 1, are identical as compared with the analytical solution in [15]. It is clear that there is a very good agreement between the present results and the previous analytic solution for uniform beam. On the other hand, the results of non-dimensional frequency obtained from the present DQM for non-uniform beam, listed in Table 2, are compared to numerical values obtained in [11] giving a good agreement with error less than 0.5%.
3.2 Results of vibration parameters for non-prismatic beams
The DQM is applied with different numbers of grid points. The optimum number of grid points is found to be 15 points. After 15 grid points, the results of DQM are fixed [16]. The DQM showed good ability for the analysis of non-prismatic beam with different end supports. The results of non-dimensional frequency and buckling parameters are obtained using the present PM and DQM for clamped–clamped ends, and different values of \(\gamma\) are presented in Tables 3, 4, 5 and 6. The results showed agreement between results for \(< 0.6\). If \(\gamma = 1\), the relative error reached about 20%. The accuracy of the PM depends on the value of \(\gamma\), so as \(\gamma\) increases, the effect of neglected terms affects the results of PM.
Figure 2 presents the percentage relative error between the PM and DQM for the first non-dimensional frequency of non-prismatic beam calculated by the following equation:
3.3 Deflection for non-prismatic beams
The deflection of non-prismatic beam with circular cross section under the effect of constant vertical load is plotted for two different cases of end supports and different values of \(\gamma\) as shown in Figs. 3 and 4. As \(\gamma\) increases, the maximum deflection decreases and the location of maximum deflection displaced toward the smaller moment of inertia as predicted.
4 Discussion
Results of DQM and PM for uniform beams, as shown in Table 1, showed perfect agreement with analytical solution for non-dimensional frequency parameter. DQM results for non-uniform beams, as shown in Table 2, proved its perfect ability in prediction of non-dimensional frequency parameter as compared with numerical results given in [11]. The error for listed cases is less than 0.1%. Good results of DQM required fifteen discretization points.
Both methods are used to predict non-dimensional frequency and buckling parameters for non-uniform beams with rectangular or circular cross sections, as shown in Tables 3, 4, 5 and 6. All cases have clamped–clamped ends. The results showed good ability of PM in prediction of non-dimensional frequency and non-dimensional buckling load when the height or the radius increasing ratios are less than 60%. The results of PM are not reliable for higher increasing ratio of height or radius.
Deflection results for clamped–clamped (Fig. 3), clamped–simply supported (Fig. 4), non-uniform beams subjected to a constant uniform load showed good ability of PM in prediction of lateral deflection and the effect of radius increasing ratio on the location of maximum lateral deflection along the beam length. As the increasing ratio of radius increases, the location of maximum lateral deflection moves toward the position of maximum height. Maximum deflection decreases as the increasing ratio of radius increases.
5 Conclusions
The present paper presents two mathematical techniques to investigate the buckling load as well as the natural frequency under axial and transverse load for non-prismatic beams. The deflection of the beam resting on an elastic foundation under transverse distributed and axial loads is also obtained for different end supports. From the present study, the following points could be concluded:
-
The PM and DQM succeeded powerfully for investigating the buckling load as well as the natural frequency for non-prismatic beam.
-
The percentage of relative error between DQM and PM doesn’t exceed than 5% for \(\gamma < 0.6\).
-
As \(\gamma\) increases, the maximum deflection decreases and the location of maximum deflection displaced toward the smaller moment of inertia.
Availability of data and material
Not applicable.
Abbreviations
- PM:
-
Perturbation method
- DQM:
-
Differential quadrature method
References
Bert CW, Malik M (1996) Differential quadrature method in computational mechanics: a review. ASME Appl Mech Rev 49(1):1–28
Hassan HN, El-Tawil MA (2012) A new technique of using homotopy analysis method for second order nonlinear differential equations. Appl Math Comput 219:708–728
Kukla S, Zamojska I (2005) Application of the Green’s function method in free vibration analysis of non-uniform beams. Sci Res Inst Math Comput Sci 1(4):87–94
Yeh Y-L, Jang M-J, Wang C-C (2006) Analyzing the free vibrations of a plate using finite difference and differential transformation method. Appl Math Comput 178:493–501
Taha MH, Abohadima S (2008) Mathematical model for vibrations of non-uniform flexural beams. EngMech 15(1):3–11
Xiao JR (2001) Boundary element analysis of unilateral supported reissner plates on elastic foundations. Comput Mech 27:1–10
Qaisi MI (1997) A power series solution solution for the non-linear vibration of beams. J Sound Vib 199(4):587–594
Zamojska I (2014) Solution of differential equation for the Euler Bernoulli beam. J Appl Math Comput Mech 13(4):157–162
Cekus D (2012) Free vibration of a cantilever tapered Timoshenko beam, Scientific Research of the Institute of Mathematics and Computer. Science 4(11):11–17
Korabathina R, Koppanati MS (2016) Linear free vibration analysis of tapered Timoshenko beams using coupled displacement field method. Math Models Eng 2(1):27–33
Sato K (1999) Transverse vibrations of linearly tapered beams with ends restrained elastically against rotation subjected to axial force. Int J Mech Sci 22:109–115
Jansen EL (2008) A perturbation method for nonlinear vibrations of imperfect structures: application to cylindrical shell vibrations. Int J Solids Struct 45(3–4):1124–1145
Du H, Lim MK, Lin RM (1994) Application of generalized differential quadrature method to structural problems. Int J Numer Eng 37:1881–1896
Chen S, Du H (1997) A generalized approach for implementing general boundary conditions in the GDQ free vibration analysis of plates. Int J Solids Struct 34:837
Chen S, Du H (1997) Implementation of clamped and simply supported boundary conditions in the GDQ free vibration analysis of beams and plates. Int J Solids Struct 34:819
Chang S (2000) Differential Quadrature and Its Application in Engineering. Springer
Wilson EL (2002) Three Dimensional Static and Dynamic Analysis of Structures, Computers and Structures. Inc
Acknowledgements
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
MA team leader who initiates the concept of the paper derived the governing equations. SA performed the analytical solution by perturbation method. ME applied the numerical method of differential quadrature and wrote the manuscript. All authors have read and approved the manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elshabrawy, M., Abdeen, M.A. & Beshir, S. Analytic and numeric analysis for deformation of non-prismatic beams resting on elastic foundations. Beni-Suef Univ J Basic Appl Sci 10, 57 (2021). https://doi.org/10.1186/s43088-021-00144-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43088-021-00144-5