Skip to main content
SpringerLink
Log in

Buckling and vibration analysis of non-homogeneous rectangular Kirchhoff plates resting on two-parameter foundation

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

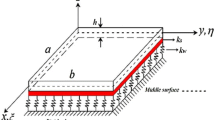
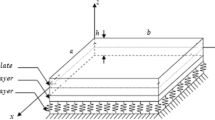
Effect of two parameter foundation has been analyzed on the transverse vibrations of non-homogeneous rectangular plates of uniform thickness when the two opposite edges are simply supported and these are subjected to linearly varying in-plane forces on the basis of Kirchhoff plate theory. The non-homogeneity of the plate material is assumed to arise due to the exponential variation in young’s modulus and density of the plate material along one direction. Using Levy approach, the partial differential equation governing the motion of such plates has been reduced to an ordinary differential equation. Differential quadrature method has been used to obtain the frequency equations for two different combinations of clamped and simply supported boundary conditions at the other two edges. These frequency equations have been solved numerically using MATLAB. The lowest three roots of these equations have been reported as first three natural frequencies corresponding to the first three modes of vibration. The effect of various parameters such as foundation parameters, non-homogeneity parameter, density parameter, aspect ratio, in-plane force parameter and loading parameter has been investigated on the frequencies. By allowing the frequency to approach zero, the critical buckling loads for various value of different parameters have been computed. Three dimensional mode shapes for a specified plate for both the boundary conditions have been plotted. A comparison of results with those available in literature has been presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Leissa AW (1969) Vibration of plates (NASA SP 160). U.S. Government Office, Washington D.C.

    Google Scholar 

  2. Reddy JN (2007) Theory and analysis of elastic plates and shells, 2nd edn. Taylor and Francis CRC Press, Philadelphia

    Google Scholar 

  3. Gorman DJ (2000) Free vibration analysis of completely free rectangular plates by the superposition-Galerkin method. J Sound Vib 237(5):901–914

    Article  ADS  MATH  Google Scholar 

  4. Manna MC (2005) Free vibration analysis of isotropic rectangular plates using a high- order triangular finite element with shear. J Sound Vib 281:735–759

    Article  Google Scholar 

  5. Wu JH, Liu AQ, Chen HL (2007) Exact solutions for free- vibration analysis of rectangular plates using Bessel’s functions. J Appl Mech 74:1247–1251

    Article  Google Scholar 

  6. Li WL, Zhang X, Du J, Liu ZG (2009) An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J Sound Vib 321(1–2):254–269

    ADS  Google Scholar 

  7. Civalek Ö (2009) A four-node discrete singular convolution for geometric transformation and its application to numerical solution of vibration problem of arbitrary straight-sided quadrilateral plates. Appl Math Model 33(1):300–314

    Article  MATH  MathSciNet  Google Scholar 

  8. Wang X, Xu S (2010) Free vibration analysis of beams and rectangular plates with free edges by the discrete singular convolution. J Sound Vib 329(10):1780–1792

    Article  ADS  Google Scholar 

  9. Zhu Q, Wang X (2011) Free vibration analysis of thin isotropic and an isotropic rectangular plate by the discrete singular convolution algorithm. Int J Numer Methods Eng 86:782–800

    Article  MATH  Google Scholar 

  10. Esen I (2012) A new finite element for transverse vibration of rectangular thin plates under a moving mass. Finite Elem Anal Des 66:26–35

    Article  MathSciNet  Google Scholar 

  11. Brush OD, Almroth OB (1975) Buckling of bars, plates and shells. McGraw-Hill, New York

    MATH  Google Scholar 

  12. Gorman DG (1983) Vibration of thermally stressed polar orthotropic annular plates. Earthq Eng Struct Dyn 11:843–855

    Article  Google Scholar 

  13. Wang CM, Wang CY, Reddy JN (2004) Exact solution for buckling of structural members. CRC, Boca Raton

    Book  Google Scholar 

  14. Gorman DJ (2000) Free vibration and buckling of in-plane loaded plates with rotational elastic edge support. J Sound Vib 229(4):755–773

    Article  ADS  MATH  Google Scholar 

  15. Devarakonda KVV, Bert CW (2004) Buckling of rectangular plate with nonlinearly distributed compressive loading on two opposite sides. Mech Adv Mat Struct 11:433–444

    Article  Google Scholar 

  16. Kang JH, Leissa AW (2005) Exact solutions for the buckling of rectangular plates having linearly varying in-plane loading on two opposite simply supported edges. Int J Solids Struct 42:4220–4238

    Article  MATH  Google Scholar 

  17. Jana B, Bhaskar K (2007) Analytical solutions for buckling of rectangular plates under non-uniform biaxial compression or uniaxial compression with in-plane lateral restraint. Int J Mech Sci 49:1104–1112

    Article  Google Scholar 

  18. Kshirsagar S, Bhaskar K (2008) Accurate and elegant free vibration and buckling studies of orthotropic rectangular plates using untruncated infinite series. J Sound Vib 314:837–850

    Article  ADS  Google Scholar 

  19. Civalek O, Korkmaz A, Demir C (2010) Discrete singular convolution approach for buckling analysis of rectangular Kirchhoff plates subjected to compressive loads on two-opposite edges. Adv Eng Softw 41:557–560

    Article  MATH  Google Scholar 

  20. Tang Y, Wang X (2011) Buckling of symmetrically laminated rectangular plates under parabolic edge compressions. Int J Mech Sci 53:91–97

    Article  Google Scholar 

  21. Tsiatas GC, Yiotis AJ (2013) A BEM-based meshless solution to buckling and vibration problems of orthotropic plates. Eng Anal Bound Elem 37:579–584

    Article  MATH  MathSciNet  Google Scholar 

  22. Rao GV, Rao BP, Raju IS (1974) Vibrations of inhomogeneous thin plates using a high-precision triangular element. J Sound Vib 34(3):444–445

    Article  ADS  Google Scholar 

  23. Tomar JS, Gupta DC, Jain NC (1982) Vibration of non-homogeneous plates of variable thickness. J Acoust Soc Am 72:851–855

    Article  ADS  MATH  Google Scholar 

  24. Chakraverty S, Jindal R, Agarwal VK (2007) Vibration of non-homogeneous orthotropic elliptic and circular plates with variable thickness. J Sound Vib 129:256–259

    Google Scholar 

  25. Dhanpati Lal R (2007) Transverse vibrations of non-homogeneous orthotropic rectangular plates of variable thickness: a spline technique. J Sound Vib 306:203–214

    Article  ADS  MATH  Google Scholar 

  26. Lal R, Kumar Y (2012) Boundary characteristic orthogonal polynomials in the study of transverse vibrations of non-homogeneous rectangular plates with bilinear thickness variation. Shock Vib 19:349–364

    Article  Google Scholar 

  27. Dhanpati Lal R (2007) Quintic splines in the study of buckling and vibration of non-homogeneous orthotropic rectangular plates with variable thickness. Int J Appl Math Mech 3(3):18–35

    Google Scholar 

  28. Kumar Y, Lal R (2011) Buckling and vibration of orthotropic non-homogeneous rectangular plates with bilinear thickness variation. J Appl Mech 78:061012-11

    Google Scholar 

  29. Winkler E (1867) Die Lehre Von Der Elastizitat Und Festigkeit. Dominicus, Prague

    Google Scholar 

  30. Hetenyi M (1946) Beams on elastic foundations. The University of Michigan Press, Ann Arbor

    Google Scholar 

  31. Filonenko-Borodich MM (1940) Some approximate theories of the elastic foundation, Uchenyie Zapiski Moskovskogo Gosudarstuennogo Universiteta Mechanika 46, 3–18 (in Russian)

  32. Pasternak PL (1954)On a new method of analysis of an elastic foundation by means of two foundation constants (in Russian), Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu i Arkhitekture, Moscow

  33. Vlasov VZ, Leontev UN (1966) Beams, plates and shells on elastic foundations (translated from Russian), Israel Program for Scientific Translation Jerusalem, Israel

  34. Kerr AD (1964) Elastic and viscoelastic foundation models. J Appl Mech 31(3):491–498

    Article  MATH  Google Scholar 

  35. Hetenyi M (1950) A general solution for the bending of beams on an elastic foundation of arbitrary continuity. J Appl Phys 21:55–58

    Article  ADS  MATH  Google Scholar 

  36. Reissner E (1967) Note on the formulation of the problem of the plate on an elastic foundation. Acta Mech 4:88–91

    Article  MATH  Google Scholar 

  37. Gupta P, Bhardwaj N (2004) Vibration of rectangular orthotropic elliptic plates of quadratically varying thickness resting on elastic foundation. J Vib Acoust 126:132–140

    Article  Google Scholar 

  38. Leung VT, Zhu B (2005) Transverse vibration of mindlin plates on two-parameter foundation by analytical trapezoidal p-elements. J Eng Mech 131(11):1140–1145

    Article  Google Scholar 

  39. Civalk O (2006) Harmonic differential quadrature-finite differences coupled approaches for geometrically nonlinear static and dynamic analysis of rectangular plates on elastic foundation. J Sound Vib 294:966–980

    Article  ADS  Google Scholar 

  40. Gupta US, Lal R, Sharma S (2008) Effect of Pasternak foundation on asixymmetric vibration of non-uniform polar orthotropic annular plates. Int J Appl Math Mech 4(5):9–25

    Google Scholar 

  41. Dhanpati Lal R (2009) Effect of nonhomogeneity on vibration of orthotropic rectangular plates of varying thickness resting on Pasternak foundation. J Vib Acoust 131:011007-1–011007-9

    Google Scholar 

  42. Sharma S, Gupta US, Lal R (2010) Effect of Pasternak foundation on axisymmetric vibration of polar orthotropic annular plates of varying thickness. J Vib Acoust 132:041001-1-13

  43. Tajeddini V, Ohadi A, Sadighi M (2011) Three-dimensional free vibration of variable thickness thick circular and annular isotropic and functionally graded plates on Pasternak foundation. Int J Mech Sci 53:300–308

    Article  Google Scholar 

  44. Khalili SMR, Abbaspour P, Malekzadeh Fard K (2013) Buckling of non-ideal simply supported laminated plate on Pasternak foundation. Appl Math Comput 219:6420–6430

    Article  MATH  MathSciNet  Google Scholar 

  45. Xiaohui R, Wanji C, Zhen W (2011) A new zig-zag theory and C0 plate bending element for composite and sandwich plates. Arch Appl Mech 81:185–197

    Article  MATH  Google Scholar 

  46. Shu C, Wu WX, Ding H, Wang CM (2007) Free vibration analysis of plates using least square-based finite difference method. Comput Methods Appl Mech Eng 196:1330–1343

    Article  ADS  MATH  Google Scholar 

  47. Ashour AS (2006) Vibration of angle-ply symmetric laminated composite plates with edges elastically restrained. Comp Struct 74(3):294–302

    Article  Google Scholar 

  48. Kerboua Y, Lakis AA, Thomas M, Marcouiller L (2007) Hybrid method for vibration analysis of rectangular plates. Nucl Eng Desig 237:791–801

    Article  Google Scholar 

  49. Chen CS, Fung CP, Chein RD (2006) A further study on nonlinear vibration of initially stressed plates. Appl Math Comput 172:349–367

    Article  MATH  MathSciNet  Google Scholar 

  50. Semnani SJ, Attarnejad R, Firouzjaei RK (2013) Free vibration analysis of variable thickness thin plates by two-dimensional differential transform method. Acta Mech 224:1643–1658

    Article  MATH  MathSciNet  Google Scholar 

  51. Bhaskar K, Sivaram A (2008) Untruncated infinite series superposition method for accurate flexural analysis of isotropic/orthotropic rectangular plates with arbitrary edge conditions. Compos Struct 83:83–92

    Article  Google Scholar 

  52. Aghdam MM, Falahatgar SR (2003) Bending analysis of thick laminated plates using extended Kantorovich method. Compos Struct 62(3–4):279–283

    Article  Google Scholar 

  53. Huanga M, Mab XQ, Sakiyamaa T, Matsudaa H, Morita C (2007) Free vibration analysis of rectangular plates with variable thickness and point support. J Sound Vib 300:435–452

    Article  ADS  Google Scholar 

  54. Bellman RE, Casti J (1971) Differential quadrature and long term integration. J Math Anal Appl 34:235–238

    Article  MATH  MathSciNet  Google Scholar 

  55. Bert CW, Jang SK, Striz AG (1988) Two new approximate methods for analyzing free vibration of structural components. AIAA J 26:612–618

    Article  ADS  MATH  Google Scholar 

  56. Liew KM, Han JB, Xiao ZM (1996) Differential quadrature method for Mindlin plates on Winkler foundation. Int J Mech Sci 38(4):405–421

    Article  MATH  Google Scholar 

  57. Bellman RE, Kashef BG, Casti J (1972) Differential quadrature: technique for the rapid solution of nonlinear partial differential equation. J Comput Phys 10:40–52

    Article  ADS  MATH  MathSciNet  Google Scholar 

  58. Bert CW, Malik M (1996) Differential quadrature method in computational mechanics: a review. Appl Mech Rev 49:1–28

    Article  ADS  Google Scholar 

  59. Shu C (2000) Differential quadrature and its application in engineering. Springer-Verleg, London

    Book  MATH  Google Scholar 

  60. Malekzadeh P, Karami G (2004) Vibration of non-uniform thick plates on elastic foundation by differential quadrature method. Eng Struct 26:1473–1482

    Article  Google Scholar 

  61. Wang X, Gan L, Wang Y (2006) A differential quadrature analysis of vibration and buckling of an SS-C-SS-C rectangular plate loaded by linearly varying in-plane stress. J Sound Vib 298:420–431

    Article  ADS  Google Scholar 

  62. Wang X, Gan L, Zhang Y (2008) Differential quadrature analysis of the buckling of thin rectangular plates with cosine-distributed compressive loads on two opposite edges. Adv Eng Softw 30:497–504

    Article  Google Scholar 

  63. Malekzadeh P, Golbahar Haghighi MR, Alibeygi Beni A (2012) Buckling analysis of functionally graded arbitrary straight-sided quadrilateral plates on elastic foundations. Meccanica 47:321–333

    Article  MATH  MathSciNet  Google Scholar 

  64. Yas MH, Jodaei A, Irandoust S, Nasiri Aghdam M (2012) Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates on elastic foundations. Meccanica 47:1401–1423

    Article  MATH  MathSciNet  Google Scholar 

  65. Tahouneh V, Naei M (2014) A novel 2-D six-parameter power-law distribution for three-dimensional dynamic analysis of thick multi- directional functionally graded rectangular plates resting on a two-parameter elastic foundation. Meccanica 49:91–109

    Article  MATH  MathSciNet  Google Scholar 

  66. Leissa AW, Kang JH (2002) Exact solution for vibration and buckling of an SS-C-SS-C rectangular plate loaded by linearly varying in plane stresses. Int J Mech Sci 44:1925–1945

    Article  MATH  Google Scholar 

  67. Jain RK, Soni SR (1979) Free vibration of rectangular plates of parabolically varying thickness. Indian J Pure Appl Math 4(3):267–277

    Google Scholar 

  68. Kumar Y, Lal R (2012) Vibrations of nonhomogeneous orthotropic rectangular plates with bilinear thickness variation resting on Winkler foundation. Meccanica 47:893–915

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors wish to express their sincere thanks to the learned reviewers for their constructive comments in improving the paper. One of the authors, Renu Saini, is thankful to Ministry of Human Resources and Development (MHRD), India for the financial support to carry out this research work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee, 247667, India

    Roshan Lal & Renu Saini

Authors
  1. Roshan Lal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Renu Saini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Renu Saini.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lal, R., Saini, R. Buckling and vibration analysis of non-homogeneous rectangular Kirchhoff plates resting on two-parameter foundation. Meccanica 50, 893–913 (2015). https://doi.org/10.1007/s11012-014-0073-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0073-0

Keywords

Search

Navigation