Abstract
The development of a dual-frequency multi-constellation satellite-based augmentation system (DFMC SBAS) is in progress worldwide. The broadcasted dual-frequency range error (DFRE) integrity parameter reflects the effects of satellite ephemeris and clock corrections. A user uses the DFRE to calculate the protection level and then determines whether the DFMC SBAS service satisfies the requirements of the current flight phase. However, the calculation of the DFRE has not been reported. Herein, a DFRE estimation method is proposed based on the projection method. Using the ephemeris–clock covariance matrix of each satellite, the maximal projection direction was solved, and the projection of the covariance matrix on this direction was used as the DFRE to form an envelope for the maximal corrected error. Results show that the DFRE can form an envelope of the maximal corrected error with a set probability, and the integrity performance in the user segment satisfies the Category I precision approach requirement.
Similar content being viewed by others
Introduction
The existing global navigation satellite systems (GNSSs) can no longer satisfy the accuracy and integrity requirements of high life-safety users, such as those in aviation. The satellite-based augmentation system (SBAS) can improve the positioning accuracy and monitor the integrity of the GNSS. When an abnormality occurs in the GNSS, the user is alerted in a timely fashion by the SBAS.
Currently, the SBASs in service are the USA’s Wide Area Augmentation System (WAAS), EU’s European Geostationary Navigation Overlay System (EGNOS), Japanese MTSAT Satellite-based Augmentation System, and Indian GPS-aided GEO augmented navigation system; all these SBASs are single-frequency (SF) SBASs (Shao et al. 2017). Owing to the effect of ionospheric anomalies, the service performance of the SF SBAS has not satisfied the requirements of Category I precision approach (CAT-I). Only WAAS and EGNOS have satisfied the requirements of the localizer performance with vertical guidance at 200 feet decision height (Jason 2016; ESSP 2016).
To reduce the effect of ionospheric anomalies on the service performance and enhance the service performance using multiple GNSSs, which can improve the geometric layout of constellations, the SBAS Interoperate Working Group and International Civil Aviation Organization DFMC SBAS SARPS Working Group are developing DFMC SBAS international standards. China has participated in the development of DFMC SBAS international standards, and is actively constructing the BeiDou Satellite Based Augmentation System (BDSBAS) in accordance with international standards and plans to provide initial service by 2020. The BDSBAS will broadcast SF SBAS messages on GEO B1C signal and DFMC SBAS messages on GEO B2a signal (Shen and Lu 2016).
The DFMC SBAS can simultaneously augment up to 92 satellites (ICAO NSP 2017), including the GPS, GALILEO, GLONASS, and BeiDou Navigation Satellite System (BDS). Using the L5 signal of the SBAS GEO satellite, the DFMC SBAS broadcasts the satellite ephemeris and clock corrections and integrity parameters, such as the dual-frequency range error (DFRE) and the covariance matrix, to improve the positioning accuracy and integrity (IWG 2016a, b). Because the user can eliminate the effect of the ionosphere in a dual-frequency positioning mode, the DFMC SBAS no longer broadcasts the corrections and integrity parameters related to the ionosphere (IWG 2016a, b).
The DFRE is an important integrity parameter of the DFMC SBAS, which reflects the effect of ephemeris and clock corrections, and is provided to users in the form of σDFRE. Users use the σDFRE to calculate the protection level (PL) and compare it with the alert limit (AL) of the current flight phase to determine whether the DFMC SBAS service is available. The DFRE (σDFRE) must envelop the maximal corrected error of the corrections with a certain probability to ensure that users can envelop the positioning error (PE) with the PL calculated using the DFRE.
Currently, the DFRE estimation method has not been published outside of China, whereas results pertaining to the DFRE have not been reported in China. This paper proposes a DFRE estimation method based on the projection method; the calculated DFRE can represent the worst case of the corrected error in the service area, and the integrity performance in the user segment satisfies the CAT-I requirement. Currently, the construction of BDSBAS is at the critical moment and the DFRE method proposed herein is expected to be applicable to BDSBAS.
DFRE calculation based on projection method
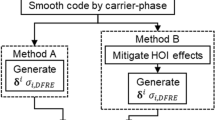
The DFRE calculation based on the projection method includes satellite ephemeris–clock correction and DFRE calculations. The process flow is shown in Fig. 1. First, the ephemeris correction, clock correction, and ephemeris–clock covariance matrix were calculated using the pseudo-range residual error; subsequently, the maximal projection direction was obtained by mathematical derivation based on the covariance matrix, and the projection of the covariance matrix on this direction was regarded as the DFRE.
Calculation of ephemeris/clock correction
Using the L1 and L5 pseudo-range measurements and carrier phase measurements from the monitoring stations, the data processing station first performs data preprocessing and subsequently eliminates the ionospheric delay, tropospheric delay, satellite ephemeris distance, satellite clock bias, and other factors from the smoothed pseudo-range. After synchronizing the interstation clock bias, the pseudo-range residual error is obtained using the following equation:
where \(\Delta \rho_{i}^{j}\) is the pseudo-range residual error of satellite j observed by monitoring station i; \(\Delta R^{j} = \left[ {\begin{array}{*{20}c} {\Delta x^{j} } & {\Delta y^{j} } & {\Delta z^{j} } \\ \end{array} } \right]^{T}\) is the ephemeris prediction error of satellite j in the X-, Y-, and Z-directions in the Earth-centered Earth-fixed (ECEF) coordinate system; \(l_{i}^{j}\) is the unit direction vector from monitoring station i to satellite j; \(\Delta B^{j}\) is the clock error of satellite j; \(v_{i}^{j}\) is the residual error whose variance is \(\sigma_{i}^{j2}\) (Shao 2012).
Using the least-squares method to solve the equation above, the ephemeris correction \(\Delta \hat{R}^{j}\), clock correction \(\Delta \hat{B}^{j}\), and covariance matrix \(P_{DFRE}^{j}\) can be calculated as follows:
where \(H^{j} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {l_{1}^{jT} } \\ \vdots \\ {l_{M}^{jT} } \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \\ \end{array} } \right]_{{\left( {M \times 4} \right)}}\), \(R^{j} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{1}^{j2} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\sigma_{2}^{j2} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ldots \\ \ldots \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \vdots \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ \ldots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ddots \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\sigma_{M}^{j2} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]_{{\left( {M \times M} \right)}}\), \(Z^{j} = \left[ {\begin{array}{*{20}c} {\Delta \rho \begin{array}{*{20}c} j \\ 1 \\ \end{array} } \\ \vdots \\ {\Delta \rho \begin{array}{*{20}c} j \\ M \\ \end{array} } \\ \end{array} } \right]_{{\left( {M \times 1} \right)}}\), M is the number of monitoring stations that observe satellite j simultaneously, \(P_{o}^{j}\) is the 3 × 3 ephemeris prediction error covariance matrix, \(P_{c}^{j}\) is the variance of the clock error, and \(P_{oc}^{j}\) is the 3 × 1 covariance matrix of the ephemeris prediction and clock errors.
DFRE calculation
The residual error obtained using the ephemeris correction \(\Delta \hat{R}^{j}\) and clock correction \(\Delta \hat{B}^{j}\) can be expressed as follows:
Let the maximal projection direction of the residual error in the service area be \({u}_{MAX}^{j}\); therefore, the projection of the residual error in the service area satisfies
where \({u}_{MAX}^{j} = \left[ {\begin{array}{*{20}c} { {l}_{MAX}^{jT} } & 1 \\ \end{array} } \right]^{T}\); \({l}_{MAX}^{jT}\) is the unit direction vector on the maximal projection direction from satellite j; \({u}_{user}^{j} = \left[ {\begin{array}{*{20}c} { {l}_{user}^{jT} } & 1 \\ \end{array} } \right]^{T}\); \({l}_{user}^{jT}\) is the unit direction vector from the user in the service area to satellite j; \({\varepsilon }^{jT} {u}_{user}^{j}\) is the corrected error; \({\varepsilon }^{jT} {u}_{MAX}^{j}\) is the maximal corrected error.
Because the residual error that follows the zero-mean normal distribution (Javier and Didier 2006) cannot be calculated in practical applications, the covariance matrix \(P_{DFRE}^{j}\) of the residual error is used to reflect the characteristics of the maximal corrected error.
where \({\text{P}}(\cdot)\) is the probability, \(Q(\cdot)\) is the cumulative probability distribution of the normal distribution, and K is the fractile.
The DFRE is a comprehensive reflection of the corrected error on the user side and needs to envelop the maximal corrected error in the service area; therefore, the DFRE can be defined as
As shown in Eq. 7, the key to calculate the DFRE is to obtain the maximum of \({u}_{user}^{jT} P_{DFRE}^{j} {u}_{user}^{j}\), which can be further transformed into
Because \(P_{oc}^{jT} {l}_{user}^{j}\) is a scalar, then \(P_{oc}^{jT} {l}_{user}^{j} = \left( {P_{oc}^{jT} {l}_{user}^{j} } \right)^{T}\); subsequently, Eq. 8 can be transformed into
According to the Cauchy–Schwarz inequality \(\left| {x^{T} y} \right| \le \sqrt {x^{T} x} \sqrt {y^{T} y}\) (Gene and Charles 2017), the following can be obtained:
Substituting Eq. 10 into Eq. 9 yields
where \(a = \sqrt {P_{oc}^{jT} P_{o}^{j - 1} P_{oc}^{j} }\).
Owing to \(a \ge 0\), \(\left( {\sqrt { {l}_{user}^{jT} P_{o}^{j} {l}_{user}^{j} } + a} \right)^{2} - a^{2} + P_{c}^{j}\) is an increasing function while \(\sqrt { {l}_{user}^{jT} P_{o}^{j} {l}_{user}^{j} }\) is in its valid domain. Therefore, obtaining the maximum of \({u}_{user}^{jT} P_{DFRE}^{j} {u}_{user}^{j}\) can be regarded as obtaining the maximum of \({l}_{user}^{jT} P_{o}^{j} {l}_{user}^{j}\).
As shown in Eq. 3, \(P_{o}^{j}\) is a real symmetric matrix; therefore, a unit orthogonal array C exists, thereby validating the following equation:
where \(\lambda_{1}\), \(\lambda_{2}\), and \(\lambda_{3}\) are the eigenvalues of \(P_{o}^{j}\) (set \(\lambda_{1} \ge \lambda_{2} \ge \lambda_{3} > 0\)); the column vector of matrix C is the eigenvector of \(P_{o}^{j}\) with respect to \(\lambda_{i} \,(i = 1,2,3)\); \(diag\left( \cdot \right)\) is the diagonal matrix.
The ECEF coordinate system can be converted to a new coordinate system by the matrix C, the origin of which is located at satellite j, and the directions of the x-, y-, and z-axes are indicated by the column vectors of C. The unit direction vector from the user to satellite j in the new coordinate system is
where \(\theta\) is the angle between \({l}_{u}\) and the XOY plane; \(\varphi\) is the angle between the projection of \({l}_{u}\) on the XOY plane and the x-axis.
The distance from any point \(\left[ {\begin{array}{*{20}c} {\sqrt {\lambda_{1} } \cos \theta \cos \varphi } & {\sqrt {\lambda_{2} } \cos \theta \sin \varphi } & {\sqrt {\lambda_{3} } \sin \theta } \\ \end{array} } \right]^{T}\) on the ellipsoidal surface \(\frac{{x^{2} }}{{\lambda_{1} }} + \frac{{y^{2} }}{{\lambda_{2} }} + \frac{{z^{2} }}{{\lambda_{3} }} = 1\) to the origin is can be expressed as follows:
From Eqs. 14 and 15, \(f\left( { {l}_{u} } \right) = d^{2}\) is obtained; therefore, obtaining the maximum of \(f\left( { {l}_{u} } \right)\) can be regarded as obtaining the maximal distance from the point on the \(\frac{{x^{2} }}{{\lambda_{1} }} + \frac{{y^{2} }}{{\lambda_{2} }} + \frac{{z^{2} }}{{\lambda_{3} }} = 1\) ellipsoidal to the origin. Because \(\lambda_{1} \ge \lambda_{2} \ge \lambda_{3}\), the maximal distance from the point on the ellipsoidal surface to the origin is \(\sqrt {\lambda_{1} }\), and the maximum direction is \({l}_{Y}^{T} = \left[ {\begin{array}{*{20}c} { \pm 1} & 0 & 0 \\ \end{array} } \right]\), i.e., the long-axis direction; therefore,
Substituting Eq. 16 into Eq. 11 yields
According to Eqs. 7 and 17, the DFRE can be calculated as follows:
Simulation
As the DFRE and user differential range error (UDRE) reflect the corrected effect of the satellite ephemeris and clock corrections, they have the same connotation. In a quarterly performance analysis report released by the WAAS, the performance of the UDRE was verified by analyzing whether it could form an envelope for the maximal corrected error \({\varepsilon }^{jT} {u}_{MAX}^{j}\) with a probability of 99.9% (\(3.29\sigma\)) (William 2018; Chen et al. 2017). The WAAS’s verification method of the UDRE was used in this study to verify the performance of the DFRE. Substituting K = 3.29 and Eq. 7 into Eq. 6 yields
The DFRE (\(\sigma_{\text{DFRE}}\)) must satisfy the condition above. To verify the effectiveness of the DFRE calculation method, the BDS and GPS were used as augmented constellations for the simulation analysis in the BDSBAS service area (east longitude 70°–140°; north latitude 5°–55°). The simulation conditions are shown in Table 1.
First, the measurements of 24 monitoring stations in China (shown as squares in Fig. 2) were simulated to calculate the DFRE of the visible satellites. Subsequently, the user measurements were simulated at a 5° interval (shown as points in Fig. 2) in the BDSBAS service area, the corrected error \({\varepsilon }^{jT} {u}_{user}^{j}\) of each user was calculated, and the maximal corrected error \({\varepsilon }^{jT} {u}_{MAX}^{j}\) was obtained. Finally, the envelope probability that was calculated as the probability of \(3.29\sigma_{\text{DFRE}}\) being greater than the maximal corrected error was used to verify whether the DFRE satisfied Eq. 19.
After the simulation, the envelope probabilities of the DFRE for the BDS and GPS are shown in Table 2.
As shown in Table 2, the maximum, minimum, and average DFRE envelope probability of the BDS are 100.0%, 99.90%, and 99.93%, respectively; the maximum, minimum, and average DFRE envelope probability of the GPS are 100.0%, 99.90%, and 99.95%, respectively. The DFREs of the BDS and GPS, which were calculated based on the projection method, satisfied the requirement of Eq. 19, and the results were consistent with the theoretical expectations.
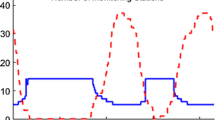
To analyze the applicability of the DFRE calculation method to different constellations and different satellite types, BDS GEO2, IGSO3, MEO18, and GPS PRN15 were selected to construct the DFRE and maximal corrected error curves, as shown in Figs. 3 and 4, respectively.
Because the ephemeris–clock covariance matrix used to obtain the DFRE was calculated based on the unit direction vectors of the satellite and the monitoring stations, the DFRE was affected by the geometrical layout between the satellite and the monitoring stations. The geometric layout between the GEO and the monitoring stations was unchanged; therefore, the GEO’s DFRE is a straight line. The geometrical layout between the IGSO (or MEO) and the monitoring stations changed constantly as the satellite moved. When the satellite entered the service area, the DFRE continued to decline, while the number of monitoring stations observing the satellite increased. When the satellite was above the service area, the number of monitoring stations observing the satellite was the same, and the DFRE tended to be stable; when the satellite left the service area, the DFRE continued increasing as the number of monitoring stations observing the satellite decreased. As shown from the figures, the DFRE can form an envelope for the maximal corrected error with a probability better than 99.9%, which shows that the DFRE calculation method based on the projection method is applicable to different constellations and satellite types.
As the DFRE is an integrity parameter, the integrity performance (the probability of integrity risk) in the user segment should be analyzed. Typically, the PE, PL, and AL are used to verify the integrity performance. The relationship between PE, PL, and AL is shown in Table 3.
To verify the integrity performance, observation data from the Crustal Movement Observation Network of China (CMONC) were used. The CMONC stations of SXTY was selected as the static user, and the horizontal PE, vertical PE, horizontal PL, and vertical PL were calculated by the method provided in SC-159 (2013) from 2018-07-11 00:00:00 to 2018-07-11 23:59:59. For CAT-I, the horizontal AL is 40 m and the vertical AL is 15 m (ICAO 2018). The horizontal and vertical performances are shown in Figs. 5 and 6, respectively.
As shown in Figs. 5 and 6, no MIs and HMIs appeared; therefore, the probability of integrity risk was 0, which satisfied the integrity requirement of CAT-I (the probability of integrity must be less than 2 × 10−7 (ICAO 2018)). However, several alarms appeared in Fig. 6, which was caused by the degradation parameters used in the calculation of the PL. Those degradation parameters were set the same as those of the WAAS. The WAAS degradation parameters could not be applied directly to the BDSBAS. Because the calculation method of the degradation parameters has not been published, studies regarding the degradation parameters of the BDSBAS will be conducted in the future.
Conclusions
The DFRE is an important integrity parameter of the DFMC SBAS, and the calculation method of the DFRE has not been published. Accordingly, a DFRE calculation method based on the projection method was proposed in this paper. The satellite ephemeris–clock-correction covariance matrix was used to obtain the maximal projection direction, and the projection of the covariance matrix on this direction was defined as the DFRE, which could form an envelope for the maximal corrected error.
Based on the observation data of 24 monitoring stations in China, the DFRE of the BDS and GPS were calculated and compared with the maximal corrected error. The DFRE calculated by the projection method could form an envelope for the maximal corrected error with a set probability, and it is suitable for monitoring the integrity of different constellations and different satellite types. According to the result obtained using CMONC observation data and the DFRE calculated by the proposed method, the probability of integrity risk in the user segment satisfied the CAT-I requirement. The results indicated that the proposed method could be applied to calculate the DFRE of BDSBAS.
Availability of Data and Materials
The data and materials can be used with the permission of the authors.
Abbreviations
- DFMC:
-
dual-frequency multi-constellation
- SBAS:
-
satellite-based augmentation system
- DFRE:
-
dual-frequency range error
- BDS:
-
BeiDou navigation satellite system
- GNSS:
-
global navigation satellite systems
- WAAS:
-
wide area augmentation system
- EGNOS:
-
European geostationary navigation overlay system
- SF:
-
single frequency
- CAT-I:
-
category I precision approach
- BDSBAS:
-
BeiDou satellite-based augmentation system
- PL:
-
protection level
- PE:
-
positioning error
- AL:
-
alert limit
- ECEF:
-
earth-centered earth-fixed
- UDRE:
-
user differential range error
- CMONC:
-
crustal movement observation network of China
References
Chen, J., Huang, Z., & Li, R. (2017). Computation of satellite clock-ephemeris corrections using a priori knowledge for satellite-based augmentation system. GPS Solutions,21(2), 663–673. https://doi.org/10.1007/s10291-016-0555-8.
ESSP. (2016). EGNOS performance and LPV implementation status. In: SBAS IWG 30, Changsha, China, May 16–17, 2016
Gene, H. G., & Charles, V. L. (2017). Matrix computations. In: Posts and Telecom Press (p. 69), Beijing.
ICAO NSP DS2. (2017). DFMC SBAS SARPs part B v1.2. In: ICAO NSP DS2 #9, Montreal Canada, October 16–20, 2017
ICAO SARPS. (2018). Annex 10: International standards and recommended practices, aeronautical telecommunications. Radio Navigation Aids. In Montreal: International Civil Aviation Organization (Vol. I), 2018.
IWG. (2016a). Satellite-based augmentation system dual-frequency multi-constellation definition document. In: SBAS IWG 31, Senegal, November 29–December 1, 2016
IWG (2016b) SBAS L5 DFMC interface control. In: SBAS IWG 31, Senegal, Nov 29 - Dec 1, 2016
Jason, B. (2016). Wide area augmentation system (WAAS) update. In: SBAS IWG 30, Changsha, China, May 16–17, 2016
Javier, V. T., & Didier, F. (2006). EGNOS. In: ESA Publications Division, Netherlands (p. 50)
SC-159. (2013). Minimum operational performance standards for global positioning system/satellite-based augmentation system airborne equipment. In: RTCA DO-229E, 2013.
Shao, B. (2012). Research on integrity key technology of user differential range error for mixed constellation. PhD thesis, School of Electronic and Information Engineering, Beihang University.
Shao, B., Geng, Y. C., Ding, Q., et al. (2017). Summarize of international satellite based augmenta-tion system. Modern Navigation,8(3), 157–161.
Shen, J., & Lu, X. C. (2016). BDS and BDSBAS status updates. In: SBAS IWG 30, Changsha, China, May 16–17, 2016
William, J. (2018). Hughes Technical Center (2018) Wide-area augmentation system performance analysis report #64, http://www.nstb.tc.faa.gov/reports/waaspan64.pdf
Acknowledgements
Thanks Dr. Li Rui and Dr. Zheng Shuaiyong of Beihang University for providing CMONC data.
Funding
This work is funded by the State Key Laboratory of Geo-Information Engineering, No. SKLGIE2018-Z-2-2.
Author information
Authors and Affiliations
Contributions
BS completed the algorithm design and simulation and contributed significantly in writing the manuscript. QD provided advice on the algorithm design and modified the manuscript. XBW provided advice on how to verify the algorithm and modified the manuscript. All authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shao, B., Ding, Q. & Wu, X. Estimation method of SBAS dual-frequency range error integrity parameter. Satell Navig 1, 9 (2020). https://doi.org/10.1186/s43020-020-00011-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43020-020-00011-1