Transient Taylor–Dean flow in a composite annulus with porous walls partially filled with porous material

Abstract

The sole aim of this article is to examine the relative contribution of suction/injection parameter on Taylor–Dean flow in a composite annular gap partially filled with porous material. In the present setup, the Newtonian fluid flow is induced by the circumferential motion of both cylinders and pressure gradient imposed in the Azimuthal direction. The mathematical model governing the flow is rendered dimensionless using appropriate dimensionless quantities transformed using the Laplace transform technique. Using suitable Ansatz, the equation is reduced to the Bessel differential equations and solved. The solution of converted to the time domain using a well-known numerical scheme known as the Riemann-sum approximation. The variation of the Newtonian fluid for different flow parameters is presented graphically. The solution method is validated by obtaining the steady-state solution and also using the implicit finite different approach (IFD); comparison of the methods is depicted in tabular form (see Tables 1, 2). It is deduced generally that the Newtonian fluid is higher when injection at the outer cylinder except when Da is small also higher interfacial velocity can be achieved by taking positive value of $\beta$.

Introduction

Several years back, the practical and theoretical steady of steady and time-dependent state of circumferential flow of Newtonian fluid in an annular duct has been of major interest to different researchers. This can be attributed to its relevance in various fields of endeavors such as biofluid mechanics, Bio-medical, mechanical, and Hemodynamics engineering. The first and pioneering work in Laminar flow in annulus due to azimuthal pressure gradient was presented by Dean [1]. This laudable and inspiring work has drawn many other researchers toward studying circumferential flow in different geometries. These include the work of Gupta and Gupta [2]. Tsangaris [3], Goldstein [4], Bhatnagar [5], Uchida [6], Rechardson [7], and Dryden and Murnaghan [8]. Gupta et al. [9] theoretically examined the analytical solution responsible for pulsatile viscous flow induced by a harmonically oscillating pressure gradient in a straight elliptic annular gap with application to the motion of the cerebrospinal fluid in the human spinal cavity.

Tsangaris et al. [10] presented laminar fully developed flow in an annular gap subject to an imposed oscillating Azimuthal pressure gradient. In a similar work, Tsangaris and Vlachakis [11] carried out an analytical solution of the Navier–Stokes equations for the fully developed laminar flow in a cylindrical annular duct. Tending the frequency of the oscillating pressure gradient to zero, the work of Goldstein is obtained as a limiting case.

Relating to the present investigation, several theoretical and experimental work using different numerical technique and analytical study has been carried out to have a better understanding of this phenomenon.

Jha and Yahaya [12] examined laminar and fully developed time-dependent flow formation in the region between two horizontally stationary impermeable concentric cylinders with an applied circumferential pressure gradient in the annulus. It is revealed that as time passes, the velocity increases till it attains a steady-state. Jha and Yahaya [13] later extended the work to the case when the walls of the cylinders are permeable. They reported that in addition to the results obtained from their previous work (see Jha and Yahaya [12]), the velocity profile is inversely proportional to the suction/injection parameter.

In the recent past, in an attempt to have an insight into the influence of unsteady pressure gradient on different flow formations, Yen and Chang [14] embarked on an investigation of the role of time-dependent pressure gradient on magnetohydrodynamic flow in a bounded channel; in their work, three cases of unsteady pressure gradient were considered; these are given as follows: pulse, step, and periodic pressure gradient. In another work, Nandi [15] examined time-dependent flow of a viscous incompressible and electrically conducting fluid within a porous annulus subject to an external radial magnetic field with an exponentially decreasing/increasing time-dependent pressure gradient. A theoretical and analytical solution of Newtonian and Non-Newtonian fluid flows in cylindrical and annular pipes due to an arbitrary time-dependent pressure gradient and arbitrary steady initial flow was investigated by McGinty et al. [16]. Similarly, Mendiburu et al. [17] utilized both Fourier series and integral transforms in theoretical examination of unsteady flow in a channel with constant and variable pressure gradient. As time increases, a constant pressure gradient is gradually achieved.

To have a better insight into the circumferential fluid flow within two cylinders, several semi-analytical works have been carried out using the Riemann-sum approximation (RSA) approach. Using this method, Jha and Gambo [18] presented an investigation of “the impact of suction/injection and an exponentially decaying/growing time-dependent pressure gradient on unsteady Dean flow through an annulus.” It is revealed that the skin frictions on both walls can be minimized by imposing an exponentially decaying pressure gradient on the flow. Using the same approach, Jha and Gambo [19] studied the impact of an exponentially decaying/growing time-dependent pressure gradient on unsteady Dean flow in an annulus. The findings revealed that maximum velocity occurs when the time-dependent pressure gradient is growing exponentially other related research works using this approach include the work of Jha and Yusuf [20]. Other relevant works include the work of Azad and Andallah [21], Sayed-Ahmed et al. [22], Tsimpoukis, Valougeorgis [23], Khali et al. [24], and Waters and Pedley [25].

The uniqueness of this work is to investigate the influence of wall porosity on unsteady Taylor–Dean flow in an annulus partly filled with porous material. It is hoped that this research work will help in understanding the procedure to better minimize wall frictional force for free flow formation. Solution of the velocity field and skin friction at both walls has been obtained using the combination Laplace transform and RSA approach. The IFD method has also been used to solve governing model while the steady-state solution has been derived equally. The effect of the various entering flow parameters on the flow formation is studied with the help of line graphs and numerical tables.

Methods

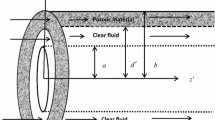
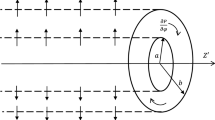
The time dependent, fully developed, and incompressible circumferential flow between two infinite co-axial horizontal porous “cylinders containing fluid and porous layer separated by a permeable thin interface with fluid occupying the interval $d^{^{\prime}} \le r^{\prime } \le r_{0}$ while the interval $r_{{{\text{in}}}} \le r^{\prime } \le d^{^{\prime}}$ is occupied by a fluid-saturated porous material of uniform permeability. r_in and r₀ are the radii of the inner and the outer cylinder, respectively, as shown in Fig. 1. The fluid is set in motion due to sudden application of constant circumferential pressure gradient and the angular, rotating with an angular velocity $\omega_{{{\text{in}}}}$ and $\omega_{0}$.” The velocity of the fluid is showed to be a function of the radial coordinate $r^{\prime }$ and time t only. The flow in the porous region is governed by the Darcy law while the flow in the clear region is governed by the usual Navier–Stokes equations. Continuity of velocity and shear stress has been used at the fluid–porous interface. In cylindrical coordinates, these equations are given as

$$\frac{{\partial u_{{\text{p}}}^{\prime } }}{{\partial t^{\prime } }} + u_{1} \left[ {\frac{1}{{r^{\prime } }}\frac{{\partial u_{{\text{p}}}^{\prime } }}{{\partial r^{\prime } }} - \frac{{u_{{\text{p}}}^{\prime } }}{{r^{\prime 2} }}} \right] = \nu_{{{\text{eff}}}} \left[ {\frac{{\partial^{2} u_{{\text{p}}}^{\prime } }}{{\partial r^{\prime 2} }} + \frac{1}{{r^{\prime } }}\frac{{\partial u_{{\text{p}}}^{\prime } }}{{\partial r^{\prime } }} - \frac{{u_{{\text{p}}}^{\prime } }}{{r^{\prime 2} }}} \right] - \frac{\nu }{{k^{\prime } }}u_{{\text{p}}}^{\prime } - \frac{1}{\rho }\frac{\partial p}{{\partial \theta }}\frac{1}{{r^{\prime } }}\quad {\text{for}}\quad r_{{{\text{in}}}} \le r^{\prime } \le d^{\prime }$$

(1)

$$\frac{{\partial u_{f}^{^{\prime}} }}{{\partial t^{\prime } }} + u_{1} \left[ {\frac{1}{{r^{\prime } }}\frac{{\partial u_{f}^{^{\prime}} }}{{\partial r^{\prime } }} - \frac{{u_{f}^{^{\prime}} }}{{r^{^{\prime}2} }}} \right] = \nu \left[ {\frac{{\partial^{2} u_{f}^{^{\prime}} }}{{\partial r^{^{\prime}2} }} + \frac{1}{{r^{\prime } }}\frac{{\partial u_{f}^{^{\prime}} }}{{\partial r^{\prime } }} - \frac{{u_{f}^{^{\prime}} }}{{r^{^{\prime}2} }}} \right] - \frac{1}{\rho }\frac{\partial p}{{\partial \theta }}\frac{1}{{r^{\prime } }}\quad {\text{for}}\quad d^{\prime } \le r^{\prime } \le r_{0}$$

(2)

Fig. 1

Flow configuration and coordinate system

The initial and the condition at the surfaces for the problem under consideration are

$$\begin{aligned} & t^{\prime } \le 0:u_{{\text{p}}}^{^{\prime}} = u_{{\text{f}}}^{^{\prime}} = 0\quad {\text{for}}\quad r_{{{\text{in}}}} \le r^{\prime } \le r_{0} \\ & t^{\prime } > 0:\quad \left[ {\begin{array}{*{20}c} {u_{{\text{p}}}^{^{\prime}} = r_{{{\text{in}}}} \omega_{{{\text{in}}}} \;\;{\text{at}}\;\;r^{\prime } = r_{{{\text{in}}}} } \\ {u_{{\text{f}}}^{^{\prime}} = r_{0} \omega_{0} \;\;{\text{at}}\;\;r^{\prime } = r_{0} } \\ \end{array} } \right] \\ \end{aligned}$$

(3)

With the dimensional matching condition at the interface given as

$$t^{\prime } > 0:\left[ {\begin{array}{*{20}l} {u_{{\text{p}}}^{^{\prime}} = u_{{\text{f}}}^{^{\prime}} = u_{{\text{i}}}^{^{\prime}} } \\ {\nu_{{{\text{eff}}}} \left[ {\frac{{\partial u_{{\text{p}}}^{^{\prime}} }}{{\partial r^{\prime } }} - \frac{{u_{{\text{p}}}^{^{\prime}} }}{{r^{\prime } }}} \right] - \nu \left[ {\frac{{\partial u_{{\text{f}}}^{^{\prime}} }}{{\partial r^{\prime } }} - \frac{{u_{{\text{f}}}^{^{\prime}} }}{{r^{\prime } }}} \right] = \frac{\beta \nu }{{\sqrt {k^{\prime } } }}u_{{\text{p}}}^{^{\prime}} } \\ \end{array} } \right]\;\;{\text{at}}\;\;r^{\prime } = d^{\prime }$$

(4)

Using the following non-dimensional quantities:

$$\begin{aligned} R & = \frac{{r^{\prime } }}{{r_{{{\text{in}}}} }} ;t = \frac{{\nu t^{^{\prime}} }}{{r_{{{\text{in}}}}^{2} }} ; \gamma = \frac{{\nu_{{{\text{eff}}}} }}{\nu } ;{\text{Da}} = \frac{{r_{{{\text{in}}}}^{2} }}{{k^{\prime } }} ;U_{{\text{p}}} = U_{{\text{f}}} = \frac{{\left( {u_{{\text{p}}}^{^{\prime}} ; u_{{\text{f}}}^{^{\prime}} } \right)}}{{u_{0} }} ; \\ u_{0} & = - r_{{{\text{in}}}} \frac{\partial p}{{\partial \theta }}\frac{1}{\rho \nu }; d = \frac{{d^{\prime } }}{{r_{{{\text{in}}}} }} ; \lambda = \frac{{r_{0} }}{{r_{{{\text{in}}}} }} ; U_{{\text{i}}} = \frac{{u_{{{\text{in}}}}^{^{\prime}} }}{{U_{0} }}, S = \frac{{u_{{\text{i}}} r_{{{\text{in}}}} }}{\nu } \\ \end{aligned}$$

(5)

Using the following dimensionless parameters defined in Eq. (5) on Eqs. (1) to (4)

$$\frac{{\partial U_{{\text{p}}} }}{\partial t} = \gamma \frac{{\partial^{2} U_{{\text{p}}} }}{{\partial R^{2} }} + \left( {\gamma - S} \right)\frac{1}{R}\frac{{\partial U_{{\text{p}}} }}{\partial R} - \frac{{\left( {\gamma + S} \right)}}{{R^{2} }}U_{{\text{p}}} - \frac{{U_{{\text{p}}} }}{{{\text{Da}}}} + \frac{P}{R}\quad {\text{for}}\quad 1 \le R \le d$$

(6)

$$\frac{{\partial U_{{\text{f}}} }}{\partial t} = \frac{{\partial^{2} U_{{\text{f}}} }}{{\partial R^{2} }} + \left( {1 - S} \right)\frac{1}{R}\frac{{\partial U_{{\text{f}}} }}{\partial R} - \frac{{\left( {1 + S} \right)}}{{R^{2} }}U_{{\text{f}}} + \frac{P}{R}\quad {\text{for}}\quad d \le R \le \lambda$$

(7)

Subject to the following dimensionless initial and boundary conditions

$$\begin{aligned} t \le 0:\;\;U_{{\text{p}}} = U_{{\text{f}}} = 0\quad {\text{for}}\quad 1 \le R \le \lambda \hfill \\ t > 0:\;\;\left[ {\begin{array}{*{20}c} {U_{{\text{p}}} = A^{*} \;\;{\text{at}}\;\;R = 1} \\ {U_{{\text{f}}} = \omega \lambda \;\;{\text{at}}\;\;R = \lambda } \\ \end{array} } \right] \hfill \\ \end{aligned}$$

(8)

With the matching condition at the interface given as

$$t > 0:\;\;\left[ {\begin{array}{*{20}l} {U_{{\text{p}}} = U_{{\text{f}}} = U_{{\text{i}}} } \\ {\gamma \left[ {R\frac{\partial }{\partial R}\left( {\frac{{U_{{\text{p}}} }}{R}} \right)} \right] - \left[ {R\frac{\partial }{\partial R}\left( {\frac{{U_{{\text{f}}} }}{R}} \right)} \right] = \frac{\beta }{{\sqrt {{\text{Da}}} }}U_{{\text{p}}} } \\ \end{array} } \right] \;\;{\text{at}}\;\;R = d$$

(9)

The Laplace domain of Eqs. (6) to (9) can be obtained using the Laplace transform technique $\overline{U}_{{\text{p}}} \left( {R,\vartheta } \right) = \int_{0}^{\infty } {U_{{\text{p}}} \left( {R,t} \right)e^{ - \vartheta t} {\text{d}}t} \;\;{\text{and}}\;\; \overline{U}_{{\text{f}}} \left( {R,\vartheta } \right) = \int_{0}^{\infty } {U_{{\text{f}}} \left( {R,t} \right)e^{ - \vartheta t} {\text{d}}t}$ (where $\vartheta > 0$ is the Laplace parameter) subject to initial condition gives:

$$\frac{{{\text{d}}^{2} \overline{U}_{{\text{p}}} }}{{{\text{d}}R^{2} }} + \frac{1}{R}\left( {\gamma - S} \right)\frac{{{\text{d}}\overline{U}_{{\text{p}}} }}{{{\text{d}}R}} - \left( {\gamma + S} \right)\frac{{\overline{U}_{{\text{p}}} }}{{R^{2} }} - \frac{1}{\gamma }\left[ {\frac{1}{{{\text{Da}}}} + \vartheta } \right]\overline{U}_{{\text{p}}} = - \frac{P}{\gamma \vartheta R}$$

(10)

$$\frac{{{\text{d}}^{2} \overline{U}_{{\text{f}}} }}{{{\text{d}}R^{2} }} + \frac{1}{R}\left( {1 - S} \right)\frac{{{\text{d}}\overline{U}_{{\text{f}}} }}{{{\text{d}}R}} - \left( {1 + S} \right)\frac{{\overline{U}_{{\text{f}}} }}{{R^{2} }} - \vartheta \overline{U}_{{\text{f}}} = - \frac{P}{\vartheta R}$$

(11)

Subject to the following boundary condition

$$t > 0:\;\;\left[ {\begin{array}{*{20}c} {\bar{U}_{{\text{p}}} = \frac{{A^{*} }}{\vartheta }\;\;{\text{at}}\;\;R = 1} \\ {\bar{U}_{{\text{f}}} = \frac{{\omega \lambda }}{\vartheta }\;\;{\text{at}}\;\;R = \lambda } \\ \end{array} } \right]$$

(12)

With the matching condition at the interface given as

$$t > 0:\;\;\left[ {\begin{array}{*{20}l} {\overline{U}_{{\text{p}}} = \overline{U}_{{\text{f}}} = U_{{\text{i}}} } \\ {\gamma \left[ {\frac{{{\text{d}}\overline{U}_{{\text{p}}} }}{{{\text{d}}R}} - \frac{{\overline{U}_{{\text{p}}} }}{R}} \right] - \left[ {\frac{{{\text{d}}\overline{U}_{{\text{f}}} }}{{{\text{d}}R}} - \frac{{\overline{U}_{{\text{f}}} }}{R}} \right] = \frac{\beta }{{\sqrt {{\text{Da}}} }}U_{{\text{i}}} } \\ \end{array} } \right] \;\;{\text{at}}\;\;R = d$$

(13)

Equations (10) and (11) can be transform to Bessel function using the following equations;

$$\overline{U}_{{\text{p}}} = \overline{U}_{{{\text{ph}}}} R^{S/2} + \frac{P}{{\vartheta \left( {\frac{1}{{{\text{Da}}}} + \vartheta } \right)R}}\;\;{\text{and}}\;\;\overline{U}_{{\text{f}}} = \overline{U}_{{{\text{fh}}}} R^{S/2} + \frac{P}{{\vartheta^{2} R}}$$

(14)

Letting $\gamma = 1$ and then applying Eq. (14) on Eqs. (10) and (11), the solutions in terms of the modified Bessel function obtained are given as:

$$\overline{U}_{{\text{p}}} = R^{S/2} \left[ {C_{5} I_{n} \left( {\eta R} \right) + C_{6} K_{n} \left( {\eta R} \right)} \right] + \frac{P}{{\vartheta \left( {\frac{1}{{{\text{Da}}}} + \vartheta } \right)R}}$$

(15)

$$\overline{U}_{{\text{f}}} = R^{S/2} \left[ {C_{7} I_{n} \left( {\sqrt \vartheta R} \right) + C_{8} K_{n} \left( {\sqrt \vartheta R} \right)} \right] + \frac{P}{{\vartheta^{2} R}}$$

(16)

where $\eta = \sqrt {\left( {\frac{1}{Da} + \vartheta } \right)} , n = \left( {\frac{S}{2} + 1} \right)$ and I_n, K_n are the modified Bessel function of a first and second kind, respectively, of order n.

using Eq. (12) and on Eqs. (15) and (16) the constants $C_{5} ,{ }C_{6} ,{ }C_{7} ,{ }C_{8} { }$ and U_i are obtained as

$$\begin{aligned} C_{5} & = a_{2} + U_{{\text{i}}} a_{3} ,\quad C_{6} = a_{4} - U_{{\text{i}}} a_{5} ,\quad C_{7} = a_{7} + U_{{\text{i}}} a_{8} ,\quad C_{8} = a_{9} - U_{{\text{i}}} a_{10} \\ U_{{\text{i}}} & = \frac{{ - a_{16} }}{{a_{17} }} \\ \end{aligned}$$

$$\begin{aligned} a_{1} & = d^{{\frac{S}{2} + 1}} \vartheta \left( {{\text{Da}}\vartheta + 1} \right) \left( {I_{n} \left( \eta \right)K_{n} \left( {d\eta } \right) - I_{n} \left( {d\eta } \right)K_{n} \left( {d\eta } \right)} \right), \\ a_{2} & = \frac{1}{{a_{1} }}\left[ {{\text{Da}}PK_{n} \left( \eta \right) + A^{*} d^{{\frac{S}{2} + 1}} K_{n} \left( {d\eta } \right) - {\text{Da}}Pd^{{\frac{S}{2} + 1}} K_{n} \left( {d\eta } \right) + A^{*} Da\vartheta d^{{\frac{S}{2} + 1}} K_{n} \left( {d\eta } \right)} \right], \\ a_{3} & = - \frac{{\left( {d\vartheta + {\text{Da}} d \vartheta^{2} } \right)K_{n} \left( \eta \right)}}{{a_{1} }}, \\ a_{4} & = - \frac{1}{{a_{1} }}\left[ {{\text{Da}}PI_{n} \left( \eta \right) + A^{*} d^{{\frac{S}{2} + 1}} I_{n} \left( {d\eta } \right) - {\text{Da}}Pd^{{\frac{S}{2} + 1}} I_{n} \left( {d\eta } \right) + A^{*} {\text{Da}}\vartheta d^{{\frac{S}{2} + 1}} I_{n} \left( {d\eta } \right)} \right], \\ a_{5} & = - \frac{{\left( {d\vartheta + {\text{Da }}d \vartheta^{2} } \right)I_{n} \left( \eta \right)}}{{a_{1} }} , \\ a_{6} & = \lambda^{{\frac{S}{2} + 1}} d^{{\frac{S}{2} + 1}} \vartheta \left( { I_{n} \left( {\lambda \sqrt \vartheta } \right)K_{n} \left( {d\sqrt \vartheta } \right) - I_{n} \left( {d\sqrt \vartheta } \right)K_{n} \left( {\lambda \sqrt \vartheta } \right)} \right), \\ a_{7} & = \frac{1}{{a_{6} }}\left[ {\lambda^{2} d^{{\frac{S}{2} + 1}} \vartheta wK_{n} \left( {d\sqrt \vartheta } \right) + \lambda^{{\frac{S}{2} + 1}} PK_{n} \left( {\lambda \sqrt \vartheta } \right) - Pd^{{\frac{S}{2} + 1}} K_{n} \left( {d\sqrt \vartheta } \right) } \right], \\ a_{8} & = - \frac{{\lambda^{{\frac{S}{2} + 1}} d\vartheta^{2} K_{n} \left( {\lambda \sqrt \vartheta } \right)}}{{a_{6} }}, \\ a_{9} & = \frac{1}{{a_{6} }}\left[ {Pd^{{\frac{S}{2} + 1}} I_{n} \left( {d\sqrt \vartheta } \right) - \lambda^{2} d^{{\frac{S}{2} + 1}} \vartheta wI_{n} \left( {d\sqrt \vartheta } \right) - \lambda^{{\frac{S}{2} + 1}} PI_{n} \left( {\lambda \sqrt \vartheta } \right) } \right] , \\ a_{10} & = - \frac{{\lambda^{{\frac{S}{2} + 1}} d\vartheta^{2} I_{n} \left( {\lambda \sqrt \vartheta } \right)}}{{a_{6} }}, \\ a_{11} & = \eta d^{n - 1} I_{n - 1} \left( {d\eta } \right) - 2d^{n - 2} I_{n} \left( {d\eta } \right) - \frac{\beta }{{\sqrt {{\text{Da}}} }}d^{n - 1} I_{n} \left( {d\eta } \right), \\ a_{12} & = \eta d^{n - 1} K_{n - 1} \left( {d\eta } \right) + 2d^{n - 2} K_{n} \left( {d\eta } \right) - \frac{\beta }{{\sqrt {{\text{Da}}} }}d^{n - 1} K_{n} \left( {d\eta } \right), \\ a_{13} & = 2d^{n - 2} I_{n} \left( {d\sqrt \vartheta } \right) - \vartheta d^{n - 1} I_{n - 1} \left( {d\sqrt \vartheta } \right), \\ a_{14} & = 2d^{n - 2} K_{n} \left( {d\sqrt \vartheta } \right) + \vartheta d^{n - 1} K_{n - 1} \left( {d\sqrt \vartheta } \right), \\ a_{15} & = \frac{2P}{{\vartheta^{2} d^{2} }} - \frac{2P}{{\vartheta \eta^{2} d^{2} }} - \frac{P\beta }{{\eta^{2} d\vartheta \sqrt {{\text{Da}}} }}. \\ \end{aligned}$$

Skin friction

To evaluate the skin friction on both the inner and the outer cylinder in the Laplace domain, we use $\left. {R\frac{\partial }{\partial R}\left( {\frac{{\overline{U}_{{\text{p}}} }}{R}} \right)} \right|_{R = 1}$ and $- \left. {R\frac{\partial }{\partial R}\left( {\frac{{\overline{U}_{{\text{f}}} }}{R}} \right)} \right|_{R = \lambda },$ respectively. On simplification, we have

$$\begin{aligned} \left. {\overline{\tau }_{1} = R\frac{\partial }{\partial R}\left( {\frac{{\overline{U}_{{\text{p}}} }}{R}} \right)} \right|_{R = 1} & = \frac{1 }{2}S\left( {C_{5} I_{n} \left( \eta \right) + C_{6} K_{n} \left( \eta \right)} \right) + C_{5} \left( {I_{n + 1} \left( \eta \right) + \frac{{nI_{n + 1} \left( \eta \right)}}{\eta }} \right)\eta \\ & \quad + C_{6} \left( {K_{n + 1} \left( \eta \right) + \frac{{nK_{n + 1} \left( \eta \right)}}{\eta }} \right)\eta - \frac{2P}{{\vartheta \eta^{2} }} \\ \end{aligned}$$

(17)

$$\begin{aligned} \left. {\overline{\tau }_{\lambda } = - R\frac{\partial }{\partial R}\left( {\frac{{\overline{U}_{f} }}{R}} \right)} \right|_{R = \lambda } & = - \frac{1 }{2}\frac{{S\lambda^{\frac{S}{2}} \left( {C_{7} I_{n} \left( {\lambda \sqrt \vartheta } \right) + C_{8} K_{n} \left( {\lambda \sqrt \vartheta } \right)} \right)}}{\lambda } \\ & \quad - \lambda^{\frac{S}{2}} \left( {C_{7} \left( {I_{n + 1} \left( {\sqrt \vartheta } \right) + \frac{{nI_{n + 1} \left( {\lambda \sqrt \vartheta } \right)}}{\lambda \sqrt \vartheta }} \right)\sqrt \vartheta + C_{8} \left( { - K_{n + 1} \left( {\lambda \sqrt \vartheta } \right) + \frac{{nK_{n + 1} \left( {\lambda \sqrt \vartheta } \right)}}{\lambda \sqrt \vartheta }} \right)\sqrt \vartheta } \right) \\ & \quad + \frac{P}{{\vartheta^{2} d^{2} }} \\ \end{aligned}$$

(18)

Before analyzing the solution above, Eqs. 15–18 need to be inverted to the time domain. However, a deep literature study in the cause of this research revealed that there is no simple analytical way to obtain the Laplace inverse of Eqs. 15–18 Hence, we follow the numerical approach used in the work of Khadrawi and Al-Nimr [26], Jha and Apere [27], and several other researchers too numerous to mention. This technique is based on the RSA. According to this method, any function in the Laplace domain can be inverted to the time domain as shown below.

$$Y\left( {R,t} \right) = \frac{{e^{\varepsilon t} }}{t}\left[ {\frac{1}{2}\overline{Y}\left( {R,\varepsilon } \right) + {\text{Re}} \mathop \sum \limits_{k = 1}^{N} \overline{Y}\left( {R,\varepsilon + \frac{ik\pi }{t}} \right)\left( { - 1} \right)^{k} } \right], \quad 1 \le R \le \lambda$$

(19)

In the equation above, $i = \sqrt { - 1}$ while Re denotes “the real part of the term with a summation. N denotes the number of terms used in the RSA and $\varepsilon$ represents the real part of the Bromwich contour used in inverting Laplace transforms. This procedure involves a single summation for the numerical process and its accuracy largely depends on the value of $\varepsilon$ and N. According to the work of Tzou [28], the value of $\varepsilon t$ that best satisfies the result is 4.7

Validation of the method

The exact solution of the steady-state velocity is obtained and used to validate the RSA approach used in this work. It is revealed that at large time, the transient state solution coincides with the steady-state velocity. This is obtained by letting $\frac{\partial ()}{{\partial t}} = 0$ in Eqs. (1) and (4) to obtain the following differential equations

$$\gamma \frac{{{\text{d}}^{2} U_{{\text{p}}} }}{{{\text{d}}R^{2} }} + \frac{{\left( {\gamma - S} \right)}}{R}\frac{{{\text{d}}U_{{\text{p}}} }}{{{\text{d}}R}} - \frac{{\left( {\gamma + S} \right)}}{{R^{2} }}U_{{\text{p}}} - \frac{{U_{{\text{p}}} }}{{{\text{Da}}}} + \frac{P}{R} = 0\quad {\text{for}}\;\;1 \le R \le d$$

(20)

$$\frac{{{\text{d}}^{2} U_{{\text{f}}} }}{{{\text{d}}R^{2} }} + \frac{{\left( {1 - S} \right)}}{R}\frac{{{\text{d}}U_{{\text{f}}} }}{{{\text{d}}R}} - \frac{{\left( {1 + S} \right)}}{{R^{2} }}U_{{\text{f}}} + \frac{P}{R} = 0\;\;{\text{for}}\;\;d \le R \le \lambda$$

(21)

Subject to the following boundary condition

$$\begin{aligned} U_{{\text{p}}} & = A^{*} \;\;{\text{at}}\;\;R = 1 \\ U_{{\text{f}}} & = \lambda w~\;\;{\text{at}}\;\;R = \lambda \\ \end{aligned}$$

(22)

With the matching condition at the interface denoted by d given as

$$\left[ {\begin{array}{*{20}l} {U_{{\text{p}}} = U_{{\text{f}}} = U_{{{\text{is}}}} } \\ {\gamma \left[ {R\frac{{\text{d}}}{{{\text{d}}R}}\left( {\frac{{U_{{\text{p}}} }}{R}} \right)} \right] - \left[ {R\frac{{\text{d}}}{{{\text{d}}R}}\left( {\frac{{U_{{\text{f}}} }}{R}} \right)} \right] = \frac{\beta }{{\sqrt {{\text{Da}}} }}U_{{{\text{is}}}} } \\ \end{array} } \right] \;\;{\text{at}}\;\;R = d$$

(23)

Equation (20) is solved by applying the transformation giving by

$$U_{{\text{p}}} = U_{{{\text{ph}}}} R^{S/2} + \frac{{P{\text{Da}}}}{R}$$

(24)

Putting $\gamma = P = 1$ and applying Eq. (24) on Eq. (20), the solution in terms of modified Bessel function is given as:

$$U_{{\text{p}}} = R^{S/2} \left[ {C_{5} I_{n} \left( {\frac{R}{{\sqrt {{\text{Da}}} }}} \right) + C_{6} K_{n} \left( {\frac{R}{{\sqrt {{\text{Da}}} }}} \right)} \right] + \frac{{{\text{Da}}}}{R}$$

(25)

Equation (21) is solved by letting $R = e^{\varphi }$ and simplifying, the resulting second-order ODE is given by

$$\frac{{{\text{d}}^{2} U_{{\text{f}}} }}{{{\text{d}}\varphi^{2} }} - S\frac{{{\text{d}}U_{{\text{f}}} }}{{{\text{d}}\varphi }} - \left( {1 + S} \right)U_{{\text{f}}} = - e^{\varphi }$$

(26)

Applying the usual method of undetermined coefficient yield

$$U_{{\text{f}}} = C_{7} R^{{\left( {S + 1} \right)}} + \frac{{C_{8} }}{R} + \frac{R}{2S}$$

(27)

Using Eqs. (22) and (23) on Eqs. (25) and (27), the constants $D_{5} ,{ }D_{6} ,{ }D_{7} ,{ }D_{8} { }$ and $U_{{{\text{is}}}}$ are obtained as.

$D_{5} = - h3 ui + h2, D_{6} = h5 ui - h4, D7 = - h8 ui - h7, D8 = h10 ui + h9$, $Ui = \frac{h16}{{h17}}$ the constant $h_{1} , h_{2} , h_{3} , \ldots ,h_{17}$ in the above equations are

$$\begin{aligned} h1 & = d^{{\frac{S}{2} + 1}} \left( {I_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)K_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) - K_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)I_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)} \right) \\ h2 & = \frac{{\left( {A^{*} d^{{\frac{S}{2} + 1}} K_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) - {\text{Da}}d^{{\frac{S}{2} + 1}} K_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) + {\text{Da}}K_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)} \right)}}{h1}, \\ h3 & = \frac{{\left( {dK_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)} \right)}}{h1} \\ h4 & = \frac{{\left( {A^{*} d^{{\frac{S}{2} + 1}} I_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) - {\text{Da}}d^{{\frac{S}{2} + 1}} I_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) + {\text{Da}}I_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)} \right)}}{h1} \\ h5 & = \frac{{\left( {dI_{n} \left( {\frac{1}{{\sqrt {{\text{Da}}} }}} \right)} \right)}}{h1},\\ h6& = 2 S\left( {\lambda^{S + 2} - d^{S + 2} } \right), \\ h7 & = \frac{{\left( { - 2\lambda^{2} Sw + \lambda^{2} - d^{2} } \right)}}{h6},\\ h8 &= \frac{2 Sd}{{h6}}, \\ h9 & = \frac{{\lambda d\left( {\lambda d^{S + 1} - d\lambda^{S + 1} - 2\lambda Sd^{S + 1} w} \right)}}{h6},\\ h10 &= \frac{{d\lambda^{S + 2} S}}{h6} \\ h11 & = \frac{1}{2}\frac{{d^{{\frac{1}{2}s}} sI_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{d} + d^{{\frac{1}{2}s}} \left( {I_{n + 1} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) + \frac{{nI_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{{\frac{d}{{\sqrt {{\text{Da}}} }}}}} \right)\frac{1}{{\sqrt {{\text{Da}}} }} \\ & \quad - d^{{\frac{1}{2}s - 1}} I_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) - \frac{{bd^{{\frac{1}{2}s}} I_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{{\sqrt {{\text{Da}}} }} \\ h12 & = \frac{1}{2}\frac{{d^{{\frac{1}{2}s}} sK_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{d} + d^{{\frac{1}{2}s}} \left( { - K_{n + 1} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) + \frac{{nK_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{{\frac{d}{{\sqrt {{\text{Da}}} }}}}} \right)\frac{1}{{\sqrt {{\text{Da}}} }} \\ & \quad - d^{{\frac{1}{2}s - 1}} K_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right) - \frac{{bd^{{\frac{1}{2}s}} K_{n} \left( {\frac{d}{{\sqrt {{\text{Da}}} }}} \right)}}{{\sqrt {{\text{Da}}} }} \\ h13 & = - \frac{{2{\text{Da}}}}{{d^{2} }} - b\frac{{\sqrt {{\text{Da}}} }}{d},\quad h14 = \frac{{d^{2 + s} s}}{{d^{2} }},\\ h15 &= \frac{ - 2}{{d^{2} }}, \\ h16 & = h11h2 - h12h4 + h14h7 - h15h9 +\\ h17 & = h10h15 + h11h3 - h12h5 - h14h8 \\ \end{aligned}$$

The accuracy of the RSA is further established using the IFD approach on Eqs. (6) to (9). The values generated using these two approaches are presented in the tables below for numerical comparison. This numerical scheme in comparison with the values obtained from the RSA approach at a large time as well as the closed-form solution of the steady-state velocity gives an excellent agreement. It is worthy to note that the numerical values obtained using the IFD method at transient state also agree significantly with the ones obtained using the RSA approach for a small value of time (see Tables 1, 2).

Table 1 Numerical values of both the steady and the transient state velocity obtained using the RSA, IFD, and the exact solution $\left( {d = 1.5, P = 10, {\text{Da}} = 0.02, A^{*} = 1, w = 0.8} \right)$

Table 2 Numerical values of both the steady and the transient state interfacial velocity (U_i) obtained using the RSA, implicit finite difference, and the exact solution $\left( {d = 1.5, b = - 0.2, P = 10, {\text{Da}} = 0.02, A^{*} = 1, w = 0.8} \right)$

Results and discussion

To have a clear insight into the effect of various parameters controlling the unified solution of the model governing the flow formation, a MATLAB code is written to compute and generate the line graphs and to obtain its numerical values for some selected entering parameters. These parameters include the Darcy number (Da), time (t), viscosity ratio $\left( \gamma \right)$, interfacial radial distance (d), adjustable coefficient of the stress jump condition $\left( \beta \right)$, the radii ratio $\left( \lambda \right)$, and the suction/injection parameter. The effect of the above parameters on fluid velocity, interfacial velocity, and skin friction on both surfaces presented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 is discussed below.

Fig. 2

Velocity profiles for different values of t $\left( {P = 10,\beta = - 0.2, d = 1.5, {\text{Da}} = 0.02, A^{*} = 1, w = 0.8 } \right)$

Fig. 3

Velocity profiles for different values of Da $\left( { t = 0.2, P = 10,\beta = - 0.2, d = 1.5, A^{*} = 1, w = 0.8 } \right)$  

Fig. 4

Velocity profiles for different values of $\beta$ $\left( { t = 0.2, P = 10,{\text{Da}} = 0.2, d = 1.5, A^{*} = 1, w = 0.8 } \right)$

Fig. 5

Interfacial Velocity profiles for different values of $\beta$ $\left( { t = 0.2, P = 10,{\text{Da}} = 0.2, d = 1.5, A^{*} = 1, w = 0.8} \right)$

Fig. 6

Interfacial Velocity profiles for different values of t and d $\left( { t = 0.2, P = 10,{\text{Da}} = 0.02, d = 1.5, A^{*} = 1, w = 0.8} \right)$

Fig. 7

Skin friction $\left( {\tau_{1} } \right)$ profiles for different values of t $\left( { \beta = - 0.2, P = 10,{\text{Da}} = 0.2, d = 1.5, A^{*} = 1, w = 0.8 } \right)$

Fig. 8

Skin friction $\left( {\tau_{\lambda } } \right)$ profiles for different values of t $\left( { \beta = - 0.2, P = 10,{\text{Da}} = 0.2, d = 1.5, A^{*} = 1, w = 0.8 } \right)$

Fig. 9

Skin friction $\left( {\tau_{1} } \right)$ profiles for different values of S and P $\left( {t = 0.2, \beta = - 0.2 ,d = 1.5, A^{*} = 1, w = 0.8} \right)$

Fig. 10

Skin friction $\left( {\tau_{\lambda } } \right)$ profiles for different values of S and P $\left( {t = 0.2, \beta = - 0.2 ,d = 1.5, A^{*} = 1, w = 0.8} \right)$

Fig. 11

Skin friction $\left( {\tau_{1} } \right)$ profiles for different values of S and d $\left( {t = 0.2, \beta = - 0.2 ,P = 10, A^{*} = 1, w = 0.8} \right)$

Fig. 12

Skin friction $\left( {\tau_{\lambda } } \right)$ profiles for different values of S and d $\left( {t = 0.2, \beta = - 0.2 ,P = 10, A^{*} = 1, w = 0.8} \right)$

Figures 2, 3 and 4 reveal the variation in velocity profiles t, Da, and $\beta,$ respectively. Figure 2 shows that fluid velocity is an increasing function of time until steady-state is attained, with injection at either the outer cylinder or the inner cylinder. However, it is observed that velocity is higher near the inner cylinder when fluid injection is at the inner cylinder for small value of Da. Figures 3 and 4 show that at transient state, fluid velocity profiles increase with increase in Da and $\beta$ for both suction and injection on both cylinders. Velocity is generally higher when fluid injection is at the outer cylinder.

Change in transient state interfacial velocity (u_i) with t, d and $\beta$ is presented in Figs. 5 and 6. It is established in both figures that u_i increases with t. To achieve higher interfacial velocity, large values of $\beta > 0$ are required (see Fig. 5); this fit can also be achieved by decreasing the region partially occupied by the porous material. The reverse occurs when the region filled with clear fluid is decreased (see Fig. 6).

Figures 7, 8, 9, 10, 11 and 12 showcase the effect of various parameters on skin friction at the outer and at the inner cylinder. It is generally observed that skin friction increases with an increase in time. Variation in skin friction at the inner cylinder for different values of s and t is shown in Fig. 7. It is important to note that shear stress is relatively lower at the inner cylinder when injection is on the outer cylinder. A similar observation is depicted in Fig. 8 as skin friction is found to be lower at the outer cylinder when injection is on the inner cylinder. The reverse situation is presented if high higher shear is desired.

The relative contribution of the azimuthal pressure gradient is illustrated in Figs. 9 and 10 and both figures show an increase in skin friction with pressure; a significant increase in the shear stress is also observed at the inner cylinder. It is interesting to note that the direction of suction/injection flow has less impact on the skin friction at the outer cylinder for pressure gradient (P > 8).

Figures 11 and 12 reveal the variation of skin friction at the inner cylinder and the outer cylinder, respectively, for different values of S and d. Figure 11 shows that shear stress at the inner cylinder increases with a decrease in the region occupied by clear fluid while an increase in the region occupied by clear fluid leads to a decrease in shear stress at the outer cylinder (see Fig. 12).

Conclusion

This paper presents the contribution of angular rotation of both cylinders on transient azimuthal pressure-driven flow partially filled with porous materials. The impact of various flow parameters on the fluid velocity, interfacial velocity, and shear stress on both cylinders is presented. The accuracy of the numerical schemes used is shown with the aid of Table. Based on the figures and the numerical values generated, the following conclusions are drawn:

• 1. Velocity is higher near the inner cylinder when fluid injection is at the inner cylinder for small value of Da.

• 2. Velocity is generally higher when injection is at the outer cylinder.

• 3. To achieve higher interfacial velocity, large values of $\beta > 0$ are required.

• 4. It is interesting to note that the direction of suction/injection flow has less impact on the skin friction at the outer cylinder for pressure gradient (P > 8).

• 5. Shear stress at the inner cylinder increases with a decrease in the region occupied by clear fluid.

• 6. It is important to note that shear stress is relatively lower at the inner cylinder when injection is on the outer cylinder.

• 7. An interesting observation in this research is that wall porosity reduces the time taken to reach steady state.