MHD Powell–Eyring dusty nanofluid flow due to stretching surface with heat flux boundary condition

Abstract

A steady MHD boundary layer flow of Powell–Eyring dusty nanofluid over a stretching surface with heat flux condition is studied numerically. It is assumed that the fluid is incompressible and the impacts of thermophoresis and Brownian motion are taken into regard. In addition, the Powell–Eyring terms are considered in the momentum boundary layer and thermal boundary layer. The dust particles are seen as to be having the same size and conform to the nanoparticles in a spherical shape. We obtain a system of ordinary differential equations that are suitable for analyzed numerically using the fourth-order Runge–Kutta method via software algebraic MATLAB by applying appropriate transformations to the system of the governing partial differential equations in our problem. There is perfect compatibility between the bygone and current results when comparing our numerical solutions with the available data for values of the selected parameters. This confirms the validity of the method used here and thus the validity of the results. The influence of some parameters on the boundary layer profiles (the velocity and temperature for the particle phase and fluid phase, and nanoparticle concentration) is discussed. The results of this study display that the profiles of the velocity for particle and fluid phases increase with increasing Powell–Eyring fluid parameter, but reduce with height in magnetic field values. Mass concentration of the dust particles decreases the temperature of both the particle and fluid phases. The results also indicate the concentration of nanoparticle contraction as Schmidt number increases.

Introduction

Magnetohydrodynamics (MHD) tends to describe the behavior of electrically conducting fluids like liquid metals, plasmas, and astrophysical systems as well as studying the magnetic field and velocity in these fluids. Characteristics of heat transfer and the effects of Hall on magnetohydrodynamic (MHD) flow in a rotating channel are analyzed by Ghosh et al. [1]. With regard to the MHD power generators, Carabineanu [2] introduced mathematical theory in the simplified form, disregarding the effect of Lorentz force contrary to the direction of fluid flow which takes the stationary flow of plasma. Some flows of MHD in a porous medium of the second-degree fluid with Darcy law for modeling the flow are investigated by Hayat et al. [3]. Alfv´en [4, 5] put the magnetohydrodynamics (MHD) equations requisite basic and he recognized the importance of the generated magnetic field as well as the electric currents loaded by plasma. Thermal radiation impact on the flow of magnetohydrodynamic (MHD) over a vertical plate with considering convective boundary condition into the model of flow has been discussed by Etwire and Seini [6]. Flow problem of mixed convection boundary layer and mass transfer over a vertical plate in the presence of a magnetic field and constant heat flux through a porous medium is illustrated by Makinde [7]. In the presence of the magnetic field, Afrand et al. [8] presented a numerical approach of natural convection flow in three-dimensional inside a vertical annulus loaded by gallium with taking lower and upper parts of the annulus in the account. The flow of MHD of Maxwell fluid caused by a moving flat plate subject to second-order slip is investigated by Liu and Guo [9]. Studying magnetohydrodynamic (MHD) flow of incompressible fluid with heat transfer effects between two circular discs has been presented by Ayaz et al. [10]. Recently, Patel [11] utilized the technique of Laplace transform to examine the flow of MHD of Casson fluid through porous medium over an oscillating vertical plate in the presence of Hall current, thermal radiation, and heat generation.

Nanofluid is a distinctive category of heat transfer fluids and can be gained by uniform dispersion of nanoparticles as well as stabilized suspension of these particles in base fluids like water, ethylene glycol, kerosene, oil, and bio-fluids. Nanofluid which has additional thermal properties achieves the largest and highest potential thermal properties utilizing particles at very small concentrations suitable. Furthermore, nanofluids are allocated by thermal conductivity. Nanoparticles are defined as metal or non-metallic particles with a size below than 100 nm that move a random movement known as Brownian motion and improve energy transfer in nanofluids. Choi [12] was the first to introduce the concept of nanofluid as a mixture of disperse particles (nanoparticles) and liquid. Among the many of nanofluid applications, we mention transportation, biomedical, power generation, and microelectronics. An important application of nanofluid is to improve the coefficient of heat transfer of the heat transfer fluids. Xuan and Li [13] offered the major reasons for improving the instrument of heat transfer of fluids by the concept of nanofluids. The research which deals with the methods of preparation of nanofluids, its applications, and its stability, as well as its thermophysical properties was presented by Yu and Xie [14]. MHD boundary layer flow with natural convection of nanofluid over a moving vertical flat plate in the presence of radiative heat flux and a magnetic field was described by Das and Jana [15]. Papers on nanofluid flow can be found by Mahdy [16] and Hady [17, 18]. Ibrahim and Makinde [19] investigated numerically the problem of heat transfer and MHD stagnation point flow with convective heating and velocity slip impacts of power-law nanofluid towards a stretching sheet. Recently, Darcy–Forchheimer model through a porous medium is applied for viscous nanofluid flow because of a curved stretchable surface by Saif et al. [20]. They noted that increasing the parameter of Brownian motion tends to reduce local Nusselt number while enhances from local Sherwood number. The method of lattice Boltzmann has been utilized by Ma et al. [21] to examine MHD natural convection of nanofluids within U-shaped enclosures with a baffle.

Powell–Eyring fluid model is regarded as an important type of non-Newtonian fluid models for its essential uses in diverse geophysical, natural, and industrial processes. Its importance is due to the fact that most fluids used in the industry have the same nature as non-Newtonian fluids. There are many patterns that have been developed to describe the behavior of non-Newtonian fluid flow; this is because of the nature of complex non-Newtonian fluids. Powell–Eyring fluid model is characterized by following the same behavior as Newtonian fluid in the case of rates of low and high shear. It is also derived from the kinetic theory of liquid but not from the empirical relation as it was before. In 1944, Powell and Eyring suggested a full and adequate mathematical model is Eyring–Powell fluid model [22]. Boundary layer flow of Powell–Eyring fluid is described across a stretching surface by many researchers in their work. This due to the importance of a stretching surface in various industrial applications including electronic chips, fiber yarn, polymer industries, and glass blowing. Here we will display a pool of previous works related to Powell–Eyring fluid. Javed et al. [23] presented Powell–Eyring fluid boundary layer flow over a stretching sheet. The numerical approach of MHD boundary layer flow of non-Newtonian Eyring–Powell fluid towards a stretching surface has been presented by Akbar et al. [24]. Hayate et al. [25] examined the problem of steady flow and heat transfer of non-Newtonian Eyring–Powell fluid in the presence of convective boundary conditions over a moving surface. The peristaltic flow with mass and heat transfer of Powell–Eyring fluid over a curved channel has been illustrated by Hina et al. [26]. Ghadikolaei et al. [27] considered the effect of Joule heating, thermal radiation, and Lorentz force when studying the unsteady problem of Eyring–Powell fluid flow by Akbari-Ganji Method (AGM). Powell–Eyring nanofluid flow due to gyrotactic microorganisms and magnetic field effect towards a stretched surface has been examined by Naseem et al. [28]. Panigrahi et al. [29] applied the method of Homotopy analysis to solve the mixed convective problem of Powell–Eyring fluid flow under the effect of Dufour number and Soret number through a nonlinear stretching surface. They found that the profiles of temperature and concentration improve with increasing Dufour number and Soret number, respectively. The problem of MHD boundary layer flow of a non-Newtonian nanofluid enforcing the model of Powell–Eyring past an impermeable nonlinear stretching sheet with variable thickness has explored by Hayat et al. [30]. They observed that an increase in the thermophoresis parameter leads to an increment of both concentration and temperature profiles. Recently, Kumar et al. [31] presented an incompressible laminar flow and the characteristics of heat transfer on non-Newtonian Powell–Eyring fluid at a shrinking wedge in the presence of the effects of the magnetic field, irregular heat source /sink, and radiative heat flow.

Dusty fluid flow phenomenon subsists in the flow of fluid compressible and incompressible such as gas and liquid, respectively, which containing solid particles in the size of the micrometer. Model of compressible gas flow through porous media in the presence of dust particles has been presented by Hamdan and Barron [32]. The flow of the boundary layer over a stretching surface of the dusty fluid under an applied magnetic field is studied numerically by Jalil et al. [33]. Ramesh and Gireesha [34] analyzed the influence of radiation on the flow of boundary layer of an incompressible dusty fluid past a stretching sheet. Dust fluid flow modeling is important because of its application's atmospheric fallout, paint spray, guided missiles, and dust collection. Furthermore, several works related to the flow of dust fluids were presented by a number of authors [35,36,37,38,39,40,41]. The object of our paper is to present an analysis of the problem of MHD flow of non-Newtonian Powell–Eyring fluid in the presence of nanoparticles and dust particles towards a stretching vertical plate with heat flux condition. The Runge–Kutta method is applied in the fourth-order to obtain numerical solutions of ordinary differential equations subject to appropriate boundary conditions. Perform a comparison to check the integrity and accuracy of the method used. The impacts of material fluid parameters, nanofluid parameters, and particle-phase parameters, Prandtl number, Grashof number, magnetic parameter (Hartmann number), and Eckert number on local Nusselt number and skin friction coefficient are estimated in tables.

Governing equations

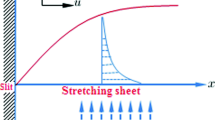
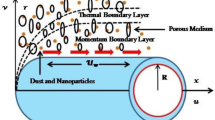
Steady MHD boundary layer flow of an incompressible Powell–Eyring nanofluid over a stretching surface in the presence of dust particles is investigated. The flow is in two-dimensional and the stretching plate coincides in Cartesian coordinates $(\widehat{x},\widehat{y})$. So that one of these coordinates $\widehat{x}$-axis is in the direction of flow and the other $\widehat{y}$-axis is in the opposite direction of flow. Figure 1 shows the geometric representation of our problem. The heat flux condition and the influences of thermophoresis and Brownian motion are taken into nanofluid model. As well as the thermophoresis effect, the normal flux of nanoparticles at the boundary is zero. The stretching velocity is denoted by ${U}_{{ }_{w}}$ and at the plate surface the temperature is given by ${T}_{w}$. Away from the stretching plate, the temperature and nanoparticle volume fraction are represented, respectively, by ${T}_{\infty }$ and ${C}_{\infty }$. Using a transverse magnetic field and uniform ${B}_{o}$, the fluid becomes electrically conductive. The induced magnetic field has very little effect because the magnetic Reynolds number is also small without applying the voltage. After the previous view, the equations of continuity, momentum, nanoparticle concentration, energy, take the following form:

Fig. 1

Schematic view and physical coordinate system

For the fluid phase:

$$\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \frac{{\partial \hat{v}}}{{\partial \hat{y}}} = 0$$

(1)

$$\begin{array}{*{20}l} {\hat{u}\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{u}}}{{\partial \hat{y}}} = \left( {\nu_{f} + \frac{1}{{\rho_{f} \beta_{f} c}}} \right)\frac{{\partial^{2} \hat{u}}}{{\partial \hat{y}^{2} }} - \frac{1}{{2\rho_{f} \beta_{f} c^{3} }}\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} \frac{{\partial^{2} \hat{u}}}{{\partial \hat{y}^{2} }} - \frac{{\sigma B_{0}^{2} }}{{\rho_{f} }}\hat{u} + } \hfill & {\frac{{\rho_{p} }}{{\rho_{f} \tau_{m} }}\left( {\hat{u}_{p} - \hat{u}} \right)} \hfill \\ { + \frac{1}{{\rho_{f} }}\left[ {\left( {1 - C_{\infty } } \right)\rho_{f} \beta g\left( {T - T_{\infty } } \right) - \left( {\rho_{np} - \rho_{f} } \right)g\left( {C - C_{\infty } } \right)} \right]} \hfill & {} \hfill \\ \end{array}$$

(2)

$$\hat{u}\frac{\partial T}{{\partial \hat{x}}} + \hat{v}\frac{\partial T}{{\partial \hat{y}}} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial \hat{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \hat{y}^{2} }}} \right) + \frac{{\alpha \sigma B_{0}^{2} }}{k}\hat{u}^{2} + \tau \left[ {D_{B} \frac{\partial C}{{\partial \hat{y}}}\frac{\partial T}{{\partial \hat{y}}} + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left[ {\left( {\frac{\partial T}{{\partial \hat{x}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial \hat{y}}}} \right)^{2} } \right]} \right] + \frac{{\rho_{p} c_{s} }}{{\tau_{T} \left( {\rho c_{p} } \right)_{f} }}\left( {T_{p} - T} \right) + \frac{{\rho_{p} }}{{\tau_{m} (\rho c_{p} )_{f} }}(\hat{u}_{p} - \hat{u})^{2} + \frac{1}{{c_{p} }}\left[ {\left( {v_{f} + \frac{1}{{\rho_{f} \beta_{f} c}}} \right)\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{2} - \frac{1}{{6\rho_{f} \beta_{f} c^{2} }}\left( {\frac{{\partial \hat{u}}}{{\partial \hat{y}}}} \right)^{4} } \right]$$

(3)

$$\hat{u}\frac{\partial C}{{\partial \hat{x}}} + \hat{v}\frac{\partial C}{{\partial \hat{y}}} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial \hat{x}^{2} }} + \frac{{\partial^{2} C}}{{\partial \hat{y}^{2} }}} \right) + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial \hat{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \hat{y}^{2} }}} \right)$$

(4)

For the dust phase:

$$\frac{{\partial \hat{u}_{p} }}{{\partial \hat{x}}} + \frac{{\partial \hat{v}_{p} }}{{\partial \hat{y}}} = 0$$

(5)

$$\hat{u}_{p} \frac{{\partial \hat{u}_{p} }}{{\partial \hat{x}}} + \hat{v}_{p} \frac{{\partial \hat{u}_{p} }}{{\partial \hat{y}}} = - \frac{1}{{\tau_{m} }}\left( {\hat{u}_{p} - \hat{u}} \right)$$

(6)

$$\rho_{p} c_{s} \left( {\hat{u}_{p} \frac{{\partial T_{p} }}{{\partial \hat{x}}} + \hat{v}_{p} \frac{{\partial T_{p} }}{{\partial \hat{y}}}} \right) = - \frac{{\rho_{p} c_{s} }}{{\tau_{T} }}\left( {T_{p} - T} \right)$$

(7)

In the above equations, there are fluid velocity components $\left( {\hat{u},\hat{v}} \right)$, particle-phase velocity components $\left( {\hat{u}_{p} ,\hat{v}_{p} } \right)$, kinematic viscosity $\nu_{f}$, density of dust particles and fluid $\rho_{p}$ and $\rho$, material parameters of Powell–Eyring model $\beta_{f}$ and $c$, volume thermal expansion coefficient of the fluid $\beta$, acceleration of gravity vector $g$, strength of the magnetic field $B_{0}$, fluid electrical conductivity $\sigma$, dust particle thermal relaxation time and dust particle velocity relaxation time $\tau_{T}$, and $\tau_{m}$, dust particles temperature and fluid temperature $T_{p}$ and $T$, fluid concentration $C$, thermal diffusivity of the base fluid $\alpha = k/(\rho c_{p} )_{f}$, nanofluid heat capacity ratio $\tau = \frac{{(\rho c_{p} )_{np} }}{{(\rho c_{p} )_{f} }}$, thermophoretic diffusion coefficient $D_{T}$, Brownian diffusion coefficient $D_{B}$, specific heat of dust particles $c_{s}$ and specific heat of fluid $c_{p}$.

The pertinent boundary conditions as follow:

$$\begin{gathered} \hat{u} = U_{w} \left( {\hat{x}} \right), \hat{v} = 0, - k\frac{\partial T}{{\partial \hat{y}}} = q_{w} , D_{B} \frac{\partial C}{{\partial \hat{y}}} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{{\partial \hat{y}}} = 0, \hat{y} = 0 \hfill \\ \hat{u},\hat{u}_{p} = 0, \hat{v}_{p} \to \hat{v}, T,T_{p} \to T_{\infty } , C \to C_{\infty } , \hat{y} \to \infty \hfill \\ \end{gathered}$$

(8)

By using the following conversions, an appropriate form of the equations to be processed is obtained:

$$\begin{gathered} \eta = \left( {\frac{a}{\nu }} \right)^{1/2} \hat{y}, \psi = \left( {a\nu } \right)^{1/2} \hat{x}f\left( \eta \right) = \left( {a\nu } \right)^{1/2} \hat{x}F\left( \eta \right),T = T_{\infty } + \frac{{q_{w} }}{k}\left( {\frac{\nu }{a}} \right)^{1/2} \theta \left( \eta \right), T_{p} = T_{\infty } + \frac{{q_{w} }}{k}\left( {\frac{\nu }{a}} \right)^{1/2} \theta_{p} \left( \eta \right), \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\infty } }} \hfill \\ \hfill \\ \end{gathered}$$

(9)

For the fluid phase:

$$\left[ {\left( {1 + \omega } \right) - \omega {\Delta }f^{{{\prime \prime }2}} } \right]f^{{{\prime \prime \prime }}} + ff^{{\prime \prime }} - f^{{{\prime 2}}} - Mf^{{\prime }} + Gr\left( {\theta - Nr\phi } \right) + D_{\rho } \alpha_{d} \left( {F^{{\prime }} - f^{{\prime }} } \right) = 0$$

(10)

$$\theta^{{\prime \prime }} + \theta^{{\prime }} \left( {Prf + Nb\phi^{{\prime }} } \right) + Nt\theta^{{{\prime 2}}} + PrEc\left[ {\left( {1 + \omega } \right)f^{{{\prime \prime 2}}} - \frac{{\omega {\Delta }}}{3}f^{{{\prime \prime 4}}} + Mf^{{\prime}{2}} } \right] + \frac{2}{3}D_{\rho } \alpha_{d} \left( {\theta_{p} - \theta } \right) + PrD_{\rho } \alpha_{d} Ec\left( {F^{{\prime }} - f^{{\prime }} } \right)^{2} = 0$$

(11)

$$\phi ^{\prime\prime} + Scf\phi ^{\prime} + \frac{Nt}{{Nb}}\theta ^{\prime\prime} = 0$$

(12)

For the dust phase:

$$FF^{\prime\prime} - F^{{\prime}{2}} + \alpha_{d} \left( {f^{\prime} - F^{\prime}} \right) = 0$$

(13)

$$F\theta ^{\prime}_{p} + \frac{2}{3}\frac{1}{{{\Gamma }Pr}}\alpha_{d} \left( {\theta - \theta_{p} } \right) = 0$$

(14)

where primes refer to differentiation for $\eta$, Prandtl number is denoted by $Pr = \frac{\nu }{\alpha }$, parameters of material fluid are given as ${\Delta } = \frac{{a^{3} \hat{x}^{2} }}{{2\nu c^{2} }}$ and $\omega = \frac{1}{{\rho_{f} \beta_{f} c\nu }}$, magnetic parameter (Hartmann number) is represented in $M = \frac{{\sigma B_{0}^{2} }}{{a\rho_{f} }}$, Grashof number is presented as $Gr = \frac{{\beta g\left( {1 - C_{\infty } } \right)\left( {T_{w} - T_{\infty } } \right)}}{{aU_{0} }}$, Schmidt number is symbolized by $Sc = \frac{\nu }{{D_{B} }}$, Buoyancy ratio parameter is written as $Nr = \frac{{\left( {\rho_{np} - \rho_{f} } \right)C_{\infty } }}{{\beta \rho_{f} \left( {1 - C_{\infty } } \right)\left( {T_{w} - T_{\infty } } \right)}}$, $Nb = \frac{{\tau D_{B} C_{\infty } }}{\alpha }$ point out the parameter of Brownian motion, $Nt = \frac{{\tau D_{T} \left( {T_{w} - T_{\infty } } \right)}}{{\alpha T_{\infty } }}$ indicates the parameter of thermophoresis, $Ec = \frac{{U_{0}^{2} }}{{c_{p} \left( {T_{w} - T_{\infty } } \right)}}$ expresses the Eckert number, $\alpha_{d} = \frac{{\hat{x}}}{{U_{0} \tau_{m} }}$ represents the parameter of fluid particle interaction, ${\Gamma } = \frac{{c_{s} }}{{c_{p} }}$ gives the specific heat ratio of the mixture, and $D_{\rho } = \frac{{\rho_{p} }}{{\rho_{f} }}$ refers the dust particles mass concentration.

Via Eq. (9), the boundary conditions (8) reduce to

$$f^{\prime} = 1, f = 0, \theta ^{\prime} = - 1, Nb\phi ^{\prime} + Nt\theta ^{\prime} = 0, \eta = 0$$

$$f^{\prime},F^{\prime} \to 0, F \to f, \theta ,\theta_{p} \to 0, \phi \to 0, \eta \to \infty$$

(15)

The dimensionless form of skin friction and Nusselt number is represented as

$$Re_{x}^{1/2} C_{fx} = \left( {1 + \omega } \right)f^{\prime\prime}\left( 0 \right) - \frac{{\omega {\Delta }}}{3}(f^{\prime\prime}\left( 0 \right))^{3}$$

(16)

$$Re_{x}^{ - 1/2} Nu_{x} = \frac{1}{\theta \left( 0 \right)}$$

(17)

where the local Reynolds number is defined as $Re_{x} = \frac{{U_{0} x}}{\nu }$.

Results and discussion

The systems of differential Eqs. (10)-(14) and (15) are solved numerically via Runge–Kutta method of fourth-order using MATLAB software. A comparison is being made with the results of Babu and Reddy [42], Malik et al. [43], and Akbar et al. [44] to determine the accuracy of the numerical method or the estimated numerical results. This comparison actually exists in Table 1 while Tables 2 and 3 present the values of local Nusselt number and skin friction coefficient under the influence of various values of the emerging physical parameters. In this study, the results obtained are valid enough after the comparison. The effect of Prandtl number, material fluid parameters, nanofluid parameters, and particle-phase parameters, etc., on the field of velocity, temperature, and concentration is examined, and the results of these tests are illustrated through figures.

Table 1 Comparison of our results for skin friction with ${\Delta } = \omega = Gr = Nr = D_{\rho } = \alpha_{d} = 0$

Table 2 Values of Nusselt number $Re_{x}^{ - 1/2} Nu_{x}$ and skin friction $Re_{x}^{1/2} C_{fx}$ for several values of $\omega$, ${\Delta }$, $M$, $D_{\rho }$, $Pr$, and $Gr$ for ${\Gamma }$ = 0.1

Table 3 Values of Nusselt number $Re_{x}^{ - 1/2} Nu_{x}$ and skin friction $Re_{x}^{1/2} C_{fx}$ for several values of $Nr$, $Nb$, $Nt$, $\alpha_{d}$, $Sc$, and $Ec$ for ${\Gamma }$ = 0.1

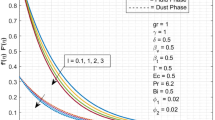
Figures 2, 3, 4 illustrate the velocity profiles in two phases: the fluid phase and particles phase with the influence of Powell–Eyring fluid parameter $\left( {\omega = 0.0,0.4,0.9,1.2} \right)$, Grashof number $\left( {Gr = 0.0,0.05,0.1,0.2} \right)$, and magnetic parameter $\left( {M = 0.9,2,3,4} \right)$ (Hartmann number). The impact of $\omega$ and $Gr$ increases the velocity profiles $f^{\prime}$ and $F^{\prime}$ in Figs. 2 and 3. There is a marked decrease in velocity profiles $f^{\prime}$ and $F^{\prime}$ due to the influence of $M$ as shown in Fig. 4. Lorentz force is an anti-flow force produced by the high values of $M$ and therefore takes place decreases in motion. It is also known that this force improves the thermal boundary layer thickness any increase in temperature. Figure 5 (a-b) is plotted to display the influence of dust parameters on the velocity and temperature profiles. It is observed from Fig. 5 (a) that an enhancement takes place in particle phase velocity $F^{\prime}$ due to improvement in values of fluid–particle interaction parameter $\left( {\alpha_{d} = 0.01,0.02,0.03,0.04} \right)$. The particle phase reduces the velocity of the fluid till it reaches the same fluid velocity; this is why the velocity of the particle phase increases, and the velocity of the fluid phase decreases. The behavior of $\theta$ and $\theta_{p}$ when studying the mass concentration of the dust particles $\left( {D_{\rho } = 0,1,10,15} \right)$ is presented in Fig. 5 (b). It is detected that the temperatures deteriorate with an increment in $D_{\rho }$. This behavior can be explained by the fact that the thermal conductivity of the particle phase is improved as a result of the increased dust particle’s mass concentration, meaning that the rate of heat transfer increases, causing a shrinking in temperature distribution.

Fig. 2

Impact of $\omega$ on velocity profile ($f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)$)

Fig. 3

Impact of $Gr$ on velocity profile ($f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)$)

Fig. 4

Impact of $M$ on velocity profile ($f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)$)

Fig. 5

a, b Impact of $\alpha_{d}$ on velocity profile $F^{\prime}\left( \eta \right)$ and $D_{\rho }$ on temperature profile ($\theta \left( \eta \right),\theta_{p} \left( \eta \right)$)

Utilizing Figs. 6 and 7, the temperature profiles for particle phase and fluid phase are depicted under the effect of Powell–Eyring fluid parameter $\left( {\omega = 0.0,0.4,0.9,1.2} \right)$, Buoyancy ratio parameter $\left( {Nr = 0.1,0.3,0.5,0.6} \right)$, Prandtl number $\left( {Pr = 0.7,0.8,0.9,1} \right)$, and Eckert number $\left( {Ec = 0.08,0.2,0.4,0.6} \right)$. Figure 6 (a) describes that for the rising values of $\omega$, the temperature profiles $\theta$ and $\theta_{p}$ diminish. Fig. 6 (b) displays the temperature profiles $\theta$ and $\theta_{p}$ for distinct values of $Nr$. The temperatures ameliorate with increased $Nr$ as shown in Fig. 6 (b). Characteristics of $Pr$ on the temperatures $\theta$ and $\theta_{p}$ are represented in Fig. 7 (a). It is clear from this figure that the temperatures diminish. The decrease in temperature distribution is due to that the increase in Pr leads to reduce the thickness of the thermal boundary layer. It is noted in Fig. 7 (b) that temperatures $\theta$ and $\theta_{p}$ positively affected by the increase in $Ec$.

Fig. 6

a, b Impact of $\omega$ and $Nr$ on temperature profile ($\theta \left( \eta \right),\theta_{p} \left( \eta \right)$)

Fig. 7

a, b Impact of $Pr$ and $Ec$ on temperature profile ($\theta \left( \eta \right),\theta_{p} \left( \eta \right)$)

The impact of several parameters like Brownian motion parameter $\left( {Nb = 0.1,0.2,0.3,0.4} \right)$, thermophoresis parameter $\left( {Nt = 0.1,0.2,0.3,0.4} \right)$, Eckert number $\left( {Ec = 0.08,0.2,0.4,0.6} \right)$, and Schmidt number $\left( {Sc = 1,2,3,4} \right)$ on the concentration profiles is captured in Figs. 8 and 9. It is clear that the concentration profile increases as $Nt$ increment and it decreases with increasing $NB$ as confirmed in Fig. 8 (a-b). The behavior of $Nt$ can be traced back to increasing the distribution of nanoparticles near the surface due to the transition of these particles from the hot fluid system to the surface, and this occurs when the surface is cold, i.e. $Nt > 0$. Progress in the concentration profile appears by $Ec$ in Fig. 9 (a). Figure 9 (b) reveals the outcome of $Sc$ effect on the concentration profile. The concentration profile deteriorates with rising values of $Sc$. Figure 10 illustrates that the magnitude of the velocity with Powell–Eyring nanofluid is greater when compared with Newtonian nanofluid, while the temperature distribution of Newtonian is higher than those of Powell–Eyring.

Fig. 8

a, b Impact of $Nt$ and $Nb$ on concentration profile $\phi \left( \eta \right)$

Fig. 9

a, b Impact of $Ec$ and $Sc$ on concentration profile $\phi \left( \eta \right)$

Fig. 10

Impact of Powell–Eyring nanofluid and Newtonian nanofluid on ($f^{\prime}\left( \eta \right),\theta \left( \eta \right)$)

Conclusions

In our work entitled numerical investigation of MHD Powell–Eyring dusty nanofluid flow towards a stretching vertical surface with heat flux boundary condition, we computed the values of Nusselt number and skin friction coefficient for various values of the governing parameters. Further inserted the numerical results of velocity, temperature, and concentration distributions for both particle and fluid phases graphically. The significant main findings of the present work are filed as follows:

• 1. The concentration of nanoparticle improves with thermophoresis parameter and Eckert number but deteriorates with Brownian motion parameter and Schmidt number.

• 2. The profiles of velocity for particle and fluid phases enhance with the increase in Powell–Eyring fluid parameter and Grashof number, while they reduce with height in magnetic parameter values. The velocity of the particle phase increases with increment fluid–particle interaction parameter.

• 3. An enhancement in Prandtl number, Powell–Eyring fluid parameter, and mass concentration of the dust particles reduces the temperature of both the particle and fluid phases.

• 4. Rising the values of both the Buoyancy ratio parameter and Eckert number tends to optimize the temperature distribution in two-particle and fluid phases.