1 Introduction

From the past decades, scientists were involved in performing a noteworthy investigation in the fluid flow area with respect to heat transfer process. Invention of special fluids paved a way for obtaining higher efficient energy during heat transfer. Researchers used several techniques and methods to improve efficiency of fluids. These fluids are termed as “nanofluids”, which are prepared by dispersing minute particles of size less than 100 nm in the conventional fluids. In modern science and nanotechnology, the rheological performance of a nanofluid is an essential feature for many applications such as cooling process, Geothermal power extraction, Coolant, Lubrication in automobiles and Microchips cooling. Therefore, significant studies have been performing on these nanofluids. Hayat et al. [1] deliberated the nano liquid flow at stagnation point with Brownian motion. They discussed the demeanour of physical parameters versus different profiles via graphical representation. Flow of a fluid consisting of nanoparticles through a revolving disk was explained by Khan et al. [2]. Kuttan et al. [3] deliberated the performance of four diverse nanoparticles on boundary layer stream through a stretching surface. Vinita and Poply [4] examined the impact of heat generation on nanofluid flow past a stretching cylinder. Mondal et al. [5] examined the impact of viscous dissipation and mixed convection on nanoliquid stream past a stretching cylinder. The combination of dual or more nanoparticles which are suspended in a convectional liquid yield’s hybrid nanofluid. Enrichment of heat transfer in hybrid nanofluid is mainly caused by fusion of two or more nanoparticles. It is experimentally verified that, hybrid nanofluids offer better thermal behaviour than that of base fluids and single nanoparticle fluids. Recently, Khan et al. [6] considered a fluid flow of consisting two nanometallic substances namely, silicon dioxide and molybdenum disulphide for determining the impact of heat source or sink. Farooq et al. [7] explored optimization of entropy on the flow of nanohybrid fluid through a revolving channel. Manjunatha et al. [8] examined the impact of convective boundary constraints on micropolar hybrid nanoliquid stream past a stretching surface. Abbas et al. [9] deliberated the stagnation point stream of a hybrid nanoliquid past a stretching cylinder.

The fluid flows along with dust particles have extensive range of mechanical applications like transport processes, cement and steel manufacturing industries, flying ash from thermal plants and chilling consequence of AC’s. The two-phase flows involving solid particles scattered in a nanofluid and hybrid nanofluid are of significant applications in industries. Recently, several researchers scrutinised the fluid flow with dust particles suspension. Turkyilmazoglu [10] provided a mathematical explanation for dusty fluid flow along with the boundary conditions. Manjunatha et al. [11] illustrated the dusty fluid flow through a stretchy cylinder on taking account of heat source. Reddy et al. [12] imposed modified Fourier law to investigate dusty hybrid nanofluid flow over a stretching surface with porous medium. Radhika et al. [13] constructed two-way flow approaching model to investigate energy transport in hybrid dusty nanofluid. Mallikarjuna et al. [14] examined effect of viscous dissipation on dusty hybrid nanoliquid stream past a stretching surface. Abdelmalek et al. [15] discussed the heat transference in dusty hybrid nano liquid stream.

The flow of different fluids over a cylinder has gained special interest in research area with many significant uses such as revolving-tube heat exchangers, cooling of electronic apparatus, and drilling of oil wells. Hayat et al. [16] used a stretched cylinder to evaluate mixed convective stream of liquid with appropriate boundary conditions. Khan et al. [17] deliberated the hydromagnetic viscous liquid flow through a cylinder. Waqas et al. [18] inspected the influence of activation energy on the nanoparticle fluid flow generated by a cylinder. The heat transfer in MHD nanofluid stream on taking account of ohmic heating over a stretching cylinder was deliberated by Mishra and Kumar [19]. Mixed convective flow and heat transfer process has enormous engineering applications like, solar cells, drying, electronic cooling devices and many others. The scrutiny of mixed convection is complex due to the convoluted interaction between the free convection with the shear motivated flow. Qayyum et al. [20] studied mixed convective two-dimensional nanofluid flow at a stagnation point over a sheet. The entropy optimization of Eyring Powell liquid flow with nanoparticles was analysed by Alsaedi et al. [21]. Further mixed convective heat transfer is scrutinized here. Akbar et al. [22] schematically illustrated mixed convective stream of nanofluid with various slip conditions. Ramesh et al. [23] deliberated the mixed convective stream of hybrid nanofluid past an upright permeable cylinder.

Fourier's law has been practically applied for studying heat transfer problems. But the most important complexity of this law is that it yields a parabolic equation of energy, which specifies that primary disturbance has established all over the entire system. To beat this difficulty, Cattaneo modified this law with the help of heat flux relaxation time. Later on, Christov improved Cattaneo's proposition with suitable explanation. Further, many authors used the modified Fourier model in their studies. Salahuddin et al. [24] examined the impact of modified Fourier heat flux on Williamson liquid past a stretching sheet. Modified Fourier model was implemented by Khan et al. [25] to estimate the hydromagnetic flow of Carreau liquid through a cylinder. Hussain et al. [26] examined the heat transfer features in viscoinelastic liquid past a stretching surface by means of modified Fourier heat flux. Ahmed et al. [27] scrutinised the mixed convective stream of maxwell liquid on taking account of Catteneo-Christov heat flux. Khan et al. [28] deliberated the impact of modified Fourier heat flux on non-Newtonian liquid stream past a stretching cylinder.

In view of the above literature survey, it is obvious to the best of writer’s knowledge, that no efforts have far been initiated with respect to modified Fourier heat flux effect on 2D-stream of a dusty hybrid nanoliquid over a stretching cylinder with mixed convection which constitutes the novelty of the present work. In this study, we discuss the consequence of hybrid nanoparticles on the dusty fluid flow through a stretching cylinder by utilising the modified Fourier heat flux law. The dusty-fluid expressions for dust and nanoparticles are discussed by using equations [1,2,3,4,5,6], and are employed with corresponding boundary conditions [7], both the dust and fluid particles are governed by the coupled set of the energy and momentum expressions. Further, we chose Molybdenum disulphide and silver as nanoparticles suspended in carrier liquid water. The governing coupled non-linear PDEs are numerically solved and the outcomes attained are presented graphically and discussed briefly. The solutions presented are not only important for practical applications but also work for further research on an ongoing topic that incorporates more complex physical factors, as quoted in the aforementioned articles in this field.

The structure of the paper consists of five parts: Sect. 1 summarizes a few published investigations and the motives for this investigation; Sect. 2 reviews the methodology used; Sect. 3 describes the Numerical method opted: the outcomes of this study and discussion are presented in Sect. 4; the conclusions and recommendations are given in the last section.

2 Mathematical formulation

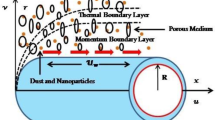
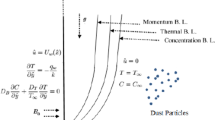
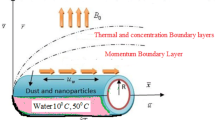
Consider a two-dimensional incompressible dusty hybrid nanofluid flow through a stretching cylinder with reference length \(L\) and stretching rate\(a\). The stretching velocity is denoted by \({U}_{w}(x)\) which is given by \({U}_{w}\left(x\right)=\frac{ax}{L}\). The axis of the cylinder is treated along the x-axis and radial direction along the r axis. The analysis of heat transfer is done by considering modified Fourier heat flux and mixed convection. The equations which represent the hybrid nanofluid flow with dust particle suspension on taking account of mixed convection through a stretching cylinder is given by (refer Manjunatha et al. [11]):

2.1 Fluid phase

$$\frac{{\partial \left( {{\text{ru}}} \right)}}{{\partial {\text{x}}}} + \frac{{\partial \left( {{\text{rv}}} \right)}}{{\partial {\text{r}}}} = 0$$
(1)
$$\left( {{\mathrm{u}}~\frac{{\partial {\mathrm{u}}}}{{~\partial {\mathrm{x}}}} + {\mathrm{v}}~\frac{{\partial {\mathrm{u}}}}{{\partial {\mathrm{r}}}}} \right) = \frac{{{\upmu _{{\mathrm{hnf}}~}}}}{{{\uprho _{{\mathrm{hnf}}}}}}\left( {\frac{{{\partial ^2}{\mathrm{u}}~}}{{\partial {{\mathrm{r}}^2}}} + \frac{1}{{\mathrm{r}}}\,\frac{{\partial {\mathrm{u}}}}{{\partial {\mathrm{r}}}}} \right) + \frac{{{\mathrm{KN}}}}{{{\uprho _{{\mathrm{hnf}}}}}}\left( {{{\mathrm{u}}_{\mathrm{p}}} - {\mathrm{u}}} \right) + \frac{{{\mathrm{g}}{{\left( {\uprho \upbeta } \right)}_{{\mathrm{hnf}}}}\left( {{\mathrm{T}} - {{\mathrm{T}}_\infty }} \right)}}{{{\uprho _{{\mathrm{hnf}}}}}}$$
(2)
$$\left( {{\text{u}} \frac{{\partial {\text{T}}}}{{ \partial {\text{x}}}} + v \frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right) + \gamma^{*} \left( {u^{2} \frac{{\partial^{2} {\text{T}}}}{{\partial {\text{x}}^{2} }} + v^{2} \frac{{\partial^{2} {\text{T}}}}{{\partial {\text{r}}^{2} }} + 2{\text{uv}}\frac{{\partial^{2} {\text{T}}}}{{\partial {\text{r}}\partial {\text{x}}}} + {\text{u}}\frac{{\partial {\text{u}}}}{{\partial {\text{r}}}}\frac{{\partial {\text{T}}}}{{\partial {\text{x}}}} + u\frac{{\partial {\text{v}}}}{{\partial {\text{x}}}}\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}} + v\frac{{\partial {\text{u}}}}{{\partial {\text{x}}}}\frac{{\partial {\text{T}}}}{{\partial {\text{x}}}} + v\frac{{\partial {\text{v}}}}{{\partial {\text{r}}}}\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right) = \frac{{{\text{k}}_{{\text{hnf }}} }}{{\left( {{\rho C}_{{\text{p}}} } \right) _{{{\text{hnf}}}} }}\left( {\frac{{\partial^{2} {\text{T}} }}{{\partial {\text{r}}^{2} }} + \frac{1}{{\text{r}}}\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right) + \frac{{{\uprho }_{{\text{p}}} }}{{\left( {{\rho C}_{{\text{p}}} } \right) _{{{\text{hnf}}}} \tau_{v} }} \left( {{\text{u}}_{{\text{p}}} - {\text{u}}} \right)^{2} + \frac{{{\uprho }_{{\text{p}}} \left( {{\text{C}}_{{\text{p}}} } \right)_{{\text{f}}} }}{{\left( {{\rho C}_{{\text{p}}} } \right) _{{{\text{hnf}}}} \tau_{t} }} \left( {{\text{T}}_{{\text{p}}} - {\text{T}}} \right)$$
(3)

2.2 Dust phase

$$\frac{{\partial \left( {{\text{ru}}_{{\text{P}}} } \right)}}{{\partial {\text{x}}}} + \frac{{\partial \left( {{\text{rv}}_{{\text{P}}} } \right)}}{{\partial {\text{r}}}} = 0$$
(4)
$$\left( {{\text{u}}_{{\text{P}}} { }\frac{{\partial {\text{u}}_{{\text{P}}} }}{{{ }\partial {\text{x}}}} + {\text{v}}_{{\text{P}}} { }\frac{{\partial {\text{u}}_{{\text{P}}} }}{{\partial {\text{r}}}}} \right) = \frac{{\text{K}}}{{\text{m}}}\left( {{\text{u}} - {\text{u}}_{{\text{P}}} } \right)$$
(5)
$$\left( {{\text{u}}_{{\text{p}}} { }\frac{{\partial {\text{T}}_{{\text{p}}} }}{{{ }\partial {\text{x}}}} + {\text{v}}_{{\text{p}}} { }\frac{{\partial {\text{T}}_{{\text{p}}} }}{{\partial {\text{r}}}}{ }} \right) = - \frac{{{\text{C}}_{{{\text{pf}}}} }}{{{\text{C}}_{{\text{m}}} {\uptau }_{{\text{T}}} }}\left( {{\text{T}}_{{\text{p}}} - {\text{T}}} \right)$$
(6)

Boundary constraints for the proposed problem are:

$$\begin{array}{ccccc} & {\mathrm{u}} = {{\mathrm{U}}_{\mathrm{w}}},{\mathrm{v}} = 0, - {{\mathrm{k}}_{{\mathrm{hnf}}}}\frac{{\partial {\mathrm{T}}}}{{\partial {\mathrm{x}}}} = {\Omega _1}\left( {{{\mathrm{T}}_{\mathrm{w}}} - {\mathrm{T}}} \right)\,{\mathrm{at}}\,{\mathrm{r}} = {\mathrm{R}}\\ & {\mathrm{u}} \to 0,{{\mathrm{u}}_{\mathrm{p}}} \to 0,{{\mathrm{v}}_{\mathrm{p}}} \to {\mathrm{v}},{\mathrm{T}} \to {{\mathrm{T}}_\infty },{{\mathrm{T}}_p} \to {{\mathrm{T}}_\infty }\,{\mathrm{as}}\,{\mathrm{r}} \to \infty \end{array}$$
(7)

The suitable similarity variables are:

$$\begin{array}{ll} {\mathrm u} &= \frac{{{\mathrm{ax}}}}{{\mathrm{L}}}{\mathrm{f}}'\left( \upeta \right),~{\mathrm{v}} = - \frac{1}{{\mathrm {r}}}\sqrt {\frac{{{{\nu }_{\mathrm {f}}}{\mathrm {a}}}}{L}} {\mathrm {Rf}}\left( \upeta \right),~\upeta = \frac{{{{\mathrm {r}}^2} - {{\mathrm {R}}^2}}}{{2{\mathrm {R}}}}\sqrt {\frac{{\mathrm {a}}}{{{{ \nu }_{\mathrm {f}}}{\mathrm {L}}}}} ,~{{\mathrm {u}}_{\mathrm {p}}} = \frac{{{\mathrm {ax}}}}{{\mathrm {L}}}{\mathrm {F}}'\left( \upeta \right),~{{\mathrm {v}}_{\mathrm {p}}} = - \frac{1}{{\mathrm {r}}}\sqrt {\frac{{{{ \nu }_{\mathrm {f}}}{\mathrm {a}}}}{{\mathrm {L}}}} {\mathrm {RF}}\left( \upeta \right)\\\uptheta \left( \upeta \right) &= \frac{{{\mathrm {T}} - {{\mathrm {T}}_\infty }}}{{{{\mathrm {T}}_{\mathrm {w}}} - {{\mathrm {T}}_\infty }}},~{\uptheta _{\mathrm {p}}}\left( \upeta \right) = \frac{{{{\mathrm {T}}_{\mathrm {p}}} - {{\mathrm {T}}_\infty }}}{{{{\mathrm {T}}_{\mathrm {W}}} - {{\mathrm {T}}_\infty }}}\end{array}$$

where \({\uprho }_{\mathrm{hnf}}, {\upmu }_{\mathrm{hnf}}, {\left({{\uprho \mathrm{C}}}_{\mathrm{p}}\right)}_{\mathrm{hnf}}, {\left({\uprho \upbeta }\right)}_{\mathrm{hnf}}\text{ and }\,{\mathrm{k}}_{\mathrm{hnf}}\) is defined by:

$$\begin{array}{lllll}\frac{{{{{\uprho}} _{{\mathrm{hnf}}}}}}{{{\uprho _{\mathrm{f}}}}} & = \left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\frac{{{\uprho _{{\mathrm{s}}1}}}}{{{\uprho _{\mathrm{f}}}}}} \right] + {\upphi _2}\frac{{{\uprho _{{\mathrm{s}}2}}}}{{{\uprho _{\mathrm{f}}}}}\\ \frac{{{{\left( {\uprho \upbeta } \right)}_{{\mathrm{hnf}}}}}}{{{{\left( {\uprho \upbeta } \right)}_{\mathrm{f}}}}} & = \left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\frac{{{{\left( {\uprho \upbeta } \right)}_{{\mathrm{s}}1}}}}{{{{\left( {\uprho \upbeta } \right)}_{\mathrm{f}}}}}} \right] + {\upphi _2}\frac{{{{\left( {\uprho \upbeta } \right)}_{{\mathrm{s}}2}}}}{{{{\left( {\uprho \upbeta } \right)}_{\mathrm{f}}}}}\\ \frac{{{{\left( {\uprho {\mathrm{C}}\uprho } \right)}_{{\mathrm{hnf}}}}}}{{{{\left( {{{\mathrm{C}}_{\mathrm{p}}}\uprho } \right)}_{\mathrm{f}}}}} & = \left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\left( {\frac{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{{\mathrm{s}}1}}}}{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{\mathrm{f}}}}}} \right)} \right] + {\upphi _2}\frac{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{{\mathrm{s}}2}}}}{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{\mathrm{f}}}}}\\ {\mu _{{\mathrm{hnf}}}} & = \frac{{{\mu _{\mathrm{f}}}}}{{{{\left( {1 - {\upphi _1}} \right)}^{2.5}}{{\left( {1 - {\upphi _2}} \right)}^{2.5}}}}\\ \frac{{{{\mathrm{k}}_{{\mathrm{hnf}}}}}}{{{{\mathrm{k}}_{{\mathrm{bf}}}}}} & = \frac{{{{\mathrm{k}}_{{{\mathrm{s}}_2}}} + 2{{\mathrm{k}}_{{\mathrm{bf}}}} - 2{\upvarphi _2}\left( {{{\mathrm{k}}_{{\mathrm{bf}}}} - {{\mathrm{k}}_{{{\mathrm{s}}_2}}}} \right)}}{{{{\mathrm{k}}_{{{\mathrm{s}}_2}}} + 2{{\mathrm{k}}_{{\mathrm{bf}}}} + {\upvarphi _2}\left( {{{\mathrm{k}}_{{\mathrm{bf}}}} - {{\mathrm{k}}_{{{\mathrm{s}}_2}}}} \right)}},~~\frac{{{{\mathrm{k}}_{{\mathrm{bf}}}}}}{{{{\mathrm{k}}_{\mathrm{f}}}}} = \frac{{{{\mathrm{k}}_{{{\mathrm{s}}_1}}} + 2{{\mathrm{k}}_{\mathrm{f}}} - 2{\upvarphi _1}\left( {{{\mathrm{k}}_{\mathrm{f}}} - {{\mathrm{k}}_{{{\mathrm{s}}_1}}}} \right)}}{{{{\mathrm{k}}_{{{\mathrm{s}}_1}}} + 2{{\mathrm{k}}_{\mathrm{f}}} + {\upvarphi _1}\left( {{{\mathrm{k}}_{\mathrm{f}}} - {{\mathrm{k}}_{{{\mathrm{s}}_1}}}} \right)}} \end{array}$$

By using above similarity transformation, the obtained reduced equations are as follow:

$$\upvarepsilon _{1} \left[ {\left( {2\upeta \updelta + 1} \right){\text{f}}^{^{\prime\prime}} + 2\updelta {\text{f}}^{^{\prime\prime}} } \right] - \left[ {{\text{f}}^{^{\prime}2} - {\text{ff}}^{^{\prime\prime}} } \right] +\upvarepsilon _{2} {\text{l}}\upbeta _{{\text{v}}} \left( {{\text{F}}^{^{\prime}} - {\text{f}}^{^{\prime}} } \right) + \frac{{\upvarepsilon _{2} }}{{\upvarepsilon _{3} }}{\text{gr}}\uptheta = 0$$
(8)
$${\upvarepsilon _4}\left( {\frac{{{{\mathrm{k}}_{{\mathrm{hnf}}~}}}}{{{{\mathrm{k}}_{{\mathrm{f}}~}}}}} \right)\left[ {\frac{1}{{\Pr }}} \right]\left[ {\left( {2\updelta \upeta + 1} \right)\uptheta '' + 2\updelta \uptheta '} \right] + {\mathrm{f}}\uptheta ' + {\upvarepsilon _4}l{\upbeta _v}{\mathrm{Ec}}{\left( {\mathrm{F' - f'}} \right)^2} + {\upvarepsilon _4}l{\upbeta _t}\left( {{\uptheta _p} + \uptheta '} \right) - \Gamma \left( {{f^2}{\uptheta ^{''}} + ff'\uptheta '} \right) = 0$$
(9)
$${\mathrm{FF''}} - {{\mathrm{F}}^{'2}} + {\upbeta _{\mathrm{v}}}\left( {{\mathrm{f'}} - {\mathrm{F'}}} \right) = 0$$
(10)
$${\mathrm{F}}\uptheta_{p}^{^{\prime}} - \upbeta_{t} \upgamma \left( {\uptheta_{p} - \uptheta } \right) = 0$$
(11)

where

$$\begin{array}{lllll} {\upvarepsilon _1} & = \frac{1}{{{{\left( {1 - {\upphi _1}} \right)}^{2.5}}{{\left( {1 - {\upphi _2}} \right)}^{2.5}}~\left[ {\left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\frac{{{\uprho _{{\mathrm{s}}1}}}}{{{\uprho _{\mathrm{f}}}}}} \right] + {\upphi _2}\frac{{{\uprho _{{\mathrm{s}}2}}}}{{{\uprho _{\mathrm{f}}}}}} \right]}}\\ {\upvarepsilon _2} & = \frac{1}{{\left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\frac{{{\uprho _{{\mathrm{s}}1}}}}{{{\uprho _{\mathrm{f}}}}}} \right] + {\upphi _2}\frac{{{\uprho _{{\mathrm{s}}2}}}}{{{\uprho _{\mathrm{f}}}}}}}\\ {\upvarepsilon _3} & = \frac{1}{{\left( {1 - {\phi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\frac{{{\uprho _{{\mathrm{s}}1}}}}{{{{\left( {\uprho \upbeta } \right)}_{\mathrm{f}}}}}} \right] + {\upphi _2}\frac{{{\uprho _{{\mathrm{s}}2}}}}{{{{\left( {\uprho \upbeta } \right)}_{\mathrm{f}}}}}}}\\ {\upvarepsilon _4} & = \frac{1}{{\left( {1 - {\upphi _2}} \right)\left[ {\left( {1 - {\upphi _1}} \right) + {\upphi _1}\left( {\frac{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{{\mathrm{s}}1}}}}{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{\mathrm{f}}}}}} \right)} \right] + {\upphi _2}\frac{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{{\mathrm{s}}2}}}}{{{{\left( {\uprho {\mathrm{C}}p} \right)}_{\mathrm{f}}}}}}} \end{array}$$

The corresponding reduced boundary constraints are:

$${\mathrm{f}}\left( 0 \right) = 0,~{\mathrm{f'}}\left( 0 \right) = 1,~\frac{{{{\mathrm{k}}_{{\mathrm{hnf}}}}}}{{{{\mathrm{k}}_{\mathrm{f}}}}}\uptheta '\left( 0 \right) = - {\mathrm{Bi}}\left( {1 - \uptheta \left( 0 \right)} \right)$$
(12)
$${\mathrm{f'}}\left( \infty \right) = 0,{\mathrm{F'}}\left( \infty \right) = 0,{\mathrm{F}}\left( \infty \right) - {\mathrm{f}}\left( \infty \right) = 0,\,\uptheta \left( \infty \right) = 0,{\uptheta _{\mathrm{p}}}\left( \infty \right) = 0$$
(13)

where,

$${\upbeta }_{{\text{t}}} = \frac{{\text{L}}}{{{\uptau }_{{\text{t}}} a}}\,{\upbeta }_{{\text{v}}} = \frac{{\text{L}}}{{{\uptau }_{{\text{v}}} a}}\,{\updelta } = \sqrt {\frac{{{\upnu }_{{\text{f}}} {\text{L}}}}{{{\text{aR}}^{2} }}} \,{\upgamma } = \frac{{{\text{C}}_{{{\text{pf}}}} }}{{{\text{C}}_{{\text{m}}} }},\,{\text{Pr}} = \frac{{\left( {{\rho C}_{{\text{p}}} } \right)_{{\text{f}}} {\upnu }_{{\text{f}}} }}{{{\text{k}}_{{\text{f}}} }},\,{\text{Re}}_{{\text{x}}} = \frac{{{\text{U}}_{{\text{w}}} {\text{x}}}}{{{\upnu }_{{\text{f}}} }},\,{\text{Gr}} = \frac{{{\text{g}}\left( {\upbeta } \right)_{{\text{f}}} \left( {{\text{T}}_{{\text{w}}} - {\text{T}}_{\infty } } \right){\text{x}}^{3} { }}}{{{\upnu }_{{\text{f}}}^{2} }},\,{\text{l}} = \frac{{{\text{mN}}}}{{{\uprho }_{{\text{f}}} }},\,{\text{ gr}} = { }\frac{{{\text{Gr}}}}{{{\text{Re}}_{{\text{x}}}^{2} }},\,{\Gamma } = \frac{{{\upgamma }^{*} {\text{a}}}}{{\text{L}}},\,Bi = \frac{{\Omega _{1} }}{{{\text{k}}_{{\text{f}}} }}\sqrt {\frac{{{\upnu }_{{\text{f}}} {\text{L}}}}{a}}$$

The skin friction coefficient is given by

$${\text{C}}_{{\text{f}}} = \frac{{{\upmu }_{{{\text{hnf}}}} }}{{{\uprho }_{{\text{f}}} {\text{u}}_{{\text{w}}}^{2} }}\left( {\frac{{\partial {\text{u}}}}{{\partial {\text{r}}}}} \right)_{{{\text{r}} = {\text{R}}}}$$
(14)

By using non-dimensional variables, we have

$${{\mathrm{C}}_{\mathrm{f}}}{{\mathop{\mathrm {Re}}\nolimits} _{\mathrm{x}}}^{\frac{1}{2}} = \frac{{{\mathrm{f''}}\left( 0 \right)~}}{{{{\left( {1 - {\upphi _1}} \right)}^{2.5}}{{\left( {1 - {\upphi _2}} \right)}^{2.5}}~}},\,{\mathrm{Where}}\,{{\mathop{\mathrm {Re}}\nolimits} _{\mathrm{x}}} = \frac{{{{\mathrm{U}}_{\mathrm{w}}}{\mathrm{x}}}}{{{{{\nu }}_{\mathrm{f}}}}}$$
(15)

3 Numerical solution

To understand the phenomena of the model, the non-linear differential Eqs. (8–11) with corresponding boundary constraints (12–13) are cracked by applying Runge–Kutta–Fehlberg–45 (RKF-45) technique along with the shooting method. The ordinary differential equations which are coupled, nonlinear with boundary constraints are numerically solved and scrutinized with the help of graphs. To solve these reduced equations, corresponding equations along with boundary conditions are transformed into accompanying arrangement of differential equations in first-order using the replacements \({\text{f}} = y\left( 1 \right),{\text{f}}^{^{\prime}} = y\left( 2 \right),{\text{f}}^{^{\prime\prime}} = {\text{y}}\left( 3 \right),\uptheta = y\left( 4 \right),\uptheta ^{^{\prime}} = {\text{y}}\left( 5 \right),{\text{F}} = {\text{y}}\left( 6 \right),{\text{F}}^{^{\prime} } = y\left( 7 \right),\,{\text{and}}\,\uptheta _{{\text{p}}} = {\text{y}}\left( 8 \right)\)\(.\)

$$\begin{array}{lllll} {\mathrm{y'}}\left( 1 \right) & = {\mathrm{y}}\left( 2 \right)\\ {\mathrm{y'}}\left( 2 \right) & = {\mathrm{y}}\left( 3 \right)\\ {\mathrm{y'}}\left( 3 \right)~ & = \frac{{ - {\upvarepsilon _1}\left[ {2\updelta {\mathrm{y}}\left( 3 \right)} \right] + \left[ {{\mathrm{y}}{{\left( 2 \right)}^2} - {\mathrm{y}}\left( 1 \right){\mathrm{y}}\left( 3 \right)} \right] - {\upvarepsilon _2}l{\upbeta _{\mathrm{v}}}\left( {{\mathrm{y}}\left( 7 \right) - {\mathrm{y}}\left( 2 \right)} \right) - \frac{{{\upvarepsilon _2}}}{{{\upvarepsilon _3}}}{\mathrm{gr}}~{\mathrm{y}}\left( 4 \right)}}{{{\upvarepsilon _1}\left( {2\upeta \updelta + 1} \right)}}\\ {\mathrm{y'}}\left( 4 \right) & = {\mathrm{y}}\left( 5 \right)\\ {\mathrm{y}}\left( 6 \right) & = {\mathrm{y}}\left( 7 \right)\\ {\mathrm{y'}}\left( 7 \right) & = \frac{{{\mathrm{y}}{{\left( 7 \right)}^2} - {\upbeta _{\mathrm{v}}}\left( {{\mathrm{y}}\left( 2 \right) - {\mathrm{y}}\left( 7 \right)} \right)}}{{{\mathrm{y}}\left( 6 \right)}}\\ {\mathrm{y'}}\left( 8 \right) & = \frac{{{\upbeta _t}\upgamma \left( {{\mathrm{y}}\left( 8 \right) - {\mathrm{y}}\left( 4 \right)} \right)}}{{{\mathrm{y}}\left( 6 \right)}} \end{array}$$

The Runge Kutta Fehlberg-45 order algorithm is given by:

$$\begin{gathered} k_{1} = hf\left( {t_{k} ,y_{k} } \right) \hfill \\ k_{2} = hf\left( {t_{k} + \frac{1}{4}h,y_{k} + \frac{1}{4}k_{1} } \right) \hfill \\ k_{3} = hf\left( {t_{k} + \frac{3}{8}h,y_{k} + \frac{3}{32}k_{1} + \frac{9}{32}k_{2} } \right) \hfill \\ k_{4} = hf\left( {t_{k} + \frac{12}{{13}}h,y_{k} + \frac{1932}{{2197}}k_{1} - \frac{7200}{{2197}}k_{2} + \frac{7296}{{2197}}k_{3} } \right) \hfill \\ k_{5} = hf\left( {t_{k} + h,y_{k} + \frac{439}{{216}}k_{1} - 8k_{2} + \frac{3680}{{513}}k_{3} - \frac{845}{{4104}}k_{4} } \right) \hfill \\ k_{6} = hf\left( {t_{k} + \frac{1}{2}h,y_{k} - \frac{8}{27}k_{1} + 2k_{2} - \frac{3544}{{2565}}k_{3} + \frac{1859}{{4104}}k_{4} - \frac{11}{{40}}k_{5} } \right) \hfill \\ z_{k + 1} = y_{k} + \frac{16}{{135}}k_{1} + \frac{6656}{{12825}}k_{3} + \frac{28561}{{56430}}k_{4} - \frac{9}{50}k_{5} + \frac{2}{55}k_{6} \hfill \\ \end{gathered}$$

We have selected a distinct value of \({\eta }_{\infty }\) so that far field boundary constraints are satisfied asymptotically. In this present study, an apt finite value of η∞ is considered as \({\eta }_{\infty }<7\) in such a way that not only numerical solutions converge but also boundary conditions defined at infinity satisfy asymptotically. The tolerance for related errors up to \({10}^{-8}\) is considered for convergence and the step size is chosen as Δη = 0.001. In addition, the CPU time to measure velocity values (1.34 s) is much shorter than the CPU time to measure temperature values (1.74 s) and the CPU concentration time is 2.01 s. We also compared the numerical results obtained in the present study with corresponding results of the published work. Table 1 is constructed for comparative table of present results with existing work and obtained a good agreement with each other.

Table 1 Comparison of the results for the dimensionless temperature gradient when \({\varvec{\varepsilon}}_{1} = \frac{{{\varvec{k}}_{{{\varvec{hnf}}}} }}{{{\varvec{k}}_{{\varvec{f}}} }} = 1\),\({{\varvec{\updelta}}} = {{\varvec{\Gamma}}} = {\varvec{\varepsilon}}_{2} = {\varvec{\varepsilon}}_{4} = 0\)
Full size table

4 Results and discussions

This segment treats the outcomes of the mixed convective flow of dusty hybrid Nano liquid over a cylinder on taking account of Cattaneo-Christov heat flux. Two phase model is implemented in the present research to characterise the fluid flow. Here, we chosen Molybdenum disulphide and silver as nanoparticles suspended in water as carrier liquid. A numerical scheme is applied to provide a clear understanding and are sufficient to depict the behaviour of flow profiles, which are strategized and deliberated with the assistance of graphs. The thermo-physical characteristics of nanoparticles and base liquid are introduced in Table 2. In this segment, we emphasis on the reliability of non-dimensional parameters that can contribute to velocity and temperature profiles containing dust and hybrid nanoparticles. The choice of the first guess and the extent of the boundary layer \(\eta_{\infty }\) depends on the parameters values which are used to find the essential solutions. The values selected in computations are based on associated earlier investigation. The physical parameter values are set and for various values of mass concentration of particles, mixed convection parameter, fluid particles interaction parameter over velocity and thermal gradients of fluid containing dust particles and hybrid nanoparticles. Further, they are exemplified with the help of graphs.

Table 2 Thermo physical properties of \({\varvec{MoS}}_{2}\), \({\varvec{Ag}}\) and water (Refer Shafie et al. [33])
Full size table

Figure 1 is plotted to see the domination of \(l\) over velocity gradient of both fluid and dust phases. The upshot in values of \(l\) deteriorates the velocity of both phases as depicted in Fig. 1. It is perceptible that the upsurge in dust particles mass concentration diminishes fluid velocity and related boundary layer thickness. The sway of curvature parameter on velocity gradient of both phases is put on a display in Fig. 2. It is very clear from Fig. 2 that the liquid velocity is just as dust stage comparing to \((\delta = 0.2)\) is least and the expansion of \((\delta )\) is to expand the velocity inside the boundary layer. Also \((\delta = 0),\) the issue diminishes to flat surface. Henceforth, the speed inside the boundary layer on account of cylinder is bigger than the flat surface. It implies that the expanding in the cylinder measurement prompts the increasing in the velocity inside the boundary layer. The inclination in velocity gradient is faster in dust phase when compared to fluid phase. Figure 3 portrays the sway of \(gr\) on velocity gradient. The rise in values of \(gr\) gradually heightens the velocity of both the phases. Enhance in mixed convection parameter causes high difference in environmental and surface temperature. This difference causes increment in thermal gradient which results in upshot of velocity in both the phases. The domination of mass concentration of the particle on thermal gradient of both phases is depicted in Fig. 4. One can detect from the figure that upsurge in \(l\) deteriorates the thermal profile. It is caused due to the dust particle mass concentration present in the liquid. Physically, it means that increasing value of \(l\) enhance the number density of dust particles and decelerate velocity of the dusty liquid and thermal gradient.

Fig. 1
figure 1

Power of \(l\) over \(f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)\)

Full size image
Fig. 2
figure 2

Power of \(\delta\) over \(f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Power of \(gr\) over \(f^{\prime}\left( \eta \right),F^{\prime}\left( \eta \right)\)

Full size image
Fig. 4
figure 4

Power of \(l\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image

Figure 5 represents the encouragement of \({\beta }_{v}\) on thermal gradient. It is detected from figure that upshot in \({\beta }_{v}\) gradually boosts up the thermal profile. The dust phase boundary layer thickness is fewer than the thickness related with liquid phase as shown in Fig. 5. The sway of \(\delta\) on thermal gradient is portrayed in Fig. 6. It is obvious from plotted figure that, upshot in curvature parameter progresses the thermal profile of both phases. Figure 7 shows the sway of \(Ec\) on thermal profile. It is observed from the plotted figure that heightening in \(Ec\) heightens the thermal gradient. It is obvious that, upsurge in \(Ec\) improve the inter-molecular motion and kinetic energy in fluid. As a result, this inter-molecular tension upsurges the thermal gradient of both the phases and of the related boundary layer. The impact of \(\Gamma\) on thermal profile for both phases are displayed in Fig. 8. The heightening of \(\Gamma\) enhances the thermal profile of both phases as displayed in Fig. 8. The fluid phase boundary layer thickness is greater than the thickness related with dust phase. Physically, the existence of heat generation effects has the ability to enhance the thermal state of the liquid which reasons for an upsurge in its temperature and hence fluid phase is more thermal than dust phase. The sway of \(Bi\) on thermal profile for both the phases are displayed in Fig. 9. The measure of the interaction among convection at its surface and conduction in the solid is called as Biot number. Here, it is essential to mention that, the extreme values of \(Bi\) enhances the thermal profile of both the phases. Here, the \(Bi\) comprises the heat transfer coefficient and which increases for higher values of \(Bi\). Physically, inclination in \(Bi\) produces large heat transfer through convection which results in inclination of thermal field. Effect of \({\beta }_{v}\) on \({{Re}_{x}}^{1/2}{C}_{f}\) is represented in Fig. 10. It is seen from figure that rise in values of \({\beta }_{v}\) enhances the\({{Re}_{x}}^{1/2}{C}_{f}\). Figure 11 portrays the influence of \(l\) on\({{Re}_{x}}^{1/2}{C}_{f}\). One can observe from figure that rise in values of \(l\) enhances the\({{Re}_{x}}^{1/2}{C}_{f}\). Further, it is evident from both the figures that \({{Re}_{x}}^{1/2}{C}_{f}\) acts as a declining function of mixed convection parameter and growing function of \(l\) and\({\beta }_{v}\).

Fig. 5
figure 5

Power of \(\beta_{v}\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image
Fig. 6
figure 6

Power of \(\delta\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image
Fig. 7
figure 7

Power of \(Ec\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image
Fig. 8
figure 8

Power of \({\Gamma }\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image
Fig. 9
figure 9

Power of \(Bi\) over \(\theta \left( \eta \right),\theta_{p} \left( \eta \right)\)

Full size image
Fig. 10
figure 10

Power of \(\beta_{v}\) on \(Re_{x}^{1/2} C_{f}\)

Full size image
Fig. 11
figure 11

Power of \(l\) on \(Re_{x}^{1/2} C_{f}\)

Full size image

5 Final remarks

Numerically we discussed the dusty hybrid nanofluid flow through a stretching cylinder on taking account of mixed convection. The heat transference analysis is deliberated by using modified Fourier heat flux model. The suspension of Molybdenum disulphide and silver particles in base fluid water is considered in the current two-phase model. The framed equations arising in the current issue is minimized to ODE’s by applying apt similarity variables. These reduced ODEs are numerically solved by using RKF-45 method by adopting shooting technique. The physical characteristics of velocity and thermal profiles of both fluid and dust phases have been deliberated under the influence of involved flow controlling physical parameters. The results conclude that, rise in values of mass concentration of particle declines the velocity and thermal gradient of dust and fluid phases. Upsurge in the diameter of cylinder leads to the increase in velocity and heat transfer within the boundary. The velocity of both the phases improves with increase in values of mixed convection parameter. Escalation in values of fluid–particle interaction parameter gradually enhances the thermal profile of both the phases. Further, improved values of mixed convection parameter declines the skin friction.

As stated in the introduction, various significant utilizations of this work are found in the polymer industry and thus later on we plan to broaden the investigation introduced here into non-Newtonian liquids in a different circumstance.