Spectral Tau method for solving general fractional order differential equations with linear functional argument

Abstract

In this paper, a numerical technique for solving new generalized fractional order differential equations with linear functional argument is presented. The spectral Tau method is extended to study this problem, where the derivatives are defined in the Caputo fractional sense. The proposed equation with its functional argument represents a general form of delay and advanced differential equations with fractional order derivatives. The obtained results show that the proposed method is very effective and convenient.

Introduction

Spectral methods have been developed through the last years for the numerical solutions of fractional differential equations. Compared to other numerical methods, spectral methods give high accuracy and have a wide range of applications in many mathematical problems and physical phenomena [1]. The Chebyshev first kind T_n(x) are the most common basis function used with the spectral methods deal many applications in numerical analysis, and numerous studies show the merits of them in various applications[2–7].

In recent years, several studies have used spectral methods to solve delay differential equations of integer order such as, numerical approximations based on Chebyshev polynomials [8], Bernoulli polynomials [9], hybrid of block-pulse functions and Taylor series [10], and Legendre wavelet [11]. Additionally, the numerical solution of delay differential equations of fractional order have been reported by many researchers [12–23]. Differential equations of advanced argument had fewer contributions in mathematics research, compared to delay differential equations, which had a great development in the last decade [24, 25]. The general form of argument (mixed type equations) have been reported by several mathematicians, where Grbz et al. used Laguerre collocation method for solving Fredholm integro-differential equations with functional arguments [26]. Yuzbasi has reported a solution of the generalized pantograph type delay differential equations with linear functional arguments[27]. Reutskiy used the backward substitution method for multi-point problems with linear Volterra-Fredholm integro-differential equations of the neutral type [28]. All previous works considered a generalization of delay and advanced differential equations (a kind of unification) with integer order derivative.

In this paper, we introduce a generalized form of delay and advanced differential equations with fractional order derivative. Our proposed problem is called general fractional order differential equations (GFDEs) with linear functional argument. Now, we consider the GFDEs with linear functional argument as follows:

$$ f(x,y(x),D^{\nu_{i}}y(p_{i}x+\xi_{i}),y^{(i)}(q_{i}x+\tau_{i}))=0, $$

(1)

where a≤x≤b, ν_i>0 and n−1<ν_i<n,i=0,1,2…,n, q_i,p_i,ξ_i,τ_i∈ℜ under the following conditions

$$ y^{(i)}(0)=\mu_{i}, $$

(2)

where (1) and the subject conditions (2) are general form of delay and advanced differential equation with fractional order.

As we focus on linear equations, we consider f(x) a linear function. Concerning the existence of solutions for delay and advanced differential equations, we refer the readers to references [24] and [25], so the solution of the proposed formula (1) exists. The general formula (1) is chosen to be multi-term of fractional order derivatives and the terms contain linear functional argument which are taken to be multi-term of fractional order derivatives as well. Chebyshev polynomials of the first kind are used here to approximate the solution of the proposed Eq. 1. The Chebyshev polynomials are defined on [−1,1], so the argument in (1) also in [−1,1]. The operational matrices of fractional derivatives are presented and employed to deal with a generalized form with the spectral Tau method. The presented operational matrices are used with the Tau method as a matrix discretization method. The obtained numerical results are compared with other methods, where they show that the proposed method gives good accuracy.

Definitions of fractional derivatives

In this section, we present notation, definitions, and recall well-known results about fractional differential equations and the Chebyshev polynomial of the first kind.

The Caputo fractional derivative

Definition 1

The Caputo fractional derivative operator D^ν of order ν is defined in the following form:

$$ D^{\nu}f(x) = \frac{1}{\Gamma(m-\nu)}\, \int_{0}^{x}\frac{f^{(m)}(t)}{(x-t)^{\nu-m+1}}dt, \quad \nu > 0, $$

(3)

where $m-1 < \nu \leq m,\ m \in \mathbb {N},\ x > 0.$

Properties 1

1− D^ν (λ f(x)+μ g(x))=λ D^ν f(x)+μ D^ν g(x), where λ and μ are constants.

2− D^ν C=0, whereCis aconstant,

$${3-} D^{\nu}\,x^{n}=\left\{ \begin{array}{ll} 0, & \quad\quad for\quad n\in \mathbb{N}_{0} \,and\, n <\lceil \nu \rceil, \\ \frac{\Gamma(n+1)}{\Gamma(n+1-\nu)}x^{n-\nu}, & {\quad\quad for\quad n\in \mathbb{N}_{0}\, and\, n\geq\lceil \nu \rceil,} \\ \end{array} \right., $$

where ⌈ν⌉ denote to the smallest integer greater than or equal to ν, and $\mathbb {N}_{0} = \{0,1, 2, \ldots \}$.

Chebyshev polynomials of the first kind

The Chebyshev polynomials T_n(x) of the first kind are orthogonal polynomials of degree n in x defined on the [−1,1]

$$T_{n}=cosn\theta, $$

(4)

where x=cosθ and θ∈[0,π].

The polynomials T_n(x) be generated by using the recurrence relations

$$T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x),\quad\,\, T_{0}(x)=1,\,\,\,\,T_{1}(x)=x,\quad\,\, n=1,2,\ldots\,.$$

The Chebyshev polynomials T_n(x) can be expressed in terms of the power xⁿ in different forms found in [29], one of them is

$$ T_{n} (x)=\sum\limits_{k=0}^{[n/2]}c_{k}^{(n)} x^{n-2k}, $$

(5)

where

$$c_{k}^{(n)} =(-1)^{k} 2^{n-2k-1} \frac{n}{n-k} \left(\begin{array}{c} {n-k} \\ {k} \end{array}\right){\; },{\; \; \; \; }2k\le n.$$

From the previous relation, we can define that: ∙ If n is even, we find

$$T_{n} (x)=T_{2l} (x)=\sum\limits_{j=0}^{l}(-1)^{l-j} 2^{2j-1} \frac{2l}{l+j} \left(\begin{array}{c} {l+j} \\ {l-j} \end{array}\right)x^{2j}. $$

∙ If n is odd, we can write

$$T_{n} (x)=T_{2l+1} (x)=\sum\limits_{j=0}^{l}(-1)^{l-j} 2^{2j} \frac{2l+1}{l+j+1} \left(\begin{array}{c} {l+j+1} \\ {l-j} \end{array}\right)x^{2j+1}. $$

Form above we can write T(x) as a general matrix form as [29]

$$ T(x)=X(x)M^{T}, $$

(6)

where T(x) and X(x) are matrices have the form:

$$T(x)=\left[\begin{array}{cccc} {T_{0} (x)} & {T_{1} (x)} & {\ldots} & {T_{N} (x)} \end{array}\right], \,\,\,\, X(x)=\left[\begin{array}{cccc} {x^{0}} & {x^{1}} & {\ldots} & {x^{N}} \end{array}\right],$$

and M is (N+1)×(N+1) matrix given by

$${} { \begin{aligned} M\,=\,\left(\!\!\begin{array}{ccccccc} {\left(\begin{array}{c} {0} \\ {0} \end{array}\right)} & {0} & {0} & {0} & {\ldots} & {0} & {0} \\ {0} & {\left(\begin{array}{c} {1} \\ {0} \end{array}\right)} & {0} & {0} & {\ldots} & {0} & {0} \\ {-\left(\begin{array}{c} {1} \\ {1} \end{array}\right)} & {0} & {2\left(\begin{array}{c} {2} \\ {0} \end{array}\right)} & {0} & {\ldots} & {0} & {0} \\ {0} & {-\frac{3}{2} \left(\begin{array}{c} {2} \\ {1} \end{array}\right)} & {0} & {2^{2} \left(\begin{array}{c} {3} \\ {0} \end{array}\right)} & {} & {0} & {0} \\ {.} & {.} & {.} & {.} & {} & {.} & {.} \\ {.} & {.} & {.} & {.} & {} & {.} & {.} \\ {.} & {.} & {.} & {.} & {} & {.} & {.} \\ {(-1)^{l} \left(\begin{array}{c} {l} \\ {l} \end{array}\right)} & {0} & {(-1)^{l-1} 2\frac{2l}{l+1} \left(\begin{array}{c} {l+1} \\ {l-1} \end{array}\right)} & {0} & {\ldots} & {2^{2l-1} \left(\begin{array}{c} {2l} \\ {0} \end{array}\right)} & {0} \\ {0} & {(-1)^{l} \frac{2l}{l+1} \left(\begin{array}{c} {l+1} \\ {l} \end{array}\right)} & {0} & {(-1)^{l-1} 2^{2} \frac{2l+1}{l+2} \left(\begin{array}{c} {l+2} \\ {l-1} \end{array}\right)} & {\ldots} & {0} & {2^{2l} \left(\begin{array}{c} {2l+1} \\ {0} \end{array}\right)} \end{array}\!\!\!\right). \end{aligned}} $$

In this case, we are going to use the last row for odd values of N=2l+1, otherwise the previous one will be the last row of matrix M (N=2l). Now, from (6) we can obtain the k^th derivative of the matrix T(x) as:

$$ T^{(k)}(x)=X^{(k)}(x)M^{T},\quad k=0,1,2,.... $$

(7)

Operational matrices

In this section, we introduce the operational matrcies for $\phantom {\dot {i}\!}D^{\nu _{i}}T(q_{i}x+\tau _{i})$ and T^(j)(q_jx+τ_j) according to fractional calculus using relations (7) and (6). The (k)^th order derivative of the row vector T(x), can be written in the following relation form [30]:

$$ X^{(k)}(x)=X(x)H^{k}, $$

(8)

where H is squar matrix writen as:

$$ H=\left(\begin{array}{cccc} 0 & 1 &0 \ldots&0 \\ 0 &0 & 2 \ldots&0 \\ \vdots&\vdots&\vdots &\vdots \\ 0 & 0 & 0..&N \\ 0 & 0 & 0..&0 \\ \end{array} \right). $$

(9)

And the row vector T(q_ix+τ_i), represents in terms of the vector X(x) in the following form:

$$ T(q_{i}x+\tau_{i})=X(q_{i}x+\tau_{i})M^{T}, $$

(10)

The (k)^th order derivative of the row vector T(q_ix+τ_i), can be represented as:

$$ \begin{aligned} T^{(k)}(q_{i}x+\tau_{i})&=X^{(k)}(q_{i}x+\tau_{i})M^{T}\\&=X(x)B_{\tau_{i}}H^{k}(ME_{q_{i}})^{T}.\\ \end{aligned} $$

(11)

Where the elements of the diagonal matrix $E_{q_{i}}$ can be written as:

$$e_{rs}=\left\{ \begin{array}{ll} 0 & \text{\quad\quad if\quad \(r\neq s\);} \\ q_{i}^{r} & \text{\quad\quad if\quad \(r=s\)} \\ \end{array} \right.,$$

where

$$B_{\tau_{i}}=\left(\begin{array}{cccc} \left(\begin{array}{c}0\\0\end{array}\right)(\tau_{i})^{0}&\left(\begin{array}{c}1\\0\end{array}\right)(\tau_{i})^{1-0}&\left(\begin{array}{c}2\\0\end{array}\right)(\tau_{i})^{2-0}\ldots&\left(\begin{array}{c}N\\0\end{array}\right)(\tau_{i})^{N-0}\\ 0 & \left(\begin{array}{c}1\\1\end{array}\right)(\tau_{i})^{1-1} & \left(\begin{array}{c}2\\1\end{array}\right)(\tau_{i})^{2-1} \ldots&\left(\begin{array}{c}N\\1\end{array}\right)(\tau_{i})^{N-1}\\ 0 & 0 &\left(\begin{array}{c}2\\2\end{array}\right)(\tau_{i})^{2-2}\ldots&\left(\begin{array}{c}N\\2\end{array}\right)(\tau_{i})^{N-2} \\ \vdots&\vdots&\vdots&\vdots\\ 0 &0&0&\ldots\left(\begin{array}{c}N\\N\end{array}\right)(\tau_{i})^{N-N} \\ \end{array} \right). $$

The $\nu _{i}^{\text {th}}$ order fractional derivative of the vector T(x) can be written as:

$$ D^{\nu_{i}}T(x)=X_{\nu_{i}}(x)H_{\nu_{i}}M^{T}, $$

(12)

where

$$ X_{\nu_{i}}(x)=[0,0,\ldots0,x^{{n-\nu_{i}}},.....x^{{N-\nu_{i}}}],\,\,\,\,\,\,\, n-1<\nu_{i}< n,\,\,n\in N, $$

(13)

and

$$ H_{\nu_{i}}=\left(\begin{array}{cccc} 0&0\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots\\ 0&0\ldots&0&0\\ 0 & 0\ldots &\frac{\Gamma(n+1)}{\Gamma(n+1-{\nu_{i}})}&0\\ \vdots&\vdots&\vdots&\vdots\\ 0 &0\ldots&0&\frac{\Gamma(N+1)}{\Gamma(N+1-{\nu_{i}})}\\ \end{array} \right),\,\,\,\,\, n-1<\nu_{i}< n,\,\,n\in N, $$

(14)

as special case, if 0<ν_i<1, then (13) and (14) can written as:

$$ X_{\nu_{i}}(x)=[0,x^{{1-\nu_{i}}},x^{{2-\nu_{i}}},.....x^{{N-\nu_{i}}}], $$

(15)

$$ H_{\nu_{i}}=\left(\begin{array}{cccc} 0&0&0\ldots&0\\ 0&\frac{\Gamma(2)}{\Gamma(2-{\nu_{i}})}&0\ldots&0\\ 0 & 0 &\frac{\Gamma(3)}{\Gamma(3-{\nu_{i}})}\ldots&0\\ \vdots&\vdots&\vdots&\vdots\\ 0 &0&0\ldots&\frac{\Gamma(N+1)}{\Gamma(N+1-{\nu_{i}})}\\ \end{array} \right). $$

(16)

Application to fractional order differential equation

In this section, the general form of operational matrices of all terms for (1) and (2) will be obtained. Now, consider the approximate solution according to Chebyshev approximation as:

$$ y(x)\cong y_{N}(x)=\sum\limits_{i=0}^{N}a_{i}T_{i}(x), $$

(17)

where the coefficients a_i are given by:

$$ a_{i}=\left\{ \begin{array}{ll} \frac{1}{\pi}\int_{-1}^{1}y(x)T_{0}(x)w(x)dx, & \text{\quad\quad if\quad \(i=0,\)} \\ \frac{2}{\pi}\int_{-1}^{1}y(x)T_{i}(x)w(x)dx, & \text{\quad\quad if\quad \(i=1,2,\ldots,N,\)} \\ \end{array} \right. $$

(18)

where $w(x)=\frac {1} {\sqrt {1-x^{2}}}.$

Form (17) we get,

$$ y_{N}(x)=T(x)A, $$

(19)

$$ y_{N}^{(i)}(q_{i}x+\tau_{i})=T^{(i)}(q_{i}x+\tau_{i})A, $$

(20)

$$ D^{\nu_{i}}y_{N}(p_{i}x+\xi_{i})=T^{(\nu_{i})}(p_{i}x+\xi_{i})A, $$

(21)

where

$$A=[a_{0},a_{1},a_{2},\ldots,a_{N}]^{T}.$$

By using (6) and (19), we get

$$ \begin{aligned} y_{N}(x)=X(x)M^{T}A, \end{aligned} $$

(22)

also, by using (11) and (20), we get

$$ \begin{aligned} y^{(i)}_{N}(q_{i}x+\tau_{i})&=X(q_{i}x+\tau_{i})H^{i}M^{T}A\\&=X(x)H^{i}B_{\tau_{i}}(M E_{q_{i}})^{T}A, \end{aligned} $$

(23)

and by substituting (12) in (21), we get

$$ \begin{aligned} D^{\nu_{i}}y_{N}(x)(p_{i}x+\xi_{i})&=X(p_{i}x+\xi_{i})H_{\nu_{i}}M^{T}A\\&=X_{\nu_{i}}(x)H_{\nu_{i}}B_{\xi_{i}}(M E_{p_{i}})^{T}A\\ \end{aligned}. $$

(24)

For non-homogeneous term g(x), using Eqs. (6), (17), and (18) can be written in the matrix form as:

$$G=X(x)M^{T}A^{'},$$

$$A^{'}=\left(\begin{array}{c} \frac{1}{\pi}\int_{-1}^{1}g(x)T_{0}(x)w(x)dx\\ \frac{2}{\pi}\int_{-1}^{1}g(x)T_{1}(x)w(x)dx\\ \vdots\\ \frac{2}{\pi}\int_{-1}^{1}g(x)T_{N}(x)w(x)dx \end{array} \right).$$

For terms that contain variable coefficients, we may use it in the matrix form as:

$$Q_{i}(x)\sim\left(\begin{array}{ccccc} Q_{i}(x)&0&0&\dots&0\\ 0&Q_{i}(x)&0&\dots&0\\ \vdots&\vdots&\vdots&\vdots&\vdots\\0&0&0&\dots& Q_{i}(x) \end{array} \right).$$

Matrix relation for the conditions

Finaly, we can obtain the matrix form for the conditions (2) by using (19) on the form:

$$ X(0)H^{i}M^{T}A=\mu_{i},\quad\quad i=0,1,2\ldots,m-1. $$

(25)

Method of solution

Now, we are ready to construct the fundamental matrix equation corresponding to (1) for this purpose, we substitute (22), (23), and (24), into (1). Thus, we have the fundamental matrix equation as:

$$ \begin{aligned} f\left(x,X(x)M^{T}A,X(x)H^{i}B_{\tau_{i}}(M E_{q_{i}})^{T}A,X_{\nu_{i}}(x)H_{\nu_{i}}B_{\xi_{i}}(M E_{p_{i}})^{T}A\right)=0, \end{aligned} $$

(26)

so, the residual R(x) of Eq. 1, can be written as:

$$ \begin{aligned} &R(x)= f\left(x,X(x)M^{T}A,X(x)H^{i}B_{\tau_{i}}(M E_{q_{i}})^{T}A,X_{\nu_{i}}(x)H_{\nu_{i}}B_{\xi_{i}}(M E_{p_{i}})^{T}A\right). \end{aligned} $$

(27)

As in a typical Tau method, we generate (N−m+1) algebraic equations by applying

$$ \begin{aligned} \langle R(x),T_{i}(x) \rangle=\int_{-1}^{1} R(x) T_{i}(x)w(x)dx, \;\;\;\;\;\;i=0, 1, \dots, N-m+1. \end{aligned} $$

(28)

Equations (25) and (28) generate (m) and (N−m+1) set of algebraic equations, respectively. Consequently, the unknown coefficients of the vector A in (17) can be calculated.

Error estimation

If the exact solution is known, then the error will be estimated from the following:

$$ e_{N}(x)=|y(x)-y_{N}(x)|, $$

(29)

where y(x) is the exact solution and y_N(x) is the approximate solution. We can easily check the accuracy of the suggested method by the residual error, since the truncated Chebyshev series (17) is an approximate solution of (1), when the solution y_N(x) and its derivatives are substituted in (1), the resulting equation must be satisfied approximately, that is, for x∈[−1,1], l=0,1,2,…

$$ \begin{aligned} e_{N} &=\left| f(x_{l}, y_{N}(x_{l}),D^{\nu_{i}}y_{N}(p_{i}x_{l}+\xi_{i}),y_{N}^{(i)}(q_{i}x_{l}+\tau_{i}))\right| \cong0, \end{aligned} $$

(30)

and e_N≤10^$ ($ positive integer). If max 10^$= 10^−L ($ positive integer) is prescribed, then the truncation limit N is increased until the difference e_N at each of the points becomes smaller than the prescribed 10^L. On the other hand, the error can be estimated by the function If e_N→0,when N is sufficiently large enough, then the error decreases.

Applications and numerical results

In this section, we introduce some numerical examples for fractional order differential equation to illustrate the above results. All results are obtained by using Mathematica 7 program.

Example 1

Consider the second-order linear fractional differential equation (mixed type delay-advanced):

$$ y^{\prime\prime}(3x+2)+y^{\prime\prime}(x)+(x^{2}+1)D^{\nu}y(x-0.3)+D^{\alpha}y(x)+y^{}(x)=g(x), $$

(31)

the connected conditions are y(0)=0, y^′(0)=1, g(x)=20.+0.445697x^0.3+1.12706x^0.4+x+1.71422x^1.3+1.61009x^1.4+x²+0.445697x^2.3+1.71422x^3.3and the exact solution when ν=0.7, α=0.6 is y(x)=x²+x. By using the truncated Chebyshev series (17) with the present method, we get algebraic equations using the following residual:

$$ {}\begin{aligned} R(x)=\left[X H^{2}B_{2}{(E_{3}M) }^{T}+XH^{2}M^{T}+Q_{0}\,X_{\nu}\,H_{\nu}B_{-0.3}M^{T}+ X_{\alpha}H_{\alpha} M^{T}+XM^{T}\right]A-G, \end{aligned} $$

(32)

where

$${}{\begin{aligned} X&=\left(\begin{array}{c} 1 \\ x \\ x^{2} \\ x^{3} \\ x^{4} \\ x^{5} \end{array} \right),X_{0.7}=\left(\begin{array}{c} 1 \\ x^{0.3} \\ x^{2.3} \\ x^{3.3} \\ x^{4.3} \\ x^{5.3} \end{array} \right),X_{0.6}=\left(\begin{array}{c} 1 \\ x^{0.4} \\ x^{2.4} \\ x^{3.4} \\ x^{4.4} \\ x^{5.4} \end{array} \right),B_{2}=\left(\begin{array}{cccccc} 1 & 2 & 4 & 8 & 16 & 32 \\ 0 & 1 & 4 & 12 & 32 & 80 \\ 0 & 0 & 1 & 6 & 24 & 80 \\ 0 & 0 & 0 & 1 & 8 & 40 \\ 0 & 0 & 0 & 0 & 1 & 10 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right)\\ E_{3}&=\left(\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 9 & 0 & 0 & 0 \\ 0 & 0 & 0 & 27 & 0 & 0 \\ 0 & 0 & 0 & 0 & 81 & 0 \\ 0 & 0 & 0 & 0 & 0 & 243 \end{array} \right),Q_{0}=\left(\begin{array}{cccccc} 1+x^{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 1+x^{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 1+x^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1+x^{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & 1+x^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1+x^{2} \end{array} \right),\\ H_{0.7}&=\left(\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1.11424 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1.71422 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2.23594 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2.71023 & 0 \\ 0 & 0 & 0 & 0 & 0 & 3.15143 \end{array} \right),M=\left(\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ -1 & 0 & 2 & 0 & 0 & 0 \\ 0 & -3 & 0 & 4 & 0 & 0 \\ 1 & 0 & -8 & 0 & 8 & 0 \\ 0 & 5 & 0 & -20 & 0 & 16 \end{array} \right),\\ H_{0.6}&=\left(\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1.12706 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1.61009 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2.01261 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2.36777 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2.69065 \end{array} \right),A^{'}=\left(\begin{array}{c} 12.0055-0.00901411 i \\ 5.92462+0.101376 i \\ 1.1573-0.216974 i \\ 0.510798+0.172611 i \\ -0.100338-0.0118752 i \\ 0.0154373-0.0681158 i \\ 0.0503126+0.0151133 i \end{array} \right).\\ H&=\left(\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 & 5 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right),B_{-0.3}=\left(\begin{array}{cccccc} 1 & -0.3 & 0.09 & -0.027 & 0.0081 & -0.00243 \\ 0 & 1 & -0.6 & 0.27 & -0.108 & 0.0405 \\ 0 & 0 & 1 & -0.9 & 0.54 & -0.27 \\ 0 & 0 & 0 & 1 & -1.2 & 0.9 \\ 0 & 0 & 0 & 0 & 1 & -1.5 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right). \end{aligned}} $$

Also, by using the conditions, we can generate two algebraic equations as:

$$ y(0)=X(0)M^{T}A=0, $$

(33)

$$ y'(0)=X(0)BM^{T}A=1, $$

(34)

by solving this algebraic equations, we have

$$ A=\left[ \begin{array}{ccccccc} \frac{1}{2}& 1& \frac{1}{2}& 0& 0 & 0&0\\ \end{array}\right]. $$

(35)

Then the solution of the problem (31) is

$$ y_{6} (x) =\frac{1}{2}T_{0}(x)+1\,T_{1}(x)+\frac{1}{2}\,T_{2}(x)+0\,T_{3}(x)+0\,T_{4}(x)+0\,T_{4}(x)+0\,T_{6}(x)=x^{2}+x, $$

(36)

which is the exact solution of the problem (31).

Example 2

Consider the linear fractional order delay differential equation [31]

$$ D^{\frac{1}{2}}y(x) +y(x)-y(x-1)=2x+\frac{\Gamma(3)}{\Gamma(1.5)}x^{1.5}-1, $$

(37)

the given condition is y(0)=0 and the exact solution is y(x)=x², in [31] the solution obtained by using the shifted Jacobi polynomial scheme, the results are shown by deriving operational matrix for the fractional differentiation and integration. We will employ the present method to (37) at N=5.

We get algebraic equations by using the following residual:

$$ \begin{aligned} R(x)=\left[\,X_{0.5} H_{0.5} M^{T}+\,XM^{T} -\,X B_{-1}M^{T}\right]A-G. \end{aligned} $$

(38)

Also, by using the given condition, we can generate algebraic equation as:

$$ y(0)=X(0)M^{T}A=0. $$

(39)

By solving this algebraic equations, we have

$$ A=\left[ \begin{array}{cccccc} \frac{1}{2}& 0& \frac{1}{2}& 0& 0 & 0\\ \end{array}\right]. $$

(40)

Then, the solution is

$$ y_{5} (x) =\frac{1}{2}T_{0}(x)+\frac{1}{2}T_{2}(x)=x^{2}. $$

(41)

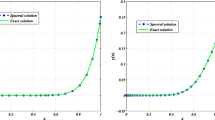
Comparison of the values of the exact and approximate solutions of the problem (37) is given in Table 1 and Fig. 1; in addition, comparison of the residual errors (depended on Eq. 30) by using the proposed method at different N is obtained in Table 2 and Fig. 2.

Fig. 1

The behavior of the exact solution and the approximate solution at N=5 for example 2

Fig. 2

Residual errors by using the proposed method at different N and α=0.5 for example 2

Table 1 Comparison of the values of exact and approximate solutions of the problem (37) for x values for example 2

Table 2 Comparison of the residual errors by using proposed method at different N for x values for example 2

Example 3

Consider the following fractional delay differential equation [32, 33]:

$$ D^{\alpha}y(x)+y(x)+y(x-0.3)=e^{-x+0.3},\,\,\,\ 2<\alpha\leq3, $$

(42)

with the conditions y(0)=1, y^′(0)=−1, ξ₀=−0.3 and the exact solution when α=3 is y(x)=e^−x. By the same way, we get the following residual:

$$ \begin{aligned} R(x)=\left[X_{\alpha} H_{\alpha} M^{T}+X M^{T} +XB_{-0.3} M^{T}\right]A-G. \end{aligned} $$

(43)

Also, by using the subjected conditions we can generate two algebraic equations as:

$$ y(0)=X(0)M^{T}A=1, $$

(44)

$$ y'(0)=X(0)BM^{T}A=-1, $$

(45)

by solving these algebraic equations at α=3, we have the solution as:

$$ A=\left[ \begin{array}{ccccccccc} 1.26604&-1.12997& 0.27146& -0.04426& 0.00546& -0.00056 & 0.00004\\ \end{array}\right]. $$

(46)

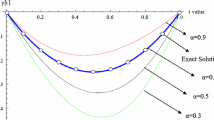
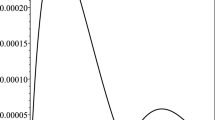
Table 4 displays the residual errors at different N, while the approximate solutions obtained for various values of x by using the present method with N=6, the Hermite wavelet method [33] for N=7 and the Bernoulli wavelet method [32] together with the exact solution are listed in Table 3. Table 3 also contains the numerical results for (42) at α=2.8 and 2.6. In addition, Fig. 3 shows the approximate solutions at different α and the exact solution (α=3) and Fig. 4 shows the residual errors at different N (Table 4).

Fig. 3

Solutions by the proposed method at different α and exact solution at α=3N=6 for example 3

Fig. 4

Residual errors by using the proposed method at different N and α=3, for example 3

Table 3 Comparison of the approximate solutions Hermite wavelet method [33], Bernoulli wavelet method [32], and the present method with the exact solution for example 3

Table 4 Comparison of the residual errors by using proposed method at different N and α=3 for x values for example 3

Example 4

Consider the fractional delay differential equation [32, 33]:

$$ D^{\alpha}y(x)-y(x-\tau)+y(x)=\frac{2}{\Gamma({3-\alpha})}x^{2-\alpha}-\frac{1}{\Gamma({2-\alpha})}x^{1-\alpha}+2\tau x-\tau^{2}-\tau, $$

(47)

with the conditions y(0)=0,y^′(0)=0 and the exact solution is y(x)=x²−x when α=1,τ=0.001, by using (17) at N=7, then the fundamental matrix equation of the problem is defined by

$$ \begin{aligned} &\left[ Q_{0}{(x)}\,X_{\alpha} H_{\alpha} M^{T}+Q^{*}_{0}{(x)}\,XM^{T} -P^{*}_{0}{(x)}\,X H_{-\tau}M^{T}\right]A-G. \end{aligned} $$

(48)

The numerical results are presented in Table 5, and the absolute errors also listed and compared with Hermite wavelet method [33].

Table 5 Comparison of the values of exact, approximate solutions for different values of x and the absolute errors at τ=0.001 for example 4

Figure 5 displays the approximate solutions obtained for values of α=1, 0.8, 0.7, 0.6, and the exact solution with N=7 and τ=0.001. From these results, it is seen that the approximate solutions converge to the exact solution.

Fig. 5

The comparison of y_N(x) for N=7,τ=0.001, with α=1, 0.8, 0.7, 0.6 and the exact solution for example 4

Example 5

Consider the fractional order delay differential equation [34]:

$$ D^{\frac{3}{10}}y(x)-y(x-1)+y(x)=1-3x+3x^{2}+\frac{2000x^{2.7}}{1071\Gamma{(0.7)}}. $$

(49)

The subjected condition y(0)=0 and the exact solution is y(x)=x³. By using the truncated Chebyshev series (17), then the fundamental matrix equation of the problem is defined by

$$ \begin{aligned} R(x)=\left[ X_{\nu}H_{\nu} M^{T}+X B_{-1}M^{T}+XM^{T}\right]A-G. \end{aligned} $$

(50)

After the augmented matrices of the system and condition are computed, we obtain the coefficient matrix on the form:

$$ A=\left[ \begin{array}{ccccccccc} 0& \frac{3}{4}& 0& \frac{1}{4}& 0 & 0& 0\\ \end{array}\right]. $$

(51)

Then, the solution is of Eq. 49

$$ y_{6} (x) =\frac{3}{4} T_{1}(x)+\frac{1}{4} T_{3}(x)=x^{3}, $$

(52)

which is the exact solution of the problem (49).

Example 6

Consider the linear fractional order delay differential equation [35]:

$$ D^{\nu}y(x)-\frac{1}{2}y'(x-\pi)+\frac{1}{2}y(x)=0, $$

(53)

with the initial condition y(0)=0,y^′(0)=1 and the exact solution when ν=2 is y(x)= sin(x), which is second-order delay differential equation with oscillatory in nature. By using (17) with N=6, we get algebraic equations by using the following residual:

$$ \begin{aligned} R(x)=\left[ X_{\nu} H_{\nu} M^{T}+Q_{1}\,X H B_{-\pi}M^{T} +Q_{0}\,X M^{T}\right]A. \end{aligned} $$

(54)

Also, by using the initial condition, we can generate two algebraic equations as:

$$ y(0)=X(0)M^{T}A=0, $$

(55)

$$ y'(0)=X(0)BM^{T}A=1, $$

(56)

by solving this algebraic system at ν=2, we have the solution as:

$$ A=\left[ \begin{array}{ccccccccc} 0& 0.880196& 0& -0.039119& 0 & 0.000488& 0\\ \end{array}\right], $$

(57)

then, the solution of Eq. (49) is:

$$ y_{6} (x) =0.880196 T_{1}(x)-0.039119T_{3}(x)+ 0.000488T_{5}(x). $$

(58)

Table 6 compares the values of exact and approximate solutions, x∈[0,1], while Table 7 lists the residual errors by using the proposed method at different N and ν=2.

Table 6 Comparison of the values of exact and approximate solutions for x values for example 6

Table 7 Comparison of the residual errors by using the proposed method at different Nand ν=2 for example 6

Conclusion

In this work, the general form of fractional order differential equations with linear functional argument is presented. The spectral Tau method is used for solving the proposed equation. All terms in the proposed equation reduced by operational matrices based on Chebyshev polynomials to matrix form. The accuracy of this method is obtained by many numerical examples. Finally, we used the Mathematica 7 to calculate our numerical results.