1 Introduction

Rarefied gas mixture flows appear in many engineering applications such as microelectro-mechanical systems (MEMSs) and aerodynamics [1,2,3]. A typical dimensionless parameter for such flows is the Knudsen number (Kn), which is defined as the ratio of the mean free path of gas molecules to the characteristic length of the system. The flow is commonly classified according to Kn into the continuum (\({Kn}<0.001\)), slip (\(0.001\le { Kn }<0.1\)), transition (\(0.1\le { Kn }<10\)), and free molecular (\({Kn}\ge 10\)) flow regimes. It is well-understood that the Euler and the Navier-Stokes (NS) equations generally fail to work when nonequilibrium effects become important (\({ Kn }>0.01\)). On the other hand, the Boltzmann equation can serve as a good model for gas mixture flows in all flow regimes [4].

The direct simulation Monte Carlo (DSMC) method [5,6,7] is an efficient and accurate method for solving the Boltzmann equation in the transition and free molecular regimes, while it faces the problems of statistical noise and large computational cost in the continuum or near continuum regimes. As a consequence, it is still a challenging task for designing efficient numerical methods for the Boltzmann equation for gas mixtures due to the complicated collision operator. Some simplified collision models have been proposed to replace the full Boltzmann collision operator [8,9,10,11,12,13], among which the Andries-Aoki-Perthame (AAP) model [9] has received particular attention. In this model, the collision operator for each species is modeled by a single Bhatnagar-Gross-Krook (BGK) operator [14]. Due to its simple structure and easy implementation, the AAP model has been widely used in the study of gas mixture flows [15,16,17], although only one transport coefficient can be given accurately by the AAP model.

Based on the AAP model, some numerical methods have been developed, such as the discrete velocity method (DVM) [18,19,20]. In the classical DVM, like the DSMC method, the numerical mesh size and time step are limited by the molecular mean free path and relaxation time, respectively, which makes them computationally expensive for flows involving continuum or near continuum regimes. In order to remove these constraints, some asymptotic preserving (AP) methods have been developed [21,22,23,24,25], which attempt to preserve the flow dynamics in the Euler limit. Furthermore, some kinetic schemes with unified preserving (UP) properties have been developed aiming to capture the corrected flow behaviors in whole flow regimes [26]. For instance, a unified gas kinetic scheme (UGKS) with UP properties has been developed for binary and multi-species mixture flows [27, 28] based on the AAP model, and recently some discrete unified gas kinetic schemes (DUGKS) have been developed for binary gas mixture flows based on the AAP model and McCormack model, respectively [29, 30]. Both UGKS and DUGKS are finite volume methods that exhibit good UP properties due to coupled particle transport and collision effect in the flux reconstruction [26, 31,32,33,34,35]. The DUGKS has already been adopted successfully for single-species gases [36,37,38,39] and binary gas mixtures [40, 41] flows from continuum to free molecular regimes.

Like the standard DUGKS for single-species flows, the previous DUGKS for binary gas mixtures designed for Maxwell molecules also evaluated the auxiliary distribution function to remove the implicitness caused by the trapezoidal rule of time integration of the collision term [29]. Due to the linear inter-species exchanges of momentum and energy of the Maxwell molecules, the macroscopic variables of each species can be solved from the moments of the auxiliary distribution function analytically, without changing the structure of the original DUGKS. But for other molecular models that usually involve complex nonlinear interactions (not considered in [29]), it is hard to calculate the macroscopic variables by taking moments of the auxiliary distribution. Although the iterative methods or interpolation methods can be employed to solve the nonlinear equation set for both species, it may introduce errors that affect the evolution of the distribution functions at a cell interface at the half-time step and even lead to numerical instability. The time-splitting technique can avoid solving complex nonlinear relations at a cell interface at the half-time step in the previous DUGKS [38, 42]. Therefore, we aim to extend DUGKS to gas mixtures composed of general molecules based on the AAP model in a more general form by employing a time-splitting technique in this paper.

The remainder of this paper is organized as follows. Section 2 will briefly introduce the AAP model for multi-species mixtures. In Section 3, the time-splitting DUGKS will be constructed based on the kinetic AAP model, and in Section 4 several numerical tests are performed to verify the present method. Finally, a brief summary is given in Section 5.

2 AAP model for multi-species mixtures

A gas mixture composed of L species can be modeled by the following multi-species Boltzmann equation [43],

$$\begin{aligned} \frac{\partial f_{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } f_{\alpha }=Q_{\alpha }, \quad \alpha =1, \ldots , L, \end{aligned}$$
(1)

where \(f_{\alpha } \equiv f_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, t)\) represents the velocity distribution function of species \(\alpha\) with particle velocity \(\boldsymbol{\xi }\) at position \(\boldsymbol{x}\) and time t. \(Q_{\alpha }\) is the collision operator for species \(\alpha\), which describes collisions between species \(\alpha\) and \(\beta\),

$$\begin{aligned} Q_{\alpha }&=\sum\limits_{\beta =1}^{L} Q_{\alpha \beta }\left( f_{\alpha },f_{\beta }\right) \\&=\sum\limits_{\beta =1}^{L} \int _{R^{3}} \int _{\boldsymbol{B}_{+}}\left( f_{\alpha }^{\prime } f_{\beta ^{*}}^{\prime }-f_{\alpha } f_{\beta ^{*}}\right) \boldsymbol{B}_{\alpha \beta }(\boldsymbol{N} \cdot \boldsymbol{V},|\boldsymbol{V}|) d \boldsymbol{\xi }_{*} d \boldsymbol{N}, \end{aligned}$$
(2)

where \(\boldsymbol{B}_{\alpha \beta }(\boldsymbol{N} \cdot \boldsymbol{V},|\boldsymbol{V}|)\) is the collision kernel, \(\boldsymbol{N}\) is a unit vector, and \(\boldsymbol{B}_{+}\) is semisphere defined by \(\boldsymbol{N \cdot V}=0\), where \(\boldsymbol{V}=\boldsymbol{\xi }-\boldsymbol{\xi }_{*}\) is relative velocity. f is pre-collision distribution that depends on pre-collision velocities \(\boldsymbol{\xi }\) and \(\boldsymbol{\xi }_{*}\); \(f^{\prime }\) is post-collision distribution that depends on post-collision velocities \(\boldsymbol{\xi }^{\prime }\) and \(\boldsymbol{\xi }_{*}^{\prime }\).

The macroscopic quantities of species \(\alpha\), such as the mass density \(\rho _{\alpha }\), velocity \(\boldsymbol{u}_{\alpha }\), and energy \(E_{\alpha }\), can be calculated from the distribution function,

$$\begin{aligned} \rho _{\alpha } = m_{\alpha } n_{\alpha } = \int f_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } \boldsymbol{u}_{\alpha } =\int \boldsymbol{\xi } f_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } E_{\alpha }= \frac{1}{2} \int \xi ^{2} f_{\alpha } d \boldsymbol{\xi }, \end{aligned}$$
(3)

where \(m_{\alpha }\) and \(n_{\alpha }\) are the molecular mass and number density of species \(\alpha\), respectively. The temperature of species \(\alpha\) is

$$\begin{aligned} T_{\alpha }= \frac{2}{3}(\rho _{\alpha } E_{\alpha }-\frac{1}{2} \rho _{\alpha } u_{\alpha }^{2})/\rho _{\alpha } R_{\alpha }, \end{aligned}$$
(4)

where \(R_\alpha =k_B/m_\alpha\) is the gas constant of species \(\alpha\) and \(k_B\) is the Boltzmann constant.

The AAP model is a relaxation approximation of collision operator in Eq. 1,

$$\begin{aligned} Q_{\alpha } =\frac{f^{M}_{\alpha }-f_{\alpha }}{\tau _{\alpha }}, \end{aligned}$$
(5)

where

$$\begin{aligned} f^{M}_{\alpha }=\rho _{\alpha }\left( \frac{m_{\alpha }}{2 \pi k_{B} T_{\alpha }^{M}}\right) ^{^{3/2}} \exp \left[ -\frac{m_{\alpha }}{2 k_{B} T_{\alpha }^{M}}\left( \boldsymbol{\xi }-\boldsymbol{u}_{\alpha }^{M}\right) ^{2}\right] \end{aligned}$$
(6)

is a local Maxwellian distribution depending on the fictitious parameters \(\boldsymbol{u}_{\alpha }^{M}\) and \(T_{\alpha }^{M}\), which can be obtained from

$$\begin{aligned} \boldsymbol{u}_{\alpha }^{M}&=\boldsymbol{u}_{\alpha }+\tau _{\alpha } \sum\limits_{\beta =1}^{L} 2 \frac{\rho _{\beta }}{m_{\alpha }+m_{\beta }} \theta _{\alpha \beta }\left( \boldsymbol{u}_{\beta }-\boldsymbol{u}_{\alpha }\right) ,\end{aligned}$$
(7a)
$$\begin{aligned} \frac{3}{2} k_{B} T_{\alpha }^{M}&= \frac{3}{2} k_{B} T_{\alpha }-\frac{m_{\alpha }}{2}\left( \boldsymbol{u}_{\alpha }^{M}-\boldsymbol{u}_{\alpha }\right) ^{2} +\tau _{\alpha } \sum\limits_{\beta =1}^{L} 4 m_{\alpha } \frac{\rho _{\beta }}{\left( m_{\alpha }+m_{\beta }\right) ^{2}}\theta _{\alpha \beta } \nonumber \\&\quad \times \left[ \frac{3}{2} k_{B} T_{\beta }-\frac{3}{2} k_{B} T_{\alpha }+\frac{m_{\beta }}{2}\left( \boldsymbol{u}_{\beta }-\boldsymbol{u}_{\alpha }\right) ^{2}\right] . \end{aligned}$$
(7b)

The collision frequency \(\nu _{\alpha }\) and relaxation time \({\tau _{\alpha }}\) are defined by

$$\begin{aligned} \nu _{\alpha }=\frac{1}{\tau _{\alpha }}= \sum\limits_{\beta =1}^{L} \frac{\rho _{\beta } \theta _{\alpha \beta }}{m_{\beta }}, \end{aligned}$$
(8)

where \(\theta _{\alpha \beta }\) is the interaction coefficient associated with the intermolecular interaction potential between species \(\alpha\) and \(\beta\)  [44]. For hard sphere molecules,

$$\begin{aligned} \theta _{\alpha \beta }=\frac{4 \sqrt{\pi }}{3}\left( 2 R_\alpha T_{\alpha }+2 R_\beta T_{\beta }\right) ^{1 / 2}\left( \frac{d_{\alpha }+d_{\beta }}{2}\right) ^{2}, \end{aligned}$$
(9)

and for Maxwell molecules,

$$\begin{aligned} \theta _{\alpha \beta }=0.422 \pi \left[ \frac{a_{\alpha \beta }\left( m_{\alpha }+m_{\beta }\right) }{m_{\alpha } m_{\beta }}\right] ^{1/2}, \end{aligned}$$
(10)

where \(d_{\alpha }\) and \(d_{\beta }\) are the molecular diameters, and \(a_{\alpha \beta }\) is the constant of the intermolecular force.

It is noted that the species collision operator \(Q_\alpha\) given by Eq. 5 conserves mass, momentum, and energy of the mixture,

$$\begin{aligned} \sum\limits_{\alpha }^L\int Q_{\alpha } d \boldsymbol{\xi }=0, \quad \sum\limits_{\alpha }^L\int \boldsymbol{\xi } Q_{\alpha } d \boldsymbol{\xi }=0, \quad \sum\limits_{\alpha }^L\int \frac{1}{2} \xi ^{2} Q_{\alpha } d \boldsymbol{\xi}=0. \end{aligned}$$
(11)

However, each operator conserves the individual mass only, but not the individual momentum and energy due to the inter-species collisions, i.e.,

$$\begin{aligned} \int Q_{\alpha } d \boldsymbol{\xi } = 0, \quad \int \boldsymbol{\xi } Q_{\alpha } d \boldsymbol{\xi }\ne 0, \quad \int \frac{1}{2} \xi ^{2} Q_{\alpha } d \boldsymbol{\xi }\ne 0. \end{aligned}$$
(12)

In order to develop an efficient time-splitting DUGKS, the collision operator given in Eq. 5 can be decomposed into an individual conservative part \(Q_{\alpha ,c}\) and an excess part \(Q_{\alpha ,e}\), namely, \(Q_{\alpha }=Q_{\alpha ,c}+Q_{\alpha ,e}\), with

$$\begin{aligned} Q_{\alpha , c} =\frac{f_{\alpha }^{e q}-f_{\alpha }}{\tau _{\alpha }}, \quad Q_{\alpha , e} =\frac{f_{\alpha }^{M}-f_{\alpha }^{e q}}{\tau _{\alpha }}, \end{aligned}$$
(13)

where \(f_{\alpha }^{e q}\) is the Maxwellian equilibrium distribution function depending on the species velocity and temperature,

$$\begin{aligned} f_{\alpha }^{e q}=\rho _{\alpha }\left( \frac{m_{\alpha }}{2 \pi k_{B} T_{\alpha }}\right) ^{3 / 2} \exp \left[ -\frac{m_{\alpha }}{2 k_{B} T_{\alpha }}\left( \boldsymbol{\xi }-\boldsymbol{u}_{\alpha }\right) ^{2}\right] . \end{aligned}$$
(14)

It is easy to verify that \(Q_{\alpha ,c}\) conserves the species mass, momentum, and energy,

$$\begin{aligned} \int Q_{\alpha ,c} d \xi =0, \quad \int \boldsymbol{\xi } Q_{\alpha ,c} d \boldsymbol{\xi }=0, \quad \int \frac{1}{2} \xi ^{2} Q_{\alpha ,c} d \xi =0. \end{aligned}$$
(15)

However, the excess part \(Q_{\alpha , e}\) does not conserve the individual momentum and energy. Actually, after some algebra we can obtain that [21]

$$\begin{aligned} & \int Q_{\alpha , e}d \boldsymbol{\xi } =0,\end{aligned}$$
(16a)
$$\begin{aligned} & \int \boldsymbol{\xi } Q_{\alpha , e} d \boldsymbol{\xi } =\sum\limits_{\beta =1}^{L} 2 \frac{\rho _{\alpha } \rho _{\beta }}{m_{\alpha }+m_{\beta }} \theta _{\alpha \beta }\left( \boldsymbol{u}_{\beta }-\boldsymbol{u}_{\alpha }\right) ,\end{aligned}$$
(16b)
$$\begin{aligned} & \int \frac{1}{2} \xi ^{2} Q_{\alpha , e} d \boldsymbol{\xi } =\sum\limits_{\beta =1}^{L} 4 \frac{\rho _{\alpha }\rho _{\beta }}{\left( m_{\alpha }+m_{\beta }\right) ^{2}} \theta _{\alpha \beta }\nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \times \left[ \frac{1}{2}\left( m_\alpha -m_\beta \right) \boldsymbol{u}_\beta \cdot \boldsymbol{u}_\alpha +m_\beta E_\beta -m_\alpha E_\alpha \right] . \end{aligned}$$
(16c)

With the above decomposition, the equation of the AAP model can be rewritten as

$$\begin{aligned} \frac{\partial f_{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } f_{\alpha }=Q_{\alpha ,c}+Q_{\alpha , e}=\frac{f_{\alpha }^{e q}-f_{\alpha }}{\tau _{\alpha }}+\frac{f_{\alpha }^{M}-f_{\alpha }^{e q}}{\tau _{\alpha }}. \end{aligned}$$
(17)

To simulate \(D<3\)-dimensional gas flow efficiently, the influence of redundant velocity components on the distribution function can be eliminated according to the method in [45]. To this end, we write the original distribution function as \(f_{\alpha } \equiv f_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, \boldsymbol{\eta }, t)\), where \(\boldsymbol{x}=\left( x_{1}, \ldots , x_{D}\right)\) and \(\boldsymbol{\xi }=\left( \xi _{1}, \ldots , \xi _{D}\right)\) are D-dimensional vectors, and the excess velocity component can be represented by the vector \(\boldsymbol{\eta }=\left( \xi _{D+1}, \ldots , \xi _{3}\right)\). Then, the following reduced distribution functions are introduced

$$\begin{aligned} & g_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, t)=\int f_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, \boldsymbol{\eta }, t) d \boldsymbol{\eta }, \end{aligned}$$
(18a)
$$\begin{aligned} & h_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, t)=\int \eta ^{2} f_{\alpha }(\boldsymbol{x}, \boldsymbol{\xi }, \boldsymbol{\eta }, t) d \boldsymbol{\eta }. \end{aligned}$$
(18b)

As such, we can obtain the following two kinetic equations from Eq. 17,

$$\begin{aligned} & \frac{\partial g_{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } g_{\alpha }=\frac{g_{\alpha }^{e q}-g_{\alpha }}{\tau _{\alpha }}+\frac{g_{\alpha }^{M}-g_{\alpha }^{e q}}{\tau _{\alpha }}, \end{aligned}$$
(19a)
$$\begin{aligned} & \frac{\partial h_{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } h_{\alpha }=\frac{h_{\alpha }^{e q}-h_{\alpha }}{\tau _{\alpha }}+\frac{h_{\alpha }^{M}-h_{\alpha }^{e q}}{\tau _{\alpha }}, \end{aligned}$$
(19b)

where

$$\begin{aligned} & g_{\alpha }^{eq}=\rho_{\alpha }\left( \frac{m_{\alpha }}{2 \pi k_{B} T_{\alpha }}\right) ^{D / 2} \exp \left[ -\frac{m_{\alpha }}{2 k_{B} T_{\alpha }}\left( \boldsymbol{\xi }-\boldsymbol{u}_{\alpha }\right) ^{2}\right] , \end{aligned}$$
(20a)
$$h_{\alpha }^{eq}=(3-D) R_{\alpha } T_{\alpha } g_{\alpha }^{eq},$$
(20b)
$$\begin{aligned} & g_{\alpha }^{M}=\rho_{\alpha }\left( \frac{m_{\alpha }}{2 \pi k_{B} T_{\alpha }^{M}}\right)^{D / 2} \exp \left[ -\frac{m_{\alpha }}{2 k_{B} T_{\alpha }^{M}}\left( \boldsymbol{\xi }-\boldsymbol{u}_{\alpha }^{M}\right)^{2}\right] , \end{aligned}$$
(20c)
$$\begin{aligned}&h_{\alpha }^{M}=(3-D) R_{\alpha } T_{\alpha }^{M} g_{\alpha }^{M}. \end{aligned}$$
(20d)

The density, velocity, and temperature of species \(\alpha\) can be obtained from the two reduced distribution functions,

$$\begin{aligned} \rho _{\alpha }=\int g_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } \boldsymbol{u}_{\alpha }=\int \boldsymbol{\xi } g_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } E_{\alpha }=\frac{1}{2} \int \left( \xi ^{2} g_{\alpha }+h_{\alpha }\right) d \boldsymbol{\xi }. \end{aligned}$$
(21)

It is noted that the kinetic equation 19 for the two reduced distribution functions have the same structure, which can be expressed as

$$\begin{aligned} \frac{\partial \phi _{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } \phi _{\alpha }=Q_{\alpha ,c}+Q_{\alpha , e}=\frac{\phi _{\alpha }^{e q}-\phi _{\alpha }}{\tau _{\alpha }}+\frac{\phi _{\alpha }^{M}-\phi _{\alpha }^{e q}}{\tau _{\alpha }}, \end{aligned}$$
(22)

where \(\phi _{\alpha }=g_{\alpha } ~\text{ or }~ h_{\alpha }\), \(\phi _{\alpha }^{eq}=g_{\alpha}^{eq}~\text{ or }~h_{\alpha }^{eq}\), and \(\phi _{\alpha }^{M}=g_{\alpha}^{M}~\text{ or }~h_{\alpha }^{M}\).

3 Numerical method

Since the collision operator of each species \(Q_{\alpha }\) does not conserve the momentum and energy of the individual species, the standard DUGKS cannot be simply employed to solve the multi-species kinetic equation 22. Here we propose a time-splitting DUGKS to solve Eq. 22 with second-order accuracy in time. Specifically, we adopt the Strang-splitting method [46] to treat the excess collision term \(Q_{\alpha ,e}\), and employ the DUGKS to solve the kinetic equation with the species conservative collision term \(Q_{\alpha ,c}\).

The scheme includes three steps, namely,

  • Pre-forcing:

    $$\begin{aligned} \frac{\partial \phi _{\alpha }}{\partial t}=\frac{1}{2} Q_{\alpha , e}=\frac{1}{2} \frac{\phi _{\alpha }^{M}-\phi _{\alpha }^{e q}}{\tau _{\alpha }}, \end{aligned}$$
    (23)

  • DUGKS:

    $$\begin{aligned} \frac{\partial \phi _{\alpha }}{\partial t}+\boldsymbol{\xi } \cdot \boldsymbol{\nabla } \phi _{\alpha }=Q_{\alpha , c}=\frac{\phi _{\alpha }^{e q}-\phi _{\alpha }}{\tau _{\alpha }}, \end{aligned}$$
    (24)

  • Post-forcing:

    $$\begin{aligned} \frac{\partial \phi _{\alpha }}{\partial t}=\frac{1}{2} Q_{\alpha , e}=\frac{1}{2} \frac{\phi _{\alpha }^{M}-\phi _{\alpha }^{e q}}{\tau _{\alpha }}. \end{aligned}$$
    (25)

The time integration in the pre-forcing is discretized as follows,

$$\begin{aligned} \phi _\alpha ^{n^*}=\phi _\alpha ^n+\frac{\Delta t}{2}\left[ \epsilon Q_{\alpha , e}^n+(1-\epsilon ) Q_{\alpha , e}^{n^*}\right] , \end{aligned}$$
(26)

where \(0 \le \epsilon \le 1\) is a parameter. Particularly, a fully explicit scheme is obtained when \(\epsilon = 1\). In this case, since the macroscopic variables \(\boldsymbol{W}^n_{\alpha }=\left( \rho ^n_{\alpha }, \rho ^n_{\alpha } \boldsymbol{u}^n_{\alpha }, \rho ^n_{\alpha } E^n_{\alpha }\right)\) and \(\boldsymbol{W}_{\alpha }^{M,n}=\left( \rho ^n_{\alpha }, \rho ^n_{\alpha } \boldsymbol{u}_{\alpha }^{M,n}, \rho ^n_{\alpha } E_{\alpha }^{M,n}\right)\) for each species at \(t^n\) are known, the equilibrium distributions \(\phi _{\alpha }^{e q,n}\) and \(\phi _{\alpha }^{M,n}\) are fully determined, and \(\phi _{\alpha }^{n^*}\) can be updated explicitly. In addition, the post-forcing step takes the same treatment explicitly as in the pre-forcing step to update \(\phi _{\alpha }^{n+1}\). To ensure numerical stability of the explicit scheme, the time step is limited by

$$\begin{aligned} \Delta t \le 1/\left( \sum\limits_{\beta =1}^L \frac{m_\beta }{m_\alpha +m_\beta } \frac{\rho _\beta ^n \theta _{\alpha \beta }}{m_\beta }\right) , \quad \Delta t \le 1/\left( \sum\limits_{\beta =1}^L \frac{2m_\alpha m_\beta }{(m_\alpha +m_\beta )^2} \frac{\rho _\beta ^{n} \theta _{\alpha \beta }}{m_\beta } \right) , \end{aligned}$$

meaning that the selection of the time step should be smaller than the relaxation time (\(\Delta t \le \tau\)). Details for the stability analysis of the explicit scheme can be found in the Appendix.

When \(\epsilon =0\), the pre-forcing is fully implicit. Now the equilibrium distribution functions \(\phi _{\alpha }^{e q,{n^*}}\) and \(\phi _{\alpha }^{M,{n^*}}\), appearing in \(\phi _{\alpha }^{e q}\) and \(\phi _{\alpha }^{M}\), respectively, are determined by the macroscopic variables \(\boldsymbol{W}_{\alpha }^{n^*}=\left( \rho _{\alpha }^{n^*}, \rho _{\alpha }^{n^*} \boldsymbol{u}_{\alpha }^{n^*}, \rho _{\alpha }^{n^*} E_{\alpha }^{n^*}\right)\) and \(\boldsymbol{W}_{\alpha }^{M,{n^*}}=\left( \rho _{\alpha }^{n^*}, \rho _{\alpha }^{n^*} \boldsymbol{u}_{\alpha }^{M,{n^*}}, \rho _{\alpha }^{n^*} E_{\alpha }^{M,{n^*}}\right)\) for each species at \(t^{n^*}\). By taking the moments of Eq. 26, one can obtain that

$$\begin{aligned} \rho _{\alpha }^{n^*}=&\rho _{\alpha }^n, \end{aligned}$$
(27a)
$$\begin{aligned} \rho _{\alpha }^{n^*} \boldsymbol{u}_{\alpha }^{n^*}=&\rho _{\alpha }^n \boldsymbol{u}_{\alpha }^n+\frac{\Delta t}{2} \sum\limits_{\beta =1}^{L} 2 \frac{\rho _{\alpha }^{n^*} \rho _{\beta }^{n^*}}{m_{\alpha }+m_{\beta }} \theta _{\alpha \beta }\left( \boldsymbol{u}_{\beta }^{n^*}-\boldsymbol{u}_{\alpha }^{n^*}\right) , \end{aligned}$$
(27b)
$$\begin{aligned} \rho _{\alpha }^{n^*} E_{\alpha }^{n^*}=&\rho _{\alpha }^n E_{\alpha }^n+\frac{\Delta t}{2}\sum\limits_{\beta =1}^L 4\frac{\rho ^{n^*}_\alpha \rho ^{n^*}_\beta }{(m_\alpha +m_\beta )^2} \theta _{\alpha \beta }\nonumber \\&\quad \quad \quad \quad \quad \quad \times \left[ \frac{m_\alpha -m_\beta }{2}\boldsymbol{u}^{n^*}_\beta \cdot \boldsymbol{u}^{n^*}_\alpha +m_\beta E^{n^*}_\beta -m_\alpha E^{n^*}_\alpha \right] . \end{aligned}$$
(27c)

For Maxwell molecules, the interaction coefficient \(\theta _{\alpha \beta }\) does not depend on the macroscopic variables according to Eq. 10, and thus the macroscopic variables \(\boldsymbol{W}_{\alpha }^{{n^*}}\) for each species can be computed by solving Eq. 27 analytically. For hard sphere molecules, \(\theta _{\alpha \beta }\) relates to the temperature. The macroscopic variables \(\boldsymbol{W}_{\alpha }^{{n^*}}\) can be obtained using certain iteration methods (here the Newton iteration is employed). Then \(\phi _{\alpha }^{{n^*}}\) can be updated implicitly from Eq. 26. Similarly, the post-forcing step takes the same treatment implicitly as in the pre-forcing step to update \(\phi _{\alpha }^{n+1}\). The stability analysis shows that the implicit scheme is unconditionally stable in the Appendix.

The DUGKS begins with the kinetic equation 24 with the conservative collision operator \(Q_{\alpha ,c}\). First, the flow domain is divided into a set of control volumes or cells. Integrating Eq. 24 on a control volume \(V_j\) centered at \(\boldsymbol{x}_j\) from time \(t^{n^{*}}\) to \(t^{n^{**}}\) with a time step \(\Delta t\), and then the midpoint rule for the convection term and trapezoidal rule for the collision term are used,

$$\begin{aligned} \phi _{\alpha , j}^{n^{**}}-\phi _{\alpha , j}^{n^{*}}+\frac{\Delta t}{\left| V_{j}\right| } \mathcal {F}_{\alpha , j}^{n^*+1/2}=\frac{\Delta t}{2}\left[ Q_{\alpha , c, j}^{n^{**}}+Q_{\alpha ,c, j}^{n^{*}}\right] , \end{aligned}$$
(28)

where \(\left| V_{j}\right|\) is the volume of \(V_{j}\), and the microflux across the cell interface \(\mathcal {F}_{\alpha , j}^{n^{*}+1/ 2}\) is given by

$$\begin{aligned} \mathcal {F}_{\alpha , j}^{n^{*}+1 / 2}=\int _{\partial V_{j}}(\boldsymbol{\xi } \cdot \boldsymbol{n}) \phi _{\alpha }\left( \boldsymbol{x}, \boldsymbol{\xi }, t^{n^{*}+1 / 2}\right) d \boldsymbol{S}, \end{aligned}$$
(29)

where \(\boldsymbol{n}\) is the outward unit vector normal to the cell surface \(\partial V_{j}\).

Then, the updated distribution function can be written as [47]

$$\begin{aligned} \phi _{\alpha ,j}^{n^{**}}=\left( 1+\frac{\Delta t}{2 \tau _{\alpha ,j}^{n^{**}}}\right) ^{-1}\left[ \phi _{\alpha ,j}^{n^{*}}-\frac{\Delta t}{\left| V_{j}\right| } \mathcal {F}_{\alpha , j}^{n^{*}+1 / 2}+\right. \left. \frac{\Delta t}{2}\left( \frac{\phi _{\alpha , j}^{eq, n^{**}}}{\tau _{\alpha , j}^{n^{**}}}+\frac{\phi _{\alpha , j}^{eq, n^{*}}-\phi _{\alpha , j}^{n^{*}}}{\tau _{\alpha , j}^{n^{*}}}\right) \right] , \end{aligned}$$
(30)

and the equilibrium function \(\phi _{\alpha , j}^{eq, n^{**}}\) and collision time \(\tau _{\alpha , j}^{n^{**}}\) can be calculated after taking the conservative moments of Eq. 28

$$\begin{aligned} \left( \begin{array}{c} \rho _{\alpha ,j}^{n^{**}} \\ \rho _{\alpha ,j}^{n^{**}} \boldsymbol{u}_{\alpha ,j}^{n^{**}} \\ \rho _{\alpha ,j}^{n^{**}} E_{\alpha ,j}^{n^{**}} \end{array}\right)&=\left( \begin{array}{c} \rho _{\alpha ,j}^{n^{*}} \\ \rho _{\alpha ,j}^{n^{*}} \boldsymbol{u}_{\alpha ,j}^{n^{*}} \\ \rho _{\alpha ,j}^{n^{*}} E_{\alpha ,j}^{n^{*}} \end{array}\right) -\frac{\Delta t}{\left| V_{j}\right| } \iint _{\partial V_{j}}(\boldsymbol{\xi } \cdot \boldsymbol{n})\left( \begin{array}{c} g_{\alpha , j}^{n^{*}+1 / 2} \\ \boldsymbol{\xi } g_{\alpha , j}^{n^{*}+1 / 2} \\ \xi ^{2} g_{\alpha , j}^{n^{*}+1 / 2}+h_{\alpha , j}^{n^{*}+1 / 2} \end{array}\right) d \boldsymbol{S} d \boldsymbol{\xi } . \end{aligned}$$
(31)

Equations 30 and 31 are the updating rules of microscopic distribution function and macroscopic conservative variables, respectively. To update \(\phi _{\alpha ,j}^{n^{**}}\), we need to evaluate the flux \(\mathcal {F}_{\alpha , j}^{n^{*}+1 / 2}\), that is, the distribution function at the cell interface at \(t^{n^{*}+1/2}=t^{n^{*}}+\Delta t/2\). To this end, Eq. 24 is integrated along the characteristic line with a time step \(s=\Delta t/2\), and the trapezoidal rule is applied to collision term again,

$$\begin{aligned} \phi _{\alpha }\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}}+s\right)&-\phi _{\alpha }\left( \boldsymbol{x}_{b}-\boldsymbol{\xi } s, \boldsymbol{\xi }, t^{n^{*}}\right) \\ &=\frac{s}{2}\left[ Q_{\alpha ,c}\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}}+s\right) +Q_{\alpha ,c}\left( \boldsymbol{x}_{b}-\boldsymbol{\xi } s, \boldsymbol{\xi }, t^{n^{*}}\right) \right] , \end{aligned}$$
(32)

where \(\boldsymbol{x}_b\) is the interface center of cell j. Obviously, Eq. 32 is implicit. In order to remove its implicit feature, we introduce

$$\begin{aligned} \bar{\phi }_{\alpha } =\phi _{\alpha }-\frac{s}{2} Q_{\alpha ,c}, \quad \bar{\phi }_{\alpha }^{+}=\phi _{\alpha }+\frac{s}{2} Q_{\alpha ,c}. \end{aligned}$$
(33)

Then, Eq. 32 can be rewritten as

$$\begin{aligned} \bar{\phi }_{\alpha }\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}+1/2}\right) =\bar{\phi }_{\alpha }^{+}\left( \boldsymbol{x}_{b}-\boldsymbol{\xi } s, \boldsymbol{\xi }, t^{n^{*}}\right) , \end{aligned}$$
(34)

where \(\bar{\phi }_{\alpha }^{+}\left( \boldsymbol{x}_{b}-\boldsymbol{\xi } s, \boldsymbol{\xi }, t^{n^{*}}\right)\) can be obtained by Taylor’s expansion of the interface distribution function

$$\begin{aligned} \bar{\phi }_{\alpha }^{+}\left( \boldsymbol{x}_{b}-\boldsymbol{\xi } s, \boldsymbol{\xi }, t^{n^{*}}\right) = \bar{\phi }_{\alpha }^{+}\left( \boldsymbol{x}_{j}, \boldsymbol{\xi }, t^{n^{*}}\right) +\left( \boldsymbol{x}_{b}-\boldsymbol{x}_{j}-\boldsymbol{\xi } {s}\right) \cdot \boldsymbol{\delta }_{j}, \end{aligned}$$
(35)

where \(\boldsymbol{\delta }_{j}\) is the slope of \(\bar{\phi }_{\alpha }^{+}\) in cell j, and the van Leer limiter [48] is applied to determine the slope for discontinuous problems. Once the distribution function \(\bar{\phi }_{\alpha }\) at the interface is known, the original distribution function \(\phi _{\alpha }\) can be obtained according to Eq. 33, i.e.,

$$\begin{aligned} \phi _{\alpha }\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}+1/2}\right) =&\frac{2 \tau _{\alpha }}{2 \tau _{\alpha }+s} \bar{\phi }_{\alpha }\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}}+s\right) +\frac{s}{2 \tau _{\alpha }+s} \phi _{\alpha }^{eq}\left( \boldsymbol{x}_{b}, \boldsymbol{\xi }, t^{n^{*}}+s\right) . \end{aligned}$$
(36)

The macroscopic variables \(\boldsymbol{W}\left( \boldsymbol{x}_{b}, t^{n^{*}}+s\right)\) required to evaluate \(\phi _{\alpha }^{eq}\) can be obtained from \(\bar{\phi }_{\alpha }\left( \boldsymbol{x}_{b}, t^{n^{*}}+s\right)\),

$$\begin{aligned} \rho _{\alpha }=\int \bar{g}_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } \boldsymbol{u}_{\alpha }=\int \boldsymbol{\xi } \bar{g}_{\alpha } d \boldsymbol{\xi }, \quad \rho _{\alpha } E_{\alpha }&=\frac{1}{2} \int \left( \xi ^{2} \bar{g}_{\alpha }+\bar{h}_{\alpha }\right) d \boldsymbol{\xi }. \end{aligned}$$
(37)

Then the equilibrium distribution \(\phi ^{eq}\) at interface center \(\boldsymbol{x}_b\) and time \(t^{n^{*}+1/2}\) can be evaluated, and subsequently the original distribution function \(\phi _{\alpha }\) at \(t^{n^{*}+1/2}\) can be updated from Eq. 36.

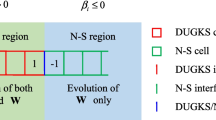
The evolution of the time-splitting DUGKS for multi-species AAP model from time \(t^{n}\) to \(t^{n+1}\) can be seen in Fig. 1, and the specific procedure is as follows:

  1. (1)

    Pre-forcing step: calculate \({\phi }_{\alpha }^{n^*}\) from \({\phi }_{\alpha }^{n}\) through explicit or implicit treatment

    Explicit treatment::

    calculate \({\phi }_{\alpha }^{n^*}\) from \({\phi }_{\alpha }^{n}\) and \(\boldsymbol{W}_{\alpha }^{n}\) at the cell center according to Eq. 26 with \(\epsilon =1\).

    Implicit treatment::

    solve the macroscopic variables \(\boldsymbol{W}_{\alpha }^{n^*}\) and \(\boldsymbol{W}_{\alpha }^{M,n^*}\) according to Eq. 27, and then calculate \({\phi }_{\alpha }^{n^*}\) from \({\phi }_{\alpha }^{n}\) and \(\boldsymbol{W}_{\alpha }^{n^*}\) at the cell center according to Eq. 26 with \(\epsilon =0\).

  2. (2)

    The DUGKS evolution from time \(t^{n^*}\) to \(t^{n^{**}}\):

    1. (a)

      Calculate \(\bar{\phi }_{\alpha }^{+}\) from \({\phi }_{\alpha }^{n^*}\) at the cell center according to Eq. 33.

    2. (b)

      Reconstruct the distribution function \(\bar{\phi }_{\alpha }^{+}\) at \(\boldsymbol{x}_{b}-\boldsymbol{\xi } s\) according to Eq. 35.

    3. (c)

      Compute the distribution function \(\bar{\phi }_{\alpha }\) at cell interface at time \(t^{n^*+1/2}\) according to Eq. 34.

    4. (d)

      Calculate the macroscopic variables \(\boldsymbol{W}\left( \boldsymbol{x}_{b}, t^{n^*+1 / 2}\right)\) according to Eq. 37.

    5. (e)

      Determine the original distribution function \(\phi _{\alpha }\) at each cell interface at time \(t^{n^*+1/2}\) according to Eq. 36.

    6. (f)

      Calculate the microflux \(\mathcal {F}_{\alpha }^{n^*+1 / 2}\) across each cell interface from \(\phi _{\alpha }^{n^*+1/2}\) according to Eq. 29.

    7. (g)

      Update conservative variables \(\boldsymbol{W}_{\alpha }^{n^{**}}\) in each cell according to Eq. 31.

    8. (h)

      Update the cell-averaged \({\phi }_{\alpha }^{n^{**}}\) in each cell according to Eq. 30.

  3. (3)

    Post-forcing step: update the macroscopic variables \(\boldsymbol{W}_{\alpha }^{n+1}\) and the distribution function \({\phi }_{\alpha }^{n+1}\) from \(\boldsymbol{W}_{\alpha }^{n^{**}}\) and \({\phi }_{\alpha }^{n^{**}}\) by the same explicit or implicit treatment as that in the pre-forcing step.

Fig. 1
figure 1

The evolution of the Strang-splitting method from time \(t^n\) to \(t^{n+1}\)

Full size image

4 Numerical Tests

In this section, several test cases are presented to validate the time-splitting DUGKS for multi-species flows.

4.1 Shock structure

The first test case is a shock structure for binary gas mixture containing species A and B [49, 50]. Two species in the simulation share the same molecular diameter \(d_A=d_B\) but have different masses \(m_A > m_B\). The molar concentrations, number densities, velocities, and temperatures are expressed as \(\chi _{-}^{A, B}\), \(n_{-}^{A, B}\), \(U_{-}\), \(T_{-}\) in the upstream and \(\chi _{+}^{A, B}\), \(n_{+}^{A, B}\), \(U_{+}\), \(T_{+}\) in the downstream, where \(\chi ^{A, B}=n^{A, B} /\left( n^{A}+n^{B}\right)\). The upstream and downstream quantities relationship for each species satisfy the Rankine-Hugoniot condition [51]. The upstream Mach number is defined as

$$\begin{aligned} M a_{-}=\frac{U_{-}}{\left( \gamma k_{\textrm{B}} T_{-} / m\right) ^{1 / 2}}, \end{aligned}$$
(38)

where \(m=m_{A} \chi ^{A}+m_{B} \chi ^{B}\). The reference mean free path is defined as [29]

$$\begin{aligned} \lambda _{\infty }=\frac{\mu _{B}}{P_{-}} \sqrt{\frac{2 k_{B} T_{-}}{m_{B}}}, \end{aligned}$$
(39)

where \(P_{-}=n_{-} k_{B} T_{-}\) and \(\mu _B\) is the viscosity of species B.

In the simulation, 100 uniform mesh points are used to divide the physical space \([-25\lambda _\infty ,25\lambda _\infty ]\). The velocity space is truncated in \([-8\sqrt{2k_B T_-/m},8\sqrt{2k_B T_-/m}]\), which is discretized by Newton-Cotes quadrature with 101 velocity points. The CFL number is 0.6. The normalized density and temperature under different Mach numbers and concentrations are shown and compared with those of the DUGKS [29] in Figs. 2, 3, 4, 5, 6 and 7. The results of SE-DUGKS and SI-DUGKS agree well with the DUGKS results for Maxwell molecules in all cases. The above comparisons illustrate that both the SE-DUGKS and SI-DUGKS methods can give accurate results with the same mesh points, hence only the results of the SI-DUGKS are shown in the following simulations of this case.

Fig. 2
figure 2

Shock structure with \(Ma_{-}=1.5\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.1\)

Full size image
Fig. 3
figure 3

Shock structure with \(Ma_{-}=1.5\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.9\)

Full size image
Fig. 4
figure 4

Shock structure with \(Ma_{-}=1.5\), \(m_B/m_A=0.25\), and \(\chi ^{A}=0.1\)

Full size image
Fig. 5
figure 5

Shock structure with \(Ma_{-}=1.5\), \(m_B/m_A=0.25\), and \(\chi ^{A}=0.9\)

Full size image
Fig. 6
figure 6

Shock structure with \(Ma_{-}=3.0\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.1\)

Full size image
Fig. 7
figure 7

Shock structure with \(Ma_{-}=3.0\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.9\)

Full size image

In addition, the normalized density and temperature for hard-sphere molecules under different Mach numbers and concentrations are calculated. The results of the SI-DUGKS with 100 mesh grids are shown and compared with those of the Boltzmann equation [49, 50] in Figs. 8, 9, 10 and 11. Good agreement can be found between the results of the SI-DUGKS and the solutions of the Boltzmann equation under \(Ma_{-}=1.5\) and \(m_B/m_A=0.5\). In Figs. 10 and 11 for \(Ma_{-}=3.0\) and \(m_B/m_A=0.5\), the results of number density predicted by the DUGKS remain good, while the temperature deviates obviously. Similar tendency can be observed in Refs. [27, 28], where the AAP model for binary gas mixture is calculated by the UGKS method. This is mainly attributed to the fact that the AAP model is the single-relaxation approximation model of the Boltzmann equation and only one transport coefficient can be produced by the AAP model. In this test case, only the viscosity coefficient is given accurately, while the thermal conductivity coefficient is not consistent with the Boltzmann equation.

Fig. 8
figure 8

Shock structure of different molecular models with \(Ma_{-}=1.5\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.1\)

Full size image
Fig. 9
figure 9

Shock structure of different molecular models with \(Ma_{-}=1.5\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.9\)

Full size image
Fig. 10
figure 10

Shock structure of different molecular models with \(Ma_{-}=3.0\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.1\)

Full size image
Fig. 11
figure 11

Shock structure of different molecular models with \(Ma_{-}=3.0\), \(m_B/m_A=0.5\), and \(\chi ^{A}=0.9\)

Full size image

Furthermore, the results of Maxwell molecules are also presented to show the difference from the hard sphere. As shown in Figs. 8 and 9 for \(Ma_{-}=1.5\), only a small deviation between different molecular models can be observed in the upstream. However, the differences between the two molecular models become prominent in the upstream and downstream under \(Ma_{-}=3.0\). Deviations between different molecular models have been also found in the simulation of the shock wave for single-species monatomic gas [52], due to the different temperature dependence on the shear viscosity and thermal conductivity, and the dependence is insensitive to changes in different molecular models at small Mach numbers [53].

4.2 Couette flow

The second test case is the Couette flow between two parallel plates with temperature \(T_0\) located at \(y = \pm H/2\) and moving with velocities \(\pm U/2\) in the x direction, respectively. The fully diffuse boundary condition is imposed on both plates and the periodic boundary condition is applied in the x direction. The initial molar fraction of the light species \(C_0\) is defined as

$$\begin{aligned} C_0=\frac{n_A^0}{n_A^0+n_B^0}, \end{aligned}$$
(40)

where \(n_A^0\) and \(n_B^0\) are the initial number density of species A and B, respectively. The characteristic molecular velocity \(v_0\) of the mixture is given as

$$\begin{aligned} v_0=\sqrt{\frac{2k_BT_0}{m}}, \end{aligned}$$
(41)

where \(m=C_0m_A+(1-C_0)m_B\) is the mean molecular mass of the mixture, and \(m_A>m_B\). The gas rarefaction parameter \(\delta\) is given as

$$\begin{aligned} \delta =\frac{H P_0}{\mu v_0}, \end{aligned}$$
(42)

where \(\mu\) is the mixture viscosity at temperature \(T_0\), and \(P_0=n_0k_BT_0\) is the initial pressure with \(n_0\) being the total number density of the two species. Here two groups of binary gas mixtures of noble gases are considered, i.e., neon-argon (Ne-Ar) and helium-xenon (He-Xe), whose molecular masses of the species are \(m_{\text{ He }}=4.0026\), \(m_{\text{ Ne }}=20.1791\), \(m_{\text{ Ar }}=39.948\), \(m_{\text{ Xe }}=131.293\) in atomic units. The viscosities are taken from Ref. [54] as, \(\mu _{\text{ He }}=19.73~\mu{\text{Pa}~\text{s}}\), \(\mu _{\text{ Ne }}=31.60~\mu{\text{Pa}~\text{s}}\), \(\mu_{\text{ Ar }}=22.39~\mu{\text{Pa}~\text{s}}\), and \(\mu _{\text{ Xe }}=22.62~\mu{\text{Pa}~\text{s}}\).

In this simulation, the physical space is divided into 2 mesh points in the x direction, and 100 uniform mesh points in the y direction. The velocity space is discretized by the half-range Gauss-Hermite quadrature [55] with 28 \(\times\) 28 velocity points for each species. The CFL number is set as 0.5. The flow field is assumed to be steady when the maximum relative change of the velocity field of the two species in two successive steps is less than \(10^{-10}\). We take \(C_0=0.5\) and \(U=0.01v_0\).

The normalized velocities under different rarefaction parameters \(\delta\) (\(\delta =0.1,1,10\), and 100) are shown and compared with results of the DUGKS [29] in Figs. 12 and 13. The results of the McCormack model for binary gaseous mixtures solved by the DVM method [56] are also shown for comparisons. As we can see, the results of SE-DUGKS and SI-DUGKS show good agreement with the DUGKS results in all cases. It is demonstrated that the present DUGKS methods provide the same results for solving the same kinetic equations. However, it can be observed that the differences in the velocities between the AAP model and the McCormack model increase with decreasing \(\delta\). Specifically, as \(\delta\) decreases from 10 to 0.1, the difference for Ne increases from \(1.4\%\) to \(7.8\%\), and the difference for Ar increases from \(0.04\%\) to \(9.1\%\). The difference for He increases from \(10.3\%\) to \(46.4\%\), and the difference for Xe increases from \(2.89\%\) to \(32.1\%\). It is clear that the differences between the two models in the He-Xe mixture with a large mass ratio are greater than that in the Ne-Ar mixture. It can be attributed to the AAP model employing a single relaxation operator to approximate the Boltzmann collision operator [29].

Fig. 12
figure 12

Velocity profiles in the Couette flow for the Ne-Ar mixture with \(C_0=0.5\)

Full size image
Fig. 13
figure 13

Velocity profiles in the Couette flow for the He-Xe mixture with \(C_0=0.5\)

Full size image

In all cases, the time step is smaller than the molecular mean collision time. Furthermore, the UP properties of the present method are validated in the continuum flow limit. First, the flow domain is divided into 10 and 20 mesh points uniformly in the y direction under \(\delta =1000\) (\({ Kn }=0.00089\)), respectively, corresponding to \(\Delta t \approx 8 \tau\) and \(\Delta t \approx 4 \tau\). The results of SE-DUGKS and SI-DUGKS for both Ne-Ar and He-Xe mixtures are shown and compared with the analytical solutions in Fig. 14. Good agreement can be found between SI-DUGKS and the analytical solution for both mesh sizes, while the results of SE-DUGKS for Ne-Ar mixture with 10 mesh points diverge. For larger \(\delta =5000\) (\({ Kn }=0.00017\)), i.e., \(\Delta t \approx 40 \tau\) and \(\Delta t \approx 20 \tau\), the results of SI-DUGKS with 10 and 20 mesh points show good agreement with the analytical solutions as shown in Fig. 15, while the SE-DUGKS diverges on both mesh grids for both mixtures. The divergence of SE-DUGKS is caused by the instability of the explicit scheme of pre-forcing or post-forcing steps, while the implicit scheme is more stable, coinciding with the theoretical analysis in the Appendix.

Fig. 14
figure 14

Velocity profiles in the Couette flow with \(\delta =1000\). M10 and M20 represent the results with 10 and 20 mesh points in the y direction, respectively

Full size image
Fig. 15
figure 15

Velocity profiles in the Couette flow with \(\delta =5000\). M10 and M20 represent the results with 10 and 20 mesh points in the y direction, respectively

Full size image

4.3 Poiseuille flow

The third test case is the pressure-driven Poiseuille flow between two parallel plates with temperature \(T_0\) located at \(y=\pm H/2\), and the fully diffuse boundary condition is imposed on both plates. A uniform pressure gradient is imposed on the gas in the flow direction (x direction), i.e., \(P_0(1+\beta _P x/H)\) with \(\beta _P\ll 1\), and the pressure condition based on a linear extrapolation scheme [57] is applied in the inlet/outlet. In this case, we consider an equimolar (\(C_0=0.5\)) Ne-Ar mixture with a molecular diameter ratio \(d_{\text{Ar}}/d_{\text{Ne}}\) of 1.406, where Ne and Ar are hard sphere molecules. The dimensionless velocity in the x direction of each species is defined as

$$\begin{aligned} U_\alpha =\frac{1}{\beta _P}\frac{u_{\alpha ,x}}{\sqrt{2k_B T_0/m}}, \end{aligned}$$
(43)

and the dimensionless particle flux is given as

$$\begin{aligned} M_\alpha =\frac{1}{\beta _P} \int \frac{u_{\alpha ,x}}{\sqrt{2k_B T_0/m}}dy. \end{aligned}$$
(44)

In this simulation, the length-to-height ratio of the channel is set to be 1, and the uniform mesh \(10 \times 10\) and \(100 \times 100\) points are used in the discretization of physical space. The velocity space is discretized by the half-range Gauss-Hermite quadrature [55] with 28 \(\times\) 28 velocity points for each species. The CFL number is set to be 0.5 and \(\beta _P\) is kept at 0.01 in the following cases. The flow field is assumed to be steady when the maximum relative errors in the velocities of the two species between two consecutive steps are less than \(10^{-10}\).

The present DUGKS is applied to predict the normalized velocity and particle flux under different rarefaction parameters \(\delta\). Firstly, it is found that the results of SE-DUGKS and SI-DUGKS are the same, and only the velocity profiles along the channel cross section predicted by SI-DUGKS under \(\delta =0.1,1\), and 10 are plotted in Fig. 16. The results of the linearized Boltzmann equation solved by a synthetic iterative scheme [58] are also included for comparisons. It can be observed that the DUGKS solutions overall agree with the solutions of the linearized Boltzmann equation, with some minor deviations that the DUGKS overestimates the velocity in the channel center by less than \(6.5\%\). In addition, the DUGKS can give sufficiently accurate results with only \(10 \times 10\) mesh points in all flows. Furthermore, the velocity profiles along the channel cross section under \(\delta =1000\) (\({Kn}=0.00089\)) are calculated by SE-DUGKS and SI-DUGKS to verify the UP properties of the present method. The results of SE-DUGKS and SI-DUGKS for Ne-Ar mixture with 10 and 100 mesh points are shown in Fig. 17. It is found that the SI-DUGKS can give accurate results with 10 grid points, while the results of SE-DUGKS with 10 mesh points diverge under \(\delta =1000\) (corresponding to \(\Delta t=8\tau\)) due to the instability of SE-DUGKS. The UP properties of DUGKS for single species in the Poiseuille flow have been also verified by Wang [36].

Fig. 16
figure 16

Velocity profiles in the Poiseuille flow for an equimolar Ne-Ar mixture. M10 and M100 represent the results with \(10 \times 10\) and \(100 \times 100\) uniform mesh points in the physical space, respectively

Full size image
Fig. 17
figure 17

Velocity profiles in the Poiseuille flow for an equimolar Ne-Ar mixture with \(\delta =1000\). M10 and M100 represent the results with \(10 \times 10\) and \(100 \times 100\) uniform mesh points in the physical space, respectively

Full size image

Then the particle flux \(M_\alpha\) for hard sphere molecules is compared between the LBE and present DUGKS in different flow regimes. Figure 18 shows that the flux of each species obtained from the LBE and DUGKS are in good agreement under different \(\delta\). It can be observed that a minimum appears for each species around \(\delta \approx 1\), which is the well-known Knudsen minimum phenomenon. Further, the results of Maxwell molecules and hard sphere molecules are also in good agreement as shown in Fig. 18, which differs from that of the single-species Poiseuille flow solved by LBE [59], where the particle flux in the free-molecular regime (small \(\delta\)) is sensitive to the molecular model. Therefore, the AAP model lacks the capability to distinguish the influence of molecular model in the Poiseuille flow for the gas mixture.

Fig. 18
figure 18

Particle flux profiles versus \(\delta\) in the Poiseuille flow of an equimolar Ne-Ar mixture

Full size image

5 Conclusion

In this paper, a time-splitting DUGKS is developed for multi-species flows over the whole flow regimes based on the AAP model. The collision operator of the AAP model is decomposed into the fully conservative part for the species and the excess part caused by inter-collision effects. The conservative part is solved by the standard DUGKS, while the excess part is treated by the Strang-splitting method, which is one feasible choice to deal with problems with non-conserved collision operator without modifying the standard DUGKS program in spite of the molecular models. Particularly, the time integration of the source term is realized by either explicit (SE-DUGKS) or implicit (SI-DUGKS) Euler scheme.

The performance of the time-splitting DUGKS is validated through numerical tests including the shock structure, the Couette flow, and the Poiseuille flow for binary gas mixture in all flow regimes. Good agreement has been obtained between the solutions of the present methods and the reference solutions. There are some deviations in the temperature profile of shock structure at high Mach numbers, and in the velocity profile of Couette flow for the He-Xe mixture with a large mass ratio. It may be caused by the limitations of the AAP kinetic model, including the fact that the model can only recover one transport coefficient. In addition, the influence of molecular model under different Mach numbers and rarefaction parameters is studied. The results of different molecular models were found to be significantly different at high Mach numbers.

Further comparisons show that the SI-DUGKS is able to reserve the UP property like the original DUGKS, while the SE-DUGKS fails to behave well, which may be caused by the instability of the explicit scheme of pre-forcing or post-forcing steps. In summary, the SI-DUGKS is preferable for gas mixture flow problems involving different flow regimes. It should be pointed out that some recently proposed kinetic models can be solved by the present DUGKS as well. In future work, it will serve as an effective tool to study multiscale flow problems based on more accurate kinetic models. For example, non-equilibrium phenomena in the gas dynamics of electrons and heavy ions based on the multiple relaxation model [12, 60] will be studied.