1 Introduction

Multiscale fluid flow problems exist widely in aerospace engineering [1,2,3], micro-electro-mechanical systems (MEMS) [4,5,6], exploration and development of shale gas [7,8,9], and so on. For example, the reference Knudsen number (Kn), which is defined as the ratio of the mean free path of molecules of the free stream flow to the characteristic physical length scale, will be changed greatly at different altitudes during the launching and landing stages of the space vehicle. Moreover, even at a certain altitude, the local Knudsen number around the space vehicle, which is usually defined by the local gradient length of the density (\({\rho \mathord{\left/ {\vphantom {\rho {\left| {\nabla \rho } \right|}}} \right. \kern-0pt} {\left| {\nabla \rho } \right|}}\)), will also cover a wide range of values with four to five orders of magnitude difference [10]. With the increase of the Knudsen number, the fluid flow will traverse the continuum regime (Kn < 0.001), slip regime (0.001 < Kn < 0.1), transition regime (0.1 < Kn < 10), and free molecular regime (Kn > 10). If different flow regimes exist in one computational domain, it is difficult to resolve this kind of problem by either the Navier–Stokes (N-S) solver [11,12,13] or the direct simulation Monte Carlo (DSMC) method [14,15,16]. Thus, an effective numerical algorithm is desired for capturing cross-scale flow physics.

Due to the use of the continuity assumption, the N-S solver is inapplicable for the above problems. Different from the N-S solver, the DSMC method resolves fluid flow problems by mimicking the streaming and collision of simulation particles. The DSMC method is first proposed by Bird [17] and further developed by many researchers [18,19,20,21], which is the most popular and effective method for solving hypersonic rarefied flows. But since the streaming and collision processes are decoupled, this method usually required that the mesh size is less than the molecular mean free path and the time step size is less than the averaged molecular collision time [22]. In the rarefied flow regime, these requirements do not influence the accuracy and efficiency of the DSMC method since the molecular mean free path and the averaged molecular collision time are larger than the mesh size and the time step size. But with the decrease of the Knudsen number, these requirements will lead to very small mesh size and time step size, thus limiting the application of the DSMC method in the near continuum and continuum flow regimes. To extend the application of the DSMC method to all flow regimes, the hybrid N-S/DSMC method has been developed [23,24,25,26,27]. The basic idea of this method is to divide the computational domain into the continuous region and the rarefied region. In the continuous region, the N-S solver is used to simulate the flow field in the macroscopic scale directly, and in the rarefied region, the DSMC method is utilized to pursue the statistical solution in the microscopic scale. In this way, the cross-scale fluid flow problems are expected to be resolved efficiently. But since the N-S solver and the DSMC method are respectively the deterministic and stochastic methods, a buffer region is needed for the information exchange between these two methods and a criterion is required for the partition of different regions. Torre et al. [28] pointed out that the results given by the hybrid N-S/DSMC method are very sensitive to the buffer region and the partitioning criterion. These issues are still open for the design of the hybrid N-S/DSMC method.

Except for the DSMC method, the discrete velocity method (DVM) has emerged as a powerful tool for solving multiscale fluid flow problems [29,30,31]. The DVM solves the Boltzmann equation in both the molecular velocity space and the physical space. In the framework of DVM, various numerical methods have been developed, such as the gas kinetic unified algorithm (GKUA) [32, 33], the unified gas kinetic scheme (UGKS) [34, 35], the discrete unified gas kinetic scheme (DUGKS) [36, 37], the improved discrete velocity method (IDVM) [38, 39], the general synthetic iterative scheme (GSIS) [40, 41], and so on. Among them, the UGKS, DUGKS and IDVM solve the discrete velocity Boltzmann equation (DVBE) by the finite volume method (FVM) and evaluate the numerical fluxes at the cell interface by coupling the motion and collision processes of molecules. Specifically, the UGKS utilizes the local integral solution to the Boltzmann-BGK equation to calculate the numerical fluxes of both the DVBE and the corresponding macroscopic governing equations. The original DUGKS uses the local discrete characteristic solution to the Boltzmann-BGK equation to evaluate the numerical fluxes of DVBE and introduces several transformations to avoid the solving of macroscopic governing equations. However, to achieve better conservativeness, the DVBE and the macroscopic governing equations are solved simultaneously in the modified DUGKS [42,43,44]. The IDVM solves the DVBE and the macroscopic governing equations with different strategies. Since the DVBE mainly takes effect in the rarefied flow regime, the IDVM calculates the numerical fluxes of DVBE without considering the collision process of molecules in order to keep the simplicity of the original DVM. But to obtain accurate results in the near continuum and continuum flow regimes, the collisional effect is introduced into the solution of macroscopic governing equations, which dominate the solution in these regimes. Although the DVM-type method can provide reasonable solutions in all flow regimes, it will lead to the curse of dimensionality since the discretizations are carried out in both the molecular velocity space and the physical space.

Like the hybrid N-S/DSMC method, several hybrid solvers based on the DVM-type method have been developed to alleviate the curse of dimensionality. Xiao et al. [45] proposed a velocity-space adaptive unified gas kinetic scheme (AUGKS) for the simulation of continuum and rarefied flows. In this method, the molecular velocity space is continuous in the near-equilibrium region and discrete in the non-equilibrium region. In the near-equilibrium region, only the macroscopic conservative variables are updated by the gas kinetic scheme (GKS) and the corresponding discrete distribution functions at the cell interface of different regions are reconstructed directly from the Chapman-Enskog expansion. In the non-equilibrium region, the UGKS is used to evolve both the discrete distribution functions and the macroscopic conservative variables. Since both the GKS and the UGKS are deterministic methods, no buffer zone is needed for the AUGKS to connect different solvers. Yang et al. [46] developed a hybrid algorithm that combines the DVM with the method of moments (DVM/MM) to simulate the rarefied gas flows in the transition regime. This hybrid method uses the DVM in the near-wall region (namely the vicinity of the Knudsen layer) where the method of moments is less accurate and utilizes the method of moments to describe the bulk flow field. Since the computational cost and the memory consumption of the method of moments are far less than those of DVM, the hybrid DVM/MM outperforms the DVM in simulating the transition flows. Besides that, Liu et al. [47] designed a hybrid method that couples the IDVM with the Grad 13-based gas kinetic flux solver (IDVM/GKFS) to simulate the non-equilibrium flows. In all the above hybrid methods, an artificial criterion concerning the local Knudsen number/Knudsen layer is required to switch different solvers. This artificial criterion will result in uncertainty in the calculation.

Whether the hybrid N-S/DSMC method or the DVM-type’s hybrid method, the criterion to switch different solvers is a key issue for their application. Even if the same local Knudsen number-based criterion is adopted, the threshold is usually set to different values for different hybrid methods [47,48,49,50]. The main reason is that a definite boundary to switch different solvers does not exist in the above methods. To overcome this defect, an adaptive partitioning-based discrete unified gas kinetic scheme (ADUGKS) is developed in this work. According to the discrete characteristic solution to the Boltzmann-BGK equation, the computational domain of multiscale fluid flow problems can be divided into the continuous region and the rarefied region. This partitioning strategy is fully based on the contribution of the initial distribution function to the calculation of free streaming fluxes, i.e., \({{\left( {2\tau - h} \right)} \mathord{\left/ {\vphantom {{\left( {2\tau - h} \right)} {\left( {2\tau + h} \right)}}} \right. \kern-0pt} {\left( {2\tau + h} \right)}}\), where \(\tau\) and \(h\) are the local collision time and the local half-time step size, respectively. If its contribution is negative, the local flow field can be regarded as the continuous flow; otherwise, it should be treated as the rarefied flow. In the continuous region, only the macroscopic conservative variables are evolved and the N-S solver is adopted directly, while in the rarefied region, both the discrete distribution functions and the macroscopic conservative variables are updated by a modified DUGKS. In this way, the computational cost of ADUGKS can be reduced gradually with the decrease of the Knudsen number. Furthermore, since this partitioning strategy is fully determined by the local flow field and the local mesh size, and both the DUGKS and the N-S solver belong to the deterministic methods, the artificial criterion to switch different solvers and the buffer zone are not needed for the ADUGKS.

2 Boltzmann-BGK equation and modified discrete unified gas kinetic scheme

The BGK model is proposed by Bhatnagar, Gross and Krook [51] to simplify the collision integral of the original Boltzmann equation. The discretization form of the Boltzmann-BGK equation in the molecular velocity space can be written as

$$\frac{\partial f_\alpha}{\partial t}+{{\varvec{\upxi}}}_{\alpha }\bullet\nabla f_\alpha=\Omega_\alpha=\frac{g_\alpha-f_\alpha}\tau,\,\alpha=1,\cdots,N_V,$$
(1)

where \(N_{V}\) and the subscript \(\alpha\) are the total number of discrete velocity points and the index in the discrete velocity space, respectively. \({{\varvec{\upxi}}}\) is the molecular velocity vector, \(\Omega\) is the collision operator, \(\tau\) is the collision time, \(f\) is the distribution function and \(g\) is its equilibrium state. For the monatomic gas, the equilibrium state is defined by the Maxwellian distribution function.

$$g = \frac{\rho }{{\left( {2\pi R_{g} T} \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\exp \left[ { - \frac{{c^{2} }}{{2R_{g} T}}} \right],$$
(2)

where \(\rho\) is the density, \(T\) is the temperature, \({\mathbf{c}} = {{\varvec{\upxi}}} - {\mathbf{u}}\) is the molecular thermal velocity vector, \({\mathbf{u}}\) is the mean flow velocity, \(c = \left| {\mathbf{c}} \right|\) is the magnitude of \({\mathbf{c}}\), and \(R_{g}\) is the gas constant. Multiplying Eq. (1) with the microscopic conservative moment \({{\varvec{\uppsi}}} = \left( {1,{{\varvec{\upxi}}},{{\xi^{2} } \mathord{\left/ {\vphantom {{\xi^{2} } 2}} \right. \kern-0pt} 2}} \right)^{T}\) and integrating the resultant equation in the molecular velocity space, the macroscopic governing equations of conservation laws can be obtained.

$$\frac{\partial\mathbf W}{\partial t}+\nabla\bullet\mathbf F=\mathbf0,$$
(3)

where the conservative flow variables \({\mathbf{W}}\) and the fluxes \({\mathbf{F}}\) are defined by

$${\mathbf{W}} = \left( {\rho ,\rho {\mathbf{u}},\rho E} \right)^{T} = \left\langle {{{\varvec{\uppsi}}}f} \right\rangle_{\alpha } = \left\langle {{{\varvec{\uppsi}}}g} \right\rangle_{\alpha },$$
(4)
$${\mathbf{F}} = \left( {F_{\rho } ,F_{{\rho {\mathbf{u}}}} ,F_{\rho E} } \right)^{T} = \left\langle {{\varvec{\upxi}} {\varvec{\uppsi }}f} \right\rangle_{\alpha }.$$
(5)

The notation \(\left\langle f \right\rangle_{\alpha } = \sum\nolimits_{{N_{V} }} {f_{\alpha } }\) defines the numerical quadrature of discrete distribution functions in the whole molecular velocity space.

The DUGKS solves Eq. (1) by the FVM and uses the discrete characteristic solution to the Boltzmann-BGK equation at the cell interface to calculate the numerical fluxes. Integrating Eq. (1) over a control volume \(V_{i}\) and using the first-order explicit scheme to discretize the temporal derivative and the trapezoidal law to approximate the collision term, we can obtain

$$f_{i,\alpha}^{n+1}=\frac{2\tau_i^{n+1}}{2\tau_i^{n+1}+\Delta t}\left[f_{i,\alpha}^n-\frac1{V_i}\sum_{j\in N\left(i\right)}S_{ij}\int_0^{\Delta t}{\mathbf n}_{ij}\bullet {{\varvec{\upxi}}}_{\alpha } f_{ij,a}\left(t\right)dt+\frac{\Delta t}2\left(\frac{g_{i,\alpha}^n-f_{i,\alpha}^n}{\tau_i^n}+\frac{\overline{g}_{i,\alpha}^{n+1}}{\tau_i^{n+1}}\right)\right],$$
(6)

where the superscripts \(n\) and \(n + 1\) represents the current time step and the new time step. \(N\left( i \right)\) is the set of neighbouring cells of the cell \(i\). \({\mathbf{n}}_{ij}\) and \(S_{ij}\) are respectively the unit outward normal vector and the area of the interface shared by the cells \(i\) and \(j\). \(\Delta t\) is the time step size, which is determined by the Courant-Friedrichs-Lewy (CFL) condition. In the original DUGKS [36, 37], to avoid the implicit computation of \(\overline{g}_{i,\alpha }^{n + 1}\), two auxiliary distribution functions are introduced into Eq. (6). But in fact, \(\overline{g}_{i,\alpha }^{n + 1}\) can also be predicted by the solution of Eq. (3) [42,43,44]. Similar to the discretization of Eq. (1), Eq. (3) can be discretized as

$$\overline{\mathbf W}_i^{n+1}-\mathbf W_i^n+\frac{\Delta t}{V_i}\sum_{j\in N\left(i\right)}S_{ij}{\mathbf n}_{ij}\bullet{\mathbf F}_{ij}=\mathbf0,$$
(7)

where the macroscopic fluxes vector is computed by

$${\mathbf{F}}_{ij} = \frac{1}{\Delta t}\left\langle {\int_{0}^{\Delta t} {{\varvec{\upxi}{\varvec{\uppsi} }}f_{ij} \left( t \right)dt} } \right\rangle_{\alpha }.$$
(8)

Once the predicted conservative variables \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) are obtained by Eq. (7), \(\overline{g}_{i,\alpha }^{n + 1}\) can be calculated by substituting \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) into Eq. (2) directly.

As shown in Eqs. (6) and (8), the key to evolving the discrete distribution functions and the conservative variables is to calculate the numerical fluxes at the cell interface, which are determined by the discrete distribution function \(f_{ij,a} \left( t \right)\). In the DUGKS, \(f_{ij,a} \left( t \right)\) is calculated by the discrete characteristic solution to the Boltzmann-BGK equation at the cell interface. Integrating Eq. (1) from \(t^{n} = 0\) to \(t^{n} + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-0pt} 2}\) along the characteristic line and applying the trapezoidal law to approximate the collision term, we can obtain

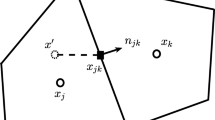
$$\begin{aligned} f_{ij,a} \left( h \right)&= f_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right) \hfill\,\\ &= \frac{2\tau - h}{{2\tau + h}}f_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) + \frac{h}{2\tau + h}\left( {g_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) + g_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)} \right), \hfill \\ \end{aligned}$$
(9)

where \({\mathbf{x}}_{ij}\) represents the location of the cell interface and \(h = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-0pt} 2}\) is the half-time step size. \(f_{a} \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) and \(g_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) are the discrete distribution function and its equilibrium state at the surrounding points of the cell interface at the current time level, which can be obtained by interpolating from those at the cell center.

$$\phi \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) = \left\{ {\begin{array}{*{20}c} {\phi^{L} \left( {{\mathbf{x}}_{ij} ,0} \right) - h{{\varvec{\upxi}}}_{\alpha } \bullet\nabla \phi \left( {{\mathbf{x}}_{i} ,0} \right)L\left( {\phi ,{\mathbf{x}}_{i} } \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } \ge 0} \\ {\phi^{R} \left( {{\mathbf{x}}_{ij} ,0} \right) - h{{\varvec{\upxi}}}_{\alpha } \bullet\nabla \phi \left( {{\mathbf{x}}_{j} ,0} \right)L\left( {\phi ,{\mathbf{x}}_{j} } \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } < 0} \\ \end{array} } \right.,$$
(10)

where \(\phi\) stands for either \(f_{a}\) or \(g_{\alpha }\). \(\phi^{L}\) and \(\phi^{R}\) denote the interfacial states of \(f_{a}\) or \(g_{\alpha }\) at the left and right sides, respectively. They can be reconstructed from those at cell centers with a slope limiter function \(L\left( {\phi ,{\mathbf{x}}} \right)\). \(g_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)\) is the equilibrium distribution function at the cell interface and the time level of \(h\), which is the function of conservative variables at the same position and time level. Multiplying Eq. (9) with the microscopic conservative moment \({{\varvec{\uppsi}}}\) and integrating the resultant equation in the molecular velocity space, we can get

$$\mathbf{W}\left({\mathbf x}_{ij},h\right)=\frac{2\tau-h}{2\tau+h}{\left\langle \varvec{\uppsi}{f}\left({\mathbf x}_{ij}-\varvec{\upxi}_{\alpha}h,0\right)\right\rangle}_{a}+\frac{h}{2\tau + h}\left\{{\left\langle\varvec{\uppsi}{g}\left({\mathbf x}_{ij}-\varvec{\upxi}_{\alpha} h,0\right)\right\rangle}_{a}+\mathbf{W}\left({\mathbf x}_{ij},h\right)\right\}.$$
(11)

As a result, the conservative variables at the cell interface can be calculated by

$${\mathbf{W}}\left( {{\mathbf{x}}_{ij} ,h} \right) = \frac{2\tau - h}{{2\tau }}\left\langle {{{\varvec{\uppsi}}}f\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)} \right\rangle_{a} + \frac{h}{2\tau }\left\langle {{{\varvec{\uppsi}}}g\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)} \right\rangle_{a}.$$
(12)

Since \(f_{a} \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) and \(g_{a} \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) have been determined by Eq. (10), \({\mathbf{W}}\left( {{\mathbf{x}}_{ij} ,h} \right)\) can be calculated explicitly, and then \(g_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)\) can be fully determined. Finally, the time integration of numerical fluxes at the cell interface can be approximated by the rectangle rule, namely taking \(f_{ij,a} \left( t \right) = f_{ij,a} \left( h \right)\).

3 Adaptive partitioning-based discrete unified gas kinetic scheme

It can be seen from Eq. (9) that, the distribution function at the cell interface consists of the initial distribution function \(f_{ij}^{fr}\) and the local equilibrium state \(f_{ij}^{eq}\), which can be rewritten into the following form:

$$f_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right) = \frac{2\tau - h}{{2\tau + h}}\underbrace {{f_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)}}_{{f_{ij}^{fr} }} + \frac{h}{2\tau + h}\underbrace {{\left( {g_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) + g_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)} \right)}}_{{f_{ij}^{eq} }}.$$
(13)

Here, \(f_{ij}^{fr}\) and \(f_{ij}^{eq}\) contribute to the calculation of free streaming fluxes and equilibrium fluxes, respectively. The contribution of \(f_{ij}^{fr}\) to the calculation of free streaming fluxes is dependent on an adaptive parameter \(\beta = {{\left( {2\tau - h} \right)} \mathord{\left/ {\vphantom {{\left( {2\tau - h} \right)} {\left( {2\tau + h} \right)}}} \right. \kern-0pt} {\left( {2\tau + h} \right)}}\), which is determined by the local flow variables and the local mesh size. Thus, its contribution will be changed in different regions of the computational domain.

In the region where \(\beta > 0\), the contribution of the initial distribution function to the calculation of \(f_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)\) is positive, which means that there is a \(\beta\) portion of “molecules” without suffering collision before crossing the cell interface. In this circumstance, the rarefaction effect has to be considered in the calculating of numerical fluxes. But in the region where \(\beta < 0\), the contribution of the initial distribution function to the calculation of \(f_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)\) is negative, which means that all “molecules” suffer at least one collision before crossing the cell interface. In other words, the local mesh size in this case is larger than the mean free path of molecules. Thus, the fluid flow in this region can be treated as the continuous flow directly. These inferences are the basis for the design of the ADUGKS in this work.

3.1 Adaptive partitioning for identification of cell types and face types

Different from other hybrid methods [23,24,25,26,27,28, 45,46,47,48,49,50], in which an artificial parameter is usually required to identify the cell types and/or a buffer region is needed to link different solvers, the ADUGKS identifies the cell types based on a local adaptive parameter and it does not need to set a buffer region. For a control volume \(V_{i}\), the adaptive parameter can be calculated by

$$\beta_{i} = \frac{{2\tau_{i} - h_{i} }}{{2\tau_{i} + h_{i} }},$$
(14)

with the collision time \(\tau_{i}\) and the half-time step size \(h_{i}\) defined by

$$\tau_{i} = \frac{{\mu_{i} }}{{p_{i} }},$$
(15)
$$h_{i} = \frac{{\Delta t_{i} }}{2} = \frac{{0.5\sigma V_{i} }}{{\xi_{x,\max } \Delta S_{x} + \xi_{y,\max } \Delta S_{y} }},$$
(16)

where, \(\sigma\) is the associated CFL number for the calculation of the time step \(\Delta t\), \(\xi_{x,\max }\) and \(\xi_{y,\max }\) are the maximum discrete velocities in the x- and y-direction, \(\Delta S_{x}\) and \(\Delta S_{y}\) are the projections of the control volume on the y- and x-plane, respectively. In this work, \(\sigma\) is taken as 0.95 to avoid extrapolation when reconstructing the initial distribution functions at the surrounding points of the cell interface.

According to the value of \(\beta_{i}\), the cell i can be classified into the DUGKS cell or the N-S cell as follows:

$$T_{cell,i} = \left\{ {\begin{array}{*{20}c} { \, 1, \, \beta_{i} > 0{\text{ is the DUGKS cell}}} \\ { - 1, \, \beta_{i} \le 0{\text{ is the N - S cell }}} \\ \end{array} } \right.,$$
(17)

where \(T_{cell,i}\) is the flag of the cell type of cell i. In addition, for the convenience of the calculation of numerical fluxes at the cell interface, the flag of the face type of the interface shared by cells i and j is defined by

$$T_{face,ij} = \frac{1}{2}\left( {T_{cell,i} + T_{cell,j} } \right).$$
(18)

It can be seen from Eq. (18) that, for the cell interface shared by the DUGKS cell and the N-S cell, we have \(T_{face,ij} = 0\). Otherwise, the value of \(T_{face,ij}\) is consistent with the flag of the cell type of the left and right cells. The details of the classification of cell types and face types are shown in Fig. 1.

Fig. 1
figure 1

Illustration of cell types and face types

Full size image

In the DUGKS cell, both the discrete distribution functions \(f_{\alpha }\) and the conservative variables \({\mathbf{W}}\) are evolved, while in the N-S cell, only the conservative variables \({\mathbf{W}}\) need to be updated. But for the convenience of evolving \(f_{\alpha }\) in the DUGKS cell close to the interface where \(T_{face,ij} = 0\), the discrete distribution functions in the N-S cell close to the same interface need to be given explicitly. According to the Chapman-Enskog expansion, the distribution function in the N-S cell can be reconstructed directly from its expansion truncated to the N-S level.

$$f_{NS} = g - \tau \left( {\frac{\partial g}{{\partial t}} + {{\varvec{\upxi}}}\bullet\nabla g} \right) + O\left( {\tau^{2} } \right).$$
(19)

For the convenience of application, the temporal and spatial derivatives of \(g\) can be further reformulated as the spatial derivatives of macroscopic flow variables. The final expression of \(f_{NS}\) can be written as [52]

$$f_{NS} = g - \tau g\left\{ {\frac{1}{T}\left( {\lambda c^{2} - \frac{5}{2}} \right)c_{i} \frac{\partial T}{{\partial x_{i} }} + 2\lambda c_{i} c_{j} \frac{{\partial u_{ < i} }}{{\partial x_{j > } }}} \right\} + O\left( {\tau^{2} } \right),$$
(20)

where

$$\frac{{\partial u_{ < i} }}{{\partial x_{j > } }} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) - \frac{1}{3}\frac{{\partial u_{k} }}{{\partial x_{k} }}\delta_{ij}$$
(21)

is the trace-free part of a symmetric tensor and \(\lambda = {1 \mathord{\left/ {\vphantom {1 {\left( {2R_{g} T} \right)}}} \right. \kern-0pt} {\left( {2R_{g} T} \right)}}\). In addition, for the convenience of evolving \({\mathbf{W}}\) in the N-S cell close to the interface where \(T_{face,ij} = 0\), the conservative variables in the DUGKS cell close to the same interface are needed. They can be calculated from \(f_{\alpha }\) by Eq. (4) directly.

3.2 Evolution of discrete distribution functions and conservative variables

In the ADUGKS, the discrete distribution functions \(f_{\alpha }\) are only stored and evolved in the DUGKS cell. This process is the same as the DUGKS and the discrete distribution functions at the cell interface \(f_{ij,a} \left( h \right)\) are calculated by Eq. (9). But note that, in the ADUGKS, \(f_{a} \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) and \(g_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) in the N-S cell close to the interface where \(T_{face,ij} = 0\) are calculated from the conservative variables and their derivatives at \({\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h\) rather than by Eq. (10) since the derivatives of discrete distribution functions in the N-S cell are unknown. The conservative variables in the N-S cell at the location \({\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h\) can be calculated by

$${\mathbf{W}}\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) = \left\{ {\begin{array}{*{20}c} {{\mathbf{W}}^{L} \left( {{\mathbf{x}}_{ij} ,0} \right) - h{{\varvec{\upxi}}}_{\alpha } \bullet\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{i} ,0} \right)L\left( {{\mathbf{W}},{\mathbf{x}}_{i} } \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } \ge 0} \\ {{\mathbf{W}}^{R} \left( {{\mathbf{x}}_{ij} ,0} \right) - h{{\varvec{\upxi}}}_{\alpha } \bullet\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{j} ,0} \right)L\left( {{\mathbf{W}},{\mathbf{x}}_{j} } \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } < 0} \\ \end{array} } \right.,$$
(22)

where \({\mathbf{W}}^{L}\) and \({\mathbf{W}}^{R}\) are the interfacial states of \({\mathbf{W}}\) at the left and right sides. They can be reconstructed from those at cell centers with a slope limiter function \(L\left( {{\mathbf{W}},{\mathbf{x}}} \right)\). \(\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{i} ,0} \right)\) and \(\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{j} ,0} \right)\) are the spatial derivatives of \({\mathbf{W}}\) at the left and right cells. Since the second-order scheme is used in this work, the spatial derivatives of \({\mathbf{W}}\) can be regarded as constant in every cell at each time step.

$$\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right) = \left\{ {\begin{array}{*{20}c} {\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{i} ,0} \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } \ge 0} \\ {\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{j} ,0} \right){, }\;{\mathbf{n}}_{ij} \bullet{{\varvec{\upxi}}}_{\alpha } < 0} \\ \end{array} } \right..$$
(23)

As a result, \(g_{\alpha } \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) can be calculated by substituting \({\mathbf{W}}\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) into Eq. (2) and \(f_{a} \left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) can be determined by substituting \({\mathbf{W}}\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) and \(\nabla {\mathbf{W}}\left( {{\mathbf{x}}_{ij} - {{\varvec{\upxi}}}_{\alpha } h,0} \right)\) into Eq. (20).

Once the discrete distribution functions at the cell interface between different DUGKS cells (\(T_{face,ij} = 1\)) and the interface shared by the DUGKS cell and the N-S cell (\(T_{face,ij} = 0\)) are obtained, the corresponding numerical fluxes of macroscopic governing equations \({\mathbf{F}}_{ij}\) can be calculated by Eq. (8). For other cell interfaces (\(T_{face,ij} = - 1\)), which are fully located in the N-S region as shown in Fig. 1, the numerical fluxes \({\mathbf{F}}_{ij}\) can be calculated by the N-S solver directly. In this work, the improved Roe scheme is used to calculate the inviscid fluxes and the central difference scheme is utilized to calculate the viscous fluxes [53]. Finally, the conservative variables of all cells can be updated by Eq. (7). For the N-S cell, we can take \({\mathbf{W}}_{i}^{n + 1} = \overline{{\mathbf{W}}}_{i}^{n + 1}\) since the discrete distribution functions in this cell can be reconstructed from the Chapman-Enskog expansion directly. But for the DUGKS cell, these evolved conservative variables \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) are only used to calculate the predicted equilibrium distributions \(\overline{g}_{i,\alpha }^{n + 1}\). With the discrete distribution functions at the cell interface \(f_{ij,a} \left( h \right)\) and the predicted equilibrium distributions \(\overline{g}_{i,\alpha }^{n + 1}\), the discrete distribution functions \(f_{i,\alpha }^{n + 1}\) and the conservative variables \({\mathbf{W}}_{i}^{n + 1}\) in the DUGKS cell can be updated by Eq. (6) and Eq. (4), respectively.

It can be seen from the above derivations that the ADUGKS can be viewed as a hybrid method of the DUGKS and the N-S solver. At first, the computational domain of ADUGKS is divided into the DUGKS region and the N-S region by the value of an adaptive parameter \(\beta_{i}\), which reflects the contribution of collisionless “molecules” to the free transport fluxes. This parameter is fully determined by the local flow variables and the local mesh size. Thus, it can be adjusted adaptively in the calculation without any manual intervention. Then, in the DUGKS cell, the discrete distribution functions and the conservative variables are updated by the modified DUGKS, and in the N-S cell, the conservative variables are updated by the N-S solver directly and the evolution of discrete distribution functions is abandoned. This is due to the fact that the discrete distribution functions in the N-S cell can be reconstructed from its expansion truncated to the N-S level directly, which is fully determined by the macroscopic flow variables and their spatial derivatives. Since the number of discrete distribution functions is far larger than that of conservative variables, the computational cost of ADUGKS is mainly determined by the number of DUGKS cells. It can be inferred that the computational cost of ADUGKS will be reduced with the decrease of the Knudsen number, in which case the computational domain is mainly occupied by the N-S region. This expectation can be verified in Section 4.

3.3 Analysis of asymptotic preserving property and computational sequence

As a multiscale kinetic scheme, it is important to analyze the asymptotic preserving property. The asymptotic behaviors of the proposed method in the collisionless limit and the continuous limit are discussed below.

  1. 1.

    Collisionless limit (\(\tau \to \infty\))

    In this case, the adaptive parameter \(\beta\) can be approximated as

$$\beta = \mathop {\lim }\limits_{{\tau \to \infty }} \frac{{2\tau - h }}{{2\tau + h }} \to 1.$$
(24)

Equation (24) shows that all cells belong to the DUGKS cell and the ADUGKS turns into the DUGKS in this situation. In other words, the ADUGKS solves the collisionless Boltzmann equation in the collisionless limit by the DUGKS.

  1. 2.

    Continuous limit (\(\tau \to 0\))

    In this case, the adaptive parameter \(\beta\) can be approximated as

$$\beta = \mathop {\lim }\limits_{{\tau \to 0}} \frac{{2\tau - h }}{{2\tau + h }} \to - 1.$$
(25)

Equation (25) indicates that all cells belong to the N-S cell and the ADUGKS turns into the N-S solver in this circumstance. As a result, the solution given by the ADUGKS in the continuous limit is indeed the result of N-S equations.

In the ADUGKS, there are two types of cells in the computational domain. One is the DUGKS cell, in which the modified DUGKS is used to update both the discrete distribution functions and the conservative variables, and the other is the N-S cell, in which only the conservative variables are evolved and the N-S solver is applied directly. The computational processes of ADUGKS are summarized as follows:

  1. (1)

    In the first step, initialize the conservative variables \({\mathbf{W}}_{i}^{n = 0}\) in all cells.

  2. (2)

    Calculate the collision time \(\tau_{i}\) and the half-time step size \(h_{i}\) in each control volume by Eqs. (15) and (16), respectively.

  3. (3)

    Compute the adaptive parameter \(\beta_{i}\) by Eq. (14) and classify all cells into the DUGKS cell or the N-S cell by Eq. (17). At the same time, identify the face types by Eq. (18).

  4. (4)

    Get the initial state of discrete distribution functions \(f_{i,\alpha }^{n}\) at the DUGKS cell and the N-S cell linked to the interface where \(T_{face,ij} = 0\). If \(f_{i,\alpha }^{n}\) does not exist in the target cell, it can be reconstructed by Eq. (20). In the first step, we can take \(f_{i,\alpha }^{n}\) as the equilibrium state directly, i.e., \(f_{i,\alpha }^{n = 0} = g_{i,\alpha }^{n = 0}\).

  5. (5)

    Calculate the derivatives of conservative variables \(\nabla {\mathbf{W}}_{i}^{n}\) at the N-S cell and the derivatives of discrete distribution functions \(\nabla f_{i,\alpha }^{n}\) at the DUGKS cell by the Green-Gauss approach or the least-square method [54].

  6. (6)

    Compute the discrete distribution functions at the surrounding points of cell interfaces where \(T_{face,ij} = 1\) and \(T_{face,ij} = 0\) by Eqs. (10) and (20), respectively, and calculate the equilibrium state at the cell interface by Eq. (12). Then, evaluate \(f_{\alpha } \left( {{\mathbf{x}}_{ij} ,h} \right)\) by Eq. (13).

  7. (7)

    For the cell interfaces where \(T_{face,ij} = 1\) and \(T_{face,ij} = 0\), calculate the macroscopic numerical fluxes by Eq. (8), and for the cell interface where \(T_{face,ij} = - 1\), compute the macroscopic numerical fluxes by the N-S solver.

  8. (8)

    Update the conservative variables \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) of all cells by Eq. (7). For the DUGKS cell, \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) are regarded as the predicted conservative variables, while for the N-S cell, we can take \({\mathbf{W}}_{i}^{n + 1} = \overline{{\mathbf{W}}}_{i}^{n + 1}\) directly since the evolution of discrete distribution functions in this cell is not needed.

  9. (9)

    For the DUGKS cell, calculate the predicted equilibrium state \(\overline{g}_{i,\alpha }^{n + 1}\) by substituting \(\overline{{\mathbf{W}}}_{i}^{n + 1}\) into Eq. (2). Then, the discrete distribution functions \(f_{i,\alpha }^{n + 1}\) and the conservative variables \({\mathbf{W}}_{i}^{n + 1}\) can be updated by Eq. (6) and Eq. (4), respectively.

  10. (10)

    Repeat steps (2) to (9) until the convergence result is obtained or the desired end time has arrived.

4 Numerical examples

In this section, the performance of ADUGKS will be verified by a series of test examples with different Knudsen/Reynolds numbers, including the lid-driven cavity flow, the flow around a flat plate, the flow around a circular cylinder and the unsteady gas expansion in a channel. The obtained results will be compared with those calculated by the modified DUGKS described in Section 2 and/or the UGKS code provided on Kun Xu’s homepage (https://www.math.hkust.edu.hk/~makxu/?menu=6). For simplicity, the monatomic gas with the specific heat ratio of \(\gamma = {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0pt} 3}\) is assumed in all simulations and the Prandtl number is set as \(Pr = 1\). In addition, all computations are conducted on a PC with a processor of Intel(R) Xeon(R) Gold 6226R CPU@2.9 GHz and the OpenMP with 4 threads is utilized to speed up the calculation.

4.1 Case 1: lid-driven cavity flow

The performance of ADUGKS is first validated by the lid-driven cavity flow with different Knudsen/Reynolds numbers. In this test example, a square cavity with the edge length \(L\) is stationary except the top wall is moving with a velocity of \(u_{W} = 0.15\sqrt {2R_{g} T_{ref} }\), where \(T_{ref}\) is the wall temperature. The solution of this test case is governed by the Knudsen number (\(Kn\)) or the Reynolds numbers (\(Re\)). To cover different flow regimes, four cases with Kn = 1, Kn = 0.075, Re = 100 and Re = 1000, are considered in our simulations. For the cases of Kn = 1 and Kn = 0.075, the dynamic viscosity \(\mu\) is calculated by

$$\mu = \mu_{ref} \left( {\frac{T}{{T_{ref} }}} \right)^{w},$$
(26)

where \(w\) is a constant related to the inter-molecular interaction model. In this work, \(w = 0.81\) is adopted for all simulations. The reference dynamic viscosity \(\mu_{ref}\) is determined by the Knudsen number.

$$\frac{{\mu_{ref} }}{L} = \frac{{5\rho_{ref} \left( {2\pi R_{g} T_{ref} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{16}Kn.$$
(27)

Here, \(\rho_{ref}\) is the reference density. For the cases of Re = 100 and Re = 1000, the dynamic viscosity \(\mu\) is determined by the Reynolds number.

$$\mu = \frac{{\rho_{ref} u_{W} L}}{Re}.$$
(28)

In addition, the computational domain is discretized uniformly by \(50 \times 50\) cells for the cases of Kn = 1 and Kn = 0.075 and by \(150 \times 150\) cells for the cases of Re = 100 and Re = 1000. For the discretization of the velocity space, the Newton–Cotes quadrature with \(101 \times 101\) points uniformly distributed in \(\left[ { - 4\sqrt {2R_{g} T_{ref} } , \, 4\sqrt {2R_{g} T_{ref} } } \right] \times \left[ { - 4\sqrt {2R_{g} T_{ref} } , \, 4\sqrt {2R_{g} T_{ref} } } \right]\) is utilized for the test case of Kn = 1, the Gauss-Hermite quadrature rule with \(28 \times 28\) points is used for the test case of Kn = 0.075, and the Gauss-Hermite quadrature rule with \(8 \times 8\) points is adopted for the test cases of Re = 100 and Re = 1000.

The comparison of the density, temperature, x-component of heat flux and y-component of heat flux contours for the lid-driven cavity flow at Kn = 1 and Kn = 0.075 are shown in Figs. 2 and 3, respectively. Evidently, the results of ADUGKS are consistent with those of UGKS and DUGKS. Figure 4 compares the velocity profiles along the vertical and horizontal central lines of the cavity. Once again, the present results compare well with those of UGKS and DUGKS as well as the numerical results of Ghia et al. [55]. The distribution of the DUGKS cell and the N-S cell for the lid-driven cavity flow with different Knudsen/Reynolds numbers is depicted in Fig. 5. It can be seen that the DUGKS cell occupies the whole computational domain for the cases of Kn = 1, Kn = 0.075 and Re = 100, namely both the DVBE and the macroscopic governing equations are solved simultaneously in all cells by the DUGKS. Thus, the computational cost and the memory consumption of ADUGKS for these cases are almost consistent with those of DUGKS. But for the case of Re = 1000, all cells belong to the N-S cell, resulting in one order of magnitude acceleration.

Fig. 2
figure 2

Comparison of density, temperature, x-component of heat flux and y-component of heat flux contours for lid-driven cavity flow at Kn = 1 (ADUGKS: colored background; DUGKS: white dash-dot line; UGKS: red dash line)

Full size image
Fig. 3
figure 3

Comparison of density, temperature, x-component of heat flux and y-component of heat flux contours for lid-driven cavity flow at Kn = 0.075 (ADUGKS: colored background; DUGKS: white dash-dot line; UGKS: red dash line)

Full size image
Fig. 4
figure 4

Comparison of velocity profiles along the vertical and horizontal central lines of the cavity at different Knudsen/Reynolds numbers

Full size image
Fig. 5
figure 5

Distribution of the DUGKS cell and the N-S cell for lid-driven cavity flow with different Knudsen/Reynolds numbers

Full size image

4.2 Case 2: flow around a flat plate

In the above test example, all cells belong to either the DUGKS cell or the N-S cell, the performance of ADUGKS for the case in which the computational domain contains both types of cells has not been examined. Thus, the flow around a flat plate with different Reynolds numbers is simulated in this subsection. In this test example, the free stream temperature is \(T_{ref} = 295{\text{ K}}\) and the Mach number is \(Ma = 0.2\) [56,57,58]. The flat plate with the length of \(L = 1{\text{ m}}\) and the temperature of \(T_{ref}\) is placed at the bottom boundary. In the simulation, the dynamic viscosity \(\mu\) is calculated by Eq. (26) and the reference dynamic viscosity \(\mu_{ref}\) is determined by

$$\mu_{ref} = \frac{Ma}{{Re}}\sqrt {\frac{\gamma }{2}},$$
(29)

where Re is the flat plate length-based Reynolds number. The Reynolds number, Mach number, and Knudsen number have a relationship as follows:

$$Kn = \frac{{2\left( {5 - 2w} \right)\left( {7 - 2w} \right)}}{15}\frac{Ma}{{Re}}\sqrt {\frac{\gamma }{2\pi }}.$$
(30)

The setting of the computational domain in the physical space is the same as that of Ref. [58]. The convergence criterion is set as the maximum error of all primitive variables between two adjacent iteration steps being less than \(5 \times 10^{ - 7}\).

First, we use the same mesh in the physical space as Ref. [58] to simulate the flow around a flat plate with the Reynolds number varying from Re = 0.2 to 50. The corresponding Knudsen number is listed in Table 1, which contains the transition flow regime, the slip flow regime and the continuum flow regime. In the simulation, the Gauss-Hermite quadrature rule with \(28 \times 28\) points is used to approximate the moment integration in the velocity space. Figure 6 compares the temperature contours around the flat plate in the transition (Re = 0.2 ~ 2) and slip (Re = 5 ~ 50) flow regimes computed by the ADUGKS and the DUGKS. The comparison of the skin friction coefficient distribution on the flat plate in the transition and slip flow regimes is displayed in Fig. 7, and the comparison of the drag coefficient with respect to the Reynolds number is depicted in Fig. 8. Clearly, the results given by the ADUGKS are consistent with those of UGKS and DUGKS, validating the accuracy of the present method in the transition and slip flow regimes. In fact, in the transition flow regime, all cells belong to the DUGKS cell and the ADUGKS turns into the DUGKS. However, with the increase of the Reynolds number, more and more cells are identified as the N-S cell, as shown in Fig. 9. The detailed numbers of total cells (\(N_{D}\)) and DUGKS cells (\(N_{A}\)) in the computational domain for the calculation of ADUGKS are listed in Table 1. With the decrease of \(N_{A}\), the efficiency of ADUGKS increases gradually. But the speed-up ratio is very limited in these cases since the DUGKS cell is still in the majority.

Table 1 Number of DUGKS cells, memory consumption (MByte) and computational time (hours) of different methods for flow around a flat plate with different Reynolds numbers
Full size table
Fig. 6
figure 6

Temperature contours around the flat plate in the (a) transition and (b) slip flow regimes (ADUGKS: colored background with black solid line; DUGKS: white dashed line)

Full size image
Fig. 7
figure 7

Distribution of skin friction coefficient on the flat plate in the transition and slip flow regimes

Full size image
Fig. 8
figure 8

Drag coefficient of the flat plate with respect to the Reynolds number in the transition and slip flow regimes

Full size image
Fig. 9
figure 9

Distribution of the DUGKS cell and the N-S cell for flow around a flat plate with different Reynolds numbers in the slip flow regime

Full size image

Second, the flow around a flat plate with the Reynolds number varying from Re = 400 to 5000 is simulated by two types of meshes in both the physical space and the velocity space. One is the fine mesh, which is the same as Ref. [58] and the velocity space is discretized by the Gauss-Hermite quadrature rule with \(28 \times 28\) points. The other is the coarse mesh as shown in Table 1 and the velocity space is discretized by the Gauss-Hermite quadrature rule with \(8 \times 8\) points. Figure 10 compares the distribution of the skin friction coefficient on the flat plate in the continuum flow regime (Re = 400 ~ 5000) obtained by the ADUGKS and the DUGKS using the fine mesh, and the comparison of the drag coefficient is depicted in Fig. 11. Figure 12 shows the distribution of the DUGKS cell and the N-S cell for these cases. It can be seen that both the results of ADUGKS and DUGKS are basically consistent with those of the N-S solver. But if we enlarge the distribution of the skin friction coefficient on the flat plate and look at the distribution of the drag coefficient, it can be found that the results of ADUGKS are closer to those of the N-S solver than the DUGKS, especially for the cases of Re = 2000 and 5000. The reason may be that there are more cells turning into the N-S cell at high Reynolds numbers in the calculation of ADUGKS, as shown in Fig. 12. To validate the performance of ADUGKS for the case in which the mesh size is far larger than the molecular mean free path, we restimulate the cases of Re = 400 ~ 5000 with the coarse mesh and display the results in Fig. 13 and Table 1. It can be seen that even though the coarse mesh is utilized, the results of ADUGKS and DUGKS are consistent with those of the N-S solver. In addition, as compared with the DUGKS, a speed-up ratio of 34 and a memory consumption ratio of 0.103 are achieved for the ADUGKS in the case of Re = 5000, as reported in Table 1.

Fig. 10
figure 10

Distribution of skin friction coefficient on the flat plate in the continuum flow regime

Full size image
Fig. 11
figure 11

Drag coefficient of the flat plate with respect to the Reynolds number in the continuum flow regime

Full size image
Fig. 12
figure 12

Distribution of the DUGKS cell and the N-S cell for flow around a flat plate with different Reynolds numbers in the continuum flow regime (Left: global view; Right: local view)

Full size image
Fig. 13
figure 13

Distribution of skin friction coefficient on the flat plate in the continuum flow regime calculated by the coarse mesh with different methods

Full size image

4.3 Case 3: flow around a circular cylinder

To assess the performance of ADUGKS for the simulation of hypersonic flows, the flow around a circular cylinder at Ma = 5 and Kn = 0.001 ~ 0.1 is simulated. In this test example, the wall temperature is fixed at the free stream temperature of \(T_{ref} = 273{\text{ K}}\). The dynamic viscosity is calculated by Eq. (26) and the reference dynamic viscosity is determined by Eq. (27), in which \(L\) is chosen as the radius of the cylinder. For the test case of Kn = 0.001, the computational domain with a far-field boundary located at \(15L\) away from the geometrical center is discretized by a non-uniform mesh with 81 and 65 points in the radial direction and circumferential direction, respectively. For the test cases of Kn = 0.01 and 0.1, the same computational domain is discretized by a non-uniform mesh with 61 and 65 points in the radial direction and circumferential direction, respectively. The moment integration in the velocity space is approximated by the Newton–Cotes quadrature with \(101 \times 101\) points uniformly distributed in \(\left[ { - 12\sqrt {2R_{g} T_{ref} } , \, 12\sqrt {2R_{g} T_{ref} } } \right] \times \left[ { - 12\sqrt {2R_{g} T_{ref} } ,{ 1}2\sqrt {2R_{g} T_{ref} } } \right]\).

The comparison of u-velocity, v-velocity, pressure and temperature contours for the flow around a circular cylinder at Kn = 0.1, 0.01 and 0.001 are shown in Figs. 14, 15 and 16, respectively. It can be seen that the results of ADUGKS are consistent with the DUGKS for all test cases. Figure 17 depicts the density, u-velocity, pressure and temperature profiles along the stagnation line and Fig. 18 presents the pressure coefficient, shear stress coefficient and normal heat flux distributions along the cylindrical wall from the stagnation point to the trailing edge. Once again, the results of ADUGKS compare well with those of DUGKS. The distribution of the DUGKS cell and the N-S cell for the flow around a circular cylinder with different Knudsen numbers is displayed in Fig. 19. Clearly, the number of the DUGKS cell reduces with the decrease of the Knudsen number. As reported in Table 2, the ratio of the number of total cells to the number of DUGKS cells is 1.819 for the case of Kn = 0.001, resulting in a speed-up ratio of 1.208 and a memory consumption ratio of 0.605 for the ADUGKS as compared with the DUGKS.

Fig. 14
figure 14

Comparison of u-velocity, v-velocity, pressure and temperature contours for flow around a circular cylinder at Ma = 5 and Kn = 0.1 (ADUGKS: colored background with black solid line; DUGKS: white dashed line)

Full size image
Fig. 15
figure 15

Comparison of u-velocity, v-velocity, pressure and temperature contours for flow around a circular cylinder at Ma = 5 and Kn = 0.01 (ADUGKS: colored background with black solid line; DUGKS: white dashed line)

Full size image
Fig. 16
figure 16

Comparison of u-velocity, v-velocity, pressure and temperature contours for flow around a circular cylinder at Ma = 5 and Kn = 0.001 (ADUGKS: colored background with black solid line; DUGKS: white dashed line)

Full size image
Fig. 17
figure 17

Comparison of density, u-velocity, pressure and temperature profiles along the stagnation line for flow around a circular cylinder with different Knudsen numbers

Full size image
Fig. 18
figure 18

Comparison of pressure coefficient, shear stress coefficient and normal heat flux distributions along the cylindrical wall from the stagnation point to the trailing edge at different Knudsen numbers

Full size image
Fig. 19
figure 19

Distribution of the DUGKS cell and the N-S cell for flow around a circular cylinder with different Knudsen numbers

Full size image
Table 2 Number of DUGKS cells, memory consumption (MByte) and computational time (hours) of different methods for flow around a circular cylinder with different Knudsen numbers
Full size table

4.4 Case 4: unsteady gas expansion in a channel

Gas expansion in a channel is a good test case to validate the newly developed method for unsteady multiscale flows [59]. In this test example, we consider a channel with the length L and the height H = L/10, which is separated by a diaphragm located at x = L/2 initially, as shown in Fig. 20. The initial Knudsen numbers of the gas at the left and right sides of the diaphragm are \(Kn_{L} = 0.00001\) and \(Kn_{R} = 1\), respectively, and the corresponding initial normalized density are \(\rho_{L} = 1\) and \(\rho_{R} = 0.00001\). The initial normalized temperature and velocity are set as \(T_{0} = 1\) and \(U_{0} = V_{0} = 1\) for the gas in the whole channel. The temperature of the upper and bottom walls of the channel is maintained at \(T_{0}\). The inlet and outlet boundary conditions are used for the left and right boundaries of the channel, respectively. The reference dynamic viscosity is determined by Eq. (27), in which the reference density, temperature and Knudsen number are consistent with the states of the gas at the left side of the diaphragm. In addition, the dynamic viscosity is calculated by Eq. (26).

In the simulation, the computational domain is discretized by a uniform mesh with 4000 cells, and the moment integration in the velocity space is approximated by the Newton–Cotes quadrature with \(101 \times 101\) points uniformly distributed in \(\left[ { - 7, \, 7} \right] \times \left[ { - 7, \, 7} \right]\). Figure 21 compares the density, u-velocity, temperature and x-component of heat flux profiles along the horizontal central line of the channel at times t = 0.01 and 0.05 calculated by the ADUGKS and the DUGKS. The results of ADUGKS are basically consistent with those of DUGKS, validating the accuracy of ADUGKS for unsteady multiscale flows. To compare the computational cost and the memory consumption of ADUGKS with DUGKS, we depict the distribution of the DUGKS cell and the N-S cell for this test example at different times in Fig. 22. It can be seen that the N-S cell occupies the left half of the channel and the interface between the DUGKS cell and the N-S cell moves toward the right as time goes on after removing the diaphragm. Thus, the computational cost of ADUGKS will be reduced gradually in the process of gas expansion in a channel.

Fig. 20
figure 20

Unsteady gas expansion in a channel

Full size image
Fig. 21
figure 21

Comparison of density, u-velocity, temperature and x-component of heat flux profiles along the horizontal central line of the channel at different times

Full size image
Fig. 22
figure 22

Distribution of the DUGKS cell and the N-S cell for unsteady gas expansion in a channel at different times

Full size image

5 Conclusions

In this work, an adaptive partitioning-based discrete unified gas kinetic scheme (ADUGKS) is developed for multiscale flow computations. This method is designed from the multiscale discrete characteristic solution to the Boltzmann-BGK equation, which contains the initial distribution function and the local equilibrium state. The initial distribution function contributes to the calculation of free streaming fluxes, and its ratio is determined by the local flow variables and the local mesh size. If its contribution is negative, the local flow field can be regarded as the continuous flow and the N-S equations can be used to obtain the solution directly. Otherwise, both the DVBE and the corresponding macroscopic governing equations are solved with the modified DUGKS. Since more and more cells turn into the N-S cell with the decrease of the Knudsen number, a significant acceleration can be achieved for the ADUGKS in the continuum flow regime as compared with the DUGKS.

The performance of ADUGKS is examined by the lid-driven cavity flow, the flow around a flat plate, the hypersonic flow around a circular cylinder and the unsteady gas expansion in a channel in different flow regimes. Numerical results show that the accuracy of ADUGKS is consistent with that of the DUGKS in all flow regimes, validating it as a multiscale approach. The computational cost and the memory consumption of ADUGKS mainly rely on the number of the DUGKS cell in the whole computational domain. With the decrease of the Knudsen number, more and more DUGKS cells turn into the N-S cell, and thus the total computational cost and memory consumption of ADUGKS can be reduced gradually. In the continuum flow regime, about one order of magnitude acceleration can be achieved for the ADUGKS as compared with the DUGKS. However, it should be indicated that the N-S region is still too small in the slip flow regime, making the acceleration of ADUGKS indistinctive. The key to further improving the efficiency of the present method while maintaining its accuracy is to enlarge the N-S region as far as possible.