Introduction

Artificial Intelligence (AI) is a scientific discipline that is concerned with the design and development of algorithms used to evolve behaviors based on empirical data. Genetic Programming (GP) and Artificial Neural Network (ANN) are two common examples of AI techniques.

Pile foundations are structural elements that are used to transfer superstructure loads deep into the ground [1]. Several methods for estimating pile bearing capacity are proposed. These include experimental, numerical and analytical methods [2, 3]. Since the interaction of pile foundations and soils is complex and not entirely understood, the applicability of these methods in predicting the bearing capacity of pile foundations is limited. This complex interaction has encouraged researchers to apply AI techniques to predict the ultimate bearing capacity of pile foundations.

The primary focus of this paper is to briefly explain the ANNs and GP techniques and provide a literature review on the application of these methods in predicting the ultimate bearing capacity of pile foundations.

Overview of artificial intelligence

Artificial intelligence is a scientific discipline focused on the design and development of algorithms used to evolve behaviors based on empirical data. AI techniques can be used in solving engineering problems [4,5,6,7,8,9,10,11] even if the underlying relationships are unknown or the physical meaning is difficult to explain. This is one of the main advantages of these techniques when compared to most physically-based empirical and statistical methods. AI has the capability of learning by examples of data inputs and outputs presented to them so that the subtle functional relationships among the data are captured. Thus, AI models do not require numerous assumptions about the physical behavior of the system and mainly rely on the data to determine the structure and parameters that govern a system. This is in contrast to most physically-based models that use physical laws to derive the underlying relationships of the system and require prior knowledge about the nature of the relationships among the data. Therefore, AI-based solutions can often provide valuable alternatives for efficiently solving problems in the geotechnical engineering.

AI uses available data to map between the system inputs and the corresponding outputs using machine learning. Mapping process is done by repeatedly presenting examples of the inputs and model outputs in order to find the function that minimizes the error between the actual outputs and the predictions of the AI model. Statistical regression analysis of data with non-linear relationship can be applied successfully only if prior knowledge of the nature of the non-linearity exists. However, for AI models, this prior knowledge of the nature of the non-linearity is not required. In the broad area of engineering problems, it is likely to encounter complex and highly non-linear conditions where traditional regression analyses are inadequate [12].

There are several AI algorithms; amongst them ANN and GP are more applicable for prediction of non-linear phenomena in engineering problems. A brief overview of these techniques is presented below.

Artificial Neural Networks were first introduced by McCulloch and Pitts [13]. ANN as described by Bendana et al. [14] is a massively parallel distributed processor which can store information taken from a data set that is supplied out of the network.

Artificial Neural Networks are computational models based on the information processing system of the human brain and nervous system [15]. They can be considered as a group of simple, highly interconnected elements that process the information by their dynamic state response to external inputs. ANNs learn from data examples presented to them. Because of this, they can be used even if the underlying relationships among the data are unknown or the physical meaning is difficult to explain. Comparing this capability with other traditional empirical and statistical methods which require prior knowledge about the nature of the relationships reveals the applicability of this method in modeling the complex behaviors between inputs and outputs [16]. Since the early 1990s, ANNs have been applied successfully to almost every problem in engineering.

A typical structure of ANNs is composed of a number of interconnected processing elements, commonly referred to as neurons. The neurons are logically arranged in layers that interact with each other via weighted connections. The main three set of layers include input layer, hidden layers, and output layer. Each neuron is connected to all the neurons in the next layer. Patterns are presented to the network via the input layer. This layer communicates to one or more hidden layers where the actual processing is done via a system of weighted connections. The hidden layers enable these networks to represent and compute complicated associations between inputs and outputs. The hidden layer subsequently links to an output layer which holds the response of the network to the input. In addition, there is also a bias with modifiable weighted connections, which is only connected to neurons in the hidden and output layers. ANNs can be autonomous and learn by input from outside “teachers” or even self-teaching from written in rules [6]. Typical structure and operation of ANNs is shown in Fig. 1.

Fig. 1
figure 1

Typical structure and operation of ANNs [17]

Full size image

The overall performance of the ANN model can be assessed by several criteria including coefficient of determination (R2), mean squared error, mean absolute error, minimal absolute error, and maximum absolute error. A well-trained model should result in R2 value close to 1 and small values of error terms [15].

Genetic Programming is an example of AI inspired by biological evolution extending from genetic algorithms. It can be considered as an evolutionary algorithm-based methodology used to find computer programs that perform a given computational task [6]. The technique was introduced by Koza [18] as a domain-independent problem-solving approach in which computer programs composed of functions and terminals are evolved to solve, or approximately solve, problems by generating a structured representation of the data. The structural representation imitates the biological evolution of living organisms, and emulates naturally occurring genetic operations. The ability to provide the relationship between a set of inputs and the corresponding outputs in a simple mathematical form accessible to the users is the main advantage of the GP over the ANNs.

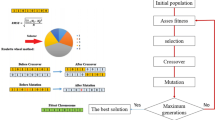
The first step of GP modelling is the creation of initial population of computer models (also called chromosomes). The initial population includes a randomly selected set of functions and terminals defined by the user to suit a certain problem. The functions and terminals represent the building blocks of the GP models and are arranged in a treelike structure to form a computer model that contains a root node, branches of functional nodes, and terminals (Fig. 2). Examples of functions and terminals used in GP are standard arithmetic operations, Boolean logic functions, trigonometric functions, numerical constants, logical constants, variables, and user-defined operators [19].

Fig. 2
figure 2

Typical example of GP tree representation for the function [(3 + X1)/(X2 − X3)]2 [6]

Full size image

Analysis in GP starts with determining a set of functions that represent the nature of the problem or data. Each individual in the population receives a measure of its fitness in the current environment. The fitness criteria are calculated by the objective function i.e., how good the individual is at competing with the rest of the population.

New population is created by applying reproduction, cross-over, and mutation to certain proportions of the computer models. Reproduction is the copying of a computer model from an existing population into the new population without any change; cross-over, as shown in Fig. 3, is the genetic recombining of randomly chosen parts of two computer models; and mutation is the replacement of a randomly selected functional or terminal node with others from the same function or terminal set. The existing population will then be replaced with the new population. This evolutionary process is continued until a termination criterion is met, which can be either an acceptable error or a maximum number of generations. Finally, the best computer model is generated by GP using the fitness function adopted.

Fig. 3
figure 3

Typical cross-over operation in GP

Full size image

AI applications in bearing capacity prediction of pile foundations

This section provides an overview of the applications of ANNs and GP in prediction of the bearing capacity of pile foundations. It should be noted that covering every single application of these techniques in pile foundations is not intended in the current paper. However, the intention is to provide a general overview of some of the more relevant applications in pile foundation’s bearing capacity estimation. In order to be able to compare the previous applications and analyze their findings, an overview of the following variables is studied: selected AI model; type of pile data and number of dataset; considered soil type; selected effective parameters; estimated output; selected error criteria and measured error value; and applied comparison method. The purpose of providing the list of applied comparison methods for each application is to demonstrate the effectiveness of these techniques compared to other traditional methods.

Load carrying capacity is often the governing factor in the design of pile foundations. This criterion has been examined by several AI researchers especially using ANNs. Table 1 summarizes the input and output parameters used for ANN in previous research.

Table 1 ANN input and output variables
Full size table

Table 2 summarizes the outcome of different applications of ANN reviewed in this paper. Overall, 25 different applications have been reviewed and the results are investigated.

Table 2 Applications of ANN in estimating the capacity of pile foundations
Full size table

The parameters that were studied for comparison of different applications include: type of ANN model, characteristics of dataset, soil type, input and output variables, error criteria used for validation with respective error value, and selected method of comparison.

Compared to ANN, the application of GP technique for estimating the capacity of pile foundations is relatively new. However, the popularity of GP shows an increased tendency in adopting this technique in estimating the capacity of pile foundations. Table 3 summarizes the input and output parameters used for GP in previous research reviewed in this paper.

Table 3 GP input and output variables
Full size table

Seven applications of GP in estimating the capacity of pile foundations are reviewed in this paper and similar to the trend applied in previous section, the following parameters of each application were analyzed for comparison purpose: type of GP model, characteristics of dataset, soil type, input and output variables, error criteria used for validation with respective error value, and selected method of comparison. Table 4 shows this information for the seven analyzed applications.

Table 4 Applications of GP in estimating the capacity of pile foundations
Full size table

Discussion

In order to better understand the different applications of AI techniques in pile capacity estimation, a statistical analysis was conducted on the input and output variables of the analyzed applications. This is useful in realizing the importance of different variables and their effects on pile capacities in previous research. It will also show which type of variables had the highest importance in previous applications and will help in selecting the proper variables for future research.

Artificial Neural Networks

The input variables adopted in the previous ANN research that are analyzed in this paper can be categorized into 4 main subdivisions. These subdivisions include pile properties, loading history, hammer/SPT/CPT information, and soil properties. Overall, in all 25 studied applications, 38 different input variables were adopted. Table 5 shows the adopted input variables categorized into 4 main groups, and their repeat numbers in all 25 analyzed ANN applications. Pile length was the most adopted variable with 21 repeat among all 25 studied applications. Pile cross sectional area and pile diameter had the highest number of repeat after pile length.

Table 5 ANN input variables
Full size table

The percentage of repeat for the four categories of ANN input variables is depicted in Fig. 4 where pile properties had the highest percentage of repeat, while, the loading history had the lowest repeat percentage. Hammer/SPT/CPT and soil properties are parameters that are used in slightly less than half of the ANN studies.

Fig. 4
figure 4

Percentage of repeat for different categories of ANN input variables

Full size image

Percentage of repeat of input variables in each category of ANN applications is shown in Fig. 5. The information in Fig. 5 helps us to see which parameters in each category has had the highest repeat percentage. Figure 5a shows that, between all parameters related to pile properties, the pile length with 31% repeat rate, was the most applied variable. Pile cross sectional area and pile diameter with 16 and 15% usage were following the pile length. For the loading history presented in Fig. 5b, the elapsed time after driving with 57% contribution, had the highest repeat percentage. In hammer/SPT/CPT information category, hammer weight, hammer drop height, driving energy delivered to the pile, and average SPT Along the pile shaft had similar repeat percentage of 16% and were the highest applied variables as an input of ANN models (Fig. 5c). In soil properties category (Fig. 5d), the effective overburden stress with 28% repeat percentage, had the highest repeat rate among previous related studies where shear resistance of the soil surrounding the pile shaft, soil type around the pile shaft, and undrained shear strength has equal usage of 12% in previous ANN studies on piles.

Fig. 5
figure 5

Percentage of repeat of input variables in ANN applications for (a) pile properties, (b) loading history, (c) hammer/SPT/CPT information, and (d) soil properties

Full size image

The variables applied as an output of ANN models together with their repeat numbers in all 25 applications are shown in Table 6. The ultimate load capacity with 14 number of repeat was the main variables of interest in previous research. Skin friction resistance and pile tip capacity had the highest repeat number after ultimate load capacity. However, both skin friction resistance and pile tip capacity are directly or indirectly used to estimate the ultimate load capacity of pile foundations.

Table 6 ANN estimated variables
Full size table

Genetic Programming

As discussed before, compared to ANN, GP is a newer technique for intelligence analysis of piles. Hence the number of parameters used in GP in each category are smaller than ANN. Overall, in 7 reviewed studies in this research, 19 different parameters have been used for GP. By following the four classification of the analyzed properties in previous AI studies on piles, Table 7 presents the input variables used for GP. Similar to parameters studied by ANN, pile length and undrained shear strength at pile tip were the most used parameters.

Table 7 GP input variables
Full size table

For pile properties category, previous studies only focused on 5 different parameters, where in ANN, 15 different parameters have been investigated. Parameters such as pile weight (Wp), amount of steel reinforcement (As), pile circumference (M), pile initial axial capacity (P), and pile–soil interface friction angle (δ) has not been investigated by GP. For hammer SPT/CPT information, ANN covered 9 parameters where GP only have covered 6 parameters. Hammer drop height (Hh), number of blows (N), and hammer weight (Wh) are parameters that are investigated in ANN but not covered by GP in previous studies. In soil properties, ANN was more developed where 11 parameters have been investigated in the literature; however, only three parameters have been used for GP. Hence, parameters such as effective soil specific weight (γe), soil friction angle (φ), soil type around the pile shaft (Ts), and etc. can be used in future GP studies on piles. In loading history category, GP used different load parameters than ANN.

The percentage of repeat for the four categories of GP input variables is illustrated in Fig. 6. Similar to ANN, pile properties had the highest percentage of repeat; however, the percentage of using pile properties in ANN (52%) was 16% larger than its usage in GP (36%). Opposite to ANN, loading history plays an important role for adopted parameters in GP with 23% where for ANN, it only contributed by 5%. Soil properties for both ANN and GP has high percentage of usage; however, it was used in GP slightly more than ANN (by 7%). Hammer/SPT/CPT for GP has usage percentage of 15% where in ANN it has a contribution of 24% in the previous studies.

Fig. 6
figure 6

Percentage of repeat for different categories of GP input variables

Full size image

Percentage of repeat of input variables in each category of GP applications is shown in Fig. 7. Figure 7a shows that, between all parameters related to pile properties, the pile length with 43% repeat rate, was the most applied variable. Pile diameter with 36% was the second frequent used parameter. For the loading history presented in Fig. 7b, the lateral force point of application, chain force angle with the horizontal, and loading rate had equal contribution of 30%. In hammer/SPT/CPT information category, all parameters had equal usage percentage in previous studies (Fig. 7d). In soil properties category (Fig. 7d), undrained shear strength at pile tip with 56% usage was the most frequent used parameter.

Fig. 7
figure 7

Percentage of repeat of input variables in GP applications for (a) pile properties, (b) loading history, (c) hammer/SPT/CPT information, and (d) soil properties

Full size image

Table 8 summarizes the output variables of GP models with their repeat numbers in all reviewed cases. Similar to ANN, The ultimate load capacity is the most interested parameter resulted from GP. The uplift capacity of suction caissons is another parameter considered in GP; however, it was not interested in ANN studies. Other parameters such as ultimate capacity of suction caissons, undrained lateral load capacity, and undrained side resistance alpha factor were also considered in GP. The comparison of the output parameters in ANN and GP showed that uplift capacity of suction caissons and ultimate capacity of suction caissons were only considered in GP.

Table 8 GP estimated variables
Full size table

Conclusions

In this review paper, initially the importance of AI in geotechnical engineering was discussed. Subsequently, the two well-known AI techniques of ANN and GP were introduced. Afterward, a detailed review of the previous studies on pile foundations was conducted and a list of applied variables as well as their usage frequencies were presented. Results of this paper will help in better understanding the importance of different variables and their effects on pile capacities in previous research. In addition, it will help in choosing other important or un-investigated parameters for future research. Based on the reviewed articles and used parameters, the followings were concluded:

  • Overall, in all 25 studied ANN applications, 38 different input variables were adopted. Pile length was the most adopted variable with 21 repeat among all variables. Pile cross sectional area and pile diameter had the highest number of repeat after pile length. Among all four main categories of variables, pile properties had the highest percentage of repeat, while, the loading history had the lowest repeat percentage. Hammer/SPT/CPT and soil properties were used in slightly less than half of the ANN studies.

  • Compared to ANN, GP is a newer technique for artificial intelligence analysis of pile capacity. Among GP applications, pile length, pile diameter, and undrained shear strength at pile tip were the most applied variables. Similar to ANN, among the four main categories of variables, pile properties had the highest percentage of repeat; however, the percentage of using pile properties in ANN (52%) was 16% larger than its usage in GP (36%). Specifically, for pile properties category, GP studies were only focused on 5 different variables, whereas in ANN, 14 different variables have been investigated. Parameters such as pile weight (Wp), amount of steel reinforcement (As), pile circumference (M), pile initial axial capacity (P), and pile–soil interface friction angle (δ) have not been investigated by GP. Overall, in the seven reviewed GP applications, only 18 different variables have been applied. Comparing this number with 38 applied variables in ANN applications shows that further studies are needed to explore more variables in GP.

  • The ultimate load capacity was the most evaluated output parameter among both ANN and GP. The uplift capacity of suction caissons was another variable considered in GP; however, it was not evaluated in ANN studies. The comparison of the output variables in ANN and GP showed that uplift capacity of suction caissons and ultimate capacity of suction caissons were only considered in GP. Hence, future ANN studies may consider these variables for characterization of soil–pile interactions.