On heterogeneous coupling of multiscale methods for problems with and without scale separation

Abstract

In this paper, we discuss partial differential equations with multiple scales for which scale resolution is needed in some subregions, while a separation of scale and numerical homogenization is possible in the remaining part of the computational domain. Departing from the classical coupling approach that often relies on artificial boundary conditions computed from some coarse grain simulation, we propose a coupling procedure in which virtual boundary conditions are obtained from the minimization of a coarse grain and a fine-scale model in overlapping regions where both models are valid. We discuss this method with a focus on interface control and a numerical strategy based on non-matching meshes in the overlap. A fully discrete a priori error analysis of the heterogeneous coupled multiscale method is derived, and numerical experiments that illustrate the efficiency and flexibility of the proposed strategy are presented.

1 Introduction

The past few years have witnessed a growing number of new numerical schemes for multiscale problems. Broadly speaking, the numerical challenge for the approximation of such problems is to avoid scale resolution, i.e., the use of a fine mesh that resolves the smallest scale in the problem. Indeed, such direct approaches are often computationally too expensive for practical applications. In this paper, we consider in a polygonal domain $\varOmega \subset \mathbb {R}^d, d=1,2,3$, with boundary $\varGamma =\varGamma _D \cup \varGamma _N$, the model problem

$$\begin{aligned} -\mathrm{{div\,}}(a^\varepsilon \nabla u^\varepsilon )&=f\quad \quad \text {in } \varOmega , \nonumber \\ u^\varepsilon&=g_D \quad \text { on}\,\varGamma _D,\nonumber \\ n \cdot (a^\varepsilon \nabla u^\varepsilon )&= g_N\quad \text { on }\varGamma _N, \end{aligned}$$

(1)

where $f\in L^2(\varOmega )$, $g_D\in H^{1/2}(\varGamma _D)$, and $g_N \in L^2(\varGamma _N)$, and where $a^\varepsilon \in (L^{\infty }(\varOmega ))^{d\times d}$ is a highly oscillatory tensor that satisfies, for $0<\alpha <\beta$,

$$\begin{aligned} \alpha |\xi |^2 \le a^\varepsilon (x)\xi \cdot \xi , \quad |a^\varepsilon (x)\xi |\le \beta |\xi | \quad \forall \xi \in \mathbb {R}^d,\quad \text { for a.e. } x\in \mathbb R. \end{aligned}$$

(2)

For such a problem, one can identify two broad classes of multiscale methods, namely numerical methods that seek to approximate an effective solution of the original problems in which the small scales have been averaged out. The existence of such effective solutions usually relies on homogenization theory [9, 21]. The attractivity of such methods is the possibility to obtain numerical approximations that correctly describe the macroscopic behavior of the multiscale problem at a cost that, however, is independent of the smallest scale. Another class of multiscale methods aims at building coarse basis functions that encode the multiscale oscillations in the problem. This class of methods usually comes with a cost that is no longer independent of the small scale, but the construction of the basis functions can be localized and, once constructed, this basis can often be reused in a multi-query context. We refer to [5] for a review and references of the first class of methods and to [15, 20, 23] for review and references of the second class of methods. The framework that makes the first class of methods efficient is that of a simultaneous coupling of a macro- and a micro-method. In such approach, a separation of the scales is often required. The second class of methods solves the fine-scale problems on overlapping patches, and it has recently been shown that convergences can also be obtained without assuming scale separation [20, 23].

In this contribution, we address an intermediate situation between separated and non-separated scales in the following sense: we assume that in a subset $\omega _2$ of the computational domain $\varOmega$ the macro-/micro-upscaling strategy can be applied but that in an other part $\omega$ of the domain one needs full resolution of the scales. Here we assume that this second domain is sufficiently small so that standard resolved finite element method (FEM) can be used. In the region $\omega _2$, we chose to use the finite element heterogeneous multiscale method (FE-HMM) [2]. While our method easily generalizes to multiple regions with and without scale separation, we assume here for simplicity that $\varOmega =\omega _2\cup \omega$. The main issue for such a coupling strategy is to set adequate boundary conditions at the interfaces of both computational domains. We note that such problems have numerous applications in the sciences; we mention, for example, heterogeneous structures with defects [10, 16] or steady flow problems with singularities [17]. Coupling strategies between fine-scale and upscaled models have already been studied in the literature, for example, in [27] where a precomputed global homogenized solution is used to provide the boundary conditions in the fine-scale subregions. More recently, a coupling strategy based on an $L^2$ projection of the homogenized solution onto harmonic fine-scale functions has been discussed [8].

The aim of this paper is to pursue the study of a new approach that we have proposed in [6, 7] relying on an optimization-based coupling strategy. By introducing small overlapping region $\omega _0$ between $\omega _2$ and $\omega$, where both fine-scale and homogenized model are valid, we consider the unknown boundary conditions for both models as (virtual) control and minimize the discrepancy of the solutions from the two models in the overlap. Two possible scenarios are illustrated in Fig. 1. Such ideas have appeared earlier in the literature for coupling different type of partial differential equations [18] or for atomistic-to-continuum methods [28]. We also note, related to our method, the recent work on the coupling of local and nonlocal diffusion models [13].

Fig. 1

Two scenarios for the domain decomposition of $\varOmega$

We briefly describe the main contribution of this paper. First, in [7], the theory and the numerics have been developed for the cost function $\left\| \cdot \right\| _{\mathrm {L}^{2}(\omega _0)}$, called distributed observation in the classical terminology of optimal control. Here we consider the cost function $\left\| \cdot \right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}$, called boundary or interface control. Such controls can reduce the cost of the iterative method to solve the optimality system compared to the cost of solving the optimization problem with distributed observation [14]. Second, in [7] we used the same mesh in the overlap $\omega _0$ with the consequence of having to use a mesh size that scales with the fine mesh of $\omega$. Here we discuss the use of independent meshes in the overlap through appropriate interpolation techniques. As a result, we have again a significant reduction in the computational cost of the coupling as the macroscopic numerical method in $\omega _2=\varOmega \setminus \omega$ does not need an increasing number of micro-solvers as the mesh in $\omega _1$ is refined. Finally, numerical examples were carried out in [7] only for the situation where $\omega \Subset \varOmega$ (Fig. 1, left); here we discuss also the scenario for which $\partial \omega \cap \partial \varOmega \ne \emptyset$ (Fig. 1, right).

The paper is organized as follows. In Sect. 2, we describe the model problem, introduce the two minimization costs functions considered in this paper, and give an a priori error analysis between the coupled and the fine-scale solutions. In Sect. 3, we define the multiscale numerical discretization of the optimization problem and perform a fully discrete a priori error analysis. Finally, Sect. 4 contains several numerical experiments that illustrate the theoretical results and the performance of the new coupling strategy.

Notations In what follows, $C>0$ is used to denote a generic constant independent of $\varepsilon$. We consider the usual Sobolev space $H^1(\varOmega )=\{u\in L^2(\varOmega )\mid D^ru\in L^2(\varOmega ), |r|\le 1 \}$,where $r \in \mathbb N^d, |r|=r_1 + \cdots + r_d$ and $D^r= \partial _1^{r_1}\ldots \partial ^{r_d}_d$. The notation $|\cdot |$ stands for the standard Euclidean norm in $\mathbb R^d$. Let Y denote the unit cube $(0,1)^d$ and define $W^1_{\mathrm{per}}(Y):=\{v\in H^1_{\mathrm{per}}(Y)\mid \int _{Y}v \text {d}y=0\}$ where the set $H^1_{\mathrm{per}}(Y)$ is the closure of $\mathcal {C}^{\infty }_{\mathrm{per}}(Y)$ for the $H^1$ norm.

2 Problem formulation

Let $\omega \subset \varOmega$ be the region without scale separation and $\omega _0$ be the overlap region. Assume that $\varGamma _1=\partial \omega _1\setminus \varGamma$ and $\varGamma _2=\partial \omega _2\setminus \varGamma$ are Lipschitz continuous boundaries. We decompose the tensor $a^\varepsilon$ of problem (1) into $a^\varepsilon =a_{\omega }+ a^\varepsilon _2$, where $a^\varepsilon _2=a^\varepsilon \mathbb {1}_{\omega _2}$ and $a_{\omega }=a^\varepsilon \mathbb {1}_{\omega }$ are tensors with and without scale separation, respectively. The tensor $a^\varepsilon _2$ H-converges toward an homogenized tensor $a^0_2$ [25]. Further, we set $a_1=a^\varepsilon \mathbb {1}_{\omega _1}$, $u_1=u^\varepsilon _1$, and $u_2=u_2^0$. The heterogeneous control restricted to Dirichlet boundary controls is given by the following problem: find $u_1^{\varepsilon }\in H^1(\omega _1)$ and $u_2^0\in H^1(\omega _2)$, such that $\frac{1}{2}\left\| u_1^{\varepsilon }-u_2^0\right\| _\mathcal {H}^2$ is minimized under the following constraints, for $i=1,2,$

$$\begin{aligned} \begin{array}{rll} -\mathrm{{div\,}}(a_i\nabla u_i)&{}=f &{}\quad \text {in }\omega _i,\\ u_i&{}= \theta _i &{}\quad \text {on } \varGamma _i,\\ u_i &{}= g_D &{}\quad \text {on } \partial \omega _i \cap \varGamma _D,\\ n \cdot (a_i\nabla v_i) &{}= g_N &{} \quad \text {on }\partial \omega _i \cap \varGamma _N, \end{array} \end{aligned}$$

(3)

where the boundary conditions $\theta _i$, called the virtual controls, are to be determined; $(\mathcal {H}, \left\| \cdot \right\| _{\mathcal {H}})$ is a Hilbert space specified below. Further, we define the space of admissible Dirichlet controls

$$\begin{aligned} \mathcal {U}^D_i=\left\{ \mu _i \in H^{1/2}(\varGamma _i)\mid \exists u\in H^1(\omega _i), u|_{\varGamma _i}=\mu _i, \text { in the sense of the trace}\right\} . \end{aligned}$$

The strategy is to solve a minimization problem in the space of admissible controls, where we minimize the cost

$$\begin{aligned} J(\theta _1, \theta _2)= \frac{1}{2}\left\| u_1^{\varepsilon }(\theta _1)-u_2^0(\theta _2)\right\| _{\mathcal {H}}^2. \end{aligned}$$

In this paper, two Hilbert spaces $(\mathcal {H}, \left\| \cdot \right\| _{\mathcal {H}})$ are considered.

Case 1. Minimization in $L^2(\omega _0)$, with

$$\begin{aligned} J(\theta _1, \theta _2)=\frac{1}{2}\left\| u_1^{\varepsilon }(\theta _1)-u_2^0(\theta _2)\right\| _{\mathrm {L}^{2}(\omega _0)}^2. \phantom {\varGamma _2} \end{aligned}$$

(case 1)

Case 2. Minimization in $L^2(\varGamma _1\cup \varGamma _2)$, with

$$\begin{aligned} J(\theta _1, \theta _2)=\frac{1}{2}\left\| u_1^{\varepsilon }(\theta _1)-u_2^0(\theta _2)\right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}^2. \end{aligned}$$

(case 2)

The solutions are split into

$$\begin{aligned} u_1^{\varepsilon }(\theta _1)= u_{1,0}^{\varepsilon }+ v_1^{\varepsilon }(\theta _1), u_2^0(\theta _2)= u_{2,0}^0 + v_2^0(\theta _2), \end{aligned}$$

where $(v_1^{\varepsilon }, v_2^0)$ are called the state variables and satisfy, for $i=1,2$,

$$\begin{aligned} \left\{ \begin{array}{rll} -\mathrm{{div\,}}(a_i\nabla v_i)&{}=0 &{}\quad \text {in }\,\omega _i,\\ v_i&{}= \theta _i &{}\quad \text {on }\,\varGamma _i,\\ v_i &{}= 0 &{}\quad \text {on }\,\partial \omega _i\cap \varGamma _D,\\ n \cdot (a_i\nabla v_i)&{}=0 &{}\quad \text {on }\,\partial \omega _i\cap \varGamma _N, \end{array} \right. \end{aligned}$$

(4)

where $v_1=v_1^{\varepsilon }$, and $v_2=v_2^0$. The functions $u_{i,0}$ are solutions of problem (3) with zero controls on $\varGamma _i$, for $i=1,2$. Let $H^1_D(\omega _i)$, $i=1,2$, denote the functions in $H^1(\omega _i)$ that vanish on $\partial \omega _i\cap \varGamma _D$. The solutions $u_{1,0}^{\varepsilon }$ and $u_{2,0}^0$ exist and are unique, thank to the Lax–Milgram lemma, and the solutions $v_1^{\varepsilon }$ and $v_2^0$ can be uniquely determined if the controls $\theta _1$ and $\theta _2$ are known. As $u_{1,0}^{\varepsilon }$ and $u_{2,0}^0$ are independent of the virtual controls $(\theta _1, \theta _2)$, they can be computed beforehand.

The well posedness of the optimization problem is proved following Lions [22]. The key point consists in proving that the cost function induces a norm over $\mathcal {U}=(\mathcal {U}_1^D, \mathcal {U}_2^D)$. One consider then the completion of $\mathcal {U}$ (still denoted by $\mathcal {U}$) with respect to the cost induced norm, and the minimization problem admits a unique solution $(\theta _1, \theta _2)\in \mathcal {U}$ satisfying the Euler–Lagrange formulation

$$\begin{aligned}&\int _{\mathcal {O}}\left( v_1^{\varepsilon }\left( \theta _1\right) -v_2^0\left( \theta _2\right) \right) \left( v_1^{\varepsilon }\left( \mu _1\right) -v_2^0\left( \theta _2\right) \right) \text {d}x \nonumber \\&\quad = - \int _{\mathcal {O}}\left( v_1^{\varepsilon }\left( \mu _1\right) -v_2^0\left( \mu _2\right) \right) \left( u_{1,0}^{\varepsilon }-u_{2,0}^0\right) \text {d}x, \end{aligned}$$

(5)

for all $(\mu _1, \mu _2)\in \mathcal {U}$, and where $\mathcal {O}$ is either $\omega _0$ or $\varGamma _1\cup \varGamma _2$. While the optimization problem with the cost function of case 1 has been considered in [7], we prove that the optimal controls problem is well posed with the cost function of case 2.

For the homogenization theory (H-convergence), we consider a family of problems (1) indexed by $\varepsilon$. In what follows, we will often assume $\varepsilon \le \varepsilon _0$, where $\varepsilon _0$ is a parameter used in a strong Cauchy–Schwarz inequality (see Lemma 6.3). We assume that $\theta _i\in \mathcal {U}_i^D$ and hence $u_i(\theta _i)$ is in $H^1(\omega _i)$, for $i=1, 2$.

2.1 Minimization over $\varGamma _1\cup \varGamma _2$

As a fist step, we write the cost in terms of the state variables $v_1^{\varepsilon }$ and $v_2^0$,

$$\begin{aligned} J\left( \theta _1, \theta _2\right)&= \frac{1}{2} \left\| v_1^{\varepsilon }\left( \theta _1\right) -v_2^0\left( \theta _2\right) \right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}^2 + \left\| \left( v_1^{\varepsilon }\left( \theta _1\right) - v_2^0\left( \theta _2\right) \right) \left( u_{1,0}^{\varepsilon }-u_{2,0}^0\right) \right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}^2 \\&\quad + \frac{1}{2} \left\| u_{1,0}^{\varepsilon }-u_{2,0}^0\right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}^2. \end{aligned}$$

We set

$$\begin{aligned} \pi \left( \left( \theta _1, \theta _2\right) ,\left( \mu _1, \mu _2\right) \right) = \int _{\varGamma _1 \cup \varGamma _2}\left( v_1^{\varepsilon }\left( \theta _1\right) -v_2^0\left( \theta _2\right) \right) \left( v_1^{\varepsilon }\left( \mu _1\right) -v_2^0\left( \theta _2\right) \right) \text {d}s \end{aligned}$$

and show that $\pi$ induce a norm over $\mathcal {U}$.

Lemma 2.1

The bilinear form $\pi$ is a scalar product over $\mathcal {U}$.

Proof

The symmetry and positivity are clear, and it remains to prove that the form is positive definite; $\pi (\theta _1, \theta _2)=0$ if and only if $\theta _1=0$ and $\theta _2=0$. We use the short-hand notation $\pi (\theta _1, \theta _2)$ to denote $\pi ((\theta _1, \theta _2),(\theta _1, \theta _2))$.

Assuming that $\theta _1$ and $\theta _2$ are zero, the state variables $v_1^{\varepsilon }$ and $v_2^0$ are solutions of boundary value problems with zero data; thus, $v_1^{\varepsilon }$ and $v_2^0$ are zero over $\omega _1$ and $\omega _2$, respectively. This leads to $\pi (\theta _1, \theta _2)=0$.

Assume now that $\pi (\theta _1, \theta _2)=0$. It holds that

$$\begin{aligned} \int _{\varGamma _1 \cup \varGamma _2}(v^{\varepsilon }_1(\theta _1)- v_2^0(\theta _2))^2 \text {d}s=\int _{\varGamma _1}(\theta _1-v_2^0(\theta _2))^2\text {d}s + \int _{\varGamma _2}(v_1^{\varepsilon }(\theta _1)-\theta _2)^2 \text {d}s =0, \end{aligned}$$

and

$$\begin{aligned} \int _{\varGamma _1}(\theta _1-v_2^0(\theta _2))^2\text {d}s=0, \int _{\varGamma _2}(v_1^{\varepsilon }(\theta _1)-\theta _2)^2\text {d}s=0. \end{aligned}$$

This implies that $v_1^{\varepsilon }(\theta _1)|_{\varGamma _1}=\theta _1= v_2^0(\theta _2)|_{\varGamma _1}$ a.e. and $v_2^0(\theta _2)|_{\varGamma _2}=\theta _2= v_1^{\varepsilon }|_{\varGamma _2}(\theta _1)$ a.e. As $v_1^{\varepsilon }$ and $v_2^0$ are $H^1$ functions on $\omega _1$ and $\omega _2$, respectively, we obtain

$$\begin{aligned} \left\| \theta _1-v_2^0(\theta _2)\right\| _{\mathrm {H}^{1/2}(\varGamma _1)}=0 \quad \text {and}\quad \left\| v_1^{\varepsilon }(\theta _1)-\theta _2\right\| _{\mathrm {H}^{1/2}(\varGamma _2)}=0. \end{aligned}$$

We now use H-convergence on the tensor $a^\varepsilon _1$, to obtain an homogenized tensor $a_1^0$ in $\omega _1$. It holds that $v_1^{\varepsilon }$ converges weakly in $H^1$ toward $v_1^0$ the homogenized solution of

$$\begin{aligned} \begin{aligned} -\mathrm{{div\,}}(a_1^0(x)\nabla v_1^0)&=0&\text { in }\,&\omega _1,\\ v_1^0&= \theta _1&\text { on }&\varGamma _1,\\ v_1^0&= 0&\text { on }&\partial \omega _1\cap \varGamma _D,\\ n \cdot (a_1^0(x)\nabla v_1^0)&=0&\text { on }&\partial \omega _1\cap \varGamma _N. \end{aligned} \end{aligned}$$

Using the compact embedding of $H^1$ in $L^2$, the solution $v_1^{\varepsilon }$ converges strongly, up to a subsequence, toward $v_1^0$ in $L^2$, and it holds that

$$\begin{aligned} \left\| v_1^0-v_2^0\right\| _{\mathrm {L}^{2}(\varGamma _1\cup \varGamma _2)}=\lim _{\varepsilon \rightarrow 0} \left\| v_1^{\varepsilon }-v_2^0\right\| _{\mathrm {L}^{2}(\varGamma _1\cup \varGamma _2)}=0, \end{aligned}$$

hence $v_1^0|_{\varGamma _2}=\theta _2=v_2^0|_{\varGamma _2}$. Consequently, it holds

$$\begin{aligned} \left\| v_1^0-v_2^0\right\| _{\mathrm {H}^{1/2}(\varGamma _1\cup \varGamma _2)}=0. \end{aligned}$$

Using the strong Cauchy–Schwarz lemma, Lemma 6.3, we obtain

$$\begin{aligned} \left\| v_1^0-v_2^0\right\| _{\mathrm {H}^{1}(\omega _0)}^2&\ge \left\| v_1^0-v_2^0\right\| _{\mathrm {L}^{2}(\omega _0)}^2\\&\ge (1-C_s)\left( \left\| v_1^0\right\| _{\mathrm {L}^{2}(\omega _0)}^2 + \left\| v_2^0\right\| _{\mathrm {L}^{2}(\omega _0)}^2\right) , \end{aligned}$$

where $C_s<1$ is the strong Cauchy–Schwarz constant. The tensors $a_2^0$ and $a_1^0$ are equal in the overlapping region $\omega _0$, due to the locality of H-convergence, the difference $v_1^0-v_2^0$ satisfies

$$\begin{aligned} -\mathrm{{div\,}}\left( a_2^0\nabla \left( v_1^0-v_2^0\right) \right) =0 \quad \text {in } \omega _0, \end{aligned}$$

and one can bound the $H^1$ norm over $\omega _0$ by the $H^{1/2}$ norm over its boundary $\varGamma _1\cup \varGamma _2$; i.e.,

$$\begin{aligned} \left\| v_1^0-v_2^0\right\| _{\mathrm {H}^{1}(\omega _0)}\le C \left\| v_1^0-v_2^0\right\| _{\mathrm {H}^{1/2}(\varGamma _1 \cup \varGamma _2)}=0. \end{aligned}$$

Collecting the results leads to $v_1^0=0$ and $v_2^0=0$ a.e. in $\omega _0$. Further from the Caccioppoli inequality, Theorem 6.1, it holds $v_1^0=0$ a.e. in $\omega _1$ and $v_2^0=0$ a.e. in $\omega _2$. We can conclude that $\theta _i=0$ a.e. in $\varGamma _i$, $i=1,2$, by using the trace inequality; i.e.,

$$\begin{aligned} \left\| \theta _i\right\| _{\mathrm {H}^{1/2}(\varGamma _i)}\le C \left\| v_i^0\right\| _{\mathrm {H}^{1}(\omega _i)}=0. \end{aligned}$$

$\square$

The norm induced from the scalar product $\pi$ is given by

$$\begin{aligned} \left\| (\mu _1, \mu _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}:= \left( \int _{\mathcal {O}} (v_1^{\varepsilon }(\mu _1)-v_2^0(\mu _2))^2 \text {d}x \right) ^{1/2}, \quad \forall (\mu _1, \mu _2)\in \mathcal {U}, \end{aligned}$$

(6)

where $\mathcal {O}$ is either $\omega _0$ or $\varGamma _1\cup \varGamma _2$.

2.2 A priori error analysis

Let $u^\varepsilon$ be the solution of the heterogeneous problem (1), and let us derive a priori error bounds between $u^\varepsilon$ and the solution of the coupling

$$\begin{aligned} \bar{u}={\left\{ \begin{array}{ll} u_1^{\varepsilon }(\theta _1) &{}\text { in } \omega ^+, \\ u_{2}^{rec}(\theta _2) &{}\text { in } \varOmega \setminus \omega ^+, \end{array}\right. } \end{aligned}$$

(7)

where $u_{2}^{rec}$ is the reconstructed homogeneous solution $u_2^0$, given by problem CITE, with periodic correctors, and $\omega ^+$ is a subdomain of $\varOmega$ such that $\omega \subseteq \omega ^+ \subseteq \omega _1$. The reconstructed homogeneous solution needs to be considered here instead of $u^0_2$, as the later is a good approximation of the heterogeneous solution $u^\varepsilon$ only in the $L^2$ norm, but fails in the $H^1$ norm. The term $u_{2}^{rec}$ is given by

$$\begin{aligned} u_{2}^{rec}(x)= u_2^0(x) + \varepsilon \sum _{j=1}^d \chi ^j(x, x/\varepsilon )\frac{\partial u_2^0(x)}{\partial x_j}, x\in \varOmega {\setminus }\omega ^+, \end{aligned}$$

(8)

where $u_2^0=u_2^0(\theta _2)$.

We consider the cost function of case 2, and we refer to [7] for an analysis of case 1. For $\varepsilon$ fixed, we consider a homogenized problem on $\omega _2$ with boundary conditions on $\varGamma _2$ given by the trace of the heterogeneous solution $u^\varepsilon$. The problem reads: find $u^0$ the solution of

$$\begin{aligned} \begin{array}{rlll} -\mathrm{{div\,}}(a^0_2 \nabla u^0)&{}= f &{}&{}\text { in } \omega _2, \\ u^0&{}= \gamma _2(u^{\varepsilon }) &{}&{} \text { on } \varGamma _2, \\ u^0&{}=g_D &{}&{}\text { on } \partial \omega _2 \cap \varGamma _D, \\ n \cdot (a^0_2 \nabla u^0)&{}= g_N &{}&{}\text { on } \partial \omega _2 \cap \varGamma _N, \end{array} \end{aligned}$$

(9)

where $\gamma _2:H^{1}(\omega _2)\rightarrow H^{1/2}(\varGamma _2)$ denotes the trace operator on $\varGamma _2$. Similarly, we define the trace operator $\gamma _1$ on $\varGamma _1$. Assuming that the tensor $a^\varepsilon _2$ is periodic in the fast variable, i.e., $a^\varepsilon _2(x)= a_2(x, x/\varepsilon )=a_2(x,y)$ is Y-periodic in y, where $Y=(0,1)^d$, explicit equations are available to compute the homogenized tensor $a^0_2$

$$\begin{aligned} a_2^0(x)= \frac{1}{|Y|} \int _{Y}a_2(x,y) \left( I + \nabla \chi \right) \text {d}y, \end{aligned}$$

where $\nabla \chi =(\nabla \chi ^1, \ldots , \nabla \chi ^d)$ and I is the $d\times d$ identity matrix. The functions $\chi ^j\in W_{per}^1(Y)$ are called the first-order correctors and, for $j=1, \ldots ,d$, $\chi ^j$ is solution of the cell problem

$$\begin{aligned} \int _{Y}a_2(x,y) \nabla \chi ^j\cdot \nabla v\text {d}y =-\int _{Y} a_2(x,y)e_j\nabla v\text {d}y, \quad \forall v\in W_{per}^1(Y), \end{aligned}$$

with periodic boundary conditions, and where $(e_i)_{i=1}^d$ denotes the canonical basis of $\mathbb R^d$. Assuming sufficient regularity on $u^0$ and on $\chi ^j$, it can be proved that

$$\begin{aligned} \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\omega _2)} \le C\varepsilon , \end{aligned}$$

(10)

where the constant is independent of $\varepsilon$. For proofs, we refer to [9, 21, 24].

Estimates for the fine solution Let us define an operator $P: \mathcal {U}\rightarrow H^1(\omega _1) \times H^1(\varOmega \setminus \omega _1)$ such that

$$\begin{aligned} P(\mu _1, \mu _2) \mapsto {\left\{ \begin{array}{ll} u_1^{\varepsilon }(\mu _1) \quad \text {in } \omega _1, \\ u_2^0(\mu _2) \quad \text {in } \varOmega \setminus \omega _1. \end{array}\right. } \end{aligned}$$

It can be split into $P=Q + U_0$, where $Q: \mathcal {U}\rightarrow H^1(\omega _1) \times H^1(\varOmega \setminus \omega _1)$ is defined by

$$\begin{aligned} Q(\mu _1, \mu _2) \mapsto {\left\{ \begin{array}{ll} v_1^{\varepsilon }(\mu _1) \quad \text {in } \omega _1, \\ v_2^0(\mu _2) \quad \text {in } \varOmega \setminus \omega _1, \end{array}\right. } \end{aligned}$$

where the state variables $v_1^{\varepsilon }$ and $v_2^0$ are solutions of (4) for $i=1,2$, respectively, and where $U_0$ is given by

$$\begin{aligned} U_0={\left\{ \begin{array}{ll} u_{1,0}^{\varepsilon } \quad \text {in } \omega _1, \\ u_{2,0}^0 \quad \text {in } \varOmega \setminus \omega _1. \end{array}\right. } \end{aligned}$$

For the cost function of case 1, it has been shown in [7] that the operator Q is bounded in the operator norm, i.e.,

$$\begin{aligned} \left\| Q\right\| :=\sup _{(\mu _1, \mu _2)\in \mathcal {U}} \frac{Q(\mu _1, \mu _2)}{\left\| (\mu _1, \mu _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}}\le C. \end{aligned}$$

Here we assume that Q is bounded for the norm in $\mathcal {U}$ induced by the scalar product (6) for the cost function of case 2.

Theorem 2.2

Let $u^\varepsilon$ be solution of (1) and $\bar{u}$ be given by (7). Assume that $u^0$ and $\chi ^j$ are smooth enough for (10) to hold, and that $\left\| Q\right\| \le C$. Then we have

$$\begin{aligned} \left\| u^\varepsilon -\bar{u}\right\| _{\mathrm {H}^{1}(\omega ^+)} \le C \varepsilon , \end{aligned}$$

where the constant C depends on the constant of the Caccioppoli inequality, the bound $\left\| Q\right\|$, and the trace constants associated with the trace operators $\gamma _1$ and $\gamma _2$ on $\varGamma _1$ and $\varGamma _2$, respectively.

To prove Theorem 2.2, we note that the difference $u^\varepsilon -\bar{u}$ is $a^\varepsilon _1$-harmonic in $\omega _1$; thus, Caccioppoli inequality (see Theorem 6.1) can be applied,

$$\begin{aligned} \left\| u^\varepsilon -\bar{u}\right\| _{\mathrm {H}^{1}(\omega ^+)}&\le C\frac{1}{\tau } \left\| u^\varepsilon -\bar{u}\right\| _{\mathrm {L}^{2}(\omega _1)} \nonumber \\&=C\frac{1}{\tau } \left\| P(\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon ))-P(\theta _1, \theta _2)\right\| _{\mathrm {L}^{2}(\omega _1)}\nonumber \\&\le \frac{C}{\tau } \left\| Q\right\| \left\| (\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon ))-(\theta _1, \theta _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}. \end{aligned}$$

(11)

Assuming that $\left\| Q\right\|$ is bounded and using Lemmas 2.3 and 6.2, we can show that $\left\| (\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon ))-(\theta _1, \theta _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}$ is bounded by $C \varepsilon$, which concludes the proof of Theorem 2.2.

Lemma 2.3

Let $u^\varepsilon$ and $u^0$ solve (1) and (9), respectively, and let $(\theta _1, \theta _2)\in \mathcal {U}$ be the optimal virtual controls. Then

$$\begin{aligned} \left\| \big (\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon )\big )-(\theta _1, \theta _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})} \le \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _1 \cup \varGamma _2)}. \end{aligned}$$

Proof

From the definition, it holds

$$\begin{aligned}&\left\| \big (\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon )\big )-(\theta _1, \theta _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})} \\&\quad =\sup _{(\mu _1, \mu _2)\in \mathcal {U}} \frac{|\pi \big ( (\gamma _1(u^\varepsilon ), \gamma _2(u^\varepsilon )), (\mu _1, \mu _2)\big ) - \pi \big ( (\theta _1, \theta _2), (\mu _1, \mu _2)\big )|}{\left\| (\mu _1, \mu _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}}. \end{aligned}$$

We look at the numerator. As the pair $(\theta _1, \theta _2)$ minimizes the cost function J, the Euler–Lagrange formulation (5) holds and

$$\begin{aligned}&\pi \left( \left( \gamma _1\left( u^\varepsilon \right) , \gamma _2\left( u^\varepsilon \right) \right) , (\mu _1, \mu _2)\right) - \pi \left( (\theta _1, \theta _2), (\mu _1, \mu _2)\right) \\&= \int _{\varGamma _1 \cup \varGamma _2}\left( v_1^{\varepsilon }\left( \gamma _1\left( u^\varepsilon \right) \right) - v_2^0\left( \gamma _2\left( u^\varepsilon \right) \right) \right) \left( v_1^{\varepsilon }\left( \mu _1\right) - v_2^0\left( \mu _2\right) \right) \text {d}s\\&\,\quad + \int _{\varGamma _1 \cup \varGamma _2}\left( v_1^{\varepsilon }\left( \mu _1\right) - v_2^0\left( \mu _2\right) \right) \left( u_{1,0}^{\varepsilon }- u_{2,0}^0\right) \text {d}s\\&= \int _{\varGamma _1\cup \varGamma _2}\left( \left( v_1^{\varepsilon }\left( \gamma _1\left( u^\varepsilon \right) \right) + u_{1,0}^{\varepsilon }\right) - \left( v_2^0\left( \gamma _2\left( u^\varepsilon \right) \right) +u_{2,0}^0\right) \right) \left( v_1^{\varepsilon }\left( \mu _1\right) -v_2^0\left( \mu _2\right) \right) \text {d}s\\&= \int _{\varGamma _1 \cup \varGamma _2}\left( u^\varepsilon -u^0\right) \left( v_1^{\varepsilon }\left( \mu _1\right) - v_2^0\left( \mu _2\right) \right) \text {d}s\le \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _1\cup \varGamma _2)} \left\| (\mu _1, \mu _2)\right\| _{\mathrm {L}^{*}(\mathcal {U})}. \end{aligned}$$

The result follows. $\square$

The next lemma gives an upper bound to the norm in Lemma 2.3.

Lemma 2.4

Let $u^\varepsilon$ and $u^0$ be solution of (1) and (9), respectively. Assume that $u^0$ and $\chi ^j$ have enough regularity for (10) to hold. Then

$$\begin{aligned} \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}( \varGamma _1 \cup \varGamma _2)} \le C \varepsilon , \end{aligned}$$

where the constant C is independent of $\varepsilon$.

Proof

It holds

$$\begin{aligned} \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _1\cup \varGamma _2)}\le \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _1)} + \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _2)}. \end{aligned}$$

Using the continuity of the traces, the first term can be bounded by

$$\begin{aligned} \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\varGamma _1)} \le C \left\| u^\varepsilon -u^0\right\| _{\mathrm {L}^{2}(\omega _2)} \le C \varepsilon , \end{aligned}$$

whereas the second term is zero because $u^0|_{\varGamma _2}=\gamma _2(u^\varepsilon )=u^\varepsilon |_{\varGamma _2}$. This prove the result.

$\square$

The proof of Theorem 2.2 follows from (11) and Lemmas 2.3 and 2.4.

Estimates for the coarse solution The a priori error estimates to the coarse-scale solver follow from [7, Theorem 3.6] using Lemma 2.4. We skip the details.

Theorem 2.5

Let $u^\varepsilon$ be solution of (1) and $u_{2}^{rec}(\theta _2)$ be given by (8). Let $a_2(x,y)\in \mathcal {C}(\overline{\omega }_2; L^{\infty }_{per}(Y))$ and $\chi ^j\in W_{\mathrm{per}}(Y)$, $j=1, \ldots , d$. If in addition, $u^\varepsilon \in H^2( \varOmega )$, $u_2^0(\theta _2) \in H^2(\omega _2)$, and $\chi ^j\in W^{1, \infty }(Y)$, $j=1, \ldots , d$, it holds

$$\begin{aligned} \left\| u^\varepsilon -u_{2}^{rec}(\theta _2)\right\| _{\mathrm {H}^{1}(\varOmega \setminus \omega ^+)}\le C \varepsilon ^{1/2}, \end{aligned}$$

where the constant C is independent of $\varepsilon$, but depends on $\tau ,$ $\tau ^+$, and the ellipticity constants of $a^\varepsilon _2$.

3 Fully discrete coupling method

In this section, we describe the fully discrete overlapping coupling method and perform an a priori error analysis. The fine-scale solver requires a triangulation of size $\tilde{h}$ sufficiently small to resolve the multiscale nature of the tensor. In contrast, the coarse-scale solver on $\omega _2$ takes full advantage of the scale separation and allows for a mesh size larger than the fine scale. We use the FEM in $\omega _1$ and the FE-HMM in $\omega _2$. As the finite elements of the fine and coarse meshes in $\omega _0$ are different, an interpolation between the two meshes should be considered. One can also chose to use the same finite elements in the overlap, leading to a discontinuity at $\varGamma _1$ in the mesh over $\omega _2$. In that latter situation, the discontinuous Galerkin FE-HMM [4] should be used instead of the FE-HMM.

In what follows, we consider for simplicity the problem (1) with homogeneous Dirichlet boundary conditions, i.e., we set $g_D=0$ and $\varGamma _N=\emptyset$. Further, we assume that $\varepsilon$ is small enough so that we can use the strong Cauchy–Schwarz lemma (Lemma 6.3) and its discrete version (Lemma 6.5) hold.

Numerical method for the fine-scale problem

Let $\mathcal {T}_{\tilde{h}}$ be a partition of $\omega _1$, in simplicial or quadrilateral elements, with mesh size $\tilde{h}\ll \varepsilon$ where $\tilde{h}=\max _{K\in \mathcal {T}_{\tilde{h}}} h_K,$ and $h_K$ is the diameter of the element K. In addition, we suppose that the family of partitions $\{\mathcal {T}_{\tilde{h}}\}$ is admissible and shape regular [11], i.e.,

• (T1) admissible: $\overline{\omega }_1=\cup _{K\in \mathcal {T}_h} K$ and the intersection of two elements is either empty, a vertex, or a common face;

• (T2) shape regular: there exists $\sigma >0$ such that $h_K/ \rho _K\le \sigma$, for all $K\in \mathcal {T}_{\tilde{h}}$ and for all $\mathcal {T}_{\tilde{h}}\in \{\mathcal {T}_{\tilde{h}}\}$, where $\rho _K$ is the diameter of the largest circle contained in the element K.

For each partition $\mathcal {T}_{\tilde{h}}$ of the family $\{\mathcal {T}_{\tilde{h}}\}$, we define a FE space in $\omega _1$

$$\begin{aligned} V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})=\left\{ w\in H^1_D(\omega _1)\mid w_{|_K}\in \mathcal {R}^{p}(K), \forall K\in \mathcal {T}_{\tilde{h}}\right\} , \end{aligned}$$

where $\mathcal {R}^p$ is the space $\mathcal {P}^p$ of polynomials of degree at most p on K if K is a triangle, and the space $\mathcal {Q}^p$ of polynomials of degree at most p in each variable if K is a rectangle. Further, $V_{0}^p(\omega _1, \mathcal {T}_{\tilde{h}})$ denotes the space of functions in $V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})$ that vanish on $\partial \omega _1$.

Let $u_{1,\tilde{h}}$ be the numerical approximation of $u_1^{\varepsilon }$ satisfying problem (3) for $i=1$. We can split $u_{1,\tilde{h}}$ into $u_{1,\tilde{h}} =u_{1,0,\tilde{h}} + v_{1,\tilde{h}}$, where $v_{1,\tilde{h}}\in V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})$ is obtained by the optimization method and $u_{1,0,\tilde{h}} \in V^p_{0}(\omega _1, \mathcal {T}_{\tilde{h}})$ satisfies

$$\begin{aligned} B_1(u_{1,0,\tilde{h}} , w_{1,\tilde{h}})=\int _{\omega _1}a_1\nabla u_{1,0,\tilde{h}} \cdot \nabla w_{1,\tilde{h}}\text {d}x= F_1(w_{1,\tilde{h}}), \forall w_{1,\tilde{h}}\in V^p_{0}(\omega _1, \mathcal {T}_{\tilde{h}}), \end{aligned}$$

where $F_1$ is given by

$$\begin{aligned} F_1(w_{1,\tilde{h}})=\int _{\omega _1}f w_{1,\tilde{h}}\text {d}x. \end{aligned}$$

Thanks to the Poincaré inequality, the coercivity and boundedness of the bilinear form $B_1$ can be proved; the existence and uniqueness of $u_{1,0,\tilde{h}}$ follow.

Numerical method for the coarse-scale problem

Let $\{\mathcal {T}_H\}$ be a family of admissible (T1) and shape regular (T2) partitions of $\omega _2$, with mesh size $H=\max _{K\in \mathcal {T}_H} h_K$. For each partition $\mathcal {T}_H$ of the family $\{\mathcal {T}_H\}$, we define a FE space over $\omega _2$

$$\begin{aligned} V^p_D(\omega _2, \mathcal {T}_H)=\left\{ v\in H^1_D(\omega _2)\mid w_{|_K}\in \mathcal {R}^{p}(K), \forall K\in \mathcal {T}_H\right\} , \end{aligned}$$

and use $V_{0}^p(\omega _2, \mathcal {T}_H)$ to denote the set of functions of $V^p_D(\omega _2, \mathcal {T}_H)$ that vanish over $\partial \omega _2$.

Quadrature formula A macroscopic quadrature formula is given by the pair $\{x_{j,K}, \omega _{j,K}\}$ of quadrature nodes $x_{j,K}$ and weights $\omega _{j,K}$, for $j=1, \ldots , J$. The sampling domain of size $\delta$ around each quadrature point is denoted by $K_{\delta _j}= x_{j,K} + \delta [-1/2, 1/2]^d$. We assume that the quadrature formula verifies the necessary assumptions to guarantee that the standard error estimates for a FEM hold [11].

The numerically homogenized tensor $a^{0,h}_2(x_{j,K})$ is obtained using numerical solutions of micro-problems defined in $K_{\delta _j}$. In each sampling domain, we consider a mesh $\mathcal {T}_h$ in simplicial or quadrilateral elements K with mesh size $h=\max _{K\in \mathcal {T}_h} h_K$ satisfying $h<\varepsilon$. The micro-FE space is

$$\begin{aligned} S^q(K_{\delta _j}, \mathcal {T}_h)=\left\{ w^h\in W(K_{\delta _j}) \mid w^h_{|_K} \in \mathcal {R}^q(K), \forall K\in \mathcal {T}_h\right\} , \end{aligned}$$

where the space $W(K_{\delta _j})$ depends on the boundary conditions in the micro-problems; $W(K_{\delta _j})= H^1_0(K_{\delta _j})$ for Dirichlet coupling, or $W(K_{\delta _j})=W_{\mathrm{per}}^1(K_{\delta _j})$ for periodic coupling. The discrete micro-problems read: find $\psi ^{i,h}_{K_{\delta _j}}\in S^q(K_{\delta _j}, \mathcal {T}_h)$, $i=1, \ldots , d$, solution of

$$\begin{aligned} \int _{K_{\delta _j}}a^\varepsilon _2(x) \nabla \psi ^{i,h}_{K_{\delta _j}}\cdot \nabla w^h_j\text {d}x= -\int _{K_{\delta _j}}a^\varepsilon _2(x) e_i \nabla w^h_j\text {d}x, \forall w^h_j\in S^1(K_{\delta _j}, \mathcal {T}_h). \end{aligned}$$

(12)

The numerically homogenized tensor can be computed by

$$\begin{aligned} {a_2^{0,h}}(x_{j,K})= \frac{1}{|K_{\delta _j}|}\int _{K_{\delta _j}}a^\varepsilon _2(x)\left( I + \nabla \psi _{K_{\delta _j}}^h\right) \text {d}x, \end{aligned}$$

where $\nabla \psi ^{h}_{K_{\delta _j}}=(\nabla \psi _{K_{\delta _j}}^{1,h}, \ldots , \nabla \psi ^{d,h}_{K_{\delta _j}})$. We define a macro-bilinear form $B_{2,H}(\cdot , \cdot )$ over $V^p_D(\omega _2, \mathcal {T}_H)\times V^p_D(\omega _2, \mathcal {T}_H)$,

$$\begin{aligned} \begin{array}{r l} \displaystyle B_{2,H}(v_{2, H}, w_{ 2,H})&\displaystyle = \sum _{K\in \mathcal {T}_H}\sum _{j=1}^J\omega _{j,K}a_2^{0,h}(x_{j,K})\nabla v_{2, H}(x_{j,K}) \cdot \nabla w_{ 2,H}(x_{j,K}). \end{array} \end{aligned}$$

The numerical homogenized solution $u_{2,H}$ is split into $u_{2,H}= u_{2,0,H}+ v_{2, H}$, where $v_{2, H}\in V^p_{D}(\omega _2, \mathcal {T}_H)$ is given by the coupling and $u_{2,0,H}\in V^p_{0}(\omega _2, \mathcal {T}_H)$ is the solution of

$$\begin{aligned} B_{2, H}(u_{2,0,H}, w_{ 2,H})=F_2(w_{ 2,H}), \forall w_{ 2,H}\in V^p_{0}(\omega _2, \mathcal {T}_H), \end{aligned}$$

with $F_2$ given by

$$\begin{aligned} F_2(w_{ 2,H})=\int _{\omega _2}f w_{ 2,H}\text {d}x. \end{aligned}$$

Numerical algorithm

In this section, we state the discrete coupling and give the main convergence results. The well posedness and the proofs of the errors estimates are done in details in [7]. In what follows, we use $\mathcal {O}$ to denote either $\omega _0$ or $\varGamma _1\cup \varGamma _2$.

The solution $(u_{1,\tilde{h}} , u_{2,H})\in V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})\times V^p_{D}(\omega _2, \mathcal {T}_H)$ satisfies

$$\begin{aligned} \min _{\mu _{1, \tilde{h}}, \mu _{2,H}} \frac{1}{2}\left\| u_{1,\tilde{h}} (\mu _{1, \tilde{h}})-u_{2,H}(\mu _{2,H})\right\| _{\mathrm {L}^{2}(\mathcal {O})}^2 \text { subject to } {\left\{ \begin{array}{ll} B_1(u_{1,\tilde{h}} , w_{1,\tilde{h}}) = F_1(w_{1,\tilde{h}}), \\ B_{2, H}(u_{2,H}, w_{ 2,H})= F_2(w_{ 2,H}), \end{array}\right. } \end{aligned}$$

for all $w_{1,\tilde{h}}\in V^p_{0}(\omega _1, \mathcal {T}_{\tilde{h}})$ and $w_{ 2,H}\in V_{0}^p(\omega _2, \mathcal {T}_H)$. We introduce discrete Lagrange multipliers for each of the constraints and obtain a discrete optimality system: find $(v_{1,\tilde{h}}, \lambda _{1,\tilde{h}}, v_{2, H}, \lambda _{2,H})\in V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})\times V_0^p(\omega _1, \mathcal {T}_{\tilde{h}})\times V_{D}^p(\omega _2, \mathcal {T}_H)\times V_{0}^p(\omega _2, \mathcal {T}_H)$ satisfying

$$\begin{aligned} \int _{\mathcal {O}}( v_{1,\tilde{h}}-v_{2, H})w_{1,\tilde{h}}\text {d}x - B_1(w_{1,\tilde{h}}, \lambda _{1,\tilde{h}})&= -\int _{\mathcal {O} }(u_{1,0,\tilde{h}} -u_{2,0,H}) w_{1,\tilde{h}}\text {d}x,\end{aligned}$$

(13)

$$\begin{aligned} B_1(v_{1,\tilde{h}}, \xi _{1,\tilde{h}})&= F_1(\xi _{1,\tilde{h}}) - B_1(u_{1,0,\tilde{h}} , \xi _{1,\tilde{h}}), \end{aligned}$$

(14)

$$\begin{aligned} \int _{\mathcal {O}}(v_{2, H}-v_{1,\tilde{h}}) w_{ 2,H}\text {d}x - B_{2, H}(w_{ 2,H}, \lambda _{2,H})&= \int _{\mathcal {O}}( u_{1,0,\tilde{h}} - u_{2,0,H}) w_{ 2,H}\text {d}x, \end{aligned}$$

(15)

$$\begin{aligned} B_{2, H}(v_{2, H}, \xi _{ 2,H})&= F_2(\xi _{ 2,H}) - B_{2, H}(u_{2,0,H}, \xi _{ 2,H}), \end{aligned}$$

(16)

for all $w_{1,\tilde{h}}\in V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})$, $\xi _{1,\tilde{h}}\in V_{0}^p(\omega _1, \mathcal {T}_{\tilde{h}})$, $w_{ 2,H}\in V_{D}^p(\omega _2, \mathcal {T}_H)$, and $\xi _{ 2,H}\in V_{0}^p(\omega _2, \mathcal {T}_H)$.

The optimality system (13)–(16) can be written in matrix form as

$$\begin{aligned} \begin{pmatrix} M &{}\quad -B^{\top } \\ B &{}\quad 0 \end{pmatrix}U = G, \end{aligned}$$

(17)

where the unknown vector U is given by $U=(v_{1,\tilde{h}}, v_{2, H}, \lambda _{1,\tilde{h}}, \lambda _{2,H})^{\top }$, and

$$\begin{aligned} M(\{v_{1, \tilde{h}}, v_{2,H}\},\{w_{1, \tilde{h}}, w_{2,H}\} )&=\begin{pmatrix} \int _{\mathcal {O}}v_{1,\tilde{h}} w_{1, \tilde{h}}\text {d}x &{}\quad -\int _{\mathcal {O}}v_{2,H} w_{1, \tilde{h}}\text {d}x\\ -\int _{\mathcal {O}}v_{1, \tilde{h}} w_{2,H}\text {d}x &{}\quad \int _{\mathcal {O}}v_{2,H} w_{2,H}\text {d}x \end{pmatrix},\\ B(\{v_{1, \tilde{h}}, v_{2,H}\}, \{\lambda _{1, \tilde{h}}, \lambda _{2,H}\})&=\begin{pmatrix} B_1(v_{1, \tilde{h}}, \lambda _{1, \tilde{h}}) &{}\quad 0 \\ 0&{}\quad B_{2,H}(v_{2,H}, \lambda _{2,H}) \end{pmatrix}. \end{aligned}$$

Fully discrete error estimates The coupling solution, denoted by $\bar{u}_{{\tilde{h}H}}$, is defined as

$$\begin{aligned} \bar{u}_{{\tilde{h}H}}= {\left\{ \begin{array}{ll} u_{1,\tilde{h}} (\theta _{1,\tilde{h}}) &{}\text { in } \omega ^+, \\ u_{2,H}^{rec}(\theta _{2,H}) &{}\text { in } \varOmega \setminus \omega ^+, \end{array}\right. } \end{aligned}$$

(18)

where $u_{2,H}^{rec}(\theta _{2,H})$ is a fine-scale approximation obtained from the coarse-scale solution $u_{2,H}(\theta _{2,H})$ using a post-processing procedure in the following way. We assume that the tensor $a^\varepsilon _2$ is Y-periodic in y, and we restrict the FE spaces to piecewise FE spaces. Periodic coupling is then used with sampling domains $K_{\varepsilon }$ of size $\varepsilon$. The reconstructed solution $u_{2,H}^{rec}(\theta _{2,H})$ is given by

$$\begin{aligned} u_{2,H}^{rec}(x)= u_{2,H}(x) + \sum _{j=1}^d \psi ^{j,h}_{K_{\varepsilon }}(x) \frac{\partial u_{2,H}}{\partial x_j}(x), x \in K, \end{aligned}$$

where $\psi ^{j,h}_{K_{\varepsilon }}$ are the micro-solutions of (12) in the sampling domain $K_{\varepsilon }$. As the numerical solutions might be discontinuous in $\omega _2$, we consider a broken $H^1$ semi-norm,

$$\begin{aligned} \left\| v\right\| _{{\bar{\mathrm {H}}}^{1}(\varOmega )}^2:= \sum _{K\in \mathcal {T}_h(\omega ^+)} \left\| \nabla v\right\| _{\mathrm {L}^{2}(K)}^2 + \sum _{K\in \mathcal {T}_H(\varOmega \setminus \omega ^+)} \left\| \nabla v\right\| _{\mathrm {L}^{2}(K)}^2. \end{aligned}$$

We next state our main convergence result for the optimization-based numerical solution. Let $u^H\in V^1_0(\omega _2, \mathcal {T}_H)$ be the FE-HMM approximation of the homogenized solution $u^0$.

Theorem 3.1

(A priori error analysis in $\omega ^+$) Let $\varepsilon _0$ be given by the strong Cauchy–Schwarz lemma, Lemma 6.3, and consider $\varepsilon \le \varepsilon _0$. Let $u^\varepsilon$ and $u^0$ be the exact solutions of problems (1) and (9), respectively, and $\bar{u}_{{\tilde{h}H}}$ be the numerical solution of the coupling (18). Further, let $u^H\in V^1_0(\omega _2, \mathcal {T}_H)$ be the FE-HMM approximation of $u^0$. Assume $u^\varepsilon \in H^{s+1}(\varOmega )$, with $s\le 1$, $u^0\in H^2(\omega _2)$, and assume that (10) holds, then

$$\begin{aligned} \left\| u^\varepsilon -u_{1, \tilde{h}}(\theta _{1,\tilde{h}})\right\| _{{\bar{\mathrm {H}}}^{1}(\omega ^+)}\le & {} C_1 \tilde{h}^s|u^\varepsilon |_{H^{s+1}(\omega _1)} \\&+ \,\frac{C_2}{\tau -\tau ^+} \left( \tilde{h}^{s+1}|u^\varepsilon |_{H^{s+1}(\omega _1)} + \varepsilon + e_{HMM, L^2}\right) , \end{aligned}$$

where the constants are independent of $\varepsilon$, H, $\tilde{h}$, and h, and where the HMM error $e_{HMM,L^2}$ is given by $e_{HMM,L^2}=\left\| u^0-u^H\right\| _{\mathrm {L}^{2}(\omega _2)}$.

Proof

It follows the lines of [7, Theorem 4.3], using a continuous macro-FEM (FE-HMM) instead of a discontinuous Galerkin FEM (DG-FE-HMM). $\square$

The analysis of the error $e_{HMM, L^2}$ is by now standard for the FE-HMM. One decompose the error into [2]

$$\begin{aligned} e_{HMM, L^2}=\left\| u^0-u^H\right\| _{\mathrm {L}^{2}(\omega _2)}\le & {} \underbrace{\left\| u^0-u^0_H\right\| _{\mathrm {L}^{2}(\omega _2)}}_{e_{MAC}} + \underbrace{\left\| u^0_H-\bar{u}^H\right\| _{\mathrm {H}^{1}(\omega _2)}}_{e_\mathrm{MOD}} \\&+\, \underbrace{\left\| \bar{u}^H-u^H\right\| _{\mathrm {H}^{1}(\omega _2)}}_{e_{MIC}}, \end{aligned}$$

where $u^0_H$ is a FEM approximation of $u^0$ with numerical quadrature and $\bar{u}^H$ is a semi-discrete FE-HMM approximation of $u^0$, where the micro-functions are in the exact Sobolev space $W(K_{\delta })$. Under suitable regularity assumption [12], we have

$$\begin{aligned} e_{MAC}\le CH^2, \end{aligned}$$

where the constant C is independent of $\varepsilon$, $\tilde{h}$, H, and h.

Next, following [1, 2] we can bound the micro- and modeling errors. If we assume the following regularity on $\psi _{K_{\varepsilon }}^{i}\in W(K_{\delta })$, the non-discretized micro-solutions of problem (12),

$$\begin{aligned} \left| \psi _{K_{\delta }}^{i}\right| _{H^{2}(K_{\delta })}\le C \varepsilon ^{-1}\sqrt{|K_{\delta }|} \quad \hbox {for }i=1, \ldots , d, \end{aligned}$$

we obtain a bound on the micro-error

$$\begin{aligned} e_{MIC}\le C \left( \frac{h}{\varepsilon }\right) ^{2}, \end{aligned}$$

where the constant C is independent of $\varepsilon$, $\tilde{h}$, H, and h (we recall that for the reconstruction we use periodic boundary conditions in the micro-problems (12) over sampling domains are of size $\delta =\varepsilon$). If we collocate (i.e., freeze) the slow variable x to the quadrature point $x_{K}$ in the tensor $a^\varepsilon _2$, i.e., we consider $a^\varepsilon _2(x_{K}, x/\varepsilon )$ in the macro- and micro-bilinear forms, we obtain an optimal modeling error

$$\begin{aligned} e_\mathrm{MOD}= 0\quad \text {with }S^1(K_{\delta }, \mathcal {T}_h)\subset W^1_{per}(K_{\delta }), \end{aligned}$$

assuming that $\delta /\varepsilon \in \mathbb {N}_{>0}$. Without collocation, the modeling error becomes

$$\begin{aligned} e_\mathrm{MOD}= C\varepsilon , \end{aligned}$$

where the constant C is independent of $\varepsilon$, $\tilde{h}$, H, and h.

Remark 3.2

When $\delta /\varepsilon \notin \mathbb {N}$ and $\delta >\varepsilon$, Dirichlet boundary conditions are used instead of the periodic conditions in the micro-problems (12), and the modeling error becomes

$$\begin{aligned} e_\mathrm{MOD}={\left\{ \begin{array}{ll} C_1\frac{\varepsilon }{\delta },&{} \text { with collocation and } S^1(K_{\delta }, \mathcal {T}_h)\subset H^1_0(K_{\delta }),\\ C_2\left( \delta + \frac{\varepsilon }{\delta }\right) , &{}\text { without collocation and } S^1(K_{\delta }, \mathcal {T}_h)\subset H^1_0(K_{\delta }),\\ \end{array}\right. } \end{aligned}$$

where the constants are independent of $\varepsilon$,$\delta$, $\tilde{h}$, H, and h.

Remark 3.3

Higher-order FE macro- and micro-spaces can also be considered, and we refer to [2, 3] for details.

Next, we state an error estimates in the coarse-scale region for the optimization-based numerical solution with correctors.

Theorem 3.4

(Error estimates in $\varOmega {\setminus }\omega ^+$) Let $u^\varepsilon$ be the exact solution of problem (1) and $\bar{u}_{{\tilde{h}H}}$ be the numerical solution of the coupling (18). Let $a^\varepsilon _2(x)=a_2(x,x/\varepsilon )$, where $a_2(x,y)$ is Y-periodic in y and satisfies $a_2(x,y)\in \mathcal {C}(\overline{\omega }_2; L^{\infty }_{per}(Y))$. Let $\psi ^j_{K_{\varepsilon }}(x)\in W_{\mathrm{per}}^1(K_{\varepsilon })$, $j=1, \ldots , d$. If in addition, $u^\varepsilon \in H^2( \varOmega )$, $u_2^0(\theta _2) \in H^2(\omega _2)$, $u_1^{\varepsilon } \in H^{s+1}(\omega _1)$, with $s\le 1$, and $\psi ^j_{K_{\varepsilon }}(x)\in W^{1, \infty }(K_{\varepsilon })$, $j=1, \ldots , d$. It holds,

$$\begin{aligned} \left\| u_{2}^{rec}(\theta _2)-u_{2,H}^{rec}(\theta _2^H)\right\| _{{\bar{\mathrm {H}}}^{1}(\varOmega \setminus \omega ^+)}&\le C_1\varepsilon ^{1/2} + C_2\left( \frac{h}{\varepsilon }\right) +C_3H |u^0_2|_{H^2(\omega _2)} \\&\quad + \frac{C_4}{\tau ^+} \left( \tilde{h}^{s+1}|u_1^{\varepsilon }|_{H^{s+1}(\omega _1)} + \varepsilon + H^2 |u_2^0|_{H^2(\omega _2)}\right) . \end{aligned}$$

where the constants are independent of $H, \tilde{h}, h,$ and $\varepsilon$.

Proof

It follows the lines of [7, Theorem 4.4], where DG-FE-HMM is replaced by FE-HMM. $\square$

Remark 3.5

We note that the above theorem is also valid when using discontinuous Galerkin macro-solver (i.e., the DG-FE-HMM [4]). This has been studied in [7] for the cost function of case case 1. A similar proof applies for the cost function of case 2.

4 Numerical experiments

In this section, we give three numerical experiments that can be seen as a complement of the ones carried in [7], where we focused on a minimization in $L^2(\omega _0)$, with interior subdomains and matching grids in the overlap $\omega _0$. In the first experiment, we still consider the minimization over $L^2(\omega _0)$ and compare matching and non-matching meshes. The second experiment illustrates the coupling with the cost function of case 2 over $\varGamma _1 \cup \varGamma _2$ and comparisons with the cost function of case 1 over $\omega _0$. In the last example, we combine non-matching grids and a minimization over the boundary. We observe several order of magnitude of saving in computational cost when compared to the method proposed in [7]. In the experiments, we will use a tensor $a^\varepsilon$ which is highly heterogeneous non-periodic and oscillate at several non-separated scales in $\omega$, and which has scale separation in $\omega _2$, with a locally periodic structure.

Comparison of matching and non-matching grids on the overlap

Experiment 1

For this experiment, we use the cost function of case 1

$$\begin{aligned} J(\mu _1, \mu _2)=\frac{1}{2}\left\| u_1^{\varepsilon }(\mu _1)-u_2^0(\mu _2)\right\| _{\mathrm {L}^{2}(\omega _0)}^2. \end{aligned}$$

Using FEM and FE-HMM in $\omega _1$ and $\omega _2$, respectively, leads to two main restrictions: the mesh size in $\omega _1$ should be smaller than the fine scale, whereas the mesh size in $\omega _2$ can be larger than the fine scales, in order to take full advantage of the FE-HMM. Since both methods are defined in $\omega _0$, we can chose to have the same FE in both meshes on the overlap, or one can impose two different meshes. With the first choice, no interpolations must be considered between $\mathcal {T}_{\tilde{h}}$ and $\mathcal {T}_H$ over $\omega _0$, but $\mathcal {T}_H$ is composed of FE with mesh size as small as the fine scales. In that situation, DG-FE-HMM is chosen instead of FE-HMM due to the discontinuity at the interface $\varGamma _1$. The second choice requires interpolation between the meshes in $\omega _0$, but $\mathcal {T}_H$ is not restricted by the size of the fine mesh $\mathcal {T}_{\tilde{h}}$. We show that both cases give similar convergence rates, but the computational cost is significantly reduced in the second case.

Let us consider a Dirichlet elliptic boundary value in $\varOmega =[0,1]^2$,

$$\begin{aligned} \begin{array}{rll} -\mathrm{{div\,}}(a^\varepsilon \nabla u^\varepsilon )&{}=f\quad \text {in } \varOmega ,\\ u&{}=0\quad \text {on } \partial \varOmega , \end{array} \end{aligned}$$

with $f\equiv 1$ and $a^\varepsilon$ is given by

$$\begin{aligned} a^\varepsilon _2(x_1, x_2)&=\frac{1}{6}\bigg ( \frac{1.1 + \sin (2\pi (x_1/\varepsilon )( x_2/\varepsilon ))}{1.1 + \sin (2\pi x_2/\varepsilon )} + \sin (4x_1^2x_2^2) +2\bigg )I_2, \\ a_{\omega }(x_1, x_2)&= 3 + \frac{1}{7} \sum _{j=0}^{4}\sum _{i=0} ^j \frac{2}{j+1} \cos \left( \lfloor 8\left( ix_2-x_1/(i+1)\right) \rfloor + \lfloor 150ix_1\rfloor + \lfloor 150x_2\rfloor \right) . \end{aligned}$$

Let $x_c$ be the center of $\varOmega$, we consider $\omega _1=x_c + [-1/4, 1/4]I_2$ and $\omega =x_c+ [-1/8, 1/8]I_2$. Let $H=1/8$, $\varepsilon =1/10$, and a micro-mesh size $h=\varepsilon /L$, so that the micro-error is negligible. We initialize the fine mesh to $\tilde{h}=1/16$. We use uniform simplicial meshes in $\omega _1$ and $\omega _2$ and assume that $\mathcal {T}_{\tilde{h}}$ is obtained from $\mathcal {T}_H$ using a uniform refinement in $\omega _0$. This allows simplification in the interpolation between the two meshes in the overlap. We couple the FEM over $\omega _1$ with the mesh $\mathcal {T}_{\tilde{h}}(\omega _1)$ with the FE-HMM over $\omega _2$ with mesh $\mathcal {T}_H(\omega _2)$ and compare it with a coupling between FEM over $\mathcal {T}_{\tilde{h}}(\omega _1)$ with DG-FE-HMM over a mesh composed of coarse FE from $\mathcal {T}_H(\omega _2\setminus \omega _0)$ with small FE from the fine mesh $\mathcal {T}_{\tilde{h}}(\omega _0)$. The reference fine-scale solution is computed on a very fine mesh, and we compare the two numerical solutions with the reference one. After three iterations, we plot the numerical approximations of the fine-scale solution $u_1^{\varepsilon }$ and coarse-scale solution $u_2^0$ (in transparent), for a coupling with minimization of the cost function of case 1 with non-matching grid (Fig. 2a) and with matching grids (Fig. 2b). A zoom of the coarse-scale solutions in the overlap region $\omega _0$ is shown in Fig. 2c for the coupling with non-matching grids and in Fig. 2d with matching grids, where the coupling is performed with the cost function of case 1 (as the fine meshes become too dense after three iterations, we plot for the zoom the solution after one iteration to better visualize the difference in the meshes).

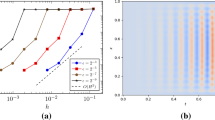
We refine either only in $\omega _1$ for the fine-scale solver (non-matching grids) or in addition in $\omega _0$ for the coarse-scale solver (matching grids). We set $\delta =\varepsilon$ for the sampling domains and consider a micro-mesh size $h=\varepsilon /L$, so that the micro-error is negligible. Figure 3a shows the $H^1$ norm in $\omega$ with non-matching grids (bullet) and with matching grids (diamond); we see that the errors are similar. We also measured the times, using MATLAB timer, to compute the numerical solutions. We see in Fig. 3b that using non-matching grids is faster as the number of micro-problems that have to be computed with the coarse solver, is smaller and fixed, whereas it increases when matching grids are used, causing a significant time overhead.

Fig. 2

Experiment 1: numerical solutions of the coupling with minimization of the cost function of case 1 using non-matching grids (a) and matching grids (b), zoom in $\omega _0$ of the coarse-scale solution with the cost function of case 1 and non-matching grids (c) and with matching grids (d)

Fig. 3

Experiment 1: a $H^1$ norm in $\omega$ with minimization of the cost function of case 1 using non-matching grids (bullet) and matching grids (diamond), b CPU time with the cost function of case 1 using non-matching grids (bullet) and matching grids (diamond)

The rate of convergence in $\omega$ is influenced by H and $\varepsilon$, and when $\tilde{h}$ is refined, we expect a saturation, depending on H and $\varepsilon$, in the convergence. Let $\varepsilon =1/20$ and initialize the fine mesh to $\tilde{h}=1/64$. We set $H=1/8, 1/16$, and 1 / 32 and refine $\tilde{h}$ in each iteration. In Fig. 4, we plot the $H^1$ norm between the reference and numerical solutions w.r.t the mesh size in $\omega$. We see indeed that the error saturates at a threshold value that depends on H.

Fig. 4

Experiment 1: $H^1$ norm between the reference and numerical solution using non-matching grids and cost function of case 1 for different macro-mesh size $H=1/8$ (dashes), $H=1/16$ (dash-dots), and $H=1/32$ (full)

Minimization with interface control

For this experiment, we compare the coupling done with the cost function of case 1 and of case 2 on an elliptic problem with $\omega \subseteq \varOmega$, i.e., when the boundaries of $\omega$ and $\varOmega$ intersect (see Fig. 1, right picture).

Experiment 2

Let us consider a Dirichlet elliptic boundary value in $\varOmega =[0,1]^2$,

$$\begin{aligned} \begin{array}{rll} -\mathrm{{div\,}}(a^\varepsilon \nabla u^\varepsilon )&{}=f \quad \text {in } \varOmega ,\\ u&{}=0 \quad \text {on } \partial \varOmega , \end{array} \end{aligned}$$

with $f\equiv 1$ and $a^\varepsilon$—plotted in Fig. 5b—is given by

$$\begin{aligned} a^\varepsilon _2(x_1, x_2)&=(\cos (2\pi x_1/\varepsilon ) + 2)I_2, \\ a_{\omega }(x_1, x_2)&= 3 + \frac{1}{7} \sum _{j=0}^{4}\sum _{i=0} ^j \frac{2}{j+1} \cos \left( \lfloor 8\left( ix_2-x_1/(i+1)\right) \rfloor + \lfloor 150ix_1\rfloor + \lfloor 150x_2\rfloor \right) . \end{aligned}$$

The tensor $a^\varepsilon$ in $\omega _2$ has scale separation and is Y-periodic in the fast variable, and the homogeneous tensor $a^0_2$ can be explicitly derived as

$$\begin{aligned} a_2^0(x)= \begin{pmatrix} \left( \int _{0}^1 \frac{1}{a(y_1)}\text {d}y_1\right) ^{-1} &{}\quad 0 \\ 0 &{}\quad 2 \end{pmatrix}. \end{aligned}$$

Let $\omega _1=[0,1/2]\times y$ and $\omega =[0,1/4]\times y$, with $y\in [0,1]$. An illustration of a numerical solution is given in Fig. 6a. At first, we consider the cost of case 1,

$$\begin{aligned} J(\mu _1, \mu _2)=\frac{1}{2}\left\| u_1^{\varepsilon }(\mu _1)-u_2^0(\mu _2)\right\| _{\mathrm {L}^{2}(\omega _0)}^2. \end{aligned}$$

Let $\varepsilon =1/50$, and $h/\varepsilon =1/L$ be small enough to neglect the micro-error. We initialize the fine mesh to $\tilde{h}=1/128$. For different macro-mesh sizes $H=1/8, 1/16, 1/32$ and 1 / 64, we refine $\tilde{h}$ and monitor the convergence rates between the numerical solution of the coupling and the reference solution. In Fig. 5a, the $H^1$ norm is displayed for $H=1/8$ (dots), $H=1/16$ (dashes-dots), $H=1/32$ (dashes) and $H=1/64$ (full lines). One can see that the error saturates at a value depending on the macro-mesh size H.

Fig. 5

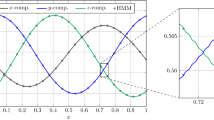
Experiment 2: a $H^1$ errors between the numerical and the reference solutions in $\omega$ using matching grids and the cost function of case 1 with different macro-mesh size $H=1/8$ (stars), $H=1/16$ (diamonds), $H=1/32$ (bullets), and $H=1/64$ (plus), b tensor $a^\varepsilon$ over $\varOmega$ for $\varepsilon =1/10$

Fig. 6

Experiment 2: numerical solutions using matching grids and the cost function of case 1 (a) and of case 2 (b), c $H^1$ error between the numerical and reference solutions in $\omega$ using matching grids and the cost function of case 1 (diamond) and the cost function of case 2 (bullet), d $L^2$ error between the numerical and reference solutions in $\omega$, using matching grids and the cost function of case 1 (diamond) and the cost function of case 2 (bullet)

Now, we compare the costs of case 1 over $\omega _0$ with the cost of case 2 over $\varGamma _1 \cup \varGamma _2$. We fix $\varepsilon =1/10$, $H=1/16$, and $h=\varepsilon /L$ small enough in order to neglect the micro-error. We initialize the fine mesh to $\tilde{h}=1/32$ and refine the mesh only in $\omega _1$. The numerical approximations of $u_1^{\varepsilon }$ and $u_2^0$ are shown in Fig. 6a, for the cost of case 1 over $\omega _0$, and in Fig. 6b, for the cost of case 2 over $\varGamma _1 \cup \varGamma _2$. The $H^1$ and $L^2$ errors between $u^H$ and a reference solution in $\omega _0$ are shown in Fig. 6c, d, respectively. Computational times are compared as well in Fig. 7, for the cost over $\omega _0$ (diamonds) and the cost over $\varGamma _1\cup \varGamma _2$ (bullets). As the number of degrees of freedom of the saddle point problem (17) is reduced when minimizing over the boundaries $\varGamma _1\cup \varGamma _2$, we see that the coupling over $\omega _0$ is more costly than the coupling over $\varGamma _1 \cup \varGamma _2$. Considering an interpolation between the two meshes in the interface $\omega _0$ gives similar results as, due to the periodicity of $a^\varepsilon _2$, we need only to resolve one cell problem to compute the homogenized tensor $a^0_2$.

Fig. 7

Experiment 2: CPU time using matching grids with the cost function of case 1 (diamond) and the cost function of case 2 (bullet)

We next vary the size of the overlap $\omega _0$ and consider $\omega _1=[0,1/4+mH]\times y$, for $m=1,4,8$, where $H=1/32$ is the coarse mesh size, and initialize $\tilde{h}=1/64$. We minimize over the overlap $\omega _0$. We observe that both couplings are influenced by the size of $\tau =\text {dist}(\varGamma _1 \cup \varGamma _2)$ and this is shown in the $H^1$ errors in Fig. 8. The rates deteriorate when $\tau$ goes to zero.

Fig. 8

Experiment 2: $H^1$ errors between the numerical and reference solutions in $\omega$ with matching grids and the cost function of case 1 (diamond) and the cost function of case 2 (bullet) for $\tau =9/32$ (dots), $\tau =10/32$ (dash-dots), and $\tau =1/2$ (full)

Minimization with interface control on non-matching grids

For the last experiment, we combine the two previous effects. The fastest coupling is obtained by performing by considering the minimization with of the cost of case 2 with interpolation of the two meshes in the overlap, whereas the slowest coupling is obtained by the minimization with the cost function of case 1 using identical meshes in the overlap.

Experiment 3

We consider a Dirichlet elliptic boundary value in $\varOmega =[0,1]^2$,

$$\begin{aligned} \begin{array}{rll} -\mathrm{{div\,}}(a^\varepsilon \nabla u^\varepsilon )&{}=f \quad \text {in } \varOmega ,\\ u&{}=0 \quad \text {on } \partial \varOmega , \end{array} \end{aligned}$$

with $f\equiv 1$ and $a^\varepsilon$ is given by

$$\begin{aligned} a^\varepsilon _2(x_1, x_2)&=\frac{1}{6}\bigg ( \frac{1.1 + \sin (2\pi (x_1/\varepsilon )( x_2/\varepsilon ))}{1.1 + \sin (2\pi x_2/\varepsilon )} + \sin (4x_1^2x_2^2) +2\bigg )I_2, \\ a_{\omega }(x_1, x_2)&= 3 + \frac{1}{7} \sum _{j=0}^{4}\sum _{i=0} ^j \frac{2}{j+1} \cos \left( \lfloor 8\left( ix_2-x_1/(i+1)\right) \rfloor + \lfloor 150ix_1\rfloor + \lfloor 150x_2\rfloor \right) . \end{aligned}$$

We set $H=1/16$ and $\varepsilon =1/10$. We initialize $\tilde{h}=1/32$. In Fig. 9a, we see the $H^1$ error for the two settings is similar, whereas the computational cost using minimization over the overlap and non-matching grid in $\omega _0$ dramatically decreases (see Fig. 9b).

Fig. 9

Experiment 3: a errors between the numerical and reference solutions with the cost function of case 1 and matching grids (diamond) and with the cost function of case 2 with non-matching grids (bullet), b CPU time with the cost function of case 1 and matching grids (diamond) and with the cost function of case 2 with non-matching grids (bullet)

5 Conclusion

In this paper, we aimed at reducing the computational cost of our optimization-based method, proposed in [6, 7]. Our focus was to reduce the total number of degrees of freedom of our method by investigating two strategies; i.e.,

• (i) to use a cost function over the boundary of the overlapping region;

• (ii) to consider independent meshes in the overlap and an interpolation procedure between the fine and coarse meshes in the overlapping region.

We derived a fully discrete a priori error analysis of the coupling method based on the new cost function and the heterogenous meshing strategy. Numerical experiments have been carried out to assess the difference between the two costs functions and the two meshing strategies, with and without matching grids in the overlap. In all numerical experiments, we observe orders of magnitude of saving in the computational cost when we compare the numerical settings used in [7] with a combination of the strategies (i) and (ii).

6 Appendix

Let us start by recalling the Caccioppoli inequality [19]. Let $\omega \subset \omega _1$ be subdomains of $\varOmega$ with $\tau =\text {dist}(\partial \omega , \partial \omega _1)$ and set $\varGamma =\partial \varOmega$. For a tensor a, the set of a-harmonic functions is denoted by $\mathcal {H}(\omega _1)$ and consists of functions $u\in L^2(\omega _1)\cap H^1_{\text {loc}}(\omega _1)$ such that

$$\begin{aligned} \int _{\omega _1}a \nabla u\cdot \nabla v \text {d}x=0 \forall v\in \mathcal {C}_0^{\infty }(\omega _1), \end{aligned}$$

where $H^1_{\text {loc}}(\omega _1):=\{u\in H^1(O)\mid \text { for any open set O with } \overline{O}\subset \omega _1\}.$

Theorem 6.1

(Caccioppoli inequality [19]) Let $u\in \mathcal {H}(\omega _1)$, then

$$\begin{aligned} \left\| \nabla u\right\| _{\mathrm {L}^{2}(\omega )}\le \frac{2\beta ^{1/2}}{\alpha ^{1/2}\tau }\left\| u\right\| _{\mathrm {L}^{2}(\omega _1)}. \end{aligned}$$

Further, it holds,

$$\begin{aligned} \left\| \nabla u\right\| _{\mathrm {L}^{2}(\omega )}\le \frac{2\beta ^{1/2}}{\alpha ^{1/2}\tau }\left\| u\right\| _{\mathrm {L}^{2}(\omega _0)}. \end{aligned}$$

We note that elliptic problems with a non-null right-hand side and problems where $\partial \omega \cap \varGamma \ne \emptyset$, can also be considered and we refer to [19] for details. We give next a bound of the $L^2$ norm over $\omega$ by the $L^2$ norm over the overlap $\omega _0$.

Lemma 6.2

Let $v_1^{\varepsilon }$ and $v_2^0$ be solutions of (4), for $i=1,2,$, respectively. The following bounds hold:

$$\begin{aligned} \left\| v_1^{\varepsilon }\right\| _{\mathrm {L}^{2}(\omega )}&\le \frac{C}{\tau }\left\| v_1^{\varepsilon }\right\| _{\mathrm {L}^{2}(\omega _0)},\\ \left\| v_2^0\right\| _{\mathrm {L}^{2}(\varOmega \setminus \omega _1)}&\le \frac{C}{\tau }\left\| v_2^0\right\| _{\mathrm {L}^{2}(\omega _0)}, \end{aligned}$$

where $\tau$ is the width of the overlap and C is a constant depending on $\alpha , \beta ,$ and the Poincaré constant is associated with $\omega _1$ and $\omega _2$, respectively.

Proof

see [7, Lemma 2.1]. $\square$

In the next lemma, we state a strong version of the Cauchy–Schwarz inequality and refer to [7] for the proof. Let us recall the problems for the state variables: find $v_i\in H^1_D(\omega _i)$ solution of

$$\begin{aligned} \begin{array}{rll} -\mathrm{{div\,}}(a_i\nabla v_i)&{}=0&{}\quad \text {in } \omega _i,\\ v_i&{}=\theta _i &{}\quad \text {on } \varGamma _i,\\ v_i &{}=0 &{} \quad \text {on }\partial \omega _i \cap \varGamma _D, \\ n_i \cdot (a_i\nabla v_i )&{}=0 &{} \quad \text {on }\partial \omega _i \cap \varGamma _N, \end{array} \end{aligned}$$

(19)

where $a_1=a_1^{\varepsilon }$ and $a_2=a_2^0$.

Lemma 6.3

(Strong Cauchy–Schwarz) Let $v_1^{\varepsilon }\in H^1_D(\omega _1)$ and $v_2^0\in H^1_{D}(\omega _2)$ be solutions of (19) for $i=1,2$. Then, there exist an $\varepsilon _0>0$ and a positive constant $C_s<1$ such that for all $\varepsilon \le \varepsilon _0$, it holds

$$\begin{aligned} \int _{\omega _0}v_1^{\varepsilon }v_2^0 \text {d}x\le C_s \left\| v_1^{\varepsilon }\right\| _{\mathrm {L}^{2}(\omega _0)} \left\| v_2^0\right\| _{\mathrm {L}^{2}(\omega _0)}. \end{aligned}$$

Discrete versions of the Caccioppoli and the strong Cauchy–Schwarz inequalities are stated below. $v^h\in V^p(\omega _1, \mathcal {T}_h)$ solution of

$$\begin{aligned} B_1(v^h, w^h):=\int _{\omega _1}a \nabla v^h\cdot \nabla w^h\text {d}x=0 \forall w^h\in V^p_0(\omega _1, \mathcal {T}_h). \end{aligned}$$

(20)

Lemma 6.4

(Discrete Caccioppoli inequality for interior domains, [26]) Let $v^h\in V^p(\omega _1, \mathcal {T}_h)$ satisfy Eq. (20) for all $w^h\in V_0^p(\omega _1, \mathcal {T}_h)$; it holds

$$\begin{aligned} \left\| \nabla v^h\right\| _{\mathrm {L}^{2}(\omega )} \le C \frac{1}{\tau } \left\| v^h\right\| _{\mathrm {L}^{2}(\omega _1)}, \end{aligned}$$

where the constant C is independent of h.

We now give the discrete strong Cauchy–Schwarz inequality, and to simplify the notations, we omit the $\varepsilon$ dependency in $v_1$.

Lemma 6.5

Let $\varepsilon <\varepsilon _0$ and $C_s <1$ be given by the strong Cauchy–Schwarz Lemma 6.3, and let $v_{1,\tilde{h}}\in V^p_D(\omega _1, \mathcal {T}_{\tilde{h}})$ and $v_{2, H}\in V_{D}^p(\omega _2, \mathcal {T}_H)$ be numerical solutions of (17). There exist ${\tilde{h}}_0>0$ and $H_0>0$ such that

$$\begin{aligned} \int _{\omega _0}v_{1,\tilde{h}}v_{2, H}\text {d}x\le C_s \left\| v_{1,\tilde{h}}\right\| _{\mathrm {L}^{2}(\omega _0)} \left\| v_{2, H}\right\| _{\mathrm {L}^{2}(\omega _0)} \quad \forall {\tilde{h}}<{\tilde{h}}_0, H<H_0. \end{aligned}$$