Error analysis of the extended Filon-type method for highly oscillatory integrals

Abstract

We investigate the impact of adding inner nodes for a Filon-type method for highly oscillatory quadrature. The error of Filon-type method is composed of asymptotic and interpolation errors, and the interplay between the two varies for different frequencies. We are particularly concerned with two strategies for the choice of inner nodes: Clenshaw–Curtis points and zeros of an appropriate Jacobi polynomial. Once the frequency $\omega$ is large, the asymptotic error dominates, but the situation is altogether different when $\omega \ge 0$ is small. In the first regime, our optimal error bounds indicate that Clenshaw–Curtis points are always marginally better, but this is reversed for small $\omega$; then, Jacobi points enjoy an advantage. The main tool in our analysis is the Peano Kernel theorem. While the main part of the paper addresses integrals without stationary points, we indicate how to extend this work to the case when stationary points are present. Numerical experiments are provided to illustrate theoretical analysis.

1 Background

The quadrature of highly oscillatory integrals plays a vital role in many research fields, such as numerical analysis, electromagnetic, acoustic scattering and quantum chemistry. Historically it was regarded as a formidable challenge, requiring large number of function evaluations (scaling roughly like the frequency), but the subject has undergone substantial revolution in the last fifteen years. Using asymptotic expansions as a major analytic tool, significant number of effective numerical methods for highly oscillatory integrals have been developed: the asymptotic expansion and Filon-type methods [9,10,11], numerical steepest descent [8], the Levin [12] method [15], complex-valued Gaussian quadrature [1, 3] and their diverse combinations.

Among these methods, a Filon-type method enjoys a number of important advantages: it is easy to implement and to generalise to a multivariate setting, and it exhibits high precision compared to the asymptotic expansion method. In particular, it gives good approximation of a highly oscillatory integral for all $\omega \ge 0$. Before we define the method, though, we first specify the subject matter of our analysis and describe its asymptotic expansion. Thus, we consider the integral

$$\begin{aligned} I_{\omega }[f] = \int _{-1}^1 f(x) \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x, \quad \omega \ge 0, \end{aligned}$$

(1.1)

where $f,g\in \mathbb {C}^\infty [-1,1]$. The restriction $\omega \ge 0$ is solely for expositional purposes: the case $\omega \le 0$ follows at once by conjugation. The asymptotic behaviour without stationary points and local property at stationary point by the method of stationary phase are presented in [14, 20, 22]. However, to study the form of the error for Filon method, it is necessary to commence from the completely explicit expansion of (1.1) derived from the integration by parts.

For the time being, $g^{\prime } \ne 0$. We assume that $g^{\prime }>0$ noting that the $g^{\prime }<0$ case can be treated in an identical manner. It is easy to derive its asymptotic expansion

$$\begin{aligned} I_{\omega }[f] \sim - \sum _{k = 0}^\infty \frac{1}{(-\mathrm {i}\omega )^{k + 1}} \left[ \frac{\sigma _{k}[f](1)}{g^{\prime }(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} - \frac{\sigma _{k}[f](-1)}{g^{\prime }(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] , \end{aligned}$$

where

$$\begin{aligned} \sigma _0[f](x)= & {} f(x),\\ \sigma _{k}[f](x)= & {} \frac{\mathrm {d}}{\mathrm {d}x}\frac{\sigma _{k-1}[f](x)}{g^{\prime }(x)}= \sum _{j = 0}^{k} \sigma _{k, j}(x) f^{(j)}(x), \quad \sigma _{k, k} = \frac{1}{{g^{\prime }}^k(x)} \ne 0, \end{aligned}$$

Iserles and Nørsett [11]. The functions $\sigma _{k,j}$ depend solely on $g^{\prime }$. The essence of the (basic) Filon-type method is to replace f by a polynomial p of degree $2s-1$ subject to the interpolation conditions

$$\begin{aligned} p^{(j)}(1) = f^{(j)}(1), \quad p^{(j)}(-1) = f^{(j)}(-1), \quad j = 0, 1, \ldots , s-1. \end{aligned}$$

The sth Filon-type method is

$$\begin{aligned} Q_\omega ^{\mathsf {F},s,0}[f]=\int _{-1}^1 p(x) \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x. \end{aligned}$$

It is easy to derive an asymptotic expansion of the error $E_\omega ^{\mathsf {F},s,0}$ committed by the Filon method $Q_\omega ^{\mathsf {F},s,0}$ applying (1.1) to the function $p-f$,

$$\begin{aligned} E_{\omega }^{\mathsf {F},s,0}[f]\sim & {} - \frac{1}{(-\mathrm {i}\omega )^{s+1}} \left[ \frac{f^{(s)}(1) - p^{(s)}(1)}{{g^{\prime }}^{s+1}(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} - \frac{f^{(s)}(-1) - p^{(s)}(-1)}{{g^{\prime }}^{s+1}(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] \nonumber \\&+\,O\left( \omega ^{-s - 2}\right) . \end{aligned}$$

(1.2)

Iserles and Nørsett [11]. Note that the precision improves as $\omega$ grows and that just 2s function and derivative evaluations are sufficient for asymptotic accuracy of $O(\omega ^{-s-2})$, $\omega \gg 1$. On the other hand, for $\omega =0$ the Filon quadrature reduces to the Birkhoff–Hermite quadrature (i.e. Gaussian quadrature using both function values and derivatives [6]). To clarify the choice of the inner nodes, we apply the interpolation conditions without derivatives at the inner nodes for a Filon-type method.

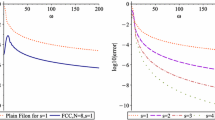
As an illustration of (1.2), in Fig. 1 we display (in logarithmic scale) the error committed by $Q_\omega ^{\mathsf {F},s,0}[\sin (x^2+x)]$ for $g(x)=x$, $s=1,2,3$ and $\omega \in [0,100]$. It is evident that while the error for $\omega =0$ is unacceptably large, it decays rapidly as $\omega$ grows—the larger s, the faster it decays, all in line with (1.2). We reiterate that all this is exceedingly cheap: all $Q_\omega ^{\mathsf {F},s,0}[f]$ is just 2s computations of f and its derivatives at the endpoints. This might come as a surprise to all those who have been led by classical numerical analysis to believe that high oscillation is inimical to computation! It is indeed inimical as long as our outlook is focussed on Taylor expansions, but asymptotic expansions invert our perspective: properly understood, high oscillation is a friend of computation.

Fig. 1

The logarithmic error $\log _{10}|Q_\omega ^{\mathsf {F},s,0}[f]-I[f]|$ for $f(x)=\sin (x^2+x)$, $g(x)=x$ and $\omega \in [0,100]$ for $s=1$ (plum), $s=2$ (navy blue) and $s=3$ (indian red)

In this paper we wish to explore in detail what happens once internal points are allowed in a Filon method.

Definition

The extended Filon method (EFM) is

$$\begin{aligned} Q_{\omega }^{\mathsf {F},s,\nu }[f]=\int _{-1}^1 p(x) \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x, \end{aligned}$$

(1.3)

where $c_1<c_2<\cdots <c_\nu$ are given in $(-1,1)$ and p is a polynomial of degree $2s+\nu -1$ defined by the Hermite-type interpolation conditions

$$\begin{aligned} p^{(j)}(1)= & {} f^{(j)}(1), \quad p^{(j)}(-1) = f^{(j)}(-1), \quad j = 0, 1, \ldots , s-1,\\ p(c_k)= & {} f(c_k),\quad k=1,\ldots ,\nu . \end{aligned}$$

Alternatively we can rewrite (1.3) in a form consistent with classical quadrature,

$$\begin{aligned} Q_\omega ^{\mathsf {F},s,\nu }[f]=\sum _{j=0}^{s-1} [b^-_j(\omega ) f^{(j)}(-1)+b^+_j(\omega ) f^{(j)}(1)]+\sum _{k=1}^\nu b_k(\omega ) f(c_k), \end{aligned}$$

where

$$\begin{aligned} b^\pm _j(\omega )= & {} \int _{-1}^1 \ell ^\pm _j(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x,\quad j=0,\ldots ,s-1,\\ b_k(\omega )= & {} \int _{-1}^1 \ell _k(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x,\quad k=1,\ldots ,\nu . \end{aligned}$$

The degree-$(2s+\nu -1)$ polynomials $\ell ^\pm _j$ and $\ell _k$ are cardinal functions of Birkhoff–Hermite quadrature,

$$\begin{aligned}&{\ell ^-_j}^{(i)}(-1)=\left\{ \begin{array}{ll} 1, &{}\;\; i=j,\\ 0, &{}\;\; i\ne j,\end{array}\right. \quad {\ell ^-_j}^{(i)}(1)=0,\quad \;\; i\,=\,0,\ldots ,s-1,\quad \;\;\ell ^-_j(c_k)\,=\,0,\quad k=1,\ldots ,\nu ,\\&{\ell ^+_j}^{(i)}(-1)=0,\quad {\ell _j^+}^{(i)}(1)=\left\{ \begin{array}{ll} 1, &{}\;\; i=j,\\ 0, &{}\;\; i\ne j,\end{array}\right. \quad \;\; i=0,\ldots ,s-1,\quad \;\; \ell ^+_j(c_k)=0,\quad k=1,\ldots ,\nu ,\\&\ell _k^{(i)}(-1)=\ell _k^{(i)}(1)=0,\quad i=0,\ldots ,s-1,\qquad \ell _k(c_r)=\left\{ \begin{array}{ll} 1, &{}\;\; r\,=\,k,\\ 0, &{}\;\; r\ne k,\end{array}\right. \quad r\,=\,1,\ldots ,\nu . \end{aligned}$$

Explicit formulæ for the above cardinal polynomials are given in Appendix A.

Fig. 2

The logarithmic error $\log _{10}|Q_\omega ^{\mathsf {F},s,3}[f]-I[f]|$ for $f(x)=\sin (x^2+x)$, $g(x)=x$ and $\omega \in [0,100]$ for $s=0$ (plum), $s=1$ (navy blue) and $s=2$ (indian red) and different choices of $c_k$, $k=1,2,3$

To illustrate the influence of internal points on the performance of EFM, we plot in Fig. 2 on the left

$$\begin{aligned} s=1{:}\,&\mathbf {c}=\left[ -\frac{\sqrt{21}}{7},\;0,\;\frac{\sqrt{21}}{7}\right] ,\\ s=2{:}\,&\mathbf {c}=\left[ -\frac{\sqrt{3}}{3},\;0,\;\frac{\sqrt{3}}{3}\right] ,\\ s=3{:}\,&\mathbf {c}=\left[ -\frac{\sqrt{33}}{11},\;0,\;\frac{\sqrt{33}}{11}\right] \end{aligned}$$

and on the right, for $s=1,2,3$, the same choice $\mathbf {c}=\left[ -\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2}\right]$—the reason for these choices will become apparent in the sequel. Comparison with Fig. 1 (which, conveniently, has been plotted to the same scale) demonstrates that while the slope of the three curves does not change (hence, the asymptotic rate of decay for $\omega \gg 1$ remains the same), the size of the error is substantially smaller. A more detailed examination reveals that the methods on the left and on the right differ in a subtle manner, which becomes apparent from Table 1. Thus, while the methods from Fig. 2 are always much better, the method on the left is better for small $\omega \ge 0$, while the method on the right is marginally better for $\omega \gg 1$. We will prove in the sequel that this represents a more general state of affairs.

Table 1 The absolute error of the three methods for $s=3$ and different values of $\omega$

There is nothing new in the incorporation of internal points into a Filon method. They have been introduced in [11], a paper that introduced Filon methods in their modern guise and analysed their asymptotic behaviour. It has been suggested there that a good choice of internal points is the zeros of the Jacobi polynomial $\mathrm {P}_\nu ^{(s,s)}$, since this maximises the (conventional) order of the Birkhoff–Hermite quadrature for $\omega =0$. We dub this method EFJ (for “Extended Filon–Jacobi”): this is the method on the left of Fig. 2.

Another choice of internal points has been proposed in [5] for the case $s=1$ and will be extended by us to all $s\ge 1$, namely the Chebyshev points of the second kind $\cos k\pi /(\nu +1)$, $k=1,\ldots ,\nu$. Such points feature in Clenshaw–Curtis quadrature, which enjoys many favourable features once compared with traditional Gaussian quadrature [21]. We call this method, corresponding to the right-hand side of Fig. 2, EFCC, standing for “Extended Filon–Clenshaw–Curtis”.

Increasing the number $\nu$ of the inner nodes contributes to reduce the whole error. In Fig. 3, still with the same f(x) and g(x) as in Fig. 2, but large $\nu = 7$, the logarithmic error $\log _{10}\left| Q^{\mathsf {F}, s, 7}_{\omega } - I[f]\right|$ of EFJ (in the left) and EFCC (in the right) is depicted, for $s = 1, 2, 3$. It is observed that the error of EFJ near $\omega = 0$ is smaller than that of EFCC. Also the error of $\nu = 7$ is much smaller than that of $\nu =3$ for the same example.

Fig. 3

The logarithmic error $\log _{10}|Q_\omega ^{\mathsf {F},s,7}[f]-I[f]|$ for $f(x)=\sin (x^2+x)$, $g(x)=x$ and $\omega \in [0,100]$ for $s=0$ (plum), $s=1$ (navy blue) and $s=2$ (indian red) and different choices of $c_k$, $k=1,2, \ldots ,7$

Insofar as interior points, inclusive of Jacobi points and Chebyshev points of the second kind, are not new and have been justified partly [5, 13], in particular for the case $\nu \gg 1$. The purpose of this paper is a rigorous and complete analysis of EFM and the establishment of realistic and tight upper bounds on its numerical error.

The asymptotic expansion of the error of (1.3) is identical to (1.2),

$$\begin{aligned} E_\omega ^{\mathsf {F},s,\nu }[f]= & {} Q_{\omega }^{\mathsf {F},s,\nu }[f]-I_\omega [f]=I_\omega [p-f]\nonumber \\= & {} -\frac{1}{(-\mathrm {i}\omega )^{s+1}} \left[ \frac{p^{(s)}(1)-f^{(s)}(1)}{{g^{\prime }}^{s+1}(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} -\frac{p^{(s)}(-1)-f^{(s)}(-1)}{{g^{\prime }}^{s+1}(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] +O\left( \omega ^{-s-2}\right) \nonumber \\= & {} -\frac{1}{(-\mathrm {i}\omega )^{s+1}} e_\omega ^{\mathsf {F},s,\nu }[f]+ O\left( \omega ^{-s-2}\right) , \end{aligned}$$

(1.4)

where

$$\begin{aligned} e_\omega ^{\mathsf {F},s,\nu }[f] = \frac{p^{(s)}(1)-f^{(s)}(1)}{{g^{\prime }}^{s+1}(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} -\frac{p^{(s)}(-1)-f^{(s)}(-1)}{{g^{\prime }}^{s+1}(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}. \end{aligned}$$

Once $\omega \gg 1$, the accuracy is to all intents and purposes determined by asymptotics. This has two ingredients: the asymptotic rate of decay, $O(\omega ^{-s-1})$, which is independent of internal points, and the size of $p^{(s)}-f^{(s)}$ at the endpoints which strongly depends on the choice of internal points. Intuitively speaking, good choice of internal points is likely to produce better approximation to f, thereby reducing $|p^{(s)}(\pm 1)-f^{(s)}(\pm 1)|$. For small $\omega \ge 0$, though, asymptotics no longer matter,

$$\begin{aligned} |E_\omega ^{\mathsf {F},s,\nu }[f]|=\left| \int _{-1}^1 [p(x)-f(x)]\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x\right| \le \int _{-1}^1 |p(x)-f(x)|\mathrm {d}x, \end{aligned}$$

and the two determinators of the error are the quality of interpolation (again!) and, for $\omega =0$, the order of the underlying Birkhoff–Hermite quadrature

$$\begin{aligned} \int _{-1}^1 f(x)\mathrm {d}x\approx \int _{-1}^1 p(x)\mathrm {d}x. \end{aligned}$$

The main tool in our analysis is the

Theorem 1

(Peano Kernel theorem (PKT), [16, p. 270–274]) Let $\mathcal {L}$ be a bounded linear functional acting on $\mathrm {C}^{m+1}(a,b)$ such that $\mathcal {L}[p]=0$ for every polynomial p of degree $\le m$ and let $f\in \mathrm {C}^{m+1}(a,b)$. Then

$$\begin{aligned} \mathcal {L}[f] = I_{\omega }[f] - Q_{\omega }^{\mathsf {F},s,\nu }[f] = \int _a^b K(\theta )f^{(m+1)}(\theta )\mathrm {d}\theta , \end{aligned}$$

(1.5)

where

$$\begin{aligned} K(\theta )=\frac{1}{m!} \mathcal {L}[(\,\cdot \,-\theta )_+^m] \end{aligned}$$

is the Peano kernel. In the formula above $\mathcal {L}$ is applied to the function $(x-\theta )_+^m$ ($\theta$ is a parameter) and $(y)_+=\max \{y,0\}$. (If $m=0$ we also need $\mathcal {L}$ to be of bounded variation.) In particular, it follows that

$$\begin{aligned} |\mathcal {L}[f]|\le \Vert K\Vert _1\Vert f^{(m+1)}\Vert _\infty . \end{aligned}$$

(1.6)

This bound on the size of $|\mathcal {L}[f]|$ neatly separates the role of $\mathcal {L}$ and of the function f, and it is sharp because there always exists $f\in \mathrm {C}^{m+1}(a,b)$ so that (1.6) is satisfied as an equality.

2 Large $\omega$

2.1 General error bounds for EFM

We recall from (1.4) that the error of EFM is

$$\begin{aligned} E_\omega ^{\mathsf {F},s,\nu }[f]=-\frac{e_\omega ^{\mathsf {F},s,\nu }[f]}{(-\mathrm {i}\omega )^{s+1}}+O(\omega ^{-s-2}), \end{aligned}$$

where

$$\begin{aligned} e_\omega ^{\mathsf {F},s,\nu }[f] = \frac{p^{(s)}(1)-f^{(s)}(1)}{{g^{\prime }}^{s+1}(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} -\frac{p^{(s)}(-1)-f^{(s)}(-1)}{{g^{\prime }}^{s+1}(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)} \end{aligned}$$

and p is an interpolating polynomial, $p^{(j)}(\pm 1)=f^{(j)}(\pm 1)$, $j=0,\ldots ,s-1$ and $p(c_k)=f(c_k)$, $k=1,\ldots ,\nu$. It follows at once that

$$\begin{aligned} \left| e_\omega ^{\mathsf {F},s,\nu }[f]\right| \le \frac{|p^{(s)}(1)-f^{(s)}(1)|}{{g^{\prime }}^{s+1}(1)} +\frac{|p^{(s)}(-1)-f^{(s)}(-1)|}{{g^{\prime }}^{s+1}(-1)} \end{aligned}$$

(2.1)

and the inequality is satisfied as an equality whenever $\omega [g(1)-g(-1)]$ is an odd multiple of $\pi$ if $[p^{(s)}(1)-f^{(s)}(1)]\cdot [p^{(s)}(-1)-f^{(s)}(-1)]>0$, an even multiple if it is negative. (Because $g^{\prime }\ne 0$ in $[-1,1]$, $g(1)-g(-1)\ne 0$). Hence, the critical point of the error analysis lies in attaining tight bounds on $|p^{(s)}(1)-f^{(s)}(1)|$ and $|p^{(s)}(-1)-f^{(s)}(-1)|$.

Define the nodal polynomial as

$$\begin{aligned} \tilde{r}(x)=(x^2-1)^s\prod _{j=1}^\nu (x-c_j). \end{aligned}$$

Since

$$\begin{aligned} \tilde{r}^{(s)}(x)=\sum _{n=0}^s{s\atopwithdelims ()n} \frac{\hbox {d}^n}{\hbox {d} x^n}(x-1)^s \frac{\hbox {d}^{s-n}}{\hbox {d} x^{s-n}} (x+1)^s \prod _{j=1}^\nu (x-c_j), \end{aligned}$$

it follows that

$$\begin{aligned} \tilde{r}^{(s)}(1)=s!2^s\prod _{j=1}^\nu (1-c_j), \quad \tilde{r}^{(s)}(-1)=(-1)^{s + \nu }s!2^s\prod _{j=1}^\nu (1+c_j). \end{aligned}$$

Shadrin [18] used the PKT to prove that

$$\begin{aligned} \left| p^{(s)}(1)-f^{(s)}(1)\right|\le & {} \frac{s!2^s}{(\nu +2s)!} \prod _{j=1}^\nu (1-c_j) \Vert f^{(\nu +2s)}\Vert _\infty ,\nonumber \\ \left| p^{(s)}(-1)-f^{(s)}(-1)\right|\le & {} \frac{s!2^s}{(\nu +2s)!} \prod _{j=1}^\nu (1+c_j)\Vert f^{(\nu +2s)}\Vert _\infty . \end{aligned}$$

(2.2)

Substituting (2.1) and (2.2) into (1.4), we derive a bound on the leading term in the asymptotic expansion of the error,

$$\begin{aligned} \left| E_\omega ^{\mathsf {F},s,\nu }[f]\right| \le \frac{s!2^s }{\omega ^{s+1} (\nu +2s)!} \left[ \frac{\prod _{j=1}^\nu (1-c_j)}{{g^{\prime }}^{s+1}(1)} + \frac{\prod _{j=1}^\nu (1+c_j)}{{g^{\prime }}^{s+1}(-1)}\right] \Vert f^{(\nu +2s)}\Vert _\infty +O(\omega ^{-s-2})\nonumber \\ \end{aligned}$$

(2.3)

for $\omega \gg 1$.

Fig. 4

The errors (to logarithmic scale) for $f(x)=\mathrm {e}^x$, $g(x)=x$, plain Filon (the top), EFJ (the left on the bottom) and EFCC (the right on the bottom) for $s=1,2,3$ (in plum, navy blue and indian red) and (for the latter two methods) $\nu =3$, each with its upper error bound (thin black line)

Figure 4 illustrates upper error bound (2.3) for $f(x)=\mathrm {e}^x$ and $g(x)=x$ for the same three methods as in Figs. 1 and 2. Note that the bounds are not “strict”, but this is only to be expected, because our function f does not maximise them. All PKT allows us to say is that for every s, $\nu$ and specific choice of the $c_k$s there exists a function f for which the bound is strict.

Note further that the bounds, while evidently correct, are useless for small $\omega \ge 0$. In that instance we need a different approach, which is described in Sect. 3.

2.2 Jacobi versus Clenshaw–Curtis

For fixed s and $\nu$, bound (2.3) depends on the choice of the inner points $c_k$, $k=1,\ldots ,\nu$. In particular, we have singled out in Sect. 1 two choices: EFJ, whereby the $c_k$s are the zeros of the Jacobi polynomial $\mathrm {P}_\nu ^{(s,s)}$, a choice that maximised the conventional order of the (nonoscillatory) quadrature for $\omega =0$ [11], and EFCC, with $c_k=\cos (k\pi /(\nu +1))$ (incidentally, these are also zeros of a Jacobi polynomial, $\mathrm {P}_\nu ^{(\frac{1}{2},\frac{1}{2})}$). The advantage of EFCC is that they are uniformly bounded [5].¹

We commence by calculating $r(1)=\prod _{k=1}^\nu (1-c_k)$ and $r(-1)=(-1)^\nu \prod _{k=1}^\nu (1+c_k)$ for the two above configurations of inner points. In both cases $r(x)=\prod _{k=1}^\nu (x-c_k)$ is a Jacobi polynomial, normalised to be monic: $\mathrm {P}_\nu ^{(s,s)}$ for EFJ and $\mathrm {P}_\nu ^{(\frac{1}{2},\frac{1}{2})}$ for EFCC. We commence by noting that

$$\begin{aligned} \mathrm {P}_\nu ^{(\alpha ,\beta )}(1)=\frac{(1+\alpha )_\nu }{\nu !},\quad \mathrm {P}_\nu ^{(\alpha ,\beta )}(x)=\frac{(1+\alpha +\beta +\nu )_\nu }{\nu !2^\nu }x^\nu +\text{ l.o.t. }, \end{aligned}$$

where $\nu \ge 0$, $\alpha ,\beta >-1$ [17, p. 254]. Letting $\tilde{\mathrm {P}}_\nu ^{(\alpha ,\beta )}$ be the monic Jacobi polynomial, we thus have

$$\begin{aligned} \tilde{\mathrm {P}}_\nu ^{(\alpha ,\beta )}(1)=\frac{2^\nu (1+\alpha )_\nu }{(1+\alpha +\beta +\nu )_\nu }, \quad \rho _\alpha ^{[\nu ]}:=\tilde{\mathrm {P}}_\nu ^{(\alpha ,\alpha )}(1)=\frac{2^\nu (1+\alpha )_\nu }{(1+2\alpha +\nu )_\nu }. \end{aligned}$$

For EFJ $\alpha =\beta =s$, hence

$$\begin{aligned} r(1)=\rho _s^{[\nu ]}=\frac{2^\nu (\nu +s)!(\nu +2s)!}{s!(2\nu +2s)!}, \end{aligned}$$

while for EFCC $\alpha =\frac{1}{2}$ and

$$\begin{aligned} r(1)=\rho _{1/2}^{[\nu ]}=\frac{\nu +1}{2^\nu }. \end{aligned}$$

Proposition 2

The function $\rho _s^{[\nu ]}$ increases strictly monotonically for $s>-1/2$ and $\nu \ge 2$, while $\rho _s^0,\rho _s^1\equiv 1$.

Proof

We compute

$$\begin{aligned} \frac{\mathrm {d}\rho _s^{[\nu ]}}{\mathrm {d} s}= & {} 2^\nu \frac{\mathrm {d}}{\mathrm {d}s} \prod _{\ell =1}^\nu \frac{\ell +s}{\ell +2s+\nu }=2^\nu \sum _{k=1}^\nu \frac{\nu - k}{\left( k + 2 s + \nu \right) ^2} \left( \prod _{\mathop {\ell \ne k}\limits ^{\scriptstyle \ell =1}}^\nu \frac{\ell +s}{\ell +2s+\nu }\right) \\= & {} \rho _s^{[\nu ]} \sum _{k=1}^\nu \frac{\nu -k}{(k+s)(k+2s+\nu )}. \end{aligned}$$

for all $s>-1/2$. Therefore ${\rho _s^{[\nu ]}}'/\rho _s^{[\nu ]}>0$, and since $\rho _{-1/2}^{[\nu ]}=2^{-\nu +1}>0$, the assertion is true. $\square$

Insofar as the value of $r(-1)$, the other ingredient we need for upper bound (2.3), is concerned, $\mathrm {P}_\nu ^{(\alpha ,\beta )}(-1)=(-1)^\nu \mathrm {P}_\nu ^{(\beta ,\alpha )}(1)=(-1)^{\nu }(1+\beta )_\nu /\nu !$ [17, p. 257] implies that $|r(-1)|=|r(1)|$.

Theorem 3

Given s and $\nu$, upper bound (2.3) is always smaller for EFCC than for EFJ.

Proof

An immediate consequence of Proposition 1. $\square$

Note however that the advantage of Clenshaw–Curtis over Jacobi is fairly minor:

$$\begin{aligned} \rho _s^{[2]}=1-\frac{1}{3+2s},\quad \rho _s^{[3]}=1-\frac{3}{5+2s},\quad \rho _s^{[4]}=1-\frac{27+12 s}{(5+2s)(7+2s)} \end{aligned}$$

etc.

3 Small $\omega \ge 0$

The analysis of Sect. 2 applies only to the case of $\omega \rightarrow \infty$, while numerical results of Sect. 1 indicate that the behaviour of EFM is altogether different for small $\omega \ge 0$. This is demonstrated in Fig. 5, where we have compared the errors of EFJ and EFCC for $s=2$, $\nu =4$ and two different functions f. Evidently, EFJ appears to be substantially more accurate for small $\omega$ and only once $\omega$ grows sufficiently, it is overtaken by EFCC (for the graph on the left) in line with the implications of Theorem 3. In the right-hand graph the asymptotic difference between EFJ and EFCC, which we know to be minor, is hidden by the oscillatory nature of the error. For the record, for much larger $\omega$ EFCC emerges as a winner, by a small margin.

Fig. 5

The error $\log _{10}\left| Q_{\omega }^{\mathsf {F},2,4}-I_{\omega }[f]\right|$, for EFJ (slate blue) and EFCC (dark goldenrod) and small $\omega \ge 0$, for two cases: $f(x) = (1+x)/(1+x^2)$, $g(x)=x$ (on the left) and $f(x)=(1+x)\cos \pi x$, $g(x)=x+x^2/4$ (on the right)

The complication for $\omega =0$ is that EFJ and EFCC are of different polynomial order: while EFJ is exact for all $f\in \mathbb {P}_{2s+2\nu -1}$ (where $\mathbb {P}_n$ is the set of nth-degree algebraic polynomials), EFCC is, on the face of it, exact just in $\mathbb {P}_{2s+\nu -1}$. The latter, however, is not entirely true. Because of the symmetry of both the integral and of the quadrature formula, all odd polynomials are computed exactly: the integral is zero and so is quadrature. Therefore, while for even $\nu$ the polynomial order of EFCC is $2s+\nu -1$, once $\nu$ is odd it increases to $2s+\nu$. However, unless $\nu =1$ (when a single Jacobi and Clenshaw–Curtis point coincides at the origin), EFJ has always higher order than EFCC.

Does it matter? According to [21], Clenshaw–Curtis is just as good as Gaussian quadrature and we can expect something similar to remain true in our setting. Except that [21] is concerned with convergence for large $\nu$, while we are interested in relatively small (and fixed) values of $\nu$. It is well known [2] that an order-p (i.e. exact for all $f\in \mathbb {P}_{p-1}$) quadrature method applied to the function f bears an error of $cf^{(p)}(\xi )$, where $c\ne 0$ is a constant, depending solely on the method (the error constant) and $\xi$ is an intermediate point. Therefore, the error is bounded by $c\Vert f^{(p)}\Vert _\infty$. The problem is that it does not allow for a comparison of EFJ and EFCC method with the same values of s and $\nu$ which lead to the different derivative order, $f^{(2s+2\nu )}$ for EFJ and $f^{(2s+\nu )}$ for EFCC. Different derivatives, incompatible top bounds!

We instead revert to Peano kernel estimations, with two twists:

• 1. We estimate the Peano kernel constant not for the order of each method but for the order of Clenshaw–Curtis. The outcome is an estimate which is compatible for both methods.

• 2. Instead of a classical PKT estimate, we use the work of Favati et al. [7]. Since the zeros of the polynomial on $[-1, 1]$ are symmetric, denote the nodes by

  $$\begin{aligned} -1< -c_{\left\lfloor \frac{\nu + 1}{2}\right\rfloor }< \cdots< -c_1< c_1< \cdots< c_{\left\lfloor \frac{\nu + 1}{2}\right\rfloor } < 1 = c_{\left\lfloor \frac{\nu + 1}{2}\right\rfloor + 1}. \end{aligned}$$

  If $\nu$ is odd, $c_1 = 0$ and when it is even, $c_1 > 0$. Thus, we have a symmetric Birkhoff–Hermite quadrature,

  $$\begin{aligned} \mathcal {I}_0[f]=\int _{-1}^1 f(x)\hbox {d} x \approx \mathcal {Q}_0[f]=\sum _{k=1}^{\left\lfloor \frac{\nu +1}{2}\right\rfloor + 1} \sum _{j=0}^{s_k-1} b_{k,j} [f^{(j)}(c_k)+(-1)^j f^{(j)}(-c_k)], \end{aligned}$$

  where $s_{\left\lfloor \frac{\nu +1}{2}\right\rfloor + 1} = s$, $s_k = 1$ for $k = 1, 2, \cdots , \left\lfloor \frac{\nu +1}{2}\right\rfloor$. If $\nu$ is odd, $b_{1,j}$ need be halved. Note that $\mathcal {I}_0[f_{\mathrm {O}}]=\mathcal {Q}_0[f_{\mathrm {O}}]=0$ for every sufficiently smooth odd function $f_{\mathrm {O}}$. This motivates a focus on the even part $f_{\mathrm {E}}(x) = (f(x)+f(-x))/2$ of the functions f(x), whereby we can restrict ourselves to [0, 1],

  $$\begin{aligned} \mathcal {I}_1[f]=\int _0^1 f_{\mathrm {E}}(x)\hbox {d} x\approx \mathcal {Q}_1[f]=\sum _{k=1}^{\left\lfloor \frac{\nu +1}{2}\right\rfloor + 1} \sum _{j=0}^{s_k-1} b_{k,j} f_{\mathrm {E}}^{(j)}(c_k), \end{aligned}$$

  where in our case $b_{k, j} = 0$ for $j \ge 1$ and $k = 1, 2, \cdots , \left\lfloor \frac{\nu + 1}{2}\right\rfloor$. It is trivial that $\mathcal {I}_1[f]=2\mathcal {I}_2[f]$.

  Suppose that the order of the method is $p\ge 1$. It has been proved in [7] that, for $\mathcal {I}_1$,

  $$\begin{aligned} K_d(\theta ) =\frac{(1-\theta )_+^{d+1}}{(d+1)!} - \frac{1}{d!} \sum _{k=1}^{\left\lfloor \frac{\nu + 1}{2}\right\rfloor } b_{k,0} (c_k-\theta )_+^{d} \end{aligned}$$

  (3.1)

  for any $d\in \{1,2,\ldots ,p-1\}$. Integrating $2|K_d|$ in [0, 1] results in the $\mathrm {L}_\infty$ PKT bound,

  $$\begin{aligned} \left| \mathcal {I}_0[f]-\mathcal {Q}_0[f]\right| \le 2 \int _0^1 |K_d(\theta )|\hbox {d} \theta \Vert f_{\mathrm {E}}^{(d)}\Vert _\infty . \end{aligned}$$

  In our case we choose $d=2s+\nu$ for odd $\nu$ or $d=2s+\nu -1$ for even $\nu$, the order of the EFCC method.

Table 2 Peano kernel constants for EFJ and EFCC methods with $\omega = 0$

Table 2 displays Peano kernel constants $2\int _0^1 |K_d(\theta )|\mathrm {d}\theta$ for a range of practical values of s and $\nu$. So, what do we learn from the table?

• 1. EFJ always beats EFCC for $\omega =0$—note that, we are comparing methods of the same order, alike with alike.

• 2. The advantage of EFJ over EFCC increases as s grows and $\nu$ is fixed. For $s=1$, it is quite minor but for $s=5$ the difference is substantial.

• 3. Likewise, the advantage of EFJ grows for fixed s and increasing $\nu$—note that for $\nu =1$ the two methods coincide.

• 4. The constants decrease strictly monotonically as a function of s or of $\nu$. Note, of course, that for different rows the constants have different meaning, because they precede different derivatives of $f_{\mathrm {E}}$, but this is interesting nonetheless.

Fig. 6

The logarithms of constants for EFCC (brighter line) and EFJ (darker line) for $s=1,\ldots ,5$ (the order is from top left to bottom right) and increasing $\nu =2,\ldots ,6$

Figure 6 displays graphically the information embedded in Table 2. The message is the same: at $\omega =0$ EFJ is always better than EFCC, the constants decrease as $\nu$ increases or as s increases.

An alternative outlook is provided by comparing methods of the same value of d (which is the order of EFCC, although not of EFJ!). For example, we have exactly six methods with $d=7$: the pairs $(s,\nu )$ in $\{(1,6),(1,5),(2,4),(2,3),(3,2),(3,1)\}$. Note that we have two such methods for each s, for some odd $\nu _s$ and for $\nu _s+1$: the latter, according to our observations, has a smaller constant.

Fig. 7

The $d=7$ sequence $(s,\nu )=(1,6),(1,5),(2,4),(2,3),(3,2),(3,1)\}$ (left), the $d=15$ sequence $\{(1,14),(2,12),(3,10),(4,8),(5,6),(6,4),(7,2),(8,0)\}$ (centre) and the $d=23$ sequence $(k,24-2k)$, $k=1,\ldots ,12$ (right), each to log scale. Cyan corresponds to EFCC and yellow orange to EFJ

In Fig. 7 we display three such sequences: on the top left for $d=7$ and all such methods, on the top right for $d=15$ and only the methods with an even (hence larger) $\nu$, and the bottom is for $d= 23$ with even $\nu$. Note that monotonicity, at least for EFCC, is no longer true, but the sequence is predictable: for sufficiently large d it first goes down, then up, while the last value (which coincides with Jacobi) may take it down again. The EFJ sequence is much nicer, and its logarithm seems to increase as a smooth function.

What is interesting, though, is once the objective is to minimise the PKT constant (with either method) for given order of the EFCC method, a good policy is to use $s=1$ and maximal $\nu$. This is an exact opposite of the right policy for $\omega \gg 1$, namely small $\nu$ and large s. Yet another example how the $\omega =0$ and $\omega \gg 1$ regimes are polar opposites.

Finally, we note that EFJ has another significant advantage vs EFCC for $\omega =0$, somewhat obscured by our comparisons: it is of a higher order! This motivates another way of looking at the PKT constants for EFJ, namely taking $d=2s+2\nu -1$, the degree of polynomials that annihilate the underlying linear functional. In that case, of course, we cannot compare with EFCC, but this provides another useful way of bounding the error of EFJ by a constant times $\Vert f_{\mathrm {E}}^{(d+1)}\Vert _\infty$.

Table 3 Peano kernel constants for EFJ and $d=2\nu +2s-1$

The PKT constants for EFJ and maximal d are displayed in Table 3: we can see that they decrease with both increasing s and increasing $\nu$—of course, the constants originate in different derivatives of $f_{\mathrm {E}}$, so direct comparison of size is of limited significance. Instead, like in Fig. 7, we can investigate constants corresponding to methods of the same order. Thus, Fig. 8 presents (in logarithmic scale) the PKT constants for EFJ and maximal d, for methods $\left( k,\frac{d+1}{2}-k\right)$, $k=1,\ldots ,\frac{d+1}{2}$, with $d=13$ and $d=23$. As before, the least error is obtained when we put all our money to increase $\nu$ , while keeping $s=1$ as small as possible. Again, this is exactly the opposite of what we need for large $\omega$!

Fig. 8

The $d=13$ (on the left) and $d=23$ (on the right) sequences for EFJ, to logarithmic scale

4 Stationary points

4.1 Filon with stationary points

Let us assume the existence of a single order-2 stationary point at $x=-1$, i.e. that $g^{\prime }(-1)=0$, $g^{\prime \prime }(-1)\ne 0$ and $g^{\prime }\ne 0$ in $(-1,1]$. Higher-order stationary point there can be dealt with in a similar manner, requiring more technical effort but no added insight, while an integral with several stationary points or with a stationary point in $(-1,1]$ can be converted through linear change of variables to possibly several integrals (1.1) of the kind addressed in this section.

As always we commence with an asymptotic expansion,

$$\begin{aligned} I[f]\sim & {} \mu _0(\omega ) \sum \limits _{k = 0}^{s - 1} \frac{\sigma _k[f](-1)}{(-\mathrm {i}\omega )^k}-\,\sum \limits _{k = 0}^{s - 1}\frac{1}{(-\mathrm {i}\omega )^{k + 1}} \nonumber \\&\times \,\left[ \frac{\sigma _k[f](1) - \sigma _k[f](-1)}{g^{\prime }(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} - \frac{\sigma '_k[f](-1)}{g^{\prime \prime }(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] \nonumber \\&+\,\frac{1}{(-\mathrm {i}\omega )^{s}} \mu _0(\omega ) \sigma _s[f](-1) -\frac{1}{(-\mathrm {i}\omega )^{s + 1}}\nonumber \\&\times \, \left[ \frac{\sigma _s[f](1) - \sigma _s[f](-1)}{g^{\prime }(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} - \frac{\sigma '_s[f](-1)}{g^{\prime \prime }(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] +\,O(\omega ^{-s-3/2}) \end{aligned}$$

(4.1)

where

$$\begin{aligned} \mu _0(\omega )= & {} \int _{-1}^1 \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x=O(\omega ^{-1/2}),\\ \sigma _0[f](x)= & {} f(x),\\ \sigma _k[f](x)= & {} \frac{\hbox {d}}{\hbox {d} x} \frac{\sigma _{k-1}[f](x) - \sigma _{k-1}[f](-1)}{g^{\prime }(x)}. \end{aligned}$$

It can be easily obtained from [11] (where the stationary point is in the interior) by a limiting process.

It is easy to observe that for every $x\in (-1,1]$ the function $\sigma _m$ is a linear combination of $f(x),f^{\prime }(x),\ldots ,f^{(k)}(x)$ with coefficients that depend on $g^{\prime }$ and its derivatives. Moreover, the coefficient of $f^{(k)}$ there is $1/{g^{\prime }}^k(x)$—all this is exactly like in Sect. 1. However, things are different at $x=-1$. Because we have there a removable singularity, we need to apply the l’Hôpital rule m times and $\sigma _m(-1)$ is a multiple of $f^{(2k)}(-1)$. By brute force, we have

$$\begin{aligned} \sigma _0(-1)= & {} f(-1),\\ \sigma _1(-1)= & {} \frac{1}{2} \frac{1}{g^{\prime \prime }(-1)} f^{\prime \prime }(-1)-\frac{1}{2} \frac{g'''(-1)}{{g^{\prime \prime }}^2(-1)}f^{\prime }(-1),\\ \sigma _2(-1)= & {} \frac{1}{8} \frac{1}{{g^{\prime \prime }}^2(-1)} f^{(4)}(-1)-\frac{5}{12} \frac{g'''(-1)}{{g^{\prime \prime }}^3(-1)}f'''(-1)\\&+\,\left[ -\frac{1}{4} \frac{g^{(4)}(-1)}{{g^{\prime \prime }}^3(-1)} +\frac{5}{8} \frac{{g'''}^2(-1)}{{g^{\prime \prime }}^4(-1)}\right] f^{\prime \prime }(-1)\\&+\,\left[ -\frac{1}{8} \frac{g^{(5)}(-1)}{{g^{\prime \prime }}^3(-1)}+\frac{2}{3} \frac{g'''(-1)g^{(4)}(-1)}{{g^{\prime \prime }}^4(-1)} -\frac{5}{8} \frac{{g'''}^3(-1)}{{g^{\prime \prime }}^5(-1)}\right] f^{\prime }(-1) \end{aligned}$$

and we assert that

$$\begin{aligned} \sigma _s(-1)= & {} \frac{f^{(2s)}(-1)}{(g^{\prime \prime }(-1))^s} \frac{1}{2^s s!} + span \{ f^{(j)}(-1), j = 0,1, 2, \ldots , 2s- 1\},\nonumber \\ \sigma _s^{\prime }(-1)= & {} \frac{f^{(2s+1)}(-1)}{(g^{\prime \prime }(-1))^s} \frac{2^s s!}{(2s+1)!} + span \{f^{(j)}(-1), j = 0,1, 2, \ldots , 2s\}. \end{aligned}$$

(4.2)

Two alternative proofs of (4.2), which are surprisingly fiddly, are presented in Appendices B and C.

The expansion (4.1) provides the necessary information towards the construction of a Filon method, whether ‘plain’ or with added inner points. As before, let $s\ge 1$, $\nu \ge 0$ and (for $\nu \ge 1$) choose distinct internal points $c_1,\ldots ,c_\nu$. Recalling that the highest derivatives in the $m=s$ terms are $f^{(2s)}(-1)$ and $f^{(s)}(1)$, we seek a polynomial $p\in \mathbb {P}_{3s+\nu }$ such that

$$\begin{aligned} p^{(j)}(-1)= & {} f^{(j)}(-1),\quad j=0,\ldots ,2s,\quad p^{(j)}(1)=f^{(j)}(1),\quad j=0,\ldots ,s-1,\\ p(c_k)= & {} f(c_k),\quad k=1,\ldots ,\nu \end{aligned}$$

and set

$$\begin{aligned} Q_\omega ^{\mathsf {F},s,\nu }[f]=\int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x. \end{aligned}$$

Since $\mu _0(\omega )=O(\omega ^{-1/2})$ [11], it follows from (4.1) that

$$\begin{aligned} E_\omega ^{\mathsf {F},s,\nu }[f]= & {} Q_\omega ^{\mathsf {F},s,\nu }[f]-I_\omega [f]=I_\omega [p-f]\\\sim & {} -\frac{1}{(-\mathrm {i}\omega )^{s+1}} \left[ \frac{\sigma _s(1)-\sigma _s(-1)}{g^{\prime }(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} -\frac{\sigma _s'(-1)}{g^{\prime \prime }(-1)}\mathrm {e}^{\mathrm {i}\omega g(-1)}\right] +O(\omega ^{-s-3/2}), \end{aligned}$$

where $\sigma _0(x)=p(x)-f(x)$. Because of the interpolation conditions, only the (2s)th derivative survives in $\sigma _s(-1)$ and the $(2s+1)$st in $\sigma _s'(-1)$ while, like in Sect. 2, the only derivative surviving on the right is $p^{(s)}(1)-f^{(s)}(1)$. Therefore

$$\begin{aligned} E_\omega ^{\mathsf {F},s,\nu }[f]\sim & {} - \frac{1}{(-\mathrm {i}\omega )^{s+1}} \left[ \frac{p^{(s)}(1)-f^{(s)}(1)}{{g^{\prime }}^{s+1}(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} -\,\frac{2^ss!}{(2s+1)!} \frac{p^{(2s+1)}(-1)-f^{2s+1)}(-1)}{{g^{\prime \prime }}^{s+1}(-1)}\mathrm {e}^{\mathrm {i}\omega g(-1)}\right] \nonumber \\&+\,O(\omega ^{-s-3/2})\nonumber \\= & {} -\frac{1}{(-\mathrm {i}\omega )^{s+1}} e_\omega ^{\mathsf {F},s,\nu }[f]+O(\omega ^{-s-3/2}). \end{aligned}$$

(4.3)

Our two distinguished choices of inner nodes can be “translated” into the present setting. This is straightforward for EFCC, where we take, as before, $c_k=\cos (k\pi /(\nu +1))$, $k=1,\ldots ,\nu$ [4], but for EFJ we need to consider different choice of nodes. To maximise classical order for $\omega =0$ we need to maximise the orthogonality of the polynomial

$$\begin{aligned} (1+x)^{2s+1}(1-x)^s\prod _{k=1}^\nu (x-c_k) \end{aligned}$$

and this takes place when the $c_k$s are zeros of the Jacobi polynomial $\mathrm {P}_\nu ^{(s,2s+1)}$.

4.2 The case $\omega \gg 1$

As before, we need to distinguish between $\omega \gg 1$ and small $\omega \ge 0$. In the first case, the pertinent information is all in (4.3) and we use again PKT and [18]

$$\begin{aligned} \left| p^{(s)}(1)-f^{(s)}(1)\right|\le & {} \frac{s!2^{2s + 1}}{(\nu +3s)!} r(1) \Vert f^{(\nu +3s+1)}\Vert _\infty ,\\ \left| p^{(2s+1)}(-1)-f^{(2s+1)}(-1)\right|\le & {} \frac{(2s+1)!2^s}{(\nu +3s)!} |r(-1)| \Vert f^{(\nu +3s+1)}\Vert _\infty , \end{aligned}$$

where

$$\begin{aligned} r(x)=\prod _{k=1}^\nu (x-c_k). \end{aligned}$$

Exactly like in Sect. 2, the choice of interior points $c_k$ determines the size of $r(\pm 1)$. Nothing changes for EFCC and

$$\begin{aligned} r(1)=|r(-1)|=\frac{\nu +1}{2^\nu }, \end{aligned}$$

while for EFJ we use, like in Sect. 2, properties of Jacobi polynomials: since $\mathrm {P}_\nu ^{(\alpha ,\beta )}(-1)=(-1)^\nu \mathrm {P}_\nu ^{(\beta ,\alpha )}(1)$ [17, p. 256], we have

$$\begin{aligned} r(1)= & {} \tilde{\mathrm {P}}_\nu ^{(s,2s+1)}(1)=\frac{2^\nu (s+1)_\nu }{(3s+\nu +2)_\nu }=\frac{2^\nu (s+\nu )!(3s+\nu +1)!}{s!(3s+2\nu +1)!},\\ r(-1)= & {} \tilde{\mathrm {P}}_\nu ^{(s,2s+1)}(-1)=(-1)^\nu \tilde{\mathrm {P}}_\nu ^{(2s+1,s)}(1)=(-1)^\nu \frac{2^\nu (2s+2)_\nu }{(3s+\nu +2)_\nu }\\= & {} (-1)^\nu \frac{2^\nu (2s+\nu +1)!(3s+\nu +1)!}{(2s+1)!(3s+2\nu +1)!}. \end{aligned}$$

Once we compare the values of r(1) for EFJ and EFCC, the same picture emerges as in Sect. 2: EFCC is smaller by a very small margin. The same situation applies to $r(-1)$. All this can be easily verified for $\nu \gg 1$ using the Stirling formula, but this adds little to our understanding.

Fig. 9

The errors, to logarithmic scale, for $f(x)=\sin (x^2)$, $g(x)=(x+1)^2$, EFJ (slate blue) and EFCC (dark goldenrod) for $s=2$ and $\nu =4$. $\omega \in [0, 20]$ on the left, $\omega \in [0, 100]$ on the right

In Fig. 9 we have sketched $\log _{10}|Q_\omega ^{\mathsf {F},2,4}[f]-I_\omega [f]|$ for $f(x)=\sin (x^2)$ and $g(x)=(x+1)^2$. The right-hand plot demonstrates asymptotic behaviour: as expected from our analysis, EFCC wins over EFJ for large $\omega$.

4.3 Small $\omega \ge 0$

It is evident from the left-hand plot in Fig. 9 that for small $\omega \ge 0$ EFJ is substantially better than EFCC. This is completely in line with the behaviour in the absence of stationary points, which we have analysed in Sect. 3 and consistent with the fact that, for $\omega =0$, EFJ and EFCC are of conventional orders $3s+2\nu +1$ and $3s+\nu +1$, respectively.

Taking a leaf from Sect. 3, we use Peano Kernel theorem for $d=3s+\nu$, the highest degree of a polynomial integrated exactly by EFCC for $\omega =0$. In the current setting, however, we have lost symmetry and, instead of the approach of [7], we need to construct functions $K(\theta )$ from first principles. Our concern is with the quadrature

$$\begin{aligned} Q_0^{\mathsf {F},s,\nu }[f]=\sum _{j=0}^{2s} b_j^- f^{(j)}(-1)+\sum _{j=0}^{s-1} b_j^+ f^{(j)} +\sum _{k=1}^\nu b_k f(c_k)\approx I_0[f]=\int _{-1}^1 f(x)\mathrm {d}x, \end{aligned}$$

where the weights $b_j^{\pm }$ and $b_k$ can be obtained from the cardinal functions of Birkhoff–Hermite interpolation,

$$\begin{aligned} b_j^{\pm }=\int _{-1}^1 \ell _j^{\pm }(x)\mathrm {d}x,\quad b_k=\int _{-1}^1 \ell _k(x)\mathrm {d}x, \end{aligned}$$

where $\ell _j^{\pm },\ell _k\in \mathbb {P}_{3s+\nu }$ and

$$\begin{aligned}&{\ell ^-}^{(i)}_j(-1)= \left\{ \begin{array}{ll}1, &{}\quad i=j,\\ 0, &{}\quad i\ne j,\end{array}\right. \quad i=0,\ldots ,2s, \qquad {\ell ^+}^{(i)}_j(1)=0,\quad i=0,\ldots ,s-1, \\&\quad \ell _j^-(c_k)=0,\quad k=1,\ldots ,\nu ,\quad j=0,\ldots ,s;\\&{\ell ^+}^{(i)}_j(-1)=0,\quad i=0,\ldots ,2s,\quad {\ell ^+}^{(i)}_j(1)=\left\{ \begin{array}{ll}1, &{}\quad i=j,\\ 0, &{}\quad i\ne j,\end{array}\right. \quad i=0,\ldots ,s-1,\\&\quad \ell _j^+(c_k)=0,\quad k=1,\ldots ,\nu ,\quad j=0,\ldots ,s;\\&\ell _k^{(i)}(-1)=0,\quad i=0,\ldots ,2s,\quad \ell _k^{(i)}(1)=0,\quad i=0,\ldots ,s-1,\\&\quad \ell _k(c_r)= \left\{ \begin{array}{ll}1, &{}\quad r=k,\\ 0, &{}\quad r\ne k,\end{array}\right. \qquad k=1,\ldots ,\nu . \end{aligned}$$

Applying formally PKT with $d\in \{1,2,\ldots ,3s+\nu \}$ to the case $\omega =0$, we have

$$\begin{aligned} |E_0^{\mathsf {F},s,\nu }[f]|\le \Vert K\Vert _1 \Vert f^{(d+1)}\Vert _\infty , \end{aligned}$$

where

$$\begin{aligned} K(\theta )=\frac{(1-\theta )^{d+1}}{(d+1)!} -\sum _{j=0}^{s-1} \frac{b_j^+}{(d-j)!} (1-\theta )^{d-j} -\frac{1}{d!} \sum _{k=1}^\nu b_k(c_k-\theta )_+^d. \end{aligned}$$

Table 4 Peano kernel constants for EFJ and EFCC in the case of a stationary point

In Table 4 we display the Peano constants $\Vert K\Vert _1$ for EFJ and EFCC and a range of values of s and $\nu$ the same as in Tables 2 and 3. It is clear that the constants associated with EFJ are substantially smaller, implying significantly smaller error at $\omega =0$—this is completely consistent with Fig. 9.

The advantage of EFJ vis á vis EFCC grows fast with s, and this is demonstrated not just in Table 4 but also in Fig. 10, where we display the relevant constants to logarithmic scale.

An alternative way to compare EFJ and EFCC for $\omega =0$ and $d=3s+\nu$ is by comparing methods with different $(s,\nu )$ but the same d, similarly to Fig. 8. Thus, in Fig. 11 we display two such sequences: $d=15$ and $\nu =15-3s$ for $s=1,\ldots ,5$ and $d=24$, $\nu =24-3s$ for $s=1,\ldots ,8$.

Fig. 10

The logarithms of constants for EFCC (brighter line) and EFJ (darker line) for $s=1,\ldots ,5$ (s increases from top left to bottom right) and $\nu =1,\ldots ,6$

Fig. 11

The cases $d=15$ (on the left) and $d=24$ (on the right) for EFJ (yellow orange) and EFCC (cyan), both to logarithmic scale

Like in Sect. 3, this comparison is somewhat unfair to EFJ, since it is of substantially higher order at $\omega =0$. Thus, in Table 5 we depict the Peano constants $\Vert K\Vert _1$ for EFJ and $d=3s+2\nu$. Again, the constants decay very rapidly indeed, similarly to Table 3 for quadrature without stationary points.

Table 5 Peano kernel constants for EFJ and $d=3s+2\nu$ in the case of a stationary point

5 Conclusions

Practical design of Filon-type methods requires the computation of moments

$$\begin{aligned} \int _{-1}^1 x^r \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x \end{aligned}$$

for a suitable range of integers $r\ge 0$. Once this is feasible, the shear simplicity, flexibility and precision of Filon-type methods arguably render them the method of choice for the computation of highly oscillatory integrals. Thus, realistic upper bounds on their error are of great importance. (We note in passing that there are variants of the Filon method, not least the algorithm from [15], which obviate the need for moments by using a suitable nonpolynomial basis. By their very nature, they do not lend themselves to analysis using the PKT).

In this paper, we have derived such bounds using the methodology of the Peano Kernel theorem. This has led to tight bounds in two cases: for $\omega \gg 1$ (which, after all, is the main objective of Filon-type methods!) and $\omega =0$. In particular, we have compared two choices of internal points: Jacobi points, which maximise classical order for $\omega =0$, and Clenshaw–Curtis points, which are cheaper when the number of internal points is large. Our conclusion is that for $\omega \gg 1$ Clenshaw–Curtis is marginally more precise, but for $\omega =0$ the honours go to Jacobi points.

All this leaves an important lacuna: What is the choice of internal points likely to deliver the least uniform (for all $\omega \ge 0$) error? In all our calculations [cf. Figs. 5 and 9 (left)] the pattern (modulo oscillations) is the same: small error for $\omega =0$, subsequent increase (‘intermediate asymptotics’) and finally, once asymptotics take over, consistent decrease. The error, thus, is likely to be maximised in the regime of intermediate asymptotics. In all our calculations, Jacobi points are a clear winner there, yet there is neither a proof of this statement nor, indeed, a rigorous uniform bound on the error.

Acknowledgements

The work is supported by the Projects of International Cooperation and Exchanges NSFC-RS (Grant No. 11511130052) and the Key Science and Technology Program of Shaanxi Province of China (Grant No. 2016GY-080).

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: An explicit expression for the Birkhoff–Hermite interpolation polynomial

Our starting point is [19], where general explicit formulæ are presented: all we need is to specialise them to our case.

The interpolation conditions are

$$\begin{aligned} p^{(j)}(1)= & {} f^{(j)}(1), \quad p^{(j)}(-1) = f^{(j)}(-1), \quad j = 0, 1, \ldots , s - 1,\\ p(c_k)= & {} f(c_k), \quad k = 1, 2, \ldots , \nu \end{aligned}$$

and, writing p in the Lagrangian form,

$$\begin{aligned} p(x) = \sum _{j = 0}^{s - 1} \left[ \ell ^-_j(x) f^{(j)}(-1) + \ell ^+_j(x) f^{(j)}(1) \right] + \sum _{k = 1}^{\nu } \ell _k(x) f(c_i), \end{aligned}$$

where the cardinal functions are explicitly

$$\begin{aligned} \ell _k(x)= & {} \frac{(1-x^2)^s}{(1-c_k^2)^s} \prod _{\mathop {j\ne k}\limits ^{\scriptstyle j=1}}^\nu \frac{x-c_j}{c_k-c_j},\quad k=1,\ldots ,\nu ,\\ \ell ^-_j(x)= & {} \frac{r(x)}{j!} (x-1)^s(x+1)^j \sum _{i=0}^{s-j-1} \frac{\phi _-^{(i)}(-1)}{i!}(x+1)^i,\quad j=0,\ldots ,s-1,\\ \ell _j^+(x)= & {} \frac{r(x)}{j!} (x-1)^j(x+1)^s \sum _{i=0}^{s-1-j} \frac{\phi _+^{(i)}(1)}{i!} (x-1)^i,\quad j=0,\ldots ,s-1, \end{aligned}$$

where

$$\begin{aligned} \phi _-(x)=\frac{1}{(x-1)^s r(x)},\quad \phi _+(x)=\frac{1}{(x+1)^sr(x)}, \quad r(x) = \prod _{k = 1}^{\nu } (x - c_k). \end{aligned}$$

In the case of stationary points, the interpolation conditions need to be changed to

$$\begin{aligned} p^{(j)}(1)= & {} f^{(j)}(1), \quad j = 0, 1, \cdots , s - 1,\quad p^{(j)}(-1) = f^{(j)}(-1), \quad j = 0, 1, \ldots , 2s,\\ p(c_{k})= & {} f(c_k), \quad k = 1, 2, \ldots , \nu . \end{aligned}$$

The interpolation polynomial p of degree $3 s + \nu$ is

$$\begin{aligned} p(x) = \sum _{\ell = 0}^{2s} \ell ^-_{\ell }(x) f^{(j)}(-1) + \sum _{\ell = 0}^{s - 1} \ell ^+_{\ell }(x) f^{(j)}(1) + \sum _{k = 1}^{\nu } \ell _k(x) f(c_i), \end{aligned}$$

where the cardinal functions can be again presented explicitly using the machinery of [19],

$$\begin{aligned} \ell _k(x)= & {} \frac{(x+1)^{2s+1}(x-1)^{s}}{(c_k+1)^{2s+1}(c_k-1)^{s}} \prod _{\mathop {j\ne k}\limits ^{\scriptstyle j=1}}^\nu \frac{x-c_j}{c_k-c_j},\quad k=1,\ldots ,\nu ,\\ \ell ^-_k(x)= & {} \frac{r(x)}{k!} (x+1)^k(x-1)^s \sum _{i=0}^{2s-k} \frac{\phi _-^{(i)}(-1)}{i!}(x+1)^i,\quad k=0,\ldots ,2s,\\ \ell ^+_k(x)= & {} \frac{r(x)}{k!} (x-1)^k(x+1)^{2s+1} \sum _{i=0}^{s-1-k} \frac{\phi _+^{(i)}(1)}{i!} (x-1)^i,\quad k=0,\ldots ,s-1, \end{aligned}$$

where

$$\begin{aligned} \phi _-(x)=\frac{1}{(x-1)^s r(x)},\quad \phi _+(x)=\frac{1}{(x+1)^{2s + 1}r(x)}, \quad r(x) = \prod _{k = 1}^{\nu } (x - c_k). \end{aligned}$$

Appendix B: A proof of (4.2)

The key is to represent $\sigma _s[f](-1)$, $\sigma '_s[f](-1)$ and $\sigma _s[f](1)$ as a linear combination of derivatives of f(x). To this end we first establish a relationship between $\sigma ^{(m)}_k[f](-1)$ and $\sigma ^{(i)}_{k-1}[f](-1)$. For brevity, we omit the argument [f] for $\sigma _k[f]$. Let

$$\begin{aligned} f(x)= & {} \sum _{m = 0}^{\infty } \frac{f^{(m)}(-1)}{m!} (x+1)^m,\quad g(x) = \sum _{m = 2}^{\infty } \frac{g^{(m)}(-1)}{m!} (x+1)^m,\\ \sigma _k(x)= & {} \sum _{m = 0}^{\infty } \frac{\sigma _k^{(m)}(-1)}{m!} (x+1)^m,\quad k = 1, 2, \ldots . \end{aligned}$$

Therefore

$$\begin{aligned} \sigma _k(x)= & {} \frac{\hbox {d}}{\hbox {d} x} \frac{\sigma _{k-1}(x) - \sigma _{k-1}(-1)}{g^{\prime }(x)}= \frac{\sigma '_{k-1}(x)g^{\prime }(x) - [\sigma _{k-1}(x) - \sigma _{k-1}(-1)]g^{\prime \prime }(x)}{{g^{\prime }}^2(x)} \nonumber \\= & {} \frac{ \sum _{m = 2}^{\infty } A_m (x+1)^m}{\sum _{m = 2}^{\infty } B_m (x+1)^m} \end{aligned}$$

(B.1)

$$\begin{aligned}= & {} \sum _{m = 0}^{\infty } \frac{\sigma _k^{(m)}(-1)}{m!} (x+1)^m, \end{aligned}$$

(B.2)

where

$$\begin{aligned} \sum _{m = 2}^{\infty } B_m (x+1)^m= & {} \left[ \sum _{m = 1}^{\infty } \frac{g^{(m+1)}(-1)}{m!} (x+1)^m\right] ^{2},\\ \sum _{m = 2}^{\infty } A_m (x+1)^m= & {} \left[ \sum _{m = 0}^{\infty } \frac{\sigma _{k-1}^{(m+1)}(-1)}{m!} (x+1)^m\right] \left[ \sum _{m = 1}^{\infty } \frac{g^{(m+1)}(-1)}{m!} (x+1)^m\right] \\&-\,\left[ \sum _{m = 1}^{\infty } \frac{\sigma _{k-1}^{(m)}(-1)}{m!} (x+1)^m\right] \left[ \sum _{m = 0}^{\infty } \frac{g^{(m+2)}(-1)}{m!} (x+1)^m\right] , \end{aligned}$$

and this implies that

$$\begin{aligned} B_m= & {} \sum _{j = 1}^{m - 1} \frac{g^{(j+1)}(-1)}{j !} \frac{g^{(m - j+1)}(-1)}{(m - j) !},\\ A_m= & {} \sum _{j = 1}^{m} \frac{2j-m-1}{j! (m-j+1)!} \sigma _{k-1}^{(j)}(-1) g^{(m-j+2)}(-1). \end{aligned}$$

Note that $A_m$ is in the span of $\sigma _{k-1}^{(j)}(-1)$, $j = 1, 2, \ldots , m$, and that $B_2 = {g^{\prime \prime }}^2(-1)$. Equating (B.1) with (B.2) results in

$$\begin{aligned} \left[ \sum _{m = 0}^{\infty } \frac{\sigma _k^{(m)}(-1)}{m!} (x+1)^m\right] \left[ \sum _{m = 2}^{\infty } B_m (x+1)^m\right] = \sum _{m = 2}^{\infty } A_m (x+1)^m. \end{aligned}$$

Comparing coefficients of $(x+1)^m$ on the both sides yields an algebraic system for the unknowns $\frac{\sigma _k^{(m)}(-1)}{m!}B_2$,

$$\begin{aligned} \sigma _k^{(0)}(-1) B_2= & {} A_2,\\ \sigma _k^{(0)}(-1) B_3 + \frac{\sigma _k^{(1)}(-1)}{1!} B_2= & {} A_3,\\ \sigma _k^{(0)}(-1) B_4 + \frac{\sigma _k^{(1)}(-1)}{1!} B_3 + \frac{\sigma _k^{(2)}(-1)}{2!} B_2= & {} A_4,\\&\vdots&\\ \sigma _k^{(0)}(-1) B_m + \frac{\sigma _k^{(1)}(-1)}{1!} B_{m-1} +\cdots \frac{\sigma _k^{(m-2)}(-1)}{(m-2)!} B_2= & {} A_m. \end{aligned}$$

Using forward substitution, we observe that

$$\begin{aligned} \sigma _k^{(m-2)}(-1) = \frac{(m-2)!}{B_2} \left[ A_m-\sum _{i=0}^{m-3} \frac{\sigma _k^{(i)}(-1)}{i!} B_{m-i}\right] , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \sigma _k^{(n)}(-1) = \frac{n!}{B_2} \left[ A_{n+2}-\sum _{i=0}^{n-1} \frac{\sigma _k^{(i)}(-1)}{i!} B_{n+2-i}\right] . \end{aligned}$$

Combining the definitions of $A_m$ and $B_m$, we obtain the relation

$$\begin{aligned} \sigma _k^{(n)}(-1) = \frac{1}{(n+2)g^{\prime \prime }(-1)} \sigma _{k-1}^{(n+2)}(-1) + \mathrm {span}\{\sigma _{k-1}^{(i)}(-1), \;i=0,1,\ldots ,n+1\}. \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} \sigma _s(-1)= & {} \frac{\sigma _{s-1}^{\prime \prime }(-1)}{2 g^{\prime \prime }(-1)} + \mathrm {span} \{ \sigma _{s-1}^{(j)}(-1), \;j = 0,1\}\\= & {} \frac{\sigma _{s-2}^{(4)}(-1)}{(g^{\prime \prime }(-1))^2} \frac{1}{2 \cdot 4} + \mathrm {span} \{ \sigma _{s-2}^{(j)}(-1), \; j = 0,1, 2, 3\}\\&\vdots&\\= & {} \frac{f^{(2s)}(-1)}{(g^{\prime \prime }(-1))^s} \frac{1}{2^s s!} + \mathrm {span} \{ f^{(j)}(-1),\; j = 0,1, 2, \cdots , 2s- 1\}. \end{aligned}$$

Likewise,

$$\begin{aligned} \sigma _s^{\prime }(-1)= & {} \frac{\sigma _{s-1}'''(-1)}{3g^{\prime \prime }(-1)} + \mathrm {span} \{ \sigma _{s-1}^{(j)}(-1),\; j = 0,1, 2\}\\= & {} \frac{\sigma _{s-2}^{(5)}(-1)}{(g^{\prime \prime }(-1))^2} \frac{1}{3 \cdot 5} + \mathrm {span} \{ \sigma _{s-2}^{(j)}(-1),\; j = 0,1, 2, 3, 4\}\\&\vdots&\\= & {} \frac{f^{(2s+1)}(-1)}{(g^{\prime \prime }(-1))^s} \frac{2^s s!}{(2s+1)!} + \mathrm {span} \{f^{(j)}(-1),\; j = 0,1, 2, \cdots , 2s\}. \end{aligned}$$

This proof can be extended to higher-order stationary points, i.e. to $r \ge 2$ in a direct manner.

Appendix C: An alternative proof of (4.2)

We assume without loss of generality that $g(-1)=0$; otherwise, we rewrite (1.1) as

$$\begin{aligned} \mathrm {e}^{\mathrm {i}\omega g(-1)} \int _{-1}^1 f(x) \mathrm {e}^{\mathrm {i}\omega [g(x)-g(-1)]}\mathrm {d}x. \end{aligned}$$

Moreover, we assume that $g^{\prime \prime }(-1)>0$–otherwise, we toggle the signs of both g and $\omega$, derive an asymptotic expansion for $\omega \ll -1$ and finally toggle the signs again.

Our assumptions imply that $g^{\prime }>0$ in $(-1,1]$; hence, $\sqrt{g(x)}$ is a strictly monotonically increasing function there. We denote its inverse function by X(t). Changing the variable $x=X(t)$ in (1.1), we obtain

$$\begin{aligned} I_\omega [f]=\int _0^\kappa f(X(t)) X^{\prime }(t)\mathrm {e}^{\mathrm {i}\omega t^2}\mathrm {d}t, \end{aligned}$$

where $\kappa =\sqrt{g(1)}$. The new integral has a first-order stationary point at the origin, and we expand it using the approach from [11] but with an important difference. We commence by rewriting it as

$$\begin{aligned} f(X(0))\int _0^\kappa X^{\prime }(t)\mathrm {e}^{\mathrm {i}\omega t^2}\mathrm {d}t+\frac{1}{2\mathrm {i}\omega } \int _0^\kappa \frac{f(X(t))-f(X(0))}{t} X^{\prime }(t)\frac{\mathrm {d}\mathrm {e}^{\mathrm {i}\omega t^2}}{\mathrm {d}t}\mathrm {d}t. \end{aligned}$$

However, $X(0)=-1$ and $\int _0^\kappa X^{\prime }(t)\mathrm {e}^{\mathrm {i}\omega t^2}\mathrm {d}t=\mu _0(\omega )$; therefore,

$$\begin{aligned} I_\omega [f]=\mu _0(\omega )f(-1)+\frac{1}{2\mathrm {i}\omega } \int _0^\kappa \frac{f(X(t))-f(-1)}{t} X^{\prime }(t)\frac{\mathrm {d}\mathrm {e}^{\mathrm {i}\omega t^2}}{\mathrm {d}t}\mathrm {d}t \end{aligned}$$

and, integrating by parts and recalling that $X(\kappa )=1$,

$$\begin{aligned} I_\omega [f]= & {} \mu _0(\omega ) f(-1)+\frac{1}{2\mathrm {i}\omega } \left[ \frac{f(1)-f(-1)}{\kappa } X^{\prime }(\kappa ) \mathrm {e}^{\mathrm {i}\omega g(1)} -f^{\prime }(-1){X^{\prime }}^2(0) \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] \\&-\frac{1}{-2\mathrm {i}\omega } \int _0^\kappa \frac{\mathrm {d}}{\mathrm {d}x} \left[ \frac{f(X(t))-f(-1)}{t} X^{\prime }(t)\right] \mathrm {e}^{\mathrm {i}\omega t^2}\mathrm {d}t. \end{aligned}$$

Like in [11], we iterate this expression, the outcome being the asymptotic expansion

$$\begin{aligned} I_\omega [f]\sim & {} \mu _0(\omega )\sum _{m=0}^\infty \frac{\tilde{\sigma }_m(0)}{(-\mathrm {i}\omega )^m} -\sum _{m=0}^\infty \frac{1}{(-\mathrm {i}\omega )^{m+1}} \nonumber \\&\left[ \frac{\tilde{\sigma }_m(1)-\tilde{\sigma }_m(0)}{\kappa } X^{\prime }(\kappa )\mathrm {e}^{\mathrm {i}\omega (1)}-\tilde{\sigma }_m^{\prime }(0){X^{\prime }}^2(0)\mathrm {e}^{\mathrm {i}\omega g(-1)}\right] , \end{aligned}$$

(C.1)

where

$$\begin{aligned} \tilde{\sigma }_0(t)=f(X(t)),\qquad \tilde{\sigma }_{m+1}(t)=\frac{1}{X^{\prime }(t)} \frac{\mathrm {d}}{\mathrm {d}t} \left[ X^{\prime }(t)\frac{\tilde{\sigma }_m(t)-\tilde{\sigma }_m(0)}{2t}\right] ,\quad m\ge 0. \end{aligned}$$

The whole point is that asymptotic expansions (4.1) and (C.1) are identical and we deduce that $\sigma _m(-1)=\tilde{\sigma }_m(0)$, $m\ge 0$.

Recall that the purpose of the exercise is to identify the coefficient of the highest derivative $f^{(2m)}(-1)$ in $\sigma _m(-1)$. We commence by assuming that $X^{\prime }\equiv \mathrm {const.}$, i.e. that g(x) is a (positive) multiple of $x^2$. In that case, it follows by easy induction from

$$\begin{aligned} F(t):=f(X(t))=\sum _{\ell =0}^\infty \frac{F^{(\ell )}(0)}{\ell !}t^\ell \;\; \mathrm {and}\;\; \tilde{\sigma }_{m+1}=\frac{\mathrm {d}}{\mathrm {d}t} \frac{\tilde{\sigma }_m(t)-\tilde{\sigma }_m(0)}{2t} \end{aligned}$$

that

$$\begin{aligned} \tilde{\sigma }_m(t)=\sum _{\ell =0}^\infty \frac{\left( \frac{\ell +1}{2}\right) _{m}}{(\ell +2m)!} F^{(\ell +2m)}(0)t^\ell ,\qquad m\ge 0, \end{aligned}$$

therefore

$$\begin{aligned} \sigma _m(-1)=\tilde{\sigma }_m(0)=\frac{F^{(2m)}(0)}{4^mm!}. \end{aligned}$$

What is the highest derivative component of $F^{(2m)}(0)$?

$$\begin{aligned} \frac{\mathrm {d}F(t)}{\mathrm {d}t}= & {} f^{\prime }(X)X^{\prime },\\ \frac{\mathrm {d}^2 F(t)}{\mathrm {d}t^2}= & {} f^{\prime \prime }(X){X^{\prime }}^2+f^{\prime }(X)X^{\prime \prime },\\ \frac{\mathrm {d}^3 F(t)}{\mathrm {d}t^3}= & {} f'''(X){X^{\prime }}^3+3f^{\prime \prime }(X)X^{\prime }X^{\prime \prime }+f^{\prime }(X)X''' \end{aligned}$$

and so on—in general, by trivial induction,

$$\begin{aligned} \frac{\mathrm {d}^{2m} F(t)}{\mathrm {d}t^{2m}}=f^{(2m)}(X){X^{\prime }}^{2m}+\text{ lower } \text{ derivatives } \text{ of } \text{ f }. \end{aligned}$$

In particular, the highest derivative component of $F^{(2m)}(0)$ is $f^{(2m)}(-1) {X^{\prime }}^{2m}(0)$. Since $t^2=g(x) =g^{\prime \prime }(0)/2 (x+1)^2+O((x+1)^3)$, it follows at once that $X^{\prime }(0)=[2/g^{\prime \prime }(0)]^{1/2}$ (this is true regardless of $X^{\prime }$ being constant!) and we deduce that (4.2) is true.

Lifting the assumption that $X^{\prime }$ is constant is somewhat of an anticlimax. Because

$$\begin{aligned} \tilde{\sigma }_{m+1}(t)=\frac{\mathrm {d}}{\mathrm {d}t} \frac{\tilde{\sigma }_m(t)-\tilde{\sigma }_m(0)}{2t} +\frac{X^{\prime \prime }(t)}{X^{\prime }(t)} \frac{\tilde{\sigma }_m(t)-\tilde{\sigma }_m(0)}{2},\quad m\ge 0, \end{aligned}$$

the highest derivative enters our considerations only through the first term, which is independent of X. This means that (4.2) is true for all strictly monotone functions X.