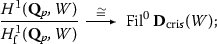Abstract
We show that the Euler system associated with Rankin–Selberg convolutions of modular forms, introduced in our earlier works with Lei and Kings, varies analytically as the modular forms vary in p-adic Coleman families. We prove an explicit reciprocity law for these families and use this to prove cases of the Bloch–Kato conjecture for Rankin–Selberg convolutions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background
Let \(p > 2\) be a prime. The purpose of this paper is to study the p-adic interpolation of étale Rankin–Eisenstein classes, which are Galois cohomology classes attached to pairs of modular forms f, g of weights \(\geqslant 2\), forming a “cohomological avatar” of the Rankin–Selberg L-function L(f, g, s).
In a previous work with Kings [19], we showed that these Rankin–Eisenstein classes for ordinary modular forms f, g interpolate in 3-parameter p-adic families, with f and g varying in Hida families and a third variable for twists by characters. We also proved an “explicit reciprocity law” relating certain specialisations of these families to critical values of Rankin–Selberg L-functions, with applications to the Birch–Swinnerton-Dyer conjecture for Artin twists of p-ordinary elliptic curves, extending earlier works of Bertolini–Darmon–Rotger [5, 6].
In this paper, we generalise these results to non-ordinary modular forms f, g, replacing the Hida families by Coleman families:
Theorem A
Let f, g be eigenforms of weights \(\geqslant 2\) and levels \(N_f, N_g\) coprime to p whose Hecke polynomials at p have distinct roots, and let \(f_\alpha , g_\alpha \) be non-critical p-stabilisations of f, g. Let \(\mathcal {F}, \mathcal {G}\) be Coleman families through \(f_\alpha , g_\alpha \) (over some sufficiently small affinoid discs \(V_1, V_2\) in weight space).
Then there exist classes
for each \(m \geqslant 1\) coprime to p and \(c > 1\) coprime to \(6pN_f N_g\), such that the specialisations of the classes \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m}\) are the Rankin–Eisenstein classes for all specialisations of \(\mathcal {F}\) and \(\mathcal {G}\), and all characters of \(\varGamma \) for which these classes are defined.
Here \(M_{V_1}(\mathcal {F})^*\) and \(M_{V_2}(\mathcal {G})^*\) are families of Galois representations over \(\mathcal {O}(V_1)\) and \(\mathcal {O}(V_2)\) attached to \(\mathcal {F}\) and \(\mathcal {G}\), and \(D^{\mathrm {la}}(\varGamma )\) is the algebra of distributions on the cyclotomic Galois group \(\varGamma \). A slightly modified version of this theorem holds for weight 1 forms as well. For a precise statement, see Theorem 5.4.2 below.
The proof of Theorem 5.4.2 reveals some new phenomena which may be of independent interest; the Galois modules in which these classes lie are, in a natural way, étale counterparts of the modules of “nearly overconvergent modular forms” introduced by Urban [32].
Theorem B
The image of the class \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{1}\) under an appropriately defined Perrin-Riou “big logarithm” map is Urban’s 3-variable p-adic Rankin–Selberg L-function for \(\mathcal {F}\) and \(\mathcal {G}\).
See Theorem 7.1.5 for a precise statement. In order to define the Perrin-Riou logarithm in this context, one needs to work with triangulations of \((\varphi , \varGamma )\)-modules over the Robba ring; we use here results of Liu [21], showing that the \((\varphi , \varGamma )\)-modules of the Galois representations \(M_{V_1}(\mathcal {F})^*\) and \(M_{V_2}(\mathcal {G})^*\) admit canonical triangulations.
Specialising this result at a point corresponding to a critical value of the Rankin–Selberg L-function, and applying the Euler system machine of Kolyvagin and Rubin, we obtain a case of the Bloch–Kato conjecture for Rankin convolutions:
Theorem C
(Theorem 8.2.1, Corollary 8.3.2) Let f, g be eigenforms of levels coprime to p and weights \(r, r'\), respectively, with \(1 \leqslant r' < r\), and let s be an integer such that \(r' \leqslant s \leqslant r-1\) (equivalently, such that L(f, g, s) is a critical value of the Rankin–Selberg L-function). Suppose \(L(f, g, s) \ne 0\). Then, under certain technical hypotheses, the Bloch–Kato Selmer groups \(H^1_{\mathrm {f}}(\mathbf {Q}, M(f) \otimes M(g)(s))\) and \(H^1_{\mathrm {f}}(\mathbf {Q}, M(f)^* \otimes M(g)^*(1-s))\) are both zero, where M(f) and M(g) are the p-adic representations attached to f and g.
One particularly interesting case is when \(f = f_E\) is the modular form attached to an elliptic curve E, and g is a weight 1 form corresponding to a 2-dimensional odd irreducible Artin representation \(\rho \). In this case, the Bloch–Kato Selmer group \(H^1_{\mathrm {f}}(\mathbf {Q}, M(f) \otimes M(g)(1))\) is essentially the \(\rho \)-isotypical part of the p-Selmer group of E over the splitting field of \(\rho \), so we obtain new cases of the finiteness of Selmer (and hence Tate–Shafarevich) groups. See Theorem 8.4.1 for the precise statement.
Remark
Since this paper was originally submitted, it has come to light that there are some unresolved technical issues in the paper [32] upon which Theorem B, and hence Theorem C, relies. We hope that these issues will be resolved in the near future; as a temporary expedient, we have given in Sect. 9 below an alternate proof of a weaker form of Theorem B which avoids these problems and thus suffices to give an unconditional proof of Theorem C.
This paper could not have existed without the tremendous legacy of mathematical ideas left by the late Robert Coleman. We use Coleman’s work in three vital ways: firstly, Coleman was the first to construct the p-adic families of modular forms along which we interpolate; secondly, the Perrin-Riou big logarithm map is a generalisation of Coleman power series in classical Iwasawa theory (introduced in Coleman’s Cambridge Part III dissertation); and finally, the results of [18] giving the link to values of p-adic L-functions, which are the main input to Theorem B, are proved using Coleman’s p-adic integration theory. We are happy to dedicate this paper to the memory of Robert Coleman, and we hope that his work continues to inspire other mathematicians as it has inspired us.
2 Analytic preliminaries
The aim of this section is to extend some of the results of Appendix A.2 of [20], by giving a criterion for a collection of cohomology classes to be interpolated by a distribution-valued cohomology class.
2.1 Continuous cohomology
We first collect some properties of Galois cohomology of profinite groups acting on “large” topological \(\mathbf {Z}_p\)-modules (not necessarily finitely generated over \(\mathbf {Z}_p\)). A very rich theory is available for groups G satisfying some mild finiteness hypotheses (see e.g. [29, §1.1]), but we will need to consider the Galois groups of infinite p-adic Lie extensions, which do not have good finiteness properties, so we shall proceed on a somewhat ad hoc basis, concentrating on \(H^0\) and \(H^1\).
Definition 2.1.1
-
(i)
If G is a profinite group, a topological G-module is an abelian topological group M endowed with an action of G which is (jointly) continuous as a map \(G \times M \rightarrow M\).
-
(ii)
For G and M as in (i), we define the cohomology groups \(H^*(G, M)\) as the cohomology of the usual complex of continuous cochains \(C^\bullet (G, M)\).
-
(iii)
We equip the groups \(C^i(G, M) = \mathrm{Maps}(G^i, M)\) with the compact-open topology (equivalently, the topology of uniform convergence).
With these definitions, the groups \(C^*(G, -)\) define a functor from topological G-modules to complexes of topological groups (i.e. the topology is functorial in M, and the differentials \(C^i(G, M) \rightarrow C^{i+1}(G, M)\) are continuous). Hence the cocycles \(Z^i(G, M)\) are closed in \(C^i(G, M)\). However, the cochains \(B^i(G, M)\) need not be closed in general, so the quotient topology on the cohomology groups \(H^i(G, M)\) may fail to be Hausdorff, and the subspace and quotient topologies on \(B^i(G, M)\) may not agree. Our next goal is to show that these pathologies can be avoided for \(i = 1\) and some special classes of modules M.
Let A be a Noetherian Banach algebra over \({\mathbf {Q}_p}\). Then any finitely generated A-module has a unique Banach space structure making it into a Banach A-module [7, Proposition 3.7.3/3].
Proposition 2.1.2
Let M be a finitely generated free A-module, equipped with a continuous A-linear action of a profinite group G. Then:
-
(1)
the space \(B^1(G, M)\) is closed in \(Z^1(G, M)\);
-
(2)
the subspace topology induced by \(B^1(G, M) \hookrightarrow Z^1(G, M)\) coincides with the quotient topology induced by \(M \twoheadrightarrow B^1(G, M)\);
-
(3)
the quotient map \(M \twoheadrightarrow B^1(G, M)\) has a continuous section (not necessarily A-linear or G-equivariant).
Proof
We begin by noting that \(Z^1(G, M)\) is, by definition, a closed subspace of the space \(C^1(G, M)\) of continuous functions from G to M, and since M is Banach, the topology of \(Z^1(G, M)\) is the Banach topology induced by the supremum norm on \(C^1(G, M)\). However, if \(M \cong A^{\oplus d}\) then we have
as a topological A-module. Since \(C^1(G, {\mathbf {Q}_p})^{\oplus d}\) is orthonormalisable as a \({\mathbf {Q}_p}\)-Banach space (every \({\mathbf {Q}_p}\)-Banach space has this property), it follows that \(C^1(G, M)\) is orthonormalisable as an A-Banach module, as orthonormalisability is preserved by base extension. However, \(B^1(G, M)\) is manifestly finitely generated as an A-module, and any finitely generated submodule of an orthonormalisable A-Banach module is closed [8, Lemma 2.8]. This proves (1).
Parts (2) and (3) now follow from the open image theorem [10, Proposition I.1.3], which shows that any continuous surjective map between \({\mathbf {Q}_p}\)-Banach spaces has a continuous section (and, in particular, a continuous bijection between \({\mathbf {Q}_p}\)-Banach spaces must be a homeomorphism). \(\square \)
Remark 2.1.3
It seems likely that this result is true for any finitely generated A-module M with G-action (without assuming that M be free), but we do not know how to prove this.
Definition 2.1.4
If X and Y are two \({\mathbf {Q}_p}\)-Banach spaces, let \(\mathcal {L}_w(X, Y)\) denote the space of continuous linear maps \(X \rightarrow Y\) equipped with the weak topology (the topology of pointwise convergence).
Now if M is a \({\mathbf {Q}_p}\)-Banach space with a continuous action of a profinite group G, then \(\mathcal {L}_w(X, M)\) also acquires a continuous G-action by composition, for any Banach space X.
Proposition 2.1.5
Suppose the differential \(d{:}\,M \rightarrow B^1(G, M)\) has a continuous section. Then the differential
also has a continuous section, for any Banach space X.
Proof
Let \(\phi {:}\,B^1(G, M) \rightarrow M\) be a section. We use this to define \(\tilde{\phi }{:}\,B^1(G, \mathcal {L}_w(X, M)) \rightarrow \mathcal {L}_w(X, M)\) as follows. Given \(\sigma \in B^1(G, \mathcal {L}_w(X, M))\), we may compose with an arbitrary \(x \in X\) to obtain an element \(\sigma _x \in B^1(G, M)\), and \(\phi (\sigma _x)\) is then an element of M. This defines a map from \(B^1(G, \mathcal {L}_w(X, M))\) to the space of linear maps \(X \rightarrow M\); however, for any \(\mu \in B^1(G, \mathcal {L}_w(X, M))\) we may write \(\mu = dL\) for some continuous L, and we can then describe the image of \(\mu (g)\) as the map obtained by composing L with  , which is thus continuous. This defines a continuous map \(\tilde{\phi }\) such that the diagram
, which is thus continuous. This defines a continuous map \(\tilde{\phi }\) such that the diagram

commutes for every \(x \in X\). However, in order to show that the top horizontal arrow is continuous, it suffices (by the definition of the weak topology) to show that the diagonal composition is continuous for every x. Since the left vertical arrow is obviously continuous, and \(\phi \) is continuous by assumption, this completes the proof. \(\square \)
Proposition 2.1.6
If M is a topological G-module, \(H \trianglelefteq G\) is a closed subgroup, and there exists a continuous section \(B^1(H, M) \rightarrow M\), then there is an exact sequence
Proof
The injectivity of the first map, and the exactness at \(H^1(G, M)\), is easily seen by a direct cocycle computation (which is valid for arbitrary topological G-modules).
Exactness at \(H^1(H, M)^{G/H}\) is much more subtle. Let \(\sigma {:}\,H \rightarrow M\) be a continuous cocycle whose class \([\sigma ] \in H^1(H, M)\) is G-invariant. Then, for any \(g \in G\), the element \(\sigma ^g - \sigma \) lies in \(B^1(H, M)\), where \(\sigma ^g\) is the cocycle \(h \mapsto g \sigma (g^{-1} h g)\). This defines a continuous map \(G \rightarrow B^1(H, M)\).
By hypothesis, the differential \(M \rightarrow B^1(H, M)\) has a continuous section. Composing this with the above map, we obtain a continuous map \(\phi {:}\,G \rightarrow M\) such that \(g\sigma (g^{-1}hg) - \sigma (h) = (h-1) \phi (g)\) for all \(h\in H\) and \(g \in G\). We may now argue as in the usual proof of the exactness of the inflation-restriction exact sequence for discrete modules [25, Proposition 1.6.5] to define a continuous 1-cochain \(\tilde{\sigma }{:}\,G \rightarrow M\) such that \(\tilde{\sigma } |_{H} = \sigma \) and \(d\tilde{\sigma } \in Z^2(G/H, M^H)\), which gives exactness at \(H^1(H, M)^{G/H}\). \(\square \)
Remark 2.1.7
The hypotheses of this proposition are satisfied, in particular, for any module of the form \(M = \mathcal {L}_w(X, N)\) where X is any Banach space, N is finitely generated and free over a Noetherian Banach algebra A, and the group H acts A-linearly on N and trivially on X. This covers all the cases we shall need below.
2.2 Distributions
For \(\lambda \in \mathbf {R}_{\geqslant 0}\), we define the Banach space \(C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) of order \(\lambda \) functions on \(\mathbf {Z}_p\) as in [11]. This has a Banach basis consisting of the functions \(p^{\lfloor \lambda \ell (n)\rfloor } \left( {\begin{array}{c}x\\ n\end{array}}\right) \) for \(n \geqslant 0\), where \(\ell (n)\) denotes the smallest integer \(L \geqslant 0\) such that \(p^L > n\). We define \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) as the continuous dual of \(C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\); for \(f \in C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) and \(\mu \in D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) we shall sometimes write \(\int f\, \mathrm {d}\mu \) for the evaluation \(\mu (f)\). The space \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) has a standard norm defined by
Proposition 2.2.1
For any integer \(h \geqslant \lfloor \lambda \rfloor \), the standard norm on \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) is equivalent to the norm defined by
Proof
See [10], Lemma II.2.5. \(\square \)
As well as the Banach topology induced by the above norms (the so-called strong topology), the space \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) also has a weak topology,Footnote 1 which can be defined as the weakest topology making the evaluation maps \(\mu \mapsto \int {f}\,\mathrm {d}\mu \) continuous for all \(f \in C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\).
Remark 2.2.2
The weak topology is much more useful for our purposes than the strong topology, since the natural map \(\mathbf {Z}_p\hookrightarrow D_0(\mathbf {Z}_p, {\mathbf {Q}_p})\) given by mapping \(a \in \mathbf {Z}_p\) to the linear functional \(f \mapsto f(a)\) is not continuous in the strong topology, while it is obviously continuous in the weak topology.
More generally, if M is a \({\mathbf {Q}_p}\)-Banach space, we define \(D_\lambda (\mathbf {Z}_p, M) = {{\mathrm{Hom}}}_{\mathrm {cts}}(C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p}), M)\); as before, this has a strong topology induced by the operator norm (which we write as \(\Vert -\Vert _\lambda \)), and a weak topology given by pointwise convergence on \(C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\).
Proposition 2.2.3
Let X be a compact Hausdorff space, and M a Banach space, and let \(\sigma {:}\,X \rightarrow D_\lambda (\mathbf {Z}_p, M)\) be a continuous map (with respect to the weak topology on \(D_\lambda (\mathbf {Z}_p, M))\). Then \(\sup \{ \Vert \sigma (x)\Vert _{\lambda }{:}\,x \in X\} < \infty \).
Proof
For each \(f \in C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\), the map \(X \rightarrow M\) given by \(x \mapsto \sigma (x)(f)\) is continuous, and hence bounded. By the Banach–Steinhaus theorem, this implies that the collection of linear maps \(\{ \sigma (x){:}\,x \in X\}\) is bounded in the uniform norm.\(\square \)
Definition 2.2.4
For \(h\ge 0\), denote by \(LP^{[0, h]}(\mathbf {Z}_p, {\mathbf {Q}_p})\) the space of locally polynomial functions on \(\mathbf {Z}_p\) of degree \(\leqslant h\). If M is a \({\mathbf {Q}_p}\)-vector space, write \(D_{\mathrm {alg}}^{[0, h]}(\mathbf {Z}_p,M)\) for the \({\mathbf {Q}_p}\)-linear homomorphisms of \(LP^{[0, h]}(\mathbf {Z}_p, {\mathbf {Q}_p})\) into M.
Remark 2.2.5
An element \(\mu \in LP^{[0, h]}(\mathbf {Z}_p, {\mathbf {Q}_p})\) is uniquely determined by a collection of values \(\int _{a+p^n\mathbf {Z}_p}x^i\mu (x)\) for \(i\in [0,h]\), \(a\in \mathbf {Z}_p\), \(n\in \mathbf {N}\), satisfying the compatibility relations
Lemma 2.2.6
Let \((\mu _n)_{n \geqslant 1}\) be a sequence of elements of \(D_\lambda (\mathbf {Z}_p, M)\) which is uniformly bounded (i.e. there is a constant C such that \(\Vert \mu _n\Vert _{\lambda } \leqslant C\) for all n), let \(\mu \in D_\lambda (\mathbf {Z}_p, M)\), and let \(h \geqslant \lfloor \lambda \rfloor \) be an integer. If we have \(\int f \, \mathrm {d}\mu _n \rightarrow \int f \, \mathrm {d}\mu \) as \(n \rightarrow \infty \) for all \(f\in LP^{[0, h]}(\mathbf {Z}_p, {\mathbf {Q}_p})\), then \(\mu _n \rightarrow \mu \) in the weak topology of \(D_\lambda (\mathbf {Z}_p, M)\).
Proof
This is immediate from the density of \(LP^{[0, h]}(\mathbf {Z}_p, {\mathbf {Q}_p})\) in \(C_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\). \(\square \)
Finally, if U is an open subset of \(\mathbf {Z}_p\), we define \(D_\lambda (U, M)\) as the subspace of \(D_\lambda (\mathbf {Z}_p, M)\) consisting of distributions supported in U; this is closed (in both weak and strong topology).
2.3 Cohomology of distribution modules
We now apply the theory of the preceding sections in the context of representations of Galois groups. Our arguments are closely based on those used by Colmez [10] for local Galois representations, but also incorporating some ideas from Appendix A.2 of [20].
We consider either of the two following settings: either K is a finite extension of \({\mathbf {Q}_p}\) and \(G = {{\mathrm{Gal}}}(\overline{K}{/}K)\), or K is a finite extension of \(\mathbf {Q}\) and \(G = {{\mathrm{Gal}}}(K^S{/}K)\), where \(K^S\) is the maximal extension of K unramified outside some finite set of places S including all infinite places and all places above p. In both cases we write \(H^*(K, -)\) for \(H^*(G, -)\); this notation is a little abusive in the global setting, but this should not cause any major confusion.
We set \(K_\infty = K(\mu _{p^\infty })\), and \(H = {{\mathrm{Gal}}}(\overline{K}{/}K_\infty )\) (resp. \({{\mathrm{Gal}}}(K^S{/}K_\infty )\) in the global case). Thus H is closed in G and the cyclotomic character identifies \(\varGamma = G{/}H\) with an open subset of \(\mathbf {Z}_p^\times \).
Remark 2.3.1
More generally, one may take for \(K_\infty \) any abelian p-adic Lie extension of K of dimension 1; see forthcoming work of Francesc Castella and Ming-Lun Hsieh for an application of this theory in the context of anticyclotomic extensions of imaginary quadratic fields.
As in Sect. 2.1 above, we let A be a Noetherian \({\mathbf {Q}_p}\)-Banach algebra, and M a finite free A-module with a continuous A-linear action of H, and we fix a choice of norm \(\Vert \cdot \Vert _M\) on M making it into a Banach A-module. We shall be concerned with the continuous cohomology \(H^1(K_\infty , D_{\lambda }(\varGamma , M))\), where \(D_{\lambda }(\varGamma , M)\) is equipped with the weak topology. Note that this cohomology group is endowed with a supremum seminorm, since every continuous cocycle \(H \rightarrow D_\lambda (\varGamma , M)\) is bounded by Proposition 2.2.3.
Proposition 2.3.2
Let \(\lambda \in \mathbf {R}_{\geqslant 0}\). Then \(H^1(K_\infty , D_\lambda (\varGamma , M))\) injects into \(H^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(\varGamma , M))\) for any integer \(h \geqslant \lfloor \lambda \rfloor \).
An element \(\mu \in H^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(K_\infty , M))\) is in the image of this injection if and only if the sequence

is bounded as \(n \rightarrow \infty \), where \(\left\| \cdot \right\| \) is the norm on \(H^1(K_\infty , M)\) induced by the norm of M. Moreover, if this condition holds, we have
where \(\Vert \mu \Vert _\lambda \) is the supremum seminorm on \(H^1(K_\infty , D_\lambda (\varGamma , M))\) and D is a constant independent of K and M.
Proof
For the injectivity, see Proposition II.2.1 of [10], where this result is proved for arbitrary Banach representations M such that \(B^1(K_\infty , M)\) is closed in \(Z^1(K_\infty , M)\); Proposition 2.1.2 shows that this is automatic under our present hypotheses on M (the argument in op.cit. is given for K local, but it applies identically in the global case too).
To describe the image of this map, we follow the argument of Proposition II.2.3 of op.cit. in which the result is shown for \(A = {\mathbf {Q}_p}\) and K local. Exactly as in op.cit., given any class in \(H^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(\varGamma , M))\) satisfying \((\star )\), then we may represent it by a cocycle \(g \mapsto \mu (g)\) in \(Z^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(\varGamma , M))\) which also satisfies \((\star )\) in the supremum norm. For each \(h \in H\), we see that \(\mu (h)\) lies in the image of \(D_\lambda (\varGamma , M) \hookrightarrow D^{[0, h]}_{\mathrm {alg}}(\varGamma , M)\). Thus \(\mu \) defines a cocycle on H with values in \(D_\lambda (\varGamma , M)\). Moreover, the values \(\Vert \mu (h)\Vert _\lambda \) for \(h \in H\) are bounded above by a constant multiple of the supremum of the sequence in \((\star )\), by Proposition 2.2.1.
It remains to check that the cocycle \(g \mapsto \mu (g)\) is continuous (for the weak topology of \(D_\lambda (\varGamma , M)\)). This is asserted without proof loc.cit., and we are grateful to Pierre Colmez for explaining the argument. Since H is a compact Hausdorff space, it suffices to show that for every convergent sequence \(g_n \rightarrow g\), the sequence \(\mu _n := \mu (g_n)\) converges to \(\mu (g)\) in \(D_\lambda (\varGamma , M)\). However, by construction we know that \(\int f\, \mathrm {d}\mu _n\) converges to \(\int f\, \mathrm {d}\mu \) for each \(f \in LP^{[0,h]}(\varGamma , {\mathbf {Q}_p})\). Since the \(\mu _n\) are uniformly bounded, Lemma 2.2.6 shows that they converge weakly to \(\mu (g)\) as required. \(\square \)
We now consider a special case of this statement. We impose the stronger assumption that M is a continuous representation of the larger group \(G = {{\mathrm{Gal}}}(\overline{K}/K)\) (resp. \({{\mathrm{Gal}}}(K^S/K)\) in the global case), rather than just of H. We equip \(D_\lambda (\varGamma , M)\) with an action of G by
where [g] is the image of g in \(\varGamma \).
Proposition 2.3.3
Let \(\lambda \in \mathbf {R}_{\geqslant 0}\), \(h \geqslant \lfloor \lambda \rfloor \) an integer, and suppose we are given elements \(x_{n, j} \in H^1(K_\infty , M)^{\varGamma _n = \chi ^j}\), for all \(n \geqslant 0\) and \(0 \leqslant j \leqslant h\), satisfying the following conditions:
-
For all \(n \geqslant 0\), we have \(\sum _{\gamma \in \varGamma _n{/}\varGamma _{n + 1}} \chi (\gamma )^{-j} \gamma \cdot x_{n+1, j} = x_{n, j}\).
-
There is a constant C such that
$$\begin{aligned} \left\| p^{-hn} \sum _{j = 0}^h (-1)^j \left( {\begin{array}{c}h\\ j\end{array}}\right) x_{n, j}\right\| \leqslant Cp^{\lfloor \lambda n \rfloor } \end{aligned}$$for all n.
Then there is a unique element \(\mu \in H^1\left( K_\infty , D_\lambda (\varGamma , M)\right) ^\varGamma \) satisfying
for all \(n \geqslant 0\) and \(0 \leqslant j \leqslant h\), and there is a constant D independent of K and of M such that
where \(\Vert \mu \Vert _\lambda \) is the seminorm on \(H^1(K_\infty , D_\lambda (\varGamma , M))\) induced by the norm of \(D_\lambda (\varGamma , M)\).
Proof
We claim first that there is a unique \(\mu ^{\mathrm {alg}} \in H^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(\varGamma , M))^\varGamma \) such that
This follows from the fact that the functions \(\phi _{n, j}(x) :=x^j \mathbf {1}_{1 + p^n \mathbf {Z}_p}(x)\) for \(n \geqslant 0\) and \(0 \leqslant j \leqslant h\), and their translates under \(\varGamma \), span the space \(LP^{[0, h]}(\varGamma , {\mathbf {Q}_p})\).
By Proposition 2.3.2, the existence of the constant C implies that \(\mu ^{\mathrm {alg}}\) is the image of a class \(\mu \in H^1(K_\infty , D_\lambda (\varGamma , M))\), which must itself be \(\varGamma \)-invariant since the injection \( H^1(K_\infty , D_\lambda (\varGamma , M)) \hookrightarrow H^1(K_\infty , D_{\mathrm {alg}}^{[0, h]}(\varGamma , M))\) commutes with the action of \(\varGamma \). This proposition also shows that \(\Vert \mu \Vert _\lambda \) is bounded above by CD. \(\square \)
Using the inflation-restriction exact sequence (and the fact that \(\varGamma \) has cohomological dimension 1) we see that \(\mu \) lifts to a class in \(H^1(K, D_{\lambda }(\varGamma , M))\). This lift is not necessarily unique, but it is unique modulo \(H^1(\varGamma , D_\lambda (\varGamma , M^{G_{K_\infty }}))\) (and thus genuinely unique if \(M^{G_{K_\infty }} = 0\)).
2.4 Iwasawa cohomology
We now show that there is an interpretation of the module \(H^1(K, D_\lambda (\varGamma , M))\) in terms of Iwasawa cohomology. Since the group G has excellent finiteness properties (unlike its subgroup H), we have the general finite-generation and base-change results of [29] at our disposal.
We now assume that A is a reduced affinoid algebra over \({\mathbf {Q}_p}\). By a theorem of Chenevier (see [9, Lemma 3.18]) we may find a Banach algebra norm on A, with associated unit ball \(A^{\circ } = \{ a \in A{:}\,\Vert a\Vert \leqslant 1\}\), and a compatible Banach A-module norm on M with unit ball \(M^{\circ } \subset M\), such that G preserves \(M^{\circ }\) and \(M^{\circ }\) is locally free as an \(A^{\circ }\)-module.
Definition 2.4.1
We set
This is evidently independent of the choice of lattice \(M^{\circ }\).
Proposition 2.4.2
The module \(H^1_{\mathrm {Iw}}(K_\infty , M)\) is finitely generated over \(D_0(\varGamma , A)\), and there are isomorphisms
Proof
Let \(A^{\circ }\) be as above. Then the ring \(B^{\circ } = D_0(\varGamma , A^{\circ }) \cong A^{\circ }[[X]]\) is Noetherian, and it is complete and separated with respect to the ideal \(I = (p, [\gamma ] - 1)\), where \(\gamma \) is a topological generator of \(\varGamma {/}\varGamma _{\mathrm {tors}}\); moreover, \(D_0(\varGamma , M^{\circ }) = B^{\circ } \otimes _{A^{\circ }} M^{\circ }\) is a flat \(B^{\circ }\)-module. Hence [29, Theorem 1.1] applies. By part (4) of the theorem, we see that \(H^1(K, D_0(\varGamma , M^{\circ }))\) is finitely generated over \(D_0(\varGamma , A^{\circ })\). Moreover, part (3) of the theorem shows that
and every power \(I^m\) contains the kernel of \(D_0(\varGamma , A^{\circ }) \rightarrow A[\varGamma {/}\varGamma _n]\) for all sufficiently large n, so we also have an isomorphism
where the last equality follows by Shapiro’s lemma. Inverting p we obtain the corresponding results with A-coefficients. Finally, we obtain the statement with locally analytic distributions by applying Theorem 1.9 of op.cit. (in the case \(n = \infty \)). \(\square \)
Corollary 2.4.3
In the above setting, for any \(\lambda \in \mathbf {R}_{\geqslant 0}\) there is a map
compatible with the natural maps to \(H^1(K, M(\chi ^{-1}))\) for each character \(\chi {:}\,M \rightarrow A^\times \).
Proof
This follows from the fact that there is a continuous homomorphism \(D_\lambda (\varGamma , A) \rightarrow D^{\mathrm {la}}(\varGamma , A)\), which gives (by the functoriality of continuous cohomology) a map
We now compose this with the second map from the previous proposition. \(\square \)
Proposition 2.4.4
If K is a global field, then for every prime \(v \ne p\), the inflation map
is an isomorphism.
Proof
The corresponding statement for Iwasawa cohomology is well known, and the result now follows by tensoring with \(D^{\mathrm {la}}(\varGamma , A)\). \(\square \)
A very slightly finer statement is possible if we consider coefficients in a field:
Proposition 2.4.5
Suppose V is a finite-dimensional p-adic representation of G. Then
Proof
In the local case, this surprisingly non-trivial result is Proposition II.3.1 of [10]. The proof relies on local Tate duality at one point, so we shall explain briefly how this can be removed in order to obtain the result in the global case as well.
Firstly, from the finite generation of \(H^2_{\mathrm {Iw}}(K_\infty , V)\) as a \(\varLambda (\varGamma )\)-module, there exists a k such that \(H^2_{\mathrm {Iw}}(K_\infty , V(k))^{\varGamma } = 0\). We may suppose (by twisting) that we have, in fact, \(H^2_{\mathrm {Iw}}(K_\infty , V)^{\varGamma } = 0\).
Let \(\nu _n = (\gamma - 1)^n\) where \(\gamma \) is a topological generator of \(\varGamma \), and let T be a lattice in V. Then the submodules \(H^2_{\mathrm {Iw}}(K_\infty , T)[\nu _n]\) are an ascending sequence of \(\varLambda (\varGamma )\)-submodules of the finitely generated module \(H^2_{\mathrm {Iw}}(K_\infty , T)\). Since \(\varLambda (\varGamma )\) is Noetherian and \(H^2_{\mathrm {Iw}}(K_\infty , T)\) is finitely generated, we conclude that this sequence of modules must eventually stabilise. But all the modules in this sequence are finite, since \(H^2_{\mathrm {Iw}}(K_\infty , V)^{\varGamma }\) vanishes by assumption; this implies that there is a uniform power of p (independent of n) which annihilates \(H^2_{\mathrm {Iw}}(K_\infty , T)[\nu _n]\) for all \(n \geqslant 1\) (compare the proof of [20, Proposition A.2.10], which is a similar argument with \(\nu _n = (\gamma - 1)^n\) replaced by \(\gamma ^{p^n}-1\)). With this in hand we may proceed as in [10]. \(\square \)
Remark 2.4.6
We do not know whether this result is valid for general p-adic Banach algebras (or even for affinoid algebras). It is also significant that the map is not an isometry with respect to the natural norms on either side; there is a denominator arising from the torsion in \(H^2_{\mathrm {Iw}}(K_\infty , T)\), which is difficult to control a priori (and, in particular, could potentially vary as we change the field K in an Euler system argument). We are grateful to Ming-Lun Hsieh for pointing this out. We shall instead control denominators by means of the proposition that follows, in which the denominator depends on an \(H^0\) rather than an \(H^2\).
Proposition 2.4.7
Suppose that V is a finite-dimensional \({\mathbf {Q}_p}\)-linear representation of G such that \(H^0(K_\infty , V) = 0\), and let \(D'\) be a constant annihilating the finite group \(H^0(K_\infty , V/T)\), for T a G-invariant \(\mathbf {Z}_p\)-lattice in V.
Let \(x_{n, j}\) be a collection of elements, and C a constant, satisfying the hypotheses of Proposition 2.3.3, and let \(\mu \in H^1(K, D_\lambda (\varGamma , V))\) be the resulting distribution. Then for every character \(\kappa \) of \(\varGamma \), we have
where on the left-hand side \(\Vert \cdot \Vert \) denotes the norm on \(H^1(K, V(\kappa ^{-1}))\) for which the unit ball is the image of \(H^1(K, T(\kappa ^{-1}))\) (and D is as in Proposition 2.3.2).
Proof
We know that \(\Vert \mu \Vert _\lambda \leqslant CD \) as elements of \(H^1(K_\infty , D_\lambda (\varGamma , V))^\varGamma \). So \(\Vert \int _\varGamma \kappa \, \mathrm {d}\mu \Vert \leqslant CD \Vert \kappa \Vert _\lambda \) as elements of \(H^1(K_\infty , V(\kappa ^{-1}))^\varGamma \).
By the definition of the supremum seminorm, this is equivalent to stating that the class \( CD \Vert \kappa \Vert _\lambda \cdot \int _\varGamma \kappa \, \mathrm {d}\mu \) is the image of a class in \(H^1(K_\infty , T(\kappa ^{-1}))\). This class is not uniquely determined, and hence not necessarily \(\varGamma \)-invariant, but the constant \(D'\) was chosen to annihilate the kernel of \(H^1(K_\infty , T(\kappa ^{-1})) \rightarrow H^1(K_\infty , V(\kappa ^{-1}))\), so \( CDD ' \Vert \kappa \Vert _\lambda \cdot \int _\varGamma \kappa \, \mathrm {d}\mu \) lifts to a \(\varGamma \)-invariant class.
Since \(H^0(K_\infty , T) = 0\), we conclude that \(H^1(K, T(\kappa ^{-1})) \rightarrow H^1(K_\infty , T(\kappa ^{-1}))^\varGamma \) is an isomorphism; thus \( CDD ' \Vert \kappa \Vert _\lambda \cdot \int _\varGamma \kappa \, \mathrm {d}\mu \) is in the image of the map \(H^1(K, T(\kappa ^{-1})) \rightarrow H^1(K, V(\kappa ^{-1}))\) as required. \(\square \)
3 Cyclotomic compatibility congruences
In this section, we establish that the Beilinson–Flach cohomology classes constructed in [19, 20] satisfy the criteria of the previous section, allowing us to interpolate them by finite-order distributions.
3.1 Modular curves: notation and conventions
For \(N \geqslant 4\), we write \(Y_1(N)\) for the modular curve over \(\mathbf {Z}[1/N]\) parametrising elliptic curves with a point of order N. Note that the cusp \(\infty \) is not defined over \(\mathbf {Q}\) in this model, but rather over \(\mathbf {Q}(\mu _N)\).
More generally, for M, N integers with \(M + N \geqslant 5\), we write Y(M, N) for the modular curve over \(\mathbf {Z}[1/MN]\) parametrising elliptic curves together with two sections \((e_1, e_2)\) which define an embedding of group schemes \(\mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}{/}N\mathbf {Z}\hookrightarrow E\) (so that \(Y_1(N) = Y(1, N)\)). We shall only consider Y(M, N) in the case \(M \mid N\), in which case the Weil pairing defines a canonical map from Y(M, N) to the scheme \(\mu _M^{\circ }\) of primitive Mth roots of unity, whose fibres are geometrically connected.
If A is an integer prime to MN, we shall sometimes also consider the curve Y(M, N(A)) over \(\mathbf {Z}[1/AMN]\), parametrising elliptic curves with points \(e_1, e_2\) as above together with a cyclic subgroup of order A.
If Y is one of the curves Y(M, N) or Y(M, N(A)), we write \(\mathscr {H}_{\mathbf {Z}_p}\) the relative Tate module of the universal elliptic curve over Y, which is an étale \(\mathbf {Z}_p\)-sheaf on Y[1 / p]. If the prime p is clear from context, we shall sometimes drop the subscript and write \(\mathscr {H}\) for \(\mathscr {H}_{\mathbf {Z}_p}\). We write \(\mathscr {H}_{{\mathbf {Q}_p}}\) for the associated \({\mathbf {Q}_p}\)-sheaf. We write \({{\mathrm{TSym}}}^k \mathscr {H}_{\mathbf {Z}_p}\) for the sheaf of degree k symmetric tensors over \(\mathscr {H}_{\mathbf {Z}_p}\); note that this is not isomorphic to the kth symmetric power, although these coincide after inverting p.
Remark 3.1.1
In this paper we will frequently consider étale cohomology of modular curves Y(M, N(A)) or products of pairs of such curves. All the coefficient sheaves we consider will be inverse systems of finite étale sheaves of p-power order, and we shall always work over bases on which p is invertible. To lighten the notation, the convention that if p is not invertible on Y, then \(H^*_{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y, -)\) is a shorthand for \(H^*_{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y[1/p], -)\).
3.2 Iwasawa sheaves
We recall some definitions and notation from [19]. Let \(M, N \geqslant 1\) be integers with \(M \mid N\) and \(M + N \geqslant 5\). Then, associated with the étale sheaf of abelian groups \(\mathscr {H}_{\mathbf {Z}_p}\) on Y(M, N)[1 / p], we have a sheaf of Iwasawa algebras \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})\) (c.f. Section 2.3 in op.cit.). For \(c>1\) coprime to 6MNp, let
be the Eisenstein–Iwasawa class, as defined in [19, §4.3]. We now recall the definition of the Rankin–Iwasawa class on the product \(Y(M, N)^2\), which is the image of \({}_c\mathcal {E}\mathcal {I}_{1,N}\) via a three-step procedure.
Firstly, let us write \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})^{[j]}=\varLambda (\mathscr {H}_{\mathbf {Z}_p}) \otimes {{\mathrm{TSym}}}^j\left( \mathscr {H}_{\mathbf {Z}_p}\right) \) for \(j \geqslant 0\). Then we have a morphism of étale sheaves on Y(M, N)[1 / p], the Clebsch–Gordan map,

as defined in [19, Definition 5.1.1].
Secondly, let \(Y(M, N)^2\) denote the fibre product \(Y(M, N) \times _{\mu _M^{\circ }} Y(M, N)\), where \(\mu _M^{\circ }\) is the group of primitive Mth roots of unity as above. We denote by \(\varLambda ^{[j, j]}\) the exterior tensor product \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})^{[j]}\boxtimes \varLambda (\mathscr {H}_{\mathbf {Z}_p})^{[j]}\) on \(Y(M, N)^2\). Pushforward along the diagonal embedding \(\varDelta {:}\,Y(M, N) \hookrightarrow Y(M, N)^2\) gives a map

Thirdly, for \(a\in \mathbf {Z}{/}M\mathbf {Z}\), denote by \(u_a\) the automorphism of \(Y(M,N)^2\) which is the identity on the first Y(M, N) factor and is given by \((E,e_1,e_2)\mapsto \left( E,e_1+a\frac{N}{M}e_2,e_2\right) \) on the second factor.
Definition 3.2.1
For integers \(M, N \geqslant 1\) with \(M \mid N\) and \(M + N \geqslant 5\), \(j \geqslant 0\), \(a \in \mathbf {Z}{/}m \mathbf {Z}\), p a prime \(> 2\), and \(c > 1\) coprime to 6M Np, define the Rankin–Iwasawa class
The primary purpose of introducing the Rankin–Iwasawa class is that it is easy to prove norm-compatibility relations for it. Our actual interest is in a second, related class, defined by pushing forward \({}_c\mathcal {RI}^{[j]}_{M, N, a}\) via a degeneracy map.
Definition 3.2.2
For integers \(m \geqslant 1\) and \(N \geqslant 4\), \(j \geqslant 0\), \(a \in \mathbf {Z}{/}m\mathbf {Z}\), and \(c > 1\) coprime to 6mNp, define the Beilinson–Flach class
to be the image of \({}_c\mathcal {RI}^{[j]}_{m,mN,a}\) under the map \((t_m\times t_m)_*\), where

is the map given in terms of moduli spaces as
Remark 3.2.3
Note that \(t_m\) corresponds to \(z \mapsto z/m\) on the upper half-plane.
Finally, recall that there are natural maps
which, for a geometric generic point \(\eta \), are given by the maps \(\varLambda (\mathscr {H}_{\eta }) \rightarrow \varLambda (\mathscr {H}_{\eta }) \otimes {{\mathrm{TSym}}}^j \mathscr {H}_{\eta }\), \([x] \mapsto [x] \otimes x^{\otimes j}\).
3.3 Compatibility congruences
We now come to the key technical result required for the rest of this paper. Let \(h \geqslant 1\). For each \(r \geqslant 1\), we would like to prove a congruence modulo \(p^{hr}\) relating the classes
for \(0 \leqslant j \leqslant h\). Here \({{\mathrm{Res}}}_{p^r}^{p^{hr}}\) denotes the pullback along the natural map
which corresponds classically to restriction of cocycles in Galois cohomology.
Definition 3.3.1
For an arbitrary m, let \(Z(m,mN) \subseteq Y(m, m N)^2\) denote the preimage of the diagonal subvariety of \(Y_1(N)\) under the natural projection map \(Y(m, m N)^2 \rightarrow Y_1(N)^2\) (i.e. the map corresponding to the identity on the upper half-plane, not the map \(t_m\)).
Note 3.3.2
The subvariety Z(m, mN) is preserved by the action of \(\varGamma _1(N) \times \varGamma _1(N)\) and in particular by the action of the element \(u_a =\left( 1, \left( {\begin{matrix}1 &{} a \\ 0 &{} 1\end{matrix}}\right) \right) \) for any \(a \in \mathbf {Z}{/}m \mathbf {Z}\). Since \(u_a\) is an automorphism, and its inverse is \(u_{-a}\), we have \((u_a)_* = (u_{-a})^*\).
There is a canonical section of the sheaf \((\mathscr {H}_{\mathbf {Z}_p} \boxtimes \mathscr {H}_{\mathbf {Z}_p})(-1)\) over the subvariety Z(m, mN), given by the Weil pairing (since along Z(m, mN) the two universal elliptic curves coincide). We call this element \(\mathcal {CG}\) (for “Clebsch–Gordan”), since the Clebsch–Gordan map \(CG^{[j]}\) is given by cup-product with the jth divided power \(\mathcal {CG}^{[j]}\) of this element. For \(t \geqslant 1\), we write \(\mathcal {CG}_t\) for the image of \(\mathcal {CG}\) modulo \(p^t\). Note that we have
for any \(a \in \mathbf {Z}{/}m\mathbf {Z}\), since \(\mathcal {CG}\) is independent of the level structure.
Let i be the inclusion of Z(m, mN) into \(Y(m, m N)^2\), so the diagonal embedding factors as

By construction, the element \({}_c\mathcal {RI}^{[j]}_{m, m N, a}\in H^3_{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y(m,mN)^2,\varLambda ^{[j,j]}(2-j))\) is given by
We now take integers \(r \geqslant 1\) and \(h \geqslant 1\) as above, and we assume \(p \not \mid m\). We also assume that the following condition is satisfied:
Assumption 3.3.3
We have \(p^{(h-1)r} \mid N\), so there is a canonical section \(Y_{hr}\) of \(\mathscr {H}_{hr}\) over \(Y(mp^r, mp^r N)\).
Under this assumption, the moment map modulo \(p^{hr}\) is given by cup-product with the element \(Y_{hr}\), so we obtain the following somewhat messy formula:
Proposition 3.3.4
For any \(a \in \mathbf {Z}{/}mp^{hr} \mathbf {Z}\), we have the following equality modulo \(p^{hr}\):
Proof
This is a straightforward exercise from the definition of multiplication in the algebra \({{\mathrm{TSym}}}^\bullet \) (the factor of \((h-j)!\) appears because \((Y \boxtimes Y)^{[h-j]} = (h - j)! Y^{[h-j]} \boxtimes Y^{[h-j]}\)). \(\square \)
We can now prove the main theorem of this section:
Theorem 3.3.5
Suppose that \(p \mid N\). Then for any \(a \in \mathbf {Z}{/}mp^{hr} \mathbf {Z}\) and any m coprime to p, we have
Proof
It follows from [19, Theorem 5.3.1] that if \(N'\) is any multiple of N with the same prime divisors as N, then \({}_c \mathcal {BF}^{[j]}_{p^{r}, N, a}\) is the image of \({}_c \mathcal {BF}^{[j]}_{p^{r}, N', a}\) under pushforward along the natural degeneracy map \(Y_1(N')\rightarrow Y_1(N)\). We can therefore assume without loss of generality that N satisfies Assumption 3.3.3.
We may factor the map \((t_{m p^r} \times t_{m p^r})_*\) as the composite of a map on the coefficient sheaves, which is a morphism
of sheaves on \(Y(mp^r, mp^r N)^2\), followed by the pushforward via \(t_{mp^r} \times t_{mp^r}\) on the underlying modular curve.
We claim that when restricted to the image of \(u_a \circ \varDelta {:}\, Y(mp^r, mp^r N) \rightarrow Z(mp^r, mp^rN)\), the section \(a \cdot Y_{r} \boxtimes Y_{r} + \mathcal {CG}_{r} \otimes \zeta _{p^{r}}\) of \(\mathscr {H}_r \boxtimes \mathscr {H}_r\) is in the kernel of \((t_{mp^r} \times t_{mp^r})_\sharp \).
This follows from the fact that the map \((t_{mp^r} \times t_{mp^r})_\sharp \) is given by quotienting out by the first component of the level structure in each factor: on the fibre at a point \((E_1, P_1, Q_1) \times (E_2, P_2, Q_2)\) of \(Y(mp^r, mp^r N)^2\), the fibre of \(\mathscr {H}\boxtimes \mathscr {H}\) is the Tate module of \(E_1 \times E_2\), and the map \((t_{mp^r} \times t_{mp^r})_\sharp \) is the quotient map \(E_1 \times E_2 \rightarrow E_1{/}\langle P_1 \rangle \times E_2{/}\langle P_2 \rangle \). A point in the image of \(u_a \circ \varDelta \) is given by \((E, P, Q) \times (E, P + a NQ , Q)\) for some point (E, P, Q) of \(Y(mp^r, mp^r N)\), and the section \(\mathcal {CG}_r \otimes \zeta _{p^r}\) is given by \( N Q \boxtimes P - P \boxtimes NQ \). Thus we have
which is annihilated by \((t_{mp^r} \times t_{mp^r})_\sharp \) as claimed.
Since this element is annihilated by \((t_{mp^r} \times t_{mp^r})_\sharp \) modulo \(p^r\), its hth tensor power is annihilated by the same map modulo \(p^{hr}\). This gives the congruence stated above. \(\square \)
Remark 3.3.6
We shall in fact use a slight refinement of this theorem. Let \(\mathcal {E}\) be the universal elliptic curve over \(Y_1(N)\), and let \(D' = C - \{0\} \subset \mathcal {E}[p]\), where C is the universal level p subgroup. Then there is a subsheaf \(\mathscr {H}_{\mathbf {Z}_p} \langle D' \rangle \) of \(\mathscr {H}_{\mathbf {Z}_p}\), which is the preimage of \(D'\) under reduction modulo p, and a corresponding sheaf of Iwasawa modules \(\varLambda (\mathscr {H}_{\mathbf {Z}_p}\langle D'\rangle )\).
The Beilinson–Flach elements for \(p \mid N\) are, by construction, the images of elements of the group
and exactly the same argument as above shows that we have a congruence modulo \(p^{hr}\) in this group. We will need this below, in order to interpolate our elements in Coleman families.
3.4 Galois representations: notation and conventions
In this section, we shall fix notations for Galois representations attached to modular forms. Let f be a normalised cuspidal Hecke eigenform of some weight \(k+2 \geqslant 2\) and level \(N_f \geqslant 4\), and let L be a number field containing the q-expansion coefficients of f.
Definition 3.4.1
For each prime \(\mathfrak {P}\mid p\) of L, we write \(M_{L_{\mathfrak {P}}}(f)\) for the maximal subspace of
on which the Hecke operator \(T_\ell \), for every prime \(\ell \), acts as multiplication by \(a_\ell (f)\). Dually, we write \(M_{L_{\mathfrak {P}}}(f)^*\) for the maximal quotient of the space
on which the dual Hecke operators \(T_\ell '\) act as \(a_\ell (f)\).
Both spaces \(M_{L_{\mathfrak {P}}}(f)\) and \(M_{L_{\mathfrak {P}}}(f)^*\) are 2-dimensional \(L_{\mathfrak {P}}\)-vector spaces with continuous actions of \({{\mathrm{Gal}}}(\overline{\mathbf {Q}}{/}\mathbf {Q})\), unramified outside S, where S is the finite set of primes dividing \(p N_f\). The twist by 1 implies that the Poincaré duality pairing
is well defined (and perfect), justifying the notation. If f is new and \(f^*\) is the eigenform conjugate to f, then the natural map \(M_{L_{\mathfrak {P}}}(f^*)(1) \rightarrow M_{L_{\mathfrak {P}}}(f)^*\) is an isomorphism of \(L_{\mathfrak {P}}\)-vector spaces, although we shall rarely use this.
If f, g are two eigenforms (of some levels \(N_f, N_g\) and weights \(k+2, k' + 2 \geqslant 2\)) with coefficients in L, we write \(M_{L_{\mathfrak {P}}}(f \otimes g)\) for the tensor product \(M_{L_{\mathfrak {P}}}(f) \otimes _{L_{\mathfrak {P}}} M_{L_\mathfrak {P}}(g)\) and similarly for the dual \(M_{L_{\mathfrak {P}}}(f \otimes g)^*\). Via the Künneth formula, we may regard \(M_{L_{\mathfrak {P}}}(f \otimes g)^*\) as a quotient of \(H^2_{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y_1(N)^2_{\overline{\mathbf {Q}}},{{\mathrm{TSym}}}^{[k,k']}(\mathscr {H}_{{\mathbf {Q}_p}})(2))\otimes _{{\mathbf {Q}_p}} L_{\mathfrak {P}}\), for any \(N \geqslant 4\) divisible by \(N_f\) and \(N_g\), where \({{\mathrm{TSym}}}^{[k,k']}(\mathscr {H}_{{\mathbf {Q}_p}})\) denotes the étale \({\mathbf {Q}_p}\)-sheaf \({{\mathrm{TSym}}}^k \mathscr {H}_{{\mathbf {Q}_p}} \boxtimes {{\mathrm{TSym}}}^{k'} \mathscr {H}_{{\mathbf {Q}_p}}\).
3.5 Consequences for pairs of newforms
We now use the congruences of Theorem 3.3.5, together with the p-adic analytic machinery of Sect. 2, in order to define “unbounded Iwasawa cohomology classes” interpolating the Beilinson–Flach elements for a given pair (f, g) of eigenforms.
Remark 3.5.1
We shall prove a considerably stronger result below (incorporating variation in Coleman families) which will mostly supersede Theorem 3.5.9: see Theorem 5.4.2. However, the proof of the stronger result is much more involved, so for the reader’s convenience we have given this more direct argument.
Let us choose two normalised cuspidal eigenforms f, g, of weights \(k + 2, k' + 2\) and levels \(N_f, N_g\), respectively, with \(k, k' \geqslant 0\). Let L be a number field containing the coefficients of f and g, and \(\mathfrak {P}\) a prime of L above p, so that the Galois representation \(M_{L_\mathfrak {P}}(f \otimes g)^*\) of Sect. 3.4 is defined. Assume that \(0\le j\le \min \{k,k'\}\), and let N be an integer divisible by \(N_f\) and \(N_g\) and having the same prime factors as \(N_f N_g\). Let \(m\ge 1\). Recall from [19, Definition 3.3.1] that we have an étale Eisenstein class
which can be constructed using Beilinson’s Eisenstein symbol (and in particular is the image of a class in motivic cohomology). By abuse of notation, we also denote by \(\mathrm {Eis}^{[k,k',j]}_{{\acute{\mathrm{e}}{\mathrm{t}}},1,mN}\) the pullback of this class to \(Y(m,mN)^2\).
Definition 3.5.2
For \(a \in \mathbf {Z}/m\mathbf {Z}\), define \(\mathcal {BF}^{[f, g, j]}_{m,a}\) to be the image of \((u_a)_*\mathrm {Eis}^{[k,k',j]}_{{\acute{\mathrm{e}}{\mathrm{t}}},1,mN}\) under the following composition of maps:

This is independent of the choice of N. For \(c > 1\) coprime to \(6mpN_f N_g\), we define
Remark 3.5.3
Note that for \(m = 1\) the class \(\mathcal {BF}^{[f, g, j]}_{m,a}\) is the Eisenstein class \(\mathrm{AJ}_{f,g,{\acute{\mathrm{e}}{\mathrm{t}}}}\left( \mathrm {Eis}^{[k, k', j]}_{{\acute{\mathrm{e}}{\mathrm{t}}},1,N}\right) \) of [18, §5.4].
Let us recall the connection between these classes and the Iwasawa-theoretic classes of the previous sections. Recall that we have maps
for each \(k \geqslant j\).
Proposition 3.5.4
([19, Proposition 5.2.3 (3)]) The class \({}_c \mathcal {BF}^{[f, g, j]}_{m,a}\) coincides with the image of
under projection to the (f, g)-eigenspace.
We now consider “p-stabilised” versions of these objects. If \(p \not \mid N_f\), we choose a root \(\alpha _f \in L\) of the Hecke polynomial of f (after extending L if necessary), and we let \(f_\alpha \) be the corresponding p-stabilisation of f, so \(f_\alpha \) is a normalised eigenform of level \(N_{f_\alpha }=p N_f\), with \(U_p\)-eigenvalue \(\alpha _f\) and the same \(T_\ell \)-eigenvalues as f for all \(\ell \ne p\). If \(p \mid N_f\), then we assume that \(a_p(f) \ne 0\), and we set \(\alpha _f = a_p(f)\) and (for consistency) \(f_\alpha = f\) and \(N_{f_\alpha }=N_f\). We define \(\alpha _g\) and \(g_\alpha \) similarly.
If \(p \not \mid N_f N_g\), then the class \({}_c \mathcal {BF}^{[f_\alpha ,g_\alpha ,j]}_{m, a}\) for m coprime to p is related to the Eisenstein class for the forms f, g as follows. There is a correspondence \({{\mathrm{Pr}}}^{\alpha _f}{:}\,Y_1(p N_f) \rightarrow Y_1(N_f)\) given by \({{\mathrm{pr}}}_1 - \frac{\beta }{p^{k + 1}} {{\mathrm{pr}}}_2\), and \(({{\mathrm{Pr}}}^{\alpha _f})_*\) gives an isomorphism
and similarly for g.
Proposition 3.5.5
For \(p \not \mid m N_f N_g\), we have
If \(p \mid N_f\) but \(p \not \mid m N_g\), then we have
Proof
This is a restatement of Lemma 5.6.4 and Remark 5.6.5 of [19]. \(\square \)
We shall now interpolate the \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha , j]}_{m, a}\) for varying m and j, under the following assumption:
Assumption 3.5.6
The automorphic representations \(\pi _f\) and \(\pi _g\) corresponding to f and g are not twists of each other.
Note 3.5.7
Assumption 3.5.6 is automatically satisfied if \(k \ne k'\).
Let m be coprime to p and \(r\ge 1\). Then Assumption 3.5.6 implies that \(H^0(\mathbf {Q}(\mu _{mp^\infty }),M_{L_{\mathfrak {P}}}(f\otimes g))=0\), so the restriction map induces an isomorphism
Convention
By abuse of notation, we write \({}_c\mathcal {BF}^{[f_\alpha ,g_\alpha ,j]}_{mp^r,a}\) for the image of the Beilinson–Flach element in \(H^1(\mathbf {Q}({\mu _{mp^\infty }}),M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*)^{\varGamma _r=\chi ^{j}}\).
These elements satisfy the following compatibility:
Lemma 3.5.8
Let \(m\ge 1\) be coprime to p, and let \(r\ge 0\). Then
Proof
This follows from the second norm relation for the Rankin–Iwasawa classes (c.f. [19, Theorem 5.4.4]). \(\square \)
We impose the following “small slope” assumption:
Theorem 3.5.9
If the small slope assumption (3.5.1) holds, then for any integers \(m \geqslant 1\) coprime to p and \(a \in (\mathbf {Z}{/}mp^\infty \mathbf {Z})^\times \), there exists a unique element
where \(\lambda = v_p(\alpha _f \alpha _g)\), such that for every \(r \geqslant 0\) and \(0 \leqslant j \leqslant \min (k, k')\), the image of \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a}\) in \(H^1(\mathbf {Q}(\mu _{m p^r}), M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*(-j))\) is given by
Remark 3.5.10
Compare Theorem 6.8.4 of [20], which is the case \(k = k' = 0\).
Proof
This amounts to reorganising the output of Theorem 3.3.5 and Proposition 2.3.3. Let \(h = \min (k, k')\). Consider the composition of maps

where \(e_h\) is the canonical basis of \(\mathbf {Z}_p(h)\) over \(\mathbf {Q}(\mu _{p^\infty })\), and the third map is given by \(({{\mathrm{mom}}}^{k-h} \cdot {{\mathrm{id}}}) \boxtimes ({{\mathrm{mom}}}^{k'-h} \cdot {{\mathrm{id}}})\). An unpleasant manipulation of factorials shows that the image of the expression in Theorem 3.3.5 under this composition of maps is equal to
where we write \(y_{r, j}\) for the quantity
The image of \(H^2_{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y_1(N)^2_{\overline{\mathbf {Q}}}, {{\mathrm{TSym}}}^{[k,k']}(\mathscr {H}_{\mathbf {Z}_p})(2)) \otimes \mathcal {O}_{\mathfrak {P}}\) in \(M_{L_{\mathfrak {P}}}(f \otimes g)^*\) is a \(\mathcal {O}_{\mathfrak {P}}\)-lattice, and hence it defines a norm \(\Vert \cdot \Vert \) on \(M_{L_{\mathfrak {P}}}(f \otimes g)^*\). So Theorem 3.3.5 gives the norm bound
where the implied constant in the O() term depends on \(k,k',h\) but not on r. Combining this fact with Lemma 3.5.8, we deduce that the quantities
satisfy the hypotheses of Proposition 2.3.3, so there exists an element
interpolating the \(x_{r,j}\). Using again that \(H^0(\mathbf {Q}(\mu _{mp^\infty }), M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*)=0\) by Assumption 3.5.6, this element lifts uniquely to
and has the required interpolation properties, which finishes the proof. \(\square \)
We now note, for future use, the following vital property of the classes \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a}\). Denote by

Perrin-Riou’s regulator map (c.f. [27] and [23, Appendix B]).
Proposition 3.5.11
If the stronger inequality
holds, then the projection of \(\mathcal {L}_{M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*}\left( {}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a}\right) \) to the \(\varphi = (\alpha _f \alpha _g)^{-1}\)-eigenspace of \(\mathbf {Q}(\mu _m) \otimes _{\mathbf {Q}} \mathbf {D}_{\mathrm {cris}}(M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*)\) is zero.
Proof
Let W be this eigenspace. It is well known that the projection of \(\mathcal {L}_{M(f \otimes g)^*}\) to W gives a map
where \(\lambda = v_p(\alpha _f \alpha _g)\) as before. So it gives a map
However, for any character of \(\varGamma \) of the form \(z \mapsto z^j \chi (z)\), with \(0 \leqslant j \leqslant \min (k, k')\) and \(\chi \) of finite order, the image of \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a}\) in \(H^1(\mathbf {Q}(\mu _m) \otimes {\mathbf {Q}_p}, M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*(-j-\chi ))\) lies in the Bloch–Kato \(H^1_\mathrm {g}\) subspace, by construction (c.f. [19, Proposition 3.3.2]). If \(\chi \) is non-trivial (so that the interpolation factors relating \(\mathcal {L}_{M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*}\) to the dual-exponential map are invertible, see [23, Theorem B.5]), then this implies that \(\mathcal {L}_{M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*}({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a})(j + \chi ) = 0\).
So the projection of \(\mathcal {L}_{M_{L_{\mathfrak {P}}}(f_\alpha \otimes g_\alpha )^*}\left( {}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, a}\right) \) to W is an element of \(D_{2\lambda }(\varGamma , {\mathbf {Q}_p}) \otimes W\) which vanishes at all but finitely many characters of the form \(j + \chi \) with \(j \in \{0, \ldots , \min (k, k')\}\) and \(\chi \) of finite order. Since \(2\lambda < 1 + \min (k, k')\), this projection must be zero as required. \(\square \)
Remark 3.5.12
We shall in fact show below that the result of Proposition 3.5.11 is actually true whenever \(\alpha _f \alpha _g\) satisfies the weaker assumption (3.5.1) (i.e. whenever the class \({}_c \mathcal {BF}^{f_\alpha , g_\alpha }_{m, a}\) is defined), by deforming Proposition 3.5.11 along a Coleman family.
This vanishing property is natural in the context of Conjecture 8.2.6 of [20], which predicts the existence of an element in \(\bigwedge ^2 H^1_{\mathrm {Iw}}(\mathbf {Q}(\mu _{mp^\infty }), M_{L_{\mathfrak {P}}}(f \otimes g)^*)\) from which the Beilinson–Flach elements (for all choices of \(\alpha _f\) and \(\alpha _g\)) can be obtained by pairing with the map \(\mathcal {L}_{M_{L_{\mathfrak {P}}}(f \otimes g)^*}\) and projecting to a \(\varphi \)-eigenspace. Clearly, pairing an element of \(\bigwedge ^2\) with the same linear functional twice will give zero.
4 Overconvergent étale cohomology and Coleman families
We now recall the construction of p-adic families of Galois representations attached to modular forms via “big” étale sheaves on modular curves. We follow the account of [1, §3], but with somewhat altered conventions (for reasons which will become clear later). We also use some results of Hansen [14] (from whom we have also borrowed the terminology “overconvergent étale cohomology”).
4.1 Set-up and notation
Definition 4.1.1
We write \(\mathcal {W}\) for the rigid-analytic space over \({\mathbf {Q}_p}\) parametrising continuous characters of the group \(\mathbf {Z}_p^\times \). For an integer \(m \geqslant 0\), we shall write \(\mathcal {W}_m\) for the wide open subspace parametrising “m-accessible” weights, which are those satisfying \(v_p(\kappa (t)^{p-1} - 1) > \frac{1}{p^m(p-1)}\) for all \(t \in \mathbf {Z}_p^\times \).
Remark 4.1.2
Note that \(\mathcal {W}\) is isomorphic to a disjoint union of \(p-1\) open unit discs, and the bounded-by-1 rigid-analytic functions on \(\mathcal {W}\) are canonically \(\varLambda (\mathbf {Z}_p^\times )\); while \(\mathcal {W}_m\) is the union of the corresponding open subdiscs of radius \(p^{-1/p^m(p-1)}\) with centres in \(\mathbf {Z}_p^\times \). Thus \(\mathcal {W}_0\) (which is the space denoted by \(\mathcal {W}^*\) in [1]) contains every \({\mathbf {Q}_p}\)-point of \(\mathcal {W}\), and in particular every weight of the form \(z \mapsto z^j\), \(j \in \mathbf {Z}\).
Now let us fix some coefficient field E (a finite extension of \({\mathbf {Q}_p}\)) with ring of integers \(\mathcal {O}_E\).
Definition 4.1.3
We let U denote a wide open disc defined over E, contained in \(\mathcal {W}_m\) for some \(m \geqslant 0\), and \(\varLambda _U\) the \(\mathcal {O}_E\)-algebra of rigid functions on U bounded by 1 (so \(\varLambda _U \cong \mathcal {O}_E[[u]]\)). We write \(\kappa _U\) for the universal character \(\mathbf {Z}_p^\times \hookrightarrow \varLambda (\mathbf {Z}_p^\times )^\times \rightarrow \varLambda _U^\times \).
The ring \(\varLambda _U\) is endowed with two topologies: the p-adic topology (which we shall not use) and the \(m_U\)-adic topology, which is the topology induced by the ideals \(m_U^n\), where \(m_U\) is the maximal ideal of \(\varLambda _U\).
Definition 4.1.4
For \(m \geqslant 0\), we write \(LA_m(\mathbf {Z}_p, \varLambda _U)\) for the space of functions \(\mathbf {Z}_p\rightarrow \varLambda _U\) such that for all \(a \in \mathbf {Z}{/}p^m \mathbf {Z}\), the function \(z \mapsto f(a + p^m z)\) is given by a power series \(\sum _{n \geqslant 0} b_n z^n\) with \(b_n \rightarrow 0\) in the \(m_U\)-adic topology of \(\varLambda _U\).
Lemma 4.1.5
If \(U \subseteq \mathcal {W}_m\), then the function \(z \mapsto \kappa _U(1 + pz)\) is in \(LA_m(\mathbf {Z}_p, \varLambda _U)\).
Proof
This is a standard computation, but we have not been able to find a reference, so we shall give a brief sketch of the proof. Let us write \(X_m\) for the affinoid rigid-analytic space over \({\mathbf {Q}_p}\) defined by \(\{ x{:}\,|x - a| \leqslant p^{-m}\text { for some } a \in \mathbf {Z}_p\} \subseteq \mathbf {A}^1_\mathrm {rig}\). Then \(LA_m(\mathbf {Z}_p, \varLambda _U)\) is precisely the space of functions \(\mathbf {Z}_p\rightarrow \varLambda _U\) which extend to rigid-analytic \(\varLambda _U\)-valued functions on \(X_m\).
Firstly, the map \(x \mapsto \frac{\log (1 + px)}{\log (1 + p)}\) is a bijection from \(\mathbf {Z}_p\) to \(\mathbf {Z}_p\) which extends to a rigid-analytic isomorphism from \(X_m\) to itself for every m, so it suffices to show that \(x \mapsto \kappa _U( (1 + p)^x )\) extends to a \(\varLambda _U\)-valued rigid-analytic function on \(X_m\) whenever \(U \subseteq \mathcal {W}_m\). It suffices to consider the universal case \(U = \mathcal {W}_m\). After enlarging the coefficient field E if necessary, we identify \(\varLambda _U\) with \(\mathcal {O}_E[[u]]\) in such a way that \(\kappa _U(1 + p) = 1 + \varepsilon u\) where \(\varepsilon \) is some element of \(\mathcal {O}_E\) of valuation \(\frac{1}{(p-1)p^m}\). Then
and we have \(\varepsilon ^n \left( {\begin{array}{c}x\\ m\end{array}}\right) \in LA_m(\mathbf {Z}_p, \mathbf {Z}_p)\) for any n, by [11, Theorem 1.29]. \(\square \)
Remark 4.1.6
It is important to use the right topology on \(\varLambda _U\), because if one takes \(U = \mathcal {W}_m\) and writes \(x \mapsto \kappa _U( 1 + p^{m+1}x )\) as a series \(\sum c_n x^n\) with \(c_n \in \varLambda _U\), the \(c_n\) tend to zero \(m_U\)-adically (the above argument shows in fact that \(c_n \in m_U^n\)), but they do not tend to zero p-adically.
4.2 The spaces \(D_U^{\circ }(T_0)\) and \(D_U^{\circ }(T_0')\)
Definition 4.2.1
Let H be the group \(\mathbf {Z}_p^{\oplus 2}\). We define subsets \(T_0, T_0' \subset H\) by
Proposition 4.2.2
The subset \(T_0\) is preserved by right multiplication by the monoid \(\varSigma _0(p) = \begin{pmatrix}{\mathbf {Z}_p^\times } &{}\quad {\mathbf {Z}_p} \\ {\mathbf {Z}_p} &{}\quad {p\mathbf {Z}_p} \end{pmatrix} \subset \mathrm{Mat}_{2 \times 2}(\mathbf {Z}_p)\), and \(T_0'\) by the monoid \(\varSigma _0'(p) = \begin{pmatrix}{\mathbf {Z}_p} &{}\quad {\mathbf {Z}_p} \\ {p\mathbf {Z}_p} &{}\quad {\mathbf {Z}_p^\times } \end{pmatrix}\). In particular, both \(T_0\) and \(T_0'\) are preserved by scalar multiplication by \(\mathbf {Z}_p^\times \). \(\square \)
Remark 4.2.3
The definition of \(T_0\) coincides with that used in [1] (and our \(\varSigma _0(p)\) is their \(\Xi (p)\)). The subspace \(T_0'\) is the image of \(T_0\) under right multiplication by \(\begin{pmatrix}{0} &{}\quad {-1} \\ {p} &{}\quad {0} \end{pmatrix}\) and conjugation by this element interchanges \(\varSigma _0(p)\) and \(\varSigma _0'(p)\).
Definition 4.2.4
For \(m \geqslant 0\), we write \(A^{\circ }_{U, m}(T_0)\) for the space of functions
which are homogenous of weight \(\kappa _U\), i.e. satisfy
for \(\gamma \in \mathbf {Z}_p^\times \), \(t \in T_0\), and are such that the function \(z\mapsto f(1, z)\) lies in \(LA_m(\mathbf {Z}_p, \varLambda _U)\). We equip this module with the topology defined by the subgroups \(m_U^n A^{\circ }_{U, m}\).
Similarly, we write \(A^{\circ }_{U, m}(T_0')\) for the space of functions \(T_0' \rightarrow \varLambda _U\) which are homogenous of weight \(\kappa _U\) and are such that \(z \mapsto f(pz, 1) \in LA_m(\mathbf {Z}_p, \varLambda _U)\), again endowed with the \(m_U\)-adic topology.
Proposition 4.2.5
If \(U \subseteq \mathcal {W}_m\), then the space \(A^{\circ }_{U, m}(T_0)\) is preserved by the left action of \(\varSigma _0(p)\) on functions \(T_0 \rightarrow \varLambda _U\) defined by
and similarly for \(A^{\circ }_{U, m}(T_0')\).
Proof
We give the proof for \(T_0'\); the proof for \(T_0\) is similar.
Unravelling the definition of the actions, we must show that if \(\gamma = \left( {\begin{matrix}a &{} \quad \\ b &{} pc\end{matrix}}\right) \quad d \in \varSigma _0'(p)\) and \(f \in A^{\circ }_U(T_0')\), then the function
is in \( LA _m(\mathbf {Z}_p, \varLambda _U)\). Since \( LA _m(\mathbf {Z}_p, \varLambda _U)\) is closed under multiplication and contains \(\mathbf {Z}_p\), it suffices to check that \(z \mapsto \kappa _U(1 + pd^{-1}bz)\) and \(z \mapsto f\left( p \cdot \frac{c + az}{d + pbz}, 1\right) \) are in this space. For the factor \(\kappa _U(1 + pd^{-1}bz)\) this follows from Lemma 4.1.5.
For the factor \(f\left( p \cdot \frac{c + az}{d + pbz}, 1\right) \), we note that the map \(z \mapsto \frac{c + az}{d + pbz}\) preserves all the rigid-analytic neighbourhoods \(X_m\) of \(\mathbf {Z}_p\), so it preserves the ring of rigid-analytic functions convergent and bounded by 1 on these spaces; thus, \(z \mapsto g\left( \frac{c + az}{d + pbz}\right) \) is in \(LA_m(\mathbf {Z}_p, \varLambda _U)\) if \(g \in LA_m(\mathbf {Z}_p, \varLambda _U)\). \(\square \)
For the rest of this section, let T denote either \(T_0\) or \(T_0'\), and \(\varSigma \) either \(\varSigma _0\) or \(\varSigma '_0\), respectively.
Note that as a topological \(\varLambda _U\)-module, \(A^{\circ }_{U, m}(T)\) is isomorphic to the space of countable sequences \((c_n)_{n=1}^\infty \) with \(c_n \in \varLambda _U\) such that \(c_n \rightarrow 0\) in the \(m_U\)-adic topology.
Definition 4.2.6
We write
and \(D_{U, m}(T) = D^{\circ }_{U, m}(T)[1/p]\).
Note that any linear functional \(\mu \in D^{\circ }_{U, m}(T)\) is necessarily continuous (where we endow both \(A^{\circ }_{U, m}(T)\) and \(\varLambda _U\) with their \(m_U\)-adic topologies). We equip \(D^{\circ }_{U, m}(T)\) with the weak (or more formally weak-star) topology, generated by sets of the form \(\{ \mu {:}\,\mu (f) \in m_U^n \}\) for \(f \in A^{\circ }_{U, m}(T)\) and \(n \geqslant 0\), i.e. the weakest topology such that all the evaluation-at-f morphisms are continuous (when the target \(\varLambda _U\) is equipped with the \(m_U\)-adic topology).
In this topology \(D^{\circ }_{U, m}(T)\) becomes compact; indeed, we have a topological isomorphism \(D^{\circ }_U \rightarrow \prod _{n=0}^\infty \varLambda _U\), with the inverse-limit topology.
Lemma 4.2.7
The formation of \(D^{\circ }_{U, m}(T)\) commutes with base change in U, in the sense that for \(V \subseteq U\) two open discs defined over E, we have
Proof
Clear by construction. \(\square \)
Lemma 4.2.8
We may write \(D^{\circ }_{U, m}(T)\) as an inverse limit
where each \({{\mathrm{Fil}}}^n\) is preserved by the action of \(\varSigma \), and the quotient \(D^{\circ }_{U, m}(T)/ {{\mathrm{Fil}}}^n\) is finite.
Proof
For \(T = T_0\) and \(m = 0\) this is [1, Proposition 3.10], and the generalisation to \(m \geqslant 1\) is given in [14, §2.1]. The case of \(T = T_0'\) is proved similarly [or, alternatively, follows from the case of \(T = T_0\) via conjugation by \(\left( {\begin{matrix}0 &{} \quad \\ -1 &{} p\end{matrix}}\right) \quad 0\)]. \(\square \)
Proposition 4.2.9
Let \(D^{\mathrm {la}}(T, E)\) be the algebra of E-valued locally analytic distributions on T. Then there is an isomorphism
given by mapping the Dirac distribution [t], for \(t \in T\), to the \(\varLambda _U\)-linear functional on \(A^{\circ }_{U, m}\) given by evaluation at t. This map commutes with the action of \(\varSigma \) on both sides and restricts to an isomorphism
Proof
We give the proof for \(T_0'\), the proof for \(T_0\) being similar. Because of the homogeneity requirement, any function in \(A^{\circ }_{U, m}(T_0')\) is uniquely determined by its restriction to \(p\mathbf {Z}_p\times 1\), and this gives an isomorphism \(D^{\circ }_{U, m}(T) \cong LA_m(\mathbf {Z}_p, \mathcal {O}_E)^* \mathop {\hat{\otimes }}_{\mathcal {O}_E} \varLambda _U\). Both results now follow by passing to the inverse limit. \(\square \)
Now let \(k \in \mathcal {W}\) be an integer weight (i.e. of the form \(z \mapsto z^k\) with \(k \geqslant 0\)); any such weight automatically lies in \(\mathcal {W}_0\). As for U above, we may define a space \(A^{\circ }_{k, m}(T)\) of m-analytic \(\mathcal {O}_E\)-valued functions on T homogenous of weight k, and its dual \(D^{\circ }_{k, m}(T)\), for any \(m \geqslant 0\).
Restriction to T gives a natural embedding \(P^{\circ }_k \hookrightarrow A^{\circ }_{k, m}(T)\), where \(P^{\circ }_k\) is the space of polynomial functions on \(\mathbf {Z}_p^2\), homogenous of degree k, with \(\mathcal {O}_E\) coefficients. Dually, we obtain a canonical, \(\varSigma _0(p)\)-equivariant projection \(\rho _k{:}\,D^{\circ }_{k, m} \rightarrow (P^{\circ }_k)^* = {{\mathrm{TSym}}}^k \mathcal {O}_E^2\).
Proposition 4.2.10
The following diagram is commutative, for any U, any m sufficiently large that \(U \subseteq \mathcal {W}_m\), and any \(k \in U\):

Here \({{\mathrm{mom}}}^k\) is as defined in [17], and the left vertical arrow is the natural inclusion \(T \hookrightarrow \mathbf {Z}_p^{\oplus 2}\).
Proof
This is clear by construction. \(\square \)
4.3 The Ohta pairing
We now define a pairing between distribution modules on \(T_0\) and \(T_0'\), following [26, §4].
Definition 4.3.1
Let \(H = \mathbf {Z}_p^{\oplus 2}\), as above. We define a bilinear map \(\phi : H \times H \rightarrow \mathbf {Z}_p\) by
This clearly restricts to a map \(T_0 \times T_0' \rightarrow \mathbf {Z}_p^\times \), so the \(\varLambda _U\)-valued function \(\Phi \) on \(T_0 \times T_0'\) given by \(\Phi (t, t') = \kappa _U(\phi (t, t'))\) is well defined, homogenous of weight \(\kappa _U\) in either variable, and m-analytic whenever \(U \subseteq \mathcal {W}_m\).
Definition 4.3.2
We write
for the bilinear map given by pairing with the function \(\Phi \in A^{\circ }_{U, m}(T_0) \mathop {\hat{\otimes }}_{\varLambda _U} A^{\circ }_{U, m}(T_0')\).
This is evidently \(\varLambda _U\)-bilinear, and it satisfies
for any \(\mu \in D^{\circ }_{U, m}(T_0)\), \(\mu ' \in D^{\circ }_{U, m}(T_0')\), and \(\gamma \in U_0(p)\), where \(U_0(p) = \varSigma _0(p) \cap \varSigma _0'(p)\) is the Iwahori subgroup of \({{\mathrm{GL}}}_2(\mathbf {Z}_p)\).
Remark 4.3.3
Let us describe the above map slightly more concretely. We take \(m = 0\), for simplicity; then, the functions \(f_n( (x, y) ) = \kappa _U(x) \cdot (y/x)^n\) are an orthonormal basis of \(A^{\circ }_{U, 0}(T_0)\), so a distribution \(\mu \in D^{\circ }_{U, 0}(T_0)\) is uniquely determined by its moments \(\mu _n = \mu (f_n)\), which can be any sequence of elements of \(\varLambda _U\). Similarly, the functions \(g_n( (px, y) ) = \kappa _U(y) (x/y)^n\) are an orthonormal basis of \(A^{\circ }_{U, 0}(T_0')\) and any \(\mu ' \in D^{\circ }_{U, 0}(T_0')\) is uniquely determined by its moments \(\mu _n' = \mu '(g_n)\).
Given such \(\mu , \mu '\), we define an element of \(\varLambda _U\) as follows: the function \(\Phi \left( (1, z), (pw, 1) \right) = \kappa _U(1 - p z w)\) can be written as a power series \(\sum a_n (wz)^n\), with \(a_n \in \varLambda _U\) such that \(a_n \rightarrow 0\) in the \(m_U\)-adic topology, by Lemma 4.1.5; then \(\{ \mu , \mu '\}\) is the value of the convergent sum \(\sum _{n \geqslant 0} a_n \mu _n \mu _n'\).
4.4 Sheaves on modular curves
Notation 4.4.1
Let M, N be integers \(\geqslant 1\) with \(M \mid N\) and \(M + N \geqslant 5\). We write Y(M, N) for the modular curve over \(\mathbf {Z}[1/N]\) defined in [15, §2.1].
We recall the construction of an étale sheaf of abelian groups \(\mathscr {H}_{\mathbf {Z}_p}\), and the corresponding sheaf of Iwasawa algebras \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})\), associated with the universal elliptic curve \(\mathcal {E}\) over Y(M, N), and more generally the sheaf of sets \(\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle \) and sheaf of \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})\)-modules \(\varLambda (\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle )\), where D is a subscheme of \(\mathcal {E}\) finite étale over Y(M, N). Cf. [19, §4.1].
We shall apply this to the curve \(Y = Y(1, N(p))\) where \(p \not \mid N\), parametrising triples (E, P, C) where E is an elliptic curves (over some \(\mathbf {Z}[1/Np]\)-algebra), P is a point of exact order N on E, and C is a subgroup of E of order p. Let \(D = E[p] - C\), which is finite étale over Y of degree \(p^2 - p\), and \(D' = C - \{ 0\}\), which is finite étale of degree \(p-1\); then the sheaves \(\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle \) and \(\mathscr {H}_{\mathbf {Z}_p} \langle D' \rangle \) are defined. Since both D and \(D'\) are contained in E[p], there is a multiplication-by-p map
and similarly for \(D'\).
Proposition 4.4.2
The pullbacks of the sheaves \(\varLambda (\mathscr {H}_{\mathbf {Z}_p})\), and \(\varLambda (\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle )\), and \(\varLambda (\mathscr {H}_{\mathbf {Z}_p}\langle D' \rangle )\) to the pro-scheme \(Y(p^\infty , Np^\infty )\) are isomorphic to the constant sheaves \(\varLambda (\mathbf {Z}_p^2)\), \(\varLambda (T_0)\), and \(\varLambda (T_0')\), respectively, and the maps \([p]_*\) are induced by the natural inclusions \(T_0 \hookrightarrow \mathbf {Z}_p^2\) and \(T_0' \hookrightarrow \mathbf {Z}_p^2\).
Proof
It suffices to check the corresponding statement for the inverse systems of sheaves of sets \(\mathscr {H}_{\mathbf {Z}_p}\), \(\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle \) and \(\mathscr {H}_{\mathbf {Z}_p}\langle D' \rangle \). However, over \(Y(p^\infty , Np^\infty )\) we have two sections \(e_1, e_2\) of \(\mathscr {H}_{\mathbf {Z}_p}\) identifying it with the constant sheaf \(\mathbf {Z}_p^2\), and since the level p subgroup C is generated by \(e_2 \bmod p\), the sheaf \(\mathscr {H}_{\mathbf {Z}_p}\langle D \rangle \) is precisely the subset of linear combinations \(ae_1 + be_2\) such that \(a \ne 0 \bmod p\), which is \(T_0\), while \(\mathscr {H}_{\mathbf {Z}_p}\langle D' \rangle \) is similarly identified with \(T_0'\). \(\square \)
Now let \(m \geqslant 0\), and U a wide open disc contained in \(\mathcal {W}_m\), as before.
Proposition 4.4.3
There are pro-sheaves of \(\varLambda _U\)-modules \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0)\) and \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0')\) on Y, whose pullbacks to \(Y(p^\infty , Np^\infty )\) are the constant pro-sheaves \(D^{\circ }_{U, m}(T_0)\) and \(D^{\circ }_{U, m}(T_0')\), respectively, and the Galois group of \(Y(p^\infty , Np^\infty ){/}Y\) acts on \(D^{\circ }_{U, m}(T_0)\) and \(D^{\circ }_{U, m}(T_0')\) via its natural identification with the Iwahori subgroup of \({{\mathrm{GL}}}_2(\mathbf {Z}_p)\).
Proof
The above trivialisation of \(\mathscr {H}_{\mathbf {Z}_p}\) over \(Y(p^\infty , Np^\infty )\) determines a homomorphism from the étale fundamental group \(\pi _1^{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y)\) to the Iwahori subgroup \(U_0(p) \subseteq {{\mathrm{GL}}}_2(\mathbf {Z}_p)\). Since \(D^{\circ }_{U, m}(T_0)\) is an inverse limit of finite right modules for \(U_0(p)\), and any finite right \(\pi _1^{{\acute{\mathrm{e}}{\mathrm{t}}}}(Y)\)-module defines an étale sheaf on Y, we obtain a pro-sheaf \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0)\), and similarly for \(D^{\circ }_{U, m}(T_0')\). These are sheaves of \(\varLambda _U\)-modules since the action of \(U_0(p)\) on the modules \(D^{\circ }_{U, m}(T_0)\) and \(D^{\circ }_{U, m}(T_0')\) is \(\varLambda _U\)-linear. \(\square \)
Remark 4.4.4
Compare [1, §3.3]; the argument is given there for the Kummer étale site on a log rigid space over \({\mathbf {Q}_p}\) (with log structure given by the cusps), but the argument works equally well in the much simpler case of affine modular curves over \(\mathbf {Q}\).
Proposition 4.4.5
For any \(k \in U\) we have commutative diagrams of pro-sheaves on Y

and

Here \({{\mathrm{mom}}}^k\) is as defined in [17].
Proof
We have the diagram of Proposition 4.2.10, which we may interpret as a diagram of constant pro-sheaves on \(Y(p^\infty , Np^\infty )\), and the morphisms in the diagram are all equivariant for the action of the Iwahori subgroup, so they descend to morphisms of sheaves on Y. \(\square \)
We can similarly construct \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0)\) and \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0')\) as sheaves on Y(U), for any sufficiently small open compact subgroup \(U \subseteq {{\mathrm{GL}}}_2(\widehat{\mathbf {Z}})\) whose image in \({{\mathrm{GL}}}_2(\mathbf {Z}_p)\) is contained in the Iwahori subgroup. Moreover, if \(g \in {\mathrm{GL}}_2(\mathbf {Q}) \cap \varSigma _0(p)\), so there is a natural map
corresponding to \(z \mapsto gz\) on the upper half-plane, then the action of g on \(D^{\circ }_{U, m}(\mathscr {H}_0)\) gives a map of sheaves on Y
the same holds with \(\mathscr {H}_0'\) and \(\varSigma _0'\) in place of \(\mathscr {H}_0\) and \(\varSigma _0\).
Definition 4.4.6
We define
We also make the same definitions for compactly supported and parabolic cohomology, which we write as \(M^{\circ }_{U, m}(\mathscr {H}_0)_c\), \(M^{\circ }_{U, m}(\mathscr {H}_0)_{\mathrm {par}}\) (and similarly for \(\mathscr {H}_0'\)).
These are profinite topological \(\varLambda _U\)-modules, equipped with continuous actions of \({{\mathrm{Gal}}}(\overline{\mathbf {Q}}{/}\mathbf {Q})\) unramified outside \(N p \infty \). As topological \(\varLambda _U\)-modules (forgetting the Galois actions) they are isomorphic to more familiar objects:
-
The space \(M^{\circ }_{U, m}(\mathscr {H}_0)\) is isomorphic to the group cohomology \(H^1\left( \varGamma , \mathcal {D}_{U, m}^{\circ }(T_0)\right) \), where \(\varGamma = \varGamma _1(N(p)) = \varGamma _1(N) \cap \varGamma _0(p)\) (since \(Y_1(N(p))(\mathbf {C})\) has contractible universal cover and its fundamental group is \(\varGamma _1(N) \cap \varGamma _0(p)\)).
-
The space \(M^{\circ }_{U, m}(\mathscr {H}_0)_c\) is isomorphic to the space of modular symbols
$$\begin{aligned} {{\mathrm{Hom}}}_{\varGamma }\left( \mathrm{Div}^0(\mathbf {P}^1_{\mathbf {Q}}), \mathcal {D}_{U, m}^{\circ }(T_0)\right) . \end{aligned}$$
The same statements hold with \(\mathscr {H}_0'\) and \(T_0'\) in place of \(\mathscr {H}_0\) and \(T_0\).
Notation 4.4.7
We shall refer to \(M^{\circ }_{U, m}(\mathscr {H}_0)\) and \(M^{\circ }_{U, m}(\mathscr {H}_0')\) as étale overconvergent cohomology (of weight U, tame level N and degree of overconvergence m).
We now state some properties of these modules:
Proposition 4.4.8
-
(1)
(Compatibility with specialisation) Let \(\varpi _k\) be the ideal of \(\varLambda _U\) corresponding to the character \(z \mapsto z^k\). For any integer \(k \geqslant 0 \in U\), there is an isomorphism
$$\begin{aligned} M^{\circ }_{U, m}(\mathscr {H}_0){/}\varpi _k \cong M^{\circ }_{k, m}(\mathscr {H}_0).\end{aligned}$$For compactly supported cohomology this is true for \(k \geqslant 1\), while for \(k = 0\) we have an injective map
$$\begin{aligned} M^{\circ }_{U, m}(\mathscr {H}_0)_c{/}\varpi _0 \hookrightarrow M^{\circ }_{0, m}(\mathscr {H}_0)_c \end{aligned}$$whose cokernel has rank 1 over \(\mathcal {O}_E\), with the Hecke operator \(U_p\) acting as multiplication by p. Similar statements hold for \(\mathscr {H}_0'\) in place of \(\mathscr {H}_0\).
-
(2)
(Control theorem) For any integer \(k \geqslant 0\), the map
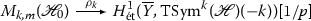
is an isomorphism on the \(U_p = \alpha \) eigenspace, for any \(\alpha \) of valuation \(< k + 1\). The same holds for compactly supported and parabolic cohomology, and for \(\mathscr {H}_0'\) and \(U_p'\) in place of \(\mathscr {H}_0\) and \(U_p\).
-
(3)
(Duality) There are \(\varLambda _U\)-bilinear, \(G_{{\mathbf {Q}_p}}\)-equivariant pairings
$$\begin{aligned} M^{\circ }_{U, m}(\mathscr {H}_0)_c \times M^{\circ }_{U, m}(\mathscr {H}_0')&\rightarrow \varLambda _U, \\ M^{\circ }_{U, m}(\mathscr {H}_0) \times M^{\circ }_{U, m}(\mathscr {H}_0')_c&\rightarrow \varLambda _U,\\ M^{\circ }_{U, m}(\mathscr {H}_0)_{\mathrm {par}} \times M^{\circ }_{U, m}(\mathscr {H}_0')_{\mathrm {par}}&\rightarrow \varLambda _U, \end{aligned}$$which we denote by \(\{ -, -\}\). For integers \(k \geqslant 0\) we have
$$\begin{aligned} \mathrm{ev}_k\left( \{ x, x'\} \right) = \left\{ \rho _k(x), \rho _k(x') \right\} _k \end{aligned}$$where \(\mathrm{ev}_k\) is evaluation at k, and on the right-hand side \(\{-, -\}_k\) signifies the Poincaré duality pairing.
-
(4)
There is an isomorphism \(W{:}\,M^{\circ }_{U, m}(\mathscr {H}_0)_{?} \rightarrow M^{\circ }_{U, m}(\mathscr {H}_0')_?\) (where \(? \in \{ \varnothing , c, \mathrm {par}\})\), intertwining the action of the Hecke operators \(T_n\) with the \(T_n'\) (including \(n = p)\); this is compatible via the maps \(\rho _k\) with the Atkin–Lehner operator \(W_{Np}\) (but not with the Galois action).
Proof
For part (1), see [1, Lemma 3.18]. For compactly supported cohomology see [2, Theorem 3.10]. (Bellaïche works with coefficients in an affinoid disc, rather than a wide open disc as we do, but the argument is the same.)
Part (2) is the celebrated Stevens control theorem; see [1, Theorem 3.16] for \(H^1\) and [28, Theorem 1.1] for \(H^1_c\).
For part (3), if we identify \(\mathbf {Z}_p(1)\) with \(\mathbf {Z}_p\) as sheaves on \(Y(p^\infty , Np^\infty )\) via the section given by the Weil pairing and our trivialisation of \(\mathscr {H}\), then the Iwahori subgroup \(U_0(p)\) acts on \(\mathbf {Z}_p(1)\) via the determinant character, and hence our pairing of \(U_0(p)\)-modules \(D^{\circ }_{U, m}(\mathscr {H}_0) \times D^{\circ }_{U, m}(\mathscr {H}_0') \rightarrow \varLambda _U\) gives a pairing of étale pro-sheaves on Y
where \(\kappa _U\) is the composite of the cyclotomic character with the canonical map \(\mathbf {Z}_p^\times \rightarrow \varLambda _U^\times \). Hence we have a cup-product pairing
and since there is a canonical isomorphism \(H^2_c(\overline{Y}, \mathbf {Z}_p(1)) \cong \mathbf {Z}_p\), this gives a pairing into \(\varLambda _U(1 + \kappa _U)\) as claimed. It is clear by construction that this is compatible with the Poincaré duality pairings with \({{\mathrm{TSym}}}^k\) coefficients for each \(k \geqslant 0\).
Part (4) follows from the fact that the action of the matrix \(\left( {\begin{matrix}0 &{} -1 \\ Np &{} 0\end{matrix}}\right) \) on H interchanges \(T_0\) and \(T_0'\). \(\square \)
Remark 4.4.9
The pairing \(\{ -, -\}\) (in any of its various incarnations) is far from perfect (since its specialisation at a classical weight \(k \geqslant 0\) factors through the maps \(\rho _k\), so any non-classical eigenclass of weight k must be in its kernel). Nonetheless, we shall see below that it induces a perfect pairing on small slope parts.
4.5 Slope decompositions
As before, let U be a wide open disc contained in \(\mathcal {W}_m\), for some m. Let \(B_U = \varLambda _U[1/p]\), and let M be one of the \(B_U\)-modules \(M_{U, m}(\mathscr {H}_0)_?\), for \(? \in \{ \varnothing , c, \mathrm {par}\}\), and let \(\lambda \in \mathbf {R}_{\geqslant 0}\).
Definition 4.5.1
We say M has a slope \(\leqslant \lambda \) decomposition if we can write it as a direct sum of \(B_U\)-modules
where the following conditions are satisfied:
-
the action of the Hecke operator \(U_p\) preserves the two summands;
-
the module \(M_U^{(\leqslant \lambda )}\) is finitely generated over \(B_U\);
-
the restrictions of \(U_p\) to \( M_U^{(\leqslant \lambda )}\) and \(M_U^{(> \lambda )}\) have slope \(\leqslant \lambda \) and slope \(> \lambda \), respectively.
Remark 4.5.2
There are several equivalent definitions of slope \(\leqslant \lambda \), see [1] for further discussion. We shall use the following formulation: the endomorphism \(U_p\) of \(M_U^{(\leqslant \lambda )}\) is invertible, and the sequence of endomorphisms \(\left( p^{\lfloor n\lambda \rfloor } \cdot (U_p)^{-n}\right) _{n \geqslant 0}\) is bounded in the operator norm.
Note that the summands \(M^{(\leqslant \lambda )}\) and \(M^{(> \lambda )}\) must be stable under the actions of the prime-to-p Hecke operators, and of the Galois group \(G_{\mathbf {Q}}\), since these commute with the action of \(U_p\).
Theorem 4.5.3
([1, Theorem 3.17]) Let \(k \geqslant 0\) and \(0 \leqslant \lambda < k + 1\). Then there exists an open disc \(U \ni k\) in \(\mathcal {W}\), defined over E, such that the module \(M_{U, 0}(\mathscr {H}_0)\) has a slope \(\leqslant \lambda \) decomposition.
The same results hold mutatis mutandis for \(M = M_{U, 0}(\mathscr {H}_0')\), using the Hecke operator \(U_p'\) in place of \(U_p\); this follows directly from the previous statement using the isomorphism between the two modules provided by the Atkin–Lehner involution. There are also corresponding statements for compactly supported and parabolic cohomology.
4.6 Coleman families
A considerably finer statement is possible if we restrict to a “neighbourhood” of a classical modular form. We make the following definition:
Definition 4.6.1
Let \(U \subseteq \mathcal {W}\) be an open disc such that the classical weights \(U \cap \mathbf {Z}_{\geqslant 0}\) are dense in U. A Coleman family \(\mathcal {F}\) over U (of tame level N) is a power series
with \(a_1(\mathcal {F}) = 1\) and \(a_p(\mathcal {F})\) invertible in \(B_U\), such that for all but finitely many classical weights \(k \in U \cap \mathbf {Z}_{\geqslant 0}\), the series \(\mathcal {F}_k = \sum _{n \geqslant 1} a_n(\mathcal {F})(k) \in \mathcal {O}_E[[q]]\) is the q-expansion of a classical modular form of weight \(k + 2\) and level \(\varGamma _1(N) \cap \varGamma _0(p)\) which is a normalised eigenform for the Hecke operators.
Remark 4.6.2
This definition is somewhat crude, since for a more satisfying theory one should also consider more general classical weights of the form \(z \mapsto z^k \chi (z)\) for \(\chi \) of finite order and allow families indexed by a finite flat rigid-analytic cover of U rather than by U itself. This leads to the construction of the eigencurve. However, the above definition will suffice for our purposes, since we are only interested in small neighbourhoods in the eigencurve around a classical point.
Definition 4.6.3
A noble eigenform of tame level N is a normalised cuspidal Hecke eigenform \(f_{\alpha }\) of level \(\varGamma _1(N) \cap \varGamma _0(p)\) and some weight \(k + 2 \geqslant 2\), with coefficients in E, having \(U_p\)-eigenvalue \(\alpha = a_p(f_\alpha )\), such that:
-
\(f_\alpha \) is a p-stabilisation of a newform f of level N whose Hecke polynomial \(X^2 - a_p(f) X + p^{k+1} \varepsilon _f(p)\) has distinct roots (“p-regularity”);
-
if \(v_p(\alpha ) = k + 1\), then the Galois representation \(M_E(f) |_{G_{{\mathbf {Q}_p}}}\) is not a direct sum of two characters (“non-criticality”).
Theorem 4.6.4
Suppose \(f_\alpha \) is a noble eigenform of weight \(k_0 + 2\). Then there exists a disc \(U \ni k_0\) in \(\mathcal {W}\), and a unique Coleman family \(\mathcal {F}\) over U, such that \(\mathcal {F}_{k_0} = f_\alpha \).
Proof
This follows from the fact that the Coleman–Mazur–Buzzard eigencurve \(\mathscr {C}(N)\) of tame level N is étale over \(\mathcal {W}\) (and, in particular, smooth) at the point corresponding to a noble eigenform \(f_\alpha \). See [2].
Remark 4.6.5
As remarked in [14], the condition that the Hecke polynomial of f has distinct roots is conjectured to be redundant, and known to be so when f has weight 2, and it is also conjectured that the only newforms f of weight \({\geqslant }2\) such that \(M_E(f)|_{G_{{\mathbf {Q}_p}}}\) splits as a direct sum are those which are of CM type with p split in the CM field.
Theorem 4.6.6
Let \(f_\alpha \) be a noble eigenform, and \(\mathcal {F}\) the Coleman family passing through \(f_\alpha \). If the disc \(U \ni k_0\) is sufficiently small, then:
-
The module
$$\begin{aligned} M_U(\mathcal {F}) :=M_{U, 0}(\mathscr {H}_0) \Big [T_n = a_n(\mathcal {F})\ \forall n \geqslant 1\Big ] \end{aligned}$$is a direct summand of \(M_{U, 0}(\mathscr {H}_0)\) as a \(B_U\)-module, free of rank 2 over \(B_U\), and lifts canonically to \(M_{U, 0}(\mathscr {H}_0)_c\).
-
The same is true of the module
$$\begin{aligned} M_U(\mathcal {F})^* :=M_{U, 0}(\mathscr {H}_0') \Big [T_n' = a_n(\mathcal {F})\ \forall n \geqslant 1\Big ]. \end{aligned}$$ -
The pairing \(\{-, -\}\) induces an isomorphism of \(B_U[G_{{\mathbf {Q}_p}}]\)-modules
$$\begin{aligned} M_U(\mathcal {F})^* \cong {{\mathrm{Hom}}}_{B_U}(M_U(\mathcal {F}), B_U). \end{aligned}$$ -
For each \(k \geqslant 0 \in U\), the form \(\mathcal {F}_k\) is a classical eigenform, and we have isomorphisms of E-linear \(G_{{\mathbf {Q}_p}}\)-representations
$$\begin{aligned} M_U(\mathcal {F}){/}\varpi _k M_U(\mathcal {F}) = M_E(\mathcal {F}_k) \quad \text {and}\quad M_U(\mathcal {F})^*{/}\varpi _k M_U(\mathcal {F})^* = M_E(\mathcal {F}_k)^*. \end{aligned}$$
Proof
The finite-slope parts of all the various overconvergent cohomology groups can be glued into coherent sheaves on the eigencurve \(\mathscr {C}(N)\). In a neighbourhood of a noble point, the eigencurve is étale over weight space and these sheaves are all locally free of rank 2, and the map from \(H^1_c\) to \(H^1\) is an isomorphism at the noble point, so it must be an isomorphism on some neighbourhood of it. See [14, Proposition 2.3.5] for further details. \(\square \)
4.7 Weight one forms
If f is a cuspidal newform of level N and weight 1, and \(f_\alpha \) is a p-stabilisation of f, then it is always the case that \(v_p(\alpha ) = k_0 + 1 = 0\) and \(M_E(f)|_{G_{{\mathbf {Q}_p}}}\) splits as a direct sum (since \(M_E(f)\) is an Artin representation). Nonetheless, analogues of Theorems 4.6.4 and 4.6.6 do hold for these forms.
Notation 4.7.1
We say that f has real multiplication by a real quadratic field K if there is a Hecke character \(\psi \) of K such that \(M_E(f) \cong \mathrm{Ind}_{G_K}^{G_\mathbf {Q}}(\psi )\).
Theorem 4.7.2
Let \(f_\alpha \) be a p-stabilisation of a p-regular weight 1 eigenform.
-
(1)
There is an open disc \(U \ni -1\) in \(\mathcal {W}\), a finite flat rigid-analytic covering
 unramified away from \(-1\) and totally ramified at \(-1\), and a family of eigenforms \(\mathcal {F}\in B_{\tilde{U}}[[q]]\), whose specialisation at \(\kappa ^{-1}(-1)\) is \(f_\alpha \). We may take \(\tilde{U} = U\) if (and only if) f does not have real multiplication by a quadratic field in which p is split.
unramified away from \(-1\) and totally ramified at \(-1\), and a family of eigenforms \(\mathcal {F}\in B_{\tilde{U}}[[q]]\), whose specialisation at \(\kappa ^{-1}(-1)\) is \(f_\alpha \). We may take \(\tilde{U} = U\) if (and only if) f does not have real multiplication by a quadratic field in which p is split. -
(2)
The module
$$\begin{aligned} M_{\tilde{U}}(\mathcal {F}) = \left( \kappa ^* M_{U, 0}(\mathscr {H}_0)\right) \left[ T_n = a_n(\mathcal {F}) \, \forall n \geqslant 1\right] \end{aligned}$$is a direct summand of \(\kappa ^* M_{U, 0}(\mathscr {H}_0)\), free of rank 2 as a \(B_{\tilde{U}}\)-module, and lifts canonically to \(\kappa ^* M_{U, 0}(\mathscr {H}_0)_c\).
-
(3)
The same is true of
$$\begin{aligned} M_{\tilde{U}}(\mathcal {F})^* = \left( \kappa ^* M_{U, 0}(\mathscr {H}_0')\right) \left[ T_n' = a_n(\mathcal {F}) \, \forall n \geqslant 1\right] , \end{aligned}$$and the pairing \(\{-, -\}\) induces an isomorphism \(M_{\tilde{U}}(\mathcal {F})^* \cong {{\mathrm{Hom}}}_{B_{\tilde{U}}}(M_{\tilde{U}}(\mathcal {F}), B_{\tilde{U}})\).
Proof
Part (1) is exactly the statement that the eigencurve is smooth at the point corresponding to \(f_\alpha \), and is étale over weight space except in the real-multiplication setting, see [3].
Part (2) for compactly supported cohomology is an instance of [2, Proposition 4.3]. However, the kernel and cokernel of the map \( M_{U, 0}(\mathscr {H}_0)_c \rightarrow M_{U, 0}(\mathscr {H}_0)\) are supported on the Eisenstein component of the eigencurve, and since \(f_\alpha \) is a smooth point on the cuspidal eigencurve \(\mathscr {C}^0(N) \subset \mathscr {C}(N)\), it does not lie on the Eisenstein component. Hence the kernel and cokernel localise to 0 at \(f_\alpha \), implying that for small enough U the \(\mathcal {F}\)-eigenspaces of \(M_U(\mathscr {H}_0)_c\) and \(M_U(\mathscr {H}_0)\) coincide.
For part (3) we use the fact that the Ohta pairings induce perfect dualities on the ordinary parts of the modules \(M_U(\mathscr {H}_0)_c\) and \(M_U(\mathscr {H}_0')\) (cf. [26]). \(\square \)
Remark 4.7.3
Parts (1) and (2) of Theorem 4.7.2 also hold for non-noble points of weight \({\geqslant }2\) corresponding to the critical p-stabilisations of ordinary CM forms, by [2, Proposition 4.5]. However, we do not know if part (3) holds in this situation.
5 Rankin–Eisenstein classes in Coleman families
5.1 Coefficient modules
Let H be a group isomorphic to \(\mathbf {Z}_p^2\) (but not necessarily canonically so), for p an odd prime. Then we can regard the modules \({{\mathrm{TSym}}}^r H\) as representations of \(\mathrm{Aut}(H) \approx \mathrm{GL}_2(\mathbf {Z}_p)\). In this section, we shall show that the Clebsch–Gordan decompositions of the groups \({{\mathrm{TSym}}}^r H \otimes {{\mathrm{TSym}}}^s H\) can themselves be interpolated as r varies (for fixed s), after passing to a suitable completion.
In this section we shall refer to morphisms as natural if they are functorial with respect to automorphisms of H.
Proposition 5.1.1
For A an open compact subset of H such that \(A \cap pH = \varnothing \), and any \(r \geqslant 1\), there is a short exact sequence

where C(A) is the space of continuous \(\mathcal {O}_E\)-valued functions on A. This short exact sequence is natural, and split (but not naturally split).
Proof
Let us begin by defining the maps. The map \(\beta \), which is the simpler of the two, is given by interpreting \({{\mathrm{Sym}}}^j H^\vee \) as a subspace of C(A) (consisting of functions which are the restrictions to A of homogenous polynomial functions on H of degree j) and composing with the multiplication map \(C(A) \otimes C(A) \rightarrow C(A)\).
The map \(\alpha \) is more intricate: it is given by including \(\bigwedge ^2(H^\vee )\) in \(H^\vee \otimes H^\vee \), and grouping the terms as
As above, we have a canonical multiplication map \(C(A) \otimes H^\vee \rightarrow H^\vee \), and multiplication in the symmetric algebra \({{\mathrm{Sym}}}^\bullet (H^\vee )\) gives a map \({{\mathrm{Sym}}}^{j-1}(H^\vee ) \otimes H^\vee \rightarrow {{\mathrm{Sym}}}^j H^\vee \), and this gives the first map in the sequence. The composite \(\beta \circ \alpha \) is clearly 0, since it factors through the map \(\wedge ^2 H^\vee \rightarrow {{\mathrm{Sym}}}^2 H^\vee \).
Having defined the maps intrinsically, we may check the exactness of the sequence after fixing a basis of H. Let x, y be the corresponding coordinate functions, so that \(x^j, x^{j-1} y, \ldots , y^j\) is a basis of \({{\mathrm{Sym}}}^j H^\vee \) and \(x \otimes y - y \otimes x\) is a basis of \(\wedge ^2 H^\vee \). With these identifications we can write the sequence as

with the maps being \((f_0, \ldots , f_{j-1}) \mapsto (-y f_0, x f_0 - y f_1, \ldots , x f_{j-1})\) and \((f_0, \ldots , f_j) \mapsto x^j f_0 + \cdots + y^j f_j\). The injectivity of \(\alpha \) is now clear, since multiplication by x (or by y) is injective in C(A).
To show that the map \(\beta \) is surjective, we write down a (non-canonical) section. We can decompose A as a union \(A_1 \sqcup A_2\) where x is invertible on \(A_1\) and y is invertible on \(A_2\). We define \(\delta (f) = (x^{-j} f, 0, \ldots , 0)\) on \(C(A_1)\) and \(\delta (f) = (0, \ldots , 0, y^{-j} f)\) on the \(C(A_2)\) factor; then \(\beta \circ \delta \) is clearly the identity, so \(\beta \) is surjective.
Finally, let \((f_0, \ldots , f_j) \in \ker (\beta )\). Choosing \(A = A_1 \sqcup A_2\) as before, we may assume either x or y is invertible on A. We treat the first case, the second being similar. We define \(\gamma (f_1, \ldots , f_j) = (g_0, \ldots , g_{j-1})\) where \(g_{j-1} = x^{-1} f_j\), \(g_{j-2} = x^{-2}(x f_{j-1} + y f_j)\), etc., down to \(g_0 = x^{-j}(x^{j-1} f_{1} + \cdots + y^{j-1} f_j)\). But then \((\alpha \circ \gamma ) + (\beta \circ \delta ) = {{\mathrm{id}}}\), so we have exactness at the middle term. \(\square \)
Now let \(C^{\mathrm {la}}(A)\) denote the space of locally analytic E-valued functions on A; exactly the same argument shows that we have an exact sequence analogous to (5.1.1),

Proposition 5.1.2
Let \(\delta {:}\,C^{\mathrm {la}}(A) \rightarrow C^{\mathrm {la}}(A) \otimes {{\mathrm{Sym}}}^j H^\vee \) be the morphism defined in a basis by
Then \(\delta \) is natural, and the composite \(\beta \circ \delta \) is the endomorphism of \(C^{\mathrm {la}}(A)\) given by \(\frac{1}{j!} \prod _{i = 0}^{j-1}(\nabla - i)\), where \(\nabla \) is given by
Proof
The morphism \(\delta \) is simply \(\tfrac{1}{j!}\) times the jth power of the total derivative map \(C^{\mathrm {la}}(A) \rightarrow C^{\mathrm {la}}(A) \otimes \mathrm{Tan}(A)^*\), combined with the identification \(\mathrm{Tan}(A) \cong \mathrm{Tan}(H) \cong H\). From this description the naturality is clear, and a computation shows that it agrees with the more concrete description above. The identity for \(\beta \circ \delta \) is easily seen by induction on j.
\(\square \)
It will be convenient to adopt the notation \(\left( {\begin{array}{c}\nabla \\ j\end{array}}\right) \) for the endomorphism \(\tfrac{1}{j!} \prod _{i=0}^{j-1}(\nabla -i)\). We may regard this as an element of the space \(D^{\mathrm {la}}(\mathbf {Z}_p^\times )\) of locally analytic distributions on \(\mathbf {Z}_p^\times \).
Proposition 5.1.3
For any \(k \geqslant j\), the restriction of \(\delta \) to the space \({{\mathrm{Sym}}}^k H^\vee \) of homogenous polynomials of degree k lands in the subspace
and the resulting map \({{\mathrm{Sym}}}^k H^\vee \rightarrow {{\mathrm{Sym}}}^{k-j} H^\vee \otimes {{\mathrm{Sym}}}^j H^\vee \) is the dual of the symmetrised tensor product map \({{\mathrm{TSym}}}^{k-j} H \otimes {{\mathrm{TSym}}}^j H \rightarrow {{\mathrm{TSym}}}^k H\).
If \(k < j\), then the restriction of \(\delta \) to \({{\mathrm{Sym}}}^k H^\vee \) is the zero map.
Proof
It is obvious that \({{\mathrm{Sym}}}^k H^\vee \) embeds naturally into \(C^{\mathrm {la}}(A)\), and its image under \(\delta \) is contained in \({{\mathrm{Sym}}}^{k-j} H^\vee \otimes {{\mathrm{Sym}}}^j H^\vee \). A straightforward computation in coordinates shows that this map sends \(x^a y^b\) to \(\sum _{s + t = j} \left( {\begin{array}{c}a\\ s\end{array}}\right) \left( {\begin{array}{c}b\\ t\end{array}}\right) \left( x^{a-s} y^{b-t} \otimes x^s y^t\right) \), which coincides with the dual of the symmetrised tensor product.
On the other hand it is obvious from Eq. (5.1.1) that \(\delta \) vanishes on any polynomial of total degree \(< j\). \(\square \)
Corollary 5.1.4
There are natural maps
and
where \(\beta ^*\) is given on group elements by \([h] \mapsto [h] \otimes h^{[j]}\), and \(\delta ^*\) satisfies
Moreover, for any \(k \geqslant 0\) we have
where \({{\mathrm{mom}}}^{k-j} \cdot 1\) denotes the composition

(where the second map is the symmetrised tensor product).
Proof
This follows by dualising the previous proposition. \(\square \)
We now consider varying j, for which it is convenient to re-label the maps \(\beta ^*, \delta ^*\) above as \(\beta _j^*\) and \(\delta _j^*\).
Lemma 5.1.5
Let \(h \geqslant j \geqslant 0\). Then the composition

where the unlabelled arrow is given by the symmetrised tensor product, is given by
Proof
Explicit computation. \(\square \)
5.2 Nearly overconvergent étale cohomology
We also have an analogue of the Clebsch–Gordan map for the distribution spaces \(D^{\circ }_{U, m}(T_0')\) introduced above, which are completions of \(D^{\mathrm {la}}(T_0')\). The rigid space \(\mathcal {W}\) has a group structure, so we can make sense of \(U - j\) for any integer j.
Proposition 5.2.1
There are natural maps
and
commuting with the action of \(\varSigma _0(p)\), such that \(\delta _j^* \circ \beta _j^*\) is multiplication by \(\left( {\begin{array}{c}\nabla \\ j\end{array}}\right) \in \varLambda _U[1/p]\).
Proof
We simply transport the constructions of Sect. 5.1 to the present setting (taking \(A = T_0'\)). The naturality of these constructions precisely translates into the assertion that the resulting maps commute with the \(\varSigma _0(p)\)-action. Since the functions in \(A_{U, m}\) are homogenous of weight \(\kappa _U\) (the canonical character \(\mathbf {Z}_p^\times \rightarrow \varLambda _U^\times \)), we have \(\frac{\mathrm {d}}{\mathrm {d}t} f(th)|_{t = 1} = \nabla \cdot f(h)\) for all \(f \in A_{U, m}\), where on the right-hand side \(\nabla \) is regarded as an element of \(\varLambda _U[1/p]\); that is, the two actions of \(\nabla \) on \(A_{U, m}\), as a differential operator and as an element of the coefficient ring, coincide. \(\square \)
Remark 5.2.2
Note that \(\delta ^*_j\) takes values in \(D_{U, m} = D^{\circ }_{U, m}[1/p]\), not in \(D^{\circ }_{U, m}\) itself; the denominator arises from the fact that the map \(\delta _j\) on \(A^{\circ }_{U, m}\) does not preserve the \(\varLambda _U\)-lattice \(A^{\circ }_{U, m}\), but rather maps \(A^{\circ }_{U, m}\) to \(\frac{1}{j! p^{1+m}} A^{\circ }_{U, m}\). Note also that if \(U \subset \mathcal {W}_0\) and U contains none of the integers \(\{0, \ldots , j-1\}\), then \(\left( {\begin{array}{c}\nabla \\ j\end{array}}\right) \) is invertible in \(\varLambda _U[1/p]\).
The maps of spaces \(\beta _j^*\) and \(\delta _j^*\) induce maps of étale sheaves on \(Y = Y_1(N(p))\) (for any N), \(\mathcal {D}^{\circ }_{U, m}(\mathscr {H}_0') \rightarrow \mathcal {D}^{\circ }_{U-j, m}(\mathscr {H}_0') \otimes {{\mathrm{TSym}}}^j \mathscr {H}\) and \(\mathcal {D}^{\circ }_{U-j, m}(\mathscr {H}_0') \otimes {{\mathrm{TSym}}}^j \mathscr {H}\rightarrow \mathcal {D}_{U, m}(\mathscr {H}_0')\), which we denote by the same symbols.
Definition 5.2.3
We shall refer to the cohomology groups \(H^*_{{\acute{\mathrm{e}}{\mathrm{t}}}}(\overline{Y}, \mathcal {D}_{U-j, m}(\mathscr {H}_0') \otimes {{\mathrm{TSym}}}^j \mathscr {H})\) as nearly overconvergent étale cohomology, and the map
as the overconvergent projector.
Remark 5.2.4
The motivation for this terminology is that the sheaves \(\mathcal {D}_{U-j, m}(\mathscr {H}_0') \otimes {{\mathrm{TSym}}}^j \mathscr {H}\), and the maps \(\beta _j^*\) and \(\delta _j^*\) relating them to the overconvergent cohomology sheaves \(\mathcal {D}_{U, m}(\mathscr {H}_0')\), are an étale analogue of the coherent sheaves appearing in the theory of nearly overconvergent p-adic modular forms (see [32]).
Recall from Corollary 5.1.4 that the composite of \(\delta _j^*\) with the moment map \(\rho _k\) is zero if \(0 \leqslant k < j\), which is somewhat undesirable. We can rectify this issue as follows. Recall that we have defined \(M_U(\mathscr {H}_0') = H^1_{{\acute{\mathrm{e}}{\mathrm{t}}}}(\overline{Y}, \mathcal {D}_{U, m}(\mathscr {H}_0')(1))\).
Proposition 5.2.5
Let U be an open disc contained in \(\mathcal {W}_0\), and \(\mathcal {F}\) a Coleman family defined over U. Suppose the following condition is satisfied: for any integer weight \(k \geqslant 0\) in U, the projection map \(M_k(\mathscr {H}'_0) \rightarrow M_k(\mathcal {F})^*\) factors through \(\rho _k\).
Then, for any \(j \geqslant 0\), the composite map

takes values in \(\nabla (\nabla - 1) \ldots (\nabla - j + 1) M_U(\mathcal {F})^*\), and hence the map
is well defined.
Proof
Note that \(\nabla \), regarded as a rigid-analytic function on \(\mathcal {W}\), takes the value k at an integer weight k. So the only points in \(\mathcal {W}_0\) at which \(\nabla (\nabla - 1) \ldots (\nabla - j + 1)\) fails to be invertible are the positive integers \(\{0, \ldots , j-1\}\), and it has simple zeroes at all of these points.
If k is one of these integers, then we have \(M_U(\mathscr {H}_0'){/}(\nabla - k) M_U(\mathscr {H}_0') = M_k(\mathscr {H}_0')\). Hence it suffices to show that \({{\mathrm{pr}}}_{\mathcal {F}} \circ \delta _j^*\) is zero on \(M_k(\mathscr {H}_0')\), but this is immediate since the specialisation of \({{\mathrm{pr}}}_{\mathcal {F}}\) at k factors through \(\rho _k\), and \(\rho _k \circ \delta _j^*\) is zero for \(0 \leqslant k < j\).
This shows that \({{\mathrm{pr}}}_\mathcal {F}\circ \delta _j^*\) lands in the stated submodule. Since \(M_U(\mathcal {F})^*\) is a free \(\varLambda _U[1/p]\)-module (and \(\varLambda _U[1/p]\) is an integral domain), the map \({{\mathrm{pr}}}_\mathcal {F}^{[j]}\) is therefore well defined. \(\square \)
Remark 5.2.6
This proposition can be interpreted as follows: we can renormalise \(\delta _j^*\) to be an inverse to \(\beta _j^*\), as long as we avoid points on the eigencurve which are non-classical but have classical weights.
By construction, the map \({{\mathrm{pr}}}^{[j]}_{\mathcal {F}}\) has the property that the following diagram commutes:

More generally, if \(0 \leqslant j \leqslant h\), then (as in Lemma 5.1.5) we can consider \(\beta _{h - j}^* \cdot \mathrm {id}\) as a map
and from Lemma 5.1.5 one computes that
5.3 Two-parameter families of Beilinson–Flach elements
Let \(N_1, N_2\) be integers such that \(p \not \mid N_i\) and \(p N_1, p N_2 \geqslant 4\). We also choose two wide open discs \(U_1\) and \(U_2\) in \(\mathcal {W}_0\), and consider the sheaf
on the affine surface \(Y_1(N_1(p)) \times Y_1(N_2(p))\).
Definition 5.3.1
Let N be any integer divisible by \(N_1\) and \(N_2\) and with the same prime factors as \(N_1 N_2\). For any \(j \geqslant 0\) and \(m \geqslant 1\), we define the element
as the image of the class
under pushforward along \(Y_1(Np)^2 \rightarrow Y_1(N_1(p)) \times Y_1(N_2(p))\), composed with the map induced by the morphisms of sheaves

for \(i = 1, 2\). Here, the first map is given by the natural maps \(\varLambda (\mathscr {H}\langle C \rangle ) \rightarrow \mathcal {D}_{U}^{\circ }\), for \(U = U_i - j\), and the second map is the overconvergent projector \(\delta ^*_j\) of Proposition 5.2.1.
Remark 5.3.2
We are using implicitly here the fact that the Beilinson–Flach elements can be lifted canonically to classes with coefficients in the sheaves \(\varLambda (\mathscr {H}_{\mathbf {Z}_p}\langle D' \rangle )\). Cf. Remark 3.3.6 above.
The Hochschild–Serre spectral sequence and the Künneth formula give a canonical surjection
and we (abusively) denote the image of \({}_c \mathcal {BF}^{[U_1, U_2, j]}_{m, N_1, N_2, a}\) under this map by the same symbol.
Proposition 5.3.3
For any integer weights \(k_1 \in U_1\) and \(k_2 \in U_2\) with \(\min (k_1, k_2) \geqslant j\), the map
sends \({}_c \mathcal {BF}^{[U_1, U_2, j]}_{m, N_1, N_2, a}\) to the pushforward of \({}_c \mathcal {BF}^{[k, k', j]}_{m, Np, a}\). On the other hand, if \(0 \leqslant k_1 < j\) or \(0 \leqslant k_2 < j\), then the image of \({}_c \mathcal {BF}^{[U_1, U_2, j]}_{m, N_1, N_2, a}\) under \(\rho _{k_1} \boxtimes \rho _{k_2}\) is zero.
Proof
This follows from the last statement of 5.1.4, since \({}_c \mathcal {BF}^{[k, k', j]}_{m, Np, a}\) is by definition the image of \({}_c \mathcal {BF}^{[j]}_{m, Np, a}\) under the map \(({{\mathrm{mom}}}^{k-j} \cdot {{\mathrm{id}}}) \boxtimes ({{\mathrm{mom}}}^{k'-j} \cdot {{\mathrm{id}}})\). \(\square \)
Now let us choose newforms f, g, of levels \(N_1, N_2\) and weights \(k_1 + 2, k_2 + 2 \geqslant 2\), and roots \(\alpha _1, \alpha _2\) of their Hecke polynomials, such that the p-stabilisations \(f_{i, \alpha _i}\) both satisfy the hypotheses of Theorem 4.6.6. The theorem then gives us families of overconvergent eigenforms \(\mathcal {F}_1\), \(\mathcal {F}_2\) passing through the p-stabilisations of f and g, defined over some discs \(U_1 \ni k_1, U_2 \ni k_2\).
Proposition 5.3.4
If the discs \(U_i\) are sufficiently small, then there exist classes
such that
where \(\nabla _i\) denotes the image of \(\nabla \) in \(\varLambda _{U_i}[1/p]\).
Proof
After shrinking the discs \(U_i\) if necessary so that all integer-weight specialisations of \(\mathcal {F}\) and \(\mathcal {G}\) are classical, so that Proposition 5.2.5 applies, we can simply define \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}, j]}_{m, a}\) as the image of \({}_c \mathcal {BF}^{[j]}_{m, a}\) under \({{\mathrm{pr}}}_{\mathcal {F}}^{[j]} \times {{\mathrm{pr}}}_{\mathcal {G}}^{[j]}\). \(\square \)
5.4 Interpolation in j
Now let \(\mathcal {F}, \mathcal {G}\) be Coleman families over open discs \(U_1, U_2\), satisfying the conditions of Proposition 5.3.4.
Proposition 5.4.1
For any \(h \geqslant 0\), and any a, there is a constant C independent of r such that the elements \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}, j]}_{mp^r, a}\), for \(0 \leqslant j \leqslant h\) and \(r \geqslant 1\), satisfy the following norm bound:
Proof
We shall deduce this from Theorem 3.3.5 (and Remark 3.3.6). This theorem gives a bound for the classes
We apply to this the map \(\mathrm{pr}_{\mathcal {F}}^{[h]} \boxtimes \mathrm{pr}_{\mathcal {G}}^{[h]}\). This maps \((1 \otimes {{\mathrm{mom}}}^{h-j})^{\boxtimes 2} {}_c \mathcal {BF}^{[j]}\) to \(\left( {\begin{array}{c}h\\ j\end{array}}\right) ^2 {}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}, j]}_{mp^r, a}\), by (5.2.1). So the image of the expression of Theorem 3.3.5 is
which is exactly \(a^h h!\) times the quantity in the proposition. We may ignore the factor \(a^h h!\), since it is nonzero and independent of r. \(\square \)
We now choose affinoid discs \(V_i\) contained in the \(U_i\) (so the \(M_{V_i}(\mathcal {F}_i)^*\) become Banach spaces).
Theorem 5.4.2
There is a element
which enjoys the following interpolating property: for any integers \((k_1, k_2, j)\) with \(k_i \in V_i\) and \(0 \leqslant j \leqslant \min (k, k')\), the image of \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a}\) at \((k_1, k_2, j)\) is
Proof
We choose an integer \(h \geqslant \lfloor \lambda _1 + \lambda _2 \rfloor \), and apply Proposition 2.3.3 with \(K = \mathbf {Q}(\mu _m)\), S the set of primes dividing \(p m N_1 N_2\), \(A = \mathcal {O}(V_1 \times V_2)\), \(M = M_{V_1}(\mathcal {F})^* \mathop {\hat{\otimes }}M_{V_2}(\mathcal {G})^*\), \(\lambda = \lambda _1 + \lambda _2\), and
for \(0 \leqslant j \leqslant h\) and \(n \geqslant 1\). These \(x_{n, j}\) are norm-compatible for \(n \geqslant 1\), and we obtain norm-compatible elements for all \(n \geqslant 0\) by defining
Moreover, the bound we have just established in Proposition 5.4.1 shows that \(\left\| p^{-nh}\sum _{j = 0}^h (-1)^j \left( {\begin{array}{c}h\\ j\end{array}}\right) x_{n, j}\right\| \leqslant Cp^{\lambda n}\), which is exactly the growth bound required for Proposition 2.3.3. It is not difficult to see that \(H^0(\mathbf {Q}_\infty , M_{V_1}(\mathcal {F})^* \mathop {\hat{\otimes }}M_{V_2}(\mathcal {G})^*) = 0\), so we obtain a class
interpolating the classes \(x_{n, j}\) for all \(n \geqslant 0\) and all \(j \in \{0, \ldots , h\}\). However, if we have two integers \(h' \geqslant h \geqslant \lfloor \lambda _1 + \lambda _2\rfloor \), then the element \(x[h']\) satisfies an interpolating property strictly stronger than that of x[h], so we deduce that x[h] is in fact independent of h and interpolates \(x_{n, j}\) for all \(j \geqslant 0\). We define \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a}\) to be this element. The interpolating property is now immediate from the interpolating property of the 2-variable classes \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}, j]}_{m, a}\) at integers \(k_1, k_2 \geqslant j\). \(\square \)
6 Phi–Gamma modules and triangulations
6.1 Phi–Gamma modules in families
Let \(\mathscr {R}\) denoteFootnote 2 the Robba ring (of \(\mathbf {Q}_p\)), which is the ring of formal Laurent series over \({\mathbf {Q}_p}\) in a variable \(\pi \), convergent on some annulus of the form \(\{x{:}\,0< v_p(x) < \varepsilon \} \subseteq \mathbf {A}^1_{\mathrm {rig}}\), and let \(\mathscr {R}^+ \subseteq {\mathbf {Q}_p}[[\pi ]]\) be its subring of elements that are analytic on the whole disc \(\{ x{:}\,v_p(x) > 0\}\). We endow these with their usual actions of Frobenius \(\varphi \) and the group \(\varGamma \cong \mathbf {Z}_p^\times \). We define a left inverse \(\psi \) of \(\varphi \) by putting
for any \(f(\pi )\in \mathscr {R}^+\).
As is well known, there is a functor \(\mathbf {D}^{\dag }_{\mathrm {rig}}\) mapping p-adic representations of \(G_{{\mathbf {Q}_p}}\) to \((\varphi , \varGamma )\)-modules over \(\mathscr {R}\) (finitely generated free \(\mathscr {R}\)-modules with commuting \(\mathscr {R}\)-semilinear operators \(\varphi \) and \(\varGamma \)), and this is a fully faithful functor whose essential image is the subcategory of \((\varphi , \varGamma )\)-modules of slope 0.
Remark 6.1.1
Strictly speaking, the definition of the functor \(\mathbf {D}^{\dag }_{\mathrm {rig}}\) depends on the auxiliary choice of a compatible system of p-power roots of unity \((\zeta _{p^n})_{n \geqslant 0}\) in \(\overline{\mathbf {Q}}_p\). We shall fix, once and for all, such a choice, and in applications to global problems we shall often assume that \(\zeta _{p^n}\) corresponds to \(e^{2\pi i{/}p^n} \in \mathbf {C}\).
Now let A be a reduced affinoid algebra over \({\mathbf {Q}_p}\), and write \(\mathscr {R}_A = \mathscr {R}\mathop {\hat{\otimes }}A\) and similarly for \(\mathscr {R}_A^+\). We define an A-representation of \(G_{{\mathbf {Q}_p}}\) to be a finitely generated locally free A-module endowed with an A-linear action of \(G_{{\mathbf {Q}_p}}\) (continuous with respect to the canonical Banach topology of M).
Theorem 6.1.2
(Berger–Colmez [4]) For any A-representation M of \(G_{{\mathbf {Q}_p}}\), we may define a finite locally free \(\mathscr {R}_A\)-module

, endowed with semilinear continuous actions of \(\varphi \) and \(\Gamma \), such that

for every \(x \in \mathrm{Max}(A)\).
Definition 6.1.3
If D is a \((\varphi , \varGamma )\)-module over \(\mathscr {R}_A\), we define cohomology groups \(H^i({\mathbf {Q}_p}, D)\) as the cohomology of the “Herr complex”

and analytic Iwasawa cohomology \(H^i_{\mathrm {Iw}}(\mathbf {Q}_{p, \infty }, D)\) as the cohomology of the complex

These groups are compatible with the usual Galois cohomology in the sense that if M is a A-representation of \(G_{{\mathbf {Q}_p}}\), then we have \(H^i({\mathbf {Q}_p}, \mathbf {D}^\dag _{\mathrm {rig}}(M)) = H^i({\mathbf {Q}_p}, V)\) and
where T is the unit ball for any \(G_{{\mathbf {Q}_p}}\)-invariant Banach module norm on M, by [16, Corollary 4.4.11].
Corollary 6.1.4
For M an A-representation of \(G_{{\mathbf {Q}_p}}\), we have a canonical isomorphism

In particular there is a canonical map
compatible with the natural maps to \(H^1({\mathbf {Q}_p}, M(\eta ))\) for every character \(\eta \) of \(\varGamma \).
Proof
Let us choose an increasing sequence of affinoid discs \(X_n \subseteq \mathcal {W}\) whose union is \(\mathcal {W}\). Since we have \(D^{\mathrm {la}}(\varGamma , {\mathbf {Q}_p}) = \mathcal {O}(\mathcal {W}) = \varprojlim _n \mathcal {O}(X_n)\), we can regard \(D^{\mathrm {la}}(\varGamma , M)\) as a locally free sheaf of \(G_{{\mathbf {Q}_p}}\)-representations on \(\mathcal {W}\times \mathrm{Max} A\), and we deduce that
by [29, Theorem 1.7]. For each n, \(X_n \times \mathrm{Max} A\) is an affinoid space, so we obtain
by [29, Proposition 2.7]. Finally, the inverse limit of the modules \(\mathbf {D}^\dag _{\mathrm {rig}}( \mathcal {O}(X_n)\mathop {\hat{\otimes }}M )\) is the module \(\mathbf {Dfm}(\mathbf {D}^\dag _{\mathrm {rig}}(M))\) considered in [16, Theorem 4.4.8], where it is shown that
for any \((\varphi , \varGamma )\)-module D over \(\mathscr {R}_A\). \(\square \)
Finally, if the base A is a finite field extension of \({\mathbf {Q}_p}\), then the functors \(\mathbf {D}_{\mathrm {cris}}(-)\) and \(\mathbf {D}_{\mathrm {dR}}(-)\) can be extended from A-linear representations of \(G_{{\mathbf {Q}_p}}\) to the larger category of \((\varphi , \varGamma )\)-modules over \(\mathscr {R}_A\), and one has the following fact:
Theorem 6.1.5
(Nakamura, see [24]) If A is a finite extension of \({\mathbf {Q}_p}\), there exist Bloch–Kato exponential and dual-exponential maps
and
for de Rham \((\varphi , \varGamma )\)-modules D over \(\mathscr {R}_A\), which are functorial in D and are compatible with the usual definitions when \(D = \mathbf {D}^{\dag }_{\mathrm {rig}}(V)\) for a de Rham representation V.
6.2 Perrin-Riou logarithms in families
Throughout this section, A denotes a reduced affinoid algebra, with supremum norm \(\Vert \cdot \Vert \), and \(\alpha \in A^\times \).
Definition 6.2.1
We write \(\mathscr {R}_A(\alpha ^{-1})\) for the free rank 1 \((\varphi , \varGamma )\)-module over \(\mathscr {R}_A\) with basis vector e such that \(\varphi (e) = \alpha ^{-1} e\) and \(\gamma e = e\) for all \(\gamma \in \varGamma \). We write \(\mathscr {R}^+_A(\alpha ^{-1})\) for the submodule \(\mathscr {R}^+_A \cdot e\) of \(\mathscr {R}_A(\alpha ^{-1})\).
Lemma 6.2.2
Suppose \(\Vert \alpha \Vert \leqslant 1\) and \(\alpha - 1\) is not a zero-divisor in A. Then
Proof
This follows from Lemma 1.11 of [12]. Cf. [14, §4.1]. \(\square \)
We use this lemma to define a Perrin-Riou big logarithm map for \(\mathscr {R}_A(\alpha ^{-1})\) when \(\alpha -1\) is not a zero-divisor, following closely the construction in [14, §4.2], as the composition

where the third arrow is the base extension to A of the Mellin transform (and \(\mathcal {W}\) is weight space). Note that our assumption that \(\alpha - 1\) is not a zero-divisor in A implies that \(\mathscr {R}_A(\alpha ^{-1})^{\varphi = 1} = 0\), and hence that \(\mathcal {L}_{\mathscr {R}_A(\alpha ^{-1})}\) is injective.
6.3 Triangulations
Definition 6.3.1
Let D be a \((\varphi , \varGamma )\)-module over \(\mathscr {R}\mathop {\hat{\otimes }}A\) which is locally free of rank 2. A triangulation of D is a short exact sequence of \((\varphi , \varGamma )\)-modules over \(\mathscr {R}\mathop {\hat{\otimes }}A\),
where the modules \(\mathscr {F}^\pm D\) are locally free of rank 1 over \(\mathscr {R}\mathop {\hat{\otimes }}A\).
Theorem 6.3.2
(Ruochuan Liu, [21]) Let \((f, \alpha )\) be as in Theorem 4.6.6. Then one can find an affinoid disc \(V \subset \mathcal {W}\) containing k such that the \((\varphi , \varGamma )\)-module

over \(\mathcal {O}(V)\) admits a canonical triangulation, with \(\mathscr {F}^- D_V(\mathcal {F})^* \cong \mathscr {R}_A(\alpha _{\mathcal {F}}^{-1})\) and \(\mathscr {F}^+ D_V(\mathcal {F})^* \cong \mathscr {R}_A(\alpha _{\mathcal {F}} \cdot \varepsilon _{\mathcal {F}}(p)^{-1})(1 + \kappa _V)\).
6.4 Eichler–Shimura isomorphisms
The last technical ingredient needed to proceed to the proof of our explicit reciprocity law is the following:
Theorem 6.4.1
(Eichler–Shimura relation in families) In the setting of Theorem 6.3.2, after possibly shrinking V, there is a canonical \(\mathcal {O}(V)\)-basis vector
such that for every integer weight \(t \geqslant 0\) in V, the specialisation of \(\omega _{\mathcal {F}}\) at t coincides with the image of the differential form \(\omega _{f_t}\) attached to the normalised eigenform \(f_t\).
This is a minor modification of results of Ruochuan Liu (in preparation); we outline the proof below. The starting point is the following theorem:
Theorem 6.4.2
(Andreatta–Iovita–Stevens, [1]) For any integer \(k_0 \geqslant 0\), and real \(\lambda < k_0 + 1\), we can find an open disc \(V \subset \mathcal {W}\) containing \(k_0\) and a Hecke-equivariant isomorphism

interpolating Faltings’ Hodge–Tate comparison isomorphisms for each \(k \in V\). Here X(w) is a rigid-analytic neighbourhood of the component of \(\infty \) in the ordinary locus of the compactification X of Y, and \(\omega ^{\dagger , \kappa _V + 2}_V\) is a certain sheaf of \(\mathcal {O}(V)\)-modules on X(w), whose specialisation at any integer \(k \geqslant 0 \in V\) is the \((k+2)\)th power of the Hodge bundle for every \(k \in V\).
Proof of Theorem 6.4.1
We translate the statement of the above theorem into the language of \((\varphi , \varGamma )\)-modules. For any family of \(G_{{\mathbf {Q}_p}}\)-representations M over an affinoid algebra A, we have a canonical isomorphism
where \(\mathbf {D}_{\mathrm {Sen}}(M)\) is defined in terms of the \((\varphi , \varGamma )\)-module \(\mathbf {D}^{\dag }_{\mathrm {rig}}(M)\).
Moreover, \(\mathbf {D}_{\mathrm {Sen}}\left( \mathscr {F}^+ D_V(\mathcal {F})(1 + \kappa _V)\right) ^{\varGamma }\) is zero. Hence, by composing \(\mathrm{comp}_V\) with the projection to \(\mathscr {F}^-\), we have an isomorphism

The left-hand side is free of rank 1, spanned by \(\tau \cdot \mathcal {F}\) where \(\tau \) is the Gauss sum of \(\varepsilon _\mathcal {F}^{(p)}\). On the other hand, since the \((\varphi , \varGamma )\)-module \(D^- = \mathscr {F}^- D_V(\mathcal {F})(1 + \kappa _V)\) is unramified, we have \(\mathbf {D}_{\mathrm {Sen}}(D^-)^\varGamma = (D^-)^{\varGamma }\). \(\square \)
Corollary 6.4.3
Under the same hypotheses as Theorem 6.4.1, possibly after shrinking V further, there is a \(\mathcal {O}(V)\)-basis vector
with the property that for every classical specialisation \(\mathcal {F}_t\) of \(\mathcal {F}\), the specialisation of \(\eta _{\mathcal {F}}\) at t is the unique vector whose cup-product with the differential \(\omega _{\overline{\mathcal {F}_t}}\) attached to the complex conjugate \(\overline{\mathcal {F}}_t\) of \(\mathcal {F}_t\) is given by
where \(\alpha \) and \(\beta \) are the roots of the Hecke polynomial of \(\mathcal {F}_t\), and \(\lambda _N(\mathcal {F}_t)\) is its Atkin–Lehner pseudo-eigenvalue.
Proof
This follows by dualising \(\omega _\mathcal {F}\) using the Ohta pairing \(\{-,-\}\); the computations are exactly the same as in the ordinary case, for which see [19, Proposition 10.1.2]. \(\square \)
7 The explicit reciprocity law
7.1 Regulator maps for Rankin convolutions
Now let us choose two newforms f, g and p-stabilisations \((\alpha _f, \alpha _g)\) satisfying the hypotheses of Theorem 4.6.4.
Notation 7.1.1
We write
and similarly for \(\mathscr {F}^{-+}\), \(\mathscr {F}^{+-}\) and \(\mathscr {F}^{++}\). We also define \(\mathscr {F}^{-\circ } D_{V_1 \times V_2}(\mathcal {F}\otimes \mathcal {G})^*=\mathscr {F}^- D_{V_1}(\mathcal {F})^*\hat{\otimes } D_{V_2}(\mathcal {G})^*\).
Theorem 7.1.2
If \(V_1\) and \(V_2\) are sufficiently small, then (for any m coprime to p) the image of \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a}\) under projection to the module \(H^1_{\mathrm {Iw}}(\mathbf {Q}(\mu _m) \otimes \mathbf {Q}_{p, \infty }, \mathscr {F}^{--} D_{V_1 \times V_2}(\mathcal {F}\otimes \mathcal {G})^*)\) is zero.
Proof
By taking the \(V_i\) sufficiently small, we may assume that \(\mathscr {F}^{--} D_{V_1 \times V_2}(\mathcal {F}\otimes \mathcal {G})^*\) is actually isomorphic to \(\mathscr {R}_A(\alpha ^{-1})\), where \(\alpha = \alpha _{\mathcal {F}} \alpha _{\mathcal {G}}\) and \(A = \mathcal {O}(V_1 \times V_2)\), and that \(\Vert \alpha ^{-1}\Vert < p^{1 + h}\) and \(\alpha - 1\) is not a zero-divisor. It suffices, therefore, to show that \(\mathcal {L}_{\mathscr {R}_A(\alpha ^{-1})}\) maps the image of \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a}\) to zero.
However, for each pair of integers \((\ell , \ell ') \in V_1 \times V_2\) with \(\ell , \ell ' \geqslant 1 + 2h\) and such that \(\mathcal {F}_\ell \) and \(\mathcal {G}_{\ell '}\) are not twists of each other, we know that the image of \(\mathcal {L}_{\mathscr {R}_A(\alpha ^{-1})}({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a})\) vanishes when restricted to \((\ell , \ell ') \times \mathcal {W}\subseteq \mathrm{Max}(A) \times \mathcal {W}\), by Proposition 3.5.11. Since such pairs \((\ell , \ell ')\) are Zariski-dense in \(\mathrm{Max}(A)\), the result follows. \(\square \)
Remark 7.1.3
Cf. [19, Lemma 8.1.5], which is an analogous (but rather stronger) statement in the ordinary case.
Hence the projection of \({}_c \mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{m, a}\) to \(\mathscr {F}^{- \circ }\) is in the image of the injection
Since \(\mathscr {F}^+ D_{V_2}(\mathcal {G})^*\) is isomorphic to an unramified module twisted by an \(A^\times \)-valued character of the cyclotomic Galois group \(\varGamma \), we may define a Perrin-Riou logarithm map for \(\mathscr {F}^{-+} D_{V_1 \times V_2}(\mathcal {F}\otimes \mathcal {G})^*\) by reparametrising the corresponding map for its unramified twist, exactly as in Theorem 8.2.8 of [19]. That is, if we define
which is free of rank 1 over \(\mathcal {O}(V_1 \times V_2)\), then we obtain the following theorem:
Theorem 7.1.4
There is an injective morphism of \(\mathcal {O}(V_1 \times V_2 \times W)\)-modules
with the following property: for all classical specialisations f, g of \(\mathcal {F},\mathcal {G}\), and all characters of \(\varGamma \) of the form \(\tau = j + \eta \) with \(\eta \) of finite order and \(j \in \mathbf {Z}\), we have a commutative diagram

in which the bottom horizontal map is given by
where \(\exp ^*\) and \(\log \) are the Bloch–Kato dual-exponential and logarithm maps, \(\varepsilon \) is the finite-order character \(\varepsilon _{g, p} \cdot \eta ^{-1}\) of \(\varGamma \), \(r \geqslant 0\) is the conductor of \(\varepsilon \), and \(G(\varepsilon ) = \sum _{a \in (\mathbf {Z}{/}p^r \mathbf {Z})^\times } \varepsilon (a) \zeta _{p^r}^a\) is the Gauss sum.
Proof
The construction of the map \(\mathcal {L}\) is immediate from (6.2.1). The content of the theorem is that the map \(\mathcal {L}\) recovers the maps \(\exp ^*\) and \(\log \) for the specialisations of \(\mathcal {F}\) and \(\mathcal {G}\); this follows from Nakamura’s construction of \(\exp ^*\) and \(\log \) for \((\varphi , \varGamma )\)-modules. \(\square \)
Theorem 7.1.5
(Explicit reciprocity law) If the \(V_i\) are sufficiently small, then we have
Here, \(L_p(\mathcal {F},\mathcal {G},1 + \mathbf {j})\) denotes Urban’s 3-variable p-adic L-function as constructed in [32], and \(\varepsilon _\mathcal {F}\) and \(\varepsilon _\mathcal {G}\) are the characters by which the prime-to-p diamond operators act on \(\mathcal {F}\) and \(\mathcal {G}\).
Proof
The two sides of the desired formula agree at every \((k, k', j)\) with \(k \in V_1\), \(k' \in V_2\) and \(0 \leqslant j \leqslant \min (k, k')\), by [18, Theorem 6.5.9]. These points are manifestly Zariski-dense, and the result follows. \(\square \)
Remark 7.1.6
The construction of \(\omega _{\mathcal {G}}\) and the proof of the explicit reciprocity law are also valid if \(\mathcal {G}\) is a Coleman family passing through a p-stabilisation \(g_\alpha \) of a p-regular weight 1 form, as in Theorem 4.7.2; the only difference is that one may need to replace \(V_2\) with a finite flat covering \(\tilde{V}_2\). In this setting, \(g_\alpha \) is automatically ordinary, so \(\mathcal {G}\) is in fact a Hida family, and one can use the construction of \(\omega _{\mathcal {G}}\) given in [19, Proposition 10.12.2].
8 Bounding Selmer groups
8.1 Notation and hypotheses
Let f, g be cuspidal modular newforms of weights \(k + 2, k' + 2\), respectively, and levels \(N_f, N_g\) prime to p. We do permit here the case \(k' = -1\). We suppose, however, that \(k > k'\), so in particular \(k \geqslant 0\), and we choose an integer j such that \(k' + 1 \leqslant j \leqslant k\). If \(j = \frac{k + k'}{2} + 1\), then we assume that \(\varepsilon _f \varepsilon _g\) is not trivial, where \(\varepsilon _f\) and \(\varepsilon _g\) are the characters of f and g.
As usual, we let E be a finite extension of \({\mathbf {Q}_p}\) with ring of integers \(\mathcal {O}\), containing the coefficients of f and g. Our goal will be to bound the Selmer group associated with the Galois representation \(M_\mathcal {O}(f \otimes g)(1 + j)\), in terms of the L-value \(L(f, g, 1 + j)\); our hypotheses on \((k, k', j)\) are precisely those required to ensure that this L-value is a critical value.
It will be convenient to impose the following local assumptions at p:
-
(p-regularity) We have \(\alpha _f \ne \beta _f\) and \(\alpha _g \ne \beta _g\), where \(\alpha _f, \beta _f\) are the roots of the Hecke polynomial of f at p, and similarly for g.
-
(no local zero) None of the pairwise products
$$\begin{aligned} \left\{ \alpha _f \alpha _g, \alpha _f \beta _g, \beta _f \alpha _g, \beta _f \beta _g\right\} \end{aligned}$$is equal to \(p^j\) or \(p^{1 + j}\), so the Euler factor of L(f, g, s) at p does not vanish at \(s = j\) or \(s = 1 + j\).
-
(nobility of \(f_\alpha \)) If f is ordinary, then either \(\alpha _f\) is the unit root of the Hecke polynomial, or \(M_E(f) |_{G_{{\mathbf {Q}_p}}}\) is not the direct sum of two characters (so the eigenform \(f_\alpha \) is noble in the sense of 4.6.3).
-
(nobility of \(g_\alpha \) and \(g_\beta \)) If \(k' \geqslant 0\), then \(M_E(g)|_{G_{{\mathbf {Q}_p}}}\) does not split as a direct sum of characters, so both p-stabilisations \(g_\alpha \) and \(g_\beta \) are noble.
Remark 8.1.1
-
(1)
In our arguments we will use both p-stabilisations \(g_\alpha \) and \(g_\beta \) of g, but only the one p-stabilisation \(f_\alpha \) of f; in particular, we do not require that the other p-stabilisation \(f_\beta \) be noble.
-
(2)
Note that the “no local zero” hypothesis is automatic, for weight reasons, unless \(k + k'\) is even and \(j = \frac{k + k'}{2}\) or \(j = \frac{k + k'}{2} + 1\) (so the L-value \(L(f, g, 1 + j)\) is a “near-central” value).
The p-regularity hypothesis implies that we have direct sum decompositions
where \(\varphi \) acts on the two direct summands as multiplication by \(\alpha _f^{-1}\), \(\beta _f^{-1}\), respectively, and similarly for g. This induces a decomposition of \(\mathbf {D}_\mathrm {cris}(M_E(f \otimes g)^*)\) into four direct summands \(\mathbf {D}_{\mathrm {cris}}(M_E(f \otimes g)^*)^{\alpha _f \alpha _g}\) etc.
Definition 8.1.2
We write
We write \({{\mathrm{pr}}}_{\alpha _f}\) for the projection
with \(\mathbf {D}_{\mathrm {cris}}(M_E(f \otimes g)^*)^{\beta _f \circ }\) as kernel.
Proposition 8.1.3
If W denotes the Galois representation \(M_E(f \otimes g)^*(-j)\), then:
-
\(H^1({\mathbf {Q}_p}, W)\) is 4-dimensional (as an E-vector space), and \(H^0({\mathbf {Q}_p}, W) = H^2({\mathbf {Q}_p}, W) = 0\);
-
we have
$$\begin{aligned} H^1_\mathrm {e}({\mathbf {Q}_p}, W) = H^1_\mathrm {f}({\mathbf {Q}_p}, W) = H^1_\mathrm {g}({\mathbf {Q}_p}, W), \end{aligned}$$and this space has dimension 2;
-
the dual-exponential map gives an isomorphism
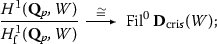
-
the projection

is an isomorphism.
Proof
This is an elementary exercise using local Tate duality, Tate’s local Euler characteristic formula, and the “no local zero” hypothesis. \(\square \)
Theorem 8.1.4
Fix some \(c > 1\) coprime to \(6p N_f N_g\). For each \(m \geqslant 1\) coprime to pc, we obtain two classes
with the following properties:
-
(i)
for every prime \(v \not \mid p\) of \(\mathbf {Q}(\mu _m)\), we have
$$\begin{aligned} \mathrm{loc}_v\left( c^{\alpha _f \alpha _g}_m\right) \in H^1_\mathrm {f}\left( \mathbf {Q}(\mu _m)_v, M_E(f \otimes g)^*(-j)\right) ; \end{aligned}$$ -
(ii)
there is a constant R (independent of m) such that
$$\begin{aligned} R c^{\alpha _f \alpha _g}_m, Rc^{\alpha _f \beta _g}_m \in H^1(\mathbf {Q}(\mu _m), M_{\mathcal {O}_E}(f \otimes g)^*(-j)){/}\{\text {torsion}\}, \end{aligned}$$where \(M_{\mathcal {O}_E}(f \otimes g)^*\) is the lattice in \(M_E(f \otimes g)^*\) which is the image of the étale cohomology with \(\mathcal {O}_E\)-coefficients;
-
(iii)
for \(\ell \not \mid m N_f N_g\), we have
$$\begin{aligned} {{\mathrm{norm}}}_{m}^{\ell m} \left( c^{\alpha _f \alpha _g}_{\ell m}\right) = P_\ell (\ell ^{-1-j} \sigma _\ell ^{-1}) \cdot c^{\alpha _f \alpha _g}_{m}, \end{aligned}$$where \(P_\ell (X)\) is the local Euler factor of L(f, g, s) at \(\ell \), and similarly for \(c^{\alpha _f \beta _g}_{\ell m}\);
-
(iv)
the images of \(c^{\alpha _f \alpha _g}_m\) and \(c^{\alpha _f \beta _g}_m\) under the map

lie in the subspaces \(\mathbf {D}_{\mathrm {cris}}(M_{E}(f)^*)^{\alpha _f \beta _g}\) and \(\mathbf {D}_{\mathrm {cris}}(M_{E}(f)^*)^{\alpha _f \alpha _g}\), respectively;
-
(v)
for \(m = 1\), the projections \({{\mathrm{pr}}}_{\alpha }\left( \exp ^* c^{\alpha _f \alpha _g}_1\right) \) and \({{\mathrm{pr}}}_{\alpha }\left( \exp ^* c^{\alpha _f \beta _g}_1\right) \) are nonzero (for some suitable choice of c) if and only if \(L(f \otimes g, 1 + j) \ne 0\).
Proof
We define the class \(c^{\alpha _f \alpha _g}\) as follows. Using the p-stabilisations \(f_\alpha \) of f and \(g_\alpha \) of g, Theorem 5.4.2 gives rise to elements
where \(\mathcal {F}\) and \(\mathcal {G}\) are Coleman families through \(f_\alpha \) and \(g_\alpha \) (which exist, since \(f_\alpha \) is noble, and \(g_\alpha \) is either noble of weight \(\geqslant 2\) or p-regular of weight 1). Specialising these at \((f_\alpha , g_\alpha , j)\), and identifying \(M_E(f_\alpha \otimes g_\alpha )^*\) with \(M_E(f \otimes g)^*\) via the maps \({{\mathrm{Pr}}}^{\alpha _f}\) and \({{\mathrm{Pr}}}^{\alpha _g}\), we obtain classes \(z_m^{\alpha _f \alpha _g} \in H^1(\mathbf {Q}(\mu _m), M_{E}(f \otimes g)^*(-j))\).
These classes satisfy (i), by Proposition 2.4.4. They also satisfy (ii), by Proposition 2.4.7 (using the fact that f and g have differing weights, by hypothesis, so we have \(H^0(\mathbf {Q}^{\mathrm {ab}}, M_E(f_\alpha \otimes g_\alpha )^*) = 0\)).
The classes \(z_m^{\alpha _f \alpha _g}\) do not satisfy (iii); instead, they satisfy the a slightly more complicated norm-compatibility relation \({{\mathrm{norm}}}_{m}^{\ell m} \left( c^{\alpha _f \alpha _g}_{\ell m}\right) = Q_\ell (\ell ^{-1-j} \sigma _\ell ^{-1}) c^{\alpha _f \alpha _g}_{m}\) where \(Q_\ell (X) \in X^{-1} \mathcal {O}_L[X]\) is a polynomial congruent to \(-X^{-1} P_\ell (X)\) modulo \(\ell - 1\). However, the “correct” Euler system relation can be obtained by modifying each class \(z^{\alpha _f \alpha _g}_m\) by an appropriate element of \(\mathcal {O}_L[(\mathbf {Z}{/}m\mathbf {Z})^\times ]\), as in [20, §7.3]. This gives classes \(c_m^{\alpha _f \alpha _g}\) satisfying (i)–(iv).
It remains to verify (iv) and (v). It suffices to prove these for the un-modified classes \(z_m^{\alpha _f \alpha _g}\). For (iv), let K denote the completion of \(\mathbf {Q}(\mu _m)\) at a prime above p, and \(K_\infty = K(\mu _{p^\infty })\). Then we have a diagram

Here W denotes the Galois representation \(M_E(f \otimes g)^*(-j)\), as above, D denotes \(\mathbf {D}^\dag _{\mathrm {rig}}(V)\), and \(\mathscr {F}^{--} D\) is the quotient of D (in the category of \((\varphi , \varGamma )\)-modules) determined by the triangulations of \(M_E(f_\alpha )^*\) and \(M_E(f_\beta )^*\). Note that this quotient depends on the choice of \(\alpha _f\) and \(\alpha _g\), although the Galois representation W does not.
The horizontal arrows in the diagram are induced by the morphism of \((\varphi , \varGamma )\)-modules \(D \rightarrow \mathscr {F}^{--} D\). We know that the image of \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_{m, 1}\) in \(H^1_{\mathrm {Iw}}(K_\infty , \mathscr {F}^{--} D )\) is zero, by Theorem 7.1.2, so its image in the bottom right-hand corner is zero. However, the projection \(\mathbf {D}_\mathrm {cris}(V) \rightarrow \mathbf {D}_\mathrm {cris}(\mathscr {F}^{--} D)\) factors through projection to the eigenspace \(\mathbf {D}_\mathrm {cris}(V)^{\alpha _f \alpha _g}\) and is an isomorphism on this eigenspace, so we recover the statement that \(\exp ^*(c^{\alpha _f \alpha _g}_m)\) projects to zero in \(\mathbf {D}_\mathrm {cris}(V)^{\alpha _f \alpha _g}\), as required.
Finally, we prove (v). For this, we use an analogous commutative diagram with \(\mathscr {F}^{-\circ }\) in place of \(\mathscr {F}^{--}\):

The projection \(\mathbf {D}_\mathrm {cris}(V) \rightarrow \mathbf {D}_{\mathrm {cris}}(\mathscr {F}^{-\circ }D)\) induces an isomorphism

Theorem 7.1.2 implies that the image of \({}_c \mathcal {BF}^{[f_\alpha , g_\alpha ]}_1\) in \(H^1_{\mathrm {Iw}}(\mathbf {Q}_{p,\infty }, V)\) lies in the image of \(H^1_{\mathrm {Iw}}(\mathbf {Q}_{p,\infty }, \mathscr {F}^{-+} D )\), and the explicit reciprocity law shows that the image of this class in \(\mathbf {D}_{\mathrm {cris}}(\mathscr {F}^{-+} D)\) is nonzero if and only if \((c^2 - c^{2j-k-k'} \varepsilon _f(c) \varepsilon _g(c)) L(f, g, 1 + j) \ne 0\). Our hypothesis that \( \varepsilon _f(c) \varepsilon _g(c)\) be non-trivial if \(j = \frac{k + k'}{2} + 1\) shows that we can choose c such that the first factor is nonzero. So, for a suitable choice of c, the projection of \(z_1^{\alpha _f \alpha _g}\) to \(\mathbf {D}_{\mathrm {cris}}(V)^{\alpha _f \beta _g}\) is nonzero if and only if \(L(f, g, 1 + j) \ne 0\).
This completes the construction of classes \(c^{\alpha _f \alpha _g}_m\) with the required properties. The construction of \(c^{\alpha _f \beta _g}_m\) is identical, using the p-stabilisation \(g_\beta \) in place of \(g_\alpha \). \(\square \)
8.2 Bounding the Bloch–Kato Selmer group
Recall that if V is a geometric p-adic representation of \({{\mathrm{Gal}}}(\overline{\mathbf {Q}}{/}\mathbf {Q})\), then we define
Theorem 8.2.1
Suppose the assumptions of Theorem 8.1.4 are satisfied, and in addition the following hypothesis is satisfied:
-
(big image) There exists an element \(\tau \in {{\mathrm{Gal}}}(\overline{\mathbf {Q}}{/}\mathbf {Q}(\mu _{p^\infty }))\) such that \(V{/}(\tau - 1) V\) is 1-dimensional, where \(V = M_E(f \otimes g)(1 + j)\).
If \(L(f, g, 1 + j) \ne 0\), then the Bloch–Kato Selmer group \(H^1_{\mathrm {f}}(\mathbf {Q}, V)\) is zero.
Remark 8.2.2
It is shown in [22] that, under fairly mild hypotheses on f and g, the “big image” hypothesis is satisfied for all but finitely many primes \(\mathfrak {P}\) of the coefficient field.
Proof
Let \(H^1_{\mathrm {strict}}(\mathbf {Q}, V)\) denote the strict Selmer group, which is the kernel of the localisation map
Let T be a lattice in V, and let \(A = V{/}T\). By Theorem 8.1.4, for some nonzero scalar R, the classes \(R \cdot c_m^{\alpha _f \alpha _g}\) form a nonzero Euler system for \(T^*(1)\) in the sense of [31, Definition 2.1.1], if we replace condition (ii) in the definition by the alternative condition (ii’)(b) of §9.1 of op.cit..
By [31, Theorem 2.2.3], the existence of any nonzero Euler system for \(V^*(1)\), together with the “big image” hypothesis, implies that the p-torsion Selmer group
is finite, where \(H^1_{\mathrm {strict}}(\mathbf {Q}_\ell , A)\) is defined as the image of the map
for \(\ell \ne p\), and \(H^1_{\mathrm {strict}}({\mathbf {Q}_p}, A) = 0\). However, the image of \(H^1_{\mathrm {strict}}(\mathbf {Q}, V)\) in \(H^1(\mathbf {Q}, A)\) is clearly contained in \(H^1_{\mathrm {strict}}(\mathbf {Q}, A)\), so we conclude that \(H^1_{\mathrm {strict}}(\mathbf {Q}, V)\) is zero.
In order to refine this, we use Poitou–Tate duality. Let \(H^1_{\mathrm {relaxed}}(\mathbf {Q}, V^*(1))\) (the “relaxed Selmer group”) denote the classes in \(H^1(\mathbf {Q}, V^*(1))\) whose localisation lies in \(H^1_\mathrm {f}\) for all \(\ell \ne p\) (but may be arbitrary at p). Then we have two exact sequences

and

where \(H^1_{\mathrm {s}}({\mathbf {Q}_p}, V^*(1)) = \frac{H^1({\mathbf {Q}_p}, V^*(1))}{H^1_{\mathrm {f}}({\mathbf {Q}_p}, V^*(1))}\) (the “singular quotient”). Local Tate duality identifies \(H^1_{\mathrm {s}}({\mathbf {Q}_p}, V^*(1))\) with the dual of \(H^1_{\mathrm {f}}({\mathbf {Q}_p}, V)\), and the Poitou–Tate global duality exact sequence implies that the images of \({{\mathrm{loc}}}^{\mathrm {f}}_p\) and \({{\mathrm{loc}}}^{\mathrm {s}}_p\) are orthogonal complements of each other; compare [31, Theorem 1.7.3].
We have constructed two classes in \(H^1_{\mathrm {relaxed}}({\mathbf {Q}_p}, V^*(1))\), namely \(c_1^{\alpha _f \alpha _g}\) and \(c_1^{\alpha _f \beta _g}\), whose images in \(\frac{H^1({\mathbf {Q}_p}, V^*(1))}{H^1_{\mathrm {f}}({\mathbf {Q}_p}, V^*(1))}\) are linearly independent (since their images under \(\exp ^*\) span distinct eigenspaces). So \({{\mathrm{loc}}}_p^{\mathrm {s}}\) is surjective, and consequently \({{\mathrm{loc}}}^{\mathrm {f}}_p\) is the zero map. As we have already shown that \(H^1_{\mathrm {strict}}({\mathbf {Q}_p}, V) = 0\), this shows that \(H^1_{\mathrm {f}}({\mathbf {Q}_p}, V)\) is zero. \(\square \)
Remark 8.2.3
The above argument is an adaptation of the ideas of [13, §6.2], in which Poitou–Tate duality is used to bound the image of the map \({{\mathrm{loc}}}^\mathrm {f}_p\) for a Galois representation arising from the product of three cusp forms. In our setting, since we have a full Euler system rather than just the two classes \(c_1^{\alpha _f \alpha _g}\) and \(c_1^{\alpha _f \beta _g}\), we can also bound the kernel of this map.
8.3 Corollaries
From Theorem 8.2.1 one obtains a rather precise description of the global cohomology groups. We continue to write \(V = M_E(f \otimes g)(1 + j)\).
Let S be any finite set of places of \(\mathbf {Q}\), containing \(\infty \) and all primes dividing \(p N_f N_g\). Then the action of \({{\mathrm{Gal}}}(\overline{\mathbf {Q}}{/}\mathbf {Q})\) on V factors through \({{\mathrm{Gal}}}(\mathbf {Q}^S\!/\mathbf {Q})\), the Galois group of the maximal extension of \(\mathbf {Q}\) unramified outside S. Since the Bloch–Kato local condition coincides with the unramified condition for \(\ell \notin S\), we have
Remark 8.3.1
Since \({{\mathrm{Gal}}}(\mathbf {Q}^S\!/\mathbf {Q})\) is the étale fundamental group of \(\mathbf {Z}[1/S]\), we may interpret any continuous \({\mathbf {Q}_p}\)-linear representation of \({{\mathrm{Gal}}}(\mathbf {Q}^S\!/\mathbf {Q})\) as a p-adic étale sheaf on \(\mathrm{Spec} \mathbf {Z}[1/S]\), and the continuous cohomology groups \(H^i(\mathbf {Q}^S\!/\mathbf {Q}, -)\) coincide with the étale cohomology groups \(H^i_{{\acute{\mathrm{e}}{\mathrm{t}}}}(\mathbf {Z}[1/S], -)\). The latter language is used in [19] for instance, but in the present work we have found it easier to use the language of group cohomology, since this makes the arguments of Sect. 2 easier to state.
Corollary 8.3.2
If the hypotheses of Theorem 8.2.1 hold, then:
-
(1)
The localisation maps
$$\begin{aligned} H^2(\mathbf {Q}^S\!/\mathbf {Q}, V)\rightarrow & {} \bigoplus _{\ell \in S} H^2(\mathbf {Q}_\ell , V)\quad \text {and}\\ H^2(\mathbf {Q}^S\!/\mathbf {Q}, V^*(1))\rightarrow & {} \bigoplus _{\ell \in S} H^2(\mathbf {Q}_\ell , V^*(1)) \end{aligned}$$are isomorphisms.
-
(2)
The space \(H^1_{\mathrm {f}}(\mathbf {Q}, V^*(1))\) is zero.
-
(3)
The space \(H^1_{\mathrm {relaxed}}(\mathbf {Q}, V^*(1))\) is 2-dimensional, and \(c_1^{\alpha _f \alpha _g}\) and \(c_1^{\alpha _f \beta _g}\) are a basis.
Proof
Again by Poitou–Tate global duality, we have an exact sequence

In the situation of the theorem, we have \(H^1_{\mathrm {f}}(\mathbf {Q}, V) = 0\), so the localisation map for \(H^2(\mathbf {Q}^S\!/\mathbf {Q}, V^*(1))\) is an isomorphism.
Now let \(c_\ell = \dim H^2(\mathbf {Q}_\ell , V^*(1))\). Using Tate’s local Euler characteristic formula, for any \(\ell \in S {\setminus } \{p\}\) we have \(\dim H^1(\mathbf {Q}_\ell , V^*(1)) = c_\ell \); while for \(\ell = p\) we have \(c_p = 0\) and \(\dim H^1_{\mathrm {s}}({\mathbf {Q}_p}, V^*(1)) = 2\). Thus \(\dim \bigoplus _{\ell \in S} H^1_{\mathrm {s}}(\mathbf {Q}_\ell , V^*(1)) = 2 + \sum c_\ell = 2 + \dim H^2(\mathbf {Q}^S\!/\mathbf {Q}, V^*(1))\). However, Tate’s global Euler characteristic formula gives \(\dim H^1(\mathbf {Q}^S\!/\mathbf {Q}, V^*(1)) = 2 +\dim H^2(\mathbf {Q}^S\!/\mathbf {Q}, V^*(1))\).
Thus the map  is a surjection between finite-dimensional vector spaces of the same dimension, so it is injective and we conclude that \(H^1_{\mathrm {f}}(\mathbf {Q}, V^*(1)) = 0\). Repeating the duality argument with \(V^*(1)\) in place of V we now deduce that the localisation map for \(H^2(\mathbf {Q}^S\!/\mathbf {Q}, V)\) is an isomorphism.
is a surjection between finite-dimensional vector spaces of the same dimension, so it is injective and we conclude that \(H^1_{\mathrm {f}}(\mathbf {Q}, V^*(1)) = 0\). Repeating the duality argument with \(V^*(1)\) in place of V we now deduce that the localisation map for \(H^2(\mathbf {Q}^S\!/\mathbf {Q}, V)\) is an isomorphism.
Finally, since \(H^1_{\mathrm {f}}(\mathbf {Q}, V^*(1)) = 0\), we deduce that \(H^1_{\mathrm {relaxed}}(\mathbf {Q}, V^*(1))\) maps isomorphically to its image in \(H^1_{\mathrm {s}}({\mathbf {Q}_p}, V^*(1))\), but the images of \(c_1^{\alpha _f \alpha _g}\) and \(c_1^{\alpha _f \beta _g}\) are a basis of \(H^1_{\mathrm {s}}({\mathbf {Q}_p}, V^*(1))\), so these two classes must be a basis of \(H^1_{\mathrm {relaxed}}(\mathbf {Q}, V^*(1))\). \(\square \)
Corollary 8.3.3
Let \(L_S(f, g, s) = \prod _{\ell \notin S} P_\ell (\ell ^{-s})^{-1}\) be the L-function without its local factors at places in S. If the hypotheses of Theorem 8.2.1 are satisfied and \(L_S(f, g, 1 + j) \ne 0\), then \(H^2(\mathbf {Q}^S\!/\mathbf {Q}, M_E(f \otimes g)^*(-j)) = 0\).
Proof
For primes \(\ell \in S\), \(\ell \ne p\), let us set
and
We define \(P_p(X) = P_p^0(X) = \det \left( 1 - X \varphi {:}\, \mathbf {D}_{\mathrm {cris}}(M_E(f \otimes g))\right) \). Then we have
where \(L(\pi _f \otimes \pi _g, s)\) (the “primitive” Rankin–Selberg L-function) and L(f, g, s) (the “imprimitive” Rankin–Selberg L-function) are both holomorphic on the whole complex plane. So if \(L_S(f, g, 1 + j)\) is nonzero, then we must have \(P_\ell (\ell ^{-1-j}) \ne 0\) for all \(\ell \in S\), and \(L(f, g, 1 + j) \ne 0\).
From the definition of \(P_\ell (X)\), the fact that \(P_\ell (\ell ^{-1-j}) \ne 0\) implies that \(H^0(\mathbf {Q}_\ell , M_E(f \otimes g)(1+j)) = 0\) for all \(\ell \in S\). Thus \(H^2(\mathbf {Q}_\ell , M_E(f \otimes g)^*(-j)) = 0\) for all \(\ell \in S\), and since the global \(H^2\) injects into the direct product of these groups, it must also vanish. \(\square \)
Remark 8.3.4
One can check that the only values of s at which the Euler factors \(P_\ell (\ell ^{-s})\) may vanish for some \(\ell \in S\) are
Note that the centre of the functional equation, with our normalisations, is at \(s = \frac{ k + k' + 3}{2}\).
8.4 Application to elliptic curves
Theorem 8.2.1 above allows us to strengthen one of the results of [19] to cover elliptic curves which are not necessarily ordinary at p:
Theorem 8.4.1
Let \(E{/}\mathbf {Q}\) be an elliptic curve without complex multiplication, and \(\rho \) a 2-dimensional odd irreducible Artin representation of \(G_{\mathbf {Q}}\) (with values in some finite extension \(L/\mathbf {Q}\)). Let p be a prime. Suppose that the following hypotheses are satisfied:
-
(i)
The conductors \(N_E\) and \(N_\rho \) are coprime;
-
(ii)
\(p \geqslant 5\);
-
(iii)
\(p \not \mid N_E N_\rho \);
-
(vi)
the map \(G_\mathbf {Q}\rightarrow \mathrm{Aut}_{\mathbf {Z}_p}(T_p E)\) is surjective;
-
(v)
\(\rho (\mathrm{Frob}_p)\) has distinct eigenvalues.
If \(L(E, \rho , 1) \ne 0\), then the group
(where F is the splitting field of \(\rho )\) is finite. In particular,

is finite.
Proof
This is exactly Theorem 8.2.1 applied with \(f = f_E\), the weight 2 form attached to E, and \(g = g_{\rho }\), the weight 1 form attached to \(\rho \). Compare Theorem 11.7.4 of [19], which is exactly the same theorem under the additional hypotheses that E is ordinary at p and \(\rho (\mathrm{Frob}_p)\) has distinct eigenvalues modulo a prime of L above p. \(\square \)
9 Addendum: remarks on the proof of the reciprocity law
In order to formulate the explicit reciprocity law of Theorem 7.1.5, one needs to invoke the main theorem of [32]: the construction of a 3-variable p-adic Rankin–Selberg L-function as a rigid-analytic function on \(V_1 \times V_2 \times \mathcal {W}\), where \(V_i\) are small discs in the Coleman–Mazur eigencurve surrounding classical p-stabilised eigenforms, and \(\mathcal {W}\) is weight space.
Unfortunately, since the present paper was submitted, it has emerged that there are some unresolved technical issues in the paper [32], so the existence of this p-adic L-function is not at present on a firm footing. We hope that this issue will be resolved in the near future, but as a temporary expedient we explain here an unconditional proof of a weaker form of explicit reciprocity law which suffices for the arithmetic applications in the present paper.
9.1 A three-variable geometric p-adic L-function
We place ourselves in the situation of Sect. 7.1, so \(f_\alpha , g_\alpha \) are noble eigenforms, obtained as p-stabilisations of newforms f, g of weights \(k_0 + 2, k_0' + 2\) and levels prime to p, and \(V_1, V_2\) are small enough affinoid discs in weight space around \(k_0\) and \(k_0'\), over which there are Coleman families \(\mathcal {F}, \mathcal {G}\) passing through \(f_\alpha \), \(g_\alpha \). We also allow the possibility that \(k'_0 = -1\), g is a p-regular weight 1 newform, and g does not have real multiplication by a field in which p splits. (The exceptional real-multiplication case can be handled similarly by replacing \(V_2\) with a ramified covering; we leave the details to the reader.)
For notational simplicity, we shall suppose that \(\varepsilon _\mathcal {F}\varepsilon _{\mathcal {G}}\) is non-trivial and is not of p-power order. Thus there is a \(c > 1\) coprime to \(6p N_f N_g\) for which the factor \(c^2 - c^{2\mathbf {j} - \mathbf {k}-\mathbf {k}'} \varepsilon _\mathcal {F}(c)^{-1} \varepsilon _{\mathcal {G}}(c)^{-1}\) is a unit in \(\mathcal {O}(V_1 \times V_2 \times \mathcal {W})\), and we may define \(\mathcal {BF}^{[\mathcal {F}, \mathcal {G}]}_{1, 1}\) (without c) by dividing out by this factor.
We shall begin by turning Theorem C on its head and defining a p-adic L-function to be the output of this theorem:
Definition 9.1.1
We define \(L_p^{\mathrm {geom}}(\mathcal {F}, \mathcal {G}) \in \mathcal {O}(V_1 \times V_2 \times \mathcal {W})\) by
Our goal is now to show that this geometrically defined p-adic L-function is related to critical values of complex L-functions.
9.2 Values in the geometric range
By construction, for integer points of \(V_1 \times V_2 \times \mathcal {W}\) in the “geometric range”—that is, the points \((k, k', j)\) with \(0 \leqslant j \leqslant \min (k, k')\)—the geometric p-adic L-function interpolates the syntomic regulators of the Rankin–Eisenstein classes. From the computations of [18], we have the following explicit formula for these syntomic regulators.
Let \(f_{k, \alpha }\) be the p-stabilised eigenform that is the specialisation of \(\mathcal {F}\) in weight \(k+2\), and let \(\lambda _{f_{k, \alpha }}\) be the unique linear functional on the space \(S_{k + 2}^\mathrm {oc}(N_f, E)\) of overconvergent cusp forms that factors through projection to the \(f_{k, \alpha }\)-isotypical subspace and sends \(f_{k, \alpha }\) to 1. We view \(\lambda _{f_{k, \alpha }}\) as a linear functional on \(S_{k + 2}^\mathrm {oc}(N, E)\), where \(N = \mathrm{lcm}(N_f, N_g)\), by composing with the trace map from level N to level \(N_f\).
Theorem 9.2.1
([18, Theorem 6.5.9]) For \((k, k', j)\) in the geometric range, with \(j > \tfrac{k}{2} -1\), we have
Here \(F^{[p]}_{k - k', k' - j + 1}\) is a nearly overconvergent p-adic Eisenstein series of weight \(k-k'\) and degree of near-overconvergence \(\leqslant k-j\), whose p-adic q-expansion (image under the unit-root splitting) is given by
Note that we have
where \(\theta = q \frac{\mathrm {d}}{\mathrm {d}q}\) and \(E^{[p]}_\kappa \), for \(\kappa \in \mathcal {W}\), denotes the weight \(\kappa \) overconvergent Eisenstein series
Since \(E^{[p]}_{r}\) is overconvergent of weight r, it follows that \(g_{k', \alpha } \cdot \theta ^{k-j}\left( E^{[p]}_{2j-k-k'}\right) \) lies in the space \(S_{k + 2}^{\mathrm {n-oc}, k-j}(N)\) of nearly overconvergent cusp forms of weight \(k + 2\) and degree of near-overconvergence \(k-j\). The condition \(j > \tfrac{k}{2}-1\) implies that \(k + 2 > 2(k-j)\), so Urban’s overconvergent projector \(\Pi ^{\mathrm {oc}}\) is defined on \(S_{k + 2}^{\mathrm {n-oc}, k-j}(N)\) [32, §3.3.3]. Thus the right-hand side of the formula in the theorem is defined.
9.3 Two-variable analytic L-functions
Let us now pick an integer \(t \geqslant 0\), and set \(j = k - t\) in the above formulae. Then, for varying k and \(k'\) (but t fixed), the forms \(g_{k', \alpha } \cdot \theta ^t\left( E^{[p]}_{k-k'-2t}\right) \) interpolate to a 2-parameter family of nearly overconvergent cusp forms over \(V_1 \times V_2\) (of weight \(\mathbf {k} + 2\) and degree t, where \(\mathbf {k}\) is the universal weight of \(V_1\)). Hence we may make sense of
as a meromorphic rigid-analytic function on \(V_1 \times V_2\), analytic except possibly for simple poles along \(V_1 \cap \{ 0, \ldots , 2t-2\}\) [32, §3.3.4].
Remark 9.3.1
The important point here is that the power of the differential operator appearing is constant in the family; this circumvents the technical issues in [32], which concern interpolation of families where the degree of near-overconvergence is unbounded.
We have the following special sets of integer points \((k, k') \in V_1 \times V_2\):
-
(i)
If \(k \geqslant \max (t, 2t-1)\) and \(k' \geqslant k-t\), then the “geometric” interpolating property above applies, showing that for these values of \((k, k')\) we have
$$\begin{aligned} L_p^{(t)}(\mathcal {F}, \mathcal {G})(k, k') = L_p^{\mathrm {geom}}(\mathcal {F}, \mathcal {G})(k, k', k-t). \end{aligned}$$Since such \((k, k')\) are manifestly Zariski-dense in \(V_1 \times V_2\), this relation must in fact hold for all points \((\kappa , \kappa ') \in V_1 \times V_2\).
-
(ii)
If \(k' \geqslant 0\) and \(k - k' \geqslant 2t + 1\), then both \(g_{k', \alpha }\) and \(E^{[p]}_{k-k'-2t}\) are classical modular forms (since, after possibly shrinking \(V_2\), we may arrange that the specialisations of the family \(\mathcal {G}\) at classical weights are classical). Thus the product \(g_{k', \alpha } \cdot \theta ^{t}\left( E^{[p]}_{k-k'-2t}\right) \) is a classical nearly holomorphic form, and on such forms Urban’s overconvergent projector coincides with the holomorphic projector \(\Pi ^{\mathrm {hol}}\). This shows that the values of \(L_p^{(t)}(\mathcal {F}, \mathcal {G})(k, k')\) for \((k,k')\) in this range are algebraic, and they compute the values of the Rankin–Selberg L-function in the usual way. This also holds for \(k' = -1\), as long as we assume that the weight 1 specialisation \(g_{k', \alpha }\) is classical (which is no longer automatic).
Combining these two statements, we deduce the following version of an explicit reciprocity law:
Theorem 9.3.2
Let \((k, k', j)\) be an integer point of \(V_1 \times V_2 \times \mathcal {W}\) with \(k \geqslant 0\), \(k' \geqslant -1\), and \(\frac{k + k' + 1}{2} \leqslant j \leqslant k\), and suppose \(f_{k, \alpha }\) and \(g_{k', \alpha }\) are p-stabilisations of classical forms \(f_k, g_{k'}\). Then we have
where the local Euler factors are given by
This suffices to prove Theorem C of the introduction when \(j \geqslant \frac{k + k' + 1}{2}\). The remaining cases of Theorem C, when \(k' + 1 \leqslant j < \frac{k + k' + 1}{2}\), are easily reduced to these cases using the functional equation.
Remark 9.3.3
It is important to be clear about what this argument does not prove: we obtain no information at all about the values of the geometric p-adic L-function at points of the form \((k, k', j + \chi )\) for a non-trivial finite-order character \(\chi \). In particular, we cannot determine by this method whether the specialisation of our 3-variable geometric L-function to \(\{k_0\} \times \{k_0'\} \times \mathcal {W}\) coincides with other existing constructions of a single-variable p-adic Rankin–Selberg L-function (cf. [30]).
Acknowledgements
During the preparation of this paper, we benefitted from conversations with a number of people, notably Fabrizio Andreatta, Pierre Colmez, Hansheng Diao, Henri Darmon, Adrian Iovita, Guido Kings, Ruochuan Liu, Jay Pottharst, Karl Rubin, and Chris Skinner. We would also like to thank the anonymous referee for several helpful comments and corrections.
Large parts of the paper were written while the authors were visiting the Mathematical Sciences Research Institute in Berkeley, California, for the programme “New Geometric Methods in Automorphic Forms”, and it is again a pleasure to thank MSRI for their support and the organisers of the programme for inviting us to participate.
The authors’ research was supported by the following grants: Royal Society University Research Fellowship (Loeffler); Leverhulme Trust Research Fellowship “Euler systems and Iwasawa theory” (Zerbes). Parts of this paper were written, while the authors were guests at MSRI in Berkeley, California, supported by NSF Grant 0932078 000.
Notes
This notation is somewhat misleading; it would be better to describe this as the \({weak\hbox {-}star\, topology}\) and to reserve the term \({weak\, topology}\) for the topology on \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) induced by its own continuous dual (for the strong topology), in line with the usual terminology in classical functional analysis. However, the above abuse of notation has become standard in the non-Archimedean theory, perhaps because the continuous duals of spaces such as \(D_\lambda (\mathbf {Z}_p, {\mathbf {Q}_p})\) are too pathological to be of much interest.
The rings \(\mathscr {R}\) and \(\mathscr {R}^+\) are often also denoted by \(\mathbf {B}^{\dag }_{\mathrm {rig}, {\mathbf {Q}_p}}\) and \(\mathbf {B}^+_{\mathrm {rig}, {\mathbf {Q}_p}}\), respectively; this notation is used in several earlier works of the present authors.
References
Andreatta, F., Iovita, A., Stevens, G.: Overconvergent Eichler–Shimura isomorphisms. J. Inst. Math. Jussieu 14(2), 221–274 (2015). doi:10.1017/S1474748013000364
Bellaïche, J.: Critical \(p\)-adic \(L\)-functions. Invent. Math. 189, 1–60 (2012). doi:10.1007/s00222-011-0358-z
Bellaïche, J., Dimitrov, M.: On the eigencurve at classical weight one points. Duke Math. J. 165(2), 245–266 (2016). doi:10.1215/00127094-3165755
Berger, L., Colmez, P.: Familles de représentations de de Rham et monodromie \(p\)-adique. Astérisque 319, 303–337 (2008). Représentations \(p\)-adiques de groupes \(p\)-adiques. I. Représentations galoisiennes et \((\phi ,\varGamma )\)-modules
Bertolini, M., Darmon, H., Rotger, V.: Beilinson–Flach elements and Euler systems I: syntomic regulators and \(p\)-adic Rankin \(L\)-series. J. Algebraic Geom. 24(2), 355–378 (2015). doi:10.1090/S1056-3911-2014-00670-6
Bertolini, M., Darmon, H., Rotger, V.: Beilinson–Flach elements and Euler systems II: the Birch and Swinnerton-Dyer conjecture for Hasse–Weil–Artin \(L\)-functions. J. Algebraic Geom. 24(3), 569–604 (2015). doi:10.1090/S1056-3911-2015-00675-0
Bosch, S., Güntzer, U., Remmert, R.: Non-Archimedean analysis. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261, Springer, Berlin (1984). doi:10.1007/978-3-642-52229-1
Buzzard, K.: Eigenvarieties. In: Burns, D., Buzzard, K., Nekovář, J. (eds.) \(L\)-Functions and Galois Representations, London Math. Soc. Lecture Note Ser., vol. 320, pp. 59–120. Cambridge University Press, Cambridge, UK (2007). doi:10.1017/CBO9780511721267.004
Chenevier, G.: Une application des variétés de Hecke des groupes unitaires. In: Stabilisation de la formule des traces, variétés de Shimura, et applications arithmétiques. II. Autour des variétés de Shimura, to appear. http://www.imj-prg.fr/fa/spip.php?article10
Colmez, P.: Théorie d’Iwasawa des représentations de de Rham d’un corps local. Ann. Math. (2) 148(2), 485–571 (1998). doi:10.2307/121003
Colmez, P.: Fonctions d’une variable \(p\)-adique. Astérisque 330, 13–59 (2010)
Colmez, P.: La série principale unitaire de \({\rm GL}_2(\mathbf{Q}_p)\). Astérisque 330, 213–262 (2010)
Darmon, H., Rotger, V.: Diagonal cycles and Euler systems II: the Birch and Swinnerton-Dyer conjecture for Hasse-Weil-Artin \(L\)-series. J. Am. Math. Soc (2016). doi:10.1090/jams/861
Hansen, D.: Iwasawa theory of overconvergent modular forms, preprint, (2015). http://www.math.columbia.edu/~hansen/bigzetaone
Kato, K.: \(P\)-adic Hodge theory and values of zeta functions of modular forms. Astérisque 295, 117–290 (2004). Cohomologies \(p\)-adiques et applications arithmétiques. III
Kedlaya, K.S., Pottharst, J., Xiao, L.: Cohomology of arithmetic families of \((\varphi,\varGamma )\)-modules. J. Am. Math. Soc. 27(4), 1043–1115 (2014). doi:10.1090/S0894-0347-2014-00794-3
Kings, G.: Eisenstein classes, elliptic Soulé elements and the \(\ell \)-adic elliptic polylogarithm. In: Coates, J., Raghuram, A., Saikia, A., Sujatha, R. (eds.) The Bloch–Kato conjecture for the Riemann zeta function, London Math. Soc. Lecture Note Ser., vol. 418, Cambridge University Press, Cambridge, UK (2015). doi:10.1017/CBO9781316163757.013
Kings, G., Loeffler, D., Zerbes, S.L.: Rankin–Eisenstein classes for modular forms, preprint. (2015). arXiv:1501.03289
Kings, G., Loeffler, D., Zerbes, S.L.: Rankin–Eisenstein classes and explicit reciprocity laws, preprint. (2015). arXiv:1503.02888
Lei, A., Loeffler, D., Zerbes, S.L.: Euler systems for Rankin–Selberg convolutions of modular forms. Ann. Math. (2) 180(2), 653–771 (2014). doi:10.4007/annals.2014.180.2.6
Liu, R.: Triangulation of refined families. Comment. Math. Helv. 90(4), 831–904 (2015). doi:10.4171/CMH/372
Loeffler, D.: Images of adelic Galois representations for modular forms, to appear in Glasgow J. Math. (2016). doi:10.1017/S0017089516000367
Loeffler, D., Zerbes, S.L.: Iwasawa theory and \(p\)-adic \(L\)-functions over \(\mathbf{Z}_p^2\)-extensions. Int. J. Number Theory 10(8), 2045–2096 (2014). doi:10.1142/S1793042114500699
Nakamura, K.: Iwasawa theory of de Rham \((\varphi,\varGamma )\)-modules over the Robba ring. J. Inst. Math. Jussieu 13(1), 65–118 (2014). doi:10.1017/S1474748013000078
Neukirch, J., Schmidt, A., Wingberg, K.: Cohomology of number fields. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 323. Springer, Berlin (2000). doi:10.1007/978-3-540-37889-1
Ohta, M.: On the \(p\)-adic Eichler–Shimura isomorphism for \(\varLambda \)-adic cusp forms. J. Reine Angew. Math. 463, 49–98 (1995). doi:10.1515/crll.1995.463.49
Perrin-Riou, B.: Fonctions \(L\) \(p\)-adiques des représentations \(p\)-adiques. Astérisque 229, 1–198 (1995)
Pollack, R., Stevens, G.: Overconvergent modular symbols and \(p\)-adic \(L\)-functions. Ann. Sci. École Norm. Sup. (4) 44(1), 1–42 (2011)
Pottharst, J.: Analytic families of finite-slope Selmer groups. Algebra Number Theory 7(7), 1571–1612 (2013). doi:10.2140/ant.2013.7.1571
Quang, M.V.: Rankin non-Archimedean convolutions of unbounded growth. Math. Sb. (N.S.) 182(2), 164–174 (1991). translation in Math. USSR-Sb. 72 (1992), no. 1, 151–161
Rubin, K.: Euler systems. Annals of Mathematics Studies, vol. 147. Princeton University Press, Princeton, NJ (2000). doi:10.1515/9781400865208
Urban, E.: Nearly overconvergent modular forms. In: Bouganis, T., Venjakob, O. (eds.) Iwasawa Theory 2012: State of the Art and Recent Advances, Contributions in Mathematical and Computational Sciences, vol. 7, pp. 401–441. Springer, Berlin (2014). doi:10.1007/978-3-642-55245-8_14
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Loeffler, D., Zerbes, S.L. Rankin–Eisenstein classes in Coleman families. Res Math Sci 3, 29 (2016). https://doi.org/10.1186/s40687-016-0077-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40687-016-0077-6




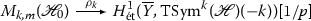
 unramified away from
unramified away from