Introduction

Three dimensional (3D) coordinate transformation is a fundamental and common issue in geodesy, engineering surveying, photogrammetry, LIDAR, GIS, robotics and computer vision, etc. (cf. Arun et al. 1987; Besl and McKay 1992; Burša 1967; Chen et al. 2004; Crosilla and Beinat 2002; Fan et al. 2015; Gargula ans Gawronek 2023; Ge and Wunderlich 2016; Horn 1987; Ioannidou and Pantazis 2020; Krarup 1985; Leick and Van Gelder 1975; Li et al. 2012; Odziemczyk 2020; Soycan and Soycan 2008; Teunissen 1988). Although it has different names in different fields, e.g. geodetic datum transformation in geodesy, absolute orientation in photogrammetry, point clouds registration in LIDAR, etc. its essence is to find the transformation parameters by a set of common points from one 3D rectangular coordinate system to another 3D rectangular coordinate system. The 3D similarity coordinate transformation is frequently used 3D coordinate transformation model. It has seven transformation parameters namely one scale factor, three rotation angles and three translations. And it is a nonlinear mathematical model. Traditionally the solution of 3D similarity coordinate transformation is implemented by the least squares (LS) estimation under the Gauss-Markov model, i.e., only the errors of coordinates in the target coordinate system are taken into account (Bektas 2022; Chen et al. 2004; Ioannidou and Pantazis 2020; Kurt 2018; Li et al. 2022; Uygur et al. 2020; Závoti and Kalmár 2016; Zeng et al. 2016, 2019;) Obviously the Gauss-Markov model is not in accord with the fact that all the coordinates in both the original coordinate system and the target coordinate system are contaminated by errors. Thus errors-in-variables (EIV) model, which considers all the errors in both the original and the target coordinate systems, is more reasonable than the Gauss-Markov model. The adjustment method oriented towards the EIV model is total least squares (TLS) named by Golub and Van Loan (1980). There are a lot of literatures on TLS, e.g. Aydin et al. (2018), Fang (2015), Lv and Sui (2020), Ma et al. (2020), Mahboub (2016), Mercan et al. (2018), Mihajlović and Cvijetinović (2017), Qin et al. (2020), Schaffrin et al. (2012); Uygur et al. (2020); Zeng et al. (2020); Zeng et al. (2022a); Xu et al. (2012); Xu et al. (2023).

Besides the classical LS or TLS adjustment methods, a few analytical algorithms of 3D coordinate transformation in the LS or TLS sense have been put forward so far. The analytical algorithms include the Procrustes algorithms (e.g. Arun et al. 1987; Crosilla and Beinat 2002; Grafarend and Awange 2003; Felus and Burtch 2009; Chang 2015; Păun et al. 2017) utilizing singular value decomposition (SVD), unit quaternion based algorithms (Horn 1987; Shen et al. 2006; Chang et al. 2017) utilizing eigenvalue–eigenvector decomposition, the orthonormal matrix based algorithm (Horn et al. 1988; Zeng 2015) utilizing eigenvalue–eigenvector decomposition, dual quaternion based algorithm (Walker et al. 1991; Wang et al. 2014; Zeng et al. 2022b) utilizing eigenvalue–eigenvector decomposition, Gibbs vector based algorithm (Zeng and Yi 2010) utilizing the property of Rodrigues matrix. The analytical algorithms are able to obtain the theoretic solutions and fast because they employ the theoretic formulae to calculate the solutions without initial values of parameters, and iterations. The disadvantages of the analytical algorithms over numerical or iterative algorithms are the former does not offer the precision estimation of computed parameters, which should be as important as the computed parameters themselves. In addition, the analytical algorithms can only deal with point-wise or identity weight matrix of observations, thus are not available for general weight matrix of observations (Zeng et al. 2022a).

As far as the iterative algorithms are concerned, good initial values of parameters are needed before iterative computations in the most situations. Otherwise the iterative computation may fail. In some cases like registration of point clouds, good initial values are hard or impossible to obtain due to the any size of rotation angles (e.g. Zeng and Yi 2011). At times good initial values of parameters are not necessary or arbitrary initial values of parameters can be available if global optimization algorithms are employed (e.g. Xu 2003). On the one hand, the 3D similarity coordinate transformation is usually not implemented real-time. On the other hand, because the number of common points is not large in the most cases, the computational time of iterations usually is short. So the iterative algorithms are tested majorly with the precision of transformation parameters rather than the efficiency.

Traditional rotation angle (Euler angle) based rotation matrix representation has a lot of trigonometric functions (Bektas 2022; Zeng et al. 2018); as a result, the iterative computation needs very good initial values of parameters. If bad initial values are provided, more time are consumed even iteration diverges (Zeng and Yi 2011). Quaternion based rotation matrix representation involves no trigonometric functions but algebraic (polynomial) functions, which has efficient computational performance (Zeng and Yi 2011). Compared to quaternion, dual quaternion represents not only the rotation matrix but also the translations by polynomials (Walker et al. 1991; Jitka 2011; Zeng et al. 2018, 2022b). In other words, the rigid transformation including rotation and translation could be represented by a dual quaternion. In addition, it is worthy of note that the established transformation model based on a unit dual quaternion does not require centralization of coordinates to exclude the translations while traditional transformation models do (Grafarend and Awange 2003; Felus and Burtch 2009). Thus it is meaningful to explore the computational performance of dual quaternion in 3D coordinate transformation, including the sensitivity of the initial values of parameters or suitability of large or small rotation angle case (bad initial values of parameters usually is caused by large rotation angle), the precision of computed parameters and effect of errors in coordinates, etc.

The remainder of the paper is organized as follows. In next section, the basic concept of quaternion and dual quaternion are introduced in brief. And the paper derives the representation of 3D rotation matrix by a quaternion and the formula of translation vector by a unit dual quaternion from the viewpoint of geometry in detail. In the Sect. “Dual quaternion algorithm (DQA) of 3D coordinate transformation”, the 3D coordinate transformation in the errors-in-variables (EIV) model is established, and then the Dual Quaternion Algorithm (DQA) is presented after the derivation of linearization of the mathematical model and WTLS solution based on the Lagrangian extremum principle with constraints. Additionally, the computation and precision estimation of traditional seven transformation parameters are fulfilled from dual quaternion considering that the seven transformation parameters are used widely in applications. Two numerical experiments including a geodetic datum transformation case and a simulated case oriented form surface fitting are demonstrated in the Sect. “Experiments and discussion”. Lastly conclusions are drawn in the last section, i.e. Sect. “Conclusions”.

Concepts of quaternion and dual quaternion

This section firstly introduces the definition and basic properties of quaternion, and emphasizes on interpreting the meaning of 3D rotation of a point around an axis, and representing the 3D rotation by means of quaternion. Next the dual quaternion is introduced and the rigid motion involving 3D rotation about an axis and translation along the axis is expressed by a unit dual quaternion. Especially the relationship between the translation and the dual quaternion is derived in detail.

Quaternion and 3D rotation matrix

Quaternion is a four-element vector invented by Hamilton in 1843, whose general form is

$${\varvec{q}} = iq_{{1}} + jq_{{2}} + kq_{{3}} + q_{{4}}$$
(1)

where \(q_{1}\), \(q_{2}\), \(q_{3}\), \(q_{4}\) are all real numbers, \(i\), \(j\) and \(k\) are imaginary units also named quaternion units with the following properties: ①\(i^{2} = j^{2} = k^{2} = - 1\), ②\(ij = - ji = k\), ③\(jk = - kj = i\), ④\(ki = - ik = j\). For \(i\), \(j\) and \(k\) are imaginary, \(q_{1}\), \(q_{2}\), \(q_{3}\) are called imaginary parts, and \(q_{4}\) is called the real part. Quaternion \({\varvec{q}}\) is usually represented in the form of vector to separate the real and imaginary parts as

$${\varvec{q}} = \left[ {\begin{array}{*{20}c} {\mathbf{q}} \\ {q_{{4}} } \\ \end{array} } \right],\,{\mathbf{q}} = \left[ {\begin{array}{*{20}c} {q_{{1}} } \\ {q_{{2}} } \\ {q_{{3}} } \\ \end{array} } \right],$$
(2)

where \({\mathbf{q}}\) is a vector used to express the imaginary parts, named vector part, \(q_{4}\) is also called the scalar part. Quaternion is called pure imaginary one when its scalar part is zero and vector part is not zero vector. Analogous to the definition of conjugate complex number, the definition of conjugate quaternion corresponding to \({\varvec{q}}\) is

$${\varvec{q}}^{*} = - iq_{1} - jq_{2} - kq_{3} + q_{4}$$
(3)

And the norm of quaternion \({\varvec{q}}\) is given as follows.

$$\left\| {\varvec{q}} \right\| = \sqrt {{\varvec{qq}}^{ * } } = \sqrt {q_{1}^{2} + q_{2}^{2} + q_{3}^{2} + q_{4}^{2} }$$
(4)

If \(\left\| {\varvec{q}} \right\| = {1}\), \({\varvec{q}}\) is called unit quaternion.

It is easy to prove the following properties utilizing the foregoing definitions.

$${\varvec{p}} + {\varvec{q}} = \left( {\begin{array}{*{20}c} {{\mathbf{p}} + {\mathbf{q}}} \\ {p_{4} + q_{4} } \\ \end{array} } \right)$$
(5)
$${\varvec{pq}} = \left( {\begin{array}{*{20}c} {{\mathbf{p}} \times {\mathbf{q}} + p_{4} {\mathbf{q}} + q_{4} {\mathbf{p}}} \\ {p_{4} q_{4} - {\mathbf{p}} \cdot {\mathbf{q}}} \\ \end{array} } \right)$$
(6)
$${\varvec{pqr}} = \left( {{\varvec{pq}}} \right){\varvec{r}} = {\varvec{p}}\left( {{\varvec{qr}}} \right)$$
(7)
$${\varvec{p}}\left( {\user2{q + r}} \right) = \user2{pq + pr}$$
(8)
$$\left( {{\varvec{pq}}} \right)^{ * } = {\varvec{q}}^{ * } {\varvec{p}}^{ * }$$
(9)
$${\varvec{q}}^{ - 1} = \frac{{{\varvec{q}}^{ * } }}{{\left\| {\varvec{q}} \right\|}}$$
(10)

where \({\varvec{p}}\), \({\varvec{q}}\) and \({\varvec{r}}\) are any quaternions, \({\varvec{q}}^{ - 1}\) denotes the inverse of \({\varvec{q}}\). The symbols \(\cdot\) and \(\times\) stand for dot and cross product of vectors respectively as follows.

$${\mathbf{p}} \cdot {\mathbf{q}} = {\mathbf{p}}^{T} {\mathbf{q}}$$
(11)
$${\mathbf{p}} \times {\mathbf{q}} = {\mathbf{C}}({\mathbf{p}}){\mathbf{q}} = \left[ {\begin{array}{*{20}c} 0 & { - p_{3} } & {p_{2} } \\ {p_{3} } & 0 & { - p_{1} } \\ { - p_{2} } & {p_{1} } & 0 \\ \end{array} } \right]{\mathbf{q}}$$
(12)

where subscript T denotes transpose computation, and \({\mathbf{C}}({\mathbf{p}})\) is called a skew symmetric matrix. From the above properties of quaternion, it is seen apparently that the multiplication of quaternion meets associativity and distributivity but non-commutativity. The product \({\varvec{pq}}\) can also be fulfilled by the product of a matrix and quaternion in the form of vector:

$$\user2{pq = }Q({\varvec{p}}){\varvec{q}} = W({\varvec{q}}){\varvec{p}}$$
(13)

where

$$Q({\varvec{p}}) = \left[ {\begin{array}{*{20}c} {p_{4} {\mathbf{I}} + {\mathbf{C}}({\mathbf{p}})} & {\mathbf{p}} \\ { - {\mathbf{p}}^{T} } & {p_{4} } \\ \end{array} } \right]$$
(14)
$${\mathbf{W}}({\varvec{q}}) = \left[ {\begin{array}{*{20}c} {q_{4} {\mathbf{I}} - {\mathbf{C}}({\mathbf{q}})} & {\mathbf{q}} \\ { - {\mathbf{q}}^{T} } & {q_{4} } \\ \end{array} } \right]$$
(15)

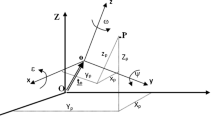
Next the relationship of 3D rotation matrix and quaternion is investigated. See Fig. 1, assume any point P in the 3D space rotates an angle of θ (be positive in the direction of counterclockwise for right-hand coordinate system) around the rotation axis represented by a unit vector n, and the corresponding point after rotation is P’. Or is the origin of 3D rectangular coordinate system, Oc is the foot of a perpendicular from pint P to the rotation axis, P⊥ is the point after 90° rotation of point P. P′⊥ is the foot of a perpendicular from pint P’ to the line of Oc to P. The vectors \(\overrightarrow {{{\mathbf{O}}_{{\mathbf{r}}} {\mathbf{O}}_{{\mathbf{c}}} }}\), \(\overrightarrow {{{\mathbf{O}}_{{\mathbf{c}}} {\mathbf{P^{\prime}}}_{ \bot } }}\), \(\overrightarrow {{{\mathbf{P^{\prime}}}_{ \bot } {\mathbf{P^{\prime}}}}}\) are computed as follows.

$$\overrightarrow {{{\mathbf{O}}_{{\mathbf{r}}} {\mathbf{O}}_{{\mathbf{c}}} }} = \, {\mathbf{n}}\left( {{\mathbf{n}} \cdot {\mathbf{p}}} \right)$$
(16)
$$\overrightarrow {{{\mathbf{O}}_{{\mathbf{c}}} {\mathbf{P^{\prime}}}_{ \bot } }} = \left( {{\mathbf{p}} - {\mathbf{n}}\left( {{\mathbf{n}} \cdot {\mathbf{p}}} \right)} \right)\cos \theta$$
(17)
$$\overrightarrow {{{\mathbf{P^{\prime}}}_{ \bot } {\mathbf{P^{\prime}}}}} = \overrightarrow {{{\mathbf{O}}_{{\mathbf{c}}} {\mathbf{P}}_{ \bot } }} \sin \theta = \left( {{\mathbf{n}} \times {\mathbf{p}}} \right)\sin \theta$$
(18)
Fig. 1
figure 1

3D rotation of a point about an axis

Full size image

So

$$\begin{aligned} {\mathbf{p^{\prime}}} =\, & \overrightarrow {{{\mathbf{O}}_{{\mathbf{r}}} {\mathbf{O}}_{{\mathbf{c}}} }} + \overrightarrow {{{\mathbf{O}}_{{\mathbf{c}}} {\mathbf{P}}^{\prime}_{ \bot } }} + \overrightarrow {{{\mathbf{P}}^{\prime}_{ \bot } {\mathbf{P}}^{\prime}}} \\ =\, & {\mathbf{n}}\left( {{\mathbf{n}} \cdot {\mathbf{p}}} \right) + \left( {{\mathbf{p}} - {\mathbf{n}}\left( {{\mathbf{n}} \cdot {\mathbf{p}}} \right)} \right)\cos \theta + \left( {{\mathbf{n}} \times {\mathbf{p}}} \right)\sin \theta \\ =\, & {\mathbf{p}}\cos \theta + \left( {{1} - \cos \theta } \right){\mathbf{n}}\left( {{\mathbf{n}} \cdot {\mathbf{p}}} \right) + \left( {{\mathbf{n}} \times {\mathbf{p}}} \right)\sin \theta \\ =\, & {\mathbf{p}}\cos \theta + \left( {{1} - \cos \theta } \right){\mathbf{n}}\left( {{\mathbf{n}}^{T} {\mathbf{p}}} \right) + \left( {{\mathbf{n}} \times {\mathbf{p}}} \right)\sin \theta \\ =\, & {\mathbf{p}}\cos \theta + \left( {{1} - \cos \theta } \right)\left( {{\mathbf{nn}}^{T} } \right){\mathbf{p}} + \left( {{\mathbf{n}} \times {\mathbf{p}}} \right)\sin \theta \\ =\, & \left( {{\mathbf{I}}_{3} \cos \theta + \left( {{1} - \cos \theta } \right)\left( {{\mathbf{nn}}^{T} } \right) + \sin \theta {\mathbf{C}}({\mathbf{n}})} \right){\mathbf{p}} \\ =\, & {\mathbf{Rp}} \\ \end{aligned}$$
(19)

where \({\mathbf{I}}_{3}\) is a 3-by-3 identity matrix and \({\mathbf{R}}\) is the 3D rotation matrix. Thus the rotation matrix is expressed by the unit vector n and rotation angle θ. Introducing a unit quaternion

$${\varvec{r}} = \left[ {\begin{array}{*{20}c} {{\mathbf{n}}\sin \frac{\theta }{{2}}} \\ {\cos \frac{\theta }{{2}}} \\ \end{array} } \right]$$
(20)

The rotation matrix \({\mathbf{R}}\) by Eq. (19) is rewritten as

$$\begin{aligned} {\mathbf{R}} =\, & {\mathbf{I}}_{3} \left( {\left( {\cos \frac{\theta }{{2}}} \right)^{{2}} - \left( {\sin \frac{\theta }{{2}}} \right)^{{2}} } \right) + {2}\left( {\sin \frac{\theta }{{2}}} \right)^{{2}} \left( {{\mathbf{nn}}^{T} } \right) + {2}\sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}}{\mathbf{C}}({\mathbf{n}}) \\ =\, & {\mathbf{I}}_{3} \left( {r_{{4}}^{{2}} - {\mathbf{r}}^{T} {\mathbf{r}}} \right) + {2}\left( {{\mathbf{rr}}^{T} + r_{{4}} {\mathbf{C}}({\mathbf{r}})} \right) \\ =\, & \left[ {\begin{array}{*{20}c} {r_{{4}}^{{2}} + r_{1}^{{2}} - r_{2}^{{2}} - r_{3}^{{2}} } & {{2}\left( {r_{1} r_{2} - r_{3} r_{4} } \right)} & {{2}\left( {r_{1} r_{3} + r_{2} r_{4} } \right)} \\ {{2}\left( {r_{1} r_{2} + r_{3} r_{4} } \right)} & {r_{{4}}^{{2}} - r_{1}^{{2}} + r_{2}^{{2}} - r_{3}^{{2}} } & {{2}\left( {r_{2} r_{3} - r_{1} r_{4} } \right)} \\ {{2}\left( {r_{1} r_{3} - r_{2} r_{4} } \right)} & {{2}\left( {r_{2} r_{3} + r_{1} r_{4} } \right)} & {r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} } \\ \end{array} } \right] \\ \end{aligned}$$
(21)

Therefore the rotation matrix is directly represented by the unit quaternion. If constructing pure quaternions \({\varvec{p}}\) and \(\user2{p^{\prime}}\) with the vectors \({\mathbf{p}}\) and \({\mathbf{p^{\prime}}}\), the rotation transformation is expressed with quaternions as (Walker et al. 1991; Zeng and Yi 2011)

$$\user2{p^{\prime} = rpr}^{*} = Q({\varvec{r}})W({\varvec{r}}^{*} ){\varvec{p}} = Q({\varvec{r}})W({\varvec{r}})^{T} {\varvec{p}} = W({\varvec{r}})^{T} Q({\varvec{r}}){\varvec{p}}$$
(22)

and \({\mathbf{W}}({\varvec{r}})^{T} Q({\varvec{r}})\) can be expanded as

$${\mathbf{W}}({\varvec{r}})^{T} Q({\varvec{r}}) = \left[ {\begin{array}{*{20}c} {\mathbf{R}} & {\mathbf{0}} \\ {{\mathbf{0}}^{T} } & 1 \\ \end{array} } \right].$$
(23)

Dual quaternion and rigid motion

Dual quaternion which was invented by William Kingdon Clifford in 1873 and originally named biquaternion (Clifford 1873), is described as

$$\begin{aligned} \overline{\user2{q}} =\, & {\varvec{r}} + \varepsilon {\varvec{s}} \\ =\, & (r_{{1}} + \varepsilon s_{{1}} )i + (r_{{2}} + \varepsilon s_{{2}} )j + (r_{{3}} + \varepsilon s_{{3}} )k + (r_{{4}} + \varepsilon s_{{4}} ), \\ =\, & q_{{d{1}}} i + q_{{d{2}}} j + q_{{d{3}}} k + q_{{d{4}}} \\ \end{aligned}$$
(24)

where \({\varvec{r}}\) and \({\varvec{s}}\) are arbitrary quaternions, and \({\upvarepsilon }\) is a basis element named dual unit. \(\varepsilon\) satisfies the following properties: \(\varepsilon^{{2}} = {0}\) and multiplication of \({\upvarepsilon }\) and quaternion units meets commutativity, e.g. \({\upvarepsilon }i\,{ = }\,i{\upvarepsilon }\). \(\left( {\begin{array}{*{20}c} {q_{{{\text{d1}}}} } & {q_{{{\text{d2}}}} } & {q_{{{\text{d3}}}} } \\ \end{array} } \right)^{T}\) is the vector (dual number vector) part, \(q_{{{\text{d4}}}}\) is the scalar (dual number) part. The product of dual quaternions \(\overline{\user2{p}} = {\varvec{u}} + {\upvarepsilon }{\varvec{v}}\) and \(\overline{\user2{q}}\) is easily deduced by the above properties of \(\varepsilon\) as

$$\user2{\overline{p}\overline{q}} = {\varvec{ur}} + {\varepsilon (}\user2{us + vr)}.$$
(25)

The conjugate of dual quaternion is defined utilizing the conjugate of quaternion:

$$\overline{\user2{q}}^{ * } = {\varvec{r}}^{ * } + {\upvarepsilon }{\varvec{s}}^{ * } .$$
(26)

And the norm of dual quaternion is a dual scalar (number) and is defined analogous to the definition of norm of quaternion as

$$\left\| {\overline{\user2{q}}} \right\| = \sqrt {\overline{\user2{q}}^{ * } \overline{\user2{q}}} = \sqrt {q_{d1}^{2} + q_{d2}^{2} + q_{d3}^{2} + q_{d4}^{2} } .$$
(27)

If \(\left\| {\overline{\user2{q}}} \right\| = 1\), \(\overline{\user2{q}}\) is called a unit dual quaternion. Unit dual quaternion \(\overline{\user2{q}}\) satisfies the following two conditions (Jitka 2011; Walker et al 1991).

$${\varvec{r}}{}^{T}\user2{r = }\,{1,}$$
(28)
$${\varvec{r}}{}^{T}\user2{s = }\,0.$$
(29)

In other words, for unit dual quaternion \(\overline{\user2{q}}\), the non-dual part i.e. \({\varvec{r}}\) is a unit quaternion, and non-dual part is perpendicular to the dual part i.e. \({\varvec{s}}\).

The rigid motion involving rotation about an axis and translation along the axis can be expressed elegantly by a unit dual quaternion (Walker et al 1991; Jitka 2011; Zeng et al. 2018). The rigid motion is depicted in Fig. 2. The O-XYZ is a rectangular coordinate system, and p is a vector starting from the origin O of coordinate system. The vector p is firstly translated by a distance d along the rotation axis denoted by the unit vector n, and then rotated by an angle θ about the rotation axis. The new rectangular coordinate system O’-X’Y’Z’, the new vector p’ after rotation, and the translation vector t from the original system to the new one are denoted in the figure. Rewriting the unit dual quaternion \(\overline{\user2{q}}\) in Eq. (24) as (Walker et al 1991)

$$\overline{\user2{q}} = \left[ {\begin{array}{*{20}c} {{\overline{\mathbf{n}}}\sin \frac{{\overline{\theta }}}{{2}}} \\ {\cos \frac{{\overline{\theta }}}{{2}}} \\ \end{array} } \right]$$
(30)

where \({\overline{\mathbf{n}}}\) and \(\overline{\theta }\) are dual vector and dual angle represented as

$${\overline{\mathbf{n}}} = {\mathbf{n}} + {\upvarepsilon }{\mathbf{p}} \times {\mathbf{n}}$$
(31)
$$\overline{\theta } = \theta + \varepsilon d$$
(32)
Fig. 2
figure 2

Rigrid motion

Full size image

Inserting the above two equations into Eq. (30) and expanding the equation and comparing with Eq. (24), one obtains

$${\varvec{r}} = \left[ {\begin{array}{*{20}c} {{\mathbf{n}}\sin \frac{\theta }{{2}}} \\ {\cos \frac{\theta }{{2}}} \\ \end{array} } \right],$$
(33)
$${\varvec{s}} = \left[ {\begin{array}{*{20}c} {\frac{d}{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}} + \sin \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \\ { - \frac{d}{{2}}\sin \frac{\theta }{{2}}} \\ \end{array} } \right]$$
(34)

where Eq. (33) is identical to Eq. (20). Thus the non-dual part of unit dual quaternion \(\overline{\user2{q}}\) i.e. \({\varvec{r}}\) is employed to express the rotation transformation as described early [see Eq. (21)], the left part of rigid body transformation i.e. translation transformation can be represented by \({\varvec{r}}\) and \({\varvec{s}}\) with derivation as follows.

From Fig. 2, the following equation is obtained.

$${\mathbf{t}} = {\mathbf{p}} + d{\mathbf{n}} - {\mathbf{p}}^{\prime} = {\mathbf{p}} + d{\mathbf{n}} - {\mathbf{Rp}}.$$
(35)

Substituting the \({\mathbf{Rp}}\) in Eq. (19) into the above equation, and considering

$${\mathbf{nn}}^{T} = {\mathbf{C}}({\mathbf{n}}){\mathbf{C}}({\mathbf{n}}) + {\mathbf{I}}_{3} ,$$
(36)

One gets

$$\begin{aligned} {\mathbf{t}} =\, & {\mathbf{p}} + d{\mathbf{n}} - {\mathbf{p^{\prime}}} \\ =\, & {\mathbf{p}} - \left( {{\mathbf{I}}_{3} \cos \theta + \left( {{1} - \cos \theta } \right)\left( {{\mathbf{C}}({\mathbf{n}}){\mathbf{C}}({\mathbf{n}}) + {\mathbf{I}}_{3} } \right) + \sin \theta {\mathbf{C}}({\mathbf{n}})} \right){\mathbf{p}} + d{\mathbf{n}} \\ =\, & {\mathbf{p}} - \left( {{\mathbf{I}}_{3} + \left( {{1} - \cos \theta } \right){\mathbf{C}}({\mathbf{n}}){\mathbf{C}}({\mathbf{n}}) + \sin \theta {\mathbf{C}}({\mathbf{n}})} \right){\mathbf{p}} + d{\mathbf{n}} \\ =\, & - \left( {{1} - \cos \theta } \right){\mathbf{C}}({\mathbf{n}}){\mathbf{C}}({\mathbf{n}}){\mathbf{p}} - \sin \theta {\mathbf{C}}({\mathbf{n}}){\mathbf{p}} + d{\mathbf{n}} \\ =\, & \left( {{1} - \cos \theta } \right){\mathbf{n}} \times \left( {{\mathbf{p}} \times {\mathbf{n}}} \right) + \sin \theta \left( {{\mathbf{p}} \times {\mathbf{n}}} \right) + d{\mathbf{n}}. \\ \end{aligned}$$
(37)

By the properties of quaternions, one can compute a new quaternion \({\varvec{t}}\) as

$$\begin{aligned} \user2{t = } & {\varvec{sr}}^{ - 1} \\ =\, & {\varvec{sr}}^{*} \\ = \,& \left[ {\begin{array}{*{20}c} { - \left( {\frac{d}{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}} + \sin \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \right) \times {\mathbf{n}}\sin \frac{\theta }{{2}} + \frac{d}{{2}}\sin \frac{\theta }{{2}}{\mathbf{n}}\sin \frac{\theta }{{2}} + \cos \frac{\theta }{{2}}\left( {\frac{d}{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}} + \sin \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \right)} \\ { - \frac{d}{{2}}\sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}} + \left( {\frac{d}{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}} + \sin \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \right) \cdot \left( {{\mathbf{n}}\sin \frac{\theta }{{2}}} \right)} \\ \end{array} } \right] \\ =\, & \left[ {\begin{array}{*{20}c} {\left( {\sin \frac{\theta }{{2}}} \right)^{2} {\mathbf{n}} \times \left( {{\mathbf{p}} \times {\mathbf{n}}} \right) + \frac{d}{{2}}\left( {\sin \frac{\theta }{{2}}} \right)^{2} {\mathbf{n}} + \frac{d}{{2}}\left( {\cos \frac{\theta }{{2}}} \right)^{2} {\mathbf{n}} + \sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \\ { - \frac{d}{{2}}\sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}} + \left( {\frac{d}{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}}} \right) \cdot \left( {{\mathbf{n}}\sin \frac{\theta }{{2}}} \right)} \\ \end{array} } \right] \\ =\, & \left[ {\begin{array}{*{20}c} {\left( {\sin \frac{\theta }{{2}}} \right)^{2} {\mathbf{n}} \times \left( {{\mathbf{p}} \times {\mathbf{n}}} \right) + \frac{d}{{2}}{\mathbf{n}} + \sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}}{\mathbf{p}} \times {\mathbf{n}}} \\ { - \frac{d}{{2}}\sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}} + \frac{d}{{2}}\sin \frac{\theta }{{2}}\cos \frac{\theta }{{2}}{\mathbf{n}} \cdot {\mathbf{n}}} \\ \end{array} } \right] \\ =\, & \frac{1}{{2}}\left[ {\begin{array}{*{20}c} {\left( {{1} - \cos \theta } \right){\mathbf{n}} \times \left( {{\mathbf{p}} \times {\mathbf{n}}} \right) + d{\mathbf{n}} + \sin \theta {\mathbf{p}} \times {\mathbf{n}}} \\ 0 \\ \end{array} } \right] \\ =\, & \frac{1}{{2}}\left[ {\begin{array}{*{20}c} {\mathbf{t}} \\ 0 \\ \end{array} } \right] \\ \end{aligned}$$
(38)

Therefore, actually \({\varvec{t}}\) is a pure imaginary quaternion constructed by half of translation vector \({\mathbf{t}}\), which can be represented by

$$\user2{t = sr}^{*} = W({\varvec{r}}^{*} )\user2{s = }W({\varvec{r}})^{T} {\varvec{s}}.$$
(39)

Dual Quaternion Algorithm (DQA) of 3D coordinate transformation

Mathematical model and its linearization

The similarity 3D coordinate transformation model is usually expressed as follows.

$${\mathbf{p}}_{i}^{t} = \lambda {\mathbf{Rp}}_{i}^{o} + {\mathbf{t}},$$
(40)

Subject to

$${\mathbf{R}}^{T} {\mathbf{R}} = {\mathbf{I}}_{3} ,\;\det ({\mathbf{R}}) = + {1,}$$
(41)

where \({\mathbf{p}}_{i}^{t} = \left[ {\begin{array}{*{20}c} {x_{i}^{t} } & {y_{i}^{t} } & {z_{i}^{t} } \\ \end{array} } \right]^{T}\) and \({\mathbf{p}}_{i}^{o} = \left[ {\begin{array}{*{20}c} {x_{i}^{o} } & {y_{i}^{o} } & {z_{i}^{o} } \\ \end{array} } \right]^{T}\) are the 3D coordinate vectors of control point, in which superscript \(t\) or \(o\) denotes target coordinate or original coordinate respectively, and subscript \(i = 1,2, \cdots ,n\) (\(n \ge 3\)) denotes the number of control point. \(\det\) represents determinant computation of matrix. \(\det ({\mathbf{R}}) = + {1}\) is imposed necessarily to ensure \({\mathbf{R}}\) stands for a rotation matrix rather than a refection one when \(\det ({\mathbf{R}}) = - {1}\). \({\mathbf{t}} = \left[ {\begin{array}{*{20}c} {t_{x} } & {t_{y} } & {t_{z} } \\ \end{array} } \right]^{T}\) is the translation vector. \(\lambda\) is the scale factor which is tightly close to 1 for most situations. Traditionally \({\mathbf{R}}\) is repressed by three rotation angles \(\theta_{x}\), \(\theta_{y}\), \(\theta_{z}\) about the X, Y, Z axes respectively as (Zeng et al. 2019)

$${\mathbf{R}} = \left[ {\begin{array}{*{20}c} {\cos \theta_{z} \cos \theta_{y} } & {\sin \theta_{z} \cos \theta_{x} + \cos \theta_{z} \sin \theta_{y} \sin \theta_{x} } & {\sin \theta_{z} \sin \theta_{x} - \cos \theta_{z} \sin \theta_{y} \cos \theta_{x} } \\ { - \sin \theta_{z} \cos \theta_{y} } & {\cos \theta_{z} \cos \theta_{x} - \sin \theta_{z} \sin \theta_{y} \sin \theta_{x} } & {\cos \theta_{z} \sin \theta_{x} + \sin \theta_{z} \sin \theta_{y} \cos \theta_{x} } \\ {\sin \theta_{y} } & { - \cos \theta_{y} \sin \theta_{x} } & {\cos \theta_{y} \cos \theta_{x} } \\ \end{array} } \right]$$
(42)

Obviously the computation of \({\mathbf{R}}\) in Eq. (42) involves lots of trigonometric functions thus the computation burden is larger than that of \({\mathbf{R}}\) in Eq. (20). If \({\mathbf{R}}\) is known or computed, the rotation angles and the quaternion can be computed as elaborated in Zeng et al. (2019).

Introducing two pure imaginary quaternions with coordinate vectors as

$${\varvec{p}}_{i}^{o} = \left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{i}^{o} } \\ 0 \\ \end{array} } \right],\;{\varvec{p}}_{i}^{t} = \left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{i}^{t} } \\ 0 \\ \end{array} } \right],$$
(43)

the similarity 3D coordinate transformation in the errors-in-variables (EIV) model is re-expressed by dual quaternion as

$${\varvec{p}}_{i}^{t} - {\varvec{e}}_{i}^{t} = \lambda {\mathbf{W}}({\varvec{r}})^{T} Q({\varvec{r}})\left( {{\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o} } \right) + 2W({\varvec{r}})^{T} {\varvec{s}},$$
(44)

subject to Eqs. (28, 29). In Eq. (44), \({\varvec{e}}_{i}^{t}\) and \({\varvec{e}}_{i}^{o}\) are the error quaternion corresponding to \({\varvec{p}}_{i}^{t}\) and \({\varvec{p}}_{i}^{o}\) respectively.

The computation of transformation parameters needs to utilize linearization and iterative procedure. Linearizing Eq. (44) by Taylor's formula, one gets

$$\begin{aligned} {\varvec{p}}_{i}^{t} - {\varvec{e}}_{i}^{t} =\, & \lambda^{j} {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o,j} ) + {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} {\varvec{s}}^{j} - \lambda^{j} {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )d{\varvec{e}}_{i}^{o,j} \\ + {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o,j} )d\lambda + \frac{\partial f}{{\partial r_{1} }}dr_{1} + \frac{\partial f}{{\partial r_{2} }}dr_{2} + \frac{\partial f}{{\partial r_{3} }}dr_{3} + \frac{\partial f}{{\partial r_{4} }}dr_{4} + {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} d{\varvec{s}} \\ \end{aligned}$$
(45)

where superscript j denotes the j-th iterative time, and

$$\frac{\partial f}{{\partial r_{i} }} = \lambda^{j} (\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{i} }}Q({\varvec{r}}^{j} ) + {\mathbf{W}}({\varvec{r}}^{j} )^{T} \frac{{\partial Q({\varvec{r}})}}{{\partial r_{i} }})({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o,j} ) + {2}\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{i} }}{\varvec{s}}^{j} ,\;i = {1,2,3,4}$$
(46)
$$\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{1} }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - 1} \\ 0 & 0 & { - 1} & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right],\,\,\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{2} }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & { - 1} \\ { - 1} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right],$$
(47)
$$\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{3} }} = \left[ {\begin{array}{*{20}c} 0 & { - 1} & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & { - 1} \\ 0 & 0 & 1 & 0 \\ \end{array} } \right],\,\,\frac{{\partial {\mathbf{W}}({\varvec{r}})^{T} }}{{\partial r_{4} }} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
(48)
$$\frac{{\partial Q({\varvec{r}})}}{{\partial r_{1} }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ 0 & 0 & { - 1} & 0 \\ 0 & 1 & 0 & 0 \\ { - 1} & 0 & 0 & 0 \\ \end{array} } \right],\,\,\frac{{\partial Q({\varvec{r}})}}{{\partial r_{2} }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ { - 1} & 0 & 0 & 0 \\ 0 & { - 1} & 0 & 0 \\ \end{array} } \right],\,$$
(49)
$$\frac{{\partial Q({\varvec{r}})}}{{\partial r_{3} }} = \left[ {\begin{array}{*{20}c} 0 & { - 1} & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & { - 1} & 0 \\ \end{array} } \right],\,\,\frac{{\partial Q({\varvec{r}})}}{{\partial r_{4} }} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right].\,$$
(50)

Considering \({\varvec{e}}_{i}^{o} = {\varvec{e}}_{i}^{o,j} + d{\varvec{e}}_{i}^{o,j}\), Eq. (45) can be rewritten as

$$\begin{aligned} {\varvec{p}}_{i}^{t} - {\varvec{e}}_{i}^{t} =\, & \lambda^{j} {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o} ) + {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} {\varvec{s}}^{j} \\ + {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o,j} )d\lambda + \frac{\partial f}{{\partial r_{{1}} }}dr_{{1}} + \frac{\partial f}{{\partial r_{{2}} }}dr_{{2}} + \frac{\partial f}{{\partial r_{{3}} }}dr_{{3}} + \frac{\partial f}{{\partial r_{{4}} }}dr_{{4}} + {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} d{\varvec{s}} \\ =\, & {\varvec{B}}_{i}^{j} {\varvec{p}}_{i}^{o} + {\varvec{C}}_{i}^{j} + {\varvec{A}}_{i}^{{{1},j}} dx_{{1}} + {\varvec{A}}_{i}^{{{2},j}} dx_{{2}} - {\varvec{B}}_{i}^{j} {\varvec{e}}_{i}^{o} \\ \end{aligned}$$
(51)

where

$$dx_{{1}} = \left[ {\begin{array}{*{20}c} {d\lambda } & {dr_{1} } & {dr_{2} } & {dr_{3} } & {dr_{4} } \\ \end{array} } \right]^{T} ,$$
(52)
$$dx_{{2}} = d{\varvec{s}} = \left[ {\begin{array}{*{20}c} {ds_{1} } & {ds_{2} } & {ds_{3} } & {ds_{4} } \\ \end{array} } \right]^{T} ,$$
(53)
$${\varvec{A}}_{i}^{{{1,}j}} = \left[ {\begin{array}{*{20}c} {{\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} )({\varvec{p}}_{i}^{o} - {\varvec{e}}_{i}^{o,j} )} & {\frac{\partial f}{{\partial r_{1} }}} & {\frac{\partial f}{{\partial r_{2} }}} & {\frac{\partial f}{{\partial r_{3} }}} & {\frac{\partial f}{{\partial r_{4} }}} \\ \end{array} } \right],$$
(54)
$${\varvec{A}}_{i}^{{{2,}j}} = {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} ,$$
(55)
$${\varvec{B}}_{i}^{j} = \lambda^{j} {\mathbf{W}}({\varvec{r}}^{j} )^{T} Q({\varvec{r}}^{j} ),$$
(56)
$${\varvec{C}}_{i}^{j} = {2}{\mathbf{W}}({\varvec{r}}^{j} )^{T} {\varvec{s}}^{j} .$$
(57)

For \(n\) (\(n \ge 3\)) control points, one has

$${\varvec{p}}^{t} - {\varvec{e}}^{t} = {\varvec{B}}^{j} {\varvec{p}}^{o} + {\varvec{C}}^{j} + {\varvec{A}}^{{{1,}j}} dx_{{1}} + {\varvec{A}}^{{{2,}j}} dx_{{2}} - {\varvec{B}}^{j} {\varvec{e}}^{o}$$
(58)

where

$$\,{\varvec{p}}^{t} = \left[ {\begin{array}{*{20}c} {{\varvec{p}}_{1}^{t} } \\ \vdots \\ {{\varvec{p}}_{n}^{t} } \\ \end{array} } \right]\user2{,e}^{t} = \left[ {\begin{array}{*{20}c} {e_{1}^{t} } \\ \vdots \\ {e_{n}^{t} } \\ \end{array} } \right],{\varvec{p}}^{o} = \left[ {\begin{array}{*{20}c} {{\varvec{p}}_{1}^{o} } \\ \vdots \\ {{\varvec{p}}_{n}^{o} } \\ \end{array} } \right]\user2{,e}^{o} = \left[ {\begin{array}{*{20}c} {e_{1}^{o} } \\ \vdots \\ {e_{n}^{o} } \\ \end{array} } \right]$$
(59)
$${\varvec{A}}^{{{1,}j}} = \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{{1}}^{{{1,}j}} } \\ {{\varvec{A}}_{{2}}^{{{1,}j}} } \\ \vdots \\ {{\varvec{A}}_{n}^{{{1,}j}} } \\ \end{array} } \right],{\varvec{A}}^{{{2,}j}} = \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{{1}}^{{{2,}j}} } \\ {{\varvec{A}}_{{2}}^{{{2,}j}} } \\ \vdots \\ {{\varvec{A}}_{n}^{{{2,}j}} } \\ \end{array} } \right],{\varvec{C}}^{j} = \left[ {\begin{array}{*{20}c} {C_{{1}}^{j} } \\ {C_{{2}}^{j} } \\ \vdots \\ {C_{n}^{j} } \\ \end{array} } \right],{\varvec{B}}^{j} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{{1}}^{j} } & {} & {} & {} \\ {} & {{\varvec{B}}_{{2}}^{j} } & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {{\varvec{B}}_{n}^{j} } \\ \end{array} } \right].$$
(60)

Introducing

$$\user2{E = p}^{t} - {\varvec{B}}^{j} {\varvec{p}}^{o} - {\varvec{C}}^{j} ,$$
(61)

Equation (58) can be rewritten as

$${\varvec{e}}^{t} = {\varvec{E}} - {\varvec{A}}^{{{1,}j}} dx_{{1}} - {\varvec{A}}^{{{2,}j}} dx_{{2}} + {\varvec{B}}^{j} {\varvec{e}}^{o}$$
(62)

Linearizing the constraints of unit dual quaternion i.e. Equations (28) and (29), one obtains

$${\varvec{C}}_{x1} dx_{1} + {\varvec{C}}_{x2} dx_{2} = {\varvec{W}}_{x}$$
(63)

where

$${\varvec{C}}_{x1} = \left[ {\begin{array}{*{20}c} 0 & {2r_{1} } & {2r_{2} } & {2r_{3} } & {2r_{4} } \\ 0 & {s_{1} } & {s_{2} } & {s_{3} } & {s_{4} } \\ \end{array} } \right],$$
(64)
$${\varvec{C}}_{x2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ {r_{1} } & {r_{2} } & {r_{3} } & {r_{4} } \\ \end{array} } \right],$$
(65)
$${\varvec{W}}_{x} = \left[ {\begin{array}{*{20}c} {1 - r_{1}^{2} - r_{2}^{2} - r_{3}^{2} - r_{4}^{2} } \\ { - r_{1} s_{1} - r_{2} s_{2} - r_{3} s_{3} - r_{4} s_{4} } \\ \end{array} } \right].$$
(66)

Derivation of formulae based on the dual quaternion

The solution of 3D similarity transformation in EIV model is based on the principle of weighted total least squares (WTLS) i.e.

$${\varvec{e}}^{tT} {\varvec{W}}^{t} {\varvec{e}}^{t} + {\varvec{e}}^{oT} {\varvec{W}}^{o} {\varvec{e}}^{o} = \min$$
(67)

where \({\varvec{W}}^{t}\) and \({\varvec{W}}^{o}\) are the weight matrices of observations in the target system and in the original system respectively. Considering the constraints in Eq. (63), a Lagrangian extremum problem with constraints is constructed as follows.

$$\mathop {\min }\limits_{{{\varvec{e}}^{o} \user2{,e}^{t} ,dx_{{1}} ,dx_{{2}} ,{\mathbf{k}}_{{1}} ,{\mathbf{k}}_{{2}} }} \left\{ \begin{gathered} l = {\varvec{e}}^{tT} {\varvec{W}}^{t} {\varvec{e}}^{t} + {\varvec{e}}^{oT} {\varvec{W}}^{o} {\varvec{e}}^{o} + {2}{\mathbf{k}}_{{1}}^{T} ({\varvec{e}}^{t} - \user2{E + A}^{{{1,}j}} dx_{{1}} + {\varvec{A}}^{{{2,}j}} dx_{{2}} - {\varvec{B}}^{j} {\varvec{e}}^{o} ) \hfill \\ + {2}{\mathbf{k}}_{{2}}^{T} ({\varvec{C}}_{{x{1}}} dx_{{1}} + {\varvec{C}}_{{x{2}}} dx_{{2}} - {\varvec{W}}_{x} ) \hfill \\ \end{gathered} \right\}$$
(68)

According to the Lagrangian extremum principle, the minimum exists if and only if the following conditions are met.

$$\frac{\delta l}{{\delta {\varvec{e}}^{o} }} = {2}{\varvec{e}}^{oT} {\varvec{W}}^{o} - {2}{\mathbf{k}}_{{1}}^{T} {\varvec{B}}^{j} = 0$$
(69)
$$\frac{\delta l}{{\delta {\varvec{e}}^{t} }} = {2}{\varvec{e}}^{tT} {\varvec{W}}^{t} + {2}{\mathbf{k}}_{{1}}^{T} = 0$$
(70)
$$\frac{\delta l}{{\delta dx_{{1}} }} = {2}{\mathbf{k}}_{{1}}^{T} {\varvec{A}}^{{{1,}j}} + {2}{\mathbf{k}}_{{2}}^{T} {\varvec{C}}_{{x{1}}} = 0$$
(71)
$$\frac{\delta l}{{\delta dx_{{2}} }} = {2}{\mathbf{k}}_{{1}}^{T} {\varvec{A}}^{{{2,}j}} + {2}{\mathbf{k}}_{{2}}^{T} {\varvec{C}}_{{x{2}}} = 0$$
(72)
$$\frac{\delta l}{{\delta {\mathbf{k}}_{{1}} }} = {2}({\varvec{e}}^{t} - \user2{E + A}^{{{1,}j}} dx_{{1}} + {\varvec{A}}^{{{2,}j}} dx_{{2}} - {\varvec{B}}^{j} {\varvec{e}}^{o} ) = 0$$
(73)
$$\frac{\delta l}{{\delta {\mathbf{k}}_{{2}} }} = {2}({\varvec{C}}_{{x{1}}} dx_{{1}} + {\varvec{C}}_{{x{2}}} dx_{{2}} - {\varvec{W}}_{x} ) = 0$$
(74)

From Eq. (69), one gets

$${\varvec{e}}^{o} { = }{\varvec{W}}^{{o}{ - {1}}} {\varvec{B}}^{jT} {\mathbf{k}}_{{1}}$$
(75)

From Eq. (70), one gets

$${\varvec{e}}^{t} { = }{\varvec{W}}^{{t}{ - {1}}} {\mathbf{k}}_{{1}}$$
(76)

Substituting Eqs. (75) and (76) into (73), and making arrangement, one gets

$${\mathbf{k}}_{{1}} = {\varvec{W}}^{ot} ( - \user2{E + A}^{{{1,}j}} dx_{{1}} + {\varvec{A}}^{{{2,}j}} dx_{{2}} ),$$
(77)

where

$${\varvec{W}}^{ot} = ({\varvec{W}}^{{t - {1}}} \user2{ + B}^{j} {\varvec{W}}^{{o - {1}}} {\varvec{B}}^{jT} )^{{ - {1}}} .$$
(78)

Substituting Eqs. (77) into (71) and introducing

$${\varvec{N}}_{{{11}}} = {\varvec{A}}^{{{1,}jT}} {\varvec{W}}^{ot} {\varvec{A}}^{{{1,}j}} ,$$
(79)
$${\varvec{N}}_{{{12}}} = {\varvec{A}}^{{{1,}jT}} {\varvec{W}}^{ot} {\varvec{A}}^{{{2,}j}} .$$
(80)

one gets

$$dx_{{1}} = - {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{N}}_{{{12}}} {\text{d}}x_{{2}} + {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{A}}^{{{1,}jT}} {\varvec{W}}^{ot} {\varvec{E}} - {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{C}}_{{x{1}}}^{T} {\mathbf{k}}_{{2}} .$$
(81)

Substituting Eqs. (81) into (72) and introducing

$${\varvec{N}}_{{{22}}} \user2{ = A}^{{{2,}jT}} {\varvec{W}}^{ot} {\varvec{A}}^{{{2,}j}} ,$$
(82)
$${\varvec{N}}_{{{21}}} = {\varvec{A}}^{{{2,}jT}} {\varvec{W}}^{ot} {\varvec{A}}^{{{1,}j}} ,$$
(83)
$${\varvec{N}}_{{{33}}} \user2{ = N}_{{{22}}} - {\varvec{N}}_{{{21}}} {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{N}}_{{{12}}} ,$$
(84)
$${\varvec{D}}_{{{11}}} = {\varvec{N}}_{{{33}}}^{{ - {1}}} ( - {\varvec{C}}_{{x{2}}}^{T} + {\varvec{N}}_{{{21}}} {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{C}}_{{x{1}}}^{T} )$$
(85)
$${\varvec{D}}_{{{10}}} = {\varvec{N}}_{{{33}}}^{{ - {1}}} ({\varvec{N}}_{{{21}}} {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{A}}^{{{1,}jT}} - {\varvec{A}}^{{{2,}jT}} )$$
(86)

one gets

$$dx_{{2}} = {\varvec{D}}_{{{11}}} {\mathbf{k}}_{{2}} - {\varvec{D}}_{{{10}}} {\varvec{W}}^{ot} {\varvec{E}}.$$
(87)

Substituting Eqs. (87) into (81) and introducing

$${\varvec{D}}_{{{21}}} = - {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{N}}_{{{12}}} {\varvec{D}}_{{{11}}} - {\varvec{N}}_{{{11}}}^{{ - {1}}} {\varvec{C}}_{{x{1}}}^{T}$$
(88)
$${\varvec{D}}_{{{20}}} = - {\varvec{N}}_{{{11}}}^{{ - {1}}} ({\varvec{N}}_{{{12}}} {\varvec{D}}_{{{10}}} + {\varvec{A}}^{{{1,}jT}} )$$
(89)

one gets

$$dx_{{1}} = {\varvec{D}}_{{{21}}} {\mathbf{k}}_{{2}} - {\varvec{D}}_{{{20}}} {\varvec{W}}^{ot} {\varvec{E}}.$$
(90)

Substituting Eqs. (90) and (87) into (74), one obtains the solution of \({\mathbf{k}}_{{2}}\) as

$${\mathbf{k}}_{{2}} = ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{20}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{10}}} ){\varvec{W}}^{ot} {\varvec{E}} + ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} {\varvec{W}}_{x}$$
(91)

Substituting Eqs. (91) into (90) and (87), one obtains

$$dx_{{1}} = {\varvec{F}}_{{1}} {\varvec{W}}^{ot} \user2{E + D}_{{{21}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} {\varvec{W}}_{x}$$
(92)
$$dx_{{2}} = {\varvec{F}}_{{2}} {\varvec{W}}^{ot} \user2{E + D}_{{{11}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} {\varvec{W}}_{x}$$
(93)

where

$${\varvec{F}}_{{1}} = {\varvec{D}}_{{{21}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{20}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{10}}} ) - {\varvec{D}}_{{{20}}} ,$$
(94)
$${\varvec{F}}_{{2}} \user2{ = D}_{{{11}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{21}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{11}}} )^{{ - {1}}} ({\varvec{C}}_{{x{1}}} {\varvec{D}}_{{{20}}} + {\varvec{C}}_{{x{2}}} {\varvec{D}}_{{{10}}} ) - {\varvec{D}}_{{{10}}} .$$
(95)

So far the derivations of formulae have been accomplished. Then one can employ the classic Gauss–Newton iterative method to seek the solution of transformation parameters. The stop condition of iteration is

$$abs(\sigma_{j}^{2} - \sigma_{j - 1}^{2} ) < \tau$$
(96)

where

$$\sigma^{2} { = }\frac{{{\varvec{e}}^{tT} {\varvec{W}}^{t} {\varvec{e}}^{t} + {\varvec{e}}^{oT} {\varvec{W}}^{o} {\varvec{e}}}}{3n - 7}$$
(97)

Subscript j and j−1 denote the present iterative times and the previous iterative times. And \(\tau\) is a threshold (1.0 × 10–14 is set in the paper).

After the iterative computation converges, the variance factor of unit weight is estimated as

$$\sigma = \pm \sqrt {\frac{{{\varvec{e}}^{tT} {\varvec{W}}^{t} {\varvec{e}}^{t} + {\varvec{e}}^{oT} {\varvec{W}}^{o} {\varvec{e}}}}{3n - 7}}$$
(98)

By Eqs. (92) and (93), the estimated variance or covariance matrices of transformation parameters \(x_{{1}}\) and \(x_{{2}}\) is derived as

$${\varvec{D}}_{{x_{1} }} = \sigma^{2} {\varvec{F}}_{{1}} {\varvec{W}}^{ot} {\varvec{F}}_{{1}}^{T} ,$$
(99)
$${\varvec{D}}_{{x_{2} }} = \sigma^{2} {\varvec{F}}_{{2}} {\varvec{W}}^{ot} {\varvec{F}}_{{2}}^{T} .$$
(100)
$${\varvec{D}}_{{x_{1} x_{2} }} = \sigma^{2} {\varvec{F}}_{{1}} {\varvec{W}}^{ot} {\varvec{F}}_{{2}}^{T}$$
(101)
$${\varvec{D}}_{{x_{2} x_{1} }} = \sigma^{2} {\varvec{F}}_{{2}} {\varvec{W}}^{ot} {\varvec{F}}_{{1}}^{T}$$
(102)

Introducing the vector of all transformation parameters

$$x_{{1,2}} { = }\left[ {\begin{array}{*{20}c} {x_{{1}} } \\ {x_{{2}} } \\ \end{array} } \right]$$
(103)

Thus the variance matrix of \(x_{{1,2}}\) is

$${\varvec{D}}_{{x_{{1,2}} }} = \left[ {\begin{array}{*{20}c} {{\varvec{D}}_{{x_{1} }} } & {{\varvec{D}}_{{x_{1} x_{2} }} } \\ {{\varvec{D}}_{{x_{2} x_{1} }} } & {{\varvec{D}}_{{x_{2} }} } \\ \end{array} } \right]$$
(104)

Computation and precision estimation of seven parameters from dual quaternion

Traditionally the similarity 3D coordinate transformation model i.e. Equation (41) includes seven parameters i.e. one scale, three rotation angles and three translations. Thus it is necessary to compute the seven parameters and estimate their precisions. Firstly one needs to construct the function of the seven parameters with dual quaternion-based transformation parameter i.e. \(x_{{1,2}}\). And then compute the variance or covariance matrices of the seven parameters according to the variance or covariance matrices propagation principle.

Utilizing Eqs. (42) and (21), the rotation angles \(\theta_{x}\), \(\theta_{y}\), \(\theta_{z}\) are computed by

$$\theta_{x} { = } - {\text{tan}}^{ - 1} \left( {\frac{{{2}\left( {r_{2} r_{3} + r_{1} r_{4} } \right)}}{{r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} }}} \right)$$
(105)
$$\theta_{y} {\text{ = sin}}^{ - 1} \left( {{2}\left( {r_{1} r_{3} - r_{2} r_{4} } \right)} \right)$$
(106)
$$\theta_{z} { = } - {\text{tan}}^{ - 1} \left( {\frac{{{2}\left( {r_{1} r_{2} + r_{3} r_{4} } \right)}}{{r_{{4}}^{{2}} + r_{1}^{{2}} - r_{2}^{{2}} - r_{3}^{{2}} }}} \right)$$
(107)

Introducing

$$s_{x} {\text{ = sin}}\theta_{x} ,\;s_{y} {\text{ = sin}}\theta_{y} ,\,s_{z} {\text{ = sin}}\theta_{z} ,c_{x} {\text{ = cos}}\theta_{x} ,\,c_{y} {\text{ = cos}}\theta_{y} ,\,c_{z} {\text{ = cos}}\theta_{z}$$
(108)

one obtains the partial derivatives of \(\theta_{x}\) with respect to \(r_{1}\) by Eq. (105)∙

$$\begin{aligned} \frac{{\partial \theta_{x} }}{{\partial r_{1} }} = & - \frac{1}{{1 + \left( {\frac{{{2}\left( {r_{2} r_{3} + r_{1} r_{4} } \right)}}{{r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} }}} \right)^{2} }} \cdot \frac{{{2}r_{4} \left( {r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} } \right) + 2r_{1} \cdot 2\left( {r_{2} r_{3} + r_{1} r_{4} } \right)}}{{\left( {r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} } \right)^{2} }} \\ = & - \frac{{{2}r_{4} \left( {r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} } \right) + 2r_{1} \cdot 2\left( {r_{2} r_{3} + r_{1} r_{4} } \right)}}{{\left( {r_{{4}}^{{2}} - r_{1}^{{2}} - r_{2}^{{2}} + r_{3}^{{2}} } \right)^{2} + \left( {{2}\left( {r_{2} r_{3} + r_{1} r_{4} } \right)} \right)^{2} }} \\ = & - \frac{{{2}r_{4} \left( {c_{x} c_{y} } \right) + 2r_{1} \left( { - s_{x} c_{y} } \right)}}{{\left( {c_{x} c_{y} } \right)^{2} + \left( { - s_{x} c_{y} } \right)^{2} }} \\ = & - \frac{{{2}\left( {r_{4} c_{x} - r_{1} s_{x} } \right)}}{{c_{y} }} \\ \end{aligned}$$
(109)

where the dots \(\cdot\) denote computation of multiplication. Similarly one obtains

$$\frac{{\partial \theta_{x} }}{{\partial r_{2} }} = - \frac{{{2}\left( {r_{3} c_{x} - r_{2} s_{x} } \right)}}{{c_{y} }}$$
(110)
$$\frac{{\partial \theta_{x} }}{{\partial r_{3} }} = - \frac{{{2}\left( {r_{2} c_{x} + r_{3} s_{x} } \right)}}{{c_{y} }}$$
(111)
$$\frac{{\partial \theta_{x} }}{{\partial r_{4} }} = - \frac{{{2}\left( {r_{1} c_{x} + r_{4} s_{x} } \right)}}{{c_{y} }}$$
(112)

Further one can get the following partial derivatives of \(\theta_{y}\), \(\theta_{z}\) with respect to \(r_{1}\), \(r_{2}\), \(r_{3}\), \(r_{4}\) by Eqs. (106) and (107) respectively.

$$\frac{{\partial \theta_{y} }}{{\partial r_{1} }} = \frac{{{2}r_{3} }}{{c_{y} }}$$
(113)
$$\frac{{\partial \theta_{y} }}{{\partial r_{2} }} = \frac{{ - {2}r_{4} }}{{c_{y} }}$$
(114)
$$\frac{{\partial \theta_{y} }}{{\partial r_{3} }} = \frac{{{2}r_{1} }}{{c_{y} }}$$
(115)
$$\frac{{\partial \theta_{y} }}{{\partial r_{4} }} = \frac{{ - {2}r_{2} }}{{c_{y} }}$$
(116)
$$\frac{{\partial \theta_{z} }}{{\partial r_{1} }} = - \frac{{{2}\left( {r_{2} c_{z} + r_{1} s_{z} } \right)}}{{c_{y} }}$$
(117)
$$\frac{{\partial \theta_{z} }}{{\partial r_{2} }} = - \frac{{{2}\left( {r_{1} c_{z} - r_{2} s_{z} } \right)}}{{c_{y} }}$$
(118)
$$\frac{{\partial \theta_{z} }}{{\partial r_{3} }} = - \frac{{{2}\left( {r_{4} c_{z} - r_{3} s_{z} } \right)}}{{c_{y} }}$$
(119)
$$\frac{{\partial \theta_{z} }}{{\partial r_{4} }} = - \frac{{{2}\left( {r_{3} c_{z} + r_{4} s_{z} } \right)}}{{c_{y} }}$$
(120)

Next, the translations can be computed by Eqs. (38) and (39) as

$$\left[ {\begin{array}{*{20}c} {t_{x} } \\ {t_{y} } \\ {t_{z} } \\ {0} \\ \end{array} } \right]{ = 2}W({\varvec{r}})^{T} {\varvec{s}}{ = }\left[ {\begin{array}{*{20}c} {r_{4} s_{1} - r_{3} s_{2} - r_{2} s_{3} - r_{1} s_{4} } \\ {r_{3} s_{1} + r_{4} s_{2} - r_{1} s_{3} - r_{2} s_{4} } \\ { - r_{2} s_{1} + r_{1} s_{2} + r_{4} s_{3} - r_{3} s_{4} } \\ {r_{1} s_{1} + r_{2} s_{2} + r_{3} s_{3} + r_{4} s_{4} } \\ \end{array} } \right]$$
(121)

It is easy to deduce the following partial derivatives as

$$\frac{{\partial t_{x} }}{{\partial r_{1} }} = - s_{4} ,\,\frac{{\partial t_{x} }}{{\partial r_{2} }} = - s_{3} ,\,\frac{{\partial t_{x} }}{{\partial r_{3} }} = - s_{2} ,\,\frac{{\partial t_{x} }}{{\partial r_{4} }} = s_{1} ,\,\frac{{\partial t_{x} }}{{\partial s_{1} }} = r_{4} ,\,\frac{{\partial t_{x} }}{{\partial s_{2} }} = - r_{3} ,\,\frac{{\partial t_{x} }}{{\partial s_{3} }} = - r_{2} ,\frac{{\partial t_{x} }}{{\partial s_{4} }} = - r_{1}$$
(122)
$$\frac{{\partial t_{y} }}{{\partial r_{1} }} = - s_{3} ,\,\frac{{\partial t_{y} }}{{\partial r_{2} }} = - s_{4} ,\,\frac{{\partial t_{y} }}{{\partial r_{3} }} = s_{1} ,\,\frac{{\partial t_{y} }}{{\partial r_{4} }} = s_{2} ,\,\frac{{\partial t_{y} }}{{\partial s_{1} }} = r_{3} ,\,\frac{{\partial t_{y} }}{{\partial s_{2} }} = r_{4} ,\,\frac{{\partial t_{y} }}{{\partial s_{3} }} = - r_{1} ,\,\frac{{\partial t_{y} }}{{\partial s_{4} }} = - r_{2}$$
(123)
$$\frac{{\partial t_{z} }}{{\partial r_{1} }} = s_{2} ,\,\frac{{\partial t_{z} }}{{\partial r_{2} }} = - s_{1} ,\,\frac{{\partial t_{z} }}{{\partial r_{3} }} = - s_{4} ,\frac{{\partial t_{z} }}{{\partial r_{4} }} = s_{3} ,\,\frac{{\partial t_{z} }}{{\partial s_{1} }} = - r_{2} ,\,\frac{{\partial t_{z} }}{{\partial s_{2} }} = r_{1} ,\,\frac{{\partial t_{z} }}{{\partial s_{3} }} = r_{4} ,\frac{{\partial t_{z} }}{{\partial s_{4} }} = - r_{3}$$
(124)

Introducing

$$y = \left[ {\begin{array}{*{20}c} \lambda & {\theta_{x} } & {\theta_{y} } & {\theta_{z} } & {t_{x} } & {t_{y} } & {t_{z} } \\ \end{array} } \right]^{T}$$
(125)
$${\varvec{J}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\partial \theta_{x} }}{{\partial r_{1} }}} & {\frac{{\partial \theta_{x} }}{{\partial r_{2} }}} & {\frac{{\partial \theta_{x} }}{{\partial r_{3} }}} & {\frac{{\partial \theta_{x} }}{{\partial r_{4} }}} & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\partial \theta_{y} }}{{\partial r_{1} }}} & {\frac{{\partial \theta_{y} }}{{\partial r_{2} }}} & {\frac{{\partial \theta_{y} }}{{\partial r_{3} }}} & {\frac{{\partial \theta_{y} }}{{\partial r_{4} }}} & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\partial \theta_{z} }}{{\partial r_{1} }}} & {\frac{{\partial \theta_{z} }}{{\partial r_{2} }}} & {\frac{{\partial \theta_{z} }}{{\partial r_{3} }}} & {\frac{{\partial \theta_{z} }}{{\partial r_{4} }}} & 0 & 0 & 0 & 0 \\ 0 & {\frac{{\partial t_{x} }}{{\partial r_{1} }}} & {\frac{{\partial t_{x} }}{{\partial r_{2} }}} & {\frac{{\partial t_{x} }}{{\partial r_{3} }}} & {\frac{{\partial t_{x} }}{{\partial r_{4} }}} & {\frac{{\partial t_{x} }}{{\partial s_{1} }}} & {\frac{{\partial t_{x} }}{{\partial s_{2} }}} & {\frac{{\partial t_{x} }}{{\partial s_{3} }}} & {\frac{{\partial t_{x} }}{{\partial s_{4} }}} \\ 0 & {\frac{{\partial t_{y} }}{{\partial r_{1} }}} & {\frac{{\partial t_{y} }}{{\partial r_{2} }}} & {\frac{{\partial t_{y} }}{{\partial r_{3} }}} & {\frac{{\partial t_{y} }}{{\partial r_{4} }}} & {\,\frac{{\partial t_{y} }}{{\partial s_{1} }}} & {\frac{{\partial t_{y} }}{{\partial s_{2} }}} & {\frac{{\partial t_{y} }}{{\partial s_{3} }}} & {\frac{{\partial t_{y} }}{{\partial s_{4} }}} \\ 0 & {\frac{{\partial t_{z} }}{{\partial r_{1} }}} & {\frac{{\partial t_{z} }}{{\partial r_{2} }}} & {\frac{{\partial t_{z} }}{{\partial r_{3} }}} & {\frac{{\partial t_{z} }}{{\partial r_{4} }}} & {\frac{{\partial t_{z} }}{{\partial s_{1} }}} & {\frac{{\partial t_{z} }}{{\partial s_{2} }}} & {\frac{{\partial t_{z} }}{{\partial s_{3} }}} & {\frac{{\partial t_{z} }}{{\partial s_{4} }}} \\ \end{array} } \right]$$
(126)

one has

$$dy = {\varvec{J}}dx_{{1,2}}$$
(127)

According to the variance or covariance matrices propagation principle, one gets

$${\varvec{D}}_{y} = {\varvec{JD}}_{{x_{{1,2}} }} {\varvec{J}}^{T}$$
(128)

Dual quaternion algorithm

The proposed algorithm namely the Dual Quaternion Algorithm is summarized in Table 1.

Table 1 The dual quaternion algorithm of the WTLS 3D coordinate transformation
Full size table

Experiments and discussion

Two numerical cases including actual geodetic datum transformation and a simulated case are demonstrated to validate the presented algorithm. The former case involves small rotation angles while the latter one involves large rotation angles. The results and analyses are as follows.

Actual geodetic datum transformation case

Mostly geodetic datum transformation involves very small rotation angles (not bigger than 1°). This case data is chosen from Grafarend and Awange (2003), which is discussed in Mercan et al. (2018), Zeng et al. (2022b), etc. The original (local) and target (global) 3D coordinates and their variances of seven control points are listed in Tables 2 and 3. The distribution of seven control points in the original coordinate system is illustrated in Fig. 3. They are almost located in a plane that is represented by the grids in the figure (the biggest distance from the control point to the plane is 68.29 m, corresponding to station Solitude, which is quite small compared to about 50 km × 50 km of the control point area. The biggest distance between the control points is 75,159.625 m). And the fitted plane equation is 0.6456x + 0.1012y + 0.7570z = 6.3655 × 106. Supposed that the components of \({\varvec{p}}_{i}^{o}\) and \({\varvec{p}}_{i}^{t}\) are isotropic and not correlative, the covariance matrices \({\varvec{D}}^{{\text{o}}}\) and \({\varvec{D}}^{t}\) of \({\varvec{p}}^{o}\) and \({\varvec{p}}^{t}\) are both diagonal as

$${\varvec{D}}^{{\text{o}}} = {\text{diag(}}\sigma_{{1}}^{o2} ,\sigma_{{1}}^{o2} ,\sigma_{{1}}^{o2} ,\sigma_{{1}}^{o2} , \cdots ,\sigma_{n}^{o2} ,\sigma_{n}^{o2} ,\sigma_{n}^{o2} ,\sigma_{n}^{o2} )$$
(129)
$${\varvec{D}}^{t} = {\text{diag(}}\sigma_{{1}}^{t2} ,\sigma_{{1}}^{t2} ,\sigma_{{1}}^{t2} ,\sigma_{{1}}^{t2} , \cdots ,\sigma_{n}^{t2} ,\sigma_{n}^{t2} ,\sigma_{n}^{t2} ,\sigma_{n}^{t2} )$$
(130)

where n is the number of point, i.e. 7 inthis case. The weight matrices \({\varvec{W}}^{o}\) and \({\varvec{W}}^{t}\) are constructed as

$${\varvec{W}}^{o} = \left( {{\varvec{D}}^{{\text{o}}} } \right)^{ - 1}$$
(131)
$${\varvec{W}}^{t} = \left( {{\varvec{D}}^{t} } \right)^{ - 1}$$
(132)
Table 2 3D coordinates in the original system
Full size table
Table 3 3D coordinates in the target system
Full size table
Fig. 3
figure 3

Distribution of the stations

Full size image

The proposed algorithm namely DQA is employed to calculate the transformation parameters. The estimated scale and unit dual quaternion by DQA are listed in Table 4. The computed traditional seven transformation parameters and their precisions by DQA are listed in Table 5. In order to compare with the quaternion algorithm (QA) in Mercan et al. (2018), the paper computes the scaled quaternion and their precisions from the estimated scale and dual quaternion by DQA as follows.

$${\varvec{q}} = \left[ {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & {q_{3} } & {q_{0} } \\ \end{array} } \right]^{T} = \sqrt \lambda {\varvec{r}}$$
(133)

where the definition of quaternion in the form of vector here is different from Mercan et al. (2018). Further, one obtains

$$d{\varvec{q}} = \left[ {\begin{array}{*{20}c} {\frac{{r_{1} }}{2\sqrt \lambda }} & {\sqrt \lambda } & 0 & 0 & 0 \\ {\frac{{r_{2} }}{2\sqrt \lambda }} & 0 & {\sqrt \lambda } & 0 & 0 \\ {\frac{{r_{3} }}{2\sqrt \lambda }} & 0 & 0 & {\sqrt \lambda } & 0 \\ {\frac{{r_{4} }}{2\sqrt \lambda }} & 0 & 0 & 0 & {\sqrt \lambda } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{d}}\lambda } \\ {{\text{d}}r_{1} } \\ {{\text{d}}r_{2} } \\ {{\text{d}}r_{3} } \\ {{\text{d}}r_{4} } \\ \end{array} } \right] = {\varvec{J}}_{q} dx_{{1}}$$
(134)
Table 4 Computed scale and dual quaternion and their precisions by DQA in the geodetic case
Full size table
Table 5 Computed seven transformation parameters and their precisions by DQA in the geodetic case
Full size table

According to the variance or covariance matrices propagation principle, one gets

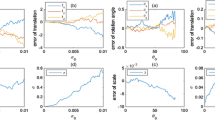
$${\varvec{D}}_{q} = {\varvec{J}}_{q} {\varvec{D}}_{{x_{{1}} }} {\varvec{J}}_{q}^{T}$$
(135)

The computed results by QA and DQA are listed in Tables 6, 7, 8 and 9. And the result by QA is directly from Mercan et al. (2018). From Table 6, it is seen that the computed scale, rotation matrix and variance component are identical regardless of the rounding errors. However the QA does not provide the precision of scale while DQA does. Table 7 shows that the computed scaled quaternion and translations are consistent if the rounding errors are ignored, but the estimated precisions are different greatly. As far as q0 is concerned, the estimated standard deviation is improved from 10–7 by QA to 10–9 by DQA. In other words, the decrease percent of standard deviations is 99.36%. For q1, q2, q3, the estimated precisions by two algorithms are slightly different. As far as the translations are concerned, the estimated standard deviations decrease 12.34%, 0.26%, 17.08% for tx, ty, tz respectively from QA to DQA. The average decrease percent is 18.28% for the scaled quaternion and translations (seven parameters). The comparison of estimated standard deviations by DQA and QA is depicted in Fig. 4. In a word, the estimated precisions are improved significantly comparing DQA to QA.

Table 6 Computed scale, rotation matrix and variance component by DQA and QA in the geodetic case
Full size table
Table 7 Computed scaled quaternion, translations by DQA and QA, and decrease percent of standard deviations from QA to DQA
Full size table
Table 8 Predicted errors of coordinates in the original and target systems by DQA and QA in the geodetic case
Full size table
Table 9 Transformation residuals by DQA and QA in the geodetic case
Full size table
Fig. 4
figure 4

Comparison of estimated standard deviations by DQA and QA

Full size image

From Tables 8 and 9, it is seen that the predicted errors of coordinates in the original and target systems by DQA and QA are the same; the transformation residuals are identical too for DQA and QA. Thus the DQA and QA are correct.

Simulated case

The adopted data in this case is originally from Felus and Burtch (2009). The data is synthesized and rounded based on a surface fitting experiment. In the experiment, the surface is surveyed in two different coordinate systems. And four control points on the surface are identified and their coordinates in the original and target coordinate systems are listed in Table 10. The area of control points are 70 m × 90 m in the original coordinate system. It is assumed that all points are not dependent on each other and the coordinate components of each point are isotropic and not correlated. And the point-wise weights are given in Table 10 too. The distribution of control points are depicted in Fig. 5. The superscript o or t denotes original coordinate system or target coordinate system respectively in the figure. The red circles represent the positions of control point regardless of the errors in the original system. And red solid lines are drawn between them. The blue asterisks represent the positions of control point regardless of the errors in the target system. And blue solid lines are drawn between them. It is easily seen that the rotation angle around the z axis is big, while rotation angles around the x and y axes are small and the scale is much greater than 1.

Table 10 Coordinates and point-wise weights of control points
Full size table
Fig. 5
figure 5

Distribution of the control points in the original and target coordinate systems

Full size image

The DQA and QA are utilized to estimate the transformation parameters. The calculated scale and unit dual quaternion by DQA are listed in Table 11. The estimated traditional seven transformation parameters and their precisions by DQA are listed in Table 12. The obtained results by QA and their counterparts by DQA are given in Tables 13, 14. Predicted errors of coordinates and estimated covariance matrix \({\varvec{D}}_{{x_{{1,2}} }}\), \({\varvec{D}}_{y}\) by DQA are listed in Tables 15, 16, 17 respectively. The transformation residuals by DQA and QA are listed in Table 18. The adjusted coordinates of points are depicted in Fig. 5. The red crosses represent the positions of control point after adjustment in the original system. And red dash-dotted lines are drawn between them. The blue squares represent the positions of control point after adjustment in the target system. And blue dash-dotted lines are drawn between them.

Table 11 Computed scale and dual quaternion and their precisions by DQA in the simulated case
Full size table
Table 12 Computed seven transformation parameters and their precisions by DQA in the simulated case
Full size table
Table 13 Computed scale, rotation matrix and variance component by DQA and QA in the simulated case
Full size table
Table 14 Computed scaled quaternion, translations by DQA and QA in the simulated case
Full size table
Table 15 Predicted errors of coordinates in the original and target systems by DQA in the simulated case
Full size table
Table 16 Covariance matrix \({\varvec{D}}_{{x_{{1,2}} }}\) obtained by DQA
Full size table
Table 17 Covariance matrix \({\varvec{D}}_{y}\) obtained by DQA
Full size table
Table 18 Transformation residuals by DQA and QA in the simulated case
Full size table

Table 12 shows that the standard deviations of seven transformation parameters are relatively big, especially those of the rotation angle which are worthy of attention are around 5°. It is seen that from Table 13, the computed scale, rotation matrix and variance component by DQA and QA are identical, however QA does not offer the standard deviation of scale while DQA does. Table 14 shows that the computed scaled quaternion, translations by DQA and QA are consistent regardless of the rounding error. Table 15 or Fig. 5 shows the predicted errors of coordinates are nearly 10 m, which are relatively big. The reason is that the original and target coordinates errors of control points are relatively big from the viewpoint of variance component in Table 13. It is shown that the transformation residuals by DQA and QA are same from Table 18.

To sum up, DQA and QA obtain the consistent results. However it is worthy of notice that the precisions of adjusted parameters are not high for this case with relatively big errors in the coordinates.

Conclusions

A unit quaternion is widely used to represent the 3D rotation matrix, and the paper presents its own derivation from the geometric meaning of 3D rotation of a point around an axis. Further, a unit dual quaternion is employed to represent not only the 3D rotation matrix but also the translation vector, and the paper gives the derivation of representation of the translation vector by the unit dual quaternion. Based on the unit dual quaternion, the 3D similarity coordinate transformation in the errors-in-variables (EIV) model is formulated. By means of linearization by Taylor's formula and Lagrangian extremum principle with constraints, the Dual Quaternion Algorithm (DQA) is proposed. The algorithm is able to output not only the computed parameters but also the full precision information of computed parameters. In addition, the traditional seven parameters and their estimated precisions are output.

The two numerical experiments including a real-world geodetic datum transformation case and a simulated case from surface fitting show that the presented algorithm i.e. DQA is not sensitive to the initial values of transformation, in other words the arbitrary initial value set in this paper is feasible regardless of the size of rotation angles. DQA obtains the consistent results with the quaternion algorithm i.e. QA from Mercan et al. (2018), no matter how big the rotation angles are, and whether the relative errors of coordinates (pseudo-observations) are large or small. On the other hand, the DQA has some advantages over the QA. The key one is the improvement of estimated precisions of transformation parameters, i.e. the average decrease percent of standard deviations is 18.28%, and biggest decrease percent is 99.36% for the scaled quaternion and translations in the geodetic datum transformation case. Another advantage is the DQA fulfills the computation and precision estimation of traditional seven transformation parameters (which still are widely applied yet) from dual quaternion, and even could perform the computation and precision estimation of the scaled quaternion.