Abstract
A series of reclamation works that took place during the twentieth century, almost completely destroyed the dune system that characterized the eastern part of the Grado-Marano perilagoonal area (NE Italy). Because of the limited data available, so far very little was known about the local subsurface conditions and the present paper presents the main outcomes of the seismic exploration accomplished with a twofold goal: collecting comprehensive data about the subsurface conditions (which geologists need to be able to reconstruct the formation processes of the local geomorphological elements) and testing a series of efficient and unconventional methodologies based on the analysis of surface waves from both active and passive seismic data. The survey was designed and accomplished also considering the local digital terrain model (DTM) and some resistivity and penetrometer data. In the present paper we focus on three main areas and, from the methodological point of view, special emphasis is given to the Holistic analysis of Surface waves (HS) and the Horizontal-to-Vertical Spectral Ratio (HVSR), since both these techniques require simple field procedures and a light equipment. It is also show the wealth of information that the simple spectral analysis of multi-offset passive data can provide in particular for the identification of possible lateral variations. In fact, in spite of the low-energy depositional environment, the area reveals extremely complex with major and abrupt lateral variations that require special care and prevent from using coarse methodologies that cannot properly handle their identification. Collected geophysical data provide a consistent overall scenario: while the area is in general dominated by soft (silty) sediments, the residual dunes are constituted by cemented sandy materials (medium-grained calcarenite) responsible for anomalously high shear-wave velocity (VS) values already at the surface. Parallel to such residual sandy dunes we also identified a series of peat channels characterized by distinctive low VS values due to a significant amount of organic components.
Graphical Abstract

Similar content being viewed by others
Introduction
In areas considerably modified by human activities, the reconstruction of the paleo-environmental conditions responsible for the formation of specific geomorphological features can be problematic. In this respect, geophysical data are able to provide information that geologists need to depict the paleo conditions that led to the formation of the local geomorphological elements.
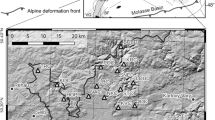
A series of geophysical data sets were acquired south of the ancient Roman city of Aquileia, around the Grado-Marano lagoon (NE Italy) (Amorosi et al. 2008; Fontana et al. 2008; Antonioli et al. 2009). The considered perilagoon area (Fig. 1) is nowadays a fundamentally flat territory that was strongly modified by a series of hydraulic reclamation works that took place mainly during the Austro-Hungarian times and the fascist regime. As a result, only few faint elements of the ancient dune system have been preserved.
Location of the investigated area: a general overview (South Europe map) and main geological, tectonic and alluvial elements (Fontana et al. 2008). The Grado-Marano lagoon is the area between the Isonzo and Tagliamento rivers; b study area with highlighted the Beligna and San Marco sites (see also Fig. 2)
Due to the lack of quantitative data necessary to formulate a well-constrained geological model, very little is known about the origin of such a dune system, since the very few geomorphological studies regarding this region are rather general and speculative (Marocco 1991; Lenardon and Marocco 1994; Arnaud-Fassetta et al. 2003).
During a preliminary seismic campaign, we identified a few sites with anomalously high shear-wave velocity (VS) values already at the surface. In fact, while the VS of the standard shallow silty sediments that dominate the area is about 100–200 m/s, in some areas the shallow layers are characterized by values of about 400–500 m/s.
The paper presents the results of the geophysical investigation accomplished to characterize the overall area through surface-wave analysis. Active and passive seismic data are analysed considering a series of efficient and unconventional methodologies able to handle the complexity of the area and properly highlight the coexistence of very different elements: peat channels (characterized by very low VS values) are found just aside sandy residual dunes characterized by stiff (cemented) sands, while ordinary silty sediments characterize the rest of the area. Such a complex stratigraphic scenario requires the adoption of effective and unconventional methodologies suitable for the acquisition and analysis of geophysical data in areas with significant lateral variations.
A defining point of the study is the extensive (but not exclusive) analysis of multi-component group velocities. Due to the fact that the seismological and applied geophysics communities hardly merge, group velocities are routinely considered in seismological studies (Dziewonski 1971; Levshin et al. 1972; Knopoff and Panza 1977; Ritzwoller and Levshin 2002, 1998; Cotte and Laske 2002; Pontevivo and Panza 2002; Fang et al. 2010; Kolínský et al. 2014; Lukešová et al. 2019; Qorbani et al. 2020) but very rarely in near-surface applications (Ritzwoller and Levshin 2002; Nguyen et al. 2009; Gaždová et al. 2015; Dal Moro et al. 2018; Dal Moro 2019a). In fact, applied geophysicists are mostly familiar with phase velocities, often processed according to the standard MASW (Multi-channel Analysis of Surface Waves) approach (Park et al. 1998; Hayashi and Suzuki 2004; O’Neill et al. 2006; O’Connell and Turner 2011). This is quite curious if we consider that the computation of the phase velocities requires the acquisition of multi-offset data, while group velocities can be defined using a single geophone. In case the acquisition is accomplished by means of a 3-component sensor, we can deal with multi-component data that allow the computation of a series of observables that can be jointly inverted so to obtain a well-constrained VS profile free from major ambiguities (Dal Moro 2019a; Dal Moro et al. 2019) otherwise inevitably affecting the analyses based on just one component (Dal Moro 2014, 2020a; Dal Moro et al. 2015a).
Although the methodologies applied for the present work are usually adopted for the definition of the VS profile in seismic–hazard studies, thanks to the simple field procedures and the limited field equipment, they reveal extremely effective for any sort of application (in this case the goal was the determination of the subsurface model useful to cast some light about the characteristics of a paleo dune system flattened out during the reclamation works that altered the original landscape).
Collected seismic data were integrated and compared with the digital terrain model (DTM) (Regione Friuli Venezia Giulia 2021), electrical resistivity tomography (Loke and Barker 1996) (ERT) and penetrometer data so to obtain a comprehensive scenario. Results show that, in spite of the low-energy depositional environment (an alluvial plain around a lagoon), the formation processes of the local geomorphological elements created large abrupt lateral variations within just a few meters.
After a brief description of the general geological setting and an introduction to the adopted geophysical methodologies, we present and comment the analyses performed on the data collected at three sites (Figs. 1, 2, 3), giving adequate emphasis on a series of methodological aspects that characterize the accomplished analyses.
Digital Terrain Model (DTM): a DTM for the whole area (vertical exaggeration 10x, shown the three investigated sites). The area approximately corresponds to the white rectangle in Fig. 1b; b DTM of the San Marco’s area (vertical exaggeration 10x). With respect to the surrounding ground level (which is almost 2 m below the sea level), the maximum height of the San Marco’s dune is about 10 m. Shown the locations where seismic data were recorded: P1 (top of the dune); P2 (base of the dune); P3 (lagoon)
Main geological elements of the investigated area
The Venetian–Friulian Plain (NE Italy) is a large piedmont basin consisting of a thick package of carbonate gravel and sand deposits from the Eastern Alps (Amorosi et al. 2008; Fontana et al. 2008; Antonioli et al. 2009) (Fig. 1a). In the southern part, the Northern Adriatic coast is dominated by fluvio-glacial sediments and extensively occupied by sandy beaches, lagoons and marshes (Arnaud-Fassetta et al. 2003).
The Grado-Marano lagoon area (Fig. 1) is a coastal shallow-water system of about 160 km2 between the Tagliamento and Isonzo river mouths. The western (Marano) and eastern (Grado) sectors, exhibit some different physico-chemical features: the Marano sector (in the western area) receives a greater amount of freshwater from its tributaries and is characterized by lower salinity and higher nutrient concentrations. On the other side, the Grado lagoon (in the eastern area) is shallower, has a weaker hydrodynamics, a more complex morphology and is geologically younger (Melis and Covelli 2013).
In the peri-lagoonal area, the sediments are dominated by silt, clay and, to a minor extent, sand and gravel (Brambati 1972; Marocco 1991; Lenardon and Marocco 1994; Melis and Covelli 2013; Dal Moro et al. 2015b; Dal Moro and Puzzilli 2017) but, according to local geologists and borehole data, peats and over-consolidated clays are pretty common as well.
Roughly speaking, the San Marco dune (the first considered site) is an L-shaped structure with two branches in the SE–NW and SW–NE directions (Fig. 2). The maximum height above the surrounding ground level is currently about 10 m but it must be considered that, over the time, the original dune was surely modified. The main elements of the dune have been preserved thanks to the presence of an ancient church and a cemetery, while the rest of the surrounding area was nearly completely flattened out because of several reclamation works that took place in particular during the twentieth century. Large parts of the area lie below sea level and are protected by a levee system (Figs. 2b and 3). The topography of the second investigated area (Beligna#1 and Beligna#2—Fig. 2a) was severely altered by the reclamation works: the top of the Beligna#1 residual dune is currently less than 2 m high (see DTM in Fig. 3), while the Beligna#2 dune is completely flattened due to intensive agricultural activities (Fig. 2a).
Applied surface-wave methodologies
For the present study, we considered a series of techniques aimed at the acquisition and analysis of surface waves according to both active and passive approaches, so to determine the subsurface conditions in terms of shear-wave velocity (Kudo et al. 2004; Dal Moro 2014). Although the paper presents just part of the data actually collected, during the exploration of the investigated area we considered several conventional (active and passive) methodologies, such as SPAC—SPatial AutoCorrelation (Aki 1957; Okada and Suto 2003; Roberts et al. 2004; Asten 2006; Ikeda et al. 2012), ESAC—Extended Spatial AutoCorrelation (Ohori et al. 2002), HVSR—Horizontal-to-Vertical Spectral Ratio (Arai and Tokimatsu 2004, 2005) and multi-component MASW (Dal Moro 2014; Dal Moro et al. 2015a, 2016, 2018), as well as a series of more recent and efficient techniques such as MAAM—Miniature Array Analysis of Microtremors (Cho et al. 2006a, b, 2013), and HS—Holistic analysis of Surface waves (Dal Moro et al. 2015b, 2018, 2019; Dal Moro and Puzzilli 2017).
The methodologies based on the analysis of passive data exploit the microtremors induced by several natural and artificial sources. Atmospheric perturbations and sea and ocean waves are considered as the main responsible for the observed ambient microtremors but also human activities can give a significant contribution and care should be taken in the identification of possible artefacts produced by industrial sources (Gutenberg 1958; Szelwis 1982; Sutton and Barstow 1990; Peterson 1993; Cessaro 1994; Withers et al. 1996; Bradley et al. 1997; Friedrich et al. 1998; Tanimoto 1999; Kedar and Webb 2005; Tanimoto et al. 2006; Webb 2007; Yang and Ritzwoller 2008; Traer et al. 2012; Stutzmann et al. 2012; Ali et al. 2013; Dal Moro 2020b).
We may incidentally mention that, together with dispersion data, HVSR certainly proves to be a valuable tool for obtaining information about the VS values in the deepest layers (Arai and Tokimatsu 2005; Dal Moro 2010, 2015, 2019a; Pischiutta et al. 2017) but its significance in estimating site effects in seismic hazard studies is highly questionable (Seekins et al. 1996; Perron et al. 2018).
The main (but not unique) difference between the MASW and HS approaches is that in the first case (MASW) we deal with several single-component geophones at various distances (offsets) from the source and consider phase velocities, while the HS technique requires just one 3-component geophone used to define (and then jointly analyse) the group-velocity spectra of the three components (vertical Z, radial R and transversal T) as well as the Rayleigh-wave Particle Motion (RPM) frequency curve (Dal Moro and Puzzilli 2017; Dal Moro et al. 2018, 2019) (the same geophone is used also for recording the passive data necessary to define the HVSR).
While group (or phase) velocities are habitually inverted considering the interpretation of modal dispersion curves (of usually just one component) (Dziewonski 1971; Levshin et al. 1972; Ritzwoller and Levshin 1998, 2002; Cotte and Laske 2002; Fang et al. 2010; Kolínský et al. 2014; Lukešová et al. 2019; Qorbani et al. 2020), the HS methodology is characterized by three main facts (for further technical details see Dal Moro et al. 2019):
-
(1)
We can easily define and jointly invert the velocity spectra of all the three components (Z, R and T);
-
(2)
Group-velocity spectra are inverted not through the interpretation of the modal dispersion curves but according to the Full Velocity Spectrum (FVS) approach, which is based on the analysis of the whole frequency–velocity matrix and is, therefore, intrinsically multimodal (Dal Moro 2014, 2015, 2019b; Dal Moro et al. 2019);
-
(3)
We can also compute (and jointly invert) the Radial-to-Vertical Spectral Ratio (RVSR) and/or the Rayleigh-wave Particle Motion (RPM) curves (Dal Moro et al. 2017, 2019; Dal Moro 2019a).
About Rayleigh waves, we should consider that the phase or group velocity spectra of the Z and R components are in general different and this is why their joint inversion (possibly according to the FVS approach) is so important: they provide complementary information that are used to avoid all the ambiguities otherwise necessarily affecting the analyses based on just one component (Dal Moro 2014, 2020a; Dal Moro et al. 2015a, 2018).
The RPM frequency-offset curve considered in the HS methodology describes the actual retrograde–prograde particle motion along the R–Z plane as a function of the frequency (and offset, in case of multi-offset data) and is obtained as the correlation coefficient between the Z component and the Hilbert transform of the R component: + 1 means a perfectly retrograde motion, while -1 indicates a purely prograde motion (Dal Moro et al. 2017). In fact, it can be underlined that, despite the simplification often made, the particle motion induced by Rayleigh waves is usually far from being retrograde and is actually a complex combination that depends on the subsurface conditions. This means that, jointly with the group or phase velocity spectra (analysed according to the FVS approach), the RPM curves are extremely useful to further constrain the subsurface model and overcome ambiguities and non-uniqueness of the solution (Dal Moro 2019a, 2020a; Dal Moro et al. 2019). In fact, the analysis of one single observable cannot provide a unique solution, since the same dispersion curve can be explained by different subsurface models and complex mode combinations can produce highly complex data and ambiguous velocity-spectra interpretation (Knopoff and Panza 1977; Panza 1981; Dal Moro 2014, 2020a). The joint analysis of multi-component data is, therefore, the only way to obtain reliable VS models (Dal Moro 2014, 2020a; Yoshizawa 2014).
The VS profiles presented in this work are obtained through the joint inversion of several observables processed in the framework of the multi-objective approach (Dal Moro and Pipan 2007; Dal Moro and Puzzilli 2017; Dal Moro 2019b; Dal Moro et al. 2019). In particular, the VS profiles shown throughout the paper are the minimum-distance models which, in the multi-objective perspective, represent the best compromise/solution for the considered combination of observables (Dal Moro and Pipan 2007; Dal Moro 2008; Dal Moro et al. 2019). It can be underlined that the considered components (or observables) can react differently to various kinds of noise inevitably present in the data (also including possible lateral variations) (Rodriguez-Castellanos et al. 2006). Therefore, while the inversion of a single observable can provide a nearly perfect misfit, when we jointly consider several observables, the solution is a compromise which, in the applied joint-inversion scheme, is defined according to the Pareto optimality (Zitzler and Thiele 1999; Dal Moro and Pipan 2007; Dal Moro 2010). For further details and a wider discussion with a series of comparative examples, the reader can refer to Dal Moro et al. (2017; 2019) and Dal Moro and Keller (2017).
From the computational point of view (surface-wave modelling), we should also underline the importance of the correct analytical computation of the eigenvalues, eigenfunctions and related integral quantities, including the energy integrals providing an estimate of the contribution of the different modes (Panza 1985, 1993; Florsch et al. 1991).
The seismic exploration of the considered area took place over a period of more than 3 years and several data sets were acquired under different weather conditions and in different seasons, also to evaluate how different conditions could affect in particular the passive data. Different sensors (Guralp CMG-40 T 3-component 30 s sensors as well as single-component and 3-component geophones from the Geospace GS-ONE 4.5 Hz LF series) have been used providing always consistent results (a detailed comparative technical report on a series of technical aspects is planned for the near future). When computing the HVSR, it is important to underline that since we are dealing with a spectral ratio, what really matters is not the natural frequency of the sensors but the fact that the three sensors (one vertical and two orthogonal horizontal) have the same response curve. This is the only fact that ensures the correctness of the Horizontal-to-Vertical Spectral Ratio and this is the reason why the low-frequency (e.g., Guralp) and higher frequency (e.g., Geospace) 3-component geophones we used for the surveys provided the same HVSR curves down to about 0.25 Hz, which is far beyond the needs of the present work. For lower frequencies and/or for different (seismological) purposes (other than the computation of the HVSR) low-frequency sensors are necessary. We should also consider that since the response curve is known, data recorded by means of high-frequency sensors can be equalized so as to recover the actual amplitude of the frequencies below the geophone eigenfrequency (Bertram and Margrave 2011). Of course, since in the very-low frequency range the amplitude (i.e., the output voltage) becomes extremely small and the signal-to-noise ratio decreases.
Acquisition parameters for the HS data considered in the present study are reported in Table 1, while passive data were recorded with a sampling frequency of 100 Hz and a record length ranging from 15 to 30 min, depending on the site conditions and specific goals. In fact, site conditions and goals determine together the lowest frequency which is necessary to consider (SESAME 2004; Dal Moro 2014). For instance, if we intend to identify a bedrock covered by a 300 m soft-sediment sequence, we might need to analyse the HVSR down to say 0.2 Hz and this may require a record length of 30 min. On the other side, if we intend to identify the gravels lying below an 8 m silty sequence, the frequency to reach might be around 4–5 Hz and the necessary record length of just about 4 min. Of course the mentioned values need to be considered just as approximate figures, since the simplicity of our rules of thumb need to cope with several possible issues and the complexities of the considered phenomena.
For the present work, passive data were used not only to define the HVSR curves but, thanks to the comparative analysis of the amplitude spectra, also to obtain straightforward information about lateral variations along the array(s). Since HVSR is particularly relevant in the low-frequency range (Arai and Tokimatsu 2005; Dal Moro 2010), during the joint inversion with dispersion data, the frequency range of the considered HVSR is systematically kept lower compared to that of the velocity spectra.
While considering HS purely active data, a simple rule of thumb is that the maximum investigated depth is approximately 1/2 (to be conservative) or 2/3 of the fixed offset. On the other hand, if the joint inversion is performed considering also the HVSR curve, the investigated depth significantly increases. Details about these issues are discussed in Dal Moro et al. (2019).
The following sections present the analyses of the data collected in three areas (Fig. 2a). In the first (San Marco’s dune), seismic data were acquired at three different sites and, at the top of the dune (P1 in Fig. 2b), a penetrometer test was also performed. In the Beligna#1 area (Fig. 3), together with the seismic data, we also carried out an Electrical Resistivity Tomography (ERT).
The San Marco’s dune
Comprehensive seismic data were acquired at three sites (Fig. 2b): the top of the dune (P1), its base (P2) and inside the lagoon, during low tide (P3). For the sake of brevity, we here focus on just the P1 and P2 data, since the VS profile obtained for P3 was very similar to that obtained at P2 (these two sites are actually pretty close to each other).
The top of the dune (P1) was the first site explored and the anomalously high VS values that were observed represented the starting point for the whole work: the presence of stiff (high velocity) sediments already at a depth of about 2–3 m was in fact quite unexpected and motivated the wider seismic exploration presented in this paper.
Figure 4 presents the HS analysis for the P1 data: the group velocities of the Z and R components were inverted according to the Full Velocity Spectrum (FVS) approach (thus avoiding the spectra interpretation in terms of modal curves) together with the RPM frequency curve (Dal Moro 2014, 2019b; Dal Moro et al. 2015a, 2019; Dal Moro and Puzzilli 2017).
HS analysis for the San Marco area—P1 site (top of the dune—see map in Fig. 2b): a group-velocity spectra of the field (background colours) and synthetic (overlying black contour lines) for the vertical (Z) component of Rayleigh waves; b group-velocity spectra of the radial (R) component of Rayleigh waves; c field (dashed magenta line) and synthetic (blue line) RPM frequency curves; d VS profile representing the minimum-distance solution of the performed multi-objective inversion (Dal Moro et al. 2019)
At a depth of about 3 m, VS reaches the considerable value of about 500 m/s, which cannot be attributed to standard shallow (unconsolidated) sands. Standard (uncemented) sands are in fact characterized by VS values around 150 m/s (for very shallow layers) and up to about 300 m/s (at depths of 5–20 m) (Dal Moro 2014; Dal Moro et al. 2015b).
To support the information provided by the seismic data, we decided to perform a penetrometer test (Fig. 5). As can be clearly seen from the performed test, the number of blows (N) quickly increases with the depth and, at a depth of about 3.7 m, the test stops because of a very hard layer that prevented the cone penetration (refusal). Penetrometer data appear in excellent agreement with the obtained VS profile (Fig. 4d) and confirm the presence of a very stiff material at a depth of about 3.7 m from the surface.
San Marco dune, penetrometer data at P1 (see map in Fig. 2b). N is the number of blows to make the cone penetrate by 10 cm while using a 10 kg weight dropping from a 30 cm height, while NSPT are the values converted to the Standard Penetration Test according to the specifications of the manufacturer. The penetrometer test stopped (refusal) at a depth of about 3.7 m because of a very hard layer
In general terms, it should always be remembered that this sort of geotechnical tests necessarily refer to very local conditions, while surface wave analysis provides an average solution between the source and receiver(s).
The simple comparison of the field seismic traces collected at different sites can provide quick and straightforward information. Figure 6 presents the comparison between the active HS seismic traces (Z, R and T components) recorded at the top (P1) and at the foot (P2) of the dune (offset is 50 m for both the data sets and the source is the same—Table 1). In qualitative terms, the difference is extremely clear already from the simple comparison of the recorded traces: terrains at P2 are looser (softer) compared to those at P1. Seismic signals gathered at P2 are in fact slower (Fig. 6a–c) and, because of the higher attenuation, with a smaller amplitude (Fig. 6d, e). These straightforward comparison provides an instantaneous evidence that at P1 (top of the dune), the sediments are significantly stiffer (higher velocities) and with higher quality factors (high frequencies are preserved thanks to the lower attenuation). Furthermore (Fig. 6a), at P2, the P-wave first arrivals due to the shallow water table can be clearly identified (Dal Moro et al. 2015b).
San Marco area. Comparison of the HS (active) seismic traces collected at P1 and P2 (offset 50 m for both the sites): a Z component (first arrivals highlighted by the P box relate to the P-wave refraction due to the shallow water table at P2) [P1—black line; P2—yellow line]; b R component; c T component (Love waves); d amplitude spectra for the P1 data; e amplitude spectra for the P2 data. See text for comments
The result of the HS joint analysis for the P2 data is presented in Fig. 7. The obtained VS values are significantly different compared to those found at P1 and are typical of good—but not cemented—sedimentary materials (compacted sands or consolidated clay).
San Marco area—P2 site. Joint analysis of the HS seismic data: a field (background colours) and synthetic (overlying black contour lines) group-velocity spectra for the vertical (Z) component of Rayleigh waves; b group velocity spectra for the radial (R) component of Rayleigh waves; c field (dashed magenta line) and synthetic (blue line) RPM frequency curves (Rayleigh-wave particle motion appears largely prograde along most of the considered frequency range); d obtained VS profile (minimum-distance model obtained from the multi-objective data inversion)
These seismic evidences suggest that while the area around the dune (now flattened because of the reclamation works) shows VS values typical of standard unconsolidated sediments, the very high VS values identified at the top of the dune represent the properties of the stiff material that constitutes the "core" of the dune itself (compare also the amplitude spectra shown in Fig. 6d, e).
The Beligna#1 residual dune
The area is about 1.4 km W-NW of the San Marco’s dune (Figs. 1 and 2a) and the remains of the original dune are apparent from the DTM (Fig. 3) as well as from the presence of superficial compact sands. Figure 8 presents the overall area and shows the positions, where seismic and resistivity data were recorded. The photo in Fig. 9a shows what can be seen at the surface when soil conditions are such that sedimentological differences are apparent (this depends on the season, weather/moisture conditions and types of agricultural activities carried out). The ERT section was planned so to be perpendicular to the elongation of the residual dune (see evidences in Figs. 3 and 8) and two sets of seismic data (HS and HVSR) were collected along two lines parallel to the dune axis: one at the centre of the sandy residual dune (HS1 and HV1) and one at its western extreme (HS2 and HV2) (Fig. 8a).
Beligna#1 area: a detailed map [satellite image] with the location of the geophysical survey (see also Figs. 2a and 3) [the POV arrow indicates the Point of View of the photo shown in Fig. 9a]; b DTM map (vertical exaggeration 20x) that highlights the slightly elevated morphological feature. The two sharp red lines in the western part are the levees of the Natissa River clearly visible in the satellite image. The orange area represents the slightly elevated sandy area (residual paleo-dune)
Some surface evidences: a Beligna#1 area from the Point of View (POV) indicated in Fig. 8a: the presence of sandy sediments (light colours in the foreground) in an area otherwise dominated by silty soils (dark colours in the background) is apparent. The dotted line highlights the abrupt passage from these two different kinds of sediments and is particularly evident in winter time when no vegetation/crop masks the superficial sediments; b large boulders of cemented sand found nearby the P2 point (see Fig. 2b)
Since in this case, we were also interested in obtaining some information about the depth of the bedrock, together with the group velocity spectra of the Z and R components we considered the HVSR obtained from the analysis of the microtremors. HVSR was computed considering the recommendations reported in (SESAME 2004). According to such guidelines, the minimum frequency (in Hz) we can soundly consider is defined as 10/lw, being lw the window length in seconds. In other words, to obtain robust amplitude spectra, the window should contain at least 10 cycles. Therefore, if we intend to define the HVSR down to 0.25 Hz, the minimum length of the window to consider is 40 s (slighlty-larger lw values can sometimes provide better results). For the present sudy, the amplitude spectra used to define the HVSR were smoothed by 15% by means of a triangular window.
The results of the data analysis are presented in Figs. 10, 11, 12, 13, 14, and 15 and provide a consistent image of the subsurface conditions. ERT and seismic data identify a central area characterized by stiff (VS of about 450–500 m/s) and high-resistivity (over 500 Ωm) sandy materials overlying slightly softer (VS of about 250 m/s) and low-resistivity (less than 1 Ωm) layers.
Beligna#1 area—ERT survey: resistivity section perpendicular to the dune elongation (dipole–dipole configuration, 3200 measurements). Also shown the positions of the sites, where HV1-North and HV2-North were recorded (see Fig. 8a). See text for comments
Beligna#1. Comparison of the HS (active) seismic traces (Z, R and T components) for the central (HS1) and western (HS2) sites (see map in Fig. 8a) [offset is 35 m for both the data sets and the source is the same—see Table 1]. Seismic traces show major differences between the two sites [HS1—black line; HS2—yellow line]: compared to HS2, HS1 signals are faster and have a larger amplitude (i.e., undergo less attenuation). These two facts provide an instantaneous evidence that, compared to the western area [HS2], in the central area (the residual sandy paleo-dune) the surficial sediments are significantly stiffer. To improve data readability, the vertical scales of the three components are different. See also traces and amplitude spectra shown in Fig. 12
Beligna#1 HS (active) data: comparing traces and amplitude spectra for the central (HS1) and western (HS2) sites (same source, stack and offset—see map in Fig. 8a and trace comparison in Fig. 11): a seismic traces and amplitude spectra (arbitrary unit) for HS1; b seismic traces and amplitude spectra for HS2 [vertical scale adapted to meet the actual data amplitudes for each site]; c comparison of the amplitude spectra of the R and T components while using the same vertical scale so to allow a clearer comparison of the data amplitudes for the central (HS1) and western (HS2) data. Due to the larger attenuation, the amplitude of the HS2 traces is considerably lower and the peak value migrates toward lower frequencies (high frequencies suffer from higher attenuation)
Beligna#1—central area (HS1). Joint analysis of the active HS and passive HVSR data: a group velocity spectra of the Z component; b group velocity spectra of the R component; c field (green lines—shown the mean curve and the standard deviation) and synthetic (blue line) HVSR curves; d obtained VS profile (down to 400 m); e close-up of the shallow part (first 15 m) of the obtained VS profile. The HVSR peak at about 0.43 Hz is related to the deep bedrock
Beligna#1—western area (HV2): directivity of the Horizontal-to-Vertical Spectral Ratio obtained from microtremor data (see also the average curve shown in Fig. 15c): the centre of the circle represents 0.3 Hz and the external circumference 19 Hz (for the joint analysis with the dispersion data we considered only the lower frequencies—see text for further comments)
Beligna#1—western area (HS2): same data as for Fig. 13 (HS1). The HVSR peak at about 2.5 Hz (not present at site#1) is due to the presence of superficial very soft (peat-like) sediments
The comparative analysis of the seismic data reported in Figs. 11, 12, 13, 14, and 15 makes clear that very soft sediments dominate the western part, where the superficial stiff sand-dominated sediments of the residual dune wedge out. In the western area the sedimentary sequence is characterized by VS values around 100 m/s in the first 7 m and the resistivity is about 1 Ωm (typical of soft and porous saturated sediments). The presence of such thick (7 m) cover of very soft sediments over harder layers (VS values increase to 200 m/s at 7 m and to approximately 500 m/s at about 15 m of depth) is responsible for the very distinctive HVSR peak at about 2.5 Hz (Figs. 14 and 15c), which is not present in the central part of the residual dune, where harder sandy sediments characterize the surface layers (see HVSR in Fig. 13c). It can be also pointed out the mild directivity of the 2.5 Hz peak (Fig. 14), which seems possibly related to the elongation of the residual dune itself. In fact, if we compare the 2.5 Hz peak and the map in Fig. 8, we can see an apparent correlation: the 2.5 Hz HVSR peak reaches a maximum value along the N30E–S30W direction, which seems closely related to the elongation of the residual dune.
On the other hand, the very low frequency HVSR peak at about 0.43 Hz clearly visible in both the data sets (Figs. 13c and 15c) can be attributed to the deep bedrock—see the borehole seismics performed in the town of Grado, about 8 km southeast of the Beligna area (Della Vedova et al. 2015).
In the central/eastern area, geophysical data unambiguously define a subsurface feature characterized by shallow (partly cemented) sandy sediments down to a maximum depth of about 7–8 m (compare ERT data in Fig. 10 and seismic data in Fig. 13). Westward, this layer gets thinner and gradually fades into very soft sediments (compare the VS profiles in Figs. 13e and 15e). Superficially, such a subsurface configuration is reflected by a slightly elevated landform (see DTM in Figs. 3 and 8b) and by the partly cemented sandy materials that can be collected at the surface in the central part of the residual dune (Fig. 9a).
To fully comprehend the paradigm to adopt while considering a joint inversion process, data shown in Fig. 15 deserve a methodological note. If we focus on the vertical component (Fig. 15a) and compare the group-velocity spectrum of the field data (background colours) and the synthetic one referred to the obtained VS profile (black contour lines), we can see that the overall match is good but not perfect. This should not surprise, since a joint inversion is a "compomise process" (the solution we obtain is the best in terms of Pareto optimality). An illustrative case study is presented for instance in Dal Moro and Puzzilli (2017), where the comparison of the solutions obtained considering single observables or several possible observable combinations is discussed. Various kinds of noise inevitably present in the data can influence in different terms the different components (see, e.g., Rodriguez-Castellanos et al., 2006). Furthermore, while HVSR is sensitive to very local conditions, dispersion data are representative of the average subsurface conditions and this can create some inconsistency in case we are working in complex area. This means that, while performing a joint inversion, usually we cannot obtain perfect (extremely small) misfits for each single observable but the obtained solution is certainly a robust (compromise) subsurface model free from major ambiguities inevitably affecting the solution in case we consider a single observable (Dal Moro and Puzzilli 2017; Dal Moro 2020a).
Because of the limited offset used for the HS active data (see Table 1 and obtained velocity spectra), the deep part of the Vs profiles shown in Figs. 13 and 15 is clearly based just on the HVSR curves and hence represent just a coarse and average solution (with limited resolution) which is geologically reasonable but which should be considered just in general terms (compare with Della Vedova et al. 2015 as well as with the geological models in Fontana et al. 2008 and Arnaud-Fassetta et al., 2003).
To obtain further seismic evidences of the subsurface 2D structure and testing the potentialities of simple procedures based on the spectral analysis of multi-component and multi-offset passive seismic data, we recorded an additional 3-component data set along a 55 m line (12 points, 5 m spaced) along the ERT line (for technical reasons just slightly shorter). The goal was the computation of the single-component amplitude spectra (for all the three components) and the HVSR 2D section to compare with the ERT line.
The HVSR 2D section reported in Fig. 16 highlights the significant difference between the central part of the line (i.e., the residual sandy dune) and the western area, where the shallow soft-sediment cover creates a significant VS contrast responsible for the large 2.5 Hz HVSR peak that indicates the western edge of the residual sandy dune. Such a seismic evidence is in fact clearly associated to the subsurface morphology of the residual dune: westward, the cemented sandy materials of the sandy dune abruptly fade away and superficial peat-like sediments with very low VS values (60–100 m/s) create a remarkable microtremor amplification for all the three components (Fig. 17) and a large variation of the HVSR (compare data shown in Figs. 13c, 15c and 17).
Beligna#1: 3-component passive seismic array along the same line of the ERT section shown in Fig. 10 (the seismic line is a bit shorter). In general terms, the overall consistency of the 2D HVSR section with the ERT data is obvious. At the beginning of the line (western part), a thick soft-sediment cover creates a large HVSR peak around 2.5 Hz which is related to the low resistivity values obtained from the ERT (Fig. 10). See also the HS analysis in Fig. 15 and the single-component amplitude spectra in Fig. 17
Beligna#1—3-component (passive) seismic data: mean amplitude spectra for the Z [vertical] (a), EW [Radial] (b) and NS [Transversal] (c) components. The magenta points indicate the location of the 12 traces along the 55 m array. Compare with data presented in Figs. 13, 15, 16 and 18. See text for further comments
This is apparent even by the simple analysis of the mean amplitude spectra of the single components (vertical, NS and EW) shown in Fig. 17 and obtained by averaging the spectra obtained by dividing the time series in a series 14 s windows (after having removed a few large-amplitude transient events related mainly to small boats along the nearby Natissa river—Fig. 8). It must be clearly pointed out that the larger amplitude in the western part is not related to any local microtremor source (we are in a remote agricultural area, where no mechanical facilities are present) but to the local stratigraphic conditions that amplify the signal in that specific frequency range (compare with data and analyses shown in Figs. 13 and 15).
Figure 18 reports the array data just about the NS component, which is actually the T component, i.e., the component perpendicular to the array (Dal Moro 2014). Plot (a) reports just a small (14 s) window: the larger amplitude of the microtremors for the first channels (traces) is apparent and is mirrored in the amplitude spectra reported in the (b) plot (the color indicates the distance from the first point of the array). The (c) plot reports the standard deviations for each trace and represent a simple and straightforward way to assess the mean amplitude trace by trace. From a computational point of view, it can be underlined that, since the transient events were removed, the value of the standard deviation computed considering the whole trace is essentially the same as the value obtained from averaging the standard deviations computed for each window (in case we divide the trace into a series of windows). The larger amplitudes of the first traces is pretty clear and the comparison of these different ways to assess the trace amplitudes can be considered for the design of simple software tools to be used during the data acquisition for a quick data check during the field operations, when sophisticate analyses cannot be easily handled. When large differences in the trace amplitude cannot be attributed to local microtremor sources, the reason is necessarily to be ascribed to non-homogenous subsurface conditions along the array. In that case, we can decide to modify our initial plans about data acquisition or, in case we are analyzing surface-wave dispersion, extract subsets of homogenous traces. For instance, in the present case, we could remove the first 3/4 traces and analyze the dispersion for the rest of the array which, according to the amplitude spectra shown in Fig. 17 (as well as by the HVSR curves in Fig. 16) appear reasonably homogenous.
Beligna#1—multi-offset passive data (T component): a small part of the recorded traces (14 s window); b normalized mean amplitude spectra (15% spectral smoothing) (color changes from green to blue as we move along the array); c standard deviations computed for all the twelve traces. The larger amplitude of the first traces is apparent from all the three graphs (three different ways to assess the mean microtremor amplitude)
In fact, the dispersion image (velocity spectrum) that we would obtain from the analysis of the entire 12-channl data set would be extremely complex and possibly unintelligible and could not be reduced to a 1D analysis (traces refer to materials with very different properties).
This is incidentally the reason why HS data presented in Figs. 13 and 15 were recorded with a source–receiver array following the dune elongation (Fig. 8), which is the direction, where minimal lateral variations are expected (as also confirmed by the computed HVSR curves).
The Beligna#2 area: a further residual dune
The last site is about 500 m east from the previous one (Fig. 2a) and differs from it for two main facts: (1) the dune elongation is slightly different (Fig. 19c); (2) the topography is totally flat (see DTM in Fig. 2a). While the similar but not identical direction is surely related to the formation process, the flat topography is due to the heavier agricultural activity carried out at this site.
Aerial view of the Beligna#2 residual dune. The lighter colours are due to shallow sandy materials while darker colours to finer (silty) alluvia sediments (see the similar conditions of the Beligna#1 area—Fig. 9a). Due to the intensive agricultural activity, DTM data does not show any evidence of such a paleo dune (Fig. 2a)
Figure 19 reports two aerial photos and a satellite view with indicated the 168 m line along which seismic data were collected. The two aerial photos show the presence of shallow lighter sandy materials surrounded by the darker silty sediments that characterize the overall area. As a matter of fact, such a major sedimentary feature (exceptionally apparent in the drone photos shown in Fig. 19a, b) is often not visible due to unfavourable soil conditions that tend to create a seemingly homogenous cover with little evidence of the different shallow sediments (the actual visibility depends on the soil humidity and on the effects of the agricultural activities carried out throughout the year).
Along the 168 m line shown in Fig. 19c we collected a series of passive data and computed the HVSR curves shown in Fig. 20, where the presence of a remarkable HVSR peak at about 5.7 Hz (inline position 100–120 m) is apparent as well as the 0.43 Hz peak already identified during the exploration of Beligna#1 (Figs. 13c and 15c) and related to the deep bedrock.
2D HVSR section for the Beligna#2 residual dune: a photo of the area with highlighted the considered line (see also Fig. 19c); b HVSR curves with indicated the two characterizing peaks related to the deep bedrock and the presence of a superficial peat channel (see text); c 2D HVSR section along the investigated line according to a 3D perspective (to highlight the shallow structure, the HVSR is shown only for frequencies higher than 2 Hz)
As for the Beligna#1 area, Fig. 21 reports the amplitude spectra trace standard deviations for the T-component data (i.e., the axis perpendicular to the array line). We just focus on the transition area, where the shallow sandy sediments of the residual paleo-dune disappear and the large 5.7 Hz HVSR peak is observed (inline position around 100 m in Fig. 20). The data (spectral ratios) presented in Fig. 21b are obtained by dividing the amplitude spectra computed at each point by the amplitude spectrum of the first considered channel so as to obtain a straightforward image of the microtremor amplitude as a function of the frequency and inline position.
Close up of the T-component passive data in the transition zone, where the stiff sandy sediments of the residual dune give way to softer sediments (inline positions 86–108 m in Fig. 20c): a normalized amplitude spectra (15% spectral smoothing); b spectral ratios with respect to the first channel; c standard deviations of the original (unfiltered) traces; d standard deviations of the traces filtered with a 5.7 Hz Gaussian filter. See text for comments
Consistently with the HVSR curves, the comparative analysis of even just the T-component amplitude spectra is useful to highlight a significant and abrupt microtremor amplitude increment in the indicated position. The amplitude increase of the horizontal components (both T and R) is a well-known consequence of a significant VS increase in the subsurface which is also responsible for the observed HVSR peak—see the similar evidences observed for Beligna#1 (Figs. 16, 17 and 18). Such an increase in the microtremor amplitude along the T component is apparent both in the frequency domain (Fig. 21a, b) as well as in the time domain (from the computation of the standard deviations of the seismic traces—Fig. 21c, d).
It can be pointed out that while computing the standard deviations of the original field data (Fig. 21c), we compare the overall amplitude of the recorded field traces. On the other side, if we compute the standard deviations after the application of a narrow Gaussian filter centred on a specific frequency, we can obtain an estimate of the amplitude differences related to that specific frequency. Figure 21d reports the standard deviations of the traces after a 5.7 Hz Gaussian filter is applied (at that frequency we observe the HVSR peak and the T-component amplitude spectra reach their maximum values—compare Figs. 20 and 21). While the standard deviations of the unfiltered seismic traces differ for about 340%, when we considered the 5.7 Hz Gaussian-filtered traces such a difference increases to about 850% (this should not surprise, since, as the spectral ratios reported in Fig. 21b clearly show, most of the difference is related to what happens around 5.7 Hz).
Data shown in Fig. 21 provide the evidence that lateral variations can be highlighted by the simple comparison of the amplitude spectra of single-component passive data (for this purpose horizontal components are often to be preferred). Needless to say that, analogously to the previous case (Figs. 16, 17 and 18 and related text), the larger amplitude spectra cannot be attributed to any local microtremor source, since no mechanical or industrial facility is present (we are in the middle of a vast agricultural area—see Figs. 19 and 20a).
Identifying the presence of significant lateral variations is important, because in case, we would analyse the dispersion considering the entire data set, we would inevitably obtain confused and meaningless velocity spectra. The analysis and comparison of the amplitude spectra or standard deviations (in case we are dealing with single-component data) or the HVSR curves (in case of 3-component data) allows to identify and extract subsets of homogenous data. If we consider the data in Fig. 20c and neglect unnecessary details about the southernmost part of the line (inline positions 130–168 m), we can divide the area (i.e., the traces/data) into three main (homogeneous) subsections: the central part (paleo sandy dune—inline positions 50–100 m) and two lateral zones with different characteristics. Dispersion should be then computed separately considering the traces of the three homogenous identified subsets.
For instance, to understand the cause of the large 5.7 Hz HVSR peak (Fig. 20c), we extracted the pertinent subset of T-component traces (inline positions 100–130 m) so to compute the Love-wave dispersion (compared to Rayleigh waves, Love waves usually provide clearer information—e.g., Safani et al. (2005), Dal Moro (2014) and Dal Moro et al. (2015a)). Obtained dispersion curve (Fig. 22a) was then jointly inverted with the HVSR (Arai and Tokimatsu 2005; Dal Moro 2010) so to obtain the VS profile shown in Fig. 22c. The presence of shallow very-soft sediments (peats) in the first couple of meters is responsible for the large HVSR peak and the low shear- and Love-wave velocities around 50–90 m/s—peats are notoriously characterized by distinctive low VS values (Dal Moro, 2014; Lorenzo et al., 2014; Zainorabidin and Said, 2015).
Inline position 110 m (see Fig. 20c): joint analysis of the HVSR and Love-wave dispersion curves (phase velocities). Shown the observed (blue) and inverted (magenta) curves for the Love-wave dispersion curve (a) and the HVSR (b). The VS model (c) represents the minimum-distance solution (i.e., the best model according to the adopted multi-objective inversion scheme) and clearly indicates the presence of a shallow 2 m-thick peat cover responsible for the low Love-wave velocities at frequencies higher than about 7 Hz and the large HVSR peak at about 5.7 Hz
Two main features can be pointed out:
-
(1)
similar to the previous dune (Beligna#1), the sandy dune is bordered by a peat channel along the southern side of the paleo dune;
-
(2)
at the northern edge of the residual sandy dune the shallow material (likely stiffer) create a minor (but still clear) feature [see HVSR around the 4–45 m inline positions in Fig. 20c].
A few geological considerations
Although the present paper intends to represent an illustrative example of the information that can be obtained from the application of a series of efficient and unconventional methodologies for the analysis of surface waves, a few geological considerations can also be put forward.
Coastal dunes are Aeolian landforms that develop in coastal zones, where the general conditions guarantee an ample supply of loose, sand-sized sediments which must be available to be transported inland by the wind (Martínez and Psuty 2004). Fundamentally, dune morphology depends on the wind directionality and on the amount of sand available for transport (Verstappen 1968; Tsoar 1983; Wasson and Hyde 1983; Gallant 1997; Radebaugh et al. 2015), while the evolution is governed by three main elements: sea, wind and vegetation.
A series of rock samples collected during a surface reconnaissance (a large block is shown in Fig. 9b) reveal to be medium-grained calcarenite mainly composed of rounded dolomite and limestone intraclasts. They appear strongly bioturbated (see the tubular aspect of the block in Fig. 9b), and their stiffness is due to recrystallization of calcitic micrite to sparitic cement (Adamovič and Mikuláš—personal communication).
Such relict samples can be found scattered all over the area and represent the remains of the dunes smoothed out during the reclamation works that strongly modified the landscape: observed high VS values along the residual dunes are due to the presence of this kind of materials in the subsurface.
The elongation and shape of the dunes can provide some hints. The local dominant wind is called Bora (a strong catabathic wind influenced by the orography of the Slovenian and Croatian coasts) and blows from N60E (Signell et al. 2010; Bellafiore et al. 2012) (Fig. 23). This direction is roughly parallel to the elongation of the local paleo-dunes. Although the actual conditions and processes cannot be interpreted in universal terms, it is generally believed that when the wind dominates with respect to the amount of available sand, the formation of longitudinal dunes (with windward slope gentler than the leeward side) is favoured (Verstappen 1968; Tsoar 1983; Wasson and Hyde 1983; Gallant 1997; Radebaugh et al. 2015).
Beligna and San Marco dunes together with the identified peat channels. Also shown the wind rose diagram that highlights the dominant wind (Bora) (Bellafiore et al. 2012) and the Point of View (POV) of the aerial photo in Fig. 19b (the yellow lines show the approximate field of view). The presence and direction of the delineated peat channels is confirmed by a series of further seismic data recorded all over the area and not reported for the sake of brevity
In the considered area, sediment deposition seems, therefore, governed by the combination of fluvial transport, distribution of lagoon channels and wind action. Consequently, the dunes should not be related to an old coastline, as originally proposed by some speculative studies (Marocco 1991; Lenardon and Marocco 1994), but could be related to the complex dynamics determined by the interactions of three main factors:
-
(a)
The Isonzo river (Fig. 1) bringing sand-sized material to the area;
-
(b)
The strong wind blowing from about N60E (possibly supporting the formation of longitudinal dunes);
-
(c)
The complex fresh-to-brackish lagoonal water system that developed within the dune field with several inner channels that were destroyed together with the dunes during the reclamation works and that were identified through the presented seismic data (peat channels).
Conclusions
In the present paper we described the results of the geophysical exploration of the eastern part of the Grado-Marano perilagoon area (NE Italy), where a vast paleodune system is present. The work was accomplished with a twofold goal:
-
(1)
Testing a series of non-conventional but efficient methodologies for the analysis of surface waves in areas characterized by significant lateral variations;
-
(2)
Obtaining information about the subsurface conditions in a complex and largely unexplored area so as to provide geologists with a bulk of information needed to properly reconstruct the paleoenvironment that led to the formation of the peculiar geomorphological features that characterize the area but that were altered by the reclamation works that strongly modified the whole area.
Our attention focused on three sites that were explored mainly by means of the surface waves extracted from both active and passive seismic data. A series of standard and unconventional methodologies were applied to verify the presence of lateral variations and depict the local VS vertical profiles.
The identification and characterization of the residual Beligna dunes (with a series of related peat channels) was possible through the integration of several evidences:
-
(1)
Detailed DEM model (this was possible just for the Beligna#1 dune, since the Beligna#2 area was completely flattened out due to intense agricultural activities);
-
(2)
Presence of superficial sand-dominated sediments (locally cemented) in an area otherwise dominated by silty soils;
-
(3)
Geophysical exploration revealing surficial stiff sandy sediments over the residual dunes and peat channels alongside them.
In case reclamation works and agricultural activities have completely flattened the original topography, DEM does not provide any clear information about the former presence of peculiar geomorphological features and the geophysical exploration is the only way to characterize large areas and reconstruct the subsurface conditions.
The paper shows how surface wave analysis can be considered an efficient tool not only for the assessment of the issues related to the seismic–hazard assessment but for any geological or geotechnical problem that requires the knowledge of the subsurface conditions.
It can be emphasized that, although we explored a low-energy depositional environment (an alluvial plain around a lagoon), strong lateral variations occur. For instance, in the Beligna area, the VS values dramatically change in just a few meters (compare the data and VS profiles shown in Figs. 13 and 15 as well as in Figs. 20 and 21) and would reflect in major differences in terms of site effects (seismic–hazard studies) as well as for the ordinary geotechnical issues (differential settlements etc.).
The analysis of the amplitude spectra and/or standard deviations of multi-offset passive data reveals extremely important to highlight possible lateral variations and should be done prior to the computation of the velocity spectra (dispersion). In fact, data collected by an array crossing different terrains (see data recorded at both the Beligna sites and shown in Figs. 16, 17, 18, 20, and 21) cannot be used to compute dispersion since refer to very different terrains. On the other side, we can extract subsets of homogenous traces (with similar amplitude spectra) to be used so to obtain meaningful velocity spectra referred to the two (or more) distinctive terrains along the seismic array.
Presented data also strongly discourage any attempt to classify the soil on the basis of large-scale geological or sedimentological maps, being necessary the detailed and precise reconstruction of the actual local VS profile.
Three main methodological facts can be, therefore, summarized:
-
(1)
HVSR can provide valuable information about possible lateral variations (e.g., Figs. 16 and 20);
-
(2)
Comparable information can be obtained by the simpler assessment of the amplitude spectra (or trace standard deviations) of passive single-component array data (e.g., Figs. 17, 18 and 21);
-
(3)
Multi-component active data recorded by means of a single 3-component geophone provide a wealth of information (group-velocity spectra for the three components and RPM frequency curve) to exploit also jointly with the HVSR with two obvious advantages: (a) simple and straightforward field procedures; (b) the possibility to jointly analyse several observables capable of constraining a robust VS subsurface model free from the ambiguities that characterize the standard MASW/SPAC/ESAC/MAAM methodologies based on the analysis of just one component.
Availability of data and materials
None.
Abbreviations
- DTM:
-
Digital terrain model
- ERT:
-
Electrical resistivity tomography
- MASW:
-
Multi-channel Analysis of Surface Waves
- HS:
-
Holistic analysis of surface waves
- HVSR:
-
Horizontal-to-Vertical Spectral Ratio
References
Aki K (1957) Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull Earthq Res Inst 35:415–456
Ali MY, Barkat B, Berteussen KA, Small J (2013) A low-frequency passive seismic array experiment over an onshore oil field in Abu Dhabi, United Arab EmiratesPassive seismic experiment in the UAE. Geophysics 78:B159–B176
Amorosi A, Fontana A, Antonioli F et al (2008) Post-LGM sedimentation and Holocene shoreline evolution in the NW Adriatic coastal area. GeoActa 7:41–67
Antonioli F, Ferranti L, Fontana A et al (2009) Holocene relative sea-level changes and vertical movements along the Italian and Istrian coastlines. Quat Int 206:102–133
Arai H, Tokimatsu K (2004) S-wave velocity profiling by inversion of microtremor H/V spectrum. Bull Seismol Soc Am 94:53–63
Arai H, Tokimatsu K (2005) S-wave velocity profiling by joint inversion of microtremor dispersion curve and horizontal-to-vertical (H/V) spectrum. Bull Seismol Soc Am 95:1766–1778
Arnaud-Fassetta G, Carre M-B, Marocco R et al (2003) The site of Aquileia (northeastern Italy): example of fluvial geoarchaeology in a Mediterranean deltaic plain/Le site d’Aquilée (Italie nord-orientale): exemple de géoarchéologie fluviale dans une plaine deltaïque méditerranéenne. Géomorphologie Reli Process Environ 9:227–245
Asten MW (2006) On bias and noise in passive seismic data from finite circular array data processed using SPAC methods. Geophysics 71:V153–V162
Bellafiore D, Bucchignani E, Gualdi S et al (2012) Assessment of meteorological climate models as inputs for coastal studies. Ocean Dyn 62:555–568
Bertram MB, Margrave GF (2011) Recovery of low frequency data from 10Hz geophones. In: expanded abstracts, recovery-CSPG CSEG CWLS convention, Calgary—Alberta, Canada
Bradley CR, Stephen RA, Dorman LM, Orcutt JA (1997) Very low frequency (0.2–10.0 Hz) seismoacoustic noise below the seafloor. J Geophys Res Solid Earth 102:11703–11718
Brambati A (1972) Clay mineral investigation in the Marano and Grado lagoons (northern Adriatic sea). Boll Soc Geol It 91:315–323
Cessaro RK (1994) Sources of primary and secondary microseisms. Bull Seismol Soc Am 84:142–148
Cho I, Tada T, Shinozaki Y (2006b) Centerless circular array method: Inferring phase velocities of Rayleigh waves in broad wavelength ranges using microtremor records. J Geophys Res Solid Earth 111:B09315. https://doi.org/10.1029/2005JB004235
Cho I, Senna S, Fujiwara H (2013) Miniature array analysis of microtremors. Geophysics 78:KS13–KS23
Cho I, Tada T, Shinozaki Y, et al (2006a) New methods of microtremor exploration: the centerless circular array method and the two-radius method. In: Third international symposium on the effects of surface geology on seismic motion. Laboratoire Central des Ponts et Chaussées Paris, pp 335–344
Cotte N, Laske G (2002) Testing group velocity maps for Eurasia. Geophys J Int 150:639–650
Dal Moro G (2008) Vs and Vp vertical profiling via joint inversion of Rayleigh waves and refraction travel times by means of bi-objective evolutionary algorithm. J Appl Geophys 66:15–24
Dal Moro G (2010) Insights on surface wave dispersion and HVSR: joint analysis via Pareto optimality. J Appl Geophys 72:129–140. https://doi.org/10.1016/j.jappgeo.2010.08.004
Dal Moro G (2014) Surface wave analysis for near surface applications. Elsevier
Dal Moro G (2015) Joint analysis of Rayleigh-wave dispersion and HVSR of lunar seismic data from the Apollo 14 and 16 sites. Icarus 254:338–349. https://doi.org/10.1016/J.ICARUS.2015.03.017
Dal Moro G (2019a) Effective active and passive seismics for the characterization of urban and remote areas: four channels for seven objective functions. Pure Appl Geophys 176:1445–1465
Dal Moro G (2019b) Surface wave analysis: improving the accuracy of the shear-wave velocity profile through the efficient joint acquisition and Full Velocity Spectrum (FVS) analysis of Rayleigh and Love waves. Explor Geophys 50:408–419
Dal Moro G (2020a) Efficient joint analysis of surface waves and introduction to vibration analysis: beyond the clichés. Springer Nature
Dal Moro G (2020b) On the identification of industrial components in the Horizontal-to-Vertical Spectral Ratio (HVSR) from microtremors. Pure Appl Geophys 177:3831–3849
Dal Moro G, Pipan M (2007) Joint inversion of surface wave dispersion curves and reflection travel times via multi-objective evolutionary algorithms. J Appl Geophys 61:56–81
Dal Moro G, Puzzilli LM (2017) Single-and multi-component inversion of Rayleigh waves acquired by a single 3-component geophone: an illustrative case study. Acta Geodyn Geomater 14:431–444. https://doi.org/10.13168/AGG.2017.0024
Dal Moro G, Moura RMM, Moustafa SSR (2015a) Multi-component joint analysis of surface waves. J Appl Geophys 119:128–138
Dal Moro G, Ponta R, Mauro R (2015b) Unconventional optimized surface wave acquisition and analysis: comparative tests in a perilagoon area. J Appl Geophys 114:158–167
Dal Moro G, Keller L, Al-Arifi NS, Moustafa SSR (2016) Shear-wave velocity profiling according to three alternative approaches: a comparative case study. J Appl Geophys 134:112–124. https://doi.org/10.1016/J.JAPPGEO.2016.08.011
Dal Moro G, Al-Arifi NS, Moustafa SSR (2017) Analysis of Rayleigh-wave particle motion from active seismics. Bull Seismol Soc Am 107:51–62
Dal Moro G, Al-Arifi N, Moustafa SR (2019) On the efficient acquisition and holistic analysis of Rayleigh waves: technical aspects and two comparative case studies. Soil Dyn Earthq Eng 125:105742
Dal Moro G, Keller L (2017) RPM Analysis and advanced joint processing of a SED (Swiss Seismological Service) dataset. In: Proceedings of the GNGTS [Gruppo Nazionale di Geofisica della Terra Solida] congress (Italy—Trieste, November 14–16 2017). pp 693–696
Dal Moro G, Moustafa SSR, Al-Arifi NS (2018) Improved holistic analysis of Rayleigh waves for single-and multi-offset data: joint inversion of Rayleigh-wave particle motion and vertical-and radial-component velocity spectra. Pure Appl Geophys 175:67–88
Della Vedova B, Petronio L, Poletto F, et al (2015) The geothermal district heating system on the Grado Island (North-eastern Adriatic Sea). In: World GEOTHERMAL CONGress. International Geothermal Association, pp 1–12
Dziewonski A (1971) A technique for the analysis of transient seismic signals. Bull Seism Soc Am 61:343–356
Fang L, Wu J, Ding Z, Panza GF (2010) High resolution Rayleigh wave group velocity tomography in North China from ambient seismic noise. Geophys J Int 181:1171–1182
Florsch N, Fäh D, Suhadolc P, Panza GF (1991) Complete synthetic seismograms for high-frequency multimodeSH-waves. Pure Appl Geophys 136:529–560
Fontana A, Mozzi P, Bondesan A (2008) Alluvial megafans in the Venetian-Friulian Plain (north-eastern Italy): evidence of sedimentary and erosive phases during Late Pleistocene and Holocene. Quat Int 189:71–90
Friedrich A, Krüger F, Klinge K (1998) Ocean-generated microseismic noise located with the Gräfenberg array. J Seismol 2:47–64
Gallant RA (1997) Sand on the move: THE story of dunes. Franklin Watts
Gaždová R, Kolínský P, Vilhelm J, Valenta J (2015) Combining surface waves and common methods for shallow geophysical survey. Near Surf Geophys 13:19–32
Gutenberg B (1958) Microseisms. In: Advances in geophysics. Elsevier, pp 53–92
Hayashi K, Suzuki H (2004) CMP cross-correlation analysis of multi-channel surface-wave data. Explor Geophys 35:7–13
Ikeda T, Matsuoka T, Tsuji T, Hayashi K (2012) Multimode inversion with amplitude response of surface waves in the spatial autocorrelation method. Geophys J Int 190:541–552
Kedar S, Webb FH (2005) The ocean’s seismic hum. Science (80-) 307:682–683
Knopoff L, Panza GP (1977) Resolution oi upper mantle structure using higher modes of Rayleigh waves. Ann Geophys 30:491–505
Kolínský P, Valenta J, Málek J (2014) Velocity model of the Hronov-Poříčí Fault Zone from Rayleigh wave dispersion. J Seismol 18:617–635. https://doi.org/10.1007/S10950-014-9433-4
Kudo K, Sawada Y, Horike M (2004) Current studies in Japan on H/V and phase velocity dispersion of microtremors for site characterization. In: Proc. 13WCEE (World Conference on Earthquake Engineering)—Vancouver, B.C., Canada, Paper No. 1144
Lenardon G, Marocco R (1994) Le dune di Belvedere-San Marco. Una antica linea di riva? 2) Considerazioni sedimentologiche. Gortania Atti Mus Friul Stor Nat 16:5–24
Levshin AL, Pisarenko VF, Pogrebinsky GA (1972) On a frequency-time analysis of oscillations. In: Annales de geophysique. Centre National de la Recherche Scientifique, pp 211–218
Loke MH, Barker RD (1996) Rapid least-squares inversion of apparent resistivity pseudosections by a quasi-Newton method1. Geophys Prospect 44:131–152
Lorenzo JM, Hicks J, Vera EE (2014) Integrated seismic and cone penetration test observations at a distressed earthen levee: Marrero, Louisiana, USA. Eng Geol 168:59–68
Lukešová R, Fojtikova L, Málek J, Kolínský P (2019) Seismic waves velocities inferred from the surface waves dispersion in the Male Karpaty Mountains, Slovakia. Acta Geodyn Geromaterialia 16:451–465
Marocco R (1991) Le dune di Belvedere-San Marco. Una antica linea di riva? 1) Considerazioni geomorfologiche. Gortania Atti Mus Friul Stor Nat 13:57–76
Martínez ML, Psuty NP (2004) Coastal dunes. Springer
Melis R, Covelli S (2013) Distribution and morphological abnormalities of recent foraminifera in the Marano and Grado Lagoon (North Adriatic Sea, Italy). Mediterr Mar Sci 14:432–450
Nguyen XN, Dahm T, Grevemeyer I (2009) Inversion of Scholte wave dispersion and waveform modeling for shallow structure of the Ninetyeast Ridge. J Seismol 13:543–559
O’Connell DRH, Turner JP (2011) Interferometric multichannel analysis of surface waves (IMASW). Bull Seismol Soc Am 101:2122–2141
O’Neill A, Safani J, Matsuoka T (2006) Rapid shear wave velocity imaging with seismic landstreamers and surface wave inversion. Explor Geophys 37:292–306
Ohori M, Nobata A, Wakamatsu K (2002) A comparison of ESAC and FK methods of estimating phase velocity using arbitrarily shaped microtremor arrays. Bull Seismol Soc Am 92:2323–2332
Okada H, Suto K (2003) The microtremor survey method. Society of Exploration Geophysicists
Panza GF (1985) Synthetic seismograms-the Rayleigh waves modal summation. J Geophys 58:125–145
Panza GF (1993) Synthetic seismograms from multimode summation theory and computational aspects. Acad Geod Geoph Mont Hung 28:1–2
Panza GF (1981) The resolving power of seismic surface waves with respect to crust and upper mantle structural models. In: The solution of the inverse problem in geophysical interpretation. Springer, pp 39–77
Park CB, Miller RD, Xia J (1998) Imaging dispersion curves of surface waves on multi-channel record. In: SEG technical program expanded abstracts 1998. Society of Exploration Geophysicists, pp 1377–1380
Perron V, Gélis C, Froment B et al (2018) Can broad-band earthquake site responses be predicted by the ambient noise spectral ratio? Insight from observations at two sedimentary basins. Geophys J Int 215:1442–1454
Peterson JR (1993) Observations and modeling of seismic background noise. US Geological Survey
Pischiutta M, Villani F, D’Amico S et al (2017) Results from shallow geophysical investigations in the northwestern sector of the island of Malta. Phys Chem Earth, Parts a/b/c 98:41–48
Pontevivo A, Panza GF (2002) Group velocity tomography and regionalization in Italy and bordering areas. Phys Earth Planet Inter 134:1–15
Qorbani E, Zigone D, Handy MR et al (2020) Crustal structures beneath the Eastern and Southern Alps from ambient noise tomography. Solid Earth 11:1947–1968
Radebaugh J, Sharma P, Korteniemi J, Fitzsimmons KE (2015) Longitudinal Dunes (or Linear Dunes). Encycl Planet Landforms 1263–1271
Regione Friuli Venezia Giulia I Cartografia Regionale. https://irdat.regione.fvg.it/CTRN/ricerca-cartografia/
Ritzwoller MH, Levshin AL (1998) Eurasian surface wave tomography: group velocities. J Geophys Res Solid Earth 103:4839–4878
Ritzwoller MH, Levshin AL (2002) Estimating shallow shear velocities with marine multicomponent seismic data. Geophysics 67:1991–2004
Roberts J, Asten M, Tsang HH, et al (2004) Shear wave velocity profiling in Melbourne silurian mudstone using the SPAC method. In: Proceedings of a conference of the Australian Earthquake Engineering Society (AEES), Mount Gambier, South Australia (November 5–7, 2004).
Rodriguez-Castellanos A, Sánchez-Sesma FJ, Luzon F, Martin R (2006) Multiple scattering of elastic waves by subsurface fractures and cavities. Bull Seismol Soc Am 96:1359–1374
Safani J, O’Neill A, Matsuoka T, Sanada Y (2005) Applications of Love wave dispersion for improved shear-wave velocity imaging. J Environ Eng Geophys 10:135–150
Seekins LC, Wennerberg L, Margheriti L, Liu H-P (1996) Site amplification at five locations in San Francisco, California: a comparison of S waves, codas, and microtremors. Bull Seismol Soc Am 86:627–635
SESAME W (2004) Guidelines for the implementation of the H/V spectral ratio technique on ambient vibrations: measurements, processing and interpretation. Eur Comm Proj No EVG1-CT-2000-00026 SESAME, D23 12:
Signell RP, Chiggiato J, Horstmann J et al (2010) High-resolution mapping of Bora winds in the northern Adriatic Sea using synthetic aperture radar. J Geophys Res Ocean 115:C04020. https://doi.org/10.1029/2009JC005524
Stutzmann E, Ardhuin F, Schimmel M et al (2012) Modelling long-term seismic noise in various environments. Geophys J Int 191:707–722
Sutton GH, Barstow N (1990) Ocean-bottom ultralow-frequency (ULF) seismo-acoustic ambient noise: 0.002 to 0.4 Hz. J Acoust Soc Am 87:2005–2012
Szelwis R (1982) Modeling of microseismic surface wave sources. J Geophys Res Solid Earth 87:6906–6918
Tanimoto T (1999) Excitation of normal modes by atmospheric turbulence: source of long-period seismic noise. Geophys J Int 136:395–402
Tanimoto T, Ishimaru S, Alvizuri C (2006) Seasonality in particle motion of microseisms. Geophys J Int 166:253–266
Traer J, Gerstoft P, Bromirski PD, Shearer PM (2012) Microseisms and hum from ocean surface gravity waves. J Geophys Res Solid Earth 117:B11307
Tsoar H (1983) Dynamic processes acting on a longitudinal (seif) sand dune. Sedimentology 30:567–578
Verstappen HT (1968) On the origin of longitudinal (seif) dunes. Zeitschrift Für Geomorphol NF 12:200–220
Wasson RJ, Hyde R (1983) Factors determining desert dune type. Nature 304:337–339
Webb SC (2007) The Earth’s ‘hum’is driven by ocean waves over the continental shelves. Nature 445:754–756
Withers MM, Aster RC, Young CJ, Chael EP (1996) High-frequency analysis of seismic background noise as a function of wind speed and shallow depth. Bull Seismol Soc Am 86:1507–1515
Yang Y, Ritzwoller MH (2008) Characteristics of ambient seismic noise as a source for surface wave tomography. Geochem Geophys Geosyst 9:Q02008. https://doi.org/10.1029/2007GC001814
Yoshizawa K (2014) Radially anisotropic 3-D shear wave structure of the Australian lithosphere and asthenosphere from multi-mode surface waves. Phys Earth Planet Inter 235:33–48
Zainorabidin A, Said MJM (2015) Determination of shear wave velocity using multi-channel analysis of surface wave method and shear modulus estimation of peat soil at Western Johore. Procedia Eng 125:345–350
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3:257–271
Acknowledgements
The authors wish to express their gratitude to Alberto Chiandussi for the ERT data and to Jiří Adamovič and Radek Mikuláš (Institute of Geology of the Czech Academy of Sciences) for the lithological and ichnological analysis. The work significanly benefited from the valuable and detailed comments of two anonymous reviewers as well as from the Editor (Prof. Kazunori Yoshizawa) and Vice Editor in Chief (Prof. Aitaro Kato). The research was supported by ELIOSOFT-Italy and by the Institute of Rock Structure and Mechanics of the Czech Academy of Sciences.
Funding
The research was supported by ELIOSOFT-Italy and by the Institute of Rock Structure and Mechanics of the Czech Academy of Sciences.
Author information
Authors and Affiliations
Contributions
GDM analyzed the seismic data, while JS managed the DTM and general geology sections. Manuscript was written jointly. All the authors read and approved the final manuscript.
Authors‘ information
GDM is senior geophysicist at the Institute of Rock Structure and Mechanics of the Academy of Sciences of the Czech Republic and is currently working in the joint inversion of seismic data with special focus on surface waves. JS is the Director of the same Institute and his research interests range from engineering geology to tectonophysics.
Corresponding author
Ethics declarations
Consent for publication
Not applicable.
Competing interests
No competing intrerests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dal Moro, G., Stemberk, J. Tools for the efficient analysis of surface waves from active and passive seismic data: exploring an NE-Italy perilagoon area with significant lateral variations. Earth Planets Space 74, 140 (2022). https://doi.org/10.1186/s40623-022-01698-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-022-01698-z
Keywords
- Shear-wave velocity (Vs)
- Surface waves
- Group velocities
- Phase velocities
- Joint Inversion
- Full Velocity Spectrum (FVS) analysis
- Rayleigh waves
- Love waves
- Rayleigh-wave Particle Motion (RPM)
- Multichannel analysis of surface waves (MASW)
- Holistic analysis of Surface waves (HS)
- Horizontal-to-Vertical Spectral Ratio (HVSR)
- NE Italy perilagoonal dune system
- Peats
- Paleodunes