Abstract
We investigated the effects of fault parameter uncertainty on the deterministic assessment of tsunami hazards for the submarine and coastal active faults in the Sea of Japan that were recently modeled by the Integrated Research Project on Seismic and Tsunami Hazards around the Sea of Japan. A key parameter in scenario-based tsunami assessment is the fault slip amount, which is usually calculated from empirical scaling relations that relate the fault size to the slip. We examined four methods to estimate the fault slip amounts and compared the coastal tsunami heights from the slip amounts obtained by two different empirical relations. The resultant coastal tsunami heights were strongly affected by the choice of scaling relation, particularly the fault aspect ratio (fault length/fault width). The geometric means of the coastal tsunami heights calculated from the two methods ranged from 0.69 to 4.30 with an average of 2.01. We also evaluated the effects of fault slip angles, which are also important parameters for controlling coastal tsunami heights, by changing the slip angles for faults in the southwestern and central parts of the Sea of Japan, where the strike-slip faults are concentrated. The effects of uncertainty of the fault slip angles (± 30° from the standard) on the coastal tsunami heights were revealed to be equal to or greater than those resulting from the choice of scaling relations; the geometric means of the coastal tsunami heights from the modified fault slip angles relative to the standard fault slip angles ranged from 0.23 to 5.88. Another important characteristic is that the locations of the maximum coastal tsunami height and the spatial pattern of the coastal tsunami heights can change with varying fault slip angles.
Graphical Abstract

Similar content being viewed by others
Introduction
There are two ways of assessing tsunami hazards: deterministic and probabilistic. Deterministic tsunami hazard assessments (DTHA) consider particular source scenarios to evaluate tsunami impacts on coastal areas, including tsunami height, inundation area, or flow velocity (e.g., Tinti and Armigliato 2003; Pranantyo et al. 2021). In evaluating tsunamis from a specified scenario, seafloor displacement due to uniform slip on fault is first computed using nine static parameters: fault location (latitude, longitude, and depth), geometry [strike, dip, and slip (rake) angles], and size (length, width, and slip amount) (e.g., Okada 1985).
Multiple uncertainties are involved in DTHA, including those derived from fault parameters, such as the fault size and geometry (Fig. 1). Submarine faults are mainly identified from seismic reflection surveys, in which the spatial intervals of the survey lines limit the estimate of the fault length to several kilometers or greater. The fault width can be estimated from the fault dip angle and the thickness of the seismogenic layer (e.g., Omuralieva et al. 2012; Sato et al, 2020), but both of these methods also include uncertainties. Geomorphological and seismological studies (e.g., seismic reflection and refraction surveys, gravity anomalies) can be used to estimate other fault parameters. However, it is difficult to estimate the fault area, slip amount and angle before the earthquake occurs. Thus, empirical scaling relations among fault parameters (e.g., fault length, rupture area, and seismic moment) that have been derived for various types of earthquakes (e.g., Wells and Coppersmith 1994; Takemura 1998; Irikura and Miyake 2001; Murotani et al. 2013) are used to estimate the slip amount or seismic moment of expected earthquakes.
Flowchart showing the setting of the tsunami fault model parameters according to the Tsunami Evaluation Subcommittee, The Nuclear Civil Engineering Committee, Japan Society of Civil Engineers (2016)
Probabilistic tsunami hazard assessments (PTHA) are typically represented as hazard curves, that is, the annual frequency of exceedance, as a function of tsunami height, and consider both aleatory and epistemic uncertainties. The aleatory uncertainty or random variability is represented by a probability distribution from repeated observations or experiments. A single hazard curve is obtained by integration over the aleatory uncertainties. Epistemic uncertainty occurs due to incomplete knowledge (i.e., models) and data, and can be reduced by improving models or collecting additional information. Weighted logic-trees are often used to treat epistemic uncertainty, with numerous hazard curves obtained for different branches of the tree (e.g., Annaka et al. 2007; Grezio et al. 2017). Recently, Mulia et al. (2020) assessed the regional probabilistic tsunami hazard associated with active faults along the eastern margin of the Sea of Japan using 60 faults proposed by the government committee (see “Previous fault models” section for more details). The maximum tsunami heights on the Sea of Japan coast are estimated to be as large as 3.7, 7.7, and 11.5 m over 100, 400, and 1000-year periods, respectively. In general, the hazard level increases from southwest to northeast, which is consistent with the number and type of identified fault systems.
In this study, we investigated the effects of fault slip amount and slip angle on DTHA, using fault parameters recently modeled by the Integrated Research Project on Seismic and Tsunami Hazards around the Sea of Japan (hereafter referred to as the JSPJ; see next section for details). A comparison of the calculated tsunami heights from the JSPJ model and the observed tsunami trace heights from twentieth century tsunamis is presented in Murotani et al. (submitted to Earth, Planets and Space). While tsunami numerical computations involve other uncertainties such as non-uniform slip (e.g., Mueller et al. 2021) and those related to the governing equations, Manning’s roughness coefficient, or the resolution and accuracy of bathymetry data (e.g., Tsunami Evaluation Subcommittee, The Nuclear Civil Engineering Committee, Japan Society of Civil Engineers 2016), our focus here is on uncertainties in fault parameters.
Fault models in the Sea of Japan
Previous fault models
Active faults in the Sea of Japan have been mapped based mainly on bathymetric data and seismic reflection survey profiles covering continental shelves to slopes (e.g., Okamura et al. 2005, 2014; Okamura 2016). For example, Okamura et al. (2014) reexamined the seismic profiles obtained by air-gun single-channel survey systems of the Geological Survey of Japan and identified faults that may be active in the shelf to slope offshore of the southwestern part of the Sea of Japan.
In 2014, a government committee jointly supported by the Ministry of Land, Infrastructure, Transport and Tourism (MLIT), the Ministry of Education, Culture, Sports, Science and Technology (MEXT), and the Cabinet Office of Japan compiled previous studies and proposed 60 rupture scenarios for submarine active faults (hereafter referred to as MLIT 2014) (Fig. 2a, b). The MLIT assumed the maximum size for these scenarios and simulated tsunami heights along the coastal areas for tsunami hazard assessments. The moment magnitudes for the 60 rupture scenarios ranged from 6.8 to 7.9, with each possibly consisting of several faults with a total length ranging from 24 to 177 km.
The fault location, length, strike, and dip angle were estimated based on seismic reflection surveys, and the widths from the thickness of the seismogenic layer (either 15 km or 18 km) and the dip angles (one of 30°, 45°, 60° and 90°). The fault slip angles were calculated from the three-dimensional tectonic stress fields estimated by Terakawa and Matsu’ura (2010) and by assuming the Wallace–Bott hypothesis (Wallace 1951; Bott 1959). The estimated fault types are dominantly reverse faults off the coast of Hokkaido and Tohoku and a mixture of strike-slip and reverse faults off the coast of the Kinki region. Strike-slip faults are dominantly distributed off the coast of the Chugoku and Kyushu regions (Fig. 2b). The fault slip angles were set at ± 35° or ± 145° for pure strike-slip faults to avoid underestimation of tsunami heights as a result of slip angle uncertainty.
The slip amount for each rupture scenario was first estimated from the fault area (length and width) using empirical scaling relations by Irikura and Miyake (2001). MLIT (2014) considered the uncertainty conservatively and increased the slip amounts by 1.5 m. The maximum slip amount was set at 6.0 m considering the above uncertainty (1.5 m) and the seismologically derived slip amounts (4.5 m) from prior large or great earthquakes (e.g., the 1993 event off the southwest coast of Hokkaido). MLIT (2014) conducted tsunami simulations using heterogeneous slip models, which included large slip patches surrounded by smaller background patches.
JSPJ fault models
The JSPJ was conducted from FY2013 to FY2020, with support from the MEXT, whereby submarine and coastal fault models along the Sea of Japan were developed through seismic and geological surveys (Fig. 2c, d). Sato et al. (2020) summarized the details of the development of fault models. Here, we selected 172 submarine or coastal fault models with lengths of 20 km or greater. In addition, we considered 28 shorter faults for the combination of segments. The lengths of these individual fault segments range from 6.7 km to 68.7 km. The locations and names of the submarine and coastal active faults considered in this study are shown in the Additional file 1: Figs. S1–S4.
In the JSPJ, crustal structures in the Sea of Japan were grouped into four types (A: oceanic crust, B: thick oceanic crust, C: back-arc rift, and D: continental crust) depending on the bathymetric and geological findings as well as seismic surveys from previous projects (e.g., No et al. 2014; Sato et al. 2014). The thickness of the seismogenic layer for each group was determined from the lower threshold depth of hypocenters and rheological examinations: 18 km (or 26 km) for the thick oceanic crust, 18 km for the back-arc rift, and 15 km for the continental crust (Sato et al. 2020).
The distribution of fault widths (Fig. 2c) depicts regional characteristics due to variations in the seismogenic layer thickness and fault dip angle. The faults off the Chugoku and Kyushu regions are narrow, where the strike-slip faults with high (~ 90°) dip angles dominate and the seismogenic layer is thin (15 km). The Hokkaido and Tohoku area faults are relatively wide, showing reverse faults with mainly gentle to moderate dip angles (30–45°) and thicker seismogenic layers (17 km or more). The fault area is determined by the fault length and width.
The fault slip angles were estimated from the three-dimensional tectonic stress fields by Terakawa and Matsu’ura (2010) and the Wallace–Bott hypothesis, an approach similar to that used by MLIT (2014), without constraining the fault slip angles for pure strike-slip faults to ± 35° or ± 145°. The estimated fault types (Fig. 2d) are similar to those from MLIT (2014), although several normal faults with gentle dip angles were newly identified in the central and southwestern parts of the Sea of Japan.
Scaling relations to estimate seismic moment and slip amount
We utilize the MLIT (2014) and three other methods (Matsuda 1975; Takemura 1998; Somerville et al. 1999; Irikura and Miyake 2001; Murotani et al. 2015) to estimate the fault slip amount and examine the effects on DTHA. A summary of the three methods is shown in Fig. 3. The parameters of the JSPJ fault models with the calculated slip amounts are shown in the Additional file 2: Tables S1 and S2.
Two methods are based on a methodology (“Recipe”) for predicting strong ground motions adopted by the Earthquake Research Committee at the Headquarters for Earthquake Research Promotion in Japan (2020). The first method (Recipe A) adopts the empirical scaling relation between fault area S and seismic moment \({M}_{0}\) by Somerville et al. (1999), Irikura and Miyake (2001) and Murotani et al. (2015), depending on the earthquake size (seismic moment),
The slip amount D is obtained by dividing the seismic moment (M0) by the fault area (S) and rigidity (μ) for single-segment rupture scenarios. We assume the rigidity as 34.3 GPa following MLIT (2014). We use a uniform slip throughout the fault area without saturation of the slip amounts. For multi-segment rupture scenarios, the total fault area is obtained by summing the fault area for the ith segment \({S}_{i}\),
The seismic moment \({M}_{0i}\) and slip amount \({D}_{i}\) for the ith segment are obtained by the following equations:
The second method (Recipe I) adopts the empirical scaling relation of Matsuda (1975), which identifies the relationship between earthquake magnitude on the JMA scale (M) and fault length (L) derived from 14 crustal earthquakes in Japan that occurred between 1891 and 1970.
The JMA magnitude M estimated from Eq. (7) is converted to the seismic moment using the relation of Takemura (1990).
The slip amount D is then obtained by dividing \({M}_{0}\) by the rigidity μ and fault area S, which is derived from the M0-S empirical relation of Somerville et al. (1999), Irikura and Miyake (2001) or Murotani et al. (2015). For multi-segment rupture scenarios, M is derived from the total length of the rupture scenario.
Li in Eq. 9 represents the fault length of the ith segment. Finally, the slip amount for the ith segment is calculated from Eq. (6), with \({S}_{i}\) as the fault area of the ith segment, as described below.
The third method (TM) uses the empirical relation of Takemura (1998), which is the association between fault length L and seismic moment \({M}_{0}\) derived from the source parameters of 33 intraplate earthquakes that occurred in Japan between 1885 and 1995. We use the scaling relations for the saturated seismogenic layer thickness (\({M}_{0 }\propto\) L2).
The slip amount D is obtained by dividing seismic moment \({M}_{0}\) by rigidity μ and fault area S, using the fault width W of each model. For the multi-segment rupture scenarios, the seismic moment and slip amount for the ith segment are determined from the following equation and Eq. (6):
A comparison of the estimated slip amounts for each single-segment rupture model is shown in Fig. 4. Slip amounts from Recipe A are mainly comparable with those from Recipe I, while those from TM are more variable than those from the other two methods. The TM slip amounts are generally larger than those from other scaling relations, especially for narrow faults and high dip angles. For example, for the single-segment rupture scenario YM08 (dip angle = 90°, fault width = 14.9 km), the TM slip amount is 3.39 m, while those from Recipe A and I are 0.96 m and 1.21 m, respectively. In contrast, the Recipe A slip amounts are larger than those from the TM for wide faults, such as with the rupture scenario RS01a (dip angle = 30°, fault width = 34.0 km), where the Recipe A slip is 2.92 m and that from TM is 2.37 m.
The histogram of moment magnitudes Mw for 349 rupture scenarios derived from Recipe A is shown in Fig. 5, and values for 172 single-segment rupture scenarios range from 6.4 to 7.5 (Additional file 2: Table S1). During the twentieth century, earthquakes with magnitudes M > 7.5 occurred, including the 1993 off the southwest coast of Hokkaido earthquake (M 7.8; Tanioka et al. 1995) and the 1983 central Sea of Japan earthquake (M 7.7; Satake 1985, 1989) that ruptured multiple fault segments (e.g., Murotani et al. submitted to Earth, Planets and Space). Thus, we also consider possible multi-segment rupture scenarios for neighboring (distance roughly < 5 km; Matsuda 1990) fault segments based on their fault geometry, and return 177 scenarios with moment magnitude ranges from 6.6 to 7.8 (Fig. 5 and Additional file 2: Table S2).
Effects of uncertainty in fault parameters on tsunami heights
Tsunami numerical simulation
For the 349 rupture scenarios, tsunami simulations were initiated using seafloor displacements obtained from Okada’s (1985) analytical solution for coseismic dislocation. Finite-difference computations were conducted for the nonlinear long-wave equation, including the bottom friction (Satake 1995). Bathymetry grids for the simulation were constructed from various data sets: JTOPO30, 30 arcsec gridded bathymetry data provided by the Japan Hydrographic Association; M7000 series, digitized bathymetry charts provided by the Japan Hydrographic Association; and the General Bathymetric Chart of the Oceans (GEBCO). We used nested bathymetry grids with spatial resolutions of 27 and 9 arcsecs. The time step for calculations was set at 0.5 s to satisfy the stability condition of the finite-difference method, and the tsunami was simulated for 5 h after the earthquake. The Manning’s roughness coefficient was assumed as 0.025 m−1/3 s (Goto and Sato 1993).
Coastal tsunami heights from various scaling relations and slip angles considering their uncertainties were compared with those calculated from Recipe A and standard slip angles, that is, slip angles evaluated from the regional stress fields, using the following geometric mean (G):
where \(n\) is the number of coastal points at which the maximum tsunami heights were evaluated. For the comparison of different scaling relations, \({H}_{i}\) and \({R}_{i}\) represent the tsunami heights at the ith coastal point using the fault slip amounts from Takemura (1998) and those from Recipe A, respectively. For the evaluation of the uncertainty of fault slip angles, \({H}_{i}\) and \({R}_{i}\) denote the tsunami heights at ith coastal point with varied fault slip angles and those from the standard fault slip angle, respectively, using the slip amount derived from Recipe A.
Effects of the fault rupture scenario
The coastal tsunami heights differ for the various fault combinations, including those with the same moment magnitude. An example is the two possible multi-segment rupture scenarios for the tsunami from the 1993 off the southwest coast of Hokkaido earthquake from the similar moment magnitude with different fault segment combinations (ST08 + ST09 + OK01; Mw 7.5 and ST09 + OK01 + OK02; Mw 7.6). The former rupture scenario (ST08 + ST09 + OK01) exhibits greater coastal tsunami heights along the southwestern coast of Hokkaido, reaching areas of the northern Hokkaido coast, such as Haboro Town and Rishiri Island. In contrast, the latter model (ST09 + OK01 + OK02) produces a lower coastal tsunami height in northern Hokkaido that becomes higher along the coast of Okushiri Island, which is similar to what was observed in the 1993 tsunami (Fig. 6). Murotani et al. (submitted to Earth, Planets and Space) further compared tsunami simulation results with the 1993 observations, both in terms of tsunami waveforms and coastal runup heights. The geometric mean K and logarithmic standard deviation κ of the observed to simulated coastal heights (Aida 1977) are 4.41 and 2.35 for ST08 + ST09 + OK01, while they are 3.56 and 2.12 for ST09 + OK01 + OK02. Murotani et al. (submitted to Earth, Planets and Space) concluded that the likely causative faults were OK03a, OK03b, and OK05 with K = 2.26 and κ = 1.54 (see Additional file 1: Fig. S1 for the locations of these faults).
Effects of scaling relations
The tsunami heights depend on the slip amounts, which were derived using the scaling relations; therefore, the tsunami heights vary significantly with the selection of these relations. The slip amounts obtained from Recipe A are larger than those obtained from TM for wide faults with gentle (~ 30°) dip angles, resulting in greater coastal heights. As an example of the single-segment rupture scenario, the fault model MMS01 off Tohoku region (L = 53.2 km, W = 33.4 km, dip angle = 25°) produces a higher maximum tsunami (6.08 m) for Recipe A due to a larger slip amount (2.88 m) than that of TM (maximum tsunami height of 4.90 m from a slip amount of 2.03 m; Fig. 7). The geometric mean G of the coastal tsunami heights from the TM compared to those of Recipe A is 0.72, which is similar to the ratio of slip amounts 0.70 (2.03/2.88). As a common characteristic of the MMS01 rupture scenario, the tsunami heights are also great along the Noto Peninsula and Oki Islands due to bathymetric effects, such as the Yamato bank. In fact, the coastal tsunami heights from the 1983 central Sea of Japan earthquake (M 7.7; Satake 1985, 1989) indicated significant tsunamis along these coasts as well as the eastern coast of the Korean peninsula, resulting in three casualties.
In contrast, the slip amounts obtained from the TM for steeply dipping faults with narrow widths, or multi-segment rupture scenarios with long total fault lengths are larger than those from Recipe A, resulting in a higher tsunami. An example is the single-segment rupture scenario YM18D off the Yamaguchi Prefecture, which is a steeply dipping fault with L = 44.6 km, W = 17.1 km, and dip angle = 60°. The tsunami is higher for TM (maximum coastal tsunami height = 5.61 m), due to a larger slip amount (3.32 m) than that of Recipe A (maximum coastal tsunami height = 2.33 m with a slip amount of 1.24 m; Fig. 8). The geometric mean G of the coastal tsunami height in this case is 2.38.
As for the multi-segment rupture scenarios, the tsunami is generally higher for the TM than that of Recipe A (Additional file 2: Table S2), due to the larger slip amounts. For example, the multi-segment rupture scenario SHN09 + MRK01 + ECG03 + ECG05 off the Niigata Prefecture that is a total length of 100.2 km based on the TM, exhibits coastal tsunami heights with a maximum of 9.39 m, which is substantially higher than those from Recipe A (maximum coastal tsunami height = 4.93 m; Fig. 9). The calculated geometric mean G of the coastal tsunami height in this case is 1.74.
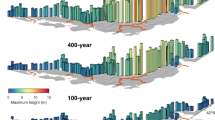
The geometric mean G histogram of the coastal tsunami heights from the TM relative to Recipe A is shown in Fig. 10a and the Additional file 2: Tables S1 and S2. The G values for both the single- and multi-segment rupture scenarios range from 0.69 to 4.30 and has an average of 2.01. Therefore, the coastal tsunami heights from the TM are on average about twice higher than those from Recipe A. For the single-segment rupture scenarios, the correlation coefficient between the slip ratios and G ratios is 1.0, indicating that the coastal heights can be predicated once they are computed for a unit slip amount. This means that the costal tsunami heights are mostly linear process. The G values range from 0.69 to 3.45 with an average of 1.84, and the distribution has clear spatial characteristics reflecting the fault aspect ratio (L/W), that is, the G values are relatively small for the faults off Hokkaido and Tohoku, while they are comparatively large for those off Chugoku and Kyushu. The G values are larger for faults with a larger aspect ratio (relatively narrow faults due to steep dip angles or thin seismogenic thickness) and vice versa (Fig. 10b). In contrast, the G values are > 1 for most of the multi-segment rupture scenarios, indicating that TM models produce higher tsunamis for multi-segment faults. The G values for multi-segment rupture scenarios range from 0.84 to 4.30 with an average of 2.17. Our results indicate that the selection of the scaling relation influences the coastal tsunami height differently depending on the fault geometry, due to systematic differences in the relation between fault geometry and slip.
a Histogram of the geometric mean (G) of coastal tsunami heights from slip amounts by the TM compared to those from Recipe A. Single-segment (green) and multi-segment (red) faults are shown in stacked bars. b Relationship between the fault aspect ratio (fault length/fault width) and geometric mean (G) for single-segment rupture scenarios
Uncertainty of fault slip angles
The effects of uncertainty of fault slip angles on coastal tsunami heights were examined by changing these angles from the standards of the regional tectonic stress fields. The effects are expected to be large for strike-slip faults; therefore, we conducted sensitivity analyses for the faults in the central and southwestern parts of the Sea of Japan, where most of the strike-slip faults are located (Fig. 2d).
Ishibe et al. (2021a) investigated the accuracy of the regional stress fields with the Wallace–Bott hypothesis in reproducing the fault slip angles of actual earthquakes using two different catalogs of focal mechanism solutions. The misfit angles between the observed and calculated fault slip angles were shown to generally be small (< 30°), except for the source and surrounding regions of large earthquakes (e.g., the 2011 earthquake off the Pacific coast of Tohoku) and the swarm-like activities started after the 2011 earthquake. Therefore, in the present study, we conducted tsunami simulations by modifying the fault slip angles by 15° or 30° from the standards estimated from three-dimensional tectonic stress fields. Here, + 15° and + 30° are in the direction of the increasing dip-slip component, while − 15° and − 30° are in the direction of the increasing strike-slip component. The varied fault slip angles saturate at ± 90° for + 15° and + 30°, and at 0° or ± 180° for the − 15° and − 30° cases (Fig. 11).
As a typical example, the changes in tsunami heights due to the variable fault slip angles for the single-segment rupture scenario FO04D off the Kyushu fault are shown in Fig. 12. The standard slip angle of this fault is 176°, which indicates an almost pure right-lateral fault, and the calculated maximum tsunami height is 0.44 m at Iki City, Nagasaki Prefecture. When the fault slip angle is changed to 161° (+ 15°), the coastal tsunami height increases to 1.03 m. The coastal tsunami height increases (1.70 m) when the fault slip angle is changed to 146° (+ 30°). Another important issue is that the coastal point with the maximum tsunami height changes from Iki City to Tsushima City (Tsushima Island, northwest of Iki Island). In contrast, cases of − 15° and − 30° show little change in tsunami heights, because slip angle changes of − 15° and − 30° result in the same fault slip angle (180°), which is the specified saturation limit explained previously, thus producing identical tsunami heights. Changes in coastal tsunami heights and the geometric means (G) for other rupture scenarios are shown in the Additional file 1: Figs. S5 and S6, Additional file 2: Table S3.
The changes in tsunami heights with fault slip angles for the multi-segment rupture scenario YM07a + YM07b + YM07c, located off Yamaguchi Prefecture, are shown in Fig. 13. Similarly, coastal tsunami heights increase as the dip-slip component of the fault slip increases. Considering uncertainties of the fault slip angles of ± 30°, the maximum tsunami heights range from 0.20 m to 1.71 m. The location of the maximum tsunami height also changes. For the standard fault slip angle, the maximum coastal tsunami height of 0.85 m is located on the coast of Mishima Island, whereas it moves eastward to Hamada at + 30° and southeastward to Hagi at − 15° and − 30°.
The variation in coastal tsunami heights due to the changes in fault slip angles in the southwestern and central parts of the Sea of Japan is summarized in Fig. 14. The G values for modifying the fault slip angles range from 0.23 to 5.88. These values are comparable or larger than the G values for the scaling relations of the TM and Recipe A. This indicates that the variation in coastal tsunami heights due to uncertainty in fault slip angle is similar or greater than those from the choice of scaling relations for pure strike-slip faults. The sensitivity of the uncertainty in the fault slip angles for coastal tsunami heights depends on the standard fault slip angle (Fig. 14b). For pure strike-slip faults, the coastal tsunami heights vary significantly, and the resulting changes in geometric means (G) are substantial. However, for pure dip-slip faults, changes in G due to the uncertainty of fault slip angles are relatively small.
Discussion
Our results indicate that the selection of the empirical scaling relation between fault dimension and slip amounts and the uncertainty of fault slip angles significantly influence the coastal tsunami heights of the DTHA. Various empirical scaling relations have been developed for various data sets. As for the scaling relations used in this study, Irikura and Miyake (2001) (Recipe A) used the largest number of earthquakes to develop their scaling relations. By assuming the average width of the source fault as W = 18 km (from the average width of Japanese inland crustal earthquakes) and the saturated surface displacement as D = 10 m, Murotani et al. (2015) proposed a three-stage scaling relationship between the rupture area and seismic moment. For the third stage with a seismic moment M0 ≥ 1.8 × 1020 Nm, the rupture area becomes proportional to the seismic moment due to the saturation of the fault slip amounts. The scaling relation of Matsuda (1975) between fault length and JMA magnitude M, which is utilized for Recipe I, was derived from only 14 crustal earthquakes in Japan between 1891 and 1970. Takemura (1998) developed a scaling relation using 33 intraplate earthquakes in Japan between 1885 and 1995, which mainly occurred on short faults. The longest fault in that data set was 85 km for the 1891 Nobi earthquake, while the fault lengths of the others were ≤ 33 km.
The MLIT (2014) assumed that the maximum slip, averaged on fault, is 6 m based on the observation that the slip amounts saturate at 4.5 m with a standard deviation of 1.5 m. In contrast, the slip amounts derived from Recipe I and the TM are not assumed to saturate for long faults and hence become unusually large. When selecting the empirical relation to evaluate the slip amounts from the fault geometry, consideration must be given to the range of application of each scaling relation to avoid under- or over-estimation.
Both MLIT and JSPJ estimated the fault slip angles using a three-dimensional tectonic stress field with the Wallace–Bott hypothesis. Recent studies validated this method using focal mechanism catalogues of recent earthquakes (Ishibe et al. 2021a) and Quaternary active faults whose fault types (slip directions) were evaluated geomorphologically (Ishibe et al. 2021b). The results indicate that the method accurately reproduced the slip angles and fault types, whereas the misfits between the observed slip angles and calculated values could be considerable for seismically inactive regions, where the uncertainty and spatial resolution of tectonic stress fields are presumed to be high. Further understanding of tectonic stress fields and their spatial and temporal heterogeneities may help to reduce the uncertainty in fault slip angles.
Conclusions
We investigated the effects of uncertainty in fault parameters on the deterministic tsunami hazard assessments for submarine and coastal active faults along the Sea of Japan. To estimate fault slip from empirical scaling relations, we examined four different methods (i.e., Recipe A, Recipe I, TM, and MLIT). Slip amounts from Recipe A and Recipe I are similar, hence the coastal tsunami heights are also similar. The geometric means of the coastal tsunami heights obtained from the TM empirical relations compared to those from Recipe A ranged from 0.69 to 4.30 with an average of 2.01, indicating that the tsunami heights were twice as large on average and up to four times at the maximum, depending on the choice of scaling relation. We also evaluated the effects of fault slip angles on coastal tsunami heights in the southwest and central parts of Japan, where strike-slip faults are dominant. The effects of slip angle uncertainty (± 30° from the standards) were similar or larger than those from the choice of scaling relations; the differences in geometric means between the standard and changed fault slip angles ranged between 0.23 and 5.88. The selection of empirical scaling relations scarcely changed the spatial pattern of tsunami heights (e.g., coastal points with the maximum tsunami height). However, the combination of fault segments for multi-segment rupture scenarios and changes in fault slip angles significantly affected both the maximum tsunami height and its spatial patterns. This indicates that it is critical to select an appropriate scaling relation and approximate the fault slip angles and geometries to reduce the uncertainty of coastal tsunami height estimates.
Availability of data and materials
More detailed tsunami simulation results are available in the annual reports of JSPJ at the following site: https://www.eri.u-tokyo.ac.jp/project/Japan_Sea/.
Abbreviations
- DTHA:
-
Deterministic tsunami hazard assessment
- JSPJ:
-
The integrated research project on seismic and tsunami hazards around the Sea of Japan
- TM:
-
Takemura (1998)
- MLIT:
-
Ministry of land, infrastructure, transport and tourism
- MEXT:
-
Ministry of education, culture, sports, science and technology
References
Aida I (1977) Simulations of large tsunamis occurring in the past off the coast of the Sanriku District. Bull Earthq Res Inst Univ of Tokyo 52:71–101 (in Japanese with English abstract)
Annaka T, Satake K, Sakakiyama T, Yanagisawa K, Shuto N (2007) Logic-tree approach for probabilistic tsunami hazard analysis and its applications to the Japanese coasts. Pure Appl Geophys 164:577–592
Bott MHP (1959) The mechanics of oblique slip faulting. Geol Mag 96(2):109–117
Earthquake Research Committee, the Headquarters for Earthquake Research Promotion (2020) Strong ground motion prediction method for earthquakes with specified source faults (“Recipe”) (as of 2020 March 6th). 53pp https://www.jishin.go.jp/main/chousa/20_yosokuchizu/recipe.pdf(in Japanese)
Goto C, Sato K (1993) Development of tsunami numerical simulation system for Sanriku coast in Japan. Report of the Port and Harbour Research Institute, Ministry of Transport, 32(2):3–44 (in Japanese with English abstract)
Grezio A, Babeyko A, Baptista MA, Behrens J, Costa A, Davies G, Geist EL, Glimsdal S, González FI, Griffin J, Harbitz CB, LeVeque RJ, Lorito S, Løvholt F, Omira R, Mueller C, Paris R, Parsons T, Polet J, Power W, Selva J, Sørensen MB, Thio HK (2017) Probabilistic tsunami hazard analysis: multiple sources and global applications. Rev Geophys 55(4):1158–1198
Irikura K, Miyake H (2001) Prediction of strong ground motions for scenario earthquakes. J Geogr 110(6):849–875 (in Japanese with English abstract)
Ishibe T, Terakawa T, Hashima A, Mochizuki M, Matsu’ura RS (2021a) Validating the Method Estimating Fault Slip Angles from Regional 3D Stress Field with the Wallace-Bott Hypothesis –Application to Two Focal Mechanism Catalogs in Japan–, Asia Oceania Geosciences Society 18th Annual Meeting (AOGS2021a) SE11-A004
Ishibe T, Terakawa T, Hashima A, Mochizuki M, Matsu’ura RS (2021b) Validating the method of estimating fault slip angles from regional 3D stress field with the Wallace-Bott Hypothesis –application to the major active fault zones in Japan–, Asia Oceania Geosciences Society 18th Annual Meeting (AOGS2021b) SE11-A005
Matsuda T (1975) Magnitude and recurrence interval of earthquakes from a fault. J Seismol Soc Jpn (Zisin) 2nd Ser 28:269–283 (in Japanese with English abstract)
Matsuda T (1990) Seismic zoning map of Japanese Islands, with maximum magnitudes derived from active fault data. Bull Earthq Res Inst Univ Tokyo 65:289–319 (in Japanese with English abstract)
Ministry of Land, Infrastructure, Transport and Tourism (2014) Investigation for large earthquakes occurring in the Sea of Japan. http://www.mlit.go.jp/river/shinngikaiblog/daikibojishinchousa(in Japanese)
Mueller C, Burbidge PW (2021) Regional tsunami forecasting: uncertainties due to non-uniform slip. Pure Appl Geophys. https://doi.org/10.1007/s00024-021-02845-5
Mulia IE, Ishibe T, Satake K, Gusman AR, Murotani S (2020) Regional probabilistic tsunami hazard assessment associated with active faults along the eastern margin of the Sea of Japan. Earth, Planets Space 72:123. https://doi.org/10.1186/s40623-020-01256-5
Murotani S, Satake K, Fujii Y (2013) Scaling relations of seismic moment, rupture area, average slip, and asperity size for M~9 subduction-zone earthquakes. Geophys Res Lett 40(19):5070–5074
Murotani S, Matsushima S, Azuma T, Irikura K, Kitagawa S (2015) Scaling relations of source parameters of earthquakes occurring on inland crustal mega-fault systems. Pure Appl Geophys 172(5):1371–1381
No T, Sato T, Kodaira S, Ishiyama T, Sato H, Takahashi N, Kaneda Y (2014) The source fault of the 1983 Nihonkai-Chubu earthquake revealed by seismic imaging. Earth Planet Sci Lett 400:14–25
Okada Y (1985) Surface deformation due to shear and tensile faults in a half-space. Bull Seismol Soc Am 75(4):1135–1154
Okamura Y (2016) Active tectonics around the junction of Southwest Japan and Ryukyu arcs: control by subducting plate geometry and pre-Quaternary geologic structure. Island Arc 25(4):287–297
Okamura Y, Satake K, Ikehara K, Takeuchi A, Arai K (2005) Paleoseismology of deep-sea faults based on marine surveys of northern Okushiri ridge in the Japan Sea. J Geophys Res Solid Earth 110:B09105. https://doi.org/10.1029/2004JB003135
Okamura Y, Inoue T, Abe S (2014) Quaternary faults offshore of the western part of San’in and northern part of Kyushu districts, west Japan. Ann Rep Active Fault Paleoearthquake Res 14:157–177 (in Japanese with English abstract)
Omuralieva AM, Hasegawa A, Matsuzawa T, Nakajima J, Okada T (2012) Lateral variation of the cutoff depth of shallow earthquakes beneath the Japan Islands and its implications for seismogenesis. Tectonophysics 518–521:93–105
Pranantyo IR, Heidarzadeh M, Cummins PR (2021) Complex tsunami hazards in eastern Indonesia from seismic and non-seismic sources: deterministic modelling based on historical and modern data. Geosci Lett 8:20. https://doi.org/10.1186/s40562-021-00190-y
Satake K (1985) The mechanism of the 1983 Japan Sea earthquake as inferred from long-period surface waves and tsunamis. Phys Earth Planet Inter 37(4):249–260
Satake K (1989) Inversion of tsunami waveforms for the estimation of heterogeneous fault motion of large submarine earthquakes: the 1968 Tokachi-oki and 1983 Japan Sea earthquakes. J Geophys Res Solid Earth 94(B5):5627–5636
Satake K (1995) Linear and nonlinear computations of the 1992 Nicaragua earthquake tsunami. Pure Appl Geophys 144(3):455–470
Sato T, No T, Kodaira S, Takahashi N, Kaneda Y (2014) Seismic constraints of the formation process on the back-arc basin in the southeastern Japan Sea. J Geophys Res Solid Earth 119(3):1563–1579
Sato H, Ishiyama T, Hashima A, Kato N, Van-Horne A, Claringbould JS, No T, Ishikawa M, Matsubara M, Koshiya S, Toyoshima T, Kobayashi K, Kosuga M (2020) Development of active fault model. Annual Progress Reports of the Integrated Research Project on Seismic and Tsunami Hazards around the Sea of Japan (FY2019), 209–239 (in Japanese)
Somerville P, Irikura K, Graves R, Sawada S, Wald D, Abrahamson N, Iwasaki Y, Kagawa T, Smith N, Kowada A (1999) Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seismol Res Lett 70:59–80
Tsunami Evaluation Subcommittee, The Nuclear Civil Engineering Committee, Japan Society of Civil Engineers (2016) Tsunami Assessment Method for Nuclear Power Plants in Japan 2016, https://committees.jsce.or.jp/ceofnp/node/140
Takemura M (1990) Magnitude-seismic moment relations for the shallow earthquakes in and around Japan. J Seismol Soc Japan (Zisin) 2nd Ser 43:257–265 (in Japanese with English abstract)
Takemura M (1998) Scaling law for Japanese intraplate earthquakes in special relations to the surface faults and the damages. J Seismol Soc Jpn (Zisin) 2nd Ser 51:211–228 (in Japanese with English abstract)
Tanioka Y, Satake K, Ruff L (1995) Total analysis of the 1993 Hokkaido Nanseioki earthquake using seismic wave, tsunami, and geodetic data. Geophys Res Lett 22:9–12
Terakawa T, Matsu’ura M (2010) The 3-D tectonic stress fields in and around Japan inverted from centroid moment tensor data of seismic events. Tectonics 29:TC6008. https://doi.org/10.1029/2009TC002626
Tinti S, Armigliato A (2003) The use of scenarios to evaluate the tsunami impact in southern Italy. Mar Geol 199(3–4):221–243
Wallace RE (1951) Geometry of shearing stress and relation to faulting. J Geol 59(2):118–130
Wells DL, Coppersmith KJ (1994) New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull Seismol Soc Am 84(4):974–1002
Wessel P, Smith WHF (1998) New, improved version of generic mapping tools released. EOS Trans AGU 79(47):579
Acknowledgements
We used Generic Mapping Tools (Wessel and Smith 1998) to draw the figures. We also used JTOPO30, 30 arcsec gridded bathymetry data around Japan provided by the Japan Hydrographic Association, M7000 series data from the Japan Hydrographic Association, and the General Bathymetric Chart of the Oceans (GEBCO) to create bathymetry data in the Sea of Japan region. We thank all the organizations and individuals who provided the data and information used in this study.
Funding
This study was supported by the Integrated Research Project on Seismic and Tsunami Hazards around the Sea of Japan, under the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan.
Author information
Authors and Affiliations
Contributions
KS led the project of tsunami forecasting under the Integrated Research Project on Seismic rand Tsunami Hazards around the Sea of Japan, designed the paper, and completed the manuscript. TI performed the numerical and statistical analyses, and drafted the initial manuscript. SM, IEM, and ARG contributed to data preparation, numerical analyses, interpretation of results, and writing of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Additional file 1.
Supplementary figures. Figure S1. Locations of submarine and coastal active faults off Hokkaido and surrounding regions that were utilized for the DTHA in this study. Parameters for each fault are shown in Tables S1 and S2. Figure S2. Locations of submarine and coastal active faults off Tohoku and surrounding regions that were utilized for the DTHA in this study. Figure S3. Locations of submarine and coastal active faults off the Chubu and Kinki regions that were utilized for the DTHA in this study. Figure S4. Locations of submarine and coastal active faults off the Chugoku and Kyushu regions that were utilized for the DTHA in this study. Figure S5. Changes in maximum coastal tsunami heights due to the uncertainty of fault slip angles. Figure S6. Geometric means of coastal tsunami heights due to the uncertainty of fault slip angles.
Additional file 2.
Supplementary tables.Table S1. Fault parameters and calculated slip amounts for three single-segment rupture scenarios. Geometric means of coastal tsunami heights TM relative to Recipe A are also shown.Table S2. Fault parameters and calculated slip amounts for three multi-segment rupture scenarios. Geometric means of coastal tsunami heights by TM relative to Recipe A are also shown.Table S3. Geometric means of coastal heights by changing fault slip angles from the standard ones. For multi-segment rupture scenarios, standard slip angle for the first fault segment is shown and plotted on Fig. 14.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Satake, K., Ishibe, T., Murotani, S. et al. Effects of uncertainty in fault parameters on deterministic tsunami hazard assessment: examples for active faults along the eastern margin of the Sea of Japan. Earth Planets Space 74, 36 (2022). https://doi.org/10.1186/s40623-022-01594-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-022-01594-6