Introduction

Boudinage structure is a key to the stress and strain analysis of deformed rocks. Pioneering deformation analysis using this structure has been performed when measuring the strain of layered boudins (Ferguson 1981, 1985, 1987; Ferguson and Lloyd 1984; Lloyd and Condliffe 2003). These studies demonstrated a significant difference in magnitude between the stress generated within boudins and that experienced by the surrounding matrix (Lloyd et al. 1982). Ferguson and Lloyd (1982) challenged existing methods of estimating palaeostress and strain. These early studies inspired Masuda and co-workers to establish a palaeopiezometer using the microboudin structure of columnar grains (e.g. tourmaline, piemontite, and glaucophane) within quartzose or calcareous metamorphic tectonites (Masuda et al. 1989, 2003, 2008; Kimura et al. 2006, 2010).

The basis of the microboudin palaeopiezometer is the theoretical probability density function for the fracturing of columnar grains (Masuda et al. 1989, 2003). The function represents the relationship between the proportion of microboudinaged grains and the aspect ratio of analysed columnar grains. The proportion of microboudinaged grains is defined as the ratio of the number of boudinaged grains to the total number of grains (microboudinaged + intact) for each aspect ratio. The probability function representation is the most important aspect of the microboudin palaeopiezometer (e.g. Masuda et al. 2011). The validity of the analysis requires the identification of an appropriate probability density function for natural microboudin data (Masuda et al. 2008, 2011; Omori et al. 2016).

Masuda and Kimura (2004) assessed the applicability of two probability density functions, assuming a columnar mineral grain surrounded by an elastic matrix and a Newtonian viscous matrix, respectively. They suggested that this comparison favoured the assumption of an elastic matrix for the microboudin palaeopiezometer. However, Maeder et al. (2009) used finite element modelling of the development of segment structures, including boudins, to show that variation in boudinaged segment shape is dependent on the viscosity contrast between competent and incompetent layers, and the kinematic vorticity number. Komoróczi et al. (2013) also performed boudinage modelling that involved coupled deformation of brittle and viscous layers. Thus, a viscous matrix remains a general assumption when considering the development of boudinaged structures.

As the evaluation by Masuda and Kimura (2004) relied on a qualitative best fit for the data, their assessment is not definitive. This approach is neither satisfactory nor quantifiable. The assessment is unable to establish a distinct difference between the functions in the qualitative best fit for newly obtained data, and Masuda and Kimura’s (2004) approach fails to support the validity of using an elastic matrix for theoretical modelling of fracturing. To better establish the basis for the microboudin palaeopiezometer, quantitative evaluation is required to assess whether the assumption of an elastic matrix is valid and reliable for microboudinage structures.

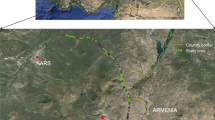
In this study, therefore, we re-examined the applicability of the two probability density functions to natural microboudin data. A quantitative comparison of the two functions was achieved through statistical evaluation using the Akaike information criterion (AIC) and a cross-validation (CV) technique. These statistical evaluations measure the relative quality of the models for a given data set, providing independent criteria to evaluate the fit of each probability density function (e.g. Burnham and Anderson 2002). Test data were obtained from columnar tourmaline grains containing microboudinaged structures, within metacherts collected from the Warrawoona greenstone belt in the East Pilbara Terrane, Western Australia.

Derivation of the probability density functions

Elastic matrix model

The fibre-loading theory and the shear-lag model, as applied to a columnar grain completely embedded within a continuous elastic matrix, assume that the matrix elastically transmits the far-field stress as a tensile stress along the grain (Fig. 1a). Using the shear-lag model, Masuda et al. (2003) proposed that the probability density function could be expressed as an elastic matrix model \(G_{E} \left( {r;\lambda } \right)\) representing the relationship between the proportion of microboudinaged grains and the aspect ratio of columnar minerals. The function \(G_{E} \left( {r;\lambda } \right)\) was referred to as \(G\left( {r;\lambda } \right)\) in previous theoretical works on the microboudin palaeopiezometer (Masuda et al. 2003, 2011; Kimura et al. 2006, 2010). In this paper, however, we represent the function as \(G_{E} \left( {r;\lambda } \right)\) to allow comparison with the Newtonian viscous matrix model. \(G_{E} \left( {r;\lambda } \right)\) is a function of the aspect ratio of columnar grains r and a non-dimensional stress parameter λ as follows (Masuda et al. 2003; Kimura et al. 2010):

$$G_{E} \left( {r;\lambda } \right) = 1 - \exp\left[ { - \frac{m - 1}{m}r\lambda^{m} \left( {\frac{{E_{f} }}{{E_{q} }}} \right)^{m} \left\{ {1 - \left( {1 - \frac{{E_{q} }}{{E_{f} }}} \right)\frac{1}{{{\text{cos}}h\left( {A_{0} r} \right)}}} \right\}^{m} } \right]$$
(1)

where m is the Weibull parameter; E f and E q are the elastic constants of the columnar grains and the matrix, respectively; and A 0 is a constant (Masuda et al. 2003). In the present study of tourmaline grains within a quartz matrix, the constants \({{E_{f} } \mathord{\left/ {\vphantom {{E_{f} } {E_{q} }}} \right. \kern-0pt} {E_{q} }}\) and A 0 have values of 2 and 0.4, respectively (Kimura et al. 2010). The relationship between λ and far-field differential stress σ 0 was defined by Kimura et al. (2010) as follows:

$$\sigma_{0} = \lambda S_{0}^{**} \frac{{K_{0} }}{{K_{c} }}\left( {\frac{1}{{\overline{w} }}} \right)^{{\frac{1}{2}}}$$
(2)

where \(S_{0}^{**}\) is the instantaneous modal fracture strength of a 1-mm cube of a columnar mineral grain, K c is the fracture toughness, K 0 is the subcritical crack growth limit, and \(\overline{w}\) is the geometric mean width of the grains. This equation considers the influence of time (Masuda et al. 2008) and the effect of size on fracture strength for columnar grains (Kimura et al. 2010). Among the parameters in Eq. (2), Kimura et al. (2006, 2010) determined that \(S_{0}^{**}\) = 39, 64, and 80 MPa for tourmaline, epidote, and amphibole, respectively. Moreover, Masuda et al. (2008) tentatively proposed that \({{K_{0} } \mathord{\left/ {\vphantom {{K_{0} } {K_{c} }}} \right. \kern-0pt} {K_{c} }}\) = 0.1. The microboudin palaeopiezometer combines the above equations to estimate σ 0 (e.g. Masuda et al. 2008, 2011).

Fig. 1
figure 1

Schematic illustration of the stress-transfer models investigated in the present study. x, y, and z are the axes in a Cartesian coordinate system. a The elastic matrix model (Masuda et al. 2003) after Zhao and Ji (1997). 2 l = length of fibre; 2r 0  = diameter of fibre; 2R 0 = length of unit cell. b The Newtonian viscous matrix model (Masuda and Kimura 2004) modified after Ramberg (1955). z c  = thickness of competent layer; z i  = thickness of matrix; l = half-length of competent layer

Full size image

Newtonian viscous matrix model

Ramberg (1955) solved the stress and strain parameters in a competent layer subjected to one-dimensional elongation as a function of the strain rate of the surrounding Newtonian viscous matrix (Fig. 1b). Drag forces acting on the Newtonian viscous matrix in the competent layer cause fracturing when the matrix flows along the layer. Based on the Ramberg (1955) solution, Masuda and Kimura (2004) proposed that the fracturing of columnar grains is equivalent to the competent layer described by the Newtonian viscous model \(G_{V} \left( {r;\psi } \right)\). \(G_{V} \left( {r;\psi } \right)\) is a function of the aspect ratio r and a dimensionless parameter ψ as follows:

$$G_{V} \left( {r;\psi } \right) = 1 - \exp\left[ { - \frac{m - 1}{m}r^{2m + 1} \psi^{m} } \right]$$
(3)

and ψ is defined as

$$\psi = \frac{{3z_{C} \sigma_{0} }}{{2z_{i} S^{*} }}$$
(4)

As the Weibull parameter depends on the fracture strength of columnar grains, we use m = 2 in the case for the elastic model. The terms z C and z i in Eq. (4) are the thicknesses of the competent layer and matrix, respectively; σ 0 is the far-field differential stress; and S* is the fracture strength of competent material at r = 1, which is regarded as a material-dependent constant (Masuda and Kimura 2004). In the Newtonian viscous model, far-field differential stress (σ 0) is defined as:

$$\sigma_{0} = \frac{\mu }{{z_{i} }}\left( { - \frac{\partial z}{\partial t}} \right) ,$$
(5)

where μ is the matrix viscosity and \({{ - \partial \left( {{z \mathord{\left/ {\vphantom {z {z_{i} }}} \right. \kern-0pt} {z_{i} }}} \right)} \mathord{\left/ {\vphantom {{ - \partial \left( {{z \mathord{\left/ {\vphantom {z {z_{i} }}} \right. \kern-0pt} {z_{i} }}} \right)} {\partial t}}} \right. \kern-0pt} {\partial t}}\) is the compressional strain rate along the z axis.

Basic data sets for model evaluation

Our statistical approach requires data to evaluate the elastic matrix and Newtonian viscous matrix models. The data we apply here are the proportion of microboudinaged columnar grains with respect to their aspect ratio (p r ), defined as the ratio of the number of microboudinaged grains to the total number of grains (microboudinaged + intact) for each aspect ratio. Such data can be obtained by measuring columnar mineral grains in samples of metamorphic tectonites. In this study, we obtained nine data sets from tourmaline grains embedded within the quartz matrix of metacherts collected from the Warrawoona Greenstone Belt around the Mount Edgar and Corunna Downs granitoid complexes in the East Pilbara Terrane (Fig. 2). It has been reported that greenstones in this area underwent greenschist-facies metamorphism, except near the margins of the associated granitoid domes, where conditions locally reach amphibolite facies as a probable result of contact metamorphism (e.g. Delor et al. 1991; Collins and Van Kranendonk 1999). The geological setting and detailed observations of this region have been provided by Collins et al. (1998, 1999) and Van Kranendonk et al. (2002, 2004, 2007). The nature of the metachert samples and the corresponding data sets are briefly described below.

Fig. 2
figure 2

Geological map of the Warrawoona greenstone belt (Collins et al. 1998; Kloppenburg et al. 2001; Van Kranendonk et al. 2004; Thébaud and Rey 2013; François et al. 2014). Sampling locations are marked by star symbols

Full size image

Analysed samples

The samples are composed mainly of equigranular quartz (grain size = tens of µm to > 0.1 mm), together with tourmaline, chlorite, and muscovite. A consistent foliation is present, defined by the alignment of muscovite- and quartz-rich layers of contrasting colours. A prominent mineral lineation is also defined within these rocks by the alignment of the long axes of tourmaline on this foliation surface, as measured using the method of Masuda et al. (1999) (Fig. 3).

Fig. 3
figure 3

Frequency distributions of the long-axis orientations of tourmaline grains on the foliation surface in each sample (EP6fb, MB28, EP10oc, MB15, EP11fi, MB14, MB23, MB39, and MB23L). Best-fit curves, based on the von Mises distribution, are also shown (for details of the method, see Masuda et al. 1999). θ is the orientation of the tourmaline grains. N is the total number of measured tourmaline grains, κ is the concentration parameter, d 0 is the confidence interval for the critical region of 0.05 (Masuda et al. 1999), and κ u and κ l are the 95% upper and lower confidence limits, respectively. The distribution is arranged to set the mean orientation = 90°, corresponding to the mean orientation of the lineation

Full size image

Microboudinage structure of tourmaline grains

Some tourmaline grains show a microboudinage structure within the quartz matrix (Fig. 4). The microboudinaged tourmaline grains have the following characteristics: (1) they are fractured perpendicular to their long axes; (2) they are generally pulled apart without any evidence of significant rotation during separation; and (3) the inter-boudin gaps are filled with quartz. These observations suggest that the morphological characteristics of the microboudinaged tourmaline grains are of the unmodified symmetric type, torn boudins group, and block (object) boudins according to the classification scheme of Goscombe et al. (2004).

Fig. 4
figure 4

Photomicrograph of a typical microboudinaged structure within a tourmaline grain viewed on the foliation surface in sample MB28 (plane-polarized light). Qtz = quartz; Tou = tourmaline

Full size image

Proportion of microboudinage

We collected nine data sets from tourmaline grains on the foliation surface according to the procedure of Masuda et al. (2011). We measured the widths and lengths of tourmaline grains and the distances of the inter-boudin gaps in microboudinaged tourmaline grains on foliation surfaces, for grains with long axes oriented within 15° of the mineral lineation (Fig. 5). The basic data for the model evaluation consist of the proportion of microboudinaged grains with respect to the aspect ratio (r). The frequency distributions of microboudinaged and intact columnar grains are shown in Fig. 6, and the proportions of microboudinaged grains are plotted in Fig. 7.

Fig. 5
figure 5

Schematic illustration of the measurement of columnar tourmaline grains, modified after Masuda et al. (2011). We measured the tourmaline grain length (L and L i ), width (W), and inter-boudin distance (G i )

Full size image
Fig. 6
figure 6

Histograms of the aspect ratios (r) of intact (white bars) and microboudinaged (grey bars) tourmaline grains in each sample

Full size image
Fig. 7
figure 7

Values of p r for each sample. The best-fit curves for the elastic and Newtonian viscous models are shown as solid and dashed curves, respectively. Error bars are 95% confidence intervals of the binomial distribution

Full size image

Model evaluation

The AIC and CV techniques were used to calculate the value of AIC and the generalization error for the elastic and Newtonian viscous matrix models for each data set. Given that both values reflect the relative predictive performance of the models when using unknown data (e.g. Burnham and Anderson 2002; Bishop 2006), we use these values as an indicator of the relative quality of the two models. We briefly explain both approaches below.

AIC

AIC is a powerful model testing criterion proposed by Akaike (1974) that has been widely used for model selection in various scientific fields (e.g. Sclove 1987; Hansen 1999; Mazerolle 2006; Ahmed et al. 2007; Posada 2008). AIC is mathematically based on the Kullback–Leibler information of distance (e.g. Kullback and Leibler 1951), which is a way of measuring differences among probability distributions. Akaike (1974) developed a rigorous method to estimate the Kullback–Leibler information based on the empirical log-likelihood function at its maximum point as the AIC (Burnham and Anderson 2002, 2004) as follows:

$$AIC = - 2\left( {lnL_{\rm max} } \right) + 2M$$
(6)

where L max is the maximum likelihood and M is the number of independently adjusted parameters. The preferred model is that with the minimum AIC value. The AIC value is used here to identify either the elastic or Newtonian model as the more appropriate. The value of M in both models is 1, which is the stress parameter λ or ψ in the elastic and Newtonian models, respectively. L max is the fundamental value used to evaluate the models by AIC, and this can be obtained from the maximum likelihood estimation.

In maximum likelihood estimation, we adopted the binomial distribution (e.g. Savage 1972) as the error function of the data at each measurement point, which consists of the proportion of microboudinaged columnar grains as a function of the aspect ratio, because columnar mineral grains are divided into two classes according to whether they are microboudinaged.

The binomial distribution is a discrete probability distribution with parameters N and p as follows:

$$P\left( y \right) = \left( {\begin{array}{*{20}c} N \\ y \\ \end{array} } \right)p^{y} \left( {1 - p} \right)^{N - y}$$
(7)

where

$$\left( {\begin{array}{*{20}c} N \\ y \\ \end{array} } \right) = \frac{N!}{{y!\left( {N - y} \right)!}}$$
(8)

In probability theory and statistics, N is the number of successes in a sequence of yes-or-no experiments, y is the number of success (y = 0, 1, 2,…, N), and p is the probability of success. Given that we treat a success as being a fractured grain, then for the microboudinage data set N is the total number of measured grains, y is the number of microboudinaged grains, and p is the ratio of the number of microboudinaged grains to the total number of grains (microboudinaged + intact). In the microboudinage case, the value of p r is represented in the elastic matrix and Newtonian viscous matrix models as follows:

$$p_{r} = G_{E} \left( {r;\lambda } \right)$$
(9)

and

$$p_{r} = G_{V} \left( {r;\psi } \right)$$
(10)

respectively. The likelihood functions L E and L V are defined by the infinite product of Eq. (7) for the elastic and Newtonian viscous matrix models in Eqs. (9) and (10) as follows:

$$L_{E} = \prod\limits_{i} {\left( {\begin{array}{*{20}c} {N_{{r_{i} }} } \\ {y_{{r_{i} }} } \\ \end{array} } \right)} \left( {G_{E} \left( {r_{i} ;\lambda } \right)} \right)^{{y_{{r_{i} }} }} \left( {1 - G_{E} \left( {r_{i} ;\lambda } \right)} \right)^{{N_{{r_{i} }} - y_{{r_{i} }} }}$$
(11)

and

$$L_{V} = \prod\limits_{i} {\left( {\begin{array}{*{20}c} {N_{{r_{i} }} } \\ {y_{{r_{i} }} } \\ \end{array} } \right)\left( {G_{V} \left( {r_{i} ;\varphi } \right)} \right)^{{y_{{r_{i} }} }} \left( {1 - G_{V} \left( {r_{i} ;\varphi } \right)} \right)^{{N_{{r_{i} }} - y_{{r_{i} }} }} }$$
(12)

respectively. \(N_{{r_{i} }}\) and \(y_{{r_{i} }}\) are N and y for the measurement point i, respectively.

We then evaluated the stress parameters λ and ψ using maximum likelihood estimation (e.g. Savage 1972). This approach provides the value of maximum likelihood L max for Eqs. (11) and (12), along with the corresponding stress parameters (λ and ψ) used to solve the optimization problem.

Cross-validation

AIC provides a useful solution for selecting the best model. However, if the available data are poor, then the best model selected might still be poor (Burnham and Anderson 2004). Thus, every effort must be made to ensure that the data used are high quality, and we acknowledge the limitation of our data in this respect. This problem commonly arises in deformation analysis of metamorphic tectonites. To rigorously evaluate the relative quality of the models, it may be necessary to obtain a test data set on which the performance of the selected model is finally evaluated.

As such, we used the CV technique to address this problem. The CV technique is an effective method for evaluating the predictive capability of a statistical model for an unknown data set based on the generalization error (GE) (e.g. Bishop 2006; Kuwatani et al. 2014), and this approach has been generally applied to model selection (e.g. Stone 1974, 1977; Geisser 1975). In the CV technique, the given data set is divided into training and testing subsets. We used the training subset to construct a statistical model and then used the test subset to evaluate the predictive performance of the model. In effect, we regard a part of the data sets as unknown data and then evaluate the predictive performance of the model for the unknown data.

In this study, we adopted the leave-one-out (LOO) method for the CV. The LOO method divides the data set into N (the number of data points) parts and then uses \({{\left( {N - 1} \right)} \mathord{\left/ {\vphantom {{\left( {N - 1} \right)} N}} \right. \kern-0pt} N}\) parts of the data as the training subset z i and the remaining part of the data as the test subset x i for the CV. This procedure is then repeated for all N possible choices (Bishop 2006). In this study, the LOO method was adopted to calculate the GE E and GE V , corresponding to the probability density functions \(G_{E} \left( {r;\lambda } \right)\) and \(G_{V} \left( {r;\psi } \right)\) as follows:

$$GE_{E} = \frac{1}{n}\sum\limits_{i = 1}^{n} {E\left( {x_{i} ,G_{E} \left( {z_{i} ;\lambda_{i} } \right)} \right)}$$
(13)

and

$$GE_{V} = \frac{1}{n}\sum\limits_{i = 1}^{n} {E\left( {x_{i} ,G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right)}$$
(14)

respectively, where n is the number of data points, and \(E\left( {x_{i} ,G_{E} \left( {z_{i} ;\lambda_{i} } \right)} \right)\) and \(E\left( {x_{i} ,G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right)\) are the error of the testing subsets x i corresponding to the probability distributions of the constructed models \(G_{E} \left( {r;\lambda } \right)\) and \(G_{V} \left( {r;\psi } \right)\), respectively. The set of statistical parameters λ i and ψ i was determined using the training subset z i that consists of all the data, apart from the testing subset x i . When using the maximum likelihood approach, the error functions \(E\left( {x_{i} ,G_{E} \left( {z_{i} ;\lambda_{i} } \right)} \right)\) and \(E\left( {x_{i} ,G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right)\) are represented as:

$$E\left( {x_{i} ,G_{E} \left( {z_{i} ;\lambda_{i} } \right)} \right) = - ln\left\{ {\left( {\begin{array}{*{20}c} {N_{i}^{{\left( {x_{i} } \right)}} } \\ {y_{i}^{{\left( {x_{i} } \right)}} } \\ \end{array} } \right)\left( {G_{E} \left( {z_{i}; \lambda_{i} } \right)} \right)^{{y_{i}^{{\left( {x_{i} } \right)}} }} \left( {1 - G_{E} \left( {z_{i} ;\lambda_{i} } \right)} \right)^{{N_{i}^{{\left( {x_{i} } \right)}} - y_{i}^{{\left( {x_{i} } \right)}} }} } \right\}$$
(15)

and

$$E\left( {x_{i} ,G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right) = - ln\left\{ {\left( {\begin{array}{*{20}c} {N_{i}^{{\left( {x_{i} } \right)}} } \\ {y_{i}^{{\left( {x_{i} } \right)}} } \\ \end{array} } \right)\left( {G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right)^{{y_{i}^{{\left( {x_{i} } \right)}} }} \left( {1 - G_{V} \left( {z_{i} ;\psi_{i} } \right)} \right)^{{N_{i}^{{\left( {x_{i} } \right)}} - y_{i}^{{\left( {x_{i} } \right)}} }} } \right\}$$
(16)

respectively. \(N_{i}^{{\left( {x_{i} } \right)}}\) is the total number of measured grains in the testing subset and x i , \(y_{i}^{{\left( {x_{i} } \right)}}\) is the number of microboudinaged grains in the testing subset x i . Equations (15) and (16) provide the function of likelihood given by the testing subset x i in each model. The model that has a smaller generalization error value is determined to be the better model, based on its higher predictive performance for the unknown data.

Results

The values of AIC, GE E , and GE V can be calculated from Eqs. (6), (13), and (14), respectively. We determined these values for both models using the nine data sets. Figure 6 shows the frequency distribution of microboudinaged tourmaline grains, which is characterized as the number of microboudinaged (grey bar) and intact grains (white bar) for each aspect ratio bin. Based on the maximum likelihood estimation applied to the data displayed in Fig. 6, we obtained the p r values and best-fit curves for \(G_{E} \left( {r;\lambda } \right)\) and \(G_{V} \left( {r;\psi } \right)\), and the values of λ and ψ for each data set (Fig. 7). These curves show that the values of p r continuously increase with increasing aspect ratio of the tourmaline grains. The 95% confidence interval of each p r value represents the proportion of data from grains with a much larger aspect ratio (r > 10) that have lower quality than the grains with a smaller aspect ratio (r < 5), because the total number of grains is small (i.e. <25 grains, as shown in Fig. 6).

According to the values of AIC, GE E , and GE V , these criteria show that the elastic model always has smaller values than the Newtonian viscous matrix model. Thus, these statistical constraints identify the elastic matrix model as the appropriate model for the fracturing of tourmaline grains in all the analysed samples (Table 1). From the perspective of the goodness of fit, the data from sample EP6fb clearly show a much better fit to the elastic matrix model than the Newtonian viscous model, whereas for the other eight samples there are no significant differences between the models. This result indicates that a qualitative assessment (e.g. Masuda and Kimura 2004 ) does not always successfully identify the appropriate model for a given data set. Values of p r for grains with a high aspect ratio (r > 10) are significantly larger than predicted by \(G_{E} \left( {r;\lambda } \right)\). These data ostensibly match \(G_{V} \left( {r;\psi } \right)\) (Fig. 7), although they are insignificant in determining the quality of the model. Given that both models have only one parameter, the AIC evaluation is essentially the same as that derived from maximum log-likelihood values.

Table 1 Summary of λ, ψ, AIC, and GE values for each sample
Full size table

Statistical criteria can be used to objectively assess the validity of the elastic matrix model applied to the microboudin palaeopiezometer. A substantial advantage of using information criteria such as AIC is that they are applicable to non-nested models (Burnham and Anderson 2002). In such models, one proposed model cannot be a subset of other models, as is the case for the elastic matrix and Newtonian viscous matrix models compared here. However, the information criteria must be chosen carefully for non-nested models due to the large possible variance in AIC (e.g. Ripley 2004). For the data sets examined in this study, AIC values for the elastic matrix model are approximately half of those for the Newtonian viscous matrix model (Table 1). These differences indicate that it is reasonable to regard the elastic matrix model as suitable for the microboudin palaeopiezometer for the analysed data sets.

Discussion

Evaluation of the results

Our result showed the validity of the elastic matrix model using for the microboudin palaeopiezometer and quantitatively supported the conclusion in Masuda and Kimura (2004); as the microboudinage occurred in the solid state during metamorphism, the elastic matrix model is acceptable. However, we do not conclude that the elastic matrix model is the best model for all microboudin data. The criteria used in this study were selected to enable comparison between the relative predictive performance of the elastic and Newtonian viscous models for nine data sets, and there are no threshold AIC or GE values that indicate the need to discard or adapt the models. It is possible that an alternative model, such as a non-Newtonian viscous model, would be more suitable than the elastic matrix model, although no other models have been proposed for the microboudin palaeopiezometer. The statistical model-selection approach could be used to undertake an objective comparison between the elastic matrix model and an alternative.

Significance of the elastic model

As the fracturing of columnar grains occurs under solid-state flow during metamorphism (e.g. Masuda et al. 2011), it is reasonable to use the elastic model to simulate the fracturing of columnar grains. Microboudinage of columnar grains into two segments can be considered to occur via the following three stages (Ferguson 1981; Lloyd et al. 1982; Masuda and Kuriyama 1988): (1) pre-fracturing; (2) fracturing; and (3) separation. The probability density function considers stages (1) and (2) and describes the proportion of microboudinaged grains as a function of aspect ratio (Fig. 7). By focussing on the duration of the fracturing and separation stages, we consider the applicability of the elastic matrix model to microboudinage.

There is a significant difference in the duration of the fracturing and separation of columnar grains. Fracturing of a columnar grain is generally assumed to occur instantaneously when the applied stress reaches the fracture strength of a microcrack within the grain (e.g. Masuda et al. 1989, 2003). However, according to the principles of fracture mechanics (e.g. Davidge 1979; Atkinson 1987; Lawn 1993; Anderson 2005; Gdoutos 2005), crack growth proceeds gradually at stresses lower than the fracture strength and results in a process with a relatively slow crack velocity, known as subcritical crack growth (e.g. Masuda et al. 2008). The slowest crack velocity estimated to date is 5 × 10−12 m/s (Wilkins 1980), with 1-mm-long cracks being produced in only 102 years. As fracturing occurs at a critical crack length, which is <50 μm in the analysed tourmaline grains, the observed fractures can form in several decades. Compared with ductile flow during metamorphism that occurs on the geological timescale (i.e. at least 106 years; e.g. Brown 2010; Hobbs and Ord 2014), cracks propagate instantaneously through intact grains to generate fractures even if the fracturing proceeded with an extremely slow crack velocity (Masuda et al. 2008).

During the separation stage, the shape of boudinaged segments is often determined by ductile deformation associated with viscous flow of the surrounding matrix (e.g. Malavieille and Lacassin 1988; Goscombe et al. 2004; Maeder et al. 2009). Previous simulations have successfully reproduced the various observed shapes of boudinaged segments (e.g. Lloyd and Ferguson 1981; Treagus and Lan 2004; Maeder et al. 2009; Komoróczi et al. 2013). Therefore, fracturing of columnar grains can be reasonably simulated under the assumption of an elastic matrix, whereas the variation in segment shape requires a ductile matrix. This discrepancy may be due to the significant difference in timescales of duration between fracturing (~102 years) and separation (~106 years). This difference suggests that the elastic and viscous matrix models can be compatible in terms of the development of microboudinage structures during metamorphism. However, the limitation of this compatibility remains problematic, although viscous theory has been applied to solid-state flow in the crust (e.g. MacKenzie 1979; Weijermars 1986; Masuda and Ando 1988; Passchier and Sokoutis 1993; Arbaret et al. 2001; Jiang 2007, 2012; Mancktelow et al. 2002; Mancktelow 2013). The technique of statistical model evaluation is a valuable approach with which to address this problem.

Conclusions

We statistically evaluated the suitability of probability density functions describing elastic and Newtonian viscous matrix models via AIC and the CV technique, using natural data from the microboudinage structure of tourmaline grains within a quartz matrix contained within metacherts. Our statistical evaluation revealed that the elastic matrix model is the more appropriate probability density function for the fracturing of columnar grains. This result supports the use of the elastic matrix model for palaeostress analysis by the microboudin palaeopiezometer. The microboudinage structure of columnar grains is one of the forms of evidence commonly used to estimate the palaeostress state imposed on metamorphic tectonites. Constructing a theoretical model for microboudinage and evaluating the model is essential to constraining geodynamics through such deformation analysis. We encourage further tests of the theoretical model for the microboudin palaeopiezometer and suggest that the statistical approach outlined here will offer an important contribution to validating such future developments in the application of stress analysis to metamorphic tectonites.