Abstract
We propose a new family of continuous distributions called the odd generalized exponential family, whose hazard rate could be increasing, decreasing, J, reversed-J, bathtub and upside-down bathtub. It includes as a special case the widely known exponentiated-Weibull distribution. We present and discuss three special models in the family. Its density function can be expressed as a mixture of exponentiated densities based on the same baseline distribution. We derive explicit expressions for the ordinary and incomplete moments, quantile and generating functions, Bonferroni and Lorenz curves, Shannon and Rényi entropies and order statistics. For the first time, we obtain the generating function of the Fréchet distribution. Two useful characterizations of the family are also proposed. The parameters of the new family are estimated by the method of maximum likelihood. Its usefulness is illustrated by means of two real lifetime data sets. AMS Subject Classification Primary 60E05; secondary 62N05; 62F10
Similar content being viewed by others
Introduction
The art of proposing generalized classes of distributions has attracted theoretical and applied statisticians due to their flexible properties. Most of the generalizations are developed for one or more of the following reasons: a physical or statistical theoretical argument to explain the mechanism of the generated data, an appropriate model that has previously been used successfully, and a model whose empirical fit is good to the data. The last decade is full on new classes of distributions that become precious for applied statisticians. There are two main approaches for adding new shape parameter(s) to a baseline distribution.
1.1 Approach 1: Adding one shape parameter
The first approach of generalization was suggested by Marshall and Olkin (1997) by adding one parameter to the survival function \(\overline {G}(x)=1-G(x)\), where G(x) is the cumulative distribution function (cdf) of the baseline distribution. Gupta et al. (1998) added one parameter to the cdf, G(x), of the baseline distribution to define the exponentiated-G (“exp-G” for short) class of distributions based on Lehmann-type alternatives (see Lehmann 1953). Following Gupta et al. ’s class, Gupta and Kundu (1999) studied the two-parameter generalized-exponential (GE) distribution as an extension of the exponential distribution based on Lehmann type I alternative. The GE distribution is also known as the exponentiated exponential (EE) distribution. Since it is the most attractive generalization of the exponential distribution, the GE model has received increased attention and many authors have studied its various properties and also proposed comparisons with other distributions. Some significant references are: Gupta and Kundu (2001a; 2001b; 2002; 2003; 2004; 2006; 2007; 2008; 2011), Kundu et al. (2005), Nadarajah and Kotz (2006), Dey and Kundu (2009), Pakyari (2010) and Nadarajah (2011). In fact, the GE model has been proven to be a good alternative to the gamma, Weibull and log-normal distributions, all of them with two-parameters. The GE distribution can be used quite effectively for analyzing lifetime data which have monotonic hazard rate function (hrf) but unfortunately it cannot be used if the hrf is upside-down, J or reversed-J shapes. Differently, the new family can have increasing, decreasing, J, reversed-J, bathtub and upside-down bathtub and, therefore, it can be used effectively for analyzing lifetime data of various types. The generalization of the exp-G class to other distributions is beyond the scope of the paper.
1.2 Approach 2: Adding two or more shape parameters
A second approach of generalization was pioneered by Eugene et al. (2002) and Jones (2004) by defining the beta-generated (beta-G) class from the logit of the beta distribution. Further works on generalized distributions were the Kumaraswamy-G (Kw-G) by Cordeiro and de Castro (2011), McDonald-G (Mc-G) by Alexander et al. (2012), gamma-G type 1 by Zografos and Balakrishanan (2009) and Amini et al. (2014), gamma-G type 2 by Ristić and Balakrishanan (2012) and Amini et al. (2014), odd-gamma-G type 3 by Torabi and Montazari (2012), logistic-G by Torabi and Montazari (2014), odd exponentiated generalized (odd exp-G) by Cordeiro et al. (2013), transformed-transformer (T-X) (Weibull-X and gamma-X) by Alzaatreh et al. (2013), exponentiated T-X by Alzaghal et al. (2013), odd Weibull-G by Bourguignon et al. (2014), exponentiated half-logistic by Cordeiro et al. (2014a), T-X{Y}-quantile based approach by Aljarrah et al. (2014) and T-R{Y} by Alzaatreh et al. (2014), Lomax-G by Cordeiro et al. (2014b), logistic-X by Tahir et al. (2015a), a new Weibull-G by Tahir et al. (2015b) and Kumaraswamy odd log-logistic-G by Alizadeh et al. (2015).
We propose a new class of distributions called the odd generalized exponential (“OGE” for short) family, which is flexible because of the hazard rate shapes: increasing, decreasing, J, reversed-J, bathtub and upsidedown bathtub. In Section 2, we define the OGE family of distributions. Two special cases of this family are presented in Section 3. The density and hazard rate functions are described analytically in Section 4. A useful mixture representation for the pdf of the new family is derived in Section 5. In Section 6, we obtain explicit expressions for the moments, generating function, mean deviations and entropies. In Section 7, we determine a power series for the quantile function (qf). In Section 8, we investigate the order statistics. Section 9 refers to some characterizations of the OGE family. In Section 10, the parameters of the new family are estimated by the method of maximum likelihood. In Section 11, we illustrate its performance by means of two applications to real life data sets. The paper is concluded in Section 12.
The new family
Consider a parent distribution depending on a parameter vector ξ with cdf G(x;ξ), survival function \(\overline {G}(x;\boldsymbol {\xi })= 1-G(x;\boldsymbol {\xi })\) and probability density function (pdf) g(x;ξ). The cdf of the GE model with positive parameters λ and α is given by Π(x)=(1−e−λx)α (for x>0). For α=1, it reduces to the exponential distribution with mean λ −1. In fact, the density and hazard functions of the GE and gamma distributions are quite similar. The GE density function is always right-skewed and can be used quite effectively to analyze skewed data. Its hrf can be increasing, decreasing and constant depending on the shape parameter in a similar manner of the gamma distribution. Its applications have been wide-spread as a model to power system equipment, rainfall data, software reliability and analysis of animal behavior, among others.
We define the cdf of the OGE family by replacing x by \(G(x;\boldsymbol {\xi })/\overline {G} (x;\boldsymbol {\xi })\) in the cdf Π(x) leading to
where α>0 and λ>0 are two additional parameters.
The pdf corresponding to (1) is given by
where g(x;ξ) is the baseline pdf. We can omit the dependence on the vector of parameters ξ and write simply G(x)=G(x;ξ). Equation 2 will be most tractable when the cdf G(x) and pdf g(x) have explicit expressions. Hereafter, a random variable X with density function (2) is denoted by X∼OGE(α,λ,ξ). The main motivations for using the OGE family are to make the kurtosis more flexible (compared to the baseline model) and possible to construct heavy-tailed distributions that are not long-tailed for modeling real data. The family (1) contains some special models as those listed in Table 1. In particular, it includes as a special case the widely known exponentiated Weibull (EW) distribution pioneered by Mudholkar and Srivastava (1993) and Mudholkar et al. (1995). For a detail survey on the EW model, the reader is referred to Nadarajah et al. (2013). It has been well-established in the literature that the EW distribution gives significantly better fits than the exponential, gamma, Weibull and lognormal distributions.
We offer a physical interpretation of X when α is an integer. Consider a system formed by α independent components following the odd exponential-G class (Bourguignon et al. 2014) given by
Suppose the system fails if all α components fail and let X denote the lifetime of the entire system. Then, the cdf of X is F(x;α,λ,ξ)=H(x;λ,ξ)α, which is identical to (1).
In Table 1, we provide some members of the OGE family.
The hrf of X is given by
Theorem 1 provides some relations of the OGE family with other distributions.
Theorem 1.
Let X∼O G E(α,λ,ξ).(a) If Y=G(X;ξ), then \(F_{Y}(y)=\left (1-\rm {e}^{-\lambda \frac {y}{1-y}}\right)^{\alpha },\,\,\,\, 0<y<1\), and (b) If \(\displaystyle Y=\frac {G(X;\boldsymbol {\xi })}{\overline {G}(X;\boldsymbol {\xi })}\), then Y∼G E(α,λ).
The OGE family is easily simulated by inverting (1) as follows: if U has a uniform U(0,1) distribution, then
has the density function (2), where Q G (·)=G −1(·) is the baseline qf.
Special OGE distributions
Lifetime distributions play a fundamental role in survival analysis, biomedical science, engineering and social sciences. Typically, lifetime refers to human life length, the life span of a device before it fails or the survival time of a patient with serious disease from the diagnosis to the death. Here, we present three special OGE distributions that can be useful in applied survival analysis.
3.1 The OGE-Weibull (OGE-W) distribution
The OGE-W distribution is defined from (2) by taking \(\phantom {\dot {i}\!}G(x;\boldsymbol {\xi })=1-\mathrm {e}^ {-\theta \,x^{\beta }}\) and \(\phantom {\dot {i}\!}g(x;\boldsymbol {\xi })=\beta \,\theta \,x^{\beta -1}\,\rm {e}^{-\theta \,x^{\beta }}\) to be the cdf and pdf of the Weibull distribution with positive parameters β and θ, respectively, and ξ=(β,θ).
The cdf and pdf of the OGE-W distribution are given by (for x>0)
and
respectively, where α>0 and β>0 are shape parameters and λ>0 and θ>0 are scale parameters.
The applications of the OGE-W and EW distributions can be directed to model extreme value observations in floods, software reliability, insurance data, tree diameters, carbon fibrous composites, firmware system failure, reliability prediction and fracture toughness, among others.
3.2 The OGE-Fréchet (OGE-Fr) distribution
The OGE-Fr distribution is defined from (2) by taking \(G(x;\boldsymbol {\xi })=\mathrm {e}^{-(b/x)^{a}}\) and \(g(x;\boldsymbol {\xi })=a\,b^{a}\,x^{-(a+1)}\,\,\mathrm {e}^{-(b/x)^{a}}\phantom {\dot {i}\!}\) to be the cdf and pdf of the Fréchet distribution with parameters a and b, respectively, and ξ=(a,b).
The cdf and pdf of the OGE-Fr distribution are given by (for x>0)
and
respectively, where α>0 and a>0 are shape parameters and λ>0 and b>0 are scale parameters.
The OGE-Fr distribution has applications ranging from accelerated life testing, rainfall and floods, queues in supermarkets, sea currents, wind speeds, and track race records, among others.
3.3 The OGE-Normal (OGE-N) distribution
The OGE-N distribution is defined from (2) by taking G(x;ξ)=Φ[(x−μ)/σ] and g(x;ξ)=σ −1 ϕ[(x−μ)/σ] to be the cdf and pdf of the normal distribution with parameters μ and σ, respectively, and ξ=(μ,σ).
The cdf and pdf of the OGE-N distribution are given by (for x∈ℜ)
and
respectively, where α>0 is a shape parameter, μ∈ℜ is a location parameter, and λ>0 and σ>0 are scale parameters.
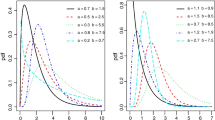
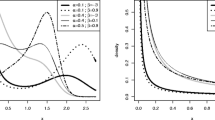
In Figures 1, 2, 3, 4 and 5, we display some plots of the pdf and hrf of the OGE-W, OGE-Fr and OGE-N distributions for selected parameter values. Figures 1, 2 and 3 indicate that the OGE family generates distributions with various shapes such as symmetrical, left-skewed, right-skewed and reversed-J. Further, Figures 4 and 5 reveal that this family can produce hazard rate shapes such as increasing, decreasing, J, reversed-J, bathtub and upside-down bathtub. This fact implies that the OGE family can be very useful to fit data sets under various shapes.
Asymptotics and shapes
Proposition 1.
The asymptotics of equations (1), (2) and (3) as G(x)→0 are given by
Proposition 2.
The asymptotics of equations (1), (2) and (3) as x→∞ are given by
The shapes of the density and hazard rate functions can be described analytically. The critical points of the OGE-G density functions are the roots of the equation:
There may be more than one root to (8). Let \(\lambda (x)=\frac {d^{2}\log [f(x)] }{d x^{2}}\). We have
If x=x 0 is a root of (8) then it corresponds to a local maximum if λ(x)>0 for all x<x 0 and λ(x)<0 for all x>x 0. It corresponds to a local minimum if λ(x)<0 for all x<x 0 and λ(x)>0 for all x>x 0. It refers to a point of inflexion if either λ(x)>0 for all x≠x 0 or λ(x)<0 for all x≠x 0.
The critical point of h(x) are obtained from the equation
There may be more than one root to (9). Let τ(x)=d 2 log[h(x)]/d x 2, then we have
If x=x 0 is a root of (9) then it refers to a local maximum if τ(x)>0 for all x<x 0 and τ(x)<0 for all x>x 0. It corresponds to a local minimum if τ(x)<0 for all x<x 0 and τ(x)>0 for all x>x 0. It gives an inflexion point if either τ(x)>0 for all x≠x 0 or τ(x)<0 for all x≠x 0.
Useful expansions
First, we consider the quantity \(M=1-\rm {e}^{-\lambda \,\frac {G(x;\boldsymbol {\xi })}{\overline {G}(x;\boldsymbol {\xi })}}\). By expanding the exponential function in power series and using the generalized binomial expansion, we obtain
The quantity M can be expressed as
where, for k≥0, b k =a k+1, and, for k≥1, \(a_{k}=\sum _{(i,j)\in I_{k}}\frac {(-1)^{i+j+1}\lambda ^{i}}{i!}\,\dbinom {-i}{j}, \,\,I_{k}=\{(i,j)|i+j=k;i=1,2,\ldots,j=0,1,2,\ldots \}. \)
Second, we can expand z α in Taylor series as
where \(f_{m}=f_{m}(\alpha)=\sum _{l=m}^{\infty }\frac {(-1)^{l-m}}{l!}\,\binom {l}{m}\,(\alpha)_{l}\). Here and from now on, we use the notation (α) l =α(α−1)…(α−l+1) for the descending factorial with (α)0=1.
We use throughout the paper a result of Gradshteyn and Ryzhik (2000, Section 0.314) for a power series raised to a positive integer n (for n≥1)
where the coefficients c n,i (for n=1,2,…) can be determined from the recurrence equation \(c_{n,i}=(i\,b_{0})^{-1}\,\sum _{m=1}^{i}\,[\!m(n+1)-i]\,b_{m}\,c_{n,i-m}\) (for i≥1), and \(c_{n,0}={b_{0}^{n}}\).
Third, based on Eqs. (10)-(12), the cdf (1) can be expressed as
where c m,k can be obtained from the quantities b 0,…,b k as in equation (12).
Then, we have
where \(d_{k}=\sum _{m=0}^{\infty }f_{m}\,c_{m,k}\) (for k≥0), H α+k (x)=G(x)α+k denotes the cdf of the exp-G distribution with power parameter α+k.
Finally, the density function of X can be expressed in the mixture form
where h α+k (x)=(α+k) G(x;ξ)α+k−1 g(x;ξ) is the exp-G density function with power parameter α+k. Equation (15) reveals that the OGE density function is a linear combination of exp-G densities. Thus, some mathematical properties of the new model such as the ordinary and incomplete moments, and moment generating function (mgf) can be derived from those properties of the exp-G distribution. Some exp-G structural properties are studied by Mudholkar and Srivastava (1993), Mudholkar et al. (1995), Mudholkar and Hutson (1996), Gupta et al. (1998), Gupta and Kundu (2001a; 2001b), Nadarajah and Kotz (2006) and Nadarajah (2011).
Mathematical properties
6.1 Moments
The need for necessity and the importance of moments in Statistics especially in applications is obvious. Some of the most important features and characteristics of a distribution can be studied through moments. Let Y k be a random variable having the exp-G pdf h α+k (x) with power parameter α+k.
A first formula for the nth moment of X follows from (15) as
Expressions for moments of several exp-G distributions are given by Nadarajah and Kotz (2006), which can be used to obtain \(\mu _{n}^{\prime }\).
We provide two applications of (16) for the OGE-W and OGE-Fr models discussed in Section 3. First, the moments of the OGE-W model can be derived from closed-forms moments of the EW distribution given by Choudhury (2005). We obtain
where the quantities A j,k (for j,k≥0) are given by
The double infinite series on the right-hand side converges for all parameter values.
Second, the moments of the OGE-Fr model (for n<a) follow immediately from the moments of the Fréchet distribution as
A second alternative formula for \(\mu _{n}^{\prime }\) is obtained from (16) in terms of the baseline qf as
where (for a>0) \(\tau (n,a)={\int _{0}^{1}} Q_{G}(u)^{n}\,u^{a} d u\). Cordeiro and Nadarajah (2011) obtained τ(n,a) for some well-known distribution such as the normal, beta, gamma and Weibull distributions, which can be applied to obtain raw moments of the corresponding OGE distributions.
The central moments (μ s ) and cumulants (κ s ) of X can be determined from the ordinary moments using the recurrence equations
where \(\kappa _{1}=\mu ^{\prime }_{1}\). The skewness \(\rho _{1}=\kappa _{3}/\kappa _{2}^{3/2}\) and kurtosis \(\rho _{2}=\kappa _{4}/{\kappa _{2}^{2}}\) can be calculated from the third and fourth standardized cumulants.
For empirical purposes, the shapes of many distributions can be usefully described by what we call the first incomplete moment which plays an important role for measuring inequality, for example, income quantiles and Lorenz and Bonferroni curves.
The nth incomplete moment of X can be expressed as
The last integral can be computed for most G distributions.
6.2 Generating function
The generating function provides the basis of an alternative route to analytical results compared with working directly with the pdf and cdf and it is widely used in the characterization of the distributions, and the application of goodness-of-fit tests. Let M(t)=E(e tX) be the mgf of X. Then, we can write from (15)
where M k (t) is the mgf of Y k . Hence, M(t) can be determined from the exp-G generating function.
Now, we provide two applications of (20) for the OGE-W and OGE-Fr models. Nadarajah et al. (2015) derived a formula for the mgf of Y k which holds for the OGE-W model depending on the complex parameter Wright generalized hypergeometric function with p numerator and q denominator parameters (Kilbas et al. 2006, Equation (1.9)) given by
for \(z\in \mathbb {C}\), where α j , \(\beta _{k} \in \mathbb {C}\), A j , B k ≠0, j=1,…,p, k=1,…,q, which converges for \(1+ \sum _{j=1}^{q}B_{j}-\sum _{j=1}^{p}A_{j}>0\).
Nadarajah et al. (2015) demonstrated that the mgf of Y k can be expressed as
Combining (20) and the last equation gives the mgf of the OGE-W distribution.
The mgf of the Fréchet distribution can be obtained by
The calculations of the integral in (21) involve the generalized hypergeometric function defined in equation (2.3.1.14) (Prudnikov et al. 1986, p. 322).
For a>0 and s>0, if b=p/q (with p≥1 and q≥1 are co-primes integers), we can write
where z=(−1)p+q s p a q/(p p q q), △(k,a) denote the sequence
m F n denotes the generalized hypergeometric function defined by
and (c) k =c(c+1)…(c+k−1) denotes the ascending factorial.
Numerical routines for computing the generalized hypergeometric function are available in most mathematical packages, e.g., Maple, Mathematica and Matlab. Nadarajah and Kotz (2005), and Nadarajah (2007) used also this result to obtain the properties of the distribution of the difference between two independent Gumbel variates, and to Iacbellis and Fiorentino (2000), and Fiorentino et al. (2006)’s model for peak streamflow.
By using (22), the mgf of the Fréchet distribution follows as
Using (15), the mgf of the OGE-Fr model can be expressed as
and then
By using (23), M(t) reduces to
A second alternative formula for M(t) can be derived from (15) as
where (for a>0) \(\rho (t,a)=\int _{-\infty }^{\infty } \rm {e}^{t\,x}\,G(x)^{a}\,g(x) dx= {\int _{0}^{1}}\,\exp [\!t\,Q_{G}(u)]\,u^{a}\,d u\).
We can obtain the mgf’s of several OGE distributions directly from equation (24). Equations (20) and (24) are the main results of this section.
6.3 Mean deviations
The mean deviations about the mean (\(\delta _{1}=E\left (|X-\mu ^{\prime }_{1}|\right)\)) and about the median (δ 2=E(|X−M|)) of X can be expressed as
respectively, where \(\mu ^{\prime }_{1}=E(X)\), M=M e d i a n(X)=Q(0.5) is the median which comes from (4), \(F\left (\mu ^{\prime }_{1}\right)\) is easily calculated from the cdf (1) and m 1(z) is the first incomplete moment determined from (19) with n=1.
Now, we provide two alternative ways to compute δ 1 and δ 2. A general formula for m 1(z) can be derived from equation (15) as
where \(J_{k}(z)=\int _{-\infty }^{z} x\,h_{\alpha +k}(x)dx\) is the first incomplete moment of Y k . Hence, the mean deviations in (25) depend only on quantity J k (z).
We give two applications of J k (z) for the the OGE-W and OGE-Fr distributions. For the first model, the EW pdf (for x>0) with power parameter α+k is given by
and then
The last integral is equal to the incomplete gamma function and then the mean deviation for the OGE-W distribution is given by
where \(\gamma (a,z)={\int _{0}^{z}}\,w^{a-1}\,\rm {e}^{-w} dw\) is the incomplete gamma function.
The first incomplete moment of the Fréchet distribution is given by
So, the first incomplete moment of the OGE-Fr model can be derived from the last equation and (15) as
where \(\Gamma (a,z)=\int _{z}^{\infty }\,w^{a-1}\,\rm {e}^{-w} dw\) is the complementary incomplete gamma function.
A second general formula for m 1(z) can be derived by setting u=G(x) in (15)
where \(T_{k}(z)=\int _{0}^{G(z)} Q_{G}(u)\,u^{\alpha +k-1} du\) depends on the baseline qf.
Applications of equations (26) and (27) can be directed to the Bonferroni and Lorenz curves defined for a given probability π by \(B(\pi) =m_{1}(q)/(\pi \mu ^{\prime }_{1})\) and \(L(\pi)=m_{1}(q)/\mu ^{\prime }_{1}\), respectively, where \(\mu ^{\prime }_{1}=E(X)\) and q=Q(π) is the qf of X at π.
6.4 Entropies
An entropy is a measure of variation or uncertainty of a random variable X. Two popular entropy measures are the Rényi and Shannon entropies (Rényi 1961; Shannon 1948). The Rényi entropy of a random variable with pdf f(x) is defined by
for γ>0 and γ≠1. The Shannon entropy of a random variable X is defined by \( \mathbb {E}\left \lbrace -\log \left [f(X)\right ]\right \rbrace \). It is the special case of the Rényi entropy when γ ↑1. Direct calculation yields
First, we define
Using Taylor and generalized binomial expansions, and after some algebraic manipulations, we obtain
So, we can write:
Proposition 3.
Let X be a random variable with pdf (2). Then,
The simplest formula for the entropy of X can be reduced to
After some algebraic developments, we obtain an expression for I R (γ)
where Y j,k has a beta distribution with parameters j+k+1 and one, and
Quantile power series
Power series methods are at the heart of many aspects of applied mathematics and statistics. Here, we derive a power series for the qf x=Q(u)=F −1(u) of X by expanding (4). If the baseline qf Q G (u) does not have a closed-form expression, it can usually be expressed in terms of a power series as
where the coefficients a i ’s are suitably chosen real numbers which depend on the parameters of the G distribution. For several important distributions, such as the normal, Student t, gamma and beta distributions, Q G (u) does not have explicit expressions but it can be expanded as in equation (29). As a simple example, for the normal N(0,1) distribution, a i =0 for i=0,2,4,… and a 1=1, a 3=1/6, a 5=7/120 and a 7=127/7560,…
Next, we derive an expansion for the argument of Q G (·) in equation (4)
For |u|<1, we have \(-\log (1-u)=\sum _{i=0}^{\infty }\,u^{i+1}/(i+1)\). Then, using the generalized binomial expansion, we obtain
where (for k≥0)
Using the generalized binomial expansion again, we can write
where \(b_{0}^{\ast }=\lambda +\alpha _{0}^{\ast }\), \(b_{k}^{\ast }=\alpha _{k}^{\ast }\) for k≥1 and the coefficient δ k (for k≥0) can be determined from the recurrence equation (for k≥1 and \(\delta _{0}=\alpha ^{\ast }_{0}/b_{0}^{\ast }\))
Then, the qf of X can be expressed from (4) as
Combining (29) and (30), we obtain
and then
where \(e_{m}=\sum _{i=0}^{\infty } a_{i}\,d_{i,m}\) and, for i≥0, \(d_{i,0}={\delta _{0}^{i}}\) and, for m>1, \(d_{i,m}=(m\,\delta _{0})^{-1}\,\sum _{n=1}^{m}[n(i+1)-m]\,\delta _{n}\,d_{i,m-n}\).
Let W(·) be any integrable function in the positive real line. We can write
Equations (31) and (32) are the main results of this section since from them we can obtain various OGE mathematical quantities. In fact, various of these properties can follow by using the second integral for special W(·) functions, which are usually more simple than if they are based on the first integral. Established algebraic expansions to determine mathematical quantities of the OGE distributions based on these equations can be more efficient then using numerical integration of the pdf (2), which can be prone to rounding off errors among others. For the great majority of these quantities, we can adopt twenty terms in the power series (31).
The effects of the shape parameter α on the skewness and kurtosis of X can be studied using quantile measures. The shortcomings of the classical kurtosis measure are well-known. The Bowley skewness is given by
Since only the middle two quartiles are considered and the outer two quartiles are ignored, this adds robustness to the measure. The Moors kurtosis is based on octiles
These measures are less sensitive to outliers and they exist even for distributions without moments. In Figures 6 and 7, we plot the measures B and M for the OGE-W and OGE-Fr distributions. These plots indicate how both measures B and M vary on the parameter α.
Order statistics
Order statistics make their appearance in many areas of statistical theory and practice. Suppose X 1,…,X n is a random sample from the OGE-G distribution. Let X i:n denote the ith order statistic. Using (14) and (15), the pdf of X i:n can be expressed as
where K=n!/[(i−1)!(n−i)!] and then
where \(\varphi _{j+i-1,0}=d_{0}^{j+i-1}\) and (for k≥1)
Hence,
where
Equation (33) is the main result of this section. It reveals that the pdf of the OGE order statistics is a triple linear combination of exp-G distributions. So, several mathematical quantities of these order statistics like ordinary and incomplete moments, factorial moments, mgf, mean deviations and several others come from these quantities of the OGE distributions.
Characterization of the OGE family
Characterizations of distributions are important to many researchers in the applied fields. An investigator will be vitally interested to know if their model fits the requirements of a particular distribution. To this end, one will depend on the characterizations of this distribution which provide conditions under which the underlying distribution is indeed that particular distribution. Various characterizations of distributions have been established in many different directions. In this section, two main characterizations of the OGE family are presented. These characterizations are based on: (i) a simple relationship between two truncated moments; (ii) a single function of the random variable.
9.1 Characterizations based on truncated moments
In this subsection we present characterizations of the OGE family in terms of a simple relationship between two truncated moments. Our characterization results presented here will employ an interesting result due to Glänzel (1987) (Theorem 2, below). The advantage of these characterizations is that, the cdf F(x) does not require to have a closed-form and are given in terms of an integral whose integrand depends on the solution of a first order differential equation, which can serve as a bridge between probability and differential equation.
Theorem 2.
Let (Ω,Σ,P) be a given probability space and let H=[a,b] be an interval for some a<b(a=−∞,b=∞ might as well be allowed). Let X:Ω→H be a continuous random variable with the distribution function F and let q 1 and q 2 be two real functions defined on H such that E[q 1(X)|X≥x]=E[q 2(X)|X≥x]η(x),x∈H, is defined with some real function η. Consider that q 1, q 2∈C 1(H), η∈C 2(H) and F(x) is twice continuously differentiable and strictly monotone function on the set H. Finally, assume that the equation q 2 η=q 1 has no real solution in the interior of H. Then, F is uniquely determined by the functions q 1, q 2 and η, particularly
where the function s is a solution of the differential equation \(s^{\prime }=\frac {\eta ^{\prime }q_{2}}{\eta q_{2}-q_{1}}\) and C is a constant chosen to make \(\int _{H}dF=1\).
Clearly, Theorem 2 can be stated in terms of two functions q 1 and η by taking q 2(x)≡1, which will reduce the condition given in Theorem 2 to E[q 1(X)|X≥x]=η(x). However, adding an extra function will give a lot more flexibility, as far as its application is concerned.
Proposition 4.
Let X:Ω→(0,∞) be a continuous random variable and let q 2(x)= \(\left [1-e^{-\lambda \left (\frac {G\left (x;\mathbf {\xi }\right) }{\overline {G}\left (x;\mathbf {\xi }\right)}\right)}\right ]^{1-\alpha }\) and \(q_{1}\left (x\right)=q_{2}\left (x\right)e^{-\lambda \left (\frac {G\left (x;\mathbf {\xi }\right)} {\overline {G}\left (x;\mathbf {\xi }\right)}\right)}\) for x>0. The pdf of X is (2) if and only if the function η defined in Theorem 2 has the form
Proof.
Let X has density (2), then
and
Finally,
Conversely, if η is given as above, then
and hence
Now, in view of Theorem 2, X has density (2). □
Corollary 1.
Let \(X:\Omega \rightarrow \mathbb {R}\) be a continuous random variable and let q 2(x) be as in Proposition 4. The pdf of X is (2) if and only if there exist functions q 1 and η defined in Theorem 2 satisfying the differential equation
Remark 1.
(a) The general solution of the differential equation in Corollary 1 is
where D is a constant. One set of appropriate functions is given in Proposition 4 with \(D=\frac {1}{2}.\)
(b) Clearly there are other triplets of functions (q 2,q 1,η) satisfying the conditions of Theorem 2. We presented one such triplet in Proposition 4.
9.2 Characterizations based on single function of the random variable
In this subsection we employ a single function ψ of X and state characterization results in terms of ψ(X).
Proposition 5.
Let X:Ω→(0,∞) be a continuous random variable with cdf F(x). Let ψ(x) be a differentiable function on (0,∞) with \({\lim }_{\mathit {x\rightarrow \infty }}\psi \left (x\right)=1\). Then for δ≠1,
if and only if
Proof.
Proof is straightforward. □
Remark 2. For \(\psi \left (x\right)=\left [1-e^{-\lambda \left (\frac {G\left (x;\mathbf {\xi }\right)}{\overline {G}\left (x;\mathbf {\xi }\right)}\right)}\right ]^{\frac {\alpha \left (1-\delta \right)}{\delta }}, x\in \left (0,\infty \right)\), Proposition 5 will give a cdf F(x) given by (1).
Estimation
Inference can be carried out in three different ways: point estimation, interval estimation and hypothesis testing. Several approaches for parameter point estimation were proposed in the literature but the maximum likelihood method is the most commonly employed. The maximum likelihood estimates (MLEs) enjoy desirable properties and can be used when constructing confidence intervals and also in test-statistics. Large sample theory for these estimates delivers simple approximations that work well in finite samples. Statisticians often seek to approximate quantities such as the density of a test-statistic that depend on the sample size in order to obtain better approximate distributions. The resulting approximation for the MLEs in distribution theory is easily handled either analytically or numerically.
Here, consider the estimation of the unknown parameters of the OGE family by the method of maximum likelihood from complete samples only. Let x 1,…,x n be observed values from this family with parameters α, λ and ξ. Let Θ=(α,λ,ξ)⊤ be the (r×1) parameter vector. The total log-likelihood function for Θ is given by
where \(V(x_{i};\boldsymbol {\xi })=G(x_{i};\boldsymbol {\xi })/\overline {G}(x_{i};\boldsymbol {\xi })\).
The components of the score function \(U_{n}(\Theta) = \left (U_{\alpha },U_{\lambda },U_{\mathbf {\xi _{k}}}\right)^{\top }\) are
where v (ξ)(·) means the derivative of the function v with respect to ξ.
Setting these equations to zero and solving them simultaneously yields the MLEs \(\widehat {\Theta }= (\widehat {\alpha }, \widehat {\lambda }, \widehat {\boldsymbol {\xi }}\,)^{\top }\) of Θ=(α,λ,ξ)⊤. These equations cannot be solved analytically, and analytical softwares are required to solve them numerically.
For interval estimation of the parameters, we obtain the 3×3 observed information matrix J(Θ)={U rs } (for r,s=α,λ,ξ k ), whose elements are listed in Appendix A. Under standard regularity conditions, the multivariate normal \(N_{3}(0, J(\widehat \Theta)^{-1})\) distribution is used to construct approximate confidence intervals for the parameters. Here, \(J(\widehat \Theta)\) is the total observed information matrix evaluated at \(\widehat {\Theta }\). Then, the 100(1−γ)% confidence intervals for α, λ and ξ k are given by \(\hat {\alpha }\pm z_{\gamma ^{*}/2}\times \sqrt {var (\hat {\alpha })}\), \(\hat {\lambda }\pm z_{\gamma ^{*}/2}\times \sqrt {var (\hat {\lambda })}\) and \(\hat {\boldsymbol {\xi _{k}}}\pm z_{\gamma ^{*}/2}\times \sqrt {var (\hat {\boldsymbol {\xi _{k}}})}\), respectively, where the v a r(·)’s denote the diagonal elements of \(\phantom {\dot {i}\!}J(\widehat {\Theta })^{-1}\) corresponding to the model parameters, and \(z_{\gamma ^{*}/2}\phantom {\dot {i}\!}\) is the quantile (1−γ ∗/2) of the standard normal distribution.
10.1 Simulation study
We evaluate the performance of the maximum likelihood method for estimating the OGE-W parameters using Monte Carlo simulation for a total of twenty four parameter combinations and the process is repeated 200 times. Two different sample sizes n=100 and 300 are considered. The MLEs and their standard deviations of the parameters are listed in Table 2. The estimates of α, β and λ are determined by solving the nonlinear equations U(Θ)=0. Based on Table 2, we note that the ML method performs well for estimating the model parameters. Also, as the sample size increases, the biases and the standard deviations of the MLEs decrease as expected.
Applications
In this section, we provide two applications to real data to illustrate the importance of the OGE family by means of the OGE-W, OGE-Fr and OGE-N models presented in Section 3. We consider θ=1, b=1 and μ=0 for the OGE-W, OGE-Fr and OGE-N models, respectively, due to the fact that one scale parameter is enough for fitting these univariate models. The MLEs of the parameters for the these models are calculated and four goodness-of-fit statistics are used to compare the new family with its sub-models.
The first real data set represents the survival times of 121 patients with breast cancer obtained from a large hospital in a period from 1929 to 1938 (Lee 1992). The data examined by Ramos et al. (2013) are: 0.3, 0.3, 4.0, 5.0, 5.6, 6.2, 6.3, 6.6, 6.8, 7.4, 7.5, 8.4, 8.4, 10.3, 11.0, 11.8, 12.2, 12.3, 13.5, 14.4, 14.4, 14.8, 15.5, 15.7, 16.2, 16.3, 16.5, 16.8, 17.2, 17.3, 17.5, 17.9, 19.8, 20.4, 20.9, 21.0, 21.0, 21.1, 23.0, 23.4, 23.6, 24.0, 24.0, 27.9, 28.2, 29.1, 30.0, 31.0, 31.0, 32.0, 35.0, 35.0, 37.0, 37.0, 37.0, 38.0, 38.0, 38.0, 39.0, 39.0, 40.0, 40.0, 40.0, 41.0, 41.0, 41.0, 42.0, 43.0, 43.0, 43.0, 44.0, 45.0, 45.0, 46.0, 46.0, 47.0, 48.0, 49.0, 51.0, 51.0, 51.0, 52.0, 54.0, 55.0, 56.0, 57.0, 58.0, 59.0, 60.0, 60.0, 60.0, 61.0, 62.0, 65.0, 65.0, 67.0, 67.0, 68.0, 69.0, 78.0, 80.0,83.0, 88.0, 89.0, 90.0, 93.0, 96.0, 103.0, 105.0, 109.0, 109.0, 111.0, 115.0, 117.0, 125.0, 126.0, 127.0, 129.0, 129.0, 139.0, 154.0.
The second data set consists of 63 observations of the strengths of 1.5 cm glass fibres, originally obtained by workers at the UK National Physical Laboratory. Unfortunately, the units of measurement are not given in the paper. The data are: 0.55, 0.74, 0.77, 0.81, 0.84, 0.93, 1.04, 1.11, 1.13, 1.24, 1.25, 1.27, 1.28, 1.29, 1.30, 1.36, 1.39, 1.42, 1.48, 1.48, 1.49, 1.49, 1.50, 1.50, 1.51, 1.52, 1.53, 1.54, 1.55, 1.55, 1.58, 1.59, 1.60, 1.61, 1.61, 1.61, 1.61, 1.62, 1.62, 1.63, 1.64, 1.66, 1.66, 1.66, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.73, 1.76, 1.76, 1.77, 1.78, 1.81, 1.82, 1.84, 1.84, 1.89, 2.00, 2.01, 2.24. These data have also been analyzed by Smith and Naylor (1987).
The MLEs are computed using the Limited-Memory Quasi-Newton Code for Bound-Constrained Optimization (L-BFGS-B) and the log-likelihood function evaluated at the MLEs (\(\hat \ell \)). The measures of goodness of fit including the Akaike information criterion (AIC), Anderson-Darling (A ∗), Cramér–von Mises (W ∗) and Kolmogrov-Smirnov (K-S) statistics are computed to compare the fitted models. The statistics A ∗ and W ∗ are described in details in Chen and Balakrishnan (1995). In general, the smaller the values of these statistics, the better the fit to the data. The required computations are carried out in the R-language.
Tables 3 and 4 list the MLEs and their corresponding standard errors (in parentheses) of the model parameters. The numerical values of the model selection statistics \(\hat \ell \), AIC, A ∗, W ∗ and K-S are listed in Tables 5 and 6. We note from the figures in Table 5 that both OGE-W and OGE-Fr models have the lowest values of the AIC, A ∗, W ∗ and K-S statistics (for the first data set) as compared to their sub-models, suggesting that the OGE-W and OGE-Fr models provide the best fits. The histogram of the first data and the estimated pdfs and cdfs of the OGE-W and OGE-Fr models and their sub-models are displayed in Figure 8. Similarly, it is also evident from Table 6 that the OGE-N gives the lowest values for the AIC, A ∗ and W ∗ statistics while OGE-W models gives the lowest values for the AIC and K-S statistics (for the second data set) as compared to their sub-models, and therefore these models can be chosen as the best ones. The histogram of the second data and estimated pdfs and cdfs of the OGE-N and OGE-W distributions and their sub-models are displayed in Figure 9. It is clear from Tables 5 and 6, and Figures 8 and 9 that the OGE-W, OGE-Fr and OGE-N models provide better fits than their sub-models to these two data sets.
Concluding remarks
The generalized continuous distributions have been widely studied in the literature. We propose a new class of distributions called the odd generalized exponential family. We study some structural properties of the new family including an expansion for its density function. We obtain explicit expressions for the moments, generating function, mean deviations, quantile function and order statistics. The maximum likelihood method is employed to estimate the family parameters. We fit three special models of the proposed family to two real data sets to demonstrate the usefulness of the family. We use four goodness-of-fit statistics in order to verify which distribution provides better fit to these data. We conclude that these three special models provide consistently better fits than other competing models. We hope that the proposed family and its generated models will attract wider applications in several areas such as reliability engineering, insurance, hydrology, economics and survival analysis.
Appendix A
The observed information matrix for the parameter vector Θ=(α,λ,ξ k )⊤ is given by
whose elements are
where \(t^{\prime }_{k}(\cdot,\boldsymbol {\xi })=\partial \,\, t(\cdot,\boldsymbol {\xi })/\partial \, \boldsymbol {\xi _{k}}\) and \(t^{\prime \prime }_{\textit {kl}}(\cdot,\boldsymbol {\xi })=\partial ^{2}\,\, t(\cdot,\boldsymbol {\xi })/\partial \,\boldsymbol {\xi _{k}}\,\,\partial \, \boldsymbol {\xi _{l}}\).
References
Alexander, C, Cordeiro, GM, Ortega, EMM, Sarabia, JM: Generalized beta-generated distributions. Comput. Statist. Data. Anal. 56, 1880–1897 (2012).
Alizadeh, M, Emadi, M, Doostparast, M, Cordeiro, GM, Ortega, EMM, Pescim, RR: A new family of distributions: the Kumaraswamy odd log-logistic, properties and applications. Hacet. J. Math Stat (2015). forthcoming.
Aljarrah, MA, Lee, C, Famoye, F: On generating T-X family of distributions using quantile functions. J. Stat. Dist. Appl. 1, Art. 2 (2014).
Alzaatreh, A, Lee, C, Famoye, F: A new method for generating families of continuous distributions. Metron. 71, 63–79 (2013).
Alzaatreh, A, Lee, C, Famoye, F: T-normal family of distributions: A new approach to generalize the normal distribution. J. Stat. Dist. Appl. 1, Art, 16 (2014).
Alzaghal, A, Famoye, F, Lee, C: Exponentiated T-X family of distributions with some applications. Int. J. Probab. Statist. 2, 31–49 (2013).
Amini, M, MirMostafaee, SMTK, Ahmadi, J: Log-gamma-generated families of distributions. Statistics. 48, 913–932 (2014).
Bourguignon, M, Silva, RB, Cordeiro, GM: The Weibull-G family of probability distributions. J. Data Sci. 12, 53–68 (2014).
Chen, G, Balakrishnan, N: A general purpose approximate goodness-of-fit test. J. Qual. Tech. 27, 154–161 (1995).
Choudhury, A: A simple derivation of moments of the exponentiated Weibull distribution. Metrika. 62, 17–22 (2005).
Cordeiro, GM: de Castro, M: A new family of generalized distributions. J. Stat. Comput. Simul. 81, 883–893 (2011).
Cordeiro, GM, Nadarajah, S: Closed-form expressions for moments of a class of beta generalized distributions. Braz. J. Probab. Stat. 25, 14–33 (2011).
Cordeiro, GM, Ortega, EMM, da Cunha, DCC: The exponentiated generalized class of distributions. J. Data Sci. 11, 1–27 (2013).
Cordeiro, GM, Alizadeh, M, Ortega, EMM: The exponentiated half-logistic family of distributions: Properties and applications. J. Probab. Statist. Art.ID. 864396, 21 (2014a).
Cordeiro, GM, Ortega, EMM, Popović, BV, Pescim, RR: The Lomax generator of distributions: Properties, minification process and regression model. Appl. Math. Comput. 247, 465–486 (2014b).
Dey, AK, Kundu, D: Discriminating among the log-normal, Weibull and generalized exponential distributions. IEEE Trans. Reliab. 58, 416–424 (2009).
El-Gohary, A, Alshamrani, A, Al-Otaibi, AN: The generalized Gompertz distribution. Appl. Math. Model. 37, 13–24 (2013).
Eugene, N, Lee, C, Famoye, F: Beta-normal distribution and its applications. Commun. Stat. Theory Methods. 31, 497–512 (2002).
Fiorentino, M, Gioia, A, Iacobellis, V, Manfreda, S: Analysis on flood generation processes by means of a continuous simulation model. Adv. Geosci. 7, 231–236 (2006).
Glänzel, W: A characterization theorem based on truncated moments and its application to some distribution families. In: Mathematical Statistics and Probability Theory (Bad Tatzmannsdorf, 1986), Vol. B, Reidel, Dordrecht, pp. 75–84 (1987).
Gradshteyn, IS, Ryzhik, IM: Table of Integrals, Series, and Products. 6th eds. Academic Press, San Diego (2000).
Gupta, RC, Gupta, PI, Gupta, RD: Modeling failure time data by Lehmann alternatives. Commun. Stat. Theory Methods. 27, 887–904 (1998).
Gupta, RD, Kundu, D: Generalized exponential distribution. Aust. N. Z. J. Stat. 41, 173–188 (1999).
Gupta, RD, Kundu, D: Generalized exponential distribution: An alternative to Gamma and Weibull distributions. Biom. J. 43, 117–130 (2001a).
Gupta, RD, Kundu, D: Generalized exponential distribution: Different methods of estimations. J. Stat. Comput. Simul. 69, 315–337 (2001b).
Gupta, RD, Kundu, D: Discriminating between the Weibull and the GE distributions. Comput. Stat. Data Anal. 43, 179–196 (2002).
Gupta, RD, Kundu, D: Closeness of gamma and generalized exponential distributions. Commun. Stat. Theory Methods. 32, 705–721 (2003).
Gupta, RD, Kundu, D: Discriminating between the gamma and generalized exponential distributions. J. Stat. Comput. Simul. 74, 107–121 (2004).
Gupta, RD, Kundu, D: On comparison of the Fisher information of the Weibull and GE distributions. J. Stat. Plann. Inference. 136, 3130–3144 (2006).
Gupta, RD, Kundu, D: Generalized exponential distribution: Existing results and some recent developments. J. Stat. Plann. Inference. 137, 3537–3547 (2007).
Gupta, RD, Kundu, D: Generalized exponential distribution: Bayesian Inference. Comput. Stat. Data Anal. 52, 1873–1883 (2008).
Gupta, RD, Kundu, D: An extension of generalized exponential distribution. Stat. Methodol. 8, 485–496 (2011).
Iacobellis, V, Fiorentino, M: Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 36, 469–482 (2000).
Jones, MC: Families of distributions arising from the distributions of order statistics. Test. 13, 1–43 (2004).
Kilbas, AA, Srivastava, HM, Trujillo, JJ: Theory and applications of fractional differential equations. Elsevier, Amsterdam (2006).
Kundu, D, Gupta, RD, Manglick, A: Discriminating between the log-normal and the generalized exponential distributions. J. Stat. Plann. Inference. 127, 213–227 (2005).
Lee, ET: Statistical Methods for Survival Data Analysis. John Wiley, New York (1992).
Lehmann, EL: The power of rank tests. Ann. Math. Statist. 24, 23–43 (1953).
Marshall, AN, Olkin, I: A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika. 84, 641–652 (1997).
Mudholkar, GS, Hutson, AD: The exponentiated Weibull family: Some properties and a flood data application. Commun. Stat. Theory Methods. 25, 3059–3083 (1996).
Mudholkar, GS, Srivastava, DK: Exponentiated Weibull family for analyzing bathtub failure data. IEEE Trans. Reliab. 42, 299–302 (1993).
Mudholkar, GS, Srivastava, DK, Freimer, M: The exponentiated Weibull family: A reanalysis of the bus-motor failure data. Technometrics. 37, 436–445 (1995).
Nadarajah, S: Exact distribution of the peak streamflow. Water Resour. Res. 43(2), W02501 (2007). doi:10.1029/2006WR005300.
Nadarajah, S: The exponentiated exponential distribution: a survey. AStA Adv. Stat. Anal. 95, 219–251 (2011).
Nadarajah, S, Cordeiro, GM, Ortega, EMM: The exponentiated Weibull distribution: a survey. Stat. Papers. 54, 839–877 (2013).
Nadarajah, S, Cordeiro, GM, Ortega, EMM: The Zografos-Balakrishnan–G family of distributions: Mathematical properties and applications. Commun. Stat. Theory Methods. 44, 186–215 (2015).
Nadarajah, S, Kotz, S: A generalized logistic distribution. Int. J. Math. Math. Sci. 19, 3169–3174 (2005).
Nadarajah, S, Kotz, S: The exponentiated type distributions. Acta Appl. Math. 92, 97–111 (2006).
Pakyari, R: Discriminating between generalized exponential, geometric extreme exponential and Weibull distribution. J. Stat. Comput. Simul. 80, 1403–1412 (2010).
Prudnikov, AP, Bruychkov, YA: Marichev, Vol. 1. Gordon and Breach, New York (1986).
Ramos, MWA, Cordeiro, GM, Marinho, PRD, Dias, CRB, Hamedani, GG: The Zografos-Balakrishnan log-logistic distribution: Properties and applications. J. Stat. Theory Appl. 12, 225–244 (2013).
Rényi, A: On measures of entropy and information. In: Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability-I, pp. 547–561. University of California Press, Berkeley (1961).
Ristić, MM, Balakrishnan, N: The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 82, 1191–1206 (2012).
Shannon, CE: A mathematical theory of communication. Bell Sys. Tech. J. 27, 379–432 (1948).
Smith, RL, Naylor, JC: A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distributuion. Appl. Statist. 36, 358–369 (1987).
Tahir, MH, Cordeiro, GM, Alzaatreh, A, Mansoor, M, Zubair, M: The Logistic-X family of distributions and its applications. Commun. Stat. Theory Methods (2015a). forthcoming.
Tahir, MH, Zubair, M, Mansoor, M, Cordeiro, GM, Alizadeh, M, Hamedani, GG: A new Weibull-G family of distributions. Hacet. J. Math. Stat. (2015b). forthcoming.
Torabi, H, Montazari, NH: The gamma-uniform distribution and its application. Kybernetika. 48, 16–30 (2012).
Torabi, H, Montazari, NH: The logistic-uniform distribution and its application. Commun. Stat. Simul. Comput. 43, 2551–2569 (2014).
Zografos, K, Balakrishnan, N: On families of beta- and generalized gamma-generated distributions and associated inference. Stat. Methodol. 6, 344–362 (2009).
Acknowledgements
The authors would like to thank the Editor and the two referees for careful reading and for their comments which greatly improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors, viz MHT, GMC, MA, MM, MZ and GGH with the consultation of each other carried out this work and drafted the manuscript together. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tahir, M.H., Cordeiro, G.M., Alizadeh, M. et al. The odd generalized exponential family of distributions with applications. J Stat Distrib App 2, 1 (2015). https://doi.org/10.1186/s40488-014-0024-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40488-014-0024-2