Adjoint-consistent formulations of slip models for coupled electroosmotic flow systems

Abstract

Background

Models based on the Helmholtz `slip' approximation are often used for the simulation of electroosmotic flows. The objectives of this paper are to construct adjoint-consistent formulations of such models, and to develop adjoint-based numerical tools for adaptive mesh refinement and parameter sensitivity analysis.

Methods

We show that the direct formulation of the `slip' model is adjoint inconsistent, and leads to an ill-posed adjoint problem. We propose a modified formulation of the coupled `slip' model, which is shown to be well-posed, and therefore automatically adjoint-consistent.

Results

Numerical examples are presented to illustrate the computation and use of the adjoint solution in two-dimensional microfluidics problems.

Conclusions

An adjoint-consistent formulation for Helmholtz `slip' models of electroosmotic flows has been proposed. This formulation provides adjoint solutions that can be reliably used for mesh refinement and sensitivity analysis.

Background

Introduction

Emerging micro- and nano-electromechanical systems (MEMS/NEMS) have a growing number of applications, ranging from lab-on-a-chip DNA analysis to micro-actuators [1]. By scaling down processes, these systems offer savings in space, cost, and energy for scientific and technological advancement [2]. However, the high manufacturing costs and complex architectures of these systems necessitate the use of numerical simulation tools for optimal design and precise control of their operation [3]. Microfluidic devices operate over various length scales and are best described using multiphysics modeling that involves hydrodynamics, electroosmosis, and chemical species transport models. The development of accurate and efficient computational simulators of these devices is therefore challenging and resource intensive.

Numerical simulations of such complex engineering systems are typically targeted towards the calculation of specific Quantities of Interest (QoI) associated with the systems. Accurate estimation of local QoIs can be achieved using goal-oriented error estimation and adaptive techniques based on the use of adjoint methods [4],[5]. Adjoint methods can also be used to improve the computational performance of parameter sensitivity analyses [6], especially for systems with a large number of parameters. However, the application of adjoint methods to such coupled flow systems is an open area of study.

The objective of the current research work is to apply an adjoint-based Adaptive Finite Element Method (AFEM) to microfluidics problems for mesh refinement and parameter sensitivity analysis. There has been a growing interest in the modeling and numerical simulation of microfluidic systems [7]-[12]. A key issue that one faces while modeling and simulating microfluidic systems is the application of `slip' boundary conditions. Prachittham et al. [13] presented a space-time adaptive finite element method applied to an electroosmotic flow using large aspect ratio elements. However, their work did not consider adjoint techniques and did not use the `slip' boundary coupling condition. On the other hand, van Brummelen et al. [14] and Estep et al. [15] have shown the importance of the treatment of boundary flux coupling for the use of adjoint-based techniques. To our best knowledge, no advances in the application of adjoint-based techniques to microfluidics applications, particularly those involving `slip' boundary coupling, have yet been published in the literature.

In this work, we investigate coupled systems arising in electroosmotic flow (EOF). We show that a naive formulation of the `slip' model leads to an ill-posed adjoint problem and adjoint inconsistency [14]. We provide numerical evidence that the corresponding adjoint solution exhibits spurious oscillations on a simple example dealing with a straight channel flow. Accordingly, we propose a modified variational formulation of the `slip' model, for which the adjoint problem is well-posed and can be computed and used in adaptive mesh refinement and parameter sensitivity analysis.

The paper is organized as follows: Section "Microfluidics modeling" describes the `slip' electroosmotic flow (EOF) model, with a brief discussion of the relevant physics and the applicability of such a model. Then, a variational formulation for a modified version of the `slip' model is presented and its adjoint is derived in Section "Variational formulation of the slip BC EOF model". An analysis of the ill-posed adjoint problem for the naive formulation is presented in Section "Ill-posedness of the adjoint problem for the naive formulation". Next, a variational formulation using penalty boundary conditions (henceforth called the penalty formulation) is proposed in Section "Penalty formulation of the slip BC EOF model". This new formulation is also employed to derive the corresponding adjoint problem and it is shown that the adjoint problem thus obtained is asymptotically consistent with the one derived in Section "Variational formulation of the slip BC EOF model". Numerical experiments are presented in Section "Results and discussion" that support the fact that the adjoint problem obtained using the penalty formulation is well-posed and that the adjoint solution is free of spurious artifacts. The adjoint obtained using the penalty formulation is used for goal-oriented adaptive mesh refinement and sensitivity analyses for a T-channel problem. Section "Conclusions" provides some concluding remarks, followed by a discussion of further work and future applications related to this class of coupled flow models. Finally, the appendix elaborates on the well-posedness of the modified formulation and presents relevant theoretical developments.

Microfluidics modeling

Microfluidics is the branch of fluid mechanics concerned with the understanding, modeling, and control of flows that occur on the micron scale, i.e. where the characteristic length (L) is of the order 10⁻⁶ m. Squires and Quake [16], and later Whitesides [17], have presented reviews of the physics and applications of microfluidics. Prominent among them are microflows driven by applied electric fields, through electroosmosis, electrophoresis, or both. In this paper, we consider electroosmotic flow devices, which find wide use in commercial and industrial applications [8],[18]. These devices utilize the properties of the electric double layer (also called the Debye layer) to drive a bulk fluid flow. More detailed descriptions of the electric double layer and electroosmotically driven microfluidic devices can be found in the microfluidics literature [1],[19],[20].

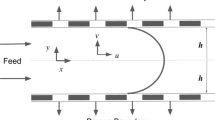
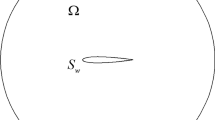
Consider a rectangular open domain $\Omega ·{\subset }^d$, with d = 2, and boundary ∂ Ω. The boundary ∂ Ω is composed of the channel wall Γ _w and its inlet/outlet Γ _io , such that $\mathrm{\partial \Omega }=\stackrel{•}{{\Gamma }_w·{\Gamma }_{\mathit{\text{io}}}}$. For simplicity, we consider a single species flow through the channel. The one-way coupled, steady-state EOF in a straight rectangular channel can be modeled with the following system of equations,

$$\begin{array}{ll}-\mathrm{\Delta \psi }=K^{2}sinh\left(\psi \right)& \text{in}\Omega ,\end{array}$$

(1a)

$$\begin{array}{ll}-\Delta ·({\sigma }_c\nabla \phi )=0& \text{in}\Omega ,\end{array}$$

(1b)

$$\begin{array}{ll}-\mathrm{\mu \Delta }\mathbf{u}+\nabla \mathit{\text{p}}=-{\rho }_{\mathit{\text{e}}}\left(\Psi \right)\nabla \phi & \text{in}\Omega ,\end{array}$$

(1c)

$$\begin{array}{ll}\nabla ·\mathbf{u}=0& \text{in}\Omega ,\end{array}$$

(1d)

where Ψ is the non-dimensional electric potential associated with the double layer, K is a non-dimensional constant, called the Debye-Huckel parameter, φ is the applied potential, σ _c is the fluid conductivity, and u and p are the flow velocity and pressure, respectively. The charge density is given by ρ _e =−2z _v n _∞ e sinh(Ψ) and μ is the viscosity of the fluid. The parameters that the charge density depends on are the ion valence z _v , electron charge e, and the bulk concentration of ions n _∞ . The above equations are supplemented with the boundary conditions,

$$\begin{array}{ll}\Psi ={\Psi }_0& \text{on}{\Gamma }_w,\end{array}$$

(2a)

$$\begin{array}{ll}\mathbf{n}·\nabla \Psi =0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(2b)

$$\begin{array}{ll}\mathbf{n}·({\sigma }_c\nabla \Phi )=0& \text{on}{\Gamma }_w,\end{array}$$

(2c)

$$\begin{array}{ll}\phi ={\phi }_{\mathit{\text{io}}}& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(2d)

$$\begin{array}{ll}\mathbf{u}=0& \text{on}{\Gamma }_w,\end{array}$$

(2e)

$$\begin{array}{ll}\mathbf{u}·\mathbf{t}=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(2f)

$$\begin{array}{ll}\mathbf{n}·(\mathit{\sigma }·\mathbf{n})=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(2g)

where Ψ₀ is the electric zeta potential on the walls Γ _w of the channel, φ _io is the external potential applied at the inlet and outlet of the channel Γ _io , n is the unit outward normal vector to ∂ Ω, t is a unit tangential vector along ∂ Ω, and σ is the stress tensor:

$$\mathit{\sigma }=-p\mathbf{I}+\mu \left(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T\right).$$

(3)

The no-slip condition (Eq. (2e)) is applied at the channel walls for the flow velocity. The no-slip conditions, in combination with the body force term in Eq. (1c), which is significant only near the boundary, lead to sharp velocity boundary layer near the wall. This makes the system given by Eq. (1) and Eq. (2) multi-scale. Note that the last two boundary (Eq. (2f) and (2g)) conditions imply that the velocity is normal to Γ _io and that the pressure vanishes on Γ _io (this is in the case of planar boundaries, see [21]), i.e.

$$p=0\text{on}{\Gamma }_{\mathit{\text{io}}}.$$

(4)

Eqs. 1 and (2) define the complete EOF model and constitute a challenging system of coupled multiscale equations. They are computationally expensive, especially for complex geometries, due to the presence of extremely sharp layers near the channel walls because of the electric double layer. Therefore, to reduce the complexity and the computational cost associated with the full model, the Helmholtz-Smoluchowski velocity approximation is introduced into the model. The approximation states that the body-force term in the Stokes equations can be replaced by an effective `slip velocity' on Γ _w as,

$${\mathbf{u}}_{\text{wall}}=\frac{є{\Psi }_0}{\mu }(-\nabla \Phi )=\lambda \mathbf{E},$$

(5)

where E denotes the applied electric field, and a new parameter λ=є Ψ₀/μ has been introduced. Here, є is the permitivity (or dielectric constant) of the fluid medium. A detailed derivation of this approximation can be found in a standard reference [19]. The validity of this approximation has been verified for several examples through both experiments and numerical simulations [10].

The associated slip model of EOF can thus be written as:

$$\begin{array}{ll}-\nabla ·({\sigma }_c\nabla \phi )=0& \text{in}\Omega ,\end{array}$$

(6a)

$$\begin{array}{ll}-\mathrm{\mu \Delta }\mathbf{u}+\nabla p=\mathbf{0}& \text{in}\Omega ,\end{array}$$

(6b)

$$\begin{array}{ll}\nabla ·\mathbf{u}=0& \text{in}\Omega ,\end{array}$$

(6c)

complemented by the boundary conditions,

$$\begin{array}{ll}{\sigma }_c{\partial }_n\phi =0& \text{on}{\Gamma }_w,\end{array}$$

(7a)

$$\begin{array}{ll}\phi ={\phi }_{\mathit{\text{io}}}& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(7b)

$$\begin{array}{ll}\mathbf{u}+\lambda \nabla \phi =\mathbf{0}& \text{on}{\Gamma }_w,\end{array}$$

(7c)

$$\begin{array}{ll}\mathbf{u}·\mathbf{t}=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(7d)

$$\begin{array}{ll}\mathbf{n}·(\mathit{\sigma }·\mathbf{n})=0& \text{on}{\Gamma }_{\mathit{\text{io}}}.\end{array}$$

(7e)

We see that the slip model spares one from solving the Poisson-Boltzmann equation, whose solution exhibits a thin layer near the wall. As a remark, the slip boundary approximation model given by Eq. (6) and (7) is widely used throughout the microfluidics research and development community for modeling and simulation [1]. The model is even included in the commercial Finite Element software package COMSOL Multiphysics [12].

The slip condition/coupling makes sense only in the direction tangent to the wall. In Eq. (7c), the no-flux boundary condition on the potential (Eq. (7a)) automatically enforces a no penetration boundary condition on the velocity. Thus, expressing the coupling condition as Eq. (5) is a matter of convenience from a notational standpoint. However, as shown in Section "Ill-posedness of the adjoint problem for the naive formulation", using Eq. (5) as such in the formulation of the coupled problem leads to an ill-posed adjoint problem. This ill-posedness will also be illustrated on numerical examples in Section "Results and discussion". We decouple one of the velocity components from the potential as follows,

$$\left\{\begin{array}{c}\mathbf{u}·\mathbf{t}+\lambda {\partial }_t\phi =0\\ \mathbf{u}·\mathbf{n}+\lambda {\partial }_n\phi =0\end{array}\right.\Rightarrow \left\{\begin{array}{c}\mathbf{u}·\mathbf{t}+\lambda {\partial }_t\phi =0,\\ \mathbf{u}·\mathbf{n}=0,\end{array}\right.$$

(8)

where we have denoted the normal (∇φ•n) and tangential (∇φ•t) derivatives of φ by ∂ _n φ and ∂ _t φ, respectively. This coupling is equivalent to the one given by Eq. (7c). We now proceed to derive the weak formulation for Eq. (6) using the modified coupling given by Eq. (8).

Methods

Variational formulation of the slip BC EOF model

Variational formulation of primal problem

We derive here the weak formulation of the equations in Eq. (6) and then combine them to give the coupled problem. The potential φ satisfies,

$$\begin{array}{ll}-\nabla ·({\sigma }_c\nabla \phi )=0& \text{in}\Omega ,\end{array}$$

(9a)

$$\begin{array}{ll}\phi ={\phi }_{\mathit{\text{io}}}& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(9b)

$$\begin{array}{ll}{\sigma }_c{\partial }_n\phi =0& \text{on}{\Gamma }_w,\end{array}$$

(9c)

We define C⁺(Ωs) as the space of continuous, strictly positive functions on Ω, and assume that the conductivity σ _c ЄC⁺(Ω). This assumption allows us to simplify the analysis later on and can be easily relaxed. We now introduce the spaces of admissible trial and test functions:

$$\begin{array}{ll}Z& =H^1\left(\Omega \right),\end{array}$$

(10)

$$\begin{array}{ll}{Z}_0& =\{vЄZ;v=0\text{on}{\Gamma }_{\mathit{\text{io}}}\},\end{array}$$

(11)

$$\begin{array}{ll}{Z}_{\mathit{\text{io}}}& =\{vЄZ;v={\phi }_{\mathit{\text{io}}}\text{on}{\Gamma }_{\mathit{\text{io}}}\}.\end{array}$$

(12)

We can use a lift function $\tilde{\phi }ЄZ_{\mathit{\text{io}}}$ such that $\phi =\phi +\tilde{\phi }$ with φЄZ₀. In this case, the weak form of the problem is given by:

$$\begin{array}{ll}\text{Given}{\sigma }_cЄ{\text{C}}^{+}\left(\Omega \right)\text{and}\tilde{\phi }ЄZ_{\mathit{\text{io}}},\text{find}& \phi ЄZ_0\text{such that}\\ \underset{\Omega }{\int }{\sigma }_c\nabla \phi .\nabla \Psi \mathit{\text{dx}}& =-\underset{\Omega }{\int }{\sigma }_c\nabla \tilde{\phi }.\nabla \psi \mathit{\text{dx}},\forall \psi ЄZ_0.\end{array}$$

(13)

We now consider the non-dimensionalized stationary Stokes equations (with μ=1) with slip boundaries,

$$\begin{array}{ll}-\Delta \mathbf{u}+\nabla \mathit{\text{p}}=\mathbf{0}& \text{in}\Omega ,\end{array}$$

(14a)

$$\begin{array}{ll}\nabla .\mathbf{u}=0& \text{in}\Omega ,\end{array}$$

(14b)

$$\begin{array}{ll}\mathbf{u}.\mathbf{t}+\lambda {\partial }_t\phi =0& \text{on}{\Gamma }_w,\end{array}$$

(14c)

$$\begin{array}{ll}\mathbf{u}.\mathbf{n}=0& \text{on}{\Gamma }_w,\end{array}$$

(14d)

$$\begin{array}{ll}\mathbf{u}.\mathbf{t}=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(14e)

$$\begin{array}{ll}\mathbf{n}.(\mathit{\sigma }.\mathbf{n})=0& \text{on}{\Gamma }_{\mathit{\text{io}}}.\end{array}$$

(14f)

We look for the velocity and pressure fields in the function spaces,

$$\begin{array}{ll}X& ={\left[H^1\left(\Omega \right)\right]}^2,\end{array}$$

(15a)

$$\begin{array}{ll}{X}_0& =\left\{\mathbf{v}ЄX;\mathbf{v}=\mathbf{0}\text{on}{\Gamma }_w,\mathbf{v}.\mathbf{t}=0\text{on}{\Gamma }_{\mathit{\text{io}}}\right\},\end{array}$$

(15b)

$$\begin{array}{ll}M& =\left\{pЄL^2\left(\Omega \right);\underset{\Omega }{\int }p\mathit{\text{dx}}=0\right\}.\end{array}$$

(15c)

Eq. (14c) requires that Φ lie in the space H²(Ω). Note that if ∂ Ω is Lipschitz and convex, or C¹-continuous, then the elliptic regularity theorem guarantees that Φ∈H²(Ω). However, to derive a well-posed adjoint problem for the slip EOF model, we need to enforce the coupling boundary conditions in a weak sense. In fact, if we enforce the condition in a weak sense, the curl theorem shows that it is sufficient to have Φ∈Z. Consider the function space $H_0^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)$,

$$H_0^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)=\{vЄH^{\frac{1}{2}}(\mathrm{\partial \Omega });v=0\text{on}{\Gamma }_{\mathit{\text{io}}}\}.$$

(16)

We have the following proposition.

Proposition 1.

Let Ω be Lipschitz. Further, let Φ∈Z, and $w,g\in H_0^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)$. Define and

(17)

is well-posed, and

$$║g{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}\le \text{c}\left(\Omega \right)\left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)},$$

(18)

where c(Ω) is a positive constant that depends only on the domain Ω.

Proof.

Since the bilinear form b(g,w) is defined using the $H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)$ inner product, it is bounded and coercive. We can use the curl theorem and a special extension of w to show the boundedness of f(w),

Consider an H¹(Ω) extension of the function w, denoted by $\tilde{w}$. From corollary B. 53, on page 488 in [22], we know that for each $wЄH^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)$, there exists an extension w^*ЄH¹(Ω), such that,

$$║w^{║}{*}_{H^1\left(\Omega \right)}\le \text{c}\left(\Omega \right)║w{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}.$$

(19)

From Proposition 12 in (F.J. Sayas: Weak normal derivatives, normal and tangential traces, and tangential differential operators on Lipschitz boundaries, unpublished), we have,

Using the fact that the gradient of the curl is the zero vector, and the vector cross product identity, we have,

$$f\left(w\right)=-\lambda \underset{\Omega }{\int }\left(\nabla \Phi \times \nabla w^{*}\right).\mathbf{k}.$$

(20)

We then easily have the following bound on |f(w)|,

$$\begin{array}{ll}\left|f\right(w\left)\right|& \le \left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)}║w^{*}{║}_{H^1\left(\Omega \right)},\\ \le \left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)}\text{c}\left(\Omega \right)║w{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}.\end{array}$$

(21)

Therefore, $║f{║}_{H^{\Omega \frac{1}{2}}}\le \text{c}\left(\Omega \right)\left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)}$, and an application of the Lax-Milgram theorem gives the well-posedness of the variational problem, and the bound $║g{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}\le \text{c}\left(\Omega \right)\left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)}$. □

We can now define the operator ℓ:Z→X,

$$\begin{array}{ll}\mathit{\ell }\left(\Phi \right)& =(g,0)\text{on}\mathrm{\partial \Omega },\text{where}g\text{satisfies Eq. (17)},\end{array}$$

(22a)

$$\begin{array}{ll}║\mathit{\ell }\left(\Phi \right){║}_X& \le \text{c}║g{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}.\end{array}$$

(22b)

The bounded extension corollary B. 53, on page 488 in [22] implies that there is at least one possible lift for any given Φ. For the purposes of deriving the variational formulation, we can pick any admissible lift. It is trivial to show that the operator ℓ is linear. Proposition 1 further gives,

$$║\mathit{\ell }\left(\Phi \right){║}_X\le \text{c}║g{║}_{H^{\frac{1}{2}}\left(\mathrm{\partial \Omega }\right)}\le \text{c}\left(\Omega \right)\left|\lambda \right|║\Phi {║}_{H^1\left(\Omega \right)}.$$

(23)

Therefore, ℓ is a bounded operator. Using this lift operator, we can write $\mathbf{u}=\mathbf{w}+\mathit{\ell }\left(\Phi \right)=\mathbf{w}+\mathit{\ell }\left(\phi \right)+\mathit{\ell }\left(\tilde{\Phi }\right)$, where w∈X₀, and write a weak form for Eq. (14),

$$\begin{array}{c}\text{Given}\Phi \in Z,\text{find}(\mathbf{w},p)\in X_0·M\text{such that},\\ \underset{\Omega }{\int }\left[\nabla \mathbf{w}.\nabla \mathbf{v}-p\nabla .\mathbf{v}-q\nabla .\mathbf{w}\right]\mathit{\text{dx}}\\ =-\underset{\Omega }{\int }\left[\nabla \mathit{\ell }\left(\phi \right).\nabla \mathbf{v}-q\nabla .\mathit{\ell }\left(\phi \right)\right]\mathit{\text{dx}}\forall (\mathbf{v},q)\in X_0·\mathrm{M.}\end{array}$$

(24)

Combining Eq. (13) and Eq. (24) together, we get the coupled variational statement:

$$\begin{array}{c}\text{Given}{\sigma }_c\in {\text{C}}^{+}\left(\Omega \right)\text{and}\tilde{\phi }\in Z_b,\text{find}(\phi ,\mathbf{w},p)\in Z_0\times X_0\times M\text{such that},\\ \underset{\Omega }{\int }{\sigma }_c\nabla \phi ·\nabla \psi \mathit{\text{dx}}\\ +\underset{\Omega }{\int }\left[\nabla [\mathbf{w}+\mathit{\ell }(\phi \left)\right]·\nabla \mathbf{v}-p\nabla ·\mathbf{v}\nabla q\nabla ·[\mathbf{w}+\mathit{\ell }(\phi \left)\right]\right]\mathit{\text{dx}}\\ =-\underset{\Omega }{\int }{\sigma }_c\nabla \tilde{\Phi }·\nabla \psi \mathit{\text{dx}}\\ -\underset{\Omega }{\int }\left[\nabla \mathit{\ell }\left(\tilde{\Phi }\right)·\nabla \mathbf{v}-q\nabla ·\mathit{\ell }\left(\tilde{\phi }\right)\right]\mathit{\text{dx}}\forall (\psi ,\mathbf{v},q)\in Z_0\times X_0\times M,\end{array}$$

(25)

where we emphasize that the integrals involving the lift velocity, which depend on the solution φ, will be part of the bilinear form for this coupled problem. We can recast the bilinear form above in more compact notation as,

$$\begin{array}{ll}\text{Given}{\sigma }_c\in {\text{C}}^{+}\left(\Omega \right)\text{and}\tilde{\phi }\in Z_b,\text{find}& \mathbf{U}\in Z_0·X_0\times M\text{such that},\\ A(\mathbf{U},\mathbf{V})& =F\left(\mathbf{V}\right)\forall \mathbf{V}\in Z_0\times X_0\times M,\end{array}$$

(26)

where U = (φ,w,p) and V = (ψ,v,q).

We have thus incorporated the coupling condition within our bilinear form and can prove that the coupled problem (26) is well-posed. We refer the interested reader to Appendix A and proceed with the derivation of the corresponding adjoint problem.

Adjoint problem

Given the primal weak form Eq. (26), we have the corresponding weak form for the adjoint problem associated with the quantity of interest $Q:Z_0\times X_0\times M\to ℝ$

$$\begin{array}{ll}\text{Given}{\sigma }_c\in {\text{C}}^{+}\left(\Omega \right),\text{find}& U^{*}\in Z_0\times X_0\times M\text{such that},\\ A(\mathbf{V},U^{*})& =Q\left(\mathbf{V}\right)\forall \mathbf{V}\in Z_0\times X_0\times M,\end{array}$$

(27)

where U^∗ = (φ^*,w^*,p^∗) is the adjoint solution and Q(U) is a linear functional that corresponds to the quantity of interest (QoI). The full weak form for the adjoint problem reads,

$$\begin{array}{l}\underset{\Omega }{\int }{\sigma }_c\nabla \psi ·\nabla {\phi }^{*}\mathit{\text{dx}}+\underset{\Omega }{\int }(\nabla \mathbf{v}·\nabla w^{*}-q\nabla ·w^{*}-p^{*}\nabla ·\mathbf{v})\mathit{\text{dx}}\\ +\underset{\Omega }{\int }(\nabla \mathit{\ell }(\psi )·\nabla w^{*}-\nabla ·\mathit{\ell }(\psi \left)p^{*}\right)\mathit{\text{dx}}\\ =Q\left(\mathbf{V}\right)\forall \mathbf{V}=(\psi ,\mathbf{v},q)\in Z_0\times X_0\times \mathrm{M.}\end{array}$$

(28)

Note that the adjoint Stokes problem solution w^* and p^* are coupled to the adjoint potential φ^* through the lift operator ℓ(.) acting on the test function ψ. The adjoint problem (28) is also well-posed, see Corollary 2 in Appendix A.

We recall that applying the forward coupling condition Eq. (14c) in a strong sense required that the forward potential φ∈H²(Ω). Correspondingly, to obtain a strong form corresponding to Eq (28), we require that the adjoint velocity w^*∈[H²(Ω)]² and the adjoint pressure p^*∈H¹(Ω). We also have the adjoint stress tensor,

$${\mathit{\sigma }}^{*}=-p^{*}\mathbf{I}+(\nabla {\mathbf{u}}^{*}+{(\nabla {\mathbf{u}}^{*})}^T).$$

(29)

Now integrating by parts we obtain,

$$\begin{array}{ll}\underset{\Omega }{\int }& -\nabla ·({\sigma }_c\nabla {\phi }^{\ast })\Psi \mathit{\text{dx}}+\underset{\mathrm{\partial \Omega }}{\int }{\sigma }_c{\partial }_n{\phi }^{\ast }\Psi \mathit{\text{ds}}\\ +\underset{\Omega }{\int }-\nabla ·{\mathit{\sigma }}^{\ast }·\left(\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right)+\underset{\mathrm{\partial \Omega }}{\int }\left(\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right)·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}\\ +\underset{\Omega }{\int }-q\nabla ·w^{\ast }\mathit{\text{dx}}=Q\left(\mathbf{V}\right).\end{array}$$

(30)

The boundary term in the formulation of the adjoint problem becomes

$$\begin{array}{c}\underset{\mathrm{\partial \Omega }}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }\underset{0}{\underset{\#}{\left(\mathbf{n}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)}}\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)+\underset{-\lambda {\partial }_t\Psi \left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)}{\underset{\#}{\left(\mathbf{t}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)}}\mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)+\underset{0}{\underset{\#}{\left(\mathbf{t}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)}}\left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }\left[{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathbf{t}\right]\Psi \mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·\mathbf{v}\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)\mathit{\text{ds}},\end{array}$$

(31)

where we have used integration by parts for the tangential derivative term along Γ _w [23],

$$\underset{{\Gamma }_w}{\int }-\left(\lambda {\partial }_t\Psi \right)(\mathbf{t}·\mathbf{z})\mathit{\text{ds}}=\underset{{\Gamma }_w}{\int }\left[{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·\mathbf{z}\right)\mathbf{t}\right]\Psi \mathit{\text{ds}},$$

(32)

where ${\nabla }_{{\Gamma }_w}·\mathbf{v}$ denotes the surface divergence of the vector v. Replacing these terms in the adjoint formulation and setting,

$$Q\left(\mathbf{U}\right)=\underset{\Omega }{\int }k\left(\mathbf{x}\right)\mathbf{u}·\mathit{\alpha }\mathit{\text{dx}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }{k}_s\left(s\right)\mathbf{u}·\mathbf{n}\mathrm{ds.}$$

(33)

We can write Eq. (31) as,

$$\begin{array}{l}\underset{\Omega }{\int }\Psi \left[-\nabla ·({\sigma }_c\nabla {\phi }^{\ast })\right]\mathit{\text{dx}}+\underset{{\Gamma }_w}{\int }\Psi \left[\mathbf{n}·({\sigma }_c\nabla {\phi }^{\ast })+{\nabla }_{{\Gamma }_w}·\left(\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathbf{t}\right)\right]\mathit{\text{ds}}\\ -\underset{\Omega }{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·\left(\nabla ·{\mathit{\sigma }}^{\ast }+k\left(\mathbf{x}\right)\mathbf{\alpha }\right)+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n}-k_s(s\left)\right)\right)\mathit{\text{ds}}\\ -\underset{\Omega }{\int }q\left[\nabla ·{\mathbf{w}}^{\ast }\right]\mathit{\text{dx}}=0\forall (\Psi ,\mathbf{v},q)\in Z_0·X_0·\mathrm{M.}\end{array}$$

(34)

The strong form of the adjoint system then reads:

$$\begin{array}{ll}\nabla ·({\sigma }_c\nabla {\phi }^{\ast })=0& \text{in}\Omega ,\end{array}$$

(35a)

$$\begin{array}{ll}-\nabla {\mathbf{w}}^{\ast }+\nabla p^{\ast }=k\mathit{\alpha }& \text{in}\Omega ,\end{array}$$

(35b)

$$\begin{array}{ll}{\mathbf{w}}^{\ast }=0& \text{in}\Omega ,\end{array}$$

(35c)

with three boundary conditions on Γ _io :

$$\begin{array}{ll}{\phi }^{\ast }=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(36a)

$$\begin{array}{ll}{\mathbf{w}}^{\ast }·\mathbf{t}=0& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(36b)

$$\begin{array}{ll}\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})=k_s& \text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(36c)

and three boundary conditions on Γ _w :

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\phi }^{\ast }+{\nabla }_{{\Gamma }_w}·\left(\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathbf{t}\right)=0& \text{on}{\Gamma }_w,\end{array}$$

(37a)

$$\begin{array}{ll}{\mathbf{w}}^{\ast }=0& \text{on}{\Gamma }_w.\end{array}$$

(37b)

We readily observe that the adjoint Stokes problem can be solved first, independently of the adjoint potential problem, but that the latter does depend on the former through the Neumann coupling condition Eq. (37a). We also note that this coupling condition involves the tangential derivatives of the adjoint stress tensor on the boundary.

Ill-posedness of the adjoint problem for the naive formulation

If both the normal and tangential coupling components are considered in the formulation of the primal problem, the corresponding adjoint boundary integrals (see Eq. (31)) would read,

$$\begin{array}{c}\underset{\mathrm{\Omega \partial }}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]·({\sigma }^{\ast }·\mathbf{n})\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }\left(\mathbf{n}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)+\underset{-\lambda {\partial }_t\Psi \left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)}{\underset{\#}{\left(\mathbf{t}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)}}\mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)+\underset{0}{\underset{\#}{\left(\mathbf{t}·\left[\mathbf{v}+\mathit{\ell }\left(\Psi \right)\right]\right)}}\left(\mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathit{\text{ds}}\\ =\underset{{\Gamma }_w}{\int }-\lambda {\partial }_n\Psi \left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)+\underset{{\Gamma }_w}{\int }\left[{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathbf{t}\right]\Psi \mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·\mathbf{v}\right)\left(\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})\right)\mathrm{ds.}\end{array}$$

The boundary conditions on Γ _w for the strong form of the adjoint system would then read:

$$\begin{array}{ll}\mathbf{n}·({\sigma }_c\nabla {\phi }^{\ast })+{\nabla }_{{\Gamma }_w}·\left(\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\right)\mathbf{t}\right)=0& \text{on}{\Gamma }_w,\end{array}$$

(38a)

$$\begin{array}{ll}\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})=0& \text{on}{\Gamma }_w,\end{array}$$

(38b)

$$\begin{array}{ll}{\mathbf{w}}^{\ast }=0& \text{on}{\Gamma }_w.\end{array}$$

(38c)

Thus the adjoint problem for the ill-posed primal problem contains four boundary conditions, despite there being only three variables. Therefore, the ill-posed primal problem leads to an adjoint inconsistent formulation, specifically in the boundary terms. Such an adjoint inconsistency can lead to oscillations in the discrete solutions of the adjoint problem [24].

Penalty formulation of the slip BC EOF model

Penalty formulation of the primal problem

The imposition of the boundary conditions for the primal and adjoint problems derived in the previous section can be extremely challenging, mainly due to the regularity requirements for the corresponding spaces in the interior and the difficulty of constructing appropriate Finite Element spaces. Therefore, we seek to impose the coupling constraint using a penalty method and relax the regularity requirements on the spaces containing the primal solution and the adjoint. The penalty method is an easy and robust approach for applying Dirichlet boundary conditions. See [25] and [26] for analysis of the method. As we shall see, the penalty method is a natural method for weak enforcement of the coupling. In addition, the penalty formulation gives us an adjoint that is asymptotically consistent with the one obtained using the lift technique. The variational formulation Eq. (25) with equivalent penalty boundary conditions can be given as:

$$\begin{array}{l}\text{Given}{\sigma }_c\in {\text{C}}^{+}\left(\Omega \right)\text{and}{\Phi }_{\mathit{\text{io}}}\in H^{\frac{1}{2}}\left({\Gamma }_{\mathit{\text{io}}}\right),\text{find}({\Phi }_{\in },{\mathbf{u}}_{\in },p_{\in })\in Z·X·M\text{such that},\\ \underset{\Omega }{\int }{\sigma }_c\nabla {\Phi }_{\in }·\nabla \Psi \mathit{\text{dx}}+\frac{1}{\in }\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }{\Phi }_{\in }\Psi \mathit{\text{ds}}+\underset{\Omega }{\int }\left[\nabla {\mathbf{u}}_{\in }·\nabla \mathbf{v}-p_{\in }\nabla ·\mathbf{v}-q\nabla ·{\mathbf{u}}_{\in }\right]\mathit{\text{dx}}\\ +\frac{1}{\in }\underset{{\Gamma }_w}{\int }({\mathbf{u}}_{\in }·\mathbf{n})(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}+\frac{1}{\in }\underset{{\Gamma }_w}{\int }({\mathbf{u}}_{\in }·\mathbf{t})(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}+\frac{1}{\in }\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }({\mathbf{u}}_{\in }·\mathbf{t})(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}\\ +\frac{1}{\in }\underset{{\Gamma }_w}{\int }\lambda \left({\partial }_t{\Phi }_{\in }\right)(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}=\frac{1}{\in }\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }{\Phi }_{\mathit{\text{io}}}\Psi \mathit{\text{ds}}\forall (\Psi ,\mathbf{v},q)\in Z·X·\mathrm{M.}\end{array}$$

(39)

As was done in Eq. (26), we can recast the bilinear form above in more compact notation as,

$$\begin{array}{ll}\text{Given}{\sigma }_c\in {\text{C}}^{+}\left(\Omega \right)\text{and}{\Phi }_{\mathit{\text{io}}}\in H^{\frac{1}{2}}\left({\Gamma }_{\mathit{\text{io}}}\right),\text{find}& {\mathbf{U}}_{\in }\in Z·X·M\text{such that},\\ A_{\in }({\mathbf{U}}_{\in },\mathbf{V})=F_{\in }\left(\mathbf{V}\right)& \forall \mathbf{V}\in Z·X·M,\end{array}$$

(40)

where U _∈ = (Φ _∈ ,u _∈ ,p _∈ ) and V = (Ψ,v,q). We now verify that the weak form in Eq. (39) is indeed consistent and converges to the BVP Eq. (9) and Eq. (14) in the limit as the penalty parameter ∈ tends to zero. Integrating Eq. (39) by parts, we obtain,

$$\begin{array}{ll}\underset{\Omega }{\int }& -\nabla ·({\sigma }_c\nabla {\Phi }_{\in })\Psi \mathit{\text{dx}}+\underset{{\Gamma }_w}{\int }{\sigma }_c{\partial }_n{\Phi }_{\in }\Psi \mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left({\sigma }_c{\partial }_n{\Phi }_{\in }+\frac{1}{\in }({\Phi }_{\in }-{\Phi }_{\mathit{\text{io}}})\right)\Psi \mathit{\text{ds}}\\ +\underset{\Omega }{\int }\left(\left(-\nabla {\mathbf{u}}_{\in }+\nabla p_{\in }\right)·\mathbf{v}-q\nabla ·{\mathbf{u}}_{\in }\right)\mathit{\text{ds}}\\ +\underset{{\Gamma }_w}{\int }\left(\mathbf{n}·({\mathit{\sigma }}_{\in }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }·\mathbf{n})\right)(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}\\ +\underset{{\Gamma }_w}{\int }\left(\mathbf{t}·({\mathit{\sigma }}_{\in }·\mathbf{n})+\frac{1}{\in }\left(\lambda {\partial }_t{\Phi }_{\in }\right)+{\mathbf{u}}_{\in }·\mathbf{t})\right)(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }(\mathbf{n}·({\mathit{\sigma }}_{\in }·\mathbf{n}\left)\right)(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{t}·(\mathit{\sigma }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }·\mathbf{t})\right)\mathbf{v}·\mathbf{t}\mathit{\text{ds}}=0\forall (\Psi ,\mathbf{v},q)\in Z\times X\times M,\end{array}$$

(41)

where σ _∈ is the stress tensor corresponding to the penalized solution,

$${\mathit{\sigma }}_{\in }=-p_{\in }\mathbf{I}+(\nabla {\mathbf{u}}_{\in }+{(\nabla {\mathbf{u}}_{\in })}^T).$$

(42)

The equivalent strong form for finite non-zero ∈ is,

$$\begin{array}{ll}-\nabla ·({\sigma }_c\nabla {\Phi }_{\in })& =0\text{in}\Omega ,\end{array}$$

(43a)

$$\begin{array}{ll}-\nabla {\mathbf{u}}_{\in }+\nabla p_{\in }& =\mathbf{0}\text{in}\Omega ,\end{array}$$

(43b)

$$\begin{array}{ll}\nabla ·{\mathbf{u}}_{\in }& =0\text{in}\Omega ,\end{array}$$

(43c)

with the boundary conditions on Γ _io :

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }+\frac{1}{\in }({\Phi }_{\in }-{\Phi }_{\mathit{\text{io}}})& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(44a)

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\in }·\mathbf{n})& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(44b)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }\ast \mathbf{t})& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(44c)

and the boundary conditions on Γ _w :

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\Gamma }& =0\text{on}{\sigma }_w,\end{array}$$

(45a)

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\in }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }·\mathbf{n})& =0\text{on}{\Gamma }_w,\end{array}$$

(45b)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }·\mathbf{n})+\frac{1}{\in }(\lambda {\partial }_t{\Phi }_{\in }+{\mathbf{u}}_{\in }·\mathbf{t})& =0\text{on}{\Gamma }_w.\end{array}$$

(45c)

One can observe that the penalty method replaces the Dirichlet boundary conditions with a Robin condition. However, upon taking the limit ∈→0 one formally recovers the original problems Eq. (9) and Eq. (14).

Adjoint problem associated with the penalty formulation

We now derive the adjoint problem corresponding to the weak form Eq. (39),

$$\begin{array}{l}\text{Find}({\Phi }_{\in }^{\ast },{\mathbf{u}}_{\in }^{\ast },p_{\in }^{\ast })\in Z\times X\times M\text{such that},\\ \underset{\Omega }{\int }{\sigma }_c\nabla {\Phi }_{\in }^{\ast }·\nabla \Psi \mathit{\text{dx}}+\frac{1}{\in }\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }{\Phi }_{\in }^{\ast }\Psi \mathit{\text{ds}}+\frac{1}{\in }\underset{{\Gamma }_w}{\int }\lambda {\partial }_t{\Psi }_{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathit{\text{ds}}\\ +\frac{1}{\in }\underset{{\Gamma }_w}{\int }({\mathbf{u}}_{\in }^{\ast }·\mathbf{n})(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}+\frac{1}{\in }\underset{{\Gamma }_w}{\int }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}+\frac{1}{\in }\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}\\ +\underset{\Omega }{\int }(\nabla {\mathbf{u}}_{\in }^{\ast }·\nabla \mathbf{v}-p_{\in }^{\ast }\nabla ·\mathbf{v}-q\nabla ·{\mathbf{u}}_{\in }^{\ast })\mathit{\text{dx}}\\ =\underset{\Omega }{\int }k\left(\mathbf{x}\right)\mathbf{v}·\mathit{\alpha }\mathit{\text{dx}}+\underset{\mathrm{\Omega \partial }}{\int }{k}_s\left(s\right)\mathbf{v}·\mathbf{n}\mathit{\text{ds}}\forall (\Psi ,\mathbf{v},q)\in Z\times X\times \mathrm{M.}\end{array}$$

(46)

Using integration by parts for the term involving the tangential derivative along Γ _w [23], i.e.

$$\underset{{\Gamma }_w}{\int }\lambda {\partial }_t{\Psi }_{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathit{\text{ds}}=-\underset{{\Gamma }_w}{\int }{\nabla }_{{\Gamma }_w}·\left((\lambda {\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathbf{t}\right){\Psi }_{\in }\mathit{\text{ds}},$$

(47)

and upon integrating by parts the higher-order terms and combining integrals with same test functions, one obtains:

$$\begin{array}{ll}\underset{\Omega }{\int }& \left(-\nabla ·({\sigma }_c\nabla {\Phi }_{\in }^{\ast })\right)\Psi \mathit{\text{dx}}+\underset{{\Gamma }_w}{\int }\left({\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }-\frac{1}{\in }{\nabla }_{{\Gamma }_w}·\left((\lambda {\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathbf{t}\right)\right)\Psi \mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left({\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }+\frac{1}{\in }{\Phi }_{\in }^{\ast }\right)\Psi \mathit{\text{ds}}+\underset{\Omega }{\int }\left(-\nabla {\mathbf{u}}_{\in }^{\ast }+\nabla p_{\in }^{\ast }-k\left(\mathbf{x}\right)\mathit{\alpha }\right)·\mathbf{v}\mathit{\text{dx}}\\ +\underset{\Omega }{\int }\left(-\nabla ·{\mathbf{u}}_{\in }^{\ast }\right)q\mathit{\text{dx}}+\underset{{\Gamma }_w}{\int }\left(\mathbf{n}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{n})\right)(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}\\ +\underset{{\Gamma }_w}{\int }\left(\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\right)(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}+\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{n}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})-k_s\left(s\right)\right)(\mathbf{v}·\mathbf{n})\mathit{\text{ds}}\\ +\underset{{\Gamma }_{\mathit{\text{io}}}}{\int }\left(\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\right)(\mathbf{v}·\mathbf{t})\mathit{\text{ds}}=0\forall (\Psi ,\mathbf{v},q)\in Z\times X\times M,\end{array}$$

(48)

where ${\mathit{\sigma }}_{\in }^{\ast }$ is the penalized adjoint stress tensor. The equivalent strong form for finite non-zero ∈ is,

$$\begin{array}{ll}-\nabla {\mathbf{u}}_{\in }^{\ast }+\nabla p_{\in }^{\ast }& =k\text{in}\Omega ,\end{array}$$

(49a)

$$\begin{array}{ll}\in ·{\mathbf{u}}_{\ast }^{\Omega }& =0\text{in}\nabla ,\end{array}$$

(49b)

$$\begin{array}{ll}\nabla ·({\sigma }_c\nabla {\Phi }_{\in }^{\ast })& =0\text{in}\Omega ,\end{array}$$

(49c)

with the three boundary conditions on Γ _io :

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\sigma }^{\in }·\mathbf{n})& =k_s\left(s\right)\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(50a)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(50b)

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }+\frac{1}{\in }{\Phi }_{\in }^{\ast }& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(50c)

and the three boundary conditions on Γ _w :

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{n})& =0\text{on}{\Gamma }_w,\end{array}$$

(51a)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})& =0\text{on}{\Gamma }_w,\end{array}$$

(51b)

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }-\frac{1}{\in }{\nabla }_{{\Gamma }_w}·\left((\lambda {\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathbf{t}\right)& =0\text{on}{\Gamma }_w.\end{array}$$

(51c)

In the next section, we show that above problem is asymptotically consistent with the previous formulation of the adjoint problem, in the sense that we recover the adjoint corresponding to the strong problem, i.e. Eq. (35), Eq. (36), and Eq. (37) as ∈ tends to zero.

Consistency of the adjoint penalty problem

The main issue is to ensure that the adjoint solution $u_{\in }^{\ast }$ to the adjoint problem obtained from the penalized formulation does in fact converge to the adjoint solution u^∗ obtained from the primal formulation as the penalty parameter ∈ tends to zero, as illustrated in Figure 1. In this case, one has to show that the resulting boundary conditions associated with the penalized and non-penalized formulations of the adjoint problems are consistent.

Figure 1

Consistency of the adjoint problems associated with the original and penalty formulations. The question here is whether the adjoint problem obtained from the penalty formulation converges to the adjoint problem derived from the original formulation in the limit when the penalty parameter ∈ tends to zero.

Recall that the non-penalized adjoint solution (Φ^∗,u^∗) for the problem of interest satisfies the following boundary conditions

$$\begin{array}{ll}{\Phi }^{\ast }& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(52a)

$$\begin{array}{ll}\mathbf{n}·({\sigma }^{\ast }·\mathbf{n})& =k\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(52b)

$$\begin{array}{ll}{\mathbf{u}}^{\ast }·\mathbf{t}& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(52c)

$$\begin{array}{ll}{\mathbf{u}}^{\ast }& =0\text{on}{\Gamma }_w,\end{array}$$

(52d)

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }^{\ast }+{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·({\sigma }^{\ast }·\mathbf{n})\mathbf{t}\right)& =0\text{on}{\Gamma }_w,\end{array}$$

(52e)

while the penalized adjoint solution (${\Phi }_{\in }^{\ast },{\mathbf{u}}_{\in }^{\ast }$) satisfies,

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }-\frac{1}{\in }{\Phi }^{\ast }& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(53a)

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})& =k\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(53b)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(53c)

$$\begin{array}{ll}\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})& =0\text{on}{\Gamma }_w,\end{array}$$

(53d)

$$\begin{array}{ll}\mathbf{n}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{n})& =0\text{on}{\Gamma }_w,\end{array}$$

(53e)

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }-\frac{1}{\in }{\nabla }_{{\Gamma }_w}·\left((\lambda {\mathbf{u}}_{\in }^{\ast }·\mathbf{t})\mathbf{t}\right)& =0\text{on}{\Gamma }_w.\end{array}$$

(53f)

To formally interpret Eq. (53f), we can substitute Eq. (53d) into Eq. (53f) as follows,

$$\begin{array}{l}\mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})+\frac{1}{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})=0\Rightarrow \frac{\lambda }{\in }({\mathbf{u}}_{\in }^{\ast }·\mathbf{t})=-\lambda \mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n}),\\ {\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }={\nabla }_{{\Gamma }_w}·\left(\left(\frac{\lambda {\mathbf{u}}_{\in }^{\ast }·\mathbf{t}}{\in }\right)\mathbf{t}\right)\Rightarrow {\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }=-{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})\mathbf{t}\right).\end{array}$$

(54)

We can thus derive the following boundary conditions for the adjoint potential

$$\begin{array}{ll}{\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }+{\nabla }_{{\Gamma }_w}·\left(\lambda \mathbf{t}·({\mathit{\sigma }}_{\in }^{\ast }·\mathbf{n})\mathbf{t}\right)& =0\text{on}{\Gamma }_w,\end{array}$$

(55a)

$$\begin{array}{ll}{\Phi }_{\in }^{\ast }+\in {\sigma }_c{\partial }_n{\Phi }_{\in }^{\ast }& =0\text{on}{\Gamma }_{\mathit{\text{io}}},\end{array}$$

(55b)

which are the same as those for the non-penalized adjoint in the limit ∈→0. Eq. 53d corresponds to a penalty representation of the tangential boundary flux. Further discussion of this representation is presented in [27]. We thus see that the penalized formulation of the electroosmotic flow problem is adjoint consistent in the limit as ∈→0, and the use of the discrete penalized adjoint solution $({\left({\Phi }_{\in }^{\ast }\right)}_h,{\left({\mathbf{u}}_{\in }^{\ast }\right)}_h,{\left(p_{\in }^{\ast }\right)}_h)$ in adjoint-based error estimation and sensitivity analysis is justified. Thus, if the forward problem is computed numerically using a discrete representation of Eq. (39), the adjoint solution can also be easily computed by taking the transpose of the stiffness matrix associated with the forward problem.