1 Introduction

In recent decades, corrosion in harsh environmental conditions has mostly harmed RC constructions. It is causing a decrease in strength and efficiency. Several researches have been carried out to boost concrete strength and tackle corrosion issues. High-strength concrete is being marketed for usage in a wide range of building applications. HSC provides greater advantages than regular-strength concrete. Its HSC is more robust, and the designer decreases the element's cross-sectional area. On the industrial side, they are creating high-strength concrete using non-corroding GFRP bars as alternative reinforcement. Reinforcement concrete constructions finished HSC with GFRP bars, extending the structural parts’ service life. To accommodate the world highly evolved human civilizations, more and higher effective designs are required nowadays (Adam et al., 2021; El-Sayed et al., 2022; Erfan et al., 2020; Nassif et al., 2021; Yu et al., 2021, 2022).

UHPFRC is a potential construction material with excellent self-consolidating properties, high durability resistance, and high mechanical strength, making it appealing for high-performance foundation designs. Currently, the majority of research is focused on exploring UHPFRC mix improvements (Xie et al., 2018a; Yoo et al., 2015), UHPFRC beams, columns and slabs flexural performance (Abadel et al., 2022a, 2023; Baby et al., 2013, 2014; El-Sayed, 2021; El-Sayed & Algash, 2021; Lachance et al., 2016; Mahmud et al., 2013), and UHPFRC elements reaction under blast pressures (Millard et al., 2010). Because of developments in concrete technology, high-performance concrete is now accessible and employed HPC. Concerns have been raised concerning the efficiency of HPC columns, as the use of HPC to reduce cross-sectional dimensions favors the building of RC columns over conventional strength concrete (Hung & Hu, 2018).

Shin et al. (Shin et al., 2015, 2017, 2018) and Hosinieh et al. (Hosinieh et al., 2015) discovered that lowering the distance between the transverse reinforcements of the short column considerably boosted the force bearing capacities and force sustainability after peak in their research of the pure axial behaviors of short columns. Adding extra crossties for transverse reinforcements with predetermined stirrup spacing would just raise the overall toughness of the short columns without considerably boosting their force bearing capacities. Steel fibers were present at the time, which kept the concrete from spalling during failure and boosted the post-peak ductility of the columns (Fang et al., 2019).

Palacios et al. (Palacios, 2015) also studied the cyclic efficiency of a column with a UHPC-fabricated plastic hinge region. The results of their research showed that using UHPC changed the typical mechanism of failure of RC columns with confinement increase and prevented concrete crushing. Several experimental and computational studies have been conducted in recent decades to examine the achievement of structures reinforced by FRP bars due to steel reinforcement corrosion, which is one of the major problems that shortens the lifetime serviceability and, thus, brittle failure of many concrete structures worldwide. FRP materials have recently become a viable material for manufacturing reinforcement bars for concrete buildings (American Concrete Institute (ACI) 2006).

Afifi et al. (Afifi et al., 2014a) studied the efficacy of circular columns reinforced with CFRP bars and spirals. He discovered that the CFRP bars were successful in sustaining compression until the concrete was crushed and provided an average of 12% of column capacity. Mohamed (Mohamed et al., 2014), also examined 14 full-scale circular RC columns under concentric axial stress with longitudinal Sand-coated GFRP bars and carbon-FRP (CFRP) restricted with circular hoops or FRP spirals. He stated that it offered enough restriction against buckling of the longitudinal FRP bars and satisfactory confinement of the concrete core in the post peak periods. Flexural and stress behavior of FRP-RC parts has recently been thoroughly studied (Canada, 2009).

However, it was still unknown how FRP-RC columns would behave under axial compression. However, FRP bars are not advised for use as longitudinal reinforcement in columns according to ACI 440.1R-06 (American Concrete Institute (ACI) 2006). Further study in this area is called for by ACI 440.1R-06 (American Concrete Institute (ACI) 2006), while Canadian standards (Canadian Standards Association, 2012) ignore the importance of FRP longitudinal reinforcement's compressive resistance in the compression zone in compressive and flexural concrete components. Previous studies have shown that FRP bars have lower strength and modulus in compression than in tension (Chaallal & Benmokrane, 1993; Wu, 1990).

CFRP bars have been found to have a compressive strength that is 78% of their tensile strength (Mallick, 1988; Wu, 1990). In addition, recent research on the bond behavior of conventional FRP rebars discovered that due to the distinctive characteristics of each FRP material and the variety of fiber/resin interfaces, it was difficult to anticipate bond behavior without doing experimental research.

In RC structures, BFRPs have gained popularity as an alternative to traditional FRPs (Refai et al., 2015). Ibrahim et al. (Ibrahim et al., 2015) used pull-out experiments to examine the bond-slip behavior among concrete and BFRP bars. He gave his OK for the reference to the well-known bond-slip presentation. BFRP is a potential substitute for other FRPs because of its lower cost, endurance to high temperatures, ease of production, and improved resistance to sulphate attack, chloride, effect stacking, and vibration (Lee et al., 2014; Li & Xu, 2009; Liu et al., 2015; Shi et al., 2011; Wei et al., 2010). BFRP bars may be incorporated into buildings in a number of different ways. A number of studies to assess the effectiveness of BFRP geopolymer concrete supporting components such columns, forbearing, and boards (Erfan et al., 2019a).

However, to effectively offer UHPC to as large a market as possible, its use must be envisioned as a catalyst for realizing innovative structural concepts, as opposed to only being limited to incrementally improving current structural concepts and element thickness reduction. In addition, this complements specialist construction techniques, such as prefabrication and additive production, the use of which is otherwise unattainable (Abadel et al., 2022b; Abdellatief et al., 2023; Al-Obaidi et al., 2022; Ozbakkaloglu et al., 2018; Shang et al., 2022; Wang et al., 2022; Xie et al., 2018b; Zhu et al., 2022).

The main importance of this study is to examine the performance of using BFRP as longitudinal bars in the production of UHPSCC columns under axial stress, with varying stirrup diameters, spacing’s, and steel reinforcement rebars. To achieve this goal, an experimental plan was carried out on twelve UHPC column specimens with dimensions 150 mm × 150 mm and height 1,200 mm that were subjected to axial loading. In addition, ANSYS® finite element code was used to create finite element models for all specimens to simulate structural behavior of each specimen. Based on such investigations, additional stiffeners and UHPC were used to increase the load capacity of columns. When compared to RC columns, test findings show that basalt bars contributed about 90% of the outcomes.

1.1 Significance of Research

Eight steel-reinforced and four basalt-reinforced RC columns that had been exposed to axial stresses each were used in the current study. The findings of the experimental investigation are contrasted with those of the analytical study. The detailed investigation would be as described in the following:

  1. 1.

    Analyzing the structural features of basalt-barred columns to ascertain their mechanism of failure

  2. 2.

    Assessing the basalt bars' compressive impact on concrete columns.

  3. 3.

    The non-linear Finite Element Model is examined by UHPC columns (FEM).

  4. 4.

    Analytical results are contrasted with experimental results. The outcomes of the analysis aid in predicting the axial stress on the column.

2 Experimental Study

2.1 Materials

  1. 1.

    Cement:

In this study, OPC-CEM I (52.5 N), compliant with EN 197/1 (EN, 2011), is employed. The silica fume used complies with ASTM (C1240-03a) and IS (15388-2003).

  1. 2.

    Aggregates

The specific density of natural quartz sand that meets ASTM (C33) standards is 2.60.

  1. 3.

    Lime powder

The specific gravity of lime powder (Ghareeb et al., 2022), a cement alternative substance, was 2.7.

  1. 4.

    Superplasticizer

The super plasticizer has a density of 1085 kg/m3.

  1. 5.

    Steel bars:

  2. •

    Type I: 24/35, 8 mm diameter.

  3. •

    Type II: 42/60, 12 mm diameter.

  4. 6.

    Basalt bars:

12 mm diameter deformed basalt bars made locally. The characteristics of basalt bars are shown in Table 1.

Table 1 Basalt bars properties (ASTM, 2021; Erfan et al., 2019b)
Full size table

2.2 Mix Design

The typical compressive strength of the design combination was estimated to be 120 MPa. Table 2 lists the properties of the mixture, while Fig. 1 display the flow of slump for this mix’s self-compacted concrete column mixtures.

Table 2 Mix design
Full size table
Fig. 1
figure 1

Typical concrete slump flow test for UHPSSC mix

Full size image

2.3 Experimental Program and Methodology

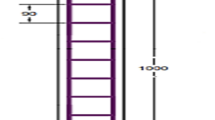
Table 3 and Fig. 2 present the information in 12 columns that used to examine the UHPSCC columns' overall behavior, cracking pattern, and final maximum capacity. The performance of concrete columns restrained by different numbers of stirrups and reinforced with either steel or BFRP reinforcements is assessed and analyzed. Table 3 presents the test matrix adopted in this study. All UHPSCC columns had a square cross section with dimensions of 150 mm × 150 mm, and a height of 1200 mm. The actual compressive strength was determined based on the average test results of nine concrete cubes (100 mm × 100 mm) tested on the same day as the start of testing of the column specimens. Two internal reinforcement schemes were employed.

Table 3 Specimen’s description
Full size table
Fig. 2
figure 2

Columns typical dimensions and internal reinforcement details

Full size image

2.4 Test Setup

All columns were examined using testing equipment with a capacity of 5000 kN. Fig. 3 depicts the column test configuration. The deformations of all the examined columns were monitored using an L.V.D.T. instrument till failure.

Fig. 3
figure 3

Test setup

Full size image

2.5 Test Results

2.5.1 Ultimate Load and Deformation

In this section, behavior of the tested column specimens in terms of ultimate load and deflection, the relationship between load and deflection, and cracking patterns are presented (see Figs. 4, 5, 6, 7). In addition, Table 4 provides a summary of experimental results.

Fig. 4
figure 4

Ultimate load of tested columns

Full size image
Fig. 5
figure 5

Ultimate deflection of tested columns

Full size image
Fig. 6
figure 6

Load–deflection curves for all tested groups

Full size image
Fig. 7
figure 7

Crack patterns for all column tested specimens

Full size image
Table 4 Test results
Full size table

2.5.2 Cracking Pattern

The cracking patterns of each column specimen are shown in Fig. 7.

3 Analytical Study

To assess the performance of the UHPC columns, a finite nonlinear analysis was conducted. Ansys was used to create FEM (ANSYS, 2005). FEM contributes in the prediction of the specimens’ ultimate axial compressive load and failure.

3.1 Elements Type

Solid 65 was used to illustrate the stress–strain curve for concrete. While element Link 180 represented the bars and stirrups. Fig. 8 depicts the geometry of the element type.

Fig. 8
figure 8

Element type’s geometry (ANSYS, 2005)

Full size image

3.2 Geometry Modeling

Columns are represented in the same manner as in the experimental test.

3.3 Modeling of Specimens

A finite nonlinear analysis was performed to evaluate the effectiveness of the UHPC columns represented in Fig. 9.

Fig. 9
figure 9

Modeling of columns

Full size image

3.4 FEM the Constitutive Model

SOLID 65 was employed in the ANSYS software to simulate concrete elements, whereas Link 180 was employed to represent steel and BFRP bar elements. The curves used are shown in Fig. 10.

Fig. 10
figure 10

Material behaviors; a solid 65- failure surface in principal stress space with nearly biaxial stress; b link180—bilinear stress–strain idealization

Full size image

3.5 Materials Properties

The material characteristics for concrete and rebars reinforcement are shown in this section:

  • Concrete

  1. 1.

    Ec = 46,147.59 MPa.

  2. 2.

    ν = 0.3 (Ibrahim et al., 2015).

  • Steel rebars

  1. 3.

    Es = 200 kN/mm2 (Ibrahim et al., 2015).

  2. 4.

    fy = 420 MPa and fyst = 240 MPa.

  3. 5.

    ν = 0.2 (Ibrahim et al., 2015).

  4. 6.

    φ10 (As = 78.5 mm2)

  5. 7.

    φ12 (As = 112 mm2)

  6. 8.

    φ8 (As = 50.3 mm2)

  7. 9.

    φ6 (As = 28.3 mm2)

  • Basalt rebars

  1. 10.

    Es = 56 kN/mm2 (Ibrahim et al., 2015).

  2. 11.

    fy = 1400 MPa (Ibrahim et al., 2015).

  3. 12.

    ν = 0.2 (Ibrahim et al., 2015).

  4. 13.

    φ12 (As = 112 mm2).

3.6 Modeling Results

3.6.1 Ultimate Load and Deformation

In this section, behavior of the modeled column specimens in terms of ultimate load and deflection, the relationship between load and deflection, and cracking patterns are presented (see Figs. 11, 12, 13, 14). In addition, Table 5 provides a summary of analytical results.

Fig. 11
figure 11

Ultimate load for modeled columns

Full size image
Fig. 12
figure 12

Ultimate deflection for modeled columns

Full size image
Fig. 13
figure 13

Load–deflection curves for all modeled groups

Full size image
Fig. 14
figure 14

Crack patterns for all modeled column

Full size image
Table 5 Modeling results
Full size table

3.6.2 Cracking Pattern

The cracking patterns of each modeled column are shown in Fig. 14.

4 Results and Discussion

4.1 Axial Load Capacity of Columns

The experimental and analytical ultimate loads for all columns are presented in Table 6 and Fig. 15. Experimentally and analytically, the ultimate for group A ranged from 1412 to 2092 kN and 1299 to 1955 kN, respectively. The influence of confinement was demonstrated in column C3-A with stirrups 8@100, which recorded greater maximum force values than column C4-A with 8@150, with a 22.8% enhancement ratio. The ultimate for group B ranged from 1776 to 2537 kN empirically and theoretically, respectively. Furthermore, employing a greater longitudinal steel reinforcement ratio for group B columns than for group A columns resulted in higher failure pressures for group B columns compared to corresponding group A columns. While for group c, the ultimate ranges from 1640 to 1700 kN and 1513 kN to 1574 kN, respectively, empirically and theoretically. Basalt RC columns handle about 90% of the axial load as compared to steel RC columns. The analytical investigation using Ansys software aided in estimating the ultimate carrying capacity of UHPC columns.

Table 6 Results for experimental and analytical
Full size table
Fig. 15
figure 15

Exp. and analytical ultimate load

Full size image

Table 6 and Fig. 16 also indicate the discrepancy between the analytical and experimental deflections. The agreement between the modeled and experimental columns was satisfactory.

Fig. 16
figure 16

Exp. and analytical ultimate deflection

Full size image

Figs. 17, 18, 19 show the load–deflection relationship for the tested columns. These data clearly show that the load and deflection for all columns can be divided into two zones, which are as follows: the first region is: the behavior was elastic up to the first signs of breaking, with a linear relationship between force and deformation. The transition from linearity to curviness marks the end of this cycle. As the test conditions varied, so did the range of this stage. While in the second zone, the slope progressively changes as a result of the expected decrease in sample stiffness caused by serial cracking.

Fig. 17
figure 17

Axial deformation response for group A

Full size image
Fig. 18
figure 18

Axial deformation response for group B

Full size image
Fig. 19
figure 19

Axial deformation response for group C

Full size image

4.2 Mode of Failure

The first set of cracking was begun at the center of the column's length, as shown in Figs. 20, 21, and 22. This is due to the experiment's invisible micro-cracks. The experimental breaking force is somewhat less. This may be acceptable, because the FE analysis specifies the status of micro fractures. The fracture patterns at each load step, on the other hand, indicated that crack propagation for molded columns differed from the experimental one due to Ansys precision.

Fig. 20
figure 20

Crack patterns for Group A

Full size image
Fig. 21
figure 21

Crack patterns for Group B

Full size image
Fig. 22
figure 22

Crack patterns for Group C

Full size image

4.2.1 Theoretical Study

The role of the basalt bars has not yet been identified by CSA (Afifi et al., 2014b) or ACI as no studies have been carried out (CSA, 2012). It was challenging to calculate the precise the ultimate loads of basalt-RC columns due to the many failure types.

As demonstrated in Eq. 1, Afifi et al. (ACI, 2015) were necessary for the CS of basalt bars. The compressive strength of basalt bars is estimated using Eq. 2 as per Tobbi et al. (Tobbi et al., 2012) linear-elastic theory. Although this model predicts a lesser strain level than the test, it yields a projected load that is lower than the exact load recorded in the research. According to Samani and Attard (Samani & Attard, 2012), the axial strain value for unconfined concrete cylinders is calculated by Eq. 3. According to the testing data, only the above three equations achieved axial loads of up to 60%, and Eq. 4 produced superior findings for both steel and basalt RC columns:

$${{\text{P}}_n} = {\text{ }}0.85{\text{ }} \times {{\text{f}}_c} \times {\text{ }}\left( {{{\text{A}}_g} - {\text{ }}{{\text{A}}_{FRP}}} \right){\text{ }} + {\text{ }}0.35{\text{ }} \times {\text{ }}{{\text{f}}_u}_{FRP} \times {\text{ }}{{\text{A}}_{FRP}}\;$$
(1)
$${\text{P}}_{n} = \, 0.85 \, \times {\text{ f}}_{c} \times \, \left( {{\text{A}}_{g} - {\text{ A}}_{FRP} } \right) \, + \, 0.002 \, \times {\text{ E}}_{FRP} \times {\text{ A}}_{FRP}$$
(2)
$${\text{P}}_{n} = \, 0.85 \, \times {\text{ f}}_{c} \times \, \left( {{\text{A}}_{g} - {\text{ A}}_{FRP} } \right) \, + \, 0.0025 \, \times {\text{ E}}_{FRP} \times {\text{ A}}_{FRP}$$
(3)
$${\text{P}}_{{\text{P}}} {\text{ = Ac Pck + As Psk}}$$
(4)

Table 7 shows the range of 60% between the estimated ultimate loads and those obtained experimentally using Eqs. 1, 2, 3. Equation 4 offered a satisfactory matching between axial capacity estimate findings depending on experimental results (IS456, 2000).

Table 7 Comparison between test results and theatrical equations
Full size table

5 Conclusions

This research was conducted as an experimental and analytical investigation of the UHPC column with basalt bars under axial compression. The experimental and analytical results can be summarized as follows:

  1. 1-

    Increasing the highly longitudinal steel ratios for UHPC columns has an impact on the column carrying capacity; particularly when employing transverse reinforcement with tight spacing, which promotes confinement and raises carrying capacity.

  2. 2-

    In comparison with steel-reinforced UHPC columns, the basalt bars supported only around 90% of the axial load. According to the study, basalt bars might successfully replace steel reinforcement in circumstances, where corrosion is a danger.

  3. 3-

    The findings of the experiment and the analytical one show good agreement. The agreement is around 92.2%, with a standard deviation of 0.005 and a coefficient of variation of 0.00002.

  4. 4-

    When lateral deformation measurements for group C using basalt columns are contrasted with those for the other group using steel bars, the results reveal improved confinement, ductility, and energy absorption.

  5. 5-

    The created UHPC columns could be effectively employed as a replacement to the conventional RC columns, and in addition to its predicted economic and environmental benefits, may be beneficial in both developed and developing nations.

  6. 6-

    Equations are employed to forecast the strength of confined concrete. Eq. 4 merely produced improved forecasts, it aids in comparing the outcomes of analytical and experimental tests.

5.1 The Limitations and Future Research Direction of the Study

The following experimental research areas should be taken into consideration for subsequent investigation to enable a more thorough examination of the observed properties:

  • Study the effect of confinement of steel stirrups with closely spaced less than 100 mm for BFRP longitudinal reinforcement for UHPC column under axial force.

  • Using BFRP bars as longitudinal reinforcement with closely space transverse BFRP stirrups instead of steel stirrups for axial force UHPC columns.

  • Effect of the eccentricity of force on UHP columns using BFRP bars instead of longitudinal steel bars.