On solving split equilibrium problems and fixed point problems of nonspreading multi-valued mappings in Hilbert spaces

Abstract

In this paper, we introduce and study iterative schemes for solving split equilibrium problems and fixed point problems of nonspreading multi-valued mappings in Hilbert spaces and prove that the modified Mann iteration converges weakly to a common solution of the considered problems. Moreover, we present some examples and numerical results for the main results.

1 Introduction

In the following, let $H_{1}$ and $H_{2}$ be real Hilbert spaces with the inner product $\langle\cdot,\cdot\rangle$ and the norm $\|\cdot\|$. Let C be a nonempty subset of $H_{1}$. The equilibrium problem is to find a point $\hat{x}\in C$ such that

$$ F_{1}(\hat{x},y)\geq0 $$

(1.1)

for all $y\in C$. Since its inception by Blum and Oettli [1] in 1994, the equilibrium problem (1.1) has received much attention due to its applications in a large variety of problems arising in numerous problems in physics, optimizations, and economics. Some methods have been rapidly established for solving this problem (see [2–5]).

Very recently, Kazmi and Rizvi [6] introduced and studied the following split equilibrium problem:

Let $C\subseteq H_{1}$ and $Q\subseteq H_{2}$. Let $F_{1}:C\times C\rightarrow\mathbb{R}$ and $F_{2}:Q\times Q\rightarrow\mathbb{R}$ be two bifunctions. Let $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator. The split equilibrium problem is to find $\hat{x}\in C$ such that

$$ F_{1}(\hat{x},x)\geq0 \quad\mbox{for all } x\in C $$

(1.2)

and such that

$$ \hat{y}=A\hat{x}\in Q \mbox{ solves } F_{2}(\hat{y},y) \geq0 \quad\mbox{for all } y\in Q. $$

(1.3)

Note that the problem (1.2) is the classical equilibrium problem and we denote its solution set by $EP(F_{1})$. The inequalities (1.2) and (1.3) constitute a pair of equilibrium problems which have to find the image $\hat{y}=A\hat{x}$, under a given bounded linear operator A, of the solution x̂ of (1.2) in $H_{1}$ is the solution of (1.3) in $H_{2}$. We denote the solution set of (1.3) by $EP(F_{2})$. The solution set of the split equilibrium problem (1.2) and (1.3) is denoted by $\Omega=\{z\in EP(F_{1}) : Az\in EP(F_{2})\}$.

A subset $C\subset H_{1}$ is said to be proximinal if, for each $x\in H_{1}$,

$$ \|x-y\|=d(x,C)=\inf\bigl\{ \|x-z\|:z\in C \bigr\} . $$

Let $CB(C)$, $K(C)$, and $P(C)$ denote the families of nonempty closed bounded subsets, nonempty compact subsets and nonempty proximinal bounded subset of C, respectively. The Hausdorff metric on $CB(C)$ is defined by

$$ H(A,B)=\max\Bigl\{ \sup_{x\in A}d(x,B), \sup_{y\in B}d(y,A) \Bigr\} $$

for all $A,B \in CB(C)$ where $d(x,B)=\inf_{b\in B}\|x-b\|$. An element $p\in C$ is called a fixed point of $T:C\rightarrow CB(C)$ if $p\in Tp$. The set of fixed points of T is denoted by $F(T)$. We say that $T:C\rightarrow CB(C)$ is:

• (1) nonexpansive if

  $$ H(Tx,Ty)\leq\|x-y\| $$

  for all $x,y\in C$;

• (2) quasi-nonexpansive if

  $$ H(Tx,Tp)\leq\|x-p\| $$

  for all $x\in C$ and $p\in F(T)$.

Recently, the existence of fixed points and the convergence theorems of multi-valued mappings have been studied by many authors (see [7–12]).

Hussain and Khan [13] presented the fixed point theorems of a *-nonexpansive multi-valued mapping and the strong convergence of its iterates to a fixed point defined on a closed and convex subset of a Hilbert space by using the best approximation operator $P_{T}x$, which is defined by $P_{T}x=\{y\in Tx:\|y-x\|=d(x,Tx)\}$. The convergence theorems and its applications in this direction have been established by many authors (for instance, see [10, 14, 15]).

In 2011, Song and Cho [16] gave the example of a multi-valued mapping T which is not necessary nonexpansive, but $P_{T}$ is nonexpansive. This is an important tool for studying the fixed point theory for multi-valued mappings.

Kohsaka and Takahashi [17] introduced a class of mappings which is called nonspreading mapping. Let C be a subset of Hilbert spaces $H_{1}$. A mapping $T:C\rightarrow C$ is said to be nonspreading if

$$ 2\|Tx-Ty\|^{2}\leq\|Tx-y\|^{2}+\|Ty-x\|^{2} $$

for all $x,y\in C$. Subsequently, Iemoto and Takahashi [18] showed that $T:C\rightarrow C$ is nonspreading if and only if

$$ \|Tx-Ty\|^{2}\leq\|x-y\|^{2}+2\langle x-Tx,y-Ty\rangle $$

for all $x,y\in C$.

Very recently, Liu [19] introduced the following class of multi-valued mappings: a multi-valued mapping $T:C\rightarrow CB(C)$ is said to be nonspreading if

$$ 2\|u_{x}-u_{y}\|^{2}\leq\|u_{x}-y \|^{2}+\|u_{y}-x\|^{2} $$

for some $u_{x}\in Tx$ and $u_{y}\in Ty$ for all $x,y\in C$. He proved a weak convergence theorem for finding a common element of the set of solutions of an equilibrium problem and the set of common fixed points.

In this paper, we introduce, by using Hausdorff metric, the class of nonspreading multi-valued mappings. We say that a mapping $T:C\rightarrow CB(C)$ is a k-nonspreading multi-valued mapping if there exists $k>0$ such that

$$ H(Tx,Ty)^{2}\leq k \bigl(d(Tx,y)^{2}+d(x,Ty)^{2} \bigr) $$

(1.4)

for all $x,y\in C$.

It is easy to see that, if T is $\frac{1}{2}$-nonspreading, then T is nonspreading in the case of single-valued mappings (see [17, 20]). Moreover, if T is a $\frac{1}{2}$-nonspreading and $F(T)\neq\emptyset$, then T is quasi-nonexpansive. Indeed, for all $x\in C$ and $p\in F(T)$, we have

$$\begin{aligned} 2H(Tx,Tp)^{2} \leq&d(Tx,p)^{2}+d(x,Tp)^{2} \\ \leq&H(Tx,Tp)^{2}+\|x-p\|^{2}. \end{aligned}$$

It follows that

$$ H(Tx,Tp)\leq\|x-p\|. $$

(1.5)

We now give an example of a $\frac{1}{2}$-nonspreading multi-valued mapping which is not nonexpansive.

Example 1.1

Consider $C=[-3,0]$ with the usual norm. Define $T:C\rightarrow CB(C)$ by

$$ Tx=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \{0\},& x\in[-2,0];\\ {[}{-}\frac{|x|}{|x|+1},0],& x\in[-3,-2). \end{array}\displaystyle \right . $$

Now, we show that T is $\frac{1}{2}$-nonspreading. In fact, we have the following cases:

Case 1: If $x,y\in[-2,0]$, then $H(Tx,Tx)=0$.

Case 2: If $x\in[-2,0]$ and $y\in[-3,-2)$, then $Tx=\{0\}$ and $Ty= [-\frac{|y|}{|y|+1},0 ]$. This implies that

$$ 2H(Tx,Ty)^{2}=2 \biggl(\frac{|y|}{|y|+1} \biggr)^{2}< 2< y^{2} \leq d(Tx,y)^{2}+d(x,Ty)^{2}. $$

Case 3: If $x,y\in[-3,-2)$, then $Tx= [-\frac{|x|}{|x|+1},0 ]$ and $Ty= [-\frac{|y|}{|y|+1},0 ]$. This implies that

$$ 2H(Tx,Ty)^{2}=2 \biggl(\frac{|x|}{|x|+1}-\frac{|y|}{|y|+1} \biggr)^{2}< 2< d(Tx,y)^{2}+d(x,Ty)^{2}. $$

On the other hand, T is not nonexpansive since for $x=-2$ and $y=-\frac{5}{2}$, we have $Tx=\{0\}$ and $Ty= [-\frac{5}{7},0 ]$. This shows that $H(Tx,Ty)=\frac{5}{7}>\frac{1}{2}= |-2- (-\frac{5}{2} ) |=\| x-y\|$.

In 1953, Mann [21] introduced the following iterative procedure to approximate a fixed point of a nonexpansive mapping T in a Hilbert space H:

$$ x_{n+1}=\alpha_{n}x_{n}+(1- \alpha_{n})Tx_{n} $$

(1.6)

for each $n\in\mathbb{N}$, where the initial point $x_{1}$ is taken in C arbitrarily and $\{\alpha_{n}\}$ is a sequence in $[0,1]$.

Motivated by the previous results, in this paper, we introduce and study the Mann-type iteration to approximate a common solution of the split equilibrium problem and the fixed point problem for a $\frac{1}{2}$-nonspreading multi-valued mapping and prove some weak convergence theorems in Hilbert spaces. Finally, we give some examples and numerical results to illustrate our main results.

2 Preliminaries

We now provide some results for the main results. In a Hilbert space $H_{1}$, let C be a nonempty closed convex subset of $H_{1}$. For every point $x\in H_{1}$, there exists a unique nearest point of C, denoted by ${{P}_{C}}x$, such that $\Vert x-{{P}_{C}}x \Vert \le \Vert x-y \Vert$ for all $y\in C$. Such a ${{P}_{C}}$ is called the metric projection from $H_{1}$ onto C. We know that ${{P}_{C}}$ is a firmly nonexpansive mapping from $H_{1}$ onto C, i.e.,

$$ {{\Vert {{P}_{C}}x-{{P}_{C}}y \Vert }^{2}} \le\langle{{P}_{C}}x-{{P}_{C}}y,x-y \rangle, \quad\forall x,y\in H_{1}. $$

Further, for any $x\in H_{1}$ and $z\in C$, $z={{P}_{C}}x$ if and only if

$$ \langle x-z,z-y \rangle\ge0, \quad\forall y\in C. $$

A mapping $A:C\to H_{1}$ is called α-inverse strongly monotone if there exists $\alpha>0$ such that

$$ \langle x-y,Ax-Ay \rangle\ge\alpha{{ \Vert Ax-Ay \Vert }^{2}},\quad \forall x,y\in C. $$

Lemma 2.1

Let $H_{1}$ be a real Hilbert space. Then the following equations hold:

• (1) $\|x-y\|^{2}=\|x\|^{2}-\|y\|^{2}-2\langle x-y,y\rangle$ for all $x,y \in H_{1}$;

• (2) $\|x+y\|^{2}\leq\|x\|^{2}+2\langle y,x+y\rangle$ for all $x,y \in H_{1}$;

• (3) $\|tx+(1-t)y\|^{2}=t\|x\|^{2}+(1-t)\|y\|^{2}-t(1-t)\|x-y\| ^{2}$ for all $t\in[0,1]$ and $x,y \in H_{1}$;

• (4) If $\{x_{n}\}_{n=1}^{\infty}$ is a sequence in $H_{1}$ which converges weakly to $z\in H_{1}$, then

  $$\limsup_{n\rightarrow\infty}\|x_{n}-y\|^{2}=\limsup _{n\rightarrow\infty }\|x_{n}-z\|^{2}+\|z-y\|^{2} $$

  for all $y\in H_{1}$.

A space X is said to satisfy Opial’s condition if, for any sequence $x_{n}$ with $x_{n}\rightharpoonup x$, then

$$ \liminf_{n\rightarrow\infty}\|x_{n}-x\|< \liminf _{n\rightarrow\infty}\| x_{n}-y\| $$

for all $y\in X$ with $y\neq x$. It is well known that every Hilbert space satisfies Opial’s condition.

Lemma 2.2

[22]

Let X be a Banach space which satisfies Opial’s condition and $\{x_{n}\}$ be a sequence in X. Let $u,v\in X$ be such that $\lim _{n\rightarrow\infty}\|x_{n}-u\|$ and $\lim_{n\rightarrow\infty}\|x_{n}-v\|$ exist. If $\{x_{n_{k}}\}$ and $\{x_{m_{k}}\}$ are subsequences of $\{x_{n}\}$ which converge weakly to u and v, respectively, then $u=v$.

Assumption 2.3

[1]

Let $F_{1}:C\times C\rightarrow \mathbb{R}$ be a bifunction satisfying the following assumptions:

• (1) $F_{1}(x,x)=0$ for all $x\in C$;

• (2) $F_{1}$ is monotone, i.e., $F_{1}(x,y)+F_{1}(y,x)\leq0$ for all $x\in C$;

• (3) for each $x,y,z\in C$, $\limsup_{t\rightarrow 0^{+}}F_{1}(tz+(1-t)x,y)\leq F_{1}(x,y)$;

• (4) for each $x\in C$, $y\rightarrow F_{1}(x,y)$ is convex and lower semi-continuous.

Lemma 2.4

[3]

Assume that $F_{1}:C\times C\rightarrow\mathbb{R}$ satisfies Assumption 2.3. For any $r>0$ and $x\in H_{1}$, define a mapping $T^{F_{1}}_{r}:H_{1}\rightarrow C$ as follows:

$$ T^{F_{1}}_{r}(x)= \biggl\{ z\in C : F_{1}(z,y)+ \frac{1}{r}\langle y-z,z-x\rangle\geq0, \forall y\in C \biggr\} . $$

Then the following hold:

• (1) $T^{F_{1}}_{r}$ is nonempty and single-valued;

• (2) $T^{F_{1}}_{r}$ is firmly nonexpansive, i.e., for any $x,y\in H_{1}$,

  $$ \bigl\| T^{F_{1}}_{r}x-T^{F_{1}}_{r}y \bigr\| ^{2}\leq\bigl\langle T^{F_{1}}_{r}x-T^{F_{1}}_{r}y, x-y\bigr\rangle ; $$

• (3) $F(T^{F_{1}}_{r})=EP(F_{1})$;

• (4) $EP(F_{1})$ is closed and convex.

Further, assume that $F_{2}:Q\times Q\rightarrow\mathbb{R}$ satisfying Assumption 2.3. For each $s>0$ and $w\in H_{2}$, define a mapping $T_{s}^{F_{2}}:H_{2}\rightarrow Q$ as follows:

$$ T_{s}^{F_{2}}(w)= \biggl\{ d\in Q : F_{2}(d,e)+ \frac{1}{s}\langle e-d,d-w\rangle\geq0, \forall e\in Q \biggr\} . $$

Then we have the following:

• (5) $T^{F_{2}}_{s}$ is nonempty and single-valued;

• (6) $T^{F_{2}}_{s}$ is firmly nonexpansive;

• (7) $F(T^{F_{2}}_{s})=EP(F_{2},Q)$;

• (8) $EP(F_{2},Q)$ is closed and convex.

Condition (A)

Let $H_{1}$ be a Hilbert space and C be a subset of $H_{1}$. A multi-valued mapping $T:C\rightarrow CB(C)$ is said to satisfy Condition (A) if $\|x-p\|=d(x,Tp)$ for all $x\in H_{1}$ and $p\in F(T)$.

Remark 2.5

We see that T satisfies Condition (A) if and only if $Tp=\{p\}$ for all $p\in F(T)$. It is well known that the best approximation operator $P_{T}$, which is defined by $P_{T}x=\{y\in Tx:\|y-x\|=d(x,Tx)\}$, also satisfies Condition (A).

3 Main results

Now, we are ready to prove some weak convergence theorem for $\frac {1}{2}$-nonspreading multi-valued mappings in Hilbert spaces. To this end, we need the following crucial results.

Lemma 3.1

Let C be a closed and convex subset of a real Hilbert space $H_{1}$ and $T:C\rightarrow K(C)$ be a k-nonspreading multi-valued mapping such that $k\in(0,\frac{1}{2}]$. If $x,y\in C$ and $a\in Tx$, then there exists $b\in Ty$ such that

$$ \|a-b\|^{2}\leq H(Tx,Ty)^{2}\leq\frac{k}{1-k} \bigl( \|x-y\|^{2}+2\langle x-a,y-b\rangle\bigr). $$

Proof

Let $x,y\in C$ and $a\in Tx$. By Nadler’s theorem (see [8]), there exists $b\in Ty$ such that

$$ \|a-b\|^{2}\leq H(Tx,Ty)^{2}. $$

It follows that

$$\begin{aligned} & \frac{1}{k}H(Tx,Ty)^{2} \\ &\quad\leq d(Tx,y)^{2}+d(x,Ty)^{2} \\ &\quad\leq\|a-y\|^{2}+\|x-b\|^{2} \\ &\quad\leq\|a-x\|^{2}+2\langle a-x,x-y\rangle+\|x-y\|^{2}+ \|x-a\| ^{2}+2\langle x-a,a-b\rangle+\|a-b\|^{2} \\ &\quad=2\|a-x\|^{2}+\|x-y\|^{2}+\|a-b\|^{2}+2\bigl\langle a-x,x-a-(y-b)\bigr\rangle \\ &\quad\leq2\|a-x\|^{2}+\|x-y\|^{2}+H(Tx,Ty)^{2}+2 \bigl\langle a-x,x-a-(y-b)\bigr\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} H(Tx,Ty)^{2}\leq\frac{k}{1-k} \bigl(\|x-y\|^{2}+2\langle x-a,y-b\rangle\bigr). \end{aligned}$$

This completes the proof. □

Lemma 3.2

Let C be a closed and convex subset of a real Hilbert space $H_{1}$ and $T:C\rightarrow K(C)$ be a k-nonspreading multi-valued mapping such that $k\in(0,\frac{1}{2}]$. Let $\{x_{n}\}$ be a sequence in C such that $x_{n}\rightharpoonup p$ and $\lim_{n\rightarrow\infty}\|x_{n}-y_{n}\|=0$ for some $y_{n}\in Tx_{n}$. Then $p\in Tp$.

Proof

Let $\{x_{n}\}$ be a sequence in C which converges weakly to p and let $y_{n}\in Tx_{n}$ be such that $\|x_{n}-y_{n}\|\rightarrow0$.

Now, we show that $p\in F(T)$. By Lemma 3.1, there exists $z_{n}\in Tp$ such that

$$\|y_{n}-z_{n}\|^{2}\leq\frac{k}{1-k} \bigl( \|x_{n}-p\|^{2}+2\langle x_{n}-y_{n},p-z_{n} \rangle\bigr). $$

Since Tp is compact and $z_{n}\in Tp$, there exists $\{z_{n_{i}}\}\subset\{z_{n}\}$ such that $z_{n_{i}}\rightarrow z\in Tp$. Since $\{x_{n}\}$ converges weakly, it is bounded. For each $x\in H_{1}$, define a function $f:H_{1}\rightarrow[0,\infty)$ by

$$\begin{aligned} f(x):=\limsup_{i\rightarrow\infty}\frac{k}{1-k}\|x_{n_{i}}-x\| ^{2}. \end{aligned}$$

Then, by Lemma 2.1(4), we obtain

$$\begin{aligned} f(x)=\limsup_{i\rightarrow\infty}\frac{k}{1-k} \bigl(\|x_{n_{i}}-p \| ^{2}+\|p-x\|^{2} \bigr) \end{aligned}$$

for all $x\in H_{1}$. Thus $f(x)=f(p)+\frac{k}{1-k}\|p-x\|^{2}$ for all $x\in H_{1}$. It follows that

$$ f(z)=f(p)+\frac{k}{1-k}\|p-z\|^{2}. $$

(3.1)

We observe that

$$\begin{aligned} f(z)&=\limsup_{i\rightarrow\infty}\frac{k}{1-k}\|x_{n_{i}}-z\| ^{2}=\limsup_{i\rightarrow\infty}\frac{k}{1-k}\| x_{n_{i}}-y_{n_{i}}+y_{n_{i}}-z\|^{2} \\ &\leq\limsup_{i\rightarrow\infty}\frac{k}{1-k}\|y_{n_{i}}-z\| ^{2}. \end{aligned}$$

This implies that

$$\begin{aligned} f(z) \leq&\limsup_{i\rightarrow\infty}\frac{k}{1-k} \|y_{n_{i}}-z\| ^{2} \\ =&\limsup_{i\rightarrow\infty}\frac{k}{1-k} \bigl(\| y_{n_{i}}-z_{n_{i}}+z_{n_{i}}-z \| \bigr)^{2} \\ \leq&\limsup_{i\rightarrow\infty}\frac{k}{1-k} \bigl( \|x_{n_{i}}-p\| ^{2}+2\langle x_{n_{i}}-y_{n_{i}},p-z_{n_{i}} \rangle\bigr) \\ \leq&\limsup_{i\rightarrow\infty}\frac{k}{1-k}\|x_{n_{i}}-p\| ^{2} \\ =&f(p). \end{aligned}$$

(3.2)

Hence it follows from (3.1) and (3.2) that $\|p-z\|=0$. This completes the proof. □

Theorem 3.3

Let $H_{1}$, $H_{2}$ be two real Hilbert space and $C\subset H_{1}$, $Q\subset H_{2}$ be nonempty closed convex subsets of Hilbert spaces $H_{1}$ and $H_{2}$, respectively. Let $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator and $T:C\rightarrow K(C)$ a $\frac{1}{2}$-nonspreading multi-valued mapping. Let $F_{1}:C\times C\rightarrow\mathbb{R}$, $F_{2}:Q\times Q \rightarrow\mathbb{R}$ be bifunctions satisfying Assumption 2.3 and $F_{2}$ is upper semi-continuous in the first argument. Assume that T satisfies Condition (A) and $\Theta=F(T)\cap\Omega\neq \emptyset$, where $\Omega=\{z\in C:z\in EP(F_{1})\textit{ and }Az\in EP(F_{2})\}$. Let $\{x_{n}\}$ be a sequence defined by

$$ \left \{ \textstyle\begin{array}{@{}l} x_{1}\in C \textit{ arbitrarily},\\ u_{n}=T_{r_{n}}^{F_{1}}(I-\gamma A^{*}(I-T_{r_{n}}^{F_{2}})A)x_{n},\\ x_{n+1}\in\alpha_{n}x_{n}+(1-\alpha_{n})Tu_{n}, \end{array}\displaystyle \right . $$

(3.3)

for all $n\geq1$, where $\{\alpha_{n}\}\subset(0,1)$, $r_{n}\subset (0,\infty)$, and $\gamma\in(0,1/L)$ such that L is the spectral radius of $A^{*}A$ and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (1) $0<\liminf_{n\rightarrow\infty}\alpha_{n}\leq\limsup _{n\rightarrow\infty}\alpha_{n}<1$;

• (2) $\liminf_{n\rightarrow\infty}r_{n}>0$.

Then the sequence $\{x_{n}\}$ defined by (3.3) converges weakly to $p\in\Theta$.

Proof

We first show that $A^{*}(I-T^{F_{2}}_{r_{n}})A$ is a $\frac{1}{L}$-inverse strongly monotone mapping. Since $T^{F_{2}}_{r_{n}}$ is firmly nonexpansive and $I-T^{F_{2}}_{r_{n}}$ is 1-inverse strongly monotone, we see that

$$\begin{aligned} \bigl\| A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax-A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ay \bigr\| ^{2} =&\bigl\langle A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay),A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay)\bigr\rangle \\ =&\bigl\langle \bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay),AA^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay)\bigr\rangle \\ \leq&L\bigl\langle \bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay), \bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay)\bigr\rangle \\ =&L \bigl\| \bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay) \bigr\| ^{2} \\ \leq&L\bigl\langle Ax-Ay,\bigl(I-T^{F_{2}}_{r_{n}}\bigr) (Ax-Ay) \bigr\rangle \\ =&L\bigl\langle x-y,A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax-A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ay\bigr\rangle \end{aligned}$$

for all $x,y\in H_{1}$. This implies that $A^{*}(I-T^{F_{2}}_{r_{n}})A$ is a $\frac{1}{L}$-inverse strongly monotone mapping. Since $\gamma\in(0,\frac{1}{L})$, it follows that $I-\gamma A^{*}(I-T^{F_{2}}_{r_{n}})A$ is nonexpansive.

Now, we divide the proof into six steps as follows:

Step 1. Show that $\{x_{n}\}$ is bounded.

Let $p\in\Theta$. Then $p=T^{F_{1}}_{r_{n}}p$ and $(I-\gamma A^{*}(I-T^{F_{2}}_{r_{n}})A)p=p$. Thus we have

$$\begin{aligned} \|u_{n}-p\| =&\bigl\| T^{F_{1}}_{r_{n}}\bigl(I- \gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)A \bigr)x_{n}-T^{F_{1}}_{r_{n}}\bigl(I-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)A\bigr)p\bigr\| \\ \leq&\bigl\| \bigl(I-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)A\bigr)x_{n}-\bigl(I-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)A\bigr)p\bigr\| \\ \leq&\|x_{n}-p\|. \end{aligned}$$

(3.4)

It follows that

$$\begin{aligned} \|x_{n+1}-p\| \leq&\alpha_{n}\|x_{n}-p\|+(1- \alpha_{n})\|z_{n}-p\| \quad\mbox{for some } z_{n}\in Tu_{n} \\ \leq&\alpha_{n}\|x_{n}-p\|+(1-\alpha_{n})d(z_{n},Tp) \\ \leq&\alpha_{n}\|x_{n}-p\|+(1-\alpha_{n})H(Tu_{n},Tp) \\ \leq&\|x_{n}-p\|. \end{aligned}$$

Hence $\lim_{n\rightarrow\infty}\|x_{n}-p\|$ exists.

Step 2. Show that $\|z_{n}-x_{n}\|\rightarrow0$ as $n\rightarrow\infty$ for all $z_{n}\in Tu_{n}$. From Lemma 2.1 and T satisfying Condition (A), we have

$$\begin{aligned} \|x_{n+1}-p\|^{2} \leq&\alpha_{n} \|x_{n}-p\|^{2}+(1-\alpha_{n})\| z_{n}-p\|^{2} -\alpha_{n}(1-\alpha_{n}) \|x_{n}-z_{n}\|^{2} \\ =&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})d(z_{n},Tp)^{2} -\alpha_{n}(1- \alpha_{n})\|x_{n}-z_{n}\|^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})H(Tu_{n},Tp)^{2} -\alpha_{n}(1- \alpha_{n})\|x_{n}-z_{n}\|^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})\|u_{n}-p\|^{2} -\alpha_{n}(1- \alpha_{n})\|x_{n}-z_{n}\| \\ \leq&\|x_{n}-p\|^{2}-\alpha_{n}(1- \alpha_{n})\|x_{n}-z_{n}\| ^{2}. \end{aligned}$$

This implies that

$$ \alpha_{n}(1-\alpha_{n})\|x_{n}-z_{n} \|^{2}\leq\| x_{n}-p\|^{2}-\|x_{n+1}-p \|^{2}. $$

From Condition (1) and the existence of $\lim_{n\rightarrow\infty}\| x_{n}-p\|$, we have

$$ \lim_{n\rightarrow\infty}\|x_{n}-z_{n} \|=0. $$

(3.5)

Step 3. Show that $\|u_{n}-z_{n}\|\rightarrow0$ as $n\rightarrow\infty$ for all $z_{n}\in Tu_{n}$. For any $p\in\Theta$, we estimate

$$\begin{aligned} \|u_{n}-p\|^{2} =&\bigl\| T^{F_{1}}_{r_{n}}\bigl(I- \gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)A \bigr)x_{n}-p\bigr\| ^{2} \\ =&\bigl\| T^{F_{1}}_{r_{n}}\bigl(I-\gamma A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)A\bigr)x_{n}-T^{F_{1}}_{r_{n}}p \bigr\| ^{2} \\ \leq&\bigl\| x_{n}-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}-p\bigr\| ^{2} \\ \leq&\|x_{n}-p\|^{2}+\gamma^{2}\bigl\| A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\| ^{2}+2 \gamma\bigl\langle p-x_{n},A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\rangle . \end{aligned}$$

Thus we have

$$\begin{aligned} \|u_{n}-p\|^{2} \leq&\|x_{n}-p \|^{2}+\gamma^{2}\bigl\langle Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n},AA^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\rangle \\ &{}+2\gamma\bigl\langle p-x_{n},A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\rangle . \end{aligned}$$

(3.6)

On the other hand, we have

$$\begin{aligned} \gamma^{2}\bigl\langle Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n},AA^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\rangle \leq&L \gamma^{2}\bigl\langle Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n},Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\rangle \\ =&L\gamma^{2}\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2} \end{aligned}$$

(3.7)

and

$$\begin{aligned} &2\gamma\bigl\langle p-x_{n},A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\rangle \\ &\quad=2 \gamma\bigl\langle A( p-x_{n}),Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\rangle \\ &\quad=2\gamma\bigl\langle A( p-x_{n})+\bigl(Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr) \\ &\qquad{}-\bigl(Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr),Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n}\bigr\rangle \\ &\quad=2\gamma\bigl\{ \bigl\langle Ap-T^{F_{2}}_{r_{n}}Ax_{n},Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\rangle -\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}\bigr\} \\ &\quad\leq2\gamma\biggl\{ \frac{1}{2}\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}-\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}\biggr\} \\ &\quad=-\gamma\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}. \end{aligned}$$

(3.8)

Using (3.6), (3.7), and (3.8), we have

$$\begin{aligned} \|u_{n}-p\|^{2} \leq&\|x_{n}-p \|^{2}+L\gamma^{2}\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}-\gamma\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2} \\ =&\|x_{n}-p\|^{2}+\gamma(L\gamma-1)\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}. \end{aligned}$$

(3.9)

It follows that, for all $z_{n}\in Tu_{n}$,

$$\begin{aligned} \|x_{n+1}-p\|^{2} =&\bigl\| \alpha_{n}x_{n}+(1- \alpha_{n})z_{n}-p\bigr\| ^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})\|z_{n}-p\|^{2} \\ =&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})d(z_{n},Tp)^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})H(Tu_{n},Tp)^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})\|u_{n}-p\|^{2} \\ \leq&\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n}) \bigl(\|x_{n}-p\|^{2}+\gamma(L \gamma-1)\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}\bigr) \\ \leq&\|x_{n}-p\|^{2}+\gamma(L\gamma-1)\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} -\gamma(L\gamma-1)\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| ^{2} \leq& \|x_{n}-p\|^{2}-\|x_{n+1}-p \|^{2}. \end{aligned}$$

Since $\gamma(L\gamma-1)<0$ and $\lim_{n\to\infty}\|x_{n}-p\|$ exists, by (3.8), we obtain

$$\begin{aligned} \lim_{n\rightarrow\infty}\bigl\| Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\| =0. \end{aligned}$$

(3.10)

Since $T^{F_{1}}_{r_{n}}$ is firmly nonexpansive and $I-\gamma A^{*}(T^{F_{2}}_{r_{n}}-I)A$ is nonexpansive, it follows that

$$\begin{aligned} &\|u_{n}-p\|^{2} \\ &\quad=\bigl\| T^{F_{1}}_{r_{n}}\bigl(x_{n}-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n} \bigr)-T^{F_{1}}_{r_{n}}p\bigr\| ^{2} \\ &\quad\leq\bigl\langle T^{F_{1}}_{r_{n}}\bigl(x_{n}- \gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n} \bigr)-T^{F_{1}}_{r_{n}}p,x_{n}-\gamma A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}-p\bigr\rangle \\ &\quad=\bigl\langle u_{n}-p,x_{n}-\gamma A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}-p\bigr\rangle \\ &\quad=\frac{1}{2}\bigl\{ \|u_{n}-p\|^{2}+ \bigl\| x_{n}-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}-p\bigr\| ^{2}-\bigl\| u_{n}-x_{n}- \gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n} \bigr\| ^{2}\bigr\} \\ &\quad\leq\frac{1}{2}\bigl\{ \|u_{n}-p\|^{2}+ \|x_{n}-p\|^{2}-\bigl\| u_{n}-x_{n}-\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n} \bigr\| ^{2}\bigr\} \\ &\quad=\frac{1}{2}\bigl\{ \|u_{n}-p\|^{2}+ \|x_{n}-p\|^{2}-\bigl(\|u_{n}-x_{n}\| ^{2}+\gamma^{2}\bigl\| A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\| ^{2} \\ &\qquad{}-2\gamma\bigl\langle u_{n}-x _{n},A^{*} \bigl(I-T^{F_{2}}_{r_{n}}-I\bigr)Ax_{n}\bigr\rangle \bigr) \bigr\} , \end{aligned}$$

which implies that

$$\begin{aligned} \|u_{n}-p\|^{2} \leq&\|x_{n}-p \|^{2}-\|u_{n}-x_{n}\|^{2}+2\gamma\bigl\langle u_{n}-x _{n},A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\rangle \\ \leq&\|x_{n}-p\|^{2}-\|u_{n}-x_{n} \|^{2}+2\gamma\|u_{n}-x _{n}\|\bigl\| A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\| . \end{aligned}$$

(3.11)

It follows from (3.4) that

$$\begin{aligned} &\|x_{n+1}-p\|^{2} \\ &\quad\leq\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})\|z_{n}-p\|^{2} \quad\mbox{for all } z_{n}\in Tu_{n} \\ &\quad\leq\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})d(z_{n},Tp)^{2} \\ &\quad\leq\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})H(Tu_{n},Tp)^{2} \\ &\quad\leq\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n})\|u_{n}-p\|^{2} \\ &\quad\leq\alpha_{n}\|x_{n}-p\|^{2}+(1- \alpha_{n}) \bigl(\|x_{n}-p\|^{2}-\| u_{n}-x_{n}\|^{2}+2\gamma\|u_{n}-x _{n}\|\bigl\| A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\| \bigr). \end{aligned}$$

Therefore, we have

$$\begin{aligned} (1-\alpha_{n})\|u_{n}-x_{n}\|^{2} \leq2\gamma\|u_{n}-x _{n}\|\bigl\| A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\| + \|x_{n}-p\|^{2}-\|x_{n+1}-p\| ^{2}. \end{aligned}$$

From Condition (1) and (3.10), we have

$$ \lim_{n\rightarrow\infty}\|u_{n}-x_{n} \|=0. $$

(3.12)

From (3.5) and (3.12), we have

$$ \|u_{n}-z_{n}\|\leq\|u_{n}-x_{n} \|+\|x_{n}-z_{n}\|\rightarrow0 $$

(3.13)

as $n\rightarrow\infty$.

Step 4. Show that $\|x_{n+1}-x_{n}\|\rightarrow0$ as $n\rightarrow\infty$. From (3.12) and (3.13), we have

$$\begin{aligned} \|x_{n+1}-u_{n}\| =&\bigl\| \alpha_{n}x_{n}+(1- \alpha_{n})z_{n}-u_{n}\bigr\| \\ \leq&\alpha_{n}\|x_{n}-u_{n}\|+(1- \alpha_{n})\|z_{n}-u_{n}\| \rightarrow0 \end{aligned}$$

(3.14)

as $n\rightarrow\infty$. From (3.12) and (3.14), we also have

$$ \|u_{n}-u_{n+1}\|\leq\|u_{n}-x_{n+1} \|+\|x_{n+1}-u_{n+1}\|\rightarrow0 $$

(3.15)

as $n\rightarrow\infty$. It follows from (3.12) and (3.14) that

$$ \|x_{n+1}-x_{n}\|\leq\|x_{n+1}-u_{n} \|+\|u_{n}-x_{n}\|\rightarrow0 $$

(3.16)

as $n\rightarrow\infty$.

Step 5. Show that $\omega_{w}(x_{n})\subset\Theta$, where $\omega_{w}(x_{n})=\{x\in H:x_{n_{i}}\rightharpoonup x, \{x_{n_{i}}\} \subset\{x_{n}\}\}$. Since $\{x_{n}\}$ is bounded and H is reflexive, $\omega_{w}(x_{n})$ is nonempty. Let $q\in\omega_{w}(x_{n})$ be an arbitrary element. Then there exists a subsequence $\{x_{n_{i}}\}\subset\{x_{n}\}$ converging weakly to q. From (3.11), it follows that $u_{n_{i}}\rightharpoonup q$ as $i\rightarrow\infty$. By Lemma 3.2 and (3.13), we obtain $q\in F(T)$.

Next, we show that $q\in EP(F_{1})$. From $u_{n}=T^{F_{1}}_{r_{n}}(I+\gamma A^{*}(I-T^{F_{2}}_{r_{n}})A)x_{n}$, we have

$$\begin{aligned} F_{1}(u_{n},y)+\frac{1}{r_{n}}\bigl\langle y-u_{n},u_{n}-x_{n}-\gamma A^{*} \bigl(I-T^{F_{2}}_{r_{n}}\bigr)Ax_{n}\bigr\rangle \geq0 \end{aligned}$$

for all $y\in C$, which implies that

$$\begin{aligned} F_{1}(u_{n},y)+\frac{1}{r_{n}}\langle y-u_{n},u_{n}-x_{n}\rangle-\frac {1}{r_{n}} \bigl\langle y-u_{n},\gamma A^{*}\bigl(I-T^{F_{2}}_{r_{n}} \bigr)Ax_{n}\bigr\rangle \geq0 \end{aligned}$$

for all $y\in C$. By Assumption 2.3(2), we have

$$\begin{aligned} \frac{1}{r_{n_{i}}}\langle y-u_{n_{i}},u_{n_{i}}-x_{n_{i}} \rangle-\frac {1}{r_{n_{i}}}\bigl\langle y-u_{n_{i}},\gamma A^{*} \bigl(I-T^{F_{1}}_{r_{n_{i}}}\bigr)Ax_{n_{i}}\bigr\rangle \geq F_{1}(y,u_{n_{i}}) \end{aligned}$$

for all $y\in C$. From $\liminf_{n\to\infty}r_{n}>0$, from (3.10), (3.12), and Assumption 2.3(4), we obtain

$$\begin{aligned} F_{1}(y,q)\leq0 \end{aligned}$$

for all $y\in C$. For any $0< t\leq1$ and $y\in C$, let $y_{t}=ty+(1-t)q$. Since $y\in C$ and $q\in C$, $y_{t}\in C$, and hence $F_{1}(y_{t},q)\leq0$. So, by Assumption 2.3(1) and (4), we have

$$\begin{aligned} 0=F_{1}(y_{t},y_{t})\leq tF_{1}(y_{t},y)+(1-t)F_{1}(y_{t},q) \leq tF_{1}(y_{t},y) \end{aligned}$$

and hence $F_{1}(y_{t},y)\geq0$. So $F_{1}(q,y)\geq0$ for all $y\in C$ by (3.15) and hence $q\in EP(F_{1})$. Since A is a bounded linear operator, $Ax_{n_{i}}\rightharpoonup Aq$. Then it follows from (3.10) that

$$\begin{aligned} T^{F_{2}}_{r_{n_{i}}}Ax_{n_{i}}\rightharpoonup Aq \end{aligned}$$

(3.17)

as $i\rightarrow\infty$. By the definition of $T^{F_{2}}_{r_{n_{i}}}Ax_{n_{i}}$, we have

$$\begin{aligned} F_{2}\bigl(T^{F_{2}}_{r_{n_{i}}}Ax_{n_{i}},y\bigr)+ \frac{1}{r_{n_{i}}}\bigl\langle y-T^{F_{2}}_{r_{n_{i}}}Ax_{n_{i}},T^{F_{2}}_{r_{n_{i}}}Ax_{n_{i}}-Ax_{n_{i}} \bigr\rangle \geq&0 \end{aligned}$$

for all $y\in C$. Since $F_{2}$ is upper semi-continuous in the first argument and (3.17), it follows that

$$\begin{aligned} F_{2}(Aq,y) \geq&0 \end{aligned}$$

for all $y\in C$. This shows that $Aq\in EP(F_{2})$. Hence $q\in\Omega$.

Step 6. Show that $\{x_{n}\}$ and $\{u_{n}\}$ converge weakly to an element of Θ. It is sufficient to show that $\omega_{w}(x_{n})$ is single point set. Let $p,q\in\omega_{w}(x_{n})$ and $\{x_{n_{k}}\}$, $\{x_{n_{m}}\} \subset\{x_{n}\}$ be such that $x_{n_{k}}\rightharpoonup p$ and $x_{n_{m}}\rightharpoonup q$. From (3.12), we also have $u_{n_{k}}\rightharpoonup p$ and $u_{n_{m}}\rightharpoonup q$. By Lemma 3.2 and (3.13), it follows that $p,q\in F(T)$. Applying Lemma 2.2, we obtain $p=q$. This completes the proof. □

If $Tp=\{p\}$ for all $p\in F(T)$, then T satisfies Condition (A) and so we can obtain the following result.

Theorem 3.4

Let $H_{1}$, $H_{2}$ be two real Hilbert spaces and $C\subset H_{1}$, $Q\subset H_{2}$ be nonempty closed convex subsets of Hilbert spaces $H_{1}$ and $H_{2}$, respectively. Let $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator and $T:C\rightarrow K(C)$ a $\frac{1}{2}$-nonspreading multi-valued mapping. Let $F_{1}:C\times C\rightarrow\mathbb{R}$, $F_{2}:Q\times Q \rightarrow\mathbb{R}$ be bifunctions satisfying Assumption 2.3 and $F_{2}$ is upper semi-continuous in the first argument. Assume that $\Theta=F(T)\cap\Omega\neq\emptyset$ and $Tp=\{p\}$ for all $p\in F(T)$, where $\Omega=\{z\in C:z\in EP(F_{1})\textit{ and }Az\in EP(F_{2})\}$. Let $\{x_{n}\}$ be a sequence defined by

$$ \left \{ \textstyle\begin{array}{@{}l} x_{1}\in C \textit{ arbitrarily},\\ u_{n}=T_{r_{n}}^{F_{1}}(I-\gamma A^{*}(I-T_{r_{n}}^{F_{2}})A)x_{n},\\ x_{n+1}\in\alpha_{n}x_{n}+(1-\alpha_{n})Tu_{n}, \end{array}\displaystyle \right . $$

(3.18)

for all $n\geq1$, where $\{\alpha_{n}\}\subset(0,1)$, $r_{n}\subset (0,\infty)$, and $\gamma\in(0,1/L)$ such that L is the spectral radius of $A^{*}A$ and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (1) $0<\liminf_{n\rightarrow\infty}\alpha_{n}\leq\limsup _{n\rightarrow\infty}\alpha_{n}<1$;

• (2) $\liminf_{n\rightarrow\infty}r_{n}>0$.

Then the sequence $\{x_{n}\}$ defined by (3.18) converges weakly to $p\in\Theta$.

Since $P_{T}$ satisfies Condition (A), we also obtain the following results.

Theorem 3.5

Let $H_{1}$, $H_{2}$ be two real Hilbert spaces and $C\subset H_{1}$, $Q\subset H_{2}$ be nonempty closed convex subsets of Hilbert spaces $H_{1}$ and $H_{2}$, respectively. Let $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator and $T:C\rightarrow P(C)$ a multi-valued mapping. Let $F_{1}:C\times C\rightarrow\mathbb{R}$, $F_{2}:Q\times Q \rightarrow\mathbb{R}$ be bifunctions satisfying Assumption 2.3 and $F_{2}$ is upper semi-continuous in the first argument. Assume that $P_{T}$ is $\frac{1}{2}$-nonspreading multi-valued mapping and $I-T$ is demiclosed at 0 with $\Theta =F(T)\cap\Omega\neq\emptyset$, where $\Omega=\{z\in C:z\in EP(F_{1})\textit{ and }Az\in EP(F_{2})\}$. Let $\{ x_{n}\}$ be a sequence defined by

$$ \left \{ \textstyle\begin{array}{@{}l} x_{1}\in C \textit{ arbitrarily},\\ u_{n}=T_{r_{n}}^{F_{1}}(I-\gamma A^{*}(I-T_{r_{n}}^{F_{2}})A)x_{n},\\ x_{n+1}\in\alpha_{n}x_{n}+(1-\alpha_{n})P_{T}u_{n}, \end{array}\displaystyle \right . $$

(3.19)

for all $n\geq1$, where $\{\alpha_{n}\}\subset(0,1)$, $r_{n}\subset (0,\infty)$, and $\gamma\in(0,1/L)$ such that L is the spectral radius of $A^{*}A$ and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (1) $0<\liminf_{n\rightarrow\infty}\alpha_{n}\leq\limsup _{n\rightarrow\infty}\alpha_{n}<1$;

• (2) $\liminf_{n\rightarrow\infty}r_{n}>0$.

Then the sequence $\{x_{n}\}$ defined by (3.19) converges weakly to $p\in\Theta$.

Proof

By the same proof as in Theorem 3.3, we have $u_{n}\rightarrow z_{n}\in P_{T}u_{n}$. This implies that

$$ d(u_{n},Tu_{n})\leq d(u_{n},P_{T}u_{n}) \leq\|u_{n}-z_{n}\|\rightarrow0 $$

(3.20)

as $n\rightarrow\infty$. Since $I-T$ is demiclosed at 0, we obtain this result. □

4 Examples and numerical results

In this section, we give examples and numerical results for supporting our main theorem.

Example 4.1

Let $H_{1}=H_{2}=\mathbb{R}$, $C=[-3,0]$, and $Q=(-\infty,0]$. Let $F_{1}(u,v)=(u-1)(v-u)$ for all $u,v\in C$ and $F_{2}(x,y)=(x+15)(y-x)$ for all $x,y\in Q$. Define two mappings $A:\mathbb{R}\rightarrow\mathbb{R}$ and $T:C\rightarrow K(C)$ by $Ax=3x$ for all $x\in\mathbb{R}$ and

$$ Tx=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \{0\},& x\in[-2,0];\\ {[}{-}\frac{|x|}{|x|+1},0],& x\in[-3,-2). \end{array}\displaystyle \right . $$

Choose $\alpha_{n}=\frac{n}{2n+1}$, $r_{n}=\frac{n}{n+1}$, and $\gamma=\frac{1}{10}$. It is easy to check that $F_{1}$ and $F_{2}$ satisfy all conditions in Theorem 3.3 and T satisfies Condition (A) such that $F(T)=\{0\}$. For each $r>0$ and $x\in C$, we divide the process of our iteration into five steps as follows:

Step 1. Find $z\in Q$ such that $F_{2}(z,y)+\frac{1}{r}\langle y-z,z-Ax\rangle\geq0$ for all $y\in Q$. Noting that $Ax=3x$, we have

$$\begin{aligned} F_{2}(z,y)+\frac{1}{r}\langle y-z,z-Ax\rangle\geq0 \quad \Longleftrightarrow&\quad(z+15) (y-z)+\frac{1}{r}\langle y-z,z-3x\rangle \geq0 \\ \quad \Longleftrightarrow&\quad r(z+15) (y-z)+(y-z) (z-3x)\geq0 \\ \quad \Longleftrightarrow&\quad(y-z) \bigl((1+r)z-(3x-15r)\bigr)\geq0. \end{aligned}$$

By Lemma 2.4, we know that $T_{r}^{F_{2}}Ax$ is single-valued. Hence $z=\frac{3x-15r}{1+r}$.

Step 2. Find $s\in C$ such that $s=x-\gamma A^{*}(I-T^{F_{2}}_{r})Ax$. From Step 1, we have

$$\begin{aligned} s =&x-\gamma A^{*}\bigl(I-T^{F_{2}}_{r}\bigr)Ax=x- \gamma A^{*}\bigl(Ax-T^{F_{2}}_{r}Ax\bigr) \\ =&x-\gamma\biggl(9x-\frac{3(3x-15r)}{1+r} \biggr) \\ =&(1-9\gamma)x+\frac{3\gamma}{1+r}(3x-15r). \end{aligned}$$

Step 3. Find $u\in C$ such that $F_{1}(u,v)+\frac{1}{r}\langle v-u,u-s\rangle\geq0$ for all $v\in C$. From Step 2, we have

$$\begin{aligned} F_{1}(u,v)+\frac{1}{r}\langle v-u,u-s\rangle\geq0 \quad \Longleftrightarrow&\quad(u-1) (v-u)+\frac{1}{r}\langle v-u,u-s\rangle \geq 0 \\ \quad \Longleftrightarrow&\quad r(u-1) (v-u)+(v-u) (u-s)\geq0 \\ \quad \Longleftrightarrow& \quad(v-u) \bigl((1+r)u-(s+r)\bigr)\geq0. \end{aligned}$$

Similarly, by Lemma 2.4, we obtain $u=\frac{s+r}{1+r}=\frac{(1-9\gamma)x+r}{1+r}+\frac{3\gamma (3x-15r)}{(1+r)^{2}}$.

Step 4. Find $x_{n+1}\in \alpha_{n}x_{n}+(1-\alpha_{n})Tu_{n}$, where $u_{n}=\frac{(1-9\gamma)x_{n}+r_{n}}{1+r_{n}}+\frac{3\gamma (3x_{n}-15r_{n})}{(1+r_{n})^{2}}$. From

$$ Tx=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \{0\},& x\in[-2,0];\\ {[}{-}\frac{|x|}{|x|+1},0],& x\in[-3,-2), \end{array}\displaystyle \right . $$

and $\alpha_{n}=\frac{n}{2n+1}$, $r_{n}=\frac{n}{n+1}$, and $\gamma =\frac{1}{10}$, we have

$$ x_{n+1}= \biggl(\frac{n}{2n+1} \biggr)x_{n}+ \biggl(1- \frac{n}{2n+1} \biggr)z_{n}, $$

(4.1)

where

$$ z_{n}\in \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \{0\},& u_{n}\in[-2,0];\\ {[}{-}\frac{|u_{n}|}{|u_{n}|+1},0 ],& u_{n}\in[-3,-2). \end{array}\displaystyle \right . $$

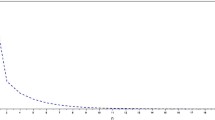
Step 5. Compute the numerical results. Choosing $x_{1}=-3$ and taking randomly $z_{n}$ in the above interval, we obtain Tables 1 and 2.

Table 1 Numerical results of Example  1.1 being randomized in the first time

Table 2 Numerical results of Example  1.1 being randomized in the second time

From Table 1 and Table 2, we see that 0 is the solution in Example 1.1.