Abstract
We compare the rate of convergence for some iteration methods for contractions. We conclude that the coefficients involved in these methods have an important role to play in determining the speed of the convergence. By using Matlab software, we provide numerical examples to illustrate the results. Also, we compare mathematical and computer-calculating insights in the examples to explain the reason of the existence of the old difference between the points of view.
Similar content being viewed by others
1 Introduction
Iteration schemes for numerical reckoning fixed points of various classes of nonlinear operators are available in the literature. The class of contractive mappings via iteration methods is extensively studied in this regard. In 1952, Plunkett published a paper on the rate of convergence for relaxation methods [1]. In 1953, Bowden presented a talk in a symposium on digital computing machines entitled ‘Faster than thought’ [2]. Later, this basic idea has been used in engineering, statistics, numerical analysis, approximation theory, and physics for many years (see, for example, [3–9] and [10]). In 1991, Argyros published a paper about iterations converging faster than Newton’s method to the solutions of nonlinear equations in Banach spaces [11, 12]. In 1997, Lucet presented a method faster than the fast Legendre transform [13]. In 2004, Berinde used the notion of rate of convergence for iterations method and showed that the Picard iteration converges faster than the Mann iteration for a class of quasi-contractive operators [14]. Later, he provided some results in this area [15, 16]. In 2006, Babu and Vara Prasad showed that the Mann iteration converges faster than the Ishikawa iteration for the class of Zamfirescu operators [17]. In 2007, Popescu showed that the Picard iteration converges faster than the Mann iteration for the class of quasi-contractive operators [18]. Recently, there have been published some papers about introducing some new iterations and comparing of the rates of convergence for some iteration methods (see, for example, [19–22] and [23]).
In this paper, we compare the rates of convergence of some iteration methods for contractions and show that the involved coefficients in such methods have an important role to play in determining the rate of convergence. During the preparation of this work, we found that the efficiency of coefficients had been considered in [24] and [25]. But we obtained our results independently, before reading these works, and one can see it by comparing our results and those ones.
2 Preliminaries
As we know, the Picard iteration has been extensively used in many works from different points of view. Let \((X, d)\) be a metric space, \(x_{0}\in X\), and \(T\colon X\to X\) a selfmap. The Picard iteration is defined by
for all \(n\geq0\). Let \(\{\alpha_{n}\}_{n\geq0}\), \(\{\beta_{n}\}_{n\geq 0}\), and \(\{\gamma_{n}\}_{n\geq0}\) be sequences in \([0, 1]\). Then the Mann iteration method is defined by
for all \(n\geq0\) (for more information, see [26]). Also, the Ishikawa iteration method is defined by
for all \(n\geq0\) (for more information, see [27]). The Noor iteration method is defined by
for all \(n\geq0\) (for more information, see [28]). In 2007, Agarwal et al. defined their new iteration methods by
for all \(n\geq0\) (for more information, see [29]). In 2014, Abbas et al. defined their new iteration methods by
for all \(n\geq0\) (for more information, see [30]). In 2014, Thakur et al. defined their new iteration methods by
for all \(n\geq0\) (for more information, see [23]). Also, the Picard S-iteration was defined by
for all \(n\geq0\) (for more information, see [20] and [22]).
3 Self-comparing of iteration methods
Now, we are ready to provide our main results for contractive maps. In this respect, we assume that \((X, \|\cdot\|)\) is a normed space, \(x_{0}\in X\), \(T\colon X\to X\) is a selfmap and \(\{\alpha_{n}\}_{n\geq 0}\), \(\{\beta_{n}\}_{n\geq0}\) and \(\{\gamma_{n}\}_{n\geq0}\) are sequences in \((0, 1)\).
The Mann iteration is given by \(x_{n+1}= (1-\alpha_{n})x_{n}+\alpha_{n} Tx_{n}\) for all \(n\geq0\).
Note that we can rewrite it as \(x_{n+1}= \alpha_{n} x_{n}+(1-\alpha_{n}) Tx_{n}\) for all \(n\geq0\).
We call these cases the first and second forms of the Mann iteration method.
In the next result we show that choosing a type of sequence \(\{\alpha_{n}\}_{n\geq0}\) in the Mann iteration has a notable role to play in the rate of convergence of the sequence \(\{x_{n}\}_{n\geq0}\).
Let \(\{u_{n}\}_{n\geq0}\) and \(\{v_{n}\}_{n\geq0}\) be two fixed point iteration procedures that converge to the same fixed point p and \(\|u_{n}-p\|\leq a_{n}\) and \(\|v_{n}-p\|\leq b_{n}\) for all \(n\geq0\). If the sequences \(\{a_{n}\}_{n\geq0}\) and \(\{b_{n}\}_{n\geq0}\) converge to a and b, respectively, and \(\lim_{n\to\infty}\frac{\|a_{n}-a\|}{\|b_{n}-b\|}=0\), then we say that \(\{u_{n}\}_{n\geq0}\) converges faster than \(\{v_{n}\}_{n\geq0}\) to p (see [14] and [23]).
Proposition 3.1
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. Consider the first case for Mann iteration. If the coefficients of \(Tx_{n}\) are greater than the coefficients of \(x_{n}\), that is, \(1-\alpha_{n} < \alpha_{n}\) for all \(n\geq0\) or equivalently \(\{\alpha_{n}\}_{n\geq0}\) is a sequence in \((\frac{1}{2}, 1)\), then the Mann iteration converges faster than the Mann iteration which the coefficients of \(x_{n}\) are greater than the coefficients of \(Tx_{n}\).
Proof
Let \(\{x_{n}\}\) be the sequence in the Mann iteration which the coefficients of \(Tx_{n}\) are greater than the coefficients of \(x_{n}\), that is,
for all n. In this case, we have
for all n. Since \(\alpha_{n} \in(\frac{1}{2}, 1)\), \(1-\alpha_{n}(1-k) < 1-\frac{1}{2}(1-k)\). Put \(a_{n} = (1-\frac{1}{2}(1-k) )^{n} \Vert x_{1}-p\Vert \) for all n. Now, let \(\{x_{n}\}\) be the sequence in the Mann iteration of which the coefficients of \(x_{n}\) are greater than the coefficients of \(Tx_{n}\). In this case, we have
for all n. Since \(1-\alpha_{n} < \alpha_{n}\) for all \(n\geq0\), we get \(1-(1-\alpha_{n})(1-k) < 1\) for all \(n\geq0\). Put \(b_{n}=\Vert x_{1}-p\Vert \) for all n. Note that \(\lim\frac{a_{n}}{b_{n}}=\lim\frac{ (1-\frac{1}{2}(1-k) )^{n} \Vert x_{1}-p\Vert }{ \Vert x_{1}-p\Vert }=0\). This completes the proof. □
Note that we can use \(1-\alpha_{n} < \alpha_{n}\), for n large enough, instead of the condition \(1-\alpha_{n} < \alpha_{n}\), for all \(n\geq0\). One can use similar conditions instead of the conditions which we will use in our results.
As we know, we can consider four cases for writing the Ishikawa iteration method. In the next result, we indicate each case by different enumeration. Similar to the last result, we want to compare the Ishikawa iteration method with itself in the four possible cases. Again, we show that the coefficient sequences \(\{\alpha_{n}\}_{n\geq 0}\) and \(\{\beta_{n}\}_{n\geq0}\) have effective roles to play in the rate of convergence of the sequence \(\{x_{n}\}_{n\geq0}\) in the Ishikawa iteration method.
Proposition 3.2
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C\) a contraction with constant \(k\in(0, 1)\), and p a fixed point of T. Consider the following cases of the Ishikawa iteration method:
and
for all \(n\geq0\). If \(1-\alpha_{n} < \alpha_{n}\) and \(1-\beta_{n} < \beta_{n}\) for all \(n\geq0\), then the case (3.2) converges faster than the others. In fact, the Ishikawa iteration method is faster whenever the coefficients of \(Ty_{n}\) and \(Tx_{n}\) simultaneously are greater than the related coefficients of \(x_{n}\) for all \(n\geq0\).
Proof
Let \(\{x_{n}\}_{n\geq0}\) be the sequence in the case (3.2). Then we have
and
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n} \in(\frac{1}{2}, 1)\), \(1-\alpha_{n}(1-k)-\alpha_{n}\beta_{n} k (1-k)< 1-\frac{1}{2}(1-k)-\frac {1}{4}k(1-k)\) for all \(n\geq0\). Put \(a_{n}= (1-\frac {1}{2}(1-k)-\frac{1}{4}k(1-k) ) ^{n} \Vert x_{1}-p\Vert \) for all \(n\geq0\). If \(\{x_{n}\}_{n\geq0}\) is the sequence in the case (3.3), then we get
and
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n} \in(\frac{1}{2}, 1)\), \(1-(1-\alpha_{n}) (1-k)-(1-\alpha_{n})(1-\beta_{n})(1-k)< 1\) for all \(n\geq0\). Put \(b_{n} =\Vert x_{1}-p\Vert \) for all \(n\geq0\). Since
we get \(\lim\frac{a_{n}}{b_{n}}=\lim\frac{ (1-\frac{1}{2}(1-k)-\frac {1}{4}k(1-k) )^{n} \Vert x_{1}-p\Vert }{\Vert x_{1}-p\Vert }=0\) and so the iteration (3.2) converges faster than the case (3.3). Now, let \(\{x_{n}\}_{n\geq0}\) be the sequence in the case (3.4). Then
and
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n}\in(\frac{1}{2}, 1)\) for all \(n\geq0\), \(-(1-k)<-\alpha_{n}(1-k)< -\frac{1}{2}(1-k)\) and \(\frac{-1}{2}k(1-k)<-\alpha_{n}(1-\beta_{n})k(1-k)<0\) for all n. Hence,
for all \(n\geq0\). Put \(c_{n} = (1-\frac{1}{2}(1-k) )^{n} \Vert x_{1}-p\Vert \) for all \(n\geq0\). Thus, we obtain
and so the iteration (3.2) converges faster than the case (3.4). Now, let \(\{x_{n}\}_{n\geq0}\) be the sequence in the case (3.5). Then we have
and
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n}\in(\frac{1}{2}, 1)\) for all n, \(-(1-k^{2})<-\alpha_{n}(1-k^{2})< -\frac{1}{2}(1-k^{2})\), and \(-\frac{1}{2}k(1-k)<-(1-\alpha_{n})\beta_{n}k(1-k)<0\) and so
for all \(n\geq0\). Put \(d_{n} = (1-\frac{1}{2}(1-k) )^{n} \Vert x_{1}-p \Vert \) for all \(n\geq0\). Then we have
and so the iteration (3.2) converges faster than the case (3.5). □
By using a similar condition, one can show that the iteration (3.5) is faster than the case (3.3).
Now consider eight cases for writing the Noor iteration method. By using a condition, we show that the coefficient sequences \(\{\alpha_{n}\}_{n\geq0}\), \(\{\beta_{n}\}_{n\geq0}\), and \(\{\gamma_{n}\}_{n\geq0}\) have effective roles to play in the rate of convergence of the sequence \(\{x_{n}\}_{n\geq0}\) in the Noor iteration method. We enumerate the cases of the Noor iteration method during the proof of our next result.
Theorem 3.1
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. Consider the case (2.3) of the Noor iteration method
for all \(n\geq0\). If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}<\gamma_{n}\) for all \(n\geq0\), then the iteration (2.3) is faster than the other possible cases.
Proof
First, we compare the case (2.3) with the following Noor iteration case:
for all \(n\geq0\). Note that
and
for all \(n\geq0\). Also, we have
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac {1}{2}, 1)\) for all n, \(-(1-k^{2})< -\alpha_{n}(1-k^{2})< -\frac{1}{2}(1 -k^{2})\), \(-k(1-k)<-\alpha_{n}\beta_{n}k(1-k)< -\frac{1}{4}k(1-k)\), and
for all n. This implies that
for all n. Put \(a_{n} = (1-\frac{1}{2}(1-k) -\frac {1}{8}k^{2}(1-k))^{n}\Vert x_{1}-p\Vert \) for all \(n\geq0\). Now for the sequences \(\{u_{n}\}_{n\geq0}\) with \(u_{1}=x_{1}\) and \(\{v_{n}\} _{n\geq0}\) in (3.6), we have
and
for all \(n\geq0\). Hence,
for all n. Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac{1}{2}, 1)\) for all n, \(-k(1-k)<-\alpha_{n}\beta_{n}k(1-k)< -\frac{1}{4}k (1-k)\) and \(\frac{1}{2}k^{2}(1-k)< -\alpha_{n}\beta_{n}(1-\gamma _{n})k^{2}(1-k) < 0 \) for all n. Hence,
for all n. Put \(b_{n}=(1-\frac{1}{2}(1-k) -\frac{1}{4}k(1-k))^{n}\| u_{1}-p\|\) for all \(n\geq0\). Then we have
Thus, \(\{x_{n}\}_{n\geq0}\) converges faster than the sequence \(\{u_{n}\} _{n\geq0}\). Now, we compare the case (2.3) with the following Noor iteration case:
for all \(n\geq0\). Note that
and
for all \(n\geq0\). Hence,
for all \(n\geq0\). Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac {1}{2}, 1)\) for all n, \(-\frac{1}{2}k(1-k)<-\alpha_{n}(1-\beta _{n})k(1-k)< 0 \), and \(-k^{2}(1-k)< -\alpha_{n}\beta_{n}(1-\gamma_{n})k^{2}(1-k) < -\frac{1}{8}k^{2}(1-k)\) and so
for all n. Put \(c_{n}=(1-\frac{1}{2}(1-k) -\frac {1}{8}k^{2}(1-k))^{n}\Vert u_{1}-p\Vert \) for all \(n\geq0\). Then we have
Thus, \(\{x_{n}\}_{n\geq0}\) converges faster than the sequence \(\{u_{n}\} _{n\geq0}\). Now, we compare the case (2.3) with the following Noor iteration case:
for all \(n\geq0\). Note that
and
and so
for all n. Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac{1}{2}, 1)\) for all n, \(-k(1-k)<-\alpha_{n}\beta_{n}k(1-k)< -\frac {1}{4}k(1-k)\), and \(-\frac{1}{2}k^{2}(1-k)< -\alpha_{n}\beta_{n}(1-\gamma _{n})k^{2}(1-k) < 0\) for all n. This implies that
for all n. Put \(d_{n}=(1-\frac{1}{2}(1-k) -\frac{1}{4}k(1-k))^{n} \Vert u_{1}-p\Vert \) for all \(n\geq0\). Then we get
and so the sequence \(\{x_{n}\}_{n\geq0}\) converges faster than the sequence \(\{u_{n}\}_{n\geq0}\). By using similar proofs, one can show that the case (2.3) is faster than the following cases of the Noor iteration method:
and
for all \(n\geq0\). This completes the proof. □
By using similar conditions, one can show that the case (3.7) converges faster than (3.8), (3.9) converges faster than (3.11), (3.11) converges faster than (3.10) and (3.10) converges faster than (3.12).
As we know, the Agarwal iteration method could be written in the following four cases:
and
for all \(n\geq0\). One can easily show that the case (3.13) converges faster than the other ones for contractive maps. We record it as the next lemma.
Lemma 3.1
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. If \(1-\alpha_{n}<\alpha_{n}\) and \(1-\beta_{n} <\beta_{n}\) for all \(n\geq0\), then the case (3.13) converges faster than (3.14), (3.15), and (3.16).
Also by using a similar condition, one can show that the case (3.16) converges faster than (3.14). Similar to Theorem 3.1, we can prove that for contractive maps one case in the Abbas iteration method converges faster than the other possible cases whenever the elements of the sequences \(\{\alpha_{n}\}_{n\geq0}\), \(\{\beta_{n}\}_{n\geq0}\), and \(\{\gamma_{n}\}_{n\geq0}\) are in \((\frac{1}{2}, 1)\) for sufficiently large n. Also, one can show that for contractive maps the case (2.6) of the Thakur-Thakur-Postolache iteration method converges faster than the other possible cases whenever elements of the sequences \(\{\alpha_{n}\}_{n\geq0}\), \(\{\beta_{n}\}_{n\geq0}\), and \(\{\gamma_{n}\}_{n\geq0}\) are in \((\frac{1}{2}, 1)\) for sufficiently large n. We record these results as follows.
Lemma 3.2
Let C be a nonempty, closed, and convex subset of a Banach space X, \(u_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\), and p a fixed point of T. Consider the following case in the Abbas iteration method:
for all n. If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}< \gamma_{n}\) for sufficiently large n, then the case (3.17) converges faster than the other possible cases.
Also by using similar conditions in the Abbas iteration method, one can show that the cases
and
converge faster than the case
Also the case
converges faster than the cases
and
and
Lemma 3.3
Let C be a nonempty, closed, and convex subset of a Banach space X, \(u_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}< \gamma_{n}\) for sufficiently large n, then the case (2.6) in the Thakur-Thakur-Postolache iteration method converges faster than the other possible cases.
Also by using similar conditions, one can show that the cases
and
converge faster than the case
Also the case
converges faster than the cases
and
and
Finally, we have a similar situation for the Picard S-iteration which we record here.
Lemma 3.4
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. If \(1-\alpha_{n} <\alpha_{n}\) and \(1-\beta_{n} <\beta_{n}\) for sufficiently large n, then the case (2.7) in the Picard S-iteration method converges faster than the other possible cases.
4 Comparing different iterations methods
In this section, we compare the rate of convergence of some different iteration methods for contractive maps. Our goal is to show that the rate of convergence relates to the coefficients.
Theorem 4.1
Let C be a nonempty, closed, and convex subset of a Banach space X, \(u_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. Consider the case (2.5) in the Abbas iteration method
the case (3.17) in the Abbas iteration method
and the case (2.6) in the Thakur-Thakur-Postolache iteration method
for all \(n\geq0\). If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}< \gamma_{n}\) for sufficiently large n, then the case (3.17) in the Abbas iteration method converges faster than the case (2.6) in the Thakur-Thakur-Postolache iteration method. Also, the case (2.6) in the Thakur-Thakur-Postolache iteration method is faster than the case (2.5) in the Abbas iteration method.
Proof
Let \(\{u_{n}\}_{n\geq0}\) be the sequence in the case (3.17). Then we have
and
for all n. Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac{1}{2}, 1)\) for sufficiently large n, we have
\(-\frac{1}{2}(1-k)<-\alpha_{n}\gamma_{n}(1-k)<0\), and \(-k(1-k)<-\alpha _{n}\beta_{n}\gamma_{n} k (1-k) <-\frac{1}{8}k(1-k)\) for sufficiently large n. Hence,
for sufficiently large n. Put \(a_{n} =k^{n} (1-\frac{1}{2}(1-k)-\frac {1}{8}k(1-k))^{n}\Vert u_{1}-p\Vert \) for all n. Now, let \(\{ u_{n}\}_{n\geq0}\) be the sequence in the case (2.6). Then we have
and
for all n. Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac{1}{2}, 1)\) for sufficiently large n, we have
\(-\frac{1}{2}(1-k)<-\alpha_{n}\beta_{n}(1-\gamma_{n})(1-k)<0\), and \(-k(1-k)<-\alpha_{n}\beta_{n}\gamma_{n} k (1-k) <-\frac{1}{8}k(1-k)\) for sufficiently large n. Hence,
for sufficiently large n. Put \(b_{n} =k^{n} (1-\frac{1}{4}(1-k) -\frac {1}{8}k(1-k))^{n}\Vert u_{1}-p\Vert \) for all n. Then
Thus, the case (3.17) in the Abbas iteration method converges faster than the case (2.6) in the Thakur-Thakur-Postolache iteration method.
Now for the case (2.5), we have
and
for all n. Since \(\alpha_{n}, \beta_{n}, \gamma_{n}\in(\frac{1}{2}, 1)\) for sufficiently large n, \(-\frac{1}{2}(1-k)<-(1-\alpha _{n})(1-k)< 0\), \(-(1-k)<-\alpha_{n}\gamma_{n}(1-k)<-\frac{1}{4}(1-k)\), and \(-\frac {1}{2}k(1-k)<-(1-\alpha_{n})\beta_{n}\gamma_{n} k (1-k) <0\) for sufficiently large n. Hence,
for sufficiently large n. Put \(c_{n} =k^{n} (1-\frac{1}{4}(1-k) )^{n} \Vert x_{1}-p\Vert \) for all n. Then we have
and so the case (2.6) in the Thakur-Thakur-Postolache iteration method is faster than the case (2.5) in the Abbas iteration method. □
By using a similar proof, we can compare the Thakur-Thakur-Postolache and the Agarwal iteration methods as follows.
Theorem 4.2
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\) and p a fixed point of T. If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}< \gamma_{n}\) for sufficiently large n, then the case (2.6) in the Thakur-Thakur-Postolache iteration method converges faster than the case (2.4) in the Agarwal iteration method and the case (2.4) in the Agarwal iteration method is faster than the cases (3.29) and (3.30) in the Thakur-Thakur-Postolache iteration method.
Also by using similar proofs, we can compare some another iteration methods. We record those as follows.
Theorem 4.3
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\), and p a fixed point of T. If \(1-\alpha_{n} <\alpha_{n}\), \(1-\beta_{n} <\beta_{n}\), and \(1-\gamma_{n}< \gamma_{n}\) for sufficiently large n, then the case (2.3) in the Abbas iteration method converges faster than the case (2.2) in the Ishikawa iteration method and the case (2.2) in the Ishikawa iteration method is faster than the cases (3.11) and (3.12) in the Abbas iteration method.
It is notable that there are some cases which the coefficients have no effective roles to play in the rate of convergence. By using similar proofs, one can check the next result. One can obtain some similar cases. This shows us that researchers should stress more the probability of the efficiency of coefficients in the rate of convergence for iteration methods.
Theorem 4.4
Let C be a nonempty, closed, and convex subset of a Banach space X, \(x_{1}\in C\), \(T\colon C \to C \) a contraction with constant \(k\in(0, 1)\), p a fixed point of T, and \(\alpha_{n}, \beta_{n}, \gamma_{n} \in(0, 1)\) for all \(n\geq0\). Then the case (2.4) in the Agarwal iteration method is faster than the case (2.1) in the Mann iteration method, the case (2.5) in the Abbas iteration method is faster than the case (2.1) in the Mann iteration method, the case (2.6) in the Thakur-Thakur-Postolache iteration method is faster than the case (2.1) in the Mann iteration method, the case (2.4) in the Agarwal iteration method is faster than the case (2.2) in the Ishikawa iteration method, the case (2.5) in the Abbas iteration method is faster than the case (2.2) in the Ishikawa iteration method and the case (2.6) in the Thakur-Thakur-Postolache iteration method is faster than the case (2.2) in the Ishikawa iteration method.
5 Examples and figures
In this section, we provide some examples to illustrate our results.
Example 1
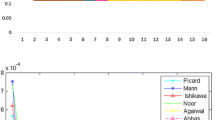
Let \(X = \mathbb{R}\), \(C=[1, 60]\), \(x_{0}=20\), \(\alpha_{n}=0.7\), and \(\beta_{n}=0.85\) for all \(n\geq0\). Define the map \(T\colon C \to C\) by the formula \(T(x)=(3x+18)^{\frac{1}{3}}\) for all \(x\in C\). It is easy to see that T is a contraction. In Tables 1-3, we first compare two cases of the Mann iteration method and also four cases of the Ishikawa and Agarwal iteration methods separately. From a mathematical point of view, one can see that the Mann iteration (3.1) is more than 2.82 times faster than the Mann iteration (2.1), the Ishikawa iteration (3.2) is more than 1.07 times faster than the Ishikawa iteration (3.4), the Ishikawa iteration (3.2) is more than 11.33 times faster than the Ishikawa iteration (3.3), the Ishikawa iteration (3.2) is more than 11 times faster than the Ishikawa iteration (3.5), the Ishikawa iteration (3.4) is more than 8.75 times faster than the Ishikawa iteration (3.5), the Agarwal iteration (3.13) is 1.22 times faster than the Agarwal iteration (3.14), the Agarwal iteration (3.13) is 1.11 times faster than the Agarwal iteration (3.15), the Agarwal iteration (3.13) is 1.22 times faster than the Agarwal iteration (3.16) and so on. We first add our CPU time in Tables 1-3 for each iteration method. Also, we provide Figure 1 by using at least 30 times calculating of CPU times for our faster cases in the methods. From a computer-calculation point of view, we get a different answer. As one can see in the CPU time table, we found that the Agarwal iteration (3.13) and the Mann iteration (3.1) are faster than the Ishikawa iteration (3.2). This note emphasizes the difference of the mathematical results and computer-calculation results which have appeared many times in the literature.
The next example illustrates Lemma 3.2.
Example 2
Let \(X = \mathbb{R}\), \(C = [0, 2000]\), \(x_{0}=1000\), \(\alpha_{n}=0. 85\), \(\beta_{n}=0. 65\), and \(\gamma_{n}=0. 75\) for all \(n\geq0\). Define the map \(T\colon C\to C\) by the formula \(T(x) =\sqrt[3]{x^{2}}\) for all \(x\in C\). Table 4 shows us that the Abbas iteration (3.17) converges faster than the other cases, the Abbas iteration (3.18) is 1.1 times faster than the Abbas iteration (3.20), the Abbas iteration (3.19) is 1.05 times faster than the Abbas iteration (3.20), the Abbas iteration (3.21) is 1.04 times faster than the Abbas iteration (3.22) and 1.3 times faster than the Abbas iteration (3.23) and the Abbas iteration (3.24). One can get similar results about difference of the mathematical and computer-calculating points of views for this example.
The next example illustrates Theorem 3.1.
Example 3
Let \(X = \mathbb{R}\), \(C = [1, 60]\), \(x_{0}=40\), \(\alpha_{n}=0.9\), \(\beta _{n}=0.6\), and \(\gamma_{n}=0.8\) for all \(n\geq0\). Define the map \(T\colon C\to C\) by \(T(x) =\sqrt{x^{2}-8x+40}\) for all \(x\in C\) (see [23]). Table 5 shows the Abbas iteration (3.17) converges 1.09 times faster than the Thakur-Thakur-Postolache iteration (2.6) and the Thakur-Thakur-Postolache iteration (2.6) is 1.16 times faster than the Abbas iteration (2.5) from the mathematical point of view. Again, we get different results from the computer-calculating point of view by checking Table 5 and Figures 2 and 3.
The next example shows that choosing the coefficients is very important in the rate of convergence of an iteration method.
Example 4
Let \(X=\mathbb{R}\), \(C=[0, 30]\), and \(x_{0}=20\). Define the map \(T\colon \mathbb{R}\to\mathbb{R}\) by \(T(x) = \frac{x}{2}+1\) for all \(x\in C\). Consider the following coefficients separately in the Thakur-Thakur-Postolache iteration (2.6):
-
(a)
\(\alpha_{n}=\beta_{n}=\gamma_{n}= 1-\frac{1}{(n+1)^{10}}\),
-
(b)
\(\alpha_{n}=\beta_{n}=\gamma_{n}= 1-\frac{1}{n+1}\),
-
(c)
\(\alpha_{n}=\beta_{n}=\gamma_{n}= 1-\frac{1}{(n+1)^{\frac{1}{2}}}\),
-
(d)
\(\alpha_{n}=\beta_{n}=\gamma_{n}=1 -\frac{1}{(n+1)^{\frac{1}{5}}}\)
for all \(n\geq0\). Table 6 shows that the Thakur-Thakur-Postolache iteration (2.6) with coefficients (a) is 1.25 times faster than the Thakur-Thakur-Postolache iteration (2.6) with coefficients (b), the Thakur-Thakur-Postolache iteration (2.6) with coefficients (a) is 1.6 times faster than the Thakur-Thakur-Postolache iteration (2.6) with coefficients (c) and the Thakur-Thakur-Postolache iteration (2.6) with coefficients (a) is 2.16 times faster than the Thakur-Thakur-Postolache iteration (2.6) with coefficients (d). This note satisfies other iteration methods of course from the mathematical point of view. Here, we find a little different computer-calculating result for the CPU time table of this example, which one can check in Figure 4.
References
Plunkett, R: On the rate of convergence of relaxation methods. Q. Appl. Math. 10, 263-266 (1952)
Bowden, BV: Faster than Thought: A Symposium on Digital Computing Machines. Pitman, London (1953)
Byrne, C: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103-120 (2004)
Dykstra, R, Kochar, S, Robertson, T: Testing whether one risk progresses faster than the other in a competing risks problem. Stat. Decis. 14(3), 209-222 (1996)
Hajela, D: On faster than Nyquist signaling: computing the minimum distance. J. Approx. Theory 63(1), 108-120 (1990)
Hajela, D: On faster than Nyquist signaling: further estimations on the minimum distance. SIAM J. Appl. Math. 52(3), 900-907 (1992)
Longpre, L, Young, P: Cook reducibility is faster than Karp reducibility in NP. J. Comput. Syst. Sci. 41(3), 389-401 (1990)
Shore, GM: Faster than light: photons in gravitational fields - causality, anomalies and horizons. Nucl. Phys. B 460(2), 379-394 (1996)
Shore, GM: Faster than light: photons in gravitational fields. II. Dispersion and vacuum polarisation. Nucl. Phys. B 633(1-2), 271-294 (2002)
Stark, RH: Rates of convergence in numerical solution of the diffusion equation. J. Assoc. Comput. Mach. 3, 29-40 (1956)
Argyros, IK: Iterations converging faster than Newton’s method to the solutions of nonlinear equations in Banach space. Ann. Univ. Sci. Bp. Rolando Eötvös Nomin., Sect. Comput. 11, 97-104 (1991)
Argyros, IK: Sufficient conditions for constructing methods faster than Newton’s. Appl. Math. Comput. 93, 169-181 (1998)
Lucet, Y: Faster than the fast Legendre transform: the linear-time Legendre transform. Numer. Algorithms 16(2), 171-185 (1997)
Berinde, V: Picard iteration converges faster than Mann iteration for a class of quasi-contractive operators. Fixed Point Theory Appl. 2004(2), 97-105 (2004)
Berinde, V, Berinde, M: The fastest Krasnoselskij iteration for approximating fixed points of strictly pseudo-contractive mappings. Carpath. J. Math. 21(1-2), 13-20 (2005)
Berinde, V: A convergence theorem for Mann iteration in the class of Zamfirescu operators. An. Univ. Vest. Timiş., Ser. Mat.-Inform. 45(1), 33-41 (2007)
Babu, GVR, Vara Prasad, KNVV: Mann iteration converges faster than Ishikawa iteration for the class of Zamfirescu operators. Fixed Point Theory Appl. 2006, Article ID 49615 (2006)
Popescu, O: Picard iteration converges faster than Mann iteration for a class of quasi-contractive operators. Math. Commun. 12(2), 195-202 (2007)
Akbulut, S, Ozdemir, M: Picard iteration converges faster than Noor iteration for a class of quasi-contractive operators. Chiang Mai J. Sci. 39(4), 688-692 (2012)
Gorsoy, F, Karakaya, V: A Picard S-hybrid type iteration method for solving a differential equation with retarded argument (2014). arXiv:1403.2546v2 [math.FA]
Hussain, N, Chugh, R, Kumar, V, Rafiq, A: On the rate of convergence of Kirk-type iterative schemes. J. Appl. Math. 2012, Article ID 526503 (2012)
Ozturk Celikler, F: Convergence analysis for a modified SP iterative method. Sci. World J. 2014, Article ID 840504 (2014)
Thakur, D, Thakur, BS, Postolache, M: New iteration scheme for numerical reckoning fixed points of nonexpansive mappings. J. Inequal. Appl. 2014, 328 (2014)
Berinde, V: Iterative Approximation of Fixed Points. Springer, Berlin (2007)
Chugh, R, Kumar, S: On the rate of convergence of some new modified iterative schemes. Am. J. Comput. Math. 3, 270-290 (2013)
Mann, WR: Mean value methods in iteration. Proc. Am. Math. Soc. 4, 506-510 (1953)
Ishikawa, S: Fixed points by a new iteration method. Proc. Am. Math. Soc. 44, 147-150 (1974)
Noor, MA: New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 251, 217-229 (2000)
Agarwal, RP, O’Regan, D, Sahu, DR: Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 8(1), 61-79 (2007)
Abbas, M, Nazir, T: A new faster iteration process applied to constrained minimization and feasibility problems. Mat. Vesn. 66(2), 223-234 (2014)
Acknowledgements
The basic idea of this work has been given to the fourth author by Professor Mihai Postolache during his visit to University Politehnica of Bucharest in September 2014. The first and fourth authors was supported by Azarbaijan Shahid Madani University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to this work. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fathollahi, S., Ghiura, A., Postolache, M. et al. A comparative study on the convergence rate of some iteration methods involving contractive mappings. Fixed Point Theory Appl 2015, 234 (2015). https://doi.org/10.1186/s13663-015-0490-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-015-0490-3