New iteration scheme for numerical reckoning fixed points of nonexpansive mappings

Abstract

The purpose of this paper is to introduce a new three step iteration scheme for approximation of fixed points of the nonexpansive mappings. We show that our iteration process is faster than all of the Picard, the Mann, the Agarwal et al., and the Abbas et al. iteration processes. We support our analytic proof by a numerical example in which we approximate the fixed point by a computer using Matlab program. We also prove some weak convergence and strong convergence theorems for the nonexpansive mappings.

MSC:47H09, 47H10.

1 Introduction

Many nonlinear equations are naturally formulated as fixed point problems,

$$x=Tx,$$

(1.1)

where T, the fixed point mapping, may be nonlinear. A solution $x^{\ast }$ of the problem (1.1) is called a fixed point of the mapping T. Consider a fixed point iteration, which is given by

$$x_{n+1}=T{x}_n.$$

(1.2)

The iterative method (1.2) is also called a Richardson iteration, a Picard iteration, or the method of successive substitution. The standard result for a fixed point iteration is the contraction mapping theorem. Indeed, the contraction mapping theorem holds on an arbitrary complete metric space; that is, if E is a complete metric space with metric d and $T:E\to E$ such that $d(Tx,Ty)\le kd(x,y)$ for some $0\le k<1$ and all $x,y\in E$, then T has a unique fixed point $x^{\ast }$ and the iterates (1.2) converge to the fixed point $x^{\ast }$. The Picard iteration has been successfully employed in approximating the fixed point of contraction mappings and its variants. This success, however, has not extended to nonexpansive mappings T even when the existence of a fixed point of T is known. Consider the simple example of a self mapping in $[0,1]$ defined by $Tx=1-x$ for $0\le x\le 1$. Then T is a nonexpansive mapping with a unique fixed point at $x=\frac{1}{2}$. If one chooses as a starting value $x=a$, $a\ne \frac{1}{2}$, then the successive iterations of T yield the sequence $\{1-a,a,1-a,a,\dots \}$. Thus when a fixed point of nonexpansive mappings exists, other approximation techniques are needed to approximate it.

Consider an average mapping of the form $T_{\frac{1}{2}}=\frac{1}{2}I+\frac{1}{2}T$, where I is the identity operator. This average mapping is nonexpansive because T is nonexpansive, and both have the same fixed point set. Krasnosel’skii [1] was first to notice the regularization effect of this average mapping. Schaefer [2] proved a convergence result for a general $T_{\lambda }=\lambda I+(1-\lambda )T$ ($0<\lambda <1$). An approximation of fixed points of a nonexpansive mapping using Mann’s algorithm [3] has extensively been studied in the literature (see, e.g., [4, 5] and references therein). Mann’s algorithm generates, for an arbitrary $x_0\in C$, a sequence $\{x_n\}$ according to the following:

$$x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,n\ge 0,$$

(1.3)

where $\{{\alpha }_n\}$ is a real control sequence in the interval $(0,1)$.

In 1974, Ishikawa [6] introduced an iteration process where $\{x_n\}$ is defined iteratively for each positive integer $n\ge 0$ by

$$\begin{array}{l}{x}_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T{y}_n,\\ y_n=(1-{\beta }_n)x_n+{\beta }_{n}T{x}_n.\end{array}\}$$

(1.4)

In 2000, Noor [7] introduced the following iterative scheme: for any fixed $x_0\in C$, construct $\{x_n\}$ by

$$\begin{array}{l}{x}_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T{y}_n,\\ y_n=(1-{\beta }_n)x_n+{\beta }_{n}T{z}_n,\\ z_n=(1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n\end{array}\}$$

(1.5)

for all $n\ge 1$, where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are sequences in $(0,1)$.

In 2007, Agarwal et al. [8] introduced the following iteration process: for an arbitrary $x_0\in C$ construct a sequence $\{x_n\}$ by

$$\begin{array}{l}{x}_{n+1}=(1-{\alpha }_n)T{x}_n+{\alpha }_{n}T{y}_n,\\ y_n=(1-{\beta }_n)x_n+{\beta }_{n}T{x}_n,n\in \mathbb{N},\end{array}\}$$

(1.6)

where $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are in $(0,1)$. They showed that this process converges at a rate that is the same as that of the Picard iteration and faster than the Mann iteration for contractions.

Recently, Abbas and Nazir [9] introduced the following iteration: for an arbitrary $x_0\in C$ construct $\{x_n\}$ by

$$\begin{array}{l}{x}_{n+1}=(1-{\alpha }_n)T{y}_n+{\alpha }_{n}T{z}_n,\\ y_n=(1-{\beta }_n)T{x}_n+{\beta }_{n}T{z}_n,\\ z_n=(1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n,\end{array}\}$$

(1.7)

where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are in $(0,1)$. They showed that this process converges faster than the Agarwal et al. [8] iteration process.

Motivated and inspired by the above work, in this paper we introduce a new iterative scheme, where the sequence $\{x_n\}$ is generated from arbitrary $x_0\in C$ by

$$\begin{array}{l}{x}_{n+1}=(1-{\alpha }_n)T{x}_n+{\alpha }_{n}T{y}_n,\\ y_n=(1-{\beta }_n)z_n+{\beta }_{n}T{z}_n,\\ z_n=(1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n,\end{array}\}$$

(1.8)

where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are real sequences in $(0,1)$.

The purpose of this paper is to prove that our process (1.8) converges faster than all of the Picard, the Mann, the Ishikawa, the Noor, the Agarwal et al., and the Abbas et al. iteration processes for contractions in the sense of Berinde [10]. We also prove weak and strong convergence theorems for nonexpansive mapping using iteration (1.8). In the last section, using a numerical example, we compare the behavior of iteration (1.8) with respect to the above mentioned iteration processes.

2 Rate of convergence

Berinde [10] proposed a method to compare the fastness of two sequences.

Definition 2.1 Let $\{a_n\}$ and $\{b_n\}$ be two sequences of real numbers that converge to a and b, respectively, and assume that there exists

$$l=\underset{n\to \mathrm{\infty }}{lim}\frac{|a_n-a|}{|b_n-b|}.$$

(2.1)

• (i) If $l=0$, then it can be said that $\{a_n\}$ converges faster to a than $\{b_n\}$ to b.

• (ii) If $0<l<\mathrm{\infty }$, then it can be said that $\{a_n\}$ and $\{b_n\}$ have the same rate of convergence.

Suppose that, for two fixed point iteration procedures $\{u_n\}$ and $\{v_n\}$, both converging to the same fixed point p, the error estimates

$$\parallel u_n-p\parallel \le a_n,n=0,1,2,\dots ,$$

(2.2)

$$\parallel v_n-p\parallel \le b_n,n-=0,1,2,\dots ,$$

(2.3)

are available, where $\{a_n\}$ and $\{b_n\}$ are sequences of positive numbers (converging to zero).

Then, in view of Definition 2.1, Berinde [10] adopted the following concept.

Definition 2.2 Let $\{u_n\}$ and $\{v_n\}$ be two fixed point iteration procedures that converge to the same fixed point p and satisfy (2.2) and (2.3), respectively. If $\{a_n\}$ converges faster than $\{b_n\}$, then it can be said that $\{u_n\}$ converges faster than $\{v_n\}$ to p.

In recent years, Definition 2.2 has been used as a standard tool to compare the fastness of two fixed point iterations. Using this technique Sahu [11] established that the Agarwal et al. iteration (1.6) converges faster than the Mann (1.3) and the Picard (1.2) iterations and supported the claim by the following example.

Example 1 Let $X=\mathbb{R}$ and $K=[0,\mathrm{\infty })$. Let $T:K\to K$ be a mapping defined by $Tx={(3x+18)}^{\frac{1}{3}}$ for all $x\in K$. For $x_0=1,000$ and ${\alpha }_n={\beta }_n=\frac{1}{2}$, $n=0,1,2,\dots$ , Agarwal et al. iteration is faster than both the Mann and the Picard iteration.

Using a similar technique Abbas and Nazir [9] established that the Abbas et al. iteration (1.7) converges faster than the Agarwal et al. iteration (1.6) and hence it converges faster than the Mann (1.3) and the Picard (1.2) iterations also. An example is also given in support of the claim.

Example 2 Let $X=\mathbb{R}$ and $K=[1,50]$. Let $T:K\to K$ be a mapping defined by $Tx=\sqrt{x^2-8x+40}$ for all $x\in K$. For $x_0=30$ and ${\alpha }_n={\beta }_n={\gamma }_n=\frac{1}{2}$, $n=0,1,2,\dots$ , the Abass et al. iteration (1.7) is faster than the Agarwal et al. iteration (1.6). Since Sahu [11] already has shown that the iteration (1.6) is faster than the Mann iteration (1.3), the iteration (1.7) is faster than the iterations (1.2), (1.3), and (1.6).

We now show that our process (1.8) converges faster than (1.7) in the sense of Berinde [10].

Theorem 2.3 Let C be a nonempty closed convex subset of a norm space E. Let T be a contraction with a contraction factor $k\in (0,1)$ and fixed point p. Let $\{u_n\}$ be defined by the iteration process (1.7) and $\{x_n\}$ by (1.8), where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are in $[\epsilon ,1-\epsilon ]$ for all $n\in \mathbb{N}$ and for some ε in $(0,1)$. Then $\{x_n\}$ converges faster than $\{u_n\}$. That is, our process (1.8) converges faster than (1.7).

Proof As proved in Theorem 3 of Abbas and Nazir [9],

$$\parallel u_{n+1}-p\parallel \le k^n{[1-(1-k)\alpha \beta \gamma ]}^n\parallel u_1-p\parallel ,$$

for all $n\in \mathbb{N}$. Let

$$a_n=k^n{[1-(1-k)\alpha \beta \gamma ]}^n\parallel u_1-p\parallel .$$

Now

$$\begin{array}{rl}\parallel z_n-p\parallel & =\parallel (1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n-p\parallel \\ \le (1-{\gamma }_n)\parallel x_n-p\parallel +k{\gamma }_n\parallel x_n-p\parallel \\ =(1-(1-k){\gamma }_n)\parallel x_n-p\parallel ,\end{array}$$

so that

$$\begin{array}{rl}\parallel y_n-p\parallel & =\parallel (1-{\beta }_n)z_n+{\beta }_{n}T{z}_n-p\parallel \\ \le (1-{\beta }_n)\parallel z_n-p\parallel +k{\beta }_n\parallel z_n-p\parallel \\ \le (1-{\beta }_n)(1-(1-k){\gamma }_n)\parallel x_n-p\parallel +k{\beta }_n(1-(1-k){\gamma }_n)\parallel x_n-p\parallel \\ =(1-(1-k){\beta }_n)(1-(1-k){\gamma }_n)\parallel x_n-p\parallel .\end{array}$$

Thus

$$\begin{array}{rl}\parallel x_{n+1}-p\parallel & =\parallel (1-{\alpha }_n)T{x}_n+{\alpha }_{n}T{y}_n-p\parallel \\ \le (1-{\alpha }_n)k\parallel x_n-p\parallel +k{\alpha }_n\parallel y_n-p\parallel \\ \le (1-{\alpha }_n)k\parallel x_n-p\parallel +k{\alpha }_n(1-(1-k){\beta }_n)(1-(1-k){\gamma }_n)\parallel x_n-p\parallel \\ =k[1-{\alpha }_n+{\alpha }_n(1-(1-k){\beta }_n)(1-(1-k){\gamma }_n)]\parallel x_n-p\parallel \\ =k[1-{\alpha }_n+({\alpha }_n-(1-k){\alpha }_n{\beta }_n)(1-(1-k){\gamma }_n)]\parallel x_n-p\parallel \\ =k[1-{\alpha }_n+{\alpha }_n-(1-k){\alpha }_n{\gamma }_n-(1-k){\alpha }_n{\beta }_n+{(1-k)}^2{\alpha }_n{\beta }_n{\gamma }_n]\parallel x_n-p\parallel \\ \le k[1-(1-k){\alpha }_n{\beta }_n{\gamma }_n-(1-k){\alpha }_n{\beta }_n{\gamma }_n+{(1-k)}^2{\alpha }_n{\beta }_n{\gamma }_n]\parallel x_n-p\parallel \\ =k(1-(1-k)(1+k){\alpha }_n{\beta }_n{\gamma }_n)\parallel x_n-p\parallel \\ =k(1-(1-k^2){\alpha }_n{\beta }_n{\gamma }_n)\parallel x_n-p\parallel .\end{array}$$

Let

$$b_n=k^n{(1-(1-k^2)\alpha \beta \gamma )}^n\parallel x_1-p\parallel .$$

Then

$$\begin{array}{rl}\frac{b_n}{a_n}& =\frac{k^n{(1-(1-k^2)\alpha \beta \gamma )}^n\parallel x_1-p\parallel }{k^n{[1-(1-k)\alpha \beta \gamma ]}^n\parallel u_1-p\parallel }\\ =\frac{{(1-(1-k^2)\alpha \beta \gamma )}^n}{{(1-(1-k)\alpha \beta \gamma )}^n}\frac{\parallel x_1-p\parallel }{\parallel u_1-p\parallel }\\ \to 0\text{as }n\to \mathrm{\infty }.\end{array}$$

Consequently $\{x_n\}$ converges faster than $\{u_n\}$. □

Now, we present an example which shows that the new iteration process (1.8) converges at a rate faster than the existing iteration schemes mentioned above.

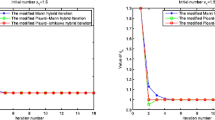
Example 3 Let $E=\mathbb{R}$ and $C=[1,50]$. Let $T:C\to C$ be a mapping defined by $T(x)=\sqrt{x^2-8x+40}$ for all $x\in C$. Choose ${\alpha }_n=0.85$, ${\beta }_n=0.65$, ${\gamma }_n=0.45$, with the initial value $x_1=40$. Our corresponding iteration process, the Abbas and Nazir iteration process (1.7), the Agarwal et al. iteration process (1.6), the Noor iteration process (1.7), the Ishikawa iteration process (1.4), the Mann iteration process (1.3), and the Picard iteration processes (1.2) are, respectively, given in Table 1.

Table 1 Comparative results

All sequences converge to $x^{\ast }=5$. Comparison shows that our iteration process (1.8) converges fastest among all the iterations considered in the example.

3 Convergence theorems

In this section, we give some convergence theorems using our iteration process (1.8); please, see Table 1 and Figure 1.

Figure 1

Convergence behavior of the Picard, the Mann, the Ishikawa, the Noor, the Agarwal et al. , the Abbas et al. iterations, and new iteration for the function given in Example 3 .

Lemma 3.1 Let C be a nonempty closed convex subset of a norm space E. Let T be a nonexpansive self mapping on C, $\{x_n\}$ defined by (1.8) and $F(T)\ne \mathrm{\varnothing }$. Then ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F$.

Proof Let $p\in F(T)$ for all $n\in \mathbb{N}$. From (1.8), we have

$$\begin{array}{rl}\parallel z_n-p\parallel & =\parallel (1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n-p\parallel \\ \le (1-{\gamma }_n)\parallel x_n-p\parallel +{\gamma }_n\parallel T{x}_n-p\parallel \\ \le (1-{\gamma }_n)\parallel x_n-p\parallel +{\gamma }_n\parallel x_n-p\parallel \\ =\parallel x_n-p\parallel \end{array}$$

(3.1)

and

$$\begin{array}{rl}\parallel y_n-p\parallel & =\parallel (1-{\beta }_n)z_n+{\beta }_{n}T{z}_n-p\parallel \\ \le (1-{\beta }_n)\parallel z_n-p\parallel +{\beta }_n\parallel T{z}_n-p\parallel \\ \le (1-{\beta }_n)\parallel x_n-p\parallel +{\beta }_n\parallel x_n-p\parallel \\ =\parallel x_n-p\parallel ,\end{array}$$

(3.2)

thus from (3.1) and (3.2)

$$\begin{array}{rl}\parallel x_{n+1}-p\parallel & =\parallel (1-{\alpha }_n)T{x}_n+{\alpha }_{n}T{y}_n-p\parallel \\ \le (1-{\alpha }_n)\parallel T{x}_n-p\parallel +{\alpha }_n\parallel T{y}_n-p\parallel \\ \le (1-{\alpha }_n)\parallel x_n-p\parallel +{\alpha }_n\parallel x_n-p\parallel \\ =\parallel x_n-p\parallel .\end{array}$$

Thus ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F(T)$. □

We need following lemma to establish our next result.

Lemma 3.2 [12]Suppose that E is a uniformly convex Banach space and $0<p\le t_n\le q<1$ for all $n\in \mathbb{N}$. Let $\{x_n\}$ and $\{y_n\}$ be two sequences of E such that ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}\parallel x_n\parallel \le r$, ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}\parallel y_n\parallel \le r$ and ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}\parallel t_n{x}_n+(1-t_n)y_n\parallel =r$ hold for some $r\ge 0$. Then ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel =0$.

We now establish a result which will be of key importance for the main result.

Lemma 3.3 Let C be a nonempty closed convex subset of a uniformly convex Banach space E. Let T be a nonexpansive self mapping on C, $\{x_n\}$ defined by (1.8), where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are in $[\epsilon ,1-\epsilon ]$ for all $n\in \mathbb{N}$ and for some ε in $(0,1)$ and $F(T)\ne \mathrm{\varnothing }$. Then ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$.

Proof By Lemma 3.1, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists. Assume that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel =c$.

From (3.1) and (3.2) we have

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel y_n-p\parallel \le c$$

(3.3)

and

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel z_n-p\parallel \le c.$$

(3.4)

Since T is a nonexpansive mapping, it follows that

$$\parallel T{x}_n-p\parallel \le \parallel x_n-p\parallel$$

and

$$\parallel T{y}_n-p\parallel \le \parallel y_n-p\parallel .$$

Taking lim sup on both sides, we obtain

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel T{x}_n-p\parallel \le c$$

(3.5)

and

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel T{y}_n-p\parallel \le c.$$

(3.6)

Since

$$c=\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-p\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel (1-{\alpha }_n)(T{x}_n-p)+{\alpha }_n(T{y}_n-p)\parallel ,$$

by using Lemma 3.2, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel T{x}_n-T{y}_n\parallel =0.$$

(3.7)

Now

$$\parallel x_{n+1}-p\parallel =\parallel (1-{\alpha }_n)T{x}_n+{\alpha }_{n}T{y}_n-p\parallel \le \parallel T{x}_n-p\parallel +{\alpha }_n\parallel T{x}_n-T{y}_n\parallel$$

yields

$$c\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel T{x}_n-p\parallel ,$$

(3.8)

so that (3.5) and (3.8) give

$$\underset{n\to \mathrm{\infty }}{lim}\parallel T{x}_n-p\parallel =c.$$

(3.9)

On the other hand, we have

$$\parallel T{x}_n-p\parallel \le \parallel T{x}_n-T{y}_n\parallel +\parallel T{y}_n-p\parallel \le \parallel T{x}_n-T{y}_n\parallel +\parallel y_n-p\parallel ,$$

which yields

$$c\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel y_n-p\parallel .$$

(3.10)

From (3.3) and (3.10) we get

$$\underset{n\to \mathrm{\infty }}{lim}\parallel y_n-p\parallel =c.$$

Since T is a nonexpansive mapping, we have from (3.1)

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel T{z}_n-p\parallel \le c.$$

(3.11)

From (3.4) and (3.11), by using Lemma 3.2 we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-T{z}_n\parallel =0.$$

(3.12)

Since

$$\parallel y_n-p\parallel \le \parallel z_n-p\parallel +{\beta }_n\parallel T{z}_n-z_n\parallel ,$$

we write

$$c\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel z_n-p\parallel ,$$

(3.13)

then

$$\parallel z_n-p\parallel =c,$$

(3.14)

so

$$\begin{array}{rl}c& =\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-p\parallel \\ =\underset{n\to \mathrm{\infty }}{lim}\parallel (1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n-p\parallel \\ =\underset{n\to \mathrm{\infty }}{lim}\parallel (1-{\alpha }_n)(x_n-p)+{\alpha }_n(T{x}_n-p)\parallel ,\end{array}$$

and by Lemma 3.2, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T{x}_n\parallel =0.$$

This completes the proof. □

Lemma 3.4 [13]

Let C be a nonempty bounded closed convex subset of a uniformly convex Banach space and $T:C\to E$ be a nonexpansive mapping. Then there is a strictly increasing and continuous convex function $g:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $g(0)=0$ such that

$$g\left(\parallel T(tx+(1-t)y)-(tTx+(1-t)Ty)\parallel \right)\le \parallel x-y\parallel -\parallel Tx-Ty\parallel$$

for all $x,y\in C$ and $t\in [0,1]$.

Lemma 3.5 For any $p_1,p_2\in F(T)$, ${lim}_{n\to \mathrm{\infty }}\parallel t{x}_n+(1-t)p_1-p_2\parallel$ exists, for all $t\in [0,1]$ under the conditions of Lemma  3.3.

Proof By Lemma 3.1, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F(T)$ and hence $\{x_n\}$ is bounded. Thus there exists a real number $r>0$ such that $\{x_n\}\subseteq D\equiv \overline{B_r(0)}\cap C$, so that D is a closed convex nonempty subset of C. Set

$$a_n(t):=\parallel t{x}_n+(1-t)p_1-p_2\parallel$$

for all $t\in [0,1]$. Then ${lim}_{n\to \mathrm{\infty }}{a}_n(0)=\parallel p_1-p_2\parallel$ and, from Lemma 3.1, ${lim}_{n\to \mathrm{\infty }}{a}_n(1)=\parallel x_n-p_2\parallel$ exist.

Now it remains to show that ${lim}_{n\to \mathrm{\infty }}{a}_n(t)$ exists for $t\in (0,1)$.

For each $n\in N$, define $W_n:D\to D$ by

$$\{\begin{array}{l}{W}_{n}x=(1-{\alpha }_n)Tx+{\alpha }_{n}T{V}_{n}x,\\ V_{n}x=(1-{\beta }_n)U_{n}x+{\beta }_{n}T{U}_{n}x,\\ U_{n}x=(1-{\gamma }_n)x+{\gamma }_{n}Tx\end{array}$$

for all $x\in D$.

We see that

$$\parallel U_{n}x-U_{n}y\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in D,$$

and

$$\parallel V_{n}x-V_{n}y\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in D,$$

hence,

$$\parallel W_{n}x-W_{n}y\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in D.$$

Set

$$R_{n,m}=W_{n+m-1}{W}_{n+m-2}\cdots W_n$$

and

$$b_{n.m}=\parallel R_{n,m}(t{x}_n+(1-t)p_1)-(t{R}_{n,m}{x}_n+(1-t)p_1)\parallel ,$$

for all $n,m\in N$. Then $R_{n,m}{x}_n=x_{n+m}$ and $R_{n,m}p=p$ $\mathrm{\forall }p\in F(T)$. Also,

$$\parallel R_{n,m}x-R_{n.m}y\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in D.$$

By Lemma 3.4, there exists a strictly increasing continuous function $g:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $g(0)=0$ such that

$$\begin{array}{rl}g(b_{n,m})& \le \parallel x_n-p_1\parallel -\parallel R_{n,m}{x}_n-R_{n,m}{p}_1\parallel \\ =\parallel x_n-p_1\parallel -\parallel x_{n+m}-p_1\parallel .\end{array}$$

Since ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F(T)$, we get ${lim}_{n,m\to \mathrm{\infty }}g(b_{n,m})=0$ and by the property of g, we get ${lim}_{n,m\to \mathrm{\infty }}{b}_{n,m}=0$.

Now,

$$\begin{array}{rl}{a}_{n+m}(t)& =\parallel t{x}_{n+m}+(1-t)p_1-p_2\parallel \\ =\parallel t{R}_{n,m}{x}_n+(1-t)p_1-p_2\parallel \\ \le b_{n,m}+\parallel R_{n,m}(t{x}_n+(1-t)p_1)-p_2\parallel \\ =b_{n,m}+\parallel R_{n,m}(t{x}_n+(1-t)p_1)-R_{n,m}{p}_2\parallel \\ \le b_{n,m}+\parallel (t{x}_n+(1-t)p_1)-p_2\parallel \\ =b_{n,m}+a_n(t).\end{array}$$

Consequently

$$\begin{array}{rl}\underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{a}_m(t)& =\underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{a}_{n+m}(t)\\ \le \underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}sup}(b_{n,m})+a_n(t).\end{array}$$

Since ${lim}_{n,m\to \mathrm{\infty }}{b}_{n,m}=0$, we get

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{a}_n(t)\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{a}_n(t).$$

This implies that ${lim}_{n\to \mathrm{\infty }}{a}_n(t)$ exists for all $t\in (0,1)$, i.e., ${lim}_{n\to \mathrm{\infty }}\parallel t{x}_n+(1-t)p_1-p_2\parallel$ exists for all $t\in [0,1]$. □

Let E be a Banach space and $S_E=\{x\in E:\parallel x\parallel =1\}$ unit sphere on E. The Banach space E is said to be smooth if

$$\underset{t\to 0}{lim}\frac{\parallel x+ty\parallel -\parallel x\parallel }{t}$$

(3.15)

exists for each x and y in $S_E$. In this case, the norm of E is called Gâteaux differentiable.

The space E is called Fréchet differentiable normed (see, e.g., [14]); for each x in E, the above limit exists and is attained uniformly for y in E, and in this case it is also well known that

$$〈h,J(x)〉+\frac{1}{2}{\parallel x\parallel }^2\le \frac{1}{2}{\parallel x+h\parallel }^2\le 〈h,J(x)〉+\frac{1}{2}{\parallel x\parallel }^2+b(\parallel h\parallel )$$

(3.16)

for all $x,h\in E$, where J is the Fréchet derivative of the function $\frac{1}{2}{\parallel \cdot \parallel }^2$ at $x\in E$, $〈\cdot ,\cdot 〉$ is the dual pairing between E and $E^{\ast }$, and b is an increasing function defined on $[0,\mathrm{\infty })$ such that ${lim}_{t\to 0}\frac{b(t)}{t}=0$.

Lemma 3.6 Assume that the conditions of Lemma  3.3 are satisfied. Then, for any $p_1,p_2\in F(T)$, ${lim}_{n\to \mathrm{\infty }}〈x_n,J(p_1-p_2)〉$ exists; in particular, $〈p-q,J(p_1-p_2)〉=0$ for all $p,q\in {\omega }_w(x_n)$, the set of all weak limits of $\{x_n\}$.

The proof of Lemma 3.6 is similar to the proof of Lemma 2.3 of Khan and Kim [15].

A Banach space E is said to satisfy the Opial condition [16] if for each sequence $\{x_n\}$ in E, $x_n\rightharpoonup x$ implies that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel x_n-x\parallel <\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel x_n-y\parallel$$

for all $y\in E$ with $y\ne x$.

A Banach space E is said to have the Kadec-Klee property if for every sequence $\{x_n\}$ in E, $x_n\rightharpoonup x$ and $\parallel x_n\parallel \to \parallel x\parallel$ together imply $x_n\to x$ as $n\to \mathrm{\infty }$.

We need the following to prove our next result.

Definition 3.7 A mapping $T:C\to E$ is demiclosed at $y\in E$ if for each sequence $\{x_n\}$ in C and each $x\in E$, $x_n\rightharpoonup x$, and $T{x}_n\to y$ imply that $x\in C$ and $Tx=y$.

Lemma 3.8 [17]

Let C be a nonempty closed convex subset of a uniformly convex Banach space E, and T a nonexpansive mapping on C. Then $I-T$ is demiclosed at zero.

Lemma 3.9 [8]

Let E be a reflexive Banach space satisfying the Opial condition, C a nonempty convex subset of E, and $T:C\to E$ an operator such that $I-T$ demiclosed at zero and $F(T)\ne \mathrm{\varnothing }$. Let $\{x_n\}$ be a sequence in C such that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$ and ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F(T)$. Then $\{x_n\}$ converges weakly to a fixed point of T.

Lemma 3.10 [18]

Let E be a real reflexive Banach space such that its dual $E^{\ast }$ has the Kadec-Klee property. Let $\{x_n\}$ be a bounded sequence in E and $x^{\ast },y^{\ast }\in {\omega }_w(x_n)$, here ${\omega }_w(x_n)$ denotes the w-limit set of $\{x_n\}$. Suppose ${lim}_{n\to \mathrm{\infty }}\parallel t{x}_n+(1-t)x^{\ast }-y^{\ast }\parallel$ exists for all $t\in [0,1]$. Then $x^{\ast }=y^{\ast }$.

We now establish a weak convergence result.

Theorem 3.11 Let E be a uniformly convex Banach space and let C, T, and $\{x_n\}$ be as in Lemma  3.3 and $F(T)\ne \mathrm{\varnothing }$. Assume that any of the following conditions hold:

• (a) E satisfies the Opial condition,

• (b) E has a Fréchet differentiable norm,

• (c) the dual $E^{\ast }$ of E satisfies the Kadec-Klee property.

Then $\{x_n\}$ converges weakly to a point of $F(T)$.

Proof Let $p\in F(T)$, by Lemma 3.1, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists.

We prove that $\{x_n\}$ has a unique weak subsequential limit in $F(T)$.

Let u and v be weak limits of the subsequences $\{x_{n_i}\}$ and $\{x_{n_j}\}$ of $\{x_n\}$, respectively. By Lemma 3.3, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$, and also $I-T$ is demiclosed with respect to zero, hence by Lemma 3.8, we obtain $Tu=u$. In a similar manner, we have $v\in F(T)$.

Next, we prove the uniqueness.

First assume that (a) holds. If $u\ne v$, then, by the Opial condition,

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-u\parallel & =\underset{i\to \mathrm{\infty }}{lim}\parallel x_{n_i}-u\parallel <\underset{i\to \mathrm{\infty }}{lim}\parallel x_{n_i}-v\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-v\parallel \\ =\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-v\parallel <\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-u\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-u\parallel .\end{array}$$

This is a contradiction, so $u=v$.

Next, assume (b) holds.

By Lemma 3.6, $〈p-q,J(p_1-p_2)〉=0$, for all $p,q\in {\omega }_w(x_n)$. Therefore, ${\parallel u-v\parallel }^2=〈u-v,J(u-v)〉=0$ implies $u=v$.

Finally, assume that (c) is true.

Since ${lim}_{n\to \mathrm{\infty }}\parallel t{x}_n+(1-t)u-v\parallel$ exists for all $t\in [0,1]$ by Lemma 3.5, $u=v$ by Lemma 3.10, and $\{x_n\}$ converges weakly to a fixed point of $F(T)$ and this completes the proof. □

A mapping $T:C\to C$ is said to be semicompact if any sequence $\{x_n\}$ in C, such that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$, has a subsequence converging strongly to some $p\in C$.

Next we establish the following strong convergence results.

Theorem 3.12 Let E be a uniformly convex Banach space and let C, T, and $\{x_n\}$ be as in Lemma  3.3. If T is semicompact and $F(T)\ne \mathrm{\varnothing }$, then $\{x_n\}$ converges strongly to a fixed point of T.

Proof By Lemma 3.3, we have ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$; since T is semicompact, $\{x_n\}$ has a subsequence converging to some $p\in C$ as C is closed. Continuity of T gives ${lim}_{j\to \mathrm{\infty }}\parallel T{x}_{n_j}-Tp\parallel \to 0$. Then by Lemma 3.3,

$$\parallel Tp-p\parallel =0.$$

This yields $p\in F(T)$. By Lemma 3.1, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in F(T)$, and therefore $\{x_n\}$ must itself converge to $p\in F(T)$ and this completes the proof. □

Theorem 3.13 Let E be a uniformly convex Banach space and let C, T, $F(T)$, and $\{x_n\}$ be as in Lemma  3.3. Then $\{x_n\}$ converges to a point of $F(T)$ if and only if ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$, where $d(x,F(T))=inf\{\parallel x-p\parallel :p\in F(T)\}$.

Proof Necessity is obvious. Suppose that ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$. As proved in Lemma 3.3, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-w\parallel$ exists for all $w\in F(T)$, therefore ${lim}_{n\to \mathrm{\infty }}d(x_n,F(T))$ exists. But by hypothesis, ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$, therefore ${lim}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$.

We will show that $\{x_n\}$ is a Cauchy sequence in C. Since ${lim}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$, for given $\epsilon >0$, there exists $n_0$ in ℕ such that, for all $n\ge n_0$,

$$d(x_n,F(T))<\frac{\epsilon }{2}.$$

Particularly, $inf\{\parallel x_{n_0}-p\parallel :p\in F(T)\}<\frac{\epsilon }{2}$. Hence, there exists $p^{\ast }\in F(T)$ such that $\parallel x_{n_0}-p^{\ast }\parallel <\frac{\epsilon }{2}$. Now, for $m,n\ge n_0$,

$$\parallel x_{n+m}-x_n\parallel \le \parallel x_{n+m}-p^{\ast }\parallel +\parallel x_n-p^{\ast }\parallel \le 2\parallel x_{n_0}-p^{\ast }\parallel <\epsilon .$$

Hence $\{x_n\}$ is a Cauchy sequence in C. Since C is a closed subset of a complete space, ${lim}_{n\to \mathrm{\infty }}{x}_n=p\in C$. Since $F(T)$ is closed, ${lim}_{n\to \mathrm{\infty }}d(x_n,F(T))=0$ gives $d(p,F(T))=0$, i.e., $p\in F(T)$. □

Definition 3.14 A mapping $T:C\to C$, where C is a subset of a normed space E, is said to satisfy Condition (I) [19] if there exists a nondecreasing function $f:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $f(0)=0$, $f(r)>0$ for all $r\in (0,1)$ such that $\parallel x-Tx\parallel \ge f(d(x,F(T)))$ for all $x\in C$ where $d(x,F(T))=inf\{\parallel x-p\parallel :p\in F(T)\}$.

Applying Theorem 3.13, we obtain strong convergence of the process (1.8) under Condition (I) as follows.

Theorem 3.15 Let e be a uniformly convex Banach space and let C, T, and $\{x_n\}$ be as in Lemma  3.3. Let T satisfy Condition (I), then $\{x_n\}$ converges strongly to a fixed point of T.

Proof We proved in Lemma 3.3 that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T{x}_n\parallel =0.$$

(3.17)

From Condition (I) and (3.17), we get

$$\underset{n\to \mathrm{\infty }}{lim}f\left(d(x_n,F(T))\right)\le \underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T{x}_n\parallel =0,$$

i.e., ${lim}_{n\to \mathrm{\infty }}f(d(x_n,F(T)))=0$. Since $f:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is a nondecreasing function satisfying $f(0)=0$, $f(r)>0$ for all $r\in (0,\mathrm{\infty })$, we have

$$\underset{n\to \mathrm{\infty }}{lim}d(x_n,F(T))=0.$$

Now all the conditions of Theorem 3.13 are satisfied, therefore, by its conclusion, $\{x_n\}$ converges strongly to a point of $F(T)$. □