Mathematical analysis and optimal control of Dengue fever epidemic model

Abstract

In this article, we are working on an SEIR-SI type model for dengue disease in order to better observe the dynamics of infection in human beings. We calculate the basic reproduction number $\mathcal{R}_{0}$ and determine the equilibrium points. We then show the existence of global stability in each of the different states depending on the value of $\mathcal{R}_{0}$. Moreover, to support the theoretical work, we present numerical simulations obtained using Python. We also study the sensitivity of the parameters included in the expression of $\mathcal{R}_{0}$ with the aim of identifying the most influential parameters in the dynamics of dengue disease spread. Finally, we introduce two functions u and v, respectively indicating the treatment of the infected people and any prevention system minimizing contact between humans and the disease causing vectors. We present the curves of the controlled system after calculating the optimal pair of controls capable of reducing the dynamics of the disease spread, still using Python.

1 Introduction

Dengue is a viral and vector-borne disease. It is transmitted to humans by the bite of infected mosquitoes. Dengue is a fairly regular disease in tropical and subtropical regions, especially in urban and semi-urban areas. The vector causing the dengue disease are mosquitoes mainly of Aedes aegypti species. These mosquitoes are also vectors of chikungunya.

According to the World Health Organization, dengue fever is manifested by a wide range of symptoms that vary from basic to severe flu-like symptoms. Although rare, some people develop a severe form of dengue fever disease, which is characterized by various complications such as severe nose bleeding. The severe form of dengue, associated with high risk of death, was first discovered in 1950 during epidemics in the Philippines and Thailand. Nowadays, the severe form of dengue affects most countries in Africa, Asia, and Latin America, where it has become a major cause of hospitalization and death. There are four distinct but closely related stereotypes that cause dengue fever: DENV-1, DENV-2, DENV-3, and DENV-4. After recovery, lifelong immunity is obtained against the type of virus that caused the infection. A dengue patient who subsequently developed the disease is at high risk of developing a severe form of dengue. Dengue fever has existed in Burkina Faso since 1925. At the time of the last epidemic in 2016, the frequency of severe forms was 33% [20] in the city of Ouagadougou, the capital of Burkina Faso.

The mathematical modeling of phenomena is essential in the field of applied sciences. In physics, chemistry, biology, and many other fields, mathematical models are the pillars of a rigorous scientific study in order to make predictions about observed phenomena. Infectious diseases are increasingly becoming a major focus of mathematical modeling. malaria, dengue, Ebola virus disease, schistosomiasis, COVID-19 [6, 26] are among many other infectious diseases that are regularly the subject of mathematical studies [7, 8, 17]. Guiro et al. [16] analyzed a model of dengue transmission with general incidence. Ivorra et al. [18] worked on an optimal control model to reduce the spread of Ebola virus disease. In the modeling of schistosomiasis, Traore et al. [5] presented a study of a discrete class of schistosomiasis models with general delay and incidence.

There are numerous mathematical models of dengue fever [2, 3, 14–16, 21], most consider the group of infected people as one simple homogeneous group. However, the infected group is almost always made up of people with simple dengue disease and some people with a more severe case of the disease. Also, several optimal control studies on epidemiological models exist [1, 7, 8, 17]. Guiro et al. [1] developed a problem of optimal control of an SIR epidemic model with a general incidence function and time delays, while Kumar et al. proposed an optimal control problem of age-structured SEIRV model with imperfect vaccination [8].

As a contribution, we work on an SEIR-SI dengue model with an infected population made up of two groups: one group with simple infected cases and another one with hemorrhagic cases. The split of the infected people into two groups is necessary to better observe the dynamics of different types of dengue patients in the population. In addition to the stability study, we perform an optimal control study on an SEIR-SI dengue model.

In this work, we subdivide the human population into five compartments: susceptible people ($S_{H}$), exposed people ($E_{H}$), people infected with simple cases ($I_{R_{H}}$), people infected with severe cases ($I_{D_{H}}$), cured people ($R_{H}$), and deceased people (D). We present the dengue vectors in two classes, one of which designates the susceptible ($S_{v}$) and the other the infected ($I_{v}$) mosquitoes.

Our paper is organized as follows. In Sect. 2, we present the system of ordinary differential equations after presenting the transfer diagram. In Sect. 3, we make sure that our mathematical model is well defined. Indeed, we exhibit the mathematical properties of the model, calculate the equilibrium points and the basic reproduction number. We then study the stability of the equilibrium points in Sect. 4. We numerically simulate the model with some real data and some estimated data using Python 3.7 in Sect. 5. We also study the sensitivity of the parameters that appear in the expression of the basic reproduction number $\mathcal{R}_{0}$ in Sect. 6. An optimal control work is done in Sect. 7, and we conclude in Sect. 8.

2 Mathematical model

At a time t in each compartment $\Delta _{i}$ ($i \in \mathbb{N}$), there are input movements $E_{i}$ and output movements $S_{i}$ of individuals.

The input movements are counted positively and the outputs negatively. The dynamics in the compartment $\Delta _{i}$ at time t denoted by $\dot{\Delta}_{i}$ is mathematically translated by the equation:

$$ \dot{\Delta}_{i}(t)= \sum_{j\geqslant 0} E_{i}^{j}(t)- \sum_{k\geqslant 0} S_{i}^{k}(t). $$

(1)

With the aim to well observe the dynamics of humans infectious classes, we propose the following diagram.

In the compartment $S_{H}$, for example, we have $\dot{S}_{H}(t)=\Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}I_{V}-\mu _{H}S_{H}$. Then, according to Fig. 1, we obtain the following system of eight differential equations:

$$\begin{aligned} \textstyle\begin{cases} \dot{S}_{H}(t) = \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}I_{V}- \mu _{H}S_{H}, \\ \dot{E}_{H}(t) = \beta _{H}\frac {S_{H}}{N_{H}}I_{V} -(\mu _{H}+ \eta _{H})E_{H}, \\ \dot{I}_{R_{H}}(t) = \eta _{H}E_{H}-(\mu _{H}+\gamma _{H_{1}})I_{R_{H}}, \\ \dot{I}_{D_{H}}(t) = (1-\theta )\gamma _{H_{1}}I_{R_{H}}-(\mu _{H}+ \gamma _{H_{2}})I_{D_{H}}, \\ \dot{R}_{H}(t) = \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}- \mu _{H}R_{H}, \\ \dot{D}_{H}(t) = (1-\rho )\gamma _{H_{2}}I_{D_{H}}, \\ \dot{S}_{V}(t) = \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}S_{V}, \\ \dot{I}_{V}(t) = \beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}I_{V}, \end{cases}\displaystyle \end{aligned}$$

(2)

with the initial conditions:

$$\begin{aligned}& S_{H}(t_{0})=S_{H_{0}}>0, \qquad E_{H}(t_{0})=E_{{H}_{0}}>0, \qquad I_{R_{H}}(t_{0})=I_{{R_{H}}_{0}}>0, \\& I_{D_{H}}(t_{0})=I_{{D_{H}}_{0}}>0,\qquad D_{H}(t_{0})=D_{{H}_{0}}>0, \qquad R_{H}(t_{0})=R_{{H}_{0}}>0, \\& S_{V}(t_{0})=S_{{V}_{0}}>0, \qquad I_{V}(t_{0})=I_{{V}_{0}}>0, \end{aligned}$$

where

Figure 1

Transfer diagram

• $S_{H}$, $E_{H}$, $I_{R_{H}}$, $I_{D_{H}}$, $I_{D_{H}}$, and $R_{H}$ denote the number of susceptible ($S_{H}$), latent ($E_{H}$), infectious ($I_{R_{H}}$, $I_{D_{H}}$), and recovered ($R_{H}$) persons at time t. $I_{R_{H}}$ and $I_{D_{H}}$ designate respectively people with classical dengue fever and those with dengue hemorrhagic fever;

• $S_{V}$ and $I_{V}$ denote the number of vectors (mosquitoes) in susceptible and infectious states at time t, respectively;

• $N_{H}=S_{H}+E_{H}+I_{R_{H}} +I_{D_{H}}+R_{H}$ and $N_{V}=S_{V}+I_{V}$ are the human and vector population size at time t, respectively;

• $\Lambda _{H}$ is the recruitment of humans, which is assumed to be constant;

• $\Lambda _{V}$ is the recruitment of mosquito population, which is assumed to be constant;

• $\beta _{H}$ is the average number of humans infected by the bites of infected mosquitoes per day and per Aedes mosquito (human.day⁻¹.vector⁻¹). The flow of people from the class of susceptible humans to the exposed humans class is therefore $\beta _{H}\frac {S_{H}}{N_{H}}I_{V}$;

• $\beta _{V}$ is the average number of Aedes mosquitoes infected by biting infected humans per day and per humans (vector.day⁻¹.human⁻¹). The flow of mosquitoes from the class of susceptible mosquitoes to the infected mosquitoes class is therefore $\beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})$;

• $\mu _{H}$ is the natural mortality rate of humans (persons.day⁻¹). This means that mortality is not due to the disease. Thus a number $\mu _{H}N_{H}$ of people leaves the dynamics of disease propagation at each time t;

• $\mu _{V}$ is the mortality rate of vectors (mosquitoes.day⁻¹). Thus a number $\mu _{V}N_{V}$ of mosquitoes leaves the dynamics of disease propagation at each time t. The infectious period of mosquito individual ends with their death;

• $\eta _{H}$ denotes the transition rate (day⁻¹) from state $E_{H}$ to $I_{R_{H}}$. We therefore consider a transfer $\eta _{H}E_{H}$ from $E_{H}$ to $I_{R_{H}}$;

• θ is simple cases infected individuals proportion (day⁻¹) who will be recovered ($R_{H}$);

• $1-\theta$ is simple cases infected individuals proportion (day⁻¹) who will be in severe cases ($I_{D_{H}}$);

• ρ is the proportion of severe cases infected individuals who will be recovered ($R_{H}$);

• $1-\rho$ is the proportion of severe cases individuals who will die ($D_{H}$);

• $\gamma _{H_{1}}$ is the transition rate (day⁻¹) from state $I_{R_{H}}$ to $R_{H}$ with proportion θ and to $I_{D_{H}}$ with proportion $1-\theta$. So $\theta \gamma _{H_{1}}I_{R_{H}}$ leaves $I_{R_{H}}$ for $R_{H}$ and $(1-\theta )\gamma _{H_{1}}I_{R_{H}}$ leaves $I_{R_{H}}$ for $I_{D_{H}}$;

• $\gamma _{H_{2}}$ is the transition rate (day⁻¹) from state $I_{D_{H}}$ to $R_{H}$ with proportion ρ and to $D_{H}$ with proportion $1-\rho$. So $\rho \gamma _{H_{2}}I_{D_{H}}$ leaves $I_{D_{H}}$ for $R_{H}$ and $(1-\rho )\gamma _{H_{2}}I_{D_{H}}$ leaves $I_{D_{H}}$ for $D_{H}$.

Remark 2.1

In model (2) we see that the state $D_{H}$ does not appear in the derivative expression of any other state. The dynamics of $D_{H}$ does not affect the dynamics of other states. We can therefore reduce the mathematical study of model (2) to that of the following one:

$$\begin{aligned} \textstyle\begin{cases} \dot{S}_{H}(t) = \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}I_{V}- \mu _{H}S_{H} \\ \dot{E}_{H}(t) = \beta _{H}\frac {S_{H}}{N_{H}}I_{V} -(\mu _{H}+ \eta _{H})E_{H}, \\ \dot{I}_{R_{H}}(t) = \eta _{H}E_{H}-(\mu _{H}+\gamma _{H_{1}})I_{R_{H}}, \\ \dot{I}_{D_{H}}(t) = (1-\theta )\gamma _{H_{1}}I_{R_{H}}-(\mu _{H}+ \gamma _{H_{2}})I_{D_{H}}, \\ \dot{R}_{H}(t) = \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}- \mu _{H}R_{H}, \\ \dot{S}_{V}(t) = \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}S_{V}, \\ \dot{I}_{V}(t) = \beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}I_{V}. \end{cases}\displaystyle \end{aligned}$$

(3)

3 Properties of the mathematical model

3.1 Positivity and boundedness of the solutions

For showing the positivity of solutions, we state the following lemma.

Lemma 3.1

[25] Suppose that $\Omega \subset \mathbb{R}\times \mathbb{C}^{n}$ is open, $f_{i} \in \mathit{C}(\Omega, \mathbb{R})$.

If $f_{i}|_{x_{i}(t)=0,X_{t}\in C^{n}_{+0}}\geqslant 0$, $X_{t}=(x_{1t},x_{2t},x_{3t},\ldots,x_{nt})^{T}$, $i=1,2,3,\ldots,n$, then $C^{n}_{+0}= \lbrace \phi =(\phi _{1},\ldots, \phi _{n}): \phi \in C( [-\tau,0 ], \mathbb{R}^{n}_{+0})\rbrace$ is the invariant domain of the following equations:

$$ \frac {dx_{i}(t)}{dt}=f_{i}(t,X_{t}), \quad t\geqslant \sigma , i=1,2,3,\ldots,n, $$

where $\mathbb{R}^{n}_{+0}=\lbrace (x_{1},\ldots,x_{n}),x_{i} \geqslant 0, i=1,2,3,\ldots,n \rbrace$.

Proposition 3.1

System (3) is invariant in $\mathbb{R}^{7}_{+}$.

Proof

By rewriting system (3), we get

$$ \textstyle\begin{cases} \frac {dX}{dt}=B(X(t)) \\ X_{0}=(S_{H_{0}},E_{{H}_{0}},I_{{R_{H}}_{0}},I_{{D_{H}}_{0}}, R_{H_{0}},S_{{V}_{0}},I_{{V}_{0}})^{T} \geqslant 0, \end{cases} $$

(4)

where $B(X(t))=(B_{1}(X), B_{2}(X),\ldots, B_{7}(X))^{T}$ and $B_{i}$ is the right-hand side of ith ($i\in \{1,\ldots,7\}$) line of system (3). □

We have

$$\begin{aligned}& \frac {dS_{H}}{dt} |_{S_{H}=0} = \Lambda _{H} \geqslant 0, \\& \frac {dE_{H}}{dt} |_{E_{H}=0} = \beta _{H} \frac {S_{H}}{N_{H}}I_{V} \geqslant 0, \\& \frac {dI_{R_{H}}}{dt} |_{I_{R_{H}}=0} = \eta _{H}E_{H} \geqslant 0, \\& \frac {dI_{D_{H}}}{dt} |_{I_{D_{H}}=0} = (1-\theta )\gamma _{H_{1}}I_{R_{H}} \geqslant 0, \\& \frac {dR_{H}}{dt} |_{R_{H}=0} = \theta \gamma _{H_{1}}I_{R_{H}}+ \rho \gamma _{H_{2}} I_{D_{H}} \geqslant 0, \\& \frac {dS_{V}}{dt} |_{S_{V}=0} = \Lambda _{V} \geqslant 0, \\& \frac {dI_{V}}{dt} |_{I_{V}=0} = \beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \geqslant 0. \end{aligned}$$

Then it follows that according to Lemma 3.1, $\mathbb{R}^{7}_{+}$ is an invariant set for model (3).

Proposition 3.2

System (3) solutions are bounded in the region

$$\Omega = \biggl\lbrace X=(S_{H},E_{H},I_{R_{H}},I_{D_{H}},R_{H},S_{V},I_{V}) \in \mathbb{R}^{7}_{+} / N_{H} \leqslant \frac {\Lambda _{H}}{\mu _{H}}\textit{ and } N_{V} \leqslant \frac {\Lambda _{V}}{\mu _{V}} \biggr\rbrace $$

with $N_{H}=S_{H}+E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H}$ and $N_{V}=S_{V}+I_{V}$.

Proof

We observe that

$$\begin{aligned}& \frac {dS_{H}}{dt}+\frac {dE_{H}}{dt}+\frac {dI_{R_{H}}}{dt}+ \frac {dI_{D_{H}}}{dt}+ \frac {dR_{H}}{dt} = \Lambda _{H}-\mu _{H}N_{H}- \gamma _{H_{1}}I_{R_{H}}-(1-\rho )\gamma _{H_{2}}I_{D_{H}}, \\& \frac {dN_{H}}{dt} \leqslant \Lambda _{H}-\mu _{H}N_{H}, \\& N_{H}(t) \leqslant N_{H_{0}}e^{-\mu _{H} t}+ \frac {\Lambda _{H}}{\mu _{H}} \end{aligned}$$

and

$$\begin{aligned}& \frac {dS_{V}}{dt}+\frac {dI_{V}}{dt} = \Lambda _{V}-\mu _{V}N_{V}, \\& \frac {dN_{V}}{dt} = \Lambda _{V}-\mu _{V}N_{V}, \\& N_{V}(t) \leqslant N_{V_{0}}e^{-\mu _{V} t}+ \frac {\Lambda _{V}}{\mu _{V}}. \end{aligned}$$

Since $t\rightarrow +\infty$, we have then $0\leqslant (N_{H}(t),N_{V}(t)) \leqslant ( \frac {\Lambda _{H}}{\mu _{H}},\frac {\Lambda _{V}}{\mu _{V}})$. Hence, system (3) solutions are bounded in Ω. □

3.2 Equilibrium points

In this subsection, we determine the equilibrium points of (3).

Let $K=(S_{H},E_{H},I_{R_{H}},I_{D_{H}},R_{H},S_{V},I_{V})$ be an equilibrium point of model (3). On the point K it follows that

$$\begin{aligned} \textstyle\begin{cases} \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}I_{V}-\mu _{H}S_{H} = 0, \\ \beta _{H}\frac {S_{H}}{N_{H}}I_{V} -(\mu _{H}+\eta _{H})E_{H} = 0, \\ \eta _{H}E_{H}-(\mu _{H}+\gamma _{H_{1}})I_{R_{H}} = 0, \\ (1-\theta )\gamma _{H_{1}}I_{R_{H}}-(\mu _{H}+\gamma _{H_{2}})I_{D_{H}} = 0, \\ \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}-\mu _{H}R_{H} = 0, \\ \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})-\mu _{V}S_{V} = 0, \\ \beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})-\mu _{V}I_{V} = 0. \end{cases}\displaystyle \end{aligned}$$

(5)

By resolving the equations of (5), we get

$$\begin{aligned}& S_{H}=\frac{\Lambda _{H}}{\mu _{H}}- \frac{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})}{\mu _{H}\eta _{H}}I_{R_{H}}, \end{aligned}$$

(6)

$$\begin{aligned}& E_{H}=\frac {\mu _{H}+\gamma _{H_{1}}}{\eta _{H}}I_{R_{H}}, \end{aligned}$$

(7)

$$\begin{aligned}& I_{D_{H}}= \frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}}I_{R_{H}}, \end{aligned}$$

(8)

$$\begin{aligned}& R_{H}= \biggl(\frac {\theta \gamma _{H_{1}}}{\mu _{H}}+ \frac {\rho \gamma _{H_{2}}(1-\theta )\gamma _{H_{1}}}{\mu _{H}(\mu _{H}+\gamma _{H_{2}})} \biggr)I_{R_{H}}, \end{aligned}$$

(9)

$$\begin{aligned}& S_{V}=\frac {\Lambda _{V}}{\mu _{V}}-I_{V}. \end{aligned}$$

(10)

Let $X^{0}$ and $X^{*}$ be respectively the disease-free equilibrium (DFE) point and the endemic equilibrium point of model (3). At the disease-free equilibrium point, there are no infectious persons ($I_{V}=I_{R_{H}}=I_{D_{H}}=0$), then $X^{0}$ is given by

$$ X^{0}= \biggl(\frac {\Lambda _{H}}{\mu _{H}},0,0,0,0, \frac {\Lambda _{V}}{\mu _{V}},0 \biggr). $$

(11)

At the endemic equilibrium point $X^{*}$, we have

$$ X^{*}= \bigl(S_{H}^{*},E_{H}^{*},I_{R_{H}}^{*},I_{D_{H}}^{*},R_{H}^{*},S_{V}^{*},I_{V}^{*} \bigr), $$

(12)

where

$$\begin{aligned}& S_{H}^{*}=\frac{\Lambda _{H}}{\mu _{H}}- \frac{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})}{\mu _{H}\eta _{H}}I_{R_{H}}^{*}, \end{aligned}$$

(13)

$$\begin{aligned}& E_{H}^{*}=\frac {\mu _{H}+\gamma _{H_{1}}}{\eta _{H}}I_{R_{H}}^{*}, \end{aligned}$$

(14)

$$\begin{aligned}& I_{D_{H}}^{*}= \frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}}I_{R_{H}}^{*}, \end{aligned}$$

(15)

$$\begin{aligned}& R_{H}^{*}= \biggl(\frac {\theta \gamma _{H_{1}}}{\mu _{H}}+ \frac {\rho \gamma _{H_{2}}(1-\theta )\gamma _{H_{1}}}{\mu _{H}(\mu _{H}+\gamma _{H_{2}})} \biggr)I_{R_{H}}^{*}, \end{aligned}$$

(16)

$$\begin{aligned}& S_{V}^{*}=\frac {\Lambda _{V}}{\mu _{V}}-I_{V}^{*}. \end{aligned}$$

(17)

3.3 Basic reproduction number $\mathcal{R}_{0}$

Proposition 3.3

The basic reproduction number $\mathcal{R}_{0}$ of model (3) is

$$\begin{aligned} \mathcal{R}_{0} =&\sqrt{ \frac {\beta _{H}\beta _{V}\eta _{H}}{\mu _{V}(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})} \biggl(1+ \frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}} \biggr)}. \end{aligned}$$

(18)

Proof

We use the next-generation matrix method [23] to calculate the reproduction number $\mathcal{R}_{0}$ of model (2). Let $\mathcal{F}$ and $\mathcal{V}$, the transmission and flow matrix between the infectious compartments E, $I_{R_{H}}$, $I_{D_{H}}$, and $I_{V}$:

$$\mathcal{F}= \begin{pmatrix} \mathcal{F}_{1} \\ \mathcal{F}_{2} \\ \mathcal{F}_{3} \\ \mathcal{F}_{4} \end{pmatrix},\qquad \mathcal{F}= \begin{pmatrix} \beta _{H}\frac {S_{H}}{N_{H}}I_{V} \\ 0 \\ 0 \\ \beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \end{pmatrix} $$

and

$$\mathcal{V}= \begin{pmatrix} \mathcal{V}_{1} \\ \mathcal{V}_{2} \\ \mathcal{V}_{3} \\ \mathcal{V}_{4} \end{pmatrix},\qquad \mathcal{V}= \begin{pmatrix} -(\mu _{H}+\eta _{H})E_{H} \\ \eta _{H}E_{H}-(\mu _{H}+\gamma _{H_{1}})I_{R_{H}} \\ (1-\theta )\gamma _{H_{1}}I_{R_{H}}-(\mu _{H}+\gamma _{H_{2}})I_{D_{H}} \\ -\mu _{V}I_{V} \end{pmatrix}.$$

On the disease-free equilibrium $X^{0}=(\frac {\Lambda _{H}}{\mu _{H}},0,0,0,0, \frac {\Lambda _{V}}{\mu _{V}},0)$, we obtain

$$\begin{aligned}& \mathcal{DF} = \begin{pmatrix} \frac {\partial \mathcal{F}_{1}}{\partial E_{H}} & \frac {\partial \mathcal{F}_{1}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{F}_{1}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{F}_{1}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{F}_{2}}{\partial E_{H}} & \frac {\partial \mathcal{F}_{2}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{F}_{2}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{F}_{2}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{F}_{3}}{\partial E_{H}} & \frac {\partial \mathcal{F}_{3}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{F}_{3}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{F}_{3}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{F}_{4}}{\partial E_{H}} & \frac {\partial \mathcal{F}_{4}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{F}_{4}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{F}_{4}}{\partial I_{V}} \end{pmatrix}, \\& F =\mathcal{DF} = \begin{pmatrix} 0 & 0 & 0 & \frac {\beta _{H}\Lambda _{H}}{\mu _{H}N_{H}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & \frac {\beta _{V}\Lambda _{V}}{\mu _{V}N_{V}} & \frac {\beta _{V}\Lambda _{V}}{\mu _{V}N_{V}} & 0 \end{pmatrix}, \\& F = \begin{pmatrix} 0 & 0 & 0 & \beta _{H} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & \beta _{V} & \beta _{V} & 0 \end{pmatrix}, \\& \mathcal{DV}= \begin{pmatrix} \frac {\partial \mathcal{V}_{1}}{\partial E_{H}} & \frac {\partial \mathcal{V}_{1}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{V}_{1}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{V}_{1}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{V}_{2}}{\partial E_{H}} & \frac {\partial \mathcal{V}_{2}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{V}_{2}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{V}_{2}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{V}_{3}}{\partial E_{H}} & \frac {\partial \mathcal{V}_{3}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{V}_{3}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{V}_{3}}{\partial I_{V}} \vspace*{3pt}\\ \frac {\partial \mathcal{V}_{4}}{\partial E_{H}} & \frac {\partial \mathcal{V}_{4}}{\partial I_{R_{H}}} & \frac {\partial \mathcal{V}_{4}}{\partial I_{D_{H}}} & \frac {\partial \mathcal{V}_{4}}{\partial I_{V}} \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} V =&\mathcal{DV}= \begin{pmatrix} -(\mu _{H}+\eta _{H}) & 0 & 0 & 0 \\ \eta _{H} & -(\mu _{H}+\gamma _{H_{1}}) & 0 & 0 \\ 0 & (1-\theta )\gamma _{H_{1}} & -(\mu _{H}+\gamma _{H_{2}}) & 0 \\ 0 & 0 & 0 & -\mu _{V} \end{pmatrix}. \end{aligned}$$

Then we get

$$ V^{-1}=- \begin{pmatrix} \frac {1}{\mu _{H}+\eta _{H}} & 0 & 0 & 0 \vspace*{3pt}\\ \frac {\eta _{H}}{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})} & \frac {1}{\mu _{H}+\gamma _{H_{1}}} & 0 & 0 \vspace*{3pt}\\ \frac {\eta _{H}(1-\theta )\gamma _{H_{1}}}{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})(\mu _{H}+\gamma _{H_{2}})} & \frac {(1-\theta )\gamma _{H_{1}}}{(\mu _{H}+\gamma _{H_{1}})(\mu _{H}+\gamma _{H_{2}})} & \frac {1}{\mu _{H}+\gamma _{H_{2}}} & 0 \vspace*{3pt}\\ 0 & 0 & 0 & \frac {1}{\mu _{V}} \end{pmatrix}, $$

and

$$ -FV^{-1}= \begin{pmatrix} 0 & 0 & 0 & a_{1} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ a_{2} & a_{3} & a_{4} & 0 \end{pmatrix}, $$

where

$$\begin{aligned}& a_{1} = \frac {\beta _{H}}{\mu _{V}}, \\& a_{2} = \frac {\beta _{V}\eta _{H}}{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})}+ \frac {\beta _{V}\eta _{H}(1-\theta )\gamma _{H_{1}}}{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})(\mu _{H}+\gamma _{H_{2}})}, \\& a_{3} = \frac {\beta _{V}}{(\mu _{H}+\gamma _{H_{1}})(\mu _{H}+\gamma _{H_{2}})}, \\& a_{4} = \frac {\beta _{V}}{\mu _{V}(\mu _{H}+\gamma _{H_{2}})}. \end{aligned}$$

The basic reproduction number $\mathcal{R}_{0}$ [23] is defined as the dominant eigenvalue of the matrix $-FV^{-1}$. Therefore,

$$\begin{aligned}& \mathcal{R}_{0}^{2} = a_{1}a_{2} \\& \mathcal{R}_{0}^{2} = \frac {\beta _{H}\beta _{V}\eta _{H}}{\mu _{V}(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})} \biggl(1+ \frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}} \biggr). \end{aligned}$$

 □

Theorem 3.1

• (i) If $\mathcal{R}_{0}>1$, then system (3) has a unique endemic equilibrium point denoted $X^{*}$.

• (ii) If $\mathcal{R}_{0}<1$, then system (3) has a unique disease-free equilibrium point denoted $X^{0}$.

Proof

i) Let consider the continuous function $\Upsilon(I_{R_{H}},I_{V})=(\Upsilon_{1}(I_{R_{H}},I_{V}), \Upsilon_{2}(I_{R_{H}},I_{V}))$ where

$$\Upsilon_{1}(I_{R_{H}},I_{V})=\frac{\eta_{H}\beta_{H}}{\mu_{H}+\eta_{H}} \frac{ S_{H}^{0}-(E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H})}{N_{V}}I_{V}-(\mu_{H}+\gamma_{H_{1}})I_{R_{H}} $$

and

$$\Upsilon_{2}(I_{R_{H}},I_{V})=\beta_{V} \frac{S_{V}^{0}-I_{V}}{N_{V}} \biggl(1+ \frac{(1-\theta)\gamma_{H_{1}}}{\mu_{H}+ \gamma_{H_{2}}} \biggr)I_{R_{H}}- \mu_{V}I_{V}. $$

Any solution of the equation $\Upsilon(I_{R_{H}},I_{V})=0$ in $(0,S_{H}^{0})\times(0,S_{V}^{0})$ corresponds to an equilibrium point with $S_{H},I_{R_{H}},S_{V},I_{V} > 0$. We remark that $\Upsilon(0,0)=0$ and $\Upsilon(S_{H}^{0},S_{V}^{0}) < 0$. The sufficient condition for the equation $\Upsilon(I_{R_{H}},I_{V})=0$ to have a solution in $(0,S_{H}^{0}) \times(0,S_{V}^{0})$ is the increasing of ϒ at the point $(0,0)$. This condition is equivalent to

$$\begin{aligned} \textstyle\begin{cases} \frac{\partial\Upsilon_{1}}{\partial I_{R_{H}} }(0,0)+\frac{\partial\Upsilon_{1}}{\partial I_{V} }(0,0) > 0 \\ \frac{\partial\Upsilon_{2}}{\partial I_{R_{H}} }(0,0)+\frac{\partial\Upsilon_{2}}{\partial I_{V} }(0,0) > 0 . \end{cases}\displaystyle \end{aligned}$$

(19)

For all $(I_{R_{H}},I_{V})\in \mathbb{R}^{2}_{+}$, we have:

$$\begin{aligned} \textstyle\begin{cases} \frac{\partial\Upsilon_{1}}{\partial I_{R_{H}} }+ \frac{\partial\Upsilon_{1}}{\partial I_{V}} = -\frac{\eta_{H}\beta_{H}}{\mu_{H}+\eta_{H}}\frac{S_{H}^{0}-(E_{H}+1+I_{D_{H}}+R_{H})}{N_{H}}I_{V}-(\mu_{H}+ \gamma_{H_{1}}) \\ \hphantom{\frac{\partial\Upsilon_{1}}{\partial I_{R_{H}} }+ \frac{\partial\Upsilon_{1}}{\partial I_{V}} =}{} +\frac{\eta_{H}\beta_{H}}{\mu_{H}+\eta_{H}}\frac{S_{H}^{0}-(E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H})}{N_{H}}\\ \frac{\partial\Upsilon_{2}}{\partial I_{R_{H}} }+ \frac{\partial\Upsilon_{2}}{\partial I_{V}} = \beta_{V}\frac{S_{V}^{0}-I_{V}}{N_{V}} (1+\frac{(1-\theta)\gamma_{H_{1}}}{\mu_{H}+ \gamma_{H_{2}}} )+\beta_{V}\frac{(S_{V}^{0}-1)}{N_{V}} (1+\frac{(1-\theta) \gamma_{H_{1}}}{\mu_{H}+\gamma_{H_{2}}} )I_{R_{H}}-\mu_{V} \end{cases}\displaystyle \end{aligned}$$

At the point $(0,0)$ we get:

$$\begin{aligned} \textstyle\begin{cases} \frac{\partial\Upsilon_{1}}{\partial I_{R_{H}} }+ \frac{\partial\Upsilon_{1}}{\partial I_{V}} = -(\mu_{H}+\gamma_{H_{1}})+\frac{\eta_{H}\beta_{H}}{\mu_{H}+\eta_{H}} \\ \frac{\partial\Upsilon_{2}}{\partial I_{R_{H}} }+ \frac{\partial\Upsilon_{2}}{\partial I_{V}} = \beta_{V} (1+\frac{(1-\theta)\gamma_{H_{1}}}{\mu_{H}+\gamma_{H_{2}}} )-\mu_{V} \end{cases}\displaystyle \end{aligned}$$

It follows that:

$$\begin{aligned}& \frac{\partial\Upsilon_{1}}{\partial I_{R_{H}}}(0,0)+ \frac{\partial\Upsilon_{1}}{\partial I_{V}}(0,0) > 0 \quad \Leftrightarrow \quad \frac{\eta_{H}\beta_{H}}{(\mu_{H}+\eta_{H})}>\mu_{H}+\gamma_{H_{1}}, \\& \frac{\partial\Upsilon_{2}}{\partial I_{R_{H}}}(0,0)+ \frac{\partial\Upsilon_{2}}{\partial I_{V}}(0,0) > 0 \quad \Leftrightarrow \quad \beta_{V} \biggl(1+\frac{(1-\theta)\gamma_{H_{1}}}{\mu_{H}+\gamma_{H_{2}}} \biggr)>\mu_{V} \end{aligned}$$

and

$$\begin{aligned}& \text{Eq. (19)} \Longleftrightarrow \frac{\beta_{H}\beta_{V}\eta_{H}}{\mu_{V}(\mu_{H}+\eta_{H}) (\mu_{H}+\gamma_{H_{1}})} \biggl(1+ \frac{(1-\theta)\gamma_{H_{1}}}{\mu_{H}+\gamma_{H_{2}}} \biggr) >1 \\& \text{Eq. (19)} \Longleftrightarrow \mathcal{R}_{0}^{2}>1. \end{aligned}$$

Since $\mathcal{R}_{0}>1$ by hypothesis, the conditions of Eq. (19) are therefore verified. These conditions implies the increasing of the function ϒ at the point $(0,0)$. The system (3) has then an unique endemic equilibrium point $X^{*}$ when $\mathcal{R}_{0}>1$.

ii) Similarly, we obtain the uniqueness of the disease free equilibrium point $X^{0}$ when $\mathcal{R}_{0}<1$. Indeed, $\Upsilon(0,0)=0$, $\Upsilon(S_{H}^{0},S_{V}^{0}) < 0$ and $\mathcal{R}_{0}<1$ then the function ϒ at $(0,0)$ is decreasing on $(0,S_{H}^{0})\times(0,S_{V}^{0})$. We deduce that $(I_{R_{H}},I_{V})=(0,0)$ is the only zero of ϒ. This point corresponds to the disease free equilibrium, hence the uniqueness of $X^{0}$. □

4 Global stability of equilibrium points

We study here the global stability of the disease-free equilibrium $X^{0}$ and the endemic equilibrium $X^{*}$, when $\mathcal{R}_{0}<1$ and $\mathcal{R}_{0}>1$ respectively.

4.1 Global stability of disease-free equilibrium point $X^{0}$

Theorem 4.1

The disease-free equilibrium $X^{0}$ of system (3) is globally asymptotically stable when $\mathcal{R}_{0}<1$.

Proof

Let us consider the infected classes $E_{H}$, $I_{R_{H}}$, $I_{D_{H}}$, and $I_{V}$.

By the equations corresponding to these states, we have at $X^{0}$ the following system:

$$\begin{aligned}& \textstyle\begin{cases} \dot{E}_{H}(t) = \beta _{H}\frac {S_{H}}{N_{H}}I_{V} -(\mu _{H}+ \eta _{H})E_{H}, \\ \dot{I}_{R_{H}}(t) = \eta _{H}E_{H}-(\mu _{H}+\gamma _{H_{1}})I_{R_{H}}, \\ \dot{I}_{D_{H}}(t) = (1-\theta )\gamma _{H_{1}}I_{R_{H}}-(\mu _{H}+ \gamma _{H_{2}})I_{D_{H}}, \\ \dot{I}_{V}(t) = \beta _{V}\frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}I_{V}. \end{cases}\displaystyle \end{aligned}$$

(20)

System (20) can be rewritten as follows:

$$\begin{aligned}& \begin{pmatrix} E_{H} \\ I_{R_{H}} \\ I_{D_{H}} \\ I_{V} \end{pmatrix}= \begin{pmatrix} -(\mu _{H}+\eta _{H}) & 0 & 0 & \beta _{H}\frac {S_{H}}{N_{H}} \\ (1-\theta )\eta _{H} & -(\mu _{H}+\gamma _{H_{1}}) & 0 & 0 \\ \theta \eta _{H} & 0 & -(\mu _{H}+\gamma _{H_{2}}) & 0 \\ 0 & \beta _{V}\frac {S_{V}}{N_{V}} & \beta _{V}\frac {S_{V}}{N_{V}} & - \mu _{V} \end{pmatrix} \begin{pmatrix} \dot{E}_{H} \\ \dot{I}_{R_{H}} \\ \dot{I}_{D_{H}} \\ \dot{I}_{V} \end{pmatrix}. \end{aligned}$$

Since $0 < \frac {S_{H}}{N_{H}}, \frac {S_{V}}{N_{V}} \leqslant 1$, we have

$$\begin{aligned}& \begin{pmatrix} \dot{E}_{H} \\ \dot{I}_{R_{H}} \\ \dot{I}_{D_{H}} \\ \dot{I}_{V} \end{pmatrix} \leqslant \begin{pmatrix} -(\mu _{H}+\eta _{H}) & 0 & 0 & \beta _{H} \\ (1-\theta )\eta _{H} & -(\mu _{H}+\gamma _{H_{1}}) & 0 & 0 \\ \theta \eta _{H} & 0 & -(\mu _{H}+\gamma _{H_{2}}) & 0 \\ 0 & \beta _{V} & \beta _{V} & -\mu _{V} \end{pmatrix} \begin{pmatrix} E_{H} \\ I_{R_{H}} \\ I_{D_{H}} \\ I_{V} \end{pmatrix} \\& \begin{pmatrix} \dot{E}_{H} \\ \dot{I}_{R_{H}} \\ \dot{I}_{D_{H}} \\ \dot{I}_{V} \end{pmatrix} \leqslant ( A+B ) \begin{pmatrix} E_{H} \\ I_{R_{H}} \\ I_{D_{H}} \\ I_{V} \end{pmatrix}. \end{aligned}$$

We consider $\bar{Y}=(\bar{E}_{H},\bar{I}_{R_{H}},\bar{I}_{D_{H}}, \bar{I}_{V})$ and the following system:

$$\begin{aligned}& \begin{pmatrix} \dot{\bar{E}}_{H} \\ \dot{\bar{I}}_{R_{H}} \\ \dot{\bar{I}}_{D_{H}} \\ \dot{\bar{I}}_{V} \end{pmatrix} = ( A+B ) \begin{pmatrix} \bar{E}_{H} \\ \bar{I}_{R_{H}} \\ \bar{I}_{D_{H}} \\ \bar{I}_{V} \end{pmatrix}, \end{aligned}$$

(21)

$$\begin{aligned}& \dot{\bar{Y}}=(A+B)\bar{Y}, \end{aligned}$$

(22)

where

$$\begin{aligned} & A = \begin{pmatrix} 0 & 0 & 0 & \beta _{H} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & \beta _{V} & \beta _{V} & 0 \end{pmatrix}, \\ &B= \begin{pmatrix} -(\mu _{H}+\eta _{H}) & 0 & 0 & 0 \\ (1-\theta )\eta _{H} & -(\mu _{H}+\gamma _{H_{1}}) & 0 & 0 \\ \theta \eta _{H} & 0 & -(\mu _{H}+\gamma _{H_{2}}) &0 \\ 0 & 0 & 0 & -\mu _{V} \end{pmatrix}. \end{aligned}$$

We remark that $F \geqslant 0$ and V is an asymptotic stable Metzler invertible matrix.

Since $\mathcal{R}_{0}=\rho (-FV^{-1})<1$, using the Varga lemma in [24], we get $M=F+V$ is asymptotically stable. That means system (21) is asymptotically stable at origin $(0,0,0,0)$. In other words,

$$ (\bar{E}_{H},\bar{I}_{R_{H}},\bar{I}_{D_{H}}, \bar{I}_{V}) \rightarrow (0,0,0,0)\quad \text{when } t \rightarrow + \infty . $$

By applying Lakshmikantham standard comparison theorem in [9], we get

$$ (E_{H},I_{R_{H}},I_{D_{H}}, I_{V}) \rightarrow (0,0,0,0) \quad \text{when } t \rightarrow +\infty . $$

We use $E_{H}=0$, $I_{R_{H}}=0$, $I_{D_{H}}=0$, $I_{V}=0$ in (3) and get $S_{H}\rightarrow S_{H}^{0}$, $R_{H} \rightarrow R_{H}^{0}$ $S_{V} \rightarrow S_{V}^{0}$, as well as $t \rightarrow +\infty$. It follows that when $\mathcal{R}_{0}<1$,

$$\begin{aligned}& \bigl(S_{H}(t),E_{H}(t),I_{R_{H}}(t), I_{D_{H}}(t), R_{H}(t), S_{V}(t), I_{V}(t) \bigr) \\& \quad \rightarrow \biggl(\frac {\Lambda _{H}}{\mu _{H}},0,0,0,0, \frac {\Lambda _{V}}{\mu _{V}},0 \biggr)\quad \text{as } t \rightarrow +\infty . \end{aligned}$$

$X^{0}= (\frac {\Lambda _{H}}{\mu _{H}},0,0,0,0, \frac {\Lambda _{V}}{\mu _{V}},0 )$ is therefore globally asymptotically stable for $\mathcal{R}_{0}<1$. □

4.2 Global stability of endemic equilibrium point $X^{*}$

Theorem 4.2

The endemic equilibrium $X^{*}$ of system (3) is globally asymptotically stable when $\mathcal{R}_{0}>1$.

Lemma 4.1

Let us consider the following function g defined by

$$g(I_{R_{H}})=I_{R_{H}}-I_{R_{H}}^{*}-I_{R_{H}}^{*} \ln \biggl( \frac {I_{R_{H}}}{I_{R_{H}}^{*}} \biggr)\quad I_{R_{H}},I_{R_{H}}^{*} \in \mathbb{R}^{+}. $$

We have that $g(I_{R_{H}}) \geqslant 0$.

Indeed, by limited development we get

$$\begin{aligned}& g(I_{R_{H}}) = g \bigl(I_{R_{H}}^{*} \bigr)+g' \bigl(I_{R_{H}}^{*} \bigr) \bigl(I_{R_{H}}-I_{R_{H}}^{*} \bigr)+ \frac {1}{2}g''(\xi ) \bigl(I_{R_{H}}-I_{R_{H}}^{*} \bigr)^{2} \\& \hphantom{g(I_{R_{H}})} = \frac {1}{2}\frac {I_{R_{H}}^{*}}{I_{R_{H}}^{2}} \bigl(I_{R_{H}}-I_{R_{H}}^{*} \bigr)^{2} \\& g(I_{R_{H}}) \geqslant \frac {1}{2} \frac {I_{R_{H}}^{*}}{(\Lambda _{H}/\mu _{H})^{2}} \bigl(I_{R_{H}}-I_{R_{H}}^{*} \bigr)^{2}. \end{aligned}$$

Proof

Consider the Lyapunov function candidate:

$$\begin{aligned} V \bigl(X(t) \bigr) =& \bigl(S_{H}-S_{H}^{*} \bigr)+ \bigl(E_{H}-E_{H}^{*} \bigr)+ \bigl(I_{R_{H}}-I_{R_{H}}^{*} \bigr) \\ &{}+ \bigl(I_{D_{H}}-I_{D_{H}}^{*} \bigr)+ \bigl(R_{H}-R_{H}^{*} \bigr) \\ &{}- \bigl(S_{H}^{*}+E_{H}^{*}+I_{R_{H}}^{*}+I_{D_{H}}^{*}+R_{H}^{*} \bigr)\ln \biggl( \frac {S_{H}+E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H}}{S_{H}^{*}+E_{H}^{*}+I_{R_{H}}^{*}+I_{D_{H}}^{*}+R_{H}^{*}} \biggr) \\ &{}+ \bigl(S_{V}-S_{V}^{*} \bigr)+ \bigl(I_{V}-I_{V}^{*} \bigr) - \bigl(S_{V}^{*}+I_{V}^{*} \bigr)\ln \biggl(\frac {S_{V}+I_{V}}{S_{V}^{*}+I_{V}^{*}} \biggr). \end{aligned}$$

• We have $V(X^{*})=0$

$$\begin{aligned}& V \bigl(X(t) \bigr) = (S_{H}+E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H}) - \bigl(S_{H}^{*}+E_{H}^{*}+I_{R_{H}}^{*}+I_{D_{H}}^{*}+R_{H}^{*} \bigr) \\& \hphantom{V (X(t) ) =}{} - \bigl(S_{H}^{*}+E_{H}^{*}+I_{R_{H}}^{*}+I_{D_{H}}^{*}+R_{H}^{*} \bigr)\ln \biggl( \frac {S_{H}+E_{H}+I_{R_{H}}+I_{D_{H}}+R_{H}}{S_{H}^{*}+E_{H}^{*}+I_{R_{H}}^{*}+I_{D_{H}}^{*}+R_{H}^{*}} \biggr) \\& \hphantom{V (X(t) ) =}{}+ (S_{V}+I_{V})- \bigl(S_{V}^{*}+I_{V}^{*} \bigr) - \bigl(S_{V}^{*}+I_{V}^{*} \bigr)\ln \biggl(\frac {S_{V}+I_{V}}{S_{V}^{*}+I_{V}^{*}} \biggr) \\& V \bigl(X(t) \bigr) = N_{H}-N_{H}^{*}-N_{H}^{*} \ln \biggl(\frac {N_{H}}{N_{H}^{*}} \biggr)+N_{V}-N_{V}^{*}-N_{V}^{*} \ln \biggl(\frac {N_{V}}{N_{V}^{*}} \biggr). \end{aligned}$$

• Using Lemma 4.1, we get $V(X(t))>0$ $\forall X\neq X^{*}$.

Differentiating with respect to time yields

$$\begin{aligned}& \dot{V} \bigl(X(t) \bigr) = \biggl(1-\frac {N_{H}^{*}}{N_{H}} \biggr) \dot{N}_{H}+ \biggl(1-\frac {N_{V}^{*}}{N_{V}} \biggr)\dot{N}_{V}, \\& \dot{V} \bigl(X(t) \bigr) = \biggl(1-\frac {N_{H}^{*}}{N_{H}} \biggr) \biggl(\Lambda _{H}- \beta _{H}\frac {S_{H}}{N_{H}}I_{V}-\mu _{H}S_{H} + \beta _{H} \frac {S_{H}}{N_{H}}I_{V} -(\mu _{H}+\eta _{H})E_{H}+\eta _{H}E_{H} \\& \hphantom{\dot{V} (X(t) ) =}{} - (\mu _{H}+\gamma _{H_{1}})I_{R_{H}} + (1-\theta ) \gamma _{H_{1}}I_{R_{H}}-( \mu _{H}+\gamma _{H_{2}})I_{D_{H}} \\& \hphantom{\dot{V} (X(t) ) =}{} + \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}-\mu _{H}R_{H} \biggr) \\& \hphantom{\dot{V} (X(t) ) =}{} + \biggl(1-\frac {N_{V}^{*}}{N_{V}} \biggr) \biggl( \Lambda _{V}-\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}S_{V} \\& \hphantom{\dot{V} (X(t) ) =}{} + \beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}})- \mu _{V}I_{V} \biggr), \\& \dot{V} \bigl(X(t) \bigr) = \biggl(1-\frac {N_{H}^{*}}{N_{H}} \biggr) (\Lambda _{H}- \mu _{H}N_{H} )+ \biggl(1- \frac {N_{V}^{*}}{N_{V}} \biggr) ( \Lambda _{V}-\mu _{V}N_{V} ) \\& \hphantom{\dot{V} (X(t) )} = \frac {N_{H}-N_{H}^{*}}{N_{H}} \bigl(\mu _{H}N_{H}^{*}- \mu _{H}N_{H} \bigr)+\frac {N_{V}-N_{V}^{*}}{N_{V}} \bigl(\mu _{V}N_{V}^{*}-\mu _{V}N_{V} \bigr), \\& \dot{V} \bigl(X(t) \bigr) = -\mu _{H}\frac {(N_{H}-N_{H}^{*})^{2}}{N_{H}}-\mu _{V} \frac {(N_{V}-N_{V}^{*})^{2}}{N_{V}}. \end{aligned}$$

• We get $\dot{V}(X(t)) \leqslant 0$. $V(X(t))$ is then a Lyapunov function. □

In addition, we get $\dot{V}(X(t))=0$ for $S_{H}=S_{H}^{*}$, $E_{H}=E_{H}^{*}$, $I_{R_{H}}=I_{R_{H}}^{*}$, $I_{D_{H}}=I_{D_{H}}^{*}$, and $R_{H}=R_{H}^{*}$. According to the LaSalle invariance theorem [10, 11], the endemic equilibrium point $X^{*}$ is globally asymptotically stable.

5 Numerical simulations and comments

In this section we have performed some numerical simulations to corroborate the theoretical work in the disease-free case and in the endemic case. In our simulations, we assume that the population is annually affected by dengue fever. This implies that the number of hemorrhagic cases in the event of dengue is considerable.

Depending on whether the number of basic reproduction is less than or greater than unity, the dynamics of the different states are observed using the Python version 3.7 programming software.

For the case of $\mathcal{R}_{0}<1$, some values are taken from the literature: $\Lambda _{H}=200$, $\Lambda _{V}=100$, $\mu _{H}=0.3$, $\mu _{V}=0.2$ in [16], and $\rho =0.99$ in [19]. Estimated, the values of the others parameters are: $\eta _{H}=0.3$, $\theta =0.4$, $\gamma _{H_{1}}=0.5$, $\gamma _{H_{2}}=0.3$, $\beta _{H}=0.5$, and $\beta _{V}=0.21$.

Indeed, with the estimated value $\beta _{H}=0.5$, we assume that for a group of one hundred (100) healthy people bitten by infected mosquitoes, fifty (50) will become ill with dengue fever. Also, by $\beta _{V}=0.21$, we assume that for one hundred (100) healthy mosquitoes biting infected people, twenty-one (21) mosquitoes become infected. With these different values, we get $\mathcal{R}_{0}=0.70156$. The first seven curves are obtained using different initial states $X_{0}$.

Comments

In each of the subfigures (a)–(d) of Fig. 2 and (a)–(c) of Fig. 3, we have presented the evolution of the population of susceptible humans, exposed humans, simple infected humans, severely infected humans, recovered humans, susceptible vectors, and infected vectors respectively.

Figure 2

The dynamics of humans, $\mathcal{R}_{0}<1$

Figure 3

The dynamics of humans and vectors, $\mathcal{R}_{0}<1$

Also, we present the evolution of susceptible persons, simple infected persons, and severe infected persons, all in the same subfigure Fig. 3(d). The evolution of infected vectors and infected persons, both severe and simple cases, are all shown in subfigure Fig. 3(e).

In a single subfigure, namely subfigure Fig. 3(g), we show the evolution of all human compartments. Similarly, we propose in the single curve Fig. 3(f) the evolution of all compartments of vectors.

Theses curves point out that the disease tends to disappear in the population. Indeed, the human and vector infectious classes $I_{R_{H}}$, $I_{D_{H}}$, and $I_{V}$ are getting closer and closer to zero with the evolution of time t. This implies the disappearance of the disease in the population.

The next curves are obtained with the estimated values grouped in Table 1. We keep the value of $\Lambda _{H}$, $\Lambda _{V}$, $\mu _{H}$, $\mu _{V}$, $\gamma _{H_{1}}$, $\gamma _{H_{2}}$ and make the following changes:

$$\rho =0.3\qquad \eta _{H}=0.8\qquad \theta =0.1\qquad \beta _{H}=0.41\qquad \beta _{V}=0.51. $$

Table 1 The values of parameters for $\mathcal{R}_{0}>1$ ($\mathcal{R}_{0}=1.289688122976037$)

Indeed, with the estimated value rho = 0.3, we assume that at the endemic equilibrium point for ten (10) haemorrhagically infected people, three (03) will recover and seven (07) will die of dengue. Also, with the estimated value theta = 0.1, we assume that for every ten (10) people infected with simple dengue, one (01) will recover and nine (09) will experience a complication. Indeed, with the estimated value rho = 0.3, we assume that at the endemic equilibrium point for ten (10) haemorrhagically infected people, three (03) will recover and seven (07) will die of dengue. Also, with the estimated value theta = 0.1, we assume that for every ten (10) people infected with simple dengue, one (01) will recover and nine (09) will experience a complication.

Comments

By the curves (a)–(e) of Fig. 4 and (a)–(f) of Fig. 5, we show respectively the dynamics as a function of time (days) of the population of susceptible humans, exposed humans, simple infected humans, severely infected humans, recovered humans, susceptible vectors, and infected vectors respectively.

Figure 4

The dynamics of humans, $\mathcal{R}_{0}>1$

Figure 5

The dynamics of humans and vectors, $\mathcal{R}_{0}>1$

We show in the same figure, subfigure 5(c), the curve of the evolution of the simple infected and the severe infected. Also we show in the single Fig. 5(d) the three curves of the three infectious classes (simple infected humans, severe infected humans, infected mosquitoes). In 5(c) and 5(d), the persistence of the three infectious classes during the dynamics of the disease can be seen.

5(e) and 5(f) show the dynamics of the different classes of vectors and the different classes of humans, respectively.

Overall, the different curves show a persistence of the disease in the population when the basic reproduction number is greater than 1.

6 Global sensitivity of $\mathcal{R}_{0}$ parameters

The normalized forward sensitivity index of $\mathcal{R}_{0}$, which depends differentiably on the parameter ζ [13, 16], is defined by

$$ \Psi ^{\mathcal{R}_{0}}_{\zeta}= \frac {\partial \mathcal{R}_{0}}{\partial \zeta}\times \frac {\zeta}{\mathcal{R}_{0}}. $$

(23)

Recall (18) that the basic reproduction number $\mathcal{R}_{0}$ is given by

$$\begin{aligned} \mathcal{R}_{0} =&\sqrt{ \frac {\beta _{H}\beta _{V}\eta _{H}}{\mu _{V}(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})} \biggl(1+ \frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}} \biggr)}. \end{aligned}$$

For each parameter ζ of $\mathcal{R}_{0}$, thanks to (23), we evaluate the impact on $\mathcal{R}_{0}$ of the parameters variation.

By calculation, the sensitivity indices of $\mathcal{R}_{0}$ with respect to $\beta _{H}$, $\beta _{V}$, $\mu _{H}$, $\mu _{V}$, $\eta _{H}$, $\gamma _{H_{1}}$, and $\gamma _{H_{2}}$ are as follows:

$$\begin{aligned}& \Psi ^{\mathcal{R}_{0}}_{\beta _{H}}=\frac {1}{2};\qquad \Psi ^{\mathcal{R}_{0}}_{\beta _{V}}=\frac {1}{2}; \\& \Psi ^{\mathcal{R}_{0}}_{\mu _{V}}=-\frac {1}{2};\qquad \Psi ^{\mathcal{R}_{0}}_{\eta _{H}}= \frac {\mu _{H}}{2(\mu _{H}+\eta _{H})}; \\& \Psi ^{\mathcal{R}_{0}}_{\mu _{H}}= \frac {-\mu _{H}(\mu _{H}+\gamma _{H_{2}})}{2(\mu _{H}+\gamma _{H_{2}}+(1-\theta )\gamma _{H_{1}})} \biggl[ \frac {2\mu _{H}+\eta _{H}+\gamma _{H_{1}}}{(\mu _{H}+\eta _{H})(\mu _{H}+\gamma _{H_{1}})} \biggl(1+\frac {(1-\theta )\gamma _{H_{1}}}{\mu _{H}+\gamma _{H_{2}}} \biggr) \\& \hphantom{\Psi ^{\mathcal{R}_{0}}_{\mu _{H}}=}{}+ \frac {(1-\theta )\gamma _{H_{1}}\gamma _{H_{2}}}{\mu _{H}+\gamma _{H_{2}}} \biggr]; \\& \Psi ^{\mathcal{R}_{0}}_{\theta}= \frac {-\theta \gamma _{H_{1}}}{2(\mu _{H}+\gamma _{H_{2}}+(1-\theta )\gamma _{H_{1}})}; \\& \Psi ^{\mathcal{R}_{0}}_{\gamma _{H_{1}}}=\frac {\gamma _{H_{1}}}{2} \biggl[ \frac {1}{\mu _{H}+\gamma _{H_{1}}}+ \frac {1-\theta +\mu _{H}+\gamma _{H_{2}}}{\mu _{H}+\gamma _{H_{2}}+(1-\theta )\gamma _{H_{1}}} \biggr]; \\& \Psi ^{\mathcal{R}_{0}}_{\gamma _{H_{2}}}= \frac {-(1-\theta )\gamma _{H_{1}}\gamma _{H_{2}}}{2(\mu _{H}+\gamma _{H_{2}}+ (1-\theta )\gamma _{H_{2}})(\mu _{H}+\gamma _{H_{2}})}. \end{aligned}$$

For the different parameters of $\mathcal{R}_{0}$, we give a value (Table 2) and obtain a numerical value of the sensitivity index (Table 2) corresponding to the parameter value.

Table 2 Sensitivity indices of $\mathcal{R}_{0}$ parameters

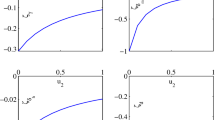
The diagram (Fig. 6) is a graphic illustration of the sensitivity indices we have calculated. Indeed, by Fig. 6, we have in picture positive or negative impact of the variation of $\mathcal{R}_{0}$ parameters. The fact that $\Psi ^{\mathcal{R}_{0}}_{\beta _{H}}=+0.5$ means that 1% increase in $\beta _{H}$, keeping all other parameters fixed, will increase the value of $R_{0}$ by 0.5%.

Figure 6

Sensitivity indices diagram

Also, when each of the parameters $\beta _{V}$, $\eta _{H}$, and $\gamma _{H_{1}}$ increases by 1% while the other parameters remain constant, the value of $\mathcal{R}_{0}$ increases by 0.5%, 0.285714285%, and 0.631883655%, respectively. On the other hand, when each of the parameters $\mu _{H}$, $\mu _{V}$, θ, and $\gamma _{H_{2}}$ increases by 1% while the other parameters remain constant, the value of $\mathcal{R}_{0}$ decreases by 0.532921918%, 0.5%, 0.00020842%, and 0.089233609%, respectively.

7 Optimal control problem

7.1 Statement of the optimal control problem

In this section, we compute the optimal function of the control (u(t), v(t)) to determine the best measures in terms of treatment and any prevention method to minimize the population of infected individuals. Indeed:

• u consists of early supportive care with rehydration and symptomatic treatment. These methods improve the patient’s survival;

• v represents any method that can reduce vector–human contact (destruction of egg nests, mosquito nets, awareness-raising, etc.).

This optimal couple minimizes at the same time the cost of implementing the treatment and the prevention strategies. So we consider the following optimal control problem:

$$ J(\bar{u},\bar{v})=\min \bigl\{ J(u,v): (u,v) \in U \bigr\} , $$

(24)

where

$$ J(u,v)= \int _{0}^{t_{f}} \biggl[ I_{R_{H}}+I_{D_{H}}+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t) \biggr]\,dt, $$

(25)

subject to the equation

$$\begin{aligned} \textstyle\begin{cases} \dot{S}_{H}(t) = \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}(1- v(t))I_{V}-\mu _{H}S_{H}, \\ \dot{E}_{H}(t) = \beta _{H}\frac {S_{H}}{N_{H}}(1- v(t))I_{V} -(\mu _{H}+\eta _{H})E_{H}, \\ \dot{I}_{R_{H}}(t) = \eta _{H}E_{H}-\gamma _{H_{1}}(1- u(t))I_{R_{H}}-\mu _{H}I_{R_{H}}, \\ \dot{I}_{D_{H}}(t) = (1-u(t)) [ (1-\theta ) \gamma _{H_{1}}I_{R_{H}}-\gamma _{H_{2}}I_{D_{H}} ]-\mu _{H}I_{D_{H}}, \\ \dot{R}_{H}(t) = (1-u(t)) [\theta \gamma _{H_{1}}I_{R_{H}}+ \rho \gamma _{H_{2}}I_{D_{H}} ]-\mu _{H}R_{H}, \\ D_{H}(t) = (1-u(t))(1-\rho )\gamma _{H_{2}}I_{D_{H}}, \\ \dot{S}_{V}(t) = \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}}(1- u(t))(I_{R_{H}}+I_{D_{H}})-\mu _{V}S_{V}, \\ \dot{I}_{V}(t) = \beta _{V}\frac {S_{V}}{N_{V}}(1- u(t))(I_{R_{H}}+I_{D_{H}})-\mu _{V}I_{V}. \end{cases}\displaystyle \end{aligned}$$

(26)

The two functions $u(t)$ and $v(t)$ represent respectively the treatment of infected persons and the different ways to prevent dengue fever. The use of insecticides, destruction of egg nests, and any other measure that reduces mosquito bites are ranked in the order of prevention methods. The functions u and v are elements of the set U defined by

$$ \Omega = \bigl\{ (u,v) \in \bigl(L^{2}(0,t_{f}) \bigr)^{2}: 0\leqslant u(t),v(t) \leqslant 1\ \forall t \in [0,t_{f}], t_{f} \in \mathbb{R}^{+} \bigr\} . $$

The two constants $A_{1} > 0$, $A_{2} > 0$ are measures of the relative cost of the interventions associated with the controls u and v respectively.

Theorem 7.1

(Existence of optimal control)

Consider the optimal control problem (24) subject to (26). Then there exists an optimal control $(\bar{u},\bar{v})$ in Ω and a corresponding solution

$$\bar{X}(t)= (\bar{ S}_{H},\bar{E}_{H}, \bar{I}_{R_{H}},\bar{I}_{D_{H}}, \bar{R}_{H}, \bar{D}_{H},\bar{S}_{V},\bar{I}_{V}) $$

that minimize $J(u,v)$ over a set of admissible controls Ω.

Proof

The existence of an optimal control can be obtained by using a result of Flemning and Rishel [4]. To use an existence result, Theorem III.4.1 from Lukes [12], we must check if the following properties are satisfied:

• (1) The set of controls and the corresponding solutions are not empty.

• (2) The set of admissible controls U is convex and closed in $L^{2}(0,T)$.

• (3) The vectors field of the state system is borned by a linear control function.

• (4) The integrand of objective function

  $$ f^{0} \bigl(X(t),u(t),v(t) \bigr)=I_{R_{H}}+I_{D_{H}}+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+ \frac{A_{2}}{2}v^{2}(t) $$

  is convex. The Hessian matrix of $f^{0}$ on U is

  $$ H= \begin{pmatrix} A_{1} & 0 \\ 0 & A_{2} \end{pmatrix}. $$

  We have $\operatorname{spec}(M)=\{A_{1},A_{2}\} \subset \mathbb{R}_{+}^{*}$, then $f^{0}$ is strictly convex.

• (5) There exist constants $k>0$ and $\rho >1$ such as the integrand $f^{0}$ of objective function verifies $f^{0}(X(t),u(t),v(t)) \geqslant k|(u,v)|^{\rho}-k_{2}$. We have

  $$\begin{aligned}& f^{0} \bigl(X(t),u(t),v(t) \bigr) = I_{R_{H}}+I_{D_{H}}+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+ \frac{A_{2}}{2}v^{2}(t) \\& \hphantom{f^{0} (X(t),u(t),v(t) )} \geqslant \frac {1}{2}\min (A_{1},A_{2}) \bigl(u(t)^{2}+v(t)^{2} \bigr)+I_{R_{H}}+I_{D_{H}}+I_{V} \\& f^{0} \bigl(X(t),u(t),v(t) \bigr) \geqslant \frac {1}{2}\min (A_{1},A_{2}) \bigl\Vert (u,v) \bigr\Vert ^{2}_{2}. \end{aligned}$$

  We get

  $$ f^{0} \bigl(X(t),u(t),v(t) \bigr) \geqslant k \bigl\Vert (u,v) \bigr\Vert ^{2}_{2} $$

  with $k=\frac {1}{2}\min (A_{1},A_{2})$.

 □

Proposition 7.1

(Hamiltonian characterization of minimization problem)

The minimization problem (24) induces to a problem of minimization of Hamiltonian H defined by

$$ H \bigl(X(t),p(t),p^{0},u(t),v(t) \bigr)=I_{R_{H}}+I_{D_{H}}+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+ \frac{A_{2}}{2}v^{2}(t)+\sum_{i=1}^{8} \lambda _{i}f_{i}, $$

(27)

where:

• $f_{i}$ is the right-hand side of the differential equation of ith state variable,

• $p(\cdot )$ is absolutely continuous application defined to $[0,t_{f}] \longrightarrow \mathbb{R}^{n}\setminus \{0\}$,

• $p^{0}$ is a positive or null real and $X(t)=(S_{H},E_{H},I_{R_{H}},I_{D_{H}},R_{H},D_{H},S_{V},I_{V})$.

Proof

Let

$$\begin{aligned}& p^{0}=1, \\& p(t)= \bigl( \lambda _{1}(t),\lambda _{2}(t),\lambda _{3}(t),\ldots, \lambda _{8}(t) \bigr), \\& f^{0} \bigl(X(t),u(t),v(t) \bigr)=I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t), \\& f \bigl(X(t),u(t),v(t) \bigr)= \bigl(f_{1} \bigl(X(t),u(t),v(t) \bigr),f_{2} \bigl(X(t),u(t),v(t) \bigr),\ldots,f_{8} \bigl(X(t),u(t),v(t) \bigr) \bigr), \end{aligned}$$

where

$$ X(t)=(S_{H},E_{H},I_{R_{H}},I_{D_{H}},R_{H},D_{H},S_{V},I_{V}) $$

and

$$\begin{aligned}& f_{1} \bigl(X(t),u(t),v(t) \bigr) = \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}} \bigl(1-v(t) \bigr)I_{V}- \mu _{H}S_{H}, \\& f_{2} \bigl(X(t),u(t),v(t) \bigr) = \beta _{H} \frac {S_{H}}{N_{H}} \bigl(1-v(t) \bigr)I_{V} -( \mu _{H}+\eta _{H})E_{H}, \\& f_{3} \bigl(X(t),u(t),v(t) \bigr) = \eta _{H}E_{H}- \gamma _{H_{1}} \bigl(1-u(t) \bigr)I_{R_{H}}- \mu _{H}I_{R_{H}}, \\& f_{4} \bigl(X(t),u(t),v(t) \bigr) = \bigl(1-u(t) \bigr) \bigl[ (1- \theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr]-\mu _{H}I_{D_{H}}, \\& f_{5} \bigl(X(t),u(t),v(t) \bigr) = \bigl(1-u(t) \bigr) [\theta \gamma _{H_{1}}I_{R_{H}}+ \rho \gamma _{H_{2}}I_{D_{H}} ]- \mu _{H}R_{H}, \\& f_{6} \bigl(X(t),u(t),v(t) \bigr) = \bigl(1-u(t) \bigr) (1-\rho ) \gamma _{H_{2}}I_{D_{H}}, \\& f_{7} \bigl(X(t),u(t),v(t) \bigr) = \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}} \bigl(1-u(t) \bigr) (I_{R_{H}}+I_{D_{H}})- \mu _{V}S_{V}, \\& f_{8} \bigl(X(t),u(t),v(t) \bigr) = \beta _{V} \frac {S_{V}}{N_{V}} \bigl(1-u(t) \bigr) (I_{R_{H}}+I_{D_{H}})- \mu _{V}I_{V}. \end{aligned}$$

Then the Hamiltonian of the optimal problem is defined by

$$\begin{aligned}& H \bigl(t,X,p,p^{0},u,v \bigr) = \bigl\langle p,f \bigl(X(t),u(t),v(t) \bigr) \bigr\rangle + p^{0}f^{0} \bigl(X(t),u(t),v(t) \bigr) \\& \hphantom{H (t,X,p,p^{0},u,v )}= \bigl\langle (\lambda _{1},\lambda _{2}, \ldots,\lambda _{8}),(f_{1},f_{2}, \ldots,f_{8}) \bigr\rangle +p^{0}f^{0} \\& \hphantom{H (t,X,p,p^{0},u,v )}= \sum_{i=1}^{8}\lambda _{i}f_{i}+ I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t) \\& H \bigl(t,X,p,p^{0},u,v \bigr) = I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t)+ \sum_{i=1}^{8} \lambda _{i}f_{i}. \end{aligned}$$

 □

Proposition 7.2

(Existence of adjoint vector $p(\cdot )$)

The application $p(\cdot )$

$$ \begin{aligned} p(\cdot ):\quad [0,t_{f}] & \longrightarrow \mathbb{R}^{8} \\ t &\longmapsto \bigl(\lambda _{1}(t),\lambda _{2}(t), \lambda _{3}(t), \lambda _{4}(t),\lambda _{5}(t), \lambda _{6}(t),\lambda _{6}(t), \lambda _{7}(t), \lambda _{8}(t) \bigr) \end{aligned} $$

and verify

$$\begin{aligned} \textstyle\begin{cases} \dot{\lambda _{1}} = \beta _{H} \frac {\lambda _{1}-\lambda _{2}}{N_{H}}(1-v(t))I_{V}+\lambda _{1} \mu _{H}, \\ \dot{\lambda _{2}} = (\lambda _{2}-\lambda _{3})\eta _{H}+\lambda _{2} \mu _{h}, \\ \dot{\lambda _{3}} = 1+(1-u(t)) ((\lambda _{3}-\lambda _{4}(1- \theta )-\lambda _{5}\theta )\gamma _{H_{1}}+(\lambda _{7}-\lambda _{8}) \beta _{V}\frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{4}} = 1+(1-u(t)) ((\lambda _{4}-\lambda _{5}\rho - \lambda _{6}(1-\rho ))\gamma _{H_{2}}+(\lambda _{7}-\lambda _{8}) \beta _{V}\frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{5}} = \lambda _{5}\mu _{H}, \\ \dot{\lambda _{6}} = 0, \\ \dot{\lambda _{7}} = (\lambda _{7}-\lambda _{8})(1-u(t))\beta _{V} \frac {1}{N_{V}}(I_{R_{H}}+I_{D_{H}})+\lambda _{7}\mu _{V}, \\ \dot{\lambda _{8}} = 1+(1-v(t)) (\lambda _{1}\beta _{H} \frac {S_{H}}{N_{H}}-\lambda _{2}\beta _{H}\frac {S_{H}}{N_{H}} + \lambda _{8}\mu _{V} ), \\ \lambda _{i}(t_{f}) = 0 \quad \forall i \in \{1,2,\ldots,8\}. \end{cases}\displaystyle \end{aligned}$$

(28)

Proof

According to Theorem (7.1) the couple of controls $(\bar{u},\bar{v})$ associated with the solution X̄ minimize $J(u,v)$ over U. According to the maximum principle of Pontryagin, there exists an absolutely continuous application

$$ \begin{aligned} p(\cdot ):\quad [0,t_{f}] & \longrightarrow \mathbb{R}^{10} \\ t &\longmapsto \bigl(\lambda _{1}(t),\lambda _{2}(t), \lambda _{3}(t), \lambda _{4}(t) \bigr),,\lambda _{5}(t),\ldots,,\lambda _{8}(t)) \end{aligned} $$

such as for almost all $t \in [0, t_{f} ]$

$$ \dot{p}(t)=-\frac{\partial H}{\partial X } \quad \text{and}\quad p(t_{f})=0. $$

Then

$$\dot{p}(t)=-\frac{\partial H}{\partial X}⟹\{\begin{array}{c}\dot{{\lambda }_1}=-\frac{\partial H}{\partial S_H},\hfill \\ \dot{{\lambda }_2}=-\frac{\partial H}{\partial E_H},\hfill \\ \dot{{\lambda }_3}=-\frac{\partial H}{\partial I_{R_H}},\hfill \\ \dot{{\lambda }_4}=-\frac{\partial H}{\partial I_{D_H}},\hfill \\ \dot{{\lambda }_5}=-\frac{\partial H}{\partial R_H},\hfill \\ \dot{{\lambda }_6}=-\frac{\partial H}{\partial D_H},\hfill \\ \dot{{\lambda }_7}=-\frac{\partial H}{\partial S_V},\hfill \\ \dot{{\lambda }_8}=-\frac{\partial H}{\partial I_V}.\hfill \end{array}$$

(29)

Then we have

$$\begin{aligned}& \dot{\lambda _{1}} = -\frac {\partial H}{\partial S_{H}} \bigl(t,X,p,p^{0},u,v \bigr) \\& \hphantom{\dot{\lambda _{1}}}= -\frac {\partial}{\partial S_{H}} \Biggl( I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac {A_{1}}{2}{u}^{2}(t)+\frac {A_{2}}{2}{v}^{2}(t)+ \sum_{i=1}^{10} \lambda _{i}f_{i}(X,u,v) \Biggr) \\& \hphantom{\dot{\lambda _{1}}}= -\sum_{i=1}^{8}\lambda _{i} \frac {\partial f_{i}}{\partial S}(X,u,v) \\& \hphantom{\dot{\lambda _{1}}} = -\lambda _{1}\frac {\partial f_{1}}{\partial S_{H}}(X,u,v) - \lambda _{2} \frac {\partial f_{2}}{\partial S_{H}}(X,u,v) \\& \hphantom{\dot{\lambda _{1}}} = -\lambda _{1}\frac {\partial}{\partial S_{H}} \biggl[\Lambda _{H}- \beta _{H}\frac {S_{H}}{N_{H}} \bigl(1-v(t) \bigr)I_{V}-\mu _{H}S_{H} \biggr] \\& \hphantom{\dot{\lambda _{1}}=} - \lambda _{2}\frac {\partial}{\partial S_{H}} \biggl[ \beta _{H} \frac {S_{H}}{N_{H}} \bigl(1-v(t) \bigr)I_{V} -(\mu _{H}+\eta _{H})E_{H} \biggr] \\& \hphantom{\dot{\lambda _{1}}} = -\lambda _{1} \biggl[-\beta _{H} \frac {1}{N_{H}} \bigl(1-v(t) \bigr)I_{V}-\mu _{H} \biggr]-\lambda _{2} \biggl[ \beta _{H}\frac {1}{N_{H}} \bigl(1-v(t) \bigr)I_{V} \biggr], \\& \dot{\lambda _{1}} = \lambda _{1}\mu _{H}+ \beta _{H} \frac {\lambda _{1}-\lambda _{2}}{N_{H}} \bigl(1-v(t) \bigr)I_{V}. \end{aligned}$$

By the same method, we have

$$\begin{aligned}& \dot{\lambda _{2}} = -\lambda _{2} \frac {\partial f_{2}}{\partial E_{H}} - \lambda _{3} \frac {\partial f_{3}}{\partial E_{H}} \\& \hphantom{\dot{\lambda _{2}} } = \frac {\partial}{\partial E_{H}} (-\lambda _{2} f_{2}-\lambda _{3}f_{3} ) \\& \hphantom{\dot{\lambda _{2}} } = \frac {\partial}{\partial E_{H}} \biggl(-\lambda _{2} \biggl( \beta _{H} \frac {S_{H}}{N_{H}} \bigl(1-v(t) \bigr)I_{V} -(\mu _{H}+\eta _{H})E_{H} \biggr) \\& \hphantom{\dot{\lambda _{2}} =}{}- \lambda _{3} \bigl(\eta _{H}E_{H}- \gamma _{H_{1}} \bigl(1-u(t) \bigr)I_{R_{H}}-\mu _{H}I_{R_{H}} \bigr) \biggr), \\& \dot{\lambda _{2}} = \lambda _{2}\mu _{H}+( \lambda _{2}-\lambda _{3}) \eta _{H} \\& \dot{\lambda _{3}} = 1+\frac {\partial}{\partial I_{R_{H}}} (- \lambda _{3} f_{3}-\lambda _{4}f_{4}-\lambda _{5}f_{5}-\lambda _{7}f_{7}- \lambda _{8}f_{8} ) \\& \hphantom{\dot{\lambda _{3}}}= 1+\lambda _{3}\mu _{H}+ \bigl(1-u(t) \bigr) \biggl( \lambda _{3}\gamma _{H_{1}}- \lambda _{4}(1-\theta ) \gamma _{H_{1}}-\lambda _{5}\theta \gamma _{H_{1}}+( \lambda _{7}-\lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}} \biggr) \\& \dot{\lambda _{3}} = 1+\lambda _{3}\mu _{H}+ \bigl(1-u(t) \bigr) \biggl(\lambda _{3} \gamma _{H_{1}}-\lambda _{4}(1-\theta )\gamma _{H_{1}}-\lambda _{5} \theta \gamma _{H_{1}}+(\lambda _{7}-\lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}} \biggr) \\& \dot{\lambda _{4}} = 1+\frac {\partial}{\partial I_{D_{H}}} (- \lambda _{4}f_{4}-\lambda _{5}f_{5}-\lambda _{6}f_{6}-\lambda _{7}f_{7}- \lambda _{8}f_{8} ) \\& \hphantom{\dot{\lambda _{4}}}= 1+\lambda _{4}\mu _{H}+ \bigl(1-u(t) \bigr) \biggl( \lambda _{4}\gamma _{H_{2}}- \lambda _{5}\rho \gamma _{H_{2}}-\lambda _{6}\gamma _{H_{2}}(1-\rho )+( \lambda _{7}-\lambda _{8})\beta _{V}\frac {S_{V}}{N_{V}}I_{R_{H}} \biggr) \\& \dot{\lambda _{4}} = 1+\lambda _{4}\mu _{H}+ \bigl(1-u(t) \bigr) \biggl(\lambda _{4} \lambda _{H_{2}}-\lambda _{5}\rho \lambda _{H_{2}}-\lambda _{6}(1- \rho ) \gamma _{H_{2}}+(\lambda _{7}-\lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}I_{R_{H}} \biggr) \\& \dot{\lambda _{5}} = \frac {\partial}{\partial R_{H}} (-\lambda _{5}f_{5} ), \\& \dot{\lambda _{5}} = \lambda _{5}\mu _{H} \\& \dot{\lambda _{6}} = \frac {\partial}{\partial D_{H}} (-\lambda _{6}f_{6} ), \\& \dot{\lambda _{6}} = 0, \\& \dot{\lambda _{7}} = \frac {\partial}{\partial S_{V}} (-\lambda _{7}f_{7}- \lambda _{8}f_{8} ) \\& \hphantom{\dot{\lambda _{7}}}= \lambda _{7}\mu _{V}+ \bigl(1-u(t) \bigr) \biggl(\lambda _{7}\beta _{V} \frac {1}{N_{V}}(I_{R{H}}+I_{D_{H}})- \lambda _{8}\beta _{V} \frac {1}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \biggr), \\& \dot{\lambda _{7}} = \lambda _{7}\mu _{V}+ \bigl(1-u(t) \bigr) (\lambda _{7}- \lambda _{8})\beta _{V}\frac {1}{N_{V}}(I_{R_{H}}+I_{D_{H}}), \\& \dot{\lambda _{8}} = 1+\frac {\partial}{\partial I_{V}} (- \lambda _{1} f_{1}-\lambda _{2}f_{2}-\lambda _{8}f_{8} ) \\& \hphantom{\dot{\lambda _{8}}} = 1+ \bigl(1-v(t) \bigr) \biggl(\lambda _{1}\beta _{H} \frac {S_{H}}{N_{H}}- \lambda _{2}\beta _{H} \frac {S_{H}}{N_{H}} \biggr), \\& \dot{\lambda _{8}} = 1+\lambda _{8}\mu _{V}+ \bigl(1-v(t) \bigr) (\lambda _{1}- \lambda _{2})\beta _{H}\frac {S_{H}}{N_{H}}. \end{aligned}$$

The condition of transversality at final time $t_{f}$ is $p(t_{f})=0$. Then

$$p(t_f)=0⟹\{\begin{array}{c}{\lambda }_1(t_f)=0,\hfill \\ {\lambda }_2(t_f)=0,\hfill \\ {\lambda }_3(t_f)=0,\hfill \\ {\lambda }_4(t_f)=0,\hfill \\ {\lambda }_5(t_f)=0,\hfill \\ {\lambda }_6(t_f)=0,\hfill \\ {\lambda }_7(t_f)=0,\hfill \\ {\lambda }_8(t_f)=0.\hfill \end{array}$$

(30)

Finally, the characteristics of the vector

$$p(\cdot ):t \longmapsto \bigl(\lambda _{1}(t),\lambda _{2}(t),\lambda _{3}(t), \lambda _{4}(t),\lambda _{5}(t),\lambda _{6}(t),\lambda _{7}(t), \lambda _{8}(t) \bigr) $$

are

$$\begin{aligned} \textstyle\begin{cases} \dot{\lambda _{1}} = +\lambda _{1}\mu _{H}+ \beta _{H} \frac {\lambda _{1}-\lambda _{2}}{N_{H}}(1-v(t))I_{V}, \\ \dot{\lambda _{2}} = \lambda _{2}\mu _{H}+(\lambda _{2}-\lambda _{3}) \eta _{H} \\ \dot{\lambda _{3}} = 1+\lambda _{3}\mu _{H}+(1-u(t)) (\lambda _{3} \gamma _{H_{1}}-\lambda _{4}(1-\theta )\gamma _{H_{1}}-\lambda _{5} \theta \gamma _{H_{1}}+(\lambda _{7}-\lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{4}} = 1+\lambda _{4}\mu _{H}+(1-u(t)) (\lambda _{4} \gamma _{H_{2}}-\lambda _{5}\rho \gamma _{H_{2}}-\lambda _{6}\gamma _{H_{2}}(1- \rho )+(\lambda _{7}-\lambda _{8})\beta _{V}\frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{5}} = \lambda _{5}\mu _{H}, \\ \dot{\lambda _{6}} = 0, \\ \dot{\lambda _{7}} = \lambda _{7}\mu _{V}+(\lambda _{7}-\lambda _{8})(1-u(t)) \beta _{V}\frac {1}{N_{V}}(I_{R_{H}}+I_{D_{H}}), \\ \dot{\lambda _{8}} = 1+\lambda _{8}\mu _{V}+(\lambda _{1}-\lambda _{2})(1-v(t)) \beta _{H}\frac {S_{H}}{N_{H}}, \\ \lambda _{i}(t_{f}) = 0 \quad \forall i \in \{1,2,\ldots,8\}. \end{cases}\displaystyle \end{aligned}$$

(31)

 □

Theorem 7.2

(Characterization of optimal control)

The optimal control $(\bar{u},\bar{v})$ is defined by

$$ \bar{u}=\min \biggl(1, \max \biggl(0,\frac {N(\bar{X}(t))}{A_{1}} \biggr) \biggr), $$

where

$$\begin{aligned} N \bigl(X(t) \bigr) =&-\lambda _{3}\gamma _{H_{1}}I_{R_{H}}+ \lambda _{4} \bigl((1- \theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr)+\lambda _{5}( \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}) \\ &{}+\lambda _{6}(1-\rho )\gamma _{H_{2}}I_{D_{H}}-( \lambda _{7}- \lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \end{aligned}$$

and

$$ \bar{v}=\min \biggl(1, \max \biggl(0, \frac {\lambda _{2}-\lambda _{1}}{A_{2}} \frac {\beta _{H}S_{H}I_{V}}{N_{H}} \biggr) \biggr). $$

Proof

To prove the characterizations of optimal control, we define the Lagrangian associated with the problem. It corresponds to Hamiltonian increased by coefficients of penalty.

$$ L(t,X,u,v,p)=H \bigl(t,X,p,p^{0},u,v \bigr)+w_{11}u+w_{12}(1-u)+w_{21}v+w_{22}(1-v), $$

where $w_{ij}(t) \geqslant 0$ are penalization coefficients that verify

$$ w_{11}u(t)=w_{12} \bigl(1-u(t) \bigr)=0\quad \text{for the control } \bar{u} $$

and

$$ w_{21}v(t)=w_{22} \bigl(1-v(t) \bigr)=0 \quad \text{for the control } \bar{v}. $$

The optimal control $(\bar{u},\bar{v})$ obtained is the resultant of application of equations of constraint

$$ \textstyle\begin{cases} \frac {\partial L}{\partial u}=0 & \text{in } \bar{u}, \\ \frac {\partial L}{\partial v}=0 & \text{in } \bar{v}, \end{cases} $$

that imply

$$ \textstyle\begin{cases} \frac {\partial H}{\partial u}-w_{11}+w_{12}=0 & \text{in } \bar{u}, \\ \frac {\partial H}{\partial v}-w_{21}+w_{22}=0 & \text{in } \bar{v}. \end{cases} $$

The partial derivative of H in relation to u is given by

$$\begin{aligned}& \frac {\partial H}{\partial u} \bigl(t,X,p,p^{0},u,v \bigr) \\& \quad = \frac {\partial}{\partial u} \Biggl( I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t)+ \sum_{i=1}^{8}\lambda _{i}f_{i} \Biggr) \\& \quad = A_{1}u+\frac {\partial}{\partial u} ( \lambda _{3}f_{3}+ \lambda _{4}f_{4}+\lambda _{5}f_{5}+ \lambda _{6}f_{6}+\lambda _{7}f_{7}+ \lambda _{8}f_{8} ) \\& \frac {\partial H}{\partial u} \bigl(t,X,p,p^{0},u,v \bigr) \\& \quad = A_{1}u+ \lambda _{3}( \gamma _{H_{1}}I_{R_{H}})- \lambda _{4} \bigl((1-\theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr)-\lambda _{5}(\theta \gamma _{H_{1}}I_{R_{H}}+ \rho \gamma _{H_{2}}I_{D_{H}}) \\& \qquad {} - \lambda _{6}(1-\rho )\gamma _{H_{2}}I_{D_{H}}+( \lambda _{7}- \lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}). \end{aligned}$$

The partial derivative of H in relation to v is given by

$$\begin{aligned}& \frac {\partial H}{\partial v} \bigl(t,X,p,p^{0},u,v \bigr) = \frac {\partial}{\partial u} \Biggl( I_{R_{H}}(t)+I_{D_{H}}(t)+I_{V}+ \frac{A_{1}}{2}u^{2}(t)+\frac{A_{2}}{2}v^{2}(t)+ \sum_{i=1}^{8}\lambda _{i}f_{i} \Biggr) \\& \hphantom{\frac {\partial H}{\partial v} (t,X,p,p^{0},u,v )}= A_{2}v+\frac {\partial}{\partial v} ( \lambda _{1}f_{1}+ \lambda _{2}f_{2} ) \\& \frac {\partial H}{\partial v} \bigl(t,X,p,p^{0},u,v \bigr) = A_{2}v+( \lambda _{1}- \lambda _{2})\beta _{H} \frac {S_{H}}{N_{H}}I_{V}. \end{aligned}$$

We obtain

$$ \textstyle\begin{cases} A_{1}u(t)+M(X(t))-w_{11}+w_{12}=0 \quad \text{for } u=\bar{u}, \\ A_{2}v(t)+(\lambda _{1}-\lambda _{2})\beta _{H}\frac {S_{H}}{N_{H}}I_{V}-w_{21}+w_{22}=0 \quad \text{for } v=\bar{v}, \end{cases} $$

where

$$\begin{aligned} M \bigl(X(t) \bigr) =&\lambda _{3}(\gamma _{H_{1}}I_{R_{H}})- \lambda _{4} \bigl((1- \theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr)-\lambda _{5}( \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}) \\ &{}-\lambda _{6}(1-\rho )\gamma _{H_{2}}I_{D_{H}}+( \lambda _{7}- \lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \end{aligned}$$

and at ū and v̄, we have:

• $A_{1}\bar{u}(t)+M(\bar{X}(t))-w_{11}+w_{12}=0$

  $$ \bar{u}=\frac {1}{A_{1}} \bigl(-M \bigl(\bar{X}(t) \bigr)+w_{11}-w_{12} \bigr) $$

• $A_{2}\bar{v}(t)+(\lambda _{1}-\lambda _{2})\beta _{H} \frac {\bar{S}_{H}}{\bar{N}_{H}}I_{V}+w_{21}-w_{22}=0$

  $$ \bar{v}=\frac {1}{A_{2}} \biggl((\lambda _{2}-\lambda _{1})\beta _{H} \frac {\bar{S}_{H}}{\bar{N}_{H}}\bar{I}_{V}-w_{21}+w_{22} \biggr). $$

Let be the set $\{t: 0<\bar{u}<1 \}$. We have

$$\begin{aligned}& w_{11}\bar{u}=w_{12}(1-\bar{u})\quad \Rightarrow\quad w_{11}=w_{12}=0,\quad \text{therefore} \\& \bar{u}= \frac {-M(\bar{X}(t))}{A_{1}}. \end{aligned}$$

Let be the set $\{t:\bar{u}=0\}$.

We have $w_{12}(1-\bar{u})=0 \Rightarrow w_{12} =0$, therefore

$$ 0=\bar{u}=\frac {-M(\bar{X}(t))+w_{11}}{A_{1}}. $$

Since $w_{11} \geqslant 0$, then $\frac {-M(\bar{X}(t))}{A_{1}} \leqslant \bar{u}=0$.

Thus, on the set $\{t: 0\leqslant \bar{u}<1 \}$, ū is defined as follows:

$$ \max \biggl(0,\frac {-M(\bar{X}(t))}{A_{1}} \biggr). $$

Let be the set $\{t:\bar{u}=1\}$. We have

$$w_{11}\times 1=w_{12}\times 0=0\quad \Rightarrow\quad w_{11}=0, \quad \text{then } 1=\bar{u}=\frac {-M(\bar{X}(t))-w_{12}}{A_{1}}. $$

Since $w_{12} \geqslant 0$, then $\frac {-M(\bar{X}(t))}{A_{1}}\bar{u}=1$.

On the set $\{t: 0 \leqslant \bar{u} \leqslant 1 \}$, ū is defined by

$$ \bar{u}=\min \biggl(1, \max \biggl(0,\frac {-M(\bar{X}(t))}{A_{1}} \biggr) \biggr). $$

By the same method, we get the expression of v̄:

$$ \bar{v}=\min \biggl(1, \max \biggl(0, \frac {-M(\bar{X}(t))}{A_{1}} \biggr) \biggr). $$

Finally, on the set U, the optimal control $(\bar{u},\bar{v})$ is given by

$$ \bar{u}=\min \biggl(1, \max \biggl(0,\frac {N(\bar{X}(t))}{A_{1}} \biggr) \biggr), $$

where

$$\begin{aligned}& N \bigl(X(t) \bigr) = -M \bigl(X(t) \bigr) \\& N \bigl(X(t) \bigr) = -\lambda _{3}\gamma _{H_{1}}I_{R_{H}}+ \lambda _{4} \bigl((1- \theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr)+\lambda _{5}( \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}) \\& \hphantom{N (X(t) ) =}{} + \lambda _{6}(1-\rho )\gamma _{H_{2}}I_{D_{H}}-( \lambda _{7}- \lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}) \end{aligned}$$

and

$$ \bar{v}=\min \biggl(1, \max \biggl(0, \frac {\lambda _{2}-\lambda _{1}}{A_{2}} \frac {\beta _{H}S_{H}I_{V}}{N_{H}} \biggr) \biggr). $$

 □

7.2 Numerical simulations

In this section, the optimal system and the results of simulations obtained by Python 3.7 (see the Annex) are presented. The optimal system is given by

$$\begin{aligned} \textstyle\begin{cases} \dot{S}_{H}(t) = \Lambda _{H}-\beta _{H}\frac {S_{H}}{N_{H}}(1- v(t))I_{V}-\mu _{H}S_{H}, \\ \dot{E}_{H}(t) = \beta _{H}\frac {S_{H}}{N_{H}}(1- v(t))I_{V} -(\mu _{H}+\eta _{H})E_{H}, \\ \dot{I}_{R_{H}}(t) = \eta _{H}E_{H}-\gamma _{H_{1}}(1- u(t))I_{R_{H}}-\mu _{H}I_{R_{H}}, \\ \dot{I}_{D_{H}}(t) = (1-u(t)) [ (1-\theta ) \gamma _{H_{1}}I_{R_{H}}-\gamma _{H_{2}}I_{D_{H}} ]-\mu _{H}I_{D_{H}}, \\ \dot{R}_{H}(t) = (1-u(t)) [\theta \gamma _{H_{1}}I_{R_{H}}+ \rho \gamma _{H_{2}}I_{D_{H}} ]-\mu _{H}R_{H}, \\ D_{H}(t) = (1-u(t))(1-\rho )\gamma _{H_{2}}I_{D_{H}}, \\ \dot{S}_{V}(t) = \Lambda _{V}-\beta _{V}\frac {S_{V}}{N_{V}}(1- u(t))(I_{R_{H}}+I_{D_{H}})-\mu _{V}S_{V}, \\ \dot{I}_{V}(t) = \beta _{V}\frac {S_{V}}{N_{V}}(1- u(t))(I_{R_{H}}+I_{D_{H}})-\mu _{V}I_{V}, \\ \dot{\lambda _{1}} = \beta _{H} \frac {\lambda _{1}-\lambda _{2}}{N_{H}}(1-v(t))I_{V}+\lambda _{1} \mu _{H}, \\ \dot{\lambda _{2}} = (\lambda _{2}-\lambda _{3})\eta _{H}+\lambda _{2} \mu _{H}, \\ \dot{\lambda _{3}} = 1+\lambda _{3}\mu _{H}+(1-u(t)) (\lambda _{3} \gamma _{H_{1}}-\lambda _{4}(1-\theta )\gamma _{H_{1}}-\lambda _{5} \theta \gamma _{H_{1}}+(\lambda _{7}-\lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{4}} = 1+\lambda _{4}\mu _{H}+(1-u(t)) (\lambda _{4} \gamma _{H_{2}}-\lambda _{5}\rho \gamma _{H_{2}}-\lambda _{6}\gamma _{H_{2}}(1- \rho )+(\lambda _{7}-\lambda _{8})\beta _{V}\frac {S_{V}}{N_{V}} ), \\ \dot{\lambda _{5}} = \lambda _{5}\mu _{H}, \\ \dot{\lambda _{6}} = 0, \\ \dot{\lambda _{7}} = \lambda _{7}\mu _{V}+(\lambda _{7}-\lambda _{8})(1-u(t)) \beta _{V}\frac {1}{N_{V}}(I_{R_{H}}+I_{D_{H}}), \\ \dot{\lambda _{8}} = 1+\lambda _{8}\mu _{V}+(\lambda _{1}-\lambda _{2})(1-v(t)) \beta _{H}\frac {S_{H}}{N_{H}}, \\ \lambda _{i}(t_{f}) = 0 \quad \forall i \in \{1,2,\ldots,8\}, \\ \bar{u} = \min (1, \max (0,\frac {N(\bar{X}(t))}{A_{1}} ) ), \\ \bar{v} = \min (1,\max (0, \frac {\lambda _{2}-\lambda _{1}}{A_{2}} \frac {\beta _{H}S_{H}I_{V}}{N_{H}} ) ) \end{cases}\displaystyle \end{aligned}$$

(32)

with

$$\begin{aligned} N \bigl(X(t) \bigr) =&-\lambda _{3}\gamma _{H_{1}}I_{R_{H}}+ \lambda _{4} \bigl((1- \theta )\gamma _{H_{1}}I_{R_{H}}- \gamma _{H_{2}}I_{D_{H}} \bigr)+\lambda _{5}( \theta \gamma _{H_{1}}I_{R_{H}}+\rho \gamma _{H_{2}}I_{D_{H}}) \\ &{}+\lambda _{6}(1-\rho )\gamma _{H_{2}}I_{D_{H}}-( \lambda _{7}- \lambda _{8})\beta _{V} \frac {S_{V}}{N_{V}}(I_{R_{H}}+I_{D_{H}}). \end{aligned}$$

With the values of Table 1, we obtain the following curves:

Comments

Figure 7(a) shows in orange color the susceptible population when there are treatment and prevention ($u \neq 0$ and $v \neq 0$) and in blue color the susceptible population when there are no treatment and prevention ($u=0$ and $v=0$). This shows that without treatment and prevention people leave the susceptible compartment for the exposed compartment.

Figure 7

Humans and vectors dynamics with and without control (u(t);v(t))

Figures 7(c), 7(d), and 7(h) represent the different dynamics of infected vectors and infected people. The orange color curves represent the dynamics when there are treatment and prevention ($u \neq 0$ and $v \neq 0$) and the blue curve represents the population when there are no vaccination and treatment ($u=0$ and $v=0$). This shows that without prevention and treatment infected individuals will be more numerous.

Again using the data in Table 1, we present the curves expressing the dynamics in the different infectious classes.

Curves (a), (b), and (c) in Fig. 8 show the population dynamics of infected humans in single cases, infected humans in severe cases, and infected vectors (mosquitoes) as a function of time, respectively.

Figure 8

Dynamics of infectious classes with v(t) and with (u(t);v(t))

In each of the three subfigures, it can be seen that when prevention alone is applied, the trend is the same as when both prevention and treatment are applied. In fact, when prevention alone is applied, the infectious classes tend towards zero after a certain time. When treatment is added, the number of individuals in the infectious classes continues to tend towards zero, but after a shorter time.

8 Conclusion

In our paper, we worked on an SEIR-SI model of dengue fever in a population regularly affected by this disease. There are considerable hemorrhagic cases of the dengue disease because of the regularity of the disease. We took full account of the hemorrhagic cases of dengue denoted by $I_{D_{H}}$. We have shown the global stability of the equilibrium points depending on whether $\mathcal{R}_{0}$ is greater or less than 1. Moreover, to corroborate the theoretical study, we presented numerical simulations using Python. We then calculated the sensitivity of each parameter affecting the basic reproduction number $\mathcal{R}_{0}$. We found that a variation of $+1\%$ in each of the parameters $\beta _{H}$, $\beta _{V}$, $\eta _{H}$, $\gamma _{H_{1}}$ separately increases the value of $\mathcal{R}_{0}$ and a variation of $+1\%$ in each of the parameters $\mu _{H}$, $\mu _{V}$, θ, $\gamma _{H_{2}}$ decreases the value of $\mathcal{R}_{0}$. Also, $\gamma _{H_{1}}$ and $\mu _{H}$ when varied by $+1\%$ are respectively the parameters that have the most positive and negative influence on the value of $\mathcal{R}_{0}$. Finally, optimal control work was carried out for finding how the optimal pair $(u(t);v(t))$ is able to drastically reduce the spread of dengue in a population regularly affected by this disease.

Appendices

Annex

Numerical method with python 3.7

In first, we implement (2), the model without control by using the function odeint of PYTHON. We obtain for example

$$\begin{aligned} \operatorname{def} F0(Y,t) :& \\ f =& [f_{1}, \\ & f_{2}, \\ & f_{3}, \\ & f_{4}, \\ & f_{5}, \\ & f_{6}, \\ & f_{7}, \\ & f_{8},] \\ \text{return } f & \\ \operatorname{sol} =& \operatorname{odeint}(F0,Y0,T), \end{aligned}$$

where Y0 is the initial condition and T is the time.

Secondly, we implement model (32) by using the method of shoot [22]. Let

$$ \textstyle\begin{cases} y=(S_{H},E_{H},I_{R_{H}},I_{D_{H}},R_{H},S_{V},I_{V},\lambda _{1},\ldots, \lambda _{8}) \\ y=(y_{1},y_{2},y_{3},y_{4},y_{5},y_{6},y_{7},y_{8},y_{9},y_{10},\ldots,y_{15},y_{16}). \end{cases} $$

(33)

By re-writing model (32), we get the two point boundary value problem

$$ \textstyle\begin{cases} \dot{y}(t)=F(t,y(t)), \\ y(0)=(S_{H}^{0},E_{H}^{0},I_{R_{H}}^{0},I_{D_{H}}^{0},R_{H}^{0}D_{H}^{0},S_{V}^{0},I_{V}^{0}, \lambda _{1}(0),\ldots,\lambda _{8}(0)))=y^{0}, \\ y(T)=(S_{H}(T),E_{H}(T),\ldots,D_{H}(T),S_{V}(T),I_{V}(T),0,\ldots,0)=y^{T}. \end{cases} $$

(34)

The solution of (34) depends on T and $y^{0}$, and is written $y(T,y^{0})$. At final time T,

$$ y \bigl(T,y^{0} \bigr)=y(T), $$

(35)

and this means

$$ y \bigl(T,y^{0} \bigr)-y(T)=0. $$

(36)

By posing $G(y^{0})=y(T,y^{0})-y(T)$, the problem becomes:

Find $y_{0}$ such that

$$ G \bigl(y^{0} \bigr)=0. $$

(37)

Solving the system of differential equations (34) is the same as finding a zero of the firing function $G(y^{0})$. This is possible with the fsolve function in Python.