1 Introduction

Discussion of the mathematical modelings of processes is an interesting part of mathematics in which the mathematicians discuss behaviors of existing systems in terms of several mathematical and computational methods. In this regard, there is a vast range of fractional operators which have a vital role in modeling different phenomena. In fact, during the past years, a large number of mathematicians have formulated well-defined operators for their purposes. For the sake of having a high accuracy of the arbitrary order modelings rather than integer order ones, the fractional versions of these new operators have been welcomed nowadays. For instance, the Caputo and the Riemann–Liouville operators in the fractional frames have appeared repeatedly for modeling the complicated mathematical systems; see [1–12]. Later, a wide range of modelings were designed utilizing the Hadamard and Caputo–Hadamard fractional operators; see [13–18]. In early 2015, Caputo and Fabrizio [19] propounded a novel nonsingular derivative named the Caputo–Fabrizio operator, and immediately after them Nieto and Losada [20] turned to checking some flexible specifications of such newly defined nonsingular operator. The applicability of this operator was such that many newly designed mathematical models were formulated with respect to the mentioned nonsingular operator; see [21–23].

In 2017, a generalization of the Caputo fractional operator called the φ-Caputo derivative was introduced by Almeida [24] in which the kernel of this operator depends on an increasing function φ. By using this newly defined operator, a limited number of papers have been published so far; see [25–29].

Belmor et al. [30] formulated a φ-fractional differential inclusion subject to φ-integral conditions as

$$ \textstyle\begin{cases} {}^{\mathcal{C}}\mathfrak{D}_{0^{+}}^{ \varsigma ^{*}; \varphi } \phi (s) \in \breve{\mathfrak{E}} (s, \phi (s)), \quad (0 \leq s\leq l), \\ \phi (0) - \delta ^{*}_{\varphi }\phi (0) = a^{*} {}^{\mathcal{RL}} \mathcal{I}_{0^{+}}^{\theta ; \varphi } \tilde{g}_{*}^{1}(p_{1}, \phi (p_{1})), \\ \phi (l) - \delta ^{*}_{\varphi }\phi (l) = b^{*} {}^{\mathcal{RL}} \mathcal{I}_{0^{+}}^{\mu ; \varphi } \tilde{g}_{*}^{2}(p_{2}, \phi (p_{2})), \end{cases} $$

where \(1 < \varsigma ^{*} < 2\), \(0 \leq p_{1} , p_{2} \leq 1\) and the constants \(a^{*}\), \(b^{*}\) are chosen arbitrarily and furthermore \(\breve{\mathfrak{E}}: [0,l]\times \mathbb{R} \to \mathfrak{P}( \mathbb{R})\) stands for a multifunction where \(\mathfrak{P}(\mathbb{R})\) denotes the family of all nonempty subsets of \(\mathbb{R}\) and \(\tilde{g}_{*}^{1} , \tilde{g}_{*}^{2}: [0,l]\times \mathbb{R} \to \mathbb{R}\) are continuous and \(\delta ^{*}_{\varphi }= \frac{1}{\varphi '(s)} \frac{\mathrm{d}}{\mathrm{d}s} \). The authors obtained the relevant criteria for the existence by utilizing the endpoint notion for ψ-weak contractions due to Moradi [31].

In the light of the new operator introduced in [24] and motivated by the aforementioned work, we design the following φ-Caputo differential inclusion boundary value problem:

$$ {}^{\mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*};\varphi } \phi (s) \in \breve{\mathfrak{E}} \bigl(s , \phi (s) \bigr), \quad \bigl(s\in [a,M], a \geq 0 \bigr), $$
(1)

supplemented with mixed integro-derivative conditions in the frame of the φ-Riemann–Liouville operators

$$ \textstyle\begin{cases} \phi (a) = \mu _{1}^{*} + {}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma _{1}; \varphi } \phi ( \xi ), \\ \phi (M) = \mu _{2}^{*} + \frac{1}{\Gamma (\varsigma _{2})} \int _{a}^{\sigma }\varphi '(r) ( \varphi (\sigma ) - \varphi (r))^{\varsigma _{2}-1}\phi (r)\,\mathrm{d}r, \end{cases} $$
(2)

so that \(1 < \varsigma ^{*} <2\), \(0 < \varsigma _{1} \leq 1\), \(\varsigma _{2} >0\) and \({}^{\mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*};\varphi }\) stands for the \(\varsigma ^{*}\)th φ-Caputo derivative with respect to an increasing function φ and \({}^{\mathcal{RL}}\mathcal{D}_{a}^{\varsigma _{1};\varphi }\) is the \(\varsigma _{1}\)th φ-Riemann–Liouville derivative and \({}^{\mathcal{RL}}\mathcal{I}_{a}^{\varsigma _{2};\varphi }\) indicates the \(\varsigma _{2}\)th φ-Riemann–Liouville integral. Besides, \(\mu _{1}^{*} , \mu _{2}^{*} \in \mathbb{R} \), \(\xi , \sigma \in (a,M)\) and \(\breve{\mathfrak{E}} : [a,M]\times \mathbb{R} \to \mathfrak{P}( \mathbb{R}) \) is a multifunction furnished with some specifications which will be indicated later.

Our basic purpose in the current research is to derive existence aspects of solutions for the above general category of the fractional inclusion boundary value problem in terms of the well-defined generalized φ-Caputo and φ-Riemann–Liouville operators. The existing boundary conditions are considered as mixed generalized φ-Riemann–Liouville bound conditions. To obtain the desired existence criteria, we utilize analytical methods on α-ψ-contractive maps and multifunctions involving the approximate endpoint specification. We emphasize that this structure of the φ-Caputo inclusion problem and φ-Riemann–Liouville integro-derivative conditions is a general case based on an arbitrary increasing function φ and we can even extend our boundary conditions to multi-strip multi-point conditions in future work. So this problem is novel and unique in this respect.

We prepare the contents of this research paper by the following settings. Some applied properties and auxiliary issues are collected in Sect. 2. Next in Sect. 3, we employ two notions of endpoint and fixed point to derive the existence aspects corresponding to the φ-inclusion boundary value problem designed by (1)–(2). In the final section, we formulate an illustrative simulation model to examine theoretical findings computationally and numerically.

2 Auxiliary preliminaries

Here, we collect and review several fundamental notions in the framework of our analytical methods applied in this paper. As is well known, the concept of the \(\varsigma ^{*}\)th Riemann–Liouville integral of a continuous function \(\phi : \mathbb{R}^{\geq 0} \to \mathbb{R}\) is

$$ {}^{\mathcal{RL}}\mathcal{I}_{0}^{ \varsigma ^{*} } \phi (s) = \int _{0}^{s} \frac{(s - r )^{ \varsigma ^{*} -1 }}{\Gamma ( \varsigma ^{*} )} \phi (r) \,\mathrm{d}r, \quad \varsigma ^{*}>0 $$
(3)

when the right hand side integral exists finitely [32, 33]. From here onwards, let \(\varsigma ^{*} \in (m-1 , m)\) with \(m = [ \varsigma ^{*} ] +1\). For a continuous function \(\phi : \mathbb{R}^{\geq 0} \to \mathbb{R}\), the \(\varsigma ^{*}\)th Riemann–Liouville derivative is represented by

$$ {}^{\mathcal{RL}}\mathcal{D}_{0}^{ \varsigma ^{*} } \phi (s) = \biggl( \frac{\mathrm{d}}{\mathrm{d}s} \biggr)^{m} \int _{0}^{s} \frac{(s - r )^{ m - \varsigma ^{*} -1 }}{\Gamma ( m - \varsigma ^{*} )} \phi (r) \,\mathrm{d}r $$
(4)

when the right hand side integral possesses finite values [32, 33]. In the next step, for an absolutely continuous function \(\phi \in AC^{(m)}_{\mathbb{R}}(\mathbb{R}^{\geq 0})\), the \(\varsigma ^{*}\)th Caputo derivative is

$$ {}^{\mathcal{C}}\mathcal{D}_{0}^{ \varsigma ^{*} } \phi (s) = \int _{0}^{s} \frac{(s - r)^{m- \varsigma ^{*} -1}}{\Gamma (m- \varsigma ^{*} )} \phi ^{(m)}(r)\,\mathrm{d} r $$
(5)

when the right hand side integral possesses values finitely [32, 33].

Definition 2.1

([33–35])

Let \(\varphi \in \mathcal{C}^{m}([a,b])\) be an increasing map so that \(\varphi '(s)> 0\) for any \(s\in [a,b]\). Then the \(\varsigma ^{*}\)th φ-Riemann–Liouville integral of an existing map \(\phi : [a,b] \to \mathbb{R}\) with respect to φ is defined as

$$ {}^{\mathcal{RL}}\mathcal{I}_{a}^{ \varsigma ^{*};\varphi } \phi (s) = \frac{1}{\Gamma ( \varsigma ^{*})} \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} -1 } \phi (r) \,\mathrm{d}r $$
(6)

provided that the right hand side of equality is finite-valued.

It is to be noted that, if \(\varphi (t) = t\), then clearly the φ-Riemann–Liouville integral (6) reduces to the standard Riemann–Liouville integral (3).

Definition 2.2

([33–35])

Let \(m = [ \varsigma ^{*} ] +1\). For a real mapping \(\phi \in \mathcal{C}(\mathbb{R}^{\geq 0})\), the \(\varsigma ^{*}\)th φ-Riemann–Liouville derivative with respect to φ is formulated as

$$ {}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma ^{*};\varphi } \phi (s) = \frac{1}{\Gamma (m- \varsigma ^{*})} \biggl( \frac{1}{\varphi '(s)} \frac{\mathrm{d}}{\mathrm{d}s} \biggr)^{m} \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ m-\varsigma ^{*} -1 } \phi (r) \,\mathrm{d}r $$
(7)

provided that the right hand side of equality is finite-valued.

In the similar manner, if \(\varphi (t) = t\), then it is obvious that the \(\varsigma ^{*}\)th φ-Riemann–Liouville derivative (7) reduces to the standard \(\varsigma ^{*}\)th Riemann–Liouville derivative (4). Inspired by these operators, Almeida presented a new φ-version of the Caputo derivative in the following formulation.

Definition 2.3

([24])

Let \(m = [ \varsigma ^{*} ] +1\) and \(\varphi \in \mathcal{C}^{m}([a,b])\) be an increasing map with \(\varphi '(s)> 0\) for any \(s\in [a,b]\). The φ-version of the \(\varsigma ^{*}\)th Caputo derivative of the absolutely continuous function ϕ with respect to φ is

$$ {}^{\mathcal{C}}\mathcal{D}_{a}^{ \varsigma ^{*};\varphi } \phi (s) = \frac{1}{\Gamma ( {m} - \varsigma ^{*})} \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ { m}-\varsigma ^{*} -1 } \biggl( \frac{1}{\varphi '(r)} \frac{\mathrm{d}}{\mathrm{d}r} \biggr)^{ {m } } \phi (r) \,\mathrm{d}r $$
(8)

when the right hand side of equality possesses values finitely.

It should be noted that, if \(\varphi (s) = s\), then it is obvious that the \(\varsigma ^{*}\)th φ-Caputo derivative (8) reduces to the standard \(\varsigma ^{*}\)th Caputo derivative (5). In the following, some useful specifications of the \(\varsigma ^{*}\)th φ-Caputo and \(\varsigma ^{*}\)th φ-Riemann–Liouville integro-derivative operators can be seen.

Proposition 2.4

([24, 33–35])

Let \(\varsigma ^{*} ,\beta ^{*} ,\varpi ^{*} > 0\) and \(\varphi \in \mathcal{C}^{m}([a,b])\) is assumed to be an increasing map with \(\varphi '(s)> 0\) for any \(a \leq s\leq b\). Then the following statements hold:

\(\mathrm{(i1)}\):

\({}^{\mathcal{RL}}\mathcal{I}_{a}^{ \varsigma ^{*};\varphi } ( {}^{ \mathcal{RL}}\mathcal{I}_{a}^{ \varpi ^{*};\varphi } \phi ) (s) = ( {}^{\mathcal{RL}}\mathcal{I}_{a}^{ \varsigma ^{*} + \varpi ^{*}; \varphi } \phi ) (s) \),

\(\mathrm{(i2)}\):

\({}^{\mathcal{RL}}\mathcal{I}_{a}^{ \varsigma ^{*}; \varphi } ( \varphi (s) - \varphi (a))^{\beta ^{*}} (y) = \frac{ \Gamma (\beta ^{*} + 1 ) }{ \Gamma ( \varsigma ^{*} + \beta ^{*} + 1 )} ( \varphi (y)- \varphi (a))^{ \varsigma ^{*} + \beta ^{*} } \),

\(\mathrm{(i3)}\):

\({}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma ^{*}; \varphi } ( \varphi (s) - \varphi (a))^{ \beta ^{*}}(y) = \frac{ \Gamma (\beta ^{*} + 1 ) }{ \Gamma ( \beta ^{*} - \varsigma ^{*} + 1 )} (\varphi (y) - \varphi (a))^{\beta ^{*} - \varsigma ^{*} }\), (\(\beta ^{*} > -1\)),

\(\mathrm{(i4)}\):

\({}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma ^{*};\varphi } ( {}^{ \mathcal{RL}}\mathcal{I}_{a}^{ \varpi ^{*};\varphi } \phi ) (s) = ( {}^{\mathcal{RL}}\mathcal{I}_{a}^{\varpi ^{*} - \varsigma ^{*}; \varphi } \phi ) (s) \), (\(\varsigma ^{*} < \varpi ^{*} \)).

Proposition 2.5

([24])

Let \(m = 1 + [ \varsigma ^{*} ] \) and \(\varphi \in \mathcal{C}^{m}([a,b])\) be same above. Then, for every \(\phi \in \mathcal{C}^{m-1} ([a,b])\), we have

$$ {}^{\mathcal{RL}}\mathcal{I}_{a}^{\varsigma ^{*};\varphi } \bigl( {}^{ \mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*} ;\varphi } \phi \bigr) (s) = \phi (s) - \sum_{j=0}^{m-1} \frac{ (\delta _{\varphi })^{j} \phi (a)}{ j!} \bigl(\varphi (s) - \varphi (a) \bigr)^{j} , \quad \biggl(\delta _{\varphi }= \frac{1}{\varphi '(s)} \frac{\mathrm{d}}{\mathrm{d}s} \biggr). $$

With due attention to the above proposition, it is simply found that the general series solution of \(({}^{\mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*};\varphi } \phi )(s) =0\) is given by

$$\begin{aligned} \phi (s) &= \sum_{j=0}^{m-1} d_{j}^{*} \bigl(\varphi (s) - \varphi (a) \bigr)^{j} \\ &= d_{0}^{*} + d_{1}^{*} \bigl(\varphi (s) - \varphi (a) \bigr) + d_{2}^{*} \bigl( \varphi (s) - \varphi (a) \bigr)^{2} + \cdots + d_{m-1}^{*} \bigl( \varphi (s) - \varphi (a) \bigr)^{ m-1 } , \end{aligned}$$

where \(m = 1 + [ \varsigma ^{*} ] \) and \(d_{0}^{*} , d_{1}^{*} ,\ldots , d_{m-1}^{*} \in \mathbb{R}\) [24]. In the subsequent stage, some concepts and the related specifications on the theory of multifunctions are reviewed.

Notation 2.6

Regard an ordered pair \((\mho , \Vert \cdot \Vert _{\mho })\) which represents a normed space. We mean by the notations \({\mathfrak{P}}( \mho )\), \(\mathfrak{P}_{bnd}( \mho )\), \(\mathfrak{P}_{cmp}( \mho )\), \(\mathfrak{P}_{cls}( \mho )\) and \(\mathfrak{P}_{cvx}( \mho )\) a representation of the category of all nonempty, all bounded, all compact, all closed and all convex subsets of ℧, respectively.

An element \(\phi ^{*}\in \mho \) is a fixed point of the given multifunction \(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}(\mho )\) whenever \(\phi ^{*}\in \breve{\mathfrak{E}}(\phi ^{*})\) [36]. We denote the collection of all existing fixed points of \(\breve{\mathfrak{E}} \) by the symbol \({\mathit{FIX}} (\breve{\mathfrak{E}})\) [36].

Definition 2.7

([36])

The Pompeiu–Hausdorff metric \(\mathrm{PH}_{d_{\mho }} : {\mathfrak{P}}(\mho ) \times {\mathfrak{P}}( \mho ) \to \mathbb{R}^{*} \) is constructed as follows:

$$ \mathrm{PH}_{d_{\mho }}(A_{1}, A_{2}) = \max \Bigl\{ \sup_{l_{1} \in A_{1}}d_{\mho }(l_{1},A_{2}), \sup_{l_{2} \in A_{2}}d_{\mho }(A_{1},l_{2}) \Bigr\} , $$

where \(d_{\mho }(A_{1},l_{2}) = \inf_{l_{1}\in A_{1}}d_{\mho }(l_{1},l_{2})\) and \(d_{\mho }(l_{1},A_{2}) = \inf_{l_{2}\in A_{2}}d_{\mho }(l_{1},l_{2})\).

Definition 2.8

([36])

An arbitrary multifunction \(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}_{cls}(\mho )\) is said to be Lipschitzian furnished with constant \(\tilde{\lambda }_{*} > 0 \) if

$$ \mathrm{PH}_{d_{\mho }} \bigl(\breve{\mathfrak{E}}(\phi ),\breve{ \mathfrak{E}} \bigl( \phi ' \bigr) \bigr) \leq \tilde{\lambda }_{*} d_{\mho } \bigl(\phi ,\phi ' \bigr) $$

is valid for each \(\phi , \phi ' \in \mho \). In addition, the given Lipschitz multifunction \(\breve{\mathfrak{E}} \) is named a contraction when \(0 < \tilde{\lambda }_{*} < 1 \).

Definition 2.9

([36, 37])

With due attention to the symbols in Notation 2.6, we have:

\(\mathrm{(i1)}\):

A multi-valued function \(\breve{\mathfrak{E}}\) is named completely continuous when \(\breve{\mathfrak{E}} (K)\) possesses the relative compactness specification for any \(K\in \mathfrak{P}_{bnd}(\mho )\).

\(\mathrm{(i2)}\):

\(\breve{\mathfrak{E}} : [0,1] \to \mathfrak{P}_{cls}(\mathbb{R})\) is named measurable when \(s \longmapsto d_{\mho }( \upsilon ,\breve{\mathfrak{E}}(s ))\) is a measurable map for all \(\upsilon \in \mathbb{R}\).

\(\mathrm{(i3)}\):

\(\breve{\mathfrak{E}}\) is a u.s.c. multifunction if, for any \(\phi ^{*} \in \mho \), \(\breve{\mathfrak{E}}(\phi ^{*})\) contained in \(\mathfrak{P}_{cls}(\mho )\) and for any open set \(\mathfrak{V}\) involving \(\breve{\mathfrak{E}}(\phi ^{*})\), a neighborhood \(\mathcal{G}_{0}^{*}\) of \(\phi ^{*}\) exists for which \(\breve{\mathfrak{E}}(\mathcal{G}_{0}^{*}) \subseteq \mathfrak{V}\).

\(\mathrm{(i4)}\):

\(\breve{\mathfrak{E}}: [0,1]\times \mathbb{R} \rightarrow \mathfrak{P}(\mathbb{R})\) is a multifunction of the Caratheodory type if \(s \mapsto \breve{\mathfrak{E}}(s ,\phi )\) is measurable for any \(\phi \in \mathbb{R}\) and \(\phi \mapsto \breve{\mathfrak{E}}(s ,\phi ) \) is u.s.c. for a.e. \(\phi \in [0,1]\).

\(\mathrm{(i5)}\):

A Caratheodory multifunction \(\breve{\mathfrak{E}}: [0,1]\times \mathbb{R} \rightarrow \mathfrak{P}(\mathbb{R})\) is named \(\mathcal{L}^{1}\)-Caratheodory if, for any \(\alpha >0\), a map \(\hslash _{\alpha }\in \mathcal{L}_{\mathbb{R}^{+}}^{1}([0,1])\) exists provided that

$$ \bigl\Vert \breve{\mathfrak{E}}(s ,\phi ) \bigr\Vert =\sup _{s \in [0,1]} \bigl\{ \vert y \vert : y \in \breve{\mathfrak{E}}(s , \phi ) \bigr\} \leq \hslash _{\alpha }(s ) $$

for every \(\vert \phi \vert \leq \alpha \) and for a.e. \(s \in [0,1]\).

\(\mathrm{(i6)}\):

\(\breve{\mathfrak{E}} \) has convex values if the set \(\breve{\mathfrak{E}}(\phi )\) is convex for every \(\phi \in \mho \).

The graph of the multifunction \(\breve{\mathfrak{E}}: \mho \to \mathfrak{P}_{cls}( \Omega )\) is constructed thus:

$$ \mathbb{G}(\breve{\mathfrak{E}})= \bigl\{ (\phi ,q)\in \mho \times \Omega : q\in \breve{\mathfrak{E}}(\phi ) \bigr\} . $$

Definition 2.10

([36, 37])

The graph \(\mathbb{G}(\breve{\mathfrak{E}})\) is closed whenever for both sequences \(\{ \phi _{n}\}_{n \geq 1} \subseteq \mho \) and \(\{q_{n}\}_{n \geq 1} \subseteq \Omega \) with \(\phi _{n} \to \phi _{0}\), \(q_{n} \to q_{0}\) and \(q_{n} \in \breve{\mathfrak{E}}( \phi _{n})\), we have the inclusion \(q_{0} \in \breve{\mathfrak{E}}( \phi _{0})\).

By [36], it is found that, if \(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}_{cls}(\Omega )\) involves a u.s.c. specification, then \(\mathbb{G}(\breve{\mathfrak{E}})\) is closed contained in \(\mho \times \Omega \). In reverse, if \(\breve{\mathfrak{E}}\) possesses both specifications of the closed graph and the complete continuity, \(\breve{\mathfrak{E}}\) is u.s.c. [36]. In addition to these, a family of existing selections of \(\breve{\mathfrak{E}} \) at \(\phi \in \mathcal{C}_{\mathbb{R}}([0,1])\) is arranged as

$$ \mathfrak{S}_{\breve{\mathfrak{E}},\phi }:= \bigl\{ \hat{\hbar }^{*} \in \mathcal{L}_{\mathbb{R}}^{1} \bigl([0,1] \bigr): \hat{\hbar }^{*} (s)\in \breve{\mathfrak{E}} \bigl(s , \phi (s ) \bigr) \bigr\} $$

for a.e. \(s \in [0,1] \) [36, 37]. It should be noted that, for any \(\phi \in \mathcal{C}_{\mho }([0,1])\), \(\mathfrak{S}_{\breve{\mathfrak{E}},\phi }\neq \emptyset \) if \(\dim (\mho ) \) possesses a value finitely [36].

Samet and Vetro et al. [38] propounded a novel construction of nondecreasing maps say \(\psi : [0,\infty )\to [0,\infty )\) by Ψ. For such \(\psi \in \Psi \), \(\sum_{k=1}^{\infty }\psi ^{k}(s)<\infty \) holds and \(s > \psi (s)\) for any \(s \in \mathbb{R}^{> 0}\) [38]. After them in 2013, Mohammadi, Rezapour and Shahzad [39] extended this structure to multifunctions in general.

Definition 2.11

([39])

A given multifunction \(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}_{cls,bnd}(\mho )\) is named a α-ψ-contraction whenever

$$ \alpha \bigl(\phi ,\phi ' \bigr) \mathrm{PH}_{d_{\mho }} \bigl( \breve{\mathfrak{E}} \phi , \breve{\mathfrak{E}}\phi ' \bigr)\leq \psi \bigl(d_{\mho } \bigl(\phi ,\phi ' \bigr) \bigr) $$

is valid for each \(\phi , \phi '\in \mho \).

Definition 2.12

([39])

Regard ℧ as a normed space. In this case:

\(\mathrm{(i1)}\):

We say that ℧ possesses the specification \((C_{\alpha })\) if for any sequence \(\{ \phi _{n} \} \subseteq \mho \) with \(\phi _{n} \to \phi \) and \(\alpha (\phi _{n} , \phi _{n+1}) \geq 1\) for \(n\in \mathbb{N}\), a subsequence \(\{ \phi _{n_{j}} \}\) of \(\{ \phi _{n} \}\) exists for which \(\alpha (\phi _{n_{j}}, \phi )\geq 1\) for each \(j\in \mathbb{N}\).

\(\mathrm{(i2)}\):

\(\breve{\mathfrak{E}}\) is named an α-admissible whenever for any \(\phi \in \mho \) and \(\phi '\in \breve{\mathfrak{E}}(\phi )\) with \(\alpha (\phi ,\phi ')\geq 1\), an inequality \(\alpha (\phi ',\phi '')\geq 1\) is valid for each \(\phi ''\in \breve{\mathfrak{E}}(\phi ')\).

Definition 2.13

([40])

Regard ℧ as a normed space. In this case:

\(\mathrm{(i1)}\):

\(\phi \in \mho \) is named an endpoint of \(\breve{\mathfrak{E}}:\mho \to \mathfrak{P}(\mho )\) if \(\breve{\mathfrak{E}}(\phi )=\{ \phi \}\).

\(\mathrm{(i2)}\):

\(\mathfrak{E}\) possesses an approximate endpoint specification if \(\inf_{\phi \in \mho }\sup_{q\in \breve{\mathfrak{E}}\phi }d_{\mho }( \phi ,q)=0 \).

The next propositions are required logical tools for establishing the desired results in this research.

Proposition 2.14

([41])

Let a Banach space ℧ be separable and

\(\mathrm{(i1)}\):

\(\breve{\mathfrak{E}} : [0, 1] \times \mho \to \mathfrak{P}_{cmp,cvx}( \mho )\) be \(\mathcal{L}^{1}\)-Carathéodory;

\(\mathrm{(i2)}\):

a linear map \(\Delta : \mathcal{L}_{\mho }^{1}([0,1]) \to \mathcal{C}_{\mho }([0,1])\) be continuous.

Then \(\Delta \circ \mathfrak{S}_{\breve{\mathfrak{E}} } : \mathcal{C}_{ \mho }([0,1]) \to \mathfrak{P}_{cmp,cvx} ( \mathcal{C}_{\mho }([0,1]))\) is another multifunction in \([\mathcal{C}_{\mho }([0,1])]^{2} \) endowed with \(\phi \mapsto (\Delta \circ \mathfrak{S}_{\breve{\mathfrak{E}} }) ( \phi ) = \Delta ( \mathfrak{S}_{\breve{\mathfrak{E}} ,\phi })\) involving a closed graph specification.

Proposition 2.15

([39])

Let a metric space \((\mho ,d_{\mho })\) be complete and

\(\mathrm{(i1)}\):

a map α be nonnegative on \(\mho \times \mho \) and \(\psi \in \Psi \) be strictly increasing;

\(\mathrm{(i2)}\):

\(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}_{cls,bnd}(\mho )\) be α-admissible and α-ψ-contraction so that \(\alpha (\phi ,\phi ' )\geq 1\) for some \(\phi \in \mho \) and \(\phi ' \in \breve{\mathfrak{E}}(\phi )\).

Then \(\breve{\mathfrak{E}}\) possesses a fixed point if ℧ involves the specification \((C_{\alpha })\).

Proposition 2.16

([40])

Let a metric space \((\mho ,d_{\mho })\) be complete and

\(\mathrm{(i1)}\):

\(\psi : \mathbb{R}^{\geq 0} \to \mathbb{R}^{\geq 0} \) be u.s.c. equipped with the property \(\psi (s)< s\) and \(\liminf_{s\to \infty }(s-\psi (s))>0\) for all \(s \in \mathbb{R}^{>0}\);

\(\mathrm{(i2)}\):

\(\breve{\mathfrak{E}} : \mho \to \mathfrak{P}_{cls,bnd}(\mho )\) be such that \(\mathrm{PH}_{d_{\mho }}(\breve{\mathfrak{E}} \phi ,\breve{\mathfrak{E}} \phi ')\leq \psi (d_{\mho }(\phi ,\phi '))\) for any \(\phi ,\phi ' \in \mho \).

Then \(\breve{\mathfrak{E}}\) possesses an endpoint uniquely iff \(\breve{\mathfrak{E}} \) possesses an approximate endpoint specification.

3 Existence theorems

After presenting some required concepts in the previous two sections, we are going to indicate our desired existence theorems. To arrive at this goal, we define \(\Vert \phi \Vert _{\mho } = \sup_{ s\in [a,M] } \vert \phi (s) \vert \) for each member of the space \(\mho = \{ \phi (s): \phi (s) \in \mathcal{C}_{ \mathbb{R} }([a,M]) \}\). In this phase, \((\mho , \Vert \cdot \Vert _{\mho } )\) will be a Banach space. In addition to this, keep in mind the following for convenience:

$$\begin{aligned} & \mathfrak{O}_{0}^{*} := 1- \frac{(\varphi (\xi ) -\varphi (a))^{-\varsigma _{1}} }{\Gamma ( 1- \varsigma _{1}) }, \quad\quad \mathfrak{O}_{1}^{*} := \frac{(\varphi (\xi ) -\varphi (a))^{1-\varsigma _{1}} }{\Gamma ( 2- \varsigma _{1}) } , \\ & \mathfrak{O}_{2}^{*} := \frac{ (\varphi (\sigma ) -\varphi (a))^{ \varsigma _{2}} }{ \Gamma ( 1 + \varsigma _{2}) } - 1, \quad \quad \mathfrak{O}_{3}^{*} := \frac{ (\varphi (\sigma ) -\varphi (a))^{1+\varsigma _{2}} }{ \Gamma ( 2 + \varsigma _{2}) } - \bigl( \varphi (M) -\varphi (a) \bigr). \end{aligned}$$
(9)

In the subsequent stage, we derive an equivalent relation as an integral equation for the generalized φ-Caputo inclusion boundary value problem (1)–(2).

Lemma 3.1

Let \(1 < \varsigma ^{*} <2\), \(\varsigma _{1} \in (0, 1] \), \(\varsigma _{2} > 0 \), \(\mu _{1}^{*} , \mu _{2}^{*} \in \mathbb{R} \) and \(\breve{\varrho } \in \mho \). Then \(\phi _{0}\) satisfies the linear φ-Caputo differential equation

$$ {}^{\mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*};\varphi } \phi (s) = \breve{\varrho }(s) $$
(10)

furnished with φ-Riemann–Liouville conditions

$$ \textstyle\begin{cases} \phi (a) = \mu _{1}^{*} + {}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma _{1}; \varphi } \phi ( \xi ), \\ \phi (M) = \mu _{2}^{*} + \frac{1}{\Gamma (\varsigma _{2})} \int _{a}^{\sigma }\varphi '(r) ( \varphi (\sigma ) - \varphi (r))^{\varsigma _{2}-1}\phi (r)\,\mathrm{d}r, \end{cases} $$
(11)

if and only if \(\phi _{0}\) is a solution of the φ-Riemann–Liouville integral equation

$$\begin{aligned} \phi (s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{h}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{h}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{h}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{h}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s) \end{aligned}$$
(12)

so that \(\tilde{\mathfrak{B}}^{*}_{1}(s)\), \(\tilde{\mathfrak{B}}^{*}_{2}(s)\) and \(\tilde{\mathfrak{B}}^{*}_{3}(s)\) are three functions depending on a variable s endowed with the following rules:

$$\begin{aligned} &\tilde{\mathfrak{B}}^{*}_{1}(s) := \frac{1}{ \mathfrak{O}^{*}} \bigl( \mathfrak{O}^{*}_{1} + \mathfrak{O}^{*}_{0} \bigl( \varphi (s) - \varphi (a) \bigr) \bigr), \quad\quad \tilde{ \mathfrak{B}}^{*}_{2}(s) := \frac{1}{\mathfrak{O}^{*}} \bigl( \mathfrak{O}^{*}_{3} - \mathfrak{O}^{*}_{2} \bigl( \varphi (s) - \varphi (a) \bigr) \bigr), \\ & \tilde{\mathfrak{B}}^{*}_{3}(s) := \mu _{1}^{*} \tilde{\mathfrak{B}}^{*}_{2}(s) - \mu _{2}^{*} \tilde{\mathfrak{B}}^{*}_{1}(s) \end{aligned}$$
(13)

and \(\mathfrak{O}^{*} = \mathfrak{O}^{*}_{0}\mathfrak{O}^{*}_{3} + \mathfrak{O}^{*}_{1}\mathfrak{O}^{*}_{2} \neq 0\).

Proof

First \(\phi _{0}\) is assumed to satisfy the generalized φ-Caputo differential equation (10). Obviously, we have \({}^{\mathcal{C}}\mathcal{D}_{a}^{\varsigma ^{*};\varphi } \phi _{0}(s) = \breve{\varrho }(s) \). By taking the \(\varsigma ^{*}\)th φ-Riemann–Liouville integral on both sides of the latter relation, we obtain

$$ \phi _{0}(s) = \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r) \,\mathrm{d}r + c^{*}_{0} + c^{*}_{1} \bigl(\varphi (s) - \varphi (a) \bigr). $$
(14)

Now, we intend to seek unknown real constants \(c^{*}_{0}\) and \(c^{*}_{1}\). If we take the \(\varsigma _{1}\)th φ-Riemann–Liouville derivative and the \(\varsigma _{2}\)th φ-Riemann–Liouville integral in s on both sides of (14), respectively, we deduce that

$$\begin{aligned} {}^{\mathcal{RL}}\mathcal{D}_{a}^{\varsigma _{1};\varphi }\phi _{0}(s) &= \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} + c^{*}_{0} \frac{(\varphi (s) - \varphi (a))^{-\varsigma _{1}}}{\Gamma (1-\varsigma _{1})} + c^{*}_{1} \frac{ (\varphi (s) - \varphi (a))^{1-\varsigma _{1}} }{ \Gamma (2-\varsigma _{1}) } \end{aligned}$$

and

$$\begin{aligned} {}^{\mathcal{RL}}\mathcal{I}_{a}^{\varsigma _{2};\varphi }\phi _{0}(s) &= \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} + c^{*}_{0} \frac{(\varphi (s) - \varphi (a))^{\varsigma _{2}}}{\Gamma (1 + \varsigma _{2})} + c^{*}_{1} \frac{ (\varphi (s) - \varphi (a))^{1 + \varsigma _{2}} }{ \Gamma (2 + \varsigma _{2}) } . \end{aligned}$$

By virtue of the mixed generalized φ-Riemann–Liouville boundary value conditions, we get

$$ \mathfrak{O}^{*}_{0} c^{*}_{0} - \mathfrak{O}^{*}_{1}c^{*}_{1} = \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{\varrho }(r)\,\mathrm{d}r + \mu ^{*}_{1} $$
(15)

and

$$\begin{aligned} \mathfrak{O}^{*}_{2}c^{*}_{0} + \mathfrak{O}^{*}_{3}c^{*}_{1} &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} - \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{\varrho }(r)\,\mathrm{d}r - \mu ^{*}_{2} , \end{aligned}$$
(16)

where \(\mathfrak{O}^{*}_{0}\), \(\mathfrak{O}^{*}_{1}\), \(\mathfrak{O}^{*}_{2}\), \(\mathfrak{O}^{*}_{3}\) are arranged in (9). After doing some straightforward calculations on (15)–(16), we obtain

$$\begin{aligned} c^{*}_{0} &= \frac{1}{\mathfrak{O}^{*}} \biggl[ \mathfrak{O}^{*}_{3} \biggl( \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{\varrho }(r)\,\mathrm{d}r + \mu ^{*}_{1} \biggr) \\ &\quad {} + \mathfrak{O}^{*}_{1} \biggl( \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} - \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{\varrho }(r)\,\mathrm{d}r - \mu ^{*}_{2} \biggr) \biggr] \end{aligned}$$

and

$$\begin{aligned} c^{*}_{1} &= \frac{1}{\mathfrak{O}^{*}} \biggl[ - \mathfrak{O}^{*}_{2} \biggl( \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{\varrho }(r)\,\mathrm{d}r + \mu ^{*}_{1} \biggr) \\ &\quad {} + \mathfrak{O}^{*}_{0} \biggl( \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} - \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{\varrho }(r)\,\mathrm{d}r - \mu ^{*}_{2} \biggr) \biggr] . \end{aligned}$$

Now we insert \(c^{*}_{0}\) and \(c^{*}_{1}\) into (14). In this case, one may write

$$\begin{aligned} \phi _{0}(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \breve{\varrho }(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \breve{\varrho }(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

which illustrates that \(\phi _{0}\) satisfies (12). Conversely, we can simply see that \(\phi _{0}\) is a solution for the generalized φ-Caputo fractional boundary value problem (10)–(11) whenever \(\phi _{0}\) satisfies (12). This finishes the argument. □

Notation 3.2

For simplicity in some required calculations, set

$$\begin{aligned} & \bigl\vert \tilde{\mathfrak{B}}^{*}_{1}(s) \bigr\vert \leq \tilde{\mathfrak{B}}^{*}_{1} := \frac{1}{ \vert \mathfrak{O}^{*} \vert } \bigl( \bigl\vert \mathfrak{O}^{*}_{0} \bigr\vert \bigl( \varphi (M) - \varphi (a) \bigr) + \bigl\vert \mathfrak{O}^{*}_{1} \bigr\vert \bigr), \\ & \bigl\vert \tilde{\mathfrak{B}}^{*}_{2}(s) \bigr\vert \leq \tilde{\mathfrak{B}}^{*}_{2} := \frac{1}{ \vert \mathfrak{O}^{*} \vert } \bigl( \bigl\vert \mathfrak{O}^{*}_{2} \bigr\vert \bigl( \varphi (M) - \varphi (a) \bigr) + \bigl\vert \mathfrak{O}^{*}_{3} \bigr\vert \bigr), \\ & \bigl\vert \tilde{\mathfrak{B}}^{*}_{3}(s) \bigr\vert \leq \tilde{\mathfrak{B}}^{*}_{3} := \bigl\vert \mu _{1}^{*} \bigr\vert \tilde{\mathfrak{B}}^{*}_{2} + \bigl\vert \mu _{2}^{*} \bigr\vert \tilde{ \mathfrak{B}}^{*}_{1} , \\ & \mathfrak{Z}^{*} = \bigl(1 + \tilde{ \mathfrak{B} }^{*}_{1} \bigr) \frac{(\varphi (M) - \varphi (a))^{ \varsigma ^{*} }}{\Gamma ( \varsigma ^{*} +1) } + \tilde{ \mathfrak{B} }^{*}_{2} \frac{( \varphi (\xi ) - \varphi (a))^{\varsigma ^{*} - \varsigma _{1}} }{\Gamma ( \varsigma ^{*} - \varsigma _{1} +1)} + \tilde{ \mathfrak{B} }^{*}_{1} \frac{( \varphi (\sigma ) - \varphi (a) )^{\varsigma ^{*} + \varsigma _{2}} }{ \Gamma ( \varsigma ^{*} + \varsigma _{2} +1)} . \end{aligned}$$
(17)

Definition 3.3

The function \(\phi \in \mathcal{AC}_{\mathbb{R}} ([a,M])\) is defined as a solution for the generalized φ-Caputo inclusion boundary value problem (1)–(2) if an integrable function \(\hat{\hbar }^{*} \in \mathcal{L}^{1}_{\mathbb{R}}([a,M])\) exists provided that \(\hat{\hbar }^{*} \in \breve{\mathfrak{E}} (s , \phi (s) ) \) for a.e. \(s\in [a,M]\) and the mixed generalized φ-Riemann–Liouville boundary value conditions

$$ \textstyle\begin{cases} \phi (a) = \mu _{1}^{*} + {}^{\mathcal{RL}}\mathcal{D}_{a}^{ \varsigma _{1}; \varphi } \phi ( \xi ), \\ \phi (M) = \mu _{2}^{*} + \frac{1}{\Gamma (\varsigma _{2})} \int _{a}^{\sigma }\varphi '(r) ( \varphi (\sigma ) - \varphi (r))^{\varsigma _{2}-1}\phi (r)\,\mathrm{d}r, \end{cases} $$

hold and also, for any \(s\in [a,M] \),

$$\begin{aligned} \phi (s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s) \end{aligned}$$

is valid.

In the following, we denote the family of existing selections of \(\breve{\mathfrak{E}} \) for each \(\phi \in \mho \) by

$$ \mathfrak{S}_{ \breve{\mathfrak{E}} ,\phi }= \bigl\{ \hat{\hbar }^{*} \in \mathcal{L}^{1} \bigl([a,M] \bigr): \hat{\hbar }^{*} (s)\in \breve{\mathfrak{E}} \bigl(s , \phi (s) \bigr) \bigr\} $$

for a.e. \(s\in [a,M]\). In addition to this, we construct the multifunction \(\mathfrak{K}: \mho \to \mathfrak{P}(\mho )\) as

$$ \mathfrak{K}(\phi )= \bigl\{ g_{*} \in \mho : \text{there is } \hat{\hbar }^{*} \in \mathfrak{S}_{ \breve{\mathfrak{E}} ,\phi } \text{ s.t. } g_{*}(s) = f_{*}(s) \text{ for all }s\in [a,M] \bigr\} ,$$
(18)

in which

$$\begin{aligned} f_{*}(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s). \end{aligned}$$

Theorem 3.4

Let \(\breve{\mathfrak{E}} : [a,M] \times \mho \to \mathfrak{P}_{cmp}( \mho )\) be a compact multifunction along with the following hypotheses:

\((\mathfrak{C}1)\):

\(\breve{\mathfrak{E}} \) is bounded and integrable and \(\breve{\mathfrak{E}} (\cdot , \phi ): [a,M] \to \mathfrak{P}_{cmp} ( \mho )\) is a measurable set for any \(\phi \in \mho \);

\((\mathfrak{C}2)\):

\(\psi \in \Psi \) and \(\breve{c} \in \mathcal{C}_{\mathbb{R}^{\geq 0}}([a,M] )\) exist provided that

$$ \mathrm{PH}_{d_{\mho }} \bigl(\breve{\mathfrak{E}} (s,\phi ), \breve{\mathfrak{E}} \bigl(s,\phi ' \bigr) \bigr) \leq \breve{c} (s) \psi \bigl( \bigl\vert \phi -\phi ' \bigr\vert \bigr) \frac{ 1 }{ \mathfrak{Z}^{*} \Vert \breve{c} \Vert } $$
(19)

for any \(s\in [a,M] \) and \(\phi ,\phi ' \in \mho \) in which \(\sup_{s\in [a,M]} \vert \breve{c}(s) \vert = \Vert \breve{c} \Vert \) and \(\mathfrak{Z}^{*}\) is formulated by (17);

\((\mathfrak{C}3)\):

a real function \(\hat{\zeta } : \mathbb{R} \times \mathbb{R} \to \mathbb{R}\) exists with \(\hat{\zeta } ( \phi , \phi ' ) \geq 0 \) for any \(\phi ,\phi ' \in \mho \);

\((\mathfrak{C}4)\):

when the sequence \(\{ \phi _{n} \}_{n\geq 1} \subseteq \mho \) approaches ϕ and \(\hat{\zeta } ( \phi _{n}(s) , \phi _{n+1}(s) ) \geq 0 \) for all \(s\in [a,M]\) and \(n\geq 1\), then a subsequence \(\{ \phi _{n_{l}}\}_{l\geq 1} \) of \(\{ \phi _{n} \} \) exists so that \(\hat{\zeta } ( \phi _{n_{l}}(s) , \phi (s) ) \geq 0 \) for every \(s\in [a,M] \) and \(l\geq 1\);

\((\mathfrak{C}5)\):

two members \(\phi _{0}\in \mho \) and \(g_{*} \in \mathfrak{K}(\phi _{0})\) exist with \(\hat{\zeta } ( \phi _{0}(s) , g_{*} (s) ) \geq 0 \) for each \(s\in [a,M]\) in which \(\mathfrak{K}:\mho \to \mathfrak{P}(\mho )\) is the same multifunction regarded in (18);

\((\mathfrak{C}6)\):

for any functions \(\phi \in \mho \) and \(g_{*} \in \mathfrak{K}(\phi )\) furnished with the property \(\hat{\zeta } ( \phi (s) , g_{*} (s) ) \geq 0\), there exists \(f_{*}\in \mathfrak{K}(\phi )\) such that \(\hat{\zeta } ( g_{*}(s) , f_{*}(s) ) \geq 0\) for each \(s\in [a,M]\).

Then the generalized φ-Caputo inclusion boundary value problem (1)–(2) possesses at least one solution on \([a,M]\).

Proof

It is an obvious issue that each solution of the generalized φ-Caputo fractional inclusion boundary value problem (1)–(2) will be a fixed point of \(\mathfrak{K}: \mho \to \mathfrak{P}(\mho )\) as demonstrated by (18). By \((\mathfrak{C}1)\), the measurability of the multifunction \(s\mapsto \breve{\mathfrak{E}} (s , \phi (s) ) \) is simply deduced and so it possesses closed values for \(\phi \in \mho \). In consequence, \(\breve{\mathfrak{E}} \) involves the measurable selection and \(\mathfrak{S}_{\breve{\mathfrak{E}} ,\phi } \neq \emptyset \). In the current position, we first prefer to check that \(\mathfrak{K}(\phi )\) is a closed set contained in ℧ for any \(\phi \in \mho \). To confirm this issue, we regard a sequence \(\{ \phi _{n} \}_{n\geq 1}\) contained in \(\mathfrak{K}(\phi )\) which goes to ϕ. For all indices n, we pick out \(\hat{\hbar }^{*}_{n} \in \mathfrak{S}_{\breve{\mathfrak{E}} ,\phi }\) so that

$$\begin{aligned} \phi _{n}(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{n}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{n}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}_{n}(r) \,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}_{n}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

for almost all \(s\in [a,M]\). Because of the compactness of the mentioned multifunction \(\breve{\mathfrak{E}} \), one can (if necessary) obtain a convergent subsequence \(\{ \hat{\hbar }^{*}_{n} \}_{n\geq 1}\) which goes to some \(\hat{\hbar }^{*} \in \mathcal{L}^{1}([a,M] )\). Consequently, \(\hat{\hbar }^{*} \in \mathfrak{S}_{\breve{\mathfrak{E}} ,\phi }\) and so

$$\begin{aligned} \lim_{n\to \infty } \phi _{n}(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s) \\ &= \phi (s) \end{aligned}$$

for any \(s\in [a,M]\). By virtue of the latter argument, we conclude that \(\phi \in \mathfrak{K}(\phi )\) and then \(\mathfrak{K}\) possesses closed values. The hypothesis of the present theorem guarantees that \(\breve{\mathfrak{E}} \) is a compact multifunction. Accordingly, the boundedness of the set \(\mathfrak{K}(\phi )\) is simply realized for every \(\phi \in \mho \). In the following, we shall review that \(\mathfrak{K}\) is α-ψ-contractive. To verify this matter, we present a function, say \(\alpha :\mho \times \mho \to [0,\infty )\) as \(\alpha (\phi ,\phi ') =1\) if \(\hat{\zeta } ( \phi (s) , \phi '(s) ) \geq 0\) and also \(\alpha (\phi ,\phi ') =0\) otherwise. In addition, let \(\phi ,\phi '\in \mho \) and \(g_{*}^{\prime } \in \mathfrak{K}(\phi ')\). We have \(\hat{\hbar }^{*}_{1} \in \mathfrak{S}_{\breve{\mathfrak{E}} , \phi '}\) provided that

$$\begin{aligned} g_{*}^{\prime }(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}_{1}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

for all \(s\in [a,M] \). The given inequality (19) guarantees that

$$ \mathrm{PH}_{d_{\mho }} \bigl( \breve{\mathfrak{E}} \bigl(s , \phi (s) \bigr), \breve{\mathfrak{E}} \bigl(s , \phi '(s) \bigr) \bigr) \leq \breve{c}(s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{ 1 }{\mathfrak{Z}^{*} \Vert \breve{c} \Vert } $$

is valid for each \(\phi ,\phi '\in \mho \) along with the specification \(\hat{\zeta } ( \phi (s) , \phi '(s) ) \geq 0 \) for \(s\in [a,M] \). Consequently, \(f_{*}\in \breve{\mathfrak{E}} ( s , \phi (s) )\) exists with \(\vert \hat{\hbar }^{*}_{1}(s)- f_{*} \vert \leq \breve{c} (s) \psi ( \vert \phi (s)-\phi '(s) \vert ) \frac{1}{ \mathfrak{Z}^{*} \Vert \breve{c} \Vert } \). In the sequel, introduce a new multifunction \(\mathfrak{R}^{*} : [a,M] \to \mathfrak{P}(\mho )\) of the following structure:

$$ \mathfrak{R}^{*}(s) = \biggl\{ f_{*}\in \mho : \bigl\vert \hat{\hbar }^{*}_{1}(s)- f_{*} \bigr\vert \leq \breve{c} (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{ 1}{\mathfrak{Z}^{*} \Vert \breve{c} \Vert } \biggr\} $$

for any \(s\in [a,M] \). But \(\hat{\hbar }^{*}_{1}\) and \(p = \breve{c} \psi ( \vert \phi -\phi ' \vert ) \frac{ 1 }{\mathfrak{Z}^{*} \Vert \breve{c} \Vert } \) are measurable, thus we conclude that \(\mathfrak{R}^{*}(\cdot ) \cap \breve{\mathfrak{E}} ( \cdot , \phi ( \cdot ) )\) is measurable. To follow the rest of the argument, we pick out \(\hat{\hbar }^{*}_{2} \in \breve{\mathfrak{E}} (s , \phi (s) )\) provided that

$$ \bigl\vert \hat{\hbar }^{*}_{1}(s)- \hat{\hbar }^{*}_{2}(s) \bigr\vert \leq \breve{c} (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{ 1}{\mathfrak{Z}^{*} \Vert \breve{c} \Vert } $$

for all \(s\in [a,M] \). Now, define \(g_{*}^{\prime \prime } \in \mathfrak{K}(\phi )\) by

$$\begin{aligned} g_{*}^{\prime \prime }(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}_{2}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

for each \(s\in [a,M] \). In this phase, we have the following estimate:

$$\begin{aligned}& \bigl\vert g_{*}^{\prime }(s) - g_{*}^{\prime \prime }(s) \bigr\vert \\& \quad \leq \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \bigl\vert \hat{\hbar }^{*}_{1}(r) - \hat{\hbar }^{*}_{2}(r) \bigr\vert \,\mathrm{d}r \\& \quad \quad {} + \bigl\vert \tilde{ \mathfrak{B} }^{*}_{1}(s) \bigr\vert \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \bigl\vert \hat{\hbar }^{*}_{1}(r) - \hat{\hbar }^{*}_{2}(r) \bigr\vert \,\mathrm{d}r \\& \quad \quad {} + \bigl\vert \tilde{ \mathfrak{B} }^{*}_{2}(s) \bigr\vert \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \bigl\vert \hat{\hbar }^{*}_{1}(r) - \hat{\hbar }^{*}_{2}(r) \bigr\vert \,\mathrm{d}r \\& \quad \quad {} + \bigl\vert \tilde{ \mathfrak{B} }^{*}_{1}(s) \bigr\vert \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \bigl\vert \hat{\hbar }^{*}_{1}(r) - \hat{\hbar }^{*}_{2}(r) \bigr\vert \,\mathrm{d}r \\& \quad \leq \biggl[ \bigl(1 + \tilde{ \mathfrak{B} }^{*}_{1} \bigr) \frac{(\varphi (M) - \varphi (a))^{ \varsigma ^{*} }}{\Gamma ( \varsigma ^{*} +1) } + \tilde{ \mathfrak{B} }^{*}_{2} \frac{( \varphi (\xi ) - \varphi (a))^{\varsigma ^{*} - \varsigma _{1}} }{\Gamma ( \varsigma ^{*} - \varsigma _{1} +1)} + \tilde{ \mathfrak{B} }^{*}_{1} \frac{( \varphi (\sigma ) - \varphi (a) )^{\varsigma ^{*} + \varsigma _{2}} }{ \Gamma ( \varsigma ^{*} + \varsigma _{2} +1)} \biggr] \\& \quad \quad {} \times \Vert \breve{c} \Vert \psi \bigl( \bigl\Vert \phi -\phi ' \bigr\Vert \bigr) \frac{ 1 }{ \mathfrak{Z}^{*} \Vert \breve{c} \Vert } = \mathfrak{Z}^{*} \Vert \breve{c} \Vert \psi \bigl( \bigl\Vert \phi -\phi ' \bigr\Vert \bigr) \frac{ 1 }{ \mathfrak{Z}^{*} \Vert \breve{c} \Vert } = \psi \bigl( \bigl\Vert \phi -\phi ' \bigr\Vert \bigr) \end{aligned}$$

for all \(s\in [a,M] \). Accordingly, we arrive at the following:

$$ \bigl\Vert g_{*}^{\prime } - g_{*}^{\prime \prime } \bigr\Vert = \sup_{s\in [a,M] } \bigl\vert g_{*}^{\prime } (s) -g_{*}^{\prime \prime } (s) \bigr\vert \leq \psi \bigl( \bigl\Vert \phi -\phi ' \bigr\Vert \bigr). $$

In conclusion, \(\alpha (\phi ,\phi ') \mathrm{PH}_{d_{\mho }} (\mathfrak{K}(\phi ) , \mathfrak{K}(\phi ')) \leq \psi ( \Vert \phi -\phi ' \Vert ) \) for each \(\phi ,\phi '\in \mho \) meaning that \(\mathfrak{K}\) is α-ψ-contractive.

In what follows, we regard \(\phi \in \mho \) and \(\phi '\in \mathfrak{K}(\phi )\) along with \(\alpha (\phi ,\phi ')\geq 1\). By virtue of the definition of ζ̂, we get \(\hat{\zeta } ( \phi (s) , \phi '(s) ) \geq 0 \). Thus a function \(f_{*}\in \mathfrak{K}(\phi ')\) exists so that \(\hat{\zeta } ( \phi '(s), f_{*}(s) ) \geq 0 \). Therefore \(\alpha (\phi ' , f_{*}) \geq 1\) and the latter inequality demonstrates that \(\mathfrak{K}\) is α-admissible.

To end the argument, let \(\phi _{0}\in \mho \) and \(\phi '\in \mathfrak{K}(\phi _{0})\) be so that \(\hat{\zeta } ( \phi _{0}(s) , \phi '(s) ) \geq 0 \) for any s. Then \(\alpha (\phi _{0} , \phi ') \geq 1\). Moreover, consider the sequence \(\{ \phi _{n} \}_{n\geq 1}\) of ℧ which goes to ϕ and \(\alpha (\phi _{n} , \phi _{n+1}) \geq 1\) for all n. In this phase, we have \(\hat{\zeta } ( \phi _{n}(s) , \phi _{n+1}(s) ) \geq 0 \). By the aid of \((\mathfrak{C}4)\), a subsequence \(\{ \phi _{n_{l}}\}_{l\geq 1} \) of \(\{ \phi _{n} \} \) exists so that \(\hat{\zeta } ( \phi _{n_{l}}(s) , \phi (s) ) \geq 0 \) for any \(s\in [a,M] \). In consequence, \(\alpha (\phi _{n_{l}}, \phi ) \geq 1\) for all \(l \geq 1\) and it follows that ℧ features the specification \(( C_{\alpha })\). Eventually, with due attention to Proposition 2.15, we understand that \(\mathfrak{K} \) possesses a fixed point and this guarantees that a solution exists for the generalized φ-Caputo fractional inclusion boundary value problem (1)–(2). □

In the following we address another criterion for the generalized φ-Caputo fractional inclusion boundary value problem (1)–(2) under new hypotheses. More precisely, we infer the existence result with respect to a new property due to Amini [40]. We invoke the approximate endpoint specification for \(\mathfrak{K} \) which is demonstrated in (18).

Theorem 3.5

Let \(\breve{\mathfrak{E}} : [a,M] \times \mho \to \mathfrak{P}_{cmp}( \mho )\) be a compact multifunction and regard the following:

\((\mathfrak{C}7)\):

the nondecreasing map \(\psi : [0,\infty )\to [0,\infty )\) involves the u.s.c. specification and \(\lim \inf_{s\to \infty }(s-\psi (s))>0\) and \(s > \psi (s)\) for \(s \in \mathbb{R}^{>0}\);

\((\mathfrak{C}8)\):

the multifunction \(\breve{\mathfrak{E}} : [a,M]\times \mho \to \mathfrak{P}_{cmp,bnd}( \mho )\) is integrable and \(\breve{\mathfrak{E}} ( \cdot , \phi ) : [a,M] \to \mathfrak{P}_{cp}( \mho )\) is measurable for any \(\phi \in \mho \);

\((\mathfrak{C}9)\):

a function \(\eta \in \mathcal{C}_{ \mathbb{R}^{\geq 0}}([a,M])\) exists for which

$$ \mathrm{PH}_{d_{\mho }} \bigl( \breve{\mathfrak{E}}(s,\phi )- \breve{\mathfrak{E}} \bigl(s,\phi ' \bigr) \bigr) \leq \eta (s) \psi \bigl( \bigl\vert \phi -\phi ' \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } $$
(20)

for any \(s\in [a,M]\) and \(\phi ,\phi ' \in \mho \), where \(\sup_{s\in [a,M]} \vert \eta (s) \vert = \Vert \eta \Vert \) and \(\mathfrak{Z}^{*}\) is illustrated in (17);

\((\mathfrak{C}10)\):

the multifunction \(\mathfrak{K}\) formulated in (18) possesses the approximate endpoint specification.

Then the generalized φ-Caputo fractional inclusion boundary value problem (1)–(2) involves a solution.

Proof

As a main purpose, we intend to check the existence of an endpoint for the multifunction \(\mathfrak{K}: \mho \to \mathfrak{P}(\mho )\). To fulfill the mentioned demand, we try to verify that \(\mathfrak{K}(\phi )\) is closed for any \(\phi \in \mho \). Due to \((\mathfrak{C}8)\) and by the measurability of the mapping \(s\mapsto \breve{\mathfrak{E}} (s , \phi (s) ) \) and closedness of it for each \(\phi \in \mho \), it is deduced that \(\breve{\mathfrak{E}} \) possesses a measurable selection and so \(\mathfrak{S}_{ \breve{\mathfrak{E}} , \phi } \neq \emptyset \) for each \(\phi \in \mho \). Accordingly, like the proof of Theorem 3.4, it is simple to confirm that \(\mathfrak{K}(\phi )\) is a closed set contained in ℧ and hence we omit it. Moreover, it is well known that \(\mathfrak{K}(\phi )\) is bounded for any \(\phi \in \mho \) for the sake of the compactness of \(\breve{\mathfrak{E}} \). We end the proof by checking \(\mathrm{PH}_{d_{\mho }} (\mathfrak{K}(\phi ), \mathfrak{K}(\phi ')) \leq \psi ( \Vert \phi -\phi ' \Vert )\) for \(\phi , \phi ' \in \mho \). To observe this issue, let \(\phi ,\phi '\in \mho \) and \(g_{*}^{\prime } \in \mathfrak{K}(\phi ')\). We have \(\hat{\hbar }^{*}_{1} \in \mathfrak{S}_{\breve{\mathfrak{E}} , \phi '}\) provided that

$$\begin{aligned} g_{*}^{\prime }(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}_{1}(r) \,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}_{1}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

for a.e. \(s\in [a,M]\). Because of (20) expressed in \((\mathfrak{C}9)\), we get

$$ \mathrm{PH}_{d_{\mho }} \bigl( \breve{\mathfrak{E}} \bigl(s , \phi (s) \bigr) , \breve{\mathfrak{E}} \bigl(s , \phi '(s) \bigr) \bigr) \leq \eta (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } $$

for a.e. \(s\in [a,M]\), thus \(f^{*} \in \breve{\mathfrak{E}} (s , \phi (s) ) \) exists for which we have

$$ \bigl\vert \hat{\hbar }^{*}_{1}(s)- f^{*} \bigr\vert \leq \eta (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } $$

for a.e. \(s\in [a,M]\). Here, we construct a new multifunction \(\mathcal{O} : [a,M]\to \mathfrak{P}(\mho )\) which is introduced by

$$ \mathcal{O}(s) = \biggl\{ f^{*} \in \mho : \bigl\vert \hat{\hbar }^{*}_{1}(s)- f^{*} \bigr\vert \leq \eta (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } \biggr\} . $$

For as far as \(\hat{\hbar }^{*}_{1}\) and \(p = \eta \psi ( \vert \phi -\phi ' \vert ) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } \) are measurable, \(\mathcal{O}( \cdot )\cap \breve{\mathfrak{E}} (\cdot ,\phi (\cdot ) ) \) is measurable. In this position, we elect the function \(\hat{\hbar }^{*}_{2}(s)\in \breve{\mathfrak{E}} (s , \phi (s) ) \) so that

$$ \bigl\vert \hat{\hbar }^{*}_{1}(s)-\hat{\hbar }^{*}_{2}(s) \bigr\vert \leq \eta (s) \psi \bigl( \bigl\vert \phi (s)-\phi '(s) \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } $$

for a.e. \(s\in [a,M]\). Furthermore, we have \(g_{*}^{\prime \prime } \in \mathfrak{K}(\phi )\) such that

$$\begin{aligned} g_{*}^{\prime \prime }(s) &= \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{s} \varphi '(r) \bigl( \varphi (s) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} ) } \int _{a}^{M} \varphi '(r) \bigl( \varphi (M) - \varphi (r) \bigr)^{ \varsigma ^{*} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (\varsigma ^{*} - \varsigma _{1} ) } \int _{a}^{\xi }\varphi '(r) \bigl( \varphi (\xi ) - \varphi (r) \bigr)^{ \varsigma ^{*} - \varsigma _{1} - 1 } \hat{\hbar }^{*}_{2}(r) \,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (\varsigma ^{*} + \varsigma _{2} ) } \int _{a}^{\sigma }\varphi '(r) \bigl( \varphi ( \sigma ) - \varphi (r) \bigr)^{ \varsigma ^{*} + \varsigma _{2} - 1 } \hat{\hbar }^{*}_{2}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s) \end{aligned}$$

for a.e. \(s\in [a,M]\). In conclusion, similar to the proof of Theorem 3.4, we have

$$ \bigl\Vert g_{*}^{\prime } - g_{*}^{\prime \prime } \bigr\Vert = \sup_{s\in [a,M] } \bigl\vert g_{*}^{\prime } (s) - g_{*}^{\prime \prime } (s) \bigr\vert \leq \mathfrak{Z}^{*} \Vert \eta \Vert \psi \bigl( \bigl\Vert \phi -\phi ' \bigr\Vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } = \psi \bigl( \bigl\Vert \phi - \phi ' \bigr\Vert \bigr). $$

The above result yields \(\mathrm{PH}_{d_{\mho }} (\mathfrak{K}(\phi ), \mathfrak{K}(\phi ')) \leq \psi ( \Vert \phi -\phi ' \Vert )\) for each \(\phi ,\phi '\in \mho \). Along with this, the condition \((\mathfrak{C}10)\) expresses that \(\mathfrak{K}\) possesses an approximate endpoint specification. In conclusion, by Proposition 2.16, we arrive at the intended purpose which confirms the issue that \(\mathfrak{K}\) possesses an endpoint uniquely; that is, \(\mathfrak{K}(\phi ^{*})=\{ \phi ^{*} \}\) for some \(\phi ^{*}\in \mho \). Hence, it is followed that \(\phi ^{*}\) is a solution for the generalized φ-Caputo fractional inclusion boundary value problem (1)–(2). □

4 Simulation example

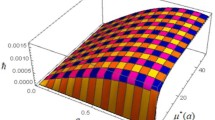
Finally, we support our results by proposing an example to demonstrate the applicability of the findings numerically. Indeed, the theoretical results obtained in Theorem 3.5 are guaranteed by a numerical example.

Example 4.1

According to the parameters \(\varsigma ^{*} =1.5\), \(\varsigma _{1} = 0.03\), \(\varsigma _{2} = 0.5\), \(\xi = 0.06\), \(\sigma = 0.07\), \(\mu ^{*}_{1} = 0.46\), \(\mu ^{*}_{2} = 0.23\), \(a=0\), \(M=1\) and also by considering the proposed boundary value problem (1)–(2), we regard the fractional generalized φ-Caputo differential inclusion

$$ {}^{\mathcal{C}}\mathcal{D}_{0}^{1.5;s^{2}} \phi (s) \in \biggl[0, \frac{125s \vert \arctan \phi (s) \vert }{ 1000 \vert \arctan \phi (s) \vert + 1000 } \biggr], \quad \bigl(s\in [0,1] \bigr) ,$$
(21)

subject to the mixed generalized φ-Riemann–Liouville boundary value conditions

$$ \phi (0) = {}^{\mathcal{RL}}\mathcal{D}_{0}^{0.04;s^{2}} \phi (0.06) + 0.46, \quad\quad \phi (1) = {}^{\mathcal{RL}}\mathcal{I}_{0}^{0.5;s^{2}} \phi ( 0.07)+ 0.23 , $$
(22)

so that \({}^{\mathcal{C}}\mathcal{D}_{0}^{1.5;\varphi } \) stands for the generalized φ-Caputo derivative of \(\varsigma ^{*} = 1.5 \) with respect to \(\varphi (s) = s^{2}\), \({}^{\mathcal{RL}}\mathcal{D}_{0}^{0.03;\varphi } \) indicates the generalized φ-Riemann–Liouville derivative of \(\varsigma _{1} = 0.03 \) with respect to \(\varphi (s) = s^{2}\) and \({}^{\mathcal{RL}}\mathcal{I}_{0}^{0.5;\varphi }\) represents the generalized φ-Riemann–Liouville integral of \(\varsigma _{2} = 0.5\) depending on \(\varphi (s) = s^{2}\). It is obvious that the function φ is increasing on \([0,1]\) and \(\varphi '(s)= 2s > 0\) on \((0,1)\). In the light of the values considered above, we obtain \(\mathfrak{O}^{*}_{0} \simeq - 0.1627\), \(\mathfrak{O}^{*}_{1} \simeq 0.00431\), \(\mathfrak{O}^{*}_{2} \simeq - 0.92102\), \(\mathfrak{O}^{*}_{3} \simeq - 0.99975\) and so \(\mathfrak{O}^{*} = \mathfrak{O}^{*}_{0}\mathfrak{O}^{*}_{3} + \mathfrak{O}^{*}_{1}\mathfrak{O}^{*}_{2} \simeq 0.1587 \neq 0\). In this position, prior to checking the specifications of desired multifunction, we firstly introduce the Banach space \(\mho =\{ \phi (s) : \phi (s) \in \mathcal{C}_{\mathbb{R}}([0,1]) \} \) endowed with \(\Vert \phi \Vert _{\mho }=\sup_{s\in [0,1]} \vert \phi (s) \vert \). Regard the multi-valued mapping \(\breve{\mathfrak{E}} : [0,1] \times \mho \to \mathfrak{P}(\mho )\)

$$ \breve{\mathfrak{E}} \bigl(s, \phi (s) \bigr)= \biggl[0, \frac{125s \vert \arctan \phi (s) \vert }{ 1000 \vert \arctan \phi (s) \vert + 1000 } \biggr] $$
(23)

for each \(s \in [0,1]\). With due attention to the method implemented in the argument of Theorem 3.5, we formulate \(\mathfrak{K}: \mho \to \mathfrak{P}(\mho )\) by the following rule:

$$ \mathfrak{K}(\phi )= \bigl\{ g_{*} \in \mho : \text{there is } \hat{ \hbar }^{*} \in \mathfrak{S}_{ \breve{\mathfrak{E}} ,\phi } \text{ so that } g_{*}(s) = f_{*}(s) \text{ for any } s\in [0,1] \bigr\} , $$

so that

$$\begin{aligned} f_{*}(s) &= \frac{1}{\Gamma ( 1.5 ) } \int _{0}^{s} 2r \bigl( s^{2} - r^{2} \bigr)^{ 1.5 - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (1.5 ) } \int _{0}^{1} 2r \bigl( 1^{2} - r^{2} \bigr)^{ 1.5 - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (1.5 - 0.03) } \int _{0}^{0.06} 2r \bigl( 0.06^{2} - r^{2} \bigr)^{ 1.5 - 0.03 - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (1.5 + 0.5 ) } \int _{0}^{0.07} 2r \bigl( 0.07^{2} - r^{2} \bigr)^{ 1.5 + 0.5 - 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s) \\ &= \frac{1}{\Gamma ( 1.5 ) } \int _{0}^{s} 2r \bigl( s^{2} - r^{2} \bigr)^{ 0.5 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (1.5 ) } \int _{0}^{1} 2r \bigl( 1 - r^{2} \bigr)^{ 0.5 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} + \tilde{ \mathfrak{B} }^{*}_{2}(s) \frac{1}{\Gamma (1.47) } \int _{0}^{0.06} 2r \bigl( 0.0036 - r^{2} \bigr)^{ 0.47 } \hat{\hbar }^{*}(r)\,\mathrm{d}r \\ &\quad {} - \tilde{ \mathfrak{B} }^{*}_{1}(s) \frac{1}{\Gamma (2 ) } \int _{0}^{0.07} 2r \bigl( 0.0049 - r^{2} \bigr)^{ 1 } \hat{\hbar }^{*}(r)\,\mathrm{d}r + \tilde{ \mathfrak{B} }^{*}_{3}(s), \end{aligned}$$

where the following estimates hold:

$$\begin{aligned} & \bigl\vert \tilde{\mathfrak{B}}^{*}_{1}(s) \bigr\vert = \bigl\vert 0.02715 - 1.0252s^{2} \bigr\vert \leq \vert 0.02715 \vert + \bigl\vert 1.0252s^{2} \bigr\vert \leq \tilde{ \mathfrak{B}}^{*}_{1} := 1.05235, \\ & \bigl\vert \tilde{\mathfrak{B}}^{*}_{2}(s) \bigr\vert = \bigl\vert -6.29962 + 5.8035s^{2} \bigr\vert \leq \vert -6.29962 \vert + \bigl\vert 5.8035s^{2} \bigr\vert \leq \tilde{ \mathfrak{B}}^{*}_{2} := 12.10312, \\ & \bigl\vert \tilde{\mathfrak{B}}^{*}_{3}(s) \bigr\vert = \bigl\vert -2.904 + 2.9054s^{2} \bigr\vert \leq \vert -2.904 \vert + \bigl\vert 2.9054s^{2} \bigr\vert \leq \tilde{ \mathfrak{B}}^{*}_{3} := 5.8094, \end{aligned}$$

for all \(s\in [0,1]\). Obviously, we get \(\mathfrak{Z}^{*} \simeq 1.54618\). In addition, the nondecreasing map \(\psi : \mathbb{R}^{\geq 0}\to \mathbb{R}^{\geq 0}\) with u.s.c. specification is given by \(\psi (s) = \frac{s}{2}\) for each \(s >0\). Also, we have \(\lim \inf_{s\to \infty }(s-\psi (s))>0\) and \(s > \psi (s)\) for all \(s \in \mathbb{R}^{>0}\). Moreover, for all \(\phi ,\phi ' \in \mho \), we obtain

$$\begin{aligned} \mathrm{PH}_{d_{\mho }} \bigl( \breve{\mathfrak{E}} \bigl(s, \phi (s) \bigr) , \breve{\mathfrak{E}} \bigl(s, \phi '(s) \bigr) \bigr) &\leq \frac{125s}{1000} \bigl( \bigl\vert \phi - \phi ' \bigr\vert \bigr) = \frac{0.25s}{2} \bigl( \bigl\vert \phi - \phi ' \bigr\vert \bigr) \\ &= 0.25s \psi \bigl( \bigl\vert \phi - \phi ' \bigr\vert \bigr) \leq \eta (s) \psi \bigl( \bigl\vert \phi - \phi ' \bigr\vert \bigr) \frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } . \end{aligned}$$

Setting \(\eta \in \mathcal{C}_{\mathbb{R}^{\geq 0}}([0,1])\) formulated by \(\eta (s)= 0.25s\) for any s, we get \(\Vert \eta \Vert = 0.25 \) for which \(\frac{1}{\mathfrak{Z}^{*} \Vert \eta \Vert } \simeq 2.58702 \). Consequently, by the aid of Theorem 3.5 on the current simulation example, it is deduced that the generalized φ-Caputo fractional inclusion boundary value problem (21)–(22) possesses a solution and accordingly, the simulation findings of the current numerical model are consistent with the analytical results discussed in Theorem 3.5. Also, since \(\eta (s) = \breve{c}(s) = 0.25s\) again \(\mathfrak{Z}^{*} \simeq 1.54618\) is obtained, thus we can conclude that all assumptions of Theorem 3.4 are valid for the suggested inclusion boundary value problem (21)–(22) with the same defined structure for \(\breve{\mathfrak{E}} : [0,1] \times \mho \to \mathfrak{P}(\mho )\) in (23) and \(\hat{\zeta } (\phi ,\phi ')= 1 \geq 0\) and, consequently, Theorem 3.4 guarantees the existence of solutions for the boundary value problem (21)–(22).

5 Conclusion

The basic purpose in the current research is to derive several existence aspects of solutions for a novel general class of inclusion problems in terms of the well-defined generalized φ-Caputo and φ-Riemann–Liouville operators. The existing boundary conditions in such inclusion problem are endowed with mixed generalized φ-Riemann–Liouville conditions. To reach this goal, we utilize two notions of endpoint and fixed point to deduce the existence aspects in relation to the existing inclusion boundary value problem (1)–(2). In other words, the analytical methods on α-ψ-contractions and multifunctions involving an approximate endpoint specification are applied to verify the required theoretical findings. Finally, we present a simulation example to examine our theoretical results computationally and numerically.