Abstract
In this paper, we are concerned with a class of quaternion-valued cellular neural networks with time-varying transmission delays and leakage delays. By applying a continuation theorem of coincidence degree theory and the Wirtinger inequality as well as constructing a suitable Lyapunov functional, sufficient conditions are derived to ensure the existence and global exponential stability of anti-periodic solutions via direct approaches. Our results are completely new. Finally, numerical examples are also provided to show the effectiveness of our results.
Similar content being viewed by others
1 Introduction
A quaternion, which was invented by Hamilton in 1843 [1], consists of a real and three imaginary parts. The skew field of quaternion is denoted by
where \(q^{R}, q^{I}, q^{J}, q^{K}\) are real numbers and the three imaginary units \(i, j\) and k obey Hamilton’s multiplication rules:
and the norm \(\Vert q \Vert =\sqrt{\bar{q}q}=\sqrt{q\bar{q}}=\sqrt{(q ^{R})^{2}+(q^{I})^{2}+(q^{J})^{2}+(q^{K})^{2}}\), where \(\bar{q}=q^{R}-iq ^{I}-jq^{J}-kq^{K}\).
Due to the non-commutativity of quaternion multiplication, the investigation on quaternion is much harder than that on plurality. Fortunately, over the past 20 years, especially in algebra area, quaternion has been a topic for the effective applications in the real world. Also, a new class of differential equations named quaternion differential equations has been already applied successfully to the fields, such as quantum mechanics [2, 3], robotic manipulation [4], fluid mechanics [5], differential geometry [6], communication problems and signal processing [7–9], and neural networks [10–13]. Many scholars tried to shed some light on the information about solutions of quaternion differential equations. For example, the authors of [14] first started the research on the existence of periodic solutions of one-dimensional first order periodic quaternion differential equation by using the coincidence degree theory approach. Subsequently, the author of [15, 16] studied the existence of periodic solution of the quaternion Riccati equation with two-sided coefficients. For more works related the problem of the existence of periodic solutions of the quaternion differential equations, we refer to [17, 18] and the references cited therein. As we know, anti-periodic functions as a special class of the quasi-periodic functions are periodic functions, but not all periodic functions are anti-periodic ones. However, up to date, very few papers have been published on the existence of anti-periodic solutions of the quaternion differential equations [19–21].
On the other hands, complex-valued neural networks (CVNNs) can be seen as an extension of real-valued neural networks (RVNNs). Naturally, CVNNs can be also generalized to quaternion-valued neural networks (QVNNs). In fact, CVNNs employing multi-state activation functions can deal with multi-level information, and have often been applied to the storage of image data [22–27]. QVCNNs can deal with multi-level information, and require only half the connection weight parameters of CVNNs [28]. Moreover, compared with RVNNs and CVNNs, QVNNs perform more prominently when it comes to geometrical transformations, like 2D affine transformations or 3D affine transformations. 3D geometric affine transformations can be represented efficiently and compactly based on QVNNs, especially spatial rotation [29]. It is well known that in the design and implementation of neural networks, the dynamics of neural networks plays a very important role. Recently, the study of QVNNs has received much attention of many scholars and some results about dynamical behaviors of QVNNs have been obtained. However, it is well known that quaternion multiplication does not meet the commutative law, so the research on quaternion is much difficult than that on plurality. Besides, the methods and techniques for analyzing CVNNs or RVNNs cannot be directly applied to study QVNNs. In order to avoid the non-commutativity of quaternion multiplication, two usually feasible methods are to decompose the QVNN into four real-valued or two complex-valued systems based on Hamilton’s multiplication rules or the plural decomposition property of quaternion. For example, by decomposing QVNNs into four real-valued systems, in [30], the author dealt with the problem of robust stability for QVNNs with leakage delay, discrete delay and parameter uncertainties; in [31], the global exponential stability for recurrent neural networks with asynchronous time delays is investigated in the quaternion field; in [32], by using Mawhin’s continuation theorem of coincidence degree theory and constructing a suitable Lyapunov function, the existence and global exponential stability of periodic solutions for quaternion-valued cellular neural networks with time-varying delays was established; in [33], the existence and global exponential stability of pseudo almost periodic solutions for neutral type quaternion-valued neural networks with delays in the leakage term on time scales was studied by using the exponential dichotomy method and Lyapunov function method; by decompose QVNNs into two complex-valued systems, in [10], some sufficient conditions on the global μ-stability of the QVNNs with unbounded time-varying delays was obtained, in [34], some sufficient conditions on the existence, uniqueness, and global asymptotical stability of the equilibrium point are derived for the continuous-time QVNNs and their discrete-time analogs, respectively.
Moreover, as far as we know, in all known results about the dynamics of quaternion-valued neural networks, the coefficients of the leakage terms in the quaternion-valued neural networks are assumed to be real numbers.
Besides, among all dynamical behaviors of neural networks, the existence and stability of anti-periodic solutions play a key role in designing and implementation of neural networks and it has been attracting the interest of many researchers, we refer to [35–38] and references therein. However, there are only few papers that consider the problems of anti-periodic solutions for QVNNs [19–21]. Thus, it is worth investigating the existence and stability of anti-periodic solutions of QVNNs.
Motivated by the above discussions and considering that various time delays may change the dynamics of a system, in this paper, we are concern with the following quaternion-valued neural network with time-varying transmission delays and leakage delays:
where \(p=1,2,\ldots,n\), \(x_{p}(t)\in \mathbb{H}\) corresponds to the state of the pth unit at time t, \(f_{q}(x_{q}(t))\), \(g_{q}(x_{q}(t- \tau _{pq}(t))\in \mathbb{H}\) denotes the output of the qth unit at time t and \(t-\tau _{pq}(t))\), \(b_{pq}(t), c_{pq}(t)\in \mathbb{H}\) denote the strength of qth unit on pth unit at time t, respectively, \(Q_{p}(t)\in \mathbb{H}\) is external input on the pth at time t, \(\tau _{pq}(t)\geq 0\) corresponds to the transmission delay along the axon of the qth unit on the pth unit at time t, \(a_{p}(t)\in \mathbb{Q}\) represents the coefficient of the leakage terms, \(\eta _{p}(t)\geq 0\) is the delay in the leakage terms.
The initial value of system (1) is given by
where \(\tau =\max_{1\leq p,q\leq n}\sup_{t\in [0,T]}\{ \tau _{pq}(t),\eta _{p}(t)\}\).
Our main purpose of this paper is by applying a continuation theorem of coincidence degree theory and the Wirtinger inequality as well as constructing a suitable Lyapunov functional to study the existence and global exponential stability of anti-periodic solutions via a direct method. That is, we do not decompose system (1) into real value systems or complex value systems, but study quaternion-valued system (1) directly. Our results are completely new and our methods are different from the previous ones, and can be used to study other types of QVNNs.
This paper is organized as follows. In Sect. 2, we recall some basic definitions and lemmas. In Sect. 3, the existence of anti-periodic solutions of (1) is discussed based on the coincidence degree and the Wirtinger inequality. In Sect. 4, the global exponential stability of anti-periodic solutions of (1) is discussed by constructing a suitable Lyapunov functional. In Sect. 5, two numerical examples are given to demonstrate the obtained results. In Sect. 6, a brief conclusion is given.
2 Preliminaries and lemmas
In this section, we introduce some definitions and recall some lemmas.
Definition 2.1
A function \(f: \mathbb{R}\rightarrow \mathbb{H}\) is called a T-periodic function if for all \(t\in \mathbb{R}\), \(f(t+T)=f(t)\).
Definition 2.2
A function \(f: \mathbb{R}\rightarrow \mathbb{H}\) is called a T-anti-periodic function if for all \(t\in \mathbb{R}\), \(f(t+T)=-f(t)\).
Remark 2.1
From the definitions above, if \(f=f^{R}+if^{I}+jf^{J}+kf^{K}: \mathbb{R}\rightarrow \mathbb{H}\), where \(f^{R},f^{I},f^{J},f^{K}: \mathbb{R}\rightarrow \mathbb{R}\), then we see that if f is a T-periodic function, then for every \(l=R,I,J,K\), \(f^{l}\) is a T-periodic function, and that if f is a T-anti-periodic function, then for every \(l=R,I,J,K\), \(f^{l}\) is a T-anti-periodic function.
Lemma 2.1
([39])
Let \(\mathbb{X},\mathbb{Y}\)be two Bananch spaces, and let \(L:D(L)\subset \mathbb{X}\rightarrow \mathbb{Y}\)be a linear operator, \(N:\mathbb{X}\rightarrow \mathbb{Y}\)is continuous. Assume thatLis one-to-one and \(\Delta:=L^{-1}N\)is compact. Furthermore, assume there exists a bounded and open subset \(\varOmega \in \mathbb{X}\)with \(0\in \varOmega \)such that the equation \(Lx=\lambda Nx\)has no solutions in \(\partial \varOmega \cap D(L)\)for any \(\lambda \in (0,1)\). Then the problem \(Lx=Nx\)has at least one solution inΩ̄.
Lemma 2.2
([39] (Wirtinger inequality))
Ifuis a \(C^{1}\)function such that \(u(0)=u(T)\), then
where \(\Vert u \Vert _{L_{2}}:=(\int _{0}^{T}|u(t)|^{2}\,dt)^{\frac{1}{2}}\)and \(\bar{u}=\frac{1}{T}\int _{0}^{T}u(t)\,dt\).
Lemma 2.3
For all \(a,b\in \mathbb{H}\), \(\bar{a}b+\bar{b}a\leq \bar{a}a+\bar{b}b\).
For convenience, we introduce the following notation:
In order to obtain our results, we introduce the following assumptions.
- (\(H_{1}\)):
For \(p,q=1,2,\dots,n\), \(\tau _{pq},\eta _{p}\in C^{1}( \mathbb{R},\mathbb{R}^{+})\), \(a_{p},b_{pq}, c_{pq},Q_{p}\in C( \mathbb{R},\mathbb{H})\) are all T-periodic functions, and \(\tau _{pq}\) and \(\eta _{p}\) satisfy \(\min_{1\leq p,q\leq n}\{1- {\dot{\tau }}^{+}_{pq}\}>0\) and \(\min_{1\leq p,q\leq n}\{1- {\dot{\eta }}^{+}_{pq}\}>0\), respectively.
- (\(H_{2}\)):
For \(q=1,2,\ldots,n\), \(f_{q}, g_{q}\in C(\mathbb{H}, \mathbb{H})\) satisfy \(f_{q}(-x)=-f_{q}(x), g_{q}(-x)=-g_{q}(x)\) for all \(x\in \mathbb{H}\).
- (\(H_{3}\)):
For \(q=1,2,\ldots,n\), there exist constants \(F,G>0\) such that \(\Vert f_{q}(x) \Vert \leq F, \Vert g_{q}(x) \Vert \leq G\) for all \(x\in \mathbb{H}\).
- (\(H_{4}\)):
For \(q=1,2,\ldots,n\), there exist constants \(L_{q}^{f}, L_{q}^{g}>0\) such that \(\Vert f_{q}(x)-f_{q}(y) \Vert \leq L_{q} ^{f} \Vert x-y \Vert , \Vert g_{q}(x)-g_{q}(y) \Vert \leq L_{q}^{g} \Vert x-y \Vert \) for all \(x,y\in \mathbb{H}\).
3 Existence of anti-periodic solutions
In this section, we will study the existence of anti-periodic solutions of (1) by applying Lemma 2.1 and the Wirtinger inequality.
Theorem 3.1
Assume that \((H_{1})\)–\((H_{3})\)hold. Suppose that
- \((H_{5})\):
For \(p=1,2,\ldots,n\), \(a^{+}_{p}T<\pi \sqrt{1- \dot{\eta }_{p}^{+}}\).
Then system (1) has at least oneT-anti-periodic solution.
Proof
Let
be two Bananch spaces equipped with the norms:
where \(\|x_{p}\|_{0}=\sup_{t\in [0,2T]}\|x_{p}(t)\|, p=1,2, \ldots,n\).
Define operators \(L:D(L)\cap \mathbb{X}\rightarrow \mathbb{Y}\) by \(Lx=\dot{x}\), where \(D(L)=\{x|x\in \mathbb{X}, \dot{x}\in \mathbb{X} \}\subset \mathbb{X}\), and \(N: \mathbb{X}\rightarrow \mathbb{Y}\) by
where
It is easy to see that \(\mathrm{Ker} L=\{\mathbf{0}\}\) and \(L(D(L))= \{y\in \mathbb{Y}, \int _{0}^{2T}y(t)\,dt=0 \}= \mathbb{Y}\). Hence, \(L: D(L)\rightarrow \mathbb{Y}\) is one-to-one. Denote by \(L^{-1}\) the inverse of L and take \(\Delta:=L^{-1}N\), then by using Arzela–Ascoli theorem, we can verify that Δ is compact. Assume that \(x\in D(L)\) is an arbitrary anti-periodic solution of the equation \(Lx=\lambda Nx\), for some \(\lambda \in (0,1)\). Then, for \(p=1,2,\ldots,n\), we have
Multiplying by \(\bar{\dot{x}}_{p}(t)\) from the left on both sides of the system (2), we have
Integrating both sides of (3) from 0 to 2T and noticing that
we obtain
that is, for \(p=1,2,\ldots,n\),
Since \(x_{p}\in C^{1}\) and \(x_{p}\) is a T-anti-periodic function, \(x_{p}\) is a 2T-periodic function, by Lemma 2.2, we have
hence
where \(p=1,2,\ldots,n\). Since \(x_{p}(t)\) is a T-anti-periodic function, there must exist constants \(\xi _{p}^{l}\in [0,2T]\) such that \(x_{p}^{l}(\xi _{p}^{l})=0, l=R,I,J,K\). Hence, we have
Moreover, obviously, \(|x_{p}^{l}(t)|\leq \|x_{p}(t)\|\), for \(l=R,I,J,K\), so we get
From (5), we obtain
thus
where \(p=1,2,\ldots,n\). Therefore,
Take \(\varOmega = \{x\in \mathbb{X}:\|x\|_{\mathbb{X}}< W+1 \}\), then it is clear that Ω satisfies all requirements of Lemma 2.1. In view of Lemma 2.1, system (1) has at least one T-anti-periodic solution. The proof is complete. □
Theorem 3.2
Assume that \((H_{1})\), \((H_{2})\)and \((H_{4})\)hold. Suppose that
- \((H_{6})\):
\(\varLambda:=1-\frac{T}{\pi } \sum_{p=1}^{n} [ \frac{a^{+}_{p}}{\sqrt{1-\dot{\eta }_{p}^{+}}} +\sum_{q=1}^{n} (b^{+}_{qp}L_{p}^{f} +\frac{c^{+}_{qp}L_{p}^{g}}{\sqrt{1- \dot{\tau }^{+}_{qp}}} ) ]>0\).
Then system (1) has at least oneT-anti-periodic solution.
Proof
Similar to the proof of Theorem 3.1, suppose that \(x\in D(L)\) is an arbitrary anti-periodic solution of the equation \(Lx=\lambda Nx\), for some \(\lambda \in (0,1)\). Then, for \(p=1,2,\ldots,n\), we have
Multiplying by \(\bar{\dot{x}}_{p}(t)\) from the left on both sides of the system (2), we have
Integrating both sides of (7) from 0 to 2T and noticing that
we obtain
that is, for \(p=1,2,\ldots,n\),
Hence, for \(p=1,2,\ldots,n\),
Since \(x_{p}\in D(L)\) and \(x_{p}\) is a T-anti periodic function, \(x_{p}\) is a 2T-periodic function, by Lemma 2.2, we have
hence
Since \(x_{p}(t)\) is a T-anti-periodic function, there must exist constants \(\xi _{p}^{l}\in [0,2T]\) such that \(x_{p}^{l}(\xi _{p}^{l})=0, p=1,2,\ldots,n, l=R,I,J,K\). Hence, we have
Moreover, obviously, \(|x_{p}^{l}(t)|\leq \|x_{p}(t)\|\), for \(l=R,I,J,K\), so we get
From (10), we obtain
Therefore,
Take \(\varOmega = \{x\in \mathbb{X}:\|x\|_{\mathbb{X}}< W+1 \}\), then system (1) has at least one T-anti periodic solution. The proof is complete. □
4 Global exponential stability
In this section, we study the global exponential stability of anti-periodic solutions of (1) by constructing a suitable Lyapunov functional.
Definition 4.1
Let \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\) be an anti periodic solution of system (1) with the initial value \(\varphi =(\varphi _{1},\varphi _{2},\ldots,\varphi _{n})^{T}\in C([-\tau,0],\mathbb{H} ^{n})\) and \(y=(y_{1},y_{2},\ldots,y_{n})^{T}\) be an arbitrary solution of system (1) with the initial value \(\psi =(\psi _{1},\psi _{2},\ldots,\psi _{n})^{T}\in C([-\tau,0],\mathbb{H}^{n})\), respectively. If there exist positive constants λ and M such that
where
then the anti-periodic solution of system (1) is said to be globally exponentially stable.
Theorem 4.1
In system (1), let \(\eta _{p}(t)\equiv 0, a_{p}\in C( \mathbb{R},\mathbb{R}^{+})\)with \(a_{p}^{-}=\inf_{t\in [0,2T]}a _{p}(t)>0, p=1,2,\ldots,n\). Assume that \((H_{1})\)–\((H_{5})\)hold, and there exists a positive constantλsuch that
- \((H_{7})\):
\(\varGamma =\max_{1\leq p\leq n} \{2\lambda +2-2a_{p}^{-}+\sum_{q=1}^{n} {b_{qp}^{+}}^{2}(L_{p}^{f})^{2}+ \sum_{q=1}^{n} {c_{q p}^{+}}^{2}(L_{p}^{g})^{2} \frac{e^{2 \lambda \tau ^{+}_{qp}}}{1-{\dot{\tau }}^{+}_{q p}} \}<0\).
Then system (1) has a uniqueT-anti periodic solution that is globally exponentially stable.
Proof
By Theorem 3.1, system (1) has an anti-periodic solution, let x be an anti-periodic solution with the initial value φ and y be an arbitrary anti-periodic solution with the initial value ψ. Taking \(z=x-y\), where \(z_{p}=x_{p}-y _{p}, p=1,2,\ldots,n\), we have
where \(\tilde{f}_{q}(z_{q}(t))=f_{q}(x_{q}(t))-f_{q}(y_{q}(t))\), \(\tilde{g}_{q}(z_{q}(t- \tau _{pq}(t)))=g_{q}(x_{q}(t- \tau _{pq}(t)))-g _{q}(y_{q}(t- \tau _{pq}(t)))\).
Define a Lyapunov function as follows:
where
Calculating the right derivatives \(D^{+}V_{1}(t)\) of \(V_{1}(t)\) and \(D^{+}V_{2}(t)\) of \(V_{2}(t)\) along with the solutions of (11), respectively, and by using Lemma 2.3, we have
and
Therefore,
That is, for \(t\geq 0\), \(V(t)\leq V(0)\). From the definition of \(V(t)\), we have
and
hence
Therefore, we have
Take \(\varTheta = \{1+\frac{\sum_{q=1}^{n} {c_{q p}^{+}}^{2}(L _{p}^{g})^{2}( e^{2\lambda \tau _{qp}^{+}}-1)}{2\lambda (1-{\dot{\tau }} ^{+}_{q p})} \}\), we have
Hence, the system (1) is globally exponentially stable. The uniqueness follows from the global stability. The proof is complete. □
Similarly, we have the following.
Theorem 4.2
In system (1), let \(\eta _{p}(t)\equiv 0, a_{p}\in C( \mathbb{R},\mathbb{R}^{+})\)with \(a_{p}^{-}=\inf_{t\in [0,2T]}a _{p}(t)>0, p=1,2,\ldots,n\). Assume that \((H_{1})\), \((H_{2})\), \((H_{4})\), \((H_{6})\)and \((H_{7})\)hold. Then system (1) has a uniqueT-anti-periodic solution that is globally exponentially stable.
5 Numerical examples
Example 5.1
Consider the following quaternion-valued cellular neural network with time-varying transmission delays and leakage delays:
where
By computing, \(T=\frac{\pi }{4}\), \(\|f_{1}(x)\|=\|f_{2}(x)\|\leq 0.089\), \(\|g_{1}(x)\|=\|g_{2}(x)\|\leq 0.097 \), \(a_{1}^{+}=1.7,a_{2}^{+}= 1.8\), \(\eta _{1}^{+}=0.13,\eta _{2}^{+}= 0.11\), \({\dot{\eta }}^{+}_{1}=0.16, {\dot{\eta }}^{+}_{2}=0.08\), \(b_{11}^{+}\leq 0.051, b_{12}^{+}\leq 0.0245, b_{21}^{+}\leq 0.055, b_{22}^{+}\leq 0.0245\), \(c_{11}^{+}\leq 0.023, c_{12}^{+}\leq 0.034, c_{21}^{+}\leq 0.034, c _{22}^{+}\leq 0.025\), \(Q_{1}\leq 0.5, Q_{2}\leq 0.55\). So \((H_{1}),(H _{2})\) and \((H_{3})\) are satisfied. Besides, it is easy to obtain
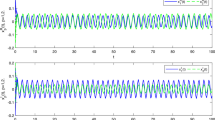
Therefore, all of the conditions of Theorem 3.1 are satisfied. Hence, system (12) has at least one \(\frac{\pi }{4}\)-anti-periodic solution. Setting the three different initial values, the transient states of four parts of system (12) are shown in Figs. 1 and 2.
Curves of \(x_{p}^{R}(t)=(x_{1}^{R}(t),x_{2}^{R}(t))^{T}\) and \(x_{p}^{I}(t)=(x_{1}^{I}(t),x_{2}^{I}(t))^{T}\) of system (12) with the initial values \((x_{1}^{R}(0),x_{2}^{R}(0))^{T}=(0.5,-0.1)^{T}, (-0.25,0.35)^{T}, (0.15,-0.45)^{T}\) and \((x_{1}^{I}(0),x_{2}^{I}(0))^{T}=(0.4,-0.2)^{T}, (0.2,-0.45)^{T}, (-0.3,0.1)^{T}\)
Curves of \(x_{p}^{J}(t)=(x_{1}^{J}(t),x_{2}^{J}(t))^{T}\) and \(x_{p}^{K}(t)=(x_{1}^{K}(t),x_{2}^{K}(t))^{T}\) of system (12) with the initial values \((x_{1}^{J}(0),x_{2}^{J}(0))^{T}=(-0.05,0.05)^{T}, (-0.15,0.2)^{T}, (-0.2,0.1)^{T}\) and \((x_{1}^{K}(0),x_{2}^{K}(0))^{T}=(-0.1,-0.05)^{T}, (0.05,0.15)^{T}, (0.2,-0.2)^{T}\)
Example 5.2
Consider the following quaternion-valued cellular neural network with time-varying transmission delays:
where
By computing, \(T=\frac{\pi }{8}\), \(\|f_{q}(x)\|\leq 0.0715, \|g_{q}(x) \|\leq 0.0561\), \(\|f_{q}(x)\|\leq \frac{1}{20}\|x-y\|, \|g_{q}(x)\| \leq \frac{1}{25}\|x-y\|\), \(a_{1}^{-}=1.4, a_{2}^{-}=1.6, a_{1}^{+}=1.41, a_{2}^{+}=1.62\), \(b_{11}^{+}\leq 0.0224, b_{12}^{+} \leq 0.0332, b_{21}^{+}\leq 0.0548, b_{22}^{+}\leq 0.0245 \), \(c_{11}^{+}\leq 0.0224, c_{12}^{+}\leq 0.0332, c_{21}^{+}\leq 0.0548, c_{22}^{+}\leq 0.0245 \), \(Q_{1}^{+}\leq 0.1334, Q_{2}^{+}\leq 0.1546\). So \((H_{1})\)–\((H_{4})\) are satisfied. Besides, \(\tau _{11}^{+}=0.091, \tau _{12}^{+}=0, \tau _{21}^{+}=0, \tau _{22}^{+}=0.015, \dot{\tau } _{11}^{+}=0.08, \dot{\tau }_{12}^{+}=0, \dot{\tau }_{21}^{+}=0, \dot{\tau }_{22}^{+}=0.04\), and it is easy to obtain
Therefore, all of the conditions of Theorem 3.1 are satisfied. Hence, system (13) has at least one \(\frac{\pi }{8}\)-anti-periodic solution. Furthermore, take \(\lambda =0.1\), we have
Therefore, all of the conditions of Theorem 4.1 are satisfied. Thus, system (13) has at least one \(\frac{\pi }{8}\)-anti-periodic solution that is globally exponentially stable. Figures 3 and 4 show the time responses of four parts of state variables of system (13) with three different initial values. Figure 5 depicts the curves of neurons \(x_{p}^{R}(t)\), \(x_{p}^{I}(t)\), \(x_{p}^{J}(t)\) and \(x_{p}^{K}(t)\) with two random initial conditions in three-dimensional space for stable case.
Curves of \(x_{p}^{R}(t)=(x_{1}^{R}(t),x_{2}^{R}(t))^{T}\) and \(x_{p}^{I}(t)=(x_{1}^{I}(t),x_{2}^{I}(t))^{T}\) of system (13) with the initial values \((x_{1}^{R}(0),x_{2}^{R}(0))^{T}=(0.01,-0.02)^{T}, (0.03,-0.04)^{T}, (0.05,-0.05)^{T}\) and \((x_{1}^{I}(0),x_{2}^{I}(0))^{T}=(-0.01,0.03)^{T}, (0.02,0.05)^{T}, (-0.05,-0.02)^{T}\)
Curves of \(x_{p}^{J}(t)=(x_{1}^{J}(t),x_{2}^{J}(t))^{T}\) and \(x_{p}^{K}(t)=(x_{1}^{K}(t),x_{2}^{K}(t))^{T}\) of system (13) with the initial values \((x_{1}^{J}(0),x_{2}^{J}(0))^{T}=(0.01,0.04)^{T}, (0.03,-0.01)^{T}, (-0.045,-0.03)^{T}\) and \((x_{1}^{K}(0),x_{2}^{K}(0))^{T}=(-0.03,0.02)^{T}, (-0.05,-0.02)^{T}, (0.01,0.05)^{T}\)
6 Conclusion
In this paper, we investigated the existence and global exponential stability of QVNNs with time-varying delays by applying a continuation theorem of coincidence degree theory and by constructing an appropriate Lyapunov functional via direct methods. Our results are new and our proposed methods can be used to study the anti-periodic problem for other types of QVNNs.
References
Sudbery, A.: Quaternionic analysis. Math. Proc. Camb. Philos. Soc. 85(2), 199–225 (1979)
Adler, S.: Quaternionic quantum field theory. Commun. Math. Phys. 104(4), 611–656 (1986)
Leo, S., Ducati, G.: Delay time in quaternionic quantum mechanics. J. Math. Phys. 53(2), Article ID 022102 (2012)
Udwadia, F., Schttle, A.: An alternative derivation of the quaternion equations of motion for rigid-body rotational dynamics. J. Appl. Mech. 77(4), Article ID 044505 (2010)
Gibbon, J.D., Holm, D.D., Kerr, R.M.: Quaternions and particle dynamics in the Euler fluid equations. Nonlinearity 19, 1969–1983 (2006)
Handson, A., Ma, H.: Quaternion frame approach to stream line visualization. IEEE Trans. Vis. Comput. Graph. 1(2), 164–172 (1995)
Ell, T., Sangwine, S.J.: Hypercomplex Fourier transforms of color images. IEEE Trans. Image Process. 16(1), 22–35 (2007)
Miron, S., Bihan, N.L., Mars, J.I.: Quaternion-music for vector-sensor array processing. IEEE Trans. Signal Process. 54(4), 1218–1229 (2006)
Took, C.C., Strbac, G., Aihara, K., Mandic, D.: Quaternion-valued short-term joint forecasting of three-dimensional wind and atmospheric parameters. Renew. Energy 36(6), 1754–1760 (2011)
Liu, Y., Zhang, D., Lu, J., Cao, J.: Global μ-stability criteria for quaternion-valued neural networks with unbounded time-varying delays. Inf. Sci. 360, 273–288 (2016)
Li, Y., Wang, H., Meng, X.: Almost automorphic synchronization of quaternion-valued high-order Hopfield neural networks with time-varying and distributed delays. IMA J. Math. Control Inf. 36(3), 983–1013 (2019)
Li, Y., Qin, J., Li, B.: Periodic solutions for quaternion-valued fuzzy cellular neural networks with time-varying delays. Adv. Differ. Equ. 2019, Article ID 63 (2019)
Xiang, J., Li, Y.: Pseudo almost automorphic solutions of quaternion-valued neural networks with infinitely distributed delays via a non-decomposing method. Adv. Differ. Equ. 2019, Article ID 356 (2019)
Campos, J., Mawhin, J.: Periodic solutions of quaternionic-valued ordinary differential equations. Ann. Math. 185(Suppl 5), S109–S127 (2006)
Wilczynski, P.: Quaternionic valued ordinary differential equations. The Riccati equation. J. Differ. Equ. 247(7), 2163–2187 (2009)
Wilczynski, P.: Quaternionic-valued ordinary differential equations II: coinciding sectors. J. Differ. Equ. 252(8), 4503–4528 (2012)
Gasull, A., Llibre, J., Zhang, X.: One-dimensional quaternion homogeneous polynomial differential equations. J. Math. Phys. 50(8), Article ID 082705 (2009)
Cai, Z.F., Kou, K.I.: Laplace transform: a new approach in solving linear quaternion differential equations. Math. Methods Appl. Sci. 41(11), 4033–4048 (2018)
Li, Y., Qin, J., Li, B.: Anti-periodic solutions for quaternion-valued high-order Hopfield neural networks with time-varying delays. Neural Process. Lett. 49(3), 1217–1237 (2019)
Li, Y., Qin, J., Li, B.: Existence and global exponential stability of anti-periodic solutions for delayed quaternion-valued cellular neural networks with impulsive effects. Math. Methods Appl. Sci. 42(1), 5–23 (2019)
Huo, N., Li, B., Li, Y.: Existence and exponential stability of anti-periodic solutions for inertial quaternion-valued high-order Hopfield neural networks with state-dependent delays. IEEE Access 7, 60010–60019 (2019)
Jankowski, S., Lozowski, A., Zurada, J.M.: Complex-valued multistate neural associative memory. IEEE Trans. Neural Netw. 7(6), 1491–1496 (1996)
Aoki, H., Kosugi, Y.: An Image Storage System Using Complex-Valued Associative Memories. Proceedings 15th International Conference on Pattern Recognition. IEEE Press, New York (2000)
Aoki, H.: A Complex-Valued Neuron to Transform Gray Level Images to Phase Information. Proceedings of the 9th International Conference on Neural Information Processing. IEEE Press, New York (2002)
Tanaka, G., Aihara, K.: Complex-valued multistate associative memory with nonlinear multilevel functions for gray-level image reconstruction. IEEE Trans. Neural Netw. 20(9), 1463–1473 (2009)
Muezzinoglu, M.K., Guzelis, C., Zurada, J.M.: A new design method for the complex-valued multistate Hopfield associative memory. IEEE Trans. Neural Netw. 14(4), 891–899 (2003)
Zheng, P.: Threshold complex-valued neural associative memory. IEEE Trans. Neural Netw. Learn. Syst. 25(9), 1714–1718 (2014)
Kobayashi, M.: Quaternionic Hopfield neural networks with twin-multistate activation function. Neurocomputing 267, 304–310 (2017)
Matsui, N., Isokawa, T., Kusamichi, H., Peper, F., Nishimura, H.: Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 15(3,4), 149–164 (2004)
Chen, X., Li, Z., Song, Q., Hu, J., Tan, Y.: Robust stability analysis of quaternion-valued neural networks with time delays and parameter uncertainties. Neural Netw. 91, 55–65 (2017)
Zhang, D., Kou, K.I., Liu, Y., Cao, J.: Decomposition approach to the stability of recurrent neural networks with asynchronous time delays in quaternion field. Neural Netw. 94, 55–66 (2017)
Li, Y., Qin, J.: Existence and global exponential stability of periodic solutions for quaternion-valued cellular neural networks with time-varying delays. Neurocomputing 292, 91–103 (2018)
Li, Y., Meng, X.: Existence and global exponential stability of pseudo almost periodic solutions for neutral type quaternion-valued neural networks with delays in the leakage term on time scales. Complexity 2017, Article ID 9878369 (2017)
Chen, X., Song, Q., Li, Z., Zhao, Z., Liu, Y.: Stability analysis of continuous-time and discrete-time quaternion-valued neural networks with linear threshold neurons. IEEE Trans. Neural Netw. Learn. Syst. 29, 2769–2781 (2018)
Pan, L., Cao, J.: Anti-periodic solution for delayed cellular neural networks with impulsive effects. Nonlinear Anal., Real World Appl. 12(6), 3014–3027 (2011)
Şaylı, M., Yılmaz, E.: Anti-periodic solutions for state-dependent impulsive recurrent neural networks with time-varying and continuously distributed delays. Ann. Oper. Res. 258(1), 159–185 (2017)
Huo, N., Li, Y.: Anti-periodic solutions for generalized inertial shunting inhibitory cellular neural networks with distributed delays. Appl. Comput. Math. 18(1), 95–107 (2019)
Li, Y., Xiang, J.: Existence and global exponential stability of anti-periodic solution for Clifford-valued inertial Cohen–Grossberg neural networks with delays. Neurocomputing 332, 259–269 (2019)
Amster, P.: Topological Methods in the Study of Boundary Value Problems. Springer, New York (2013)
Acknowledgements
Not applicable.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Funding
This work is supported by the National Natural Science Foundation of China under Grant 11861072.
Author information
Authors and Affiliations
Contributions
The two authors contributed equally to the manuscript and typed, read, and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Xiang, J. Existence and global exponential stability of anti-periodic solutions for quaternion-valued cellular neural networks with time-varying delays. Adv Differ Equ 2020, 47 (2020). https://doi.org/10.1186/s13662-020-2523-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-2523-4