1 Introduction

RNNs have a natural time depth and are adaptable to any sequence data, that is, RNNs are very suitable to solve problems when there is a correlation between samples. The recurrent structure has a natural advantage in modeling variable length data. In a sense, RNNs are the best matching model for sequence data processing. At the same time, time delays are ubiquitous and may change the long-term behavior of dynamical systems. Therefore, RNNs with or without delays have been extensively studied and applied in many fields [1–15].

On the one hand, it is well known that the dynamics of neural networks plays an important role in their design, implementation, and application. Recurrence oscillation of neural networks is an important dynamic behavior of neural networks, such as periodic oscillation, almost periodic oscillation, almost automorphic oscillation, and so on. Many scholars have studied these oscillation problems of neural networks [16–21]. The pseudo-almost-periodic functions as a generalization of almost periodic functions were introduced into the research field of mathematics by Zhang [22]. At present, the existence of pseudo-almost-periodic solutions of differential equations has been studied as an important qualitative behavior of differential equations. At the same time, pseudo-almost-periodic oscillations of ecological and neural network models have also been regarded as one of their important dynamic properties, which has attracted the interest of many researchers [23–30].

On the other hand, a quaternion consists of a real and three imaginary parts [31]. The skew field of quaternions is defined by

$$ \mathbb{H}:=\bigl\{ x\mid x=x^{R}+ix^{I}+jx^{J}+kx^{K} \bigr\} , $$

where \(x^{R},x^{I},x^{J},x^{K} \in \mathbb{R}\) and i, j, k obey the following multiplication rules:

$$ i^{2}=j^{2}=k^{2}=ijk=-1,\qquad ij=-ji=k,\qquad jk=-kj=i,\qquad ki=-ik=j, $$

and the norm of x is defined by \(\vert x \vert _{\mathbb{H}}=\sqrt{(x^{R})^{2}+(x^{I})^{2}+(x^{J})^{2}+(x^{K})^{2}}\). Quaternions can be used in pure and applied mathematics, especially in the calculation of three-dimensional rotation, such as three-dimensional computer graphics, computer vision, and crystal texture analysis. These characteristics make quaternion-valued neural networks more advantageous than the real- and complex-valued neural networks in dealing with problems such as high-dimensional data and spacial rigid body rotations, and so on. Therefore, the research on quaternion-valued neural networks has become a hot topic in the theory and applications of neural networks. However, due to the noncommutativity of quaternion multiplication, the results of quaternion-valued neural network dynamics are very few [32–41]. Especially, the results obtained by a method of not decomposing quaternion-valued systems into real- or complex-valued systems are even rarer. Also, up to date, there has been no paper published on the existence of pseudo-almost-periodic solutions for RNNs with time-varying delays by using direct methods.

Inspired by the above discussion, in this work, we consider the following quaternion-valued RNN with mixed delays:

$$\begin{aligned} \begin{aligned}[b] \dot{x}_{p}(t) &= -a_{p}(t)x_{p}(t)+\sum_{q=1}^{n}b_{pq}(t)f_{q} \bigl(x_{q}(t)\bigr)+ \sum_{q=1}^{n}c_{pq}(t)g_{q} \bigl(x_{q}\bigl(t-\tau _{pq}(t)\bigr)\bigr) \\ &\quad{} +\sum_{q=1}^{n}d_{pq}(t) \int _{-\infty }^{t}\theta _{pq}(t-s)h_{q} \bigl(x_{q}(s)\bigr)\,ds+Q_{p}(t), \end{aligned} \end{aligned}$$
(1)

where \(p=1,2,\ldots,n\), \(x_{p}(t)\in \mathbb{H}\) corresponds to the state of the pth unit at time t, \(f_{q}, g_{q},h_{q}: \mathbb{H}\rightarrow \mathbb{H}\) denote the activation functions, \(b_{pq}(t), c_{pq}(t), d_{pq}(t)\in \mathbb{H}\) represent the connection weights, the discretely delayed connection weights and the distributively delayed connection weights between the qth neuron and the pth neuron at time t, respectively; \(Q_{p}(t)\in \mathbb{H}\) is the external input on the pth neuron at time t, \(\tau _{pq}(t)\geq 0\) denotes the transmission delay, \(a_{p}(t)\in \mathbb{R}\) represents the rate with which the pth unit will reset its potential to the resting state when disconnected from the network and external inputs. The kernel is a positive continuous integrable function and it such that \(\int _{0}^{+\infty }\theta _{pq}(s)\,ds=1\).

The initial value of system (1) is

$$ x_{p}(s)=\varphi _{p}(s),\quad s\in (-\infty ,0], p=1,2, \ldots,n, $$

where \(\varphi _{p}:(-\infty ,0]\rightarrow \mathbb{H}\) is a bounded continuous function.

Our main aim in this paper is by using a direct method to study the existence and global exponential stability of pseudo-almost-periodic solutions of (1). To our knowledge, this is the first paper to study the existence and global exponential stability of pseudo-almost-periodic solutions to system (1). Our results are completely new, and our methods can be used to study other quaternion-valued neural networks.

The rest of this paper is structured as follows. Some basic definitions and lemmas are stated in Sect. 2. The existence of pseudo-almost-periodic solutions of (1) is studied in Sect. 3. In Sect. 4, the global exponential stability of pseudo-almost-periodic solutions of (1) is established. In Sect. 5, a numerical example is given to illustrate the feasibility of the obtained results. Finally, a concise conclusion is given in Sect. 6.

2 Preliminaries and lemmas

Let \(\operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\) denote the set of all bounded continuous functions from \(\mathbb{R}\) to \(\mathbb{H}^{n}\). Then it is easy to check that \(\operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\) with the norm \(\Vert x \Vert =\max_{1\leq p\leq n} \{\sup_{t\in \mathbb{R}} \vert x_{p}(t) \vert _{\mathbb{H}} \}\) is a Banach space. For \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\in \mathbb{H}^{n}\), we denote \(\vert x \vert _{\mathbb{H}^{n}}=\max_{1\leq p\leq n} \vert x_{p} \vert _{ \mathbb{H}}\).

We give the following definition of almost periodic functions in the sense of Bohr [42].

Definition 2.1

A function \(f\in \operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\) is said to be almost periodic, if for every \(\varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\) such that in every interval with length \(l(\varepsilon )\), one can find a number \(\tau =\tau (\varepsilon )\) in this interval satisfying \(\vert f(t+\tau )-f(t) \vert _{\mathbb{H}^{n}}<\varepsilon \) for all \(t\in \mathbb{R}\). The collection of such functions will be denoted by \(\operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\).

From the above definition, following similar proof methods used to prove the corresponding results in [43], one can easily establish the following four lemmas.

Lemma 2.1

If\(f\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\), thenfis bounded and uniformly continuous.

Lemma 2.2

If\(f,g\in \operatorname{AP}(\mathbb{R},\mathbb{H})\), then\(f\pm g,fg\in \operatorname{AP}(\mathbb{R},\mathbb{H})\).

Lemma 2.3

If\(f\in C(\mathbb{H},\mathbb{H}^{n})\)satisfies the Lipschitz condition and\(\varphi \in \operatorname{AP}(\mathbb{R},\mathbb{H}) \), then\(f(\varphi (\cdot ))\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\).

Lemma 2.4

If\(x\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\)and\(\tau \in \operatorname{AP}(\mathbb{R},\mathbb{R})\), then\(x(\cdot -\tau (\cdot ))\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\).

Let

$$ \operatorname{PAP}_{0}\bigl(\mathbb{R},\mathbb{H}^{n} \bigr)= \biggl\{ f\in \operatorname{BC}\bigl(\mathbb{R}, \mathbb{H}^{n} \bigr)\Bigm| \lim_{T\rightarrow +\infty } \frac{1}{2T} \int _{-T}^{T} \bigl\vert f(t) \bigr\vert _{\mathbb{H}^{n}}\,dt=0 \biggr\} . $$

Then we give the following definition of pseudo-almost-periodic functions in the sense of Zhang [22].

Definition 2.2

A function \(f\in \operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\) is said to be pseudo-almost-periodic if it can be expressed as \(f=f_{1}+f_{0}\), where \(f_{1}\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\) and \(f_{0}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H}^{n})\). The collection of all such functions will be denoted by \(\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Similar to the proof of Proposition 5.6 in [44], one can easily prove

Lemma 2.5

If\(f=g+h\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\), then\(g(\mathbb{R})\subset \overline{f(\mathbb{R})}\)and

$$ \Vert f \Vert \geq \Vert g \Vert \geq \inf_{t\in \mathbb{R}} \bigl\vert g(t) \bigr\vert _{\mathbb{H}^{n}} \geq \inf_{t\in \mathbb{R}} \bigl\vert f(t) \bigr\vert _{\mathbb{H}^{n}}. $$

Based on Lemma 2.5, similar to the proof of Lemma 5.8 in [44], one can prove

Lemma 2.6

If\(\{\varphi _{m}\}_{m\in \mathbb{N}}\subset \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\)such that\(\Vert \varphi _{m}-\varphi \Vert \rightarrow 0\)as\(n\rightarrow \infty \), then\(\varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Lemma 2.7

\((\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n}), \Vert \cdot \Vert )\)is a Banach space.

Proof

Obviously, \(\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\subset \operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\). In view of Lemma 2.6, \(\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\) is a closed subspace of \(\operatorname{BC}(\mathbb{R},\mathbb{H}^{n})\). Consequently, \((\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n}), \Vert \cdot \Vert )\) is a Banach space. The proof is complete. □

It is not difficult to prove the following three lemmas.

Lemma 2.8

If\(f,g\in \operatorname{PAP}(\mathbb{R},\mathbb{H})\), then\(fg\in \operatorname{PAP}(\mathbb{R},\mathbb{H})\).

Lemma 2.9

If\(\varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\)and\(h\in \mathbb{R}\), then\(\varphi (\cdot -h)\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Lemma 2.10

Let\(f\in C(\mathbb{H},\mathbb{H}^{n})\)satisfy the Lipschitz condition and\(\varphi \in \operatorname{PAP}(\mathbb{R}, \mathbb{H})\), then\(f(\varphi (\cdot ))\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Lemma 2.11

If\(x\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\), \(\nu \in \operatorname{AP}(\mathbb{R},\mathbb{R})\cap C^{1}(\mathbb{R},\mathbb{R})\)and there exist positive constants\(\nu ^{+}\)and\(\dot{\nu }^{+}\)such that\(\vert \nu (t) \vert \leq \nu ^{+}\)and\(\dot{\nu }(t)\leq \dot{\nu }^{+}<1\), then\(x(\cdot -\nu (\cdot ))\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Proof

Since \(x\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\), we can write \(x=x_{1}+x_{0}\), where \(x_{1}\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n}) \) and \(x_{0}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H}^{n})\), so we have

$$ x\bigl(t-\nu (t)\bigr)=x_{1}\bigl(t-\nu (t)\bigr)+x_{0} \bigl(t-\nu (t)\bigr). $$

Noticing that \(x_{1}(\cdot -\nu (\cdot ))\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\), by Lemma 2.1, \(x_{1}\) is uniformly continuous. Thus, for every \(\varepsilon >0\), there is a constant \(0<\zeta =\zeta (\varepsilon )<\frac{\varepsilon }{2}\) such that

$$\begin{aligned} \bigl\vert x_{1}(t)-x_{1}(s) \bigr\vert _{\mathbb{H}^{n}}< \frac{\varepsilon }{2},\quad \vert t-s \vert < \zeta . \end{aligned}$$
(2)

Since ν and \(x_{1}\) are almost periodic, for this \(\zeta >0\), there exists an \(l(\zeta )>0\) such that in every interval with length \(l(\zeta )\), there is a δ satisfying

$$\begin{aligned} \bigl\vert \nu (t+\delta )-\nu (t) \bigr\vert < \zeta ,\quad\quad \bigl\vert x_{1}(t+\delta )-x_{1}(t) \bigr\vert _{ \mathbb{H}^{n}}< \zeta < \frac{\varepsilon }{2},\quad t\in \mathbb{R}. \end{aligned}$$
(3)

It follows from (2) and (3) that

$$\begin{aligned}& \bigl\vert x_{1}\bigl(t+\delta -\nu (t+\delta ) \bigr)-x_{1}\bigl(t-\nu (t)\bigr) \bigr\vert _{\mathbb{H}^{n}} \\& \quad \leq \bigl\vert x_{1}\bigl(t+\delta -\nu (t+\delta ) \bigr)-x_{1}\bigl(t+\delta -\nu (t)\bigr) \bigr\vert _{ \mathbb{H}^{n}} \\& \quad\quad {} + \bigl\vert x_{1}\bigl(t+\delta -\nu (t) \bigr)-x_{1}\bigl(t-\nu (t)\bigr) \bigr\vert _{\mathbb{H}^{n}} \\& \quad < \frac{\varepsilon }{2}+\frac{\varepsilon }{2}, \end{aligned}$$

which implies that \(x_{1}(\cdot -\nu (\cdot ))\in \operatorname{AP}(\mathbb{R},\mathbb{H}^{n})\).

Moreover, let \(s=t-\nu (t)\), we find

$$\begin{aligned}& \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \bigl\vert x_{0}\bigl(t- \nu (t)\bigr) \bigr\vert _{\mathbb{H}^{n}}\,dt \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T+\nu (-T)}^{T+ \nu (T)} \bigl\vert x_{0}(s) \bigr\vert _{\mathbb{H}^{n}}\frac{1}{1-\dot{\nu }(t)}\,ds \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \biggl[ \int _{-T- \nu (T)}^{T+\nu (T)} \bigl\vert x_{0}(s) \bigr\vert _{\mathbb{H}^{n}} \frac{1}{1-\dot{\nu }(t)}\,ds \\& \quad\quad {} - \int _{-T-\nu (T)}^{-T+\nu (-T)} \bigl\vert x_{0}(s) \bigr\vert _{\mathbb{H}^{n}} \frac{1}{1-\dot{\nu }(t)}\,ds \biggr] \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T-\nu (T)}^{T+ \nu (T)} \bigl\vert x_{0}(s) \bigr\vert _{\mathbb{H}^{n}}\frac{1}{1-\dot{\nu }(t)}\,ds \\& \quad \leq \lim_{T\rightarrow +\infty } \frac{1}{1-\dot{\nu }^{+}}\frac{T+\nu ^{+}}{T} \frac{1}{2(T+\nu ^{+})} \int _{-T-\nu ^{+}}^{T+\nu ^{+}} \bigl\vert x_{0}(s) \bigr\vert _{\mathbb{H}^{n}}\,ds \\& \quad = 0, \end{aligned}$$

which implies that \(x_{0}(\cdot -\nu (\cdot ))\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H}^{n})\).

Hence, \(x(\cdot -\nu (\cdot ))\in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\). The proof is completed. □

In what follows, we will adopt the following notation:

$$\begin{aligned}& a_{p}^{-}=\inf_{t\in \mathbb{R}}a_{p}(t), \quad\quad b_{pq}^{+}= \sup_{t\in \mathbb{R}} \bigl\vert b_{pq}(t) \bigr\vert _{\mathbb{H}},\quad\quad c_{pq}^{+}= \sup_{t\in \mathbb{R}} \bigl\vert c_{pq}(t) \bigr\vert _{\mathbb{H}}, \\& d_{pq}^{+}=\sup_{t\in \mathbb{R}} \bigl\vert d_{pq}(t) \bigr\vert _{\mathbb{H}}, \quad\quad \tau ^{+}=\max_{1\leq p,q\leq n}\sup_{t\in \mathbb{R}}\bigl\{ \tau _{pq}(t)\bigr\} ,\quad\quad \dot{\tau }^{+}=\max _{1 \leq p,q\leq n}\sup_{t\in \mathbb{R}}\bigl\{ \dot{\tau }_{pq}(t)\bigr\} \end{aligned}$$

and make the following assumptions:

(\(H_{1}\)):

For \(p,q=1,2,\ldots,n\), \(a_{p}\in \operatorname{AP}(\mathbb{R},\mathbb{R}^{+})\) with \(\inf_{t\in \mathbb{R}}a_{p}(t)>0\), \(b_{pq},c_{pq}, d_{pq}, Q_{p}\in \operatorname{PAP}(\mathbb{R}, \mathbb{H})\), \(\tau _{pq}\in C^{1}(\mathbb{R},\mathbb{R}^{+})\cap \operatorname{AP}(\mathbb{R}, \mathbb{R}^{+})\) and \(\dot{\tau }^{+}<1\).

(\(H_{2}\)):

For \(p,q=1,2,\ldots,n\), the kernels \(\theta _{pq}\in C(\mathbb{R},\mathbb{R}^{+})\) are such that \(\int _{0}^{+\infty }\theta _{pq}(s)\,ds=1\) and there exists a positive constant \(\beta _{\vartheta }\) such that \(\int _{0}^{+\infty }\theta _{pq}(s)e^{\beta _{\vartheta }s}\,ds<+ \infty \).

(\(H_{3}\)):

Functions \(f_{p},g_{p},h_{p}\in C(\mathbb{H},\mathbb{H})\) and there exist constants \(L_{p}^{f}\), \(L_{p}^{g}\), \(L_{p}^{h}\) such that

$$\begin{aligned}& \bigl\vert f_{p}(x)-f_{p}(y) \bigr\vert _{\mathbb{H}} \leq L_{p}^{f} \vert x-y \vert _{\mathbb{H}}, \\& \bigl\vert g_{p}(x)-g_{p}(y) \bigr\vert _{\mathbb{H}} \leq L_{p}^{g} \vert x-y \vert _{\mathbb{H}}, \\& \bigl\vert h_{p}(x)-h_{p}(y) \bigr\vert _{\mathbb{H}} \leq L_{p}^{h} \vert x-y \vert _{\mathbb{H}}, \end{aligned}$$

and \(f_{p}(0)=g_{p}(0)=h_{p}(0)=0\), where \(p=1,2,\ldots,n\).

\((H_{4})\):

\(r:=\max_{1\leq p\leq n} \{\frac{1}{a_{p}^{-}} [ \sum_{q=1}^{n}b_{pq}^{+}L_{q}^{f}+\sum_{q=1}^{n}c_{pq}^{+}L_{q}^{g}+ \sum_{q=1}^{n}d_{pq}^{+}L_{q}^{h} ] \}<1\).

3 The existence of pseudo-almost-periodic solutions

In this section, we study the existence of pseudo-almost-periodic solutions of system (1).

Lemma 3.1

Assume that\((H_{1})\)–\((H_{3})\)hold. If\(x_{q} \in \operatorname{PAP}(\mathbb{R},\mathbb{H})\), then for\(p,q=1,2,\ldots, n\), functions\(\varphi _{pq}:t\rightarrow \int _{-\infty }^{t}\theta _{pq}(t-s)h_{q}(x_{q}(s))\,ds\)belong to\(\operatorname{PAP}(\mathbb{R},\mathbb{H})\).

Proof

It follows from Lemma 2.10 that \(h_{q}(x_{q}(\cdot ))\in \operatorname{PAP}(\mathbb{R},\mathbb{H})\). Let \(h_{q}(x_{q}(t))=u_{q}(t)+v_{q}(t)\), in which \(u_{q}\in \operatorname{AP}(\mathbb{R},\mathbb{H}) \) and \(v_{q}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\), then

$$\begin{aligned} \varphi _{pq}(t) =& \int _{-\infty }^{t}\theta _{pq}(t-s) \bigl[u_{q}(s)+v_{q}(s)\bigr]\,ds \\ =& \int _{-\infty }^{t}\theta _{pq}(t-s)u_{q}(s) \,ds+ \int _{-\infty }^{t} \theta _{pq}(t-s)v_{q}(s) \,ds \\ :=&\varphi _{p}^{1}(t)+\varphi _{p}^{0}(t). \end{aligned}$$

Now, we prove that \(\varphi _{pq}\in \operatorname{PAP}(\mathbb{R},\mathbb{H})\). To this end, firstly, we will prove that \(\varphi _{p}^{1}\in \operatorname{AP}(\mathbb{R},\mathbb{H})\). Since \(u_{q}\in \operatorname{AP}(\mathbb{R},\mathbb{H})\), for every \(\varepsilon >0\), there exists a number \(L({\varepsilon })>0\) such that in every interval of length L, one finds a number τ such that

$$ \bigl\vert u_{q}(t+\tau )-u_{q}(t) \bigr\vert _{\mathbb{H}}< \varepsilon . $$

Hence, we have

$$\begin{aligned}& \bigl\vert \varphi _{p}^{1}(t+\tau )-\varphi _{p}^{1}(t) \bigr\vert _{\mathbb{H}} \\& \quad = \biggl\vert \int _{-\infty }^{t+\tau }\theta _{pq}(t+\tau -s)u_{q}(s)\,ds- \int _{-\infty }^{t}\theta _{pq}(t-s)u_{q}(s) \,ds \biggr\vert _{\mathbb{H}} \\& \quad \leq \int _{-\infty }^{t}\theta _{pq}(t-s) \bigl\vert u_{q}(s+\tau )-u_{q}(s) \bigr\vert _{ \mathbb{H}} \,ds \\& \quad \leq \varepsilon \int _{0}^{+\infty }\theta _{pq}(t)\,dt= \varepsilon , \end{aligned}$$

which implies that \(\varphi _{p}^{1}\in \operatorname{AP}(\mathbb{R},\mathbb{H})\).

Then, we will prove that \(\varphi _{p}^{0}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\). In view of \(v_{q}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\) and the Lebesgue’s dominated convergence theorem, we have

$$\begin{aligned}& \lim_{T\rightarrow \infty }\frac{1}{2T} \int _{-T}^{T} \biggl\vert \int _{-\infty }^{t}\theta _{pq}(t-s)v_{q}(s) \,ds \biggr\vert _{ \mathbb{H}}\,dt \\& \quad = \lim_{T\rightarrow \infty }\frac{1}{2T} \int _{-T}^{T} \biggl\vert \int _{0}^{+\infty }\theta _{pq}(\delta )v_{q}(t-\delta )\,d \delta \biggr\vert _{\mathbb{H}}\,dt \\& \quad \leq \lim_{T\rightarrow \infty }\frac{1}{2T} \int _{-T}^{T} \int _{0}^{+\infty }\theta _{pq}(\delta ) \bigl\vert v_{q}(t-\delta ) \bigr\vert _{ \mathbb{H}}\,d\delta \,dt \\& \quad \leq \int _{0}^{+\infty }\theta _{pq}(\delta )\lim _{T \rightarrow \infty }\frac{1}{2T} \int _{-T}^{T} \bigl\vert v_{q}(t- \delta ) \bigr\vert _{ \mathbb{H}}\,dt\,d\delta \\& \quad = 0, \end{aligned}$$

which implies that \(\varphi _{p}^{0}\in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\). Therefore, \(\varphi _{p}\in \operatorname{PAP}(\mathbb{R},\mathbb{H})\). The proof is completed. □

Let \(\varphi _{0}(t)=(\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{1}(u)\,du}Q_{1}(s)\,ds,\ldots,\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{n}(u)\,du}Q_{n}(s)\,ds)^{T}\) and take a constant \(\alpha > \Vert \varphi _{0} \Vert \). Consider the set \(\mathbb{X}_{0}= \{ \varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n}): \Vert \varphi -\varphi _{0} \Vert \leq \frac{r\alpha }{1-r} \}\), then for every \(\varphi \in \mathbb{X}_{0}\), we have \(\Vert \varphi \Vert \leq \Vert \varphi -\varphi _{0} \Vert + \Vert \varphi _{0} \Vert \leq \frac{r\alpha }{1-r}+\alpha = \frac{\alpha }{1-r}\).

Theorem 3.1

Assume that\((H_{1})\)–\((H_{4})\)hold. Then system (1) has a pseudo-almost-periodic solution in\(\mathbb{X}_{0}\).

Proof

For every \(\varphi =(\varphi _{1},\varphi _{2},\ldots,\varphi _{n})^{T}\in \operatorname{PAP}( \mathbb{R},\mathbb{H}^{n})\), if φ satisfies

$$\begin{aligned} \varphi _{p}(t) =& \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{p}(u)\,du} \Biggl[\sum _{q=1}^{n}b_{pq}(s)f_{q}\bigl( \varphi _{q}(s)\bigr) \\ & {} + \sum_{q=1}^{n}c_{pq}(s)g_{q} \bigl(\varphi _{q}\bigl(s-\tau _{pq}(s)\bigr)\bigr) \\ & {} +\sum_{q=1}^{n}d_{pq}(s) \int _{-\infty }^{t}\theta _{pq}(t-s)h_{q} \bigl( \varphi _{q}(s)\bigr)\,ds \\ & {} +Q_{p}(s) \Biggr]\,ds,\quad p=1,2,\ldots,n, \end{aligned}$$
(4)

then by differentiating (4), we have

$$\begin{aligned} \dot{\varphi }_{p}(t) =&-a_{p}(t)\varphi _{p}(t)+\sum_{q=1}^{n}b_{pq}(t)f_{q} \bigl( \varphi _{q}(t)\bigr)+\sum_{q=1}^{n}c_{pq}(t)g_{q} \bigl(\varphi _{q}\bigl(t- \tau _{pq}(t)\bigr)\bigr) \\ & {} +\sum_{q=1}^{n}d_{pq}(t) \int _{-\infty }^{t}\theta _{pq}(t-s)h_{q} \bigl( \varphi _{q}(s)\bigr)\,du +Q_{p}(t), \end{aligned}$$

which implies that φ is a solution of (1).

Define an operator \(\mathcal{F} :\mathbb{X}_{0}\rightarrow \operatorname{BC}(\mathbb{R},\mathbb{H}^{n}) \) as follows:

$$ \mathcal{F}\varphi =(\mathcal{F}_{1}\varphi ,\mathcal{F}_{2} \varphi ,\ldots,\mathcal{F}_{n}\varphi )^{T}, $$

where for every \(\varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\) and \(p=1,2,\ldots,n\),

$$\begin{aligned}& (\mathcal{F}_{p}\varphi ) (t)= \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{p}(u)\,du} (\varGamma _{p}\varphi ) (s)\,ds, \\ & \begin{aligned} (\varGamma _{p}\varphi ) (s)&=\sum_{q=1}^{n}b_{pq}(s) f_{q}\bigl( \varphi _{q}(s)\bigr)+\sum _{q=1}^{n}c_{pq}(s) g_{q}\bigl( \varphi _{q}\bigl(s- \tau _{pq}(s)\bigr)\bigr) \\ &\quad {} +\sum_{q=1}^{n}d_{pq}(s) \int _{-\infty }^{s}\theta _{pq}(s-u)h_{q} \bigl( \varphi _{q}(u)\bigr)\,du+Q_{p}(s). \end{aligned} \end{aligned}$$

From Lemmas 2.8–2.11 and 3.1, we have \(\varGamma _{p}\varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H})\), which implies that \(\varGamma _{p}\varphi \) can be written as \(\varGamma _{p}\varphi =\varGamma _{p}^{1}\varphi +\varGamma _{p}^{0}\varphi \), where \(\varGamma _{p}^{1}\varphi \in \operatorname{AP}(\mathbb{R},\mathbb{H})\), \(\varGamma _{p}^{0} \varphi \in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\), \(p=1,2,\ldots,n\). Therefore,

$$\begin{aligned} \begin{aligned} (\mathcal{F}_{p}\varphi ) (t)&= \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{p}(u)\,du}\bigl( \varGamma _{p}^{1}\varphi \bigr) (s)\,ds+ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{p}(u)\,du}\bigl( \varGamma _{p}^{0}\varphi \bigr) (s)\,ds \\ &:=\bigl(\mathcal{F}_{p}\varGamma _{p}^{1} \varphi \bigr) (t)+\bigl(\mathcal{F}_{p} \varGamma _{p}^{0} \varphi \bigr) (t),\quad p=1,2,\ldots,n. \end{aligned} \end{aligned}$$

In order to show that \(\mathcal{F}_{p}\varGamma _{p}\varphi \in \operatorname{PAP}(\mathbb{R},\mathbb{H})\), we will first prove that \(\mathcal{F}_{p}\varGamma _{p}^{1}\varphi \in \operatorname{AP}(\mathbb{R},\mathbb{H})\). Since \(a_{p}\in \operatorname{AP}(\mathbb{R},\mathbb{R})\), \(\varGamma _{p}^{1}\in \operatorname{AP}(\mathbb{R}, \mathbb{H})\), for every \(\epsilon >0\), there exists \(l>0\) such that every interval of length l contains a number τ satisfying

$$ \bigl\vert \bigl(\varGamma _{p}^{1}\varphi \bigr) (t+ \tau )-\bigl(\varGamma _{p}^{1}\varphi \bigr) (t) \bigr\vert _{\mathbb{H}}< \varepsilon ,\quad\quad \bigl\vert a_{p}(t+ \tau )-a_{p}(t) \bigr\vert < \varepsilon ,\quad t\in \mathbb{R}. $$

Thus,

$$\begin{aligned}& \bigl\vert \bigl(\mathcal{F}_{p}\varGamma _{p}^{1} \varphi \bigr) (t+\tau )-\bigl( \mathcal{F}_{P}\varGamma _{p}^{1}\varphi \bigr) (t) \bigr\vert _{\mathbb{H}} \\& \quad = \biggl\vert \int _{-\infty }^{t+\tau } e^{-\int _{s}^{t+\tau } a_{p}(u)\,du} \bigl(\varGamma _{p}^{1}\varphi \bigr) (s)\,ds- \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u)\,du} \bigl(\varGamma _{p}^{1}\varphi \bigr) (s)\,ds \biggr\vert _{\mathbb{H}} \\& \quad \leq \biggl\vert \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u+\tau )\,du} \bigl(\varGamma _{p}^{1}\varphi \bigr) (s+\tau )\,ds- \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u)\,du} \bigl(\varGamma _{p}^{1}\varphi \bigr) (s+\tau )\,ds \biggr\vert _{\mathbb{H}} \\& \quad\quad {} + \biggl\vert \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u)\,du} \bigl(\varGamma _{p}^{1} \varphi \bigr) (s+\tau )\,ds- \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u)\,du} \bigl(\varGamma _{p}^{1}\varphi \bigr) (s)\,ds \biggr\vert _{\mathbb{H}} \\& \quad \leq \int _{-\infty }^{t} \bigl\vert e^{-\int _{s}^{t} a_{p}(u+\tau )\,du}-e^{- \int _{s}^{t} a_{p}(u)\,du} \bigr\vert \bigl\vert \bigl(\varGamma _{p}^{1}\varphi \bigr) (s+ \tau ) \bigr\vert _{\mathbb{H}}\,ds \\& \quad \quad {} + \int _{-\infty }^{t} \bigl\vert e^{-\int _{s}^{t} a_{p}(u)\,du} \bigr\vert \bigl\vert \bigl( \varGamma _{p}^{1}\varphi \bigr) (s+\tau )-\bigl(\varGamma _{p}^{1}\varphi \bigr) (s) \bigr\vert _{\mathbb{H}}\,ds \\& \quad \leq \bigl\Vert \varGamma _{p}^{1}\varphi \bigr\Vert \int _{-\infty }^{t}e^{-a_{p}^{-}(t-s)}(t-s) \epsilon \,ds+ \varepsilon \int _{-\infty }^{t} e^{-a_{p}^{-}(t-s)}\,ds \\& \quad = \bigl\Vert \varGamma _{p}^{1}\varphi \bigr\Vert \frac{\epsilon }{(a_{p}^{-})^{2}}+\frac{\varepsilon }{a_{p}^{-}}, \end{aligned}$$

which implies that \(\varGamma _{p}^{1}\varphi \in \operatorname{AP}(\mathbb{R},\mathbb{H})\).

Then, we will prove that \(\mathcal{F}_{p}\varGamma _{p}^{0} \in \operatorname{PAP}_{0}(\mathbb{R},\mathbb{H})\). In fact,

$$\begin{aligned}& \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \bigl\vert \bigl( \mathcal{F}_{p}\varGamma _{p}^{0}\varphi \bigr) (t) \bigr\vert _{\mathbb{H}}\,dt \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \biggl\vert \int _{-\infty }^{t} e^{-\int _{s}^{t} a_{p}(u)\,du} \bigl(\varGamma _{p}^{0} \varphi \bigr) (s)\,ds \biggr\vert _{\mathbb{H}}\,dt \\& \quad \leq \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \int _{- \infty }^{t} \bigl\vert e^{-\int _{s}^{t} a_{p}(u)\,du} \bigr\vert \bigl\vert \bigl(\varGamma _{p}^{0} \varphi \bigr) (s) \bigr\vert _{\mathbb{H}}\,ds \,dt \\& \quad \leq \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \int _{- \infty }^{t} e^{-a^{-}_{p}(t-s)} \bigl\vert \bigl( \varGamma _{p}^{0}\varphi \bigr) (s) \bigr\vert _{\mathbb{H}}\,ds \,dt \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{-T}^{T} \int _{0}^{+ \infty }e^{-a_{p}^{-}u} \bigl\vert \bigl( \varGamma _{p}^{0}\varphi \bigr) (t-u) \bigr\vert _{\mathbb{H}}\,du\,dt \\& \quad = \lim_{T\rightarrow +\infty } \int _{0}^{+\infty }e^{-a_{p}^{-}u} \frac{1}{2T} \int _{-T}^{T} \bigl\vert \bigl(\varGamma _{p}^{0}\varphi \bigr) (t-u) \bigr\vert _{\mathbb{H}} \,dt \,du. \end{aligned}$$

By Lebesgue’s dominated convergence theorem, we have that \(\mathcal{F}_{p}\varGamma _{p}^{0}\varphi \in \operatorname{PAP}_{0}(\mathbb{R}, \mathbb{H})\). Therefore, \(\mathcal{F}\) maps \(\mathbb{X}_{0}\) into \(\operatorname{PAP}(\mathbb{R},\mathbb{H}^{n})\).

Now, we prove that the mapping \(\mathcal{F}\) is a self-mapping from \(\mathbb{X}_{0}\) to \(\mathbb{X}_{0}\). In fact, for each \(\varphi \in \mathbb{X}_{0}\), we have

$$\begin{aligned}& \Vert \mathcal{F}\varphi -\varphi _{0} \Vert \\& \quad \leq \max_{1\leq p\leq n} \Biggl\{ \sup_{t\in \mathbb{R}} \Biggl[ \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du} \sum _{q=1}^{n}b_{pq}(s)f_{q} \bigl(\varphi _{q}(s)\bigr) \Biggr\vert _{ \mathbb{H}} \,ds \\& \quad \quad {} + \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du} \sum _{q=1}^{n}c_{pq}(s)g_{q} \bigl(\varphi _{q}\bigl(s-\tau _{pq}(s)\bigr)\bigr) \Biggr\vert _{ \mathbb{H}} \,ds \\& \quad\quad {} + \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du}\sum _{q=1}^{n}d_{pq}(s) \int _{-\infty }^{s}\theta _{pq}(s-u)h_{q} \bigl(x_{q}(u)\bigr)\,du \Biggr\vert _{\mathbb{H}} \,ds \Biggr] \Biggr\} \\& \quad \leq \max_{1\leq p\leq n} \Biggl\{ \sup_{t\in \mathbb{R}} \Biggl[ \int _{-\infty }^{t}e^{-a_{p}^{-}(t-s)}\sum _{q=1}^{n}b_{pq}^{+}L_{q}^{f} \Vert \varphi \Vert \,ds \\& \quad \quad {} + \int _{-\infty }^{t}e^{-a_{p}^{-}(t-s)}\sum _{q=1}^{n}c_{pq}^{+}L_{q}^{g} \Vert \varphi \Vert \,ds+ \int _{-\infty }^{t}e^{-a_{p}^{-}(t-s)}\sum _{q=1}^{n}d_{pq}^{+}L_{q}^{h} \Vert \varphi \Vert \,ds \Biggr] \Biggr\} \\& \quad \leq \Vert \varphi \Vert \max_{1\leq p\leq n} \Biggl\{ \frac{1}{a_{p}^{-}} \Biggl[\sum_{q=1}^{n}b_{pq}^{+}L_{q}^{f} + \sum_{q=1}^{n}c_{pq}^{+}L_{q}^{g} +\sum_{q=1}^{n}d_{pq}^{+}L_{q}^{h} \Biggr] \Biggr\} \\& \quad \leq \frac{r\alpha }{1-r}, \end{aligned}$$

which means that \(\mathcal{F}\varphi \in \mathbb{X}_{0}\). Hence the mapping \(\mathcal{F}\) is a self-mapping from \(\mathbb{X}_{0}\) to \(\mathbb{X}_{0}\).

Finally, we prove that \(\mathcal{F}\) is a contraction mapping. In fact, for any \(\varphi ,\psi \in \mathbb{X}_{0}\), we have

$$\begin{aligned}& \Vert \mathcal{F}\varphi -\mathcal{F}\psi \Vert \\& \quad = \max_{1\leq p\leq n} \Bigl\{ \sup_{t\in \mathbb{R}} \bigl\vert \mathcal{F}_{p}\varphi (t)-\mathcal{F}_{p}\psi (t) \bigr\vert _{\mathbb{H}} \Bigr\} \\& \quad \leq \max_{1\leq p\leq n} \Biggl\{ \sup_{t\in \mathbb{R}} \Biggl[ \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du} \sum _{q=1}^{n}b_{pq}(s) \bigl[f_{q}\bigl(\varphi _{q}(s)\bigr)-f_{q} \bigl( \psi _{q}(s)\bigr) \bigr] \Biggr\vert _{\mathbb{H}}\,ds \\& \quad \quad {} + \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du}\sum _{q=1}^{n}c_{pq}(s) \bigl[g_{q}\bigl(\varphi _{q}\bigl(s-\tau _{pq}(s) \bigr)\bigr)-g_{q}\bigl( \psi _{q}\bigl(s-\tau _{pq}(s)\bigr)\bigr) \bigr] \Biggr\vert _{\mathbb{H}}\,ds \\& \quad \quad {} + \int _{-\infty }^{t} \Biggl\vert e^{-\int _{s}^{t}a_{p}(u)\,du}\sum _{q=1}^{n}d_{pq}(s) \int _{-\infty }^{s}\theta _{pq}(s-u) \\& \quad\quad {} \times \bigl[h_{q}\bigl(\varphi _{q}(u) \bigr)-h_{q}\bigl(\psi _{q}(u)\bigr)\bigr]\,du \Biggr\vert _{ \mathbb{H}}\,ds \Biggr] \Biggr\} \\& \quad \leq \max_{1\leq p\leq n} \Biggl\{ \frac{1}{a_{p}^{-}} \Biggl[ \sum _{q=1}^{n}b_{pq}^{+}L_{q}^{f} \Vert \varphi _{q}-\psi _{q} \Vert + \sum _{q=1}^{n}c_{pq}^{+}L_{q}^{g} \Vert \varphi _{q}-\psi _{q} \Vert \\& \quad\quad {} +\sum_{q=1}^{n}d_{pq}^{+}L_{q}^{h} \Vert \varphi _{q}-\psi _{q} \Vert \Biggr] \Biggr\} \\& \quad \leq r \Vert \varphi -\psi \Vert , \end{aligned}$$

which, combined with \((H_{4})\), implies that the mapping \(\mathcal{F}\) is a contraction. Therefore, \(\mathcal{F}\) has a unique fixed point, that is, system (1) has a unique-pseudo-almost periodic solution. The proof is completed. □

4 Global exponential stability

In this section, for \(z\in C(\mathbb{R},\mathbb{H}^{n})\) and \(\phi \in \operatorname{BC}((-\infty ,0],\mathbb{H}^{n})\), we denote \(\Vert z(t) \Vert = \max_{1\leq p\leq n} \{ \vert z_{p}(t) \vert _{\mathbb{H}} \}\) and \(\Vert \phi \Vert _{0}=\max_{1\leq p\leq n} \{\sup_{t \in (-\infty ,0]} \vert \phi (t) \vert _{\mathbb{H}} \}\).

Definition 4.1

Let \(x=(x_{1},x_{2},\ldots,x_{n})^{T}\) be a pseudo-almost-periodic solution of system (1) with the initial value \(\varphi =(\varphi _{1},\varphi _{2},\ldots,\varphi _{n})^{T}\in C([- \infty ,0],\mathbb{H}^{n})\) and let \(y=(y_{1},y_{2},\ldots,y_{n})^{T}\) be an arbitrary solution of system (1) with the initial value \(\psi =(\psi _{1},\psi _{2},\ldots,\psi _{n})^{T}\in C([-\infty ,0], \mathbb{H}^{n})\), respectively. If there exist positive constants λ and M such that

$$ \bigl\Vert x(t)-y(t) \bigr\Vert \leq M \Vert \varphi -\psi \Vert _{0}e^{-\lambda t},\quad \forall t>0, $$

then the pseudo-almost-periodic solution x of system (1) is said to be globally exponentially stable.

Theorem 4.1

Assume that\((H_{1})\)–\((H_{4})\)hold. Then system (1) has a unique pseudo-almost-periodic solution that is globally exponentially stable.

Proof

By Theorem 3.1, system (1) has a pseudo-almost-periodic solution, let \(x(t)\) be a pseudo-almost-periodic solution with initial value \(\varphi (t)\) and \(y(t)\) be an arbitrary solution with initial value \(\psi (t)\). Taking \(z_{p}(t)=y_{p}(t)-x_{p}(t)\), \(\phi _{p}(t)=\psi _{p}(t)-\varphi _{p}(t)\), we have

$$\begin{aligned}& \dot{z}_{p}(t)+a_{p}(t)z_{p}(t) \\& \quad =\sum_{q=1}^{n}c_{pq}(t) \bigl[f_{q}\bigl(z_{q}(t)+x_{q}(t) \bigr)-f_{q}\bigl(x_{q}(t)\bigr) \bigr] \\& \quad\quad{} +\sum_{q=1}^{n}c_{pq}(t) \bigl[f_{q}\bigl(z_{q}\bigl(t-\tau _{pq}(t) \bigr)+x_{q}\bigl(t- \tau _{pq}(t)\bigr)\bigr)-f_{q} \bigl(y_{q}\bigl(t-\tau _{pq}(t)\bigr)\bigr) \bigr] \\& \quad\quad{} +\sum_{q=1}^{n}d_{pq}(t) \int _{-\infty }^{t}\theta _{pq}(t-s) \bigl[h_{q}\bigl(z_{p}(s)+x_{q}(s) \bigr)-h_{q}\bigl(x_{q}(s)\bigr)\bigr]\,ds. \end{aligned}$$
(5)

Let \(\varTheta _{p}\) be defined by

$$ \varTheta _{p}(\omega )=a_{p}^{-}-\omega -\sum _{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f}+c_{pq}^{+}L_{q}^{g}e^{ \omega \tau ^{+}}+d_{pq}^{+}L_{q}^{h} \int _{0}^{+\infty }\theta _{pq}(s)e^{ \omega s} \,ds \biggr], $$

where \(p=1,2,\ldots,n\), \(\omega \in [0,+\infty )\). Then by \((H_{2})\) and \((H_{4})\), for each \(p=1,2,\ldots,n\), we have \(\varTheta _{p}(0)>0\), moreover, since \(\varTheta _{p}(\omega )\rightarrow -\infty \) as \(\omega \rightarrow +\infty \), there exists \(\varepsilon _{p}^{*}>0\) such that \(\varTheta _{p}(\varepsilon _{p})>0\) for \(\varepsilon _{p}\in (0,\varepsilon _{p}^{*})\). Let \(\eta =\min \{\varepsilon _{1}^{*},\varepsilon _{2}^{*},\ldots, \varepsilon _{n}^{*}\}\), then we have \(\varTheta _{p}(\eta )\geq 0\), \(p=1,2,\ldots,n\). So we can take a positive constant λ satisfying \(0<\lambda <\min \{\eta ,a_{1}^{-},a_{2}^{-},\ldots,a_{n}^{-},\beta _{ \vartheta }\}\) such that \(\varTheta _{p}(\lambda )>0\), which implies that

$$\begin{aligned} \frac{1}{a_{p}^{-}-\lambda }\sum_{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}}+d_{pq}^{+}L_{q}^{h} \int _{0}^{+ \infty }\theta _{pq}(s)e^{\lambda s} \,ds \biggr]< 1, \quad p=1,2,\ldots,n. \end{aligned}$$
(6)

Multiplying both sides of (5) by \(e^{\int _{0}^{s}a_{p}(u)\,du}\) and integrating on \([0,t]\), we have

$$\begin{aligned}& z_{p}(t) \\& \quad =\phi _{p}(0)e^{-\int _{0}^{t}a_{p}(u)\,du}+ \int _{0}^{t}e^{-\int _{s}^{t}a_{p}(u)\,du} \sum _{q=1}^{n} \biggl\{ b_{pq}(t) \bigl[f_{q}\bigl(z_{q}(t)+x_{q}(t)\bigr) \\& \quad\quad{} -f_{q}\bigl(x_{q}(t)\bigr) \bigr]+c_{pq}(t) \bigl[f_{q}\bigl(z_{q}\bigl(t- \tau _{pq}(t)\bigr)+x_{q}\bigl(t- \tau _{pq}(t) \bigr)\bigr)-f_{q}\bigl(y_{q}\bigl(t-\tau _{pq}(t) \bigr)\bigr) \bigr] \\& \quad\quad{} +d_{pq}(t) \int _{-\infty }^{s}\theta _{pq}(s-\mu ) \bigl[h_{q}\bigl(z_{p}(\mu )+x_{q}( \mu ) \bigr)-h_{q}\bigl(x_{q}(\mu )\bigr)\bigr]\,d\mu \biggr\} \,ds. \end{aligned}$$
(7)

Let

$$ M=\max_{1\leq p\leq n} \Biggl\{ a_{p}^{-} \Biggl[ \sum_{q=1}^{n}\bigl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}+d_{pq}^{+}L_{q}^{h} \bigr] \Biggr]^{-1} \Biggr\} . $$

By \((H_{4})\), \(M>1\), and

$$\begin{aligned} \Biggl(\frac{1}{M}-\frac{1}{a_{p}^{-}-\lambda }\sum _{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}}+d_{pq}^{+}L_{q}^{h} \int _{0}^{+\infty }\theta _{pq}(s)e^{\lambda s} \,ds \biggr] \Biggr)\leq 0, \end{aligned}$$
(8)

where \(0<\lambda <\min \{\eta ,a_{1}^{-},a_{2}^{-},\ldots,a_{n}^{-},\beta _{0} \}\).

Obviously,

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert \leq \Vert \phi \Vert _{0}\leq M \Vert \phi \Vert _{0}e^{-\lambda t},\quad t \in (-\infty ,0]. \end{aligned}$$

We show that

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert \leq M \Vert \phi \Vert _{0}e^{-\lambda t}, \quad t>0. \end{aligned}$$
(9)

To prove (9), we show for any \(\xi >1\),

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert \leq \xi M \Vert \phi \Vert _{0}e^{-\lambda t},\quad t>0. \end{aligned}$$
(10)

If (10) is false, then there must be some \(t_{1}>0\) and some \(p\in \{1,2,\ldots,n\}\) such that

$$\begin{aligned} \bigl\Vert z(t_{1}) \bigr\Vert = \bigl\Vert z_{p}(t_{1}) \bigr\Vert = \xi M \Vert \phi \Vert _{0}e^{-\lambda t_{1}}, \quad t>0 \end{aligned}$$
(11)

and

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert < \xi M \Vert \phi \Vert _{0}e^{-\lambda t}, \quad t\in (-\infty ,t_{1}). \end{aligned}$$
(12)

By (6)–(8), (12) and \((H_{3})\), we have

$$\begin{aligned}& \bigl\Vert z_{p}(t_{1}) \bigr\Vert \\& \quad \leq \Vert \phi _{p} \Vert _{0}e^{-t_{1}a_{p}^{-}}+ \int _{0}^{t_{1}}e^{-(t_{1}-s)a_{p}^{-}} \sum _{q=1}^{n} \biggl\{ b_{pq}^{+}L_{q}^{f} \bigl\Vert z_{q}(s) \bigr\Vert +c_{pq}^{+}L_{q}^{g} \bigl\Vert z_{q}\bigl(s-\tau _{pq}(s)\bigr) \bigr\Vert \\& \quad\quad {} +d_{pq}^{+} \int _{-\infty }^{s}\theta _{pq}(s-\mu )L_{q}^{h} \bigl\Vert z_{q}(s) \bigr\Vert \,d\mu \biggr\} \,ds \\& \quad \leq \Vert \phi _{p} \Vert _{0}e^{-t_{1}a_{p}^{-}}+ \int _{0}^{t_{1}}e^{-(t_{1}-s)a_{p}^{-}} \sum _{q=1}^{n} \biggl\{ b_{pq}^{+}L_{q}^{f} \xi M \Vert \phi \Vert _{0}e^{- \lambda s} \\& \quad \quad {} +c_{pq}^{+}L_{q}^{g} \xi M \Vert \phi \Vert _{0}e^{-\lambda (s-\tau _{pq}(s))}+d_{pq}^{+} \int _{-\infty }^{s}\theta _{pq}(\mu )L_{q}^{h}\xi M \Vert \phi \Vert _{0}e^{- \lambda (s-\mu )} \,d\mu \biggr\} \,ds \\& \quad \leq \Vert \phi _{p} \Vert _{0}e^{-t_{1}a_{p}^{-}}+ \int _{0}^{t_{1}}e^{-(t_{1}-s)a_{p}^{-}} \xi M \Vert \phi \Vert _{0}e^{-\lambda s}\sum_{q=1}^{n} \Biggl\{ b_{pq}^{+}L_{q}^{f} \\& \quad \quad {} +\sum_{q=1}^{n}c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}} + \sum_{q=1}^{n}d_{pq}^{+} \int _{-\infty }^{s}\theta _{pq}( \mu )L_{q}^{h} e^{\lambda \mu }\,d\mu \Biggr\} \,ds \\& \quad \leq \xi M \Vert \phi \Vert _{0}e^{-\lambda t_{1}} \Biggl\{ \frac{e^{(\lambda -a_{p}^{-})t_{1}}}{\xi M}+ \frac{1}{a_{p}^{-}{-}\lambda }\sum_{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}} \\& \quad \quad {} +d_{pq}^{+} \int _{-\infty }^{s}\theta _{pq}(\mu )L_{q}^{h} e^{ \lambda \mu }\,d\mu \bigl(1-e^{(\lambda -a_{p}^{-})t_{1}} \bigr) \biggr] \Biggr\} \\& \quad \leq \xi M \Vert \phi \Vert _{0}e^{-\lambda t_{1}} \Biggl\{ e^{(\lambda -a_{p}^{-})t_{1}} \Biggl(\frac{1}{M}-\frac{1}{a_{p}^{-}-\lambda }\sum _{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}} \\& \quad \quad {} +d_{pq}^{+}L_{q}^{h} \int _{0}^{+\infty }\theta _{pq}(s)e^{\lambda s} \,ds \biggr] \Biggr)+ \biggl(\frac{1}{a_{p}^{-}-\lambda } \biggl[b_{pq}L_{q}^{f} +c_{pq}L_{q}^{g}e^{ \lambda \tau ^{+}} \\& \quad\quad {} +d_{pq}L_{q}^{h} \int _{0}^{+\infty }\theta _{pq}(s)e^{\lambda s} \,ds \biggr] \biggr) \Biggr\} \\& \quad \leq \xi M \Vert \phi \Vert _{0}e^{-\lambda t_{1}} \Biggl\{ \frac{1}{a_{p}^{-}-\lambda }\sum_{q=1}^{n} \biggl[b_{pq}^{+}L_{q}^{f} +c_{pq}^{+}L_{q}^{g}e^{\lambda \tau ^{+}}+d_{pq}^{+}L_{q}^{h} \int _{0}^{+ \infty }\theta _{pq}(s)e^{\lambda s} \,ds \biggr] \Biggr\} \\& \quad < \xi M \Vert \phi \Vert _{0}e^{-\lambda t_{1}}, \end{aligned}$$

which contradicts (11), and so (10) holds. Letting \(\xi \rightarrow 1\), shows that (9) holds. Hence, the pseudo-almost-periodic solution of (1) is globally exponentially stable. The uniqueness follows from the global exponential stability. The proof is complete. □

5 An example

In this section, we give a numerical example and computer simulations.

Example 5.1

In system (1), let \(n=2\) and for \(p,q=1,2 \), consider

$$\begin{aligned}& x_{p}(t)=x^{R}_{p}(t)+ix^{I}_{p}(t)+jx^{J}_{p}(t)+kx^{K}_{p}(t) \in \mathbb{H},\qquad \theta _{pq}(t)=e^{-t}, \\& f_{q}(x_{q})=\frac{1}{40}\sin 6 x_{q}^{R}+ \frac{1}{45}i\sin 3 x_{q}^{I}+ \frac{1}{42}j\sin 5x_{q}^{J}+\frac{1}{54}k\sin 13x_{q}^{K}, \\& g_{q}(x_{q})=\frac{1}{45}\sin 3x_{q}^{R}+ \frac{1}{45}i\sin 6 x_{q}^{I}+ \frac{1}{55}j\sin 7x_{q}^{J}+\frac{1}{48}k\sin 4x_{q}^{K}, \\& h_{q}(x_{q})=\frac{1}{55}\sin 6x_{q}^{R}+ \frac{1}{45}i\sin 7 x_{q}^{I}+ \frac{1}{48}j\sin 10x_{q}^{J}+\frac{1}{55}k\sin 11x_{q}^{K}, \\& \begin{pmatrix} a_{1}(t) \\ a_{2}(t) \end{pmatrix}= \begin{pmatrix} 2.6+0.11\sin 3t \\ 2.5+0.12\cos \sqrt{2} t \end{pmatrix}, \\& \begin{pmatrix} b_{11}(t) &b_{12}(t) \\ b_{21}(t)&b_{22}(t) \end{pmatrix} \\& \quad = \begin{pmatrix} \frac{1}{9+t^{2}}+0.001i\sin \sqrt{6}t+0.002j\sin \sqrt{3}t & 0.013+0.001k \sin \sqrt{7}t \\ 0.015-0.001i\cos \sqrt{13} t+0.002k\cos \sqrt{15}t & 0.011+0.02j\sin \sqrt{2}t \end{pmatrix}, \\& \begin{pmatrix} c_{11}(t) &c_{12}(t) \\ c_{21}(t)&c_{22}(t) \end{pmatrix} \\& \quad = \begin{pmatrix} 0.01\sin t+0.06 i\sin \sqrt{5} t & 0.13+ 0.1 k\sin \sqrt{7}t \\ \frac{1}{16+t^{2}}- 0.11 i\cos \sqrt{13}t+ 0.2 k\cos \sqrt{6}t & 0.11+ 0.2 j\sin \sqrt{8} t \end{pmatrix}, \\& \begin{pmatrix} d_{11}(t) &d_{12}(t) \\ d_{21}(t)&d_{22}(t) \end{pmatrix} \\& \quad = \begin{pmatrix} 0.1\sin t+ 0.0 2 i\sin \sqrt{3} t & \frac{1}{25+t^{2}}+0.1 k\sin \sqrt{15} t \\ 0.15-0.01 i\cos \sqrt{14}t+0.02 j\cos \sqrt{17}t & 0.11+0.2 k\sin \sqrt{5} t \end{pmatrix}, \\& \begin{pmatrix} \tau _{11}(t) &\tau _{12}(t) \\ \tau _{21}(t)&\tau _{22}(t) \end{pmatrix}= \begin{pmatrix} 0.02\sin 8 t+0.12& 1-0.3\sin t \\ 3-0.2\cos t &0.01\sin 8 t+0.11 \end{pmatrix}, \\& \begin{pmatrix} Q_{1} (t) \\ Q_{2} (t) \end{pmatrix}= \begin{pmatrix} \frac{1}{1+t^{2}}+\frac{1}{2}i\sin \sqrt{6}t+\frac{1}{12}j\cos \sqrt{3}t+ \frac{1}{15}k\sin \sqrt{5}t \\ \frac{1}{1+t^{2}}+\frac{1}{8}i\sin \sqrt{7}t+\frac{1}{10}j\cos \sqrt{5}t+ \frac{1}{5}k\sin \sqrt{11}t \end{pmatrix}. \end{aligned}$$

By straightforward computation, \(\vert f_{q}(x)-f_{q}(y) \vert _{\mathbb{H}}\leq \frac{1}{40} \vert x-y \vert _{\mathbb{H}}\), \(\vert g_{q}(x)-g_{q}(y) \vert _{\mathbb{H}}\leq \frac{1}{45} \vert x-y \vert _{\mathbb{H}}\), \(\vert h_{q}(x)-h_{q}(y) \vert _{\mathbb{H}}\leq \frac{1}{45} \vert x-y \vert _{\mathbb{H}}\), \(q=1,2\), \(a_{1}^{-}=2.49\), \(a_{2}^{-}=2.38\), \(b_{11}^{+}\leq 0.1112\), \(b_{12}^{+}\leq 0.014\), \(b_{21}^{+}\leq 0.016\), \(b_{22}^{+} \leq 0.023\), \(c_{11}^{+}\leq 0.07\), \(c_{12}^{+}\leq 0.165\), \(c_{21}^{+}\leq 0.282\), \(c_{22}^{+} \leq 0.229\), \(d_{11}^{+}\leq 0.102\), \(d_{12}^{+}\leq 0.170\), \(d_{21}^{+} \leq 0.152\), \(d_{22}^{+}\leq 0.229\). So \((H_{1})\)–\((H_{3})\) are satisfied. Besides, it is easy to obtain that

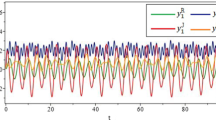
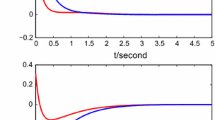
$$ \max_{1\leq p\leq 2}\frac{1}{a_{p}^{-}} \Biggl[\sum _{q=1}^{2}b_{pq}^{+}L_{q}^{f}+ \sum_{q=1}^{2}c_{pq}^{+}L_{q}^{g}+ \sum_{q=1}^{2}d_{pq}^{+}L_{q}^{h} \Biggr]\approx 0.058< 1. $$

That is, \((H_{4})\) is verified. Therefore, by Theorem 4.1, system (1) has a unique pseudo-almost-periodic solution that is globally exponentially stable (see Figs. 1–4).

Figure 1
figure 1

Curves of \(x_{p}^{R}(t)\) and \(x_{p}^{I}(t)\), \(p=1,2\)

Full size image
Figure 2
figure 2

Curves of \(x_{p}^{J}(t)\) and \(x_{p}^{K}(t)\), \(p=1,2\)

Full size image
Figure 3
figure 3

Curves of \(x_{1}^{R}(t)\), \(x_{1}^{I}(t)\), \(x_{1}^{J}(t)\), and \(x_{1}^{K}(t)\) in 3-dimensional space for the stable case

Full size image
Figure 4
figure 4

Curves of \(x_{2}^{R}(t)\), \(x_{2}^{I}(t)\), \(x_{2}^{J}(t)\), and \(x_{2}^{K}(t)\) in 3-dimensional space for the stable case

Full size image

6 Conclusion

In this paper, we studied the existence and global exponential stability of pseudo-almost-periodic solutions for a class of quaternion-valued RNNs by a direct method. Our results and methods are new. At the same time, our method can be used to study the existence and stability of other functional solutions of other types of quaternion numerical neural network models.