Abstract
This paper investigates a periodic Nicholson’s blowflies equation with multiple time-varying delays. By using differential inequality techniques and the fluctuation lemma, we establish a criterion to ensure the global exponential stability on the positive solutions of the addressed equation, which improves and complements some existing ones. The effectiveness of the obtained result is illustrated by some numerical simulations.
Similar content being viewed by others
1 Introduction
Recently, the global exponential stability of positive periodic solutions and almost-periodic solutions for the famous Nicholson’s blowflies equation with multiple time-varying delays:
has been intensively studied in [1–3]. Here, \(\beta (t), \alpha _{j}(t), \sigma _{j}(t)\), and \(\gamma _{j}(t)\) are all continuous and nonnegative functions, \(\beta (t) \) and \(\gamma _{j}(t)\) are bounded below by positive constants, \(\beta (t) x(t)\) is the death rate of the population which depends on time t and the current population level \(x (t)\), \(\alpha _{j}(t) x(t-\sigma _{j} (t) )e^{- \gamma _{j}(t) x(t-\sigma _{j}(t))}\) is the time-dependent birth function which involves maturation delay \(\sigma _{ j}(t)\), and reproduces at its maximum rate \(\frac{1}{\gamma _{ j}(t)}\), and \(j\in \varPi:=\{1,2, \dots, m\}\).
It should be mentioned that, by restricting the existence of the periodic and almost-periodic solutions for (1.1) in a small interval \([\kappa, \widetilde{\kappa }]\approx [0.7215355, 1.342276]\), all results in [1–3] were obtained under the crucial assumption:
where \(\kappa \in (0, 1)\) and \(\tilde{\kappa }\in (1,+\infty )\) satisfy
Most recently, the authors in [4–6] pointed out that it is interesting that when the maximum reproduction rate is not limited (i.e., \(\frac{1}{\gamma _{j}(t)}\) maybe sufficiently large), the stability of a class of delayed nonlinear density-dependent mortality Nicholson’s blowflies models without the assumption (1.2) can be established. However, there are no research works on the global exponential stability of periodic solutions for Nicholson’s blowflies equation (1.1) without assumption (1.2) and \([\kappa, \widetilde{\kappa }]\) as the existence interval for the periodic solutions.
Based on the above discussions, in this paper, avoiding assumption (1.2) and without adopting \([\kappa, \widetilde{\kappa }]\) as the existence interval of periodic solutions, we establish the global exponential stability of periodic solutions for system (1.1). The proposed criterion improves and complements some existing results in the recent publications [1–3], and its effectiveness is demonstrated by a numerical example.
From now on, we suppose that \(\beta, \gamma _{j}:[ t_{0}, +\infty ) \rightarrow (0, +\infty ) \) and \(\sigma _{j}, \alpha _{j}:[ t_{0}, + \infty )\rightarrow [0, +\infty )\) are continuous T-periodic functions with \(T>0\) and \(j\in \varPi \). Let
and
Furthermore, consider the following initial value conditions:
We let \(x(t; t_{0}, \varphi ) \) denote a solution of the initial value problem (1.1) and (1.4), and the maximal right-interval of existence of \(x(t; t_{0}, \varphi )\) is marked by \([t_{0}, \eta (\varphi ))\). Then, the existence and uniqueness of \(x(t; t_{0}, \varphi )\) is straightforwardly established in [1].
2 Preliminary results
In this section, we give three lemmas which will play important roles in the next section.
Lemma 2.1
LetAandδbe constants such that \(A>1, e<\frac{1}{\delta }\leq e^{2}\), and \(\delta =Ae^{-A}\). Then, \(\delta A> \frac{1}{e}\).
Proof
Evidently,
Define \(f(u)=\frac{e^{u}}{u}\) for \(u\in (0, +\infty )\) and \(f(x_{0})=e^{2}\) with \(x_{0}>1\). Then, \(f'(u)= \frac{e^{u}(u-1)}{u^{2}}>0 (u>1)\), and \(f(u)\) is monotonously increasing on \((1,+\infty )\). Clearly, \(f(1)=e, f(e)=e^{e-1}< e^{2}\), which, together with (2.1), suggests that \(A\in (1,x_{0} ]\), and \(x_{0}>e\).
Now, letting \(G(u)=u^{2}e^{-u}\) on \((0, +\infty )\), it suffices to show that \(G(A)>\frac{1}{e}\). In fact, \(G'(u)= e^{-u}u(2-u)\), \(G(u)\) increases on \((1, 2)\) and decreases on \((2, x_{0})\), \(G(1)=e^{-1}=\frac{1}{e}\), as well as
Consequently, \(G(A)>\min \{G(1), G(x_{0})\}=\frac{1}{e}\). The proof is complete. □
Lemma 2.2
\(x (t; t_{0},\varphi )\)is positive and bounded on \([t_{0}, \eta ( \varphi )) \), and \(\eta (\varphi )=+\infty \).
Proof
First, it follows from Theorem 5.2.1 in [7], p. 81, that \(x_{t}(t_{0}, \varphi )\in C_{+}\) for all \(t \in [t_{0}, \eta (\varphi ))\). Let \(x (t )= x (t; t_{0},\varphi )\). Noting that \(x(t_{0})=\varphi (0)>0\), we gain
Second, due to the positivity and periodicity of coefficient functions, we can choose a positive constant M such that
Therefore, in view of the fact that \(\sup_{u\geq 0} ue^{-u}=\frac{1}{ e}\), we obtain
Finally, we have from Theorem 2.3.1 in [8] and the boundedness of \(\varLambda (t)\) that \(\eta (\varphi )=+\infty \), and \(x (t )\) is positive and bounded on \([t_{0}, +\infty )\). □
Lemma 2.3
Let
and
Then,
where
Proof
From (2.2), (2.5) and Lemma 2.1, one can see that
We claim that \(\liminf_{t\to +\infty } x(t)=l>0\). Otherwise, \(l=0\). For any \(t\geq t_{0} \), we set
We conclude from \(l=0\) that \(\nu (t) \to +\infty \) as \(t\to +\infty \) and \(\lim_{t\to +\infty }x(\nu (t))=0\). On the other hand, \(x(\nu (t))=\min_{t_{0} \leq s\leq t}x(s)\), and \(x'(\nu (t)) \leq 0 \text{ for all } \nu (t)>t_{0}\). Then, (1.1) leads to
and
where \(\nu (t)>t_{0}, j\in \varPi \), which, together with the fact that \(\lim_{t\to +\infty }x (\nu (t))=0 \), suggests that
From (2.2), (2.7), (2.8) and the fact that
letting \(t\rightarrow +\infty \) results in
which is a contradiction. Hence, \(l>0\).
Now, by the fluctuation lemma [9], Lemma A.1., there are two sequences \(\{q_{k}^{*}\}_{k=1}^{+\infty }\) and \(\{q_{k}^{**}\}_{k=1}^{+\infty }\) obeying
and
respectively. Without loss of generality, regarding the periodicity of delays and coefficients, we can assume that \(\lim_{k \rightarrow + \infty } \beta (q_{k}^{*}), \lim_{k \rightarrow + \infty } \alpha _{j} (q_{k}^{*}), \lim_{k \rightarrow + \infty } \gamma _{j}(q_{k}^{*}), \lim_{k \rightarrow + \infty } x(q_{k}^{*}-\sigma _{ j} (q_{k}^{*})), \lim_{k \rightarrow + \infty } \beta (q_{k}^{**}), \lim_{k \rightarrow + \infty }\alpha _{j}(q_{k}^{**}), \lim_{k \rightarrow + \infty } \gamma _{j}(q_{k}^{**}) \) and \(\lim_{k \rightarrow + \infty }x(q_{k}^{**}-\sigma _{ j} (q _{k}^{**})) \) exist for all \(j\in \varPi \).
Likewise, (1.1), (2.6) and (2.9) yield
and
Consequently, let \(j_{0}\in \varPi \) such that
and
It follows from (1.1), (2.10) and the fact that \(\min_{[a, b]\subseteq [0, +\infty )}ue^{-u}=\min \{ae^{-a}, be ^{-b}\}\) that
If \(le^{-l}=\min \{le^{-l}, Le^{-L}\}\), (2.3) and (2.12) yield
If \(Le^{-L}=\min \{le^{-l}, Le^{-L}\}< le^{-l}\), then (2.11) implies
which, together with (2.3) and (2.12), entails that
which, together with (2.11) and (2.13), establishes (2.4). This finishes the proof of Lemma 2.3. □
3 Main results
The main results in this paper will now be presented as the subsequent proposition and theorem.
Proposition 3.1
Suppose that all assumptions in Lemma 2.3are satisfied. Then, for \(\varphi,\psi \in C_{+}\)with \(\varphi (0)>0\)and \(\psi (0)>0\), there exist constants \(Q_{\varphi, \psi }>t_{0}\), \(K _{\varphi, \psi }>0\)and \(\lambda >0\)such that
Proof
Denote \(x^{\varphi }(t)= x(t; t_{0}, \varphi )\) and \(x^{\psi }(t)= x(t; t_{0}, \psi )\). By Lemma 2.3 and the fact that \(\gamma ^{+}\leq 1\), there exists \(Q_{\varphi, \psi }>t_{0} \) such that
for all \(t\in [Q_{\varphi, \psi }-\sigma, +\infty ) \) and \(j\in \varPi \). According to (2.2), we can take \(\lambda >0\) such that
Define \(z(t)= x^{\varphi }(t)-x^{\psi }(t)\) and \(M (t) = |z(t)|e^{ \lambda t}\) for all \(t\in [t_{0}-\sigma, +\infty )\). Consequently,
and
Now, we show that
Suppose on the contrary and pick \(Q_{*}>Q_{\varphi, \psi }\) such that
From the definition of κ, we have
which, together with (3.2), (3.3), (3.4), (3.6), and (3.7), results in
and
which is a contradiction, validating (3.5). This implies that (3.1) holds, and the proof of the Proposition 3.1 is now finished. □
Theorem 3.1
Under the assumptions of Proposition 3.1, system (1.1) has exactly one globally exponentially stable positiveT-periodic solution \(x^{*}(t)\in [\frac{\kappa }{\gamma ^{-}}, A]\).
Proof
According to Proposition 3.1 and Lemma 2.3, one can follow the argument of Theorem 3.1 in [1] to demonstrate that \(x(t+qT)=x(t+qT;t _{ 0},\varphi )\) is not only convergent on every compact interval as \(q\to +\infty \), but also converges uniformly to a continuous function \(x^{*}(t)\), where \(x^{*}\) is a T-periodic solution of (1.1), and such that
Furthermore, by applying a similar argument as in Lemma 2.3, we can validate the global exponential stability of \(x^{*}(t)\). This completes the proof of Theorem 3.1. □
By applying Theorem 3.1, we can obtain the following result.
Corollary 3.1
Assume that \(\beta \in (0, +\infty )\)and \(\sigma _{j}, \alpha _{j}\in [0, +\infty )\)are constants, and
Then, the classical autonomous Nicholson’s blowflies equation,
has a globally exponentially stable positive equilibrium point \(x^{*}\in [ \kappa, A]\), where
Remark 3.1
Under the conditions (3.8), the stability of the classical autonomous Nicholson’s blowflies equation in the main results of [10, 11] can be concluded from the above Corollary 3.1. In addition, in [10, 11], the exponential stability and existence range of a positive equilibrium point have not been considered for the classical autonomous Nicholson’s blowflies equation with the conditions (3.8), which implies that the obtained results of this present paper improve and complement some existing ones.
4 Example
In this section, we present a numerical example to verify the theoretical results derived in the previous section.
Example 4.1
Consider the delayed Nicholson’s blowflies equations described by
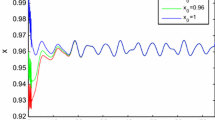
Obviously, it is observed that (4.1) satisfies (2.2) and (2.3). Therefore, from Theorem 3.1, one can see that (4.1) has exactly one globally exponentially stable positive 2π-periodic solution. This fact is also supported by the numerical simulations in Fig. 1 (numerical solutions of (4.1) for different initial values).
Numerical solutions on the state trajectories of state variables x of system (4.1) for differential initial values: \(\varphi (s) =0.9, 1, 1.2, s\in [-100,0]\)
Remark 4.1
It should be pointed out that in (4.1),
do not satisfy assumption (1.2) mentioned in Sect. 1. In addition, the results concerning on population dynamics in [12–16] give no clue about the problem of periodic solutions of Nicholson’s blowflies model without assumption (1.2). This implies that all the results in [1–6, 10–57] cannot be used to show the global exponential stability on the positive periodic solution of system (4.1).
5 Conclusions
In this paper, we combine the Lyapunov function method with the differential inequality method to establish some new criteria ensuring the existence and exponential stability of positive periodic solutions for a class of Nicholson’s blowflies equation with multiple time-varying delays. Avoiding the assumption that the maximum reproduction rate is less than 1, these criteria are obtained without assuming that \([\kappa, \widetilde{\kappa }] \approx [0.7215355, 1.342276] \) is the existence region of periodic solutions, and the analogous results in the recently published literature are summarized and refined. The approach presented in this article can be used as a possible way to study other population models involving multiple time-varying delays, for example, neoclassical growth model, Mackey–Glass model, epidemical system or age-structured population model, and so on.
References
Liu, B.: Global exponential stability of positive periodic solutions for a delayed Nicholson’s blowflies model. J. Math. Anal. Appl. 412, 212–221 (2014)
Liu, B.: New results on global exponential stability of almost periodic solutions for a delayed Nicholson’s blowflies model. Ann. Pol. Math. 113(2), 191–208 (2015)
Xiong, W.: New results on positive pseudo-almost periodic solutions for a delayed Nicholson’s blowflies model. Nonlinear Dyn. 85, 563–571 (2016)
Xu, Y.: New stability theorem for periodic Nicholson’s model with mortality term. Appl. Math. Lett. 94, 59–65 (2019)
Son, D.T., Hien, L.V., Anh, T.T.: Global attractivity of positive periodic solution of a delayed Nicholson model with nonlinear density-dependent mortality term. J. Qual. Theory Differ. Equ. 8, 1–21 (2019)
Ding, H., Fu, S.: Periodicity on Nicholson’s blowflies systems involving patch structure and mortality terms. J. Exp. Theor. Artif. Intell. (2019). https://doi.org/10.1080/0952813X.2019.1647567
Smith, H.L.: Monotone Dynamical Systems. Math. Surveys Monogr. Amer. Math. Soc., Providence (1995)
Hale, J.K., Verduyn Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (1993)
Smith, H.L.: An Introduction to Delay Differential Equations with Applications to the Life Sciences. Springer, New York (2011)
Liz, E., Tkachenko, V., Trofimchuk, S.: A global stability criterion for scalar functional differential equation. SIAM J. Math. Anal. 35(3), 596–622 (2003)
Berezansky, L., Braverman, E., Idels, L.: Nicholson’s blowflies differential equations revisited: main results and open problems. Appl. Math. Model. 34, 1405–1417 (2010)
Huang, C., Yang, Z., Yi, T., Zou, X.: On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 256, 2101–2114 (2014)
Huang, C., Qiao, Y., Huang, L., Agarwal, R.: Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 186 (2018). https://doi.org/10.1186/s13662-018-1589-8
Huang, C., Zhang, H., Huang, L.: Almost periodicity analysis for a delayed Nicholson’s blowflies model with nonlinear density-dependent mortality term. Commun. Pure Appl. Anal. 18(6), 3337–3349 (2019)
Huang, C., Zhang, H., Cao, J., Hu, H.: Stability and Hopf bifurcation of a delayed prey–predator model with disease in the predator. Int. J. Bifurc. Chaos 29(7), 1950091 (2019)
Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 100, 106027 (2020). https://doi.org/10.1016/j.aml.2019.106027
Huang, C., Yang, X., Cao, J.: Stability analysis of Nicholson’s blowflies equation with two different delays. Math. Comput. Simul. (2019). https://doi.org/10.1016/j.matcom.2019.09.023
Tan, Y., Huang, C., Sun, B., Wang, T.: Dynamics of a class of delayed reaction–diffusion systems with Neumann boundary condition. J. Math. Anal. Appl. 458(2), 1115–1130 (2018)
Duan, L., Fang, X., Huang, C.: Global exponential convergence in a delayed almost periodic Nicholson’s blowflies model with discontinuous harvesting. Math. Methods Appl. Sci. 41(5), 1954–1965 (2018)
Hu, H., Zou, X.: Existence of an extinction wave in the Fisher equation with a shifting habitat. Proc. Am. Math. Soc. 145(11), 4763–4771 (2017)
Wang, J., Huang, C., Huang, L.: Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle-focus type. Nonlinear Anal. Hybrid Syst. 33, 162–178 (2019)
Wang, J., Chen, X., Huang, L.: The number and stability of limit cycles for planar piecewise linear systems of node-saddle type. J. Math. Anal. Appl. 469(1), 405–427 (2019)
Cai, Z., Huang, J., Huang, L.: Periodic orbit analysis for the delayed Filippov system. Proc. Am. Math. Soc. 146(11), 4667–4682 (2018)
Liu, J., Yan, L., Xu, F., Lai, M.: Homoclinic solutions for Hamiltonian system with impulsive effects. Adv. Differ. Equ. 2018(1), 326 (2018)
Chen, T., Huang, L., Yu, P., Huang, W.: Bifurcation of limit cycles at infinity in piecewise polynomial systems. Nonlinear Anal., Real World Appl. 41, 82–106 (2018)
Yang, X., Wen, S., Liu, Z., Li, C., Huang, C.: Dynamic properties of foreign exchange complex network. Mathematics 7, 832 (2019). https://doi.org/10.3390/math7090832
Iswarya, M., Raja, R., Rajchakit, G., Cao, J., Alzabut, J., Huang, C.: Existence, uniqueness and exponential stability of periodic solution for discrete-time delayed BAM neural networks based on coincidence degree theory and graph theoretic method. Mathematics 7(11), 1055 (2019). https://doi.org/10.3390/mathxx010005
Li, J., Ying, J., Xie, D.: On the analysis and application of an ion size-modified Poisson–Boltzmann equation. Nonlinear Anal., Real World Appl. 47, 188–203 (2019)
Li, X., Liu, Z., Li, J.: Existence and controllability for nonlinear fractional control systems with damping in Hilbert spaces. Acta Mech. Sin. Engl. Ser. 39(1), 229–242 (2019)
Zhu, K., Xie, Y., Zhou, F.: Pullback attractors for a damped semilinear wave equation with delays. Acta Math. Sin. Engl. Ser. 34(7), 1131–1150 (2018)
Zhao, J., Liu, J., Fang, L.: Anti-periodic boundary value problems of second-order functional differential equations. Bull. Malays. Math. Sci. Soc. 37(2), 311–320 (2014)
Huang, C., Yang, L., Liu, B.: New results on periodicity of non-autonomous inertial neural networks involving non-reduced order method. Neural Process. Lett. 50, 595–606 (2019)
Huang, C.: Exponential stability of inertial neural networks involving proportional delays and non-reduced order method. J. Exp. Theor. Artif. Intell. (2019). https://doi.org/10.1080/0952813X.2019.1635654
Huang, C., Wen, S., Huang, L.: Dynamics of anti-periodic solutions on shunting inhibitory cellular neural networks with multi-proportional delays. Neurocomputing 357, 47–52 (2019)
Huang, C., Zhang, H.: Periodicity of non-autonomous inertial neural networks involving proportional delays and non-reduced order method. Int. J. Biomath. 12(2), 1950016 (2019)
Huang, C., Liu, B.: New studies on dynamic analysis of inertial neural networks involving non-reduced order method. Neurocomputing 325(24), 283–287 (2019)
Zhang, H.: Global large smooth solutions for 3-D hall-magnetohydrodynamics. Discrete Contin. Dyn. Syst. 39(11), 6669–6682 (2019)
Li, W., Huang, L., Ji, J.: Periodic solution and its stability of a delayed Beddington–DeAngelis type predator–prey system with discontinuous control strategy. Math. Methods Appl. Sci. 42(13), 4498–4515 (2019)
Qian, C., Hu, Y.: Novel stability criteria on nonlinear density-dependent mortality Nicholson’s blowflies systems in asymptotically almost periodic environments. J. Inequal. Appl. (2020). https://doi.org/10.1186/s13660-019-2275-4
Huang, C., Long, X., Huang, L., Fu, S.: Stability of almost periodic Nicholson’s blowflies model involving patch structure and mortality terms. Can. Math. Bull. (2019). https://doi.org/10.4153/S0008439519000511
Hu, H., Yi, T., Zou, X.: On spatial-temporal dynamics of Fisher–KPP equation with a shifting environment. Proc. Am. Math. Soc. 148(1), 213–221 (2020)
Wang, F., Yao, Z.: Approximate controllability of fractional neutral differential systems with bounded delay. Fixed Point Theory 17, 495–508 (2016)
Hu, H., Yuan, X., Huang, L., Huang, C.: Global dynamics of an SIRS model with demographics and transfer from infectious to susceptible on heterogeneous networks. Math. Biosci. Eng. 16(5), 5729–5749 (2019)
Wei, Y., Yin, L., Long, X.: The coupling integrable couplings of the generalized coupled Burgers equation hierarchy and its Hamiltonian structure. Adv. Differ. Equ. 2019, 58 (2019). https://doi.org/10.1186/s13662-019-2004-9
Zhang, J., Lu, C., Li, X., Kim, H.-J., Wang, J.: A full convolutional network based on DenseNet for remote sensing scene classification. Math. Biosci. Eng. 16(5), 3345–3367 (2019)
Hu, H., Liu, L.: Weighted inequalities for a general commutator associated to a singular integral operator satisfying a variant of Hormander’s condition. Math. Notes 101(5–6), 830–840 (2017)
Huang, C., Liu, L.: Boundedness of multilinear singular integral operator with non-smooth kernels and mean oscillation. Quaest. Math. 40(3), 295–312 (2017)
Huang, C., Cao, J., Wen, F., Yang, X.: Stability analysis of SIR model with distributed delay on complex networks. PLoS ONE 11(8), e0158813 (2016). https://doi.org/10.1371/journal.pone.0158813
Li, X., Liu, Y., Wu, J.: Flocking and pattern motion in a modified Cucker–Smale model. Bull. Korean Math. Soc. 53(5), 1327–1339 (2016)
Xie, Y., Li, Q., Zhu, K.: Attractors for nonclassical diffusion equations with arbitrary polynomial growth nonlinearity. Nonlinear Anal., Real World Appl. 31, 23–37 (2016)
Xie, Y., Li, Y., Zeng, Y.: Uniform attractors for nonclassical diffusion equations with memory. J. Funct. Spaces 2016, Article ID 5340489 (2016). https://doi.org/10.1155/2016/5340489
Wang, F., Wang, P., Yao, Z.: Approximate controllability of fractional partial differential equation. Adv. Differ. Equ. 2015, 367 (2015). https://doi.org/10.1186/s13662-015-0692-3
Liu, Y., Wu, J.: Multiple solutions of ordinary differential systems with min-max terms and applications to the fuzzy differential equations. Adv. Differ. Equ. 2015, 379 (2015). https://doi.org/10.1186/s13662-015-0708-z
Yan, L., Liu, J., Luo, Z.: Existence and multiplicity of solutions for second-order impulsive differential equations on the half-line. Adv. Differ. Equ. 2013, 293 (2013). https://doi.org/10.1186/1687-1847-2013-293
Liu, Y., Wu, J.: Fixed point theorems in piecewise continuous function spaces and applications to some nonlinear problems. Math. Methods Appl. Sci. 37(4), 508–517 (2014)
Zhou, S., Jiang, Y.: Finite volume methods for N-dimensional time fractional Fokker–Planck equations. Bull. Malays. Math. Sci. Soc. 42(6), 3167–3186 (2019)
Liu, F., Feng, L., Vo, A., Li, J.: Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time-space fractional Bloch–Torrey equations on irregular convex domains. Comput. Math. Appl. 78(5), 1637–1650 (2019)
Acknowledgements
We would like to thank the anonymous referees and the editor for very helpful suggestions and comments which led to improvements of our original paper.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 11971076, 11771059, 51839002), the Foundation of Hunan Provincial Education Department of China (Grant No. 14C0806), and the Natural Scientific Research Fund of Hunan Provincial of China (Grant No. 2016JJ6104).
Author information
Authors and Affiliations
Contributions
The three authors contributed equally to this work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cao, Q., Wang, G. & Qian, C. New results on global exponential stability for a periodic Nicholson’s blowflies model involving time-varying delays. Adv Differ Equ 2020, 43 (2020). https://doi.org/10.1186/s13662-020-2495-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-2495-4